Background

Most river systems worldwide are anthropogenically influenced, which leads to changes in the sediment household and, resulting, to changes in the river’s morphology (Ekka et al. 2020; Hoffmann et al. 2022; Mondal and Patel 2018; Vörösmarty et al. 2003; Wohl et al. 2021). In Germany, large navigable rivers are well monitored (Asselman 1999; Blöthe et al. 2018; Hoffmann et al. 2020; Horowitz 2003), and between 1990 and 2010 a significant decline in the suspended sediment concentration (SSC) could be observed, which very likely is linked to anthropogenic measures (Hoffmann et al. 2022). However, typical mid-European river types are mid-sized low-mountain gravel bed and sand-prone lowland rivers (Muhar et al. 2016; Poppe et al. 2016), monitored to a smaller extent. This study aims to identify and quantify anthropogenic impacts on the suspended sediment transport of a typical mid-sized European river based on practicable, easily repeatable own measurements.

As Frings (2022) states: “Rivers are complex systems, in which local morphodynamics strongly depend on the sediment flux coming from upstream. To understand rivers, basin-scale knowledge about sediment fluxes, their sources, and their sinks is indispensable”. He found fine sediments to be an important driver for river development, even in coarse-material-rich rivers (Frings 2022). Besides the long-time river development, sediment-driven short-time processes can cause problems in river management. Examples are sediment accumulation in reservoirs, which reduces the reservoir capacity and water quality if sediments are contaminated, local erosion due to sediment deficits, colmation, and floodplain sedimentation, potentially leading to pollutant hotspots.

Heavy rainfall and erosive land use lead to high sediment input rates (Cobaner et al. 2009; Estrany et al. 2009; Piest 1963), and particularly forest clearing and reforestation significantly affect the river’s sediment budget (Collins et al. 1997). Land use may even explain different priority sediment sources during flood events in sub-basins (Collins et al. 1997; Hughes et al. 2012).

Another important sediment source in a waterbody is the streambed itself, as material erodes (Bull 1997; Collins et al. 1997). Zhou and Lin (1998), as well as Ahn and Steinschneider (2019), found that bank erosion and deposition must be considered when evaluating the fine sediment input into the river system.

Deposition occurs nearly uniformly across the riverbed, whereas erosion occurs mainly along the thalweg and in cohesive material at the banks of the river (Zhou and Lin 1998). Overall, the suspended sediment concentration (SSC) at a river’s cross-section results from the sediment availability, mobilization, and storage from its upstream section (Bača 2008; Chalov et al. 2017; Williams 1989).

The correlation between runoff and sediment yield is described in the sediment rating curve (cf. equation 1) (Campbell and Bauder 1940; Ferguson 1986; Miller 1951; Piest 1963) as follows:

$$\begin{array}{*{20}c} {SSC} \\ {or} \\ {SSL} \\ \end{array} = \alpha \cdot Q^{\beta } + {\epsilon }_{i}$$
(1)

after Campbell and Bauder (1940), Ferguson (1986).

With: \(SSC\, (e.g. \left[\frac{mg}{l}\right])\) suspended sediment concentration.

\(SSL\, (e.g. \left[\frac{g}{sek.}\right])\) suspended sediment load.

\(Q\) discharge.

\(\alpha ,\beta\) parameters fitted by least squared regression.

\({\epsilon }_{i}\) normally distributed independent error.

This strict correlation only between the suspended sediments and discharge is spurious because more components play into account (McBean and Al‐Nassri 1988). Generally, errors up to \(\pm\) 50%, and a large scatter occur when the sediment rating curve is used for SSC-Q correlations (Asselman 1999, 2000; Hoffmann et al. 2020; Horowitz 2003; Walling 1977b). In long-time observations, underprediction in low concentrations and overprediction in high concentrations balance each other out, as studies from Europe and the USA show (Horowitz 2003). In this study, we aim to rephrase the sediment rating curve to predict SSCs further downstream and to reduce the errors on a small time scale by incorporating the impact of anthropogenic measures.

Ferguson (1986) and Asselman (2000) found that wash load, bed, as well as suspended load, are underestimated with this relation and proposed adding a correction factor or an additive term covering the error. The correction must be adjusted for every river (Ferguson 1986). Furthermore, seasonal contrasts lead to large scatter in the SSC predicted from sediment rating curves and influence hystereses patterns (Estrany et al. 2009; Oeurng et al. 2010), which reflects that additional factors to discharge control the supply of suspended sediment.

For navigable German rivers, such as the Rhine River, Weser River, Ems River, Danube River, and Elbe River, regular suspended sediment monitoring by the Federal Waterways and Shipping Administration (Wasserstraßen- und Schifffahrtsverwaltung des Bundes, WSV) started in 1965 (Blöthe et al. 2018; Hoffmann et al. 2020). Results indicate that additional anthropogenic controlling factors from within the river system and from the catchment, such as dams and weirs, influence the SSC-Q relation. About 50% of the annual suspended load is transported in 10% of the time with the highest discharges, with summer discharges having higher sediment loads than comparable winter discharges (Blöthe et al. 2018; Hoffmann et al. 2020). The Rhine River is additionally monitored by the Federal Institute of Hydrology (Bundesanstalt für Gewässerkunde, BfG) (Asselman 1999; Horowitz 2003). Two years of data, 1982–1983, were used to analyze transport behavior. Results indicate sediment storage along the channel during low flows and high sediment introduction by tributaries during winter and early spring floods, which results in clockwise hysteresis patterns (Asselman 1999). The results are in good agreement with Blöthe et al. (2018).

Girolamo et al. (2018) examined the alpine, temporary aquiferous Celone River in Italy and found a correlation between measured streamflow and SSC of 0.81 with an R2 of 0.66. They concluded that 66% of the variance of SSC could be explained by streamflow, and 34% is influenced by other factors, like rainfall, vegetation cover, and soil management (Girolamo et al. 2018). Also, they found it helpful to stratify data by discharge and recommended sampling different flow events, especially flood events (Girolamo et al. 2018).

By linking the respective hydrograph with the pattern of sediment concentration during the flood event, information about the sediment source can be obtained as a function of the emerging pattern. Five general classes of (hysteresis) patterns can occur in the relationship between suspension load and flood wave: a purely linear pattern, clockwise turning, counterclockwise turning, a more linear pattern with turning at maximum values, and hysteresis with two loops, i.e., shaped like the number eight (Williams 1989). Williams (1989) identifies various underlying precipitation events and the availability or source of the fine sediment as reasons why different patterns develop in the relationship between suspension load and discharge. Hamshaw et al. (2018) further distinguish between a total of 14 hysteresis patterns within Williams (1989) five classes according to different rainfall events and initial conditions, such as baseflow and soil moisture. Oeurng et al. (2010) identified total precipitation, peak discharge, total water volume, flood intensity, and sediment supply as influencing variables for different shapes. In addition, the clockwise rotation of hysteresis indicated sediment sources near the river (Klein 1984; Oeurng et al. 2010; Smith and Dragovich 2009).

Cobaner et al. (2009) systematically studied different neural networks fed with hydrometeorological data to predict the SSC in the Mad River, New Hampshire, USA. They found that the best results were obtained by incorporating the current stream flow, and rainfall, one previous stream flow, and two previous suspended sediment values (Cobaner et al. 2009).

Although the relationship between discharge and the suspension load is very strong, additional factors of the system need to be considered. Between two observation points of the suspended sediment concentration, both the discharge and the sediment load can change. Rainfall within the sub-catchment, as well as tributaries, increases the discharge (cf. Figure 1). An increase in discharge without further sediment input leads to a decrease in the SSC unless sediment is eroded from within the riverbed. Depending on the erosivity of the catchment, sediment loads enter the riverbed after rainfall, which increases the SSC. Large dams often reduce the discharge, being a water storage. Also, through sedimentation, due to a reduction of the flow velocity, the sediment load in the water is reduced. Although the discharge regulation, dams lead to a reduction in the SSC. Last, during high flows, overbank flooding can lead to floodplain sedimentation, which also reduces the SSC.

Fig. 1
figure 1

Schematic illustration of water and sediment pathways within a sub-catchment between two observation points of the suspended sediment concentration (SSCi and SSCi+1). The SSC changes with the amount of sediment and discharge transported in the river, and possible changes in sediment and discharge are illustrated. “ + ” indicates an increase in discharge or sediment, “–“ indicates the local storage within the system. Water and sediment input are additionally influenced by catchment characteristics, such as land use and geology

Full size image

Although many aspects of the suspended sediment transport in rivers are known (cf. Table 1), SSC-Q relations are mostly investigated in large, well-monitored, navigable rivers. However, typical mid-sized European rivers do not have comparable monitoring but are nevertheless the focus of water management measures to achieve the objectives of the European Water Framework Directive (EU-WFD) (Muhar et al. 2016). The aims are to evaluate if the sediment rating curve is suited for SSC prediction over a river section in a typical mid-sized European river and to improve the prediction by incorporating additional terms based on thoughts on mass conservation (c.f. Hinderer 2012) (cf. Table 1). The influence of different parameters on the sediment concentration within a river section is to be discussed to support future water resource management.

Table 1 Known influence of different possible processes within a sub-catchment on the SSC
Full size table

Study area

The Rur River is situated in North Rhine-Westphalia in western Germany. It is a typical upland to lowland mid-European River. In the uplands, the Rur River is rich in coarse materials, in the lowlands, the Rur River is a gravel-embossed lowland river. The Rur River originates in the swamps of High Fens in Belgium in the Eifel mountains at an altitude of 600 m.a.s.l. The middle and lower reach of the Rur River are situated in the lowlands of the Lower Rhine Embayment.

After 165 km, at an altitude of 30 m.a.s.l, the Rur River flows into the Meuse River in the city of Roermond, Netherlands. The catchment shows different land use patterns and is dominated by forestry and grassland in the uplands and agriculture in the lowlands (Kufeld et al. 2010). The catchment area of 2.361 km2 holds approximately 15 to 20% of urban and industrial areas, almost 50% of agricultural areas, and over 30% of natural or forest areas (Nilson 2006).

Due to its proximity to the Atlantic Ocean, the catchment is characterized by a comparatively humid but cool climate (Bressers et al. 2016; Kufeld et al. 2010). Precipitation in the Eifel mountain region is significantly higher than in the northern lowlands (Kufeld et al. 2010). The year-round aquiferous Rur River has a rain and snow-influenced discharge regime (Lehmkuhl 2011). Flood events after snowmelt and the lack of water during the summer months (Paul 1994), led to the construction of large dams with a capacity of 45 Mio m3 as early as 1900 (Polczyk 1999). Today, the Rur reservoir (Rurtalsperre Schwammenauel) has a capacity of 203 Mio m3 (Wasserverband Eifel-Rur 2017a). The reservoir has an upstream auxiliary dam (Wasserverband Eifel-Rur 2017a) to prevent siltation. Two main rivers flow in the Rur reservoir, the Rur River and the Urft River. The Rur reservoir is followed by the Obermaubach basin 18 river-km (rkm) downstream, which holds 1.65 Mio m3 (Wasserverband Eifel-Rur 2017b).

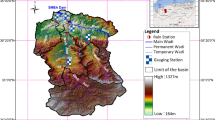
In this study, we investigated 55 km within the upper and mid catchment in Germany, from 5 km upstream of Monschau to 3 km downstream of the mouth of the Inde River tributary (cf. Figure 2). The Rur River is strongly anthropogenically influenced since the sustentation of mill ditches in the middle ages but has experienced river straightening between the 1940s and 70s, especially in the lowlands (MNULV 2005). Nevertheless, near-natural sections can still be found (MNULV 2005).

Fig. 2
figure 2

Overview of the study area and sampling sites, which are marked with “SSC-1 – SSC-14”. Countries are abbreviated with GER for Germany, B for Belgium, NL for the Netherlands, LUX for Luxembourg, CH for Switzerland, and AUS for Austria. Sources: DEM25: European Environment Agency (2016), river system: Geofabrik GmbH (2018), country borders: Eurostat (2020)

Full size image

The three main tributaries of the Rur River are the Urft River, the Inde River, and the Wurm River. The 43 km-long Urft River is situated in the Eifel mountains (Demoulin 2011) and discharges into the Urft dam, which is connected to the Rur reservoir (cf. Figure 2). The 54 km-long rich in fine to coarse siliceous substrates Inde River flows from the uplands to the lowlands and is famous for its 12 km-long river relocation around an open pit mine (Maaß et al. 2018). The 58 km-long low mountain stream of the Wurm River is rich in fine cohesive sediments (Maaß and Schüttrumpf 2019a).

In our study, data from the Wurm River is used for validation. The Wurm River catchment is embossed by agricultural land use (MKULNV NRW 2015). Its source is situated in the urban area of the city of Aachen, where the Wurm River, as well as its confluences, are mainly piped. Near Aachen, the wastewater treatment plant “Soers” discharges into the Wurm River and accounts for the majority of the Wurm Rivers discharge on dry days (Buchty-Lemke and Lehmkuhl 2018). The Wurm River is a gravel-embossed river with relatively high suspended sediment concentrations (Maaß and Schüttrumpf 2019b).

Methods

Suspended sediment concentration

For investigating the SSC of the Rur River, from 16th October 2019 to 1st February 2021, on 11 field trips, in total, 129 samples of 2 × 1 L or 2 × 0.5 L (sample and reference sample) from 14 sampling sites were taken along the Rur River. Sampling sites were chosen based on site visits, and between two sampling sites, characteristic sections of the Rur River were covered respectively (cf. Table 2). Thus, dams and near natural sections are bracketed by two sampling sites. Long monotonous straightened river sections, such as between sampling sites SSC-11 and SSC-12 are not further divided. For investigating the SSC development between two sampling sites, 78 pairs of samples were compiled from 98 samples since SSCi+1 of the previous pair is SSCi for the next pair (cf. Table 2). For the sampling pairs, samples needed to be collected within one field trip and in chronological order within flow direction as fast as possible to track the suspended sediment flow as accurately as possible. The quarterly field trips were scheduled when characteristic weather changes with corresponding changes in discharge occurred, such as intensified rainfall in autumn, snowmelt at the end of winter, and periods of droughts in the summertime. We identified sampling sites SSC-3, SSC-13, and SSC-14 as relevant for flood scenarios since they give us insights into the differences between uplands and lowlands, as well as the impact of the Inde River, one of the main tributaries of the Rur River. As a mid-sized river, the Rur River’s warning time ranges around a few hours. Thus, we used mobile warnings (see LUBW (2022) for more information) for existing gauging stations and were prepared to initiate an unscheduled field trip as soon as information value 1 (indicating a channel overflow) was exceeded.

Table 2 Data from the Rur River for model identification, local features of data sets
Full size table

The data sets are used to test and expand the sediment rating curve for SSC prediction along a river (cf. Data Matrix and SSC-Equation-Formulation).

At the Wurm River, samples from two sampling sites from previous studies (cf. Maaß and Schüttrumpf 2019b) are still collected monthly. 16 samples, collected from September 30th, 2019 to June 29th, 2021 from this database serve to validate findings from the Rur River (13 each at SSC-W-1 and SSC-W-2). Data from the Wurm River and the Rur River are comparable since they are collected in the same way and by the same person (Table 3).

Table 3 Data from the Wurm river for evaluation of the transferability
Full size table

For compiling sediment hysteresis patterns, a heavy rainfall event leading to high discharges on 29th January 2021 was sampled over several hours, including follow-up samples until 31st January 2021. We collected 19 samples at sampling site SSC-3, 9 samples at sampling site SSC-13, and 20 samples at sampling site SSC-14.

The SSC is determined by filtration using a vacuum pump as described in Maaß and Schüttrumpf (2019b). The SSC of the reference sample is divided by the SSC of the 1st sample. Out of those factors, the 5% percentile and the 95% percentile mark the lower and upper boundary of the range, in which values are treated as comparable. For the Rur River, those values are 0.47 and 1.81, and for the Wurm River, 0.33 and 1.39, respectively. If the reference sample falls below or exceeds the range, the following error in sample taking is assumed: if the sampler hits the riverbed soil, often unnoticed, sediments are swirled up, and false high concentrations are sampled. In those cases, the smaller value is considered. Otherwise, a mean value between the two samples is computed. Still, we assume that samples collected from the middle of the stream represent the sediment transport within the cross-section.

Rainfall-runoff modeling

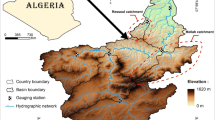
Since the 14 sampling sites at the Rur River are not identical to gauging stations and only 7 gauging stations exist (cf. Figure 2), sub-catchments for the rainfall-runoff model were set between a sampling location and a gauging station. Within five sub-models for the Rur River, the discharge between sampling locations is modeled (cf. Figure 3). The BlueM software package, a rainfall-runoff model based on the Soil Conservation Service method (SCS) incorporating the Curve Number (Bach et al. 2009; Bach and Ostrowski 2013; ihwb 2021; Mockus 1965), is used to estimate the discharges corresponding with the SSC samples. Also, for calculating the translation and retention properties of the open channel, the Kalinin-Miljukov method is implemented within BlueM (Bach et al. 2009; Bach and Ostrowski 2013). The SCS-CN approach is suitable for modeling rural as well as urban sub-catchments of different sizes based on a small data basis (Jehanzaib et al. 2022; Sitterson et al. 2018). The rainfall-runoff model can reach volume errors of less than 2% and correlations of over 95% (Bach 2011). We ran the serial simulation on a computer with an Intel® Xenon® CPU E5504 2 GHz processor with 24 GB of workspace.

Fig. 3
figure 3

Modeled areas in the rainfall-runoff simulation. Blue arrows mark sub-catchments which could be supplemented by discharge data from the gauging station. Sources: river system: Geofabrik GmbH (2018)

Full size image

Between gauging stations Altenburg and Selhausen, linear interpolation was chosen to obtain discharge at sampling site 13 since the section is impacted by groundwater pumping in the lignite open-cast mine, which cannot be incorporated into our model.

Data from the existing eight gauging stations (cf. Figure 3) was incorporated and not only used for model validation. Also, we cut out the reservoirs and fed the reservoir runoff into the next sub-model.

For the validation data set, a rainfall-runoff model for the Wurm River is set up. The sampling site SSC-W-2 is situated at the gauging station Herzogenrath, whereas here, the discharge is known. For the sampling site SSC-W-1, at the wastewater treatment plant Aachen Soers, the discharge is unknown. Hence, at the Wurm River, only one model was incorporated. The Wurm River’s model area is characterized by urban catchments. In the sub-catchment of the urban area in Aachen, the Wurm River is canalized and is modeled as such, according to Bach et al. (2009). The models are provided in Supplement 4 and Supplement 5.

Input parameters for the simulation are the hydrological state in nature of the sub-catchments and their channels. Flow path length, length of river sections and their slope, elevations of sub-catchments as well as sub-catchment areas were determined based on the EU DEM 25 (European Environment Agency 2016).

The SCS-method also requires the runoff curve number from the individual sub-catchments of the sub-models as an input variable. The curve number value (CN value) can be used to derive the runoff-effective portion of a precipitation event, dependent on the respective prevailing hydrological soil group (Maniak 2016; Mockus 1965). As a basis for determining the CN value served the soil map of North Rhine-Westphalia, the roughness coefficient of the soil, and the CORINE Land Cover data set (EEA 2016; Geologischer Dienst NRW 2016). Mean precipitation for the sub-catchments was provided as raster data by LfU (2019). Timelines for temperature and rainfall were calculated for the sub-catchments from 17 climate stations for the Rur Rivers model and three climate stations for the Wurm Rivers model. The LANUV and the DWD provided data from the climate stations.

The rainfall-runoff models were calibrated using the discharge data of the gauging stations. The calibration target was set to a maximum deviation of 10%, which was achieved for the Wurm River model and largely achieved (79%) for the Rur Rivers models. In the remaining cases (20.35%), minor deviations from the calibration target occurred (cf. Table 4). The hydrological derivation describes a weighted mean error based on peak flows, and values between 3 and 0 are considered to be excellent (Schultz 1968). The Nash–Sutcliffe Efficiency, however, compares the whole hydrograph, and the closer the value is to 1, the better the fit. We conclude that the simulated discharge data of the models created is satisfactory.

Table 4 Goodness of fit of the rainfall-runoff-modeling after calibration
Full size table

Data matrix and SSC-equation-formulation

Discharge values from rainfall-runoff modeling (cf. section “Rainfall-Runoff Modeling”) are assigned to the SSC sample values. Further, the characteristics of sub-catchments between two sampling sites are determined and transferred to a data matrix (cf. Figure 4 and Supplement 2). Columns hold an index for each pair of sampling sites (SSC-1–SSC-2, SSC-2–SSC-3 to SSC-13 to SSC-14), SSCi, SSCi+1, Qi (discharge during sampling of SSCi), Qi+1 (discharge during sampling of SSCi+1) and parameters \({\mathrm{p}}_{\text{rkm}}\), \({\mathrm{p}}_{\mathrm{d}}\), \({\mathrm{p}}_{\mathrm{t}}\), \({\mathrm{p}}_{\mathrm{EROS}}\) and \({\mathrm{p}}_{\mathrm{r}}\) (cf. Table 5). Rows hold an entry for each pair of samples, whereas parameters are constant for each sub-catchment between two sampling sites. The parameter for erosivity, \({\mathrm{p}}_{\mathrm{EROS}}\), can be based on various model approaches. We tested two data sets for \({\mathrm{p}}_{\mathrm{EROS}}\) with significant differences to rule out that a possible poor model performance is solely based on an improper database. Data set a) (cf. Table 5) describes an estimation of the mean annual soil loss by water in sheet and rill erosion in 2016 with a resolution of 100 m (Panagos et al. 2020). The data is based on the revised universal soil loss equation (RUSLE) (Panagos et al. 2020), which was established in 1997 and has proven to generate valid results (Renard et al. 1997). A special feature of the RUSLE data set by Panagos et al. (2020) is the incorporation of data from surveyors describing land cover and soil conditions on a small scale. The second data set is the Global Soil Erosion (GloSEM) from 2012, with a resolution of 250 m (Borrelli et al. 2013). Borrelli et al. (2013) incorporate dynamic land cover changes between 2001 and 2012, and although the data set is based on the RUSLE-equation as well, different results are reached. The correlation between \({p}_{RUSLE}\) and \({p}_{GloSEM}\) for the 13 sub-catchments of the Rur model is very low (R2 = 0.0046).

Fig. 4
figure 4

Overview of the Model Identification Process: based on the sediment rating curve (Base Equation, Eq. 2), the SSC (suspended sediment concentration) at sampling site i + 1 is determined by the discharge Q at both sampling sites and the SSC at sampling site i. Possible extensions to the Base Equation are obtained from the data matrix, which contains specific information for the reach between sampling sites. Using permutations, extensions reaching the best SSC-forecast are kept; the final fitting of the equation is executed without permutations

Full size image
Table 5 Definition and description of parameters contained in the data matrix for model identification
Full size table

An equation for the suspended sediment concentration at a sampling site (SSCi+1) to the previous sampling site (SSCi) is derived from a systematic approach starting with the relation of the sediment rating curve (cf. Eq. 2). This approach is based on literature (cf. Eq. I). Hence, Equation 2 is our “base equation” (cf. Figure 4):

$${\text{SSC}}_{{\text{i + 1}}} {\text{ = SSC}}_{{\text{i}}} + \left( {\alpha_{{\text{Q}}} \cdot {\text{Q}}_{{\text{i + 1}}}^{{\beta_{{\text{ Q}}} }} - \alpha_{{\text{Q}}} \cdot {\text{Q}}_{{\text{i}}}^{{\beta_{{\text{ Q}}} }} } \right)$$
(2)

Equation II is systematically extended according to processes described in Table 1 (cf. also Figure 1). For the extensions, mathematical expressions of described processes of sediment erosion and deposition as well as changes in discharge are formulated. Whenever more than one possible formulation seems logical, variations for extensions are tested.

First, the length of the river section is integrated into the equation since the probability of influences on the suspension load increases with distance (Eq. 3). The first additional option is multiplying the delta of the sediment rating curves between two sampling sites with a parameter for the river length between them.

$$SSC_{i \, + \, 1} \, = \, SSC_{i} + \left( {\alpha_{Q} \cdot Q_{i \, + \, 1}^{{\beta_{ \, Q} }} {-}\alpha_{Q} \cdot Q_{i}^{{\phi_{ \, Q} }} } \right)$$
(3)

With: \({\alpha }_{Q}\) coefficient fitting the correlation with discharge.

\({\beta }_{Q}\) exponent fitting the correlation with discharge.

The first extension is:

$${[} \cdots {]} \cdot p_{{{\text{rkm}}}}$$
(Ext-I)

Next, an additional term to the equation for the biggest anthropogenic disturbance variable, the two dams, is proposed. Here, the relation to the dammed river section (Ext-II-1) and the relation between the dammed river section as well as the change in discharge (Ext-II-2) are tested:

$$p_{d} \cdot \alpha_{d}$$
(Ext-II-1)
$$p_{d} \cdot \left( {Q_{i + 1} - Q_{i} } \right) \cdot \alpha_{d}$$
(Ext-II-2)

With: \({\alpha }_{d}\) coefficient fitting the influence of damming.

Since damming leads to a reduction in the SSC, the term needs to be negative.

An additional term to describe the sediment input by tributaries is proposed. Again, two variations are tested, whereat erosivity is incorporated optionally.

$$p_{t} \cdot p_{r} \cdot a_{t}$$
(Ext-III-1)
$$p_{t} \cdot p_{EROS} \cdot p_{r} \cdot a_{t}$$
(Ext-III-2)

With: \({\alpha }_{t}\) coefficient fitting the influence of the activation of the sediment entry by tributaries.

The larger the tributary, the more sediment can be discharged into the main stream. Hence, \({p}_{t}\) is a factor of the additional term Ext-III. Usually, the larger the sub-catchment between two sampling sites, the more likely tributaries drain the surface. We only compute one mean value for the erodibility for the whole sub-catchment area between two sampling sites, which we apply in the additional term once, and we don’t distinguish between sub-catchments of the tributaries. Further, the higher the rainfall, the higher the impact of the tributaries since they react faster to rainfall than the main stream.

Also, an additional term to describe the sediment entry through surface erosion within the sub-catchment between two sampling sites is proposed:

$$p_{EROS} \cdot \left( {\frac{{p_{{{\text{rkm}}}} }}{{p_{subc} }}} \right) \cdot p_{r} \cdot a_{subc}$$
(Ext-IV-1)
$$p_{EROS} \cdot p_{subc} \cdot p_{r} \cdot a_{subc}$$
(Ext-IV-2)

With: \({\alpha }_{subc}\) coefficient fitting the influence of the activation of the sub-catchment by rainfall.

Unless the majority of the surface is almost sealed or consists of surface water bodies, surface erosion and sediment entry into the river is expected. The higher the erodibility, the higher the mean RUSLE-value of the sub-catchment and the more sediment can be transported into the river. Also, the higher the rainfall, the more sediment is eroded (Ext-IV-2). The factor \(\frac{{p}_{\text{rkm}}}{{p}_{subc}}\) increases when hillslopes are closer to the river, which makes sediment entry more likely (Ext-IV-1).

Last, along a river section, riverbed erosion and floodplain deposition can occur either by increasing or reducing the SSC. Since it is not known which processes the sediment rating curve can represent, extension V fills possible gaps.

$$p_{rkm} \cdot \frac{{Q_{i} }}{Qi + 1} \cdot a_{rkm}$$
(Ext-V-1)
$$p_{rkm} \cdot \left( {Q_{i + 1} - Q_{i} } \right) \cdot a_{rkm}$$
(Ext-V-2)

With: \({\alpha }_{rkm}\) coefficient fitting the influence of additional processes along the river section.

Constructing the equation is a theoretical approach; all possible extensions must be tested on their pertinence afterward. All possible extensions and their composition to equation II are displayed in Table 6.

Table 6 Possible extensions to the sediment rating curve based on a basic understanding of sediment transport
Full size table

Model identification for SSC-equation

Leave-one-out cross-validation (see Fig. 4, “Model Selection”) is implemented with Matlab 2018b to select suitable model extensions to minimize the percentual difference between the calculated and the measured \({\text{SS}}{\text{C}}_{\text{i+1}}\). Therefore, the data from the Rur River is divided into training and test data, whereas one pair of sampling sites (one data set) is left out as test data, respectively (cf. Figure 4). First, the model is fitted to the training data by solving the non-linear weighted least squares problem with a hybrid of particle swarm optimization and gradient-based local search. The optimizer searches for model coefficients, which predict the training data as accurately as possible. Afterward, the validation error is calculated by evaluating the model on the independent training set. This procedure is repeated \(j\) times such that each data set is used as testing data exactly once.

Leveraging the leave-one-out cross-validation methodology, model extensions, which improve average validation performance most, are successively added one by one to the SSC model. First, possible extensions are tested individually, and the best extension is kept. Afterward, a combination between the kept extension and the remaining extension is tested. Again, the best addition is kept. This is repeated until all extensions are evaluated. The algorithm uses particle swarm optimization for parameter fitting of the coefficients. Particle swarm optimization is robust against non-linear functions with varying data sets, such as our example, and cost-efficient since parameters are optimized parallel (Kennedy and Eberhart 1995; Poli et al. 2007). The cross-validation checks how good results are obtained with the training data set performed on the test data set.

Parameters, cf. Table 5, are standardized by dividing values by the corresponding maximum value. Also, each data set is constrained with a weighting depending on how many data pairs are available to prevent the overrepresentation of certain data pairs. We use 1000 particles and repeat the optimization 10 times to check if the results are robust. As a result, the RSME (root squared mean error) for the test- and training data is plotted. Also, the process is repeated twice, one time with \({p}_{RUSLE}\) and one time with \({p}_{GloSEM}\) for \({p}_{EROS}\).

After a first evaluation (cf. Table 8), the simulation is repeated, leaving out data set 1, since it is the most error-prone in the rainfall-runoff modeling and discharge is a key input parameter (cf. Table 4). After this second training circle, extensions are evaluated, which improve the forecast performance on new data sets. Last, for the identified extensions, a parameter fitting with the complete data set is performed to obtain optimal coefficients and exponents for the equation. Again, 10 batches are run, and the result with the lowest WRMSE (weighted root mean squared error) is chosen. Each run with cross-validation had a computing time of about 30 min. The final runs without cross-validation and with given extensions took about 3 min, both on a single core.

Afterward, the equation is manually tested on the Wurm Rivers data set to evaluate its transferability within MS-Excel (cf. Table 3).

Results

Overall, the suspended sediment concentration in the Wurm River is higher than in the Rur River (cf. Table 7). Within our sampling periods, the mean SSC in the Rur River is 9.8 mg/l vs. 23.4 mg/l in the Wurm River. During the flood event in late January 2021, SSCs up to 133.4 mg/l were measured in the Rur River, which are lower than the highest SSC value of 149.3 mg/l in the Wurm River within our sampling period, which does not contain flood events.

Table 7 Value ranges of the data bases for model identification of an SSC-equation and compilation of hysteresis patterns
Full size table

Hystereses from the flood event in January 2021

During a flood event at the end of January 2021, several samples were collected with 30 to 60 min timing at three locations; SSC-3: a rural location in the uplands, SSC-13: a straightened river section towards the lowlands upstream of the Inde River tributary, and SSC-14: a rather straightened river section, but with lower floodplains downstream of the Inde River tributary.

Using the results of the rainfall-runoff modeling, the SSC is potted against the discharge (cf. Figure 5). Results show that all hysteresis turn clockwise. At sampling site SSC-3 the pattern is the clearest. The flood peak and the peak of the sediment concentration occur almost at the same time, but the peak of the sediment concentration is a few hours earlier. Nevertheless, the peaks are shaped relatively similarly.

Fig. 5
figure 5

Flow Sediment Hysteresis during a flood event in late January 2021; samples were taken every 30 to 60 min. at sampling site SSC-3 in the uplands upstream of the Rur dam (cf. a)), at SSC-13 towards the lowlands upstream of the Inde tributary (cf. b)), and at sampling site SSC-14 downstream of the Inde tributary (cf. c)). The hystereses patterns and the SSC and discharge curve are plotted (a), b), c)). d) gives an overview of the location of the three sampling sites

Full size image

At the sampling site SSC-13, the discharge has no clear peak due to flow regulations by the Rur dam and Obermaubach basin. The sediment concentration peaks earlier than the peak discharge at SSC-13 and is generally lower than at SSC-3 and SSC-14. At sampling site SSC-14, downstream of the Inde tributary, the peak in SSC is measured over 12 h before the peak discharge and is the highest.

Model identification for SSC-equation

Measured values for the SSC of the Rur River range between 0.19 mg/l and 92.19 mg/l with an overall mean of 9.80 mg/l (cf. Table 7 and Supplement 2).

First, we evaluate the reproducibility of the identification approach by repeating it ten times. We also test which possible extensions to the base equation (Eq. II) improve our results and critically examine at the 13 data sets. Overall, we see the optimization is consistent since the standard deviation of the mean error in predicting the SSCi for data sets of all 10 batches mostly ranges about 0.00% (cf. Table 8).

Table 8 Model Identification performance over 10 batches with all 13 data sets, results with \({p}_{RUSLE}\) for \({p}_{EROS}\)
Full size table

However, no improvements could be reached on the test data when adding extensions. When excluding data set 1, as described in the section ‘Model Identification for SSC-Equation’, Extensions Ext-II (1), Ext-V (1), and Ext-I (cf. Table 6) improve the model performance on the test data set from a mean WRMSE of 176% to a mean RMSE (root mean squared error) of 159% to 158% (cf. Table 9 and Table 10). Both approaches, using \({\mathrm{p}}_{\mathrm{RUSLE}}\) or \({\mathrm{p}}_{\mathrm{GloSEM}}\) for \({\mathrm{p}}_{\mathrm{EROS}}\) lead to similar results, although \({\mathrm{p}}_{\mathrm{GloSEM}}\) and \({\mathrm{p}}_{\mathrm{EROS}}\) have no linear correlation (R2 = 0.0046).

Table 9 Mean test-WRMSE over 10 batches when adding extensions, excluding data set 1 and using \({p}_{RUSLE}\)
Full size table
Table 10 Mean test-WRMSE over 10 batches when adding extensions, excluding data set 1 and using \({p}_{GloSEM}\)
Full size table

However, the model performs very poorly for test data sets 4 and 7 (cf. Table 11 and Table 12), with errors of 2767% and 618%. Data sets 4 and 7 include the large Rur reservoir and the smaller Obermaubach basin. Again, using \({p}_{RUSLE}\) or \({p}_{GloSEM}\) for \({p}_{EROS}\) leads to almost identical results.

Table 11 Model Identification performance over 10 batches without data set 1, results with \({p}_{RUSLE}\) for \({p}_{EROS}\)
Full size table
Table 12 Model identification performance over 10 batches without data set 1, results with pGloSEM for pEROS
Full size table

Overall, the final equation based on data sets 2–13 with a WRMSE of 131.90% and an RMSE of 131.83% is:

$${\text{SSC}}_{{\text{i + 1}}} {\text{ = SSC}}_{{\text{i}}} + \left( {\alpha_{{\text{Q}}} \cdot {\text{Q}}_{2}^{{\beta_{{\text{ Q}}} }} { - }\alpha_{{\text{Q}}} \cdot {\text{Q}}_{1}^{{\beta_{{\text{ Q}}} }} } \right) \cdot p_{rkm} - p_{d} \cdot \alpha_{d} + p_{rkm} \cdot \frac{{Q_{i} }}{Qi + 1} \cdot a_{rkm}$$
(IV)

With: \({\upalpha }_{{\text{Q}}} = 39,085.756\)

$${\upbeta }_{{\text{ Q}}} = 9.17{\text{E}} - 06.$$
$$\alpha_{d} = 0.9519.$$
$$\alpha_{rkm} = {-}{ }0.2186.$$

A correlation of 0.878 is achieved between the measured and computed \({\text{SS}}{\text{C}}_{\text{i+1}}\), whereas the correlation between \({\text{SS}}{\text{C}}_{\text{i}}\) and \({\text{SS}}{\text{C}}_{\text{i+1}}\) is 0.876. The RMSE between \({\text{SS}}{\text{C}}_{\text{i}}\) and \({\text{SS}}{\text{C}}_{\text{i+1}}\) is 152.27% and is improved to 131.83% when computing \({\text{SS}}{\text{C}}_{\text{i+1}}\) based on equation IV (cf. Table 13).

Table 13 Results of the model identification for the SSC-Equation
Full size table

The correlation of the errors between \({\text{SS}}{\text{C}}_{\text{i}}\) and \({\text{SS}}{\text{C}}_{\text{i+1}}\) and the errors between the measured and computed \({\text{SS}}{\text{C}}_{\text{i+1}}\), which underly the computation of the RMSE, is 0.9988. Thus, the data is not independent, and not normally distributed. Therefore, we chose the Wilcoxon Signed Rank Test (Rey and Neuhäuser 2011) to test if the improvement from an RMSE of 152.27% to an RMSE of 131.83% is statistically significant. Our null hypothesis is that both RMSEs originate from the same population, which we want to reject. With a p-value of 0.073, we see the improvement as very likely statistically significant since we can reject our null hypothesis with 93.7%.

Afterward, the equation is tested on the 13 data points from the Wurm River (cf. Table 3). Here, a correlation of 0.340 is achieved between the measured and computed \({\text{SS}}{\text{C}}_{\text{i+1}}\), whereas the correlation between \({\text{SS}}{\text{C}}_{\text{i}}\) and \({\text{SS}}{\text{C}}_{\text{i+1}}\) is 0.333, but the RMSE of 54.97% between \({\text{SS}}{\text{C}}_{\text{i}}\) and \({\text{SS}}{\text{C}}_{\text{i+1}}\) is slightly better than between the measured and computed \({\text{SS}}{\text{C}}_{\text{i+1}}\) (55.54%) (cf. Table 13).

Discussion

We used a model identification approach to identify an SSC equation based on the sediment rating curve to predict the sediment concentration \({\text{SS}}{\text{C}}_{\text{i+1}}\) on a location downstream of the measured value \({\text{SS}}{\text{C}}_{\text{i}}\). Possible extensions for the equation describe the river length between the locations of \({\text{SS}}{\text{C}}_{\text{i+1}}\) and \({\text{SS}}{\text{C}}_{\text{i}}\) (Ext-I), sediment deposition due to damming (Ext-II), sediment entry by tributaries (Ext-III), sediment entry due to hillslope erosion (Ext-IV) as well as riverbed erosion or floodplain deposition (Ext-V) (cf. Table 6). Incorporating the river length between the two locations as well as sediment deposition due to damming improved the prediction of \({\text{SS}}{\text{C}}_{\text{i+1}}\) based on \({\text{SS}}{\text{C}}_{\text{i}}\). We evaluated the improvement of computing \({\text{SS}}{\text{C}}_{\text{i+1}}\) based on \({\text{SS}}{\text{C}}_{\text{i}}\) in comparison to the relation of \({\text{SS}}{\text{C}}_{\text{i+1}}\) and \({\text{SS}}{\text{C}}_{\text{i}}\) (cf. Table 13). We could improve the RMSE from 152.27 to 131.83% with a p-value of 0.073 in the Wilcoxon Signed Rank Test. But, when transferring the equation to the Wurm River validation data set, the RMSE did not improve. It changed from 54.97 to 55.54% (cf. Table 13). Results indicate that a catchment-wide prediction of \({\text{SS}}{\text{C}}_{\text{i+1}}\) based on a known \({\text{SS}}{\text{C}}_{\text{i}}\) is generally possible but with limited accuracy and transferability to sub-catchments.

Sub-catchment characteristics and model transferability

The Rur River is characterized as a coarse-material-rich, siliceous low mountain stream in the uplands, which is relevant for the first two data sets (SSC-1 to SSC-3) (cf. Table 2) (LAWA 2013). Afterward, it is characterized as a silicatic, fine- to coarse-material-rich low mountain range river, which changes to a gravel-dominated lowland river 12 rkm downstream of our last sampling site (SSC-14) (LAWA 2013). The Wurm River is characterized as a coarse-material-rich, siliceous low mountain stream within our study area (LAWA 2013). However, it is rich in fine sediments and characterized by high SSC with large organic compounds due to riverbank erosion. The Wurm River generally transports higher suspended sediment concentrations than the Rur River (cf. Table 7). The study area of the Rur River is located at a meso catchment scale, while the validation area, a section of the Wurm River, operates on a micro catchment scale (Maaß 2019; Maaß et al. 2021). The fast behavior of the micro catchments (Ahn and Steinschneider 2019; Hinderer 2012; Maaß et al. 2021) could be one of the aspects of why the final equation (Eq. IV) is not transferable to the section of the Wurm River, although river types are the same. Since the correlation between \({\text{SS}}{\text{C}}_{\text{i}}\) and \({\text{SS}}{\text{C}}_{\text{i+1}}\) at the Wurm River is low, a very fast behavior of the sub-catchment in between is suspected (cf. Table 13). Walling (1977a) already predicted that the transferability of a sediment rating curve approach to another catchment might not be possible based on larger scale parameters, like climate. Asselman (2000) found a comparable behavior in the suspended sediment-discharge relation at sampling sites along the Rhine River but differences in tributaries, similar to our finding. Although those parameters should be similar for the Rur River and the Wurm River on a larger scale, differences in the micro catchment characteristics are suspected to be the cause for the bad transferability. This finding is in good agreement with the generally accepted statement that drainage basin size is relevant to the sediment input (Maner 1963; Phillips et al. 1999).

Sectioning the Rur River in 13 data pairs (of which 12 were used), we divide the river into small sub-catchments. However, we observe a continuous behavior in its suspended sediment mobilization from the upper to the middle reach since all three hystereses patterns are similar, showing a clockwise movement (Figure 5). A clockwise turning pattern means that sediments stored in the river channel are mobilized with the first flow (Hughes et al. 2012; Williams 1989), a counterclockwise hysteresis indicates sediments eroded from the farther away slopes (Hughes et al. 2012) but can also form due to different processes. Usually, during high flows, the sediment wave is transported downstream with a slower velocity than the flood wave (Marcus 1989), leading to a change in the hysteresis from clockwise to counterclockwise in lower reaches (Tena et al. 2014). We can observe a small trend towards this effect between the hysteresis from sampling sites SSC-3 and SSC-14 (cf. Figure 5), but the increase of the sediment peak from sampling site SSC-13 to sampling site SSC-14 is more significant and shows the sediment input by the Inde tributary. Overall, the hystereses from sampling sites SSC-3 and SSC-13 tend towards a class-IV behavior after Hamshaw et al. (2018), first linear and then clockwise, which is typical for floods after long rainfall periods. Since the underlying event of the hysteresis was triggered by a combination of snowmelt and rainfall in the uplands, leading to in-channel erosion as the main sediment source, the pattern is a good fit.

Additionally, for upland catchments, bank erosion is a typical supply of suspended sediments during flood events (Bull 1997). Not only the catchment characteristics but also the characteristics of the flood event scientifically influence the response behavior, respectively, the SSC-entry into the river (Oeurng et al. 2010; Smith and Dragovich 2009). Overall, the behavior of the Rur River, in comparison with the Wurm River, seems to be more stable, even over multiple small sub-catchments.

Interpretation of the model behavior

The sediment rating curve can describe the SSC to Q with an error, which is an independent, additive, normally distributed value (Ferguson 1986). Correlations using the sediment rating curve are prone to over- and underestimating the SSC (Walling 1977a, 1977b). Grouping data by seasons could improve the predictions (Campbell and Bauder 1940) but still lead to relatively high errors (Walling 1977a), which we aimed to meet with additional terms (cf. Table 6). Results improve when sediment deposition due to damming is incorporated (cf. Table 9 and Table 10). As shown in a previous study on the Rur River, even for coarse-material-rich rivers, the deposition of fine sediments due to damming reduces the SSC, but only short term, since the local lithostratigraphy and tributaries have a balancing effect for sediment supply (Wolf et al. 2022).

As Bača (2008) states, based on altering hysteresis patterns, the suspended sediment load is not only dependent on the energy in a river system but also the sediment availability. Energy is applied to the channel by the discharge, which is incorporated into the sediment rating curve, but sediment availability is not. The sediment availability could be mapped by the length of the river section, the sub-catchment characteristics, or the sediment input by tributaries. When describing suspended sediment transport processes, several researchers stress the importance of considering local bank erosion (e.g., Bull 1997; Meade and Moody 2009; Smith and Dragovich 2009; Zhou and Lin 1998). With a longer distance between sampling sites, a larger section of riverbanks is available for bank erosion. However, on small timescales, channel networks often act as short-term sinks (Bull 1997; Llena et al. 2021). Hence, it is comprehensible that a negative coefficient for \({a}_{rkm}\) (= -0.2186, cf. equation IV) results from the model identification. Affecting the erosion and storage processes, channel routing and channelization is the main driver for the shape of hysteresis patterns (Ahn and Steinschneider 2019; Bača 2008; Maner 1963; Tena et al. 2014). Incorporating the river’s section length into the SSC-prediction is potentially of great value for river management since channelization leads to a decrease and river restoration to an increase of the parameter “\({p}_{rkm}\)” (cv. Table 5). Meade and Moody (2009) already provide a case example for this observation, since at the Missouri–Mississippi River system between 1987 and 2006, large declines in the transported suspended sediment load were only partly caused by the closure of large dams. Meander cuttings, river training structures, river restorations, and soil conservation measures were identified as the cause for the change of the river system from a transport limited to a supply limited system (Meade and Moody 2009). River systems in an active morphological state, e.g., with active channel migration and meander formation, might need to be incorporated into a SSC prediction differently than systems that tend to be in a more statically equilibrium (c.f. Lauer and Parker 2008). Hence, the transferability of our results to different catchments is limited since their supply and transport behavior differs by factors like the catchment connectivity.

As indicated by the patterns of the hysteresis from the Rur River, the Inde tributary plays a key role in the suspended sediment transport of the Rur River. However, extensions describing the sediment and discharge input by tributaries (EXT-III (1) & (2), cf. Table 6) do not improve the prediction. Tributaries feed sediment and discharge into the main river, and the increase in discharge is already implemented into the base equation (Eq. III), which could explain the model not improving when adding terms describing the tributaries. Ghanbarynamin et al. (2020) systematically tested soft computing approaches against the sediment rating curve approach and offered their models different hydrological and hydraulically parameters, such as precipitation, temperature, a flow depth index, and a season index. Similar to our study, they observed that additional parameters to the discharge potentially lead to overfitting and do not improve the prediction of suspended sediment transport (Ghanbarynamin et al. 2020).

In our study, incorporating additional terms which account for the rainfall of the last 72 h did not improve the SSC prediction either, since both formulations of Ext-III and Ext-IV did not improve the WRMSE (cf. Table 9 and Table 10). However, Cobaner et al. (2009) indicated rainfall as an important parameter for SSC prediction with neuronal networks. Their findings do not necessarily contradict ours since rainfall in a sub-catchment between two sampling sites increases the discharge deviation between those sites, which we incorporated in our base equation (Eq. III).

Also, we incorporated the sum of the last 3 days as a rainfall factor. A possible extension to our approach would be to extend the timeframe and maybe even incorporate flexible time frames. Walling (1977a) already stated for the stationary sediment rating curve that results could be different if parameters were fitted on different timescales. Peterson (1963), for example, incorporated rainfall data from the current month and the previous month to compute a monthly sediment yield. Hence, the duration of incorporated rainfall data was twice as long as the timeframe of the result. However, sediment yields are on a different time scale than single SSC-samples, which limits the transferability. Further, Peterson (1963) did not additionally incorporate discharge data into the rainfall data. Khan et al. (2019) found that when predicting SSC with artificial neural networks, incorporating rainfall data or a combination of rainfall and discharge performed worse than using discharge data alone. They suspect that rainfall data needs to be coupled with the catchment characteristics to predict an influence on the SSC.

Geology, soil properties, and land use are often interrelated (Striffler 1963). Thus, it makes sense to incorporate combined data sets, like the two data sets we tested, RUSLE (Panagos et al. 2020) and GloSEM (Borrelli et al. 2013). Although both are based on the RUSLE equation, data sets from Borrelli et al. (2013), describing soil loss in 2012, and Panagos et al. (2020), describing soil erosion by water in 2015, show no correlation. Both approaches incorporate the same input variables but obtain those from slightly different GIS databases and in different special resolutions; 100 m x 100 m vs. 250 m x 250 m (Borrelli et al. 2013; Panagos et al. 2020). Also, land cover management parameters are incorporated and for crops, mean values are considered (Borrelli et al. 2013). Seasonal changes in those parameters, however, are known to have a significant influence on sediment entry into river systems (Lusby 1963; Peterson 1963). Erosion is induced by rainfall; hence we coupled erosion parameters with rainfall data within our model approach. But the land cover and land management, as well as the geology, influence the rainfall-runoff and for example, less erosive agricultural covers also lead to a reduced runoff (Ahn and Steinschneider 2019; Copeland and Otis 1963; Lusby 1963; Noble 1963; Piest 1963; Ursic 1963). The runoff reduction by land use and land cover is already considered in the underlying rainfall-runoff modeling. One of the reasons why none of the terms describing the erosivity led to improvements in the prediction could be that the main impact is already mapped via the rainfall-runoff modeling. This assumption agrees with the findings of Baartman et al. (2020) who stress that the functional aspect of connectivity is more important than the structural one.

Wagner (2020), in good agreement with Llena et al. (2021), identifies the flashiness of a flood event, describing the height, frequency, and duration of a flood wave in comparison to the rivers base flow, as well as soil-related land use management as the main impact on the suspended sediment transport independent of the climate zone. Accordingly, it was observed that during small flood events, similar amounts of sediment were deposited in the river in forested catchments and with mixed land use, but during larger flood events, the land use had a significant impact (Hughes et al. 2012). Small agricultural sub-catchments are an important sediment source for the suspended load (Bača 2008). On the other hand, in mostly forested catchments, bank erosion was observed as the main source of suspended sediments (Striffler 1963).

For different river systems, either surface erosion or in-channel erosion can be the more dominant source of fine sediments, which is dependent on various factors, like sediment availability, land use, and geology (Ahn and Steinschneider 2019; Grimshaw and Lewin 1980). The potential surface erosion is hereby based on various factors, such as underlying soil properties, topographic aspects, soil moisture, land cover, and land use or land management (Ahn and Steinschneider 2019; Noble 1963; Renard et al. 1997). Further studies should include an underlying sediment source fingerprint study to evaluate sediment sources based on geochemical properties (Chalov et al. 2017).

Overall accuracy in the combined approach

First, one has to state that the reached accuracies are not high (cf. Table 13), although improvements were reached and our approach is proven valid. To classify the reached RMSE of 131.83%, underlying uncertainties and variances need to be considered to evaluate if higher accuracies would have been possible. The two most important base data sets in our study are SSC values, which are field data, and corresponding discharge, which is obtained from rainfall-runoff modeling in between gauging stations.

Over a cross-section and within different depths, the SSC varies due to the shear stress profile and the formation of sediment pulses. In a seminar at the Institute of Hydraulic Engineering and Water Resources Management, RWTH-Aachen University, in the summer semester of 2022, a group of students collected a total of 15 SSC samples of 0.5 l along a cross-section at SSC-W-1 at the Wurm River. Their results help estimate the SSC variation over a cross-section. Values range between 2.5 mg/l and 83.7 mg/l with the highest values (83.7 mg/l, 45.4 mg/l, 43.6 mg/l, and 41.5 mg/l) measured at the riverbed near the banks and in the main channel. When leaving out those 4 values, the mean is 4.3 mg/l with a standard deviation of 52%. For the C-51 Canal to Lake Worth in Florida, the SSC values within a cross-section varied between 5 mg/l and 30 mg/l (Lietz and Debiak 2006), which is a range that is in good agreement with our findings. Hence, a single SSC-value consisting of a sample and a control sample, as implemented in our study, has at least an error of 50%, probably higher. Both the prediction of SSC by sampling or turbidity measurements comes with inaccuracies, simply due to the nonuniform sediment transport in suspension. Furthermore, the determination of suspended sediment concentration with vacuum filtration has an error of approximately 10% (Davies-Colley and Smith 2001).

Fluctuation in sediment concentration is hard to determine by direct sampling (Walling 1977a). Especially in rivers with high variances in the annual discharge pattern, high variability was observed, and results improved with data stratification by flow regime (Girolamo et al. 2018; Jung et al. 2020). Since the sediment rating curve tends to underestimate the SSC during high discharge and to overestimate values during low discharge (Hapsari et al. 2019), a systematic data division and separate model identification for at least low to mid and mid to high flows is recommended for the future. Unfortunately, our data set is not suited for the proposed division since some data sets between two sampling sites do not contain enough samples.

Also, the temporal resolution in which samples are collected does influence the results (Hoffmann et al. 2017). For catchments with low sediment transport rates, high-volume sampling is recommended to increase accuracy (Wagner 2020). However, those samples take longer than manually sampling smaller volumes, which increases the time lag between the sampling sites. This causes further inaccuracies since the measurements should follow the flow as well as possible. Additionally, larger water volumes are more prone to contain higher organic matter, leading to problems with algae formation in the sample (Gilvear and Petts 1985). Nevertheless, to implement a more differentiated sampling approach, which accounts for high and low levels in SSC, a pumping sampler and discharge measurement in the field are inevitable (Thomas 1985). Continuous turbidity measures are a promising measure to improve the timescale of the data basis (Walling 1977a), but they are scattered by organic particles (Chalov et al. 2017) and strongly depend on the particle shape and size (Hoffmann et al. 2017; Hughes et al. 2012) and therefore should be used with caution.

When rainfall-runoff modeling is incorporated into the SSC-prediction, the goodness of the discharge modeling plays a crucial part in the overall model accuracy (e.g., Sakai et al. 2005). Hence, an additional error is incorporated in the model identification for the SSC equation and makes up to 24% of the total volume; on average, the volume error is below 10%. Single values could be better or worse, which is displayed via the hydrological deviation and the nash sutcliffe efficiency (cf. Table 4). Hence, we made a valid decision when excluding data set 1 from the model identification approach, but using rainfall-runoff modeling when no gauging measurement can be installed at sampling sites incorporates an additional error. Although the error range due to the input data cannot be fully estimated, it relativizes the reached RMSE of 131.83%.

Conclusion and outlook

A sediment rating curve was used to predict the SSC at a sampling site further downstream. The accuracy of the prediction using additional linear terms, which describe sediment input, sediment storage, and dilution, achieved an uncertainty in the underlying simulations and field measurement in this study. When predicting SSC, both temporal and spatial variations within the cross-section of the river need to be considered. Especially when sampling manually, a good compromise needs to be found between the expense of the sampling and the sampling time. Further, knowing the discharge at sampling locations is crucial (e.g., Thomas 1985), but rainfall-runoff modeling can offer a solution where field measurements are missing and if a high model accuracy is reached.

Linear terms can increase the mode accuracy by incorporating the river section length and sediment deposition due to damming. Along the river section length, sediment sinks were mapped, being related to the small timescale of direct discharge (Bull 1997; Llena et al. 2021). Incorporating sub-catchment parameters, such as erosivity and relative sub-catchment size, as well as information on tributaries and rainfall data, did not improve the SSC prediction. We assume that most incorporated parameters directly influence the discharge relation between two sampling locations and, therefore, lead to overfitting.

The equation fitted to the Rur River is not transferable to the Wurm River, although it is one of the Rur River’s main tributaries. The failed transferability of the equation, although both rivers are located in the same catchment, is proof of the significance of the natural boundaries of catchments and sub-catchments. In our case, the failed transferability indicates the different spatial scales of the two model regions (meso-scale and micro-scale, cf. Maaß et al. (2021)).

We conclude that the most important aspect in SSC-prediction between two sampling sites is the spatial scale; the time scale equals the flow duration between two sampling sites and, therefore, is set. The size of the sub-catchment between two sampling sites does not seem significant, but the scale on which the catchment itself operates appeared relevant. River systems on a micro catchment scale have shorter response times and a different connectivity behavior than larger systems (Baartman et al. 2020). Related to these findings is whether surface or in-channel erosion is the more dominant source of fine sediments for the sub-catchment. For the Rur River, the main source is in-channel or near-channel erosion. It is likely that the model identification will lead to different results in study areas with surface erosion as the main source of fine sediments.

For a universally applicable equation, more data from different catchments need to be collected and grouped based on the spatial scale of the catchment area. A sufficiently diversified data set with sufficient accuracy in both SSC and discharge values could lead to a universally applicable equation, which contains variations for (sub-)catchments on different spatial scales, but maybe more characteristics need to be considered. Hence, first, a (sub-)catchment characterization needs to be developed together with the model identification approach.