Introduction

Modeling of hydraulic structure has received much attention in recent years due to its effect on increasing hydro system performance (Dehdar-behbahani and Parsaie 2016; Parsaie et al. 2015b). Weirs are common structures, which are widely used in most water engineering projects such as hydropower systems, irrigation and drainage networks and sewage networks (Haghiabi 2012). Side weir is a type of weir which has many possible uses in hydraulic engineering and has been investigated as an important structure in hydro systems as well (Chen 2015; Laycock 2007). Side weir is a hydraulic structure placed on the side of the channel and sometime is used as water surface controller structure in dam and irrigation projects whereas the main task of side weirs is removing the excess flow from the hydro systems (Bagheri et al. 2014; Haddadi and Rahimpour 2012). Study on side weirs hydraulics is conducted by the physical and numerical approaches (Parsaie 2016). In the field of physical studies, researchers attempted to improve the performance of side weirs by proposing various shapes for the crest of the side weir and compared its performance with rectangular shape as standard form for side weir. In this regard, labyrinth, oblique, semi-elliptical, curved plan-form and trapezoidal sharp and broad-crested could be mentioned. Based on reports, performance of nonlinear weirs is much more than the conventional side weir (Borghei and Parvaneh 2011; Cheong 1991; Coşar and Agaccioglu 2004; Emiroglu and Kaya 2011; Emiroglu and Kisi 2013; Emiroglu et al. 2011a; Haddadi and Rahimpour 2012; Jalili and Borghei 1996; Kaya et al. 2011). In the field of numerical modeling, in addition to solving the governing hydraulic equations by numerical approaches such as Runge–Kutta Method, the computational fluid dynamic (CFD) techniques has been used to simulate the flow over side weir. Numerical solution of governing equations leads to defining hydraulic parameters such as water surface profile, distribution of velocity and pressure and flow pattern (Aydin and Emiroglu 2013; Parsaie and Haghiabi 2015b). Another way for numerical modeling is related to the use of soft computing techniques for predicting the hydraulic properties of side weirs such as discharge coefficient (Azamathulla et al. 2016). In this regard, researchers used artificial neural network (ANNs), group method of data handling (GMDH), gene expression programming (GEP), and adaptive neuro-fuzzy inference system (ANFIS). Developing ANN models is based on data set, which means that to predict the hydraulic phenomenon by neural network techniques, parameters that influence the phenomenon should be measured in the past. ANN models could be used as standalone and be applied as participant of numerical methods in numerical simulation as well to increase the accuracy of the numerical modeling. The results of using the mentioned neural network models indicate that ANN models are more accurate (Bilhan et al. 2010; Bilhan et al. 2011; Ebtehaj et al. 2015a, b; Emiroglu and Kisi 2013; Emiroglu et al. 2011b; Kisi et al. 2012; Parsaie and Haghiabi 2015b). In this research, the radial basis function (RBF) neural network that has high performance in pattern recognition and image processing is used for predicting the side weir discharge coefficient, and its performance is compared with empirical formula and multilayer perceptron neural network as common ANN model, which is used by most researchers.

Materials and method

Figure 1 shows a schematic shape of a side weir in subcritical flow condition. The discharge coefficient of side weir is a function of hydraulic characteristics and geometry of side weir and main channel. Most hydraulic and geometry parameters are shown in Fig. 1.

Fig. 1
figure 1

Sketch of side weir structure in subcritical flow condition

Full size image

As could be seen in Fig. 1, V1 and Q1 are the velocity and discharge of flow at beginning the side weir respectively; B: width of main channel; E: specific energy; h1: depth of flow at beginning the side weir; h: the flow over side weir; h2: depth of flow at the end of side weir; L: side weir length; P: weir height and the longitudinal slope of the channel (S0). Defining the effect of each effective parameter requires conducting experiments in the condition that other parameters are constant. Researchers who conducted experimental studies on the hydraulics of side weirs proposed empirical equations for calculating the side weir discharge coefficient. A summary of the most famous empirical formulas is given in Table 1.

Table 1 Some empirical formulas to calculate side weir discharge coefficient
Full size table

Researchers attempt to reduce the number of experiments using the dimensional analysis techniques such as Buckingham \(\pi\) theory. Using analysis techniques leads to derive dimensionless parameters. Dimensionless parameters which influence the discharge coefficient of side weirs are given in Eq. (1) (Emiroglu et al. 2011a).

$$Cd_{sw} = f_{2} \left( {Fr_{1} ,\frac{L}{B},\frac{L}{{h_{1} }},\frac{P}{{h_{1} }}} \right)$$
(1)

In Eq. (1), \(Fr_{1}\) is the Froude number, \(\frac{L}{B}\) describes the ratio of weir length to the width of main channel, \(\frac{L}{{h_{1} }}\) describes the ratio of weir length to the flow depth at beginning the weir, and \(\frac{P}{{h_{1} }}\) describes the ratio of weir height to the flow depth at the beginning the weir. As presented in Table 1, most empirical formulas have used dimensionless parameters. Using dimensionless parameters in ANN model preparation leads to developing optimal structure. Developing MLP and RBF models similar to other neural network models is based on data set. To do so, 477 data sets related to side weir discharge coefficient, published in creditable journals were collected. Some of resources used for data derivation are given as follows (Bagheri et al. 2014; Borghei et al. 1999; Emiroglu et al. 2011a; Singh et al. 1994; Subramanya and Awasthy 1972). The range of collected data is given Table 2.

Table 2 Range of collected data related to the side weir discharge coefficient
Full size table

Multilayer perceptron (MLP) neural network

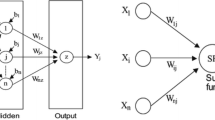
ANN is a nonlinear mathematical model that is able to simulate arbitrarily complex nonlinear processes, which relate inputs and outputs of any system. In many complex mathematical problems that lead to solving complex nonlinear equations, Multilayer perceptron networks are common types of ANN widely used by researchers. To use MLP model, definition of appropriate functions, weights and bias should be considered. Due to the nature of the problem, different activity functions in neurons could be used. An ANN may have one or more hidden layers. Figure 2 demonstrates a three-layer neural network consisting of inputs layer, hidden layer (layers) and outputs layer. As shown in Fig. 2, \(nw_{i}\) is the weight and \(b_{i}\) is the bias for each neuron. Weight and biases values will be assigned progressively and corrected during training process comparing the predicted outputs with known outputs. Such networks are often trained using back propagation algorithm. In the present study, ANN was trained by Levenberg–Marquardt technique because this technique is more powerful and faster compared to the conventional gradient descent technique (Parsaie and Haghiabi 2015a; Parsaie et al. 2015a).

Fig. 2
figure 2

A three-layer ANN architecture

Full size image

Radial basis function (RBF) neural network

Radial basis function (RBF) neural network is a type of artificial neural network widely used in image processing, pattern recognition and nonlinear system modeling. RBF model as shown in the Fig. 3, consists of two layers, the first layer considered as hidden layer and the second one as output layer. The radial function is considered as transfer function for neurons, which are in hidden layer and linear function as output layer transfer function. Designing RBF neural network is based on defining the center of these functions. In other words, the aim of RBF model training is mapping the input space to output space as \(f:R^{n} \to R\). Transfer function of the RBF model is defined as Eq. (2).

$$f\left( \nu \right)\, = \,\mathop \sum \limits_{i = 1}^{n} w_{i} \varphi \left( {\left| {\left| {\nu - c_{i} } \right|} \right|} \right)$$
(2)

where \(\nu\) is the inputs variable, \(w_{i}\) is the weight coefficients, \(\varphi\) is Gaussian function, which is the basic function used as kernel function in RBF model development and is defined as Eq. (3).

$$\varphi \left( \nu \right)\, = \,e^{{\left( {\frac{{ - \nu^{2} }}{{2\sigma^{2} }}} \right)}}$$
(3)
Fig. 3
figure 3

A RBF model structure

Full size image

RBF model training usually is carried out by Gradient Descent approach. The aim of RBF model is defining the value of kernel function parameters and weights. Initial value of weights is defined randomly. The error for each sample of the data set is calculated as Eq. (4).

$$e_{i} = t_{i} - y_{i} = t_{i} - \mathop \sum \limits_{j = }^{N} w_{j} \varphi \left( {\left| {\left| {\nu_{i} - c_{i} } \right|} \right|} \right)$$
(4)

The error for total input data set is calculated as Eq. (5).

$$E\, = \,\frac{1}{2}\mathop \sum \limits_{i = 1}^{p} \left| {e_{i} } \right|^{2}$$
(5)

RBF model preparation is finished when error of RBF model for all data sets is lower than the threshold error which is defined by the designer (Liu 2013).

Results and discussion

Performance of empirical formulas, MLP and RBF models was assessed by data collected the range of which is given in Table 2. Accuracy of empirical formulas and MLP and RBF models was assessed by statistical error indices such as correlation coefficient, root mean square error (RMSE), mean square error (RMSE). It is noticeable that these indices provide an average value for error and do not provide any information about error distribution. All stages of MLP and RBF models’ development have been programed in Matlab software.

Results of experimental formulas

Performance of empirical formulas was evaluated for calculating the \(Cd_{sw}\) using data collection (Table 2) and the results of them were compared with measured data. Figure 4 and Table 3 present the results of empirical formulas. As could be seen in Table 3, most empirical formula do not provide suitable performance. Emiroglu formula with error indices (R2 = 64 and RMSE = 0.03) is the most accurate one among empirical formulas.

Fig. 4
figure 4figure 4

Results of empirical formulas versus measured data

Full size image
Table 3 Performance of empirical formulas
Full size table

Results of ANNs models

ANNs model development

Developing ANNs model as a common type of soft computing technique is based on data set. Therefore, the collected data set was divided into three groups as training, validation and testing. Validation data set was considered to avoid over-training of MLP model. The dimensionless parameters presented in Eq. (1), were desirable as input parameters for ANNs model development and discharge coefficient was considered as model output. Data selection for preparation of MLP model was carried out randomly. 70 % of total data set was considered for training, 15 % for validation and the rest (15 %) for testing. Designing the structure of MLP model is more based on the designer experience whereas recommendation of investigators who conducted similar researches is useful. In this paper, the recommendation of Parsaie and Haghiabi (2015c) was used. Preparation of ANNs model included the type of ANNs model, number of the hidden layer(s), number of the neurons in each hidden layer, defining suitable transfer function for neurons of hidden layer(s), defining suitable transfer function for output layer and learning algorithm. To obtain an optimal structure for MLP model, first, one hidden layer was considered and then, the number of neurons in hidden layer was increased one by one. Various types of transfer functions such as log-sigmoid (logsig), tan-sigmoid (tansig), linear (purelin), etc. were tested. This process continues to obtain a model with suitable performance. It is notable that Levenberg–Marquardt technique was used for MLP model learning. All stages of MLP preparation were conducted in Matlab software.

Results of MLP models

MLP model contains two hidden layers. The first hidden layer contains ten (10) neurons with tangent sigmoid (tansig) as transfer function and the second one contains five neurons with Log-sigmoid transfer function. The linear transfer function was considered as neuron of output layer. The structure of developed MLP model is shown in Fig. 5. Training of MLP model was performed with Levenberg-Marquat technique. 70 % of data set was used for training, 15 % for validation and the rest (15 %) was considered for testing the model. Performance of MLP model in each stage of development (training, validation and testing) is shown in Figs. 6, 7, 8 and to assess the performance of this model, error indices for each stage of preparation were calculated and presented in these figures. Figures 6, 7, 8) show that accuracy of MLP model is suitable for prediction of the \(Cd_{sw}\). In addition to calculation, standard error indices the error distribution were also plotted for the all data, which were used for training, validation and testing. To evaluate error density, error histogram was plotted. As could be seen in histogram, distribution of error is normal and more concentrated around zeros.

Fig. 5
figure 5

Structure of MLP model

Full size image
Fig. 6
figure 6

Performance of MLP model during training stage

Full size image
Fig. 7
figure 7

Performance of MLP model during validation stage

Full size image
Fig. 8
figure 8

Performance of MLP model during testing stage

Full size image

Results of RBF models

To assess the accuracy of RBF model to predict \(Cd_{sw}\) and compering its performance with MLP model, it has been attempted to hold similar conditions for model development. In other words, it has been attempted to hold similar number of the training, validation and testing data set. In addition, it has been attempted to hold similar number of neurons in input layer. The architect of RBF model is shown in Fig. 9. As shown in Fig. 9, the input layer neurons were considered equal to MLP model input later. Performance of RBF model during training, validation and testing model is shown in Figs. 10, 11, 12. As shown in these figures, performance of RBF model to predict \(Cd_{sw}\) is not suitable. Comparing performance of RBF model with MLP model in training, validation and testing stages shows that MLP model is more accurate.

Fig. 9
figure 9

Architecture of RBF model

Full size image
Fig. 10
figure 10

Performance of RBF model during training stage

Full size image
Fig. 11
figure 11

Performance of RBF model during validation stage

Full size image
Fig. 12
figure 12

Performance of MLP model during validation stage

Full size image

Conclusion

In this study, side weir discharge coefficient (\(Cd_{sw}\)) was calculated and predicted by empirical formulas and radial basis function (RBF) neural network along with multilayer perceptron (MLP) neural network. Results of this study indicate that Emiroglu formula is the most accurate one among empirical formulas. To achieve more accuracy in \(Cd_{sw}\) prediction, MLP model and RBF model were developed and to prepare MLP and RBF models, about 477 data sets related to \(Cd_{sw}\) were collected. Results of assessing performance of MLP show that MLP model has suitable performance to predict \(Cd_{sw}\). Results of RBF model development indicated the accuracy of this model is a little better compared to empirical formals. In general, performance of MLP model is much more compared to RBF and empirical formulas.