Abstract
Background: most methods of uncertainty quantification for digital image correlation are orientated towards the research environment and it remains difficult to quantify all of the uncertainty introduced along the measurement chain in an industrial environment. This gap in capability can become critical when physical tests are required for certification purposes. Objective: To develop and demonstrate an uncertainty quantification method that was independent of a specific DIC system, easily integrated with the measurement workflow, applicable at the measurement location and capable of capturing the contributions from all sources of uncertainty. Methods: an elegant new method utilises the calibration target, commonly used with DIC systems to evaluate their intrinsic and extrinsic parameters, through reference measurements before and after relative motion between the measurement system and the object of interest. The method is described and demonstrated for quantifying the field of uncertainty associated with maps of displacement and deformation in a large-scale industrial component. Results: The fields of uncertainty associated with measurements, using stereoscopic DIC, of x-, y- and z- displacement components during a compression buckling test on an aircraft fuselage panel are presented. The derived uncertainty has independently been corroborated along one axis by moving a calibrated translation stage. Conclusions: A new method has been proposed that allows the quantification of the fields of uncertainty arising from all sources when DIC measurements are performed on a large-scale object of interest in an industrial environment. The method requires no additional equipment and can be readily included in the workflow of a measurement campaign.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
In recent years, full-field optical methods for measuring shape, displacement and strain in components have gained in popularity in both research and industry as tools for design and development. Digital image correlation (DIC) has become ubiquitous because it requires only grey-scale images that can be acquired using relatively simple and low-cost equipment and it provides global distributions of the three-dimensional components of shape, displacements and deformation [1, 2]. DIC can be used to identify the location and amplitude of the maximum surface strain, to characterise crack growth behaviour and, via inverse analysis, to evaluate material properties for both elastic and plastic deformation as well as to understand the global behaviour of large structures.
However, the quantification of the uncertainty in DIC measurements is less advanced and less widely practised than the measurement technique. There is a considerable and evolving literature on the uncertainty in DIC measurements, including by Reu and his collaborators [e.g. 3, 4], Lavatelli et al. [5] and Thai et al. [6]. A number of different approaches have been investigated including noise floor determination, measurement of rigid body movements, error propagation and using physical reference materials [3]. However, most of these approaches are orientated towards the use of DIC in a research environment and it remains difficult to quantify all of the uncertainties introduced along the entire measurement chain, particularly when measurements in industrial environments are required. However, the need to quantify measurement uncertainty becomes greater in the industrial environment where physical tests are often conducted for certification purposes, or to provide data for the validation of computational models that are used to support decisions with socio-economic consequences. In these circumstances, a knowledge of the measurement uncertainties is required to assess the significance of differences between predictions and measurements [7, 8].
Outside of the controlled environment of a laboratory, the influence of conditions in an industrial environment, including the scale of the object of interest, the ambient lighting conditions and the difficulties associated with creating a suitable speckle pattern, poses a significant challenge to the quantification of the uncertainties in measurements of a real test object. In practice, these obstacles often lead to quantification of the uncertainties associated with a DIC system in the laboratory, for instance using a reference material to provide a continuous chain of comparison to a national standard [9, 10], which is assumed to be the minimum uncertainty achievable in measurements made in the industrial environment. This assumption leads to conservative judgments on the extent to which predictions represent a physical test and might result in additional costs when reliable predictions are unnecessarily rejected. Hence, a need was identified for a straightforward but reliable assessment of the uncertainty associated with measurements acquired using stereoscopic digital image correlation in an industrial environment. Based on advice from practitioners in industry, the aim was to develop a method with the following features: independence from specific DIC system or manufacturer; ease of integration with workflow in any measurement process; applicable at the measurement location; and capability to capture the contributions from all sources of uncertainty [11].
The method was developed in an international collaboration involving a DIC vendor, a major industrial user, two national laboratories and two university research groups. And, it is based on a series of measurements of the object of interest and the calibration target of the DIC system both before and after a relative rigid body motion between the measurement system and the object of interest. The method and its application to a 1 m2 panel from the fuselage of an aircraft are described in the following sections. The output from the method are fields of uncertainty for the x-, y- and z- displacement measurements in the field of view of the DIC system.
Measurement Uncertainty Quantification
The calibration of a stereoscopic DIC system provides the projection parameters of the DIC system together with an estimate of the uncertainty associated with the reconstructed x-, y-, z-components of the coordinates. However, an uncertainty quantification should be performed in industrial environments with the DIC system located in front of the object of interest and set-up to acquire the desired measurements.
The objective of the uncertainty quantification is to capture the effects of error sources associated with the object of interest and the environmental conditions. In addition, some DIC systems may use a different correlation algorithm for determining the positions of the features in the target compared to the one used for correlation of the speckle pattern on an object surface; and this is also accounted for in the uncertainty quantification. The uncertainty quantification is performed by introducing a rigid body motion between the measurement system and the object of interest. This motion is the same for the entire region of interest and is compared to the motion evaluated by the measurement system to yield a field of deviations which are a direct measure of the deformation uncertainty. This could be achieved by acquiring images of the region of interest on the test object before and after introducing the relative rigid body motion between the measurement system and the object; and then, by correlating the images to obtain a field of values that can be compared to the applied relative motion, to obtain the field of deviations. However, this requires detailed information about the applied motion; and, since it is difficult to introduce a known rigid-body motion of the required accuracy, it is preferable to measure the applied rigid-body motion. This is done by fixing the reference target, Fig. 1, in the field of view of the measurement system in front of the object and acquiring images of it before and after applying the motion. Consequently, the uncertainty quantification consists of four measurement steps sandwiching a physical movement and followed by a correlation step, Fig. 2, namely:
Flowchart for the uncertainty quantification which is conducted in front of the object of interest using a reference/calibration target and rigid body motion of the DIC system; the steps A to G are described in Measurement Uncertainty Quantification section
-
A.
Acquire images of the object of interest and use them to calculate the shape and position of the object;
-
B.
Place the reference target in the field of view in front of the object of interest and acquire images;
-
C.
Apply a rigid body motion to the measurement system. The amount and direction should be in the range of the expected deformation during the test;
-
D.
Acquire images of the reference target in the field of view in front of the object;
-
E.
Remove the reference target and acquire images of the object of interest and use them to calculate the shape and position of the object again;
-
F.
Correlate images from B and D to determine the rigid-body motion relative to the reference target;
-
G.
Transform the object coordinates from step A using the rigid-body motion from step F and compare with the object coordinates from step E.
Steps A and E both generate fields of measurements with x-, y- and z- coordinates of the object of interest and the difference between them can be compared quantitatively with the measured value of the rigid body motion from step F to yield fields of deviation for each component of displacement that are a direct measure of the corresponding uncertainties. In order to avoid introducing errors, it is important no changes are made to the DIC system between steps A and B, that the location of the calibration target relative to the object of interest must not change between steps B and D, and that the DIC system and its location relative to the object of interest are not changed during steps D and E.
Application of Measurement Uncertainty Quantification
Set‐up of Experiment
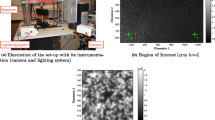
The use of the proposed method for quantifying the measurement uncertainty associated with using a stereoscopic DIC system was demonstrated during a measurement campaign conducted on a 1 m2 piece of an Airbus A-340 fuselage shown in Fig. 3. The piece of fuselage consisted of the aircraft skin riveted to a framework of stringers and frames. The skin had transverse and longitudinal joints that were also riveted. The edges of the panel parallel to the frames (top and bottom in Fig. 3) were bonded into U-shaped channels, or potting boxes, in order to allow it to be loaded in compression in an Instron 1346 testing machine, as shown in Fig. 4. The two printed speckle patterns provided by Airbus and Dantec Dynamics were respectively pasted to the left and right halves of the outside face of the fuselage panel. The size of speckle in the two areas was 2–3 pixels and 3–5 pixels approximately for the Airbus and Dantec Dynamics patterns, respectively, and the morphology of the patterns was different as shown in Fig. 4.
Set-up for measurement campaign showing panel from A-340 fuselage in test machine arranged for compression test and calibration/reference target in position with stereoscopic DIC system in foreground (top) and speckle patterns on sticky-backed plastic applied to outer surface (bottom) with close-up images of speckle pattern on left (top close-up) and right (bottom close-up) with the facet size illustrated (centre close-up)
A commercially available stereoscopic DIC system (Q-400, Dantec Dynamics GmbH) consisting of two cameras (Baumer VCXG-51 M) with 12 mm lenses (Schneider Kreuznach) and a LED light system was set up to view the outer surface of the panel as shown in Fig. 4. The stand-off distance of the DIC system from the panel was approximately 1.9 m with a distance of 0.64 m between the cameras giving a stereoscopic angle of about 18 degrees. The stereoscopic angle was smaller than the recommended value of 27 degrees [11] due to the constraints imposed by the pillars of the test machine which would otherwise obstruct the field of view.
Once the DIC system was set up to view the entire fuselage panel, a calibration was performed following the procedure described by the manufacturer and using a 50 × 50 cm calibration target with a chessboard pattern that had been engraved by a laser. The values of the calibration parameters are given in Table 1. The corners of the squares in the chessboard pattern formed the features used in the new method of uncertainty quantification. Their positions had been measured by an accredited laboratory with an uncertainty of 2.5 µm for the x- and y- directions, which defined the plane of the chessboard, and 5 µm for the z-direction, which was normal to the chessboard [12]. The size of these uncertainties is sufficiently small that they will not introduce a significant error into the method.
Image correlation of the speckle pattern was performed using a facet size of 23 × 23 pixels and a pitch of 17 pixels. No filters or smoothing were used in the calculations of shape and displacements. The results were presented in a Cartesian coordinate system with the x-axis along the front horizontal edge of the lower potting box, the xy-plane defined by a point on the front edge of the upper potting box, and the z-axis pointing from the lower potting box towards the DIC system.
Determination of Measurement Uncertainty
After performing the calibration process following the instructions provided by the vendor of the DIC system, a pair of stereoscopic images (image pair A) was captured of the object of interest in its unloaded state with the speckle pattern applied. Then, the reference target, which in this case was the vendor supplied calibration target, was introduced again directly in front of the fuselage panel, and fixed in position. A pair of stereoscopic images of the reference target (image pair B) were captured without adjusting the DIC system.
Subsequently, the DIC system was moved by a small amount to introduce a rigid body motion between the measurement system and the object of interest (step C) by moving its tripod perpendicular to and away from the fuselage panel. The rigid-body motion was perpendicular to the panel because the principal direction of deformation of the panel in the compression test was expected to be out-of-plane.
After moving the DIC system, a second pair of stereoscopic images (image pair D) were acquired of the reference target in its fixed position without adjusting the optical arrangement of the system. Finally, the reference target was removed from the field of view without disturbing anything else, a second pair of stereoscopic images of the fuselage panel (image pair E) were captured.
The applied rigid-body motion of the DIC system was calculated using the two sets of image pairs (B & D) of the reference target captured before and after the motion. Although the intention had been to move the DIC system in a direction perpendicular to the fuselage panel, the correlation of these image pairs revealed a translation of 4.53 mm in the x-direction (horizontal in-plane), 1.69 mm in the y-direction (vertical in-plane) and − 2.71 mm in the z-direction (positive away from the panel) with a small rotation of 0.23 degrees around the z-axis. These movements are of approximately the same order of magnitude as the expected displacements and hence the in-plane translations should not influence the results because the principal contributions to the uncertainty are independent of the displacements.
The calculated rigid-body motion, based on image pairs B & D, was applied to the coordinates of the object of interest which defined its shape as calculated from image pair A. These translated coordinates of the panel were compared to its measured coordinates obtained from image pair E following the rigid-body motion of the DIC system. The deviation between the translated and measured coordinates are shown in Fig. 5 and describe the uncertainty of the measurement system set-up to perform the measurement campaign, including errors arising from the DIC system, speckle pattern on the panel and environmental influences, such as ambient lighting conditions. The same data is combined in Fig. 6 to show the magnitude of the deviations as a distance from the three-dimensional shape of the fuselage panel and also shown in Fig. 7 as a ‘box and whisker’ plot.
Fields of deviations in millimetres of the x- (top), y- (middle) and z- (bottom) displacements plotted over the shape of the fuselage panel and potting boxes obtained by comparing the translated and measured coordinates of the fuselage panel. Above each plot the following statistical data is provided: maximum value, minimum value, mean, median, mean of absolute values and the standard deviation
Magnitude of the deviations in microns over the shape of the fuselage panel and potting boxes obtained by comparing the translated and measured coordinates of the fuselage panel from Fig. 5; the statistical data provided above the plot relates to: maximum value, minimum value, mean, median, and the standard deviation, all in mm
Box and whisker plot for the deviations in x-, y- and z-direction in millimetres including all of the measurement points of Fig. 5, showing the median (red line), mean (red cross), and intervals of 16–84 % (blue box) and 2–98 % (black error bars) of the distribution of deviations
The three-dimensional presentation of the data in Figs. 5 and 6 allow an assessment to be made about whether any systematic error is present, which does not appear to be the case in this example. It should be noted that the elevated lines of data running parallel to the x-axis in these figures represent the potting boxes at the top and bottom of the fuselage panel. It is clear from Fig. 5 that the fields of deviations for the y- and z-displacements are larger (absolute means of 0.015 and 0.018 mm, respectively) than those for the x-displacement (absolute mean of 0.007 mm). This is likely due to the small stereo angle in the DIC system which was set up with the cameras on a common line approximately parallel to the x-axis. However, the distributions of deviations are clearer in the box and whisker plot where it can be seen that mean and median values for the x-, y- and z-directions are approximately the same in absolute terms although the x-values are the closest to zero. However, the scatter in the values for the z-displacement is substantially larger with an expanded uncertainty [13] (\(2\sigma =42 \mu m\)) four times larger than the corresponding intervals for the x- (\(2\sigma =8 \mu m\)) and y-displacements (\(2\sigma =12 \mu m\)). It is worth noting that the form of the fields of deviations in Fig. 5 is similar to effects caused by heat waves as observed by previous investigators, e.g. [14]; however, there is no evidence available from our experiment to corroborate this observation.
The measurement campaign on the fuselage panel was then conducted as part of the Horizon 2020 Clean Sky 2 project, MOTIVATE [15] and a video is available of the process of capturing the data as described above [16].
Verification of Measurement Uncertainty
In order to verify the outcomes of the procedure described above, an alternative method was used to evaluate the measurement uncertainty using a speckled plate mounted on a single-axis motorised stage whose uncertainty of movement had been previously verified using an interferometer and found to be 8 μm over a travel of 50 mm with a systematic error of 0.2 μm/mm [12]. The motorised stage (PI 405. DGII, Physik Instrumente GmbH & Co. KG) was mounted in front of the fuselage panel with its direction of travel in the negative x-direction. The speckled plate of dimensions 115 × 115 mm was attached to the motorized stage with its plane parallel to the xy-plane and its speckled surface facing the DIC system, as shown in Fig. 8. The stage was moved in steps of 10 mm up to 40 mm in one direction followed by an additional 5 mm step in the same direction, before reversing the direction of motion applying 10 mm steps so that the steps in the two directions were interlaced, as shown in Fig. 9. At each step, three pairs of images were captured and the whole process was repeated four times so that a total of 12 image pairs were acquired at each position of the stage. In Fig. 9, an image is shown, collected at the farthest position, i.e. -45 mm from the starting position, together with the displacement measured from the starting position based on correlation of the images. The mean value of displacement for the plate obtained from the image correlation was subtracted from the known position of the stage to obtain a deviation based on each of the 12 image pairs for each position, i.e. 108 (= 12 repeats for 9 positions) values of deviation in total and these values are plotted in Fig. 10.
Graph (top) showing axial position of motorized stage as a function of time, stereoscopic pairs of images were acquired of the speckled plate mounted in the stage at each pause in the motion; and displacement (bottom) from initial position at the maximum excursion of -45 mm based on correlation of the images
The standard deviation is about 4µm for each stage position in Fig. 10 which is of the same order as the standard deviation from the DIC measurements of the object. The data in Fig. 10 imply that the uncertainty for a 10 mm movement is about 0.18 µm/mm based on fitting a regression line to all of the data.
Discussion
A new method has been described for quantifying the uncertainty in measurements made with a digital image correlation system in an industrial environment. The main features of the method are that: it can be easily integrated in the workflow of a measurement campaign; no additional equipment is required; the uncertainties associated with the whole measurement process are captured, including those arising from the object of interest and environmental conditions; and it provides values for the uncertainty in the x-, y- and z-displacements independently and for the entire measured surface of the object. The new method is based on the known geometric features in the calibration target used in the usual calibration of a DIC system to establish its projection parameters. A chain of traceability to the national standard for length can be established by measuring the position of the features in the calibration target using certified instrumentation; this is an essential feature when the intention is to establish the uncertainty in a set of measurements. The use of the calibration target also provides results that are independent of the object of the measurement campaign which provides a stronger basis for comparisons between datasets. In addition, the approach allows the full field of view to be considered rather than only the domain occupied by the test object. These factors will be important when more than one test object is to be measured and might not be positioned in precisely the same location in the field of view. Further, Reu [17] identified the importance of using a high-quality calibration target in order to reduce uncertainty in the projection parameters determined through the calibration process, and, hence, this approach will complement his recommendations.
Many investigations of errors in DIC measurements have used rigid-body motions [e.g. 18–21]; however, most of these investigations were laboratory-based and orientated towards enhancing knowledge of uncertainties and their sources. Whereas the method proposed here is designed to be implemented in an industrial environment and on a large scale, for example on full scale tests of aircraft structures [22], and to yield fields of uncertainties for the x-, y- and z-components of displacement measurements. Hence, the new method provides uncertainty values across the field of view of the DIC system rather than a single value for the whole field as in previous work based on reference materials [9, 10] or based on evaluating standard deviations or root mean square errors (RMSE) in measurements [e.g. 23, 24]. It incorporates error sources from the instrumentation, the environmental conditions and from the object of interest and its speckle pattern. The effect of the former has been investigated extensively [e.g. 3, 4] and the latter was modelled analytically and numerically by Lavatelli et al. [5], Su et al. [25] and experimentally by Badadani et al. [26] and Jee et al. [27]. While recently, Matthews et al. [28] have considered the influence of external or environmental factors on digital image correlation. However, the method presented above represents an attempt to capture the effect of all sources of uncertainty in measurements made in industrial environments using digital image correlation. Its applicability in a measurement campaign on a large-scale panel for the aerospace industry has been successfully demonstrated.
The method has been designed for use in an industrial environment where the object of the measurement campaign is likely to be large and hence it will usually be easier to move the DIC system rather than the object and calibration target. However, it is a relative movement that is required and so it is acceptable to move either the DIC system or the object and calibration target providing that the relative position of the object and target remain unchanged. The easier option was adopted in this demonstration, which was to move the DIC system. The DIC system was moved on its tripod after ensuring that the set-up was secure and rigid so that the calibration of the system was not disturbed. When a very small relative movement is required because the expected displacements of the test object are small, then it might be appropriate to include translation stages to ensure very small movements of the DIC system can be made reliably.
Developing an approach for use in industrial environments also motivated the choice of the calibration target rather than a ‘perfect’ speckled reference plate with a known minimum uncertainty that was substantially less than other sources of uncertainty. The design of such a speckled plate would be system dependent and necessitate its preparation for each test setup thus rendering it substantially less practical than a readily available calibration target. While in the demonstration a calibration target was employed which had been supplied with the DIC system by the vendor, any calibration target would suffice providing that the DIC software can determine the position of the features in the target. As this is a pre-requisite for every calibration target, it renders the approach independent of a particular calibration target. It is important that any errors in the feature positions of the calibration target are sufficiently small as to have an insignificant influence on the method; and, this was ensured in the demonstration by measuring the calibration target in an accredited laboratory which also provided traceability to the international standard for length. It is good practice to provide traceability and it will be a requirement for many measurement campaigns in industry, especially when the measurements are required to support regulatory cases.
The results from the application of the new method to a measurement campaign focussed on 1 m2 panel cut from an A-340 fuselage have been verified by comparison to those obtained using a single-axis motorised stage with a flat, speckled plate placed in the field of view of the DIC system. The results were found to be in good agreement. However, there are some restrictions associated with the new method, including that there is no relative movement between the measurement system and the object of interest other than the applied rigid body motion, and that the optical set-up of the measurement system is not altered throughout the process. If these restrictions are not fulfilled then an offset might be introduced into the measured uncertainties.
Conclusions
A new method has been proposed that allows the quantification of the uncertainty arising from all sources when DIC measurements are to be performed on a large-scale object of interest in an industrial environment. The method requires no additional equipment and can be readily included in the workflow of a measurement campaign. The method uses the calibration target employed in the usual calibration of a DIC system which provides traceability to the national standard for length, independence from the object of interest and uncertainty for the full field of view. The method has been demonstrated as part of the measurement campaign on a 1 m2 panel from an aircraft fuselage set up for a compression buckling test and yielded fields of deviations that characterised the uncertainties in the x-, y- and z-components of displacement measured over the entire surface of the panel.
References
Lava P, Cooreman S, Debruyne D (2010) Study of systematic errors in strain fields obtained via DIC using heterogeneous deformation generated by plastic FEA. Opt Lasers Eng 48(4):457–468
Sutton MA, Orteu JJ, Schreier H (2009) Image correlation for shape, motion and deformation measurements. Springer, Berlin
Reu PL, Toussaint E, Jones E, Bruck HA, Iadicola M, Balcaen R, Turner DZ, Siebert T, Lava P, Simonsen M (2018) DIC challenge: developing images and guidelines for evaluating accuracy and resolution of 2D analyses. Exp Mech 58(7):1067–1099
Fayad SS, Seidl DT, Reu PL (2020) Spatial DIC errors due to pattern-induced bias and grey level discretization. Exp Mech 60(2):249–263
Lavatelli A, Balcaen R, Zappa E, Debruyne D (2019) Closed-loop optimization of DIC speckle patterns based on simulated experiments. IEEE Trans Instrum Meas 68(11):4376–4386
Thai TQ, Hansen RS, Smith AJ, Lambros J, Berke RB (2019) Importance of exposure time on DIC measurement uncertainty at extreme temperatures. Exp Tech 43(3):261–271
CEN Workshop Agreement 16779 (2014) Validation of computational solid mechanics models. Comité Européen de Normalisation, Brussels
Dvurecenska K, Graham S, Patelli E, Patterson EA (2018) A probabilistic metric for the validation of computational models. R Soc Open Sci 5(11):180687
Patterson EA, Hack E, Brailly P, Burguete RL, Saleem Q, Siebert T, Tomlinson RA, Whelan MP (2007) Calibration and evaluation of optical systems for full-field strain measurement. Opt Lasers Eng 45(5):550–556
Hack E, Lin X, Patterson EA, Sebastian CM (2015) A reference material for establishing uncertainties in full-field displacement measurements. Meas Sci Technol 26(7):075004
International Digital Image Correlation Society, Jones EMC, Iadicola MA (eds) (2018) A good practices guide for digital image correlation. https://doi.org/10.32720/idics/gpg.ed1
Crosbie LJ (2018) Quantification of uncertainties in measurements using Digital Image Correlation (DIC), Master Thesis, Hochschule Ulm University of Applied Sciences, September 2018
JCGM 100:2008, Evaluation of measurement data — Guide to the expression of uncertainty in measurement, Joint Committee for Guides in Metrology (JCGM/WG 1)
Jones E, Reu P (2018) Distortion of Digital Image Correlation (DIC) displacements and strains from heat waves. Exp Mech 58:1133–1156
MOTIVATE, Matrix optimization for testing by interaction of virtual and test environments, H2020 Grant Agreement No. 754660 and Swiss SERI contract No. 17.00064, see https://www.engineeringvalidation.org/overview. Accessed 9 Feb 2021
https://youtu.be/YH6uDNPKO0c (Video Showing the process of Uncertainty Quantification). Accessed 9 February 2021
Reu PL (2013) A study of the influence of calibration uncertainty on the global uncertainty for digital image correlation using a Monte Carlo approach. Exp Mech 53(9):1661–1680
Wattrisse B, Chrysochoos A, Muracciole JM, Némoz-Gaillard M (2001) Analysis of strain localization during tensile tests by digital image correlation. Exp Mech 41(1):29–39
Schreier HW, Braasch JR, Sutton MA (2000) Systematic errors in digital image correlation caused by intensity interpolation. OptEn 39:2915–2921
Bergonnier S, Hild F, Roux S (2005) Digital image correlation used for mechanical tests on crimped glass wool samples. J Strain Anal Eng Des 40(2):185–197
Hild F, Roux S (2006) Digital image correlation: from displacement measurement to identification of elastic properties–a review. Strain 42(2):69–80
Littell J (2017) Large field digital image correlation used for full-scale aircraft crash testing: methods and results. In: International Digital Imaging Correlation Society. Springer, Cham, pp 235–239
Reu PL (2013) Uncertainty quantification for 3D digital image correlation. In: Imaging Methods for Novel Materials and Challenging Applications, Volume 3. Springer, New York, pp 311–317
Zappa E, Hasheminejad N (2017) Digital image correlation technique in dynamic applications on deformable targets. Exp Tech 41(4):377–387
Su Y, Gao Z, Zhang Q, Wu S (2018) Spatial uncertainty of measurement errors in digital image correlation. Opt Lasers Eng 110:113–121
Badadani V, Sriranga TS, Srivatsa SR (2018) Analysis of uncertainty in digital image correlation technique for strain measurement. Mater Today Proc 5(10):20912–20919
Jee C, Salata G, Nobes D, Duke K (2018) Investigating the effect of a speckle pattern on measurement uncertainty in a three-dimensional digital image correlation (3D-Dic) system, CSME Conference Proceedings. https://doi.org/10.25071/10315/35392
Matthews SJC, Jesson D, Smith P, Heliker M, Beavis L, James B, Livesey R (2017) Evaluation of external errors relating to portable use of Digital Image Correlation. In: Proceedings of iDICs 2017 Conference & Workshop. International Digital Image Correlation Society, Barcelona, Spain, available at https://epubs.surrey.ac.uk/848765/. Accessed 9th Feb 2021
Acknowledgements
The authors would like to acknowledge helpful discussions with Richard Burguete of the National Physical Laboratory, Ksenija Dvurecenska of the University of Liverpool and Eszter Szigeti of Airbus Operations Ltd. This research has received funding from the Clean Sky 2 Joint Undertaking under the European Union’s Horizon 2020 research and innovation programme under grant agreement No 754660 MOTIVATE and was supported by the Swiss State Secretariat for Education, Research and Innovation (SERI) under contract number 17.00064.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Ethical Statement/Conflict of Interest
There are no ethical issues associated with the research reported here and the authors declare that they have no conflicts of interest. The views expressed are those of the authors and not the Clean Sky 2 Joint Undertaking.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Siebert, T., Hack, E., Lampeas, G. et al. Uncertainty Quantification for DIC Displacement Measurements in Industrial Environments. Exp Tech 45, 685–694 (2021). https://doi.org/10.1007/s40799-021-00447-3
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40799-021-00447-3