Abstract
The present work introduces a different data processing strategy, proposed in order to improve sub-surface defect detection on industrial composites; in addition, a resume of thermal data processing with most common algorithms in literature is presented and applied with new data. A deep comparison between the common absolute contrast, DAC, PCT, TSR and derivative methods and a new proposed contrast mapping procedure is implemented. Thermographic inspection was done in reflection mode on a Glass Fiber Reinforced Plastic plate, with flat bottom hole defects. Thermal data computation method is found to be critical for simultaneous defect detection and automatic mapping, optimized to identify defect boundaries at specific depth, with help of accurate image processing, implemented in a Matlab GUI for a reliable and rapid characterization of internal damage. The new processing approach, the Local Boundary Contrast method, elaborates different contrast maps and facilitates recognition of damage extension. Tanimoto criterion and the signal-to-noise ratio method were applied as a criterion to assess defect detectability of various processing methods.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Non-destructive testing with active thermography involves verification of mechanical properties and material integrity [1, 2], investigating discontinuities and internal defects present in analyzed component [3]. The main advantages of IRT enhanced international interest for thermal inspection systems in several applications, i.e. the industrial, military defense, archaeological or medical fields [4,5,6,7]. IRT procedures provide accurate analyses that established these techniques as effective tools for real time monitoring of different structures, particularly in case of composite laminates [8,9,10]. Manufacturing, repair processes and in service load history could induce several flaw typologies in composite components, as delamination, diffused porosity, or fiber-matrix cracking [11,12,13]; interest on active thermographic methods is provided in numerous applications on large and complex composite surfaces [14, 15], for which wide inspected parts of elevated value, as for aeronautical parts, are easily detected by temperature response under thermal pulses with reliable results. The thermal sequence acquisition of temperature decay curve on inspected sample after pulsed heat induction and the post-processing analysis between regions of interest [16, 17], after a proper experimental setup, allows for damage detection in composites; image processing approaches and results are widely discussed [2, 4]. Since the IRT inspections are focused on rapid and real-time application in the production field, thermal-processing and software tools are continuously improved to overcome thermal NDE limitations [18, 19]. The main IRT challenge is represented by the automatic thermal processing of large data sets and the easily/reliable detection of all anomalies, avoiding false negative information.
In literature, several image processing techniques have been developed for active infrared thermography, successfully improved for defect detectability, subjected to suitable integration to other existing techniques. A simple classification [2] is based on image processing groups, such as thermal contrast techniques [20, 21], techniques based on transforms [22] and techniques using statistical methods [23]. Thermal contrast represents the main thermographic parameter in IR examinations and different computation methods are defined in literature [24]. Other important processing procedures include differential absolute contrast (DAC) or interpolated differential absolute contrast (IDAC) [25, 26]. On the other hand, Statistical methods include the well-established thermal signal reconstruction (TSR) approach, allowing reduction of temporal noise [27], methods based on derivative images [28], while new processing techniques based on transforms offer good results, as in the case of Pulsed phase thermography (PPT) [29] and the principal component thermography approach (PCT) [22, 30], developed to enhanced defect detection.
These well-established processing methods guarantee robust references for an innovative promising approach, a different contrast processing method, where defect boundaries are automatically visualized on modified thermal contrast maps, optimized to facilitate inspections on large areas even for small defects and developed for better defect shape reconstruction, using thermal contrast thresholds in similar way of ultrasonic c-scans. The main goal of this paper consists of improving and evaluating the proposed processing approach [31] implemented on different material, to be verified with respect to actual reference methods; the proposed algorithm is based on thermal contrast evaluation and subset calculation in a correlation zone, whose main goal consists of improving and evaluating the proposed approach introduced previously by authors on GFRP material, performing deep comparison with different well-established procedures, more suitable defect detection, reducing problematics in terms of cost and longer computing times.
Thermographic tests were conducted on GFRP plate with numerous flat bottom holes reproducing different size and depth of damage. A quantification of goodness through the Tanimoto criterion [32] and signal to noise ratio (SNR) [2, 33] was implemented both on the standard processing techniques (DAC, PCT, TSR, and derivative) and the proposed method. A simplified block diagram briefly summarizes the methodology selected in this work, as shown in Fig. 1, for data processing of GFRP specimen.
Materials and Methods
This work presents preliminary evaluation of thermal-image processing for thermographic ND controls inspect FRP component, to be compared with thermographic analysis, enhanced by accurate data processing.
GFRP Plate and Experimental Setup
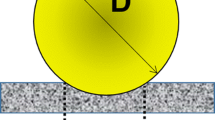
Actually, this paper estimates the inspection reliability and capability to Inspected parts in GFRP plate, since low cost composites are still improved and widely used for maritime, energy and other applications. This GFRP plate (Dim. 315 × 290 mm × [2 ÷ 20.6]) was laminated in vacuum bag and hand lay-up process, whose constituent characteristics are reported in Table 1. Defects have been realized with flat bottom holes and defect configuration is shown in Fig. 2. Different drill holes of 8 to 20 mm diameter allow to study the defect properties influence, as size or depth. Inspected plate surface is preliminary covered with matte black paint to eliminate reflections, especially for difficult inspection of smaller diameter defects.
Previous experimental campaigns defined the suitable set-up possibilities for a better characterization of defects on similar size GFRP plate [34] employing an appropriate arrangement of camera/specimen/lamps position, as shown in Fig. 3(a) [34].
As shown in Fig. 3(b), the thermographic setup includes four halogen 1000 W lamps, employed as thermal source, a signal generator with single square wave form to synchronize thermal pulse and acquisition using heating times described in Table 2; a FLIR 7500 M IR camera, with a FPA cooled detector, endowed with NETD 25 mK In-Sb sensor and image resolution of 320 × 256 pixels is coupled with proprietary PC connection. This experimental configuration proved to ensure uniform heating of the exposed surface, as demonstrated by experience and in previous heating tests carried out on a black body of equivalent size. Suitable heating times [for simplicity, denotated as tH] are determined in the range 12 ÷ 40 s to better identify defect depths in 2–6 mm range. Eight total tests are conducted in a controlled ambient temperature between 21 ÷ 25 °C, monitored by Humidity / Temperature Data Logger.
Image-Processing Techniques
In the following paragraph, the mathematical theory of processing techniques is reported.
Thermal contrast method
Absolute Contrast Analysis
Basically, the Source Distribution Image (SDI) consists in the manually selection of free-defects zone that is heated receives by the same thermal flow of corresponding inspected defective spot [13, 16, 35]. The absolute contrast parameter CA [°C] is defined by difference between temperatures of defective and free-defect zones, as the following formula:
Where the two terms TDZ and TIZ are temperatures in defected region and defect-free regions respectively, preliminary selected through an isothermal line in the first thermogram of cooling phase. Most of thermal processing algorithms are based on the SDI approach, therefore the authors implement the SDI processing algorithm in the MATLAB GUI environment for standard absolute contrast evaluation of GFRP defects.
Differential Absolute Contrast (DAC)
The CA results require the need to prior location of free-defect zone, strongly depending by operator selection. Processing technique using differential absolute contrast is based on the one-dimensional solution of Fourier’s diffusion equation for a pulsed thermal wave (Dirac delta function) [36]. The application of this processing technique enables to model the time evolution profiles of the specimen surface temperature, obtaining the values of the thermal energy transferred in each point of the surface.
Therefore, the processing technique of differential absolute contrast (DAC) is developed as SDI solution, enabling a suitable computation of intact reference zone based on the assumption that all pixel shows a similar thermal behavior as a free-defect reference area in the first few thermograms [25, 36]. According to previous simplification, the thermal response [°C] for a semi-infinite surface could be determined as function of thermal effusivity of material [e], of the absorbed energy [Q] is x is representative of depth [37]. The start point is provided by the assumption that a specific time t’, defined as the precise moment when first defective spot appears, produces a thermal contrast in the related thermogram with no visible defect. Consequently, the temperature of free-defect area [°C] is obtained at a selected t’ as
Therefore, the resulting differential absolute contrast (DAC) definition [°C] could be evaluated as a simple manipulation of term Q/e between the thermal response solution for a semi-infinite surface and equation (2) and computed as [38].
As function of time t’ and relative temperature T(t’). DAC contrast definition is extended for all pixel of thermal map processing and provide optimal result reducing the effects of the non-uniform heating on the surface. The limitation in the selection process of t’ is removed with the automation method designed for this technique (IDAC) [21].
Statistical techniques: signal reconstruction and derivative images techniques
The authors include three processing techniques based on statistical methods: the signal reconstruction or TSR, first and second derivative methods.
Thermal signal reconstructed (TSR) technique from polynomials provides significant sensitivity improvement, used especially in noise filtering and data reduction that increases the SNR performance [39, 40]. The mathematical origin of TSR technique comes from the Fourier’s one-dimensional heat-transfer equation on a semi-infinite surface previously subjected to thermal excitation (Dirac delta) [37, 39]. Basically, this thermal response equation of step-heating surface could be described as temperature evolution [°C] of free-defect zones in logarithmic scale with a slope of −1/2 and a constant of Q/e, by equation:
in the logarithmic domain to linearize data regardless of thermal properties. Thermal deviations from ideal slope provide an automatic recognition of defective zones [41]. Thermal signal reconstruction [°C] process the thermal evolution of a pixel using a polynomial of nth degree, fitting the polynomial to a logarithmic sequence performing with least squares [42] as follows:
However, the common experience demonstrates that temperature behavior shows a different response does not practically follow the semi-infinite response. The choice of small nth order provides satisfactory results in terms of reducing oscillations in the processed sequence and a fourth and fifth-order polynomial order effectively acts as a low pass filter to smooth the data without reconstructing the noise [4, 39, 43, 44].
Taking the derivatives of the raw signal is problematic when the signal possesses a high noise content. Polynomial thermal response provides also processing methods based on derivative images [45] that allow a proper facilitating detection of maximum contrast in early time [46]. The first and second derivative methods of the thermal sequence are respectively evaluated in the logarithmic domain as [39].
Transform technique: principal component thermography (PCT)
The Fourier transform represent the most robust and well-established decomposing mode of thermal signals to the phase-frequency space employing sinusoidal functions that indeed could not proper for representing either transient heating signals [22]. Principal component thermography (PCT) is a completely different technique, based on an eigenvector transform that applies an orthogonal transformation to acquired thermal data through singular value decomposition (SVD) method [47]. This processing technique provides many processing advantages to reduce high-dimensional data into fewer dimensions and to achieve compact data using orthogonal empirical functions (EOF) in a statistical representation of contrasts variations, associated with defects presence [22, 48]. Before applying decomposition, the 3D thermal matrix of the image sequence is reshaped into 2D array, whose columns and rows contain the temporal and the spatial dimension, respectively [49]. Thus, the original image sequence (Nx × Ny × Nt with Nt number of thermograms) is transformed in matrix A decomposition (M × Nt with M = Nx × Ny) as formula
Where the U columns represent the empirical orthogonal functions (EOF) describing the spatial variations, D is a diagonal matrix containing singular values of A present in the diagonal and VT columns represent the main components of the temporal variations [50].
A new thermal image mapping
The selected processing methods represent the reference established techniques for evaluation of IRT measurements for detect artificial defects in a GFRP component. As demonstrated in previous works [31, 51, 52], a recent image processing was proposed by authors as different approach that combines thermal contrast theory equations (1) and (4). The suggested processing method elaborates acquired thermal sequence in contrast images where defect boundaries are automatically visualized on modified thermal contrast maps [52], optimized to facilitate inspections on large areas even for small defects at critical depths and developed for better defect shape reconstruction, using thermal contrast thresholds in similar way of ultrasonic c-scans [53, 54]. The proposed method leads from the assumption that the processed image could show the intact area and defective areas in different surface location with similar threshold values, due to pre-heating accumulation or non-uniform heat distribution. Therefore, the anomalous thermal behavior could provide the damage detection using a different thermal contrast’s evaluation, the Local Boundary Contrast (LBC), through the difference between the temperature of central spot and the temperature of a pixels area that circumscribes the spot itself; obviously, in the ideal case LBC procedure should provide a null contrast value for the non-defective areas, however thermal values of free-defective contrast are measured in a range of few cents temperatures.
Therefore, the authors propose a different processing approach through an algorithm that processes temperatures of whole thermal map in iterative manner and returns a dissimilar contrast maps, without choosing an intact reference zone, inspired by sub-set correlation in reference zones of Digital Image Correlation (DIC) procedure [55, 56]. As shown in Fig. 4, for each (i, j)th pixel of a selected thermogram, the new procedure computes the absolute LBC contrast between two ROIs, defined as the mean temperature of an image subset IROI(i,j) and the mean temperature of its neighborhood NROI(i,j), in a similar automatization procedure proposed by other author [2, 57]. At a given time, t, the proposed local contrast [°C] for each pixel of general location [i, j] comes from the formula:
Where the TI (i, j) and TN (i, j) represents the temperature in a reference rectangular matrix zone (Dim. 3 × 3)] and all around [i, j]th calculation point matrix zone (Dim. p × p, with p > 3), respectively. The reference temperatures are evaluated around the inspected spot and provides to maximize different values when incorporate the pixels lying on defect border, leading to display local contrast variations, clearly distinguishing defect boundaries.
Results and Discussion
Image-Processing Results
Thermal contrast processing
Absolute Contrast
In Fig. 5(a), an example of thermal map analysis on GFRP plate allows to estimate heat distribution quality and presence of heat pre-accumulation; in the cooling phase more uniform temperature maps and local temperature gradients in the defected regions are observed. Since flat bottom hole sample is suitable for defect analysis in terms of depth and size, heat pre-accumulation appears only at depth around 1 mm (see Fig. 2(a)), disturbing thermal processing as illustrated in example Fig. 5(b).
The preliminary algorithm need selection of the reference intact spots, corresponding to previously selected defective regions, as indicated for defect D10 in example Fig. 2, which shows critical inspection zones, due to elevate depth or located at specimen borders, where thermal variation and gradients take place. In general, absolute contrast algorithm provides an interactive analysis procedure for selected defective and intact zones, iterated many times for all defects; Table 3 lists scheduled inspection results for various heating times. As presented in Fig. 6, typical processing contrast examples are illustrated in a similar manner for difd15 defect with 18 mm diameter and depth 10.8 mm (see Fig. 6(a)) and for difD27 defect with 8 mm diameter and depth 5.4 mm (see Fig. 6(b)) and relative reference intact zones.
The MATLAB GUI with routine elaborates the absolute contrasts and Fig. 6 shows examples of typical absolute contrast behavior of selected intact and defective areas, giving CA values from 0,15 °C up to 2 °C, indicating the defect intensity. Usually a different behavior of damaged or intact zones is easily identified, considering the maximum achieved temperature and the slopes of cooling phases during the test [22].
In terms of maximum absolute contrast, the optimal heating time might range for defects with different depth and size; however, the optimal heating time could be estimated for various groups of defects with similar characteristics and therefore multiple analysis must be performed for the whole plate; as shown in Fig. 7, diagrams report maximum absolute contrast values CA_MAX, showing respectively influence of heating time and defect depth for two example defects. General result is a significant maximum contrast convergence at a 25 s time distance, for most of defect types, as function of selected heating time. Therefore, the higher heating times provide higher values of absolute temperatures for free-defect and defective zones than those observed with lower heating times. It may happen also to observe Temperature difference between two selected spots decrease because higher heating temperatures determine pre-accumulation that reduces the contrast value and thermal decay between the two areas.
Differential Absolute Contrast
Higher depth and smaller dimensions represent a physical threshold for detection due to thermal profile similar to reference intact zone. The effective DAC approach is capable to reduce this problem and present the main advantage in terms of selecting different frame where defects at different depths could be emphasized in contrast respect to others.
Therefore, in order to improve analysis, the GFRP plate is considered in two sub-set images, associated to different defect disposition zone and manufacturing characteristics (as shown in Fig. 2). The Fig. 8(a) and (b) are selected on the base of previous assumption and the of inspected defects is maximized in the two sub-zones; in these Figures, defects d5, d10, d4, d9, d3, d8, d2, d7 are clearly distinguished. In particular, after other data processing, Fig. 9(a) and (b) better reveals the left-bottom zone’s defects in plate; in this case, defects d5, d4, d3, d2, D10, D20, D30, D9, D19, D18 are clearly distinguished.
Statistical Methods: TSR and Derivative Approaches
Several processing techniques could be applied to the cooling phase only, based on the assumption that the thermal profiles follow an appropriate linear decay on a double-logarithmic scale as predicted by the 1D solution of the heat diffusion equation, i.e. TSR, DAC, PPT [4, 58]. Therefore, based on the above observations regarding variation of surface diffusivity on defect detectability and data interpretation, all processing methods were applied to the whole thermal sequence (heating and cooling phases), i.e. 2000 thermograms for a heating time of 15 s (as reported in Table 2). This processing strategy brings interesting advantages such as that so more information could be available about different defects that could provide a detectable contrast during the heating phase. For instance, defect d10, d20, d30, d9, d19, d29 could be better distinguished very early during the heating stage when higher contrast level is appeared.
The suggested statistical methods provide an automation process for processing and final elaborated maps present suitable visibility improvements of defect detections and shape indications. The MATLAB codes for TSR and derivative processing elaborates the thermal acquired data in the resulting sequences, reported in Figs. 10 and 11. Defects d5, d4, d3, d2, D10, D20 and D30 are clearly distinguished in Figs. 10(b), (c), 11(b) and (c), while defects d5, d4, d3, d2, d10, d9, d8 and d7 are clearly identified in Figs. 10(a) and 11(a).
The TSR and the derivative images related to heating time 25 s and 30s are respectively displayed. The signal reconstruction and noise reduction with TSR technique proved to be beneficial in processing GFRP specimen; derivative images provided visible and consistent defect contrast enhancement, at least in a qualitative manner. The derivative technique is also able to reveal fiber orientation, highlighting sensitivity and resolution of first and second derivative images to detect superficial glass-fiber positioning, leading to some improvement of detectability thresholds, previously found for both absolute contrast and DAC method, as recognized in Figs. 10(b), (c), 11(b) and (c).
PCT Processing Method
The PCT approach shows mainly the detectability of flat holes depends on the selected choice of the first EOF reference images and indicative results are presented in Figs. 12 and 13. Results seem to offer solid data, but it was found the total time for sampling, useful to improve the PCT results and first seven EOF images seem to give better results.
Example maps of first seven orthogonal statistical functions are reported for acquired sequence employing thermal excitation of 25 s and 30s respectively. Reducing number of frames offers faster defects detectability, particularly in case of bottom defects. This promising analysis demonstrates that the consistent variance of first orthogonal statistical functions contain the most relevant data, although some variability and dispersion occur in the higher order of EOF and defect maps may result less precise and smooth [45].
In Fig. 13(a) and (b), second EOF images highlight slightly fiber orientation and manufacturing damage in laminate as seen in previous derivatives images, therefore these maps clearly provide the influence of thermal time excitation in terms of inspected defect. However, the second and third EOFs describe the characteristic variability in the thermal data for fourteen defects [d5, d4, d3, d2, d10, d9, d8, d7, D10, D20, D30, D9, D19]; several deeper defects are then analyzed in Figs. 13(b) [D8, D18, D28] and 12c [D8, D18, D28, D7, D17, D27], generally non-detected in previous image-processing methods, however effects of signal noise and possible cooling effect near plate boundaries may occur, providing some misjudgment of defects difficult to detect. The top and bottom right corner of each EOF images shows a remarkably defect scratching type of composite plies. In all cases, defects d11÷d20 appears with a very weak contrast, due to difficult inspection depth near the surface for IRT technique.
LBC approach procedure
As shown in Fig. 14(a) and (b), the processed maps obtained with new LBC method, conceived by authors, enable to increase the level of contrast between defective and undamaged areas, allowing a better identification and shape analysis of damage effects in the component. The LBC algorithm provides rapid and automatic contrast evaluation in the processed image, highlighting local contrast differences, as calculated from equation (9), able to identify defect boundaries in unique way onto the analyzed component. Following new imaging procedure indicated equation (10), all pixels of thermographic images are post-processed employing a MATLAB GUI, capable to highlight local temperature variation between two 2D-dimensional pixel matrixes in the computation point. Figures 8(a) and 14(b) could be directly compared as processed maps based on contrast techniques; the DAC image (as seen in Fig. 14(a)) for example and the proposed LBC image (as shown in Fig. 14(b)) of bottom hole Plate, obtained after 238 cooling seconds after heating pulse of 25 s. Similar results are observed for other cases.
First and second lines of detected defects with different diameter at a depth of 2.6 mm and 6.6 mm respectively are clearly distinguished in the contrast map. As observed, since longer heating times are required for a suitable inspection of defects at the higher depths, still an uncertain identification of less than 10 mm diameter defects is to be confirmed up to now, as for previous DAC, TSR and PCT analyses.
Defects denoted D10, D20, D19, d12, d13, d14, d15 (the four last defects at a deeper depth of 10.8 mm) are clearly investigated in Fig. 15, showing the method allows to better distinguish all of them, but the physical limit of higher depth remains and very small defects are still not visible. As any processing techniques, the LBC method is needed to be optimized, choosing appropriate dimension of subset correlation zone around [i, j]th point and rearranging the image scale, in order to define the LBC contrast numerical limits between 0 and 1. In Fig. 15, selected maximum contrast of 0.22 °C and minimum contrast of 0.02 °C represents the thermal difference threshold optimized for indicated defects in the zoomed image in Fig. 15. Defect d5, d4, d3, d2, d10, d9, d8 and d7 are simply detected. Although number of inspected defects is comparable to previous method, LBC processed maps show an optimized selected threshold of contrast limits to separate and localize thermal anomalies of damage areas, distinguishing in optimal way defect in shape and location. This LBC method combines main advantage of absolute and DAC contrast method, allowing an instantaneous thermal contrast mapping of IRT test controls.
Evaluation of Processing Results
Tanimoto criterion
Firstly, the Tanimoto criterion [20, 21, 59] is employed for rapid data comparison and for preliminary evaluation on suitable image processing technique. The Tanimoto criterion is dimensionless parameter evaluated as
where Nr. d., Nm. d., Nf. d. represent the number of real, missed and false reading defects respectively inspected on acquired images by different methods [60, 61]. Figure 16(a) shows a schematic representation with colored defect location considered in the calculation of the statistical parameter avoiding negative value of Tanimoto parameters. In this study, the pareto chart is evaluated for Tanimoto criterion of different processing approaches in the thermal acquisition of heating time 25 s; for each method, specific thermograms selected were selected because it corresponds to the best visibility time for a maximum number of defects [60]. The capabilities of the various processing methods are evaluated the defect detectability assessment, indicating a detection efficiency around 7 to 60% by the Tanimoto criterion. to compare the different approaches capabilities to detect artificial defect. The GFRP plate provide Tanimoto values TC ~ 40% appeared in the case of LBC and PCT processing analysis, but other procedures (DAC, TSR and derivate) present Tanimoto values not exceeding the 10%. Therefore, the LBC method allows a suitable ND detection in terms of higher number of inspected defects respect to other processing techniques, but the resulting low TC value is due to a higher number of false positives, due to the construction at different plate’s thicknesses.
Signal to Noise Ratio
However, the suitable defect detection and characterization should provide using the signal to noise ratio analysis, that enables to determine the more appropriate processing techniques in terms of accuracy of detectability [2, 33, 62]. The SNR of each defects is measured in decibels (dB) and determined as
Where Imean and Dmean are the arithmetic mean of all pixels inside the free-defective and the defective regions, respectively, while σ is the standard deviation of all pixels inside the free-defective.
The absolute contrast in equation (11) were computed between two ROIs of 5 × 5 pixel between a defective area and its neighborhood free-defect zone, establishing a dynamic decibel range [2]. For the specific test of 30s, the corresponding SNR results are listed in Tables 4, based on the processed image with maximum number of inspected defects with ID number identified in Fig. 16(a). Four group of defects are analyzed defects are at the same depth but with different dimensions, showing the defect parameters influence on the SNR values. In fact, SNR data depend on the defect dimension, varying from NAN or SNR < 0 if defects result undetected/ smaller to SNR > 0 in case of bigger and better identified defects [2]. In the case of the DAC, first and second derivative results, the values of the SNR parameter clearly depend on the defects depth and diameter, where the deeper and smaller d9 defect computes the worse signal to noise ratio (SNR < 0). However, D10 and D9 defects show minor SNR value that the corresponding D20 and D19 of lower diameter; this behavior could be determined from the position on the specimen, strongly influenced by the edge effect. It is observed that the PCT based data significantly enhanced the SNR of defects, where the differences in SNR between different EOF are low as compared; therefore, EOF-6 seems to provide the more suitable SNR values. The SNR depends by the applied processing technique, they will not be detected (ND) and the LBC approach seems to enhance the SNR of defects, so the further accuracy of detectability is improved. The defect depth seems less influence SNR values of proposed approach that shows a clear dependence; therefore, TSR approach provides higher value of SNR for D10, D20 and D19 defects.
Conclusions
This paper presented mainly a comparison between several experimental results of established and standard image processing techniques for NDA thermal inspection on composites, compared with a different algorithm, based on new proposed approach, applied to GFRP flat bottom holes’ plate. Preliminary results show it has been confirmed experimentally that a suitable set-up, with procedures and image-processing phase represent needful tools for pulsed thermography on composite elements. In the raw images, large and sub-superficial defects are easily observed; however, signal processing techniques such as TSR, DAC, PCT and proposed LBC allow to detect the smaller and deeper defects within certain limits. Some differences in performances are observed and the damage extension and location maps onto specimens result to be different in terms of graphic quality and visualization effectiveness.
The innovative processing approach was proposed to combine processing techniques based on thermal contrast evaluation and data management for better defect boundary identifications. The new algorithm provides improved defect maps that allow better detectability of numerous defects, even that similar detection limits are still present, in the same range of reference methods. The resulting LBC images showed that contrast-based data fused with advanced processing mode provide enhanced results in the same way as PCT approach and others, given evaluation results in terms the Tanimoto criterion values and SNR technique, applied for some defects analysis and with respect to other methods.
Abbreviations
- DAC:
-
Differential Absolute Contrast
- DIC:
-
Digital Image Correlation
- EOF:
-
Empirical Orthogonal Function
- FPA:
-
Focal-Plane Array
- GFRP:
-
Glass-Fibre Reinforced Plastic
- IDAC:
-
Interpolated Differential Absolute Contrast
- IRT:
-
Infrared thermography (IRT)
- NAN:
-
Not a number
- NDT:
-
Non-Destructive Testing
- NETD:
-
Noise Equivalent Temperature Differences
- PCT:
-
Principal Component Thermography
- PPT:
-
Pulsed phase thermography
- PT:
-
Pulsed Thermography
- SNR:
-
Signal to noise
- TSR:
-
Thermal Signal Reconstruction
References
Shull PJ (2002) Nondestructive evaluation: theory, Techniques and Applications. Marcel Dekker, New York
Hidalgo-Gato R, Andrés JR, López-Higuera JM, Madruga FJ (2013) Quantification by signal to noise ratio of active infrared thermography data processing techniques. Opt Photon J. https://doi.org/10.4236/opj.2013.34A004
Gade R, Moeslund TB (2014) Thermal cameras and applications: a survey. Mach Vis Appl. https://doi.org/10.1007/s00138-013-0570-5
Galietti U, D’Accardi E, Palumbo D, Tamborrino R (2018) A quantitative comparison among different algorithms for defects detection on aluminum with the pulsed thermography technique. Metals. https://doi.org/10.3390/met8100859
Vainer BG (2012) In: Meola C (ed) Applications of Infrared Thermography to Medicine. Chapter 3, Infrared Thermography: Recent Advances and Future Trends, Part II-Applications (Section 1: Medicine and Veterinary). Bentham Science, New York, pp 61–84
Carlomagno GM, Di Maio R, Fedi M, Meola C (2011) Integration of infrared thermography and high-frequency electromagnetic methods in archaeological surveys. J Geophys Eng. https://doi.org/10.1088/1742-2132/8/3/S09
Jiang Z, Hu M, Fan L, Pan Y, Tang W, Zhai G, Lu Y (2020) Combining visible light and infrared imaging for efficient detection of respiratory infections such as covid-19 on portable device. Comput Sci-Comput Vision Pattern Recognition. https://arxiv.org/abs/2004.06912
Montesano J, Fawaz Z, Bougherara H (2013) Use of infrared thermography to investigate the fatigue behavior of a carbon fiber reinforced polymer composite. Comp Struct. https://doi.org/10.1016/j.compstruct.2012.09.046
Schroeder JA, Ahmed T, Chaudhry B, Shepard S (2002) Non-destructive testing of structural composites and adhesively bonded composite joints: pulsed thermography. Comp Part A: App Sci Manu. https://doi.org/10.1016/S1359-835X(02)00139-2
Bai W, Wong BS (2001) Evaluation of defects in composite plates under convective environments using lock-in thermography. Meas Sci Technol. https://doi.org/10.1088/0957-0233/12/2/303
Naebe M, Abolhasani MM, Khayyam H, Amini A, Fox B (2016) Crack damage in polymers and composites: a review. Polym Rev. https://doi.org/10.1080/15583724.2015.1078352
Birt EA, Smith RA A review of NDE methods for porosity measurement in fibre-reinforced polymer composites. Insight-Non-destruct Test Cond Monit. https://doi.org/10.1784/insi.46.11.681.52280
Cheng L, Tian GY (2012) Comparison of nondestructive testing methods on detection of delaminations in composites. J Sensors. https://doi.org/10.1155/2012/408437
Avdelidis NP, Hawtin BC, Almond DP (2003) Transient thermography in the assessment of defects of aircraft composites. NDT E Int. https://doi.org/10.1016/S0963-8695(03)00052-5
Usamentiaga R, Venegas P, Guerediaga J, Vega L, López I (2012) Non-destructive inspection of drilled holes in reinforced honeycomb sandwich panels using active thermography. Infrared Phys Technol. https://doi.org/10.1016/j.infrared.2012.08.002
Danesi S, Salerno A, Wu D, Busse G (1998) Cooling down thermography: principle and results for NDE. Proc SPIE, Thermosense XX. https://doi.org/10.1117/12.304736
Almond DP, Angioni SL, Pickering SG (2017) Long pulse excitation thermographic non-destructive evaluation. NDT E Intern. https://doi.org/10.1016/j.ndteint.2017.01.003
Meola C, Carlomagno GM, Giorleo L (2004) Geometrical limitations to detection of defects in composites by means of infrared thermography. J Nondestruct Eval. https://doi.org/10.1007/s10921-004-0819-z
Popow V, Gurka M (2019) Possibilities and limitations of passive and active thermography methods for investigation of composite materials using NDT simulations. SPIE 10973. https://doi.org/10.1117/12.2518226
Maldague X (2001) Theory and practice of infrared Technology for Nondestructive Testing. John Wiley & Sons, Inc., Wiley Series in Microwave and Optical Engineering, Hoboken
Ibarra-Castanedo C, Maldague X (2013) In: Czichos H (ed) Handbook of Technical Diagnostics: Fundamentals and Application to Structures and Systems. Part II: Methods and Techniques for Diagnostics and Monitoring, Cap. 10: Infrared Thermography. Springer Science & Business Media, Berlin
Rajic N (2002) Principal component thermography for flaw contrast enhancement and flaw depth characterization in composite structures. Comp Struct. https://doi.org/10.1016/S0263-8223(02)00161-7
Zalameda JN, Rajic N, Winfree WP (2003) A comparison of image processing algorithms for thermal non-destructive evaluation. Proc. SPIE 5073. Thermosense XXV. https://doi.org/10.1117/12.485869
Madruga FJ, Ibarra-Castanedo C, Conde OM, López-Higuera JM, Maldague X (2010) Infrared thermography processing based on higher-order statistics. NDT E Int. https://doi.org/10.1016/j.ndteint.2010.07.002
Pilla M, Klein M, Maldague X, Salerno A (2002) New absolute contrast for pulsed thermography. In: Balageas D, Busse G, Carlomagno G (eds) Proc. of QIRT02. https://doi.org/10.21611/qirt.2002.004
Gonzalez D, Ibarra-Castanedo C, Pilla M, Klein M, Lopez-Higuera J, Maldague X (2004) Automatic interpolated differentiated absolute contrast algorithm for the analysis of pulsed thermographic sequences. Proc. Quan Infrared Thermograph. https://doi.org/10.21611/qirt.2004.014
Ramirez-Granados JC, Paez G, Strojnik M (2010) Reconstruction and analysis of pulsed thermographic sequences for nondestructive testing of layered materials. Appl Opt. https://doi.org/10.1364/AO.49.001494
Shepard SM, Lhota JR, Rubadeux BA, Ahmed T, Wang D (2002) Enhancement and reconstruction of thermographic NDT data. Proc Thermosense XXIV - Aero-Sense. https://doi.org/10.1117/12.459603
Ibarra-Castanedo C, Maldague X (2004) Pulsed phase thermography reviewed. Quan InfraRed Thermograph J. https://doi.org/10.3166/qirt.1.47-70
Hoult NA, Take WA, Lee C, Dutton M (2013) Experimental accuracy of two-dimensional strain measurements using digital image correlation. Eng Struct. https://doi.org/10.1016/j.engstruct.2012.08.018
Dattoma V, Panella FW, Pirinu A, Saponaro A (2019) Advanced NDT methods and data processing on industrial CFRP components. Appl Sci. https://doi.org/10.3390/app9030393
Vavilov VP, Bison PG, Grinzato EG (1996) Statistical evaluation of thermographic NDT performance applied to CFRP. Proc. SPIE 2766, Thermosense XVIII. An Int Confer Thermal Sens Imaging Diagnostic Appl. https://doi.org/10.1117/12.235396
Shrestha R, Kim W (2018) Non-destructive testing and evaluation of materials using active thermography and enhancement of signal to noise ratio through data fusion. Infrared Phys Tech. https://doi.org/10.1016/j.infrared.2018.08.027
Dattoma V, Giancane S, Palano F, Panella FW (2012) Non-destructive small defects detection of GFRP laminates using pulsed thermography. Integritet I Vek Konstrukcija-Struct Integ Life 12(2):109–116
Susa M, Maldague X, Boras I (2010) Improved method for absolute thermal contrast evaluation using source distribution image (SDI). Infrared Phys Tech. https://doi.org/10.1016/j.infrared.2009.11.008
Benitez H, Ibarra-Castanedo C, Bendada A, Maldague X, Loaiza H, Caicedo E (2008) Definition of a new thermal contrast and pulse correction for defect quantification in pulsed thermography. Infrared Phys Tech. https://doi.org/10.1016/j.infrared.2007.01.001
Carslaw H, Jaeger J (1986) Conduction of heat in solids, 2nd edn. Claredon Press, Oxford
Ibarra-Castanedo C, Bendada A, Maldague X (2005) Image and signal processing techniques in pulsed thermography. GESTS Int'l Trans Comput Sci Engr 22(1):89–100
Shepard SM, Lhota JR, Rubadeux BA, Wang D, Ahmed T (2003) Reconstruction and enhancement of active thermographic image sequences. Opt Eng. https://doi.org/10.1117/1.1566969
Omar MA, Zhou Y (2008) A quantitative review of three flash thermography processing routines. Infrared Phys Tech. https://doi.org/10.1016/j.infrared.2007.09.006
Sun JG (2006) Analysis of pulsed thermography methods for defect depth prediction. J Heat Transf. https://doi.org/10.1115/1.2165211
Balageas D, Roche JM (2014) Common tools for quantitative time-resolved pulse and step-heating thermography – part I: theoretical basis. Quantitative InfraRed Thermography J. https://doi.org/10.1080/17686733.2014.891324
Zheng K, Chang YS, Wang KH, Yao Y (2015) Improved non-destructive testing of carbon fiber reinforced polymer (CFRP) composites using pulsed thermograph. Polym Test. https://doi.org/10.1016/j.polymertesting.2015.06.016
Shepard SM, Hou J, Lhota JR, Golden JM (2007) Automated processing of thermographic deriviatives for quality assurance. Opt Eng. https://doi.org/10.1117/1.2741274
Ibarra-Castanedo C, González D, Klein M, Pilla M, Vallerand S, Maldague X (2004) Infrared image processing and data analysis. Infrared Phys Tech. https://doi.org/10.1016/j.infrared.2004.03.011
Shepard SM (2006) Understanding flash thermography. Materials Evalu 64(5):460–464
Marinetti S, Grinzato E, Bison PG, Bozzi E, Chimenti M, Pieri G, Salvetti O (2004) Statistical analysis of IR thermographic sequences by PCA. Infrared Phys Tech 46(1–2):85–91
Liu W, Huang J, Zhao Y (2006) Image fusion based on PCA and undecimated discrete wavelet transform. Int Conf Neural Inform. https://doi.org/10.1007/11893257_54
Rajic N (2002) Principal component thermography. Defense Science and Technology Organization Victoria (Australia) Aeronautical and Maritime Research Laboratory, Technical report DSTO-TR-1298. https://apps.dtic.mil/dtic/tr/fulltext/u2/a405857.pdf. Accessed 15 October 2020
Rajic N (2000) A quantitative approach to active thermographic inspection for material loss evaluation in metallic structures. Res Nondestruct Eval. https://doi.org/10.1080/09349840009409654
Dattoma V, Nobile R, Panella FW, Saponaro A (2017) NDT thermographic techniques on CFRP structural components for aeronautical application. Pro Struct Integrity. https://doi.org/10.1016/j.prostr.2017.12.045
Dattoma V, Panella FW, Pirinu A, Saponaro A (2020) Ultrasonic and thermographic studies for CFRP inspections with real and simulated defects. Mater Today: Proc. https://doi.org/10.1016/j.matpr.2020.02.915
Scarponi C, Briotti B (2000) Ultrasonic technique for the evaluation of delaminations on CFRP, GFRP. KFRP Comp Mater Comp Part B: Eng. https://doi.org/10.1016/S1359-8368(99)00076-1
Kas YO, Kaynak C (2005) Ultrasonic (C-scan) and microscopic evaluation of resin transfer molded epoxy composite plates. Polym Test. https://doi.org/10.1016/j.polymertesting.2004.07.002
Sutton S, Wolters MJ, Peters WH, Ranson WF, McNeill SR (1983) Determination of displacements using an improved digital correlation method. Image Vis Comput. https://doi.org/10.1016/0262-8856(83)90064-1
Dattoma V, Giancane S, Nobile R, Panella FW (2010) Fatigue damage evolution of fiber reinforced composites with digital image correlation analysis. Proc Eng. https://doi.org/10.1016/j.proeng.2010.03.142
Usamentiaga R, Venegas P, Guerediaga J, Vega L, Molleda J, Bulnes FG (2014) Infrared thermography for temperature measurement and non-destructive testing. Sensors. https://doi.org/10.3390/s140712305
Sfarra S, Theodorakeas P, Ibarra-Castanedo C, Avdelidis NP, Ambrosini D, Cheilakou E, Paoletti D, Koui M, Bendada A, Maldague X (2015) How to retrieve information inherent to old restorations made on frescoes of particular artistic value using infrared vision? Int J Thermophys. https://doi.org/10.1007/s10765-015-1962-8
Bossi RH, Giurgiutiu V (2015) Nondestructive testing of damage in aerospace composites. Polymer Compos Aerospace Ind. https://doi.org/10.1016/B978-0-85709-523-7.00015-3
Vavilov VP, Bison PG, Grinzato EG (1996) Statistical evaluation of thermographic NDT performance applied to CFRP. Int Soc Opticsd Photonics. https://doi.org/10.1117/12.235396
Sojasi, S., Fariba Khodayar, F., Lopez, F., Ibarra-Castando, C., Maldague, X., Vavilov VP, Chulkov AO (2015) Infrared Testing of CFRP Components: Comparisons of Approaches using the Tanimoto Criterion. Proceedings of NDT in Canada 2015 Conference, https://www.ndt.net/events/NDTCanada2015/app/content/Paper/27_Sojasi.pdf (2015). Accessed 15 October 2020
Shrestha R, Park J, Kim W (2016) Application of thermal wave imaging and phase shifting method for defect detection in Stainless steel. Infrared Phys Tech. https://doi.org/10.21611/qirt.2016.057
Funding
Open access funding provided by Università del Salento within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of Interest
The authors declare that they have no conflict of interest.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Panella, F., Pirinu, A. & Dattoma, V. A Brief Review and Advances of Thermographic Image - Processing Methods for IRT Inspection: a Case of Study on GFRP Plate. Exp Tech 45, 429–443 (2021). https://doi.org/10.1007/s40799-020-00414-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40799-020-00414-4