1 Introduction

During the last decades the growing use of non-standard employment has received extensive attention in the literature (see, e.g. Deakin et al. 2007; Eurofound 2020; European Commission 2010). Millward et al. (2000), for instance, report that in Britain the share of workers hired on the basis of temporary as well as part-time and self-employment contracts has increased since the 1980s. Keune (2013), Cappelli and Keller (2013) and Allmendinger et al. (2013) confirm similar trends in other countries.Footnote 1 While the rising incidence of non-standard employment is often associated with the firm’s need to cope with an uncertain and volatile market environment (Kalleberg 2011; ILO 2015), recent works document that firm-specific factors can play an important role as well. Arrighetti et al. (2021), in particular, show that the asymmetric distribution of managerial resources accounts for large part of the within-industry heterogeneity in the use of temporary and fixed-term contracts and dominates conventional context-based explanations.

In this paper we contribute to this line of research by studying how the heterogeneous use of non-standard employment is affected by the existence of interlocking complementarities between job design and labour contracts. We suggest that in presence of incomplete contracts and market uncertainty, firms face two alternative organizational equilibria: in one of them, job designs characterized by high routine task intensity are matched with an extensive use of non-standard employment; in the other, low routine task intensity is combined with a relatively small use of non-standard contracts. These complementarities exist because while non-standard contracts allow firms to adjust to external shocks, they also provide little incentive to invest in firm-specific knowledge. The cost associated with the lack of such knowledge is lower in firms with high routine task intensity, which are thus more likely to use this type of contracts. The opposite reasoning holds for the relationship between small use of non-standard contract and low routine task intensity.

We build a formal model of such interlocking complementarities and test the related predictions using linked employer-employee (LEED) data which combines two sources: (a) worker- and firm-level information taken from the SILER-ARTER system, which collects all mandatory communications firms from the Emilia Romagna region (Italy) submitted to regional administrative offices in the cases of major employment events (e.g. hiring, firing, changes of contractual status) between January 2008 and December 2017; and (b) accounting and financial information derived from the AIDA-BVD database, which contains disaggregated balance sheet and profit and loss statement information for all Italian firms between 2008 and 2017. This gives us an open panel with detailed firm- and worker-level yearly information, including contractual basis and occupation. Moreover, we match this data with the INAPP survey on Italian professions, which links occupational titles included in the Italian occupational classification (in turn linked to the International Standard Classification for Occupation, ISCO08) to 255 variables measuring either importance and complexity of tasks, knowledge and skills related to each occupation based on the O*Net content model. In this way, we build a firm-level index of routine task intensity based on the within-firm distribution of occupations. The empirical evidence (pooled OLS, Panel FE and IV) provides strong support for our theoretical predictions: routine task intensity and the use of non-standard contracts are indeed positively associated. This result holds under different model specifications and following a wide range of robustness checks, including panel and IV estimations.

We add to the literature in two distinct ways. First, we contribute to the stream of research that discusses the diffusion and impact of non-standard employment. In particular, many contributions investigate how this type of employment affects different components of firm performance such as job creation (Houseman 2001; Saint-Paul 1996), returns on equity (Lepak et al. 2003), productivity growth (Boeri et al. 2013; Ichino and Riphahn 2005; Valverde et al. 2000; Bardazzi and Duranti 2016; Lucidi and Kleinknecht 2010; Damiani et al. 2016), innovation and R&D (Kleinknecht et al. 2014; Reljic et al. 2021) as well as workers’ motivations (Blanchard and Landier 2002; Battisti and Vallanti 2013) and the propensity to accumulate firm-specific skills (Lepak and Snell 2002). Less attention, however, has been paid on the driver of non-standard employment in the first place. On this respect we expand on previous research by strengthening the idea that decision to rely on non-standard employment is not simply driven by the characteristics of the competitive context in which firms operate, but it is rather the consequence of broader evaluations concerning the organization of work, including the design of jobs and their complementarity with different contractual forms.

Second, we extend the growing literature on the design of organizations in presence of techno-institutional complementarities (Aoki 2001).Footnote 2 Pagano and Rowthorn (1994) develop one of the first formalization of organisational equilibria in presence of complementarities between technology and property rights. A similar approach has later been used to study the source of organizational diversity in many contexts such as: knowledge intensive industries (Landini 2012, 2013; Gurpinar 2016a, 2016b), automation (Belloc et al. 2020); corporate governance models (Barca et al. 1999; Earle et al. 2006; Nicita and Pagano, 2016; Landini and Pagano 2020). Recently, Dughera et al. (2021) exploit a framework based on multiple organizational equilibria to study the relationship between the firm’s technological and hiring strategies. In this paper we rely on these previous works to investigate how complementarities in the organization of work contribute to explain the heterogeneous use of non-standard employment among firms.

The remainder of the paper is organized as follows. Section 2 presents the theoretical model and the related predictions. Sections 3 describes the data and some initial descriptive evidence. Section 4 discusses the results. Finally, Sect. 5 comments and concludes.

2 The model

2.1 Setup and assumptions

Consider a situation where two managers \(M\) and \(N\), have to hire an (additional) employee \(E\) to run their business. The cost of labour, \(w>0\), is exogenously determined by market conditions and it is assumed to satisfy E’s participation and incentive compatibility constraint, so that E finds it rational to participate in the firm and exert the required level of effort when receiving a job offer.

To produce its output, the firm needs fulfilling a unit-measure of different tasks that may be more or less routinized, depending on the feature of the job-design. More specifically, we assume that the labour process is organized as to include a fraction \(0\le \phi \le 1\) of complex tasks and a fraction \(1-\phi \) of routinary tasks. In this specification, the higher (resp., lower) is \(\phi \), the greater the degree of task complexity (resp, routine-task intensity). The timing of a typical period is as follows.

At stage 1, \(M\) and \(N\) choose in different domains of labour organization taking each other’s decision as given. In this framework, complementarities may arise because of the managers’ inability to coordinate their actions. The plausible reasons behind this coordination problem are multiple, spanning from the classic bounded rationality argument developed by Milgrom and Roberts (1990b), to issues of costly communication analyzed in the team-theoretic tradition initiated by Marschck and Radner (1972). Following Milgrom and Robert’s (1990b: 513, 525) original idea, the organization can be understood “as an extensive system of complementarities [whose management] requires coordinated action between the traditionally separate functions of design, engineering, manufacturing, and marketing”. In this framework “only coordinated changes among all the variables will allow the firm to achieve its optimum”. However, when coordination is both costly and imperfect due to cognitive or informational constraints (Simon 1991), a multiplicity of self-sustaining organizational designs may simultaneously exist, each of which constitute a Nash equilibrium without necessarily ensuring Pareto-optimality. In our framework, \(M\) selects an optimal job design \(\phi \) that defines the task-complexity of E’s occupation, while N selects the type of labour contract \(C\), choosing whether to hire \(E\) on a permanent (\(C=P\)) or temporary basis (\(C=T\)), so that \(C\in \left\{P,T\right\}\). In the second stage of the game, E decides how intensively to learn the firm-specific skills required by her job. After that, she exerts the required level of effort, revenues are collected, and the game ends. Our working assumption is that the productivity of routine activities does not depend on E’s learning decision, while complex tasks need firm-specific human capital to be efficient.

During the production phase, the economy experiences an adverse technological shock with exogenous probability \(0<s<1,\) in which case, \(E\)’s productivity is driven to zero, regardless of the time allocation chosen by \(M\) and the type of contract chose by N.Footnote 3 To model the idea that labour flexibility allows firms to adjust easily to the outside economic environment, we assume that temporary workers can be dismissed at no cost, whereas permanent workers must be compensated with a severance payment that is exogenously set by the labour law.Footnote 4 To keep things simple, we assume that this indemnity is large enough so that firms find it rational not to dismiss their permanent workers upon the arrival of the productivity shock. This admittedly limiting assumption allows us to focus on a trade-off that is quite common in contemporary labour markets: although permanent contracts may promote organizational performance in several ways (in our framework, by fostering the accumulation of firm-specific human capital) flexible tenures allow firms to adapt to unanticipated changes in the outside economic environment. The game is solved by backward induction, starting from E’s human capital decision at stage 2, to M’s and N’s complementary choices at stage 1.

2.2 Stage 2: human capital investments

At stage 2, \(E\) works under the labour contract chosen by \(N\) and decides how intensively to invest in firm-specific skills. Borrowing from the field of educational psychology (Marton and Säljö 1976), we assume that E chooses between two learning strategies, respectively characterized as ‘deep’ (\(\lambda =1\)) and ‘surface’ (\(\lambda =0\)) learning. In the first mode, E adopts an affirmative learning attitude and chose to understand the full meaning of her assignment at a private cost \(k>0\). The second mode involves a learning performance of a minimally acceptable sort. The cost of surface learning is normalized to zero.

As in Kräkel (2016) and Dughera et al. (2021), we assume that learning reduces the cost of effort when \(E\) works for \(M\) and \(N\). In addition, and always in line with both in Kräkel (2016) and Dughera et al. (2021), we assume that \(E\) may be able to recover some of her human capital investments also when changing occupation, depending on the degree \(0\le p\le 1\) of portability (or generality) of the acquired skills. In this framework, the closer the parameter \(p\) is to unity, the more general are the capabilities that E acquires on the job. Formally, we assume that the cost of effort follows a two-point distribution over \([{e}_{l}, {e}_{h}]\), where \({e}_{l}\ge 0\) (resp., \({e}_{h}>{e}_{l}\)) indicates a low (resp., high) cost of effort. For future reference, define \({e}_{h}-{e}_{l}=e>0\).

As anticipated, the key difference between temporary and permanent contracts is that non-standard workers are immediately dismissed upon the arrival of a productivity shock. Hence, when N chooses \(C=T\), with probability \(s\) \(E\) is endogenously separated from \(M\) and \(N\). In this case, she enters the unemployment pool and further exits the latter with probability \(0<a<1\), where \(a\) is the job-finding rate measuring how tight the labour market is. When unemployed, E receives her outside option, which we normalize to zero. For the sake of simplicity, we assume that permanent workers have no incentives to leave their current employers, so that \(E\) remains with \(M\) and \(N\) along the entire duration of the game—see Table 1 for a summary of the parameters’ interpretation.

Table 1 Worker’s payoffs
Full size table

Given the above, we assume that E chooses \(\lambda \in \left\{\mathrm{0,1}\right\}\) to maximize:

$${V}_{P}=w-\left(1-\lambda \right){e}_{h}-\lambda {e}_{l} -k\lambda $$
(1)
$${V}_{T}=\left(1-s\right)\left[w-\left(1-\lambda \right){e}_{h}-\lambda {e}_{l}\right]+sa\left\{w-\left(1-\lambda \right){e}_{h}-\lambda \left[\left(1-p\right){e}_{h}+p{e}_{l}\right]\right\}-k\lambda $$
(2)

from which we derive the following Lemma, which summarizes \(E\)’s learning decision:

Lemma 1

When N chooses a permanent contract, \(E\) finds it rational to invest in deep-learning iff \(k\le \overline{k}\) . Similarly, when N chooses a temporary contract, \(E\) finds it rational to invest in deep-learning iff \(k\le \underline{k}\) , where \(\overline{k}=e\) and \(\underline{k}=\left[1-s\left(1-ap\right)\right]e\) .

Proof

See Appendix A.

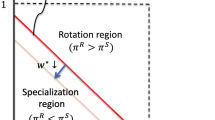
The key insight from Lemma 1 is that the interval of learning costs that induces E to invest in deep learning is larger under permanent contracts. The upshot is that there exist situations where permanent contracts generate learning incentives (and thus, productivity gains) that are missed under temporary contracts. More specifically, we have three cases—see Fig. 1 for a visualization:

  1. 1.

    If \(k\in \left[0,\underline{k}\right]\), E chooses \(\lambda =1\) regardless of the type of labour contract.

  2. 2.

    If \(k\in \left[\underline{k}, \overline{k}\right]\), E chooses \(\lambda =1\) when offered a permanent contract and \(\lambda =0\) otherwise.

  3. 3.

    If \(k\in \left[\overline{k},\infty \right]\), E chooses \(\lambda =0\) regardless of the type of labour contract.

Fig. 1
figure 1

Learning incentives

Full size image

In what follows, we shall restrict our attention to the second (and more interesting) of these cases, which is also the one which generates the possibility of multiple equilibria. In this scenario, the tradeoff between permanent and temporary contracts is straightforward. While the use of non-standard labour allows firms to better adjust to the outside economic environment, permanent contracts generate learning incentives that do not exist under more flexible tenures. The key strategic dilemma, in this case, is that between flexibility and human capital. For future reference, we define \({\lambda }_{P}=1\) and \({\lambda }_{T}=0\) as summarizing E’s learning decisions across the different contracts when \(k\in \left[\underline{k}, \overline{k}\right]\).

2.3 Stage 1: labour contracts and task complexity

At stage 2, \(M\) selects the fraction \(0<\phi <1\) of non-routinary activities that defines the task-complexity of E’s occupational assignment. Our working assumption, as anticipated, is that the productivity of routine activities is independent from E’s learning decision, while the latter is crucial in determining E’s performance at complex tasks. Several intuitions can be provided in support for this key, and yet reasonable assumption. First, by routinizing the labour process, managers define a series of step-by-step procedures that workers need follow, thus leaving little space for interpretation and creativity. In this framework, any piece of tacit knowledge accumulated by E is of little use, as the entire production process relies heavily on well-codified sources of organizational knowledge. Conversely, when tasks are less routinary and require workers to use their knowledge and engage in creative thinking, learning investments become crucial. Second, repetitive tasks likely require less social interaction among coworkers, so that soft and interpersonal skills cannot be profitably used in activities of this sort. In this framework, social bonding at the workplace is not as crucial as it is in the case of complex tasks, where good social relationships among organizational agents are key to promote team effort and collective problem solving. Given this, we specify E’s productivity as:

$${y}_{C}=\gamma \left(1-\phi \right)+\left[\alpha {\lambda }_{C}+\beta \left(1-{\lambda }_{C}\right)\right]\phi $$
(3)

where the subscript \(C\in \left\{P,T\right\}\), as before, indicates the type of labour contract and \(\alpha >\beta >\gamma >0\) are parameters that model the above assumptions. In addition, we assume that organizing the different activities performed by E entails coordination costs \(c\left(\phi \right)\) that increase (at an increasing rate) with the level of task complexity, so that \(c\left(0\right)>0\), \({c}^{^{\prime}}\left(\phi \right)>0\) and \({c}^{{{\prime}}{{\prime}}}\left(\phi \right)>0\). Assuming that \(M\) and \(N\) split the operating profit 50:50, the firm’s revenue is given by:

$${\Pi }_{P}=\frac{1}{2}\left[\left(1-s\right){y}^{P}-w-c\left(\phi \right)\right]$$
(4)
$${\Pi }_{T}=\frac{1}{2}\left[\left(1-s\right)\left({y}^{T}-w\right)-c\left(\phi \right)\right]$$
(5)

The decision rules that define the managers’ equilibrium strategy are as follows. When \(N\) chooses \(C=P\), \(M\) maximizes equation \((4)\) with respect to \(\phi \). Denote as \({\phi }_{P}\) the argument that maximizes \({\Pi }_{P}\). Conversely, when \(N\) chooses \(C=T\), \(M\) maximizes equation \((5)\) with respect to \(\phi \). Denote as \({\phi }_{T}\) the arguments that maximize \({\Pi }_{T}\). N, in turn, takes M’s decision as given and chooses the type of labour contract that provides the higher returns. Hence, applying a tie-breaking rule whereby \(N\) chooses to hire on a permanent base when s/he is indifferent between the two types of labour contracts, s/he chooses \(C=P\) when \({\Pi }_{P}\ge {\Pi }_{T}\) and chooses \(C=T\) when \({\Pi }_{T} >{\Pi }_{P}\).

2.4 Theoretical results: organizational equilibria

When \(N\) recruits E on a permanent basis, M maximizes equation \(\left(4\right)\) w.r.t. \(\phi \) Inserting the results of Lemma 1 in equation \((3)\) under the assumption that \(k\in \left[\underline{k}, \overline{k}\right]\), the first order condition for optimal profit is given by:

$$\frac{\partial {\Pi }_{P}}{\partial \phi }=\left(1-s\right)\left(\alpha -\gamma \right)-{c}^{^{\prime}}\left(\phi \right)=0$$
(6)

Denote as \({\phi }_{P}\) the degree of task complexity of E’s occupational assignment when N hires on a permanent basis.

Similarly, when \(N\) recruits E on a temporary basis, M maximizes equation \(\left(5\right)\) w.r.t. \(\phi \). In this case, the first order condition for optimal profit is given by:

$$\frac{\partial {\Pi }_{T}}{\partial \phi }=\left(1-s\right)\left(\beta -\gamma \right)-{c}^{^{\prime}}\left(\phi \right)=0$$
(7)

As before, denote as \({\phi }_{T}\) the degree of task complexity when N chooses \(C=T\). Given the assumption that \(\alpha >\beta >\gamma >0\), it is cleat that \({\phi }_{P}>{\phi }_{T}\), that is, that the level of task complexity selected by M is larger when N chooses \(C=P\). With these facts in mind, we can put forward the following Proposition, which summarizes the equilibrium outcome of the game and derives condition for the existence of multiple equilibria:

Proposition 1

Under the assumption that \(k\in \left[\underline{k}, \overline{k}\right]\) , M’s job-design and N’s hiring strategy are characterized by interlocking complementarities. In this case, a unique “complexity equilibrium” where low-routine-task-intensity is combined with the use of permanent contracts exists if \({\phi }_{T}\ge \widehat{\phi }\) , where \(\widehat{\phi }\equiv sw/\left(1-s\right)\left(\alpha -\beta \right).\) Conversely, a unique “routine equilibrium” where high-routine-task-intensity is combined with the use of temporary contracts exists if \({\phi }_{P}\le \widehat{\phi }\) , Finally, when \({\phi }_{T}<\widehat{\phi }<{\phi }_{P}\) , multiple equilibria may exist. In addition, \(\widehat{\phi }\) is increasing in the probability of adverse probability shocks.

Proof

See Appendix A.

The expression of the critical threshold \(\widehat{\phi }\) reported in Proposition 1 is illuminating as far as the relationship between the different types of labour contracts and the frequency of productivity shocks is concerned. Indeed, while the numerator measures the flexibility gains enjoyed by firms relying on non-standard labour (i.e., when \(s=1\), M and N can dismiss E, adjust their labour demand, and save the cost of labour \(w\)), the denominator captures the higher returns from firm-specific human capital enjoyed by firms using permanent contract (i.e., when \(s=0\), E’s productivity at complex tasks is greater under permanent contracts, due to the greater learning incentives they generate). While the numerator (resp., denominator) is increasing (resp. decreasing) in the arrival rate \(s\) of exogenous shocks, the denominator is increasing in the difference between \(\alpha \) and \(\beta \), which captures the productivity gains associated with learning. Hence, our model suggests that, everything else equal, temporary contracts are relatively more efficient in turbulent environments. On the other hand, permanent contracts are more convenient when firm-specific human capital is an important driver of firm’s competitiveness.

2.5 Welfare and Pareto-efficiency

In this section, we further analyze the situation characterized by multiple equilibria by studying the Pareto-efficiency of the latter. To do so, we compare M’s and N’s profit and E’s utility across the “complexity” and the “routine” equilibrium. To do so, we need to make specific assumptions on the functional form of \(c\left(\phi \right).\) To keep things simple, we assume that \(c\left(\phi \right)=\frac{1}{2}{\phi }^{2}\). Making use of equations \(\left(1\right)\), \(\left(2\right)\), \(\left(3\right)\), \(\left(4\right)\) and \(\left(5\right)\) the assumptions that \(k\in \left[\underline{k}, \overline{k}\right]\) and \({\phi }_{T}<\widehat{\phi }<{\phi }_{P}\), we can put forward the following Proposition:

Proposition 2

Under the assumption of multiple equilibria, E is always better off in the “complexity” equilibrium, while M and N are better off in the “complexity” equilibrium iff:

$$\frac{1}{2}{\left(1-s\right)}^{2}\left[{\left(\alpha -\gamma \right)}^{2}-{\left(\beta -\gamma \right)}^{2}\right]-sw\ge 0$$
(8)

In which case, the “complexity” equilibrium is Pareto-efficient.

Proof

See Appendix A.

According to Proposition 2, the “complexity” equilibrium is the only candidate to be Pareto-efficient for both \(E\), \(M\) and \(N\). Therefore, when condition \(\left(8\right)\) is satisfied but the system has gravitated towards the “routine equilibrium” due to adverse initial conditions or poor equilibrium selection, agents are stuck in what may be called an “organizational poverty trap”.

This can be used as a policy argument against the plea for deregulation that has characterized the public debate over the last couple of decades or so. If our reasoning is correct, in fact, the liberalization of temporary contracts not only has negative repercussions on worker well-being, which is somewhat unsurprising, but it also endangers profitability, conversely to what suggested by the advocates of the “flexibility thesis” (Saint-Paul 1996; Houseman 2001; Bassanini and Ernst 2002; Scarpetta and Tressel 2004).

Since the key determinant of the workers’ decision to accumulate firm-specific knowledge is the length of time they will remain within the firm, permanent contracts seem the only institutional arrangement capable of incentivizing human capital formation. The policy suggestion that can be derived is rather straightforward: institutional reforms aimed at improving labour market flexibility should be discouraged. In addition, given the interlocking character of institutional complementarities, the tipping from the less to the more efficient equilibrium requires interventions in labour market institutions to be coupled with the fine-tuning of organizational practices aimed at increasing task complexity. If either of the two policies is implemented without the other, the system may remain stuck in an “organizational poverty trap” due to self-reinforcing character of organizational equilibria.

2.6 From theory to data

Basically, our model predicts that each time a firm has to hire a new employee (or set of employees) there will be interlocking complementarities between the choice of the labour contract and job design. The existence of multiple equilibria characterized by strategic synergies between high-routine-task intensity and non-standard labour on the one hand, and low-routine-task-intensity and standard labour on the other, in fact, suggests a clear testable prediction: the share of temporary workers at the firm-level should be positively correlated with the degree of routine task intensity. Hence, our model not only provides a possible channel to explain the variability in the use of permanent workers among firms, but it also illustrates a plausible mechanism to understand why firms may vary their use of non-standard labor over time. Indeed, the decision to hire on a permanent basis is always conditional on the type of task-assignment chosen by the firm. We thus go and test this prediction using administrative data concerning manufacturing firms from one Italian region (Emilia-Romagna) by regressing the incidence of non-standard employment at the firm level against a measure of routine task intensity. In recognition of the fact that causality can be reverse, we refine our study by focusing on one direction of causality only, from job design to labour contract, and we then implement several robustness checks to rule out possible confounding factors. We want to explicit, however, that the nature of the exercise remains intrinsically correlational as we do acknowledge the existence of interlocking complementarities between these two dimensions.

Ideally, to analyze empirically our model’s prediction, we should have task-level data on the different activities performed by each employee in our sample. Unfortunately, the information we have is not that granular, as it contains indications on routine-intensity at the occupational level—for a detailed description of our data, see the next section. Hence, in the empirical approach described in what follows, we first calculate a series of measures that capture the degree of task-complexity of each occupation, and then, using these, we construct a routine-intensity-index and rank the firms in our sample according to the latter. The relationship between the task-based approach of our theoretical model and the occupation-based approach of our empirical analysis can be rationalized by considering the existence of a job-designer that first identifies a cluster of required tasks, and then, matches such tasks with an occupation that best fits the job duties. In this sense, the occupation becomes itself an indicator of how routinary/complex the job is.

3 Data

To test our hypothesis, we combine data from three different sources. The first source is represented by Sistema Informativo Lavoro–Emilia-Romagna (SILER), an administrative Linked Employers-Employees microData (LEED) system run by Italian regions along with the national government. SILER collects mandatory communications (i.e. Comunicazioni obbligatorie, in Italian) that all private employers (except for agriculture, fishery and forestry sectors) are required to submit for all occurrences concerning the employment relationships (hiring, termination, conversion and/or prolonged duration of fixed-term contracts). For our analysis we consider employment relationships associated with occurrences that took place in the manufacturing sector of the Emilia Romagna region from January 2008 to December 2017. An interesting feature of SILER is that once an employment relationship enters the system via a mandatory communication, all information concerning the individual worker is reconstructed going backward until the initial hiring. It follows that employment relationships that began before 2008 and ended or were transformed after 2008 are also included in the dataset. This feature, together with the relatively long time span covered by our data, allow us to reproduce rather closely the distribution of the stock of employees across firms.Footnote 5

For each employment relationship the available information includes data concerning the two parties and the characteristics of the relation as well. In particular, we retrieve data concerning the legal basis of the relationship (i.e. the type of contract), its date of start/end, the related occupational code (ISCO08) and the municipality in which the relationship was established. As far as employers are concerned, information includes the economic sector of activity (Ateco/Nace, 2-digit-level) and total employment at a firm-level, as measured in terms of full-time equivalent employees (FTE). In addition, we also retrieve entries concerning the employees’ working experience.

The second source of information in our analysis consists of the survey on Italian occupations (Indagine Campionaria sulle Professioni, ICP hereafter) run every 6 years by the Italian Institute for Public Policy Evaluation (Istituto Nazionale per l'Analisi delle Politiche Pubbliche, INAPP hereafter) in collaboration with the National Statistical Institute (ISTAT). The ICP is a very detailed dataset exploring 255 variables based on the O*Net content model and referred to knowledge, tasks and skills for more than 800 occupations as identified at the 6-digit-level in the Italian classification for occupation (named CP and in turn based on ISCO08 and its ISCO occupational codes). The first wave of this survey, the one used in our analysis, was held in 2007 and engaged some 16,000 workers in self-assessing the relative difficulty of the 255 variables on a 1–100 points scale when making reference to their job position.

Moreover, as the extent to which firms rely on NSE can be affected by other firms’ characteristics, namely performance and economic dimensions, we retrieve data from firms’ balance sheets included in the Aida-BVD online archive, that thus comes to constitute our third main source of information. We retrieve data concerning firms operating only in the manufacturing sectors in the Emilia-Romagna region and go on excluding those organizations with negative values of turnover and with no valid entries for all of the explanatory variables (see below, the ‘Controls’ subsection).Footnote 6 The resulting sample consists of a 10-years panel (i.e. 2008–2017) accounting up to 31,807 observations relative to 4508 firms.Footnote 7 We then go on and compare the sample obtained after this merge and cleaning procedure with census data deriving from Istat’s Archivio Statistico delle Imprese Attive (ASIA) using 2011 as a reference year to assess the overall representativeness of the sample itself. The distribution of firms across different manufacturing industries highlights two interesting facts. First, the overall representativeness in terms of frequencies across the different industries is preserved. Second, firms included in our sample account for nearly 8.5% of all the firms operating in the manufacturing sectors in the Emilia-Romagna region in the reference year. Taken together, these two highlights constitute a genuine endorsement for the representativeness of our sample (see Tables B.2 and B.3 in the Appendix B).

3.1 Dependent variables

Our dependent variable is represented by the share of non-standard employment (NSE) on total employment at a firm level, where employment is measured in FTE, i.e. based on the actual presence of each employee on the job in each year and weighted for full and part time working arrangements (0.5 if part-time, 1.0 if full-time). In this study, NSE is defined based on the contractual basis of the employment relationship. We thus consider employment as non-standard if the employee holds a fixed-term contract or is an agency worker and go on summing all FTE non-standard employees thus dividing this figure by the firm’s total employment FTE.

NSE shares are unevenly distributed across firms in the sample and while the overall average equals 12.8%, the median does not exceed 9.7%. However, 15% of firms in the sample do not use NSE at all whereas the top 1% of firms in the distribution extensively resort to it (i.e., NSE share accounting for more than 60% of total employment at firm level). In addition, the distribution asymmetry remains rather similar even after controlling for sectoral differences, as Fig. 2 shows. In this figure we report kernel distributions for firm-level deviations from the relevant sectoral means of NSE shares. In this case, the economic sector of activity is defined at the 2-digit level of the Italian classification ATECO (in turn based onto NACE international standard), thus identifying 22 different manufacturing industries (i.e., groupings 11, 13–33 of the 2-digit Ateco2007 code) for which we computed the relative mean NSE rates. The majority of firms shows NSE rates that fall below their relative sectoral mean whereas a persistent tail of the distribution suggests how a minority of firm, once again, massively relies on such contractual bases.

Fig. 2
figure 2

Kernel density estimate for non-standard employment, measured as the deviation at firm level from the sectoral mean of NSE

Full size image

All in all, the low diffusion of NSE and the detected within-industry heterogeneity suggests that individual and/or firm-specific characteristics may play a relevant role in shaping the extent to which firms differentiate in terms of NSE use. In fact, even when comparing firms operating within the same industry, we find a relatively high degree of heterogeneity that is impossible to explain by making reference solely to common/contextual factors, such as the competitive environment. For this reason, and following our theoretical model, in the next section we introduce a firm-specific routine task intensity index in an attempt to test whether the latter can indeed account for (at least) part of the observed heterogeneity.

3.2 Focal regressor

Our focal regressor is a firm-level Routine Task Intensity (RTI, henceforth) index. To compute the latter, we rely on the approach first proposed by Autor et al. (2003) applying a desk-based analysis on the 41 items included in the ICP survey (2007 wave) representing “general working activities” (i.e., tasks). In this case, we use such items as a proxy for measuring the relative complexity of the constituent tasks of each job title included in the Italian occupational classification (Classificazione delle Professioni in Italian, in turn based onto ISCO08 and ISCO codes) at the 6-digit level. We then divide tasks into 4 broad categories, applying the usual ALM two-way discrimination between routine and non-routine tasks on the one hand and thus between manual and cognitive tasks on the other hand. Following this taxonomy, routine tasks are the ones that “can be exhaustively specified with programmed instructions and performed by machines”. On the contrary, non-routine tasks entail “rules that are not sufficiently well understood to be specified in computer code and executed by machines”. The further above-mentioned discrimination is thus run between manual and non-manual tasks, the latter of which can be further divided between analytical, cognitive and interactive. Table 2 summarizes the 4 major tasks categories to which items from the ICP are allocatedFootnote 8 based on our desk analysis following ALM approach.

Table 2 Task families according to ALM approach
Full size table

For each of these 4 main categories we calculate a mean complexity score of each task in each 6-digit occupation (thus neglecting the ‘importance’ scale included in the ICP survey) to obtain the RTI following the standard procedure usually adopted in the relevant literature (Goose et al. 2014), explicated in Eq. (9):

$${RTI}_{o}=ln\left(\frac{{RM}_{o} + {RC}_{o}}{{NRM}_{o}+\left({NRA}_{o}+{NRI}_{o}\right)}\right)$$
(9)

where RM, RC, NRM, NRA and NRI are the average complexity scores, respectively, for all Routine Manual, Routine Cognitive, Non-Routine Manual, Non-routine Analytical and Non-Routine Interactive tasks in occupation o. Having attached a RTI to all occupations included at the 6-digit level ISCO code in the Italian classification for occupations, we go on and assign the relevant RTI to each employee of the Emilia-Romagna manufacturing firms included in the SILER dataset. In fact, SILER provides occupational information (ISCO code) for all employees included in the dataset and we thus use this information as a key to match workers with their relevant occupation RTI. Finally, we calculate the median RTI at a firm level, based on FTE weights. This index captures the median degree of routineness for the jobs available in a firm, in a given year.

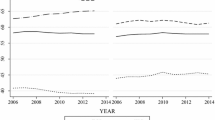
Figure 3 shows kernel density estimates for firms’ deviations from sectoral means of the RTI index. In this case, the distribution appears less skewed than the NSE one, as median and mean virtually coincide (both measuring about 0.35), even if the kernel analysis highlights how the left tail of the distribution decreases relatively more gradually compared to the right one. When reference is made to the evolution over time of the demand for routine tasks, Fig. 4 shows a diverging trend in the aftermath of the 2008 crisis as the demand for low routines tasks outpaced that of high routine ones, stabilizing from 2012 onwards. In this case, we have estimated the fractions of workers employed in firms characterized by a RTI, respectively, higher (RTI_HIGH) and lower (RTI_LOW) than the median RTI in the year 2008. The diverging pattern indicates that a polarizing effect took place between 2008 and 2012 as employment grew relatively more rapidly in low RTI firms than in high RTI ones or, alternatively, that the median RTI at firm level in the sample decreased over time up until 2012 at least. Cirillo et al. (2021) show that similar trends at the occupation level persisted also in the following years.

Fig. 3
figure 3

Kernel density estimate for RTI, measured as the deviation at firm level from the sectoral mean of RTI

Full size image
Fig. 4
figure 4

Evolution over time of shares of employment in low (RTI_LOW) and high (RTI_HIGH) routine jobs, 2008–2017

Full size image

In our view, firms’ median RTI represents an individual characteristic potentially capable to explain at least a part of the within industry heterogeneous use of NSE. Namely, we postulate that the higher firms’ RTI is, the larger firms’ NSE incidence will be. As a first preliminary exercise, we thus run an analysis of variance to test whether low, medium and high RTI firms showed significant mean differences in terms of NSE use.

Table 3 displays estimates from ANOVA, showing that a higher RTI brings about significantly larger shares of NSE within firms’ employment. As expected, firms characterized by low, medium, and high levels of RTI display increasing NSE shares with significant differences in means. These latter are reported in columns (1)–(3) of Table 3, while a standard t-test is available in column (4) reporting a significance level at 1%. Figure 5 depicts the same estimates showing the potential positive relationship between the two dimensions of interest.

Table 3 Analysis of variance, differences in means of non-standard employment across low, medium and high RTI firms
Full size table
Fig. 5
figure 5

Mean NSE in terms of FTE employees, by groups of firms (low, medium and high RTI)

Full size image

3.3 Controls

We include in our analysis several other variables that can account for the firms’ propensity to rely on NSE. The predominant view, both in the literature and in policy debates, is that the use of NSE is mainly due to contextual/structural factors, such as competitive pressure (Landini et al. 2020), technological volatility (Mayer and Nickerson 2005) and/or market uncertainty (Volberda 1996; Saint-Paul 1996, Kalleberg 2011). Our analysis thoroughly acknowledges for these possible explanations by including a composite set of covariates. In particular, alongside conventional fixed-effect controls, we consider two additional sets of variables. The first one includes measures for sales volatility and yearly sales growth rates. Sales volatility can be considered a firm-level proxy for demand uncertainty and is computed as the ratio between the average standard deviation and the average level of sales over the 10-year period for each firm i (for a similar approach see Devicienti et al. 2018 and Arrighetti et al. 2021). The sales growth rate is a firm-specific proxy for demand uncertainty as well and it is measured taking into account sectoral differences among firms, following Bianchini et al. (2018) and Alessandro et al. (2021). Namely, we use first differences of total sales (expressed in natural logarithms) after subtracting their annual sectoral average, where sectors are defined at the 2-digits level of the Italian ATECO classification. In this way, we can account for sectoral trends that are common across firms operating within the same industry, such as demand variability and inflation.

To control for technological volatility and production regimes, we include two measures representing production inputs endowments at a firm level. In fact, among the contextual drivers of the firms’ propensity to rely on NSE or, specularly, to select among internal and external work flexibility, the relevant literature stresses the importance of production regimes. For instance, knowledge intensive productions usually heavily rely on highly qualified/skilled workers and/or advanced manufacturing machineries and equipment. Accordingly, we use measures of labour productivity, workers’ average working experience at firm level and physical asset trends at a firm level as a firm-specific proxy of production regimes. Labour productivity is measured for each firm i at time t as the natural logarithm of the ratio between value added and total employment (FTE). Physical asset trend, on the other hand, is measured as the ratio between the value of total tangible asset at time t for firm i and the mean value of total tangible assets for firm i over the 10-years period.

In addition, we consider variables that can affect the use of NSE beyond conventional external and contextual factors. On this respect, Arrighetti et al. (2021a) document that the firm-specific endowment of managerial resources exerts strong influence on the firms’ propensity to rely on work organization based on numerical flexibility. This is particularly relevant for us as the distribution of such resources is likely to be highly heterogeneous both across and within industries. Therefore, we include in our analysis a proxy of the firm-level availability of managerial resources based on the span of control (for a similar approach see Arrighetti et al. 2021). In particular, we define our measure at the firm level as the natural logarithm of the ratio between the total number of manual workers (major groups 4–8 at the 1-digit level of the ISCO code) and the number of clerical workers, executives and managers (major groups 1–3 at the 1-digit level of the ISCO code). In theory, this latter ratio signals the overall cognitive workload that managers are required to perform in order to orchestrate the knowledge and activities of subordinates. When this ratio is high the coordination activity of managers is likely to be bound by cognitive constraints whereas a low ratio potentially signals a situation of resource slack.

Finally, we also include in our analysis a set of conventional firm-level characteristics, such as: a proxy for firm size measured as the natural logarithm of total employment (FTE); the natural logarithm of firm age as computed by year of foundation stated in the balance sheet; a proxy of the firm’s propensity to rely on outsourcing calculated as the natural logarithm of the ratio between total expenses for purchasing external services over total production costs. A summary of all variables’ descriptions and the relative main descriptive statistics is reported in Table 4.

Table 4 Variables’ description and descriptive statistics
Full size table

4 Estimation strategy

Our theoretical framework postulates a mutual dependency between NSE and the routineness of job design. From the empirical point of view this implies the existence of reverse causality between our dependent variable and the focal regressor, leading to the habitual endogeneity issues. For these reasons, and taking into account that a clear-cut causal identification goes beyond the aim of the paper, we organize the empirical analysis as follows. First, in our baseline estimates, we look for correlation between NSE and RTI. Then, we carry out some robustness checks where we put such correlation under stricter causal scrutiny. To design the robustness checks we exploit both the panel structure of our data and exogenous sources of variation in RTI.

The baseline estimates consist of a pooled OLS model over the period 2008–2017 adopting a stepwise approach to assess the fraction of variability of NSE potentially affected by median RTI at a firm level, as robust to different specifications controlling for four sets of covariates. Our pooled OLS model is thus as follows:

$${NSE}_{i,t}=\alpha +{\beta }_{1}*{RTI}_{i,t}+{\beta }_{2}*{X{^{\prime}}}_{i,t}+{\epsilon }_{i,t}$$
(10)

where \({NSE}_{i,t}\) is the share of workers hired with NSE contracts in firm i at time t, \({RTI}_{i,t}\) is the median RTI index for firm i at time t, \({X{^{\prime}}}_{i,t}\) is a horizontal vector of controls and the \({\epsilon }_{i,t}\) is the idiosyncratic error. When reference is made to controls, we only included time, industry and province dummies in the first specification thus gradually adding the three sets of covariates described in Sect. 3. Namely, the second specification includes contextual factors that are common to all firms operating within a same industry, such as sales volatility and sales growth. In the third specification we add controls representing production regimes (i.e., workers’ median working experience, physical assets trend, firm size) and span of control. Finally, we include additional firm-specific characteristics such as firm age and the propensity to outsource.

One issue that potentially affects our baseline estimates is existence of unobservable characteristics that are not adequately controlled for in the empirical model. The latter can be time variant or invariant and can lead to biased estimates. For this reason, the first robustness check that we implement is based on a panel estimation with firm fixed effects (FE). Such specification solves problems related to time invariant unobservable characteristics, whose effect is captured by the individual fixed effects included in the relative model. Our FE model is thus as follows:

$${NSE}_{i,t}={\alpha }_{i}+{\beta }_{1}*{RTI}_{i,t}+{\beta }_{2}*{X{^{\prime}}}_{i,t}+\theta *{T}_{t}+{\epsilon }_{i,t}$$
(11)

where, compared to Eq. (10), we include time dummies capturing common time trends (\({T}_{t}\)) and individual intercepts \({\alpha }_{i}\) capable to capture time invariant unobservable characteristics.

Nonetheless, there may be also time variant unobservable characteristics affecting the same relationship which are not taken into account in our FE model. To address this issue, we resort to an instrumental variable (IV) approach. Ideally, we would have to find an instrument capable to affect the dependent variable only indirectly, thus meeting the exclusion restriction requirements. Having to identify an instrument that directly affects the median firm-specific RTI but not the NSE share within the firm total employment, our choice falls onto the coverage of broadband fibers at a municipality level. The underlying assumption is that the availability of broadband coverage affects the costs of technology adoption at the firm level and it thus impacts on the firm’s demand of relatively routine vs. non-routine tasks.Footnote 9 At the same time, local availability of broadband connection should not directly affect the firm-level use of non-standard employment.Footnote 10 To build the instrument, we use open data from the Italian Ministry of Economic Development’s BUL project (acronym for Progetto “Banda Ultra Larga”, meaning ‘ultra-broadband project’ in Italian) that report the relative percentage of territory that is covered by broadband infrastructures (FTTH, FTTB and/or FTTDPFootnote 11) at a municipal level, for the year 2015.

Table 5 provides some empirical evidence that our exclusion restrictions are likely be met. Broadband penetration is negatively correlated with RTI as expected. This correlation is statistically significant. In addition, broadband penetration is not correlated with NSE shares at a firm level as the t-statistics associated with its pairwise correlation coefficient fails to reject the null hypothesis that the same coefficient is equal to zero. Incidentally, the same table shows a positive and significant pairwise correlation between RTI and NSE thus providing preliminary evidence in line with our postulated positive relationship between the two dimensions.

Table 5 Correlation matrix with Pearson pairwise correlation coefficients, year of reference: 2015; significance levels: 0.90 (*), 0.95(**) and 0.99 (***)
Full size table

5 Results

Tables 6 and 7 show estimates for the relationship between median RTI indexes and NSE shares at firm level. In particular, Table 6 reports estimates obtained from four different specifications (columns 1–4) of the same pooled OLS model applied to the whole sample of firms over the period 2008–2017. When moving from column (1) to (4) we progressively add sets of covariates as outlined in Sect. 4. Results show a positive and significant correlation between RTI and NSE at firm level, robust to all the different specifications. The evidence is in line with our expectations.

Table 6 Pooled OLS estimates, dependent variable: NSE share for each firm i at time t; SILER data, 2008–2017
Full size table
Table 7 Robustness checks
Full size table

As far as the other covariates are concerned, we find that sales volatility and sales growth show a positive and significant (across all the relative specifications) effect on the incidence of NSE on the total firm employment. Moving to production regimes factors, we find contradictory evidence of a positive relationship between labour productivity and NSE share as well as a negative relationship between working experience and NSE. While the latter evidence is in line with the prevailing explanations in the relevant literature (i.e., the use of NSE is relatively more abundant in less productive firms with possibly less experienced/tenured employees), the former one can only be understood within the framework of the core-periphery hypothesis (Kalleberg 2011; Atkinson 1984), according to which most productive and technologically advanced firms differentiate their labour force. In this way, a core group of highly skilled and highly productive workers is somewhat protected from demand fluctuations by a buffer of precarious and easily replaceable workers, making it possible for high productivity levels and relatively large NSE shares to coexist within a same firm. Somewhat in line with this explanation, firm size and firm age exhibit positive effects on NSE incidence, reinforcing the idea that relatively more productive, larger and well-established firms are more likely to promote an internal polarization of jobs. Physical assets trend, on the other hand, does not seem to play a relevant role in shaping NSE share. Finally, the span of control impacts positively on NSE use, in line with prior evidence that scarce managerial resources may represent an incentive to reduce coordination and operating costs via NSE (Arrighetti et al. 2021).

Table 7 reports the results of our robustness checks. Columns (1) and (2) show estimates from the same panel FE model as differently specified to account for different set of covariates. In this setting, a 1% increase in the relative routine task intensity at firm level is associated with an increase in the incidence of NSE on the total employment of about 10% on average. Compared to the estimates reported in Table 6, this result would suggest a downward bias in our baseline specification.Footnote 12

Columns (3) and (4) present estimates from the first and second stage of the IV, respectively. In this case, given that data concerning the instrument (i.e., broadband penetration) are referred to 2015 we restrict the analysis to that year only. In line with our expectations, in the first stage of the IV regression local broadband penetration is negatively associated with firm-level RTI. Moreover, when entered in the NSE regression, the coefficient of the instrumented RTI remains positive and significant. The magnitude of the coefficient roughly doubles compared to that assessed with alternative estimators, which can be due to the fact that the latter were assessing a yearly average effect over a 10-years period whereas in the IV the analysis is restricted to just one particular year. As usual in IV models, standard errors are inflated if compared with OLS and FE. Reassuringly, usual IV diagnostic tests for instrument relevance and exogeneity are passed.

As compared to pooled OLS estimates, results associated with the other covariates show minor differences. On the one hand, a positive impact of firm size, sales growth and propensity to outsourcing is still there even after implementing different estimators. The same holds true for the negative impact of workers’ experience and the inconclusiveness of the effect of physical assets trend on NSE incidence. On the other hand, we obtain mixed evidence for span of control, firm age and labour productivity. This mixed evidence, however, does not contradict the core-periphery explanation according to which relatively high productivity levels and NSE incidence may well coexist at firm level.

6 Conclusion

Our study sheds light on the interplay between jobs design and labor contracts. While most of the conventional approaches relate the use of non-standard employment to contextual factors such as the uncertainty and volatility of marked demand, empirical evidence reveals that (if anything) their impact is weak. Within the same competitive context, firm’s use of non-standard labor is highly heterogeneous, which suggests that firm-specific factors are important drivers too. In this paper we focus on the existence of interlocking complementarities between the nature of job design and the type of labor contract. These complementarities lead to multiple organizational equilibria: in one of them, firms with high incidence of routine jobs hire workers mainly via non-standard contracts; in the other, firms combine complex jobs with hiring based on standard contracts. When both such organizational equilibria exist, the one featuring non-routine tasks and standard employment may Pareto dominates the other, which implies that “organizational poverty trap” may exist.

Using linked employer-employee data for a large sample of manufacturing firms in the Emilia Romagna region (Italy) we provide strong support for our theoretical predictions, as far as the correlation between routine task intensity and non-standard employment is concerned. In fact, firms where the former is higher, which we measure using task characteristics at the occupation level, exhibit higher incidence of the latter. This relationship holds after controlling for several firm-specific and context-depended factors. The structure of the data allows us to deal with potential unobserved confounders panel fixed effects. Moreover, we exploit the availability of local broadband coverage to instrument the features of jobs design, purging the estimates from remaining endogeneity issues. In all these different specifications the use of non-standard employment remains positively and significantly associated with routine task intensity thus constituting a robust and consistent endorsement for our argument. Further research may be needed, however, to explore the causal nature of this two-way relationship.

Overall, the results of our study have interesting implications for both managers and policy makers. With respect to the former, the existence of interlocking complementarities between job design and labor contracts introduces the risk that firms end up in a sub-optimal organizational equilibrium. Managers need to be aware of this possibility and eventually envisage potential exit strategies. Given the nature of the equilibrium, such strategies need to be forcefully multidimensional and combine simultaneous changes in job design and labor contracts. A smooth coordination of decisions that are taken across different human resource management departments is a necessary condition for transition to a superior equilibrium to actually take place.

Our analysis contributes also to contemporary policy discussions about labor market regulation. During the last decades most of such debates focused on the introduction of some degree of contractual flexibility, which was mainly motivated by the firm’s need to cope with the changed conditions of the competitive environment. Recently, especially as a tool to fight the rising level of unemployment, the focus has shifted toward active labor market policies, aimed at providing workers with the right skills to find new jobs. For both such types of intervention, the result of our study are relevant. First, our results suggest that, far from being efficiency-enhancing, further flexibilization of the labor markets can increase the risk that firms get caught in “organizational poverty traps”. To avoid this outcome, policy makers should design interventions that while making non-standard employment less attractive, they also provide incentive to introduce more complex job designs within firms. Moreover, with respect to active labor market policy, the existence of a relatively large number of companies that combine routine jobs with non-standard employment implies that the demand for skilled labor should not be taken as given. Rather, it depends on how work is organized inside firms. To be successful, labor market policy should be complemented with other interventions aimed at favoring the adoption of less routinized and more protected jobs. The latter may include support to workforce training, team organization and employee participation.