Rate transient analysis for multilateral horizontal well in natural gas hydrate: superposition principle and reciprocity

Abstract

Due to high energy density, clean combustion products and abundant resources, natural gas hydrates (NGHs) have been regarded as an important clean energy source with the potential for large-scale development and utilization. However, pilot tests in NGHs show that their production rates are far below commercial needs. Multilateral well technology may lead to a solution to this problem because it can dramatically expand the drainage area of production wells. This paper presents the practical rate transient analysis for multilateral horizontal wells in NGHs. In developing solution to the diffusivity equation of multilateral horizontal wells in NGHs, the superposition principle and reciprocity are applied. We wrote the governing equation in cylindrical coordinates to describe the NGH flow process. We used the moving boundaries and dissociation coefficients to model the solid-to-gas transition process in hydrates. To obtain solutions for flow in hydrate reservoirs, we used Laplace transforms and the Stehfest numerical inversion method. Superposition principle and Gaussian elimination are applied to obtain the desired solution for multilateral horizontal wells. We validated our proposed model with a commercial numerical simulator. By performing sensitivity analyses, effects on production behavior of the number of branches, dissociation coefficient, radius of the region with dissociated hydrate, and dispersion ratio are determined. A synthetic case study is conducted to show the typical production behaviors.

1 Introduction

The transformation from traditional fossil energy to clean energy is a key technical approach to reduce climate warming and achieve carbon neutrality (Li 2021; Zhou et al. 2022). Figure 1 shows that, due to its high energy density, clean combustion products (only small amounts of CO₂ and water) and abundant geological resources, natural gas hydrates (NGHs) have become an important new clean energy source (Ma et al. 2023). The total amount of NGH resources in the world is 1 × 10¹⁵ to 1 × 10¹⁸ m³, which is twice the total carbon content of conventional fossil energy sources such as coal and petroleum (Wang et al. 2021). 99% of the world's identified NGH resources exist in marine sediments at depths of 300 to 2500 m (White et al. 2018; Chibura et al. 2022).

Fig. 1

The distribution of NGH resources in the world (Aghajari et al. 2019)

NGHs are stable at high pressure and low temperature (Zhang et al. 2022a). To break the temperature–pressure equilibrium conditions and separate CH₄ gas from NGH, the heating stimulation method, CO₂ displacement method and depressurization method are commonly applied (Lall et al. 2022; Dufour et al. 2019). However, the heating stimulation method and CO₂ replacement method are currently limited by technical difficulties such as cost, timeliness, and CH₄ separation. As Fig. 2 shows, the depressurization method is the major technique of NGH recovery; it has been applied in several pilot plant tests in Japan, China, Canada, and the United States (Aghajari et al. 2019; Konno et al. 2017). The maximum average gas production rate in Shenhu area of the South China Sea is 2.87 × 10⁴ m³/d, which is difficult to meet the industrial demand of 5 × 10⁵ m³/d (Ye et al. 2020). Multilateral wells and hydraulic fracturing are potential ways to increase the production rate of NGH. But due to the physical properties and high permeability of NGH reservoirs, hydraulic fracturing only slightly impacts long-term gas production performance (Feng et al. 2019). Multilateral wells can expand the drainage area of wells, allowing more dissociated gas to flow into the wellbore (Yin et al. 2010; Ye et al. 2022). Since NGH reservoirs are formed by the accumulation of sediments, multilateral well technology has cost and technology advantages (Zhang et al. 2022a). Furthermore, compared with multilateral vertical wells, the lengths of multilateral horizontal wells can further expand the drainage area.

Fig. 2

Location map of NGH depressurization production pilot tests in the world (Chibura et al. 2022)

Production modeling is a prerequisite to obtaining the maximum economic benefits of NGH (Sangnimnuan et al. 2018; Wan et al. 2022; Mabuza et al. 2022). Current production modeling methods are primarily divided into analytical methods and numerical methods. Roostaie and Leonenko (2020) developed analytical models including dissociated and undissociated zones to investigate the heat and mass transfer during vertical well extraction of NGH. Mao et al. (2021) developed a 3D numerical model of multilateral horizontal wells. The influence of well type and reservoir properties on hydrate production is quantitatively evaluated. Zhang et al. (2022b) used the numerical code HydrateResSim to demonstrate the impact of reservoir boundaries on the production of four-branch vertical wells. Ning et al. (2022) conducted a study on the combination of multilateral wells and reservoir reformation technology. The impact of reservoir reformation technology on multilateral well production is elucidated. Ye et al. (2022) systematically compared the impact of well type on the production performance of multilateral wells. The cluster horizontal well has been proven to have the greatest potential for NGH production. Zhang et al. (2023) utilized a thermal–hydrological–mechanical coupling model to study the geomechanical response of multilateral wells during the NGH production. Wang et al. (2023) developed a coupled numerical model of a four-branch horizontal well to describe the phase transition, two-phase flow, and mass transfer during NGH production.

To the best of our knowledge, current NGH production modeling research includes analytical, semi-analytical and numerical works on vertical wells, horizontal wells and multilateral vertical wells (Tsimpanogiannis et al. 2007; Roostaie and Leonenko 2020; Li et al. 2022; Zhang et al. 2022a). A numerical simulator can analyze the relationship between the temperature field, flow field, and stress field during the production of NGH. However, the recovery of NGH is accompanied by a phase transition process from solid to gas (Wan et al. 2022; Wang et al. 2023). This will make convergence of the numerical solution difficult and require more CPU time. In addition, the structure of a multilateral horizontal well is complex, which requires local grid refinement to describe its branch structure. This increases the difficulty of numerical simulation. Some previous works about analytical and semi-analytical models are mainly focused on the well testing process of vertical wells and multilateral vertical wells (Chen et al. 2022; Chu et al. 2023a). The pressure and production decline behavior of multilateral vertical wells are investigated respectively. The typical curves for production behavior only include decline curves analysis. This limitation allows previous models to only analyze production behavior under constant bottom hole pressure conditions.

To fill this gap, this paper proposes a semi-analytical model of a multilateral horizontal well during NGH recovery. The dissociation process of NGH is considered as a moving boundary with production time and dissociation coefficient. We used Laplace transforms and Stehfest numerical inversion methods to obtain analytical flow solutions, as well as the superposition principle to model the interference between various branches to obtain a semi-analytical solution for a multilateral horizontal well. We validated our model with a commercial numerical simulator, studied the factors that influence NGH production with a sensitivity analysis. The rate normalized pressure (RNP) is used to analyze production rate behavior under variable bottom hole pressure conditions. Finally, we performed a synthetic case study to show the typical production behaviors.

The innovations of this paper mainly include (1) a new model for multilateral horizontal wells is proposed; (2) the RNP is introduced to analyze the typical production behavior; (3) the typical flow stages for multilateral horizontal wells are clarified.

2 Methodology

2.1 Conceptual model and application condition

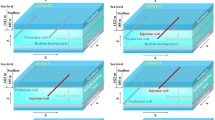
NGH on the seabed maintains a solid state under the pressure of the water above. The dissociation of hydrate from the solid state into natural gas is related to production time and reservoir pressure, which is the motivation for depressurization methods. Offshore drilling platforms occupy only a limited space. A multilateral horizontal well in the platform can effectively increase the drainage area between the wellbore and the reservoir. Figure 3a shows a schematic diagram of a multilateral horizontal well in the ocean for exploiting NGH. Hydrates in marine environments are usually recovered by ships or drilling platforms. In this limited surface environment, the potential of multilateral wells can be maximized. Figure 3b shows a multilateral well in a hydrate reservoir from a top view and a side view respectively. The multilateral well is simplified as a combination of points and lines. The multilateral well can have branches with the number of m. Each branch is approximated as consisting of N_m segments in the boundary element method. The angle, length and other attributes of each branch can be different. For the hydrate reservoir, the whole formation is divided into the dissociated region and the original formation. The pressure reduction during the production of multilateral wells will cause hydrates near the well to first decompose into natural gas in the dissociated region. As the pressure continues to decrease, the dissociated region in the near-well zone gradually expands. Other assumptions are as follows:

• (1) The single-phase gas flow obeys Darcy's law;

• (2) During the flow process, the effects of gravity and capillary force are ignored;

• (3) NGH reservoir has a uniform pressure distribution during the initial stage without recovery. When various wells are used for NGH production, the pressure distribution in the reservoir is no longer uniform;

• (4) The NGH reservoir is isotropic;

• (5) The NGH reservoir has impermeable boundaries in vertical direction;

• (6) The area of the dissociated region increases radially.

Fig. 3

a Schematic diagram of a multilateral horizontal well (modified from Wang et al. 2020) and b The physical model of a multilateral horizontal well in a hydrate reservoir. DR refers to the dissociated region

It is worth mentioning that using the pseudo-pressure method proposed by Xie et al. (2016) and Chen et al. (2018), the main conclusions obtained in this paper are still valid under two-phase flow conditions.

2.2 Development of flow model

According to the principle of mass conservation, the continuity equation in the NGH reservoir is:

$$\frac{{\partial \left( {\rho_\text{g} v_{x} } \right)}}{\partial x} + \frac{{\partial \left( {\rho_{g} v_{y} } \right)}}{\partial y} + \frac{{\partial \left( {\rho_\text{g} v_{z} } \right)}}{\partial z} = - \frac{{\partial \left( {\phi \rho_\text{g} } \right)}}{\partial t}$$

(1)

where $\phi$ is porosity, $\upnu$ is velocity, $t$ is time, $\rho_\text{g}$ is gas density, $x,y,z$ are coordinates in three-dimensional space. As Fig. 3b illustrates, the entire NGH reservoir is divided into two regions. Introducing Darcy's law from Eq. (40), the stress relation from Eq. (39) and the equation of state from Eq. (41), the governing equation in the dissociated region, in Cartesian coordinates, is:

$$\nabla \left( {\frac{{p_{1,f} }}{\mu Z}\nabla p_{1,f} } \right) = \frac{{\varphi \mu C_\text{t} }}{{k_{i} e^{{ - \alpha \left( {p_{i} - p_{1,f} } \right)}} }}\left( {\frac{{p_{1,f} }}{\mu Z}\frac{{\partial p_{1,f} }}{\partial t}} \right)$$

(2)

where $\mu$ is viscosity, $Z$ is gas-law compressibility factor, $C_\text{t}$ is total system compressibility, and $\alpha$ is stress sensitivity coefficient. Substituting the pseudo-pressure from Appendix B, the inner boundary condition for a producing well is:

$$\left( {r\frac{{\partial \psi_{1} }}{\partial r}} \right)_{r \to 0} = \frac{{3.684 \times 10^{ - 3} q_{\text{sc}} \mu B_\text{g} }}{{hk_{i} e^{{ - \alpha \left( {\psi_{i} - \psi_{1} } \right)}} }}$$

(3)

where $h$ is formation thickness and $B_\text{g}$ is gas volume factor. Differing from a conventional gas reservoir development process, there is a transition from solid to gas states in the recovery of NGH. Therefore, this phase transition process is related to the production time during constant-rate production. According to Goel et al. (2001), the front edge position of the phase transition region is a function of time.

$$R^{ * } = 2\sqrt {\frac{{\lambda t_{\text{D}} k_{i} }}{{\phi \mu C_{\text{t}} }}}$$

(4)

where $R^{ * }$ is front edge position and $\lambda$ is dissociation coefficient. Additionally, the flow rate defining the phase transition region satisfies Eq. (6).

$$- \frac{{\partial \psi_{1} }}{\partial r} - \frac{F}{M}\left( {\frac{{\partial \psi_{2} }}{\partial r}} \right)^{2} = 2ZTB_\text{H} S_\text{H} \frac{{\uppi k_{i} hL\mu p_\text{sc} }}{{FBq_\text{sc} T_\text{sc} }}\sqrt {\frac{{\phi k_{i} }}{{\mu C_{\text{t}} t}}} = \frac{\lambda }{\sqrt t }$$

(5)

$$F = \frac{{k_{i} hL}}{{3.684 \times 10^{ - 3} \mu^{2} B_\text{H} q_\text{sc} Z}}$$

(6)

where the subscript $\text{sc}$ refers to standard state, $S_\text{H}$ is NGH saturation, and $T$ is temperature, $M$ is mobility ratio. As Fig. 3b illustrates, the pressure at the interface of two regions satisfies the compatibility condition given by Eq. (8).

$$\psi_{1} \left( {R^{ * } ,t} \right) = \psi_{2} \left( {R^{ * } ,t} \right)$$

(7)

The initial conditions of the NGH reservoir are:

$$\psi_{1} \left( {r,0} \right) = \psi_{2} \left( {r,0} \right) = \psi_{i}$$

(8)

Substituting the definitions of dimensionless quantities from Appendix A and taking Laplace transforms, we can write the continuity equation as:

$$\frac{{\partial^{2} \psi_\text{1D} }}{{\partial r_\text{D}^{2} }} + \frac{1}{{r_\text{D} }}\frac{{\partial \psi_\text{1D} }}{{\partial r_\text{D} }} - \gamma_\text{D} \left( {\frac{{\partial \psi_\text{1D} }}{{\partial r_\text{D} }}} \right)^{2} = e^{{\gamma_\text{D} \psi_\text{1D} }} \frac{{\partial \psi_\text{1D} }}{{\partial t_\text{D} }}$$

(9)

The nonlinear term on the right side of Eq. (9) can be processed using the perturbation transformation method (Pedrosa 1986), and it can be given as:

$$\frac{{\partial^{2} \overline{{\xi_\text{1D} }} }}{{\partial r_\text{D}^{2} }} + \frac{1}{{r_\text{D} }}\frac{{\partial \overline{{\xi_\text{1D} }} }}{{\partial r_\text{D} }} = u\overline{{\xi_\text{1D} }}$$

(10)

Correspondingly, the boundary conditions and initial conditions are:

$$r_\text{D} \frac{{\partial \overline{{\xi_\text{1D} }} }}{{\partial r_\text{D} }} = - \frac{1}{u}$$

(11)

$$\overline{{\xi_\text{2D} }} \left( {r_\text{D} \to \infty ,u} \right) = 0$$

(12)

$$\overline{{\xi_\text{1D} }} \left( {R^{ * } ,u} \right) = \overline{{\xi_\text{2D} }} \left( {R^{ * } ,u} \right)$$

(13)

$$\frac{{\overline{{\partial \xi_\text{1D} }} }}{{\partial r_\text{D} }}\left| {_{{r_\text{D} = R^{ * } }} } \right. - \frac{1}{M}\frac{{\overline{{\partial \xi_\text{2D} }} }}{{\partial r_\text{D} }}\left| {_{{r_\text{D} = R^{ * } }} } \right. = \frac{{\lambda_\text{D}^{\prime } }}{\sqrt u }$$

(14)

Thus, the general solution is:

$$\overline{{\xi_{{1,f}\text{D}} }} = \frac{{VK_{1} \left( {\sqrt u } \right)I_{0} \left( {r_\text{D} \sqrt u } \right) + K_{0} \left( {r_\text{D} \sqrt u } \right)I_{1} \left( {\sqrt u } \right)}}{{I_{1} \left( {\sqrt u } \right) - KI \times K_{1} \left( {\sqrt u } \right)}} - \frac{{KI \times K_{0} \left( {r_\text{D} \sqrt u } \right) + I_{0} \left( {r_\text{D} \sqrt u } \right)}}{{u^{1.5} \left[ {I_{1} \left( {\sqrt u } \right) - KI \times K_{1} \left( {\sqrt u } \right)} \right]}}$$

(15)

where V is:

$$V = \frac{{\lambda_\text{D}{\prime} K_{0} \left( {R^{*} \sqrt {u\eta_{12} } } \right)}}{{\frac{u}{M}K_{0} \left( {R^{*} \sqrt u } \right)K_{1} \left( {R^{*} \sqrt {u\eta_{12} } } \right)\sqrt {\eta_{12} } - uK_{0} \left( {R^{*} \sqrt {u\eta_{12} } } \right)K_{1} \left( {R^{*} \sqrt u } \right)}}$$

(16)

where $\eta_{12} { = }{M \mathord{\left/ {\vphantom {M W}} \right. \kern-0pt} W}$ and $KI$ is:

$$KI = \frac{{K_{0} \left( {R^{*} \sqrt {u\eta_{12} } } \right)I_{1} \left( {R^{*} \sqrt u } \right) + {1 \mathord{\left/ {\vphantom {1 {M\sqrt {u\eta_{12} } I_{0} \left( {R^{*} \sqrt u } \right)K_{1} \left( {R^{*} \sqrt {u\eta_{12} } } \right)}}} \right. \kern-0pt} {M\sqrt {u\eta_{12} } I_{0} \left( {R^{*} \sqrt u } \right)K_{1} \left( {R^{*} \sqrt {u\eta_{12} } } \right)}}}}{{K_{0} \left( {R^{*} \sqrt {u\eta_{12} } } \right)K_{1} \left( {R^{*} \sqrt u } \right) - {1 \mathord{\left/ {\vphantom {1 {M\sqrt {u\eta_{12} } K_{0} \left( {R^{*} \sqrt u } \right)K_{1} \left( {R^{*} \sqrt {u\eta_{12} } } \right)}}} \right. \kern-0pt} {M\sqrt {u\eta_{12} } K_{0} \left( {R^{*} \sqrt u } \right)K_{1} \left( {R^{*} \sqrt {u\eta_{12} } } \right)}}}}$$

(17)

2.3 Superposition principle and reciprocity for multilateral well

Since the equation is linear, the reciprocity of different branch segments between multilateral horizontal well can be introduced using the superposition principle.

$$\overline{{\xi_{\text{D},ji}}} = \sum\limits_{l = 1}^{m} {\sum\limits_{k = 1}^{{N_{m} }} {\overline{{q_{Dkl} }} } } \overline{{\psi_{\text{1D,}ji} }}$$

(18)

where $q_{\text{D}kl}$ is flow rate item of the l-th segment on the k-th branch and $\psi_{\text{1D},ji}$ is pressure item of the i-th segment on the j-th branch. The dimensionless distance in the Cartesian coordinate system can be used to account for the influence of branch angles and positions:

$$r_{\text{D},ji} = \sqrt {\left( {x_\text{D} - x_{{w}\text{D}} + l\cos \theta } \right)_{ji}^{2} + \left( {y_\text{D} - y_{{w}\text{D}} + l\sin \theta } \right)_{ji}^{2} }$$

where $\theta$ is branch angle and $l$ refers to the length of each lateral segment. To obtain the unknown bottom hole pressure, we write the inner boundary equation for the constant rate condition as:

$$\sum\limits_{l = 1}^{m} {\sum\limits_{k = 1}^{{N_{m} }} {\overline{{q_{\text{D}{kl} }}} } } = \frac{1}{u}$$

(19)

From Eqs. (18) and (19), we express the system of linear algebraic equations as:

$$\left[ {\begin{array}{*{20}c} A & 0 & { - 1} \\ 0 & 1 & { - 1} \\ 1 & 0 & 0 \\ \end{array} } \right] \times \left[ {\begin{array}{*{20}c} {\overline{q} } \\ {\overline{\xi } } \\ {\overline{{\xi_{{w}\text{D}} }} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ 1 \\ \end{array} } \right]$$

(20)

where $A$ is the coefficient matrix between various segments and $\xi_{{w}\text{D}}$ is the dimensionless bottom hole pressure. For the final production solution, its relationship with the pressure solution in Laplace space can be given as Eq. (21) (Van Everdingen 1953).

$$\overline{q\left( t \right)}_{{w}\text{D}} = \frac{1}{{u^{2} \overline{{\xi_{{w}\text{D}} }} }}$$

(21)

The RNP and material-balance time was also used to analyze the obtained production solutions. The definition of RNP and its derivatives can be given as:

$$RNP = \frac{{p_{i} - \xi_{w} }}{q\left( t \right)}$$

(22)

$$RNP^{\prime} = \frac{\text{d}RNP}{{\text{d}\ln t_{\text{e}} }}$$

(23)

The material-balance time can be given as Eq. (25). The influence of wellbore storage effect and skin effect on production data can be considered through Eq. (26).

$$t_{\text{e}} = \frac{Q\left( t \right)}{{q\left( t \right)}}$$

(24)

where $Q\left( t \right)$ is cumulative production volume.

$$\overline{{\psi_{{w}\text{D}} }} = \frac{{S + u \times \overline{{\psi_{{w}\text{D}} }} \left( u \right)}}{{u\left\{ {1 + C_{D} u\left[ {S + u \times \overline{{\psi_{{w}\text{D}} }} \left( u \right)} \right]} \right\}}}$$

(25)

where $S$ is skin factor and $C_\text{D}$ is wellbore storage coefficient.

2.4 Solution procedure

Figure 4 shows the solution flow chart of the proposed model. After Laplace transformation and dimensionless treatment, the flow model of NGH production in multilateral horizontal well is composed of the continuity equation in Eq. (10), the inner boundary equation in Eq. (11), the outer boundary equation in Eq. (12), the interface equation in Eq. (13). The unknowns in the flow model include $\sum\nolimits_{i = 1}^{m} {N_{i} }$ pressures terms, $\sum\nolimits_{i = 1}^{m} {N_{i} }$ flow rate terms and the bottom hole pressure. The total number of unknowns is $2 \times \sum\nolimits_{i = 1}^{m} {N_{i} } + 1$. The linear algebraic equations include the general solutions in Eq. (18) and the inner boundary condition in Eq. (19). The total number of equations is $\sum\nolimits_{i = 1}^{m} {N_{i} } + 1$. In order to equate the number of unknown quantities to the number of equations, the $\sum\nolimits_{i = 1}^{m} {N_{i} }$ unknown pressure terms are considered to be equal to the bottom-hole pressure term. The numbers of unknowns and equations all are $\sum\nolimits_{i = 1}^{m} {N_{i} } + 1$ and the system becomes well-defined. The Gaussian elimination method is used to obtain the point source solution in a system of linear algebraic equations. Since the equations are linear, a multilateral horizontal well can be regarded as consisting of an infinite number of points. The superposition principle is used to consider the reciprocity between various points. The Stehfest numerical inversion method is chosen to obtain the production solution in time domain (Stehfest 1970).

Fig. 4

The calculation flow chart of the production solution for multilateral horizontal well in natural gas hydrate

3 Methodology validation

There are some simulators that can simulate the hydrate dissociation process. However, in addition to the dissociation of hydrates, the complex structure of multilateral wells also brings great challenges to the modeling process. Current commercial software capable of modeling hydrate dissociation is difficult to efficiently simulate multilateral wells. Thus, we validated the proposed model using the KAPPA commercial numerical simulator. Figure 5a shows that, a multilateral horizontal well and two concentric zones with different radii were established. The well length is 250 m and it has 4 branches. These branches are distributed at the same formation and are all perpendicular to the horizontal wellbore. The distance between two adjacent branches is 62.5 m and the branch length is 250 m. Other input parameters can be found in Table 1 and Fig. 6. The total number of grids in the numerical model is 14,620. Since the current commercial numerical simulator cannot describe the dissociation process, the NGH dissociation coefficient is specified as 0. Numerical data from commercial software and the proposed model solutions are compared in the Fig. 5b. The matching results show that the proposed model is reliable and accurate.

Fig. 5

a Schematic diagram of a multilateral horizontal well and two concentric zones with different radii and b The comparison of numerical data from commercial software and the proposed model solutions

Table 1 Input parameters of multilateral horizontal well and reservoir in the numerical validation

Fig. 6

The input gas volume factor, density, compressibility factor, viscosity in methodology validation

In summary, multilateral horizontal wells require traditional numerical methods using fine discrete grids to describe the gas flow in each branch. The number of grids and grid generation process affect the computational efficiency and stability of numerical methods. Compared with traditional numerical methods, the proposed meshless method only needs to be discretized at the inner boundary where the multilateral horizontal well is located. Thus, the proposed method has advantages in computational efficiency and stability.

4 Sensitivity analysis

4.1 Effect of number of branches

We increase the number of branches from 2 to 4 while held the length of the multilateral horizontal well constant. Figure 7 shows that the number of branches affects the early stages of production behavior of the multilateral horizontal well. As the number of branches increases, the early production rate also increases. In the earliest production stage, the production rate shows a linear upward trend while the number of branches increasing. This result indicates that interference between branches has not occurred at this time. The total drainage area is equal to the sum of the drainage areas of the individual branch. With production continues, branches interfere mutually and the drainage area of each branch coalesces with adjacent branches. Multilateral horizontal wells can increasingly be viewed as a whole. The influence of the number of branches on production gradually decreases. RNP and its derivative curves indicate that the number of branches affects the linear flow of multilateral horizontal wells. As the number of branches increases, the inter-branch interference becomes significant and the linear flow is gradually obscured.

Fig. 7

Effect of number of branches on production rate and rate normalized pressure of multilateral horizontal well

4.2 Effect of initial radius of dissociated zone

Solid NGHs can flow when they are dissociated into natural gas vapor. The initial radius of the region where the dissociated gas is located is called the initial dissociation radius $r$, as given in Eq. (26) and Fig. 3. The dissociated radius increases as the formation pressure decreases during depressurization production. The initial dissociated radii were chosen to be 300, 500, 800, 1000, 1500 m respectively. According to the production rate curve in Fig. 8, the change of radius affects only the middle stage of the rate curve. The production value is positively correlated with the dissociated radius. The affected starting and ending time of the production curve also increase with the dissociated region radius increases. The permeability difference between the dissociated region and the original formation leads to a response in RNP curves, which is similar to the closed boundary effect. The initial radius of dissociated zone is directly proportional to the effected period of the response and the linear flow.

$$r_\text{D} = \frac{r}{L}$$

(26)

where $L$ is the reference length and $r_\text{D}$ is the dimensionless radial distance.

Fig. 8

Effect of dissociated radius on production rate and rate normalized pressure of multilateral horizontal well

4.3 Effect of dispersion ratio

As given in Eq. (27), the dispersion ratio $W$ is the ratio of the fluid storage capacity between the dissociated region and the original formation. Figure 9 shows the impact of dispersion ratio on production behavior. The dimensionless dispersion ratios gradually increase from 2 to 100. Comparison of production curves shows that the change of dispersion ratios impacts production rates only slightly. The change of dispersion ratios mainly affects rates in the middle and late stages of production. As dispersion ratio increases, production rates during middle and late stages also increase. In addition, the change in production rate is time dependent. As production time increases, this rate increases first and then decreases. From the flow stage shown by RNP curves, the dispersion ratio affects both linear flow and the convex effect brought by moving boundaries. The dispersion ratio is proportional to the duration of linear flow. As the dispersion ratio increases, the convex effect gradually disappears.

$$W = \frac{{\left( {\varphi C_{\text{t}} } \right)_{1} }}{{\left( {\varphi C_{\text{t}} } \right)_{2} }}$$

(27)

Fig. 9

Effect of dispersion ratio on production rate and rate normalized pressure in multilateral horizontal wells

4.4 Effect of dissociation coefficient

Dissociation coefficient $\lambda$ in Eq. (28) represents the ability of a unit volume of solid NGH to dissociate into gas. In the proposed model, the dissociation coefficient also affects the speed of front edge movement of the phase transition region. The production curves of multilateral horizontal wells with different dissociation coefficients are plotted in Fig. 10. The results show that the change of coefficient mainly affects the middle and later stages of production curves. As the dissociation coefficient increases, the production rate in the middle and late stages also increases. In addition, the influence of the coefficient on rate also increases with the increase of the dissociation coefficient. When the dissociation coefficient increases from 0.00001 to 0.0001, stages of the rate curve are most affected. However, as the dissociation coefficient increases from 0.01 to 0.1, the affected region is concentrated in the middle and late stages of the curve. The change of production rate in the middle stage is larger than the change in the later stage. The dissociation coefficient also affects the convex effect caused by moving boundaries. As the dissociation coefficient increases to 0.1, the dissociation rate of hydrate into natural gas becomes fast enough. The dissociation zone occupies most of the reservoir through which the pressure response has propagated.

$$R^{ * } = 2\sqrt {\frac{{\lambda t_\text{D} k_{i} }}{{\phi \mu C_{\text{t}} }}}$$

(28)

Fig. 10

Effect of dissociation coefficient on production rate and rate normalized pressure in multilateral horizontal well

5 Synthetic examples

5.1 Parameter preparation

Due to the lack of actual data on NGH production using multilateral wells, a synthetic case was used to demonstrate typical production behaviors. As shown in Table 2, the input parameters of the synthetic case include reservoirs, wells and gas hydrates. Although the data in this case are not explicitly targeted, some of the input model parameters are derived from actual NGH in Nankai Trough. The synthetic NGH reservoir is assumed to have a reservoir thickness of 30 m. The porosity and permeability for the synthetic NGH reservoir are 0.43 and 800 mD respectively. The investigated multilateral well is a horizontal well with four mutually perpendicular branches. To reduce model uncertainty, the length of each branch is set to 250 m. The length of the horizontal wellbore is chosen as 300 m.

Table 2 Input reservoir and well properties in the synthetic examples (parameters sources include Zhu et al. 2020; Yu et al. 2019; Sun et al. 2016; Chen et al. 2022)

5.2 Typical production behaviors

The proposed model is chosen to obtain typical production and RNP behaviors of hydrate production in multilateral wells. The composite two-zone model is used to simulate the dissociated natural gas zones and original hydrate reservoirs. As hydrate recovery continues, the dissociated area near the well gradually increases. The branches and wellbores of a multilateral well are treated as lines in 3D space. Each line can be composed of multiple segments in the boundary element method. The initial state of hydrate formation is assumed to satisfy a uniform pressure distribution. With these above parameters as input, the production profiles of the multilateral horizontal well are plotted in Fig. 11. The typical production profile of multilateral horizontal wells can be divided into three stages. The first stage is the rapid production rates decline stage, affected mainly by the structure of multilateral horizontal well. In the early period of this stage, the rate curve exhibits the characteristics of linear flow and is a straight line with a slope of -1/2. Linear flow here refers to the fact that the fluid in the 3D space flows to the wellbore linearly. As the formation pressure response gradually propagates to the junction of the dissociated zone and the original formation, the production curve begins to enter the second phase. The second stage mainly reflects the physical properties of the NGH dissociated zone. After sufficient production time, the pressure response has extended to the original formation. The third stage at this time is affected by the properties of the original reservoir, including the properties of solid gas hydrates and the physical properties of the formation.

Fig. 11

The production profile comparison between the conventional radial composite model and proposed model for multilateral horizontal well in eastern Nankai Trough

By setting the dissociation coefficient in the proposed model to 0, the proposed model is simplified into a conventional radial composite model. The production performance generated from the conventional radial composite model are plotted in Fig. 11 for comparison. Since the conventional model ignores the dynamic dissociation effect of hydrate, results show that the daily production rate of the conventional model is smaller than the value of the proposed model. This feature appears in the middle stages of production. As time increases, the production rate difference between the two models increases. This is due to the increment of the hydrate dissociation area.

The RNP behaviors is further analyzed to reveal the flow process of hydrate production in multilateral wells. The RNP and derivative curves in Fig. 12 show that the flow of hydrate can be divided into linear flow, transitional flow, dissociation flow and radial flow. The RNP behavior during linear flow appears as a straight line with a slope of 1/2. The causes of transitional flow are complex, including the interference of various branches, the expansion of the dissociated zone, and the flow abilities difference between the inner and outer zones. The solid hydrate in the outer zone begins to dissociate and flows toward the inner zone. At this time, the RNP derivative shows a response, which is similar to the closed boundary effect. Finally, the RNP derivative curve appears as a horizontal line with a slope of 0 in the radial flow.

Fig. 12

The typical RNP and derivative profile for multilateral horizontal well in eastern Nankai Trough

6 Conclusions

This paper presents a practical production model for multilateral horizontal wells in NGH reservoirs. The hydrate reservoir is assumed to be isotropic. We used Laplace transforms and Stehfest numerical inversion methods to obtain solutions for flow in isotropic hydrate reservoirs. The superposition principle and reciprocity are applied in model development. We validated our model, performed sensitivity analyses, and conducted synthetic case studies. Based on this analysis, we drew the following conclusions:

A commercial numerical simulator validated the rate forecasts in proposed model. The typical production behaviors show that the rate profile can be divided into three parts. The early stage exhibits the characteristics of linear flow and it is a straight line on a log–log plot with a slope of -1/2. The middle stage of production curve reflects the physical properties of NGH dissociated zone. The later stage is affected by the properties of original reservoir. The predicted cumulative production value using the conventional model only accounts for 47% of the predicted value of the proposed model.

The flow of hydrate production in multilateral wells includes linear flow, transitional flow, dissociation flow and radial flow. The RNP behavior during linear flow appears as a straight line with a slope of 1/2. The RNP derivative during dissociation flow shows a convex characteristic similar to the closed boundary effect. There is a horizontal line with a slope of 0 in the final radial flow.

The limitation of this paper mainly lies in the lack of field data and the neglect of some physical phenomena in hydrate. The published hydrate field data are all for vertical wells. As a potential future technology, field reports of hydrate production in multilateral wells exist but no field data have yet been disclosed. In addition, the multiphase flow during the hydrate dissociation process and reservoir anisotropy bring severe challenges to the modeling process. Our next step will focus on the application of the model to field data and the modeling of multiphase flow. The effects of reservoir anisotropy should also be studied separately.

Appendices

Appendix A: Dimensionless variables

Dimensionless time,

$$t_\text{D} = \frac{3.6kt}{{\mu \varphi C_{\text{t}} L^{2} }}$$

(29)

Dimensionless pressure,

$$\xi_\text{D} = \frac{{kh\left( {\xi_{i} - \xi } \right)}}{{3.684 \times 10^{ - 3} \mu^{2} B_{\text{g}} Zq_{\text{sc}} }}$$

(30)

Dimensionless horizontal length,

$$L_{{\text{h}}\text{D}} = \frac{{L_{\text{h}} }}{L}$$

(31)

Dimensionless branch length,

$$L_{{\text{b}}\text{D}} = \frac{{L_{\text{b}} }}{L}$$

(32)

Dimensionless distance,

$$x_\text{D} = \frac{x}{L},y_\text{D} = \frac{y}{L},z_\text{D} = \frac{z}{L}$$

(33)

Dimensionless production rate,

$$q_{{w}\text{D}} = \frac{{3.684 \times 10^{ - 3} \mu^{2} B_{\text{g}} Z}}{{kh\left( {\xi_{i} - \xi_{w} } \right)}}q_{\text{sc}}$$

(34)

Dimensionless dissociated radius,

$$r_\text{D} = \frac{r}{L}$$

(35)

Dimensionless dispersion ratio,

$$W = \frac{{\left( {\varphi C_{\text{t}} } \right)_{1} }}{{\left( {\varphi C_{\text{t}} } \right)_{2} }}$$

(36)

Dimensionless mobility ratio,

$$M = \frac{{\left( {k_{i} } \right)_{1} \left( \mu \right)_{2} }}{{\left( {k_{i} } \right)_{2} \left( \mu \right)_{1} }}$$

(37)

Dimensionless wellbore storage coefficient,

$$C_\text{D} = \frac{C}{{2\pi \varphi C_{\text{t}} hL^{2} }}$$

(38)

Appendix B: Derivation of flow equations

As bottom-hole pressure decreases, pore pressure also decreases in the depressurization process to recover NGH. We model the relationship between effective stress and permeability with the Eq. (39) (Pedrosa 1986).

$$\alpha = \frac{1}{k}\frac{\partial k}{{\partial p}} \Rightarrow k = k_{i} e^{{ - \alpha \left( {p_{i} - p} \right)}}$$

(39)

where $\alpha$ is permeability modulus and $k_{i}$ is the permeability at the initial pressure. The flow of NGH follows Darcy's law and the equation of motion is:

$$v = \frac{k}{\mu }\nabla p$$

(40)

The equation of state for the gas is:

$$pM_\text{g} = \rho ZRT$$

(41)

where $M_\text{g}$ is gas molar mass, $\rho$ is gas density, $Z$ is gas-law compressibility factor and $R$ is gas constant. The definition of pseudo pressure is given as:

$$\psi = 2\int_{{p_{i} }}^{p} {\frac{p}{\mu Z}} \text{d}p$$

(42)