1 Introduction

In the field of blasting engineering, there is a pressing need to address the challenges of enhancing the utilization rate of blasting energy, improving the effectiveness of rock-breaking during blasting operations, and reducing overall blasting costs. The introduction of high-power water-resistant explosives, such as water-based and emulsion explosives, has led to the practical application of borehole water-coupled charge blasting in various engineering projects. This technique finds utility in tunnel smooth blasting (Li and Li 2022), open-pit mining blasting (Ebrahim et al. 2012), and controlled demolition blasting (Liu et al. 2009). Water-coupled blasting involves utilizing water as a medium to transmit explosive energy, with the charge coming into direct contact with the water medium. By leveraging the incompressibility and other properties of water, the propagation pattern of shock waves generated by the explosion can be altered, thereby influencing the overall blasting effect. Extensive research has been conducted on the theory of water-coupled blasting. The formation and propagation laws of underwater shock waves have been analyzed through theoretical derivation(Du and Luo 2003), the peak pressure on the hole wall has been determined using elastic wave theory (Du et al. 2007), the range of rock failure zones has been calculated based on strength theory (Zong et al. 2012), and specific examples have been provided to demonstrate that water-coupled charges can enhance the utilization rate of explosion energy compared to air-uncoupled charges (Zong et al. 2004). Furthermore, the “water-wedge effect” exhibited by water media has also been investigated. Chen et al. (Chen and Lin 1996) considered the “water-wedge effect” as a means to expand cracks and analyzed the relevant conditions for crack propagation and arrest in the presence of water media. Experimental research on the water coupling coefficient involves model experiments focused on the stress distribution characteristics around the borehole (Wang and Li 2010, Zong and Luo 2006). Talhi et al. (TALHI and BENSAKER 2004) conducted measurements of the peak pressure of P-waves during water-coupling blasting processes. Huang et al. (2014, 2015) conducted water-coupling blasting model experiments to determine the crack range of fractured coal bodies and analyze the crack propagation law of fractured coal and rock masses during hydraulic fracturing. Zhang et al. (2018) conducted experiments with varying water-coupling coefficients and compared the peak pressure on the pore wall to identify the optimal coefficient. However, the stress-wave intensity curve in the immediate vicinity of the explosion is absent, which prevents an accurate assessment of the influence of phase transformation in the water medium on stress distribution near the explosion zone. The attenuation law of peak pressure can only be calculated using the detonation-wave pressure of the charge as the initial value of the shockwave pressure, leaving the stress distribution pattern near the explosion zone unclear. Therefore, further investigation is required to elucidate the mechanism of water-containing blast-hole blasting. Numerical simulation methods are widely employed due to their ability to replicate the overall impact of blasting. Wang et al. (2005) utilized numerical simulation methods to explore the distribution of damage and failure zones, as well as the relationship between hole wall pressure, acceleration, velocity, and radial uncoupling coefficients. Yang et al. (2018) employed the explicit dynamic finite element software LS-DYNA to establish a two-dimensional numerical calculation model. They evaluated the rock damage distribution, hole wall pressure distribution, and blasting efficiency as criteria and conducted a comparative analysis of factors such as radial uncoupling coefficient, axial uncoupling charging position, and axial uncoupling coefficient.

In summary, significant progress has been made in theoretical research and understanding the blasting effect of water coupling blasting. However, there is still limited research on the specific impact of the water coupling coefficient on its blasting effect, with most studies relying on on-site experiments. To gain a more comprehensive understanding of the relationship between the water coupling coefficient and the blasting effect, this study begins with theoretical derivations and analyzes the correlation between the water coupling coefficient and the hole wall pressure. This will provide a more intuitive observation of their relationship.

Second, water coupling blasting experiments are conducted, utilizing CT technology to reconstruct the morphology of the specimen after blasting and visually display the blasting effects under different water coupling coefficients. Finally, numerical simulation is employed to facilitate fractal analysis and verify the theoretical derivation and experimental results through simulations. This study serves as a valuable reference for the practical application of water-coupled blasting technology in engineering projects.

2 Analysis on the mechanism of water coupled blasting

2.1 Basic assumptions

When utilizing water-coupled blasting, the presence of a water medium introduces notable distinctions in the blasting effect compared to other methods. The measurement of hole wall pressure serves as a precise indicator of the vibration intensity generated by blasting and the extent of damage inflicted on the surrounding rocks. By assessing the hole-wall pressure, blasting parameters can be adjusted to achieve the desired blasting effect while minimizing unnecessary environmental impacts. Calculating the hole wall pressure of water-coupled blasting is crucial for analyzing the underlying mechanism of this technique.

However, the process of water-coupled blasting involves complex phenomena, including explosive detonation, shock wave propagation in water, and the interaction between shock waves and borehole walls. To simplify the analysis, the following assumptions are made: (1) The interface between the detonation wave and the water medium is approximated, and the interaction between the shock wave in water and the borehole wall is assumed to occur on a plane surface. (2) The water–rock interface is considered as an elastic wall, and the shock wave in water is assumed to directly impact the interface, resulting in the generation of transmitted and reflected waves.

2.2 Initial parameters of shock waves in water

The detonation product parameters were calculated using the Chapman–Jouguest detonation theory model, which included the initial pressure \(p_{{\text{h}}}\), particle velocity \({u}_{{\text{h}}}\), density \(\rho_{{\text{h}}}\), and sound velocity of the detonation product \(c_{{\text{h}}}\).

$$p_{{\text{h}}} = \frac{1}{{\gamma + 1}}\rho _{0} D^{2} ,{\text{ }}\rho _{{\text{h}}} = \frac{\gamma }{{\gamma + 1}}\rho _{0} ,{ u}_{{\text{h}}} = \frac{1}{{\gamma + 1}}D,{\text{ }}c_{{\text{h}}} = \frac{\gamma }{{\gamma + 1}}D$$
(1)

where, the isentropic index of the detonation product is the initial density of the explosive charge and D is the detonation velocity.

Following the explosion, the detonation products, characterized by high temperature and pressure, disperse outward. When the detonation wave encounters the water medium, it undergoes transmission and reflection at the interface, resulting in the formation of a transmitted shock wave in the water. Additionally, due to the higher density of the explosives compared to water, the reflected detonation products manifest as sparse waves. Figure 1 illustrates the parameter distribution in the vicinity of the explosive–water interface subsequent to the interaction with the detonation wave.

Fig. 1
figure 1

Distribution of parameters at the explosive water interface

Full size image

When sparse waves are introduced into the detonation products, they undergo isentropic expansion to obtain additional velocities (Compiling Group of Explosion and Its Functions of the Eighth Department of Beijing Institute of Technology 1979). The interface between the detonation products and water media must meet continuous conditions; thus, the interface particle velocity

$${u}_{{{\text{x}}1}} = {u}_{{\text{h}}} + {u}_{{{\text{r}}1}}$$
(2)

Additional speed \(u_{{{\text{r1}}}}\)

$$u_{{{\text{r1}}}} = u_{{{\text{x1}}}} - u_{{\text{h}}} = \int_{{p_{{{\text{x1}}}} }}^{{p_{{\text{h}}} }} {\frac{\text{d}p}{{\rho _\text{c}}}}$$
(3)

In the equation, \(p_{{{\text{x1}}}}\) is the interface pressure.

The isentropic equation and sound velocity formula of detonation products are as follows:

$$P = A\rho^{\gamma }$$
(4)
$${c}^{2} = \left( {\frac{{{\text{d}p}}}{{{\text{d}}\rho }}} \right)_{{\text{s}}}$$
(5)

Simultaneous equation to obtain the velocity of interface particles \(u_{{{\text{x1}}}}\)

$$u_{{{\text{x1}}}} = \frac{D}{\gamma + 1}\left\{ {1 + \frac{2\gamma }{{\gamma - 1}}\left[ {1 - \left( {\frac{{p_{{{\text{x1}}}} }}{{p_{{\text{h}}} }}} \right)^{{\frac{\gamma - 1}{{2\gamma }}}} } \right]} \right\}$$
(6)

Based on the aforementioned assumptions, the interface between the detonation products and water medium is simplified as elastic interface 1–1 as shown in Fig. 2.

Fig. 2
figure 2

Elastic interface 1–1

Full size image

Establishing a system of mass and momentum conservation equations for shockwaves in water, we get,

$$\left\{ \begin{gathered} \rho_{{{\text{w0}}}} D_{2} = \rho_{{{\text{wx}}}} \left( {D_{2} - u_{{\text{x}}} } \right) \hfill \\ p_{{{\text{wx}}}} - p_{{{\text{w0}}}} = \rho_{{{\text{w0}}}} D_{2} u_{{{\text{wx}}}} \hfill \\ \end{gathered} \right.$$
(7)

Owing to the continuous initial pressure and particle velocity of the shock wave at the interface between the detonation product and water medium,

$$u_{{{\text{wx}}}} = u_{{{\text{x1}}}} , \, p_{{{\text{wx}}}} = p_{{{\text{x1}}}}$$
(8)

The particle velocity of the initial shock wave in the inherent water medium is \(u_{{{\text{x1}}}}\)

$$u_{{{\text{x1}}}} = u_{{{\text{wx}}}} = \sqrt {\left( {p_{{{\text{wx}}}} - p_{{{\text{w0}}}} } \right)\left( {\nu_{{{\text{w0}}}} - \nu_{{{\text{wx}}}} } \right)} = \sqrt {\left( {p_{{{\text{x1}}}} - p_{{{\text{w0}}}} } \right)\left( {\nu_{{{\text{w0}}}} - \nu_{{{\text{wx}}}} } \right)}$$
(9)

In the equation, \(p_{{{\text{wx}}}} , \, \nu_{{{\text{wx}}}}\) represents the initial pressure and specific volume of the shock wave in water, and \(p_{{{\text{w0}}}} , \, \nu_{{{\text{w0}}}}\) represents the original pressure and specific volume of the water medium when undisturbed.

Owing to the initial pressure of the shock wave in the water, \(p_{{{\text{wx}}}} \gg p_{{{\text{w0}}}}\). Equation (9) can be simplified as follows:

$$u_{{{\text{x1}}}} = u_{{{\text{wx}}}} = \sqrt {p_{{{\text{wx}}}} \left( {\nu_{{{\text{w0}}}} - \nu_{{{\text{wx}}}} } \right)} = \sqrt {p_{{{\text{x1}}}} \left( {\nu_{{{\text{w0}}}} - \nu_{{{\text{wx}}}} } \right)}$$
(10)

The equation of state for the water medium under the action of shock waves is as follows (Huang et al. 2015):

$$p_{{{\text{wx}}}} = A^{\prime } \left[ {\left( {\frac{{\rho_{{{\text{wx}}}} }}{{\rho_{{{\text{w0}}}} }}} \right)^{{B^{\prime } }} - 1} \right]$$
(11)

In the equation, \(A^{\prime }\) and \(B^{\prime }\) are constants, usually taken as \(A^{\prime }\) = 304.7 MPa, \(B^{\prime }\) = 7.15.

Equations (6), (10), and (11) can be used simultaneously to obtain all the initial parameters of the underwater shock waves. Taking DDNP explosive as an example, the surrounding medium is red sandstone, and the relevant material parameters are as follows: explosive density ρ = 1600 kg/m3, detonation velocity D = 6800 m/s, isentropic index of detonation products γ = 3. The initial parameters of the underwater explosion shock waves are listed in Table 1.

Table 1 Initial parameters of underwater explosion shock wave
Full size table

2.3 Attenuation law of shock wave parameters in water medium

Wave propagation in water interacts with the blast hole wall after propagating for a certain distance. Because of the high-temperature and high-pressure characteristics of the blast wave near the explosion, it is difficult to directly measure the attenuation law of the peak pressure of the shock wave. The following empirical formula is used to extend the overpressure with relative distance when the charge explodes in infinite water (Wang et al. 2008):

$$\left\{ \begin{gathered} \Delta p = \frac{{A_{1} }}{{\bar{r}^{{2.49}} }},1 < \bar{r} \le 2 \hfill \\ \Delta p = \frac{{A_{2} }}{{\bar{r}^{{1.45}} }},2 < \bar{r} \le 5 \hfill \\ \Delta p = \frac{{A_{3} }}{{\bar{r}^{{0.63}} }},5 < \bar{r} \le 240 \hfill \\ \end{gathered} \right.$$
(12)

In the formula, \(\overline{r}\) is the relative distance, \(\overline{r} = R/R_{0}\), where R is the distance from the explosion center, R0 is the diameter of the charge roll, and A1 is the initial peak pressure of the shock wave in water.

The provided equation serves as an approximation for the attenuation law of overpressure in water. By integrating the mass and momentum conservation Eq. (7), the state equation of water (Eq. (11)), and the overpressure attenuation law (Eq. (12)) of the shock wave in water, approximate parameters for the shock wave in water at the interface between water and rock can be obtained.

2.4 Interaction process between shock wave and borehole wall in water medium

Interface 2–2 between the water shock waves and rock media is simplified as shown in Fig. 3.

Fig. 3
figure 3

Interface 2–2

Full size image

The mass and momentum conservation equations for shock waves penetrating into rocks are as follows:

$$\left\{ \begin{gathered} \rho_{{{\text{mx}}}} \left( {D_{4} - u_{{{\text{m0}}}} } \right) = \rho_{{{\text{mx}}}} \left( {D_{4} - u_{{{\text{mx}}}} } \right) \hfill \\ p_{{{\text{mx}}}} - p_{{{\text{m0}}}} = \rho_{{{\text{m0}}}} \left( {D_{4} - u_{{{\text{m0}}}} } \right)\left( {u_{{{\text{mx}}}} - u_{{{\text{m0}}}} } \right) \hfill \\ \end{gathered} \right.$$
(13)

Based on the initial particle velocity in the rock medium, the aforementioned equations can be simplified as follows:

$$\left\{ \begin{gathered} \rho_{{{\text{m0}}}} D_{4} = \rho_{{{\text{mx}}}} \left( {D_{4} - u_{{{\text{mx}}}} } \right) \hfill \\ p_{{{\text{mx}}}} = \rho_{{{\text{m0}}}} D_{4} u_{{{\text{m0}}}} \hfill \\ \end{gathered} \right.$$
(14)

However, the impact compressibility law of solid dense media can be expressed as follows.

$$p_{3} = \rho_{{{\text{m0}}}} (a + bu_{{{\text{mx}}}} )u_{{{\text{mx}}}}$$
(15)

In Eq. (15), the velocity of the shockwave particle in the rock is the only unknown variable, which can be determined using the following method: When the shock wave in water encounters a rock medium characterized by high density and low compressibility, it generates both a transmitted shock wave and a reflected shock wave. The distribution of parameters at the rock interface is illustrated in Fig. 4.

Fig. 4
figure 4

Distribution of water rock interface parameters

Full size image

The reflected shock wave will reduce the particle velocity of the shock wave in water to the particle velocity at the interface \(u_{{{\text{x2}}}}\); the interface between the detonation product and the water medium needs to meet continuous conditions, that is \({u}_{{{\text{r2}}}}\). Moreover, there is an additional velocity to increase the particle velocity at the interface \({u}_{{{\text{x2}}}} \text{ =} {u}_{\text{w}} { + u}_{{{\text{r2}}}}\). At the same time, the transmitted shock wave \({u}_{{{\text{x2}}}}\) is analyzed to obtain the particle velocity at the interface.

$${u}_{{{\text{x2}}}} \text{ =} {u}_{\text{w}} \text{ + }{u}_{{{\text{r2}}}} = {u}_{\text{w}} - \sqrt {\left( {p_{{{\text{x2}}}} - p_{{\text{w}}} } \right)\left( {\nu_{\text{w}} - \nu_{{{\text{x2}}}} } \right)}$$
(16)
$$e_{{{\text{mx}}}} - e_{{{\text{m}}0}} = \frac{1}{2}\left( {p_{{{\text{mx}}}} + p_{{{\text{m0}}}} } \right)\left( {\nu_{{{\text{m0}}}} - \nu_{{{\text{mx}}}} } \right)$$
(17)

Equation (17) is the Hugonio equation of the reflected shock wave, which represents the change in the internal energy of the water medium before and after the reflected shock wave front passes through it, simplifying the isentropic equation of the detonation products to Eq. (18).

$$\frac{{\nu_{{{\text{x2}}}} }}{{\nu_{{\text{w}}} }} = \frac{{\left( {\gamma + 1} \right)p_{{\text{w}}} + \left( {\gamma - 1} \right)p_{{{\text{x2}}}} }}{{\left( {\gamma + 1} \right)p_{{{\text{x2}}}} + \left( {\gamma - 1} \right)p_{{\text{w}}} }} = \frac{{(\gamma - 1)\pi + \left( {\gamma + 1} \right)}}{(\gamma + 1)\pi + (\gamma - 1)}$$
(18)

In the equation, \({\uppi} = \frac{{p_{{{\text{x2}}}} }}{{p_{\text{w}} }}\).

Substituting this into Eq. (16), we obtain:

$$u_{{{\text{x2}}}} = u_{\text{w}} - \sqrt {p_{\text{w}} \nu_{\text{w}} ({\uppi} - 1)\left[ {1 - \frac{{(\gamma - 1){\uppi} + \left( {\gamma + 1} \right)}}{{(\gamma + 1){\uppi} + \left( {\gamma - 1} \right)}}} \right]}$$
(19)

The continuity of velocity at the interface enables us to observe this phenomenon. In Eq. (19), the unknown variables can be solved simultaneously by utilizing the parameters and attenuation laws of underwater shock waves mentioned in Sects. 2.1 and 2.2. Consequently, by combining Eqs. (15) and (19) with the underwater shock wave parameters, the initial parameters of the shock wave in the rock medium can be determined, with the initial shock wave pressure transmitted into the rock representing the hole wall pressure.

2.5 Relationship between water coupling coefficient and pore wall pressure

The water-coupling coefficient is a crucial parameter for characterizing the configuration of the water-coupling blasting charge, and it significantly influences the blasting effect. In Eq. (12), the relative distance represents the decay of shock wave overpressure over time, while the expression for the relative distance at the borehole wall coincides with the water coupling coefficient Kd. For instance, when considering sandstone, calculations demonstrate that its density is 2500 kg/m3, and the Hugo-Neo parameters a = 2100 m/s and b = 1.63 are employed to describe its impact compressibility law. Based on the calculation results in Table 1, the underwater shock wave parameters at the interface of the hole wall were calculated according to Eq. (12), and the hole wall pressure was obtained by combining Eqs. (15) and (19). The calculation results are presented in Fig. 5.

Fig. 5
figure 5

Relationship between pore wall pressure and water coupling coefficient

Full size image

The calculation results presented in Fig. 5 demonstrate that an increase in the water coupling coefficient leads to several effects. First, if the borehole size remains constant, the relative distance increases, resulting in a decrease in shock wave parameters at the borehole wall. This decrease in parameters corresponds to a decrease in particle velocity within the rock medium, ultimately leading to a reduction in peak pressure on the borehole wall. This adjustment prevents excessive crushing around the hole wall, allowing sufficient energy to be directed toward the rock medium to create crack zones. As a result, rock cracking is promoted, ultimately achieving an optimal explosion effect.

However, notably, the aforementioned research is based on the assumption that the explosion load acts vertically on the hole wall. The effects of oblique incidence and reflection of the explosion load have not been fully considered in this analysis.

The use of assumptions and empirical formulas in analyzing the attenuation law of explosion shock waves in a water medium can introduce limitations in obtaining accurate theoretical solutions. To address this challenge, high-precision numerical simulation methods are employed in the subsequent analysis to examine the relationship between the hole wall pressure and the water coupling coefficient.

3 Blasting tests with different water coupling coefficients

3.1 Protocol

To facilitate a comparative analysis of the blasting effects on rock specimens under various water coupling coefficients, experiments were conducted while ensuring consistency in other conditions such as charge quantity and borehole diameter. The water coupling blasting experiments involved modifying the diameter of the charge to adjust the water coupling coefficient. Four distinct sets of water coupling coefficients were designed for the experiment. Table 2 provides specific details regarding the parameters of the charge and water coupling coefficients.

Table 2 Package parameters and water coupling coefficient
Full size table

3.2 Preparation of test pieces and drug packages

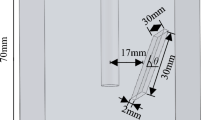
The test pieces used in the experiment were obtained by cutting and processing large blocks of red sandstone sourced from Jiaoxi Township, Liuyang City, Hunan Province. The red sandstone had an average density of 2500 kg/m3 and a uniaxial compressive strength of approximately 76.30 MPa. To ensure reliable and consistent results, red sandstone with good integrity and uniformity was selected, avoiding the presence of discontinuous interfaces such as internal joints and cracks in the rock specimen that could influence crack propagation. The red sandstone was shaped into a cube specimen measuring 100 mm × 100 mm × 100 mm. A blast hole with a diameter of 6 mm and length of 70 mm was drilled from the top to the bottom of the specimen, as illustrated in Fig. 6.

Fig. 6
figure 6

Schematic diagram of red sandstone specimen and charge structure

Full size image

The drug package used in the experiment was constructed as follows: First, the DDNP explosive was loaded into a 30 mm long straw, and both ends of the straw were sealed with rubber mud. Additionally, a suction pipe of the same height was placed outside the loaded straw, creating a "pipe sleeve" structure. The bottoms of the two suction pipes were bonded with rubber mud, and the space between them was filled with a water medium, creating a water-coupling blasting cartridge structure.

To set up the experiment, the prepared cartridge was positioned at the bottom of a small hole in the test piece. The upper 40 mm space of the hole was filled with a mixture of fine sand and glue to ensure proper sealing. The explosive charge was connected to a digital high-energy pulse initiator using a wire.

After completing the above work, the specimen will be placed in a specially designed cube device to constrain it.

3.3 Test result

3.3.1 Overall shape of the specimen after explosion

After the cartridge detonates inside the blast hole, the detonation pressure rapidly increases to tens of thousands of megapascals, generating a shock wave in the water. Due to the incompressibility of water, the shock wave pressure uniformly acts on the rock at the blast hole wall for an extended period. As the wave propagates into the rock medium, it transforms into a stress wave, which leads to the formation of radial cracks near the blast hole wall under compression.

As the explosion process progresses, the explosive gas and water medium infiltrate the cracks, creating a “wedge” effect. This causes the radial cracks to continue extending and developing, leading to further damage and fracturing of the rock mass.

The crack morphologies of the specimens after the explosion were visually examined and analyzed. In Fig. 7a, which corresponds to a water-coupling coefficient of 1.2, the red sandstone specimen exhibited a complex failure pattern. The radial crack extended from the blast hole to the rock surface, dividing the specimen into two parts. The crack direction within each plane was relatively consistent, indicating a uniform division of Specimen 1. Additionally, small microcracks were observed on the top surface of the specimen, probably caused by the reflected tension after the propagation of the stress wave to the free surface. These observations highlight the influence of the water-coupling coefficient on the formation and distribution of cracks in the rock mass. The reflected tensile stress wave increases the stress field at the crack tip, promoting crack propagation in multiple directions. However, when this small microcrack reaches the middle part of the specimen, its growth ceases, preventing the formation of a complete through crack. Consequently, further cracking occurs in the specimen. Figure 7b illustrates the surface crack morphology of the red sandstone specimen with a water coupling coefficient of 1.33, which is similar to that of the specimen with a water coupling coefficient of 1.2. Specimen 2 is divided into two parts, exhibiting significant surface spalling. Notably, an angle of 30° is observed between the direction of the main crack on the top surface of the specimen and the vertical direction. Two small microcracks developed from the blast hole position. One of them stopped developing at the top of the specimen, while the other propagated downward along the surface. The direction of the second microcrack on the front surface of the specimen was consistent with that of the main crack and intersected with it again on the bottom surface. The presence of increased water medium resulted in more explosive energy being utilized for crack propagation, leading to a greater propagation distance of the surface microcracks in specimen 2 compared to specimen 1. Figure 7c depicts the surface crack morphology of the red sandstone specimen with a water coupling coefficient of 1.5, which exhibits significant differences from the previous two groups of specimens. The specimen exhibited a division into three parts due to the presence of two perpendicular cracks: one large and two small. The cracks displayed notable bending and flaking on different planes, accompanied by the formation of secondary branch cracks. The surface failure morphology of the specimens became more complex. Figure 7d illustrates the surface crack morphology of the red sandstone specimen with a water coupling coefficient of 2.0. The three cracks, located at the top and bottom of the specimen, formed an angle of approximately 120°, resulting in the specimen being fragmented into three equal parts. When comparing Specimen 3, which fragmented into three uneven parts, with Specimen 4, it can be observed that the increase in the water coupling coefficient led to a more uniform failure pattern of the specimen. As the water coupling coefficient increased, a larger amount of water participated in the blasting process, resulting in a decrease in peak pressure at the borehole wall, a reduced area of destruction and crushing near the explosion, and a greater utilization of explosion energy for crack propagation and development in the middle zone of the specimen. The presence of water medium at the crack tip further facilitated the rapid and extensive expansion of cracks, resulting in an increased number of cracks and a more complex failure morphology of the specimen. Overall, the variation in water coupling coefficient had a significant influence on the blasting effects, with higher coefficients promoting more efficient crack propagation and a more uniform failure pattern.

Fig. 7
figure 7

Surface crack morphology of specimen after explosion

Full size image

3.3.2 Fractal dimension of surface crack

Xie et al. (2005) introduced fractal theory to the field of rock mechanics, recognizing that the development, propagation, penetration, and distribution of cracks in rock material under explosive loads exhibit a statistically self-similar behavior. The distribution of cracks on the rock surface after blasting provides insights into the extent of specimen damage. Therefore, the fractal method can be utilized to quantitatively analyze the blasting effects on red sandstone specimens subjected to water-coupled blasting loads. The box-counting dimension, a widely used dimension, directly reflects the spatial occupation of cracks on a plane. To calculate the fractal dimension of a plane crack, the process involves determining the number of squares, denoted as N(ε), that contain the point set F for a given side length ε. This process is repeated by varying ε to obtain a series of ε-N(ε) data. By plotting N(ε) against 1/ε and calculating the slope of the resulting double logarithmic scatter diagram using the least square method, the fractal dimension D can be determined.

$$D = - \mathop {\lim }\limits_{\varepsilon \to 0} \frac{\lg N(\varepsilon )}{{\lg \varepsilon }} = \mathop {\lim }\limits_{\varepsilon \to 0} \frac{\lg N(\varepsilon )}{{\lg (1/\varepsilon )}}$$
(20)

To analyze the surface cracks of the specimens after the explosion, the top and bottom planes of the four groups of specimens were selected for calculation, as these planes displayed significant differences. Utilizing the image box dimension calculation method in MATLAB, the surface cracks were converted into a binary form. The point set consisting of surface cracks was then overlaid with square grids of varying sizes, enabling the quantitative calculation of the box dimensions of the surface cracks. Figure 8 presents the binary and double logarithmic scatter diagrams of the cracks observed on the top and bottom surfaces of test piece 3. The scatter-fitting straight line exhibited a high correlation coefficient (R2) of > 0.99, indicating a strong correlation. The surface cracks in the test piece displayed distinct fractal characteristics following the explosion.

Fig. 8
figure 8

Binary diagram and double logarithmic scatter diagram of cracks on the top and bottom surfaces of specimen 3

Full size image

The scatter comparison diagram in Fig. 9 illustrates the fractal dimensions of the surface cracks on the top and bottom surfaces of the four specimen groups. The extent of damage to the specimens under different water coupling coefficients can be evaluated by analyzing the fractal dimension of the surface cracks. A higher fractal dimension indicates a greater complexity and occupation of cracks in the plane, indicating a higher degree of damage to the specimens. The fractal dimension of the top surface cracks of the specimens after the explosion ranged from 1.44 to 1.56, while the fractal dimension of the bottom surface cracks ranged from 1.22 to 1.38. Specimen 3 exhibited the highest fractal dimension, which correlates with the severe surface spalling and the presence of numerous secondary cracks. Overall, the fractal dimension of the surface cracks exhibited a trend of first increasing and then decreasing with an increasing water-coupling coefficient for the four groups of specimens. The use of water as an energy transfer medium, characterized by its high density and viscosity, resulted in a slower expansion of the detonation products in water. This led to a slow decay of the explosion stress wave in the surrounding rock medium, thereby prolonging the duration of action and increasing the degree of rock damage. The external water medium penetrated the cracks under high pressure as the detonation products expanded, acting as a “water wedge.” The presence of more water in the medium resulted in a more pronounced stress concentration at the crack tip. The tangential tensile stress exceeded the tensile strength of the rock, leading to the formation of radial cracks and the subsequent fracturing of the rock. Consequently, as the water-coupling coefficient increased, the development and expansion of cracks were further enhanced, resulting in more complex crack morphologies on the rock surface. However, when the water medium reached a certain threshold, the incompressibility of the water caused a more uniform distribution of explosion energy in the rock medium. As a result, the surface cracks of the rock specimen became more evenly distributed. This led to a lower fractal dimension of the surface crack for Specimen 4 compared to Specimen 3. Additionally, the fractal dimension of the top surface crack was larger than that of the bottom surface crack, indicating that the degree of damage on the top surface was more complex than that on the bottom surface. When an explosive detonates, the stress wave travels through the rock medium and is reflected and superimposed on the free surface. As the wave propagates toward the upper part of the rock specimen, it encounters the blocking structure, which is less uniform compared to the red sandstone material. This leads to a more complex stress field in the upper part of the rock specimen compared to the lower part. Consequently, there is a significant difference in the geometric distribution of cracks between the top and bottom surfaces of the rock specimen, resulting in a larger fractal dimension for the top surface compared to the bottom surface.

Fig. 9
figure 9

Scatter diagram of fractal dimension of specimen surface

Full size image

3.3.3 CT scanning and 3D reconstruction of specimen

This test used an X-ray Industrial CT detection system (actis300_320/225) from the State Key Laboratory of Coal Resources and Safe Mining, as shown in Fig. 10. CT technology can perform non-contact scanning of samples, and based on the relative action of rays and materials, it can quantitatively analyze the pore and fracture characteristics of red sandstone specimens.

Fig. 10
figure 10

X-ray Industrial CT detection system

Full size image

The main parameters of the scanning scheme are voltage 280 kV, current 3 mA, magnification 2.078, voxel size 0.048, total number of frames 1201, tomography interval 0.1 mm, CT image size 55 mm × 55 mm, pixel size 1850 × 1850. After the explosion, the red sandstone samples were scanned using CT, and 1000 32 bit gray images were obtained. The gray images were binarized and imported into Avizo software to reconstruct the rock samples damaged after the explosion. Figure 11 shows a typical CT slice image and a three-dimensional reconstruction model of the specimen after the explosion.

Fig. 11
figure 11

CT Slice image and 3D reconstruction model of post explosion specimen

Full size image

Through a comparison between the three-dimensional reconstruction of the specimen after the explosion and the actual damaged specimen shown in Fig. 7, a high degree of similarity and coincidence was observed. CT scanning and three-dimensional reconstruction techniques were employed to accurately capture the distribution of the three-dimensional fracture network within the rock specimen. This enabled an intuitive analysis of the internal failure characteristics of the rock under the influence of the explosion load.

Figure 12 presents a perspective view of the internal crack structure of the test piece after the explosion. In Fig. 12a, which corresponds to a water-coupling coefficient of 1.2, the internal crack structure of the test piece is depicted. The main crack is observed to penetrate the rock and divide the test piece into two parts. Additionally, a microcrack is visible vertically aligned with the main crack at the top, extending downward for a certain distance before ceasing further development. The internal crack structure of the test piece exhibits increased complexity. In Fig. 12b, corresponding to a water-coupling coefficient of 1.33, the crack structure forms a "Y" shape overall. All three cracks extend to the surface of the test piece, but due to incomplete penetration in the horizontal direction, test piece 2 is also divided into two parts.

Fig. 12
figure 12

Internal fracture structure

Full size image

Figure 12c illustrates the internal crack structure when the water-coupling coefficient is 1.5. The morphology becomes even more complex compared to a water-coupling coefficient of 1.33. The crack structure becomes more intricate and extensive as the water coupling coefficient increases. In Fig. 12d, representing a water-coupling coefficient of 2.0, three through-cracks with angles of 120° can be observed inside the test piece, and all three cracks extend to the rock surface. Each test piece is divided into three equal parts.

The increase in the water coupling coefficient leads to a greater number of cracks in the model. The presence of water as a medium during crack propagation acts as a “water wedge.” Following an explosion, the interaction between the high-temperature and high-pressure explosive gas and the water medium results in the formation of a high-speed liquid jet. This liquid jet generates significant pressure and tensile stress, thereby facilitating the growth and development of cracks. Simultaneously, the explosion energy was highly concentrated in the jet head and quickly transferred to the rock medium. During the entire process, the energy dissipation was low, and the utilization rate of the explosion energy was high. More explosive energy was used to promote crack growth and development.

3.3.4 Volume fractal dimension and damage degree of specimen after explosion

To calculate the volume fractal dimension of the specimens after blasting under different water coupling coefficients, the method involves extending the square lattice to a cube box and covering the target set F with a cube box of side length a. By changing the value of a, multiple boxes are created, and the number of small boxes N(a) containing the set is calculated. Then, a scatter plot of the relationship between lg(a) and lg N(a) is generated. The slope of the fitted straight line from the scatter points represents the volume fractal dimension. This approach enables the quantitative calculation of the volume fractal dimension by covering the point set consisting of cracks in the three-dimensional reconstruction model of rock specimens with cubes of varying sizes. The presence of initial microcracks, microholes, and other defects in rock materials contributes to the initial damage of the rock. When an explosion occurs, the combined effects of the explosion stress wave, explosion-generated gas, and water medium further enhance the development of these internal defects, leading to an increase in the overall damage of the rock. This increase in damage is observed through the proliferation of cracks and an increase in the fractal dimension of the rock after the explosion. Yang et al. (2017) have established a relationship between the material damage degree caused by blasting, represented by ω, and the corresponding fractal dimension Dt of the “crack field” in the specimen. This relationship can be utilized to quantify the damage degree of the specimen after the explosion, and it is expressed as follows:

$$\omega = \frac{{D_{\text{t}} - D_{0} }}{{D_{\text{t}}^{\max } - D_{0} }}$$
(21)

where, Dt is the fractal dimension of the damaged area inside the medium after the explosion; D0 is the fractal dimension of the initial damaged area in the medium before the explosion, and it is considered that D0 = 0; Dtmax is the fractal dimension when the medium reaches the maximum damaged area. For plane problems, Dtmax = 2, and for three-dimensional problems, Dtmax = 3.

The scatter diagrams in Fig. 13 illustrate the relationship between the volume fractal dimension and the damage degree of the specimen after the explosion under different water coupling coefficients. These diagrams show a similar trend to the surface fractal dimension scatter diagram. When the water coupling coefficient is low, the volume fractal dimension of the specimen after the explosion tends to increase as the water coupling coefficient increases. However, when the water coupling coefficient reaches a certain threshold, the failure morphology of the specimen after the explosion becomes more uniform, leading to a decrease in the volume fractal dimension. This indicates that as the water coupling coefficient increases, the damage degree of the specimen shows a complex relationship with the fractal dimension, influenced by factors such as failure morphology and uniformity of the cracks. The water medium is incompressible. When the explosion energy acts on the rock with the water medium, the water can disperse the energy to the surface of the target object faster and more evenly, avoiding the uneven explosion impact load inside the rock medium to accelerate and increase crack propagation, and ensure the efficient and uniform failure of the rock. Therefore, the volume fractal dimension first increases and then decreases.

Fig. 13
figure 13

Volume fractal dimension and damage degree scatter diagram

Full size image

The fractal damage degree of the specimens varied with different water coupling coefficients. Specimens with a water coupling coefficient of 1.2 had the lowest fractal damage degree of 0.7, while specimens with a water coupling coefficient of 1.5 had the highest fractal damage degree of 0.81. This indicates that as the water coupling coefficient increased, the degree of fractal damage generally increased for specimens 1–3. The participation of the water medium in the blasting process further promoted the development and expansion of cracks, leading to increased internal damage and fracture intensity in the rock. However, from specimens 3–4, the fractal damage degree decreased. Although the overall damage degree of specimen 4 was still higher than that of specimens 1 and 2, this suggests that there may be a threshold or optimal water coupling coefficient beyond which the damage degree starts to decrease. Equation (21) shows that the damage degree of the rock specimen after blasting is positively correlated with the volume fractal dimension, and the relationship between the rock damage degree and the volume fractal dimension is linear. Therefore, the above analysis of the change law of the volume fractal dimension is also applicable to the analysis of the change law of the degree of damage of rock specimens after blasting.

4 Numerical simulation

4.1 Determination of material model and parameters

The multicore finite element software LS with the complex and accurate material model DYNA was used for the numerical simulation analysis. Four materials were involved in the numerical modeling process: explosive, water, rock, and the plugging medium. The selection of the material model is listed in Table 3.

Table 3 material model and state equation
Full size table

4.1.1 Explosive material parameter

In LS-DYNA, the JWL equation of state is generally used to describe the process of simulating explosive rapid combustion to generate shock waves. The JWL equation reflects the change in chemical energy during an explosion and is expressed as follows (HALLQUIST 2012):

$$p = A\left( {1 - \frac{\omega }{{R_{1} V}}} \right)e^{{ - R_{1} V}} + B\left( {1 - \frac{\omega }{{R_{2} V}}} \right)e^{{ - R_{2} V}} + \frac{\omega E}{V}$$
(22)

where, A, B, R1, R2 and ω are the material constants of explosives; P is the detonation pressure; V is the relative volume of detonation products; E is the internal energy per unit volume of explosive. The selection of the explosive parameters used in this study is presented in Table 4.

Table 4 Explosives and parameters of equation of state
Full size table

4.1.2 Water medium material

The Gruneisen equation of state is a mathematical model used to describe the dynamic mechanical behavior of a material, in this case, a water medium, under the influence of an explosion load. It provides a relationship between the pressure, density, and initial internal energy of the water medium during the blasting process. The equation is expressed as follows (Hallquist 2012):

$$P = \frac{{\rho_{0} {\text{C}}^{2} \mu \left[ {1 + \left( {1 - \frac{{\gamma_{0} }}{2}} \right)\mu - \frac{\alpha }{2}\mu^{2} } \right]}}{{\left[ {1 - \left( {S_{1} - 1} \right)\mu - S_{2} \frac{{\mu^{2} }}{\mu + 1} - S_{3} \frac{{\mu^{2} }}{\mu + 1}} \right]}} + (\gamma_{0} + a\mu )E_{\omega }$$
(23)

where, Eω is the internal energy of water material per unit volume, and the initial value is Eω0; C is the intercept of VS-VP curve; γ0 is the Gruneisen gamma constant. α is the order volume correction factor of γ0; μ is the compression of water material, μ = (ρ/ρ0) − 1, where ρ and ρ0 is the current density and initial density of the material respectively; S1, S2 and S3 are slope coefficients of VS-VP curve respectively. The selection of the water medium parameters for this study is presented in Table 5.

Table 5 Water and its equation of state parameters
Full size table

4.1.3 Rock material

The RHT material model can reflect the impact of compression damage and tensile damage on the mechanical properties of the rock mass and can accurately reflect the dynamic mechanical response of rock after being subjected to an explosion impact load. Therefore, the RHT material model was used to simulate the process of the rock material being subjected to an explosion impact and damage. The RHT rock parameters selected in this study are listed in Table 6 (Xie et al. 2017).

Table 6 RHT physical and mechanical parameters of materials
Full size table

4.2 Establishment of numerical model

To accurately simulate the interaction between various materials involved in the calculation process, a fluid–structure coupling algorithm was employed in the numerical analysis. Specifically, the Lagrange algorithm was used to model the behavior of the rock, while the arbitrary Lagrangian–Eulerian (ALE) algorithm was used for the explosives and air. This approach enabled a more realistic representation of the dynamic response of the system.

To simplify the computational complexity, an axisymmetric model was adopted. A 1/4 cube model with dimensions of 50 mm × 50 mm × 100 mm was created, effectively reducing the computational burden. The blast hole, with a radius of 3 mm, contained the explosive material at the bottom, followed by a water medium in the middle, and a blocking structure at the top. Non-reflective boundary conditions were applied to the upper, right, and rear sides of the model to minimize the influence of boundaries on the experiment.

The LS-DYNA finite element software was utilized to establish the numerical calculation model, as depicted in Fig. 14. In the figure, the red, blue, and green parts represent the explosive, water medium, and blocking structure, respectively. This computational model enabled the analysis of the dynamic response of the system and the evaluation of the effects of different materials and configurations on the explosion process.

Fig. 14
figure 14

Schematic diagram of numerical calculation model

Full size image

4.3 Calculation results

4.3.1 Simulation results of rock internal damage

Figure 15 presents the internal damage nephograms of the rock mass after blasting under different water-coupling coefficients. In this analysis, half of the section of the rock model after blasting under each working condition was taken for examination.

Fig. 15
figure 15

Nephogram of internal damage of rock mass after blasting with different water coupling coefficients

Full size image

In Fig. 15a, corresponding to a water coupling coefficient of 1.2, the rock damage range spans a duration of 0.6 μs. The damage pattern forms a conical shape, with complete destruction near the blast hole. As time progresses to 1.6 μs, the damage scope expands to its maximum extent, and the main propagation of damage occurs upward and downward, resulting in an approximately circular overall damage range. At 2.6 μs, the damage range continues to extend upward from the blast hole and downward to the boundary of the rock specimen. This progression demonstrates the evolution of damage within the rock mass and provides insight into the spatial distribution of the internal damage under different water-coupling conditions. At this stage, the damage range after the explosion reaches its maximum extent and remains relatively constant over time. Figure 15b, c illustrate the damage range after the explosion with water coupling coefficients of 1.33 and 1.5, respectively, showing a similar trend to that observed with a water coupling coefficient of 1.2. In Fig. 15d, for a water coupling coefficient of 2.0, the damage range after the explosion is 0.6 μs, diffusing from the blast hole to the surrounding area. At 1.6 μs, the damage scope only expands vertically along the axial direction of the blast hole, with no significant development observed in other directions. Comparing the four groups of models with different water coupling coefficients, it was observed that an increase in the water coupling coefficient led to a decrease in the internal damage range of the model after the explosion. This indicates that the water coupling coefficient has a significant impact on the distribution of damage within the rock. Based on the stress distribution of the rock mass following explosive blasting and the dynamic compressive strength of the rock, it can be determined that an area with a damage factor greater than 0.9, between 0.1 and 0.9, and between 0 and 0.1, can be classified as the crushing area, fracture area, and elastic area, respectively. When the water coupling coefficient is small, the explosive generates a powerful shock wave that directly impacts the walls of the blast hole after passing through the water medium. The intensity of the shock load from the explosion exceeds the dynamic compressive strength of the rock, leading to the crushing of the rock and the formation of a crushing area. Additionally, a significant amount of energy is consumed by the shock wave during the rock crushing process. Hence, the shock wave is unable to create additional fracture areas beyond the crushing area.

However, as the water coupling coefficient increases and the water medium becomes more prominent, the water's characteristics, such as high density, high viscosity, and low compressibility, enable the uniform dispersion of explosion energy throughout the model medium along with the shock wave. This leads to a more balanced distribution of energy, enabling the formation of fracture areas beyond the initial crushing area. The shock wave strength at the blast hole wall is significantly reduced, and the crushing area caused by the explosion shock wave is reduced, leading to a reduction in the damage range inside the rock.

4.3.2 Characteristics of stress wave propagation under different water coupling coefficients

Figure 16 depicts a cloud chart illustrating the internal stress evolution of the rock model under two different working conditions, corresponding to water coupling coefficients of 1.2 and 2.0. In Fig. 16a, which represents the case with a water coupling coefficient of 1.2, the stress wave is generated at the initial stage of the explosion from the explosive position at the bottom of the blast hole. It propagates in a diffusive manner, spreading from the bottom of the blast hole toward the four sides. By 2.1 μs, the stress wave reaches the boundary of the rock model.

Fig.16
figure 16

Stress evolution nephogram of rock under different water coupling coefficients

Full size image

Similarly, in Fig. 16b, representing the case with a water coupling coefficient of 2.0, the internal stress evolution process follows a similar pattern. At 0.5 μs, the stress wave begins to diffuse outward from the bottom of the blast hole, exhibiting propagation characteristics comparable to those observed with a water coupling coefficient of 1.2. By 2.1 μs, the stress wave also reaches the boundary of the rock model.

These cloud charts provide a visual representation of the temporal and spatial distribution of stress within the rock model under different water coupling coefficients. Comparing the internal stress wave propagation process of the rock model under different water coupling coefficients, there is no obvious difference in the generation time and location of the stress wave under the two groups of coefficients; however, from the stress wave propagation range at the same time, it can be clearly seen that the stress wave strength when the water coupling coefficient is 1.2 is greater than that when the water coupling coefficient is 2.0. When the stress wave propagated to the boundary of the model, the stress distribution around the borehole tended to stabilize. When the water-coupling coefficient was 1.2, the stress at the borehole wall was approximately 96.8 mPa, while when the water coupling coefficient is 2.0, the stress at the borehole wall is reduced by 51.5% to 46.9 mPa. In other words, with an increase in the water coupling coefficient, the detonation products interacted with more water media during the process of propagating to the hole wall, the stress value at the hole wall decreased, and the stress wave intensity inside the model decreased.

The propagation of shock waves in water is closely related to the density, viscosity, and other medium parameters. The density and viscosity of the water medium are relatively high, and the interaction between water molecules is strong. This leads to a corresponding increase in the resistance to shock wave propagation, thus weakening the strength of the shock wave. In addition, the existence of the water medium also results in a thermal diffusion effect, and the explosive releases a large amount of heat after the explosion, which is absorbed and transferred by the water medium. Water molecules escape from the high-temperature area and remove some of the heat, which reduces the temperature in the high-temperature area, whereas the water molecules in the surrounding low-temperature area are heated and then spread to the surrounding low-temperature area, and the heat is transferred to the surroundings. If there is no coupling water medium between the explosive and rock models, the heat release rate in the high-temperature and high-pressure regions is higher, which can enhance the generation and propagation of rock stress waves. However, the thermal diffusion effect of the water medium reduces the temperature in the explosion region, which affects the propagation speed and amplitude of the stress waves in the rock medium. This results in a reduction in the propagation energy of the stress wave, thus weakening the strength of the stress wave. Therefore, with an increase in the water coupling coefficient and water medium, the weakening effect is further enhanced, resulting in a reduction in the initial parameters of the stress wave at the hole wall, thus weakening the strength of the stress wave in the model.

4.3.3 Analysis of time history curve of hole wall pressure

Through numerical simulations, the effects of different water coupling coefficients on the propagation of the explosion stress wave in the blasting rock mass and the dynamic mechanical response of stress elements within the rock mass can be determined. To analyze the variation patterns of hole wall pressure under different water coupling coefficients, the observation point selected was the grid element located at the blast hole wall. Figure 17 illustrates the results of this analysis.

Fig.17
figure 17

Pressure time curve of hole wall with different water coupling coefficients

Full size image

As shown in Fig. 17, with an increase in the water-coupling coefficient, the hole wall pressure at the blast hole wall decreased. This result is consistent with the theoretical derivation, which indirectly confirms the accuracy of the numerical simulation. During water-coupling blasting, the detonation wave compresses the water medium around the explosive and propagates outward. Owing to the high density, large flow viscosity, and incompressibility of the water medium, the expansion speed of the detonation product in water is low, which slows the propagation speed of the shock wave, and the water medium plays a good buffering role. When the water coupling coefficient is 1.2, 1.33, 1.5, 2, the peak pressure of the hole wall is 644.16 MPa, decreases by 38.66% to 395.11 MPa, decreases by 49.89% and 197.99 MPa compared with the former, decreases by 38.37% and 122.02 MPa compared with the former, respectively. Furthermore, the pressure–time curves of the hole wall under the four different working conditions exhibit distinct patterns. At the 200 μs mark, an inflection point is observed, indicating the rapid increase in pressure. This corresponds to the initial impact of the shock wave generated by the detonation products passing through the water medium on the blast hole wall. The pressure at the hole wall quickly reaches its peak, causing crushing damage to the surrounding rock mass and forming the crushing area.

Subsequently, the pressure–time curve of the hole wall enters the attenuation stage, and the hole wall pressure for all four groups of specimens gradually decreases to approximately 50 MPa. The pressure shows slight fluctuations but tends to stabilize. Moreover, the slope of the pressure–time curve in both the rising and falling sections decreases with an increase in the water coupling coefficient. This implies that as the water coupling coefficient increases, the growth and attenuation speed of the stress wave slow down, the duration of the explosion shock wave increases, and the degree of rock damage intensifies.

4.3.4 Analysis of explosion energy time history curve

Figure 18 shows the time–history curves of the explosion energy for different water-coupling coefficients. The image shows that the energy transmitted by the explosion to the rock mass tended to be stable and reached its peak over time. This peak is considered to be the explosion energy brought to the rock mass by an underwater shock wave. When the water coupling coefficient is 1.2, 1.33, 1.5, and 2, the maximum explosion energy obtained by the rock mass is approximately 19.8 MPa, 13.6 MPa, 9.4 MPa, and 3.1 MPa, approximately. With an increase in the water coupling coefficient, the energy obtained by the rock mass decreases. However, the result reflected in the experiment is that the water coupling coefficient increases, and the blasting effect improves. In fact, there is no conflict between the two. When the water coupling coefficient is small, a significant portion of the energy transferred to the rock medium dissipates during the formation of the fracture zone, resulting in only a small fraction of the energy being utilized for rock breaking. However, as the water coupling coefficient increases, more water medium occupies the gap between the blast hole wall and cartridge. The presence of water medium acts as a buffer, reducing the initial pressure at the hole wall and within the crushing area. This enables the explosion energy to be primarily used for the formation and expansion of cracks, resulting in further damage to the rock and an improved blasting effect.

Fig. 18
figure 18

Time history curves of explosion energy under different water coupling coefficients

Full size image

The explosion energy curves for all four working conditions exhibit a rapid rise within approximately 100 μs after the explosion, with the slope of the curve in the rising phase decreasing as the water coupling coefficient increases. The rising stage of the curve corresponds to the process of the explosion energy acting on the hole wall and being transferred to the rock. The smaller the slope of the rising stage, the more explosion energy that can act on the rock medium for a long time and further promote the destruction of the rock.

5 Conclusions

This study mainly analyzes the water-coupling blasting process based on the detonation wave theory, explores the relationship between the hole wall pressure and water coupling coefficient, conducts rock blasting experiments and numerical simulation analysis under different water coupling coefficients, and studies the impact of changes in the water coupling coefficient on the blasting effect. The main conclusions are as follows.

  1. (1)

    Based on the detonation and elastic wave theories, the formation and attenuation laws of shock waves during water-coupled blasting were analyzed, and the relationship between the hole wall pressure and water coupling coefficient was clarified. The specific calculation results showed that the larger the water-coupling coefficient, the smaller was the peak value of the hole wall pressure.

  2. (2)

    During water-coupled blasting, owing to the high density and viscosity of the water medium, the expansion speed of the detonation products in the water was slow, and the explosion energy was evenly dispersed onto the rock medium with the shock wave. The intensity of the shock wave at the borehole wall decreased, resulting in a decrease in the borehole wall pressure and crushing area. More explosion energy is used for crack propagation, making the post-explosion morphology more complex.

  3. (3)

    The results of the CT scanning and 3D reconstruction of the post-explosion specimens show that the post-explosion cracks have good statistical self-similarity, and the fractal dimension can be used to quantitatively characterize the damage and fracture degree of the post-explosion specimens. With an increase in the water coupling coefficient, the degree of damage of the post-explosion specimens first increased and then decreased owing to the uniformity of the failure forms of the specimens.

  4. (4)

    Using the LS-DYNA software to establish blasting models with different water coupling coefficients, we observed the changes in the internal damage area, stress cloud map, and explosion energy time history curve with the water coupling coefficient. The water medium plays a buffering role in the blasting process, causing the damaged area, stress wave intensity, and peak explosion energy received by the rock to decrease with an increasing water-coupling coefficient. In addition, the variation characteristics of the pore wall pressure time–history curve were consistent with the theoretical derivation results.