1 Introduction

In the process of underground mine tunnelling in fault areas, water inrush causes a large number of casualties and property losses every year (Cao et al. 2022). From 2001 to 2009, there were 511 serious mine water inrush accidents, resulting in 3245 fatalities and missing with an economic loss of up to 12 billion RMB (Zhou et al. 2017a). In the water inrush accident, a large amount of groundwater and mud was poured into the tunnel within a short time. The flooding of the tunnel causes the difficulty of rescue work, serious damage to the equipment and machinery, and the stagnation of engineering (Bayati and Khademi Hamidi 2017). In addition, the abnormal inflow of groundwater could also lead to structure strength loss and instability of rock mass, resulting in tunnel collapse and severe structure deformation (Wu et al. 2021; Yuan et al. 2019). In a word, the prevention and control of water inrush disasters are urgent to be solved in the construction of underground mining tunnel.

Due to the severe damage of water inrush hazards, the water inrush prediction has been highlighted. In the previous studies, a series of mathematical models (methods) were used to predict water inrush disasters, such as the statistical method (Qiu et al. 2017; Shi et al. 2018a), GIS-based prediction model (Chen et al. 2018a; Li and Li 2014; Marquínez et al. 2003; Wu et al. 2011), fuzzy system theory (Wang et al. 2012; Zhou et al. 2017b), analytic hierarchy process (Chen et al. 2018b; Wang et al. 2019b, 2012; Wu et al. 2011; Zhang and Yang 2018), artificial neural network model (Zhou et al. 2017b), grey model (Li and Yang 2018; Zhang and Yang 2018), Fisher discriminant model (Chen et al. 2016), evidence theory (Li et al. 2017; Qiu et al. 2017), ideal point method (Wang et al. 2019b). These models have positive implications for the prediction of water inrush disasters. However, most of them are concentrated on the probability characteristics of water inrush, instead of the variation of hydraulic characteristics during water inrush.

To study the evolution laws of hydraulic properties before the water inrush accidents, a series of seepage experiments (Li et al. 2019a; Yang et al. 2018) and numerical simulations (Li et al. 2019b; Osman and Bruen 2002) were carried out. In some seepage experiments and engineering sites, the phenomenon of two-phase mixed seepage has attracted the attention of scholars (Li and Li 2014; Xue et al. 2018). When the confined water flows through the rock fracture zone (e.g. faults and karst collapse pillar), fine particles are forced to migrate, forming a water–rock mixed flow, so that the permeability of the rock mass increases continuously (Li et al. 2018a; Liu et al. 2018a). Meanwhile, the increase in permeability can increase the velocity and transportation capacity of water flow, so that more particles are migrated and lost. This mixed flow effect can induce a water inrush pathway, leading to a water inrush accident eventually (Liu et al. 2018b; Ma et al. 2023). In order to study the relationship between particle migration and water inrush, a series of two-phase flow experiments were conducted (Ma et al. 2017; Zhang et al. 2017). Ma et al. (2022a) designed a set of experimental systems for radial particle migration, and conducted a series of radial sandstone erosion-seepage experiments. However, due to the constraints of experimental instrument design and experimental conditions, only the temporal evolution of porosity, permeability, and fluid velocity were observed in the previous experiments. The spatial distribution of these parameters was difficult to be measured. In addition, variables such as water pressure and particle concentration cannot be studied experimentally. Therefore, the temporal and spatial evolution of the seepage field cannot be fully explored.

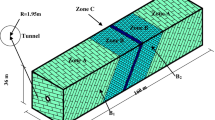
To make up for the lack of experimental research, numerical models were established to predict the evolution of the seepage field during particle migration. Bai et al. (2016) developed a numerical model to predict the suspended-particle migration for short-time constant-concentration injections and repeated three-pulse injections. Liu et al. (2017) established an erosion seepage model and discussed the effect of the thickness of the grout layer on the seepage. Based on the discrete element method, Wang et al. (2019a) established a particle migration model in the fractured sandstone during the groundwater inrush process. When the water-bearing fault fracture zone is encountered in the mining tunnel construction, the confined groundwater gathers from the periphery to the side wall of the tunnel (see Figs. 1, 2a) (Li et al. 2018b; Ma et al. 2022b; Ye and Liu 2018). Under such a condition of radial seepage, the path of particle migration will be more complicated; and the temporal-spatial evolution of term parameters is difficult to be measured.

Fig. 1
figure 1

Tunneling advance through fault fracture zone above a confined aquifer

Full size image
Fig. 2
figure 2

Principle of rock granules migration system. Symbols: rA- radius of the lower boundary, rB- radius of the upper boundary, pA-pore pressure at the lower boundary, pB-pore pressure at the upper boundary, σB-uniform external stress, σr- radial stress, σθ-tangential stress

Full size image

Another issue is the instability of the rock mass caused by water inrush (Hui et al. 2018; Meng et al. 2020; Wang et al. 2022). During water inrush, as seepage proceeds, the rock mass undergoes softening and disintegration, making it susceptible to large deformations under the effect of excavation disturbance. Many researchers (Li et al. 2019a; Wang et al. 2022) have studied the mechanical response characteristics of rock masses during water inrush, but most of these studies have focused on the effect of the fracture propagation and damage on the permeability of rock mass, failing to take into account the rock particle migration effect under water pressure. In fact, as the particles migrate, the structural strength of the rock mass decreases and is prone to collapse and damage under the stress-seepage effect, which eventually makes the surrounding rock mass unstable.

In this paper, considering the mass conservation, pore evolution, and nonlinear motion law during the migration of fine rock particles, a water–rock mixed flow model is established. Then, the reliability of the model is verified by the data from a previous experimental study. After, the temporal-spatial evolution of the hydraulic and stress fields during radial erosion seepage is predicted by the proposed mixed flow model, which reveals the precursory properties of water inrush and instability of fault rocks. Finally, the applicability and limitations of the proposed model are scrutinized through a comparative analysis with the existing water inrush model.

2 Computational models

2.1 Model descriptions and assumptions

When the fault fracture zone is encountered in mining tunnel construction, the surrounding rock of the tunnel is filled with broken and loose fault fillers. These fillers are composed of broken rock with different sizes, in which fine rock particles are easy to be migrated under the effect of confined groundwater and stress, then water inrush pathways are formed (see Fig. 2a). In order to facilitate the experimental verification of the model, the fault fracture rock model is simplified in this paper. As shown in Fig. 2b, a part of the annular model (sector shape) is intercepted as a seepage-stress model. The radius of the upper boundary is \(r_{\text{B}}\), and the radius of the lower boundary is \(r_{\text{A}}\). For the seepage field, the pore pressure at the upper boundary of the model is \(p_{\text{B}}\), and the pore pressure at the lower boundary is \(p_{\text{A}}\). Due to the difference in pressure between the upper and lower water, the fluid flows radially to the centre point of the tunnel. At the same time, the fractured rock is affected by the stress field, where the radial stress is \(\sigma_{r}\), tangential stress is \(\sigma_{\theta }\), and uniform external stress is \(\sigma_{\text{B}}\).

The model also contains the following basic assumptions:

  1. (1)

    The rock mass comprises three phases, namely, solid skeleton, water and fluidized rock particles. The solids phases are insoluble in water.

  2. (2)

    The pores in the rock mass are saturated with water and fluidized particles.

  3. (3)

    The porosity of the rock mass is effective porosity, while closed pores are considered part of the solid skeleton.

  4. (4)

    During the migration of fluidized particles, there is no deformation of the solid skeleton, and the fluid is incompressible.

  5. (5)

    The velocities of fluidized particles and water are consistently maintained at the same value.

  6. (6)

    The rock mass exhibits isotropic properties.

2.2 Definitions

The broken rock is viewed as a three-phase material with the representative volume element \(\text{d}V\), consisting of (0) solid skeleton with volume \(\text{d}V_{\text{s}}\) and mass \(\text{d}m_{\text{s}}\); (1) liquid water with volume \(\text{d}V_{\text{f}}\) and mass \(\text{d}m_{\text{f}}\); (2) fluidized particles with volume \(\text{d}V_{\text{fs}}\) and mass \(\text{d}m_{\text{fs}}\). According to assumption a), the porosity \(\phi\) and the volume concentration of the fluidized particle \(c\) are defined as:

$$\phi = \frac{{\text{d}V_{\text{f}} + \text{d}V_{\text{fs}} }}{\text{d}V}$$
(1)
$$c = \frac{{\text{d}V_{\text{fs}} }}{{\text{d}V_{\text{f}} + \text{d}V{}_{\text{fs}}}}$$
(2)

The partial densities of the three phases ((0) solid skeleton; (1) liquid water; (2) fluidized particles) are respectively defined by the following equations:

$$\left\{ {\begin{array}{*{20}l} {\rho^{\left( 0 \right)} = \frac{{\text{d}m_{\text{s}} }}{\text{d}V} = \rho_{\text{s}} \frac{{\text{d}V_{\text{s}} }}{\text{d}V} = \rho_{\text{s}} \frac{{\text{d}V - \left( {\text{d}V_{\text{f}} + \text{d}V_{\text{fs}} } \right)}}{\text{d}V} = \left( {1 - \phi } \right)\rho_{\text{s}} } \hfill \\ {\rho^{\left( 1 \right)} = \frac{{\text{d}m_{\text{f}} }}{\text{d}V} = \rho_{\text{f}} \frac{{\text{d}V_{\text{f}} }}{\text{d}V} = \rho_{\text{f}} \frac{{\phi \text{d}V - \text{d}V_{\text{fs}} }}{\text{d}V} = \left( {1 - c} \right)\phi \rho_{\text{f}} } \hfill \\ {\rho^{\left( 2 \right)} = \frac{{\text{d}m_{\text{fs}} }}{\text{d}V} = \frac{{\rho_{\text{s}} \text{d}V_{\text{fs}} }}{\text{d}V} = \rho_{\text{s}} \frac{c\phi \text{d}V}{{\text{d}V}} = c\phi \rho_{\text{s}} } \hfill \\ \end{array} } \right.$$
(3)

where \(\rho_{\text{s}}\) and \(\rho_{\text{f}}\) are the density of rock and water. The partial density of the water–rock mixture flow \(\overline{\rho }\) is:

$$\overline{\rho } = \frac{{\text{d}m_{\text{f}} + \text{d}m_{\text{fs}} }}{{\text{d}V_{\text{f}} + \text{d}V_{\text{fs}} }}{\kern 1pt} = c\rho_{\text{s}} + \left( {1 - c} \right)\rho_{\text{f}}$$
(4)

Velocities of three phases are defined as \(v_{i}^{(0)}\), \(v_{i}^{(1)}\), \(v_{i}^{(2)}\) (\(i = 1,2,3\)). According to assumptions (b) and (c), there are:

$$v_{i}^{\left( 0 \right)} { = }0$$
(5)
$$v_{i}^{\left( 1 \right)} = v_{i}^{\left( 2 \right)}$$
(6)

The volume discharge rate of water and fluidized particles can be defined as:

$$q_{i}^{\left( 1 \right)} = \left( {1 - c} \right)\phi v_{i}^{\left( 1 \right)}$$
(7)
$$q_{i}^{\left( 2 \right)} = c\phi v_{i}^{\left( 1 \right)} = {{cq_{i}^{\left( 1 \right)} } \mathord{\left/ {\vphantom {{cq_{i}^{\left( 1 \right)} } {\left( {1 - c} \right)}}} \right. \kern-0pt} {\left( {1 - c} \right)}}$$
(8)

The volume discharge rate of the mixture fluid \(\overline{q}_{i}\) is defined as:

$$\overline{q}_{i} = \phi \left( {v_{i}^{\left( 1 \right)} - v_{i}^{\left( 0 \right)} } \right) = \phi v_{i}^{\left( 1 \right)}$$
(9)

2.3 Governing equations of the seepage field

2.3.1 Mass balance equation

According to the fluid mass conservation equation (Bear 1972), based on partial densities and velocity of three phases, the three-phase mass conservation equation is obtained:

$$\frac{{\partial \rho^{\left( n \right)} }}{\partial t} + \text{div}\left( {\rho^{\left( n \right)} {{v}}^{\left( n \right)} } \right) = j^{\left( n \right)}$$
(10)

where \(j^{\left( n \right)}\) is the mass loss rate of the nth phase under the action of confined water (\(n = 0,1,2\)). Combining Eqs. (3) and (5)–(10), the mass balance equation of the three phases is obtained as follows:

  • Solid skeleton phase:

$$\frac{\partial \phi }{{\partial t}} = - \frac{{j^{\left( 0 \right)} }}{{\rho_{\text{s}} }}$$
(11)

  • Liquid phase:

$$\frac{{\partial \left( {1 - c} \right)\phi }}{\partial t} + \text{div}\left[ {\left( {1 - c} \right)\overline{q}_{i} } \right] = j^{\left( 1 \right)}$$
(12)

  • Fluidized particles phase:

$$\frac{{\partial \left( {c\phi } \right)}}{\partial t} + \text{div}\left( {c\overline{q}_{i} } \right) = \frac{{j^{\left( 2 \right)} }}{{\rho_{\text{s}} }}$$
(13)

Assuming that all fluidized particles are stemmed from the skeleton, i.e., \(j^{\left( 2 \right)} = - j^{\left( 0 \right)}\). As there is no mass change in the liquid phase, \(j^{\left( 1 \right)} = 0\). Combining Eqs. (11)–(13), we can obtain a continuous equation for the water–rock mixed flow:

$$\text{div}{\kern 1pt} {\kern 1pt} {\kern 1pt} \overline{q}_{i} = 0$$
(14)

2.3.2 Constitutive equations of particle migration

Sakthivadivel (Sakthivadivel 1967) summarized the experimental and theoretical work of non-colloidal solid particles filtration in porous media materials and obtained the basic equations for controlling filtration kinetics.

The fluidized particles can be calculated by the following equation:

$$j^{\left( 2 \right)} = j_{\text{tr}}^{\left( 0 \right)} - j_{\text{de}}^{\left( 2 \right)}$$
(15)

where \(j_{\text{tr}}^{\left( 0 \right)}\) is the mass variable rate of skeleton solid transportation due to the action of confined water, \(j_{\text{de}}^{\left( 2 \right)}\) is the mass variable rate of fluidized particles due to deposition.

According to the research of Sakthivadivel, the relationship among \(j_{\text{tr}}^{\left( 0 \right)}\), \(j_{\text{de}}^{\left( 2 \right)}\), \(\phi\), and \(c\) are shown as follows:

$$j_{\text{tr}}^{\left( 0 \right)} = \lambda \rho_{\text{s}} \left( {1 - \phi } \right)c\left| {\overline{q}_{i} } \right|$$
(16)
$$j_{\text{de}}^{\left( 2 \right)} = \lambda \rho_{\text{s}} \left( {1 - \phi } \right)\frac{{c^{2} }}{{c_{\text{cr}} }}\left| {\overline{q}_{i} } \right|$$
(17)

where \(\lambda\) is a particle migration parameter; \(c_{\text{cr}}\) is a critical value of c between transportation and deposition. Then, Eqs. (16) and (17) are substituted into Eq. (15) as:

$$j^{\left( 2 \right)} = \lambda \rho_{\text{s}} \left( {1 - \phi } \right)\left[ {c - \frac{{c^{2} }}{{c_{\text{cr}} }}} \right]\left| {\overline{q}_{i} } \right|$$
(18)

In fact, according to test results (Bendahmane et al. 2008; Chang and Zhang 2011), the fractured rock mass cannot be completely migrated under a certain pore pressure gradient. It is indicated that \(j^{\left( 2 \right)}\) approaches zero at a certain moment, and the porosity reaches a stable value \(\phi {}_{\text{s}}\). Therefore, Eq. (18) can be rewritten as:

$$j^{\left( 2 \right)} = \lambda \rho_{\text{s}} \left( {\phi_{\text{s}} - \phi } \right)\left[ {c - \frac{{c^{2} }}{{c_{\text{cr}} }}} \right]\left| {\overline{q}_{i} } \right|$$
(19)

2.3.3 Non-Darcy flow equation in the broken rock mass

On the basis of previous research (Mathias and Todman 2010), the Forchheimer equation (a kind of non-Darcy flow equation) is often used to describe the quadratic relationship between the pore pressure gradient \(\nabla p\) and the volume discharge rate of mixed fluid \(\overline{q}_{i}\), namely:

$$- \nabla p = \frac{{\mu \overline{\rho }}}{k}\overline{q}_{i} + \overline{\rho }\beta \left| {\overline{q}} \right|\overline{q}_{i}$$
(20)

where \(\mu\) is the kinematic viscosity of water; \(k\) is the permeability; \(\beta\) is the non-Darcy factor, which indicates that the volume discharge rate is determined not only by the viscous force but also by the inertial force (Thauvin and Mohanty 1998).

According to the research of Li et al. (2001), the non-Darcy factor \(\beta\) has the following empirical relationship between permeability \(k\) and porosity \(\phi\):

$$\beta = \beta_{0} k^{ - 1} \phi^{ - 1}$$
(21)

where \(\beta_{0}\) is the non-Darcy parameter. Combining Eqs. (20) and (21), the non-Darcy equation of water–rock mixture flow can be obtained as:

$$- \nabla p = \frac{{\mu \overline{\rho }}}{k}\overline{q}_{i} + \frac{{\overline{\rho }\beta_{0} }}{k\phi }\left| {\overline{q}} \right|\overline{q}_{i} = \frac{{\overline{\rho }}}{k}\overline{q}_{i} \left( {\mu + \frac{{\beta_{0} }}{\phi }\left| {\overline{q}} \right|} \right)$$
(22)

The change in porosity is bound to cause changes in the permeability of skeleton particles. Ma et al. (2022a) predict the evolution of fault rock mass permeability, the result shows the Carman-Kozeny equation has the highest fitting accuracy, that is

$$k = k_{\text{c}} \frac{{\phi^{3} }}{{\left( {1 - \phi } \right)^{2} }}$$
(23)

where \(k_{\text{c}}\) is the permeability parameter independent of the porosity of the rock sample.

2.3.4 Governing equations of the radial erosion process

According to the model features shown in Fig. 2, the fluid flows radially to the center of the tunnel. Based on Eq. (14), there are \(\overline{q}_{2} = \overline{q}_{3} = 0\) and:

$$\overline{q}_{r} = \overline{q}_{1} = - q\left( t \right)\quad \left( {q > 0} \right)$$
(24)

Under radial seepage conditions, Eqs. (4), (13), (14), (19), and (22)–(24) are combined, the governing equations of the water–rock mixture flow model system can be obtained as:

$$\left\{ {\begin{array}{*{20}l} {\frac{\partial \phi }{{\partial t}} = \overline{q}_{r} \frac{\partial c}{{\partial r}} + \frac{{\partial \left( {c\phi } \right)}}{\partial t}} \hfill \\ {\frac{\partial \phi }{{\partial t}} = \lambda \left( {\phi_{\text{s}} - \phi } \right)\left[ {c - \frac{{c_{{}}^{2} }}{{c_{\text{cr}} }}} \right]\left| {\overline{q}_{r} } \right|} \hfill \\ { - \frac{\partial p}{{\partial r}} = \frac{{\overline{\rho }}}{k}\overline{q}_{r} \left( {\mu + \frac{{\beta_{0} }}{\phi }\left| {\overline{q}_{r} } \right|} \right)} \hfill \\ {\frac{{\overline{q}_{r} }}{r} + \frac{{\partial \overline{q}_{r} }}{\partial r} = 0} \hfill \\ {\overline{\rho } = c\rho_{\text{s}} + \left( {1 - c} \right)\rho_{\text{f}} } \hfill \\ {k = k_{\text{c}} \frac{{\phi^{3} }}{{\left( {1 - \phi } \right)^{2} }}} \hfill \\ \end{array} } \right.$$
(25)

2.4 Governing equations of the stress field

2.4.1 Constitutive equations of stress and strain

In this paper, the total stress tensor \(\sigma_{ij}\) is considered as the sum of the stress on the mixed fluid \(\sigma_{ij}^{\left( \text{f} \right)}\) and the solid skeleton \(\sigma_{ij}^{\left( \text{s} \right)}\), that is,

$$\sigma_{ij} = \sigma_{ij}^{\left( \text{f} \right)} + \sigma_{ij}^{\left( \text{s} \right)}$$
(26)

In the above equation, the stress on the mixed fluid is described by the pore pressure, i.e.

$$\sigma_{ij}^{\left( \text{f} \right)} = - \phi p\delta_{ij}$$
(27)

And the stress on the solid skeleton is

$$\sigma_{ij}^{\left( \text{s} \right)} = \left( {1 - \phi } \right)\overline{\sigma }_{ij}$$
(28)

where the \(\overline{\sigma }_{ij}\) is the strain-dependent constitutive stress, and it could be calculated in the isotropic linear elastic model:

$$\overline{\sigma }_{ij} = \Lambda \varepsilon_{kk} \delta_{ij} + 2G\varepsilon_{ij}$$
(29)

where \(\Lambda\) and \(G\) are Lame coefficients, which are defined through Poisson’s ratio \(\nu\) and elasticity modulus \(\overline{E}\):

$$\Lambda = \frac{{\overline{E}\nu }}{{\left( {1 - \nu } \right)\left( {1 - 2\nu } \right)}},G = \frac{{\overline{E}}}{{2\left( {1 - \nu } \right)}}$$
(30)

In combination with Eqs. (28) and (29), porosity \(0 < \phi < 1\) can be used to describe the internal damage of the fault rocks, and it can be defined as the damage parameter:

$$E = \overline{E}\left( {1 - \phi } \right)$$
(31)

According to the Terzaghi effective stress principle, the total stress is divided into two components, the effective stress \(\sigma^{{\prime }}\) and the pore pressure, i.e.

$$\sigma_{ij} = \sigma_{ij}^{\prime } - p\delta_{ij}$$
(32)

Combining Eqs. (26)–(28) and (32), the relation among effective stress, constitutive stress and pore pressure is:

$$\sigma_{ij}^{\prime } = \left( {1 - \phi } \right)\left( {\overline{\sigma }_{ij} + p\delta_{ij} } \right)$$
(33)

As particle migration occurs, the increase in porosity and the decrease in cohesion between solid particles will further facilitate the migration of fine particles. Based on the previous experimental phenomena, the migration of fine particles can be described by using the interaction between cohesion C and porosity as follows.

$$C = \overline{C}\left( {1 - \phi } \right)$$
(34)

Based on the above equations and the Mohr–Coulomb failure criterion, the effective principal stress is modified as:

$$\frac{1}{2}\left( {\sigma_{1}^{\prime } + \sigma_{2}^{\prime } } \right)\sin \gamma - \frac{1}{2}\left( {\sigma_{1}^{\prime } - \sigma_{2}^{\prime } } \right) = C\cos \gamma = \overline{C}\left( {1 - \phi } \right)\cos \gamma$$
(35a)

or,

$$\tau_{\text{m}} = - \sigma_{\text{m}} \sin \gamma + C\cos \gamma$$
(35b)

where, \(\gamma\) is the friction angle; \(\sigma_{1}^{\prime }\) and \(\sigma_{2}^{\prime }\) are the maximum and minimum principal effective stress, respectively; \(\tau_{\text{m}}\) is tangential stress; \(\sigma_{\text{m}}\) is the average stress; \(\tau_{\text{m}}\) and \(\sigma_{\text{m}}\) could be calculated by the following equation:

$$\tau_{\text{m}} = - \frac{1}{2}\left( {\sigma_{1}^{\prime } - \sigma_{2}^{\prime } } \right),\sigma_{\text{m}} = \frac{1}{2}\left( {\sigma_{1}^{\prime } + \sigma_{2}^{\prime } } \right)$$
(36)

2.4.2 The instability properties of fault rocks

Based on the above analysis, the instability of rocks is simplified to a plane strain axisymmetric deformation problem for investigation. In combination with Eqs. (26)–(30), the elastic constitutive relationship between the total stress and the total strain is established as

$$\sigma_{r} = \frac{{\overline{E}\left( {1 - \phi } \right)}}{{\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)}}\left[ {\left( {1 - \nu } \right)\varepsilon_{r} + \nu \varepsilon_{\theta } } \right] - \phi p$$
(37)
$$\sigma_{\theta } = \frac{{\overline{E}\left( {1 - \phi } \right)}}{{\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)}}\left[ {\left( {1 - \nu } \right)\varepsilon_{\theta } + \nu \varepsilon_{r} } \right] - \phi p$$
(38)

The strain could be expressed by radial displacement \(u_{r} = u\left( {r,t} \right)\):

$$\varepsilon_{r} = \frac{\partial u}{{\partial r}}$$
(39)
$$\varepsilon_{\theta } = \frac{u}{r}$$
(40)

For the stress balance equations of \(\sigma_{r} = \sigma_{r} \left( {r_{\text{A}} ,t} \right)\) and \(\sigma_{\theta } = \sigma_{\phi } \left( {r_{\text{A}} ,t} \right)\), ignoring body force, we get:

$$\frac{{\partial \sigma_{r} }}{\partial r} + \frac{{\sigma_{r} + \sigma_{\theta } }}{r} = 0$$
(41)

Substituting Eqs. (37)–(40) into Eq. (41), the radial displacement can be described by the following differential equation, that is,

$$\frac{{\partial^{2} u}}{{\partial r^{2} }} + g_{1} \frac{\partial u}{{\partial r}} - g_{2} u = g_{3} \frac{{\partial \left( {\phi p} \right)}}{\partial r}$$
(42)

where \(g_{i} = g_{i} \left( {r,t} \right)\) are the parameters related \(\nu\) and \(\phi = \phi \left( {r,t} \right)\), i.e.,

$$g_{1} = \frac{1}{r} - \frac{1}{1 - \phi }\frac{\partial \phi }{{\partial r}},g_{2} = \frac{1}{{r^{2} }} + \frac{1}{r}\frac{\nu }{1 - \nu }\frac{1}{1 - \phi }\frac{\partial \phi }{{\partial r}},g_{3} = \frac{{\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)}}{{\overline{E}\left( {1 - \nu } \right)\left( {1 - \phi } \right)}}$$
(43)

2.5 Computational conditions

For the seepage field, since the nonlinear differential equations contain four unknowns, namely \(\phi\), \(c\), \(q\) and \(p\), the corresponding boundary conditions and initial conditions need to be established. According to Fig. 2b, the following boundary conditions exist on the lower and upper boundary surfaces of the model:

$$c\left( {r_{\text{B}} ,t} \right) = c_{\text{B}} ,p\left( {r_{\text{A}} ,t} \right) = p_{\text{A}} ,p\left( {r_{\text{B}} ,t} \right) = p_{\text{B}}$$
(44)

The initial conditions for the porosity and volume concentration are:

$$\phi \left( {r,0} \right) = \phi_{0} ,c\left( {r,0} \right) = c_{0} = c_{\text{B}} ,k\left( {r,0} \right) = k_{0} = \frac{{k_{\text{c}} \phi_{0}^{3} }}{{\left( {1 - \phi_{0} } \right)^{2} }}$$
(45)

It is noted that due to the hyperbolic nature of Eq. (23), the initial conditions regarding \(\phi\) and \(c\) may result in non-smooth solutions. According to Eqs. (23), (25) and (44), the initial values of the volume discharge rate \(q\left( {r,0} \right)\) and pore pressure \(p\left( {r,0} \right)\) of the system can be obtained as follows:

$$q\left( {r,0} \right) = \frac{{C_{1} }}{r}$$
(46)
$$p\left( {r,0} \right) = a_{1} C_{1} \ln r - \frac{{a_{2} C_{1}^{2} }}{r} + C_{2} = p\left( {r_{\text{A}} } \right) + a_{1} C_{1} \ln \left( {{r \mathord{\left/ {\vphantom {r {r_{\text{A}} }}} \right. \kern-0pt} {r_{\text{A}} }}} \right) + \frac{{a_{2} C_{1}^{2} }}{{rr_{\text{A}} }}\left( {r - r_{\text{A}} } \right)$$
(47)

where \(a_{1} = \frac{{\overline{\rho }\mu }}{{k\left( {r,0} \right)}}\), \(a_{2} = \frac{{\overline{\rho }\beta_{0} }}{{k\left( {r,0} \right)\phi \left( {r,0} \right)}}\), \(C_{1}\) and \(C_{2}^{{}}\) are parameters related to the \(a_{1}\), \(a_{2}\), \(r_{\text{A}}\), \(r_{\text{B}}\), \(p_{\text{A}}\) and \(p_{\text{B}}\).

For the stress field, according to Fig. 2, the boundary conditions of stress are:

$$\sigma_{r} \left( {r_{\text{A}} ,t} \right) = - P_{\text{A}} ,\sigma_{r} \left( {r_{\text{B}} ,t} \right) = - \sigma_{\text{B}}$$
(48)

And the boundary conditions of displacement are:

$$\left. {\frac{\partial u}{{\partial r}}} \right|_{{r = r_{\text{A}} }} = - \frac{\nu }{1 - \nu }\frac{{u\left( {r_{\text{A}} } \right)}}{{r_{\text{A}} }}{ + }g_{3} \left( {r_{\text{A}} ,t} \right)\left[ {\phi \left( {r_{\text{A}} ,t} \right)p_{\text{A}} - p_{\text{A}} } \right]$$
(49)
$$\left. {\frac{\partial u}{{\partial r}}} \right|_{{r = r_{\text{B}} }} = - \frac{\nu }{1 - \nu }\frac{{u\left( {r_{\text{B}} } \right)}}{{r_{\text{B}} }} + g_{3} \left( {r_{\text{B}} ,t} \right)\left[ {\phi_{0} p_{\text{B}} - \sigma_{\text{B}} } \right]$$
(50)

The initial boundary of radial displacement could be obtained by solving Eqs. (42), (49) and (50). When \(u\) and \({{\partial u} \mathord{\left/ {\vphantom {{\partial u} {\partial r}}} \right. \kern-0pt} {\partial r}}\) are obtained, the initial boundary of stress could be obtained by substituting them into Eqs. (37)–(40).

3 Numerical solution of the water–rock mixed flow model

3.1 Parameters calibration

Before solving the mixed flow model, the material element characteristic parameters of the model should be calibrated, including the fine particle migration parameter \(\lambda\), the permeability parameter of the fractured rock mass \(k_{\text{c}}\), non-Darcy parameter β0 and the stable porosity of the material unit \(\phi_{\text{s}}\). The calibration experiment is carried out in the calibrated test system, as shown in Fig. 3a; the calibrated test procedure is shown in Fig. 3b. From the test conditions in Ma et al.’s research (Ma et al. 2022a) and the calibrated test, the fixed parameters of the numerical model are determined and shown in Table 1. The variable parameters for the numerical simulation of Sample A-F are shown in Table 2. The simulation time is set as 1600 s.

Fig. 3
figure 3

The calibrated test system and test procedure a Calibrated test system b Calibrated test procedure

Full size image
Table 1 Fixed parameters of the mixture flow model
Full size table
Table 2 Variable parameters for numerical simulation of Samples A–F
Full size table

3.2 Computational conditions and analysis algorithms

In this study, COMSOL Multiphysics is adapted to solve the proposed model. For the spatial domain, the Galerkin finite element method is used to approximate the partial differential equations. Then, the implicit difference method is adopted to discretize the model in the time domain and the Newton iteration method is employed to solve for the result at each time step. The results of the seepage field are obtained first by solving the governing equations of the seepage field, and then these results would be substituted into the governing equations of the stress field and output the corresponding solutions. The mesh type employed is a structured quadrilateral mesh, with the following parameters: maximum element size of 1.98 cm, minimum element size of 0.088 cm, maximum element growth rate of 1.15 and curvature factor of 0.3. The time-stepping method used is BDF (backward differentiation formula), and the solver is MUMPS (multifrontal massively parallel sparse direct solver), which belongs to implicit solvers.

4 Results and discussion

4.1 Comparison of model and test results

Porosity is an important index of hydraulic property. In this paper, the prediction accuracy of the model is analysed by comparing the porosity values obtained by the model and the previous experiment (Ma et al. 2022a) (In Ma et al.’s research, a conical cylinder was utilized to perform a series of radial erosion tests on the fractured rocks). According to the theoretical model, the calculated value of porosity at time ti (\(\phi_{\text{c}i}\)) is:

$$\phi_{\text{c}i} = \frac{{\int_{{r_{\text{A}} }}^{{r_{\text{B}} }} {\phi_{\text{c}i} \left( r \right)\text{d}r} }}{{r_{\text{B}} - r_{\text{A}} }},\left( {i = 1, \ldots ,n} \right)$$
(51)

In this paper, the absolute percentage error (APE) is used to evaluate the difference between the calculated value and tested value at each moment, and the mean absolute percentage error (MAPE) is used to evaluate the accuracy of the numerical model during the whole seepage process, namely:

$$\text{APE}_{i} = \left| {\frac{{\phi_{i} - \phi_{\text{c}i} }}{{\phi_{i} }}} \right|\times100\%$$
(52)
$$\text{MAPE} = \frac{1}{n}\sum\limits_{i = 1}^{n} {\left| {\frac{{\phi_{i} - \phi_{\text{c}i} }}{{\phi_{i} }}} \right|}\times100\%$$
(53)

where \(\phi_{i}\) is the tested value, which is measured in Ma et al.’s research (Ma et al. 2022a).

Figure 4 shows the comparison of tested values with calculated values and APE for all samples. It can be seen that, both calculated and tested values increase over time, and show faster growth in the initial stage than that in the late stage of the seepage. At the end of the test, the growth of both values is stopped. As shown in Fig. 4b, APE of all samples shows a growth in the early stage of seepage, which is related to the formation of the seepage pathway and the fluctuation of the particles in the sample. In addition, in the steady flow phase, APEs of all samples increase, and the calculated value is greater than the tested value at the end of seepage, due to the stable porosity \(\phi_{\text{s}}\) being greater than the final porosity of the sample \(\phi_{n}\). This difference is probably caused by the heterogeneity of the pores inside the rock mass caused by radial seepage.

Fig. 4
figure 4

Comparison of the test and predictive results for porosity and APE of samples a Porosity; b APE CV: calculated value TV: tested value

Full size image

Figure 5 depicts the MAPE of each sample, it can be observed that the MAPE of all samples is within 3.5%, indicating that the calculated values of the model coincide with tested values. The MAPE of Sample A-C is similar, both at about 2%. It shows that the particle size distribution (PSD) has little effect on the prediction accuracy of the model; the prediction accuracy of Sample D-F gradually increases, the MAPE of Sample D is 3.1%, and that of Sample F is only 1.5%. This is probably caused by the smoother particle migration in the sample under large pore pressure.

Fig. 5
figure 5

MAPE for all samples

Full size image

The spatial distribution of porosity is also compared between the testing values and the calculated values. To compare the spatial distribution, the sample is divided into 6 sections from top to bottom according to the equal sample height. And these sections are labelled as Sect. 1 to Sect. 6 from top to bottom. And the calculated value of porosity in Section j (\(\phi_{cj}\)) can be obtained by:

$$\phi_{cj} = \frac{{\int_{{r_{j + 1} }}^{{r_{j} }} {\phi_{\text{c}n} \left( r \right)\text{d}r} }}{{r_{j} - r_{j + 1} }},\left( {j = 1, \ldots ,6} \right)$$
(54)

where \(r_{j} = r_{\text{B}} - \frac{{\left( {j - 1} \right)\left( {r_{\text{B}} - r_{\text{A}} } \right)}}{6}\).

From the calculated results, the porosity from top to bottom gradually increases and reaches the maximum at the bottom fluid outlet (see Fig. 6). The final porosity is between the second and third parts, which is mainly consistent with the tested results.

Fig. 6
figure 6

Comparison of the test and predictive results for porosity of the six sections a Samples A–C, b Samples D–F CV: calculated value TV: tested value

Full size image

The above result indicates the high accuracy of the proposed model, and the applicability of the proposed model is verified for the temporal-spatial evolution prediction of the flow field. In the next chapter, Sample F is taken as an example to predict the temporal-spatial evolution of several hydraulic parameters (including porosity, volume concentration of fluidized particles, flow rate, pore pressure, and permeability).

4.2 Temporal-spatial evolution of the seepage field

4.2.1 Porosity

Figure 7 shows the temporal-spatial evolution surface of the porosity in Sample F. For the temporal evolution of porosity at different positions, the porosity is gradually increased by the migration of fine particles. In addition, the closer to the fluid outlet, the more intense the porosity increases. It indicates that the migration of fine particles tends to occur near the fluid outlet. The porosity increases rapidly before 600 s and then stabilizes, which is consistent with the rapid increase in porosity at the initial stage of the experimental observation. Besides, it can be concluded that the further away from the fluid outlet, the longer the duration of porosity growth.

Fig. 7
figure 7

Temporal-spatial distribution of porosity

Full size image

For the spatial distribution of porosity at different times, it can be seen that as the distance from the fluid outlet increases, the porosity decreases gradually, indicating that the particle migration effect in the upper parts of the sample is weaker than that in the lower parts. At the beginning of the seepage, the spatial distribution of porosity in the container is relatively uniform. From 60 to 660 s, the porosity near the fluid outlet increases greatly within a short time, resulting in the uneven spatial distribution of porosity. Although the porosity growth in the upper part of the sample has the longest duration, the porosity of the upper parts of the sample is still lower than that of the lower part at the end of the seepage process. The result is consistent with the test observation.

4.2.2 Volume concentration of the fluidized particle

The temporal-spatial evolution results of the volume concentration of fluidized particles in Sample F are depicted in Fig. 8. It is concluded in terms of temporal evolution that, the volume concentration of fluidized particles at a position close to the fluid outlet (r < 18.6 cm) can increase rapidly to a peak value, but much smaller than the critical volume concentration value of 0.3. After reaching the peak value, the volume concentration drops rapidly, and it decreases slowly and eventually tends to a stable value after 800 s. However, the volume concentrations of the fluidized particle far from the fluid outlet (r > 18.6 cm) show a different temporal evolution law. Volume concentrations slowly decrease from the initial values and eventually tend to be stable.

Fig. 8
figure 8

Temporal-spatial distribution of sandstone particle volume concentration

Full size image

In terms of the spatial distribution of the volume concentration of the fluidized particle at different times, it can be observed that the highest volume concentration of the fluidized particle occurs at the closest position to the fluid outlet. The reasons are explained as follows. First, there are more intense erosion occurs near the fluid outlet, leading to more fluidized rock particle production. Second, due to the downward migration of fine particles in the upper parts, the volume concentration of particles in the fluid is higher than that in the upper positions. As the seepage progresses, the particle migration effect gradually slows down, the volume concentration of solid particle decreases, and the spatial distribution of the particle concentration becomes more uniform. At 1560 s, volume concentrations of all positions drop below 1‰, indicating the end of the particle migration.

4.2.3 Volume discharge rate

The temporal-spatial evolution of the volume discharge rate is depicted in Fig. 9. With regard to the temporal evolution, at the beginning of the seepage, the volume discharge rate near the fluid outlet is greater than that away from the fluid outlet, due to the smaller cross section of the sample near the fluid outlet. As the seepage processes, the volume discharge rate gradually increases. This is caused by the migration of particles. Since the porosity of the sample increases, more fluid can pass through. Meanwhile, it can be found that, the volume discharge rates of the positions near the fluid outlet have a larger increase than that of the positions away from the fluid outlet. This is probably caused by the more pronounced particle migration here.

Fig. 9
figure 9

Temporal-spatial distribution of volume discharge rate

Full size image

With regard to the spatial distribution of the volume discharge rate, it can be seen that the closer the fluid outlet is, the larger the flow rate values are. As the seepage progresses, the flow rate near the fluid outlet greatly increases, leading to a more uneven spatial distribution of the volume discharge rate.

4.2.4 Permeability

Figure 10 shows the temporal-spatial evolution of permeability in Sample F. It can be found that the temporal evolution of permeability is similar to the evolution of porosity. The permeability at the positions near the fluid outlet (r < 14.5 cm) has a greater growth than that away from the fluid outlet (r > 14.5 cm). For the positions near the fluid outlet, the permeability increases sharply at the initial seepage, then gradually slows down and eventually ends. For the positions away from the fluid outlet, the permeability increases slowly and grows to the steady seepage phase.

Fig. 10
figure 10

Temporal-spatial distribution of permeability

Full size image

In respect of the spatial distribution of permeability, the spatial distribution of permeability within the rock mass is relatively uniform in the initial stage of seepage, due to the uniform distribution of porosity at the beginning of seepage. As the particle migration progresses, the permeability near the fluid outlet is much larger than that away from the fluid outlet, resulting in a spatial distribution with uneven permeability. At 1560 s, the permeability of that closest to the fluid outlet reaches 345.7 μm2, which is 6 times higher than the permeability of the upper boundary.

4.2.5 Pore pressure

As shown in Fig. 11, the temporal evolution of the pore pressure at different positions in Sample F can be obtained. Unlike the assumptions in the previous tests, the pore pressure fluctuates with the seepage. During the seepage, the pore pressure first decreases rapidly and then stabilizes. The closer the fluid outlet is, the greater the pressure drop and the shorter the duration is. For example, at r = 10.49 cm (near outlet), the pore pressure drops by 0.04 MPa within 0–480 s, whereas at r = 40.37 cm (near inlet), the pore pressure only decreases by 0.016 MPa within 0–1080 s. This fluctuation in pore pressure is mainly caused by rock particle migration.

Fig. 11
figure 11

Temporal-spatial distribution of pore pressure

Full size image

Figure 11 shows the spatial distribution of pore pressure at different times in the sample as well. It can be seen that the spatial distribution of pore pressure is not linear and changes with seepage. The water pressure at each point after 60 s tends to decrease. The change in water pressure spatial distribution is also related to the particle migration process. At the initial stages of seepage, skeletal particles are rearranged by the fluid force, and a large number of fine particles keep moving under the action of water flow. A large amount of fluid kinetic energy is consumed during these processes, resulting in a high pore pressure at each position. As the particle migration effect is weakened, the fluid consumption kinetic energy is small, and then the pore pressure is significantly reduced.

To sum up, under the action of pore pressure, skeleton particles near the fluid outlet are first liquefied to form fine particles. Then, the volume discharge rate of the mixture flow is gradually increased, which improves the migration ability of fine particles. During the seepage process, the fine particles migrate and flow out, which rapidly increases the porosity and permeability of the broken rock mass sample. The pathways of the particle migration are rapidly formed, causing more fine particles to be migrated, and then the volume concentration of the fluidized particle is rapidly increased to a certain peak. Subsequently, fine particles that can be migrated out from the fluid outlet are highly reduced, and the decrease in volume discharge rate causes the low capacity of fine particles migration in the mixture flow. Therefore, the volume concentration of the fluidized particle in the sample is gradually reduced until there are no more fine particles. When the fine particle migration is finished, the porosity and permeability of the sample finally tend to be stable.

4.3 Temporal-spatial evolution of the stress field and the properties of rock instability

4.3.1 Radial displacement

The temporal evolution of the radial displacements in Sample F is shown in Fig. 12, from which it can be found that downward displacements occurred at all positions of the sample, and the displacements increase before 1000 s, and then keep stable. Combining the result in Sect. 4.2, it is clear that the fault rock is unstable and moves downward under the effect of particle migration.

Fig. 12
figure 12

Temporal-spatial distribution of radial displacement

Full size image

Figure 12 also reflects the spatial distribution of radial displacement. It can be seen that a significant increase in displacement occurred in the position far away from the fluid outlet. At the same time, the displacement at the fluid outlet (r = 7.7 cm) is greater than that at r = 11.3 cm, which means the rock mass at the fluid outlet experiences instability and collapses under the combined effect of stress and particle migration, while the rocks at r = 11.3 m remain relatively stable.

4.3.2 Effective stress

The temporal-spatial distribution of the effective radial stress is shown in Fig. 13. It can be found that the effective radial stress gradually decreases as the particle migration proceeds, which is caused by the increase of porosity. The further the distance from the fluid outlet, the higher the effective radial stress.

Fig. 13
figure 13

Temporal-spatial distribution of radial effective stress

Full size image

The temporal-spatial distribution of the effective tangential stress is illustrated in Fig. 14. For positions close to the fluid outlet, a significant decrease in effective tangential stress is found within 400 s and then remains stable, while for positions away from the fluid outlet, a slight increase in effective tangential stress is observed. The further away from the fluid outlet, the lower the effective tangential stress.

Fig. 14
figure 14

Temporal-spatial distribution of tangential effective stress

Full size image

4.3.3 Instability properties of rocks

Considering the elastic stress boundary problem, the instability (failure) characteristics of the fractured rock mass sample can be analysed by Eq. (35). The results of the calculations are given in Figs. 15 and 16. Figure 15 illustrates the gradual decrease in the failure envelope of the rock material, together with the gradual decrease in shear stress. The decrease in the failure envelope is caused by a reduction in the cohesion of the rock material, while the reduction in the shear stress is due to the particle migration effect mitigating the stress concentration near the fluid outlet. Figure 16 shows the temporal evolution of the instability envelope and stress field (shear stress) on the fluid outlet. Both Figs. 15 and 16 show that the reduction in shear strength (cohesion) on the fluid outlet is greater than the reduction in shear stress after 480 s, which means the rock mass is unstable at this time.

Fig. 15
figure 15

Failure envelopes and corresponding critical stresses at the fluid outlet

Full size image
Fig. 16
figure 16

Time variation of failure envelope and the stress field at the fluid outlet

Full size image

4.4 The applicability of the proposed model

To discuss the applicability of the proposed model, several existing types of water inrush models are analysed in this chapter, and their advantages, disadvantages and applicability are compared. Then, combined with the results of this research, the applicability and limitations of the proposed model are discussed.

Currently, there exist various types of water inrush models that can be categorized based on their underlying principles. These include probability-based water inrush models (Chen et al. 2018a; Li et al. 2013; Wu et al. 2011), fracture evolution-based water inrush models (Yang et al. 2014, 2007), and flow regime transformation-based water inrush models (Shi et al. 2018b; Zhang et al. 2021), and all of which are extensively employed within engineering applications. The probability-based water inrush models predict the possibility of water inrush by means of hierarchical analysis, machine learning, etc. They have the advantages of simple operation, but it does not involve the evolution characteristics of local rock seepage and mechanical properties. For fracture evolution-based water inrush models, the propagation law of fractures in rocks is obtained by analysing the stress field evolution in potential water inrush areas, enabling the prediction of the evolution of water inflow. However, this model rarely takes into account the activation characteristics of rock fracture zone (e.g., faults and karst collapse pillar), thus it is primarily applicable for analysing water inrush from intact strata. Through analysing the transition of the fluid regime (from Darcy flow to non-Darcy flow to turbulent flow) in the rock fracture zone, the flow regime transformation-based water inrush models can accurately predict the timing and location of water inrush, but they fail to consider the rock erosion effect and stress field evolution.

Based on the principles of mass balance and filtration kinetics theory, this research proposes a model to analyse the erosion evolution characteristics of fault fractured zones and explains fault activation and water inrush phenomenon from the perspective of particle migration. Meanwhile, the instability characteristics of rock mass under erosion effects are also analysed and the temporal-spatial evolution law of the stress field is obtained. Experimental results have verified its high accuracy in predicting porosity evolution in fractured rock masses, demonstrating its applicability for analysing water inrush from faults.

Nevertheless, the proposed model still has some limitations. Firstly, it only analyses the water inrush law in fractured rock mass, and fails to consider the complex geometry and geological features of fault structure. Secondly, the model ignores the dissolution of minerals with high solubility during water inrush. Finally, limited by the model assumptions, it cannot account for the influence of rock particle size and pore geometry. To address these limitations, further modifications to the model are necessary for future research.

5 Conclusions

In order to study the temporal-spatial evolution law of the seepage field, a water–rock mixture flow model is established. Based on the experimental data from a previous study, the reliability of the water–rock mixed flow model is verified. Then, according to the established mixed flow model, the temporal-spatial evolution laws of several hydraulic properties (porosity, the volume concentration of the fluidized particle, volume discharge rate, pore pressure, and permeability) and mechanical properties (radial displacement, effective stress and instability properties) are analysed. Finally, the applicability and limitations of the proposed model are analysed through a comparison with the existing water inrush model. The main conclusions are as follows.

The two-phase flow model is established with excellent precision. In the process of seepage, the fluctuation caused by particle migration and the deviation of the set value of porosity stability will affect the accuracy of the model. Comparing the accuracy of the model under different conditions, it is found that different PSD has little effect on the accuracy of the model, the mean absolute percentage error of the model is around 0.2. With the increase of pore pressure, the accuracy of the model increases significantly. In terms of spatial distribution, the proposed model also has a high accuracy.

By the solutions of the two-phase flow model, it can be found that, in the initial stage of seepage, the spatial distribution of porosity and permeability is relatively uniform. Under the action of pore pressure, high volume discharge rates occur near the fluid outlet, and a severe particle migration appears. While the volume discharge rates away from the fluid outlet are still small, and the particle migration is also weak. These phenomena result in greater porosity, particle volume concentration, and permeability at the position closer to the fluid outlet. Besides, it can be found that the volume concentration of particles near the exit decreases rapidly after reaching a peak, indicating that the particle migration process is slowing down. Thereafter, the flow rate of growth is reduced, and the migration ability of fine particles is weakened. The increasing rate of permeability and porosity slows down in the sample. The volume fraction of fine particles in the sample gradually decreases until no fine particles can be migrated out. Finally, particle migration ends, and the internal porosity and permeability of the sample tend to be stable. It is worth noting that the simulation shows that the pore pressure decreases with the particle migration processes, which may be related to energy consumption during the rock particle migration. In addition, unlike the assumptions made in the previous experiments, the pore pressure is not a uniform spatial distribution during the seepage process but varies with the seepage process.

Based on the two-phase flow model, the stress field evolution and the instability properties of fault rock mass during water inrush are analysed. As particle migration proceeded, the downward radial displacement and decrease in effective radial stress are observed in the fractured rock mass. Both the displacement and the effective stress show significant non-uniform characteristics. The further away from the fluid outlet, the greater the radial displacement and effective radial stress and the lower the effective tangential stress. At the same time, both the cohesion and shear stress of the rock material decreased during the erosion process, and the rock mass at the fluid outlet becomes unstable after 480 s.

By the proposed model, the water conduction phenomenon of fault is explained from the perspective of rock particle migration, and the instability characteristics of fault rocks under the erosion effect are obtained, which means the model has good applicability in analysing water inrush from faults. Meanwhiles, the proposed model has limitations in considering fault structure and geological characteristics, dissolution effects of minerals with high solubility, and the influence of rock particle size and pore geometry on seepage. Further study is required to address these issues.