1 Introduction

The western blown-sand area in China is becoming the main coal-producing base. This area has several small desert lakes, which not only supply water for plants in sandy areas, but also serve as the main water source of surrounding residents and agriculture. Therefore, they play an important role in protecting the ecosystem of the blown-sand area. In recent years, large scale mining activities have caused a sharp decline in the number and area of desert lakes (Liu et al. 2017; Nie et al. 2018; Wang et al. 2020; Xu et al. 2019a, b; Zheng et al. 2021). Reducing the impact of coal mining on the fragile ecosystem, especially the desert lakes, has become a problem that needs to be solved urgently at present. Therefore, obtaining the lake information accurately and rapidly is of great significance for the ecological environment protection and sustainable development in the mining area.

The development of remote sensing technology offers a promising tool for desert lake monitoring as it has outstanding advantages compared with traditional ground observation methods. The water area, water quality and other parameters can be obtained based on the optical remote sensing images (Ma et al. 2018; Wang et al. 2019a, b; Zhang et al. 2021a, b; Zhou and Dong 2019; Zhou et al. 2004). The extraction methods mainly include the threshold method, classifier method, object-oriented method, data mining method, water body index method, etc. (Jiang et al. 2011; Li et al. 2020; Liu 2020; Qiao and Sun 2020; Su et al. 2021; Wang et al. 2019a, b; Zhang et al. 2021a, b).

Among these methods, the water body index method is the most widely used one. It involves the formulation of a mathematical model of the water index through the selection of the bands closely related to the water body to enhance the contrast between the water body and the background, and then realize the rapid extraction of the water information (Zhang et al. 2022). Commonly used water body indices mainly include the normalized difference water index (NDWI), the modified NDWI (MNDWI), the automatic water extraction index (AWEI), and others. The NDWI is based on the spectral characteristics of water and surrounding vegetation in the near-infrared and green bands and can be used to extract water information from the image. The MNDWI uses the mid-infrared band to replace the near-infrared band to mitigate the influence of buildings when extracting water information within urban environments. The AWEI integrates the blue, green, near-infrared, short-wave infrared and mid-infrared band to construct a water index and inhibit the influence of shadows and buildings (Xu 2005; Feyisa et al. 2014).

Due to the limited spatial resolution of the remote sensing images, small lake areas and shallow water bodies, there are many mixed pixels near the water boundaries in the images, which affect the extraction precision.

In order to solve the problem of mixed pixels, researchers concentrating on feasible methods for mixed pixels in remote sensing images have developed a variety of spectral unmixing methods (Chen et al. 2016; Chen and Vierling 2006; Fan et al. 2009; Li et al. 2008, 2009, 2020; Wu 2004). Cui et al. (2019) combined decision tree and linear spectral unmixing methods to extract bamboo forest information in China. Yang et al. (2010) proposed an image unmixing method based on the posterior probability of relevance vector machines. Zhang et al. (2019) analyzed the factors influencing the decomposition precision of mixed pixels based on the constraint linear spectral mixing model. Liu et al. (2008) proposed a method for decomposing mixed pixels that combined self-organizing map (SOM) neural networks and fuzzy membership in the fuzzy theory. Li et al. (2016) presented a nonlinear spectral unmixing for optimizing per-pixel end member sets. Kong and Chen (2017) used the fully constrained least squares (FCLS) method to extract different reservoir surface water information.

Most of the traditional unmixing methods use spectral information to calculate the coverage of water bodies in a mixed pixel (Lai et al. 2019; Wang et al. 2008). However, it is difficult to describe the water spatial distribution state in the mixed pixel due to ignoring the spatial correlation information of the ground features, which affects the accuracy of lake information extraction.

The cellular automata model (CA) can be used in a sub-pixel level for the analysis of remote sensing images (Li et al. 2015). Feng and Han (2012) used CA to study the spatial distribution of coastlines using remote sensing images. Gao and Dai (2020) simulated water pollution dispersion based on improved CA model.

This paper selects a mining area in the Shenmu City, ShaanXi Province, China, as the research region. It uses the Sentinel-2 images as the data source and the high spatial resolution UAV images as the reference. The lake information extraction at a sub-pixel level is achieved by combining the dimidiate pixel model and FCLS with the CA model. This method not only considers the image spectral information, but also makes full use of the water body spatial correlation. Consequently, it can improve the accuracy of remote sensing image recognition and classification.

The remainder of the paper is organized as follows. In Sect. 2, the natural geographical conditions and the main data sets used in this study are described. Study methods are described in Sect. 3. The experimental process and accuracy analysis are presented in Sect. 4. A summary of the main conclusions and prospects of the research detailed in the paper is discussed in Sect. 5.

2 Study area and data processing

2.1 Overview of the study area

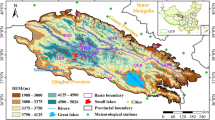
The study area is situated on the southeast edge of Maousu Desert at a distance of about 47 km from the Shenmu City, Shaanxi Province, China. It is in the arid to semi-arid transition zone of temperate continental monsoon climate and has the characteristics of drought, low rainfall and high annual evaporation. The surface is largely covered by quaternary blown-sand in the form of semi-fixed and fixed dunes. The ground elevation is between 1325.60 and 1234.10 m, with a relative maximum height difference of 91.50 m.

The surface water in the study area is mainly comprised of small lakes and the water storage volume changes in different seasons. The water depth is associated with geographical morphology, mostly between 0.3 and 5.0 m. The surface vegetation is mainly sandy vegetation. Figure 1 shows the desert lakes and surrounding environments.

Fig. 1
figure 1

Study area and photos of desert lakes

Full size image

2.2 Data acquisition and preprocessing

The remote sensing data for this experiment are based on the Sentinel-2 image that was acquired on 5 October 2020. It is downloaded from the Copernicus Open Access Hub (https://scihub.copernicus.eu/) and the product level is L2A, which has been passed through radiation calibration and atmospheric correction. The Sentinel-2 images have 13 bands with different spatial resolutions of 10, 20 and 60 m. Table 1 provides detailed information about the bands of Sentinel-2 images.

Table 1 Some bands information of Sentinel-2 image
Full size table

In order to verify the correctness of the proposed method, a UAV at a flight altitude of 80 m is used to collect high resolution images of the lake. The data qualities of these aerial images are first checked, and the images with relatively poor quality are removed. The remaining images are imported into the PhotoScan software to carry out image matching, aerial triangulation and irregular triangle network model construction, subsequently generating dense point clouds and a 3D model to obtain a Digital Orthophoto Map (DOM) with a spatial resolution of 0.02 m (Fig. 2), then some samples of lakes are obtained with a supervised method using the ENVI software as a reference for accuracy evaluation (Fig. 3).

Fig. 2
figure 2

DOM of UAV

Full size image
Fig. 3
figure 3

Lake samples

Full size image

3 Study methods

3.1 Water coverage index calculation based on dimidiate pixel (DP) model

When the desert lake body is extracted using medium spatial resolution remote sensing images, there are many mixed pixels that could affect the accuracy near the boundaries between the land and water. Therefore, it is necessary to un-mix the pixels to estimate the percentage of water, subsequently providing the foundation for water boundary mapping at the sub-pixel level (Lai et al. 2019). In this paper, we use the dimidiate pixel (DP) model to analyze mixed pixels and calculate water area proportion based on the normalized difference water index (NDWI).

  1. (1)

    The NDWI was proposed by McFeeter in 1996. It is based on the spectral characteristics of water and surrounding vegetation in the near-infrared and green bands. The information is used to suppress the vegetation and enhance the water signal to obtain water information in the image. It can be calculated using Eq. (1) (Gu et al. 2020; McFeeter 1996; Wang et al. 2017; Xu 2005):

    $$\text{NDWI} = (G - \text{NIR})/(G + \text{NIR})$$
    (1)

    where G and NIR are the values of green band and near-infrared band respectively.

  2. (2)

    Dimidiate pixel (DP) model.

    Assuming that the reflectance of each pixel is composed of a water part (RW) and a land part (RL), then its value can be expressed as a linear weighted sum of the two parts, as shown in Eq. (2):

    $$R = R_{\text{W}} + R_{\text{L}}$$
    (2)

    If the water area proportion in a mixed pixel is fw, which is the water coverage index of the pixel, then the land part is 1–fw. If the pixel is entirely composed of water, the reflectance can be represented as Rwater; if there is no water in the pixel, the reflectance is Rland. Therefore, the information contributed by the water part (which is RW) can be expressed as the product of the pure water end-member reflectance Rwater and the water coverage index fw, while RL can be expressed as the product of the land part reflectance Rland and 1 − fw, as shown in Eqs. (3) and (4):

    $$R_{\text{W}} = f_{\text{w}} * R_{\text{water}}$$
    (3)
    $$R_{\text{L}} = (1 - f_{\text{w}} ) * R_{\text{land}}$$
    (4)

    Then, the water coverage index fw can be calculated using Eq. (5) (Ding and Liu 2020).

    $$f_{\text{w}} = (R - R_{\text{land}} )/(R_{\text{water}} - R_{\text{land}} )$$
    (5)

    According to the principle of the DP model, the NDWI value of a pixel is a composition of the water and land parts, so the equation for calculating the water coverage index can be expressed as Eq. (6):

    $$f_{\text{w}} = (\text{NDWI} - \text{NDWI}_{\text{land}} )/(\text{NDWI}_{\text{water}} - \text{NDWI}_{\text{land}} )$$
    (6)

    where fw is the water coverage index in a mixed pixel, and NDWIwater and NDWIland are the NDWI values of a pure water pixel and a pure land pixel, respectively.

3.2 Water coverage index calculation based on fully constrained least squares (FCLS) pixel unmixing model

The linear spectral unmixing model is a common method to solve the problem of mixed pixels in low-resolution remote sensing images. In this approach, the spectrum of a mixed pixel is considered to be a linear combination of various ground object spectra in the instantaneous field of view, as expressed using Eq. (7).

$$R_{i} = \sum\limits_{j = 1}^{n} {f_{j} } * R_{e,i,j} + \varepsilon_{i}$$
(7)
$${\text{s}}.{\text{t}}.\;\sum\limits_{j = 1}^{n} {f_{j} } = 1,\quad 0 \le f_{j} \le 1$$

where Ri is the reflectance of band i; fj is the percentage of ground of class j in the pixel; Re, i, j is the reflectance of ground of class j in band i; and εi is the error of band i.

Linear spectral unmixing can be considered as a nonlinear optimization problem with the constraints expressed as Eq. (8).

$$F = \min D(S,XF)$$
(8)
$${\text{s}}.{\text{t}}.\;\sum\limits_{j = 1}^{n} {f_{j} } = 1,\quad 0 \le f_{j} \le 1$$

where D(S,XF) is the objective function representing the distance between the target mixed pixel reflection spectrum S and the estimated spectrum XF (Chang et al. 2003; Kong and Chen 2017)

The water coverage index fw can be obtained from Eq. (8) using FCLS.

3.3 Sub-pixel position based on the Cellular Automata model

3.3.1 Cellular automata

Cellular automata (CA) refer to dynamic systems defined in a cellular space composed of cells with discrete and finite states, evolving under certain local rules along a discrete time dimension. These systems follow the bottom-to-top strategy for simulating the change of a complex system. The change of each cell’s state at the next generation is determined by its initial state and the influence of the neighboring cells around it. Therefore, small changes in local cells will eventually cause substantial changes in the composition, layout, properties and dynamics of the system (Chen et al. 2020; Fisher et al. 2016; Li and Ye 2002; Li and Yen 2005; Luo et al. 2005; Yang 2008).

A CA-based system consists of a set of cells, the cellular space, neighbors and rules. These can be represented with four tuples, as shown in Eq. (9):

$$C_{A} \, = \,\left( {Zn,S,N,f} \right)$$
(9)

where CA is the CA system, Zn denotes the cellular space, S is a set of finite discrete cellular states, N represents the neighboring cell states, and f is a local state transition function that uses the current state of the cell and the states of all its neighbors to determine the evolution of the state.

As the CA is a computational system that performs complex tasks on the basis of simple items, it is used in the fields of geography, society, environment, etc. (Li and Ye 2002; Liu et al. 2012; Yuan and Liao 2005; Zhang et al. 2016).

3.3.2 Lake body optimization in sub-pixel level based on CA model

The original low-resolution pixel is divided into N × N sub-pixels in order to determine the water distribution in the mixed pixel. The number of sub-pixels occupied by the water body can be determined through the water coverage index. Subsequently, the spatial distribution of the water body can be estimated based on the CA model. The specific methods are introduced as follows:

  1. (1)

    Cellular space: The original low-resolution mixed pixel and its neighboring pixels are divided into a set of sub-pixels that constitute the cellular space. In order to improve operational efficiency, the cells involved in the transition are limited within the operation space, which is set to the scope of the original mixed pixel. Figure 4 shows the division of cellular space.

    Fig. 4
    figure 4

    Schematic diagram of cellular space division

    Full size image
  2. (2)

    Cellular states: The initial state of each cell is determined according to the water coverage index.

  3. (3)

    Neighborhood: The Moore neighborhood is adopted in this study.

  4. (4)

    Transition rules: First, the CA evolves through the influence of the neighboring cells and its current state; then, the cellular state is calculated via the constraint of water proportion in a mixed pixel. Lastly, the layout of water body cell is optimized based on the spatial association of the cells. The detailed CA evolution is as follows:

  5. I.

    Cellular state initialization.

    The initial state values of a pure water pixel, pure land pixel and mixed pixel are set to 1, 0, and k \(\in (0,1)\) according to the water coverage index, respectively.

  6. II.

    System evolution.

    ① Evolution based on the influence of neighboring cells.

    The state transition probability of a cell in a mixed pixel is calculated using Eq. (10).

    $$S_{t + 1} (i,j) = \sum {W(m,n) \times S_{t} } (m,n)$$
    (10)

    where \(S_{t + 1} (i,j)\) represents the state of cell (i,j) at time t + 1, \(S_{t} (m,n)\) is the state of the neighboring cell (m,n) at time t, and is the weight of the neighboring cell (m,n), and (m,n) is used as the identifier of the neighborhood.

    ② Evolution based on the constraints of water coverage in the mixed pixel.

    After the first-stage evolution, the cellular state values in the mixed pixel can be differentiated. Subsequently, the number of cells that should be converted to water bodies can be calculated according to the water coverage index and the cellular probabilities in descending order. The calculation is as shown in Eq. (11):

    $$N_{w} = N_{k} \times f_{w}$$
    (11)

    where Nw is the number of cells whose state values are set to 1 in the mixed pixel, Nk is the total number of cells in the mixed pixel, and fw is the water coverage index of the mixed pixel.

    ③ Optimization of the spatial location.

    The cell state can be readjusted to achieve layout optimization according to the spatial connectivity in a mixed pixel. If an exchange of the states of two cells improves the water body pixels’ spatial correlation, then the water body’s spatial distribution can be optimized.

3.4 Implementation of the model

The water coverage indices of the dimidiate pixel model and FCLS are implemented using the ENVI software with IDL (Interactive Data Language) support, and the CA model is implemented using the ArcGIS software with Python tools. Figure 5 shows the flow chart of the implementation.

Fig. 5
figure 5

Flow chart of the study

Full size image

3.5 Accuracy evaluation

Accuracy evaluation is an important means to test the reliability of image information extraction method. This is generally achieved by comparing the classification results with ground measured values. A confusion matrix is often established to calculate various classification accuracy metrics. In this study, the lake water boundary extracted from the UAV image is taken as the ground reference to verify the water extraction results obtained using different methods. The commonly used accuracy indices are commission, omission, producer accuracy, user accuracy, overall accuracy and Kappa coefficient. (Pontius Jr and Millones 2011; Li et al. 2021; Xu et al. 2019a, b).

4 Experimental analyses

4.1 Calculation of water coverage index based on DP model

The NDWI of the study area was calculated according to Eq. (1) and the result is shown in Fig. 6. Water and land samples were selected respectively. The maximum value, minimum value, mean and standard deviation of the NDWI were analyzed (the details are provided in Table 2), and the threshold values for water and land were chosen based on their respective frequency distribution histograms. Subsequently, the distribution of the water coverage index was calculated using Eq. (6) and the result is shown in Fig. 7.

Fig. 6
figure 6

NDWI Value

Full size image
Table 2 Sample information statistics of NDWI
Full size table
Fig. 7
figure 7

Distribution of water coverage index

Full size image

4.2 Calculation of water coverage index using FCLS pixel unmixing model

Depending on the land characteristics of the study area, the land cover was classified into three types, namely vegetation, water and soil land. Then, the pure end elements were selected to calculate the coverage index of the land type using the FCLS tool provided by ENVI. The results are shown in Fig. 8.

Fig. 8
figure 8

Coverage index distribution for different land types

Full size image

4.3 CA simulation

4.3.1 CA Model Construction

In order to facilitate the division of the cellular spaces and reduce the error of data processing, the size of the CA is recommended to be an integer division of the resolution for segmentation. So, the water coverage index image of 10 m spatial resolution was subdivided into 2 m spatial resolution in ArcGIS for CA generation using the nearest neighbor method, which does not change the values of the cells.

The neighborhood was set to 3 × 3 and the weight of the neighborhood cells was assigned based on the distance to the central cell according to the following rules.

The weight value of central cell shall be the largest because it will contribute the most information in next generation the during CA evolution. The weight value of cells that adjoin the central cell with a edge shall be moderate, while for cells that adjoins the central cell with a point, the weight value shall be the lowest. The sum of all weight values of neighborhood shall be equal to one.

4.3.2 CA simulation

Based on the transition rule given by Eq. (10), the intermediate results after CA evolution are shown in Fig. 9. It can be observed that the cellular state values of the mixed images are strongly correlated with the spatial layout of the water body, and the spatial shape is finer than before CA evolution.

Fig.9
figure 9

Local details about the mixed pixel

Full size image

Allocation for the cellular state of the lake body was based on water coverage constraints in a mixed pixel. The number of cellular states of the lake body was determined according to the water coverage in the mixed images, and the value of cellular state was changed to water according to the probabilities sorted in descending order after cell evolution.

Although the proportion of water cells in the mixed pixel can be determined after the previous step, there are a few opening holes or discontinuities in the partial layout of a water body. Therefore, the spatial distribution of water cells was adjusted based on the spatial correlation. The corresponding results are shown in Fig. 10. It can be observed that the spatial connectivity of water body is improved and the distribution is more logical after CA evolution.

Fig. 10
figure 10

Spatial optimization for the water cell

Full size image

4.4 Accuracy analysis

13 samples about of the lake body were obtained from the UAV image. Next, the extraction results of the lake body using the NDWI, DP-CA, FCLS and FCLS-CA methods were compared with the reference value in Fig. 11. The confusion matrix was calculated by comparing the location and class of each truth pixel with the corresponding location and class in the classification image, respectively.

Fig. 11
figure 11

Comparative analysis of the extracted results

Full size image

Subsequently, the commission, omission, producer accuracy, user accuracy, overall accuracy and Kappa coefficient indices were calculated to evaluate the accuracy of different methods. Further details are given in Table 3.

Table 3 Accuracy evaluation of different water extraction methods
Full size table

The results show that the FCLS-CA model can identify most water bodies in the study area, and its overall accuracy and Kappa coefficient were higher than those of other methods. This method also achieved a better balance between the indices of commission and omission percentage.

There were some small lakes that could not be identified due to the limited spatial and spectral resolutions of the original remote sensing image.

5 Conclusions

Desert lakes are important wetland resources and hold great significance for maintaining the regional ecological environment. Information extraction relevant to the lakes via remote sensing images is affected by many mixed pixels present in the images. This paper presented a new method to obtain the position and size of water from a mixed pixel in a remote sensing image. Through the use of CA, the distribution of water body can be obtained automatically and the impact of inappropriate threshold value selection, which is a common occurrence in water body index methods, are reduced. The experiments show that the CA model can improve the sub-pixel positioning accuracy for lake bodies in mixed pixel image and improve classification accuracy. Compared with other methods, the FCLS-CA model has a higher accuracy and can identify most water bodies in the study area.

There were some small lakes that could not be accurately identified, so the method still needs further improvement in the future to increase the information extraction accuracy with higher spatial and spectral resolution remote sensing images.