Abstract
Discrete element calculations of the top-coal drawing process for different gangue-coal density ratios were conducted to investigate the effect of the gangue-coal density ratio on the drawing mechanism in longwall top-coal caving. The effects were analyzed for the drawing body, the top-coal boundary, and the recovery of top coal. The results show that for increasing density ratio, the initial drawing body on the goaf side is farther away from the drawing support and its width and volume gradually increase. The upper part of the sickle-shaped drawing body extends near the initial drawing body with increasing density ratio in the normal cycling stage, and the distance from the drawing body to the initial drawing body is its maximum width. The larger the density ratio, the smaller the height of the top coal above the goaf at the end of the initial drawing process. The height of the top-coal boundary decreases with increasing density ratio, until it reaches a limit. In a normal cycle, due to hysteretic development, the top-coal boundary moves toward the goaf until the density ratio is approximately 2.0, which is consistent with the physical experiment results. Finally, increasing the advance length of the working face is beneficial for increasing the overall recovery of top coal.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In recent years, longwall top-coal caving (LTCC) has been widely used for mining thick coal seams with various complicated conditions (Alehossein and Poulsen 2010; Jangara and Ozturk 2021; Le et al. 2017; Song and Konietzky 2019; Wang 2009; Wang et al. 2017; Yang et al. 2016). In LTCC, the key technology is top-coal drawing, which affects the amount of coal produced (Wang et al. 2020a, 2020b; Zhang et al. 2018a, b). The main factors that affect top-coal drawing include the drawing parameters, coal seam conditions (such as dip angle, shape, density, etc.), and the method of drawing the coal. Wang et al. (2019, 2020c, 2021a, 2021b) studied the effect of the size distribution of granular top coal on the drawing mechanism using a theoretical analysis. By restoring the drawn top coal to its original position, scholars have used the boundary-body-ratio (BBR) research system to describe the relationships between the drawing body, the boundary of the top coal, and the recovery ratio (Wang et al. 2016a; Wang and Zhang 2015). Zhang et al. (2018a, b) investigated the effect of seam dip angle on the drawing mechanism in LTCC based on the BBR research system. Using numerical simulations and physical experiments, researchers have analyzed the stress, the deformation, and movement of top coal under different cutting–caving ratios and caving intervals, and improved the recovery ratio (Wang et al. 2014, 2016b; Yasitli and Unver 2005; Zhang et al. 2015). Using an experimental model, Klishin et al. (2019) described the stress distribution in the rock mass, as well as the position, shape, and size.
In addition, scholars have studied the effect of gangue and coal density on coal drawing, such as the dynamics of the particle flow under different conditions (such as different densities) (Bi et al. 2016; Shi et al. 2007; Yi and Hill 2015). Sheng et al. (2021) investigated the dynamic behavior and segregation of particles of different densities in a rough, inclined chute. Liao et al. (2017) studied the sinking dynamics of a heavy granular ring caused by buoyancy in a binary mixture with identically sized particle and various particle densities in a shear cell device. Tripathi and Khakhar (2013) analyzed the segregation of spheres of equal size and different densities flowing over an inclined plane, theoretically and computationally with distinct element method (DEM) simulations. Xiao et al. (2016) studied the kinematics of density-bidisperse flows using a DEM simulation and proposed an approach for predicting the segregation of density-bidisperse granular materials in a quasi-2D-bounded heap.
Similarly, the stress state (Aguado and Gonza 2009; Navarro et al. 2019), discrete element model (Hamdi et al. 2018; Regassa et al. 2018), failure mechanism (Lupo 1997; Woo et al. 2013), granular caving, and displacement (Melo et al. 2008, 2009; Sepehri et al. 2017; Vivanco and Melo 2013) are also key aspects of sublevel caving research. These researchers analyzed the recovery rate and surface subsidence by examining the movement of granular particles with a discrete element model. This type of model is suitable for studying granular flows in top-coal and sublevel caving, so the research results are applicable to both coal and metal mines.
By analyzing the flow of particles in the drawing frame, this research investigates the effect of particle density on the drawing of granular top coal. Based on the BBR research system, a theoretical analysis and discrete element numerical simulation are adopted. The work provides a theoretical foundation for optimizing top-coal drawing with different gangue-coal density ratios.
A theoretical model is used to explain the drawing of multi-layer particles with different densities under gravity (Unver and Yasitli 2006; Wang and Song 2015). The density range of particles in the model is determined by investigating the density of various rocks in a mine (Li 2013; Wu and He 2011). The density ranges of different minerals and rocks are shown in Table 1.
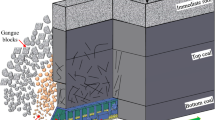
Generally, an underground coal mine is in sedimentary rock, whereas a non-coal mine is in magmatic or metamorphic rock (Song et al. 2021; Xu 2008). Schematic diagrams of a coal mine and a metal mine are shown in Figs. 1 and 2, respectively. Due to the different geological conditions, the densities of coal, ore, and gangue in different mines are quite different. Based on data from a wide range of mining conditions, the density of coal is about 1.2–1.8 g/cm3, and the density of sedimentary rock is about 1.8–3.3 g/cm3. Furthermore, the density of non-coal ore is 2.2–4.7 g/cm3, and the density of magmatic rock is about 2.2–6.2 g/cm3. Thus, in coal mines, the density of coal is generally lower than that of the gangue, while in metal mines, the density of the ore is generally higher than that of the rock. Due to the differences in particle densities for a numerical simulation model of a coal mine or a metal mine, the ellipsoid theory of ore drawing may not be fully applicable to the drawing of top coal in a coal mine. Therefore, a deep investigation of top-coal drawing based on the ratio of the particle densities in the upper and lower layers is necessary.
Schematic diagram of a coal mine showing the gangue and coal (Wang et al. 2016a)
Schematic diagram of a metal mine showing the mineral and rock (non-pillar sublevel caving) (Atlas Copco 2007)
In this research, the ratio of the densities of the upper and lower layers of particles (gangue particles and coal particles, respectively, in a coal mine) is defined as:
where ρg and ρc are the densities of the gangue and coal, respectively.
2 Theory
Gangue-coal column theory (Zhang et al. 2018a, b) is adopted here to analyze theoretically the development of the top-coal boundary. In Fig. 3a, we consider two regions at different places on the hydraulic support (both of which have base areas of δ). The gangue and coal above these two regions are in two columns. The left column is gangue-coal column No. 1, and the right column is gangue-coal column No. 2.
Thus, the masses of the two columns are:
where G1 and G2 are the masses of the gangue-coal column No. 1 and 2; δ is the basal area of the gangue-coal column, h1 and h2 are the heights of the gangue in the two gangue-coal columns, respectively, and h1' and h2' are the heights of the top coal in the two columns, respectively. γ is the gangue-coal density ratio. The heights of the two columns at the beginning of the initial drawing are equal, i.e., h1 + h1' = h2 + h2'.
The difference in mass between the two columns can easily be obtained from Eqs. (2) and (3):
From Fig. 3a, it is obvious that h1–h2 > 0. From Eq. (4), if γ > 1, then ΔG > 0, and G1, G2, and ΔG all increase with an increase of γ, which indicates that the stress between the loose particles in the model increases with increasing γ. Furthermore, an increase of the stress between the loose particles means that the particle velocity is higher at the drawing opening (DO).
Similarly, the difference between the floor pressures (ΔG') in Fig. 3b can be calculated:
In Fig. 3b, which is before the initial drawing process, (h1'– h2') is equal to the height of the hydraulic support. During the initial drawing of top coal, the inequality (h1'– h2') > 0 still holds. Therefore, in the initial drawing stage, the goaf pressure on the floor is always greater than the pressure above the hydraulic support. Thus, the flow velocity and drawn volume on the goaf side are greater than above the hydraulic support.
Figure 4 shows the gangue-coal columns during a normal cycle. In Fig. 4, the total height of the left column is greater than that of the right column, so that h1 > h2. Thus, from Eqs. (2) and (3), ∆G > 0. While the drawing is in the normal cycling stage, the number of top-coal particles decreases in the goaf and the number of gangue particles increases significantly, so that the pressure of the goaf on the floor gradually increases. The intrusion of gangue particles into the top coal increases significantly, and the volume of undrawn top coal increases above the hydraulic support, which causes the top-coal boundary to bend and move toward the goaf so that it eventually moves over the DO, as shown in Fig. 4. These changes of the top-coal boundary are called hysteretic development.
Through the establishment of the theoretical model of gangue-coal column, the motion mechanism of top coal and the evolution of top-coal boundary are preliminarily investigated and analyzed. The main results are as follows:
(1) In the initial drawing stage, with increasing γ, the stress at the top-coal boundary above the goaf is greater than that above the hydraulic support, and the top-coal boundary in the goaf drops faster than that above the hydraulic support.
(2) In the normal drawing stage, when γ is larger than 1, gangue is drawn out of DO in advance with the progressive advance of hydraulic support, and the phenomenon of hysteretic development of top-coal boundary appears, which are gradually significant with the increase of γ.
To examine the development of the top-coal boundary and study the variation of the drawing body shape and recovery ratio, a series of numerical simulation models are established, calculated and analyzed in the following sections.
3 Numerical model set-up
3.1 Simulation schemes
According to Table 1, the density of sedimentary rock is in the range 1.8–3.3 g/cm3, and that of coal is in the range 1.2–1.8 g/cm3. To analyze the drawing efficiency of top coal and the characteristics of the drawing body under different density conditions, in the model, the density of top-coal particles was set as 1.5 g/cm3. To have sufficient comparison schemes (including γ ≥ 1.0 and γ ≤ 1.0), the density range of gangue obtained from the investigation can be included by the density range set, and 9 schemes for theoretical simulation research are set with a gradient interval of 0.3 g/cm3, as shown in Table 2.
3.2 Microscopic parameters and boundary conditions
Nine numerical models of LTCC based on the different density ratios in Table 2 were established using the discrete element method Particle Flow Code (PFC2D) which is an effective approach to simulate the mechanical properties of rocks and top coal drawing (Song et al. 2018, 2019, 2020; Ajamzadeh et al. 2019). After an initial drawing process, each model simulated 15 cycles of advancing the support and drawing top coal to analyze the drawing mechanism under different γ, including the development of the drawing body, the evolution of the top-coal boundary, the variation of the top-coal drawing volume, and the recovery of top coal. The initial state and parameters of the model is shown in Fig. 5.
When the hydraulic support moves forward in LTCC panels, the top coal and immediate roof above DO are fractured and broken into blocks under the mining-induced stress in soft or medium hard coal seams. Considering the immediate roof above the soft coal seams are always carbonaceous mudstone or sandy mudstone, which can easily break into pieces under the mining induced abutment pressure in front of the working face, the coal and rock are simplified as granular media without bond in this simulation.
As shown in Fig. 5, the white particles at the top of the model are broken gangue (with a height of 11 m), and the black particles at the bottom are the coal seam (with a height of 9 m). To show the flow of the particles, five marked lines with different colors were arranged at equal intervals along the vertical direction in the coal seam. To simplify the model, the right part of the coal seam, to the same height as the hydraulic support, was ignored as it does not affect the experimental study. The wall element was used to simulate the drawing support (with a height of 3 m) and model boundary in the model. Walls 1 and 2 simulated DO and the shield beam, respectively, with a dip angle of 50°. The vertical projection height of DO was 1.3 m and that of the shield beam was 1.5 m. Furthermore, a small vertical Wall 3 simulated the back edge of the rear AFC, and its height was 0.2 m. Wall 4 was employed to simulate the canopy, with a length of 4 m. Walls 5 and 6 were used to simulate the left and right boundaries of the model, respectively. The bottom boundary of the model consists of a row of particles with equal size and fixed position, simulating the rough floor of the goaf. The physical and mechanical parameters of bottom particles, top coal and gangue, are shown in Table 3. The size of coal and gangue in Table 3 were referred to Wang et al. 2019.
In the drawing process, the drawing interval is 1.0 m, and DO is closed when the first gangue is seen. The opening and closing of DO are controlled by FISH language, and each model performs the drawing process of 16 times. The velocity and acceleration of the model boundary are fixed at 0, and the initial velocity of the particles is also 0. Coal and gangue particles are affected only by gravity, and the gravitational acceleration is 9.81 m/s2.
3.3 Hardware requirements and calculation time
The dimension of the model is 20 m in height and 43 m in width. The calculation time and hardware information are shown in Table 4.
Among the 9 model schemes, some of the them were calculated on personal computer with 8G RAM, and the calculation time is 21.5 h per model; while others were calculated on computer workstation with 64G RAM, and the calculation time is 9.2 h per model.
The DEM approach is avoided due to space (computer) and time requirements, especially when it is compared with the continuous medium approach. However, DEM shows obvious advantages when it comes to the discharge issues of granular coal and gangue blocks in top coal caving mining. Based on the authors’ experience and the calculation time recorded in Table 4, the computational efficiency is acceptable to some extent when the Two-dimensional Particle Flow Code (PFC2D) was used and the number of the particles is not very large.
4 Simulation results and analysis
4.1 Effect of the density ratio on the drawing body
The top-coal drawing bodies for each of the nine models were deduced by inverting the drawn particles. The effect of γ on the drawing body shape was studied at the initial drawing stage and the normal cycling stage.
4.1.1 Initial drawing stage
The inversion works as follows. To show the original position of the drawn particles intuitively, the IDs of all drawn particles were recorded and the corresponding particles were then deleted in the initial model one by one. The shape of the drawing body is reflected by the resulting cavity, as shown in Fig. 6.
Figure 6 shows that the initial drawing body was above the rear canopy of the support. Its top was tangential to the bottom of the gangue layer, which indicates that the height of the initial drawing body was approximately equal to the thickness of the coal seam. When γ was in the range 1.4–2.2, there was a small amount of residual top coal (particles in the red ellipses) at the top of the drawing body. However, the volume of residual coal was relatively small and did not have an increasing trend. The volume and shape of the initial drawing body are depicted in Fig. 7.
Figure 7a shows that for the nine models, the volume of the initial drawing body (Vi) slowly increased with increasing γ. Figure 7b indicates that, as γ increased, the width of the drawing body varied significantly, while the drawing body height was basically unchanged. By calculating the transverse coordinates of the particles, the width of the drawing body (Wi) can be calculated, as shown in Fig. 7c. When γ was in the range 0.6–2.2, the width of the drawing body fluctuated from 8.1 to 9.2 m. The general trend is that the width of the initial drawing body increased with increasing γ, which indicates that Vi increased with an increase of γ. The horizontal distance between the bottom left of the boundary and the origin is defined as D1, and the distance from the bottom right of the boundary to the origin is D2, as shown in Fig. 7b. The variation of D1 and D2 with increasing γ is shown in Fig. 7d. Notably, with an increase of γ, basically D2 did not increase or decrease; however, D1 increased significantly. When γ was in the range 0.6–2.2, D1 varied in the range 3.3–5.0 m. The trend for D1 is similar to that for Wi.
In summary,
-
(1)
Vi fluctuated with an increase of γ, with an overall rising trend.
-
(2)
With increasing γ, the right boundary did not move but the left boundary moved leftward, resulting in an increase of Wi and Vi.
In these drawing experiments with two layers of granular particles with different γ, due to gravity, an increase of ρg relative to ρc led to an increase in the force that the upper particles exerted on the lower particles. This larger force increased the velocity of the granular particles, which was the root reason for the increase of Vi.
4.1.2 Normal cycling
In the normal cycling stage, the drawing body develops under the top-coal boundary from the previous cycle, so that it is essentially different from the initial drawing stage. The volume of coal drawn in the normal cycling stage is closely related to the output of the mine. Therefore, during normal cycling, it is important to study the influence of γ on the drawing body, especially the shape of the drawing body and the top-coal yield.
For each of the nine schemes, the initial drawing process was simulated followed by 15 normal cycles of drawing. After each drawing process, the drawing body was inverted using the initial model, resulting in an inversion diagram. Figure 8 shows inversion diagrams for three representative schemes. The five colored marked lines are shown. Also shown in different colors are the 16 inverted drawing bodies (DB1 to DB16).
Figure 8 shows that in normal cycling, the bending of DB2 to DB16 to the left becomes more significant with increasing γ. Since the height of a drawing body is basically equal to the thickness of the coal seam, we can study the bending by analyzing the width of the drawing body. The width of a drawing body in normal cycling can be obtained from the abscissas of the particles in the original model. Taking DB13 as an example, the width of the sickle-shaped drawing body (Ws) and the relation between Ws and γ are illustrated in Fig. 9. Figure 9b shows that Ws increased significantly with increasing γ, which indicates that the larger the γ, the more evident the delay in the drawing of the upper coal seam. The increase of the weight of the gangue relative to the weight of the coal with increasing γ is the fundamental reason for these changes in the drawing bodies.
Figure 10 shows the volume of DBn (Vn) for the nine schemes with different γ. Due to the effect of the initial drawing process, V2 and V3 were much lower than V1, whereas V4–16 were relatively normal. Cycles 4–16 of the drawing process can be divided into three stages: cycles 4–7 are stage I (SI), cycles 8–11 are stage II (SII), and cycles 12–16 are stage III (SIII).
To further analyze the influence of γ on Vn in normal cycling, the average volume of the drawing bodies (\(\overline{{V_{n} }}\)) was calculated for the three stages for different γ, as shown in Fig. 11. With increasing γ, the average volume in SI gradually decreased, the average volume in SII hardly changed, whereas the average volume in SIII increased. By comparing the linear fitting lines of the three stages, we can see that \(\overline{{V_{{{\text{S}}_{{\text{I}}} }} }} < \overline{{V_{{{\text{S}}_{{{\text{II}}}} }} }} < \overline{{V_{{{\text{S}}_{{{\text{III}}}} }} }}\). In other words, for fixed γ, the volume of each drawing body increased as the support advanced in normal cycling. Moreover, the larger the γ, the greater the increase in the volume.
The drawing body develops from the top-coal boundary formed in the previous round of drawing. The top-coal boundary after each drawing cycle was significantly different for different γ, so that the shape of the drawing body also significantly varied in normal cycling, as shown in Fig. 12. Although, the shapes of the drawing bodies are different in the normal cycling, the stages shown in Fig. 10 are still used here in investigating the drawing body shape.
The average width (\(\overline{W}\)) and average height (\(\overline{H}\)) of the drawing bodies are shown for each stage for different γ in Fig. 13. Overall, \(\overline{{W_{{\text{I}}} }}\) approximately decreased, while \(\overline{{W_{{{\text{II}}}} }}\) and \(\overline{{W_{{{\text{III}}}} }}\) increased with increasing γ. All the average heights of the drawing bodies decreased with increasing γ. In addition, the average height in each stage was greater than the average width. The width and volume increased with increasing γ, which indicates that the change in the volume was mainly due to change in the width of the drawing body.
To analyze the influence of \(\overline{W}\) and \(\overline{H}\) on the volume of the drawing body in normal cycling, the average width-to-height ratios of drawing bodies in different stages are plotted in Fig. 14. \(\overline{W} /\overline{H}\) increased with an increase of γ. The rate of increase for SII was similar to that for SIII, whereas the rate of increase for SI was relatively smaller. From Fig. 10, it can be seen that the trend for \(\overline{W} /\overline{H}\) has little correlation with the trend for the volume, which confirms that the change in the width is the main reason for the change in the volume. Therefore, if γ is relatively large, the best way to optimize the on-site top-coal drawing is to increase the width of the drawing body. This would increase the average output of top coal in normal cycling, which would increase the recovery ratio of top coal in LTCC.
4.2 Effect of density ratio on the top-coal boundary
4.2.1 Initial drawing stage
The top-coal boundary at the end of the initial drawing process is called the initial top-coal boundary (Wei et al. 2018; Yang et al. 2020, 2021). To visualize the shapes of the initial top-coal boundaries for the nine schemes for different γ, they were sketched using trace points, as shown in Fig. 15. The relative distance (D) is the horizontal axis, the height (H) is the longitudinal axis, and the center of the DO is the origin. As illustrated in Fig. 15, the curves on the right side of the DO interweave with increasing γ, whereas those on the left are relatively separate. The left curves basically conform to the law that the height decreases with increasing γ, which means that the volume of drawn top coal increases. Therefore, the drawn volume for the left side increased with increasing γ.
To study the internal mechanism for the change in the height of the initial top-coal boundary, the shape of the boundary, the displacement field diagram, and a force chain diagram (Jin et al. 2017; Sun et al. 2019; Wang et al. 2019, 2020c) for when the first gangue appeared are shown in Fig. 16 for γ = 0.6, 1.0, and 1.4. From the shapes of the boundaries, it can be seen that the difference in the thicknesses of the left and right coal seams was due to the hydraulic support on the right side of the DO. Furthermore, due to the asymmetrical shape of the DO, the left granular particles were more likely to be drawn. With increasing γ, the coal seam was subjected to higher pressure, and the resulting increase in the particle velocity led to a decrease of the height of the top-coal boundary on the left side.
In the displacement field diagram in Fig. 16, the gradual variation of the particle color from red to blue represents a decrease in the particle displacement during the drawing process. Compared with the displacement field for γ = 0.6, there were more large-displacement (red) particles in the displacement field than for γ = 1.0 or 1.4, which indicates that with increasing γ, more distant particles flow toward the DO and the velocity increases. This is the main mechanism for the increase of the top-coal yield with increasing γ.
In the force chain diagram, each short line represents an interaction force between particles. The color gradient from red to blue represents a decrease in the force from large to small. As can be seen, the number of strong chains (red lines) increased with increasing γ. When γ = 0.6, the strong chains were only in the goaf and the front of the working face. They did not connect to form an arch above the support. When γ = 1.4, a weak chain developed to the DO, and there were a large number of strong-chain arches, which indicates that with increasing γ, the number of strong chains increased and that the strong chains gradually connected to form strong-chain arches.
Figure 17 is a fusion graph of the force chains and the top-coal boundary at a certain moment in the initial drawing process for γ = 0.6. The pre-drawing body is under the strong-chain arch, and the position of the weak-chain arch is basically coincident with that of the DO. In the initial drawing stage, the weak chain gradually develops toward the DO under the control of the strong-chain arch, resulting in top-coal particles being mainly unconstrained and drawn from the opening.
4.2.2 Normal cycling
Similarly, the top-coal boundary at the end of the 16th drawing process is called the final top-coal boundary. The shapes of the final top-coal boundaries for different γ are shown in Fig. 18. The amount of bending of the boundary increased with increasing γ, which is called hysteretic development. As the density ratio increases, the bending first appears and then becomes more severe. The entire curve basically moves to the left. Eventually, the bending becomes less severe.
Furthermore, taking the 16th drawing process as an example, the shape of the boundary, displacement field diagram, and force chain diagram for normal cycling for γ = 0.6, 1.0, or 1.4 are shown in Fig. 19. With increasing γ, some phenomena deserve further analysis. The shape of the boundary diagram shows that the top-coal boundary bends and moves toward the goaf, eventually moving over the DO, which is the hysteretic development.
In the displacement field diagram in Fig. 19a, a small large-displacement crest appears after the first large-displacement crest. In the displacement field map for γ = 1.4 in Fig. 19c, there are two large-displacement crests of similar size. When γ = 1.0 in Fig. 19b, there are more large-displacement particles. However, the large-displacement crests are chaotic. In general, during the drawing process and as the support moves forward, the first large-displacement crest forms. Then, due to the increase of the distance between the DO and the first large-displacement crest, the effect of the drawing process on the first large-displacement crest gradually decreases, and then a new large-displacement crest forms. By comparing the displacement field diagrams for different γ, it can be seen that with increasing γ, the pressure exerted by gangue particles on the top-coal particles increases and the intrusiveness also increases. This promotes the periodic formation and termination of crests, which leads to a decrease in the widths of the crests and an increase in the formation speed.
The force chain diagram shows that when γ was relatively small, there were only weak-chain arches but they span a large area. These weak-chain arches gradually developed toward the DO, and a few strong chains appeared in the goaf. With increasing γ, the pressure exerted by gangue particles on the lower particles increased. Strong chains formed and lengthened in the goaf, the roof above the hydraulic support, and the front of the working face. They gradually connected to form a strong-chain arch. Under the control of a large number of strong-chain arches, the weak-chain arches developed toward the DO, and the difficulty of drawing top coal above the DO increased, resulting in the hysteretic development of the top-coal boundary.
4.3 Effect of density ratio on the recovery of top coal
Improving the recovery of top coal is an important way to optimize the output of a coal mine. Two indexes measuring the recovery of top coal are the raw coal recovery ratio and the pure coal recovery ratio. The latter is calculated as:
where \(V_{1}\) is the volume of pure coal produced and \(V_{2}\) is the volume of the reserves of pure coal.
\(V_{1}\) and \(V_{2}\) of each scheme are obtained by the following methods: In the initial model, the distance from the canopy of the hydraulic support to the top of the coal seam is taken as the height of a rectangle, and the advance distance of the hydraulic support is defined as the length of the rectangle. The \(V_{2}\) is the volume of top coal within this rectangle. In the numerical model at the end of the last drawing, the unreleased top coal between the initial position and the present position of the drawing opening is called residual coal. The volume of pure coal produced (\(V_{1}\)) is equal to the difference between pure coal reserves and the volume of residual coal. The recovery rates of schemes with different density ratios were calculated from Formula 6, as shown in Fig. 20a. The pure coal recovery ratio for different γ varies between 83% and 87%. When 1.0 ≤ γ ≤ 2.2, the average recovery rate of top coal is about 86%, while when γ < 1.0, the recovery rate of top coal is relatively lower. Although the theoretical recovery value is not equal to the actual recovery value of the mine site, it can be seen that when the density ratio is less than 1, it is not conducive to the improvement of top coal recovery.
As for the influence of random seed number in numerical simulation on experimental results, 5 models with different random seed numbers under the condition of γ = 1.0 were generated. The top coal recovery results from models with different random seed numbers and initial random seed number (10,030) were calculated and shown in Fig. 20b. It can be seen that the top coal recovery rate under different random numbers is basically the same, which is similar to the calculation result of the original model. Hence, it is generally acceptable to default to random numbers or ignore the influence of random numbers on the motion law of top coal.
Next, we consider the recovery of top coal for different γ in different stages of the whole process. The initial stage S0 is when the hydraulic support has advanced a distance of 0–2 m from its initial position. SI, SII, and SIII correspond to the support advancing distances of 3–6, 7–10, and 11–15 m, respectively. The pure coal recovery ratio for increasing γ is shown in Fig. 21 for the different stages. When 0.6 ≤ γ ≤ 2.2, the recovery ratios in SI and SII are both greater than 90% and are directly proportional to γ. The recovery ratios in SO is in the range of 77% to 88%, which is also directly proportional to γ. Affected by the hysteretic development of the boundary of top coal, the recovery ratios in S0 is lower than 78% and inversely proportional to γ.
The following two points can be drawn:
-
(1)
In fully mechanized caving mining, the top coal loss at both ends is generally greater than that at the normal cycle drawing stage, so the method to reduce the top coal loss at both ends is worth studying in the future work.
-
(2)
With the variation of γ, the recovery ratio of top coal is stable at γ ≤ 1.2 and fluctuates greatly at γ > 1.2. At 1.0 ≤ γ ≤ 2.0, the recovery ratio of top coal at each stage is relatively high. That is to say, the condition of 1.0 ≤ γ ≤ 2.0 is conducive to the increase of top coal recovery ratio.
In general, 1.0 ≤ γ ≤ 2.0 is conducive to improving the recovery of top coal, especially in the middle of the normal cycling stage. Therefore, when designing a production system, to increase the top-coal yield and the recovery of top coal, the advance length of the working face should be as long as possible.
5 Discussion
The range of γ used in the above numerical simulations basically covers the general geological conditions of coal mines. However, to further explore some of the phenomena described above, we ran tests with a higher γ, namely 5.0, and compared the results with those from the previous tests. We analyzed the shape of the initial drawing body, Ws in normal cycling, the initial top-coal boundary, and the characteristics of the hysteretic development.
5.1 The drawing body
5.1.1 Initial drawing coal stage
The shape of the initial drawing body for different γ and the relation between D1, D2, and γ are plotted in Fig. 22. Figure 22a shows that when γ = 5.0, the left boundary has shifted significantly toward the goaf, while the position of the right boundary is basically unchanged, which is consistent with Fig. 7b. Figure 22b shows that D1 is positively correlated with γ, while D2 basically does not change.
5.1.2 Normal cycling drawing coal stage
The bending of the drawing body was analyzed with the sickle-shaped DB13 as an example. Figure 23a shows that DB13 was severely bent and its upper part extended to near the initial drawing body. Figure 23b indicates that Ws basically has a positive correlation with γ, although the overall trend is an S-shaped rise. It is easy to conclude that DB13 extended further in the direction of the initial drawing body with increasing γ and that its distance from the initial drawing body is its maximum width.
5.2 The initial top-coal boundary
5.2.1 Initial drawing coal stage
Figure 24 shows the initial top-coal boundary for different γ. Unlike Fig. 15, with γ = 5.0, the height of the left boundary no longer decreases with increasing γ which suggest that there is a limit to this trend. This indicates that for a larger γ, it is more difficult to reduce the height of the initial top-coal left boundary.
5.2.2 The hysteretic development in normal cycling drawing coal stage
The hysteretic development occurs at the top-coal boundary above the hydraulic support in the normal cycling stage. Using data from Figs. 18, 25 shows the final top-coal boundaries after the 16th drawing process and the hysteretic development for various γ including γ = 5.0. γ was divided into three ranges according to the degree of hysteretic development.
Figure 25a shows that when 0.6 ≤ γ ≤ 1.0, the bottom of the top-coal boundary shifted to the right with increasing γ, resulting in an increase of the curvature and the start of hysteretic development. Figure 25b indicates that when 1.0 ≤ γ ≤ 2.0, with increasing γ, the degree of hysteretic development of the boundary was basically unchanged. However, the boundary above the hydraulic support moved toward the goaf as a whole. Figure 25c shows that when 2.0 ≤ γ ≤ 5.0, there was no obvious or regular change of the top-coal boundary. In summary, when γ ≤ 1.0, the hysteretic development basically does not occur. This is called the formation stage of hysteretic development. When 1.0 ≤ γ ≤ 2.0, the hysteretic development occurs and becomes more obvious with an increase of the density ratio. This is called the expansion stage. When 2.0 ≤ γ, the hysteretic development reaches a maximum, and this is called the limit stage.
5.3 Physical experiments validation
To validate the results obtained from numerical calculation, physical experiments with three representative gangue-coal density ratios (γ < 1.00, γ = 1.00 and γ > 1.00) were conducted. Particles made of polycarbonate and aluminum alloy with densities of 1.18 g/cm3 and 2.7 g/cm3 respectively were used in the experiments. Images during the experimental process are shown in Fig. 26.
It can be seen from Fig. 26 that in the physical experiment, during the top coal drawing progress with support advancing, the phenomenon of hysteretic development of top coal boundary consistent with the numerical simulation results, as shown in Fig. 19a.
After the experiment, the recovery of top coal was canulated and compared with the numerical results data, as shown in Fig. 27. The results show that the recovery ratio of top coal under different γ is different. The method of “seeing gangue close the door” is used in numerical simulation experiments, and a small amount of gangue is often released in physical experiments. This leads to some inconsistency between the experimental results of the two experimental methods. Nevertheless, the physical experiment results are still within the range of numerical simulation results. Hence, the physical experimental data validated the results obtained from numerical modeling.
In summary, this paper mainly uses theoretical analysis and numerical simulation methods to investigate the effect of γ on the top coal drawing mechanism in the advancing direction of working face. In the subsequent research, more systematic physical experiments, field data analysis and other more approaches will be employed to verify, analyze and utilize this research results, and the effect of other physical and mechanical properties (shape, size, stiffness, etc.) of coal and gangue particles on the top coal motion law will also be further studied.
6 Conclusions
Using the method of density gradient division, discrete element numerical simulations were performed for the top-coal drawing process in LTCC with different γ. Based on the BBR research system, the effect of γ on the top-coal drawing mechanism was investigated from the perspectives of drawing body, top-coal boundary, and recovery of top coal. The main conclusions are as follows.
-
(1)
With increasing γ, the initial drawing body on the goaf side is farther away from the hydraulic support, which is the fundamental reason for the increase of the width and volume of the initial drawing body.
-
(2)
In normal cycling, with increasing γ, the drawing body bends and its upper part extends near to the initial drawing body. Ws basically has a positive correlation with γ, and the overall trend has an S-shaped rise.
-
(3)
The larger the γ is, the smaller the height of the top coal above the goaf at the end of the initial drawing process. However, the decrease in the height of the initial top-coal boundary with increasing γ has a limit. The larger the γ is, the smaller the decrease of the height of the initial top-coal boundary above the goaf.
-
(4)
There are three stages of hysteretic development: formation stage, expansion stage, and limit stage. When γ ≤ 1.0, the hysteretic development basically does not occur. When 1.0 ≤ γ ≤ 2.0, the hysteretic development occurs and becomes more obvious with an increase of the density ratio. When γ ≥ 2.0, the hysteretic development has reached a maximum.
-
(5)
Increasing the advance length of the working face is beneficial for increasing the overall recovery rate.
References
Aguado Ã, Gonza C (2009) Influence of the stress state in a coal bump-prone deep coalbed: a case study. Int J Rock Mech Min Sci 46:333–345. https://doi.org/10.1016/j.ijrmms.2008.07.005
Ajamzadeh M, Sarfarazi V, Dehghani H (2019) Evaluation of plow system performance in long-wall mining method using particle flow code. Int J Coal Sci Technol 6:518–535. https://doi.org/10.1007/s40789-019-00266-3
Alehossein H, Poulsen BA (2010) Stress analysis of longwall top coal caving. Int J Rock Mech Min Sci 47:30–41. https://doi.org/10.1016/j.ijrmms.2009.07.004
Copco A (2007) Mining methods in underground mining, 2nd edn. Atlas Copco, Sweden
Bi Y, He S, Li X, Ouyang C (2016) Effects of segregation in binary granular mixture avalanches down inclined chutes impinging on defending structures. Environ Earth Sci 75:236. https://doi.org/10.1007/s12665-015-5076-1
Hamdi P, Stead D, Elmo D, Töyrä J (2018) Use of an integrated finite/discrete element method-discrete fracture network approach to characterize surface subsidence associated with sub-level caving. Int J Rock Mech Min Sci 103:55–67. https://doi.org/10.1016/j.ijrmms.2018.01.021
Jangara H, Ozturk CA (2021) Longwall top coal caving design for thick coal seam in very poor strength surrounding strata. Int J Coal Sci Technol. https://doi.org/10.1007/s40789-020-00397-y
Jin A, Sun H, Wu S, Gao Y (2017) Confirmation of the upside-down drop shape theory in gravity flow and development of a new empirical equation to calculate the shape. Int J Rock Mech Min Sci 92:91–98. https://doi.org/10.1016/j.ijrmms.2016.12.005
Klishin VI, Fryanov VN, Pavlova LD, Opruk GY (2019) Modeling top coal disintegration in thick seams in longwall top coal caving. J Min Sci 55:247–256. https://doi.org/10.1134/S1062739119025527
Le TD, Mitra R, Oh J, Hebblewhite B (2017) A review of cavability evaluation in longwall top coal caving. Int J Min Sci Technol 27:907–915. https://doi.org/10.1016/j.ijmst.2017.06.021
Li W (2013) Mineral and rock identification method. Petroleum Industry Press, Beijing
Liao CC, Hsiau SS, Hu YM (2017) Density-driven sinking dynamics of a granular ring in sheared granular flows. Adv Powder Technol 28:2597–2604. https://doi.org/10.1016/j.apt.2017.07.011
Lupo JF (1997) Progressive failure of hanging wall and footwall Kiirunavaara Mine, Sweden. Int J Rock Mech Min Sci Geomech Abstr 34:684. https://doi.org/10.1016/S1365-1609(97)00277-3
Melo F, Vivanco F, Fuentes C, Apablaza V (2008) Kinematic model for quasi static granular displacements in block caving: dilatancy effects on drawbody shapes. Int J Rock Mech Min Sci 45:248–259. https://doi.org/10.1016/j.ijrmms.2007.07.005
Melo F, Vivanco F, Fuentes C (2009) Calculated isolated extracted and movement zones compared to scaled models for block caving. Int J Rock Mech Min Sci 46:731–737. https://doi.org/10.1016/j.ijrmms.2008.09.012
Navarro J, Schunnesson H, Ghosh R, Segarra P, Johansson D, Sanchidrián JÁ (2019) Application of drill-monitoring for chargeability assessment in sublevel caving. Int J Rock Mech Min Sci 119:180–192. https://doi.org/10.1016/j.ijrmms.2019.03.026
Regassa B, Xu N, Mei G (2018) An equivalent discontinuous modeling method of jointed rock masses for DEM simulation of mining-induced rock movements. Int J Rock Mech Min Sci 108:1–14. https://doi.org/10.1016/j.ijrmms.2018.04.053
Sepehri M, Apel DB, Hall RA (2017) Prediction of mining-induced surface subsidence and ground movements at a Canadian diamond mine using an elastoplastic finite element model. Int J Rock Mech Min Sci 100:73–82. https://doi.org/10.1016/j.ijrmms.2017.10.006
Sheng LT, Hsiau SS, Hsu NW (2021) Experimental study of the dynamic behavior and segregation of density-bidisperse granular sliding masses at the laboratory scale. Landslides 18:2095–2110. https://doi.org/10.1007/s10346-021-01629-1
Shi Q, Sun G, Hou M, Lu K (2007) Density-driven segregation in vertically vibrated binary granular mixtures. Phys Rev e: Stat Nonlinear Soft Matter Phys 75:3–6. https://doi.org/10.1103/PhysRevE.75.061302
Song Z, Konietzky H (2019) A particle-based numerical investigation on longwall top coal caving mining. Arab J Geosci 12:556. https://doi.org/10.1007/s12517-019-4743-z
Song Z, Konietzky H, Herbst M (2019) Bonded-particle model-based simulation of artificial rock subjected to cyclic loading. Acta Geotech 14:955–971. https://doi.org/10.1007/s11440-018-0723-9
Song Z, Konietzky H, Herbst M (2020) Drawing mechanism of fractured top coal in longwall top coal caving. Int J Rock Mech Min Sci 130:104329. https://doi.org/10.1016/j.ijrmms.2020.104329
Song Z, Wang Y, Konietzky H, Cai X (2021) Mechanical behavior of marble exposed to freeze-thaw-fatigue loading. Int J Rock Mech Min Sci 138:104648. https://doi.org/10.1016/j.ijrmms.2021.104648
Song Z, Wei W, Zhang J (2018) Numerical investigation of effect of particle shape on isolated extracted zone (IEZ) in block caving. Arab J Geosci 11:310. https://doi.org/10.1007/s12517-018-3669-1
Sun H, Gao Y, Elmo D, Jin A, Wu S, Dorador L (2019) A study of gravity flow based on the upside-down drop shape theory and considering rock shape and breakage. Rock Mech Rock Eng 52:881–893. https://doi.org/10.1007/s00603-018-1514-1
Tripathi A, Khakhar DV (2013) Density difference-driven segregation in a dense granular flow. J Fluid Mech 717:643–669. https://doi.org/10.1017/jfm.2012.603
Unver B, Yasitli NE (2006) Modelling of strata movement with a special reference to caving mechanism in thick seam coal mining. Int J Coal Geol 66:227–252. https://doi.org/10.1016/j.coal.2005.05.008
Vivanco F, Melo F (2013) The effect of rock decompaction on the interaction of movement zones in underground mining. Int J Rock Mech Min Sci 60:381–388. https://doi.org/10.1016/j.ijrmms.2013.01.013
Wang J (2009) Theory and technology of thick coal seam mining. Metallurgical Industry Press, Beijing
Wang J, Song Z (2015) Characteristic and control method of initial interface between coal and rock under fully mechanized loose top coal caving. J China Coal Eng 47:1–4. https://doi.org/10.11799/ce201507001
Wang J, Zhang J (2015) BBR study of top-coal drawing law in longwall top-coal caving mining. J China Coal Soc 40:487–493. https://doi.org/10.13225/j.cnki.jccs.2015.0278
Wang J, Yang S, Li Y, Wei L, Liu H (2014) Caving mechanisms of loose top-coal in longwall top-coal caving mining method. Int J Rock Mech Min Sci 71:160–170. https://doi.org/10.1016/j.ijrmms.2014.04.024
Wang J, Zhang J, Li Z (2016) A new research system for caving mechanism analysis and its application to sublevel top-coal caving mining. Int J Rock Mech Min Sci 88:273–285. https://doi.org/10.1016/j.ijrmms.2016a.07.032
Wang J, Song Z, Zhang J, Chen Y (2016b) Theoretical model of drawing body in LTCC mining. J China Coal Soc 41:352–358. https://doi.org/10.13225/j.cnki.jccs.2015.1750
Wang J, Wei W, Zhang J, Xie F (2017) Stability analysis of support around the longwall top-coal caving mining in steeply thick coal seam. J China Coal Soc 42:2783–2791
Wang J, Wei W, Zhang J (2019) Effect of the size distribution of granular top coal on the drawing mechanism in LTCC. Granul Matter 21:1–18. https://doi.org/10.1007/s10035-019-0923-5
Wang J, Wang Z, Li Y (2020a) Longwall top coal caving mechanisms in the fractured thick coal seam. Int J Geomech 20:06020017. https://doi.org/10.1061/(asce)gm.1943-5622.0001722
Wang J, Wei W, Zhang J (2020b) Theoretical description of drawing body shape in an inclined seam with longwall top coal caving mining. Int J Coal Sci Technol 7:182–195
Wang J, Wei W, Zhang J, Mishra B, Li A (2020c) Numerical investigation on the caving mechanism with different standard deviations of top coal block size in LTCC. Int J Min Sci Techno 30:583–591. https://doi.org/10.1016/j.ijmst.2020.06.001
Wang J, Wei W, Zhang J, Mishra B (2021a) Laboratory and field validation of a LTCC recovery prediction model using relative size of the top coal blocks. B Eng Geol Environ 80:1389–1401. https://doi.org/10.1007/s10064-020-01970-0
Wang J, Yang S, Wei W, Zhang J, Song Z (2021b) Drawing mechanisms for top coal in longwall top coal caving (LTCC): a review of two decades of literature. Int J Coal Sci Technol. https://doi.org/10.1007/s40789-021-00453-1
Wei W, Song Z, Zhang J (2018) Theoretical equation of initial top-coal boundary in longwall top-coal caving mining. Int J Min Miner Eng 9:157–176. https://doi.org/10.1504/IJMME.2018.091972
Woo KS, Eberhardt E, Elmo D, Stead D (2013) Empirical investigation and characterization of surface subsidence related to block cave mining. Int J Rock Mech Min Sci 61:31–42. https://doi.org/10.1016/j.ijrmms.2013.01.015
Wu T, He G (2011) General geology, 2nd edn. Peking University Press, Beijing
Xiao H, Umbanhowar PB, Ottino JM, Lueptow RM (2016) Modelling density segregation in flowing bidisperse granular materials. Proc R Soc A Math Phys Eng Sci 472:20150856. https://doi.org/10.1098/rspa.2015.0856
Xu J (2008) Geology, 4th ed. Metallurgical Industry Press.
Yang L, Li L, Wei W (2021) Optimization of caving technology in an extrathick seam with longwall top coal caving mining. Adv Mater Sci Eng 2021:7725159. https://doi.org/10.1155/2021/7725159
Yang S, Zhang J, Chen Y, Song Z (2016) Effect of upward angle on the drawing mechanism in longwall top-coal caving mining. Int J Rock Mech Min Sci 85:92–101. https://doi.org/10.1016/j.ijrmms.2016.03.004
Yang S, Wei W, Zhang J (2020) Top coal movement law of dynamic group caving method in LTCC with an inclined seam. Mining, Metall Explor 37:1545–1555. https://doi.org/10.1007/s42461-020-00254-1
Yasitli NE, Unver B (2005) 3D numerical modeling of longwall mining with top-coal caving. Int J Rock Mech Min Sci 42:219–235. https://doi.org/10.1016/j.ijrmms.2004.08.007
Yi F, Hill KM (2015) Shear-induced segregation of particles by material density. Phys Rev E 022211:1–14. https://doi.org/10.1103/PhysRevE.92.022211
Zhang J, Pan W, Li Z, Song Z (2015) Development and application of 3D simulation test device for loose top-coal drawing under caving mining technique. Chinese J Rock Mech Eng 34:3871–3879. https://doi.org/10.13722/j.cnki.jrme.2014.0620
Zhang J, Wang J, Wei W (2018a) Effect of face dip angle on the drawing mechanism in longwall top-coal caving mining. J China Univ Min Technol 47:805–814. https://doi.org/10.13247/j.cnki.jcumt.000889
Zhang J, Wang J, Wei W et al (2018b) Experimental and numerical investigation on coal drawing from thick steep seam with longwall top coal caving mining. Arab J Geosci 11:96. https://doi.org/10.1007/s12517-018-3421-x
Acknowledgements
This work was supported by the Natural Science Foundation of China, China (Grant No. 51904305), the Research Fund of the State Key Laboratory of Coal Resources and Safe Mining, China University of Mining and Technology (Grant No. SKLCRSM19KF023), the Fundamental Research Funds for the Central Universities (Grant No.2022YQNY03), the Research Fund of Key Laboratory of Safety and High-efficiency Coal Mining, Ministry of Education (Grant No. JYBSYS2021204), and the Open Fund of State Key Laboratory of Coal Resources and Safe Mining (Grant No. SKLCRSM21KFA09).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no conflicts of interest.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zhang, J., Cheng, D., Yang, Y. et al. Numerical and theoretical investigations of the effect of the gangue-coal density ratio on the drawing mechanism in longwall top-coal caving. Int J Coal Sci Technol 9, 31 (2022). https://doi.org/10.1007/s40789-022-00501-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40789-022-00501-4