1 Introduction

The enhanced internal drainage of open-pit mines reduces the floor space of external drainage, decreases the stripping distance, and improves the efficiency of equipment operation. It is also the best measure for controlling the spontaneous combustion of coal, dust, and slope stability. However, once the inner dump slope has been formed, its stability directly affects the development of the open-pit coal mine stripping project and the safety of personnel and equipment. The inner dumps of some large-scale open-pit coal mines in China have experienced a certain degree of deformation or instability, which seriously threatens the safe production of open-pit coal mines. For example, in September 2014, the Huolinhe open-pit coal mine found that the inner dump was in a creeping state. Although the overall deformation was relatively stable, a bottom heave with a height of about 1 m appeared near the coal seam floor, and extended 700 m along the north–south direction. A landslide with a volume of about 770,000 m3 occurred in February 2015, causing the + 828 m horizontal dumping pan to move forward by 75 m, and the height of the bottom drum near the F4 fault to shift between 0 and 29 m (Tang et al. 2016). The inner dump in the Shenhua Baorixile open-pit coal mine began to settle in April 2009. In May of the same year, the deformation of the inner dump site + 660 m horizontal dumping transportation platform accelerated, and a 2-h landslide occurred. The landslide area covered about 750 m from north to south and about 600 m from east to west. The sliding distance was 200 m and the volume of the sliding body was estimated at about 10 million cubic meters, causing serious damage to the drainage system of the blind ditch in the basement (Yang et al. 2018). The main controlling factors of the inner dump slope are the weak base and groundwater. As the base rock mass of such dumps is highly hydrophilic, it is difficult to quantify the effect of conventional draining and drainage measures (Lu et al. 2019). If a substrate treatment is performed, the peeling cost will increase; additionally, when the weak substrate layer is thick, it is difficult to obtain an ideal treatment effect (Zhang and Wang 2015). Retaining coal pillars are an important means of improving the stability of the inner dump slope. For example, Ji (2013) analyzed the stability of the inner dump under three potential landslide modes, and analyzed the influence of the width of the coal pillar on the stability of the inner dump. Wang et al. (2019) examined the mechanical effects of supporting coal pillars and revealed the quantitative relationship between coal pillar morphological parameters and other factors and supporting effects. Previous studies have only considered the two-dimensional supporting effect of coal pillars and have not investigated the impact of the discharge load on the supporting effect of the coal pillar, resulting in the remaining coal pillar being too large. Therefore, there is an urgent need to find a new method for analyzing the stability of the inner dump slope under the pillar supporting effect that takes into account the development position of the dump, so as to realize the safe and economical operation of open-pit coal mines.

2 Characterization of three-dimensional mechanical effects of supporting coal pillar

2.1 Analysis of instability mechanism of supporting coal pillarn

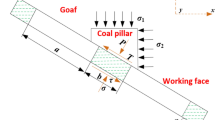
Given the current status of stripping projects in open-pit coal mines and the associated equipment operation requirements, the spatial form of the supporting coal pillar of the inner dump can be approximated as a hexahedron with a trapezoidal section. The plane position of the supporting coal pillar is shown in Fig. 1.

Fig. 1
figure 1

Location of supporting coal pillar

Full size image

The shape of the section along the direction of the supporting coal pillar (I-I') is shown in Fig. 2a. The shape of the section along the inclination of the supporting coal pillar (II-II') is shown in Fig. 2b.

Fig. 2
figure 2

Section shape of supporting coal pillar

Full size image

The sectional shape of the supporting coal pillar in the I-I' section can be regarded as an inverted trapezoid, and the sectional shape in the II-II' section can be regarded as a trapezoid. Assuming that the slope angle of the end slope is αd, based on the positional relationship between the supporting coal pillar and the inner dump, the bottom angle of the trapezoid near the inner dump is the inner bottom angle ω of the supporting coal pillar, and the trapezoid near the goaf side of the bottom angle is the outside corner β of the supporting coal pillar. The height of the trapezoid is the height of the supporting coal pillar h, the top width of the trapezoid is the top width of the supporting coal pillar b, and the width of the open pit bottom is the strike length d of the supporting coal pillar.

The coal pillar is subjected to the static earth pressure F behind the inner dump, the squeezing force F1 and F2 of the side edges, the shear resistance T1 and T2 of the side interfaces, and the supporting force of the bottom interface N. Under the effect of shear resistance S and gravity W (the resultant force of the weight of the coal pillar and the gravity load of the discharged material), the spatial shape and force analysis of the coal pillar are depicted in Fig. 3.

Fig. 3
figure 3

Spatial shape and force state of supporting coal pillar

Full size image

Although the supporting coal pillar is subjected to three-dimensional mechanics, it can be approximated using rock beam theory for analysis. It is well known that the supporting coal pillar is prone to shear failure on both sides of the end slope, and cracking damage can easily occur in the middle of the supporting coal pillar. When the supporting coal pillar is first broken by the static earth pressure F behind the inner dump, it can be roughly approximated as two cantilever beams. If the overall instability of the inner dump is induced, the two cantilever beams on either side of the end slope will undergo shear failure. In this study, the failure mechanism of the supporting coal pillar is similar to the shear failure of the lowermost rock strata in the inner row of the cross-mining in the Zhundong open-pit mine (Tian 2019). According to a large number of landslide engineering examples (Wang et al. 2020; Liu et al. 2020; Wei and Nei 2013), shear failure occurred in the lower rock mass and tensile fracture failure occurred in the upper rock mass, which eventually induced a landslide. Therefore, when the failure of the supporting coal pillar induces the overall instability of the slope, shear failure occurs near the end edge positions on both sides of the supporting coal pillar.

When the supporting coal pillar undergoes shear failure on both sides of the end slope, the resultant force must be greater than the shear resistance of the supporting coal pillar. The position at which the resultant shear force T is the least likely to undergo shear failure can be determined as follows. Assuming that the shape of the side interface of the supporting coal pillar is the same and the height of the discarded material at the upper part does not change, the shear resistance and the resultant shear force of the side interface are 2T1 and 2T2. According to the Mohr–Coulomb strength criterion:

$$T{ = }2\iint\limits_{A} {\left( {\sigma \tan \varphi_{\text{m}} + c_{\text{m}} } \right){\text{d}}A}$$
(1)

where \(\varphi_{\text{m}}\) is the internal friction angle of the coal pillar, \(c_{\text{m}}\) is the cohesion of the coal pillar, A is the area of the coal pillar side interface, and σ is the normal stress acting on the side interface of the coal pillar.

As the height of the supporting coal pillar is fixed in its strike direction, the self-weight stress at the same level of any section (such as sections GE', PE', QF', and KF' in Fig. 4) is the same as the Poisson effect (G1, P1, Q1, K1). Therefore, the shear resistance T is only related to the section area. According to the triangular function relationship, the section where the supporting coal pillar is most likely to undergo shear failure is the vertical plane that crosses the end of the supporting coal pillar at its bottom interface. Taking into account the horizontal base and the inclined base, the spatial shape of the supporting coal pillar can be approximated as a quadrangular prism with a quadrilateral cross-section.

Fig. 4
figure 4

Failure position of supporting coal pillar

Full size image

According to the limit equilibrium condition in the x-direction:

$$F{ = }S + T_{1} + T_{2}$$
(2)

Thus, the condition for the coal pillar to remain stable and exert the maximum supporting effect is \(F < S + T_{1} + T_{2}\). Therefore, the supporting effect of the coal pillar is three-dimensional, and its magnitude is \(S + T_{1} + T_{2}\). As the ratio of the width of the coal pillar to the length of the end slope on both sides is small, additional force is generated by the triangular vertical load (Shao and Wei 1998). This implies that S is determined by the self-weight of the supporting coal pillar and the load of the upper waste, the morphological parameters of the bottom interface of the supporting coal pillar, and the lithology of the inner dump base. T is determined by the normal stress of the side interface, the properties of the supporting coal pillar, and the morphological parameters of the site interface.

2.2 Characterization of three-dimensional mechanical effects of supporting coal pillar

The three-dimensional supporting effect of the coal pillar is affected by the load of the upper waste. Thus, it is necessary to characterize the three-dimensional mechanical effect of the coal pillar in the inner dump at different development positions. In this study, three working conditions were considered: (1) development of the dumping to the side of the supporting coal pillar, (2) development of the dumping to the top surface of the supporting coal pillar, and (3) development of the entire supporting coal pillar for dumping. The cross-sections of each working condition are shown in Fig. 5. Corner points B and A of the top surface of the supporting coal pillar denote the boundary points of working conditions I and II, and of working conditions II and III, respectively.

Fig. 5
figure 5

Section indication under three working conditions

Full size image

According to the coal pillar morphological parameters, coal pillar height equations \(H_{\text{I}} \left( x \right)\), \(H_{\text{II}} \left( x \right)\), and \(H_{\text{III}} \left( x \right)\) are established as follows for areas AOE, AEBF, and BFC, respectively:

$$\left\{ {\begin{array}{*{20}l} {H_{\text{I}} \left( x \right) = x\tan \left( {\beta + \alpha } \right),x \subseteq \left[ {0,\frac{h}{{\tan \left( {\beta + \alpha } \right)}}} \right]} \hfill \\ {H_{\text{II}} \left( x \right) = h,x \subseteq \left[ {\frac{h}{{\tan \left( {\beta + \alpha } \right)}},b + \frac{h}{{\tan \left( {\beta + \alpha } \right)}}} \right]} \hfill \\ \begin{gathered} H_{\text{III}} \left( x \right) = h + \left[ {b + \frac{h}{{\tan \left( {\beta + \alpha } \right)}} - x} \right]\tan \left( {\omega - \alpha } \right) \\ x \subseteq \left\{ {b + \frac{h}{{\tan \left( {\beta + \alpha } \right)}},\frac{{h + \left[ {\frac{h}{{\tan \left( {\beta + \alpha } \right)}} + b} \right]\tan \left( {\omega - \alpha } \right)}}{{\tan \left( {\omega - \alpha } \right) + \tan \alpha }}} \right\} \\ \end{gathered} \hfill \\ \end{array} } \right.$$
(3)

The slope equation of the inner dump is \(z_{\text{p}}\), and the base morphological equation of the inner dump is \(H_{\text{d}} \left( x \right)\):

$$\left\{ {\begin{array}{*{20}c} {z_{\text{p}} = h_{\text{p}} + x\tan \beta_{\text{p}} } \\ {H_{\text{d}} \left( x \right) = x\tan \alpha ,x \subseteq \left( {0,h + \left[ {\frac{h}{{\tan \left( {\beta + \alpha } \right)}} + b} \right]\tan \left( {\omega - \alpha } \right){/}\left[ {\tan \left( {\omega - \alpha } \right) + \tan \alpha } \right]} \right)} \\ \end{array} } \right.$$
(4)

2.2.1 Three-dimensional supporting effect under the development of dumping to coal pillar side

Taking the outer corner of the coal pillar bottom interface as the origin of the coordinates, the trapezoidal section is divided into four areas: the triangle AOE, trapezoid AEFB, quadrilateral BFMG, and triangle GMC. The area division is shown in Fig. 6. The shear resistance T of the interface on both sides of the end slope is twice the sum of the side interface shear resistance of the four regions, and the bottom interface shear resistance S is the sum of the bottom interface shear resistance of the four regions.

Fig. 6
figure 6

Development of dumping to coal pillar side

Full size image

(1) Shear resistance T of side interface.

The shear resistance of the side interface in AOE is \(T\), that in AEBF is \(T\), that in BFMG is \(T\), and that in GMC is \(T ^{\prime}\). These quantities can be written as follows:

$$\left\{ {\begin{array}{*{20}l} {T_{\text{I}} = \int_{0}^{{\frac{h}{{\tan \left( {\beta + \alpha } \right)}}}} {\int_{x\tan \alpha }^{{x\tan \left( {\beta + \alpha } \right)}} {\left\{ {\tan \varphi_{\text{m}} k\gamma_{\text{m}} \left[ {H_{\text{I}} \left( x \right) - z} \right] + c_{\text{m}} } \right\}} } {\text{d}}z{\text{d}}x} \hfill \\ {T_{\text{II}} = \int_{{\frac{h}{{\tan \left( {\beta + \alpha } \right)}}}}^{{\frac{h}{{\tan \left( {\beta + \alpha } \right)}} + b}} {\int_{x\tan \alpha }^{h} {\left\{ {\tan \varphi_{\text{m}} k\gamma_{\text{m}} \left[ {H_{\text{II}} \left( x \right) - z} \right] + c_{\text{m}} } \right\}} } {\text{d}}z{\text{d}}x} \hfill \\ {T_{\text{III}} = \int_{{\frac{h}{{\tan \left( {\beta + \alpha } \right)}} + b}}^{{\frac{{h + \left[ {\frac{h}{{\tan \left( {\beta + \alpha } \right)}} + b} \right]\tan \left( {\omega - \alpha } \right) - h_{\text{p}} }}{{\tan \beta_{\text{p}} + \tan \left( {\omega - \alpha } \right)}}}} {\int_{x\tan \alpha }^{{h + \left[ {b + \frac{h}{{\tan \left( {\beta + \alpha } \right)}} - x} \right]\tan \left( {\omega - \alpha } \right)}} {\left\{ {k\tan \varphi_{\text{m}} \gamma_{\text{m}} \left[ {H_{\text{III}} (x) - z} \right] + c_{\text{m}} } \right\}} } {\text{d}}z{\text{d}}x} \hfill \\ {T_{\text{III}} ^{\prime} = \int_{{\frac{{h + \left[ {\frac{h}{{\tan \left( {\beta + \alpha } \right)}} + b} \right]\tan \left( {\omega - \alpha } \right) - h_{\text{p}} }}{{\tan \beta_{\text{p}} + \tan \left( {\omega - \alpha } \right)}}}}^{{\frac{{h + \left[ {\frac{h}{{\tan \left( {\beta + \alpha } \right)}} + b} \right]\tan \left( {\omega - \alpha } \right)}}{{\tan \left( {\omega - \alpha } \right) + \tan \alpha }}}} {\int_{x\tan \alpha }^{{h + \left[ {b + \frac{h}{{\tan \left( {\beta + \alpha } \right)}} - x} \right]\tan \left( {\omega - \alpha } \right)}} {\left\{ {\tan \varphi_{m} k\left\{ \begin{gathered} \gamma_{\text{m}} \left[ {H_{\text{III}} \left( x \right) - z} \right] \hfill \\ + \gamma_{\text{p}} \left[ {z_{\text{p}} - H_{\text{III}} \left( x \right)} \right] \hfill \\ \end{gathered} \right\} + c_{\text{m}} } \right\}} } {\text{d}}z{\text{d}}x} \hfill \\ \end{array} } \right.$$
(5)

(2) Shear resistance S of the bottom interface.

The shear resistance of the bottom interface in AOE is \(S_{\text{I}}\), that in AEBF is \(S_{\text{II}}\), that in BFMG is \(S_{\text{III}}\), and that in GMC is \(S_{\text{III}} ^{\prime}\). These quantities can be written as follows:

$$\left\{ {\begin{array}{*{20}l} {S_{\text{I}} = \int_{0}^{d} {\int_{0}^{{\frac{h}{{\tan \left( {\beta + \alpha } \right)}}}} {\tan \varphi_{j} \gamma_{\text{m}} \left[ {x\tan \left( {\beta + \alpha } \right) - x\tan \alpha } \right]} {\text{d}}x} {\text{d}}y + \int_{0}^{d} {\int_{0}^{{\frac{h}{{\cos \alpha \tan \left( {\beta + \alpha } \right)}}}} {c_{j} } {\text{d}}x} {\text{d}}y} \hfill \\ {S_{\text{II}} = \int_{0}^{d} {\int_{{\frac{h}{{\tan \left( {\beta + \alpha } \right)}}}}^{{\frac{h}{{\tan \left( {\beta + \alpha } \right)}} + b}} {\tan \varphi_{j} \gamma_{\text{m}} \left( {h - x\tan \alpha } \right){\text{d}}} } x{\text{d}}y + \int_{0}^{d} {\int_{{\frac{h}{{\cos \alpha \tan \left( {\beta + \alpha } \right)}}}}^{{\frac{h}{{\cos \alpha \tan \left( {\beta + \alpha } \right)}} + \frac{b}{\cos \alpha }}} {c_{j} {\text{d}}} } x{\text{d}}y} \hfill \\ {S_{\text{III}} = \int_{0}^{d} {\int_{{A_{7} }}^{{A_{10} }} {\tan \varphi_{j} \gamma_{\text{m}} \left\{ {h + \left[ {A_{7} - x} \right]\tan \left( {\omega - \alpha } \right) - x\tan \alpha } \right\}{\text{d}}} } x{\text{d}}y + \int_{0}^{d} {\int_{{\frac{{A_{7} }}{\cos \alpha }}}^{{\frac{{A_{10} }}{\cos \alpha }}} {c_{j} {\text{d}}} } x{\text{d}}y} \hfill \\ {S_{\text{III}} ^{\prime} = \int_{0}^{d} {\int_{{A_{10} }}^{{A_{8} }} {\tan \varphi_{\text{m}} \left\{ {\gamma_{\text{m}} \left[ {A_{6} - A_{5} x - A_{3} x} \right] + \gamma_{\text{p}} \left[ {h_{\text{p}} + xA_{4} + xA_{5} - A_{6} } \right]} \right\}{\text{d}}} } x{\text{d}}y + \frac{{dc_{j} }}{\cos \alpha }(A_{8} - A_{10} )} \hfill \\ \end{array} } \right.$$
(6)

where

$$\left\{ {\begin{array}{*{20}l} {A_{3} = \tan \alpha } \hfill \\ {A_{4} = \tan \beta_{\text{p}} } \hfill \\ {A_{5} = \tan \left( {\omega - \alpha } \right)} \hfill \\ {\begin{array}{*{20}l} {\begin{array}{*{20}l} {A_{6} = h + \tan \left( {\omega - \alpha } \right)\left[ {h/\tan \left( {\beta + \alpha } \right) + b} \right]} \hfill \\ {A_{7} { = }h{/}\tan \left( {\beta { + }\alpha } \right) + b} \hfill \\ \end{array} } \hfill \\ {A_{8} = \left\{ {h + \tan \left( {\omega - \alpha } \right)\left[ {h/\tan \left( {\beta + \alpha } \right) + b} \right]} \right\}/\left[ {\tan \alpha + \tan \left( {\omega - \alpha } \right)} \right]} \hfill \\ {A_{10} = \left\{ {h + \tan \left( {\omega - \alpha } \right)\left[ {h/\tan \left( {\beta + \alpha } \right) + b} \right] - h_{\text{p}} } \right\}/\left[ {\tan \beta_{\text{p}} + \tan \left( {\omega - \alpha } \right)} \right]} \hfill \\ \end{array} } \hfill \\ \end{array} } \right.$$

Based on Eqs. (5) and (6), the three-dimensional supporting effect under the development of dumping to the coal pillar side is given by:

$$S + T = {2}\left( {T_{\text{I}} + T_{\text{II}} + T_{\text{III}} + T_{\text{III}} ^{\prime}} \right) + \left( {S_{\text{I}} + S_{\text{II}} { + }S_{\text{III}} { + }S_{\text{III}} ^{\prime}} \right)$$
(7)

2.2.2 Three-dimensional supporting effect under the development of dumping to coal pillar top

Because the side interface shear force and bottom interface shear force of the triangular AOE area are the same for the development of dumping to the coal pillar side and to the coal pillar top, we need only consider the other regions here. The regional division is shown in Fig. 7.

Fig. 7
figure 7

Development of dumping to coal pillar top

Full size image

(1) Shear resistance T of side interface.

The shear resistance of the side interface in AEMG is \(T_{2\text{II}}\), that in GMFB is \(T_{2\text{II}} ^{\prime}\), and that in BFC is \(T_{2\text{III}}\). These quantities can be written as follows:

$$\left\{ {\begin{array}{*{20}l} {T_{2\text{II}} = \int_{{\frac{h}{{\tan \left( {\beta + \alpha } \right)}}}}^{{\frac{{h - h_{\text{p}} }}{{\tan \beta_{\text{p}} }}}} {\int_{x\tan \alpha }^{h} {\left[ {\tan \varphi_{\text{m}} k\gamma_{\text{m}} \left( {h - z} \right) + c_{\text{m}} } \right]} } {\text{d}}z{\text{d}}x} \hfill \\ {T_{2\text{II}} ^{\prime} = \int_{{\frac{{h - h_{\text{p}} }}{{\tan \beta_{\text{p}} }}}}^{{\frac{h}{{\tan \left( {\beta + \alpha } \right)}} + b}} {\int_{x\tan \alpha }^{h} {\left\{ {\tan \varphi_{\text{m}} k\left[ {\gamma_{\text{m}} \left( {h - z} \right) + \gamma_{\text{p}} \left( {h_{\text{p}} + x\tan \beta_{\text{p}} - h} \right)} \right] + c_{\text{m}} } \right\}} } {\text{d}}z{\text{d}}x} \hfill \\ {T_{2\text{III}} = \int_{{A_{7} }}^{{A_{8} }} {\int_{x\tan \alpha }^{{h + \left[ {b + \frac{h}{{\tan \left( {\beta + \alpha } \right)}} - x} \right]\tan \left( {\omega - \alpha } \right)}} {\left\{ {k\tan \varphi_{\text{m}} \left[ \begin{gathered} \gamma_{\text{m}} \left( {A_{6} - A_{5} x - z} \right) \hfill \\ + \gamma_{\text{p}} \left( {h_{\text{p}} + A_{4} x + A_{5} x - A_{6} } \right) \hfill \\ \end{gathered} \right] + c_{\text{m}} } \right\}} } {\text{d}}z{\text{d}}x} \hfill \\ \end{array} } \right.$$
(8)

(2) Shear resistance S of the bottom interface.

The shear resistance of the bottom interface in AEMG is \(S_{2\text{II}}\), that in GMFB is \(S_{2\text{II}} ^{\prime}\), and that in BFC is \(S_{2\text{III}}\). These quantities can be written as follows:

$$\left\{ {\begin{array}{*{20}c} {S_{2\text{II}} = \int_{0}^{d} {\int_{{\frac{h}{{\tan \left( {\beta + \alpha } \right)}}}}^{{\frac{{h - h_{\text{p}} }}{{\tan \beta_{\text{p}} }}}} {\tan \varphi_{j} \gamma_{\text{m}} \left( {h - x\tan \alpha } \right){\text{d}}} } x{\text{d}}y + \int_{0}^{d} {\int_{{\frac{{A_{1} }}{\cos \alpha }}}^{{\frac{{A_{9} }}{\cos \alpha }}} {c_{j} {\text{d}}} } x{\text{d}}y} \\ {S_{2\text{II}} ^{\prime} = \int_{0}^{d} {\int_{{\frac{{h - h_{\text{p}} }}{{\tan \beta_{\text{p}} }}}}^{{\frac{h}{{\tan \left( {\beta + \alpha } \right)}} + b}} {\tan \varphi_{j} \left[ {\gamma_{\text{m}} \left( {h - x\tan \alpha } \right) + \gamma_{\text{p}} \left( {h_{\text{p}} + x\tan \beta_{\text{p}} - h} \right)} \right]{\text{d}}} } x{\text{d}}y} \\ {S_{2\text{III}} = \int_{0}^{d} {\int_{{A_{7} }}^{{A_{8} }} {\tan \varphi_{j} \left[ \begin{gathered} \gamma_{\text{m}} \left( {A_{6} - A_{5} x - A_{3} x} \right) \hfill \\ + \gamma_{\text{p}} \left( {h_{\text{p}} + A_{4} x + A_{5} x - A_{6} } \right) \hfill \\ \end{gathered} \right]{\text{d}}} } x{\text{d}}y + \int_{0}^{d} {\int_{{\frac{{A_{7} }}{\cos \alpha }}}^{{\frac{{A_{8} }}{\cos \alpha }}} {c_{j} {\text{d}}} } x{\text{d}}y} \\ \end{array} } \right.$$
(9)

where \(A_{9} = \left( {h - h_{\text{p}} } \right)/\tan \beta_{\text{p}}\).

Based on Eqs. (8) and (9), the three-dimensional supporting effect under the development of dumping to the coal pillar top is given by:

$$S + T = 2\left( {T_{\text{I}} + T_{2\text{II}} + T_{2\text{II}} ^{\prime} + T_{2\text{III}} } \right) + \left( {S_{\text{I}} + S_{2\text{II}} { + }S_{2\text{II}} ^{\prime}{ + }S_{2\text{III}} } \right)$$
(10)

2.2.3 Three-dimensional supporting effect under the development of dumping to entire coal pillar

The mechanical boundary of the side interface and the bottom interface of the triangular BFC area under the development of dumping to the coal pillar top is different from that in the case of development of dumping to the entire coal pillar. In particular, the shear resistance can be expressed Eqs. (8) and (9). We now derive expressions for the other areas. The regional division is shown in Fig. 8.

Fig. 8
figure 8

Development of dumping to entire coal pillar

Full size image

(1) Shear resistance T of side interface.

The shear resistance of the side interface in AOE is \(T_{3\text{I}}\) and that in AEFB is \(T_{3\text{II}}\). These quantities can be written as follows:

$$\left\{ {\begin{array}{*{20}c} {T_{3\text{I}} = \int_{0}^{{\frac{h}{{\tan \left( {\beta + \alpha } \right)}}}} {\int_{x\tan \alpha }^{{x\tan \left( {\beta + \alpha } \right)}} {\tan \varphi_{\text{m}} k\left\{ \begin{gathered} \gamma_{\text{m}} \left[ {x\tan \left( {\beta + \alpha } \right) - z} \right] \hfill \\ + \gamma_{\text{p}} \left[ {z_{\text{p}} - x\tan \left( {\beta + \alpha } \right)} \right] + c_{\text{m}} \hfill \\ \end{gathered} \right\}} } {\text{d}}z{\text{d}}x} \\ {T_{3\text{II}} = \int_{{\frac{h}{{\tan \left( {\beta + \alpha } \right)}}}}^{{\frac{h}{{\tan \left( {\beta + \alpha } \right)}} + b}} {\int_{x\tan \alpha }^{h} {\left\{ {\tan \varphi_{\text{m}} k\left[ {\gamma_{\text{m}} \left( {h - z} \right) + \gamma_{\text{p}} \left( {z_{\text{p}} - h} \right)} \right] + c_{\text{m}} } \right\}} } {\text{d}}z{\text{d}}x} \\ \end{array} } \right.$$
(11)

where \(A_{2} { = }\tan \left( {\beta + \alpha } \right)\).

(2) Shear resistance S of bottom interface.

The shear resistance of the bottom interface in AOE is \(S_{3\text{I}}\) and that in AEFB is \(S_{3\text{II}}\). These quantities can be written as follows:

$$\left\{ {\begin{array}{*{20}c} {S_{3\text{I}} = \int_{0}^{d} {\int_{0}^{{\frac{h}{{\tan \left( {\beta + \alpha } \right)}}}} {\tan \varphi_{j} \left\{ \begin{gathered} \gamma_{\text{m}} \left[ {x\tan \left( {\beta + \alpha } \right) - x\tan \alpha } \right] \hfill \\ + \gamma_{\text{p}} \left[ {h_{\text{p}} + x\tan \beta_{\text{p}} - x\tan \left( {\beta + \alpha } \right)} \right] \hfill \\ \end{gathered} \right\}} {\text{d}}x} {\text{d}}y + \int_{0}^{d} {\int_{0}^{{\frac{h}{{\cos \alpha \tan \left( {\beta + \alpha } \right)}}}} {c_{j} } {\text{d}}x} {\text{d}}y} \\ {S_{3\text{II}} = \int_{0}^{d} {\int_{{\frac{h}{{\tan \left( {\beta + \alpha } \right)}}}}^{{\frac{h}{{\tan \left( {\beta + \alpha } \right)}} + b}} {\tan \varphi_{j} \left[ \begin{gathered} \gamma_{\text{m}} \left( {h - x\tan \alpha } \right) \hfill \\ + \gamma_{\text{p}} (h_{\text{p}} + x\tan \beta_{\text{p}} - h) \hfill \\ \end{gathered} \right]{\text{d}}} } x{\text{d}}y + \int_{0}^{d} {\int_{{\frac{h}{{\cos \alpha \tan \left( {\beta + \alpha } \right)}}}}^{{\frac{h}{{\cos \alpha \tan \left( {\beta + \alpha } \right)}} + \frac{b}{\cos \alpha }}} {c_{j} {\text{d}}} } x{\text{d}}y} \\ \end{array} } \right.$$
(12)

Based on Eqs. (11) and (12), the three-dimensional supporting effect under the development of dumping to the entire coal pillar is given by:

$$S + T = 2\left( {T_{2\text{III}} + T_{3\text{I}} + T_{3\text{II}} } \right) + \left( {S_{2\text{III}} + S_{3\text{I}} + S_{3\text{II}} } \right)$$
(13)

We have established mathematical expressions for the three-dimensional supporting effect of the coal pillar when the inner dump is developed in different engineering positions. As a result, a quantitative characterization of the three-dimensional mechanical effect of the supporting coal pillar of the inner dump has been realized.

In engineering applications, it is first necessary to select a reasonable calculation method according to the location of the project development. Using the design parameters of the open-pit coal mine and the physical and mechanical parameters of the rock and soil, the mechanical effects of the supporting coal pillar can be analyzed.

3 Two-dimensional equivalent method for determining the supporting effect of the coal pillar

The inner dump slope is homogeneous and loose. There is little evidence of force from the end slope on both sides, and so this can be neglected as a first approximation. The resulting formulation can be regarded as a plane strain problem. Therefore, the two-dimensional rigid body limit equilibrium method can be used for analysis. To apply this approach to engineering, we need to transform the three-dimensional supporting effect into a two-dimensional effect. Obviously, the three-dimensional supporting effect of the coal pillar is the combined shear force of the side interface and the bottom interface. When the two-dimensional rigid body limit equilibrium method is used, the supporting effect of the coal pillar is only reflected in the shearing force of the bottom interface. Finding a suitable method for equating the shear force on the side interface to the bottom interface will result in the two-dimensional equivalent of the three-dimensional supporting effect.

Based on Eqs. (5)–(12), the three-dimensional supporting effect of the coal pillar is essentially the resultant force of the cohesion and internal frictional resistance between the side interface and the bottom interface. These components are provided by the cohesion and the internal friction angle of the shear strength parameters. The former is only related to the morphological parameters of the coal pillar, and the latter is affected by the vertical external load above the coal pillar due to the development of the dumping project. This is influenced by the composition type of the shear reaction force at the bottom interface of the block in the two-dimensional rigid body limit equilibrium method, which is consistent with the influencing factors. Therefore, the equivalent cohesion of the bottom interface and the equivalent internal friction angle (or the equivalent internal friction angle coefficient) can be solved by combining similar terms to achieve the two-dimensional equivalent of the pillar supporting effect.

(1) Equivalent cohesion \(c_{d}\).

The shear reaction force provided by the cohesive force is independent of the load of the dump material. Thus, this force is only related to the cohesive force of the supporting coal pillar and its morphological parameters, and the cohesive force of the base rock of the inner dump. The equivalent cohesion \(c_{d}\) under the three working conditions can be written as follows:

$$c_{d1} = \frac{{c_{\text{m}} \cos \alpha \left\{ \begin{gathered} A_{1}^{2} \left( {A_{2} - A_{3} } \right) + b(2h - 2A_{1} A_{3} - bA_{3} ) \hfill \\ + (A_{7} - A_{8} )\left[ {(A_{5} + A_{3} )(A_{7} + A_{8} ) - 2A_{6} } \right] \hfill \\ \end{gathered} \right\}}}{{d\left[ {A_{1} + b + \left( {\frac{{h + A_{5} A_{7} }}{{A_{3} + A_{5} }} - A_{7} } \right)} \right]}} + c_{j}$$
(14)

where \(A_{1} = h{/}\tan \left( {\beta { + }\alpha } \right)\).

(2) Equivalent internal friction coefficient \(\tan \varphi_{d}\).

The equivalent internal friction coefficient \(\tan \varphi _{{d_{{11}} }}\) under the development of dumping to the coal pillar side can be written as follows:

$$\tan \varphi_{d11} = \frac{{k\tan \varphi_{\text{m}} }}{3d}\frac{{\left\{ \begin{gathered} \frac{{h^{3} \left[ {\tan \left( {\beta + \alpha } \right) - \tan \alpha } \right]^{2} }}{{\tan^{3} \left( {\beta + \alpha } \right)}} \\ + \left[ {A_{1}^{3} ( - A_{3}^{2} ) + 3A_{1}^{2} A_{3} h - 3A_{1} h^{2} + A_{7} (A_{3}^{2} A_{7}^{2} - 3A_{3} A_{7} h + 3h^{2} )} \right] \\ + \left[ {(A_{3} + A_{5} )^{2} (A_{8}^{3} - A_{7}^{3} + 3A_{6} (A_{3} + A_{5} )(A_{7}^{2} - A_{8}^{2} ) + 3A_{6}^{2} (A_{8} - A_{7} )} \right] \\ + \frac{{\gamma_{\text{p}} }}{{\gamma_{\text{m}} }}(A_{10} - A{}_{8})\left\{ \begin{gathered} (A_{3} + A_{5} )\left[ {2(A_{5} + A_{4} )(A_{10}^{2} + A_{10} A_{8} + A_{8}^{2} ) + 3h_{\text{p}} (A_{10} + A_{8} )} \right] \hfill \\ + 3A_{6} (A_{8} - A_{10} )(A_{3} + 2A_{5} + A_{4} ) - 6A_{6} h_{\text{p}} + 6A_{{6}}^{2} \hfill \\ \end{gathered} \right\} \\ \end{gathered} \right\}}}{{\left\{ \begin{gathered} \frac{{h^{2} \left[ {\tan \left( {\beta + \alpha } \right) - \tan \alpha } \right]}}{{\tan^{2} \left( {\beta + \alpha } \right)}} + b\left\{ {\left[ {\frac{2h}{{\tan \left( {\beta + \alpha } \right)}} + b} \right]\tan \alpha - 2h} \right\} \\ + 2\left[ {(A_{3} + A_{5} )(\frac{{A_{7}^{2} }}{2} - \frac{{A_{8}^{2} }}{2}) + A_{6} (A_{8} - A_{7} )} \right] \\ + \frac{{\gamma_{\text{p}} }}{{\gamma_{\text{m}} }}(A_{8} - A_{10} )\left[ {A_{4} (A_{10} + A_{8} ) + A_{5} A_{10} + A_{5} A_{8} + 2h_{\text{p}} - 2A_{6} } \right] \\ \end{gathered} \right\}}} + \tan \varphi_{j}$$
(15)

The equivalent internal friction coefficient \(\tan \varphi _{{d_{{21}} }}\) under the development of dumping to the coal pillar top can be written as follows:

$$\tan \varphi_{d21} = \frac{{\tan \varphi_{\text{m}} k}}{3d}\frac{{\left\{ \begin{gathered} \left[ { - A_{1}^{3} A_{3}^{2} + 3A_{1}^{2} A_{3} h - 3A_{1} h^{2} + A_{9} (A_{3}^{2} A_{9}^{2} - 3A_{3} A_{9} h + 3h^{2} )} \right] \\ + A_{1}^{3} \left( {A_{2} - A_{3} } \right)^{2} \\ + \left[ {A_{9}^{3} ( - A_{3}^{2} ) + 3A_{9}^{2} A_{3} h - 3A_{9} h^{2} + A_{7} (A_{3}^{2} A_{7}^{2} - 3A_{3} A_{7} h + 3h^{2} )} \right] \\ + \frac{{\gamma_{\text{p}} }}{{\gamma_{\text{m}} }}(A_{9} - A_{7} )\left\{ \begin{gathered} A_{3} \left[ {2A_{4} (A_{7}^{2} + A_{7} A_{9} + A_{9}^{2} ) - 3(A_{9} + A_{7} )(h - h_{\text{p}} )} \right] \hfill \\ - 3h\left[ {A_{4} (A_{9} + A_{7} ) - 2h + 2h_{p} } \right] \hfill \\ \end{gathered} \right\} \\ + \left\{ {(A_{3} + A_{5} )^{2} (A_{8}^{3} - A_{7}^{3} ) + 3A_{6} (A_{3} + A_{5} )(A_{7}^{2} - A_{8}^{2} ) + 3A_{6}^{2} (A_{8} - A_{7} )} \right\} \\ + \frac{{\gamma_{p} (A_{7} + A_{8} )}}{{\gamma_{m} }}\left\{ \begin{gathered} (A_{3} + A_{5} )\left[ {2(A_{5} + A_{4} )(A_{7}^{2} + A_{7} A_{8} + A_{8}^{2} ) + 3h_{\text{p}} (A_{7} + A_{8} )} \right] \hfill \\ - 3A_{6} (A_{7} - A_{8} )(A_{3} + 2A_{5} + A_{4} ) - 6A_{6} h_{\text{p}} + 6A_{6}^{2} \hfill \\ \end{gathered} \right\} \\ \end{gathered} \right\}}}{{\left\{ \begin{gathered} A_{1}^{2} \left( {A_{2} - A_{3} } \right) + (A_{1} - A_{9} )(A_{1} A_{3} + A_{9} A_{3} - 2h) \\ + (A_{9} - A_{7} )(A_{9} A_{3} + A_{7} A_{3} - 2h) \\ + \frac{{\gamma_{\text{p}} }}{{\gamma_{\text{m}} }}(A_{7} - A_{9} )(A_{7} A_{4} + A_{9} A_{4} - 2h + 2h_{\text{p}} ) \\ + 2\left[ { - (A_{5} + A_{3} )(\frac{{A_{8}^{2} }}{2} - \frac{{A_{7}^{2} }}{2}) + A_{6} (A_{8} - A_{7} )} \right] \\ - \frac{{\gamma_{\text{p}} }}{{\gamma_{\text{m}} }}(A_{7} - A_{8} )(A_{4} (A_{7} + A_{8} ) + A_{5} A_{7} + A_{5} A_{8} + 2h_{\text{p}} - 2A_{6} ) \\ \end{gathered} \right\}}} + \tan \varphi_{j}$$
(16)

The equivalent internal friction coefficient \(\tan \varphi _{{d_{{31}} }}\) under the development of dumping to the entire coal pillar can be written as follows:

$$\tan \varphi_{d31} = \frac{{\tan \varphi_{\text{m}} k}}{3d}\frac{{\left\{ \begin{gathered} A_{1}^{3} \left( {A_{2} - A_{3} } \right)^{2} - \frac{{\gamma_{\text{p}} }}{{\gamma_{\text{m}} }}A_{1}^{2} (A_{2} - A_{3} )\left[ {2A_{1} (A_{2} - A_{4} ) - 3h_{\text{p}} } \right] \hfill \\ b\left[ {3A_{1}^{2} A_{3}^{2} + 3A_{1} A_{3} (bA_{3} - 2h) + b^{2} A_{3}^{2} - 3bA_{3} h + 3h^{2} } \right] \hfill \\ + \frac{{\gamma_{\text{p}} }}{{\gamma_{\text{m}} }}b\left\{ \begin{gathered} - 6A_{1}^{2} A_{3} A_{4} + 6A_{1} \left[ {A_{3} ( - bA_{4} + h - h_{\text{p}} ) + hA_{4} } \right] \hfill \\ - 2b^{2} A_{3} A_{4} + 3b(A_{3} h - A_{3} h_{\text{p}} + hA_{4} ) + 6h(h_{\text{p}} - h) \hfill \\ \end{gathered} \right\} \hfill \\ + \left[ {(A_{3} + A_{5} )^{2} (A_{8}^{3} - A_{7}^{3} ) + 3A_{6} (A_{3} + A_{5} )(A_{7}^{2} - A_{8}^{2} ) + 3A_{6}^{2} (A_{8} - A_{7} )} \right] \hfill \\ + \frac{{\gamma_{\text{p}} }}{{\gamma_{\text{m}} }}(A_{7} - A{}_{8})\left\{ \begin{gathered} (A_{3} + A_{5} )\left[ {2(A_{5} + A_{4} )(A_{7}^{2} + A_{7} A_{8} + A_{8}^{2} ) + 3h_{\text{p}} (A_{7} + A_{8} )} \right] \hfill \\ - 3A_{6} (A_{7} - A_{8} )(A_{3} + 2A_{5} + A_{4} ) - 6A_{6} h_{\text{p}} + 6A_{6}^{2} \hfill \\ \end{gathered} \right\} \hfill \\ \end{gathered} \right\}}}{{\left\{ \begin{gathered} A_{1}^{2} (A_{2} - A_{3} ) + \frac{{\gamma_{\text{p}} }}{{\gamma_{\text{m}} }}A_{1} \left[ {A_{1} (A_{4} - A_{2} ) + 2h_{\text{p}} } \right] \\ + b(A_{1} A_{3} + A_{7} A_{3} - 2h) + \frac{{\gamma_{\text{p}} }}{{\gamma_{\text{m}} }}b(A_{1} A_{4} + A_{7} A_{4} - 2h + 2h_{\text{p}} ) \\ + 2\left[ {( - A_{3} - A_{5} )(\frac{{A_{8}^{2} }}{2} - \frac{{A_{7}^{2} }}{2}) + A_{6} (A_{8} - A_{7} )} \right] \\ - \frac{{\gamma_{\text{p}} }}{{\gamma_{\text{m}} }}(A_{7} - A_{8} )\left[ {A_{4} (A_{7} + A_{8} ) + A_{5} A_{7} + A_{5} A_{8} + 2h_{\text{p}} - 2A_{6} } \right] \\ \end{gathered} \right\}}} + \tan \varphi_{j}$$
(17)

4 Calculation method of slope stability of inner dump under coal pillar support

Slope stability analysis is commonly performed using the residual thrust method (Feng et al. 2014; Zhou et al. 2019; Ram et al. 2019). Also called the transfer coefficient method or the unbalanced force method, this is suitable for determining the stability coefficient of any slip surface. Here, the two-dimensional equivalent shear strength parameters are introduced into the residual thrust method, and a method for calculating the slope stability of the inner dump slope under the effect of coal pillar support and taking into account the development position of dumping is established.

The shapes of the slope and the supporting coal pillar are shown in Fig. 9. The landslide model is a circular arc–base combined sliding formulation in which the sliding mass is divided into several vertical blocks. To ensure the accuracy of the calculations, the blocks near the supporting coal pillar need to be encrypted, and the inflection point of the slope step, intersection point of the sliding surfaces, and the rock layer need to be divided into separate blocks.

Fig. 9
figure 9

Slope and supporting coal pillar shapes

Full size image

Under arc–base combined sliding, the bottom surface of the upper blocks on the circular sliding surface is different from that of the upper blocks on the base sliding surface. Therefore, the circular sliding surface mass is divided into a total of n blocks. The upper sliding mass is divided into k blocks and the upper base sliding mass is divided into nk blocks; there are u blocks containing coal pillars, n-k-u blocks without coal pillars, and q blocks from the inner corner of the coal pillar to the intersection of the circular arc sliding surface and the base sliding surface.

(1) Residual thrust of the upper blocks on the arc sliding surface.

Let us consider block i on the upper part of the arc sliding surface, i = 0, 1, …, k. The bottom inclination of block i is \(\delta_{i}\), the bottom inclination of block i-1 is \(\delta _{{i_{{ - 1}} }}\), the residual thrust of block i is \(D_{i}\), and the residual thrust of block i-1 is \(D_{{i{ - }1}}\).

Then, the equilibrium equation for the direction parallel to the bottom of block i can be established as:

$$D_{i} = W_{i} \sin \delta_{i} + D_{i - 1} \cos (\delta_{i - 1} - \delta_{i} ) - S_{i}$$
(18)

where \(W_{i}\) is the weight of block i and \(S_{i}\) is the tangential force at the bottom of block i.

The equilibrium equation for the direction perpendicular to the bottom of block i is:

$$N_{i} = W_{i} \cos \delta_{i} + D_{i - 1} \sin (\delta_{i - 1} - \delta_{i} )$$
(19)

where \(N_{i}\) is the normal force at the bottom of block i.

According to the Moore–Coulomb strength criterion (Cai et al. 2013; Yuan et al. 2019; Naeini et al. 2012):

$$S_{i} = \frac{{c_{i} l_{i} + N_{i} \tan \varphi_{i} }}{K}$$
(20)

where \(l_{i}\) is the length of the bottom of block i, \(c_{i}\) is the cohesion of the bottom of block i, \(\varphi_{i}\) is the internal friction angle of the bottom of block i, and K is the reduction coefficient.

Based on Eqs. (18)–(20), the residual thrust of block i is given by:

$$D_{i} = W_{i} \sin \delta _{i} + D_{i - 1}\, \cos (\delta _{{i - 1}} - \delta _{i} ) - \frac{{c_{i} l_{i} + \left[ {W_{i} \cos \delta _{i} + D_{i - 1} \, \sin (\delta _{{i - 1}} - \delta _{i} )} \right]\tan \varphi _{i} }}{K}$$
(21)

The residual thrust \(D_{k}\) of the upper sliding mass on the arc sliding surface can then be written as follows:

$$\left\{ {\begin{array}{*{20}c} {D_{{2}} = W_{{2}} \sin \delta_{{2}} + D_{{1}} \cos (\delta_{{1}} - \delta_{{2}} ) - \frac{{c_{{2}} l_{{2}} + \left[ {W_{{2}} \cos \delta_{{2}} + D_{{1}} \sin (\delta_{{1}} - \delta_{{2}} )} \right]\tan \varphi_{{2}} }}{K}} \\ {D_{3} = W_{{3}} \sin \delta_{{3}} + D_{{2}} \cos (\delta_{{2}} - \delta_{{3}} ) - \frac{{c_{{3}} l_{{3}} + \left[ {W_{{3}} \cos \delta_{{3}} + D_{{2}} \sin (\delta_{{2}} - \delta_{{3}} )} \right]\tan \varphi_{{3}} }}{K}} \\ {......} \\ {D_{k} = W_{k} \sin \delta_{k} + D_{k - 1} \cos (\delta_{k - 1} - \delta_{k} ) - \frac{{c_{k} l_{k} + \left[ {W_{k} \cos \delta_{k} + D_{k - 1} \sin (\delta_{k - 1} - \delta_{k} )} \right]\tan \varphi_{k} }}{K}} \\ \end{array} } \right.$$
(22)

(2) Residual thrust of the upper blocks with coal pillars on the base sliding surface.

Let us consider block r with a coal pillar on the base sliding surface, r = 0, 1, …, u. We assume that the base inclination angle of the inner dump is α:

$$\delta_{1} { = }\delta_{2} ... = \delta_{u} = \alpha$$
(23)

The equilibrium equation for the direction parallel to the bottom of block r can be written as:

$$D_{r} = W_{r} \sin \alpha + D_{r - 1} - S_{r}$$
(24)

where \(W_{r}\) is the weight of block r, given by:

$$W_{r} = A_{r\text{m}} \gamma_{\text{m}} + \left( {A_{r} - A_{r\text{m}} } \right)\gamma_{\text{p}}$$
(25)

The equilibrium equation for the direction perpendicular to the bottom of block r is given by:

$$N_{r} = W_{r} \cos \alpha$$
(26)

According to the Moore–Coulomb strength criterion:

$$S_{{\text{r}}} = \frac{{c_{d} l_{r} + N_{r} \tan \varphi_{d} }}{K}$$
(27)

Thus, the residual thrust of block r is given by:

$$\begin{aligned}D_{r} &= D_{r - 1} + \left[ {A_{r\text{m}} \gamma_{\text{m}} + \left( {A_{r} - A_{r\text{m}} } \right)\gamma_{\text{p}} } \right]\left( {\sin \alpha - \frac{{\cos \alpha \tan \varphi_{d} }}{K}} \right)\\ &\quad- \frac{{c_{d} l_{r} }}{K}\end{aligned}$$
(28)

(3) Residual thrust of the upper blocks without coal pillars on the base sliding surface.

The residual thrust of the upper blocks with and without coal pillars satisfies an equilibrium condition in the parallel and perpendicular directions. The essential difference lies in the tangential force on the bottom surface. Take upper block p without a coal pillar as an example, p = 1, 2, …, n-k-u. According to the Moore–Coulomb strength criterion:

$$S_{p} = \frac{{c_{j} l_{p} + N_{p} \tan \varphi_{j} }}{K}$$
(29)

From Eqs. (24), (26), and (29), the residual thrust of block p is given by:

$$D_{p} = D_{p - 1} + W_{p} \left( {\sin \alpha - \frac{{\cos \alpha \tan \varphi_{j} }}{K}} \right) - \frac{{c_{j} l_{p} }}{K}$$
(30)

From Eqs. (22), (28), and (30), the residual thrust of the sliding mass is given by:

$$\left\{ {\begin{array}{*{20}c} {D_{2} = W_{2} \sin \delta_{2} + D_{1} \cos (\delta_{1} - \delta_{2} ) - \frac{{c_{2} l_{2} + \left[ {W_{2} \cos \delta_{2} + D_{1} \sin (\delta_{1} - \delta_{2} )} \right]\tan \varphi_{2} }}{F}} \\ {...} \\ {D_{k} = W_{k} \sin \delta_{k} + D_{k - 1} \cos (\delta_{k - 1} - \delta_{k} ) - \frac{{c_{k} l_{k} + \left[ {W_{k} \cos \delta_{k} + D_{k - 1} \sin (\delta_{k - 1} - \delta_{k} )} \right]\tan \varphi_{3} }}{F}} \\ {\begin{array}{*{20}c} {...} \\ {D_{k + q} = D_{k + q - 1} + W_{k + q} \left( {\sin \alpha - \frac{{\cos \alpha \tan \varphi_{j} }}{F}} \right) - \frac{{c_{j} l_{k + q} }}{F}} \\ {\begin{array}{*{20}c} {...} \\ {\begin{array}{*{20}c} {D_{k + q + j} = D_{k + q + u - 1} + \left[ {A_{{\left( {k + q + u} \right)m}} \gamma_{m} + \left( {A_{{\left( {k + q + u} \right)}} - A_{{\left( {k + q + u} \right)m}} } \right)\gamma_{p} } \right]\left( {\sin \alpha - \frac{{\cos \alpha \tan \varphi_{d} }}{F}} \right) - \frac{{c_{d} l_{r} }}{F}} \\ {\begin{array}{*{20}c} {...} \\ {D_{n} = D_{n - 1} + W_{n} \left( {\sin \alpha - \frac{{\cos \alpha \tan \varphi_{j} }}{F}} \right) - \frac{{c_{j} l_{n} }}{F}} \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right.$$
(31)

Under the development of dumping to the coal pillar side or top, the residual thrust of the sliding mass can be written as follows:

$$D_{n} = D_{n - 1} + \left[ {A_{n\text{m}} \gamma_{\text{m}} + \left( {A_{n} - A_{n\text{m}} } \right)\gamma_{\text{p}} } \right]\left( {\sin \alpha - \frac{{\cos \alpha \tan \varphi_{d} }}{K}} \right) - \frac{{c_{d} l_{r} }}{K}$$
(32)

By adjusting the reduction coefficient K so that \(D_{n} = 0\), the stability of the inner dump under the sliding surface position can be calculated. Then, by adjusting the position of the sliding surface, K can be readjusted to make \(D_{n} = 0\). Kmin is the stability coefficient corresponding to the most dangerous sliding surface, and is also the stability coefficient Fs of the inner dump. When calculating the overall stability coefficient of the slope, the top width of the section is generally set to twice the height of the slope.

5 Engineering applications

Shengli East No. 2 open-pit coal mine has a design production capacity of 30 million t/a and an economical and reasonable strip ratio of 6 m3/t. To maximize the mining resources, the coal pillar is mined using the single-bucket-truck process, with a step flat plate width of 15 m, a step height of 12 m, and a step slope angle of 60°. The inner dumping operation is also based on the single-bucket-truck process. The inner dumping yard has a flat plate width of 50 m, a slope angle of 33°, and a step height of 15 m.

To shorten the transportation distance, thus reducing the transportation costs and increasing the economic benefits of the mine, Shengli East No. 2 open-pit coal mine is advancing westward, during which time the inner dump is being developed. As the southern slope is in a creeping state, some of the discharged materials are placed on the roof of the coal seam to avoid large-scale landslides. The inclination angle of the basement of the inner dump is 2°, the lithology of the basement is mainly mudstone, such as kaolinite and montmorillonite, and the primary characteristic is serious softening with water. Waste mainly comes from quaternary clay, tertiary glutenite, mudstone of clay, and coal-measure strata, which have the characteristics of a loose structure and low strength. The typical engineering geology of the inner dump is shown in Fig. 10. According to previous rock test results and slope stability research, the geotechnical physical mechanics indices are presented in Table 1.

Fig. 10
figure 10

Typical engineering geology of inner dump

Full size image
Table 1 Geotechnical physical mechanics indices
Full size table

5.1 Factors affecting slope stability of inner dump

(1) Sensitivity analysis of factors affecting the stability of the inner dump.

The sensitivity of the factors affecting the stability of the inner dump was analyzed using an orthogonal test design method. Orthogonal test calculation results of inner dump stability are presented in Table 2 and a range analysis of these orthogonal tests is presented in Table 3.

Table 2 Orthogonal test calculation results of inner dump stability
Full size table
Table 3 Range analysis of orthogonal tests of inner dump stability
Full size table

Table 3 indicates that the degree of influence of various factors on the stability of the inner dump runs in the order \(\beta_{\text{p}}\) > α > d > h > b > ω > \(h_{\text{p}}\) > β.

In summary, for a specific open-pit coal mine, the coal pillar strike length d, slope angle \(\beta_{\text{p}}\), and dip angle α of the base are all fixed values. When a coal pillar is used to support the inner dump, the height h and top width b are prioritized in the optimization of the coal pillar shape parameters, and the outer bottom angle β and inner bottom angle ω are adjusted to satisfy the engineering operation. Thus, only the height h and top width b of the coal pillar should be optimized among the supporting coal pillar shape parameters of the inner dump in Shengli East No. 2 open-pit coal mine.

(2) Influence of various factors on the stability of the inner dump.

We now quantitatively describe the functional relationship between the stability of the inner dump and the various factors, based on the mechanical parameters of the rock and soil mass, and the slope shape of the end slope in Shengli East No. 2 open-pit coal mine. Through Eqs. (14) and (15), the numerical value of the coal pillar supporting effect was calculated using MATLAB. The relationships between the stability of the inner dump and the various factors were fitted using Eq. (31) and the Origin software. The results are shown in Fig. 11.

Fig. 11
figure 11

Inner dump stability with respect to various factors (longitudinal intercept of the slope line of the inner dump is determined by the slope angle, the distance from the coal pillar to the slope toe, and the height of the inner dump)

Full size image

The results reveal that the slope stability coefficient has a linear relation with the top width and height of the coal pillar, the slope angle, and the base inclination angle. It has an exponential relation with the coal pillar strike length and the slope height increment. The coefficient has a quadratic relation with the coal pillar outer and an absolute value relation with the inner bottom angle.

5.2 Optimization of morphological parameters of supporting coal pillar in the inner dump

Based on the stratum occurrence information and the present situation of stripping engineering, it is known that the inclination angle α is 2° and the coal pillar strike length d is 108 m. To meet the requirements of stripping engineering operations, 15-m-wide transportation flats must be set at the + 816 m and + 804 m levels. The slope angle of the steps is 65°, and the width of the flat of the inner dump is 50 m; The slope angle of the step is 33°, the height of the step is 15 m, and the slope angle of the inner dump is about 12°. Under the above conditions and for a typical engineering geological section, when h and b are given, ω, β, d, α, and \(h_{\text{p}}\) can be determined. Therefore, the unknown parameters of the shape of the coal pillar in Shengli East No. 2 open-pit coal mine are the height h and top width b. We designed five working conditions, with the minimum coal pillar volume as the criterion, and determined the optimal shape parameters of the coal pillar in the inner dump of Shengli East No. 2 open-pit coal mine. The calculation parameters and results under various working conditions are presented in Table 4, and the resulting coal pillar volumes under each condition are listed in Table 5.

Table 4 Calculation parameters and results under various working conditions
Full size table
Table 5 Calculation of coal pillar volume
Full size table

It can be seen from Table 4 that, when the shear resistance T of the side interface of the supporting coal pillar is considered, the minimum value of the equivalent cohesion is 27 kPa and the maximum value is 38.56 kPa. The minimum equivalent internal friction angle is 13.68° and the maximum value is 15.55°. If the shear resistance T of the side interface of the supporting coal pillar is neglected, the cohesion of the bottom interface is 10 kPa and the internal friction angle is 10°. Thus, the cohesion and the internal friction angle increase by at least 170% and 36.8%, respectively, when T is considered. Therefore, the shear resistance of the side interface of the supporting coal pillar cannot be ignored, and the three-dimensional supporting effect of the coal pillar should be considered in the process of coal pillar shape design to avoid any waste of resources.

Analysis of Table 5 shows that the top width of the coal pillar in the inner dump of Shengli East No. 2 open-pit coal mine should be at the level of + 824 m. This gives the optimum size of the coal pillar, with a top width of 15 m and a height of 36.7 m.

5.3 Numerical simulation of instability mechanism of the coal pillar and stability of inner dump

To verify the rationality of the instability mechanism of the supporting coal pillar and the stability of the inner dump obtained from the theoretical analysis, the FLAC3D software, which is based on the fast Lagrangian method, was used for analysis (Chatra and Ma 2019; Hamed et al. 2020; Ravi et al. 2017). Considering the applicability of ANSYS for building numerical models and meshing complex engineering-geological bodies and the powerful functions of FLAC3D for geotechnical engineering, the two packages were combined to perform the numerical simulations. The numerical calculations are based on strength reduction theory. The fast Lagrangian finite difference method was used to solve the slope stability coefficient and obtain the slope instability characteristics. The numerical model was meshed using tetrahedrons with a mesh size of 40 m. Numerical simulations were performed to determine the optimal coal pillar shape parameters and slope shape parameters under the five working conditions when considering the shear resistance of the side interface of the supporting coal pillar. The cross-sectional shapes of the supporting coal pillars for each working condition are shown in Fig. 12, and the numerical simulation results are shown in Fig. 13.

Fig. 12
figure 12

Cross-sections of the optimal coal pillar shapes under five working conditions

Full size image
Fig. 13
figure 13

Numerical simulation model

Full size image

Following several previous studies (Saxena et al. 2019; Wang et al. 2020; Singh et al. 2020; Makowski et al. 2020), suitable boundary conditions were imposed on the numerical model. The boundary conditions for the five working conditions are to impose displacement constraints on the x = 0, x = 950, z = 0, y = 0, and y = 1100 planes.

(1) Instability mechanism of supporting coal pillar.

It can be seen from Fig. 14 that the displacement of the inner dump slope is relatively small, the displacement of the supporting coal pillar is slightly greater, and the displacement from the fourth flat plate (+ 905 m level) from the top to the local slope of the supporting coal pillar is relatively large. Based on the relative stability analysis theory of the slope, the stability of the entire lower part of the inner dump is relatively good, whereas the stability of the central part of the slope is poor. Taking the densest displacement increment contour as the critical sliding surface, the supporting coal pillar fails vertically above the intersection of the end edge and the bottom interface of the supporting coal pillar. It can be seen from the distribution of the plastic zone that, when the supporting coal pillar becomes unstable, the plastic zone mainly suffers from shear failure, local tensile failure occurs, and the shear failure penetrates the entire supporting coal pillar. Therefore, the mechanism of supporting coal pillar instability is a shear failure.

Fig. 14
figure 14

Distribution of displacement and plastic zone

Full size image

(2) Stability of inner dump.

Taking the horizontal displacement mutation point of the top of the slope surface as the slope instability criterion, the stability calculation results of the inner dump are presented in Table 6.

Table 6 Stability calculation result of inner dump
Full size table

It can be seen from Table 6 that, under the five working conditions, the stability coefficient of the inner dump calculated by the two-dimensional calculation method is generally lower than that from the numerical simulations. One possible reason for this phenomenon is that the research method used in this study ignores the influence of the end slope on the stress distribution of the supporting coal pillar. Analysis of the relative error shows that the maximum relative error of the two methods is 4.76%, which verifies the rationality of the proposed method for calculating the slope stability of the inner dump considering the development position of dumping.

6 Conclusions

Supporting the coal pillar is an essential component of improving the inner dump stability. This paper has proposed a novel and effective method for ensuring the slope stability of the inner dump under the effect of coal pillar support. Taking an open-pit coal mine as the engineering background, the influence of factors such as the supporting coal pillar shape parameters on the stability was discussed. For a specific open-pit coal mine, the coal pillar strike length, slope angle, and base inclination angle are all fixed; the height and top width of the coal pillar are then prioritized in the shape parameter optimization. The slope stability coefficient has a linear relation with the coal pillar’s top width and height, the slope angle, and the base inclination angle, and has an exponential relation with the coal pillar strike length and the slope height increment. Quadratic and absolute value relations have been established with the coal pillar outer and inner bottom angle, respectively. The top width of the coal pillar in the inner dump of Shengli East No. 2 open-pit coal mine should be at the level of + 824 m, and the optimum size of the coal pillar is with a top width of 15 m and a height of 36.7 m. The instability mechanism of the supporting and retaining coal pillar obtained through numerical simulations and the inner dump’s stability are in good agreement with the theoretical analysis results. The results presented in this paper provide a theoretical basis for the design, treatment, and safety implementation of similar open-pit mine slope engineering.