Influence of stress wave-induced disturbance on ultra-low friction in broken blocks

Abstract

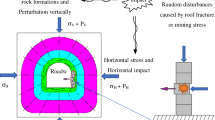
Deep rock mass tends to be broken into blocks when mining for materials deep below the surface. The rock layer of the roof of the mine can be regarded as a system of blocks of fractured rock mass. When subjected to high ground stress and mining-induced disturbance, the effect of the ultra-low friction of the block system easily becomes apparent, and can induce rock burst and other accidents. By taking the block of rock mass as research object, this study developed a test system for ultra-low friction to experimentally examine its effects on the broken blocks under stress wave-induced disturbance. We used the horizontal displacement of the working block as the characteristic parameter reflecting the effect of ultra-low friction, and examine its characteristic laws of horizontal displacement, acceleration, and energy when subjected to the effects of ultra-low friction by changing the frequency and amplitude of the stress wave-induced disturbance. The results show that the frequency of stress wave-induced disturbance is related to the generation of ultra-low friction in the broken block. The frequency of disturbance of the stress wave is within 1–3 Hz, and significantly increases the maximum acceleration and horizontal displacement of the broken blocks. The greater the intensity of the stress wave-induced disturbance is, the higher is the degree of block fragmentation, and the more likely are effects of ultra-low friction to occur between the blocks. The greater the intensity of the horizontal impact load is, the higher is the degree of fragmentation of the rock mass, and the easier it is for the effects of ultra-low friction to occur. Stress wave-induced disturbance and horizontal impact are the main causes of sliding instability of the broken blocks. When the dominant frequency of the kinetic energy of the broken block is within 20 Hz, the effects of ultra-low friction are more likely.

Introduction

The demand for mineral resources and developments in mining technology has long driven economic development (Bamford et al. 2021). The mining roadway is deformed and broken into small blocks under the action of deep and high stress, which threatens safe mining (Li et al. 2019b, a). For example, the rock surrounding a mine (Baryakh et al. 2021) can be broken during mining and delay work on it. Under the action of long-term and high ground stress, the deep rock mass is usually an intermittent structure with joints and fissures. Under repeated vertical disturbances and horizontal impacts caused by roof fracture and mechanical vibrations, the rock mass around the stope and roadway constantly vibrates, deforms, and breaks to form a broken structure. In particular, the layers of rock gradually transform from intermittent to loose and broken. When stress wave-induced disturbance and the effect of load reach critical values, the vibrations subject the block of broken rock mass to positive pressure as a tensile force. The blocky rock mass is prone to sudden interlayer slippage under the surrounding load, which instantly causes the roof, rock strata, and bottom plate to slip. The slip velocity along the surface of the contact structure increases nonlinearly and frictional resistance is weakened such that the effect of ultra-low friction of the block fractured rock mass becomes prominent.

The effect of the ultra-low friction of rock mass was identified by the Russian scholars Kurlenya and Oparin in 1996. They claimed that when a dynamic impulse acts on the rock mass, the compaction between rock masses changes with time due to vibrations. At certain times when the rock masses are loose, frictional resistance between them is significantly reduced (by several times, on occasion), leading to its "disappearance" (Kurlenya et al. 1996, 1999; Oparin et al. 2001). Aleksandrova and Sher (2004) confirmed and explained the effect of ultra-low friction between rock masses by establishing a one-dimensional (1D) model of a block system. Many researchers agree that ultra-low friction is universally present in the block structure of rock masses and the effect of ultra-low friction in rock masses is an important issue in deep mining (Qian 2004). The large drop in stress means that small disturbances in lateral stress may lead to the appearance of ultra-low friction (Cui et al. 2005). The shear effect of low friction leads to the release of a large amount of energy in earthquakes and rock fractures in deep underground mines (Tarasov and Randolph 2007).

The above findings show that the effect of ultra-low friction has a significant impact on underground engineering. To overcome problems caused by ultra-low friction, examining its mechanism is crucial. Wang et al. (2006) established a dynamic model of a block of rock mass by experimentally describing ultra-low friction in it, and preliminarily revealed its internal mechanism through a comparison between the results of numerical analysis and experimental data (Wang et al. 2007). Xu et al. (2009) used a multi-functional test system to examine the dynamic characteristics of blocks of rock under vertical impact-induced load and horizontal tension, and established relations between the impact energy, and the characteristic friction force and coefficient of reduction in friction. Li et al. (2018) developed a test system to examine the dynamic mechanical properties of a block of rock mass through physical simulations of slip in rock blocks induced by impact. They determined the key mechanical mechanisms of irreversible displacement and the instability of dynamic slip. Once the mechanism of ultra-low friction has been clarified, a number of researchers seek to solve this problem by establishing physical models and obtaining analytical solutions through numerical calculations. Wu et al. (2008) established a 1D dynamic model of a deep block system of rock mass, and obtained an analytical expression for the horizontal displacement of the working block (Wu and Fang 2009, 2010; Wu et al. 2009a, b). Li et al. (2019b, a) proposed the concept of ultra-low friction-induced rock burst, established a block model for it, and derived the relation of normal dynamic load at the interface of lump coal and the rock mass over time. Studies have shown that the nature of the rock mass is important, and external factors that lead to the effect of ultra-low friction are key.

The FLAC3D numerical software has been used to simulate ultra-low friction owing to the combined action of vertical impact and horizontal static force, and vertical and horizontal impacts on a granite block. The residual displacement and law of evolution of the normal force of the working block in the model were thus obtained. The distributions of the vertical and horizontal stresses of the block model have also been obtained (Lv 2015). Wang et al. (2016) used the theory of self-balanced in-situ stress in a hierarchical block system to study the law of energy transformation between the rock block and the surrounding weak medium during the propagation of a pendulum wave, and analyzed the law of energy transfer in the block of rock mass. Liu et al. (2018) carried out static and dynamic action tests on the load joint, simulated the process of rock burst damage induced by the roadway, analyzed the state and shape of fragmentation, and developed a method to determine rock burst induced by dynamic load. Jiang et al. (2019) simplified the block system of rock mass into an equivalent viscoelastic mass model, introduced a model for the weakening of the frictional slip rate of rock, and obtained a model to calculate the slip instability of the rock mass. Zhao et al. (2018) analyzed the influence of the characteristics of the block system of rock mass and those of external load on friction between the rock blocks to establish a 1D model of jointed rock mass, and used it to discuss the influence of these characteristics on the law of propagation of the stress wave. They found that the stress wave-induced disturbance has a significant impact on the generation of ultra-low friction.

The investigations above show that theoretical models of blocks of rock mass have been used to only examine dynamic response under vertical impact loads and horizontal static forces. There is a lack of analysis of the influence of such parameters as the degree of block fragmentation, and the frequency of disturbance and amplitude of the stress wave on the effects of ultra-low friction of blocks of rock mass. In this study, on the basis of the direction of research scholars, the effect of ultra-low friction was designed and developed to load test device, in under the action of stress wave-induced disturbance crushing block of effect of ultra-low friction test, to work for the parameter block horizontal displacement and horizontal acceleration, the study of the frequency of stress wave-induced disturbance and intensity of disturbance of the broken block of ultra-low friction effect. The results are compared with those of past work, and provide a scientific basis for predicting and preventing accidents caused by the effects of ultra-low friction.

Theoretical model of the effect of ultra-low friction in block of rock mass

When establishing a theoretical model of the effect of ultra-low friction, springs or spring dampings are often used to simulate the mechanical characteristics of the weak interlayer, and the overall model is established by connecting the mass points. Many mechanical models have been proposed to study the dynamics of blocks of rock mass in recent years (Wu and Fang 2009, 2010; Wu et al. 2009a, b; Zhang et al. 2021), and provide a theoretical basis for examining ultra-low friction in systems of broken rock mass.

Model establishment

The deep rock mass is divided by such geological structures as fissures and joints. The mechanism of the effect of ultra-low friction is closely related to the dynamic deformation of the interface of the block and the stability of the block system. To study the characteristics of deformation of deep block media, we must first identify the normal and tangential dynamic characteristics of the block interface. Based on previous research, we regarded the block as a rigid body. The theoretical model of the effect of ultra-low friction is then as shown in Fig. 1, where the size of the block is the same, its mass is m_i, vertical impact is $P_{\text{v}} \left( t \right) = P_{\text{v}} \sin \omega_{\text{v}} t$ and axial pressure $\gamma H$ acts on the surface of block 1. Springs and dampers are set between the blocks to describe the energy transfer and retardation of the weak connecting medium between them. The stiffness coefficient is k_i and the damping coefficient is c_i. The movement of the block consists of two stages. The first stage is forced vibration under the action of a vertical impact and the second one is the free vibration of the block starting from moment t₀, with the state at this time set as the initial condition.

Fig. 1

Theoretical model of effect of ultra-low friction

The block system is composed of n blocks stacked vertically. Suppose the positive direction is vertically upward, and position l at the center of the bottom surface of the nth block is the origin of the coordinate system. The equations of motion in the vertical direction are then given by:

$$\left. \begin{gathered} m\ddot{z}_{1} + k_{1} \left( {z_{1} - z_{2} - l} \right) + c_{1} \left( {\dot{z}_{1} - \dot{z}_{2} } \right) = mg + P_{\text{v}} \sin \left( {\omega t} \right) + F_{\text{v}} \\ m\ddot{z}_{2} + k_{2} \left( {z_{2} - z_{3} - l} \right) + c_{2} \left( {\dot{z}_{2} - \dot{z}_{3} } \right){ - }k_{1} \left( {z_{1} - z_{2} - l} \right){ - }c_{1} \left( {\dot{z}_{1} - \dot{z}_{2} } \right) = mg \\ \cdots \cdots \\ m\ddot{z}_{i} + k_{i} \left( {z_{i} - z_{i + 1} - l} \right) + c_{i} \left( {\dot{z}_{i} - \dot{z}_{i + 1} } \right){ - }k_{(i - 1)} \left( {z_{i - 1} - z_{i} - l} \right){ - }c_{(i - 1)} \left( {\dot{z}_{i - 1} - \dot{z}_{i} } \right) = mg \\ \cdots \cdots \\ m\ddot{z}_{n} + k_{{{n}}} \left( {z_{n} - l} \right) + c_{n} \dot{z}_{n} { - }k_{(n - 1)} \left( {z_{n - 1} - z_{n} - l} \right){ - }c_{{({{n - 1}})}} \left( {\dot{z}_{n - 1} - \dot{z}_{n} } \right) = mg \\ \end{gathered} \right\}$$

(1)

where m_i is the mass of the block, z_i is the ordinate of block i, l is the free length of the spring, g is the acceleration due to gravity, and F_v is the resultant force of ground stress in the vertical direction of the model.

We simplify the above formula into a matrix form to get:

$$M{\varvec{\ddot{z}}} + C{\dot{\varvec{z}}} + K{\varvec{z}} = F\left( t \right) + b$$

(2)

where

$$M = \left( {\begin{array}{*{20}c} {m_{1} } & 0 & 0 & 0 & \cdots & 0 & 0 \\ 0 & {m_{2} } & 0 & 0 & \cdots & 0 & 0 \\ 0 & 0 & {m_{3} } & 0 & \cdots & 0 & 0 \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ 0 & 0 & 0 & 0 & \cdots & {m_{(n - 1)} } & 0 \\ 0 & 0 & 0 & 0 & \cdots & 0 & {m_{{\text{n}}} } \\ \end{array} } \right)\quad K = \left( {\begin{array}{*{20}c} {{ - }k_{1} } & {k_{1} } & 0 & 0 & \cdots & 0 & 0 \\ { - k_{1} } & {k_{1} + {\text{k}}_{2} } & {{ - }k_{2} } & 0 & \cdots & 0 & 0 \\ 0 & {{ - }k_{2} } & {k_{2} + {\text{k}}_{3} } & {{ - }k_{3} } & \cdots & 0 & 0 \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ 0 & 0 & 0 & 0 & \cdots & {k_{(n - 2)} + {\text{k}}_{(n - 1)} } & { - k_{(n - 1)} } \\ 0 & 0 & 0 & 0 & \cdots & { - k_{(n - 1)} } & {k_{(n - 1)} + {\text{k}}_{n} } \\ \end{array} } \right)$$

$$C = \left( {\begin{array}{*{20}c} {c_{1} } & { - c_{1} } & 0 & 0 & \cdots & 0 & 0 \\ { - c_{1} } & {c_{1} + c_{2} } & { - c_{2} } & 0 & \cdots & 0 & 0 \\ 0 & { - c_{2} } & {c_{2} + c_{3} } & { - c_{3} } & \cdots & 0 & 0 \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ 0 & 0 & 0 & 0 & \cdots & {c_{(n - 2)} + c_{(n - 1)} } & { - c_{(n - 1)} } \\ 0 & 0 & 0 & 0 & \cdots & { - c_{(n - 1)} } & {c_{(n - 1)} + c_{n} } \\ \end{array} } \right)$$

$$F\left( t \right) = P_{{\text{v}}} \left( {\begin{array}{*{20}c} {\sin \omega t} \\ 0 \\ \cdots \\ 0 \\ \end{array} } \right) \, z = \left( {\begin{array}{*{20}c} {z_{1} } \\ {z_{2} } \\ \vdots \\ {z_{n} } \\ \end{array} } \right)b{ = }\left\{ {\begin{array}{*{20}c} {mg + k_{1} l + F_{{\text{v}}} } \\ {mg + k_{2} - k_{1} )l} \\ \ldots \\ {mg + (k_{n} - k_{(n - 1)} )l} \\ \end{array} } \right\}$$

Suppose the third block is the working block that is acted on by the horizontal force $P_{\text{h}} \left( t \right)$. The equation of motion in the horizontal direction is:

$$m\ddot{u} = P_{\text{h}} (t) - \mu_{\text{d}} N(t)$$

(3)

where u is the horizontal displacement of the block, $\mu_{\text{d}}$ is the dynamic coefficient of friction between blocks, and $N(t)$ is the normal force on the block.

We set $z = z^{0} + y$, the vertical balance then is:

$$Kz^{0} = b$$

(4)

We solve the initial coordinates of each block along the z-axis as:

$$z_{i}^{0} = (n - i + 1)l + \sum\limits_{j = i}^{n} {\left( {\frac{{jmg + F_{v} }}{{k_{j} }}} \right)} \quad (i = {1},{ 2}, \ldots ,n)$$

(5)

By substituting $z = z^{0} + y$, $Kz^{0} = b$ into the matrix equation, we get:

$$M{\ddot{{y}}} + C\dot{y} + K{{y}} = F\left( t \right)$$

(6)

We set k₁ = k₂ = … = k_n, c₁ = c₂ = … = c_n, and m₁ = m₂ = … = m_n. Then, the approximate solution of the acceleration of the block in the model is:

$$\ddot{z}_{i} = \frac{{2P_{{\text{v}}} l^{2} }}{{{\text{m}}\omega_{{\text{v}}} \left( {\gamma t} \right)^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-\nulldelimiterspace} 3}}} }}\sqrt{\frac{k}{m}} \frac{1}{\uppi }\int_{0}^{\infty } {\sin \left( {\zeta z + {{z^{3} } \mathord{\left/ {\vphantom {{z^{3} } 3}} \right. \kern-\nulldelimiterspace} 3}} \right){\text{ e}}^{{{ - }\mu {\text{z}}^{{2}} }} z{\text{d}}z}$$

(7)

where $\gamma = \frac{{c_{1} l^{2} }}{8}(1 + \frac{{3c^{2} }}{mk})$, $\zeta = \frac{{il - c_{1} t}}{{\left( {\gamma t} \right)^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}}} }}$, $\mu = \frac{\alpha t}{{\left( {\gamma t} \right)^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-\nulldelimiterspace} 3}}} }}$, $\alpha = \frac{{cl^{2} }}{m}$, and $c_{1} = l\sqrt{\frac{k}{m}}$, $l$ is the parameter of the free length of the spring, in m, k_i is its stiffness coefficient, and m_i is block mass, in kg.

Equation (7) has been deduced and verified in detail by Li et al. (2019a, b).

Comparative analysis of test theory

To study the influence of stress wave-induced disturbance on the effect of ultra-low friction in sandstone blocks, we designed a test in which axial compression and stress wave-induced disturbance were simultaneously applied to the blocks. The size of each sandstone block was 100 mm × 100 mm × 100 mm and its mass was 2.56 kg. The test model consisted of five vertically stacked blocks without weak interlayers. An axial pressure of 4 MPa was applied to block No. 1 to simulate the pressure of the overburden. The amplitude of the stress wave-induced disturbance was 40 kN, and the disturbance frequencies were 1, 3, 5, 10 and 20 Hz. We installed an acceleration sensor at the center of each sandstone block and connected them to a computer. The type of acceleration sensor used was a PCB, with voltage type 352C04, sensitivity of 10 mV/g, range of frequency of 0.3–15,000 Hz, weight of 5.8 g, and a sampling rate of 2 kHz.

The calculation in the theoretical formula was consistent with the test parameters:$P_{\text{v}} = 40 \,{\text{kN}}$, $\omega_{\text{v}} = 31.42$ (f = 5 Hz), c = 60 N s/m, k = 4.0 × 10⁶ N/m, l = 0.005 m, and m_i = 2.56 kg. The working block was the third block(No. 3 black block in Fig. 2). Its acceleration was used as a parameter, the test data were calculated, and the results were compared with the accelerations derived from the theoretical model as shown in Fig. 3.

Fig. 2

Schematic diagram of verification test device

Fig. 3

Curves of maximum acceleration with disturbance frequency

Figure 3 shows that the maximum accelerations of the test block and the theoretical block both decreased with increasing frequency. The amplitude of acceleration of the working block can be divided into three stages: a stage of steep decline, one of slow decline, the steady stage. When the perturbation frequency was in the range of 1–5 Hz, the amplitude of changes in acceleration was large, indicating that low-frequency perturbations had a significant impact on the movement of the block. When the disturbance frequency was 1 Hz, the maximum accelerations were, respectively, 14.13 m/s² and 49.52 m/s². With the increase in the disturbance frequency, changes in the amplitude of acceleration of the block decreased and stabilized. Due to the difference between the theoretical model and the experimental conditions, their maximum accelerations were different, but their trends of change were consistent with the frequency of the stress wave-induced disturbance. Therefore, the reasonableness of the setup was verified.

Ultra-low friction test of broken block

Ultra-low friction test system

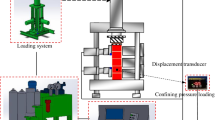
The equipment used in the test could be used to represent the loading of 3D stress on the broken rock mass, and could adequately simulate empirical stress when the ultra-low friction-induced rock burst occurred. The loading equipment was composed of four main parts: the mechanisms for loading axial pressure, confining pressure, impact, and disturbance. This design used a hydraulic transmission and control system. The size of the model of the test block could be adjusted according to the test requirements. The range of length and width was 0–200 mm, and that of height was 0–600 mm. Confining pressure could be applied to the front and back of the test body in the range of 0–30 MPa; horizontal impact was applied to the left side over the range of 0–30 MPa. Axial pressure and vertical disturbance could be applied in the vertical direction at the same time. The range of axial pressure was 0–30 MPa and that of vertical disturbance was 0–3 MPa, and frequency could be adjusted to within 0–50 Hz, as shown in Fig. 4. The horizontal displacement of the block was measured by a Panasonic mini-laser sensor.

Fig. 4

Ultra-low friction test system

Preparation of test pieces

Red sandstone has a uniform grain size, and is widely found underground. We used it as the rock sample in the test. To make the results comparable, all samples were drawn from the same kind of sandstone, with good integrity and homogeneity. The samples were processed into cylinders, each with a diameter of 50 mm and a height of 100 mm, and were polished to ensure that the parallelism of the surfaces at both ends was within 0.05 mm and surface flatness was within 0.02 mm. The uniaxial compression test of the rock samples was carried out in a mechanics’ laboratory. All the tests used the displacement-controlled loading method, and the loading rate was constant at 0.15 mm/min. We discuss the influence of the disturbing action of the stress wave on the ultra-low friction of the sandstone block. The complex ground stress was simplified into axial pressure and confining pressure. The experimental axial pressure was set to 10% of the uniaxial compressive strength (Fig. 5).

Fig. 5

Standard rock sample and the broken sample after test

Test plan

The test involved developing a test device to study the effects of the frequency of stress wave-induced disturbance and the intensity of disturbance on the effect of ultra-low friction of the broken blocks. The intensity of stress wave-induced disturbance was characterized by the amplitude of disturbance of the test device (Fig. 6). Using a method described by Wu et al. (2010), each group in this experiment consisted of four complete blocks with dimensions of 100 mm × 100 mm × 100 mm, and a working block in the middle. We set the working block to block number 3. In the three sets of tests, the working blocks consisted of one 100 mm × 100 mm × 100 mm sandstone block, two 100 mm × 100 mm × 50 mm sandstone blocks, and four 100 mm × 100 mm × 25 mm sandstone blocks. Axial pressure and disturbance were applied to the uppermost block in the vertical direction (Table 1). The stress wave-induced disturbance was a sine wave. We did not consider the effect of delay, and applied horizontal impact to the rock block at t₀.

Fig. 6

Block placement and loading model

Table 1 Physical and mechanical parameters

The experimental steps are as follows:

(1) The intact sandstone block was placed in the testing machine from top to bottom in the vertical direction. Axial pressure of 4 MPa was applied in the vertical direction and the confining pressure was set to 15 MPa.

(2) The stress wave-induced disturbance was applied in the vertical direction. The initial amplitude of disturbance was 0.3 MPa and the vibrational frequency was 1 Hz.

(3) Horizontal impact was applied to the No. 3 working block, and its horizontal displacement was measured by an optical fiber-based noncontact displacement sensor. Acceleration was measured by the acceleration sensor.

(4) The frequency of stress wave-induced disturbance, amplitude of disturbance, and horizontal impact were changed in turn during the test.

(5) The working block was replaced with two and four sandstone blocks, steps (1)–(4) were repeated, and the data were recorded.

Influence of stress wave-induced disturbance

Influence of stress wave-induced disturbance frequency

Influence of horizontal displacement of broken block

As the frequency of the stress wave-induced disturbance increased, the horizontal displacements of blocks of different levels of fragmentation all showed the characteristic of increasing first and then decreasing. When the frequency of the stress wave-induced disturbance was 1–3 Hz, an area of large displacement of the working block was formed. Under the same level of impact and frequency of the stress wave, the horizontal displacement of the four sandstone rock blocks was the largest, followed by the two sandstone rock blocks and the intact sandstone block.

As shown in Fig. 7, as the frequency of stress wave-induced disturbance increased, blocks with different levels of fragmentation recorded large displacements. Under the same disturbance frequency, the residual displacement of the four sandstone rock blocks was the largest, followed by the two sandstone rock blocks and the intact sandstone block. In the area of large displacement, when the frequency was 2.5 Hz, the horizontal displacement of the block was the largest, indicating that the effect of ultra-low friction of the block was the strongest at this frequency during the process of dynamic disturbance. Taking a horizontal impact of 1.5 MPa as an example, when the disturbance frequency was increased from 1 Hz to 1.5, 2.5, and 3 Hz, the residual displacements of the four sandstone rock blocks and the intact sandstone block were, respectively, 0.0302 mm, 0.0702 mm, 0.0618 mm, and 0.0983 mm, and 0.037 mm. Under a low-frequency disturbance, the degree of fragmentation of the block affected the strength of ultra-low friction of the block during impact. The more broken the rock mass of the block system was, the greater was the horizontal displacement of the blocks, and the easier it was for engineering accidents to occur. As the depth of mining increased, the rock blocks tended to be more broken, and thus stronger support should be used in projects to increase the strength of rocks around the roadway to avoid accidents.

Fig. 7

Relationship between horizontal displacement of broken block and frequency of stress wave-induced disturbance

Influence of acceleration of broken blocks

When the blocks were disturbed by the stress wave, the working block oscillated back and forth in the vertical direction at the equilibrium position. At this time, a horizontal impact was applied, and the acceleration of the working block increased suddenly, and was greater than its acceleration without stress wave-induced disturbance. Figure 8 shows that when the frequency of the stress wave-induced disturbance was in the range of 1–3 Hz, the working block had a prominent effect of ultra-low friction under horizontal impact. The greater the energy of horizontal impact of the working block was, the greater was the extreme acceleration, and the stronger was the effect of ultra-low friction. Under the same impact and frequency of the stress wave, the horizontal displacement of the four sandstone rock blocks was the largest, followed by the two sandstone rock blocks and the intact sandstone block. With a gradual increase in the disturbance frequency from 3 Hz, the maximum acceleration of the broken block gradually decreased and returned to the level when there was no disturbance. The effect of ultra-low friction of the broken block decreased. During the propagation of the stress wave, the accumulated energy of the block increased; and when the block was more broken, the stability of the entire rock mass decreased during disturbance, and the phenomenon of "separation" between blocks frequently occurred. Therefore, when the block was subjected to strong impact and disturbance, friction between the blocks weakened, the acceleration of the blocks increased, and the effect of ultra-low friction increased. The more broken the block tended to be, the greater was the amplitude of its acceleration. Wang et al. (2016) have reported results consistent with these.

Fig. 8

Curves of the maximum acceleration of blocks broken to varying degrees with changes in the disturbance frequency

Influence of intensity of stress wave-induced disturbance

The frequency of stress wave-induced disturbance applied in the experiment was fixed at 3 Hz. As the intensity of stress wave-induced disturbance increased, the maximum acceleration and horizontal displacement of blocks with different levels of fragmentation increased. Under the same impact and intensity of stress wave-induced disturbance, the maximum acceleration and horizontal displacement of the four sandstone rock blocks were the largest, followed by the two sandstone rock blocks and the intact sandstone block.

Influence of horizontal displacement of broken block

Figure 9 shows that with an increase in the intensity of disturbance, the horizontal displacements of the working blocks of different degrees of fragmentation all increased almost linearly, and the degree of fit was high. This enhanced the effect of ultra-low friction. Under the same impact and intensity of stress wave-induced disturbance, the horizontal displacement of the four sandstone rock blocks was the largest, followed by the two sandstone rock blocks and the intact sandstone block. When the horizontal impact was 1.5 MPa, the horizontal displacement of the four sandstone rock blocks under a strength of disturbance of 1 MPa increased by 16.6% compared with the horizontal displacement without disturbance, that of the two sandstone rock blocks increased by 15.4%, and in the intact sandstone block increased by 15.1%. When the horizontal impact was 2.5 MPa, the horizontal displacement of the four sandstone rock blocks under a strength of disturbance of 1 MPa increased by 31.6% compared with the horizontal displacement without disturbance, that in the two sandstone rock blocks is increased by 25.6%, and in the intact sandstone block increased by 23%. By comparison, the increase in the intensity of disturbance slightly increased the horizontal displacement of the working block, and the increase in the horizontal impact accentuated this phenomenon.

Fig. 9

Relationship between horizontal displacement and disturbance amplitude under different levels of horizontal impact

Influence of acceleration of broken blocks

Figure 10 shows that with the increase in the intensity of disturbance, the maximum acceleration of the working block broken to varying degrees increased at different degrees, and this increased the effect of ultra-low friction effect. Under the same impact and intensity of stress wave-induced disturbance, the maximum acceleration of the four sandstone rock blocks was the highest, followed by the two sandstone rock blocks and the intact sandstone block. When the horizontal impact was 1.5 MPa, the maximum acceleration of the four sandstone rock blocks under a strength of disturbance of 1 MPa increased by 19.3% compared with the acceleration without disturbance, that of the two sandstone rock blocks increased by 38.1%, and that of the intact sandstone block increased by 35%. When the horizontal impact was 2.5 MPa, the maximum acceleration of the four sandstone rock blocks under a strength of disturbance of 1 MPa increased by 42.3% compared with the horizontal acceleration without disturbance, that of the two sandstone rock blocks increased by 55.8%, and that of the intact sandstone block increased by 48.5%. By comparison, an increase in the disturbance intensity increased the maximum acceleration of the working block, and the increase in the horizontal impact accentuated this phenomenon. The more broken the blocks tended to be, the lower was the stability of the blocks when the intensity of the stress wave-induced disturbance increased, and the greater was the separation between them. Thus, the intensity of ultra-low friction was greater (Table 2).

Fig. 10

Relationship between the maximum acceleration and the disturbance amplitude under different levels of horizontal impact

Table 2 Differences in the horizontal displacement of broken blocks under different horizontal impacts

Influence of differences in horizontal displacement of broken block

The difference in horizontal displacement is the difference between the horizontal displacement of the broken rock mass with and without stress wave-induced disturbance. The above table shows that when the horizontal impact load of the working block was increased from 1.5 to 2.5 MPa, the difference in horizontal displacement of the block increased, and the effect of ultra-low friction increased. Under the same impact and stress wave-induced disturbance, the difference in horizontal displacement of the four sandstone rock blocks was the largest, followed by the two sandstone rock blocks and the intact sandstone block. Under a horizontal impact of 1.5 MPa, the horizontal displacements of the four sandstone rock blocks and the two sandstone rock blocks were 1.69 times and 1.37 times larger than that of the intact sandstone block, respectively. Under a horizontal impact of 2.5 MPa, the horizontal displacements of the four sandstone rock blocks and the two sandstone rock blocks were 1.61 times and 1.21 times larger than that of the intact sandstone block, respectively. The intensity of the horizontal impact load had little effect on the difference in horizontal displacement. This shows that the more broken the rock mass tended to be, the more prone was a roadway damaged by stress to the effect of ultra-low friction. This was identical to the results of field observations. With an increase in the mining depth, the rock mass tended to be broken and intermittently formed a block structure. Under the combined action of ground stress and mining disturbance, the broken block was more prone to dislocation, resulting in increasing effect of ultra-low friction. This can lead to accidents, such as rock bursts.

Energy-related characteristics of effect of ultra-low friction

Rock burst occurs owing to the instantaneous release of energy (Wang et al. 2018). In case of dynamic disturbance, Wang et al. (2015) have shown that the effect of the disturbance makes the rock block vibrate, and the equivalent vibration generated by the kinetic energy W of the disturbed block is:

$$W = \frac{{1}}{{2}}{m}v^{{2}}$$

(8)

where $v$ is the equivalent vibrational velocity. Equation (8) can be rewritten as

$$\frac{{W}}{{m}} = \frac{1}{2}v^{2}$$

(9)

We set $\frac{{W}}{{m}}$ as the kinetic energy per unit mass.

The horizontal displacement of the working block obtained from the experiment was derived to obtain the velocity of the block, and was used to obtain its kinetic energy per unit mass in the time domain. This was Fourier-transformed to obtain its curve of power spectral density.

Energy characteristics of effect of ultra-low friction of different broken blocks

The frequency of the stress wave-induced disturbance applied in the experiment was set to 3 Hz and the intensity of disturbance was set to 0.3 MPa.

• (1) The curves of change in the kinetic energy per unit mass in Figs. 11 and 12 shows that under horizontal impacts of 1.5 MPa and 2.5 MPa, the maximum kinetic energy of the working block was obtained after 125 ms, that is, when the working block was subjected to horizontal impact for a short time, due to the effects of impact and ultra-low friction. Its kinetic energy quickly increased to its maximum value. The smaller the friction between the blocks was, the greater was the kinetic energy of the working blocks. Due to the constraint on axial pressure and the energy consumption during horizontal impact, the energy of the block was greatly attenuated within 4 ms of impact. After this, the working block returned to a stable vibrational state, and the kinetic energy of the block increased with the horizontal impact load. Therefore, when rock masses with different levels of fracture were disturbed by vertical stress waves and had an ultra-low friction effect, their kinetic energy underwent transient accumulation and transient peak effects. Under the same impact load, the kinetic energy of the four sandstone rock blocks was the largest and that of the intact sandstone block was the smallest. At this time, the effect of ultra-low friction of the block was the strongest.

• (2) The test adequately simulated the occurrence and development of rock burst. The effect of ultra-low friction of the broken rock mass was caused by the stress wave-induced disturbance. In this process, the amplitude of power spectral density increased instantaneously and fluctuated significantly. The frequency corresponding to the maximum power spectral density of the working block is called the extreme frequency. The more broken the working block tended to be, the closer was its extreme frequency to the lowest frequency. When ultra-low friction-type rock impact occurred, the kinetic energy of the working block changed from high to low frequency. The more broken the working block tended to be, the greater was the maximum power spectral density. Energy was concentrated in the low-frequency area and decreased in the transition area. Energy in the high-frequency area was small, and the effect of ultra-low friction was small. When the working block was subjected to a large impact load, energy increased significantly, and it was easier to produce the effect of ultra-low friction under the action of the stress wave.

Fig. 11

Kinetic energy per unit mass and curves of power spectral density of different degrees of fracture under a horizontal impact of 1.5 MPa

Fig. 12

Kinetic energy per unit mass and curves of power spectral density of different degrees of fracture under a horizontal impact of 2.5 MPa

Comparative analysis of parameters of energy of ultra-low friction

• (1) Table 3 shows that the kinetic energy of blocks broken to different degrees increased with the horizontal impact load, and the energy of the four sandstone rock blocks reached their maximum value when the effect of ultra-low friction was evident, and the intact sandstone block had the least energy. Under a horizontal impact of 1.5 MPa, the energies of the four sandstone rock blocks and the two sandstone rock blocks were, respectively, 2.90 times and 1.68 times larger than that of the intact sandstone block. Under a horizontal impact of 2.5 MPa, the energies of the four sandstone rock blocks and the two sandstone rock blocks were, respectively, 2.12 times and 1.62 times larger than that of the intact sandstone block. When blocks with different levels of fracture had been subjected to horizontal impacts during stress wave-induced disturbance, energy accumulation was different. The blocks tended to be broken, the roadways had stress-induced defects, and weaker and less stable rock blocks were affected by the impact. The block energy accumulated to the maximum in a short period, and the effect of ultra-low friction was easy to observe, and in turn induced accidents due to rock impact. Therefore, the degree of rock fragmentation was the main factor affecting the strength of ultra-low friction of the block.

• (2) The more broken the block tended to be, the lower was the dominant frequency in case of ultra-low friction. The higher the horizontal impact load of the block was, the lower was the dominant frequency in case of ultra-low friction. When the horizontal impact was 1.5 MPa, the main frequency of the block was within 20 Hz, and when the horizontal impact was 2.5 MPa, it was within 10 Hz. This is consistent with the conclusion that the underground effect of ultra-low friction occurred in the low-frequency range.

• (3) The more broken the block tended to be, the higher was the power spectrum density is when ultra-low friction occurred. The higher the horizontal impact load of the block was, the higher was the power spectral density in case of ultra-low friction. The more broken the block tended to be, the stronger was the horizontal impact to which it was subjected, the more significant was the dynamic response, and the more prone to ultra-low friction it was. This caused rock burst accidents.

Table 3 The parameters of the effect of ultra-low friction of blocks with different degrees of fragmentation

Discussions

With the gradual reduction and depletion of shallow resources, countries around the world have engaged in deep mining (Ranjith et al. 2017; Zhao et al. 2018; Chen et al. 2020). Therefore, this article developed a test of ultra-low friction to differentiate among the degrees of fragmentation of rock blocks. We used the confining axial compression to simulate the state of stress of the deep rock formation. Vertical and horizontal impacts were used to simulate blasting, rock transportation, and mechanical operation. The conclusions obtained were compared with those of previous studies. Experimental research by Su et al. (2016) showed that in the frequency range of 0–3 Hz, the kinetic energy of rock burst-induced ejection first increased and then decreased as the frequency of axial disturbance-induced load increased. Pan and Wang (2014) and other researchers have reported that the frequency of external disturbances changes the maximum stretch between rock blocks. When the frequency of disturbance is close to the quasi-resonant frequency of the rock mass of the block system, the maximum stretch increases sharply. Compared with the above experiments, we found that ultra-low friction was likely to occur when the perturbation frequency was 1–3 Hz, due to differences in loading conditions, and the physical and mechanical properties as well as dimensions of the specimens used. The conclusions of this article thus need to be verified through experiments. In future work, we plan to conduct ultra-low friction tests under field conditions so that the results have theoretical and practical value for the prediction and prevention of deep rock bursts.

Conclusions

• (1) The frequency of stress wave-induced disturbance influences the ultra-low friction of broken rock mass. Frequency within the range of 1–3 Hz was considered here. The maximum horizontal displacement and acceleration of the block subjected to dynamic response increased significantly, and the effect of ultra-low friction was the strongest in this case. As the frequency of disturbance of the stress wave increased, the maximum horizontal displacement and acceleration of the block gradually fell back into those of the state without disturbance. The more broken the blocks were, the greater was the dynamic response.

• (2) The influence of intensity of the stress wave-induced disturbance on the effect of ultra-low friction of the crushed block changed linearly. The more broken the block was, the greater was the intensity of the stress wave-induced disturbance, and the more prominent was the effect of ultra-low friction of the block.

• (3) Under the same impact, the effect of ultra-low friction of the blocks decreased among the four combined blocks, two combined blocks, and a complete sandstone block. The horizontal impact load also influenced the effect of ultra-low friction of the block.

• (4) Under the combined action of axial compression, horizontal impact, and stress wave-induced disturbance, the kinetic energy of the block had the characteristics of agglomeration and a short-term peak value. When the effect of ultra-low friction was the strongest, it was manifested in the unit mass kinetic energy of the block, its power spectral density, and maximum kinetic energy. The frequency shifted from high to low, and the waveform tended to consist of low-frequency waves. The block exhibited prominent effects of ultra-low friction within a frequency of 20 Hz.