1 Introduction

China’s coal resources are abundant, with demonstrated coal reserves that account for approximately 11.1% of global reserves (Wang et al. 2019a). Open-pit mining is an important technique for recovering coal resources, and has advantages such as safe operation, large output, environmental efficiency, good working conditions, and high mining intensity. Recently, open-pit mining has developed rapidly and its application is becoming increasingly widespread. In China, the proportion of open-pit coal mining has grown from 4% in the early 1990s to 16.2% in 2010 (Song et al. 2016). Although the advantages of open-pit mining have been highlighted in actual engineering practice, this method often leaves a large amount of residual coal that cannot be recovered (Zhao et al. 2020a, b). The advent of the LDC100 highwall miner provides an effective approach for recovering this residual coal in the highwall.

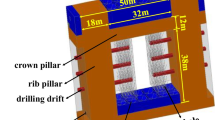
The highwall miner is a new open-pit highwall mining technology that combines the advantages of open-pit mining and underground mining to achieve highwall mining in soft and thick coal seams (Sasaoka et al. 2016; Ross et al. 2019). The mining and transporting process is fully automatic and remotely controlled (Wang et al. 2019b), allowing unmanned intelligent mining and transportation operations to be carried out in the coal chamber. In the highwall mining process, web pillars are set up between the chambers to support the overlying strata and prevent landslides, the burial of equipment, and other disasters (Wang et al. 2019c; Huang et al. 2021). When the web pillars become partially unstable, a chain of instability may be induced in the pillar group. This results in slope instability and landslides (Chandar et al. 2014, 2015), which endanger the safety of mining equipment and cause substantial loss of resources. Therefore, the stability of web pillars should be investigated and a reasonable web pillar size should be designed.

Globally, current research on web pillar stability in open-pit mining is mainly based on empirical formulas describing the coal pillar strength to determine the width of the web pillar (Bunting et al. 1911; Greenwald et al. 1939; Holland et al. 1957, 1964; Salamon et al. 1967; Bieniawski et al. 1968; Sheorey 1992; Galvin et al. 1999). Porarthur et al. adopted hybrid empirical and numerical modeling techniques for web pillar design in India, and proposed the introduction of a correction factor into the empirical pillar strength equation for slender pillars with a width to height ratio of less than unity. This enabled a more reasonable design of the coal pillar parameters to be achieved (Porarthur et al. 2013). Lukáš et al. (2017) used rockbolt supports to address the issue of coal pillar stability and stabilization, and sufficiently reinforced several existing pillars. Deliveris and Benardos (2017) investigated approximate solutions using two-dimensional (2D) numerical simulation techniques and three-dimensional (3D) numerical analyses, and evaluated the geomechanical responses of the lignite pillar formed by the room and pillar mining method. They pointed out that 2D approximation techniques adequately approximate the actual 3D problem. Hikaru et al. (2013) considered the recovery ratio and used numerical analysis to develop an appropriate design for the width of the web coal pillar. Zhang et al. (2011) used the FLAC3D (Fast Lagrangian Analysis of Continua in Three Dimensions; Itasca Consulting Group Inc., Minneapolis, Minnesota, USA) numerical simulation software to systematically investigate the laws governing the stress increase coefficient of the coal pillar and the pillar’s stability. They obtained a function describing the relationships among the stress increase coefficient of the upper and lower pillars, the properties of the interstratified rock, and the geometrical parameters.

However, the results obtained in the abovementioned studies are not necessarily suitable for the geological conditions and the occurrence of coal and rock in China. Notably, the quality of coal in most parts of China is soft. Moreover, previous studies have not provided a detailed description of the instability mechanism or a reasonable instability criterion for the web pillar. As a result, the designed width of the web pillar is not necessarily reliable (Jiang et al. 2021). Therefore, taking an open-pit coal mine in Inner Mongolia, China, as the engineering geological background, this paper systematically studies the instability mechanism and the web pillar width by means of experimental analysis, numerical simulations, and cusp catastrophe theory. Our results are expected to provide a basis for the design and safety implementation of highwall mining schemes, as well as guidance for similar projects.

2 Engineering background

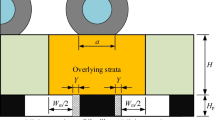
This paper focuses on the geological background of an open-pit mine located in Inner Mongolia Province, China. The strike length of the mine is 5.1 km. Two main coal seams, numbered 19 and 21, contain high-quality lignite. The expected advance length of the open cut operations is 360 m per year, and it is necessary to cut the coal in the No. 21 seam along the seam floor to allow for reasonable internal coal transport. The tracking distance of the internal transport is 50 m. The strata at the west end-slope of the open-pit mine are almost horizontally distributed, and there is no obvious change in lithology along the strike direction. The slope strata consists of surface soil, gritstone, siltstone, coal, and base sandstone from top to bottom (Fig. 1).

Fig. 1
figure 1

Schematic diagram of lithology distribution of slope strata

Full size image

The LDC100 highwall miner (Han et al. 2014) is used to extract the coal left under the west highwall of the open-pit mine. This is an unmanned mining machine with a production capacity of 60 t/h and a suited coal-rock hardness factor of f ≤ 2, which is applicable for recovery from lignite open-pit mines. The recovery chamber has a rectangular cross-section measuring 2 m (width) × 2.5 m (height). The maximum mining depth is 100 m and the mining process can be completed once every 3 days. The mechanical properties of the rocks and soil mass at the highwall of the open-pit mine are listed in Table 1.

Table 1 Mechanical properties of the rocks and soil mass
Full size table

3 Numerical modeling of the instability mechanism of web pillars

3.1 Model construction and experiment schemes

Taking the west highwall of an open-pit coal mine in Inner Mongolia as the engineering background, numerical simulation models of the web pillars under four slope angles (i.e., 20°, 30°, 40°, and 50°) are established separately using the finite difference modeling software FLAC3D. These models allow the instability mechanism of web pillars to be studied at different slope angles and mining depths. The models represent the geological conditions around the target area shown in Fig. 1. To eliminate the boundary effect, coal pillars with a width of 60 m are retained at each side of the chambers, based on the theory of elastic–plastic mechanics (Ghaednia et al. 2017). As the element size has a great impact on the modeling results (Mo et al. 2018), the meshing elements in the target area should be precisely arranged to minimize the influence of numerical errors. The element width was set to be 1 m along the pillar strike direction. Ten elements were set in each horizontal and vertical direction of the pillar cross-section. A total of 100 elements are used to discretize the pillar area. Horizontal constraints are imposed on both sides of the model, that is, the horizontal displacement was set to be zero, and the base boundary of the model was fixed, which means the horizontal and vertical displacements of the base boundary are both zero. The top surface and the slope face of the model are free boundaries. The loading stress is gravity, and the Mohr–Coulomb elastic–plastic constitutive model is used for calculation and analysis. The failure criteria used in the Mohr–Coulomb model are the Mohr–Coulomb failure criterion and the maximum tensile stress criterion. The relationship between the three principal stresses is σ1 ≤ σ2 ≤ σ3; the failure criterion in the (σ1, σ3) plane is represented in Fig. 2.

Fig. 2
figure 2

Mohr–Coulomb failure criterion

Full size image

According to the specifications of the LDC100 highwall miner, the chamber measures 2.5 m in height (h = 2.5 m) and 2 m in width (a = 2 m); the maximum mining depth is 100 m (l = 100 m), and one mining process can be completed in 3 days. As the slope angle and mining depth increase, the thickness of the overburden gradually increases, and the bearing stress of the coal pillar increases. A larger pillar width provides greater ultimate strength. At larger values of the slope angle and mining depth, larger coal pillars should be designed to support the overburden load. The accuracy of the pillar width should be within 0.2 m to satisfy the engineering requirements. To analyze the abutment stress, the yield zone distribution, and the instability mechanism of the web pillar at different slope angles and mining depths, four modeling schemes are designed. Tables 2, 3, 4 and 5 present the modeling schemes under slope angles of 20°, 30°, 40°, and 50°, respectively. For each scheme, four mining depths are considered, i.e., l = 50 m, 65 m, 80 m, and 100 m, and there are four chambers for each mining depth. Each chamber has h = 2.5 m and a = 2 m, and three web pillars are retained between the chambers. We design four pillar widths for each mining depth, giving a total of 16 simulation models (Fig. 3) in each scheme. Details of the web pillar sizes are listed in Tables 2, 3, 4 and 5.

Table 2 Simulated web pillar widths (m) under different mining depths (m) at slope angle 20°
Full size table
Table 3 Simulated web pillar widths (m) under different mining depths (m) at slope angle 30°
Full size table
Table 4 Simulated web pillar widths (m) under different mining depths (m) at slope angle 40°
Full size table
Table 5 Simulated web pillar widths (m) under different mining depths (m) at slope angle 50°
Full size table
Fig. 3
figure 3

Numerical model

Full size image

3.2 Analysis of abutment stress distributions of web pillars

By examining the shear resistance of the web pillars, the abutment stress distribution before pillar failure can be obtained. Analyzing the characteristics of the abutment stress distributions in the web pillar along both the strike direction and the dip direction, the position with the maximum abutment stress under the condition of “triangular loading” is determined. Additionally, the variations in the loading sustained in this position at different slope angles, mining depths, and pillar widths is revealed.

Due to space limitations, this paper only presented the modeling results of the abutment stress distributions for web pillars at a slope angle of 40° (Fig. 4). The engineering positions with the maximum abutment stress under varying pillar widths, mining depths, and slope angles were recorded in Table 6. There is an “end effect” in highwall mining. This is because the stiffness of the web pillar is smaller than the stiffness of the solid slope barrier, which shares some of the overburden load upon the web pillar. The maximum abutment stresses occur somewhere ahead of the web pillars towards the end of chamber excavations. Additionally, the locations of the maximum abutment stresses are not related to the pillar width, but are closely associated with the maximum mining depth and the slope angle (burial depth). Notably, the riskiest web pillar position is at the site where the coal pillar bears the maximum abutment stress. If instability occurs in this position, it may produce a chain reaction and lead to instability of the entire pillar group. The positions with the maximum abutment stress (Pd) are fitted in Fig. 5, and Eq. (1) is derived to demonstrate the relationship between Pd, the slope angle, and the mining depth.

$$P_{\text{d}} = 2.54 - 0.15\theta + 0.9689L$$
(1)

where, Pd is the position bearing the maximum abutment stress; θ is the slope angle, and L is the mining depth.

Fig. 4
figure 4

Abutment stress distributions under different mining widths and pillar sizes at slope angle of 40°

Full size image
Table 6 Maximum abutment stress positions at different slope angles and mining depths
Full size table
Fig. 5
figure 5

Fitted maximum abutment stress positions at different slope angles and mining depths

Full size image

Based on the positions with the maximum abutment stress at different slope angles and mining depths, the stress distributions along the dip direction and the variation of the loading sustained in these positions are studied. In this paper, we only present the results of the stress distributions in the riskiest positions under different pillar widths and mining depths at a slope angle of 40° (Figs. 6 and 7). The results show that the abutment stress is distributed symmetrically along the center of the pillar. As the coal pillar does not break, the stress concentration factor is relatively large at either side of the pillar, but smaller in the center. The stress distribution is approximately bowl-shaped. The maximum and minimum abutment stresses of the web pillars with different widths and mining depths at slope angles of 20°, 30°, 40°, and 50° are recorded in Tables 7, 8, 9 and 10, respectively.

Fig. 6
figure 6

Side abutment stress distributions for different pillar widths at slope angle 40° and depth 65 m

Full size image
Fig. 7
figure 7

Side abutment stress distributions for different pillar widths at slope angle 40° and depth 100 m

Full size image
Table 7 Maximum and minimum bearing stress values of different pillar widths at slope angle 20°
Full size table
Table 8 Maximum and minimum bearing stress values of different pillars widths at slope angle 30°
Full size table
Table 9 Maximum and minimum bearing stress values of different pillars widths at slope angle 40°
Full size table
Table 10 Maximum and minimum bearing stress values of different pillars widths at slope angle 50°
Full size table

3.3 Analysis of instability mechanism and ultimate strength of web pillars

Based on the distributions of positions at which the maximum abutment stress occurs, namely, the positions at which the web pillars are most vulnerable to instability, the distribution characteristics of the side abutment stress are analyzed under varying pillar widths and mining depths and at slope angles of 20°, 30°, 40°, and 50°. Taking the case of a 40° slope angle for detailed analysis (Figs. 8 and 9), it is evident that, as the pillar width decreases, the stress profile changes from a saddle shape to an approximate platform shape, and finally to an arch shape. Correspondingly, the web pillar undergoes the following evolution process: “stable state–critical equivalent state–ultimate failure state”. This is because, with the narrowing of the pillar width, the pillar’s ultimate strength decreases as the abutment stress grows. The abutment stress of the web pillar is initially smaller than the pillar’s ultimate strength (Fig. 8a) and then becomes equal to the pillar strength (Fig. 8b), implying that the web pillar is in a stable state. Finally, the abutment stress becomes larger than the ultimate strength of the coal pillar (Fig. 8c, d), suggesting that the web pillar is damaged. According to the limit equilibrium theory (Xiong et al. 2019), the ultimate strength of the web pillar can be determined as a function of its width. Under different slope angles and mining depths, web pillars with the same width have almost the same ultimate strength, indicating that the ultimate strength is independent of the slope angle and the mining depth, but is positively correlated with the pillar width. That is, the larger the pillar width, the greater will be the pillar’s ultimate strength, as illustrated in Fig. 10.

Fig. 8
figure 8

Side abutment stress distributions for different pillar widths at slope angle 40° and depth 65 m

Full size image
Fig. 9
figure 9

Side abutment stress distributions for different pillar widths at slope angle 40° and depth 100 m

Full size image
Fig. 10
figure 10

Ultimate strengths of coal pillars with different widths

Full size image

3.4 Analysis of yield zone distribution

The modeling results of the yield zone distribution in web pillars at different mining depths and a slope angle of 40° are now analyzed in detail (Figs. 11, 12, 13, 14). The results show that the failure pattern of the web pillars is shear failure. If the web pillar has a small width, failure occurs when the yield zones at either side of the web pillar merge with each other (Fig. 11a, b). As the pillar width increases, an elastic core zone (Fig. 11c, d) appears in the center of the web pillar and the yield zones do not meet, implying that the web pillar is in a stable state. The modeling results of the web pillar stability are consistent with the previous analysis of the state identification of web pillars based on the abutment stress distribution. By combining the relationship between the abutment stress and the ultimate strength of the web pillar with the failure characteristics of the yield zones, the instability mechanism of the web pillar in highwall mining can be determined, that is, when the abutment stress of the web pillar exceeds its ultimate strength, shear failure occurs. To improve the recovery rate, the appropriate retaining widths for web pillars under different slope angles and mining depths are identified in Table 11.

Fig. 11
figure 11

Yield zone distributions of web pillars with different widths at slope angle 40° and depth 50 m

Full size image
Fig. 12
figure 12

Yield zone distributions of web pillars with different widths at slope angle 40° and depth 65 m

Full size image
Fig. 13
figure 13

Yield zone distributions of web pillars with different widths at slope angle 40° and depth 80 m

Full size image
Fig. 14
figure 14

Yield zone distributions of web pillars with different widths at slope angle 40° and depth 100 m

Full size image
Table 11 Retaining widths of web pillars at different slope angles and mining depths
Full size table

4 Instability criterion of web pillars

4.1 Cusp catastrophe model of web pillars

The maximum abutment stress positions of web pillars under the “triangular loading” effect are different from those under a uniform distribution of the overburden rock. The modeling results of the abutment stress distributions indicate that the abutment stress in the riskiest position along the dip direction has a bowl-shaped distribution, rather than the uniform distribution described by effective region theory. Accordingly, a bearing model of the web pillar is established (Fig. 15). The arch-shaped solid curve in the model illustrates the actual distribution of the abutment stress, which is symmetrically distributed along the center of the web pillar. Provided that the actual stress curve follows the two broken lines in the figure, the overburden load of the web pillar (P) can be calculated by Eq. (2).

$$P = \frac{{\sigma_{\min } + \sigma_{\max } }}{2}w_{\text{s}}$$
(2)

where, σmin is the minimum abutment stress; σmax is the maximum abutment stress, and ws is the pillar width.

Fig. 15
figure 15

Bearing model of web pillar

Full size image

By substituting the maximum and minimum abutment stress values in Tables 7, 8, 9 and 10 into Eq. (2), the overburden load of the web pillar can be calculated for different pillar widths, mining depths, and slope angles. Equation (3) describes the best-fit curve of the bearing stress of the web pillar with respect to the slope angle, mining depth, and pillar width:

$$P = 0.0638\theta { + }0.0023L^{2} + 0.195w_{\text{s}}^{2}$$
(3)

Mining activities induce stress redistribution and an overburden load concentrated in the coal pillar, forming symmetrical yield zones at either side of the pillar. Let the yield zone width and the chamber width be denoted by xp and wm, respectively. The constitutive relation of the elastic core zone is different from that of the yield zone (Guo et al. 2005) (Fig. 16), and exhibits linearity in the elastic core zone. The coal pillar in the elastic core zone has high strength, conforming to elasticity theory, and has the elastic or strain-hardening property. However, in the yield zone, the constitutive relation curve is nonlinear and has the strain-softening property. Once the coal pillar reaches its peak strength, it will release stress quickly and the pillar strength will drop rapidly, resulting in reduced ability to resist deformation as the deformation grows.

Fig. 16
figure 16

Constitutive relation curves of the coal pillar

Full size image

The relationship between the stress of the coal pillar (σ), the strain (ε), and the damage parameter (D) can be expressed as follows (Guo et al. 2004):

$$\sigma = E\varepsilon \left( {1 - D} \right)$$
(4)

where, \(D = 1 - \exp \left( { - \frac{\varepsilon }{{\varepsilon_{0} }}} \right)\); ε0 is the strain variable of the coal pillar under a certain load, and E is the elasticity modulus of the coal pillar.

The yield zones have a total width of 2xp, and the coal seam thickness is h. Hence, the relation between the bearing stress in the yield zones (Ps) and the deformation value in these zones (u) can be described as:

$$P_{{\text{s}}} = \frac{{2x_{\text{p}} Eu}}{h}\exp \left( { - \frac{u}{{u_{0} }}} \right)$$
(5)

where, u0 is the deformation value of the coal pillar under the maximum bearing stress, u0 = σch/E.

The width of the elastic core zone is ws−2xp, which conforms to the elasticity principle. The corresponding bearing stress in this zone is given by:

$$P_{\text{e}} = \frac{Eu}{h}\left( {w_{\text{s}} - 2x_{\text{p}} } \right)$$
(6)

Thus, the strain energy (Vs) and the elastic potential energy (Ve) of the coal pillar in the yield zones and the elastic core zone can be written as:

$$V_{\text{s}} = \frac{{2Ex_{\text{p}} }}{h}\int_{0}^{u} {\exp \left( { - \frac{u}{{u_{0} }}} \right)} \text{d}u$$
(7)
$$V_{\text{e}} = \frac{{2E\left( {w_{\text{s}} - 2x_{\text{p}} } \right)}}{h}\int_{0}^{u} {u\text{d}u}$$
(8)

The potential energy of the overburden (Vp) is expressed as follows:

$$V_{\text{p}} = \left( {0.0638\theta + 0.0023L^{2} + 0.195w_{\text{s}}^{2} } \right)u$$
(9)

The total potential energy function in the mechanical model shown in Fig. 17 can be calculated by:

$$V = \frac{{2Ex_{\text{p}} }}{h}\int_{0}^{u} u \left( { - \frac{u}{{u_{0} }}} \right)\text{d}u + \frac{{2E\left( {w_{\text{s}} - 2x_{\text{p}} } \right)}}{h}\int_{0}^{u} {u\text{d}u} - \left( {0.0638\theta { + }0.0023L^{2} + 0.195w_{\text{s}}^{2} } \right)u$$
(10)
Fig. 17
figure 17

Mechanical model of chamber and surrounding rocks

Full size image

Here, u is considered as the state variable for analysis using cusp catastrophe theory. Setting the first derivative of V equal to zero (i.e., V' = 0), the equation for the equilibrium surface (M) can be derived as:

$$V^{\prime} = \frac{{2Ex_{\text{p}} }}{h}u\exp \left( { - \frac{u}{{u_{0} }}} \right) + \frac{{E\left( {w_{\text{s}} - 2x_{\text{p}} } \right)}}{h}u - 0.0638\theta - 0.0023L^{2} - 0.195w_{\text{s}}^{2} = 0$$
(11)

Equation (11) is the equilibrium condition of the mechanical model. To establish the cusp catastrophe model, we take the derivative of the equilibrium surface equation and set the second derivative (i.e., V″) equal to zero:

$$V^{\prime\prime} = 2\left( {w_{\text{s}} - x_{\text{p}} } \right)x_{\text{p}} \frac{E}{{u_{0} }}\left( {2 - \frac{u}{{u_{0} }}} \right) + \left( { - 4w_{\text{s}} x_{\text{p}} + 2w_{\text{s}} x_{\text{p}} \frac{u}{{u_{0} }} + 4x_{\text{p}}^{2} - 2x_{\text{p}}^{2} \frac{u}{{u_{0} }}} \right)\left( {\frac{1}{{u_{0} }}} \right)e^{{ - \frac{u}{{u_{0} }}}} = 0$$
(12)

The solution of V″ = 0 is u = u1 = 2u0. Expanding Eq. (12) about u = u1 = 2u0 according to Taylor’s formula and neglecting powers above the cubic term, we have:

$$\frac{{4x_{\text{p}} Eu_{1} e^{ - 2} }}{3h}\left\{ {\left( {\frac{{u - u_{1} }}{{u_{1} }}} \right)^{3} + \frac{{3\left( {u - u_{1} } \right)}}{2u}\left[ {\frac{{\left( {w_{\text{s}} - 2x_{\text{p}} } \right)e^{2} }}{{2x_{\text{p}} }} - 1} \right] + \frac{3}{2}\left[ {1 + \frac{{\left( {w_{\text{s}} - 2x_{\text{p}} } \right)e^{2} }}{{2x_{\text{p}} }} - \frac{{Phe^{2} }}{{2x_{\text{p}} Eu_{1} }}} \right]} \right\} = 0$$
(13)

Let the dimensionless quantity z be the state variable, and let p and q be the control variables:

$$z = \frac{{u - u_{1} }}{{u_{1} }},\quad p = \frac{3}{2}\left( {k_{0} - 1} \right),\quad q = \frac{3}{2}\left( {1 + k_{0} - t} \right)$$
(14)
$$k_{0} = \frac{{k_{\text{e}} }}{{k_{\text{s}} }} = \frac{{E\left( {w_{\text{s}} - 2x_{\text{p}} } \right)/h}}{{2x_{\text{p}} Ee^{ - 2} /h}} = \frac{{\left( {w_{\text{s}} - 2x_{\text{p}} } \right)e^{2} }}{{2x_{\text{p}} }},\quad t = \frac{{he^{2} }}{{2x_{\text{p}} Eu_{1} }}\left( {0.0638\theta + 0.0023L^{2} + 0.195w_{\text{s}}^{2} } \right)$$
(15)

where, ke and ks are the material stiffness in the elastic core zone and in the yield zone, respectively; t is a parameter related to highwall mining conditions, that is, it is relevant to the mining height, retaining width, mining depth, overburden bulk density, coal deformation parameter, and other factors.

According to Eqs. (13)–(15), the standard equilibrium equation of the cusp catastrophe model is obtained as:

$$z^{3} + pz + q = 0$$
(16)

The derivative of Eq. (16) gives the singular point equation of the system:

$$3z^{2} + p = 0$$
(17)

Combining Eqs. (16) and (17), the bifurcation set equation of the system can be obtained as:

$$\Delta = 8p^{3} + 27q^{2} = 0$$
(18)

Substituting Eq. (14) into Eq. (18), we obtain the simplified expression:

$$\Delta = 2\left( {k_{0} - 1} \right)^{3} + 9\left( {1 + k_{0} - t} \right)^{2} = 0$$
(19)

Finally, substituting Eq. (15) and u0 = σch/E into Eq. (19), we obtain the following fitted expression:

$$\Delta = 2\left[ {\frac{{\left( {w_{\text{s}} - 2x_{\text{p}} } \right)e^{2} }}{{2x_{\text{p}} }} - 1} \right]^{3} + 9\left[ {1 + \frac{{\left( {w_{\text{s}} - 2x_{\text{p}} } \right)e^{2} }}{{2x_{\text{p}} }} - \frac{e}{{4x_{\text{p}} \sigma_{\text{c}} }}\left( {0.0638\theta + 0.0023L^{2} + 0.195w_{\text{s}}^{2} } \right)} \right]^{2} = 0$$
(20)

A value of Δ > 0 means the system is in a stable state, and Δ = 0 implies the system is in the critical equilibrium state. Only when Δ < 0 can the system cross the bifurcation set and fail instantly. Therefore, the sufficient and necessary conditions for the instability catastrophe of coal pillars are as follows:

$$2[\frac{{\left( {w_{\text{s}} - 2x_{\text{p}} } \right)e^{2} }}{{2x_{\text{p}} }} - 1]^{3} + 9\left[ {1 + \frac{{\left( {w_{\text{s}} - 2x_{\text{p}} } \right)e^{2} }}{{2x_{\text{p}} }} - \frac{{e^{2} }}{{4x_{\text{p}} \sigma_{\text{c}} }}(0.0638\theta + 0.0023L^{2} + 0.195w_{\text{s}}^{2} )} \right]^{2} < 0$$
(21)

4.2 Yield zone width calculation

In view of the problems with the classical elastic–plastic analysis of rock mechanics, and based on limit equilibrium theory, it is further assumed that the coal seam roof and floor have the same lithology and have greater strength than the coal (Wilson et al. 1973). A mechanical model (Gu et al. 2014, 2015) of the chamber and the surrounding rock is established without considering the body force (Fig. 17).

As the yield zone is the limit equilibrium zone, the shear stress τ and the vertical stress σy at the interface between the coal seam roof and floor satisfy the following conditions:

$$\tau = c_{0} + \sigma_{y} \tan \varphi_{0}$$
(22)

where, c0 and φ0 are the internal friction angle and the cohesion of the coal seam interface. The equilibrium equation in the x-direction is established as:

$$h\sigma_{x} + 2\pi \text{d}x - h\left( {\sigma_{x} + \frac{{\partial \sigma_{x} }}{\partial x}\text{d}\sigma_{x} } \right) = 0$$
(23)

According to the Mohr–Coulomb failure criterion, when the yield zone of the coal body is in the limit equilibrium state, we have:

$$\sigma_{1} { = }\frac{1 + \sin \varphi }{{1 - \sin \varphi }}\sigma_{3} + \frac{2c\cos \varphi }{{1 - \sin \varphi }}$$
(24)

Given the assumed symmetry of the problem, the vertical and horizontal stresses in the x-axis are the principal stresses. In Eq. (24), σ1 = σy, σ3 = σx, c is the internal friction angle, and φ is the cohesion of the coal body. Taking the derivative of Eq. (24), the following expression is obtained:

$$\frac{{\partial \sigma_{y} }}{\partial x} = \frac{1 + \sin \varphi }{{1 - \sin \varphi }}\frac{{\partial \sigma_{x} }}{\partial x}$$
(25)

If A = (1 + sinφ)/(1−sinφ), then

$$\frac{{\partial \sigma_{y} }}{\partial x}{ = }A\frac{{\partial \sigma_{x} }}{\partial x}$$
(26)

Substituting Eq. (26) into Eq. (24), we derive the following expression:

$$\frac{{\partial \sigma_{y} }}{\partial x}{ - }\frac{{2A\tan \varphi_{0} }}{h}\sigma_{y} = \frac{{2c_{0} A}}{h}$$
(27)

Considering the boundary condition σx=0 = 0 and setting N = (2ccos φ)/(1 + sin φ), the vertical stress and the horizontal stress in the x-axis of the yield zone can be deduced as:

$$\left\{ {\begin{array}{*{20}l} {\sigma^{p}_{y} = \left( {NA + \frac{{c_{0} }}{{\tan \varphi_{0} }}} \right)e^{{\frac{{2A\tan \varphi_{0} }}{h}x}} - \frac{{c_{0} }}{{\tan \varphi_{0} }}} \hfill \\ {\sigma^{P}_{x} = \left( {N + \frac{{c_{0} }}{{A\tan \varphi_{0} }}} \right)(e^{{\frac{{2A\tan \varphi_{0} }}{h}x}} - 1)} \hfill \\ \end{array} } \right.(0 \le x \le x_{\text{p}} )$$
(28)

In combination with stress balance theory, after the chamber has been excavated, the load imposed on the original coal body along the length of the chamber is transferred to the adjacent coal body. Provided that the vertical stress and the horizontal stress in the x-axis are equal to the average stress along the height of the coal seam, and according to the assumption of symmetry, the following equation can be obtained:

$$\frac{{w_{\text{m}} }}{2}\gamma H = \int_{0}^{{x_{\text{p}} }} {(\sigma^{p}_{y} - \gamma H)\text{d}x + \int_{{x_{\text{p}} }}^{ + \infty } {(\sigma^{e}_{y} - \gamma H)\text{d}x} }$$
(29)

Integrating both sides of Eq. (29), if X = 2Atan φ0xph, then xp = Xh2Atan φ0, and:

$$\frac{{w_{\text{m}} \gamma HA\tan \varphi_{0} }}{h} = \left\{ {\left( {NA + \frac{{c_{0} }}{{A\tan \varphi_{0} }}} \right)(X + 1)e^{x} - 2\left( {\gamma H + \frac{{c_{0} }}{{\tan \varphi_{0} }}} \right)X - \left( {NA + \frac{{c_{0} }}{{\tan \varphi_{0} }}} \right)} \right\}$$
(30)

Rearranging this expression, we have:

$$x_{\text{p}} = \ln \left[ {\frac{{\frac{{2(\gamma H\tan \varphi_{0} + c_{0} )}}{{(NA\tan \varphi_{0} + c_{0} )}}X + \frac{{w_{m} \gamma H\tan^{2} \varphi_{0} }}{{h(NA\tan \varphi_{0} + c_{0} )}} + 1}}{(X + 1)}} \right]$$
(31)

5 Case study

The burial depth of the No. 21 coal seam is H = 100 m, the average bulk density of the overlying strata is γ = 23.6 kN/m3, the chamber width is wm = 2.0 m, the chamber height is h = 2.5 m, the mining depth is 100 m, the cohesion is c = c0 = 0.30 MPa, the internal friction angle is φ = φ0 = 17.6°, and the compressive strength of the web pillar is σc = 17.66 MPa. Substituting these parameters, along with the depths and retaining pillar widths provided in Table 11, into Eqs. (31) and (21), the yield zone widths at each side of the web pillars and the instability criteria of the web pillars under different slope angles and mining depths are as displayed in Table 12. It can be seen that the instability criteria for the retaining pillar widths are all greater than zero (Δ > 0), implying that the web pillars are in a stable state. Therefore, the designed web pillar widths are reasonable.

Table 12 Instability criteria for coal pillar widths under different slope angles and mining depths
Full size table

6 Conclusions

  1. (1)

    From the modeling results, the maximum abutment stress in the web pillar along the pillar strike direction is located somewhere ahead of the web pillar towards the maximum mining depth, and the abutment stress distribution along the dip direction is approximately bowl-shaped. By combining the relationship between the abutment stress and the ultimate strength of the web pillar with the failure characteristics of the yield zone, the instability mechanism of the web pillar has been revealed. Specifically, when the abutment stress of the web pillar is greater than its ultimate strength, shear failure occurs. Based on the characteristics of the abutment stress distribution and the yield zone distribution, it is possible to design and evaluate the retaining widths of the web pillars.

  2. (2)

    According to the characteristics of the abutment stress distributions, a mechanical bearing model of the web pillar has been established. An equation describing the coal pillar load under different slope angles, mining depths, and pillar widths was established by fitting numerical data to a mathematical expression. Based on cusp catastrophe theory, a pillar-overburden model was constructed, and the sufficient and necessary conditions for the web pillar instability were derived.

  3. (3)

    Using the mechanical model of the chamber and surrounding rock established in this study, the formula for calculating the yield zone width, considering the width of the chamber either side of the web pillar, was obtained. This formula can be used in combination with the instability criterion of web pillars to validate the rationality of the designed pillar widths and provide theoretical guidance on safe mining operations and high recovery efficiency in open-pit highwall mining.