1 Introduction

Permeability of coal reservoirs reflect the flow performance of fluids such as coal gas in coal seams and it is important for the simulation and identification of fluid systems in coal seams (Harpalani and Schraufnagel 1990).

It is important to understand the factors that influence coal permeability for the successful exploration of coalbed methane. Therefore, many studies have been conducted on factors that control coal permeability such as fissures, coal rank, fracture aperture, geological structures, and stress on strata (Shen et al. 2010; Shi et al. 2018a, b; Zhang et al. 2019). Cracks are the main channels for the transport of gas, brine, and other fluids in coal. Cracks in coal are classified as exogenous and endogenous (Gamson et al. 1993; Yao and Liu 2009). Endogenous cracks occur due to the shrinkage in coal volume and internal tensions in coal caused by the influence of temperature and pressure during coal formation. Exogenous cracks are formed by tectonic structures such as faults and folds (Yao et al. 2014). In a previous study, micron-level cracks were studied using micro-CT scanning and fractal theory, and the results showed that micro-crack networks in coals of low ranks have good connectivity and as the rank of coal increases its micro-crack structure becomes more complex (Shi et al. 2018b). As an organic-rich dual-porosity medium, the permeability of coal undergoes a unique evolution because of adsorption/desorption. Unlike elastic strain, sorption-induced strain displays a non-linear behavior with continuously sorbing gas injections, and both types of strains are competing processes in causing the volumetric change in coal (Fan and Liu 2018). Coal’s permeability is related to effective stress and the mechanism of stress loading and unloading. The average permeability damage of a coal specimen is more sensitive to the maximum loading stress and the loading–unloading path compared to gas-injection pore pressure and holding period. Gas-adsorption induced swelling significantly reduces initial permeability and average permeability damage during cyclic loading (Fan and Liu 2019).

Geological structures have major influences on the permeability of coal. The permeability of coal near a fracture zone of a tensile structure is larger than that in a fracture zone where stress is concentrated (e.g., the high-pressure area squeezed between tectonic movement and thrust nappe structure). The permeability gradients of coal reservoirs in the Shanxi Formation are controlled by the principal stress exerted by the tectonic stress field (Qin et al. 1999). Shi et al. (2018a) conducted coal permeability measurements under constant confining pressure and effective stress and showed that it evolves due to expansion and contraction that are induced by adsorption, instantaneous effective stress, and matrix–fracture interactions. The relationship between coal permeability and pressure sensitivity was studied using coal samples collected from the Xinyuan coal mine in Yangquan city. The study showed the following: (1) permeability of coal exhibits anisotropy, (2) permeability along the strike of the coal seam is higher than that along the direction of propensity (Wang et al. 2018). These observations indicate that coal permeability is highly sensitive to stress anisotropy. Shen et al. (2010) used structural curvature to describe the undulating form of coal seams and analyzed its influence on permeability. They also calculated structural curvature based on contours of the floor of the No. 3 coal seam of the Shanxi Formation in the Qinshui Basin and showed that it is negatively correlated with coal reservoir pressure and positively correlated with coal permeability. These studies analyzed the effect of geological factors on permeability and provided guidance for further analysis.

Observation data containing multiple variables are required to understand the effects of geological influencing factors on coal permeability. Large multivariate data sets can provide a wealth of information for this study. More importantly, in many cases, there may be correlations among various geological factors, thereby increasing the complexity of the analysis. The complex sets of information in the multivariate data sets cannot be fully utilized by analyzing each geological factor separately. Therefore, the reduction of factors without reasoning will lead to the loss of useful information, resulting in erroneous conclusions. Principal component analysis (PCA) is an algorithm for dimensionality reduction, which eliminates redundant indicators, and at the same time, minimizes the loss of information. The principal components are orthogonal to each other. Therefore, each principal component can represent a geological control mode. Our study aims to analyze the relationships between geological factors and coal permeability in the Sihe coal mine. We tested the permeability of coal in the Sihe coal mine. Other parameters such as porosity, structural curvature, and vitrinite reflectance of the coal samples obtained from the Sihe coal mine were also measured. Subsequently, the relationships between the coal parameters on the permeability of coal were analyzed. PCA was employed to understand the factors controlling the permeability of coal.

2 Coal sample preparation of Sihe coal mine

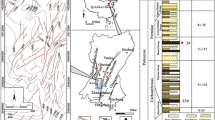
In this study, anthracite coal samples were collected from the Sihe coal mine, which is located on the No. 3 coal seam of the Lower Permian Shanxi Formation in Jincheng city, Shanxi Province.

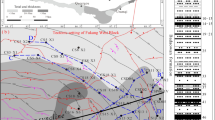
Figure 1 displays the contour map of the No. 3 coal seam in the west mining area based on seismic data. The No. 3 coal seam has folds in the axial direction of NNE. The anticline is located in the western part of the zone with an NNE-trending axis, the two limbs are basically asymmetrical, the inclination of the western limb is 6°–10°, the inclination of the eastern limb is slightly greater at 7°–14°. The syncline is located in the eastern part of the zone; the axis trends close to NE, the inclination of the two limbs is 6°–9°. There are nineteen faults in the fold. A total of 12 coal samples were taken from the No. 3 coal seam. The samples were protected with plastic wrap to ensure that they are not exposed to the air and to prevent damage during transportation. The distance between the sampling point and the nearest fault can be calculated from the map.

Fig. 1
figure 1

Contour map of the floor of the No. 3 coal seam and distribution of sampling positions

Full size image

3 Principal component analysis

The goal of PCA is to recombine initial variables with a certain correlation into a new set of unrelated comprehensive variables (principal components) to replace the original variables. Studying a certain problem involves many variables; if there is a correlation between these variables, then there must be one or more common factors that dominate the data. Based on variable covariance or correlation matrices, original variables are combined to form comprehensive variables (principal components) (Makinde and Lee 2019). These comprehensive variables play a critical role in simplifying the problem while preserving the main information of the original variables, thereby making it easier to understand the main contradictions when studying complex problems (Lam et al. 2020; Mao et al. 2018).

3.1 Theory of principal component analysis

Assume that there are n random variables X1, X2, …, Xn; the n-dimensional random vector is \({\varvec{X}} = \left( {X_{1} ,X_{2} , \ldots ,X_{p} } \right)^{\prime}\); the mean value of the random vector X is μ; and the covariance matrix is ∑. PCA is used to express these n random variables as n new comprehensive random variables F1, F2, …, Fn through linear transformation as follows:

$$\left\{ {\begin{array}{*{20}c} {F_{1} = a_{11} X_{1} + a_{12} X_{2} + \cdots + a_{1n} X_{1n} } \\ {F_{2} = a_{21} X_{1} + a_{22} X_{2} + \cdots + a_{2n} X_{2n} } \\ \cdots \\ {F_{n} = a_{n1} X_{1} + a_{n2} X_{2} + \cdots + a_{nn} X_{nn} } \\ \end{array} } \right.$$
(1)

Equation (1) can be expressed in the matrix form as follows:

$${\varvec{F}} = {\varvec{AX}},$$
(2)

where \({\varvec{F}} = \left( {F_{1} ,F_{2} , \ldots ,F_{n} } \right)^{\prime}\) and \({\varvec{A}} = \left( {\begin{array}{*{20}c} {a_{11} } & \ldots & {a_{1n} } \\ \vdots & \ddots & \vdots \\ {a_{n1} } & \cdots & {a_{nn} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {{\varvec{a}}_{1}^{\prime} } \\ {{\varvec{a}}_{2}^{\prime} } \\ \cdots \\ {{\varvec{a}}_{n}^{\prime} } \\ \end{array} } \right)\).

Since the linear transformation of Eq. (1) can be arbitrarily performed on the original variables, comprehensive variables F1, F2,…, Fn that are obtained through different linear transformations are also different. Therefore, for better linear transformation, Fi (i = 1, 2,…, n) should be mutually independent, and the variance of Fi (i = 1, 2,…, n) should be as large as possible.\(D\left( {F_{i} } \right)\) represents the variance of Fi and is expressed as follows:

$$D(F_{i} ) = D({\varvec{a}}_{i}^{\prime } {\varvec{X}}) = {\varvec{a}}_{i}^{\prime } \sum {\varvec{a}}_{i} .$$
(3)

However, it is not enough to limit the maximum variance, because for any constant \(c\), there is

$$D(c{\varvec{a}}_{i}^{\prime } {\varvec{X}}) = c^{2} {\varvec{a}}_{i}^{\prime } \sum {\varvec{a}}_{i} .$$
(4)

Therefore, if there is no restriction on a, and D(Fi) is changed arbitrarily, the problem cannot be clarified. Therefore, linear transformation is constrained by the following principles:

  1. (1)

    \({\varvec{a}}_{i}^{\prime} {\varvec{a}}_{i} = 1\), i.e., \(a_{i1}^{2} + a_{i2}^{2} + \cdots + a_{in}^{2} = 1(i = 1,2, \ldots ,n)\);

  2. (2)

    Fi is not related to Fj, i.e., \(Cov(F_{i} ,F_{j} ) = 0(i,j = 1,2, \ldots ,n;i \ne j)\);

  3. (3)

    F1 is the largest variance among the linear combinations of X1, X2,…, Xn that satisfy Eq. (1); F2 is the largest variance of all linear combinations of X1, X2,…, Xn that are not related to F1; Fn is has the largest variance among all linear combinations of X1, X2,…, Xn that are not related to F1, F2,…, Fn–1.

Based on these three principles, the integrated variables F1, F2, …, Fn are the first, second, …, and n-th principal components of the original variable, respectively. Equation (3) sequentially decreases the proportion of each principal component in the total variance. In practical problems, the principal components with the largest variances can be selected to replace the original variables. These new comprehensive variables are composed of multiple old variables; thus, they represent the controlling effect of the variables (Du and Du 2018; Ha et al. 2017).

3.2 Geometric meaning of principal component analysis

From an algebraic point of view, PCA is a special linear combination of n random variables X1, X2,…, Xn. From a geometric point of view, these linear combinations are obtained by rotating the coordinate system of the original variables X1, X2,…, Xn by a certain angle to obtain a new coordinate system. In the new coordinate axis, the maximum possible original variable information (with the largest variance) is included. For example (to illustrate the principle), there are n samples, and each sample has two observed random variables (X1 and X2). The distribution of n samples is in the ellipse form as shown in Fig. 2.

Fig. 2
figure 2

Geometric interpretation of principal component analysis

Full size image

Figure 2 shows that n samples have greater dispersion along the X1 or X2 axis direction, and the degree of dispersion can be quantitatively determined by the variance of variables X1 and X2. If only one of the two variables is considered, then the information in the original data will have a greater loss, which implies that X1 and X2 jointly express the information in the original data. Both are essential when analyzing problems with X1 and X2. However, through a certain linear combination, the original data can be characterized by new variables F1 and F2. In geometrical terms, the coordinate axis is rotated counterclockwise by an angle of θ to obtain new coordinate axes F1 and F2. The coordinate rotation formula is as follows:

$$\left\{ {\begin{array}{*{20}c} {F_{1} = X_{1} \cos \theta + X_{2} \sin \theta } \\ {F_{2} = - X_{1} \sin \theta + X_{2} \cos \theta } \\ \end{array} } \right.$$
(5)

The matrix form is expressed as follows:

$$\left( {\begin{array}{*{20}c} {F_{1} } \\ {F_{2} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\cos \theta } & {\sin \theta } \\ { - \sin \theta } & {\cos \theta } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {X_{1} } \\ {X_{2} } \\ \end{array} } \right) = {\varvec{AX}}$$
(6)

where A is the rotation transformation matrix; A is an orthogonal matrix, i.e., \({\varvec{A}}^{\prime} = {\varvec{A}}^{ - 1}\).

A new coordinate system was obtained after rotation, as shown in Fig. 2. The n samples have more dispersion in the direction of the F1 axis indicating that variable F1 contains more information. If variable F2 is not considered, there will be no loss of the original variable information. Therefore, after the rotation transformation, the information in the original variables can be concentrated on the F1 axis, which condenses the information in the data and facilitates analysis. From a geometric point of view, PCA is the rotation process of the coordinate system. The direction of the coordinate axis of each principal component is the direction with the largest degree of dispersion, capturing most of the original variable information (Tran et al. 2019).

4 Analysis of the influence of geological factors on permeability

Tests for porosity, permeability, isothermal adsorption, fracture aperture, and vitrinite reflectance were performed on 12 coal samples collected from the No. 3 coal seam in the Sihe mining area. The test results are presented in Table 1. Porosity was measured using a Coberly–Stevens porosimeter. Permeability was measured by the transient method using nitrogen. Standard nitrogen gas adsorption–desorption measurements using liquid nitrogen at a temperature of 77.4 K were performed on the coal samples. Surface area of each adsorbent was determined using the Brunauer–Emmett–Teller (BET) plot of nitrogen adsorption data. The Frenkel–Halsey–Hill (FHH) model usually uses low-temperature liquid nitrogen adsorption data to obtain the pore fractal dimension of coal. Vitrinite reflectance of these samples was measured using a DM4500P polarizing microscope photometer. Structural curvature was calculated from the contours of the floor of the No. 3 coal seam. Based on these results, the controlling effects of porosity, structural curvature, vitrinite reflectance, and pore structure of coal on permeability were studied. Using the results of the PCA, the mode of control of geological factors on coal permeability was elucidated.

Table 1 Test results of coal samples
Full size table

4.1 Relationship between porosity and permeability

To study the effect of porosity on permeability, the Kozeny–Carman (KC) equation was used as a porosity–permeability model. The KC equation has been widely used for studying porous media such as sand, mudstone, soil, and oil and gas reservoirs, and is expressed as follows:

$${{k}} = C_{\text{kc}} \frac{{\phi^{3}}}{{\left( {1 - \phi } \right)^{2} }} = \frac{c}{{\left( {8a_{v}^{2} \tau } \right)}}\frac{{\phi^{3} }}{{\left( {1 - \phi }\right)^{2} }}$$
(7)

where, k is the permeability; \(\phi\) is the porosity; c is introduced as an empirical geometric parameter; \(a_{v}\) is the ratio of exposed surface to solid volume; and \(\tau\) is the tortuosity, which is defined as the square of the ratio of the effective channel length \(Le\) to the length \(L\) of the porous body \(({\tau } = (Le{/}L)^{2})\). Because it is not easy to directly measure tortuosity \(\tau = (Le{/}L)^{2}\), it is common to use the conductivity measured for the same rock saturated with an electrolyte solution as an analogy. For this, we used the following equation:

$$F = (Le{/}L)^{2} {/}\phi .$$
(8)

The ratio F is called the formation factor, and the value of F is the same as that in the Archie formula:

$$F = b/\phi^{m}$$
(9)

where b is an empirical factor (0.6 < b < 2), and m is the cementation index or tortuous factor (1 < m < 4).

Equations (8) and (9) were combined to obtain (10) (Bayles et al. 1989):

$$k = \frac{c}{{8a_{v}^{2} }}\frac{{\phi^{2 + m} }}{{\left( {1 - \phi } \right)^{2} }}$$
(10)

where all the components represent the same factors as those given above.

Equation (10) expresses the relationship between permeability and porosity. This equation contains only two parameters (c and m). If the semi-empirical constant \(c\) and cementation index m are determined, the model can be used to predict permeability. Parameters c and m can be determined by minimizing the standard deviation \(\sigma\) of the regression, which is expressed as follows:

$$\sigma^{2} = \frac{1}{N - P}\mathop \sum \limits_{j = 1}^{N} W_{j} [Y_{j} (exp) - Y_{j} (calc)]^{2}$$
(11)

where, \(W_{j}\) is the weighting factor; \(P\) is the number of parameters; N is the number of data points, and \(Y_{j} (exp)\) and \(Y_{j} (calc)\) represent measured and calculated values, respectively.

The improved KC equation model was used to fit the porosity and permeability of 12 coal samples (Fig. 3). Case 1 represents the fitting situation of all samples, while Case 2 is the fitting situation after the removal of SH2 and SH6 samples. The correlation coefficients between permeability and porosity were 0.18 and 0.68 in Case 1 and Case 2, respectively. The permeability of coal increased with increasing porosity. The low correlation coefficient indicated that permeability was affected by many factors and not by porosity alone.

Fig. 3
figure 3

Fitting curve of coal porosity and permeability based on the extended KC equation

Full size image

4.2 Relationship between structural curvature and permeability

Structural curvature that affects coal permeability is caused by the tectonic force field, which can accurately reflect the degree of crack development due to the tensile stress in curved rock layers (Liu et al. 2015; Cao et al. 2020). Figure 4 shows the curvature descriptions of anticline, syncline, monocline, and flat layers. In the context of the geological structure, the curvature of the anticline is positive, that of the syncline is negative, and those of the plane and monoclinic systems are 0. In a two-dimensional space, for any surface S, the curvature can be uniquely determined by z = f (x, y), and the principal curvature at point P can be determined using Eq. (12).

$$K_{1} ,K_{2} = \frac{1}{2}(r + t) \pm \sqrt {\frac{1}{4}(r + t)^{2} + s^{2} }$$
(12)

where \(r = \frac{{\partial^{2} f}}{{\partial x^{2} }}\;{\text{and}}\;S = \frac{{\partial^{2} f}}{\partial x\partial y}.\) The parameters r, s, and t are obtained via the difference method.

Fig. 4
figure 4

Geological folds and their curvatures

Full size image

The curvature of the sampling point (Table 1) was calculated using the contours of the floor of the coal seam (Fig. 1). The relationship diagrams of structural curvature, permeability, and porosity are displayed in Fig. 5. Figure 5a shows the relationship between structural curvature and porosity. The porosity at the anticline (structural curvature value > 0) was relatively skewed. As structural curvature values of synclines approached zero, porosity values increased. This shows that structural curvature has a significant effect on coal porosity in the No. 3 coal seam, an effect which increased and decreased at anticlines and synclines, respectively.

Fig. 5
figure 5

Interaction of permeability with structural curvature and porosity. a the relationship between structural curvature and porosity, b the relationship between structural curvature and permeability, c the relationship between porosity and permeability at an anticline, d the relationship between porosity and permeability at a syncline

Full size image

However, structural curvature did not always increase at anticlines. When structural curvature reached a certain level, porosity showed a downward trend probably because as structural curvature increased, pores in coal are filled with minerals. Fig. 5b shows the relationship between structural curvature and permeability. Figure 5b shows that permeability of coal at the syncline was low, and the sensitivity to structural curvature was weak. Figure 5c, d show the relationship between porosity and permeability at an anticline and a syncline, respectively; coal porosity and permeability were strong in both. Coal reservoir permeability is related to coal seam fissures and in situ stress, while the geological structure is an underlying factor that controls these two factors.

4.3 Relationship between vitrinite reflectance and permeability

With the gradual increase in average vitrinite reflectance, the permeability of the No. 3 coal seam tended to first decrease and then increase. The permeability of coal was the minimum at an average vitrinite reflectance of 2.86%. Figure 6 shows the relationship between average vitrinite reflectance and permeability, after excluding the samples that were collected near faults (SH-2, SH-3, and SH-6). Combined with the analysis of geological data, we observed that average vitrinite reflectance of coal was below 2.86%, coal had a shallow burial depth, and pressure in the reservoir was relatively small. With the increase in burial depth, a higher degree of coal metamorphism was manifested by a higher vitrinite reflectance; the pressure of the formation increased, the level of coalification increased, coal macromolecular functional groups contracted, carbon content increased, and moisture and permeability decreased. However, when the average vitrinite reflectance was greater than 2.86%, the evolution continued and the coal generated lighter hydrocarbons (Yu et al. 2020); further, the number of micropores and small pores gradually increased, causing an increase in the permeability of coal.

Fig. 6
figure 6

Relationship between average vitrinite reflectance and permeability

Full size image

4.4 Relationship between pore structure characteristics and permeability

Many classification schemes for pore structures are available as they vary widely in different types of coals. This study employed the International Union of Pure and Applied Chemistry (IUPAC) classification system, in which pores are divided into large pores (> 50 nm), mesopores (2–50 nm), and micropores (< 2 nm). A static liquid nitrogen adsorption instrument (JW-BK122F) was used to test the pore structures of coal samples using low-temperature liquid nitrogen.

The low-temperature N2 adsorption/desorption isotherms of the coal samples are shown in Fig. 7. The adsorption loops of the coal samples were of type A, which displays a distinct hysteresis loop that develops as capillary condensation occurs in the mesopores indicating that the coal samples had many mesopores. The pores were cylindrical, and the pore shape was open. The loop characteristics of SH-2 and SH-6 were similar, but not precisely like the B-type of the IUPAC classification.

Fig. 7
figure 7

Low-temperature N2 adsorption/desorption isotherms of the coal samples

Full size image

SH-2 and SH-6 presented characteristics of an AB-type hysteresis loop, which was a comprehensive reflection of the true shape of pores of the samples. This indicated that SH-2 and SH-6 coal samples had fractured and cylindrical pores.

The pore shape of the coal samples was irregular, and the pore sizes were also different. The pore shape was characterized by pore volume distribution parameters in different pore size ranges from which the pore size distribution can be calculated based on isothermal adsorption data. Figure 8 displays the distribution of pore volumes and sizes of the 12 samples using the Barrett–Joyner–Halenda (BJH) pore size method. Pore sizes of the samples were approximately 2–8 nm, indicating the development of many mesopores and micropores in the coal samples. Macropores were less developed.

Fig. 8
figure 8

Pore volume–pore size differential distribution in coal samples

Full size image

Figure 9 displays the histogram of pore volume distribution based on the IUPAC classification. The pore volumes of 12 coal samples were dominated by mesopores (pore diameter was 2–50 nm), except for in SH-2 coal sample. As the SH-2 coal sample was dominated by fracture-shaped pores generated by stress fracturing, the proportion of large pores exceeded that of micropores. The pore size distributions of the remaining 11 coal samples were studied based on the volume of micropores (pore diameter < 2 nm) and the largest pores (pore diameter > 50 nm). Meso-, large and micro- pore volumes accounted for 71.38%, 18.17%, and 10.45%, respectively.

Fig. 9
figure 9

Histogram of pore volume distribution based on the IUPAC classification

Full size image

Fractal geometric features can characterize the pore structure and surface irregularities of porous materials. According to the FHH model, the fractal dimensions of the coal samples were obtained from low-temperature N2 adsorption data. Table 1 shows that the FHH fractal dimensions were between 2 and 3 in all coal samples. The fractal dimensions of SH-2 and SH-6 are 2.51 and 2.49, respectively, which are larger than those of the other coal samples. Their corresponding BJH adsorption, average pore size, and porosity values were also higher, indicating higher permeability compared to other coals. A larger average pore diameter of coal implies higher fractal dimension (more complex pores of coal), higher porosity, better connectivity of pores, and thus higher permeability. The other 10 samples had lower fractal dimensions, smaller pore sizes, and less developed pores, resulting in poor connectivity and low coal permeability.

Linear correlation analyses between permeability and pore structure parameters were carried out and are shown in Fig. 10. Average pore size had the highest correlation coefficient with permeability followed by the most probable pore size, fractal dimension, and specific surface area. This analysis shows that, in the study area, within the average pore size range of 5–13 nm, as the pore size increases, permeability increases.

Fig. 10
figure 10

Linear regression relationship between pore structure and permeability

Full size image

4.5 Principal component analysis of permeability control modes

Although factors that affect permeability of coal are complex, it is important to understand its controlling factors for practical applications. The analysis thus far has indicated that each factor is related to permeability but no individual factor controls it. For example, a close relationship exists between porosity and permeability. However, the correlation coefficient between permeability and porosity is low indicating that permeability is also affected by other factors. Similar findings on the influence of other geological factors on permeability were obtained. Various degrees of correlation exist between these factors; thus, analyses considering these variables individually may introduce redundancy.

The PCA method can transform a group of potentially correlated variables into a group of linearly uncorrelated variables through orthogonal transformation, thus allowing us to identify the primary mode controlling permeability. In PCA, groups of linearly independent attributes comprise the components, and the contribution of an attribute to each principal component is different. Therefore, this study considered coal porosity, structural curvature, vitrinite reflectance, specific surface area, and fractal dimensions to identify principal component modes that control coal permeability.

The properties of the coal samples measured in the experiment are summarized in Table 1. IBM SPSS software was used for the PCA. The coal parameter data were standardized, and then, principal components were determined. We obtained the eigenvalues of the correlation coefficient matrix and their corresponding contributions to variance (Table 2). The variance contribution of the first principal component was 52.585% (the highest among the components), and the cumulative contribution of the variance of the first three principal components was 84.7%. Therefore, the first three principal components largely explain the variance in the data, and thus, three main modes of permeability control are present in the study area.

Table 2 Eigenvalues of the correlation coefficient matrix and their corresponding contributions to variance
Full size table

Table 3 presents the calculated coefficient score matrix of the components. The absolute value of coefficient score has a directly proportional relationship with the degree of influence of a variable on a principal component. BJH adsorption–based average pore size, depth, and fractal dimensions are the top three variables within the first principal component. These variables involve pore diameter and complexity of coal pore structure, indicating that they have the highest influence on coal permeability.

Table 3 Scores of the first, second, and third principal components for different variables
Full size table

Correlation analysis of permeability and PCA results showed that correlation coefficients were 0.711 between permeability and the first principal component, 0.072 between permeability and the second principal component, and 0.01 between permeability and the third principal component. The correlation coefficient between permeability and the first and second principal components is 0.751; the correlation coefficient between permeability and the first and third principal components is 0.714; the correlation coefficient between permeability and the second and third principal components is 0.074, and the correlation coefficient between permeability and the first, second and third principal components is 0.754. The results indicate that permeability is controlled by the first principal component. According to the previous analysis, the major geological factors in the first principal component are pore size, depth, and fractal dimension. Based on the KC equation, the correlation coefficient between porosity and permeability is 0.18, which is relatively low. However, after removing the two sample points near the fault structure, the correlation coefficient increases to 0.68. In addition to the correlation coefficient between permeability and the first principal component, the results show that the depth of burial influences pore connectivity and structure influences the complexity of pore shapes (characterized by fractal dimension). Therefore, pore size, burial depth, and fractal dimension are major factors controlling permeability.

The study area features high-rank coal. The coal sampled from the mines was black with a striped structure, black streaks, stepped fractures, and a glassy luster. In terms of abundance, bright coal was followed by dark coal, bright light coal, and simple coal seam structures. The coal was semi-hard, and the dominant gangue was mudstone. Thus, the influencing factors of coal permeability determined via PCA were consistent with the study area’s simple geological structure and relatively underdeveloped coal fractures.

In summary, the factors affecting coal permeability are multiple and diverse. The first, second, and third principal components represented different control modes of permeability. The influence of geological factors on permeability varied based on geological conditions. Overall, the main factors affecting permeability of coal were properties of the coal itself, such as the average pore size based on BJH adsorption, depth, and fractal dimensions.

5 Conclusions

This study examined the physical properties of 12 coal samples obtained from the No. 3 coal seam in the Sihe coal mine. Coal characteristics such as porosity, permeability, isothermal adsorption–based pore size, and vitrinite reflectivity were evaluated. Structural curvature was calculated based on the contour of the floor of the coal seam, and the pore fractal dimensions were calculated using the FHH model.

Geological factors influencing coal permeability characteristics were determined, and the main controlling factors were analyzed using PCA. The main conclusions are as follows:

  1. (1)

    Coal permeability and porosity were analyzed based on the porosity–permeability model derived from the Archie formula and the KC equation. Coal permeability increased with an increase in porosity (porosity increased from 8% to 16%, and permeability increased from 0.0012 to 0.018 md).

  2. (2)

    The effect of structural curvature on permeability was most evident when the curvature of the anticline structure was 0.015–0.030 m−1. Curvatures lower than 0.015 m−1 or higher than 0.03 m−1 were not conducive to high levels of permeability. As structural curvature increased from − 0.0239 to − 0.0068 m−1, permeability increased from 0.0008 to 0.008 md.

  3. (3)

    With a gradual increase in the average vitrinite reflectance, permeability tended to first decrease and later increase. The minimum permeability value was reached at an average vitrinite reflectance of 2.86%.

  4. (4)

    At the microscopic level, the degree of pore development can be characterized based on porosity and pore fractal dimensions. The greater the porosity, the more complex the pore structure. The higher the degree of micropore development, the better the connectivity of pores (permeability). On the other hand, the lower the porosity, the lower the degree of pore development. The more uniform the pore size, the lower the permeability.

  5. (5)

    The control mode of coal permeability in the Sihe coal mine was analyzed using PCA. The data were divided into three principal components. Since each principal component is a combination of multiple geological factors, the principal components are orthogonal to each other, each representing a permeability control mode. The first principal component represented the influence of pore size, burial depth, and pore complexity on permeability. The second principal component represented the influence of specific surface area, structural curvature, and porosity. The third principal component included specific surface area, porosity, and average vitrinite reflectance. In general, pore diameter and pore complexity of coal had a major impact on its permeability.

The results of the present study, which explored factors influencing coal permeability, suggest that researchers and stakeholders in the coal industry need to consider not only distinct properties but also interactions among multiple properties of coal. The results of the present study could facilitate the efficient utilization of coalbed methane resources.