1 Introduction

Retractable adaptive pier columns offer a new way to support a roadway. The filler material used is compressible and can be adapted to a given deformation caused by the overall subsidence of the overburden (Qian et al. 2003; Jia et al. 2014; Guo et al. 2018; Jack et al. 2019). The advantages are simple manufacturing technology, low economic cost, and high early support strength at the support site. Moreover, the rapidly increasing resistance offers good lane retention (Wang et al. 2015; Li et al. 2015; He et al. 2017; Ju et al. 2019). However, since the pier column is made of two nested steel tubes, it is relatively long and thick. Under the continuous roof load, the central lap position of the pier column is prone to bending failure due to eccentric pressure, as shown in Fig. 1. Local instability of the pier column leads to insufficient bearing capacity, and the shrink quantity cannot meet the pressure relief requirements. Therefore, it is necessary to improve and reinforce the vulnerable points of the structure.

Fig. 1
figure 1

Characteristics of pier column failure on site

Full size image

To date, there has been much beneficial research on the strengthening of concrete-filled steel tube (CFST) structures. To improve the structural bearing capacity, Dong et al. proposed using steel tubes filled with concrete reinforced by carbon-fiber-reinforced polymer (CFRP) (Dong et al. 2013; Ganesh and Sundarraja 2013; Park and Choi 2013). They analyzed the structural composition and mechanical mechanism theoretically, and a comparative test of the bearing capacity showed its superiority. Li et al. (2012) and Hassanein et al. (2013) proposed a strengthening measure of outer bread steel pipe to enhance the bearing capacity of a CFST. Referring to the common reinforcement methods of CFST columns, such as pasting CFRP, outer bread steel pipe method, enlarged section strengthening method and so on, CFRP has high tensile strength and favorable fatigue resistance, but its disadvantages include anisotropy, poor shear strength, and high price. External steel reinforcement is more suitable for shorter CFST columns, but the construction process is complex.

In this paper, a stiffener ring (SR) is set up in the plastic hinge area in the middle of the pier column, and an axial compression test is carried out. Comparing the failure modes of the pier column before and after stiffening shows how the mechanical properties of the pier column change after stiffening. Finally, finite-element (FE) analysis is used to optimize the parameters of the stiffener and select the optimal stiffener size suitable for the pier column. This method is simple in operation, flexible in strengthening position, and low in cost, thereby helping to minimize pipe buckling and increase the overall stability. Furthermore, it provides a reference for the stiffening design of collapsible pier columns for mines, which should help to further the popularity and applicability of collapsible pier columns.

2 Experiment

2.1 Analysis of stiffening form and reinforcing mechanism of pier column

As a pier column is essentially a CFST, when it bears an axial load, the steel tube provides transverse constraint for the internal filling material so that the latter is in a state of three-way stress, thereby improving its bearing capacity. Meanwhile, as the internal filling material is compressed and expands, the steel pipe is subjected to the reaction of the radial stress of the internal filling material while providing constraints, thereby limiting its own deformation and delaying buckling. The steel pipe of the pier column is composed of two nested steel pipes. The outer radius of the upper steel tube is φ351 mm × 8 mm, and the inside radiu is 339 mm; the outer radius of the lower steel tube is φ325 mm × 8 mm, and the inside radius is 309 mm. Thus, the steel tube can be regarded as a thin-walled cylinder (Guo et al. 2013a, b). The section of which is shown in Fig. 2. From the formula for calculating the stress of a thin-walled cylinder, we have

$$\sigma_{r} = \frac{{a^{2} }}{{b^{2} - a^{2} }}\left( {1 - \frac{{b^{2} }}{{r^{2} }}} \right)p_{\text{i}} - \frac{{b^{2} }}{{b^{2} - a^{2} }}\left( {1 - \frac{{a^{2} }}{{r^{2} }}} \right)p_{0}$$
(1)
$$\sigma_{\theta } = \frac{{a^{2} }}{{b^{2} - a^{2} }}\left( {1 + \frac{{b^{2} }}{{r^{2} }}} \right)p_{\text{i}} - \frac{{b^{2} }}{{b^{2} - a^{2} }}\left( {1 + \frac{{a^{2} }}{{r^{2} }}} \right)p_{0}$$
(2)

where a is the inner radius, b is the outer radius, r (a < r<b) is any radius, pi is the internal pressure, p0 is the external pressure, and t is the thickness of the steel tube.

$$\sigma_{\theta {\text{max}}} = \sigma_{\theta r - a} = \frac{{b^{2} + a^{2} }}{{b^{2} - a^{2} }}p_{\text{i}}$$
(3)

where pi is the internal pressure, \(p_{\text{i}} = k q = \left( {1 - \sin \theta } \right) q\),where k is the coefficient of lateral pressure (\({k} = 1 - \sin \theta\))

$$\sigma_{\theta {\text{max}}} = \frac{{b^{2} + a^{2} }}{{b^{2} - a^{2} }}(1 - \sin \theta ) q = f_{y}$$
(4)
$$q = \frac{{f_{y} \left( {b^{2} - a^{2} } \right)}}{{b^{2} + a^{2} }} \cdot \frac{1}{1 - {\text{sin}}\,\theta } = \frac{{f_{y} \left( {b + a} \right)t}}{{b^{2} + a^{2} }} \cdot \frac{1}{1 - {\text{sin}}\,\theta }$$
(5)

According to Eq. (5), when the inner radius of the steel pipe is fixed, the ultimate bearing capacity of the thin-walled cylinder can be improved by increasing its outer radius, which means adding lateral constraints to the outer wall of the steel pipe. When local buckling or expansion occurs, the reserved additional lateral constraints and the gap between the steel tubes are gradually eliminated. At this time, the existence of additional transverse constraints subjects the steel pipe to its radial stress, thereby putting the internal filling material into a more effective three-way stress state and improving the mechanical performance of the steel pipe and the internal filling material. At the same time, by setting additional transverse constraints, the section stiffness of the steel pipe in the restrained part changes before and after buckling, thereby improving the plastic deformation capacity of the specimen, delaying the buckling failure of the steel pipe, and improving the ultimate bearing capacity of the specimen (Xiao and He 2003). Figure 3 shows the stress state of the specimen, from which it can be seen that the additional constraints have no effect on the deformation of the steel tube before it bends. As long as the reserved void disappears because of the buckling deformation of the steel pipe, the additional constraints will come into play, thereby limiting the transverse deformation of the steel pipe. Because the additional constraint is only applied to the middle of the specimen and the lower section is on the free face, the vertical load cannot be transferred. Therefore, the additional constraint is in the state of bidirectional stress, that is, it bears the circumferential stress while receiving the radial compressive stress transferred from the steel pipe. The stress state in both directions is similar to that of the steel pipe.

Fig. 2
figure 2

Schematic of sections of steel pipe

Full size image
Fig. 3
figure 3

Additional lateral restraint mechanism of pier column

Full size image

Referring to the common reinforcement methods for existing long CFST columns, an effective way to avoid premature local buckling of the steel tube is to increase the lateral additional constraint of the CFST column and improve the flexural and compressive strength of the steel tube by locally setting a stiffening steel casing on the outside of the steel tube (Xiao and He 2003). Therefore, in view of the buckling failure of the steel pipe at the pier-column lap joint, combined with the construction convenience and cost saving, the present paper proposes the reinforcement measure of setting an SR in the plastic hinge area in the middle of the pier column. The size of the SR can be determined by referring to the strengthening provisions of the axial force members in the technical specification for steel structure reinforcement (Guo et al. 2013a, b). To meet the requirements of the net cross-sectional area of the members after reinforcement, the length of the SR is 150 mm and the thickness of the steel pipe wall is 8 mm.

2.2 Test plan design

The test is designed using a similarity model. The type of pier column used in the Wutongzhuang Mine in Hebei Province, China is taken as the prototype structure. The scale reduction ratio is approximately 1:3 and the total height of the model is designed to be 1.2 m. The size parameters of the prototype pier column and test model are given in Table 1. The SR is set on the outer surface of the steel pipe on the pier column. The size of the SR refers to the technical specification for steel structure reinforcement (GB 50017–2003 2003), which determines the length as 150 mm and the thickness of the steel tube wall as 8 mm. The axial compressive properties of unstiffened and stiffened pier specimens are tested and studied. The width of the SR is set as 40, 50, or 60 mm, and three parallel tests are conducted on the pier specimens of the same size, making a total of 12 groups. The specific stiffening is shown schematically in Fig. 4, and the sample numbers are given in Table 2.

Table 1 Dimensions of original structure and model
Full size table
Fig. 4
figure 4

Schematic of pier column

Full size image
Table 2 Specimen numbers and dimensions
Full size table

2.3 Specimen design and production

The steel pipe of the pier column is composed of two nested steel pipes. The upper and lower steel tubes are overlapped and the length of the upper and lower steel tubes is 700 mm, and the length of the overlapped part is 200 mm. The wall thickness of the steel pipe is 3 mm. The reinforcing ring and the steel pipe are fixed at the lower end of the upper steel pipe by means of interval spot welding. The steel tube specimens after lapping is shown in Fig. 5.

Fig. 5
figure 5

Lapped steel tube specimens

Full size image

Regarding the specimen pouring and curing, the filling material is placed on a vibrator to vibrate it fully. When filling, the upper pier column is fixed with a bracket, and a vibrating rod with a diameter of 3 cm is used to vibrate it fully. The specimen is maintained at room temperature for 14 d.

2.4 Test equipment and loading system

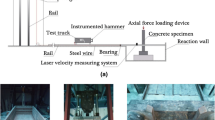
The test loading device is a YAJ servo hydraulic press produced by Zhubang Co., Ltd., with a maximum load of 1000 kN and a maximum loading displacement of 100 mm. The test device is shown schematically in Fig. 6 and physically in Fig. 7. The whole test process is conducted by the electro-hydraulic servo test system, and the test stress–strain data are collected in real time by the static strain data acquisition system on the computer. The specific parameters of the strain gauges are given in Table 3.

Fig. 6
figure 6

Schematic of test device

Full size image
Fig. 7
figure 7

Photograph of test equipment

Full size image
Table 3 Specifications of strain gauges used in experiment
Full size table

The loading method of this test adopts the combination of displacement control and force control. Before loading, a force load of 5 kN is preloaded on the specimen. Within the elastic range, force loading method is adopted and the loading speed is 0.05 kN/s. When the loading curve bends, the displacement loading mode is adopted, and the loading speed is 0.01 mm/s. When the loading curve shows a gentle trend, the displacement loading speed is adjusted to 0.008 mm/s, and the number of data collected is increased. The test is terminated when the bearing capacity of the specimen falls below 85% of the ultimate load.

The data collected by the test include load value applied by the loading machine, displacement value of the displacement meter, strain gauge strain value, etc. The vertical force exerted by the jack on the specimen is measured by the force sensor on the loading head of the servo hydraulic press. The vertical displacement and lateral deflection of the specimen are measured by a displacement meter. Four longitudinal and circumferential resistance strain gauges are affixed at 90° intervals to the parts on the outer surface of the steel tubes prone to local buckling. The positions and numbers of the displacement gauges are shown in Fig. 8, and the arrangement of the strain gauges is shown in Fig. 9.

Fig. 8
figure 8

Layout of displacement meters

Full size image
Fig. 9
figure 9

Arrangement of strain gauges

Full size image

2.5 Material properties

The test-piece steel pipe is a 3 mm thick seamless round steel pipe with material quality Q325B. Standard test pieces are selected to conduct a uniaxial tensile test on an electronic universal test machine. The uniaxial tensile test results are given in Table 4.

Table 4 Mechanical properties of steel
Full size table

The steel pipe is filled with sand, stone, hydrated lime and other materials. The filling quality refers to the mining pier columns. The quality ratio is sand:gravel:hydrated lime:water = 1:1.6:0.5:0.3. The average quality of each pier-column filling material is given in Table 5.

Table 5 Quality of pier filling material
Full size table

The technical requirements for the filling materials are that the sand should be medium sand in zone II, and no less than 15% of the sand should be able to pass through 0.315 mm sieve holes. When artificial sand is used, the stone powder content should not exceed 3%. Gravel is selected with a continuous gradation of 5–16.5 mm. The mud content (by mass) should not exceed 1%, and the mud content should not exceed 0.5%.

A grading sieve (5 mm, 16.5 mm) is used to sieve the coarse aggregate of the stone as the supporting material. Large particles are selected and removed manually so that the proportion of flaky particles in the test material does not exceed 10%. The principle of aggregate screening is based on the maximum diameter of the screening aggregate.

3 Test phenomenon

Because the macroscopic phenomena and failure modes of the specimens in each group of parallel tests are similar, only one of the specimens in each group is selected for analysis of the test phenomena.

3.1 A3: unstiffened specimen

In the initial loading stage, the vertical displacement of the specimen is large, the upper section of steel pipe has a significant downward displacement, and the specimen has no lateral deformation.

(1) When the load reaches 37.5 kN, the load–displacement curve shows a diagonal straight upward trend, and the transverse deformation of the steel pipe is small.

(2) When the load reaches 125 kN, the steel pipe begins to yield, especially the upper end of the lower section of steel pipe. There is an obvious lateral deformation, the diameter of the steel pipe becomes thicker. As the loading continues, the overall deformation of the specimen increases, and a large lateral deflection appears at the joints of the steel pipes.

(3) When the load reaches 162.5 kN, the vertical displacement of the specimen reaches approximately 31 mm, the load–displacement curve exhibits a descending section, the lateral deflection of the specimen increases sharply, and the upper end of the lower section of steel pipe exhibits an obvious bulge.

(4) When the load drops to around 130 kN, the test ends.

3.2 B1-2: 40-mm-wide stiffener ring

In the initial loading stage, the specimen is in the compaction stage and the vertical displacement is large.

(1) When the load reaches 50 kN, the sliding of the upper section of steel pipe slows down, and the specimen has no obvious lateral deformation.

(2) When the load reaches 150 kN, the diameter of the steel pipe becomes obviously thicker, and the lower section of steel pipe appears to yield. As the loading continues, the deflection of the middle part of the specimen grows.

(3) When the load reaches 182.5 kN, the vertical displacement of the specimen reaches approximately 34 mm, the load–displacement curve begins to fall, the bearing capacity of the specimen decreases, the overall structural deformation is large, and the upper end of the lower section of steel pipe has a larger lateral deformation.

(4) When the load drops to around 157.5 kN, the test ends.

3.3 B2-2: 50-mm-wide stiffener ring

With the application of the load, the specimen enters the compaction stage, the load–displacement curve shows a slowly rising trend, and the appearance of the specimen does not change.

(1) When the load reaches 50 kN, the vertical displacement of the specimen slows down. The load–displacement curve shows that the specimen is in the elastic compression stage at this time, and the lateral deformation of the steel pipe is not obvious.

(2) When the load reaches 175 kN, the specimen shows lateral bending at the joint of the steel pipes. As loading continues, the diameter of the steel pipe becomes thicker, the lateral deformation of the specimen is obvious, and the load–displacement curve enters the curved segment from the straight-line segment.

(3) When the load reaches 210 kN, the vertical displacement of the specimen reaches approximately 38 mm, the yielding of the steel pipe is obvious, the lateral deformation of the specimen increases continuously, and the bearing capacity of the specimen decreases gradually.

(4) When the load drops to around 177.5 kN, the test ends.

3.4 B3-3: 60-mm-wide stiffener ring

In the initial stage of loading, the vertical displacement of the specimen is large.

(1) When the load reaches 57.5 kN, the filling material is compacted, and the specimen enters the elastic compression stage. The lateral deformation is not obvious, and the vertical displacement increases slowly.

(2) When the load reaches 207.5 kN, lateral bending occurs at the joint of the specimen, the diameter of the steel pipe gradually becomes larger, local buckling occurs, the vertical displacement of the specimen decreases, but the lateral deformation is obviously increased.

As the lateral deflection of the specimen continues to increase, the buckling of the upper end of the lower section of steel pipe becomes obvious.

(3) When the load reaches 235 kN, the specimen reaches the ultimate load, the corresponding ultimate displacement is 44 mm, and the load–displacement curve appears to fall. As the lateral deflection of the specimen increases, the upper end of the lower section of steel pipe yields significantly.

(4) When the load drops to around 190 kN, the test ends.

4 Analysis of test results

4.1 Analysis of load–displacement curves

Figure 10 shows the load–displacement curve of each specimen. Combined with the test phenomena, it can be seen that the curve comprises the compaction phase, the elastic phase, the elastoplastic phase, and the plastic failure phase. The filling material of the pier-column specimen is a three-phase aggregate composed of sand-stone solid particles, pore water, and air. The stress generated by the external load in the filling material is transmitted mainly by the mutual contact between the sand and stone particles. This contact stress causes the solid particles of the sand to undergo extrusion deformation, thereby changing the strength of the solid particles of the filler.

Fig. 10
figure 10

Load–displacement curves

Full size image

In the initial stage of loading, the sand and stone inside the pier column are compressed and compacted, and the water is discharged, showing that the elastic modulus is gradually increasing. At this stage, the upper section of steel pipe is basically not involved in the force, and the load–displacement curve is slowly rising.

In the second stage, the filling material of the pier column has been compressed to a compact state. At this time, the pier column can be regarded as an elastic body obeying Hooke’s law, and the load–displacement curve exhibits linear elasticity and shows a straight upward trend.

In the third stage, when the loading reaches around 80% of the ultimate load, the steel pipe exhibits yield deformation locally, and the load–displacement curve increases in bending, the slope decreases, and the load increase becomes smaller.

In the fourth stage, the stress on the pier column reaches the ultimate strength, the load decreases with the increase of the displacement, and the load–displacement curve enters the descending segment. The sand and stone particles inside the pier are crushed under the joint action of the steel pipe and the axial pressure, the steel-pipe yield deformation is serious, and the bearing capacity of the pier column is reduced until it is destroyed. The setting of the SR increases the lateral restraint ability of the steel pipe to the internal filling material, delays the yield time of the steel pipe, and significantly increases the axial bearing capacity of the pier-column specimen.

4.2 Analysis of load–deflection curves

The load–deflection curve reflects the process of instability and failure of the specimen. The lateral deflection f in the middle of the specimen is calculated as

$$f = \varDelta - \left( {\varDelta_{1} + \varDelta_{2} } \right)/2,$$

where Δ is the displacement at the middle of the specimen, Δ1 is the displacement at L/6 along the specimen, and Δ2 is the displacement at 5L/6 along the specimen.

The overall variation of the load–deflection curve of each specimen is similar, as shown in Fig. 11. In the elastic phase, compared with the unstiffened specimens, the load–deflection curve shows a linear relationship and the linear slope of the stiffened specimens is larger, that is, the increase speed of the lateral displacement of the stiffened specimens is lower. In the elastic–plastic phase, the average lateral deflections of specimens A, B1, B2, and B3 decrease sequentially. When the critical load is reached, the horizontal section corresponding to the load–deflection curve of the stiffened specimen is shorter, and the lateral deformation of the specimen is not large. After the loading is completed, the ultimate deflection values corresponding to specimens A, B1, B2, and B3 are 28.69, 25.99, 23.15, and 18.72 mm, respectively. Compared with specimen A, the lateral deflection values of stiffened specimens B1, B2, and B3 decreased by 9.4%, 19.3%, and 34.7%, respectively.

Fig. 11
figure 11

Load–deflection curves

Full size image

The load–lateral displacement curve of specimens under different loads are plotted in Fig. 12, where the vertical coordinate is the relative height (h/L) between each measuring point and the bottom of the pier column, and the horizontal coordinate is the lateral deflection of the specimen at different positions during the loading process. It can be seen that during the loading process, the lateral deflection of each section of the specimen increases gradually, and the setting of the SR provides additional lateral constraints for the steel pipe. The lateral deformation of the specimen is constrained effectively, and the wider the SR, the better the lateral constraint effect. The transverse deformation of the unreinforced section of L/6 and 5L/6 of the specimen increases, indicating that the SR (1) strengthens the cooperative working ability between the steel tube and the internal filling material, (2) improves the restraint effect of the steel tube on the internal filling material, (3) delays the buckling deformation of the steel tube in the middle of the specimen, and (4) improves the overall mechanical properties of the specimen.

Fig. 12
figure 12

Load–lateral displacement curves

Full size image

4.3 Analysis of load–strain curves

According to the paste position of strain gauge, take the average strain value at the four sections of 1/6 section, 1/3 section, 1/2 section and 3/4 section respectively to draw the load–strain curves. In the Fig. 13, εv is the longitudinal strain and εh is the transverse strain. According to Fig. 13, the curve can be divided into three stages: linear growth, nonlinear increase, and horizontal development. During the loading process, the transverse stress at each section of the specimen is smaller than the longitudinal stress. The strain values of the 1/2 and 3/4 sections of each specimen are generally small because the steel tube of the upper section does not yield during the loading process, and setting the SR has little influence on the stress distribution of the two sections. The curves of the stiffened specimens bifurcate relatively late compared with those of the unstiffened specimens in the early stage of loading. When the A3 curve bifurcates, the load is 32.5 kN; when the load–strain curves of the B1-2, B2-2, and B3-3 specimens bifurcate, the loads are 55, 62.5, and 80 kN, respectively. Before the ultimate load is reached, the corresponding strain value of the stiffened specimen is smaller than that of the unstiffened specimen under the same load. After loading, the longitudinal and transverse strain values at the 1/6 section increase with increasing width of the SR, indicating that the existence of the SR gives full play to the material properties of the steel tube. After the SR is set, the longitudinal and transverse strain values are significantly reduced at the 1/3 cross section near the weak point of the pier column. As the width of the SR increases, the corresponding strain value becomes smaller and smaller, which shows that the existence of the SR is effective at improving the bending deformation of the pier-column specimens. The greater the width of the SR, the better the reinforcing effect.

Fig. 13
figure 13

Load–strain curves

Full size image

4.4 Analysis of bearing capacity and ductility

The bearing capacity and corresponding displacement data of all specimens are listed in Table 6. Bearing capacity is an important reference index for the stiffening design of pier columns. Table 6 shows that the yield bearing capacity and ultimate bearing capacity of the specimens increase significantly after setting the SRs. Compared with the group-A specimens, the yield bearing capacities of the specimens of groups B1–B3 increase by 13%, 29%, and 51%, respectively, and the ultimate bearing capacities increase by 10%, 29%, and 44%, respectively. When the SR is 60 mm wide, the bearing capacity increases the most, which indicates that the larger the contact area between the SR and the steel tube, the stronger the clamp effect of the steel tube on the inner filling material when the specimen enters the elastic–plastic stage under axial pressure, and the better the cooperative working ability between the two, so as to improve the overall bearing capacity of the specimen.

Table 6 List of test data
Full size table

Ductility refers to the capacity of a structure, component, or material to continue to increase its deformation after it has reached yield. It is usually measured by the ductility coefficient, which is the ratio of the maximum displacement Δmax of the specimen to the yield displacement Δy (Ross and Etheridge 2000). In practical calculation, Δmax generally takes the deformation corresponding to the load falling to 85% of the ultimate load. According to existing research, the yield point is determined and the corresponding yield displacement Δy is found by geometric drawing method on load displacement curve (Zha et al. 2012).

From the increase coefficient of the yield load and the yield displacement of the specimens in Table 6, it can be concluded that the ductility of the specimen is increased by 7%, 9%, and 12% when the SR width is 40, 50, and 60 mm, respectively. This shows that the existence of the SR improves the ductility of the specimen, but only because in the loading process the diameter of the steel pipe in the lower section gradually becomes thicker under the expansion and extrusion of the internal filler material. When the gap between the upper and lower steel pipes is filled, the two steel pipes and the SR can be regarded as a whole, and the restraining area of the SR is smaller than the total cross-sectional area of the steel-pipe cross section, and the change of SR width has little effect on the proportion of the area of the restraint. So as the width of the SR changes, the increase in ductility is not significant.

5 Finite-element analysis

5.1 Establishment and verification of finite-element model

5.1.1 Establishment of finite-element model

An FE model of the pier-column specimen is established. The steel is subjected to an ideal elastic–plastic reinforced model. The composition and properties of the filler in pier-column studies are similar to those of concrete. Based on research into the constitutive relation of concrete (Niu 2012), the Drucker–Prager yield criterion is adopted for the failure criterion (Liu 2017). The parameters of the filling materials for pier column are derived from those of sand and gravel filling in geotechnical engineering (Wang et al. 2015). The specific physical and mechanical parameters are given in Table 7.

Table 7 Model physical and mechanical parameters
Full size table

An eight-node linear reduced integral solid element (C3D8R) is used for the pier-column model elements. To ensure convergence, an end plate is defined as an elastic rigid body at both ends of the pier column. The elastic modulus of the end plate is increased to E = 206 MPa, and the Poisson’s ratio is 0.0001, and the constraint between the end plate and the pier-column interface is a binding constraint. Reference points are fitted near the upper and lower end plates and are coupled with each other. The contact relationship between the steel pipe and its internal filler is surface-to-surface contact. Hard contact is used to simulate the normal contact behavior. The inner surface of the steel tube is the main control surface, and the outer surface of the inner filling material is the subordinate surface. The contact surfaces of the two sections of steel pipes are surface-to-surface contact, the tangential friction coefficient is 0.1, and there is hard contact in the normal direction. The restraint between the SR and the steel pipe is a binding restraint.

The FE analysis model based on the above method is shown in Fig. 14. According to the boundary condition that all loading ends are articulated, the top of the model is selected as the loading end, and the load and boundary conditions of the model are applied to the end plate. The displacements U1 and U2 and the rotation angles UR1 and UR3 of the upper end plate are constrained, and the displacement is allowed to develop along the direction of U3, namely the z axis, with the load. Displacement control is applied to U3 of the upper end plate to simulate the axial compression loading.

Fig. 14
figure 14

Schematic of finite-element (FE) model

Full size image

5.1.2 Validation of finite-element model

Figure 15 shows the failure modes of axially compressed specimens calculated by the FE method. It can be seen that all the failure modes are local bending failure. The lateral deflection of the stiffener specimen decreases significantly, and the local buckling amplitude of the lower section steel tube weakens. The existence of SRs is effective at reducing the buckling of the steel tube wall and limiting the overall lateral displacement of the pier-column specimens. Also, the numerically calculated failure mode is consistent with that of the axial compression test.

Fig. 15
figure 15

Comparison of failure modes under axial compression

Full size image

The stress nephograms of the unstiffened specimen, a stiffened specimen, and the internal filler are shown in Fig. 16. These show that the coverage area of the ultimate stress of the steel tube and internal filler decreases gradually with the increase of the width of the SR, and the distribution of axial compressive stress of the steel tube and internal filler is more uniform.

Fig. 16
figure 16

Comparison of nephograms of axial compressive stress

Full size image

The load–displacement curves calculated by the FE method are shown in Fig. 17. The curves are smooth and above but consistent with the experimental curves obtained by the axial compression test. Generally speaking, the results of the FE calculation agree with the experimental results.

Fig. 17
figure 17

Comparison of load–strain curves

Full size image

5.2 Analysis of finite-element results

The above FE model is used to perform numerical simulations of SRs whose width is either less than 40 mm or more than 60 mm, for which no experimental studies were performed. The thickness changes of the SRs are determined to be 2, 3, 4, and 5, and the widths of the SR are 30, 40, 50, 60, 70, and 80 mm.

The relationship between the thickness t of the SR and the ultimate bearing capacity is plotted in Fig. 18, and the relationship between the width B of the SR and the ultimate bearing capacity is plotted in Fig. 19. From Fig. 18, the variation of the ultimate bearing capacity of the pier column is small for B ≤ 40 mm. For B > 40 mm, the Fu–t curve shows a trend of rapid rise initially, then slow rise, and finally decline. The curve has its maximum at t = 4 mm, and the ultimate bearing capacity of the pier column strengthened with an SR of various width reaches the maximum value. The reasons for the above trend are as follows. When the width of the SR is small, its lateral restraint force on the pier column is equal to the effect of stirrups on the pier column, the thickness of the SR is equal to the diameter of the stirrups, and a single stirrup has less influence on the pier column as a whole. When the width of the SR is larger than 40 mm, the contact area between the SR and the steel tube increases, which is equivalent to the joint work of several stirrups. The transverse restraint effect provided to the steel tube is strengthened. When the thickness of the SR exceeds 4 mm, the ultimate bearing capacity of the pier decreases, and the thickness of the SR is too large, resulting in its strong effect on the hoop of the steel pipe. When the gap reserved at the lap joint is filled, the transverse deformation of the lower section of steel pipe at the bottom of the lap joint exceeds the transverse deformation of the upper section of the steel pipe, where the steel pipe will yield in advance.

Fig. 18
figure 18

Curves of Fu–t relationship

Full size image
Fig. 19
figure 19

Curves of Fu–B relationship

Full size image

As shown in Fig. 19, when B ≤ 40 mm, the bearing capacity of the pier column does not change much with the width of the SR. When 40 mm < B<70 mm, the ultimate bearing capacity of the pier column increases with the increase of the width of the SR. When B > 70 mm, changing the SR width has little effect on the ultimate bearing capacity of the pier column. When the width of the SR is small, the contact area with the steel pipe is small, which has little effect on the bearing capacity of the pier column. When the width of the SR is too large, the contact area with the steel tube increases, but there are redundant areas that are not involved in the work. Only when the width of the SR is appropriate can the cooperative working ability between the steel pipe and the filling material be improved through transverse restraint, and the full section of the SR be guaranteed to work, causing the bearing capacity of the pier column to reach its optimum value. According to the curve, the optimal width of the SR is 70 mm.

The optimal size of the SR is determined by FE software as being B = 70 mm, t = 4 mm, and the ultimate bearing capacity of the specimens is 267.55 kN, which is about 592% higher than that of unstiffened specimens. Based on this result, the optimum stiffening dimensions of solid pier columns for roadside support in the Wutongzhuang Mine in Hebei Province are determined as B′ = 200 mm, t′ = 10 mm. The bearing capacity of the prototype pier column after stiffening is verified. Figure 20 compares the stress nephograms before and after stiffening. The comparison results of the FE load–displacement curves are shown in Fig. 21. According to Fig. 21, the ultimate bearing capacity of the prototype pier column is 1645.11 kN, the ultimate bearing capacity of the stiffened pier column is 2609.25 kN, and the increase of bearing capacity after stiffening is 58.61%. It is proved that the effect of stiffening is better.

Fig. 20
figure 20

Comparison of FE stress nephograms

Full size image
Fig. 21
figure 21

Comparison of FE load–displacement curves

Full size image

6 Conclusions

  1. (1)

    Additional transverse constraints are effective for stiffening the pipe wall and enhancing the cooperative working ability between the steel pipe and the internal filling material, thereby improving the bearing capacity of the pier-column specimens.

  2. (2)

    Setting an SR is effective for improving the yield bearing capacity and ultimate bearing capacity of the pier-column specimens.

  3. (3)

    The presence of the SR is effective for restricting the lateral deformation of the pier-column specimens. As the width of the SR increases, the transverse restraint effect is better, the deflection value of the pier column decreases, and the overall stability of the pier column is higher.

  4. (4)

    Setting an SR improves the ductility of the specimens to some extent, but their ductility is insensitive to changing the width of the SR because the constraint area of the SR is small relative to the total section area of the specimens.

  5. (5)

    The ultimate bearing capacity of the pier column is related to the width and thickness of the SR. The optimal stiffening dimensions of the model pier column are determined as a width of 70 mm and a thickness of 4 mm, the choice of which increases the ultimate bearing capacity of the pier column by 58.61%.