1 Introduction

Escalation of greenhouse gas emission and its contribution towards global warming due to prevalent power generation technologies using fossil fuels is a burning problem for mankind. The recently published IPCC report (Barros et al. 2015) also advocated for reduction in the release of greenhouse gases as a solution to it. The deteriorating quality of fossil fuel and lack of proper technology to use such fuels that will arrest carbon dioxide emission in the power generating plants has further complicated the above problem. From the last decade, various efforts are being made for the development of technologies with total carbon capturing facilities such as chemical looping combustion.

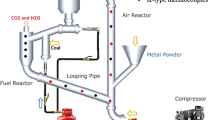
The history of chemical looping process dates back to 1951 when Lewis and Gilliland proposed a patented process in which carbonaceous materials can be oxidize as fuel to generate pure carbon dioxide. In the chemical looping combustion process, carbonaceous fuel, such as coal; first reacts in a fuel reactor with a metal oxide which acts as an oxygen carrier and subsequently gets reduced to metal. The above reaction yields carbon dioxide and steam as products from which carbon dioxide is readily separable by condensing steam. The reduced metal in the fuel reactor is oxidized again by air in air reactor for its regeneration to metal oxide. The metal oxide is then recycled back to the fuel reactor for reuse. The cyclic process is shown as in Fig. 1.

Fig. 1
figure 1

Cyclic chemical looping process

Full size image

The continued development of clean technologies for power generation are pushing the limits of chemical looping combustion process, by improving reactors, fuels, oxygen carriers, etc., through research (Lyngfelt 2011). Xiao et al. (2010) have investigated the pressurized chemical looping combustion by using Chinese bituminous coal in a medium-pressure, high temperature fixed bed reactor with iron (Companhia Valedo Rio Doce iron ore) ore as oxygen carrier. They also estimated the effect of operating pressure and concluded that pressurized condition suppresses the initial reaction of coal pyrolysis while it enhances the coal char gasification and reduction of iron ore in steam. Thus, limited pressurized chemical looping combustion has a potential to exhibit added advantage. Labiano et al. (2006) have analyzed the effects of reactor parameters on Cu, Fe, and Ni based oxygen carrier in syngas fueled chemical looping combustion and concluded that the dependence of reaction rates on temperature has been low while total pressure has a negative effect on oxygen carrier reactions.

Abad et al. (2013) developed a mathematical model, only for the fuel reactor, to determine the effect of key parameters such as reactor temperature, solids circulation rate and solid inventory on the efficiency of carbon dioxide capture. They validated their simulated results against a 100 kWth chemical looping combustion unit. Their result showed carbon dioxide capture efficiency as 98.5 % when operating temperature of fuel reactor was 1000 °C. Thunman et al. (2004) developed model for large scale fluidized beds using kinetic data obtained from chemical looping experiments at lab-scale. Their model was used to evaluate the performance of large scale fuel reactor including the effect of variation in different inputs, operation strategies such as locations of feeding point for oxygen carriers and fuels, physical properties of oxygen carriers and fuel, and operating condition such as fluidization velocity and pressure drop. Jin et al. (2009) developed CFD model for chemical looping combustion using hydrogen as fuel and CaSO4 as an oxygen carrier incorporating reaction kinetics. They studied the effects of partial pressure of hydrogen on the system performance and concluded that higher partial pressure accelerated the reaction rate.

Wadhwani (2014) discussed the development of a CFD based model for the pilot plant described by Kim et al. (2013) using coal and iron (III) oxide as an oxygen carrier. For commercial development of CLC process, computational model of the process is a necessity to study the physical and chemical behavior of the process and to optimize the operating parameters.

From the above piecemeal studies it has been established that operating pressure is a key parameter affecting the efficiency of different segments of the process. However, in above studies, its integrated effect on complete process is missing. Thus, the present work attempts to fill this gap by developing a computational model for complete process to study the effect of operating pressure on the process as whole. For this, the process described by Kim et al. (2013) was considered. Further, this work utilizes the geometry developed by Wadhwani (2014) for the pilot plant reported by Kim et al. (2013) and a 2D model of the system developed on the basis of equivalent volume for various sections of plant unit. A preliminary study by Wadhwani (2014) shows that the number of reactions employed by Kim et al. (2013) does not help in developing accurate model. A set of significant reactions (discussed in Table 6) which were reported by Wadhwani (2014) when included showed better prediction of pilot-plant results had been considered in the present work. The simulated results showed a qualitative agreement with the results obtained by different investigators during study of the effect of operating pressure on different segments of the CLC process (Lee et al. 1991; Labiano et al. 2006; Xiao et al. 2010; Abad et al. 2013).

2 Problem description

The 2D model of the system is developed on the basis of equivalent volume for various sections of plant unit discussed and shown in Fig. 2 and is taken from Wadhwani (2014). The geometrical parameters are tabulated in Table 1. The CFD model is developed for two fuels namely sub-bituminous coal (SBC) and metallurgical coke (MC) discussed by Kim et al. (2013) and are used one at a time in the pilot plant with ferric oxide as an oxygen carrier.

Fig. 2
figure 2

Sub-pilot chemical looping system

Full size image
Table 1 Geometry parameters
Full size table

Table 2 provides the details about the properties of oxygen carrier that has been used in the pilot plant developed at Ohio State University, USA and also considered for the present study. Tables 3 and 4 describe the proximate analysis and ultimate analysis (on dry basis) for two types of coal i.e., MC (average particle size 36.5 μm) and SBC (average particle size 89.8 μm) respectively that were used for the pilot plant described by Kim et al. (2013) and also for the present investigation for comparison of results in Wadhwani (2014).

Table 2 Properties of oxygen carrier
Full size table
Table 3 Proximate analysis of fuels (%)
Full size table
Table 4 Ultimate analysis of fuels (%)
Full size table

3 Model development

A 2-D CFD model for inter-connected system of fuel and air reactors to simulate CLC process was solved using the computational software, FLUENT 6.3.26 and mesh for the above assembly was developed using GAMBIT 2.3.16. The solid–gas mixture contains solid particles (as fuel and oxygen carrier in the range of 36–1500 μm particle size) with gases present in the system (due to injection and creation from the reaction). The amount of gases in this solid–gas mixture amounts more than 94 % by volume. Due to the above fact, this mixture is assumed to flow as a fluid inside both the reactors and their inter-connecting parts while solids remain in fluidized state. The kinetic parameters of solid–solid reactions were incorporated in the model to simulate real system. Eighteen sets of reaction are incorporated for the present CFD model as suggested by Wadhwani (2014) out of which eleven sets of reaction were same as proposed by Kim et al. (2013). Before a complicated two phase CFD model was selected for the accurate analysis of the present problem, it was thought logical to use the least complicated model as the system handles large volume of gaseous species (about 94 % by volume) which makes the solid–gas mixture flow like a gas mixture only. Further, in such a situation incorporation of kinetic parameters for reaction between solid and solid in the proposed model would cause no loss of accuracy even if a complicated two phase model is not considered in its place. Thus, the Species-Transport model with volumetric reactions was used in the present model to validate the pilot plant data which in fact predicted the results considerably well.

Following governing equations were solved on FLUENT 6.3.26 for the present model:

Mass conservation equation The equation for mass conservation/continuity equation can be written as:

$$\frac{\partial \rho }{\partial t} + \nabla (\rho \overrightarrow {v} ) = S\!_{m}$$
(1)

The mass conservation Eq. (1) is valid for compressible and incompressible flows.

  1. (1)

    For momentum conservation equations:

    In an inertial frame, the momentum conservation equation is described as below Eq. (2):

    $$\frac{{\partial (\rho \overrightarrow {v} )}}{\partial t} + \nabla .(\rho \overrightarrow {v} \overrightarrow {v} ) = - \nabla p + \nabla .(\overline{\overline{\tau }} ) + \rho \overrightarrow {g} + \overrightarrow {F}$$
    (2)
    $$\overline{\overline{\tau }} = \mu \left[(\nabla \overrightarrow {v} + \nabla \overrightarrow {v}^{\text{T}} ) - \frac{2}{3}\nabla. \overrightarrow {v} I\right].$$
    (3)
  2. (2)

    For energy conservation equation

    The conservation of energy is defined by the following Eq. (4):

    $$\frac{\partial \rho E}{\partial t} + \nabla .(\overrightarrow {v} (\rho E + P) = \nabla .\left( {\kappa_{eff} {\nabla T} - \sum_j {h_{j} \overrightarrow {{J_{j} }} + (} \overline{\overline{\tau}}_{eff} .\overrightarrow {v} )} \right) + S_{h}$$
    (4)
    $$E = h - \frac{P}{\rho } + \frac{{v^{2} }}{2}$$
    (5)

    For ideal gases as:

    $$h = \sum\limits_{j} {Y_{j} h_{j} }$$
    (6)

    And at T ref = 298.15 K, h j is defined as:

    $$h_{j} = \int_{T_{ref}}^{T} C_{P,j} {\text{d}}T$$
    (7)
  3. (3)

    For species transport equations:

    The local mass fraction of each species (Y i ) through the solution of a convection–diffusion equation for the ith species is solved. It takes the following general form:

    $$\frac{\partial }{\partial t}(\rho Y_{i} ) + \nabla. (\rho \overrightarrow {v} Y_{i} ) = - \nabla .\overrightarrow {{J_{i} }} + R_{i}^{{}} + S_{i}$$
    (8)
  4. (4)

    For mass diffusion in Laminar flows:

    In the above Eq. (8), which arises due to concentration gradients; in the present model, dilute approximation was assumed, which is defined as follows:

    $$\overrightarrow {{J_{i} }} = - \rho D_{i,m} \nabla Y_{i}$$
    (9)

    For the Laminar finite-rate model:

    The net source of chemical species ith, due to reaction is computed as the sum of the Arrhenius reaction sources over the N R reactions, the species participate in:

    $$R_{i} = M_{w,i} \sum\limits_{r = 1}^{{N_{R} }} \overbrace{R_{i,r}}$$
    (10)

    The forward rate constant k f,r for reaction r, is computed using the Arrhenius expression

    $$k_{f,r} = A_{r} T^{{\beta_{r} }} {\text{e}}^{{ - {E}_{R} }} /RT$$
    (11)

    For reversible reactions, the backward rate constant k b,r for reaction r, is computed from the forward rate constant using the following relation:

    $$k_{b,r} = \frac{{k_{f,r} }}{{K_{r} }}$$
    (12)
    $$k_{r} = \text{e}^{{\left( {\frac{{\Delta S_{r}^{0} }}{R} - \frac{{\Delta H_{r}^{0} }}{RT}} \right)}} \left( {\frac{{p_{\text{atm}} }}{RT}} \right)\sum\limits_{i = 1}^{N} {\left( {v_{i,r}^{{{\prime \prime }}} - v_{i,r}^{{\prime }} } \right)}$$
    (13)

    where \(\frac{{\Delta S_{r}^{0} }}{R} = \sum\limits_{i = 1}^{N} {(v_{i,r}^{''} - v_{i,r}^{'} )}\) and, \(\frac{{\nabla H_{r}^{0} }}{RT} = \sum\limits_{i = 1}^{N} {\left( {v_{i,r}^{\prime \prime } - v_{i,r}^{\prime } } \right)} \frac{{h_{i}^{0} }}{RT}\)

  5. (5)

    For reactions kinetics:

    The coal devolatilization reaction (Reaction 1) discussed by Kim et al. (2013) mainly occurs in the fuel reactor and is numerically deduced (Reactions 1.1, 1.2) from Govind (2012) and Strezov et al. (2000) for the present study. In Table 5, 11 reactions proposed by Kim et al. (2013) are described along with their kinetics; while in, Table 6 additional significant reactions with their kinetics are described. Preliminary study (Wadhwani 2014) showed that the amount of Fe3O4 formed in fuel reactor was very less in molar concentration and thus, its formation and reaction have been ignored in the present study.

    Table 5 Proposed reactions for coal direct chemical looping process
    Full size table
    Table 6 Other significant reactions for coal direct chemical looping process
    Full size table
  6. (6)

    For effect of pressure:

    The present model uses Lindemann form to represent the rate expression in pressure dependent reactions which makes a reaction dependent on both pressure and temperature. In Arrhenius form, the parameters for high pressure limit (k) and low pressure limit (k low) are described as follows:

    $$k = A_{r} T^{\beta } {\text{e}}^{ - E/RT}$$
    (14)
    $$k_{\text{low}} = A_{\text{low}} T^{\beta_{low} } {\text{e}}^{ - E_{low}/RT}$$
    (15)

    The net rate constant at any pressure is given by,

    $$k_{\text{net}} = k \left( {\frac{{p}_{r} }{{1 + p_{r} }}} \right)F$$
    (16)
    $$p_{r} = \frac{{k_{\text{low}} [M]}}{k }$$
    (17)

    [M] is conc. of gas mixture, and function F is unity for Lindemann form.

  7. (7)

    For the standard k-ε turbulence model:

    The standard k-ε turbulence model described by Launder and Spalding in 1974 was used for the present study.

    $$\frac{{\partial \left( {\rho{k}} \right)}}{\partial t } + \frac{{{\mathbf{\partial }}\left({\varvec{\rho}{ku}_{i} } \right)}}{{\partial{x}_{\varvec{i}} }} = \frac{\partial }{{{\mathbf{\partial}}{x}_{i} }}\left[ \left( {\mu + \frac{{\mu_{t}}}{\sigma_{k}}} \right)\frac{\partial {k}}{{\partial}{x}_{j}}\right] + {G}_{k} +{G}_{b} - \rho\! \in - {Y}_{M} + {S}_{k}$$
    (18)
    $$\frac{{\partial \left( {\rho\varepsilon } \right)}}{{\partial{t}}} + \frac{{{\mathbf{\partial }}\left({\varvec{\rho}\varepsilon {u}_{i} }\right)}}{{\partial {x}_{\varvec{i}} }} = \frac{\partial}{{{\mathbf{\partial }}{x}_{i} }}\left[ {{\left( {\mu + \frac{{\mu_{t} }}{{\sigma_{k} }}}\right)}\frac{\partial \varepsilon }{{\delta {x}_{j} }}}\right] + {C}_{1\varepsilon } \frac{\varepsilon}{k}\left( {{G}_{k} + {C}_{3\varepsilon } {G}_{b} } \right) - {C}_{2\varepsilon }\varvec{\rho}\frac{{\varepsilon^{2}}}{k} + {S}_{\varepsilon }$$
    (19)
  8. (8)

    For mass-weighted average of rate of reaction:

    The mass-weighted average of rate of reaction are computed by dividing, the summation of the values of the rate of reaction multiplied by the absolute value of the dot product of the facet area and momentum vectors, by the summation of the absolute value of the dot product of the facet area and momentum vectors as given in Eq. (20):

    $$\frac{{\int {\overbrace{{{R}_{r} }}\rho\left| {\overrightarrow {v} \cdot {d}\overrightarrow {A} } \right|} }}{{\int {\rho\left| {\overrightarrow {v} \cdot {d}\overrightarrow {A} } \right|} }} = \frac{{\sum\nolimits_{{{i} = 1}}^{n} {\overbrace{{{R}_{i,r} }}\rho_{i} \left| {\overrightarrow {{{v}_{\text{i}} }}. \overrightarrow {{{A}_{i} }} } \right|} }}{{\sum\nolimits_{{{i} = 1}}^{n} {\rho_{i} \left| {\overrightarrow {{{v}_{i} }}. \overrightarrow {{{A}_{i} }} } \right|} }}$$
    (20)

4 Solution technique

The sub- pilot plant dimensions were taken from the mechanical drawing of the sub-pilot plant described in Kim et al. (2013) on equivalent volume basis. The boundary condition for air inlet and coal inlet were defined as velocity inlet and mass flow inlet respectively whereas, that for fuel reactor exhaust and cyclone exhaust it were defined as pressure outlets Further, no slip conditions was kept at wall boundary. The grid independency test was carried out on mesh size ranging from 0.005 to 0.025 (m) at steps of 0.005 (m), based on grid independence test grid size of 0.01 (m) was selected. Unsteady state simulation with a time step of 0.001 s and 40 iteration/time step was selected. In Table 7, other details of solution techniques are listed.

Table 7 Computational and simulation parameters for the present study
Full size table

5 Results and discussion

In this section, result obtained from the 2D CFD simulation study of CLC process using MC and SBC as fuels are discussed. It draws a considerable inferences from the preliminary study conducted by Wadhwani (2014) which showed that the simulation of chemical looping combustion process using eleven reaction as proposed by Kim et al. (2013) were not adequate enough to validate the pilot plant data accurately. Further, an in-depth study Wadhwani (2014) revealed that there is a need to include seven more significant reactions as discussed in Table 6 to describe the process accurately for developing a computational model for CLC process which is used for the present investigation.

Figure 3 shows that for pressure ranging from 5 to 25 atm, the coal devolatilization reaction (Reaction no. 1 (1.1/1.2) of Table 5) is one of the most dominating reactions taking place in the fuel reactor. Figure 3a, b shows the variation of mass average rate of reaction (calculated using Eq. 20) with pressure for the most dominating reactions (Reaction Nos. 1, 13, 14) that are taking place in fuel reactor for MC and SBC respectively. The negative effect of pressure on coal devolatilization is due to the external pressure exerted on volatile species escaping in this process (Lee et al. 1991). Further, the effect of pressure on water gas shift reaction (Reaction 13) is negligible due to Le Châtelier’s principle whereas, it has a negative effect on steam reforming reaction (Reaction 14).

Fig. 3
figure 3

Effect of pressure on most dominating reaction in fuel reactor section. a For MC. b For SBC

Full size image

Figure 4 shows the effect of simulated operating pressure on key parameters such as reactors temperature, fuel conversion and carbon dioxide purity in the fuel reactor exhaust when MC is used as a fuel. The simulation results showed negative impact of operating pressure on the temperature of fuel reactor and air reactor. As suggested by Labiano et al. (2006), during their experiment on limited pressurized operation, an increased pressure during the startup helps to improve the reduction reactions of oxygen carrier (similar to reaction Nos. 2 & 4) while at the later stage it exhibits a negative impact on coal devolatilization reaction. Similar effects were observed for SBC by Lee et al. (1991) also. Further, as per the simulation results of present investigation, an increase in operating pressure increases the purity of carbon dioxide while, it decreases the percentage fuel conversion.

Fig. 4
figure 4

Effect of operating pressure on MC for chemical looping combustion

Full size image

Similar to Figs. 4 and 5 shows the effect of operating pressure on key parameters such as reactors temperature, fuel conversion and carbon dioxide purity in fuel reactor exhaust is shown when SBC is used as a fuel. The simulation results showed negative impact of operating pressure on the temperature of fuel reactor and air reactor as has already been observed in the case when MC when it is used as a fuel. Further, an increase in operating pressure increases the purity of carbon dioxide while, it decreases the percentage fuel conversion when SBC is used as a fuel. This observation is also similar to the simulated results when MC is used as a fuel. Thus, both fuels SBC and MC, show similar trends with variation in pressure.

Fig. 5
figure 5

Effect of operating pressure on SBC for chemical looping combustion

Full size image

For an optimal condition, the temperature of the reactors should be high enough to provide sufficient energy to keep endothermic reactions (reduction reaction) of oxygen carrier going. The higher value of carbon dioxide purity and fuel conversion are the desired objective of this process, and thus a trade-off between these two parameters based on economics of the process is required to select the optimal operating pressure. Higher value of operating pressure can be selected in case of SBC fuel as compared to MC fuel as can be seen from Figs. 4 and 5 respectively. This is primarily due to higher conversion values observed for SBC as a fuel even at high operating pressures. Fuel and air reactor temperatures, when SBC is used as a fuel, are more than when MC is used as a fuel. This is despite of the fact that SBC offers lower calorific value than MC and thus during operation (using SBC) it engages more amount of fuel in inlet in comparison to the operation when MC is used as a fuel. The percentage change in carbon dioxide purity for MC and SBC with change in pressure in the simulated range is approximately ~2 % and ~3 % respectively. The percent change in carbon dioxide purity with change in pressure for El Cerrejón coal with ilmenite (FeTiO3) as an oxygen carrier is also found to be ~3 % which provides a quantitative agreement of the simulated result with experimental values Abad et al. (2013).

6 Conclusion

The simulated results obtained through the simple 2D CFD Species-Transport model with volumetric reactions developed in the commercial CFD software shows similar behavior observed in experimental studies discussed in literature. The CFD model provides a cost-effective method to developed CLC process and optimum operating conditions. The operating pressure has a negative effect on reactor temperatures (fuel and air reactor), and the rate of decrease in reactor temperature increases at higher pressure. The efficacy of CLC process lies on the higher value of two key parameters i.e., purity of carbon dioxide in fuel reactor exhaust and fuel conversion. The carbon dioxide purity in fuel reactor exhaust and fuel conversion increases and decreases respectively, with increase in operating pressure. The opposite effect of operating pressure on above two key desired parameters requires a trade-off to select the optimum operating pressure.