Abstract
Coal and ore underground mining generates subsidence and deformation of the land surface. Those deformations may cause damage to buildings and infrastructures. The environmental impact of subsidence will not be accepted in the future by the society in many countries. Especially there, where the mining regions are densely urbanized, the acceptance of the ground deformations decreases every year. The only solution is to limit the subsidence or its impact on the infrastructure. The first is not rentable for the mining industry, the second depends on the precise subsidence prediction and good preventing management involved in the mining areas. The precision of the subsidence prediction depends strictly on the mathematical model of the deformation phenomenon and on the uncertainty of the input data. The subsidence prediction in the geological conditions of the raw materials used to be made on the basis of numerical modeling or the stochastic models. A modified solution of the stochastic model by Knothe will be presented in the paper. The author focuses on the precise description of the deposit shape and on the time dependent displacements of the rock mass. A two parameters’ time function has been introduced in the algorithm.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Specialists dealing with the protection of mining areas have recently discussed the issue of reliability and higher accuracy of deformation occurrence predictions (Kowalski 2005; Niedojadło 2008; Hejmanowski and Malinowska 2009). Such considerations stem from the increasing financial and social costs of damage done by this type of mining activity. The reliability issue is mainly connected with the quality of geologic-mining data (Naworyta and Sroka 2005; Stoch 2005), whereas higher accuracy of predictions may be related with the appropriate model of deposit and accuracy of the estimated parameters of the calculation model. Bearing in mind the popularity of Knothe theory and its common applicability in the Polish mining, the discussion may be focused on model parameters a and r (or interchangeably “tgβ”), and also additionally horizontal displacement parameter \(B\) (Budryk 1953) and time coefficient c (Knothe 1953). Over the years of study of deformations and predictions of their occurrence, the author noticed that deposit models used for calculations are frequently simplified (Knothe 2005), which results in considerable inaccuracies of the obtained results. The discrepancies of predictions and the actual deformations on the surface clearly indicate that such simplifications should never be made. The influence of a simplified description of deposit on the accuracy of model calculations is presented in this paper. An exemplary model employing author’s prediction system MODEZ (Hejmanowski and Kwinta 2009) is also presented. This program can be used for accurate modeling of deposition in a reservoir and the mining process itself.
2 Classic modeling of displacements in a function of time
The most popular model of rock mass displacement in Poland and in many other countries all over the world is Knothe model worked out in 1953 (Knothe 1953), called the influence function model or stochastic model.
In this case, the vertical displacements of any point in the rock mass or on the surface can be modeled with this dependence:
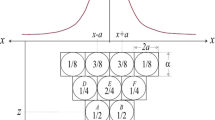
where \(\varphi (x, y)\) is the influence function in Knothe model, which will be simplified to the form: \(\varphi \left( {x,y} \right) = {\text{e}}^{{ - \pi \frac{{x^{2} + y^{2} }}{{r_{z}^{2} }}}}\), for a point located at the origin of the coordinates system, a is the extraction coefficient which defines the way in which mining voids should be filled; g is the thickness of the deposit under production; and r z is the radius of major influences in Knothe model, at a level z over the mined deposit. For z = H, this will be a dependence of the angle of major impact zone β and depth of extraction H (Fig. 1):
and then
where H is the depth of extraction (m); β is the angle of major impact zone (grad), and n is the rock mass parameter, characterizing propagation of deformations in the space above the deposit. The n value does not matter for the terrain surface, though according to many authors n < 1, 0 (Krzysztoń 1965; Drzęźla 1979; Preuße 1990).
This model (1) was originally worked out for predicting static states of vertical displacements, however, later Knothe supplemented it by the function of time. This function was written in the form of a linear differential equation describing the subsidence rate as a function difference of final and momentary subsidence:
where S k (t) is the subsidence of a point when the mining has been stopped at a moment t; S(t) is the actual subsidence of a point at a moment t, and c is the time parameter-proportionality coefficient in Eq. (4), characterizing delaying properties of the rock mass as far as mining impacts effects appearing in time [1/year] are concerned.
A general solution of (4) is (5):
This model well describes subsidence of the analyzed point of the terrain surface after the mining operations on a given mining field (or fragment of the lot) are finished. It can be hardly applied for the advancing longwall fronts, as in this case calculations should be made for fragments (strips) of the lot. The author of this model also noticed this regularity and suggested a solution for the advancing extraction front (Knothe 1984). A similar application of Knothe model for the calculation of dynamic subsidence of terrain was presented by a group of Chinese scientists (Hu et al. 2011).
If part of the deposit has been mined and depleted instantly (i.e. S K (t) = constants and S(t) t = 0 = 0), the solution takes the form of Eq. (4):
As observed earlier (Kwinta et al. 1996), this function has a drawback, i.e. the subsidence is described from the moment of t = 0, when the subsidence rate is the maximum. This shortcoming can be liquidated by simulating the advancing extraction front in the form of strips (for longwall coal extraction), or deposit elements in the form of a cuboid.
3 Numerical modeling of displacements in time-reservoir elements model
This method was used in the calculation model based on the division of reservoir into reservoir elements (Hejmanowski 1993). In this case, the subsidence of an arbitrary point caused by mining activity can be written as:
and mining-induced subsidence of the entire mining lot or part of the reservoir is a sum of elementary impacts:
where N is the number (quantity) of exploitation elements; i is the number of a subsequent individual exploitation element; j is the number of the (individual) calculation point; V i (t) is the volume of the post-exploitation elementary subsidence bowl at the time t, due to mining of the layer volume in the ith element of exploitation; H i is the local mining depth in (m); t is the time difference between exploitation date of every reservoir element and date of the prediction (years); d i,j is the (horizontal) distance between the point calculation, and the centre of the exploitation element (m); and φ z (d i,j , H i ) is the influence function, given with the formulae:
The model of reservoir division is presented in figure (Fig. 2). The horizontal dimension (square) is adjusted to the distance of the reservoir from the calculation level, accounting for the accuracy issue. The size of such elements is considerable, i.e. length L usually ranges from 30 to 60 m for extraction depth to 1000 m and predictions made for the surface. The height of the element corresponds with the thickness of the mined reservoir g i .
3.1 Modeling of geology and mining technology
The division of reservoirs into elements has a very important utility aspect. All attributes connecting with geologic conditions and technological parameters of mining, which are locally variable, can be attributed to elements. In this situation the reservoir element may bring about information about the reservoir, which is especially significant for the prediction of deformation occurrence, and also spatial analyses and for evaluation of mining hazards.
3.1.1 Deposit thickness variable
The average thickness of extracted deposit layer is a typical generalization assumed in the traditional prediction models. It is not very important for coal seams, though in the metal ore deposits the thickness may vary significantly (Fig. 3).
The reservoir element model allows including this attribute in displacement calculations for thus diversified thicknesses of mined layers (Fig. 4). Consequently, the picture of the summary subsidence basin will vary, depending on the varying thickness of deposit.
3.1.2 Mixed mining system
The accuracy of displacement predictions is known to depend on the correct parametrization of the mathematical model. The parameters should correspond to the local geologic-mining conditions. The extraction coefficient a and angle of major impact β were the most important parameters in Knothe model, on the basis of which the presented modified model was worked out. In view of the planned extraction system, the extraction coefficient can also be simulated for the locally varying conditions, e.g. hydraulic backfilling (Fig. 5). In the presented example the room and pillar system with roof deflection is predicted for extraction coefficient of ca. 0.6. The system including hydraulic backfill better minimizes displacements and the extraction coefficient usually ranges between 0.2 and 0.3.
3.1.3 Varying abundance of deposit and its modeling
The reservoir elements model allows for very accurate modeling of local changes in the ore resources thanks to which they can be selectively extracted. The influence of a given fragment of reservoir on the rock mass displacements can be modelled by introducing information about the surface of the planned mining area within the reservoir element as compared to the total reservoir element area. Figure 6 illustrates a reservoir pillar which will not be extracted. Numbers corresponding to the percentage of mined area of a given reservoir element are introduced in particular cells of the model. Thanks to this the volume of an arbitrary reservoir element, i.e. its influence on rock mass displacement, can be calculated from dependence (10):
where \(V_{i}^{E}\) is the volume of reservoir element to be mined; \(E_{i} {\text{ is the }}\) ratio of surface of mining area to total surface in a given reservoir element; \(L_{i}\) is the length of the edge of reservoir element; and \(g_{i}\) is the local thickness of deposit layer to be mined.
3.1.4 Tectonic disturbances and reservoir tilt
The biggest problem in modeling displacements is usually stratigraphy and tectonics of the reservoir formation. Unlike the presented model, classic models are frequently insufficiently flexible for modeling tectonic disturbances or variable reservoir tilt, e.g. within the coal longwall itself. Another advantage of the improved model is the local height datum as well as local direction and angle of dip of the deposit. Figure 7 reveals the way in which the difference of depth of deposition is accounted for. This affects the mining impact area of particular elementary basins on the surface. The summaric subsidence basin, being a sum of elementary basins, will show a visible asymmetry in the cross section parallel to the dip of deposit. This effect is observed in practice and no asymmetric influence functions need to be applied.
Additional information about the angle of inclination of deposit layers and the direction of the dip of the layer can be used for deviating the basin (m i ) i.e. shifting elementary basin towards the dip by a value calculated from dependence (11) (Fig. 8).
where α is the angle of dip of deposit layer or roof formation (grad), 0 < α < 50 grad; μ is the deviation coefficient determined empirically for local geologic conditions, μ < 1.
3.2 Time as important attribute of the model
Most importantly, the division of a reservoir into elements allows one to very accurately describe the mining development in time, and so to simulate the advancement of the extraction longwall or development of the room and pillar field, even for varying mining rates.
The extraction time of a given reservoir element as compared to the time, for which the subsidence has been calculated, is a unique pair of variables (dates) in the calculation algorithms. An arbitrary function of time can be used for this pair of variables to obtain a result which would be closest to the real conditions of mining deformation propagation in a given area. In this way the course of time in which manifests itself the mining impact at a given calculation point will automatically account for the space and time conditions referred to in the model.
It seems obvious that the surface deformation rate reaches the maximum after some time, but begins from the preliminary phase when the distance of the extraction from the given point on the surface is relatively big. Thus Knothe time model (4–6) will not be a suitable tool for describing this type of displacements. A far better solution will be the two-parameter function of time proposed by Sroka and Schober (Schober and Sroka 1983). This function, whose properties were discussed in detail (Kwinta et al. 1996) relates the cause of deformation, i.e. convergence of working with the subsidence basin. The volume of elementary basin needed in the forecast of displacements (7) is expressed with the formula (12).
where θ(t) is the function of time.
where ξ is the convergence coefficient characterizing delaying properties of roof rocks in the workings area, (year−1); ϑ is the coefficient characterizing delaying properties of the cap rock in displacement propagation, (year−1).
These two time parameters characterize time in which appear all mining impacts on the surface it can be assumed that they are the same as time coefficient introduced by Knothe. Then:
For traditional hard coal and ore extraction, the values of these coefficients take the following values:
-
(1)
For hard coal (goaf system), 15 < ξ < 50;
-
(2)
For copper ores (room and pillar), 0.2 < ξ < 1.5, 1 < ϑ< 15.
Graphic characteristics of the presented function of time are presented for exemplary values of time coefficient in figures (Figs. 9, 10).
The function of time has zero rate and acceleration at the initial stage of movement. Then the displacement rate increases to the maximum in the linear phase of movement, delays, and the rate lowers at the vanishing movement stage. These properties of the function of time show to its adequacy to the actual conditions of displacement propagation in the rock mass as compared to Knothe function. Nonetheless the two-parameter function requires a much broader scope of studies to determine both these parameters. For the sake of determining the convergence coefficient, convergence measurements need to be performed in similar geologic and mining conditions, which is not always possible.
4 Concluding remarks
The problem of modeling displacements in the coal or ore rock mass shows considerable advantages of a model based on Knothe influence function model. Modifications in the article in Knothe model refer to the space and time. The division of reservoir has the following advantages:
-
(1)
this model gives much better possibility of including local variability of geologic properties of the rock mass and deposit as compared to Knothe model,
-
(2)
properties characteristic of the designed extraction system (backfill, working convergence rate, leaving off pillars and unmined deposit remains) can be accounted for,
-
(3)
time-modeling of extraction in planned reservoir lots, accounting for delays in displacements propagation in the rock mass.
Utilization of this model and author’s computer software MODEZ (Hejmanowski and Kwinta 2009; Hejmanowski and Zespol (2009)) makes prediction of the rock mass deformations and displacements much easier in the coal and copper ore mining conditions. The introduction of this software to the mining practice will increase the accuracy of predictions.
References
Budryk W (1953) Wyznaczanie wielkości poziomych odkształceń terenu. Archiwum Górnictwa i Hutnictwa, t.1, z.1, Warszawa
Drzęźla B (1979) Zmienność zasięgu wpływów w górotworze, Przegląd Górniczy, nr 10, Katowice
Hejmanowski R (1993) Zur Vorausberechnung förderbedingter Bodensenkungen über Erdöl- und Erdgaslagerstätten. Praca doktorska, TU Clausthal
Hejmanowski R, Zespół I (2009) Dokładność prognoz deformacji powierzchni terenu górniczego “Lubin I” i “Małomice I”, w aspekcie zmian dynamiki ruchów powierzchni w odniesieniu do prognoz krótko- i długookresowych. Praca nauk-badawcza na zlecenie KGHM Polska Miedź SA. (niepublik.)
Hejmanowski R, Kwinta A (2009) System prognozowania deformacji Modez. Materiały konferencji X Dni Miernictwa Górniczego i Ochrony Terenów Górniczych”, Kraków
Hejmanowski R, Malinowska A (2009) Evaluation of reliability of subsidence prediction based on spatial statistical analysis. Int J Rock Mech Min Sci 46:432–438
Hu QF, Cui XM, Wang G, Wang MR, Ji YX, Xue WW (2011) Key technology of predicting dynamic surface subsidence based on Knothe time function. J Softw 6(7):1273–1280
Knothe S (1953) Równanie profilu ostatecznie wykształconej niecki osiadania. Archiwum Górnictwa i Hutnictwa, t.1, z.1, Warszawa
Knothe S (1984) Prognozowanie wpływów eksploatacji górniczej. Wyd. Śląsk
Knothe S (2005) Asymetryczna funkcja rozkładu wpływów eksploatacji górniczej w ośrodku zmieniającym swoje własności. Archiwum Górnictwa 50(4):401–415
Kowalski A (2005) O błędach prognozy wskaźników deformacji powierzchni spowodowanych błędami parametrów teorii. Materiały konferencji, VIII Dni Miernictwa Górniczego i Ochrony Terenów Górniczych, Ustroń
Krzysztoń D (1965) Parametr zasięgu niecek osiadania w ośrodku sypkim, Archiwum Górnictwa, tom X, zesz.1, str. 29–51, Kraków
Kwinta A, Hejmanowski R, Sroka A (1996) A time function analysis used for the prediction of rock mass subsidence.//96 International symposium on mining science and technology, Xuzhou, pp 16–18
Naworyta W, Sroka A (2005) Ocena niepewności prognozy wskaźników deformacji terenu metodą symulacji geostatystycznej. Materiały konferencji, VIII Dni Miernictwa Górniczego i Ochrony Terenów Górniczych, Ustroń
Niedojadło Z (2008) Problematyka eksploatacji złoża miedzi z filarów ochronnych szybów w warunkach LGOM. Rozprawy i monografie nr 177. Wydawnictwo AGH, Kraków
Popiołek E, Ostrowski J (1981) Próba ustalenia głównych przyczyn rozbieżności prognozowanych i obserwowanych poeksploatacyjnych wskaźników deformacji. Ochrona Terenów Górniczych nr 58, Katowice
Preuße A (1990) Markscheiderische analyse und prognose der vertikalen beanspruchungvon Schachtsäulen im Einwirkungsbereich untertägigen Steinkohlenabbaus. Praca doktorska, TU Clausthal, Clausthal-Zellerfeld
Schober F, Sroka A (1983) Die Berechnung von Bodenbewegungen uber Kavernen unter Berucksichtigung des zeitlichen Konvergenz und Gebirsverhaltens. Kahli und Steinsaltz Bd.8, Heft 10 (in German)
Stoch T (2005) Wpływ warunków geologiczno-górniczych eksploatacji złoża na losowość procesu przemieszczeń i deformacji powierzchni terenu. Akademia Górniczo-Hutnicza w Krakowie, Kraków (praca doktorska)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Hejmanowski, R. Modeling of time dependent subsidence for coal and ore deposits. Int J Coal Sci Technol 2, 287–292 (2015). https://doi.org/10.1007/s40789-015-0092-z
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40789-015-0092-z