1 Introduction

Spur gears is commonly applied in the driving system of the mining machinery and equipment, such as scraper conveyer, gearbox, mining drilling and excavator, etc. and mainly used for the transmission of rotary motion between two shafts. Using traditional machining method to manufacture spur gear has some drawbacks and insufficiencies, such as severe erosion and abrasion, poor strength and service life, lower transmission efficiency and huge material waste, etc. which satisfies the requirements poorly in complex and bad environment of the coal mine (Jing and Xing 2006; Can and Misirli 2008; Lee et al. 2011). The recent trend of manufacturing spur gear is characterized by cold precision forging and enhanced strength of gear with lower cost and higher productivity in the mining machinery industry (Lee et al. 2001; Altinbalik et al. 2007; Hu et al. 2007; Politis et al. 2014).

As more and more types and sizes of forging gears are needed, the accuracy of billet volume plays an extremely important role in fully filling the die cavity during the cold precision forging of spur gear (Balendra and Qin 2000; Abrinia and Makaremi 2008). In order to obtain the complete filling of the die cavity form, the billet is supposed to have the exact volume needed for the finished part (Behrens et al. 2007). The change of billet volume will affect dimensional accuracy of the gear as is demonstrated by Xu and Chi (2000). This is because the billet volume is equal to the volume of the gear in cold precision forging. Reference circle method is a traditional method to calculate the billet volume, which is not taken into account the clearances between the working teeth and tooth modification factors. Three-dimensional solid modeling is an accurate and feasible method to obtain the billet volume (Jin et al. 2012), but it is extremely complicated and will cost long modeling time. Choi et al. (1996) suggested a trapezoidal tooth profile theory to obtain the billet volume in spur gear precision forging. Eyercioglu et al. (2009) proposed a thick wall cylinder model to take the reference diameter as bore diameter without considering gear tooth shape. Up to now, there is no simple method to obtain gear billet volume precisely (Chen et al. 2010). Methods above may be far from the practical application and do not meet large-scale applications in spur gear cold precision forging.

A new engineering method named average circle method is put forward to calculate the volume of spur gear billet on the basis of our long-term practice and experiment in this article. It is an accurate and convenient way to obtain spur gear billet volume by evaluating the accuracy with relative errors between average circle method and traditional method.

2 Details of reference circle method

By comparison and analysis of different spur gear models, model structure of gear can be divided into two parts that is the wheel part within the dedendum circle and the teeth part out of the dedendum circle. Therefore, in order to simplify theoretical analysis for the forging of spur gear, the gear billet volume can be considered as the wheel volume and tooth volume. Gear wheel is a geometrical rotating body, whose volume can be calculated by relevant mathematical formulas. While gear teeth are some irregular trapezoidal cylinders, there are no accurate formulas to calculate the volume of the gear teeth (Fig. 1).

Fig. 1
figure 1

Composition of cylindrical spur gear

Full size image

In general, reference circle method is the most common way to calculate cylindrical gear volume in cold precision forging. According to above theory, the structure of gear wheel can be assumed to be a regular solid cylinder whose height is equal to tooth width. Cylindrical gear volumes are calculated by following theoretical formulas:

$$V_{\text{wheel}} = \frac{\pi }{ 4}d_{f}^{2} B$$
(1)
$$V_{\text{teeth}} = \frac{\pi }{ 4}d_{r}^{2} B - \frac{\pi }{ 4}d_{f}^{2} B$$
(2)
$$V_{\text{gear}} = V_{\text{teeth}} + V_{\text{wheel}} = \frac{\pi }{ 4}d_{r}^{2} B$$
(3)

It is concluded that reference circle diameter above is imprecise to calculate the cylindrical gear volume, because it is not associated with modification coefficient, addendum coefficient, tip clearance coefficient as shown in Eq. (4). Gear volumes (modulus is 6 mm, width is 30 mm) will be described in the following figures.

$$d_{r} = mz$$
(4)
$$V_{\text{gear}} = \frac{\pi }{ 4}m^{2} z^{2} B$$
(5)

where \(V_{\text{wheel}}\) is the volume of gear wheel, d f is the diameter of dedendum circle, B is the gear width, \(V_{\text{teeth}}\) is the volume of gear teeth, d r is the diameter of reference circle, m is the modulus and z is the number of tooth.

3 Details of average circle method

Mohamed et al. (2012) investigated the objective function. The gear volume considered in calculations would be the volume of the pinion only. The pinion volume can be simplified to a truncated cone at the pitch cone (Fang 2000; Deng et al. 2001; Lin et al. 2001). The volume of a truncated cone is given as below:

$$V = \frac{\pi }{3}F\,\cos (\gamma_{p} )\left[ {\left( {\frac{n}{{2P_{d} }}} \right)^{2} + \left( {\frac{n}{{2P_{d} }}\, \times \,\frac{A - F}{A}} \right)^{2} + \frac{n}{{2P_{d} }}\left( {\frac{n}{{2P_{d} }}\, \times \,\frac{A - F}{A}} \right)} \right]$$
(6)
$$V = \frac{\pi }{3}b\,\cos (\gamma_{p} )\left[ {\left( \frac{mz}{2} \right)^{2} + \left( {\frac{mz}{2}\, \times \,\frac{R - b}{R}} \right)^{2} + \frac{mz}{2}\left( {\frac{mz}{2}\, \times \,\frac{R - b}{R}} \right)} \right]$$
(7)

The volume of the pinion pitch frustum is determined by a function of the number of teeth z, module m, face-width F, cone distance A, helical angle γ ρ , slant height b, the height of truncated cone h and the frustum of a cone radius R, revolving speed n and distance of face-width P d .

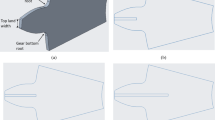
Equations (6) and (7) can be used to calculate truncated cone volume when D > d or D < d, which are very complicated and circumscribed without considering the strength of gear in practical engineering applications. In order to solve above problems, a new engineering method is put forward when D = d in cold precision forging, which assumes the truncated cone volume (Fig. 2a) as regular cylinder volume (Fig. 2b). The average of the top diameter d and the bottom diameter D of the irregular truncated cone can be taken as below:

Fig. 2
figure 2

Volume transformational relations: a truncated cone; b regular cylinder

Full size image
$$d_{\text{average}} = (d + D)/2$$
(8)

For a standard modified cylindrical spur gear, addendum circle diameter d a and dedendum circle diameter d f are calculated as follows:

$$d_{a} = mz + 2\left( {h_{a}^{ * } + \chi } \right)m$$
(9)
$$d_{f} = mz - 2(h_{a}^{ * } + c^{ * } - \chi )m$$
(10)

The average of addendum circle diameter and dedendum circle diameter is calculated as below:

$$d_{\text{average}} = (d_{a} + d_{f} )/2 = m(z - c^{*} + 2\chi )$$
(11)
$$V = \frac{\pi }{ 4}Bd_{\text{average}}^{ 2}$$
(12)

where \(d_{\text{average}}\) is the average diameter, h * a , the addendum coefficient, χ, the modification coefficient, c*, the top clearance coefficient, m, the modulus, z, the number of tooth and B is the gear width.

Taking the cylindrical volume whose height is equal to the tooth width as the volume of the gear teeth, the hypothetical diameter of cylinder is considered as the average diameter of outside circle diameter and inside circle diameter. This approximate algorithm is called average circle method. Similarly, assuming that the structure of gear wheel is a solid cylinder with the same height as tooth width, cylindrical gear volumes are calculated by using Eq. (12). Gear volumes which are calculated with average circle method (modulus is 6 mm, width is 30 mm) are given in Sect. 5.1.

4 Three-dimensional solid modeling

Solid modeling of cylindrical gear is constructed by taking advantage of Pro/E4.0 software as higher accuracy, feature modeling and parameter-driving (Jin et al. 2012). The precise values of gear billet volume were obtained to evaluate the accuracy of above method. Choose ‘measurement’ and ‘model’ commands in Pro/E4.0 main window menu and then click ‘tools’ and ‘parameters’ to change a series of basic parameters, such as gear teeth, modulus, tooth widths, and so on, in order to obtain different gear solid models (Palermo et al. 2013). The specific operating steps were shown as follows:

  1. (1)

    Put basic parameters of the gear such as modulus, tooth number, tooth thickness and pressure angle into ‘Tools’ and ‘Parameters’ in Pro/E4.0 main window.

  2. (2)

    Dedendum circle, reference circle, base circle and addendum circle with different sizes were respectively drawn by electing the FRONT datum plane as the basic surface in Pro/E sketched curve window. Next, constraints of the relationship of four circles were drawn by clicking ‘Tools’ and ‘Relations’ with the following formulas:

    $$\begin{aligned} d &=mz \\ db &= d\,{ \cos }(a) \\ da &= d + 2m(ha + x) \\ df &= d - 2m(ha + c - x) \\ sd0 &= db \\ sd1 &= df \\ sd2 &= d \\ sd3 &= da \\ \end{aligned}$$

    Circles under the restriction of above relations were gained by ‘Regenerate’ in Pro/E4.0 sketched feature window as shown in Fig. 3a.

    Fig. 3
    figure 3

    Three-dimensional solid modeling: a the circles to be constrained; b the involutes to be generated; c dynamic trimmed closed curves; d remove material along a closed curve; e gear teeth array; f gear solid model to be obtained

    Full size image
  3. (3)

    Formation of the involutes: Clicked the toolbar ‘Insert Benchmark Curve’, selected ‘From Eq’, ‘Cartesian coordinates’ and set ‘t = 0 − 1’, then entered the involute Eqs. in the pop-up text page. Finally, saved the text and ensured generating an involute as presented in Fig. 3b.

    $$\begin{aligned} r &= db/2 \\ \theta &= 45t \\ x &= r\,{ \cos }(\theta) + r\,{ \sin }(\theta) \times \theta \times \pi/180 \\ y &= r\,{ \sin }(\theta) - r\,{ \cos }(\theta) \times \theta \times \pi/180 \\ \end{aligned}$$
  4. (4)

    Constructing a benchmark, mirroring the involute: Defined the intersection between the involute and the reference circle as the benchmark PNT0 and the line formed by RIGHT datum plane and TOP datum plane as a benchmark axis A_1, then PNT0 and A_1 formed the datum plane DTM1. Datum plane DTM2 was created by a benchmark axis A_1 and the datum plane DTM1 which were turned 90°/z (z refers to tooth number). Used datum plane DTM2 as symmetry plane to mirror another involute as observed in Fig. 3c.

  5. (5)

    Generating the transition curve: According to properties of the involute, there is no involute in the base circle. If d f  > d b , the whole tooth profile is involute curve, if d f  < d b , the tooth profile curve is comprised of external involute curve of the base circle and inside transition curve of tooth profile of the base circle. Tooth root was not engaged in actual process of gear transmission. Consequently, transition curve of fillet between involute curve and dedendum circle could be added when d f  > d b or d f  < d b .

  6. (6)

    Generating tooth shape: The addendum circle was extruded whose depth was B (B is tooth width) by using ‘Extrude’ and ‘Solid’ commands. Clicked ‘Extrude’ and ‘Cut’ buttons to remove redundant material (Fig. 3d), then sketched a curve shaped by two involutes, the addendum circle, the dedendum circle and two transition curves, and obtained the solid model. Then arrayed extruding results above and obtained the entire circumference of tooth profile with benchmark axis A_1, the angle 360°/z and teeth number z as given in Fig. 3e, f.

By using three-dimensional solid modeling, gear volumes with modulus of \(6 {\text{ mm}}\), tooth width of 30 mm, the modification coefficients varies from −0.6 to 0.6 are shown in Fig. 4c.

Fig. 4
figure 4

Gear volumes varied with different modification coefficients and number of teeth a reference circle method; b average circle method; c three-dimensional modeling method

Full size image

5 Results and discussion

5.1 Volume calculation results

Figure 4 shows the variation of spur gear billet volumes with various modification coefficients and gear teeth by using above three methods. When modification coefficients are identical, gear volumes rise with increasing of the number of gear tooth. Also, when gear tooth are identical, the change of modification coefficient has little influence on the gear volume. Gear volume curves with above three methods are some increasing exponential function curves, which the fitting functions are defined as below:

$$y = y_{0} + A\,{ \exp }( - x/t)$$
(13)

By analyzing sample curves of spur gear billet volumes, the value of offset y0 = 1; the amplitude A = 2; decay constant t = 1. Although volume calculation methods are different, the fitting degree of the volume curve is very well and their variation trends are basically identical. Therefore, the consistency of volume curves provides a foundation for calculation and analysis of relative errors as below.

5.2 Theoretical calculation of relative errors

By using Pro/E three-dimensional solid modeling method to calculate gear billet volume as a standard in cold precision forging, calculation formulas of relative errors are respectively shown as below. Relative errors of reference circle method and Pro/E solid modeling method are shown in Fig. 5a. Relative errors of the average circle method and the Pro/E solid modeling method are shown in Fig. 5b.

Fig. 5
figure 5

Relative error curves with different modification coefficients and number of teeth a reference circle method; b average circle method

Full size image
$$F_{a} = \left| {\frac{{V_{a} - V_{\text{proe}} }}{{V_{\text{proe}} }}} \right| \times 100\,\%$$
(14)
$$F_{r} = \left| {\frac{{V_{r} - V_{\text{proe}} }}{{V_{\text{proe}} }}} \right| \times 100\,\%$$
(15)

Figure 5a shows reference circle method to calculating gear volume with different number of tooth and modification coefficients. It is seen that the bigger degree of modification increases, the bigger the relative error is. When the absolute value of modification coefficient is 0.6, the relative errors vary from 2.10 % to 10.41 %. While modification coefficient is 0, the relative errors reach the maximum of 1.105 %. When modification coefficients are identical, the relative errors also increase with decrease of tooth number.

Figure 5b shows average circle method for calculating gear volume with different numbers of tooth and modification coefficients. Relative errors fluctuate with the change of modification coefficient. Relative errors decrease sharply with the increase of absolute value of modification coefficient. When the absolute value of modification coefficient is 0.6, relative errors vary from 0.002 % to 0.38 %. While modification coefficient is 0, the relative errors reach the minimum 1.491 %. When modification coefficients are identical, the relative errors increase with decrease of tooth number.

The relative error is determined by the number of tooth, modification coefficient and top clearance coefficient, etc. With regard to modified gear, relative errors with average circle method are lower than that of reference circle method, which are both increased with decrease of teeth number. This may be attributed to modification degree of the spur gear that is considered by using average circle method. As the gear tooth increase, the shape of gear is much closer to a regular cylinder. This is because the relative error of the gear billet volume is less affected by the irregular tooth shape.

6 Experimental verification

The cold precision forging experiment was carried out with pure industrial aluminum. The shape sizes of the top die and the bottom die assembled in cylindrical spur gear forming mould were processed by W-EDM (wire-cut EDM machine) in accordance with the size of standard spur gear. The experiments were conducted on the 2,000 kN hydraulic press with the speed of \(1.0\,{\text{mm/min}}\) at room temperature and the cylindrical billet was lubricated by dipping into mineral oil. The die structure of cold precision forging was designed as shown in Fig. 6 and basic parameters of experimental standard gear are listed in Table 1.

Fig. 6
figure 6

Die structure of gear cold precision forging: (1) lower platen; (2) guide bushing; (3) hexagon socket head cap screws; (4) shrink ring; (5) bottom die; (6) hexagon socket head cap screws; (7) gear billet; (8) upper platen; (9) hexagon socket head cap screws; (10) support plate; (11) upper die holder; (12) guide pin; (13) floating die holder; (14) spring; (15) top die; (16) ejector; (17) ejector beam; (18) hexagon socket head cap screws; (19) cushion block; (20) hexagon socket head cap screws

Full size image
Table 1 Basic parameters of experimental spur gear
Full size table

It can be observed that the tooth profile of formed cylindrical gear by experiment (Fig. 7) is fully filled and with a good integrity. The volumes of formed cylindrical spur gear calculated by above three methods were measured with Archimedes drainage method. Relative errors of billet volume of cylindrical spur gear between the calculated and the experimental were presented in Table 2. The relative error with average circle method is less than 1.5 %, indicating a higher calculation accuracy than traditional reference circle method. Moreover, the experimental gear billet volume is lower than that of the calculated one due to the limitation of experimental conditions, such as billet internal metallurgical defects, machining precision of forged part, experimenter, etc. It is concluded that the experimental result with average circle method can completely fulfill the engineering requirements in cylindrical spur gear cold precision forging.

Fig. 7
figure 7

Photos of experiment die and formed cylindrical spur gear: a die structure; b bottom die; c cylindrical billet; d forged gear

Full size image
Table 2 Relative errors for spur gear billet volume (mm3) between the calculated and the experimental
Full size table

7 Conclusions

The spur gear billet volumes with different gear teeth and various modification coefficients are obtained by using the reference circle method, average circle method and three-dimensional modeling method, respectively. The cold precision forging experiments are carried out with various gear billet volumes. The conclusions can be summarized as follows:

  1. (1)

    Observing relative error curves of two alternative calculating methods, the maximum relative error of average circle method is less than 1.5 %. The maximum relative error of the average circle method is nearly equal to the minimum relative error of the reference circle method. Therefore, the average circle method is a more accurate way to obtain the gear billet volume.

  2. (2)

    By experimental verification in the cold precision forging of spur gear, the relative error of the calculated with reference circle method is 0.98 %, while the average circle method is 0.42 %. Relative error of the experimental with reference circle method is 1.78 %, while the average circle method is 1.32 % in the experiment, which agrees well with the theoretical calculation. With brief calculating process, convenient operation and higher precision, average circle method possesses an obvious advantage in calculating the billet volume in spur gear cold precision forging.