1 Introduction

At the present time, spiral ropes are widely used in lightweight cable-supported structural systems such as sports stadia, suspended bridges and large Ferris wheels. A rope can be a critical load carrier of these structures (Beltrán and Williamson 2011; Stanova et al. 2011a).

With the increase of demand in predicting the behavior of ropes, many advanced digital techniques had been used in the strand and rope analysis. Computer-aided design and the finite element method created powerful sophisticated tools for the modeling and analysis of ropes. Judge et al. (2012) developed full 3D elastic–plastic finite element models of the multi-layer spiral strand cables subjected to quasi-static axial loading using LS-DYNA. Nawrocki and Labrosse (2000) presented a finite element model of a simple straight wire rope strand and studied all the possible inter-wire motions. The role of contact conditions in pure axial loading and axial loading combined with bending were investigated. Stanova et al. (2011b) established a geometric model of a multi-layered strand by CATIA V5 and analyzed force-strain relationship of the strand by ABAQUS/Explicit. Jiang et al. (2000, 2008), Jiang (2012) performed concise finite element models for 1 × 7 wire strand under axial extension and pure bending load, and studied the contact stress among wires, wire radial displacement, global response of the strand and predicted the detailed progressive nonlinear plastic behaviors of the strand wires. Ma et al. (2008, 2009) reported the 6 × 19 IWS right lang lay and right ordinary lay rope models with ANSYS software. Wang et al. (2012, 2013) proposed finite element models for 6 × 19 wire rope from the viewpoint of determination of fretting parameters. Many scholars (Bradon et al. 2007; Ghoreishi et al. 2007a, b; Usabiaga and Pagalday 2008; Argatov 2011; Beltrán and Williamson 2011; Paczelt and Belezna 2011; Beltra’n and Vargas 2012; Prawoto and Mazlan 2012) dealt with theoretical models, fiber ropes and broken ropes using 3D finite element analyses.

However, few models with different twisting manners of open spiral ropes had been reported.

In this study, three geometric models of open spiral wire rope 1 × 37 with different twisting manners of wires were built by CAD software Pro/ENGINEER. The models were imported into the ANSYS/Workbench. Behavior of the models obtained from finite element analysis was compared with theoretical and experimental data. The effect of twisting manner on open spiral rope was analyzed.

2 Geometric models generation

2.1 The parameters of models

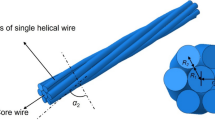
The cross-section of an open spiral rope 1 × 37 with a structure of wires 1 + 6 + 12 + 18 in the three wire layers is shown in Fig. 1.

Fig. 1
figure 1

The structure of an open spiral rope 1 × 37

Full size image

In wire ropes (Feyrer 2007), spiral ropes were round strands as they had an assembly of layers of wires laid helically over a center with at least one layer of wires being laid in the opposite direction to that of the outer layer. To predict the effect of twisting manner on open spiral rope 1 × 37 under tensile loads, three cables with different twisting manners and equal diameters of wires are modeled. The parameters of the three investigated ropes (Feyrer 2007) are shown in Table 1. The lay radius of wires in the individual layers of the strand is

$$ r_{\text{1}} = \frac{{d_{0} + d_{1} }}{\text{2}} = \frac{{\text{1}\text{.35} + \text{1}\text{.25}}}{\text{2}} = \text{1}\text{.3 mm} $$
$$ r_{2} = r_{1} + \frac{{d_{1} + d_{2} }}{2} = \text{1}\text{.3} + \frac{{\text{1}\text{.25} + \text{1}\text{.25}}}{\text{2}} = \text{2}\text{.55 mm} $$
$$ r_{3} = r_{2} + \frac{{d_{2} + d_{3} }}{2} = \text{2}\text{.55} + \frac{{\text{1}\text{.25} + \text{1}\text{.25}}}{\text{2}} = \text{3}\text{.8 mm} $$
Table 1 The parameters of models
Full size table

2.2 CAD modeling

The parameter of the helical curve of the wire centerline in a straight spiral rope as fellows (Feyrer 2007):

$$ \begin{aligned} x & = - r \cdot {\text{sin}}\, \phi \\ y & = r \cdot \text{cos}\,\phi \\ z & = \frac{r}{\tan \alpha } \cdot \phi \\ h_{w} & = \frac{{2\uppi \cdot r}}{\tan \left| \alpha \right|} \\ \end{aligned} $$
(1)

where ϕ is the angle of rotation (the direction of rotation in anti-clockwise is positive, the clockwise is negative), h w is lay length, α is the angle of lay and \( r = r_{i} \,(i = \text{0, 1, 2, 3)} \) (see Fig. 2).

Fig. 2
figure 2

Wire space curve in a straight spiral rope

Full size image

The lay length of first layer is

$$ h_{w1} = \frac{{2\pi r_{1} }}{{\tan \alpha_{1} }} = \frac{2 \times 3.14 \times 1.33}{\tan 14} = 32.74 \, \text{mm} $$

The lay length of second layer is

$$ h_{w2} = \frac{{2\pi r_{2} }}{{\tan \alpha_{2} }} = \frac{2 \times 3.14 \times 2.55}{\tan 14} = 64.23 \, \text{mm} $$

The lay length of third layer is

$$ h_{w3} = \frac{{2\pi r_{3} }}{{\tan \alpha_{3} }} = \frac{2 \times 3.14 \times 3.8}{\tan 14} = 96.42 \, \text{mm} $$

The helical curve of the wire centerline of rope can be represented by cylindrical coordinates in PRO/ENGINEER. The spiral curve in cylindrical coordinates is written as

$$ \begin{aligned} R & = r \\ \text{theta} & = \text{360} \times n \times t \\ z & = t \times h \\ \end{aligned} $$
(2)

where r is the radius of helix, n is the number of helix, the valve of t between 0 and 1, and h the pitch of helix.

By Eq. (2), turn Eq. (1) into Eq. (3) as the following:

$$ \begin{aligned} x & = r \times \cos (360 \times n \times t\text{)} \\ y & = r \times \sin (360 \times n \times t) \\ z & = t \times h \\ \end{aligned} $$
(3)

The defined geometric parametric equations are used to generate the spatial curves of the wires centerline in the individual layers of the rope (see Table 2).

Table 2 The equations of helical curve
Full size table

In Pro/ENGINEER, the helical curve of the wire centerline in first layer of model 1 is constructed according to equations (see Table 2). The wire is generated by the sweep function and arrayed the wire in accordance with the number of wires in first layer. Consequently, the generation of six wires in first layer is finished. The mentioned approach is repeated for the other wires in all layers of the rope. Topology of the generated wires in the second, third layer and core wire. It should be noted that wires of all layers are modeled as the same way whereas the adequate parametric equations with the corresponding values of the wire diameter and the lay radius for the actual layer must be used.

The other two models are created analogously. Three models of spiral ropes are shown in Fig. 3. It can be seen from Fig. 3a that the twisting manner of wires in the first layer of the first model is clockwise, that of the second layer is anti-clockwise and that of the third layer is clockwise. The twisting manner in the first layer of second model is clockwise, that of the second layer and third layer is anti-clockwise (see Fig. 3b). The twisting manner in the first layer of third model is anti-clockwise, that of the second layer is anti-clockwise and third layer is clockwise (see Fig. 3c).

Fig. 3
figure 3

The three models of spiral ropes

Full size image

3 The generation of 3D FE models

The geometric models of spiral ropes created in PRO/ENGINEER are imported into the finite element software of ANSYS/Workbench, which are used for finite element numerical analysis. These CAD models are exported as XT files to ANSYS/Workbench software.

3.1 Material properties and contacts

The assumed modulus of elasticity of the wire material is E = 188 GPa, the density is q = 7,800 kg/m3, the Poisson’s ratio is v = 0.3 (Beltrán and Williamson 2011).

The frictional contact types are defined between the surfaces of the individual adjacent wires of ropes. The coefficient of friction between wires is \( \mu = \text{0}\text{.2} \). The pairs of contact are 329. The formulation of contact is Augmented Lagrange.

3.2 Finite element mesh generation

The mesh method is sweep method. The size of element in sweep method is 0.5 mm. Face meshes with dimensions of 0.3 mm are used for the finite element analysis. The sizing of relevance center is fine. The skewness of mesh size is 0.56. The meshes for each wire are generated independently. Three models are composed of 195,395 elements and 941,117 nodes.

3.3 Supports

The supports of one end in the models are fixed support (fully fixed in all degrees of freedom) and the supports of other end in the models are submitted to a force. Four different loading forces: F1 = 13,680 N, F2 = 20,000 N, F3 = 25,000 N and F4 = 30,000 N are considered for each model.

4 Results and discussion

4.1 Comparison of normal stresses with theoretical and experimental data

For previous literature (Feyrer 2007; Beltrán and Williamson 2011; Stanova et al. 2011a, b) reported the twisting manner of rope as those of first model, the first model is compared with theoretical and experimental data. The normal stresses of four wires at the X positive direction (see Fig. 3a) are studied. The normal stresses along Z axis of model 1 are presented in Fig. 4 and Table 3. The normal stress nephogram along Z axis of model 1 and model 2 at tensile force (F1 = 13,680 N) are presented in Fig. 5. For the rope has equal magnitude of lay angle for all wire layers, the tensile stress of four wires in the three layers are nearly the same. The center wire of the rope has a higher stress than the other wires.

Fig. 4
figure 4

The normal stress along Z axis of model 1: a core wire, b the first layer, c the second layer and d the third layer

Full size image
Table 3 Average normal stresses of model 1 along the Z axis obtained from Fig. 4
Full size table
Fig. 5
figure 5

The normal stress nephogram along Z axis of model 1 and model 2

Full size image

Numerical stress values of model 1 obtained by the present finite element analysis are compared with those of the analytical approach proposed by Feyrer (2007). The tensile stress \( \sigma_{{\text{tk}}} \) in a wire of a specific wire layer k is

$$ \sigma_{tk} = \frac{{\frac{{\cos^{2} \alpha_{k} }}{{1 + \upsilon_{k} \cdot \sin^{2} \alpha_{k} }} \cdot E_{k} }}{{\sum\nolimits_{i = 0}^{n} {(\frac{{z_{i} \cdot \cos^{3} \alpha_{i} }}{{1 + \upsilon_{i} \cdot \sin^{2} \alpha_{i} }} \cdot E_{i} \cdot A_{i} )} }} \cdot S $$
(4)

where E i and/or E k is the modulus of elasticity of the wire, A i is the cross-sectional area of the wire, υ i and/or υ k is the Poisson’s ratio, α i and/or α k is the lay angle, n is the number of wire layers counted from the inside with n = 0 to the core wire and z i is the number of wires in the wire layer, S is the tensile force. Stresses of the wires for the rope calculated according to Feyer’s method (Feyrer 2007) and Eq. (4) are used in the calculating process. The obtained results are presented in Table 4.

Table 4 The calculated stresses of rope
Full size table

The relative differences e σ are calculated according to the following equation.

$$ e_{\sigma } = \frac{{\sigma^{\text{FEM}} - \sigma^{\text{TD}} }}{{\sigma^{\text{TD}} }}100\;\% $$
(5)

\( \sigma^{{\text{FEM}}} \) is the stress obtained by the finite element analysis. \( \sigma^{{\text{TD}}} \) is the stress according to the theoretical data. The relative differences are shown in Table 5. When a straight spiral rope becomes longer and thinner under a tensile force, the wire helix will be deformed. Beside the tensile stresses, there exist bending stresses, torsion stresses and radial pressures from the small length-related radial force of the wires. Additionally, the wire stresses in the straight spiral rope neglected in Eq. (4), the numerical stress values of the model obtained by the present finite element analysis are slightly higher than those of theoretical data.

Table 5 Relative differences e σ
Full size table

The results show that the strain discrepancies do not exceed 9 %. The mesh quality determines calculation accuracy. If mesh is refined, the relative differences will be smaller at cost of computational time.

The force-strain relationship of the studied rope obtained by the present finite element analysis is compared with those obtained experimentally and theoretically by Nakai et al. (1975). The compared results are shown in Fig. 6.

Fig. 6
figure 6

Comparison of the force-strain relationship of the ropes obtained by the present finite element analysis with those obtained experimentally and theoretically by Nakai et al. (1975)

Full size image

The relative differences e ɛ are calculated according to the testing results (Nakai et al. 1975).

$$ e_{\varepsilon } = \frac{{\varepsilon^{{\text{FEM}}} - \varepsilon^{{\text{TEST}}} }}{{\varepsilon^{{\text{TEST}}} }}\times 100\;\% $$
(6)

where \( \varepsilon^{{\text{FEM}}} \) is the strain obtained by the finite element analysis. \( \varepsilon^{{\text{TEST}}} \) is the strain according to the testing results.

The results show that the strain discrepancies do not exceed 4.74 %.

The present FE model is in an acceptable level of accuracy as compared with theoretical and experimental data. The model is validated.

4.2 Comparison the force-strain relationship of three models

The resultant elongations of three models are shown in Fig. 7. The resultant elongations of model 2 are larger than those of model 1 and model 3.

Fig. 7
figure 7

Resultant elongations of three models

Full size image

The resultant strain is expressed as

$$ \varepsilon = \frac{\Delta L}{{L_{0} }} $$
(7)

where ΔL is the resultant elongations of the model.

The force-strain relations of three models are compared, shown in Fig. 8. The force-strain relationship of model 1 is similar with that of model 3. The first twisting manner of model 1 is contrary to the twisting manner of model 3 and the other twisting manner of two models are identical. The third twisting manner of model 2 is contrary to the twisting manner of model 1 and the other twisting manner of two models are the same. For the resultant elongations and the strain of model 2 are higher than that of other models, it indicates that the relation of twisting manner between first layer and second layer has little influence on strain and stress and those between second layer and third layer has influence on the response of the rope under tension.

Fig. 8
figure 8

Force-strain relations of three models

Full size image

4.3 Comparison of the equivalent stresses for different models

For the resultant elongations and the strain of model 1 are similar with those of model 3, only the equivalent stresses of the four wires in model 1 and model 2 at the X positive direction (see Fig. 3a, b) along Z direction are studied.

The equivalent stresses of layers in two models at tensile forces: F1 = 13,680 N, F2 = 20,000 N, F3 = 25,000 N and F4 = 30,000 N are shown in Fig. 9 and Table 6.

Fig. 9
figure 9

The equivalent stress of two models at different tensile forces: a core wire, b first layer, c second layer and d third layer

Full size image
Table 6 Average equivalent stresses obtained from Fig. 9
Full size table

The equivalent stress nephogram of two models at tensile force (F1 = 13,680 N) are shown in Fig. 10, and the contacting stress distribution nephogram between inner and outer wire layers of two models are shown in Fig. 11.

Fig. 10
figure 10

The equivalent stress nephogram of two models

Full size image
Fig. 11
figure 11

The contacting stress distribution nephogram between inner and outer wire layers of two models

Full size image

The equivalent stress of the first layer in model 2 is larger than the yield stress 1,580 MPa (Beltrán and Williamson 2011) from F2 = 20,000 N to F4 = 30,000 N. Plastic deformation happens on the wires of first layer. Though the twisting manner of model 2 are satisfied with that spiral ropes were round strands as they had an assembly of layers of wires laid helically over a center with at least one layer of wires being laid in the opposite direction to that of the outer layer (Feyrer 2007), it can be seen that the equivalent stresses of layers in model 2 are higher than that of model 1 which further confirms the second and third twisting manner have effect on ropes.

The structures of model 2 are different from model 1 in twisting manner of outer and the strain and stresses of model 2 are higher than model 1. The structures of model 3 are different from model 1 in twisting manner of first layer and these two models are similar in strain and stresses. Contrasting the structures of three models, it means that the second twisting manner of open spiral rope 1 × 37 should be contrary to that of the outer layer. In processing of manufacture the twisting manner similar to twisting manner of model 2 do not choose.

5 Conclusions

In order to simulate the complex geometry of open spiral ropes by finite element analysis, the geometric parametric equations were established and implemented in PRO/ENGINEER software for the geometric models. The methodology of their implementation and the approach for creation of the geometric model for the open spiral ropes were demonstrated. Three models had been established in order to predict the behaviors of the models under different tensile loads by ANSYS/Workbench.

The finite element models of spiral ropes with complicated geometry and contact conditions had been developed in this study. The normal stresses and force-strain relationship of the studied ropes obtained by the present finite element analysis were compared with those obtained theoretically and experimentally. The present FE model was proved to be accurate sufficiently as compared with theoretical and experimental result, which can be utilized to optimize key geometric parameter-twisting manner.

Further development is ongoing to analyze the equivalent stresses which was induced by the twisting manner of cables. The twisting manner in each layer was important to ropes and the twisting manner of open spiral ropes with three layers should not choose the twisting manner of model 2. The outer twisting manner should be contrary to that of the second layer, no matter what is the first twisting manner of wires.