1 Introduction

Injecting CO2 into coal seams could enhance coal bed methane recovery (CO2-ECBM). The effectiveness of this technique depends on the different adsorption abilities of coal for CO2 and CH4 and the displacement of CH4 as the result of injection of a certain quantity of CO2 into deep coal seams. In 1995, CO2-ECBM experiments were first conducted in the Burlington Allison Unit in the San Juan basin in the United States, resulting in a 15 % increase in coal bed methane output, despite remarkable differences in the different wells (White et al. 2005). Pilot experiments were performed later in Canada, Poland, and Japan. The experimental results indicated that injecting CO2 into coal seams could enhance CBM recovery, and under appropriate conditions, could sequester certain amounts of CO2 (Gunter et al. 2004; White et al. 2005; Shi et al. 2008). Since 2002, additional CO2-ECBM experiments have been performed in a number of places in China, such as Qinshui basin in Shanxi, Luling in Huaibei, and Encun in Jiaozuo. Some wells yielded good results with respect to methane output, but others did not perform satisfactorily. These results demonstrated that successful CO2 injection depends upon certain conditions (Wong et al. 2007; Ye et al. 2007).

Currently, CO2-ECBM research is mainly focused on the different adsorption abilities of coal for CO2 and CH4 and the changes in coal permeability caused by CO2 adsorption. With respect to the difference in the adsorption of CO2 and CH4, some laboratory experiments have shown that more CO2 is adsorbed in coal than CH4 under the same conditions, and CO2 may displace CH4 adsorbed by coal (Reznik et al. 1984; Zuber 1998; Clarkson and Bustin 2000; Wu and Guo 2001; Zhang et al. 2005; Tang et al. 2006; Lv et al. 2011). With respect to coal matrix expansion and permeability changes due to CO2 adsorption, mathematical and physical models of coal matrix expansion and contraction during the adsorption/desorption process based on surface chemistry and elastic mechanics theories have been confirmed with experimental data (Wu et al. 2005; Zhou et al. 2011; Ni et al. 2013). In addition, coal matrix expansion and contraction and permeability changes during the adsorption/desorption process have been measured using coal adsorption, deformation, and permeability testers; a regularity of the changes was discovered that has provided a theoretical basis for additional field CO2 injection studies (Fang et al. 2009; Liu et al. 2010; Duan et al. 2012).

In fact, coal contains clay minerals such as kaolinite, illite, and montmorillonite, which after reacting with carbonic acid formed from injected CO2 (Pi et al. 2009) may affect the permeability of coal seams to some degree. Montmorillonite is a silicate mineral with two silicon-oxygen tetrahedra and an aluminum-oxygen octahedron. Studies of the dissolution and precipitation behavior of montmorillonite in hydrochloric and mud acid solutions and the dissolution profiles of Si and Al from montmorillonite have revealed that the secondary precipitation of montmorillonite may reduce the permeability of coal seams (Wei and Tian 1998; Zhong 2006; Yan et al. 2007). It has also been found that the dissolution processes for Si and Al from montmorillonite into an aqueous solution are different (Sondi et al. 2008). Furthermore, montmorillonite has been shown to dissolve more readily in alkaline (NaOH, Na2CO3) solutions with an obvious increase in Si and Al ions in the solutions, and generally more Si ions than Al ions (Xiong et al. 2009).

CO2, after being injected into coal seams, may form carbonic acid, which is more acidic than water and alkaline solutions and less acidic than hydrochloric and mud acid solutions. Under different conditions (solution acidity, pH value, and temperature), montmorillonite exhibits different dissolution and precipitation profiles in carbonic acid solutions. The study of the Si and Al dissolution/precipitation profiles in carbonic acid solutions after acidification of montmorillonite may promote the understanding of the micromechanisms and reaction behavior of montmorillonite after the injection of CO2 into coal seams; thus, the study is important for reducing coal seam damage caused by CO2 injection and enhancing coal bed methane recovery.

2 Experimental

2.1 Sample preparation

Samples of montmorillonite ores were taken from Lingshou in China’s Hebei province. The ores were first crushed and sifted using a sieve (>100 mesh per square inch). The montmorillonite particles were analyzed using an X-ray diffractometer; subsequently, elemental analysis was performed on more than 90 % of the montmorillonite powder using an energy-dispersive X-ray spectrometer. The results are listed in Table 1.

Table 1 Elemental composition of the original montmorillonite sample
Full size table

2.2 Experimental procedure

The deeper the coal seam, the higher the temperature. Generally, the geothermal gradient is 1–3 °C/100 m. At present, the mining depth of coal bed methane wells is generally no more than 1,200 m. When the surface temperature is 15 °C, given a geothermal gradient of 2 °C/100 m, the coal seam temperature at a depth of 500 m will be around 25 °C, and the temperature at a depth of 1,250 m will be 45 °C. At ambient temperature, the pH value of lab-made saturated carbonic acid solutions is 4.3. When CO2 is released and the carbonic acid solution becomes unsaturated, the pH value is greater than 4.3. Therefore, in order to simulate the reactions of montmorillonite in carbonic acid solutions under varying saturation conditions and at varying depths, lab experiments were conducted at different temperatures (25, 35, and 45 °C) and pH conditions (4.3, 5.0, and 5.7) as follows: montmorillonite (2 g weighed using a precision weighing balance) was placed in an inert plastic bottle. A carbonic acid solution was then added in a solid: liquid ratio (g/mL) of 1:15, and the bottle was sealed and placed in a constant-temperature box set at 25, 35, or 45 °C. Liquid-phase composition and solid-phase elemental and structural analyses were performed after varying periods of reaction time (1, 4, 9, 24, 48, 72, 96, 120, and 144 h).

2.2.1 Liquid-phase composition analysis

The analysis of the composition of the liquid phase was performed in order to determine the changes in the concentrations of Si and Al in solution. A sample of supernatant was removed from the reaction bottle using a syringe and filtered through filter paper. The Si concentration in the solution was determined using the ammonium molybdate spectrophotometric method, and the Al concentration was determined using the chrome azurol photometric method (Chen et al. 2003). A Shanghai Youke 721-type visible spectrophotometer was used for the analysis.

2.2.2 Solid-phase composition analysis

Analysis of the montmorillonite was performed in order to determine the structural and elemental changes that occurred after reaction with carbonic acid. The samples (original mineral samples and reacted samples) were placed in an oven and dried at 80 °C to a constant weight and subjected to X-ray diffraction and energy-dispersive X-ray analysis. A D8ADVANCE X-ray diffractometer and an INCA-ENERAGY 250-type energy-dispersive X-ray spectrometer were used for the analyses.

3 Results and discussion

3.1 Liquid-phase composition

3.1.1 Experimental results

The changes in the Si and Al concentrations in solution after reaction of the montmorillonite in carbonic acid solutions at different temperatures and pH values are shown in Figs. 1 and 2, respectively.

Fig. 1
figure 1

Changes in the Si and Al concentrations in solution with time at different temperatures

Full size image
Fig. 2
figure 2

Changes in the Si and Al concentrations in solution with time at different pH values

Full size image

As can be seen in Figs. 1 and 2, several observations can be made regarding to the dissolution of Si and Al in carbonic acid solutions.

3.1.1.1 Effect of reaction temperature on dissolution

In carbonic acid solutions of the same pH, for a given reaction time the Si concentration increased as the temperature increased. At pH 4.3, the maximum Si concentration at 25, 35, and 45 °C was 16.06, 19.15, and 26.05 mg/L respectively. On the other hand, there was little change in the Al concentration, which remained below 1.0 mg/L.

3.1.1.2 Effect of the carbonic acid solution pH on dissolution

At given temperatures and reaction times, the Si concentration increased as the pH value decreased but only slightly. At 45 °C, the maximum Si concentration at pH 4.3, pH 5.0, and pH 5.7 was 26.05, 25.24, and 22.52 mg/L, respectively. Again, there was little change in the Al concentration, which remained at 1.0 mg/L, as the pH decreased.

3.1.1.3 Effect of reaction time on dissolution

At a given carbonic acid solution pH, the Si concentration in solution initially increased and then decreased with reaction time. In addition, at higher temperatures, the time to reach the maximum Si concentration decreased. Thus, at 25, 35, and 45 °C, the maximum Si concentration was observed at approximately 96, 72, and 48 h, respectively. Furthermore, when the Si concentration reached a certain level, an Si(OH)4 colloidal precipitate was formed (Wei and Tian 1998), resulting in a decrease in the Si concentration. The colloidal precipitate was then adsorbed on the surface of the montmorillonite. The dissolution rate for Si increased with increasing temperature; at 45 °C, the maximum Si concentration in solution was reached and the precipitate was formed, leading to a decrease in the Si concentration. The dissolution of Al led to the formation of an Al(OH)3 colloidal precipitate. Compared to Si, Al reached its solubility equilibrium more rapidly, and thus dissolved more readily.

3.1.2 Si dissolution kinetic analysis

According to the profile for Si dissolution from montmorillonite into the reaction solution, the Si concentration increased and then decreased. In order to calculate the Si dissolution rate and apparent activation energy and determine the fitting of solid–liquid kinetic equations to the changing Si dissolution rates, the point at which the maximum Si concentration was reached (48 h) at 45 °C was used as the critical point for distinguishing Si dissolution from precipitation.

The Si dissolution rate was defined as follows:

$$ X(\text{Si}) = \frac{m}{M}, $$
(1)

where X(Si) is the Si dissolution rate, m is the mass of dissolved Si (g), and M is the Si concentration in the sample and was calculated using the mass of the sample and the mass fraction of Si (g).

Solid–liquid–phase kinetic reaction models for mineral dissolution in acidic solutions mainly include first-order reaction models, interfacial reaction models, and capacity models (Zhong 2006).

The reaction rate equation for the first-order reaction model is:

$$ \text{d}M/\text{d}t = - KM^{m} \left[ {H^{ + } } \right]^{n} = - K'M^{m} $$
(2)

where m and n are the reaction orders; K and K’ are the reaction rate constants and m = 1. Through integration, we obtain:

$$ \text{ln}\left( {1 - X} \right) = K'\,t $$
(3)

The interfacial model can be divided into a reaction-controlled interfacial model and a diffusion-controlled interfacial model.

The reaction rate equation for the reaction-controlled model is:

$$ \text{d}X/\text{d}t = K\left( {3V/r_{0}^{3} } \right)\left( {1 - X} \right)^{2/3} $$
(4)

where r0 is the particle size of the mineral, V is the molar volume, and X is the cation leaching rate.

Through integration, we obtain the following equation:

$$ 1 - \left( {1 - X} \right)^{1/3} = k'\,t $$
(5)

The kinetic equation for the diffusion-controlled model is as shown below:

$$ 1 - 3\left( {1 - X} \right)^{2/3} \,+\, 2\left( {1 - X} \right) = k'\,t $$
(6)

If diffusion is omitted, then the reaction rate equation for the capacity model is as shown below:

$$ \text{d}X/\text{d}t = K\left[ {\text{H}^{ + } } \right]^{m} (1 - X)^{n} $$
(7)

When there is an extraordinary excess of acid solution, [H+] may be regarded as a constant value and is as shown below:

$$ \text{d}X/\text{d}t = k'\left( {1 - X} \right)^{n} $$
(8)

The fitting results for the different kinetic models to the Si dissolution rates at different reaction times are listed in Table 2. As can be seen from the data, the capacity model did not fit the reaction order well. On the other hand, the diffusion-controlled model had the highest correlation coefficient, and thus was the best fit.

Table 2 Fitting results for the Si dissolution kinetic constants for different models
Full size table

3.1.3 Calculation of the apparent activation energy

The reaction rate constants at different temperatures (25, 35, and 45 °C) obtained from the fitting of the diffusion-controlled model are listed in Table 3.

Table 3 Reaction rate constants (Ln K and 1/T) at different temperatures obtained from fitting the diffusion-controlled model
Full size table

Using the Arrhenius formula:

$$ K = A{ \exp }\left( { - E{\text{a}}/RT} \right), $$
(9)

A plot of the Ln K and 1/T values (Table 3) was created, and the apparent activation energies for Si dissolution during the reaction of montmorillonite in carbonic acid solutions with different pH values were obtained (Yang et al. 1999; Zhang 2008) (Table 4).

Table 4 Apparent activation energies for Si dissolution at different pH values
Full size table

As indicated in Table 4, all of the apparent activation energies for Si dissolution were below 42 kJ/mol. This result suggests that the reaction proceeds via a diffusion-controlled mechanism. The apparent activation energy decreased with a decrease in the solution pH. However, it should be noted that while these results indicate that Si dissolved more readily at lower pH values, due to the weak acidity of carbonic acid, the apparent activation energies were all close in value.

3.2 Solid-phase composition

3.2.1 Energy-dispersive X-ray spectroscopy analysis

The results of the energy–dispersive x-ray spectroscopy analysis of the montmorillonite samples reacted for different periods of time in carbonic acid solutions at pH 4.3 and 45 °C are listed in Table 5 and shown in Fig. 3.

Table 5 Results of the energy-dispersive x-ray analysis of montmorillonite reacted for different times in a pH 4.3 carbonic acid solution at 45 °C
Full size table
Fig. 3
figure 3

Energy–dispersive X-ray spectrum of montmorillonite reacted for different times in a pH 4.3 carbonic acid solution at 45 °C

Full size image

As can be seen in Table 5 and Fig. 3, both the Si and Al content initially decreased and then increased, but the Al concentration changed much less than that of Si. This result corresponds to the Si and Al concentration changes in the reaction solution, in which the Si concentration initially increased and gradually declined. The Si concentration solution reached a maximum at 48 h and was low at 144 h. In the solid-phase montmorillonite, the Si concentration was the lowest at 48 h and higher at 144 h due to Si dissolution and precipitation, respectively. When the Si concentration in solution reached a high level, the solid-phase Si concentration decreased, and when Si precipitation occurred in solution, the Si concentration in the solid phase increased. In addition, the concentrations of Mg, Ca, and Na in the solid phase decreased with reaction time due to Mg, Ca, and Na dissolution. Interestingly, the O concentration in the solid phase initially increased and then decreased, likely because the initial quantity of dissolved O was relatively small, resulting in a relative concentration increase followed by a decrease upon precipitation of Si and other elements at 144 h. Finally, there was no significant change in the K and Cl concentrations in the solid phase.

3.2.2 Structural analysis

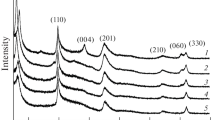
The X-ray diffraction patterns before and after reaction of the montmorillonite in a pH 4.3 carbonic acid solution at 45 °C for 144 h are shown in Fig. 4.

Fig. 4
figure 4

X-ray diffraction patterns before and after reaction of montmorillonite in a pH 4.3 carbonic acid solution at 45 °C for 144 h

Full size image

As can be seen in Fig. 4, the X-ray diffraction patterns before and after reaction of the montmorillonite in the carbonic acid solution were nearly the same, with no newly-generated or missing peaks. Carbonic acid is weak acid, and thus its reaction with montmorillonite is mild and results in little damage to the crystal structure of the mineral.

4 Conclusions

The reaction of montmorillonite in carbonic acid solutions at pH 4.3, 5.0, and 5.7 was performed, and the dissolution behavior of Si and Al and the elemental and structural changes in the montmorillonite were investigated. Based on the results of the analyses, the following conclusions were drawn:

  1. (1)

    At a given carbonic acid solution pH, the concentration of dissolved Si increased as the reaction temperature increased from 25 to 45 °C, but that of dissolved Al remained nearly the same. At a constant solution pH and temperature, the Si concentration in the solution initially increased and then gradually decreased with vibrations. The Si concentration in solution reached a maximum at approximately 48, 72, and 96 h at 45, 35, and 25 °C, respectively. The Al concentration, on the other hand, increased rapidly, reaching a maximum level in approximately 1 h and remaining stable thereafter.

  2. (2)

    At a constant temperature, the Si concentration in the carbonic acid solution increased with a decrease in the pH from 4.3 to 5.7, but the change was insignificant. The dissolution of Si from montmorillonite into the carbonic acid solution fit the diffusion-controlled interfacial reaction model. Under the conditions used in this study, the apparent activation energies for Si dissolution in pH 4.3, 5.0, and 5.7 carbonic acid solutions were 34.40, 35.27, and 35.68 kJ/mol, respectively. These results indicate that the higher the acidity of the carbonic acid solution, the easier it was for Si to dissolve.

  3. (3)

    Carbonic acid is a weak acid. Therefore, the reaction of montmorillonite in carbonic acid solution caused little damage to the crystal structure of the montmorillonite.