Statistics of intermittent granular flow from confined tabletop experiments

Abstract

It is often said that “granular matter is ubiquitous”. Many natural components and human products look and behave like grains: stones, debris, soils, on the one hand; food, pharmaceuticals, building materials, etc., on the other. However, the physics involved is still poorly understood due to its inherent difficulties. In fact, granular materials are an example of frictional, dissipative, nonlinear, out-of-equilibrium systems. One consequence is that they exhibit, under various circumstances, large and irregular fluctuations, finite size effects, and poor reproducibility (as everyone knows from trying to slowly pour sugar or coffee powder). This article summarizes some experimental results on the response of horizontal grain beds subjected to low rate shear stress. In this case, the response is often intermittent and irregular, the so-called stick–slip regime, and can only be described statistically. Small-scale experiments are the best way to collect the necessary large amount of data and, despite the difference in scale, can provide the basis for a better understanding of larger scale phenomena such as avalanches, landslides and earthquakes.

1 Introduction

“There are some, king Gelon, who think that the number of the sand is infinite in multitude; and I mean by the sand not only that which exists about Syracuse and the rest of Sicily but also that which is found in every region whether inhabited or uninhabited. Again there are some who, without regarding it as infinite, yet think that no number has been named which is great enough to exceed its multitude.” So says Archimedes in his book of the III century B.C. “The Sand-Reckoner” [1]. He had conceived the idea of the power of numbers and he wanted to demonstrate that these could express huge quantities. Therefore, when he wanted to think of something that could be found in almost unlimited amounts, he thought of sand grains. He also drew on the ideas of Aristarchus of Samos about a heliocentric universe, much larger than was then believed, to show that he could express numbers so large as to exceed the mass of sand that could fill that universe.

This introductory quote may help to recall how granular matter pervades our world and lives in, one might say, a multitude of forms and uses, both in the natural world and in human activities. Most of the earth’s constituents are in the form of grains, from powder to soil, debris, gravel, stones, rocks, and fault gouges. Main products of agriculture are seeds, grains, fruits. Construction, pharmaceuticals, chemicals, all are goods mostly produced, transported and stored in the form of grains.

In addition to the consequent impact on the economy and quality of life, granular matter is interesting from a scientific point of view, not only for its practical implications, but also because it is a visible example of a complex non-equilibrium system that includes phenomena such as non-linearities and energy dissipation. It can sometimes behave like common forms of matter such as solids, liquids, or gases, but even small perturbations can suddenly and inhomogeneously change its state. The physics of granular matter has overlaps with several other branches, such as the physics of fluids, glasses, soft matter, fracture, soil, and seismology. Among other complex systems, granular matter has the advantage that many of its properties can be studied with small and relatively simple experimental setups. The main objective of this paper is to illustrate and discuss some experimental results obtained by shearing a confined granular medium while it exhibits irregular and fluctuating dynamics, under normal conditions of temperature, pressure and humidity (dry grains). The main focus will be on the behavior of macroscopic quantities and on highlighting the common features observed in different experiments. Despite the chaotic and random nature of the dynamics, many statistical regularities emerge, making research in this field extremely exciting, challenging and maximally important for practical applications.

In the following, after a brief review in Sect. 2 of some phenomenology and shear properties of granular matter Sect. 3 describes the statistical properties of stress observed in experiments, and Sect. 4 deals with the statistics of quantities characterizing the intermittent shear. Section 5 illustrates some stochastic models that succeed in reproducing some of the main features observed experimentally, while Sect. 6 attempts to place these models in a broader theoretical framework. The last section, Sect. 7, tries to summarize the main findings, draw some conclusions, and envision possible future developments.

2 General aspects of granular matter

2.1 Phenomenology

Since everyone’s experience of granular matter is somewhat intuitive, it may seem superfluous to define it. In any case, it can be useful to quickly list the main properties that it should satisfy. Granular materials are defined as aggregates of macroscopic particles in the sense that their kinetic or potential energies are insensitive to thermal fluctuations. At room temperature, this means that their energies are greater than $\simeq 5\cdot 10^{-21}$ Joule. Grain interactions are hard-core and dissipate energy in collisions and sliding. In some cases, they can have low adhesion, on very short scales with respect to their dimension, and their size, shape, and roughness can be different even in the same assembly. Granular systems can be found in several different states, resembling ordinary matter, quasi-solid or quasi-fluid, but they can give rise to phenomena that are specific to these materials. Examples include segregation, stratification, compaction, local clustering in fluids, formation of shear bands, anomalous wave propagation, and many others [2].

Because of its relevance in engineering and geophysics, the mechanical response of granular matter has long been studied experimentally and is the subject of soil mechanics, which has become a very broad discipline in itself [3,4,5]. However, physicists famous for their important contributions in various fields have also studied granular materials. Examples are Charles-Augustin de Coulomb, Michael Faraday, Lord Rayleigh, Osborne Reynolds, and most recently the Nobel laureate Pierre-Gilles Gennes (a short historical introduction can be found in the book by Jaques Duran [6]). Certainly, a significant impulse to the physics of granular matter must be attributed to Ralph A. Bagnold, who, in a series of studies in the second half of the last century, gave fundamental contributions to this discipline, also addressing complex problems such as the formation and evolution of sand dunes [7].

Fig. 1

Stratification, an example of an unpredictable and non-equilibrium configuration of a granular pile formed by pouring an initially well homogeneous mixture of grains with different properties

The intrinsic non-equilibrium nature of granular matter, mainly due to frictional contacts and energy dissipation, and the variety of different situations in which it can be found make a unified approach difficult, if not impossible. Theories for different systems have been developed starting from microscopic kinetic theory or from continuous elasto-visco-plastic approaches. We refer to specific reviews for both general descriptions and more specialized expositions [2, 8,9,10,11,12,13,14,15,16,17,18,19,20].

In the late 80s, there was a surge of interest in granular matter in the physics community. It is hard not to think that this was in great part due to a seminal paper in which a pile of sand was used as a prototype or metaphor for self-organized out-of-equilibrium systems [21], as will be illustrated later. The increased interest stimulated many more studies [22] and led both to a better description and explanation of sometimes known but poorly understood phenomena, such as compaction and size segregation under vibration, flow stratification, and to the discovery of new manifestations of nonlinearity such as oscillons [23,24,25,26], Recently, granular shear experiments have also been performed in microgravity [27]). A laboratory realization of stratification is shown in Fig. 1 as an example of such phenomena. A key role in granular flow dynamics is played by shear and the next section is devoted to a brief introduction to some of its general aspects.

2.2 Shear stress and onset of stick slip

As briefly recalled above, the phenomenology of granular media is extremely broad, and there is no single description, and probably never will be, but there are theories or models adapted to specific situations, although they do not always work well. Quoting Charles Campbell [13] “Yet the design of granular systems is still something of a black art, in part because even the most basic flow mechanisms of granular materials are not well understood. In fact, science has not identified the set of material properties that control flow behavior”. Fortunately, however, there are several situations in which good predictions can be made. They generally correspond to homogeneous and not too low packing fractions (the ratio of the volume occupied by the grains to the available volume), or high normal pressure, or rapid flow, but no general rule can be given.

For what follows, it is not necessary to recall the full notions of stress and strain tensors. It is sufficient to define the normal stress component $\sigma =F_n/A$, where $F_n$ is the force perpendicular to a plane surface of area A, and the shear stress component $\tau =F_t/A$, which is tangential to the given plane. When applied to an elastic solid, the shear stress $\tau$ results in a shear strain, which can be roughly defined as the displacement relative to some characteristic size of the sample. For most solids and not too large stresses, $\gamma$ is proportional to $\tau$ and the solid is elastic. Therefore, applying a constant shear will also result in a constant stress. However, in a viscous fluid, to get a constant $\tau$, shear must be applied continuously at a certain rate $\dot{\gamma }$. If the shear stress is proportional to the rate, the fluid is said to be Newtonian. A granular material responds to small forces elastically like a solid, but above a certain value the material yields and begins to flow like a fluid, a property common to elasto-visco-plastic materials. If the shear stress (along a slip plane) is proportional to the normal stress, the material is also called a Coulomb material, in analogy to ordinary friction. By neglecting the elastic deformation, which is usually small compared to the post-yielding deformations, the yield stress $\tau _Y$ can be written as

$$\begin{aligned} \tau _Y = \mu \sigma + c, \end{aligned}$$

(1)

where $\mu$ is the coefficient of friction and c is a parameter. Experiments show that there is a critical density at which the granular medium flows steadily under constant stress, leading to the notion of critical state in soil mechanics [4], which is distinct from criticality discussed later.

A property closely related to shear flow and peculiar to granular materials is dilatancy, studied by Reynolds [28]. In order to flow, the material must expand. Then, the shear strain is accompanied by an increase in volume, the dilation or dilatancy, also defined as the volumetric strain $\gamma _V=-\delta V/V$. Therefore, for a horizontal granular bed sheared by an upper plate, the stress–strain curves appear as shown in Fig. 2a) and the shear causes a vertical displacement of the plate as shown in Fig. 2b). It may happen that if the material is initially loose, the shear strain starts to occur without a peak in force. However, it gradually compresses under the subsequent shear and usually reaches a point where a peak appears when the shear is stopped and then restarted. The shear stress then reaches a constant value, as does the volumetric strain, although it can sometimes be observed to increase even at constant stress [29].

A simple argument to relate the stress to the dilation [3] is to assume that in order to flow, some layers of grains overcome interlocked grains. Under the shear stress $\tau$ and the normal stress $\sigma$, the medium deforms by dx and dy in the horizontal and vertical directions, respectively. Equating the mechanical work and the frictional work

$$\begin{aligned} \tau A dx - \sigma A dy = \mu \sigma dx, \end{aligned}$$

(2)

where $\mu$ is the coefficient of friction of the granular medium, one gets the yield stress as

$$\begin{aligned} \tau _Y = \sigma (\tan \theta + \tan \psi ) \end{aligned}$$

(3)

which has the form of Eq. (1), where $\psi$ is the dilatancy angle and $\theta$ is the friction angle. This equation also defines a relation between static (yield) friction and dilatancy

$$\begin{aligned} \mu _s=\mu + \tan \psi . \end{aligned}$$

(4)

In fact, other factors may contribute to the onset of finite yield stress, such as intergranular friction or adhesion. In any case, the response of a granular medium to shear is closely related to grain friction and geometry. As shown by Bagnold [30, 31], with increasing shear the response of the granular medium ceases to be Newtonian and becomes quadratic: $\tau ~\propto ~\sigma \dot{\gamma }^2$, where the proportionality constant is also related to the dilatancy angle $\psi$. This is also known as friction or shear hardening and will appear in several of the results reported in the following sections. For extensive studies on continuously sheared granular systems, we refer to Refs. [32, 33] and their extensive bibliography.

Closely related to yield stress and friction is intermittent motion, also known as stick–slip. Probably the simplest system in which intermittent dynamics can be observed is the so-called spring-block system, in which a massive block slides over a surface while being pulled by a spring driven at a constant speed (see, for example, Ref. [34] and references therein). The block is initially at rest and begins to slide when the spring is sufficiently stretched. If the sliding speed of the block exceeds the driving speed, the spring unloads, the driving force decreases and the block slows to a stop. Then, the driving recharges the spring until the static friction is overcome, and so on. As everyone’s daily experience shows, stick–slip can occur with different characteristics and also not occur. In particular, driving fast enough will result in continuous slip. A simple example of the transition from stick–slip to continuous sliding is provided by a system in the presence of Coulomb friction, but the specific dynamics depend on the friction law obeyed by the interface, as do the slip characteristics [35]. An enlightening phase diagram is given in Fig. 3. The diagram shows that, for a given system, the character of the motion depends essentially on the spring constant and the driving speed. Varying these parameters, it can exhibit continuous sliding, periodic stick–slip or chaotic stick–slip, as can be seen from the frequency spectrum.

Fig. 2

Schematics of shear stress responses in a shear strain and b dilatation (from Ref. [4])

Bagnold [31] studied a horizontal layer of dry sand being bulldozed to a constant depth by a plate against a wall. After some grains have piled up, avalanches begin to fall occasionally as the slope of the pile increases, and the plate suffers a jump. Assuming a slab moving at a constant speed, he calculated the size and periodicity of the jumps for both sand and glass beads, distinguished between primary larger (yield) jumps and smaller jumps as a function of driving speed, and predicted that above a critical speed the grains would begin to fall continuously from the pile and the slab motion would become continuous. He also verified his prediction experimentally by driving the slab through a spring long enough for the jumps not to change its strength. But stick–slip has sometimes been considered a complication. In Ref. [36], it was reported that for glass beads, it occurred only at low shear rates, close to the yield stress, but that for sand, the behavior could be observed from the yield point up to much higher shear rates, presumably because it is related to the angularity of sand. It was concluded that “this interesting phenomenon merits future study, but since it complicates the interpretation of the steady-flow problem, the shear rates were restricted to avoid this unsteady complication”.

Stick slip is the basis of seismicity. In general, an earthquake consists of a shear motion between two tectonic plates defining a 2-dimensional fault, with the consequent propagation of seismic waves through the surrounding crust. It is now clear that a key role is played by the granular material accumulated between the plates, the “gauge” [37]. The conditions under which a granular material can fail and the stick–slip dynamics are, therefore, also fundamental issues in earthquake dynamics [34]. For this reason, many laboratory experiments have been carried out paying more attention to seismic quantities [38, 39] or trying to reproduce some seismic condition, such as high pressure, slow or very high driving (rocks), different temperatures, hydraulic fracture. See among many [40,41,42], references in [43] and [44] for fluid-induced seismicity, and [45] for a general review of seismic faulting. As with earthquakes and as shown in the diagram in Fig. 3, stick–slip can occur as an irregular phenomenon, which implies fluctuations in the forces shown in the next section.

Fig. 3

Dynamic phase diagram in spring constant, k, and driving velocity, c. The upper color bar encodes the range of the power spectrum as $\log (\omega _{max}/\omega _{min})$ if greater than 1. The right color bar expresses its maximum in the periodic regime. The map, with unavoidable uncertainties, linearly interpolates experimental measurement points (black dots) in log space. The top line shows $k = \infty$ as the slider is pulled with a chain (from Ref. [46])

2.3 Chains, arching and force fluctuations

Granular media also differ from molecular fluids in that they are insensitive to temperature and subject to internal friction, cannot relax fluctuations, and can remain in a static configuration indefinitely or evolve on very rapid scales during flow. Forces can be transmitted along paths that screen large regions essentially stress-free, a property that gives rise to arches. l Arches are capable of transferring normal stress to shear stress and vice versa, a mechanism at the basis of the Janssen effect. While in a vertical solid or liquid column the pressure increases linearly with depth (Stevino’s law), in a granular column it reaches a maximum value and remains constant below. Friction between the grains produces horizontal components of the forces acting on the walls, transferring part of the normal load. Considering the combined effect of tangential friction and stress on the walls, Jansen [47] derived an expression that correctly predicts that the pressure saturates exponentially with depth. Both the exponential rate and the maximum pressure depend linearly on the column diameter, and this is why sand flows at a constant rate through a funnel like an hourglass, at least until its height is more than two times the opening diameter [5].

Janssen’s law correctly predicts average values, but the disordered arrangement of the particles makes the force distributions at the bottom and walls of the container far from Gaussian. In fact, in most situations they have exponential tails, which are responsible for the catastrophic collapses that occur in grain elevators, as shown by simple experiments [48]. In addition, friction and geometry often make the interactions between individual grains discontinuous, meaning that an apparently solid granular structure can fail abruptly. In fact, the network structure of the forces renders the continuous limit ineffective in many situations, and simple theoretical models indicate that relative fluctuations do not disappear with increasing size [49, 50].

Contact forces in granular media follow intricate paths, resulting in a network of “force chains”. This can be revealed by birefringence techniques. In photoelastic materials, stress changes the refractive index along the corresponding direction. Sending polarized light through a 2-D array of photoelastic disks allows the stress field to be detected, as shown in Fig. 4. This technique has been in use for many years and is still widely used (see, e.g., Ref. [51] for a historical review). Images can be taken in both static [52] and dynamic [53] regimes, revealing important details. The transmission of forces through the irregular network is responsible for many of the peculiarities of granular mechanics (such as the height independence of normal pressure discussed above), but also for stress fluctuations and the tendency of the medium to dilate under shear [28, 31]. The study of contact forces in sheared photoelastic systems has shown not only that the stress is carried by a small subset of grains, especially near the jammed state, but that its distribution is also broad in this case, with exponential tails [54]. Force chains are also sensitive to the shear direction, making them anisotropic. In the presence or after a shear, they are preferentially aligned along the loading direction, as shown by pure shear experiments with photoelastic disks [55]. For this reason, granular materials have also been considered “fragile” [56], in the same sense that a column can support large loads along its axis but not perpendicular to it. A detailed and up-to-date introduction to the application of photoelastic techniques to the measurement of stresses in granular materials can be found in Ref. [57].¹

Fig. 4

Visualization of force chains in a Couette cell filled with photoelastic disks (from Ref. [58])

The microscopic behavior of grains can be studied not only with optical techniques, but also with passive tracers, as in a recent work [59], where the motion of a grain-scale intruder driven by a spring through a 2-D annular channel has been investigated. In this way, quantitative information can be collected about the dynamics and how friction between grains and the channel bottom influences the force network and thus the granular behavior. Also, properties such as particle shape, roughness and adhesion can strongly influence the internal force chain structure and the discontinuous evolution it undergoes.

It is easy to understand how the instability of chain networks can cause granular properties, including quantities such as friction coefficient, Young’s modulus, and shear modulus, to change in a discontinuous and unpredictable manner, and cause the periodic stick–slip motion to become chaotic and characterized by erratic and intermittent events. It will be seen in the next sections that in many situations fluctuations are not only not negligible, but are in fact characterizing features of a system. In addition to providing useful information for understanding the dynamics, they also suggest the possibility of attributing them to a non-equilibrium critical point underlying the observed phenomenology.

2.4 Experimental approach

The previous section described how force transfer in granular media can be highly inhomogeneous and anisotropic. At low shear rates, this phenomenon causes the system to exhibit intermittent and erratic activity in the form of bursts, or avalanches, characterized by wild fluctuations of physical quantities, also called crackling noise [60]. Thus, the behavior of the system can only be characterized on a statistical level. Statistical properties of physical quantities, besides being significant in themselves, can also provide important clues about the mechanisms underlying the observed phenomenology and about which models might be suitable to describe it (some of these models will be discussed later in Sect. 5). Besides the probability distributions of dynamical variables, such as position, velocity, slip extent and duration, and frequency spectrum, the average behavior of physical quantities along the slips is also useful information. It can help to distinguish between different models [61], and in many cases, it is scale invariant, a property shared by other systems such as sheared amorphous solids, but which can also be broken under certain circumstances, signaling the onset of different dynamics, as will be seen later.

As mentioned before , fluctuating dynamics can be observed if both the shear rate and the elastic coupling to the driving are low enough (Fig. 3). When experiments are performed at a slow fixed shear rate, i.e., in the absence of a spring, stick cannot be properly observed in the plate motion, but it can be reflected in a highly discontinuous behavior of the shear stress, consisting of more or less linear increases followed by sudden decreases, corresponding to internal relaxations releasing some of the applied force, which can be identified with internal avalanches. The next two sections are devoted to illustrating the statistics of several quantities obtained from experimental studies of irregular stick slip. Unfortunately, for some quantities, such as dilation, there does not seem to be enough data for fluctuating dynamics.

Fig. 5

Example of a linear pure shear cell (on the left) (from Ref. [62]) and of a circular shear cell (on the right), of the Walker type

The main difference between the setups used in the experiments comes from the geometry, which can be linear or circular, as shown in Fig. 5. A circular cell made of two concentric vertical walls, one of which can rotate, is also called a Couette cell, after the French physicist who used such a device to measure the viscosity of liquids (in this case, a thickness of a few millimeters was sufficient, so there was a small difference between the inner and outer cylinder radii). An annular cell with a rotating lid is sometimes called a Walker shear cell [63]. Linear shear cells can apply shear in different ways. These include pure shear, where the volume is maintained. Shear can also be applied horizontally or vertically. Each configuration has its advantages and disadvantages. In the linear configuration, the shear rate is nominally homogeneous within the granular medium, but with necessarily finite time and displacement. The circular geometry allows shear to be applied for an indefinite time and extent, but the shear rate is inhomogeneous due to the decreasing circumference from the outside to the inside. Due to different bibliographic sources, similar quantities may be represented by different symbols in the figures presented here. The notation for displacement, velocity and stress can also change depending on the experimental setup, referring to angles, angular velocity or frequency, torque, etc. for circular geometries. In the main text, we will use the notation for a linear system, where the forces are denoted by f, the space coordinate by x and their time derivatives by v or points. Explanations of the symbols are given in the figure captions when necessary.

3 Stress fluctuations

The randomness of contacts within the medium described in the previous section is reflected in a randomness of stress values in both static and dynamic regimes. Since shear stress is generally proportional to normal stress, it will be considered analogous to frictional force and the two terms will be used interchangeably.

Although mainly focused on periodic, stick–slip, those reported in Refs. [64, 65] were among the first systematic studies on the intermittent dynamics of a granular medium, capturing some important features also shared by irregular dynamics. Experiments were performed using a linear slider, connected to a leaf spring, driven at a constant low velocity V on spherical glass particles (70-110 $\mu$m in diameter) or clean sieved nonspherical coarse sand (100–600 $\mu$m). For regular particles, irregular stick–slip was observed at low V and large spring constant k, with a transition to approximately periodic stick–slip and then to continuous sliding at larger values of V. Periodic motion was never observed with coarse particles, and both small and large slip events occurred in a chaotic manner. Along each slip, a vertical displacement of the slider could be observed, signaling the dilation of the granular medium. An important observation is that the instantaneous frictional force is not a single-valued function of the instantaneous velocity. Each slip corresponds to a hysteresis cycle, some of which are shown in Fig. 6, with the friction going from higher to lower values. Moreover, in fast slips, the friction shows a relative minimum in the accelerating part, thence exhibiting both velocity weakening and hardening, a feature frequently encountered in different situations, as will be seen. In the following, various experimental results on the fluctuating behavior of the shear stress are reported, in particular its statistical distributions and some dependencies of the mean values.

3.1 Yield stress distribution

As illustrated in Sect. 2.2, a major distinguishing property of dry granular matter with respect to a standard fluid is the need to apply a finite stress to mobilize it. The granular medium starts to flow only when the applied stress exceeds a critical value, the yield stress. Otherwise, it can exhibit finite deformation like viscoelastic solids, although it can also undergo creeping, i.e., small local rearrangements of the internal structure that do not manifest macroscopically (and are, therefore, not considered here). This property is shared by many non-Newtonian fluids [66] and solids [67]. The yield stress corresponds to the boundary between elastic and plastic behavior, but is also often referred to as static friction. In a spring-block system, the distribution of static friction $f_s$ can be easily derived from the distribution of spring strain at the beginning of each slip: $f_s=-\kappa \Delta x$, with $\Delta x = x-x_0$, where $x_0$ is the equilibrium distance of the spring of elastic constant $\kappa$ (in the case of circular geometry, friction force usually corresponds to torque). In the absence of the spring, for example in constant shear experiments, other methods can be used, such as measuring the instantaneous power applied to the driving motor or a load cell.

Fig. 6

Dynamic friction along periodic slips exhibits hysteresis, cycling from higher to lower values. At zero velocity, friction increases during spring loading until another slip begins. For larger slips, the friction shows relative minima (from Ref. [64])

As recalled in Sect. 2.3, forces within a granular medium form a random network of contacts that depends on the specific and detailed grain configuration, from which the macroscopic stress results. Consequently, the yield stress is a random quantity. Since the stress results from the sum of innumerable contributions, one might expect to observe Gaussian distributions. Experiments in which glass beads of about 1 mm filling a horizontal annular cell were sheared at the top by a rotating plate free to move vertically [68], have shown that this is not the case and that the distribution is generally asymmetric, as seen in Fig. 7. This is due to strong correlations between the force chains within the system. In fact, the sum of a large number of independent variables converges to the Gaussian distribution by the central limit theorem when the variables are uncorrelated. In the correlated case, different distributions may result (see, e.g., Ref. [69] and references therein). Some authors [70] have also argued that certain asymmetric distributions of this kind, which take the place of Gaussians when the variables are highly correlated, may be stable distributions in the sense of Lèvy [71]. Sums of random variables that follow a stable distribution have the same distribution as the individual variables (an example of a stable distribution for independent variables is just the Gaussian). An experimental test of this conjecture has been performed [72] using a setup similar to that of Ref. [68], integrating both yield and dynamic shear stress data on windows of different widths. The distributions obtained with different widths have indeed shown the same shape, a result that implies a form of self-similarity and can help to understand how the macroscopic stress arises from the force network.

Fig. 7

The distribution in the stick–slip regime of the dynamic, $f_r$ (o), static, $f_s$ ($\triangle$), and stationary (see text), $f_d$ (x), friction forces and their log-normal fits (lines). The inset shows the distributions for two experiments, one at low velocity (solid-like regime) (o), one at high speed (liquid-like regime) (x), and the corresponding log-normal and Gaussian fits on semilog axes (from Ref. [68])

To investigate how the shear stress depends on the grain smoothness a slider was pulled by a spring on the top of a 2-D linear vertical bed of gravity-packed photoelastic grains sandwiched between two vertical glass plates [73]. The bed consisted of a mixture of grains which were bidisperse in size but had the same shape of a regular polygon, each characterized by the number of vertices, which could take the values 3, 4, 5, 6, 7, and $\infty$ (circular grains). The results have shown that the yield stress is sensitive to shape, as is the dynamic stress (see below). In particular, the PDF has shown a growth of the tails, especially on the right side.

The average yield stress also shares some properties with static friction is solids, but within some limits. It is proportional to the normal stress, but in a granular medium, an increase of pressure can cause a sudden compaction and a consequent sharp change of the yield stress [74]. As in solids (see Sect. 5.1), it increases roughly logarithmically with time. However, this seems to happen only if a shear stress is applied during the waiting time [75], a property that has been shown to hold even at very high normal pressures [76].

3.2 The shear stress

As for the yield stress, the evaluation of the dynamic frictional force $f_r$ along the slip can be done by measuring the position x and the associated acceleration $\ddot{x}$, or by piezoelectromechanical devices when the shear stress is applied by a rigid load plate. Data from the circular geometry experiments [68] have shown a first clear distinction between the statistical behavior of the force in the stick–slip regime and in continuous sliding. In Fig. 7, the distribution of the dynamic friction $f_r$ is shown, together with those of the static friction $f_s$ and of $f_d$, corresponding to stationary points where the plate has zero acceleration. All distributions have the same type of asymmetry and are close to log-normal curves. Differently, the distribution of $f_r$ during continuous sliding assumes a narrower Gaussian profile, as shown in the inset. The observed statistics have been shown to be robust with respect to changes in parameters such as the spring constant and the driving speed [72]. As recalled in the previous subsection, a Gaussian distribution signals that the motional resistance is the resultant of many independent or at most weakly correlated forces. On the contrary, skewed shapes signal the presence of strong correlation. In particular, log-normal shapes do not necessarily result from the product of independent contributions, but may result from the contribution of many correlated variables [69].

Fluctuations were also measured in a circular cell where sub-millimeter glass beads were sheared at a constant rate from the top of the channel [79]. Averages of minimum and maximum values taken along the motion were found to be proportional to the normal load. As the driving speed increases, the amplitude of the shear stress variations decreases and eventually disappears along with the stick–slip.

Even the normal stress shows large fluctuations during shear. These have been measured in an annular cell filled with monodisperse glass spheres of diameters from 1.0 to 5 mm sheared by a top plate for different plate weights [53]. Their distributions assume asymmetric shapes, again characterized by long right-handed tails that shorten with increasing shear rate and are independent of grain diameter. The normal stress distributions were then measured in a similar system where not only monodisperse but also bidisperse mixtures of 2 mm and 3 mm steel spheres were tested, to avoid crystallization [80]. Again, they were observed to decay exponentially from the maximum, with a slope that was greater for monodisperse systems and that increased with normal pressure. In fact, a wavelet transform highlighted a strong sensitivity of the intermittency properties to the nature of the mixture, and a slightly greater dependence on grain size was observed than in Ref. [53].

In the experiments cited above with particles of different shapes [73], the spring constant and driving speed were chosen such that the system was in the stick–slip dynamic regime for all particle shapes. It was found that as the number of angles decreases, the PDF of the total stress increases its average value and also widens, preferentially towards higher values, similar to the yield stress. The PDF of the stress at the end of the slip behaves in the same way.

Fig. 8

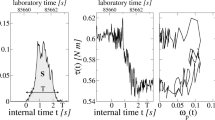
Left panel: friction evolution along irregular slips as a function of instantaneous plate velocity (lines) and its average (circles) (from Ref. [77]). Right panel: a average friction as a function of instantaneous plate velocity shows clear weakening and hardening regimes separated by a minimum. The inset b shows the power spectrum of the shear stress compared to a Lorentzian (from Ref. [78])

3.3 Friction dependencies

The random nature of friction does not preclude the study of its dependence on physical quantities. In the previous section, dependencies of its distribution on normal weight or shear rate were reported. In addition, at the beginning of this section were reported results [64, 65] on its hysteretic behavior, then showing to be a not univocal function of the velocity (a property not exclusive to granular matter but that can be observed also in solid-solid friction, as will be recalled later).

Fig. 9

Main panel: the residual average friction, $f_a$, obtained by subtracting the average velocity dependence $f_v$ Eq. (5), as function of the instantaneous acceleration. Inset: the residual friction after also subtracting $f_a$ (from Ref. [74])

While friction reproduces more or less the same cycle along regular slips, as in Fig. 6, things are more chaotic during irregular motion, as shown in the left panel of Fig. 8, but even here a hysteretic behavior can be seen. As a first step, such an effect can be neglected in order to point out a possible velocity dependence by calculating the average value of $f_r$ as a function of the instantaneous velocity v: $f_v(v)=\langle f_r(v)\rangle$. The values obtained in this way [78] are represented by circles in the figure, showing that, as for regular stick–slip, the average friction exhibits a velocity weakening at low speeds and a hardening at higher speeds. The two regions are separated by a relative minimum whose position has been found to be independent of parameters such as spring constant or driving speed. The circles in Fig. 8 are well interpolated by a rate-dependent friction law of the type

$$\begin{aligned} f_v(v)=f_0 + \Gamma [v -2v_0 \ln (1+v/v_0)]. \end{aligned}$$

(5)

where $f_0$ is the average static friction, $v_0$ is the minimum, and $\Gamma$ is the high velocity damping. A friction curve with weakening and hardening regimes separated by a minimum, also known as a Stribeck curve, strongly influences the dynamics, as will be discussed in Sect. 4.5.

It is interesting, and far from well understood, that while in the present case the plate velocity changes continuously, and the hysteresis cycles clearly show that friction does not depend on it alone, similar Stribeck curves can be observed under very different circumstances, as already mentioned. Experiments at constant shear have been performed with both natural beach sand ($\approx$ 300 $\mu$m ) and milled quartz grains filling a cylinder, with the rotational speed of a top plate systematically varied over 5 orders of magnitude [33]. Shear stress was measured at both constant normal stress and constant volume on the different materials, and showed in all cases the presence of a more or less deep minimum separating a velocity weakening at low rates from the Bagnold regime at high rates.

In principle, friction can also depend on other dynamical variables, including higher order spatial derivatives and integrals:

$$\begin{aligned} f=f\left( x,\dot{x},\ddot{x},\dots , \int x(t) dt, \dots \right) \end{aligned}$$

(6)

Examining the behavior of the residual force $f_a = f_r-f_v$, with $f_v$ from Eq. (5), as a function of $\dots {x}$, it was found [74] that the instantaneous acceleration can account for another part of the average friction, $f_a$, shown in Fig. 9, as would be expected from the hysteretic behavior (Fig. 6). The inset of the figure shows the residual friction after also subtracting $f_a$. It can be seen that a large part of the average friction is accounted for by an empirical dependence on velocity and acceleration. A quantitative study of the remaining part $f_r-f_a-f_v$ [74], shows that its variance grows with slip size. A similar dependence on slip size is shown by the maximum slip velocity. It will be seen in Sect. 6.1 that this feature is also present in a model equation commonly used to describe intermittent dynamics in various systems, which will be discussed in Sect. 5 (Eq. 19). Even if the above empirical friction dependence is a good approximation of the observed average behavior, it is known that memory terms (the integral in Eq.6), are also determinant for the fluctuating sliding dynamics, a point that will be discussed in Sect. 5 devoted to models.

In order to investigate how the depth of the granular medium influences the response to shear, experiments were also performed where the number of layers of interstitial granular material was varied [81]. It has been seen that, as expected, the presence of interstitial material initially reduces friction with respect to solid–solid shear, acting as a lubricant. However, further increases in grain thickness cause an increase in shear stress, likely due to the increased mass of grains dragged during motion. At first glance, it would seem that this phenomenon should prevent slippage. On the contrary, the fraction of time spent slipping also increases, despite the increased friction. This behavior is particularly pronounced at driving speeds close to the continuous sliding speed for the deep system. In this region, even a small increase in the granular depth causes a sudden and large increase in friction, but at the same time the fraction of time spent slipping increases by several orders of magnitude. Therefore, the plate continues to slide much more frequently even when it is more restrained, indicating that the flow is not determined by friction alone. Shear bands typically do not include too many layers from the shear surface and the behavior of the system is seen to stabilize above a certain depth.

4 Statistical characterization of slips

In his experiment cited in Sect. 2.2 [31], Bagnold had observed that when perturbed at a low rate, a sand pile does not respond continuously, but in the form of bursts or avalanches, which can be observed in several situations [82,83,84]. When a granular bed is sheared slowly enough by a compliant force, neither the shear stress nor the shear rate can be predicted, and the system finds itself in a state between jamming and mobility, exhibiting stick–slip dynamics. As already observed, such behavior can also exhibit a chaotic character, and the statistical distributions of several physical quantities can span a wide range of values with very long tails, generally close to power laws. Even when shear is applied at a constant rate, there are sudden drops in stress or energy, due to internal slips, followed by nearly constant linear increases corresponding to sticks. This behavior is common to many different natural phenomena where a system responds in an unpredictable way to a small external perturbation. Examples are fracture [85], structural phase transitions [86], plastic deformation [87], hysteresis in ferromagnets [88], and many others, among which earthquakes are probably the most well known, with the famous Gutenberg–Richter law (Sect. 6.)

For a statistical characterization of the avalanches, measurable quantities can be recorded and statistically analyzed, such as duration, size, velocity, stress and energy drop. The slip duration T is defined as the time between the beginning and the end of a slip. The slip extension S is the integral of v(t) between these two points and is the total displacement experienced by the slider. Another important property related to slipping and sliding is also dilatation, but unfortunately, there does not seem to be enough data on its behavior during irregular dynamics to discuss its statistical properties.

Power laws, i.e., distributions of the form $P(x) \simeq x^{-b}$, manifest the absence of characteristic scales, as is easily seen from their functional invariance under a scale transformation by a factor $\lambda$: $x \rightarrow \lambda x$: $P(x) \rightarrow \lambda ^{-b} P(x)$. The self-similarity of power laws is opposite to e.g., exponential or Gaussian distributions whose scales are characterized by some parameter. In general, it describes fractal objects. For example, the distribution of domains in a ferromagnet or of droplets in a critical fluid is geometrically self-similar near the critical point, a property that is reflected in the dependence of their density on the sampled volume. Thus, knowledge of the fluctuation statistics is not only necessary for testing any theoretical or numerical approach to the problem, but also the hypothesis of being in the vicinity of some critical point (in the acceptation of equilibrium thermodynamics). This is because critical phase transitions exhibit power laws resulting from the divergence of correlation lengths in the system. Equilibrium critical phase transitions possess some universal properties that do not depend on the particular system or the interaction of its microscopic components. The presence of the same phenomenology common to different disordered systems thus reveals the possibility of a universal and scale-independent description of the dynamics [60].

4.1 Slip distributions in size and time

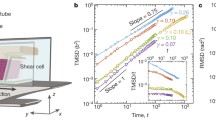
As mentioned earlier, many physical quantities characterizing the slips exhibit probability distributions close to power laws. Such behavior has been observed in a granular medium consisting of highly polydisperse tapioca particles [89] (diameter between 5 $\mu$m and 2 mm) confined in a Walker-type shear cell consisting of a horizontal annular channel (of width 80 mm and mean diameter 280 mm). The grains were sheared at the top by a rotating plate, free to move vertically and connected to a motor by a helical spring. Keeping the system in the stick–slip regime, clean power laws could be observed for the probability density distributions of event sizes $p(S) \simeq S^{-\tau }$, durations $p(T) \simeq T^{-\alpha }$ and energies $p(E) \simeq E^{-\beta }$, with $\tau =1.94$, $\alpha =2.08$ and $\beta =1.88$, Fig. 10a). Curiously, the study of statistics was not motivated by rheological investigation, but by the search for power laws related to the theory of Self Organized Criticality (SOC) (recalled in Sects. 2 and  6). The theory, introduced in the 1980s [21, 91], aimed to explain the appearance of power laws and frequency spectra s(f) behaving like 1/f in many natural phenomena as a manifestation of critical behavior. For this reason, the frequency spectrum of plate displacement was also analyzed (see below).

Fig. 10

a Distributions for different quantities from a [89], b [90] and c adapted from [39]. The plots in b and c compare distributions for homogeneous quantities that differ in range, cutoff, and possibly peaks at large value due to the different compactness of the medium obtained from the preparation in b and the increased normal pressure in c

Further investigation has shown that distributions are not always clean power laws. Using the same setup described in Ref. [89], it has been observed that the distribution tails can show an excess or depletion of events [90], as seen in Fig. 10b). This has been related to different packing fractions associated with different preparation methods, resulting in different responses to shear. Similar differences have been observed in the series of 2-D experiments reported in Ref. [62], a work motivated by the search for similarities between granular slip and earthquake statistics. By shearing two horizontal photoelastic plates, separated by a narrow gap (1 cm) and filled with a bidisperse mixture of vertical photoelastic rods, the stress-induced birefringence has allowed the determination of the spatial and temporal properties of both the elastic plate deformations and the microscopic motion of the granular material. In particular, it has been observed that increasing the packing density increases the temporal range of the slips, but also turns the distribution towards an exponential and favors the transition from aperiodic to periodic stick–slip. In this experiment, as the shear rate was kept constant, the sum of the individual grain displacements was used as the slip extension from the images, yielding an exponent approaching $\tau \simeq 1.5$ in the power-law regime. Other experiments performed in a similar system [39], have confirmed that increasing the packing fraction can produce similar effects. It can be seen that the distributions in panel c) of Fig. 10 tend to change similarly to those in panel b), despite the many differences in experimental conditions and measurement methods: the discriminating parameter that generated a peak or moving cutoff at large events was the average torque (low, medium, high) in panel b) [90], the normal pressure in panel c) [39]. The volume was 2-D and fixed in one case [39], and 3-D and not fixed in the other case [90]. As will be shown below, the large peak seen in b) for the denser system is likely due to the granular inertia, which is much smaller in the 2-D system, and where it was also seen that only avalanches that span the entire system contribute to the peak. The slip size exponent was confirmed to be $\tau \approx 3/2$ in Ref. [39] or ranging from $\simeq 4/3$ to 2 in Ref. [90].

Fig. 11

Probability distributions of a slip size, and b slip duration for different driving speeds (from Ref. [78]) The points refer to experimental data, while the curves are obtained by the stochastic model described in Sect. 5.2

In another experiment inspired by earthquake dynamics [92], a biaxial compressive test has been applied to a vertical cell in the form of a parallelepiped (85 $\cdot$ 55 $\cdot$ 25) mm$^3$, filled with polydisperse glass beads of diameter around 100 $\mu$m at a pressure of 30 kPa. The analogous of the seismic moment, in fact proportional to the shear displacement [93], has shown a distribution with an exponent $\tau \simeq 2.1$ independent of the compression velocity. It should be remembered, however, that this experiment was conducted in a different way than usual.

In another experiment inspired by earthquake dynamics [92], a biaxial compression test was applied to a vertical cell in the form of a parallelepiped (85 $\cdot$ 55 $\cdot$ 25) mm$^3$ filled with polydisperse glass beads of diameter about 100 $\mu$m at a pressure of 30 kPa. The analog of the seismic moment, which is actually proportional to the shear displacement, has shown a distribution with an exponent $\tau \simeq 2.1$ independent of the compression velocity. It should be noted, however, that this experiment was carried out in a different way than usual.

In experiments performed with millimeter-sized glass beads in a Walker cell [78] similar to the one described in Ref. [89], distributions close to power laws were again found. The effect of changing several parameters, including the speed of the driving motor and the spring constant, was also tested, and it was found that the shape of the distributions is rather insensitive to these parameters (as long as the system exhibits stick–slip), as can be seen in Fig. 11, where the experimental data are represented by symbols. At the same time, as in some of the observations cited above, P(S) and P(T) show peaks at high values. At least an important part of the peaks in the distributions can be attributed to resonant frequencies of the system. In fact, when the moment of inertia of the plate, $I_0$, was changed, it was observed that the peak location moved according to $T_0=\sqrt{(}I_0/\kappa )$, while it was independent of the driving speed [78], which instead influences the cutoff, as seen in Fig. 12. The best quantitative agreement with experiments is actually obtained by considering a larger inertia $I > I_0$, which implies that the granular layers move together with the disk. This behavior is expected due to the formation of shear bands [94], and has been confirmed by measurements where the depth of the granular medium was varied [95]. When the height of the granular bed was decreased below about five bead diameters (identified with the thickness of the shear band), the peak moved towards larger values, while $\tau$ changed only a little between 1.5 and 1.7, demonstrating that the inertia of the mobilized granular system, which can also strongly depend on the shear, plays an essential role in the dynamics.

Fig. 12

Inset: distributions of the slip duration P(T) for different moments of inertia of the circular shear plate. They look like power laws superimposed with a peak, here fitted by a Weibull distribution. The main panel shows that the mean and mode of the Weibull peak increase with the square root of the moments of inertia, while the power-law exponent remains approximately constant (from Ref. [72])

4.2 Stress drops and dissipated energy

As already noted, when experiments are performed at a slow fixed shear rate, i.e., without a spring, stick–slip dynamics cannot be observed in the constant velocity of the plate, but can be reflected in the highly discontinuous behavior of the shear stress, manifested by smooth increases followed by sudden decreases due to internal relaxations of the applied force. These stress avalanches also have statistical distributions that follow power laws and can be considered approximately proportional to an effective slip extension, defined as the sum of the individual grain displacements, so that no distinction is made, also avoiding a proliferation of exponents. This assumption is supported by the fact that the exponents for the two quantities are often similar.

Stress avalanches have been measured in a linear 3-D system of soft spheres [96] with a diameter of 1.5 mm and a polydispersity of 5%, in a cell of (10 $\cdot$ 10 $\cdot$ 10) cm$^3$ sheared from the top at fixed normal pressure, yielding $\tau =3/2$, along with an exponent for durations $\alpha \simeq 2$ (a similar system, with grains immersed in an index-matching liquid [97], had shown a similar exponent $\tau \approx 3/2$ for stress avalanches, together with a shear rate-dependent cutoff that decreases with increasing shear rate).

As the stress decreases, a certain amount of energy is dissipated in the slip. The associated distribution also follows a power law $P(E) \approx E^{-\beta }$. For disks of 12.7 and 15.9 mm filling a 2-D pure shear cell (of rectangular dimensions (44 $\cdot$ 40) cm$^2$) and sheared in small step cycles of different duration [98], the energy avalanches were found to follow an exponent $\beta = 1.24$, as shown in Fig. 13. Using the photoelastic visualization technique, also local avalanches, i.e., those involving only particles displacing above a certain threshold, have been studied, finding for them a different exponent $P(E)\simeq E^{-2}$. In this case, the results were shown to be stable with respect to different packing fractions and friction coefficients. In the same experiment, the number of particles involved in an avalanche has also been measured, observing power-law distributions, but with exponents depending on the method of measurement. As already mentioned [89], energy avalanches were also investigated in a circular experiment, where $\beta = 1.88$ was found (Fig.10a)).

Fig. 13

Probability distribution of dissipated energy in slips for different packing fraction, $\phi$, and grain friction coefficient $\nu$ (from Ref. [98])

In another experiment [99], a 4 mm thick monolayer of 3D-printed disks with diameters of 6.4 mm and 7.0 mm was sandwiched between two fixed transparent and concentric cylinders, finding $\beta = 1.72$ for the probability distribution of the slip energy and $\tau = 1.67$ for the stress drop distribution. A different monolayer was investigated in the experiments reported in Ref. [100], where a slider of 25 cm length and variable mass was pulled by a spring moving at constant velocity on a vertical bed (9.5 cm deep and 1.5 m long) of bidisperse cylindrical photoelastic particles of 0.4 and 0.5 cm in diameter. Different regimes were investigated, from very intermittent stick–slip at low shear to irregular and periodic motion for increasing shear, finding $\beta =1.22$ for the distribution of dissipated energy in slips. For the polygonal grains described in Sect. 3.2 [73], an exponent $\beta =1$ was found to be approximately stable with respect to shape of the particles.

4.3 Power spectrum and correlations

Another quantity useful to characterize the behavior of a systems is the power spectrum s(f). It is defined as the square modulus of the Fourier transform of the signal, and the Wiener–Khintchin theorem shows that it is also the Fourier transform of the associated time autocorrelation function [101]. The high-frequency power spectrum thus provides information about the short-time correlation properties of the system.

In an experiment cited above [53], power spectra of the normal stress behaving as $1/f^\delta$ with $\delta =2$ have been observed, with the interesting property of becoming independent of the shear rate when the frequency is rescaled with the angular velocity of the shear plate. As mentioned in Sect. 4.1, some experiments [89, 90] were motivated by a comparison with the values of the exponents predicted by SOC models, in particular for the power spectrum, which initially appeared to be $\delta =1$ but was later found to be $\delta =2$. An exponent of $\delta =2$ has actually been observed [89]. Although at first glance similar, the behavior described by the two exponents can be substantially different, as the second can be the long tail of a Lorentzian spectrum, as shown in the right panel of Fig. 8, corresponding to an autocorrelation decaying exponentially in time, while the first implies a much slower, logarithmic decay.

Using the same setup described in Ref. [100], different regimes were studied, from very intermittent stick–slip at low shear to irregular and periodic motion for increasing shear [46]. Correspondingly, frequency spectra for the shear stress were observed continuously progressing from power laws with exponent $\delta \approx 2.4$ for stick–slip to $\delta \approx 0$ (white noise) for irregular sliding, to a peak corresponding to periodic motion.

In Ref. [92], a time autocorrelation function with exponent 0.7 has been reported, corresponding to $\delta =0.3$. As noted above, the experiment, being a biaxial test, was inherently different from the others, but confirmed the existence of time correlations in the dynamics.

4.4 Exponents and scaling

Table 1 summarizes the results reported in the previous section for slip size and shear stress drop S (assumed to have the same exponent), duration T, energy drop E, and power spectrum s. Another assumption that could be made, but should be checked, is that $E \propto S^2$, which would give $\beta \simeq (\tau +1)/2$.

Table 1 Summary of experimental and expected from mean field exponents from different models (Sect. 6)

Note that in some cases, $\tau$ and $\alpha$ were found to be the mean-field values. In other cases, slightly larger values were obtained. This may possibly be due to the presence of cutoffs in the distributions, which, if properly accounted for, could make the exponents closer to the expected ones. The values observed for $\beta$ seem far from those of the mean field, but some of them are close to $\beta \simeq (\tau +1)/2$. The values of the spectral exponent mostly agree with the mean field.

Fig. 14

Scatter plot of extension, S vs. duration, T of single slips; different regions (colors) refer to different classes of duration. The white dots are the corresponding mean values for each class. In the inset, the average nominal velocity $<S>/<T>$ as a function of the average slip duration clearly shows a transition to another regime (from Ref. [102])

As mentioned earlier, power-law distributions are often associated with self-similarity and with critical phenomena. Figure 14 shows a plot of the size versus the duration of each individual slip [102]. Although the points are scattered, there is a well-defined scaling between the two quantities. It can be made clearer by considering average values. By dividing the slips into classes according to their duration, identified by different colors in the graph, averages can be made on the slips belonging to the same class. The average length and duration of each class are shown in the inset. A clear scaling $\langle S\rangle \simeq \langle T\rangle ^{\zeta _{ST}}$ can be seen, at least up to a crossover (the reasons for this will be seen later). In fact, in analogy to equilibrium-critical phenomena, well-defined relations can be expected between the exponents characterizing different distributions. To make the connection between them let us also write $\langle S \rangle \simeq \langle E\rangle ^{\zeta _{SE}}$. At the same time it must be true that

$$\begin{aligned} \int p(T) \langle S(T)\rangle dT = \int p(E) \langle S(E)\rangle dE. \end{aligned}$$

(7)

Using similar relations for the other quantities, one obtains other equations from which the following relations among the exponents are derived [89, 103]:

$$\begin{aligned} \zeta _{ST}= \dfrac{\alpha -1}{\tau -1}; \quad \zeta _{SE}= \dfrac{\beta -1}{\tau -1}. \end{aligned}$$

(8)

The data shown in Fig. 14 give an exponent $\zeta _{ST} \approx 2.2$, which is roughly consistent with the mean-field values for $\alpha$ and $\tau$. In Ref. [89], scatter plots for $\langle E(S)\rangle$, $\langle T(S)\rangle$and $\langle T(E)\rangle$ are shown to exhibit quite clean power laws, with exponents $\zeta _{ES} = 1/\zeta _{SE} =1.13$, $\zeta _{TS} =0.87$ and $\zeta _{TE} =0.81$, respectively. A similar value $\zeta _{TE} =0.79$ is reported in Ref. [100]. These values and those found for the probability distributions are consistent with the relations in Eqs. (8) and with mean-field values, except for the value of $\beta$ which in general seems to be more scattered across different experiments.

4.5 Slip scaling and average profiles

In general, one can also expect self-similarity relations between function averages. In particular, one can consider the average value of some physical quantity Q in a slip as a function of some parameter p describing the slip evolution: $\langle Q(p)\rangle _P$, where the average is over all slips ending in $p=P$. Although the average velocity profile $\langle Q(p)\rangle _P$ depends on both p and P, self-similar scaling implies that there is an invariant function $\Omega$ such that it can be expressed as

$$\begin{aligned} \langle Q(p)\rangle _P= g(P) \Omega (p/P), \end{aligned}$$

(9)

where the function g(P) is the scaling factor of $\langle Q \rangle _P$ with respect to P, and $\Omega$ is an invariant function of the rescaled parameter p/P describing the avalanche shape. This scaling scenario is supported by several theoretical models of critical dynamics [61], some of which will be briefly illustrated in the next section.

The study of slip shapes and their scaling properties has been carried out in many different systems. Introduced in the context of Barkhausen noise in ferromagnetic materials [104], the average avalanche shape can provide a much sharper tool for testing theory against experiment than the simple comparison of critical exponents characterizing probability distributions [61], since, as shown for simple stochastic processes, the geometric and scaling properties of the average shape depend on the temporal correlations of the dynamics [105,106,107]. Average avalanche shapes have been studied for a variety of systems, well beyond magnetic ones [108, 109]: from intermetallic compounds and crystals [110, 111] to glassy and amorphous systems [112,113,114]. In living matter, it has been studied in cortical outbursts [115, 116], in transport processes in living cells [117], in ants [118] and in human activity [119]. It has also been studied in stellar processes [120], Earth magnetospheric dynamics [121], and earthquakes [122].

One quantity that has been studied in granular systems is the average rate of stress decay over time [96]. It was observed that the shape of the resulting curves was self-similar and symmetric for avalanches of short duration. However, it became progressively slightly asymmetric, more tilted to the left, as the duration increased, so the avalanche scaling is tested for the short avalanches. Another quantity analyzed is the rate of dissipated energy dE/dx along the slip extension x, assimilable to friction [98]. Also in this case, symmetric and rescalable average profiles were observed only below a certain event size, above which they became asymmetric, showing a strong initial increase and then a slow decrease.

The shape of the dissipated power dE/dt has also been observed to break symmetry and scaling for driving rates at which the sequence of avalanches is periodic [46], in contrast to the small avalanche shapes in the crackling regime. The asymmetry is less pronounced than in other experiments, but the system was inherently different since the granular surface was free outside the slider while in the others it was confined everywhere. The average velocity has been studied as a function of time [102], observing also in this case the breaking of symmetry and scaling in larger avalanches. In the rising part, the slip velocity is greater than it would be for symmetric slides. After the maximum it decays more slowly, analogous to what is described in Ref. [98], with the asymmetry becoming more pronounced as the slip duration increases. Shorter slips show average profiles that are rescalable with duration, while larger slips do not, as shown in Fig. 15 a) for profiles corresponding to the classes of slips individuated in Fig.14, from which it also emerges that the expected $S-T$ scaling stops when slips become asymmetric [102].

Fig. 15

Top: profiles of the rescaled average (angular) velocity as function of the normalized time for the five classes of slip duration shown in Fig. 14. The profiles are approximately symmetric and scale invariant for short slip (top left); for long slip, the velocity increases faster at short times and decreases slower at long times, and the profiles are no longer self-similar (top right). Bottom: friction curves along the corresponding slips shown above exhibit a change in behavior from nearly constant for short slip (bottom left) to highly hysteretic (bottom right) (from Ref. [102])

Despite the different experimental conditions and quantities analyzed, all experiments show symmetric and rescalable shapes for small slips, and the onset of left-skewed asymmetric shapes, with less or no similarity for large slips. This generality makes this symmetry breaking look like a key phenomenon, although it is not clear whether the origin in the different experimental observations could be the same. In Ref. [96], the authors suggest that this could be a delayed damping effect related to time scales inherent to the friction between the granular particles. In addition, because the particles were relatively soft, there could be a significant microscopic delay in the onset of slip. In Ref. [98], on the other hand, it is speculated that the softness of the particles could induce nonlinear elasticity, with a fast relaxation at the onset of slip followed by a slower one, but also hypothesized a role for the basal static friction between the particles and the supporting glass. As shown above (Fig.14), the slip size at which the symmetry of the $\langle v(t)\rangle$ profile breaks corresponds to a crossover in the $S-T$ scaling [102]. A detailed study of the dynamics has shown that this is accompanied by a change in the friction along the slip, visible in Fig. 15b), which goes from approximately constant during short slips to a behavior similar to that in Fig. 6. Noteworthy, the critical velocity $V_c=\langle S\rangle /\langle T\rangle$, at which the scaling breaks, corresponds to the minimum of the average friction $\langle f(v)\rangle$, between the velocity weakening and the velocity hardening regions (see also Sect. 3.3). The evolution of friction with slip length, therefore, looks to play an important role, But other factors cannot be excluded, an important one being inertia. However, the latter is expected to break the symmetry in the opposite direction, as has been shown for Barkhausen noise [107, 123], a different phenomenon whose models are sometimes borrowed to describe granular stick–slip, as will be discussed in the following sections.

It is worth recalling that experiments have also been carried out on granular-fluid mixtures, as recently reported in Ref. [124]. These systems can offer some advantages, such as the possibility of making gravity irrelevant, as in Ref. [30], or the visualization of dark tracers in an otherwise transparent ensemble of glass beads using a refractive index-matching liquid (see, e.g., Ref. [125] and references therein). Several of the observed statistical features are common to dry granular systems, such as the transition from irregular stick–slip to sliding and from symmetric to asymmetric torque distributions, power-law regimes, frictional weakening and hardening. Other properties, such as average shape, do not seem to have been measured yet. On the other hand, it is obvious that these systems are inherently different from dry ones, as can be seen from the fact that some properties depend on the viscosity of the fluid. The subject is quite wide and would deserve a separate review. Therefore, we refer to the specific literature, such as the already cited Refs. [125] and [124].

5 Stochastic models

Models and theories for rapid flow are generally not suited to account for intermittency. An exception is the model recently studied in Ref. [126], where, building on the results of Ref. [127], continuous equations are derived which are coupled with an order parameter describing the transition between fluid and static components of the granular system. The model is able to describe periodic stick–slip, but not irregular, at least in its present form. Irregular motion can be reproduced by direct numerical simulation, but it is desirable to have analytical models for both practical and scientific reasons, and this brings the necessity to include stochastic components. However, it seems that not many such models have been proposed. In the present section, some of them are described.

5.1 Yield stress—static friction

A model in which the force chains are considered as a bundle of elastic brittle fibers with finite failure strength has been introduced in Ref. [128]. When a fiber fails, its load is randomly redistributed among the remaining fibers. The model is inspired by the fiber bundle model (FBM) for fracture [129, 130], but introduces a novel random load redistribution mechanism that, although crude, appears to produce many features consistent with experimental observations, such as an exponential distribution of internal stress [58] and a log-normally shaped distribution of global failure stress ( Sect. 5.1). These features are robust to the choice of the fiber failure distribution and the details of the stress redistribution. Moreover, the distribution scales with the number of fibers and collapses in the limit of infinite fibers to a non-zero deterministic value of the residual strength, corresponding to a finite yield stress. Other models deserve to be studied in this context, among them the FBM on a complex network [131], and one including dissipation and restructuring [132], which can describe the formation of new force chains.

5.2 Stochastic space-dependent friction

As argued in Sect. 2.3, the random fluctuations of shear friction can be attributed to the disordered structure of the force chain network present in the granular medium. At the same time it has been seen that some mean values are stable (see Sect. 3.3). One can, therefore, think of separating the random components from the deterministic ones and try to model them as random processes.

One of these models describes the random component of friction via a space-dependent stochastic process [78]. Equations with similar space-dependent noise have also been introduced in various contexts and will be illustrated in Sect. 6.1. As the shear stage slips by a small distance, one expects the random component of the friction $f_c$ to increase or decrease by a small random amount $df_c$, which depends only on the coordinate and expresses the rearrangement of the granular structure. Assuming a completely random change, one can write it as $df_c(x+dx)= \eta (x)dx$ and take $\eta (x)$ as white noise. On the other hand, as the slipped distance increases, the grain configurations become more and more different from the initial ones, whose memory is gradually lost. This corresponds to making the friction decorrelated with the distance. The simplest stochastic equation describing such an evolution is an Ornstein–Uhlembeck process [133], but with the role usually played by time being taken over by space:

$$\begin{aligned} \frac{df_c(x)}{dx} = \eta (x) -\ell f_c, \end{aligned}$$

(10)

where $\ell$ is the correlation length and $\eta$ is a Gaussian white noise whose variance D defines the average amplitude of the force. This equation can be used to describe the evolution of the random component of friction in the equation of motion for the shear plate:

$$\begin{aligned} I\ddot{x}= -\kappa (v_0 t -x) -f_v(v)-f_c(x), \end{aligned}$$

(11)

where $f_v$ is the deterministic component of Eq. (5), derived empirically from experiments [78]:

$$\begin{aligned} f_v(v)=f_0 + \Gamma [v -2v_0 \ln (1+v/v_0)]. \end{aligned}$$

(12)

The correlation length $\ell$ and the amplitude D of the random component of friction can be measured directly from the experimental power spectrum, as the one shown in Fig. 8. The other parameters, mass and spring constant, are known, so time series for x and the associated quantities can be easily obtained by simulating the process numerically. This equation has been shown to be able to adequately model the stick–slip motion, reproducing many features of the observed statistics [78], as can be seen in Fig. 11, where the reproduced probability distributions for s, v and T, corresponding to the lines, show a very good agreement with the experimental observation for different driving speeds. Moreover, the inclusion of inertia also seems to explain well the peaks that characterize the distributions at large values [134] (Sect. 4.1).

Another model that includes randomness in friction resorts to a coarse-grained description of the granular medium, representing it as particles on a D-dimensional regular lattice [135]. In this model, each lattice site i can be randomly occupied by a grain, and is associated with a strain $u_i$ and a stress $\tau _i$. Shear is applied to the system by moving a boundary of the lattice with constant velocity V. If the stress at a location exceeds a local random yield threshold, a proportional strain is accumulated until it falls below a local arrest threshold, which is also randomly assigned at each location. As the system slips, the local failure thresholds are lowered, simulating the global weakening of friction often observed experimentally. A slip ends when there are no more sites with stress above the local arrest threshold. When a slip ends, the local yield stresses return to their initial values. In the mean-field approximation, where one site interacts with all others, and neglecting the inertial term, the resulting shear stress at site i at time t is given by [135]

$$\begin{aligned} \tau _i(t)= J \left( \bar{u}-u_i\right) + \kappa (Vt-u_i(t)), \end{aligned}$$

(13)

where $\bar{u}= \sum _j u_j/N$ is the average strain, the sum being on the occupied sites (packing fraction). The model has been shown to reproduce many features observed in experiments. In particular, the exponents for avalanche size, duration, and power spectrum are $\tau =3/2$, $\alpha =2$, $\delta =2$. In addition, the associated distributions show bounds depending on the occupation probability (packing fraction), as observed in Ref. [39], and a parabolic shape of the average velocity is reproduced (Sect. 4.5).

5.3 Rate-and-state friction laws

Friction is a very broad subject [136,137,138]. Nevertheless, a discussion of granular shear stress cannot ignore the so-called rate-and-state (R &S) laws that describe the frictional interaction between solids. In contrast to the simple Da Vinci–Amonton–Coulomb laws where time and velocity play no role, they take into account some effects that can be observed in friction. It can decrease at relatively slow speeds and increase at higher speeds. Furthermore, when two bodies remain in static contact for a long period of time, the frictional force between them is observed to increase with the logarithm of the contact age, both effects that can also be observed in some granular systems, as discussed in Sect. 3. Bowden and Tabor [139] understood that the static frictional force between two sliding surfaces is strongly dependent on the actual contact area due to asperities. In a long series of papers, various authors elaborated on this concept in order to establish more refined properties and constitutive laws for the behavior of frictional bodies, capable of describing the properties observed experimentally. They came to formulate friction laws with similar time and velocity dependence (see Refs. [140,141,142] and, e.g., Ref. [137] for a review on the historical evolution of friction laws).

R &S-dependent laws have been widely used in the description and simulation of coseismic activity [37, 143] and have been shown to reproduce many features of crustal earthquakes [144]. They retain some features of time-independent friction, such as independence of contact area and proportionality to load. In the formulation of Refs. [140, 145], the time and velocity dependence of the friction coefficient $\mu$ is expressed as

$$\begin{aligned} \mu = \mu _0+ a\ln \left( 1+\frac{v}{v_0}\right) +b \ln \left( 1+\frac{\phi v_0}{D_0}\right) \end{aligned}$$

(14)

where $\mu _0$ is the static friction coefficient, $v_0$ is a reference velocity, usually very small and mainly to avoid the logarithmic divergence, and $D_0$ is a characteristic length related to the asperity spatial size and correlation. The state variable $\phi$ ages with time while rejuvenating with velocity and can be interpreted as a characteristic contact lifetime:

$$\begin{aligned} \dot{\phi } = 1-\frac{v\phi }{D_0}. \end{aligned}$$

(15)

R &S laws account for both the strengthening of quasi-static contacts and the velocity dependence of sliding friction, and do so with the same state variable (14).

The coefficients a and b determine the weight of the rate-dependent and state-dependent terms, respectively. Note that in a steady state $\phi =D_0/v$ and, therefore, $\mu =\mu _0 +(a-b)\ln (v/v_0)$. R &S laws can sustain stick–slip. For the overdamped case, it can be shown that the motion can perform stick–slip for $a - b \le 0$, and always performs continuous sliding otherwise [141]. Although well consistent for solids, the R &S friction laws appear to be of limited validity for granular materials. Tested on a wide range of different granular materials [146], it has been observed that the same system can have different values of the parameters a, b and $D_0$ in different ranges of velocity or normal pressure.

5.4 R &S friction in fluctuating granular systems

As previously reported, frictional aging and a Stribeck curve in a granular system are often observed in different situations. Expressions similar to Eq. (12) have also been derived from theoretical arguments [147]. As just recalled above, also in sheared granular systems, it is observed that the friction depends not only on the instantaneous velocity but also on some time-dependent state variable that accounts for the lifetime of contacts between asperities, although not as stably as for solid-on-solid [146].

It seems that there have not been many attempts to include R &S laws in the description of the irregular dynamics of a granular system. One has been done by rethinking the model [78] based on the Ornstein–Uhlembeck process in Sect. 5.2, which uses an empirical expression of the average friction as a function of the single velocity, $f_v(\dot{x})$, derived from the experiments, Eq.(12). Note that it contains a quadratic term at large shear, consistent with Refs. [30, 31] and other observations. However, it has been seen that friction is not a unique function (Sects.3.2, 4.5) and, as shown in Fig. 6, different values of friction are observed for positive or negative acceleration, even at the same instantaneous speed. It is likely that one of the causes of friction hysteresis is contact aging. Therefore, instead of considering the acceleration dependence empirically, as in Fig. 9, an expression that includes both nonlinear viscosity and contact aging has been used in Eq. (11) in place of the simple Eq. (5) [77]:

$$\begin{aligned} f_{v_\pm }(v, \phi ) = \left( 1+\frac{\chi }{A_0} v^2\right) \left( A_0 +A_\phi \ln \left( 1+\frac{\phi }{\tau }\right) \right) , \end{aligned}$$

(16)

where the evolution of $\phi$ is given by Eq. (15) and the parameters are derived from experiments. This expression allows for both weakening and hardening of the average force, that in this way appear as dynamical effects through the state variable $\phi$. Performing numerical simulations of the chaotic stick–slip motion of the plate on the granular bed, the average friction along the slips has been calculated considering positive and negative accelerations as separate instances. Both curves and their average, which does not distinguish the acceleration, show the Stribeck shape, but with minima at different locations. At low v, friction is greater for positive accelerations, as expected. A comparison with the experiment is shown in Fig. 16, where it is interesting to note that in both cases the curves cross at a unique point. These results, although qualitative, show that reliable models for granular shear cannot be built without considering contact aging.

Fig. 16

Top: experimental average friction as a function of instantaneous velocity for positive (squares) and negative (diamonds) acceleration. At sufficiently low velocities, the force is greater for positive acceleration, but crosses the negative acceleration curve at larger values, and decelerating events show higher friction. Bottom: Corresponding average friction curves from the stochastic model Eq. (11) with a rate-state law of the type Eq. (16) (from Ref. [77])

To test whether the average friction evolution along a slip can be described by the R &S equations, a fitting procedure was performed on the average friction and velocity curves extracted from experimental data [148]. For this purpose, the slips were divided into classes according to their duration (as described in Sect. 4.4 [102]). For each class, the average velocity profile has been considered and employed to fit the corresponding average friction evolution with different forms of friction laws, among which R &S in the form of Eq. (14) and its other usually adopted [149]. Both forms have been shown to be able to reproduce to some extent the average behavior of experimental friction better than other laws, but without some important details. In addition, the parameter values obtained from the fits are not always realistic. It should be noted that the R &S laws do not seem to have been experimentally tested along slips with continuous, long-lasting velocity changes. Thus, their validity for granular media, already limited in velocity step experiments as recalled above, may be even weaker under these circumstances. Fluidization along the motion can change the internal contact network, and the random nature of the motion makes it difficult to extract parameters from individual slips. Moreover, in the presence of nonlinear relations as in R &S, the average friction does not necessarily depend to the average velocity, and therefore, the adopted fitting procedure itself could be inconsistent. It may be worth noting that, nevertheless, the experimentally derived rheology of the granular material, imposed as a boundary condition in the numerical simulation of a fault, reproduces the basic features of both sub-shear and super-shear crustal earthquakes, with spontaneous acceleration up to some terminal rupture speed [148] in a way that is difficult to distinguish from when using R &S.

6 Fluctuating response as a critical phenomenon

As discussed earlier, power laws and scale invariance are often taken as manifestations of some non-equilibrium critical transition that, as for equilibrium systems [150], could cause systems that are microscopically very different to exhibit similar and universal statistical features in their critical properties. Some theoretical frameworks potentially relevant to this description are briefly illustrated below. However, it is necessary to keep in mind that the need for time-dependent dynamics to describe non-equilibrium systems makes the concept of universality, developed in the context of equilibrium-critical phenomena, possibly dependent on the dynamical rules.

6.1 The ABBM model

It was mentioned in Sect. 5.2 that the random modeling of friction has analogies to noise in other systems. The common features are the dependence of the noise on space, not on time as in the usual stochastic process, and the autocorrelation properties. Among the paradigmatic models of this type is the one describing Barkhausen noise [151], i.e., the (magnetic) noise emitted by a ferromagnet during a hysteresis cycle. Although the magnetization signal in the $H-M$ plane is apparently smooth, it shows fluctuations (avalanches) on small scales [88, 107, 152]. As the external magnetic field changes, domains aligned with the external fields grow, while opposite domains shrink due to the motion of the interfaces. Fluctuations in the motion due to defects generate the Barkhausen noise which, although known for almost a century [151], has received a quantitative description derived from microscopic considerations only in the last decades [153]. This is formulated by a stochastic equation which is simple enough to allow exact analytical results and is similar to Eq. (11):

$$\begin{aligned} \frac{dx}{dt}=-\kappa (x-Vt)+F \end{aligned}$$

(17)

where x is a quantity directly proportional to the magnetization and V is the rate of change of the external field H, $\kappa$ is the demagnetization factor and F is a random perturbation given by

$$\begin{aligned} \frac{dF}{dx}=\eta (x). \end{aligned}$$

(18)

The model, named ABBM after the initials of its authors, is also representative of a class of stochastic models where the randomness comes from a spatial noise term, generally called depinning models, which describe the dynamics of an elastic (hyper-) surface or of interacting particles over a rough landscape in the presence of a viscous force. Besides the ABBM model [107, 154], they can describe, e.g., the crack propagation in a disordered medium [155] and the slip of dislocations in solids [156, 157]. The random potential accounts for the roughness and can exert a pinning force. If F is greater than the driving force, the system will stall until the driving force is large enough. The depinning transition exhibits all the features of criticality (such as power-law distribution and long-range correlations) and universality (see [158] for a recent review). Equations of the form (17) are obtained by replacing the local interactions by suitable averages, leading to a mean-field formulation of the problem where the interface moves with intermittent motion for $V <1$ and continuous sliding for $V>1$. In fact, a Fokker–Planck equation [159] equivalent to the same process was first introduced by Feller [160] to describe a problem of population dynamics. Later, the process was rederived in the form of a stochastic (Langevin) equation [161], known as the CIR model, to explain the evolution of interest rates. The CIR equation can be obtained from ABBM, Eqs. (17) and (18), by deriving with respect to time and taking into account the rules for time transformation in stochastic processes, obtaining

$$\begin{aligned} \dot{v} =-\kappa (v-V)+\sqrt{v} \eta (x(t)), \end{aligned}$$

(19)

with $v=dx/dt$. In this equation, the noise is coupled to the velocity (as in the Fokker–Planck–Feller equation mentioned above), so it does not act when the system sticks, but its amplitude grows with velocity (this has been observed experimentally ([74], Sect. 3.3). From this equation it is easy to derive power-law distributions for avalanches, as well as parabolic and self-similar average shapes. A detailed discussion of the latter property, also in connection with other processes, can be found in Ref. [162]. A very relevant point is that depinning and similar models can describe different systems giving rise to identical critical exponents, which can, therefore, be expected to be observed in different phenomena, at least in some situations (in the case of short-range interaction, the exponents are sensitive to the driving velocity V).

As noted above, these models are formulated in the overdamped limit, that is, neglecting the inertial terms with respect to the viscous term linear in velocity. However, there are situations where inertia cannot be neglected. Cases have been seen in the dependence of time distributions, Fig. 12, and in the reproduction of experimental observations with Eq. (11). There seems to have been only one attempt to add inertia to the ABBM equation. For this purpose, the equation in the form of (19) is more manageable than Eq. (17), but the inclusion of inertia gives rise to a complicated history dependence, due to possible oscillations with consequent backward motion, which creates problems with both the square root and the spatially dependent noise. The study, therefore, requires the definition of some protocols and regularizations that affect the original model. The results do indeed show the presence of negative slip, which decreases with increasing drive speed and decreasing mass. Both positive and negative branches of the velocity distribution appear at low speeds, with regions of power-law behavior. Further investigations are needed to see to what extent such a model can reproduce experimental results, where negative velocities are not observed.

6.2 Self-organized criticality

When sand is poured over a limited area, a pile of increasing slope grows until an avalanche detaches from the surface. When the avalanche runs out, adding more sand will eventually start a new avalanche, and so on. It is as if the system would self-organize into a statistically stationary state where avalanches occur intermittently, as in Bagnold’s experiment recalled in Sect. 2.2. This metaphor of a sand pile [163], called self-organized criticality (SOC) and translated into a cellular automaton [21], has shown to be capable of generating large and intermittent fluctuations, statistically distributed as power laws [91]. Initially proposed mainly as a mechanism for generating 1/f noise spectra [21], it was eventually found to generate $1/f^2$ instead. SOC gained great popularity, spawning a number of variants and several other models inspired by it [164, 165], and has the credit of proposing a link between critical phenomena and intermittent self-similar fluctuations. But it has also attracted criticism and raised questions that have not yet been resolved. Among the former is the one that it is not really self-organizing [166]. In fact, as their name implies, SOC systems seem to drive themselves at a critical point, in contrast to equilibrium systems, which exhibit critical behavior only when deliberately brought close to the critical point by a fine tuning of parameters. In fact, some care is required in how slow driving and fast dissipation are realized [166].

As mentioned above, an open question concerns the real possibility of defining universality classes [165, 167]. The concept of universality, developed in the context of equilibrium-critical phenomena [150], is not readily transferable to non-equilibrium systems. The main reason is the need for dynamic rules that can make the difference. Another point concerns the relationship of SOC to real systems. In particular, it is far from clear how parameters and variables of a real system can be translated into a SOC model. As the model is based on the idealization of a sand pile, it gave impetus to the investigation of real granular systems, revealing among other things that real sand piles hardly show power laws due to inertial effects neglected in the model, another instance that scale symmetry can be broken by mass.

6.3 RFIM and crackling noise

Another approach to the critical dynamics observed in several systems starts from equilibrium-critical phase transitions [168] and considers as a prototypical model the random field Ising model (RFIM) [60]. In this model, binary variables, spins, are assigned to each site of a D-dimensional lattice. They are coupled to their nearest neighbors by a ferromagnetic coupling J, to an external magnetic field H, and to a local quenched random field $h_i$ that accounts for disorder, so that the total energy is given by

$$\begin{aligned} { \mathcal {E}} = -J\sum _{i,j \in nn} \sigma _i\sigma _j -\sum _i (h_i+H)\sigma _i. \end{aligned}$$

(20)

There are no thermal fluctuations, but by slowly changing the external field, avalanches of arbitrary size are triggered when disorder and field are in certain critical ranges. Through renormalization group calculations [60], it has been shown that around the critical point avalanches can be generated with exponents shared by different systems. Particularly suitable for magnetic systems, as for the case of Barkhausen noise, it has, therefore, been suggested that similar approaches can be used for various phenomena, from earthquakes to crumpled paper, which emit “crackling noise” in response to small perturbations. And that, to better discriminate between theories, progress can be made by comparing other statistical quantities besides distributions, such as scaling functions and avalanche shapes (Sect. 4.5). These quantities have also proven to be useful tools for understanding how complex non-equilibrium systems may differ from equilibrium-critical systems.

6.4 Relation with other phenomena

The above models are perhaps the most common reference for the search for universality in non-equilibrium systems. Actually, the associated scaling exponents for the different quantities depend on the space dimensionality and the interaction range [60, 107, 165, 167]. For short interactions, they are somewhat different but sometimes very similar from one model to another. Nevertheless, in the mean-field limit (infinite interaction range or space dimension), they all give the identical exponents listed in Table 1, which are often observed in experiments, as reported here. It has been mentioned several times how many different phenomena share similar intermittent and scale invariant behavior, despite their different nature and size scale. It may be worthwhile to recall some systems that, as granular systems, manifest these properties under shear, and that appear to be related in many natural phenomena.

Intermittent motion is exhibited during the sliding of two solid surfaces in contact. Experiments have shown that different regimes are possible at varying driving velocity, mass and spring, and power laws can be observed in the distributions of slip extension, stress drop and frequency spectrum [169,170,171,172,173] also in different configurations [174].

Among many phenomena that show statistical scale invariance, fault dynamics has gained great visibility also for its relevance. Among the statistical distributions, the Gutenberg–Richter law for the magnitude of earthquakes is certainly the best known. It relates the frequency of seismic events to their magnitude:

$$\begin{aligned} P(m)\propto 10^{-bm}, \end{aligned}$$

where P(m) is the probability of an event having a magnitude greater than m. This exponential law takes on the aspect of a power law when rewritten in terms of physical quantities. In fact, the magnitude is related to the seismic moment M, which in turn is proportional to the radiated energy [93], so that

$$\begin{aligned} m=\frac{2}{3}\log E + c, \end{aligned}$$

which yields $P(E) \propto E^{1-\beta }$ with $\beta =\frac{2}{3}b+1$, and, therefore, a density

$$\begin{aligned} p(E) \simeq E^{-\beta }. \end{aligned}$$

For the typical value $b \approx 1$, this implies $\beta \approx 5/3$, a value close to that observed in some granular shear experiments (Sect. 4), but a bit larger than the value 5/4 derived in Sect. 4.4 from the assumption $E \propto S^2$, and than the mean field value 4/3 (Table 1). However, it is compatible with larger values of $\tau$ often observed when inertial effects are present. At the same time, smaller values of b are also observed. Several stochastic models have been developed to reproduce seismic activity. Besides chaotic deterministic models, such as that of Burridge and Knopov [175] and its variants, [176], others have been inspired by SOC [177, 178] and ABBM [179], in analogy to those discussed in Refs. [135] and [180]. Seismic self-similarities obey a very rich catalog, so we refer to the literature for an overview (see, e.g., Refs. [181,182,183]).

Another phenomenon with self-similar aspects, and also strictly related to earthquakes and friction [183], is crack propagation. The slow propagation of a crack in a heterogeneous medium also occurs by avalanches [85], its profile is self-similar [155, 184] and can be related to the depinning transition mentioned above [185].

Finally, it is worth recalling that scale-invariant properties in the plastic deformation of solids [186], known for many years [110, 187], have recently been enriched by the study of slip profiles in some compounds such as metallic glasses [96], where it has been observed that symmetric and self-similar profiles of short slips deform gradually for increasing size in the same direction as in granular systems and earthquakes [122].

7 Conclusions and perspectives

This paper summarizes and discusses the results of some tabletop shear experiments on the fluctuating dynamics of a confined granular system. As a general feature, physical quantities are observed to exhibit wide probability distributions, generally skewed, as for example the shear stress. The quantities characterizing the slip, such as strain, duration, stress, and energy drop, follow distributions close to power laws, sometimes with similar exponents in different experiments, even with different dimensionality, and possibly close to mean field values. Other times, however, power laws appear more as stylized facts, with sensible differences, especially in the tails. More detailed and systematic studies of the factors influencing the distributions at large values are needed, including the system size, which is not easy to vary in experiments. The cutoff of the distributions and the corresponding shapes at large values seem to be sensitive to other factors as well. In addition to controllable granular properties, such as compaction and normal stress, which can modify or even suppress the intermittency, the inertial component dynamically related to the fluidization of the medium, i.e., the granular mass mobilized in the slip, seems also to contribute in a fundamental way to the inertial peaks. Large changes in the cutoff may also be the reason why the distributions sometimes look essentially exponential.

Apart from some very general theoretical approaches inspired by equilibrium-critical phenomena, there is a lack of stochastic models able to take into account the random aspects of granular dynamics and to reproduce experimental results at a realistic level. At present, only a few very simple mean-field models, borrowed from other systems and sometimes neglecting inertia, seem to have been proposed and partially tested. Continuous descriptions could be fruitful, if not necessary, by extending Bagnold’s findings on the transition from stick–slip to continuous sliding, while no explanation of the transition from irregular to periodic stick–slip seems to be available, even on a qualitative level.

A key point in this regard is the friction law. In fact, the modification of friction in long slips seems to be one of the factors that can break the scale invariance of statistical features, which instead appears very clearly in some circumstances. In particular, the self-similarity is clearly broken in large slips, where asymmetric average shapes and peaks in the probability distributions are observed. The friction law should account, at least on a phenomenological level, for the Stribeck behavior, i.e., the velocity weakening and subsequent hardening that can be seen in many different situations, as well as for the random fluctuations. At present, rate-and-state (R &S) friction laws seem to be the best approximation available to describe granular friction and, although some experiments show that they are not really adequate, their inclusion in simple models produces promising results. More systematic experiments and simulations are desirable, not only varying the usual parameters influencing friction, such as packing fraction, system size and normal stress, but also carefully analyzing the entire dynamic evolution of the system, trying to model also random components of friction in an appropriate way, possibly taking into account the changes in granular motion during the flow. The dynamic variation along the slip of parameters such as contact aging, granular inertia, degree of fluidization, are factors that certainly need to be considered in order to model also random components of friction in an appropriate way.

By systematically collecting large amounts of data from experiments and numerical simulations, artificial intelligence, which is already used in related fields such as seismology, could perhaps be of great help in addressing some of the above issues, such as the formulation of effective friction laws and the discrimination of factors influencing distribution shapes. A deeper knowledge of the mechanisms governing intermittent granular flow in laboratory experiments would also be a step towards understanding these dynamics at larger scales, such as in industrial and natural systems.