Abstract
Quantum information processing is nowadays an established branch of quantum mechanics applications. Recent results in different areas, ranging from communications to computing, show that quantum technologies are advancing towards being mature platforms with substantial advantages over traditional classical protocols. Quantum optics and photonic apparatuses are one of the best candidates for the realization of quantum processors. In this context, integrated photonic technologies are essential components towards miniaturisation of such complex optical systems. Integrated optical devices enabled an important improvement in the level of complexity in the generation and processing of quantum states of light. This review aims at providing an exhaustive framework of the advances of integrated quantum photonic platforms, for what concerns the integration of sources, manipulation, and detectors, as well as the contributions in quantum computing, cryptography and simulations.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Quantum states of light are fundamental resources for the implementation of quantum information protocols since the pioneering tests on nonlocality and quantum teleportation [1, 2]. The advantages of single-photon state encoding are several and include the lack of decoherence phenomena, the possibility to realize information processing at room temperature and to send photons through fibers and free space channels. In the last ten years, improvements in photonic quantum technologies enabled an increase in the complexity of the implemented system, supporting relevant advances in various branches of quantum information, including the demonstration of quantum advantage [3,4,5] and satellite quantum communications [6, 7].
One of the technological steps which allowed such an improvement was the adoption of integrated photonic device components for manipulating the quantum state of the light [8,9,10]. Integrated photonics envisages the fabrication of waveguides and of tunable optical elements to realize multi-port programmable optical circuits [11, 12]. Further developments in the integration manufacturing stage allow nowadays to have both the generation and processing of quantum states in a single monolithic programmable nano-processor [13,14,15]. The integration of single-photon detectors still presents relevant challenges, but recent results have opened promising perspective toward the implementation of fully integrated photonic platforms [16,17,18,19]. In this review, we aim at picturing the recent advances of integrated photonics for quantum technologies. The most recent achievements, limitations and future perspectives in the various application ranges, like computing, cryptography and simulation, are presented.
To ease the consultation of this document, we illustrate briefly the structure of the presentation. The review is organized in two main parts. The first part is an overview on the generation, encoding, processing and detection methods of single-photon states in integrated platforms. We begin by first presenting the principal fabrication technologies of optical waveguides. As a second step, the integration of parametric and deterministic single-photon sources is discussed. The third subsection is dedicated to integrated optical circuit designs and various single-photon encodings. The first part ends with a review of single-photon detector integration. The second part of this work regards an overview of recent applications of integrated photonic technologies in quantum information. In particular, we focus on the results in quantum cryptography and communication and then, on various on-chip realizations of schemes for universal quantum computing. Other applications in the quantum simulation field are presented. In the end, the review will illustrate the paradigms to prove quantum advantage with photons via sampling algorithms.
2 Quantum information processing in integrated photonics platforms
Quantum information protocols have been investigated in several physical systems. Each platform displays some advantages and drawbacks and, consequently, there is not a clear or definitive evidence regarding the best physical system for future quantum technologies [20]. In this context, photonic quantum states are optimal information carriers thanks to the weak interaction with the environment which made optical operations nearly decoherence-free and the possibility to send photons both through fibers or free space for long distances [1]. These features have been exploited in recent years for first demonstrations of quantum cryptography, computing and simulation as well as quantum mechanics foundation tests, until the latest experiments which have proven quantum advantage with photons [3,4,5]. Many of these examples took advantage from integrated optical platforms which are essential for compact and scalable realisation of quantum information protocols. Before illustrating the various techniques and applications of such integrated devices, it is helpful to review the principal information encoding adopted in the photonics community.
One approach for quantum information processing is via discrete variables. The operations are defined in Hilbert spaces individuated by \(\{|i\rangle \}_{i=0}^{d-1}\) discrete levels [21]. Many of the existent quantum computing and quantum cryptography schemes have been realised in such a framework, exploiting photonic qubit (\(d=2\)) and qudit (\(d>2\)). In fact, various degrees of freedom (DOFs) of single photons are highly appropriate for the task. The polarization individuates a two-level system which is equivalent to the Hilbert space associated to a qubit. Photon states can be prepared even in high-dimensional DOFs to encode qudit [1, 22, 23] such as a discrete set of time intervals or frequencies [24,25,26], the optical path [8, 15, 27], the spatial modes supported by optical fibers [28, 29], orbital and transverse momentum [30, 31].
A second approach is via continuous variables (CV) in quantum optics. This quantum information framework exploits physical observables which assume continuous values instead of making use of discrete levels as in qubits or qudits registers [32]. In quantum optics, the physical observables are expressed in the phase space of the quantum harmonic oscillator associated with each mode of the electromagnetic field [33]. Protocols for quantum computing [34, 35], quantum cryptography [36], and, recently, sampling algorithm from photon counting experiments [37,38,39,40] have been proposed in the CV framework. This work will focus mainly on the use of single-photon in discrete variables, except in the last section of the review, in which squeezed states and, more generally, Gaussian states of light are employed to prove quantum advantage via sampling algorithms. We suggest the following reviews collection for a deepening of CV quantum information [32, 34, 41, 42].
The fundamental phenomenon which allows the optical processing of the information is the interference among photons or among the DOFs of single-photon states. Multi-port interferometers are thus essential elements of any quantum optical protocol, together with single-photon sources and detection. In this context, integrated photonics aims at providing compact and miniaturised devices which include all the elements mentioned above. As we will see in the following sections, the engineering of waveguides’ materials, optical properties and fabrication methodologies has allowed the verification of first proof-of-principle quantum protocols in single chips.
2.1 Materials and fabrications technologies
The principal methods for the integration of optical elements in monolithic chips envisage the fabrication of optical waveguides. The material and the fabrication technology determine important features of the resulting platform. The various approaches differ, for example, for the range of operating wavelengths, the level of miniaturization, the geometry of the waveguides disposition, the presence of nonlinear processes, the coupling efficiencies with fiber connections, just to mention a few. Therefore, there is not a unique and well-established technology which outperforms the others in the integration of optical circuits.
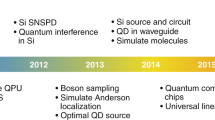
Integration technologies. Summary of the features of the principal fabrication technologies for what concerns the operating wavelengths, circuits geometry, integration of sources and detectors, and the interface with external fibers. Each method is labeled by a different colour. On the timeline, the milestones achievements of quantum integrated photonics in the last ten years. The coloured circles highlight the manufacturing technology, Silica-on-Silicon (SoS), UV-writing, femtosecond-laser-writing (FLW), silicon (Si) and silicon nitride (SiN)
One adopted material for the waveguides is fused silica (SiO\(_2\)) thanks to various advantages. Depending on the fabrication process, silica waveguides can display low birefringence and propagation losses, as well as transparency from the visible to infrared wavelengths and high coupling efficiency with fibers. We can distinguish among two main fabrication methods: the silica-on-silicon (SoS) [43] and laser-written waveguides, which includes in turn UV-writing [44] and femtosecond-laser-writing (FLW) [45]. Other important and advanced manufacturing for integration are Silicon-on-insulator (SoI) platforms, including silicon (Si) [46] and silicon nitride (SiN) waveguides [47]. The silicon-based circuit offers one of the highest levels of miniaturization which derives from the know-how of the silicon-based integrated-electronics circuits.
Other waveguides technologies based on the employment of active materials such as LN [48, 49], GaAs [50], and InP [51], present large electro-optical properties that allow for fast operations on single photon states. For a more comprehensive discussion on active materials platforms, we suggest the following collection of reviews [9, 48,49,50,51].
In the next subsections, we review the main features of the principal methods cited so far, namely SoS, UV-writing, FLW, Si and SiN manufacturing technologies.
2.1.1 Silica-on-silicon waveguides (SoS)
The fabrication method of SoS waveguides follows these steps. A layer of undoped silica that is the core material of the waveguides is deposited on a substrate of Silicon. The core is then patterned via standard optical lithography techniques and covered by a second layer of doped silica. One of the first examples of integrated circuits for observing quantum interference and testing quantum gate on path-encoded qubits were realized with such technology [43, 52]. SoS platforms were also one of the first instances of re-programmable optical circuits [53, 54], including the first universal 5-mode quantum processor [11]. However, some intrinsic limitations of this technology have prevented further developments of SoS devices. In fact, the waveguides present a rectangular cross-section which is not symmetric around the propagation axis. This implies that only two polarization modes are guided, namely, the TE mode, in which the electric field is transverse and the magnetic field does not, and the TM mode where the magnetic field is transverse. The size of the rectangular shape allows one of such components, more precisely the mode TE\(_{10}\). It follows that integrated devices with rectangular waveguides work only with one linear polarization component. The fabrication process requires the use of a mask which allows only for the planar arrangement of the waveguides. In addition, the integration of single photon sources is challenging since it requires a nonlinear response of the material (see Sect. 2.2.1) that is weak in these waveguides.
2.1.2 Silica laser-written waveguides
Direct UV-writing. An alternative method is the direct UV-writing, in which SoS waveguides are fabricated by focusing a continuous wave laser at the wavelength of \(244\, nm\) in a photosensitive doped silica layer which induces a permanent change in the refractive index of the material. Such a layer is placed within two layers of undoped silica on top of a third silicon layer [44]. The waveguides are then etched translating the sample with respect to the laser beam. Consequently, the writing technique does not require the adoption of masks as the previous SoS method. This simplifies the process of fabrication and allows for 3D geometry architectures and for circular cross-sections of the waveguides. There are examples of multi-mode static [55] and reconfigurable circuits [56, 57] up to 20 modes. This fabrication method shows also remarkable results in the integration of parametric single-photon sources in SoS. waveguides [58, 59]. The UV-writing demonstrated to realize separately all the components required for the full integration of optical setups, such as integrated sources [58, 59], directional couplers [55,56,57], optical gratings [60,61,62], polarizers [63] and detectors [64]. However, the assembly in a single device has not been carried out yet.
Femtosecond-laser-writing (FLW). The femtosecond laser writing is a further method for silica waveguide fabrication [45, 65]. The mechanism of the process is the non-linear absorption of strong laser pulses tightly focused in the silica sample. Such absorption results in a permanent and localized modification in the refractive index. Waveguides are directly written by translating the silica sample at a constant speed with respect to the laser beam, without needing any preliminary preparation of substrate or layers of different materials as in the previous methods. The cross-section is circular and presents a very low birefringence. Such characteristics together with the 3D geometry capability have allowed the realization of devices insensitive from polarization [66,67,68] as well as devices able to manipulate polarization as waveplates or partially polarizing beamsplitter [69, 70]. The 3D geometry has other advantages regarding the range of possible schemes for optical circuit decomposition. FLW devices demonstrated to realize circuits according to the traditional networks of integrated beam-splitter in planar [67, 71,72,73,74] and 3D geometries [75,76,77] and continuously-coupled waveguide lattices [78,79,80,81,82]. We have instances of re-programmable circuits in small [83,84,85,86] and large scale [87] realization of integrated devices. The integration of single-photon sources which exploits nonlinear effects is still challenging due to the low birefringence and null \(\chi ^{(3)}\) of these waveguides (see Sect. 2.2.1). Notwithstanding, the FLW can be exploited to write waveguides in a nonlinear material to generate pairs of photons in parametric processes. These kinds of sources have been interfaced successfully with FLW chips in [88]. The FLW waveguides display also a good coupling with external fibers, enabling the interface of the optical circuit with remote users or solid-state sources [85, 86].
2.1.3 Silicon-on-insulator (SoI)
Silicon (Si). The previously cited fabrication technologies present some limitations for what concerns the level of miniaturization and thus for the number of optical elements that can be integrated in a single chip. Silicon devices are characterized by a high refractive index which allows both for reduced-size circuits and for nonlinear processes. The fabrication of these waveguides is through optical lithography [46]. Si-based circuits show one of the highest densities of optical elements in the same device including integrated tunable beam-splitter and phase-shifter, optical gratings, waveguide crossings, resonators and single-photon sources. Many recent experiments exploit Si circuits in the various fields of quantum information like quantum teleportation [89], computing [13, 15, 90], simulation [91, 92] and entanglement generation [27, 93, 94]. The integration of single-photon sources by means of nonlinear processes is also very advanced [95, 96]. Arrays up to 16 identical sources in the same chip have been demonstrated [15, 27, 90]. Some advantages of the Si waveguides such as the high-birefringence result in some collateral limitations for what concerns photons absorption, low transparency at the visible wavelengths and not optimal couplings with external fibers. Some improvements can be achieved using alternative semiconductor materials such as InP [97], GaAs [98] and GaN [99].
Silicon nitride (SiN). Si\(_3\)N\(_4\) waveguides are emerging as a promising alternative to silicon photonics. These optical circuits share many features of the Si device regarding miniaturization and integration of single-photon sources. Furthermore, these waveguides are transparent in a wide range of wavelengths like the silica ones and display the lowest level of photon absorption and losses [100]. Recently, quantum protocols have been demonstrated in re-programmable multi-port optical circuits with high-level of reconfigurability [12, 101]. The integration of single-photon sources is possible also in these platforms. We have examples of entanglement generation and measurement in the same chip [102], optical resonator for the generation of high-dimensional entangled states in the frequency domain [24, 25, 103], as well as quantum algorithms run in a fully integrated device [14].
2.2 Integrated non-classical light sources
One of the main fundamental components for photonic integrated quantum apparatuses consists in photon sources. Several sources based on different technologies have been implemented, starting from bulk sources based on second-order parametric processes to recent developments on solid-state devices. However, sources producing single-photon or entangled-states off-chip require the capability of an efficient interface with integrated photonic devices, to avoid adding additional losses that can prevent the successful application of quantum information protocols. Thus an integrated approach encompassing photon sources may be preferable to go in the direction of fully integrated systems with complete functionalities. In the following, we review recent advances in the implementation of integrated photon sources.
2.2.1 Integrated single-photon sources
The engineering of single-photon sources is tailored to generate on-demand indistinguishable and entangled photon states. The principal difficulty in the design of photon sources is to fulfill all the requirements mentioned so far in the same system. In fact, single-photon sources can be separated into probabilistic and deterministic ones. The first family of sources exploits nonlinear processes which generate intrinsically pairs of correlated photons. Probabilistic sources have found a straightforward realization in integrated circuits thanks to the nonlinear properties of the waveguides materials [104]. The second class of sources exploits deterministic emissions of photons from atomic-like structures grown on semiconductor materials [105]. Let us illustrate in more detail the efforts for single-photon sources integration in these two frameworks.
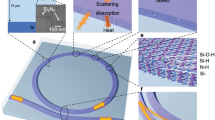
Among probabilistic sources, we can recognize two generation mechanisms. The first one is the spontaneous parametric down-conversion (SDPC) which is a second-order nonlinear process linked to the \(\chi ^{(2)}\) value of the material. The geometry of this kind of source consists of straight waveguides etched inside or near a material with a high \(\chi ^{(2)}\), such as periodically poled crystals in FLW waveguides [88, 106], in LN [107] and AlGaAs waveguides [108] (see Fig. 2a). To increase the generation efficiency and purity, the nonlinear waveguides can be eventually designed inside a resonant ring interferometer [109]. The second mechanism is the spontaneous four-wave mixing (FWM) which is the typical phenomenon in materials with high \(\chi ^{(3)}\) coefficient. Examples of integrated FWM are in UV-writing silica waveguides [58, 110], Si [96, 111, 112], SoI [113] and SiN [14, 102, 114, 115] platforms. Ring resonators and long waveguides coiled in spirals are widely employed to enhance the brightness of the sources and the purity of the single-photon states [95, 104] (see Fig. 2b). One of the great advantages of integrated probabilistic sources is that they can be fabricated in arrays of identical emitters [13, 15, 27, 58]. The most important limitations of nonlinear processes are due to their probabilistic nature that prevents to have high pair emission probabilities and to scale the number of photons without post-selection and heralding procedures [116]. Possible solutions to such issues are time-multiplexed techniques which can increase the generation probability. This method has been performed only in a bulk-optics experiment [117] and the adaptation in integrated circuits is still under investigation.
The other type of sources are the deterministic emitters in solid-state physics. These architectures are generally composed of a quantum dot, an artificial atom structure, that generates a single photon when excited by a laser pulse. A first method for solid-state sources is based on micro-pillar cavities. The quantum dot is placed inside two Bragg mirrors. The cavity and the dot are grown together in the same hetero-structure [118,119,120,121,122]. This quantum dot technology has the advantage of producing very bright sources with high photon purity and indistinguishability. However, these structures are very hard to integrate. The experiment carried out with such micro-pillars exploit integrated circuits that can be efficiently coupled with the fibers coming from the sources [85, 86] (see Fig. 2c). Others solid-state emitters are defects in diamond crystals that have shown promising features towards the integration in the waveguide. Demonstrations of quantum entanglement and photon indistinguishability have been demonstrated [123, 124]. An alternative method to exploit defects engineering in a photonic-crystal waveguide [125]. Also this quantum dot structure has the advantage to put the source directly inside the waveguides. The creation of such a photonic crystal in waveguides is still challenging and the sources do not display the same performances as the micro-cavity dots. One common issue with deterministic sources is that the current state-of-the-art fabrication procedure is not sufficiently precise to produce identical dots in the same sample. Multi-photon experiments are thus performed by time-demultiplexing of photons generated by the same dot at different excitation. The cost of such a synchronization procedure is in the overall generation rate and indistinguishability [85, 126].
Integrated sources of quantum light. Principal schemes for the integration of probabilistic (a, b) and deterministic c) sources. a Waveguides written in materials with high \(\chi ^{(2)}\) such as periodically poled KTP, generate pairs of photons through the SPDC process. One possible fabrication of these waveguides is FLW. b Examples of single-photon sources which exploit third-order nonlinear processes as spontaneous FWM in doped silica, Si and SiN waveguides. The generation is enhanced via integrated optical resonators like the ring micro-resonator or by a very long waveguide coiled in a spiral. c The integration of deterministic sources is still challenging. Besides the first attempt in photonic crystal waveguides, the most adopted solution is via fiber connections from the source to the chip
2.2.2 Integrated squeezed light sources
A different type of quantum light employed in the continuous-variable framework is squeezing. Squeezed light shows very peculiar properties useful for quantum computation and metrology tasks. The major issues with squeezed light manipulation are the losses that can destroy the quantum properties of such sources. The on-chip generation and manipulation are thus essential since insertion losses in the fibers/chip interface could damage the quality of squeezed states. In recent years, the advances in the integrated photonic allowed several implementations of on-chip squeezed light sources. Since the first attempt in 2017 [127], now there are various implementations for different wavelengths [128, 129] and different materials [130, 131]. The principal geometry used to implement this kind of source are \(\chi ^{(2)}\) and \(\chi ^{(3)}\) materials inside resonators [131, 132]. This technology allows the fabrication of multiple squeezed sources into a linear array whit high photon indistinguishability [14, 90].
2.3 Optical circuits design
Integrated photonic tool-kits have been designed to prepare and process single-photon states in various DOFs [9, 133]. The manipulation of the single-photons states is performed by exploiting the optical properties of the waveguides such as the birefringence for polarization control, the refractive index which regulates the relative optical phases between the modes, and by mean of directional couplers for making photons interfere. They consist of two (or more) waveguides placed very close one to another for a given length in such a way that the radiation can be coupled in the waveguides by evanescent waves. Integrated beamsplitters, partially polarizing beamsplitters and resonators are realized through such a physical phenomenon. In the following, we analyze the optical circuit designs for the on-chip manipulation of the various DOFs of single-photon states. We will focus mainly on the path encoding framework since it is the most suitable for integration.
2.3.1 Path encoding
Photon states distributed among multiple waveguides are employed to encode qubit/qudit states and to observe quantum interference effects due to bosonic statistics. Such information encoding has been one of the most investigated in quantum integrated photonics. Path-encoded single- and multi-photon states can be arbitrarily prepared, manipulated and measured using re-programmable Mach–Zehnder interferometers (MZIs). The effect of the MZI is equivalent to the operations made by a beamsplitter with a tunable splitting ratio and by a phase shift (Fig. 3a). This unit for path encoding processing envisages two unbiased directional couplers and two integrated tunable phase shifts. Relative phases between paths in integrated devices are the results of the geometric deformation of waveguides. The recent developments in the field have demonstrated the capability to realize reconfigurable phase shifters, thus allowing the implementation of several unitary transformations on the same device [11, 12, 101]. There are several examples of programmable integrated devices in SoS [11, 53], Si [13, 15, 27, 90, 92,93,94], SiN [12, 14, 101] silica laser written waveguides with FLW [83,84,85] and UV-writing [56, 57]. The re-programmable elements inside the MZI are the two phase shifts that are controlled generally through the thermo-optic effect. Heaters placed nearby the location of the waveguide allow for local changes in the refractive index of the material. Such reconfigurable units are sufficient to encode, process and measure any qubit in two optical paths. The complexity reached from integrated devices is nowadays very remarkable allowing for full integration of qubit- and qudit-based quantum gates and algorithms in SoS [53] and Si-chips [15, 27, 93, 94]. In particular, the most recent silicon quantum processors count up to 16 integrated single-photon sources, more than 100 heaters and likewise integrated optical elements [13, 15, 27].
Universal schemes. More generally, optical circuits made by a network of several layers of tunable MZIs are universal, i.e. the circuits can be programmed to realize any unitary evolution on quantum states encoded in m paths. The first work which proved such a feature was Ref. [134]. Any \(m\times m\) unitary matrix representing the evolution of the m modes in the interferometer can be decomposed in the elementary operations of \(M=\frac{m (m-1)}{2}\) MZIs. The resulting network, shown in Fig. 3b presents a triangular structure. A universal and fully-programmable five-mode processor was realized in an SoS device in Ref. [11]. A more recent algorithm for the decomposition was introduced [135]. This scheme provides a fully symmetric arrangement of the optical elements which results in a more compact structure with reduced propagation losses and sensitivity to fabrication errors (see Fig. 3c). The most recent programmable universal processors exploit this design. The largest covers up to 20 optical modes [12, 101], together with an 8-mode processor equipped with four integrated sources [14], both realized in SiN waveguides. The last cited experiment was tailored to perform sampling tasks and quantum algorithms in the continuous variables framework.
Fast schemes. There are some schemes for specific families of transformation, such as Fourier and Hadamard matrices, which require a smaller number of optical elements. The symmetries of these matrices allow simplifying the process of decomposition, namely a number of MZI equal to \(M=\frac{m}{2} \log _2 m\) [136]. However, these schemes known as fast architectures need coupling between non-adjacent optical modes that result in a non-planar disposition of the directional couplers and phase shifts. Therefore, only fabrication techniques that can realize waveguides in different planes are compatible with the fast schemes. In particular, the tritter [75], the Fourier [76], the Sylvester [77], and cyclic transformations [86] have been fabricated in silica waveguides via FLW, for implementing tests on multi-photon interference.
Path encoding and integrated multi-port interferometers. a MZI unit for qubit path-encoding and for multi-port re-programmable circuits. The red phase shifter (PS) between the two unbiased directional couplers (DC) controls the reflectivity of the equivalent beamsplitter (on the right). The external PS introduces a phase between the two states \(|0\rangle \) and \(|1\rangle \). b, c Examples of universal 4-mode interferometers according to the triangular [134] and rectangular [135] decomposition. d Continuously-coupled devices comprise parallel waveguides organized in lattices of different geometries
Continuously coupled optical lattices. The MZI networks are not the only possible designs for operations on path-encoded quantum states. The laser-writing technologies present the capability of enabling 3-dimensional architectures for waveguide fabrication. This allows the possibility of fabricating arrays of several waveguides placed parallel one to the other, and are continuously coupled by evanescent-field interaction. This represents an alternative approach to implement large-scale circuits with a further favorable scaling with respect to losses and fabrication imperfections. However, it is worth noting that in the literature there is still not a systematic and complete study on the universality of such an approach for multi-mode interferometers fabrication. In this scheme, the geometry of the lattice determines the Hamiltonian H of the system. The latter can be expressed in terms of the annihilation and creation operators of the electromagnetic field as \(H = \sum _i k_i a^{\dagger }_ia_i + \sum _{i\ne j} c_{ij} a^{\dagger }_ia_j\) where the \(k_i\) are the site energies and the coefficients \(c_{ij}\) are the coupling coefficients among neighbor sites. Then, the equation that regulates the propagation of the field in the circuit is expressed via the operator \(U = \exp {-i/\hbar \int H(z) dz}\) where z is the propagation length through the lattice. Continuously-coupled devices are particularly suitable for quantum simulation since it is possible to map the hamiltonian of a system in the circuit as shown in [78,79,80,81]. Furthermore, modulations of the \(k_i\) and \(c_{ij}\) in various ways during the fabrication stage make these circuits particularly appropriate to implement Haar-random extracted matrix. For example, the random modulations of k(z) have been realized in square and linear lattices with the FLW by changing the writing speed of the waveguides [82]. However, this methodology can reproduce only a static circuit or, equivalently, a single random extracted unitary transformation. It is possible to introduce dynamical modulation of the circuit parameters and thus obtain a reconfigurable device able to realize several Haar-random matrices as reported recently in a 32-mode integrated device [87], making continuously-coupled device viable solutions for photonic sampling algorithms.
2.3.2 Other encodings
Quantum states encoded in other DOFs of single-photon states such as polarization, time and frequency bins, can be converted in the path-encoding to be processed by the interferometers described above. Notwithstanding, dedicated integrated toolboxes have been developed for polarization qubit, frequency and time bins qudits. They still present technological challenges for what concern re-programmability and universality. For example, an option for on-chip operations on the polarization is the use of the birefringence of the waveguides. Integrated waveplates and partially polarized beam-splitters have been realized in FLW silica waveguides [69, 70] which present near-circular profiles, while their realization is challenging in planar waveguides. Waveplates with arbitrary orientation of the optical axis are the result of a tilted focusing on the laser beam during the writing process [70]. Partially polarizing beamsplitters are directional couplers in which the interaction length is chosen to drive the two polarization components in different paths according to a given splitting ratio. In this way polarization qubits can be processed as shown in [69].
Quantum states encoded in a superposition of frequency bins can be generated in optical resonators. On-chip micro-ring resonators have been demonstrated to be effective for generating entangled and cluster states in such a DOF [24,25,26, 103, 114] that are feasible for measurement-based quantum computing schemes. On-chip generation and measurement of entangled states in the time-bin encoding has been recently demonstrated in SiN device [102].
Structured light DOFs which are employed in qudits encoding in the orbital and transverse momentum are still challenging to transmit and manipulate in waveguides. Besides some works on integrated optical vortex single-photon emitters [137] and on waveguides supporting angular momentum states of light [138], alternative technologies based on metasurfaces [139, 140] are promising solutions towards miniaturization of the optical elements that manipulate these DOFs.
2.4 Integrated single-photon detection
When aiming to the fully scalable approach of integrated photonics, some key ingredients must be taken into consideration. The first one is the reconfigurability of the system which allows for active routing of photons. The second one is the integration of single-photon sources and single-photon detectors (SPD) which turns out to be crucial to increase the overall performance by highly reducing losses at interconnections between fibres and the waveguides. Then, on-chip detector manufacturing is central for the development of quantum information protocols for increasing the compactness, reliability and stability of the devices. The scientific community has devoted many efforts at improving the number of detectors within the single device as well as the photon-number resolution (PNR) capability, jitter timing and many other parameters that play a crucial role in single-photon detection. The recent results in this field open the possibility to a new class of experiments and more innovative methods to interface and address in a monolithic photonic device many quantum information protocols. The integration of superconducting elements for single-photon detection is crucial for the entire development of complex and effective integrated devices. The principal types of single-photon detectors and the integration methods are discussed in the following paragraphs.
The different options for single-photon detectors range from avalanche photodiodes, superconducting nanowire single-photon detectors (SNSPDs) to transition edge sensors (TESs). From the first integration of SPD within chip devices performed in 2011 by Sprengers et al. [141], several works have been published demonstrating the efficient overcome of this major barrier in quantum technologies [142, 143]. The main challenge when building systems with multiple SNSPDs remains the residual fabrication defects at the nanoscale [144], a problem that increases even more when aiming to the insertion of the detector into the integrated devices. This problem can be solved by exploiting a micrometer-scale flip-chip process [145]. The integration of SPD technologies can be patterned on different materials ranging from GaAs [141], Si [142] to Si\(_{3}\)N\(_{4}\) [146]. The choice of the material will impact on the compactness, transmittivity and overall performance of the integrated device. It is well known that some quantum protocols require PNR detection [147,148,149]. Thus some efforts have been directed to the construction of this kind of detectors within chips. In particular, PNR TESs have been integrated on silica [150] and LN waveguides [151] demonstrating the capacity of resolving up to five photons while the maximum number of photons resolving was four in SNSPDs on GaAs [152]. The development of SNSPDs with pseudo PNR, is another potential solution to increase the capacity of detection relying on spatial multiplexing in arrays of superconducting nanowires [153]. PNR capabilities of a single SNSPD enabled by tapered transmission lines for measuring Hong-Ou-Mandel interference have been demonstrated in a recent article of 2020 [19], where the authors have demonstrated a PNR detector at telecommunication wavelengths based on a single superconducting nanowire with an integrated impedance-matching taper. The prototyping device was able to resolve up to four absorbed photons with 16 ps timing jitter and less than 2 Hz device dark count rate.
For the correct operation of SNSPDs and TESs a cryogenic temperature is required and thus represents an issue to overcome. Waveguide-coupled germanium-on-silicon avalanche photodiodes were already demonstrated with promising detection efficiencies at 1310 nm while operating at 80 K [16, 18]. TESs would also be able to provide the possibility for PNR, but they require to operate at low temperatures close to 100 mK range and show high dead times and low time resolution.
In general, to achieve GHz detection rates, it is required to reduce the reset time of the detectors to the sub-nanosecond range. Another potential solution consists on decreasing the length of the integrated device that would reduce the kinetic inductance and, consequently, the detection pulse decay time. On the other hand, shortening the length of the chips results in a smaller waveguide-detector interaction length which limits the on-chip detection. Thus a compromise between circuit size and detection efficiency must be taken into consideration. One of the best performances of on-chip detection was reported in 2018. A detection efficiency >90% with a timing jitter <20 ps and recovery times enabling count rates higher than 1 GHz. [17].
3 Applications
This section of the review is entirely dedicated to the adoption of integrated devices in quantum information protocols. We focus on experiments and methods which exploit fully integrated or hybrid bulk-integrated solutions. For other experiments in free space or bulk apparatuses we refer to other reviews in the field [1, 2].
3.1 Quantum communication and cryptography
In the last years, there has been an increasing interest for the development of more complex, stable and compact setups. This requirement promoted integrated photonics as one of the most promising approaches. Quantum physics has contributed to the development of fields ranging from quantum information processing to quantum communications. In particular, for quantum communications it is required to have at least two separated nodes, and a natural solution is found using single photons as information carriers [154]. Photon capabilities allow us to encode information in different degrees of freedom such as polarization, path, orbital angular momentum, frequency, etc. Another reason to exploit photons is due to the fact that they have very low interaction with the environment, in particular for free-space and fiber communications, thus preserving the encoded information.
Within this section, we will review some of the most recent progress of quantum communication and cryptography exploiting integrated photonics. Nowadays, open challenges include the connection between different interfaces such as chip with optical fibers, chip-to-chip, and certainly integrated optics with classical telecommunications. Other problems to solve when aiming to scalable communications with integrated photonics involve quantum memories and quantum repeaters [155, 156] with the aim of successfully developing quantum networks with complex structures [157]. The guiding principle is to go towards higher integration of electronics and photonics, leading to improvements in the clock rates, low cost and portability. Nowadays, it is common to rely on signal post-processing such as post-selection of probabilistic measurement outcomes, as well as quantum state analysis to overcome some limitations.
It is important to notice that integrated devices have already an impact on quantum communications offering advantages in terms of physical footprint, weight, energy consumption, compactness, stability, portability and manufacturability with respect to current state-of-the-art demonstrations in table-top experiments. In the past decade, a handful of research groups have performed interesting experiments proving the capabilities of integrated photonics in the communication field. One of the seminal papers involved the experimental implementation of quantum teleportation in a photonic chip [56]. It is well known that quantum teleportation is at the core of many applications such as quantum cryptography, quantum relays [158], quantum repeaters [155, 156] and linear optics quantum computing [159]. The authors exploited a reconfigurable photonic chip to perform the teleportation protocol with state encoding, entanglement preparation, Bell-state analysis and state tomography, all carried out on chip. Fourfold events of 5MHz at one output of the Bell-state measurement were registered and a fidelity of the initial state of \(89\% \pm 3 \%\) which is higher than the 2/3 value of the classical limit.
Currently, Quantum Key Distribution (QKD) is one of the most developed and fruitful fields of quantum information [160, 161]. The working principle permits the exchange of a private secret key between two trusted parties over an untrusted quantum channel, provided that the parties can access to 1) an authenticated classical channel and 2) true random number sources for the development of the algorithm. On-chip sources of random numbers have been already implemented [162,163,164,165]. This field has been recently extended to the cases for which quantum dots are exploited in the generation of photons thus improving the overall security [166, 167]. Very recently, some QKD experiments with integrated photonic components have been reported [168,169,170,171]. In particular, on-chip measurement-device-independent quantum key distribution has been demonstrated [170]. The authors experimentally proved that 1 kbps of secret key can be exchanged at 100 km, and predict positive key rates at more than 350 km. The system removes detector vulnerabilities, and represents a viable solution for near-term metropolitan quantum networks.
Another important step forward has been a protocol of chip-to-chip quantum teleportation [89]. In this experiment, the devices were able to produce, process, transmit and measure multiphoton multi-qubit states. The fidelity obtained in the mentioned work was almost \(90\%\) which is one of the highest obtained when exploiting integrated photonics. The results obtained up to now encourage the construction of worldwide communication exploiting hybrid technologies and thus several research groups are continuously contributing to this research topic.
3.2 Quantum computing schemes
The principal universal schemes of computation are the circuit model [21], the measurement-based quantum computing (MBQC) [172,173,174] and blind-quantum computing (BQC) [175]. The circuit model is the direct adaptation of the traditional set of gates in operations with qubits and qudits. The MBQC is a different formulation which requires the generation of a large entangled state with many qubits followed by single-qubit measurements. In the BQC paradigm a client delegates to a server the information processing without previous knowledge of the client’s state. Single-photon states are perfect information carriers since are quite free from decoherence and can be shared among users. However, the absence of interaction among photonic qubits puts important limitations in the realizations of such schemes of quantum computing. The first scheme to implement quantum computing via the circuit model in linear optics was formulated by Knill, Laflamme and Milbourn in [159] (KLM scheme). In this paradigm, the interaction necessary to implement two-qubit gates is introduced by the employment and measurement of ancillary photons. This means that the number of photons and of optical elements grows unfavorably with the number of qubits. The MBQC results to be a more convenient solution in photonic qubits. In this paradigm, the problem of the interaction is shifted to the generation stage of multi-partite entangled states. To this aim, a combination of entangled single-photon sources, time-multiplexing, and linear interferometer have been proposed [176,177,178]. Also, the BQC can find in principle convenient realization in photonic platforms since photons can be sent through fibers between clients and servers and then processed by a linear interferometer.
Quantum computing in integrated photonics. a Examples of on-chip realization of heralded quantum gates. On the left, a CNOT gate on two path encoded qubits in a SoS chip [43]. On the right, the most recent scheme of Refs. [13, 15] to implement controlled gates by exploiting the entanglement between photons generated by an array of integrated sources in Si waveguides. The operations and measurements on idlers photons (orange circles) control the gates on the two qubits encoded in the signal photons (green circles). b On chip generation of 4 qubits cluster states for MQBC reported in [179] and [93]. The quantum resource of MQBC is a complex and fully connected cluster entangled state in which each circle represents a qubit and the edges the entanglement correlations. c Scheme of BQC with integrated photonics. A proof-of-principle on-chip demonstration of a BQC variant has been recently reported [180]
Circuit model. The first attempts in the early integrated chips regarded single- and two-qubit gates on path [43] and polarization [69] encoded qubits (see also Fig. 4a). In particular, these two examples aimed at realize a probabilistic CNOT gate which represents together with the Hadamard gate the basic unit for universal computation. Another integrated device was designed to perform Shor factorization algorithm with two integrated CNOT [52]. The next generation of integrated devices showed the capability to encode different operations in the same device thanks to reconfigurability and to universal schemes for decomposing any transformation over the photons modes [11, 12, 101]. However, these instances are demonstrations of a single gate operations rather than the integration of a quantum processor. The latter would require many ancillary photons and cascaded gates such as the KLM scheme suggests. Examples of CNOT gates performed according to the KLM scheme are reported in Ref. [56] in UV-writing silica waveguides and in Ref. [11] in a SoS platform. The most recent proof-of-principle demonstrations of quantum algorithms in two-qubit and two-qudit processors in Si-photonics exploit a scheme which is halfway between KLM and MQBC. Quantum algorithms are performed by local operations and measurements on maximally entangled states. In this approach, arrays of integrated parametric sources are coherently excited to produce a state which is the superposition of the different ways to have a pair of signal-idler photons. One- and two-particle operations result in the signal photons detection conditioned by the measurement of the corresponding idler signals (see Fig. 4a). Two path-encoded processors, one with two qubits [13] and the other with two ququarts [15], have been developed according to this scheme in Si devices. Four FWM integrated sources are excited and the local operations are performed by tunable MZI on each qubit or ququart. These processors proved to perform with high fidelity and good success probability several gates and quantum algorithms. Furthermore, these chips are one of the most complex quantum integrated devices for what concerns the number of integrated optical elements and numbers of tunable MZI.
Measurement-based quantum computing (MQBC). A genuine MQBC requires the generation of large entangled states, such as GHZ, cluster or graph states. Nowadays, on-chip entanglement generation is a well-established and mature technology. One method is through the scheme reported in Fig. 4a in Si-chip. This approach allowed to generate two-qudit with \(d=16\) entangled states in path encoding [27] as well as cluster states [93]. Other examples of entanglement generation in time bin encoding are provided in [102, 181] and in frequency bins [24, 25]. The first example of on-chip MQBC operations was the work [179] in FLW waveguides. The authors generate a four qubit cluster states encoded in polarization and path of two photons. Two type of cluster states such as the linear chain and the four-vertex box were investigated (see Fig. 4b). Furthermore, a proof-of-principle Grover search algorithm was demonstrated. A further demonstration of MQBC is given by Refs. [25]. In this work cluster states were generated in frequency bins from an integrated micro-resonator. As most recent implementations of MQBC, we mention the fully on-chip generation and manipulation of cluster states in Si-photonic platforms. The key element is the engineering of array of identical integrated sources and their excitement. In Ref. [93] different graph cluster states geometry were demonstrated with such technology (Fig. 4b).
Blind quantum computing (BQC). The BQC scheme is based on the secured exchange of classical and quantum data between a client and a server. A crucial requirement of this scheme is that the server processes the information for the client, i.e. perform a function f(x), where x are the client’s quantum or/and classical data, without previous knowledge of x. Some technological challenges of the scheme regard the need for quantum memories or quantum repeaters to store and exchange quantum states. Integrated photonic platforms can be employed for example to prepare photonic qubits by clients and to process them in the server station. However, besides the first proof-of-principle implementation of BQC in a bulk optics apparatus [182], no demonstrations of such a scheme in fully integrated devices have been reported. A variant of BQC which relaxes some hypotheses of the original proposal such as the universality [183], has been demonstrated in FLW four-mode chip [180]. The authors proved the effectiveness of homomorphic encryption to perform delegated computational tasks in the spirit of BQC.
3.3 Quantum simulation
Quantum simulations aims at solving problems related to a physical system in a quantum processor. In other words, a quantum simulator maps a given system in a controlled quantum platform which can be programmed. A possible way to perform quantum simulation with photons is through quantum walks, a paradigm which allows to encode hamiltonians in the information processing [184]. Another approach is via quantum algorithms for phase estimation and variational eigensolvers [21]. These algorithms are tailored for the calculation of the ground state energy of molecules or chemical substances. Recently, photonic platforms which exploit squeezed light sources have demonstrated potentiality for molecular vibronic spectra simulations [185, 186] as well as for solving graph-theory problems [187,188,189]. The last emerging branch regards machine learning and quantum machine learning [190]. In the following, we review these principal quantum simulation approaches in integrated photonics.
Quantum walks. Quantum walks are important paradigms for quantum simulation with photons. They are the adaptation of random walks on lattices in a quantum framework, i.e the walker lives in a Hilbert space. The evolution of such a walker can be performed in two different fashions, via discrete-time quantum walks, where the evolution takes place in discrete steps, and via continuous-time quantum walks, in which the evolution is described by a Hamiltonian. The discrete-time version is realized in integrated chips by muli-port interferometers. Quantum transport phenomena such as single- and two-particles Anderson localization and entanglement growth in a spin chain have been simulated in polarization insensitive FLW devices [67, 68]. Fermionic and bosonic statistics effect in two-particle interference have been observed with the same fabrication technology [66, 67]. Quantum transport properties such as diffusion and ballistic diffusion have been simulated recently also in Si-device [191]. Dynamics and energy transport in 4 atoms molecule have been simulated in a 5-mode SoS device [192]. The laser writing methods are feasible also to realize continuous-time quantum walk. The engineering of the couplings among waveguides written in one- and two-dimensional optical lattices allow to map different Hamiltonian in the device. Continuously coupled circuits have been employed to observe bosonic statics [78, 81] and the effect on Fano resonance [193]. Furthermore, the previously cited phenomena of quantum transport like localization, diffusion, and ballistic spreading have been simulated also in these architectures [79, 80, 194].
Simulation via quantum algorithms. Quantum algorithms such as phase estimation have been exploited to determine the energy levels of atoms and molecular systems. The idea of phase estimation is to individuate with high precision the values of the complex phase \(e^{i\phi }\) by mean of an oracle U such that \(U |\psi \rangle =e^{i\phi }|\psi \rangle \) where \(|\psi \rangle \) is the qubit register of the quantum processor [21]. A quantum simulator based on this algorithm maps the hamiltonian and the corresponding evolution U of the system in a way that \(\phi \) will be the energy estimation. This quantum algorithm has been demonstrated in Si-based device in Refs. [92] with a circuit scheme equivalent to the one showed in Fig. 4a. More precisely, this work combines a phase estimation with a variational eigensolver. In this second method the qubit register \(|\psi \rangle \) is initialized according to some initial ansatz on the ground state of the system. The state preparation is iteratively optimized to reach the minimum of the energy estimation. This algorithm is generally assisted by a classical optimization routine to change on-line the circuit setting in the preparation stage. The first demonstration was performed in 2014 in SoS chip [54].
Quantum simulators with squeezed light. Recently, many studies on photon counting experiments performed on squeezed single-photon states in multi-port optical networks have been carried out [185, 189]. One result regards the possibility to retrieve from the photon counting samples molecular vibronic spectra. This was proved theoretically [185, 186] and recently demonstrated in a SiN chip with 4 integrated squeezed light sources and 8 ports [14]. On the same device, other properties of squeezed light have been investigated. Graph adjacency matrices can be encoded in the circuit. This allows to solve some graph problems such as dense-subgraph estimation [188], graph-isomorphism and similarity [189].
Learning algorithms. Another emerging branch in quantum computing is quantum machine learning. This field aims at looking for advantages in computation from interfacing quantum processors with classical machine learning methods and from a direct translation of learning algorithms in the quantum framework. Hybrid and fully quantum learning algorithms can provide new solutions for quantum simulations as such as traditional machine learning did in many scientific fields. In Ref. [91] Hamiltonian learning by a quantum photonic Si-chip has been performed. In this work, the hamiltonians of molecules are individuated from a combination of a bayesian learning method and information processing by the quantum photonic chip. For what concerns fully quantum learning methods, we have examples of quantum reinforcement learning in a Si-chip [195] and the realization of quantum memristors in a FLW chip for neuromorphic computing [196]
3.4 Integrated circuits for photonic sampling devices
Among the different fields of applications, integrated circuits have been employed as one of the main ingredients for quantum devices dedicated to solve specifically tailored sampling problems. This class is composed by those tasks whose aim is to obtain a finite sample from a given distribution. The interest relies in that some of these problems cannot be solved efficiently with a classical approach, while they can be solved with quantum hardware. Building a quantum device capable of solving a sufficiently large instance of one of these problems would provide an unambiguous demonstration of the quantum advantage regime [20], namely those scenarios where a quantum approach outperforms any classical system. In this context, photonic integrated circuits have been employed to tackle sampling problems based on the evolution of photon input states in linear networks [197].
The original formulation of the Boson Sampling is due to S. Aaronson and A. Arkhipov [37]. More specifically, the related task requires to draw a finite sample distributed according to the output obtained from the propagation of a set of n non-interacting bosons injected in different input ports of an \(m \times m\) linear transformation. In this seminal paper, it was demonstrated that such a sampling task belongs to the \(\#\)-P complexity class, and is exponentially hard (in the number of photons n) to tackle with a classical approach. This is due to the connection between the transition amplitudes between input and output configurations and a matrix function known as permanent, which cannot be efficiently calculated or approximated classically for complex and sufficiently random entries. Conversely, a quantum device composed of single-photon sources, linear optical interferometers and single-photon detectors can be in principle employed to perform such a task in a shorter time than any classical approach, if the number of photons n is sufficiently large.
Given these requirements for the quantum implementation, photon circuits have represented the most employed approach to implement the constituting quantum hardware components since the very early implementations [55, 71, 72, 198]. In particular, the formal recipe for Boson Sampling requires interferometers with a number of modes scaling at least as \(m \sim n^2\), being n the number of photons, with a universal layout so as to implement arbitrary unitary transformations to avoid symmetric structures affecting the complexity of the calculation. To this end, given their inherent stability and their compact structure, integrated interferometers have been employed to perform different Boson Sampling implementations [199,200,201,202] using layouts corresponding or inspired by universal schemes [134, 135], or circuits with the fast architecture to test validation protocols [76, 77]. Recent implementations with integrated photonic circuits have also employed reconfigurable interferometers with universal layouts [11] as well as tested novel geometries for a more compact and low-loss implementation of arbitrary unitary transformations [87]. Furthermore, experiments with quantum dot sources have been recently reported [133, 203,204,205]
Photonic sampling machines. a Boson Sampling (BS) and the variants b Scattershot Boson Sampling (SBS) and c Gaussian Boson Sampling GBS). These non-universal machines solve the problem of sampling from the photon counting distribution of the quantum states of light reported in the figure for each case after the evolution in a random interferometer. These variants have been introduced to increase the samples generation rates and for looking at further applications beyond the original sampling task
Starting from the original proposal of Ref. [37], different variants of Boson Sampling have been proposed and tested experimentally (see Fig. 5). The aim of the variants was mainly due to obtain the formal of equivalent sampling tasks in terms of classical complexity while exploiting more efficiently the available hardware for quantum photon implementations. The first proposed variant, called Scattershot Boson Sampling [38], was defined in this exact spirit to fully exploit the potential of probabilistic spontaneous down-conversion sources. The first experimental implementations relied on integrated components for the linear optical evolution [73], and subsequently encompassed integration of both sources and evolution in the same device [90]. For a detailed review of all Boson Sampling implementations, including those not relying on integrated circuits, we refer to [197].
A second and relevant variant is found in the Gaussian Boson Sampling problem [40], which replaces single-photon sources with single-mode squeezing sources. This task shares the same complexity class of the original Boson Sampling formulation, albeit the available photonic technology enabled recent implementations of large-scale experiments with bulk optics [3, 4] or fiber components [5]. Furthermore, the interest in this variant is also found in the connection with graph theory [187,188,189] and quantum simulation of certain molecular systems [185, 186], thus opening first perspectives of application of photonic sampling problems beyond the quest for quantum advantage. Integrated circuits have been employed for different Gaussian Boson Sampling instances [14, 90], with systems encompassing both sources and photon evolution on the same chip. Implementations based on integrated technology are characterized by the large degree of reconfigurability of the platform and the universality of the layout. These ingredients are both relevant to fully satisfy the hypothesis behind the Gaussian Boson Sampling problem, as well as for the potential adoption of the quantum hardware towards the aforementioned applications. Future challenges to scale up these systems to a larger scale involve the integration of all components (sources, evolution, and detectors) on the same low-loss platform.
4 Conclusions and outlook
In this work, we have overviewed the different technologies to realize integrated circuits, and the level of miniaturization reached by the various components which also involves photon sources and detectors. These devices have proved to be viable solutions to realize nano-processors for qubits [13], qudits [15] and sampling machines for quantum advantage demonstrations [12, 14, 87, 90]. Significant results have been reported even in the field of communications, cryptography and quantum random number generation [89]. One of the most mature manufacturing technology is silicon photonics, which provides a feasible solution for large-scale instances of programmable photonic quantum processors. Notwithstanding, Si-photonics present some issues that need to be addressed towards further developments of progressively larger photonic chips. One of the main limitations regards the two-photon absorption that can be mitigated in SiN waveguides. The latter are nowadays alternative and important candidates for future quantum integrated photonic technologies. Finally, other technologies present their own advantages, such as for instance femtosecond laser-writing circuits having unique properties in terms of three-dimensional capabilities and supporting polarization encoding.
The next challenges of integrated photonics regard scalable implementations of computing and entanglement generation schemes, possibly avoiding the need of ancillary photons and post-selection. On-chip demonstrations of the MQBC paradigm, which could circumvent such resource overhead in photonic platforms, still require post-selection methods for the generation of cluster states. A fundamental technological step towards scalable computing schemes is the integration of feed-forward systems. This seems to be the next challenge of integrated photonics for the implementation of universal quantum computing. Possible solutions can be found in the fabrication of heterogeneous circuits with passive and active waveguides such as LN which allow for fast modulation of the optical operations [9, 10]. Furthermore, the interface between deterministic sources and fast on chip-manipulation of time and spatial degrees of freedom represents a promising route to employ such a high-efficiency approach for photon generation, as recently shown by bulk experiment with dot sources [206].
Data availability statement
There are no data associated with the paper.
References
F. Flamini, N. Spagnolo, F. Sciarrino, Photonic quantum information processing: a review. Rep. Prog. Phys. 82, 016001 (2018). https://doi.org/10.1088/1361-6633/aad5b2
S. Slussarenko, G.J. Pryde, Photonic quantum information processing: A concise review. Appl. Phys. Rev. 6(4), 041303 (2019). https://doi.org/10.1063/1.5115814
H.-S. Zhong, H. Wang, Y.-H. Deng, M.-C. Chen, L.-C. Peng, Y.-H. Luo, J. Qin, D. Wu, X. Ding, Y. Hu, P. Hu, X.-Y. Yang, W.-J. Zhang, H. Li, Y. Li, X. Jiang, L. Gan, G. Yang, L. You, Z. Wang, L. Li, N.-L. Liu, C.-Y. Lu, J.-W. Pan, Quantum computational advantage using photons. Science 370(6523), 1460–1463 (2020). https://doi.org/10.1126/science.abe8770
H.-S. Zhong, Y.-H. Deng, J. Qin, H. Wang, M.-C. Chen, L.-C. Peng, Y.-H. Luo, D. Wu, S.-Q. Gong, H. Su, Y. Hu, P. Hu, X.-Y. Yang, W.-J. Zhang, H. Li, Y. Li, X. Jiang, L. Gan, G. Yang, L. You, Z. Wang, L. Li, N.-L. Liu, J.J. Renema, C.-Y. Lu, J.-W. Pan, Phase-programmable gaussian boson sampling using stimulated squeezed light. Phys. Rev. Lett. 127, 180502 (2021). https://doi.org/10.1103/PhysRevLett.127.180502
L.S. Madsen, F. Laudenbach, M.F. Askarani, F. Rortais, T. Vincent, J.F.F. Bulmer, F.M. Miatto, L. Neuhaus, L.G. Helt, M.J. Collins, A.E. Lita, T. Gerrits, S.W. Nam, V.D. Vaidya, M. Menotti, I. Dhand, Z. Vernon, N. Quesada, J. Lavoie, Quantum computational advantage with a programmable photonic processor. Nature 606(7912), 75–81 (2022). https://doi.org/10.1038/s41586-022-04725-x
S.-K. Liao, W.-Q. Cai, W.-Y. Liu, L. Zhang, Y. Li, J.-G. Ren, J. Yin, Q. Shen, Y. Cao, Z.-P. Li, F.-Z. Li, X.-W. Chen, L.-H. Sun, J.-J. Jia, J.-C. Wu, X.-J. Jiang, J.-F. Wang, Y.-M. Huang, Q. Wang, Y.-L. Zhou, L. Deng, T. Xi, L. Ma, T. Hu, Q. Zhang, Y.-A. Chen, N.-L. Liu, X.-B. Wang, Z.-C. Zhu, C.-Y. Lu, R. Shu, C.-Z. Peng, J.-Y. Wang, J.-W. Pan, Satellite-to-ground quantum key distribution. Nature 549(7670), 43–47 (2017). https://doi.org/10.1038/nature23655
J.-G. Ren, P. Xu, H.-L. Yong, L. Zhang, S.-K. Liao, J. Yin, W.-Y. Liu, W.-Q. Cai, M. Yang, L. Li, K.-X. Yang, X. Han, Y.-Q. Yao, J. Li, H.-Y. Wu, S. Wan, L. Liu, D.-Q. Liu, Y.-W. Kuang, Z.-P. He, P. Shang, C. Guo, R.-H. Zheng, K. Tian, Z.-C. Zhu, N.-L. Liu, C.-Y. Lu, R. Shu, Y.-A. Chen, C.-Z. Peng, J.-Y. Wang, J.-W. Pan, Ground-to-satellite quantum teleportation. Nature 549(7670), 70–73 (2017). https://doi.org/10.1038/nature23675
J. Wang, F. Sciarrino, A. Laing, M.G. Thompson, Integrated photonic quantum technologies. Nat. Photonics 14(5), 273–284 (2020). https://doi.org/10.1038/s41566-019-0532-1
E. Pelucchi, G. Fagas, I. Aharonovich, D. Englund, E. Figueroa, Q. Gong, H. Hannes, J. Liu, C.-Y. Lu, N. Matsuda, J.-W. Pan, F. Schreck, F. Sciarrino, C. Silberhorn, J. Wang, K.D. Jöns, The potential and global outlook of integrated photonics for quantum technologies. Nature Reviews Physics 4(3), 194–208 (2022). https://doi.org/10.1038/s42254-021-00398-z
G. Moody, V.J. Sorger, D.J. Blumenthal, P.W. Juodawlkis, W. Loh, C. Sorace-Agaskar, A.E. Jones, K.C. Balram, J.C.F. Matthews, A. Laing, M. Davanco, L. Chang, J.E. Bowers, N. Quack, C. Galland, I. Aharonovich, M.A. Wolff, C. Schuck, N. Sinclair, M. Lončar, T. Komljenovic, D. Weld, S. Mookherjea, S. Buckley, M. Radulaski, S. Reitzenstein, B. Pingault, B. Machielse, D. Mukhopadhyay, A. Akimov, A. Zheltikov, G.S. Agarwal, K. Srinivasan, J. Lu, H.X. Tang, W. Jiang, T.P. McKenna, A.H. Safavi-Naeini, S. Steinhauer, A.W. Elshaari, V. Zwiller, P.S. Davids, N. Martinez, M. Gehl, J. Chiaverini, K.K. Mehta, J. Romero, N.B. Lingaraju, A.M. Weiner, D. Peace, R. Cernansky, M. Lobino, E. Diamanti, L.T. Vidarte, R.M. Camacho, 2022 roadmap on integrated quantum photonics. Journal of Physics: Photonics 4(1), 012501 (2022). https://doi.org/10.1088/2515-7647/ac1ef4
J. Carolan, C. Harrold, C. Sparrow, E. Martín-López, N.J. Russell, J.W. Silverstone, P.J. Shadbolt, N. Matsuda, M. Oguma, M. Itoh, G.D. Marshall, M.G. Thompson, J.C.F. Matthews, T. Hashimoto, J.L. O’Brien, A. Laing, Universal linear optics. Science 349(6249), 711–716 (2015). https://doi.org/10.1126/science.aab3642
C. Taballione, M.C. Anguita, M. de Goede, P. Venderbosch, B. Kassenberg, H. Snijders, N. Kannan, D. Smith, J.P. Epping, R. van der Meer, P.W.H. Pinkse, H.v.d. Vlekkert, J.J. Renema, 20-Mode Universal Quantum Photonic Processor (2022). arXiv:abs/2203.01801
X. Qiang, X. Zhou, J. Wang, C.M. Wilkes, T. Loke, S. O’Gara, L. Kling, G.D. Marshall, R. Santagati, T.C. Ralph, J.B. Wang, J.L. O’Brien, M.G. Thompson, J.C.F. Matthews, Large-scale silicon quantum photonics implementing arbitrary two-qubit processing. Nat. Photonics 12(9), 534–539 (2018). https://doi.org/10.1038/s41566-018-0236-y
J.M. Arrazola, V. Bergholm, K. Brádler, T.R. Bromley, M.J. Collins, I. Dhand, A. Fumagalli, T. Gerrits, A. Goussev, L.G. Helt, J. Hundal, T. Isacsson, R.B. Israel, J. Izaac, S. Jahangiri, R. Janik, N. Killoran, S.P. Kumar, J. Lavoie, A.E. Lita, D.H. Mahler, M. Menotti, B. Morrison, S.W. Nam, L. Neuhaus, H.Y. Qi, N. Quesada, A. Repingon, K.K. Sabapathy, M. Schuld, D. Su, J. Swinarton, A. Száva, K. Tan, P. Tan, V.D. Vaidya, Z. Vernon, Z. Zabaneh, Y. Zhang, Quantum circuits with many photons on a programmable nanophotonic chip. Nature 591(7848), 54–60 (2021). https://doi.org/10.1038/s41586-021-03202-1
Y. Chi, J. Huang, Z. Zhang, J. Mao, Z. Zhou, X. Chen, C. Zhai, J. Bao, T. Dai, H. Yuan, M. Zhang, D. Dai, B. Tang, Y. Yang, Z. Li, Y. Ding, L.K. Oxenløwe, M.G. Thompson, J.L. O’Brien, Y. Li, Q. Gong, J. Wang, A programmable qudit-based quantum processor. Nat. Commun. 13(1), 1166 (2022). https://doi.org/10.1038/s41467-022-28767-x
N.J.D. Martinez, M. Gehl, C.T. Derose, A.L. Starbuck, A.T. Pomerene, A.L. Lentine, D.C. Trotter, P.S. Davids, Single photon detection in a waveguide-coupled ge-on-si lateral avalanche photodiode. Opt. Express 25(14), 16130–16139 (2017). https://doi.org/10.1364/OE.25.016130
S. Ferrari, C. Schuck, W. Pernice, Waveguide-integrated superconducting nanowire single-photon detectors. Nanophotonics 7(11), 1725–1758 (2018). https://doi.org/10.1515/nanoph-2018-0059
P. Vines, K. Kuzmenko, J. Kirdoda, D.C.S. Dumas, M.M. Mirza, R.W. Millar, D.J. Paul, G.S. Buller, High performance planar germanium-on-silicon single-photon avalanche diode detectors. Nat. Commun. 10(1), 1086 (2019). https://doi.org/10.1038/s41467-019-08830-w
D. Zhu, M. Colangelo, C. Chen, B.A. Korzh, F.N.C. Wong, M.D. Shaw, K.K. Berggren, Resolving photon numbers using a superconducting nanowire with impedance-matching taper. Nano Lett. 20(5), 3858–3863 (2020). https://doi.org/10.1021/acs.nanolett.0c00985
A.W. Harrow, A. Montanaro, Quantum computational supremacy. Nature 549, 203 (2017). https://doi.org/10.1038/nature23458
M.A. Nielsen, I.L. Chuang, Quantum Computation and Quantum Information: 10th, Anniversary. (Cambridge University Press, Cambridge, 2010). https://doi.org/10.1017/CBO9780511976667
M. Erhard, M. Krenn, A. Zeilinger, Advances in high-dimensional quantum entanglement. Nature Reviews Physics 2(7), 365–381 (2020). https://doi.org/10.1038/s42254-020-0193-5
D. Cozzolino, B. Da Lio, D. Bacco, L.K. Oxenløwe, High-dimensional quantum communication: Benefits, progress, and future challenges. Advanced Quantum Technologies 2(12), 1900038 (2019). https://doi.org/10.1002/qute.201900038
C. Reimer, M. Kues, P. Roztocki, B. Wetzel, F. Grazioso, B.E. Little, S.T. Chu, T. Johnston, Y. Bromberg, L. Caspani, D.J. Moss, R. Morandotti, Generation of multiphoton entangled quantum states by means of integrated frequency combs. Science 351(6278), 1176–1180 (2016). https://doi.org/10.1126/science.aad8532
C. Reimer, S. Sciara, P. Roztocki, M. Islam, L. Romero Cortés, Y. Zhang, B. Fischer, S. Loranger, R. Kashyap, A. Cino, S.T. Chu, B.E. Little, D.J. Moss, L. Caspani, W.J. Munro, J. Azaña, M. Kues, R. Morandotti, High-dimensional one-way quantum processing implemented on d-level cluster states. Nat. Phys. 15(2), 148–153 (2019). https://doi.org/10.1038/s41567-018-0347-x
P. Imany, J.A. Jaramillo-Villegas, M.S. Alshaykh, J.M. Lukens, O.D. Odele, A.J. Moore, D.E. Leaird, M. Qi, A.M. Weiner, High-dimensional optical quantum logic in large operational spaces. npj Quantum Information 5(1), 59 (2019). https://doi.org/10.1038/s41534-019-0173-8
J. Wang, S. Paesani, Y. Ding, R. Santagati, P. Skrzypczyk, A. Salavrakos, J. Tura, R. Augusiak, L. Mančinska, D. Bacco, D. Bonneau, J.W. Silverstone, Q. Gong, A. Acín, K. Rottwitt, L.K. Oxenløwe, J.L. O’Brien1, A. Laing, M.G. Thompson, Multidimensional quantum entanglement with large-scale integrated optics. Science (2018). https://doi.org/0.1126/science.aar7053
G.B. Xavier, G. Lima, Quantum information processing with space-division multiplexing optical fibres. Communications Physics 3(1), 9 (2020). https://doi.org/10.1038/s42005-019-0269-7
S. Leedumrongwatthanakun, L. Innocenti, H. Defienne, T. Juffmann, A. Ferraro, M. Paternostro, S. Gigan, Programmable linear quantum networks with a multimode fibre. Nat. Photonics 14(3), 139–142 (2020). https://doi.org/10.1038/s41566-019-0553-9
M. Erhard, R. Fickler, M. Krenn, A. Zeilinger, Twisted photons: new quantum perspectives in high dimensions. Light: Science & Applications 7(3), 17146 (2018). https://doi.org/10.1038/lsa.2017.146
L. Marrucci, E. Karimi, S. Slussarenko, B. Piccirillo, E. Santamato, E. Nagali, F. Sciarrino, Spin-to-orbital conversion of the angular momentum of light and its classical and quantum applications. J. Opt. 13, 064001 (2011). https://doi.org/10.1088/2040-8978/13/6/064001
S.L. Braunstein, P. van Loock, Quantum information with continuous variables. Rev. Mod. Phys. 77, 513–577 (2005). https://doi.org/10.1103/RevModPhys.77.513
R. Loudon, The Quantum Theory of Light (Oxford science publications. Clarendon Press, Oxford, 1983)
C. Weedbrook, S. Pirandola, R. García-Patrón, N.J. Cerf, T.C. Ralph, J.H. Shapiro, S. Lloyd, Gaussian quantum information. Rev. Mod. Phys. 84, 621–669 (2012). https://doi.org/10.1103/RevModPhys.84.621
D. Gottesman, A. Kitaev, J. Preskill, Encoding a qubit in an oscillator. Phys. Rev. A 64, 012310 (2001). https://doi.org/10.1103/PhysRevA.64.012310
E. Diamanti, A. Leverrier, Distributing secret keys with quantum continuous variables: Principle, security and implementations. Entropy 17(9), 6072–6092 (2015). https://doi.org/10.3390/e17096072
S. Aaronson, A. Arkhipov, The Computational Complexity of Linear Optics. In: Press, A. (ed.) Proceedings of the 43rd Annual ACM Symposium on Theory of Computing, pp. 333–342 (2011). https://doi.org/10.1145/1993636.1993682
A.P. Lund, A. Laing, S. Rahimi-Keshari, T. Rudolph, J.L. O’Brien, T.C. Ralph, Boson sampling from a gaussian state. Phys. Rev. Lett. 113, 100502 (2014). https://doi.org/10.1103/PhysRevLett.113.100502
S. Rahimi-Keshari, A.P. Lund, T.C. Ralph, What can quantum optics say about computational complexity theory? Phys. Rev. Lett. 114, 060501 (2015). https://doi.org/10.1103/PhysRevLett.114.060501
C.S. Hamilton, R. Kruse, L. Sansoni, S. Barkhofen, C. Silberhorn, I. Jex, Gaussian boson sampling. Phys. Rev. Lett. 119, 170501 (2017). https://doi.org/10.1103/PhysRevLett.119.170501
G. Adesso, S. Ragy, A.R. Lee, Continuous variable quantum information: Gaussian states and beyond. Open Systems & Information Dynamics 21(01n02), 1440001 (2014). https://doi.org/10.1142/S1230161214400010
U.L. Andersen, G. Leuchs, C. Silberhorn, Continuous-variable quantum information processing. Laser & Photonics Reviews 4(3), 337–354 (2010). https://doi.org/10.1002/lpor.200910010
A. Politi, M.J. Cryan, J.G. Rarity, S. Yu, J.L. O’Brien, Silica-on-silicon waveguide quantum circuits. Science 320(5876), 646–649 (2008). https://doi.org/10.1126/science.1155441
M. Svalgaard, C. Poulsen, A. Bjarklev, O. Poulsen, Direct uv writing of buried singlemode channel waveguides in Ge-doped silica films. Electron. Lett. 30(17), 1401–1403 (1994). https://doi.org/10.1049/el:19940935
R.R. Gattass, E. Mazur, Femtosecond laser micromachining in transparent materials. Nat. Photonics 2(4), 219–225 (2008). https://doi.org/10.1038/nphoton.2008.47
L. Vivien, L. Pavesi, Handbook of Silicon Photonics (CRC press, Boca Raton, Florida, 2013). https://doi.org/10.1201/b14668
D.J. Moss, R. Morandotti, A.L. Gaeta, M. Lipson, New cmos-compatible platforms based on silicon nitride and hydex for nonlinear optics. Nat. Photonics 7(8), 597–607 (2013). https://doi.org/10.1038/nphoton.2013.183
A. Boes, B. Corcoran, L. Chang, J. Bowers, A. Mitchell, Status and Potential of Lithium Niobate on Insulator (LNOI) for Photonic Integrated Circuits. Laser & Photonics Reviews 12(4), 1700256 (2018). https://doi.org/10.1002/lpor.201700256
Y. Jia, L. Wang, F. Chen, Ion-cut lithium niobate on insulator technology: Recent advances and perspectives. Appl. Phys. Rev. 8(1), 011307 (2021). https://doi.org/10.1063/5.0037771
C.P. Dietrich, A. Fiore, M.G. Thompson, M. Kamp, S. Höfling, GaAs integrated quantum photonics: Towards compact and multi-functional quantum photonic integrated circuits. Laser & Photonics Reviews 10(6), 870–894 (2016). https://doi.org/10.1002/lpor.201500321
M. Smit, K. Williams, J. van der Tol, Past, present, and future of inp-based photonic integration. APL Photonics 4(5), 050901 (2019). https://doi.org/10.1063/1.5087862
A. Politi, J.C.F. Matthews, J.L. O’Brien, Shor’s quantum factoring algorithm on a photonic chip. Science 325(5945), 1221 (2009). https://doi.org/10.1126/science.1173731
P.J. Shadbolt, M.R. Verde, A. Peruzzo, A. Politi, A. Laing, M. Lobino, J.C.F. Matthews, M.G. Thompson, J.L. O’Brien, Generating, manipulating and measuring entanglement and mixture with a reconfigurable photonic circuit. Nat. Photonics 6(1), 45–49 (2012). https://doi.org/10.1038/nphoton.2011.283
A. Peruzzo, J. McClean, P. Shadbolt, M.-H. Yung, X.-Q. Zhou, P.J. Love, A. Aspuru-Guzik, J.L. O’Brien, A variational eigenvalue solver on a photonic quantum processor. Nat. Commun. 5(1), 4213 (2014). https://doi.org/10.1038/ncomms5213
J.B. Spring, B.J. Metcalf, P.C. Humphreys, W.S. Kolthammer, X.-M. Jin, M. Barbieri, A. Datta, N. Thomas-Peter, N.K. Langford, D. Kundys, J.C. Gates, B.J. Smith, P.G.R. Smith, I.A. Walmsley, Boson sampling on a photonic chip. Science 339(6121), 798–801 (2013). https://doi.org/10.1126/science.1231692
B.J. Metcalf, J.B. Spring, P.C. Humphreys, N. Thomas-Peter, M. Barbieri, W.S. Kolthammer, X.-M. Jin, N.K. Langford, D. Kundys, J.C. Gates, B.J. Smith, P.G.R. Smith, I.A. Walmsley, Quantum teleportation on a photonic chip. Nat. Photonics 8(10), 770–774 (2014). https://doi.org/10.1038/nphoton.2014.217
P.L. Mennea, W.R. Clements, D.H. Smith, J.C. Gates, B.J. Metcalf, R.H.S. Bannerman, R. Burgwal, J.J. Renema, W.S. Kolthammer, I.A. Walmsley, P.G.R. Smith, Modular linear optical circuits. Optica 5(9), 1087–1090 (2018). https://doi.org/10.1364/OPTICA.5.001087
J.B. Spring, P.L. Mennea, B.J. Metcalf, P.C. Humphreys, J.C. Gates, H.L. Rogers, C. Söller, B.J. Smith, W.S. Kolthammer, P.G.R. Smith, I.A. Walmsley, Chip-based array of near-identical, pure, heralded single-photon sources. Optica 4(1), 90–96 (2017). https://doi.org/10.1364/OPTICA.4.000090
M.T. Posner, T. Hiemstra, P.L. Mennea, R.H.S. Bannerman, U.B. Hoff, A. Eckstein, W.S. Kolthammer, I.A. Walmsley, D.H. Smith, J.C. Gates, P.G.R. Smith, High-birefringence direct uv-written waveguides for use as heralded single-photon sources at telecommunication wavelengths. Opt. Express 26(19), 24678–24686 (2018). https://doi.org/10.1364/OE.26.024678
C. Sima, J.C. Gates, H.L. Rogers, P.L. Mennea, C. Holmes, M.N. Zervas, P.G.R. Smith, Ultra-wide detuning planar bragg grating fabrication technique based on direct uv grating writing with electro-optic phase modulation. Opt. Express 21(13), 15747–15754 (2013). https://doi.org/10.1364/OE.21.015747
C. Holmes, J.C. Gates, L.G. Carpenter, H.L. Rogers, R.M. Parker, P.A. Cooper, S. Chaotan, F.R.M. Adikan, C.B.E. Gawith, P.G.R. Smith, Direct uv-written planar bragg grating sensors. Meas. Sci. Technol. 26(11), 112001 (2015). https://doi.org/10.1088/0957-0233/26/11/112001
Q.S. Ahmed, P.C. Gow, C. Holmes, P.L. Mennea, J.W. Field, R.H.S. Bannerman, D.H. Smith, C.B.E. Gawith, P.G.R. Smith, J.C. Gates, Direct uv written waveguides and bragg gratings in doped planar silica using a 213 nm laser. Electron. Lett. 57(8), 331–333 (2021). https://doi.org/10.1049/ell2.12126
M.T. Posner, N. Podoliak, D.H. Smith, P.L. Mennea, P. Horak, C.B.E. Gawith, P.G.R. Smith, J.C. Gates, Integrated polarizer based on 45\(^\circ \) tilted gratings. Opt. Express 27(8), 11174–11181 (2019). https://doi.org/10.1364/OE.27.011174
B. Calkins, P.L. Mennea, A.E. Lita, B.J. Metcalf, W.S. Kolthammer, A. Lamas-Linares, J.B. Spring, P.C. Humphreys, R.P. Mirin, J.C. Gates, P.G.R. Smith, I.A. Walmsley, T. Gerrits, S.W. Nam, High quantum-efficiency photon-number-resolving detector for photonic on-chip information processing. Opt. Express 21(19), 22657–22670 (2013). https://doi.org/10.1364/OE.21.022657
T. Meany, M. Gräfe, R. Heilmann, A. Perez-Leija, S. Gross, M.J. Steel, M.J. Withford, A. Szameit, Laser written circuits for quantum photonics. Laser & Photonics Reviews 9(4), 363–384 (2015). https://doi.org/10.1002/lpor.201500061
L. Sansoni, F. Sciarrino, G. Vallone, P. Mataloni, A. Crespi, R. Ramponi, R. Osellame, Two-particle bosonic-fermionic quantum walk via integrated photonics. Phys. Rev. Lett. 108(1), 010502 (2012). https://doi.org/10.1103/physrevlett.108.010502
A. Crespi, R. Osellame, R. Ramponi, V. Giovannetti, R. Fazio, L. Sansoni, F.D. Nicola, F. Sciarrino, P. Mataloni, Anderson localization of entangled photons in an integrated quantum walk. Nature Photonics 7, 322–328 (2013). https://doi.org/0.1038/nphoton.2013.26
I. Pitsios, L. Banchi, A.S. Rab, M. Bentivegna, D. Caprara, A. Crespi, N. Spagnolo, S. Bose, P. Mataloni, R. Osellame, F. Sciarrino, Photonic simulation of entanglement growth and engineering after a spin chain quench. Nat. Commun. 8(1), 1569 (2017). https://doi.org/10.1038/s41467-017-01589-y
A. Crespi, R. Ramponi, R. Osellame, L. Sansoni, I. Bongioanni, F. Sciarrino, G. Vallone, P. Mataloni, Integrated photonic quantum gates for polarization qubits. Nat. Commun. 2(1), 566 (2011). https://doi.org/10.1038/ncomms1570
G. Corrielli, A. Crespi, R. Geremia, R. Ramponi, L. Sansoni, A. Santinelli, P. Mataloni, F. Sciarrino, R. Osellame, Rotated waveplates in integrated waveguide optics. Nat. Commun. 5(1), 4249 (2014). https://doi.org/10.1038/ncomms5249
M. Tillmann, B. Dakić, R. Heilmann, S. Nolte, A. Szameit, P. Walther, Experimental boson sampling. Nature Photon. 7(7), 540–544 (2013). https://doi.org/10.1038/nphoton.2013.102
A. Crespi, R. Osellame, R. Ramponi, D.J. Brod, E.F. Galvão, N. Spagnolo, C. Vitelli, E. Maiorino, P. Mataloni, F. Sciarrino, Integrated multimode interferometers with arbitrary designs for photonic boson sampling. Nature Photon. 7(7), 545–548 (2013). https://doi.org/10.1038/nphoton.2013.112
M. Bentivegna, N. Spagnolo, C. Vitelli, F. Flamini, N. Viggianiello, L. Latmiral, P. Mataloni, D.J. Brod, E.F. Galvão, A. Crespi, R. Ramponi, R. Osellame, F. Sciarrino, Experimental scattershot boson sampling. Sci. Adv. 1(3), 1400255 (2015). https://doi.org/10.1126/sciadv.1400255
M. Tillmann, S.-H. Tan, S.E. Stoeckl, B.C. Sanders, H. de Guise, R. Heilmann, S. Nolte, A. Szameit, P. Walther, Generalized multiphoton quantum interference. Phys. Rev. X 5, 041015 (2015). https://doi.org/10.1103/PhysRevX.5.041015
N. Spagnolo, C. Vitelli, L. Aparo, P. Mataloni, F. Sciarrino, A. Crespi, R., R., R. Osellame, Three-photon bosonic coalescence in an integrated tritter. Nature Commun. 4, 1606 (2013). https://doi.org/10.1038/ncomms2616
A. Crespi, R. Osellame, R. Ramponi, M. Bentivegna, F. Flamini, N. Spagnolo, N. Viggianiello, L. Innocenti, P. Mataloni, F. Sciarrino, Suppression law of quantum states in a 3d photonic fast fourier transform chip. Nat. Commun. 7(1), 10469 (2016). https://doi.org/10.1038/ncomms10469
N. Viggianiello, F. Flamini, L. Innocenti, D. Cozzolino, M. Bentivegna, N. Spagnolo, A. Crespi, D.J. Brod, E.F. Galvão, R. Osellame, F. Sciarrino, Experimental generalized quantum suppression law in sylvester interferometers. New J. Phys. 20(3), 033017 (2018). https://doi.org/10.1088/1367-2630/aaad92
K. Poulios, R. Keil, D. Fry, J.D.A. Meinecke, J.C.F. Matthews, A. Politi, M. Lobino, M. Gräfe, M. Heinrich, S. Nolte, A. Szameit, J.L. O’Brien, Quantum walks of correlated photon pairs in two-dimensional waveguide arrays. Phys. Rev. Lett. 112, 143604 (2014). https://doi.org/10.1103/PhysRevLett.112.143604
P.M. Preiss, R. Ma, M.E. Tai, A. Lukin, M. Rispoli, P. Zupancic, Y. Lahini, R. Islam, M. Greiner, Strongly correlated quantum walks in optical lattices. Science 347(6227), 1229–1233 (2015). https://doi.org/10.1126/science.1260364
F. Caruso, A. Crespi, A.G. Ciriolo, F. Sciarrino, R. Osellame, Fast escape of a quantum walker from an integrated photonic maze. Nat. Commun. 7, 11682 (2016). https://doi.org/10.1038/ncomms11682
Z.-Q. Jiao, J. Gao, W.-H. Zhou, X.-W. Wang, R.-J. Ren, X.-Y. Xu, L.-F. Qiao, X.-M. Jin, Two-Dimensional Quantum Walk of Correlated Photons (2020). arXiv:abs/2007.06554
H. Tang, L. Banchi, T.-Y. Wang, X.-W. Shang, X. Tan, W.-H. Zhou, Z. Feng, A. Pal, H. Li, C.-Q. Hu, M.S. Kim, X.-M. Jin, Generating haar-uniform randomness using stochastic quantum walks on a photonic chip. Phys. Rev. Lett. 128, 050503 (2022). https://doi.org/10.1103/PhysRevLett.128.050503
F. Flamini, L. Magrini, A.S. Rab, N. Spagnolo, V. D’Ambrosio, P. Mataloni, F. Sciarrino, T. Zandrini, A. Crespi, R. Ramponi, R. Osellame, Thermally reconfigurable quantum photonic circuits at telecom wavelength by femtosecond laser micromachining. Light: Science & Amp; Applications 4, 354 (2015). https://doi.org/10.1038/lsa.2015.127
E. Polino, M. Riva, M. Valeri, R. Silvestri, G. Corrielli, A. Crespi, N. Spagnolo, R. Osellame, F. Sciarrino, Experimental multiphase estimation on a chip. Optica 6(3), 288–295 (2019). https://doi.org/10.1364/OPTICA.6.000288
C. Antón, J.C. Loredo, G. Coppola, H. Ollivier, N. Viggianiello, A. Harouri, N. Somaschi, A. Crespi, I. Sagnes, A. Lemaître, L. Lanco, R. Osellame, F. Sciarrino, P. Senellart, Interfacing scalable photonic platforms: solid-state based multi-photon interference in a reconfigurable glass chip. Optica 6(12), 1471–1477 (2019). https://doi.org/10.1364/OPTICA.6.001471
M. Pont, R. Albiero, S.E. Thomas, N. Spagnolo, F. Ceccarelli, G. Corrielli, A. Brieussel, N. Somaschi, H. Huet, A. Harouri, A. Lemaître, I. Sagnes, N. Belabas, F. Sciarrino, R. Osellame, P. Senellart, A. Crespi, Quantifying \(n\)-photon indistinguishability with a cyclic integrated interferometer. Phys. Rev. X 12, 031033 (2022). https://doi.org/10.1103/PhysRevX.12.031033
F. Hoch, S. Piacentini, T. Giordani, Z.-N. Tian, M. Iuliano, C. Esposito, A. Camillini, G. Carvacho, F. Ceccarelli, N. Spagnolo, A. Crespi, F. Sciarrino, R. Osellame, Reconfigurable continuously-coupled 3d photonic circuit for boson sampling experiments. npj Quantum Information 8(1), 55 (2022). https://doi.org/10.1038/s41534-022-00568-6
S. Atzeni, A.S. Rab, G. Corrielli, E. Polino, M. Valeri, P. Mataloni, N. Spagnolo, A. Crespi, F. Sciarrino, R. Osellame, Integrated sources of entangled photons at the telecom wavelength in femtosecond-laser-written circuits. Optica 5(3), 311–314 (2018). https://doi.org/10.1364/OPTICA.5.000311
D. Llewellyn, Y. Ding, I.I. Faruque, S. Paesani, D. Bacco, R. Santagati, Y.-J. Qian, Y. Li, Y.-F. Xiao, M. Huber, M. Malik, G.F. Sinclair, X. Zhou, K. Rottwitt, J.L. O’Brien, J.G. Rarity, Q. Gong, L.K. Oxenlowe, J. Wang, M.G. Thompson, Chip-to-chip quantum teleportation and multi-photon entanglement in silicon. Nat. Phys. 16(2), 148–153 (2020). https://doi.org/10.1038/s41567-019-0727-x
S. Paesani, Y. Ding, R. Santagati, L. Chakhmakhchyan, C. Vigliar, K. Rottwitt, L.K. Oxenløwe, J. Wang, M.G. Thompson, A. Laing, Generation and sampling of quantum states of light in a silicon chip. Nat. Phys. 15(9), 925–929 (2019). https://doi.org/10.1038/s41567-019-0567-8
J. Wang, S. Paesani, R. Santagati, S. Knauer, A.A. Gentile, N. Wiebe, M. Petruzzella, J.L. O’Brien, J.G. Rarity, A. Laing, M.G. Thompson, Experimental quantum hamiltonian learning. Nat. Phys. 13(6), 551–555 (2017). https://doi.org/10.1038/nphys4074
R. Santagati, J. Wang, A.A. Gentile, S. Paesani, N. Wiebe, J.R. McClean, S. Morley-Short, P.J. Shadbolt, D. Bonneau, J.W. Silverstone, D.P. Tew, X. Zhou, J.L. O’Brien, M.G. Thompson, Witnessing eigenstates for quantum simulation of hamiltonian spectra. Science Advances 4(1), (2018). https://doi.org/10.1126/sciadv.aap9646
J.C. Adcock, C. Vigliar, R. Santagati, J.W. Silverstone, M.G. Thompson, Programmable four-photon graph states on a silicon chip. Nat. Commun. 10(1), 3528 (2019). https://doi.org/10.1038/s41467-019-11489-y
C. Vigliar, S. Paesani, Y. Ding, J.C. Adcock, J. Wang, S. Morley-Short, D. Bacco, L.K. Oxenløwe, M.G. Thompson, J.G. Rarity, A. Laing, Error-protected qubits in a silicon photonic chip. Nat. Phys. 17(10), 1137–1143 (2021). https://doi.org/10.1038/s41567-021-01333-w
M. Borghi, C. Castellan, S. Signorini, A. Trenti, L. Pavesi, Nonlinear silicon photonics. J. Opt. 19(9), 093002 (2017). https://doi.org/10.1088/2040-8986/aa7a6d
S. Paesani, M. Borghi, S. Signorini, A. Maïnos, L. Pavesi, A. Laing, Near-ideal spontaneous photon sources in silicon quantum photonics. Nat. Commun. 11(1), 2505 (2020). https://doi.org/10.1038/s41467-020-16187-8
C. Abellan, W. Amaya, D. Domenech, P.M. noz, J. Capmany, S. Longhi, M.W. Mitchell, V. Pruneri, Quantum entropy source on an InP photonic integrated circuit for random number generation. Optica 3(9), 989–994 (2016). https://doi.org/10.1364/OPTICA.3.000989
J. Wang, A. Santamato, P. Jiang, D. Bonneau, E. Engin, J.W. Silverstone, M. Lermer, J. Beetz, M. Kamp, S. Höfling, M.G. Tanner, C.M. Natarajan, R.H. Hadfield, S.N. Dorenbos, V. Zwiller, J.L. O’Brien, M.G. Thompson, Gallium arsenide (GaAs) quantum photonic waveguide circuits. Optics Communications 327, 49–55 (2014). https://doi.org/10.1016/j.optcom.2014.02.040
C. Xiong, W. Pernice, K.K. Ryu, C. Schuck, K.Y. Fong, T. Palacios, H.X. Tang, Integrated GaN photonic circuits on silicon (100) for second harmonic generation. Opt. Express 19(11), 10462–10470 (2011). https://doi.org/10.1364/OE.19.010462
M. Poot, C. Schuck, X.-S. Ma, X. Guo, H.X. Tang, Design and characterization of integrated components for SiN photonic quantum circuits. Opt. Express 24(7), 6843–6860 (2016). https://doi.org/10.1364/OE.24.006843
C. Taballione, R. van der Meer, H.J. Snijders, P. Hooijschuur, J.P. Epping, M. de Goede, B. Kassenberg, P. Venderbosch, C. Toebes, H. van den Vlekkert, P.W.H. Pinkse, J.J. Renema, A universal fully reconfigurable 12-mode quantum photonic processor. Materials for Quantum Technology 1(3), 035002 (2021). https://doi.org/10.1088/2633-4356/ac168c
C. Xiong, X. Zhang, A. Mahendra, J. He, D.-Y. Choi, C.J. Chae, D. Marpaung, A. Leinse, R.G. Heideman, M. Hoekman, C.G.H. Roeloffzen, R.M. Oldenbeuving, P.W.L. van Dijk, C. Taddei, P.H.W. Leong, B.J. Eggleton, Compact and reconfigurable silicon nitride time-bin entanglement circuit. Optica 2(8), 724–727 (2015). https://doi.org/10.1364/OPTICA.2.000724
M. Kues, C. Reimer, P. Roztocki, L.R. Cortés, S. Sciara, B. Wetzel, Y. Zhang, A. Cino, S.T. Chu, B.E. Little, D.J. Moss, L. Caspani, J. Azaña, R. Morandotti, On-chip generation of high-dimensional entangled quantum states and their coherent control. Nature 546(7660), 622–626 (2017). https://doi.org/10.1038/nature22986
S. Signorini, L. Pavesi, On-chip heralded single photon sources. AVS Quantum Science 2(4), 041701 (2020). https://doi.org/10.1116/5.0018594
I. Aharonovich, D. Englund, M. Toth, Solid-state single-photon emitters. Nat. Photonics 10(10), 631–641 (2016). https://doi.org/10.1038/nphoton.2016.186
P. Vergyris, T. Meany, T. Lunghi, G. Sauder, J. Downes, M.J. Steel, M.J. Withford, O. Alibart, S. Tanzilli, On-chip generation of heralded photon-number states. Scientific Reports 6(1), (2016). https://doi.org/10.1038/srep35975
S. Krapick, B. Brecht, H. Herrmann, V. Quiring, C. Silberhorn, On-chip generation of photon-triplet states. Opt. Express 24(3), 2836–2849 (2016). https://doi.org/10.1364/OE.24.002836
C. Autebert, N. Bruno, A. Martin, A. Lemaitre, C.G. Carbonell, I. Favero, G. Leo, H. Zbinden, S. Ducci, Integrated algaas source of highly indistinguishable and energy-time entangled photons. Optica 3(2), 143–146 (2016). https://doi.org/10.1364/OPTICA.3.000143
X. Guo, C.-L. Zou, C. Schuck, H. Jung, R. Cheng, H.X. Tang, Parametric down-conversion photon-pair source on a nanophotonic chip. Light: Science & Applications 6(5), 16249 (2016). https://doi.org/10.1038/lsa.2016.249
Z. Yan, Y. Duan, L.G. Helt, M. Ams, M.J. Withford, M.J. Steel, Generation of heralded single photons beyond 1100nm by spontaneous four-wave mixing in a side-stressed femtosecond laser-written waveguide. Appl. Phys. Lett. 107(23), 231106 (2015). https://doi.org/10.1063/1.4937374
J.W. Silverstone, D. Bonneau, K. Ohira, N. Suzuki, H. Yoshida, N. Iizuka, M. Ezaki, C.M. Natarajan, M.G. Tanner, R.H. Hadfield, V. Zwiller, G.D. Marshall, J.G. Rarity, J.L. O’Brien, M.G. Thompson, On-chip quantum interference between silicon photon-pair sources. Nat. Photonics 8, 104 (2013). https://doi.org/10.1038/nphoton.2013.339
S. Signorini, M. Sanna, S. Piccione, M. Ghulinyan, P. Tidemand-Lichtenberg, C. Pedersen, L. Pavesi, A silicon source of heralded single photons at 2 \(\mu \)m. APL Photonics 6(12), 126103 (2021). https://doi.org/10.1063/5.0063393
P. Kultavewuti, E.Y. Zhu, X. Xing, L. Qian, V. Pusino, M. Sorel, J.S. Aitchison, Polarization-entangled photon pair sources based on spontaneous four wave mixing assisted by polarization mode dispersion. Scientific Reports 7(1), (2017). https://doi.org/10.1038/s41598-017-06010-8
C. Reimer, L. Caspani, M. Clerici, M. Ferrera, M. Kues, M. Peccianti, A. Pasquazi, L. Razzari, B.E. Little, S.T. Chu, D.J. Moss, R. Morandotti, Integrated frequency comb source of heralded single photons. Opt. Express 22(6), 6535–6546 (2014). https://doi.org/10.1364/OE.22.006535
K. Wu, Q. Zhang, A.W. Poon, Integrated si3n4 microresonator-based quantum light sources with high brightness using a subtractive wafer-scale platform. Opt. Express 29(16), 24750–24764 (2021). https://doi.org/10.1364/OE.429921
A. Christ, C. Silberhorn, Limits on the deterministic creation of pure single-photon states using parametric down-conversion. Phys. Rev. A 85, 023829 (2012). https://doi.org/10.1103/PhysRevA.85.023829
F. Kaneda, P.G. Kwiat, High-efficiency single-photon generation via large-scale active time multiplexing. Sci. Adv. 5(10), 8586 (2019). https://doi.org/10.1126/sciadv.aaw8586
N. Somaschi, V. Giesz, L. De Santis, M.P. Loredo, J.C. Almeida, G. Hornecker, S.L. Portalupi, T. Grange, C. Antón, J. Demory, C. Gómez, I. Sagnes, N.D. Lanzillotdti-Kimura, A. Lemaítre, A. Auffeves, A.G. White, L. Lanco, P. Senellart, Near-optimal single-photon sources in the solid state. Nature Photon. 10, 340–345 (2016). https://doi.org/10.1038/nphoton.2016.23
F. Olbrich, J. Höschele, M. Müller, J. Kettler, S.L. Portalupi, M. Paul, M. Jetter, P. Michler, Polarization-entangled photons from an InGaAs-based quantum dot emitting in the telecom c-band. Appl. Phys. Lett. 111(13), 133106 (2017). https://doi.org/10.1063/1.4994145
G. Kiršansk, H. Thyrrestrup, R.S. Daveau, C.L. Dreeßen, T. Pregnolato, L. Midolo, P. Tighineanu, A. Javadi, S. Stobbe, R. Schott, A. Ludwig, A.D. Wieck, S.I. Park, J.D. Song, A.V. Kuhlmann, I. Söllner, M.C. Löbl, R.J. Warburton, P. Lodahl, Indistinguishable and efficient single photons from a quantum dot in a planar nanobeam waveguide. Phys. Rev. B 96, 165306 (2017). https://doi.org/10.1103/PhysRevB.96.165306
A. Schlehahn, S. Fischbach, R. Schmidt, A. Kaganskiy, A. Strittmatter, S. Rodt, T. Heindel, S. Reitzenstein, A stand-alone fiber-coupled single-photon source. Scientific Reports 8(1), (2018). https://doi.org/10.1038/s41598-017-19049-4
H. Snijders, J.A. Frey, J. Norman, V.P. Post, A.C. Gossard, J.E. Bowers, M.P. van Exter, W. Löffler, D. Bouwmeester, Fiber-coupled cavity-qed source of identical single photons. Phys. Rev. Applied 9, 031002 (2018). https://doi.org/10.1103/PhysRevApplied.9.031002
A. Sipahigil, R.E. Evans, D.D. Sukachev, M.J. Burek, J. Borregaard, M.K. Bhaskar, C.T. Nguyen, J.L. Pacheco, H.A. Atikian, C. Meuwly, R.M. Camacho, F. Jelezko, E. Bielejec, H. Park, M. Lončar, M.D. Lukin, An integrated diamond nanophotonics platform for quantum-optical networks. Science 354(6314), 847–850 (2016). https://doi.org/10.1126/science.aah6875
C. Bradac, W. Gao, J. Forneris, M.E. Trusheim, I. Aharonovich, Quantum nanophotonics with group iv defects in diamond. Nat. Commun. 10(1), 5625 (2019). https://doi.org/10.1038/s41467-019-13332-w
M. Arcari, I. Söllner, A. Javadi, S. Lindskov Hansen, S. Mahmoodian, J. Liu, H. Thyrrestrup, E.H. Lee, J.D. Song, S. Stobbe, P. Lodahl, Near-unity coupling efficiency of a quantum emitter to a photonic crystal waveguide. Phys. Rev. Lett. 113, 093603 (2014). https://doi.org/10.1103/PhysRevLett.113.093603
F. Lenzini, B. Haylock, J.C. Loredo, R.A. Abrahão, N.A. Zakaria, S. Kasture, I. Sagnes, A. Lemaitre, H.-P. Phan, D.V. Dao, P. Senellart, M.P. Almeida, A.G. White, M. Lobino, Active demultiplexing of single photons from a solid-state source. Laser & Photonics Reviews 11(3), 1600297 (2017). https://doi.org/10.1002/lpor.201600297
M. Stefszky, R. Ricken, C. Eigner, V. Quiring, H. Herrmann, C. Silberhorn, Waveguide cavity resonator as a source of optical squeezing. Phys. Rev. Applied 7, 044026 (2017). https://doi.org/10.1103/PhysRevApplied.7.044026
F. Mondain, T. Lunghi, A. Zavatta, E. Gouzien, F. Doutre, M.D. Micheli, S. Tanzilli, V. D’Auria, Chip-based squeezing at a telecom wavelength. Photon. Res. 7(7), 36–39 (2019). https://doi.org/10.1364/PRJ.7.000A36
J. Ali, P. Youplao, K. Chaiwong, I.S. Amiri, S. Punthawanunt, N. Pornsuwancharoen, P. Yupapin, Broadband photon squeezing control using microring embedded gold grating for LiFi-quantum link. SN Applied Sciences 1(5), (2019), https://doi.org/10.1007/s42452-019-0487-3
F. Lenzini, J. Janousek, O. Thearle, M. Villa, B. Haylock, S. Kasture, L. Cui, H.-P. Phan, D.V. Dao, H. Yonezawa, P.K. Lam, E.H. Huntington, M. Lobino, Integrated photonic platform for quantum information with continuous variables. Sci. Adv. 4(12), 9331 (2018). https://doi.org/10.1126/sciadv.aat9331
V.D. Vaidya, B. Morrison, L.G. Helt, R. Shahrokshahi, D.H. Mahler, M.J. Collins, K. Tan, J. Lavoie, A. Repingon, M. Menotti, N. Quesada, R.C. Pooser, A.E. Lita, T. Gerrits, S.W. Nam, Z. Vernon, Broadband quadrature-squeezed vacuum and nonclassical photon number correlations from a nanophotonic device. Sci. Adv. 6(39), 9186 (2020). https://doi.org/10.1126/sciadv.aba9186
A. Dutt, K. Luke, S. Manipatruni, A.L. Gaeta, P. Nussenzveig, M. Lipson, On-chip optical squeezing. Phys. Rev. Appl. 3, 044005 (2015). https://doi.org/10.1103/PhysRevApplied.3.044005
H. Wang, W. Li, X. Jiang, Y.-M. He, Y.-H. Li, X. Ding, M.-C. Chen, J. Qin, C.-Z. Peng, C. Schneider, M. Kamp, W.-J. Zhang, H. Li, L.-X. You, Z. Wang, J.P. Dowling, S. Höfling, C.-Y. Lu, J.-W. Pan, Toward scalable boson sampling with photon loss. Phys. Rev. Lett. 120, 230502 (2018). https://doi.org/10.1103/PhysRevLett.120.230502
M. Reck, A. Zeilinger, H.J. Bernstein, P. Bertani, Experimental realization of any discrete unitary operator. Phys. Rev. Lett. 73, 58–61 (1994). https://doi.org/10.1103/PhysRevLett.73.58
W.R. Clements, P.C. Humphreys, B.J. Metcalf, W.S. Kolthammer, I.A. Walmsley, Optimal design for universal multiport interferometers. Optica 3(12), 1460–1465 (2016). https://doi.org/10.1364/OPTICA.3.001460
R. Barak, Y. Ben-Aryeh, Quantum fast fourier transform and quantum computation by linear optics. J. Opt. Soc. Am. B 24(2), 231–240 (2007). https://doi.org/10.1364/JOSAB.24.000231
X. Cai, J. Wang, M.J. Strain, B. Johnson-Morris, J. Zhu, M. Sorel, J.L. O’Brien, M.G. Thompson, S. Yu, Integrated compact optical vortex beam emitters. Science 338(6105), 363–366 (2012). https://doi.org/10.1126/science.1226528
S. Zheng, J. Wang, On-chip orbital angular momentum modes generator and (de)multiplexer based on trench silicon waveguides. Opt. Express 25(15), 18492–18501 (2017). https://doi.org/10.1364/OE.25.018492
E. Karimi, S.A. Schulz, I. De Leon, H. Qassim, J. Upham, R.W. Boyd, Generating optical orbital angular momentum at visible wavelengths using a plasmonic metasurface. Light: Science & Applications 3(5), 167 (2014). https://doi.org/10.1038/lsa.2014.48
F. Di Colandrea, A. Babazadeh, A. Dauphin, P. Massignan, L. Marrucci, F. Cardano, Ultra-long photonic quantum walks via spin-orbit metasurfaces (2022). arXiv:abs/1708.06232
J.P. Sprengers, A. Gaggero, D. Sahin, S. Jahanmirinejad, G. Frucci, F. Mattioli, R. Leoni, J. Beetz, M. Lermer, M. Kamp, S. Höfling, R. Sanjines, A. Fiore, Waveguide superconducting single-photon detectors for integrated quantum photonic circuits. Appl. Phys. Lett. 99(18), 181110 (2011). https://doi.org/10.1063/1.3657518
W.H.P. Pernice, C. Schuck, O. Minaeva, M. Li, G.N. Goltsman, A.V. Sergienko, H.X. Tang, High-speed and high-efficiency travelling wave single-photon detectors embedded in nanophotonic circuits. Nat. Commun. 3(1), 1325 (2012). https://doi.org/10.1038/ncomms2307
D. Sahin, A. Gaggero, T.B. Hoang, G. Frucci, F. Mattioli, R. Leoni, J. Beetz, M. Lermer, M. Kamp, S. Höfling, A. Fiore, Integrated autocorrelator based on superconducting nanowires. Opt. Express 21(9), 11162–11170 (2013). https://doi.org/10.1364/OE.21.011162
A.J. Kerman, E.A. Dauler, J.K.W. Yang, K.M. Rosfjord, V. Anant, K.K. Berggren, G.N. Gol’tsman, B.M. Voronov, Constriction-limited detection efficiency of superconducting nanowire single-photon detectors. Appl. Phys. Lett. 90(10), 101110 (2007). https://doi.org/10.1063/1.2696926
F. Najafi, J. Mower, N.C. Harris, F. Bellei, A. Dane, C. Lee, X. Hu, P. Kharel, F. Marsili, S. Assefa, K.K. Berggren, D. Englund, On-chip detection of non-classical light by scalable integration of single-photon detectors. Nat. Commun. 6(1), 5873 (2015). https://doi.org/10.1038/ncomms6873
C. Schuck, X. Guo, L. Fan, X. Ma, M. Poot, H.X. Tang, Quantum interference in heterogeneous superconducting-photonic circuits on a silicon chip. Nat. Commun. 7(1), 10352 (2016). https://doi.org/10.1038/ncomms10352
G. Brassard, N. Lütkenhaus, T. Mor, B.C. Sanders, Limitations on practical quantum cryptography. Phys. Rev. Lett. 85, 1330–1333 (2000). https://doi.org/10.1103/PhysRevLett.85.1330
W.J. Munro, K. Nemoto, R.G. Beausoleil, T.P. Spiller, High-efficiency quantum-nondemolition single-photon-number-resolving detector. Phys. Rev. A 71, 033819 (2005). https://doi.org/10.1103/PhysRevA.71.033819
R.H. Hadfield, Single-photon detectors for optical quantum information applications. Nat. Photonics 3(12), 696–705 (2009). https://doi.org/10.1038/nphoton.2009.230
T. Gerrits, N. Thomas-Peter, J.C. Gates, A.E. Lita, B.J. Metcalf, B. Calkins, N.A. Tomlin, A.E. Fox, A.L. Linares, J.B. Spring, N.K. Langford, R.P. Mirin, P.G.R. Smith, I.A. Walmsley, S.W. Nam, On-chip, photon-number-resolving, telecommunication-band detectors for scalable photonic information processing. Phys. Rev. A 84, 060301 (2011). https://doi.org/10.1103/PhysRevA.84.060301
J.P. Höpker, M. Bartnick, E. Meyer-Scott, F. Thiele, S. Krapick, N. Montaut, M. Santandrea, H. Herrmann, S. Lengeling, R. Ricken, V. Quiring, T. Meier, A. Lita, V. Verma, T. Gerrits, S.W. Nam, C. Silberhorn, T.J. Bartley, Towards integrated superconducting detectors on lithium niobate waveguides (2017).arXiv:abs/1708.06232
D. Sahin, A. Gaggero, Z. Zhou, S. Jahanmirinejad, F. Mattioli, R. Leoni, J. Beetz, M. Lermer, M. Kamp, S. Höfling, A. Fiore, Waveguide photon-number-resolving detectors for quantum photonic integrated circuits. Appl. Phys. Lett. 103(11), 111116 (2013). https://doi.org/10.1063/1.4820842
F. Mattioli, Z. Zhou, A. Gaggero, R. Gaudio, S. Jahanmirinejad, D. Sahin, F. Marsili, R. Leoni, A. Fiore, Photon-number-resolving superconducting nanowire detectors. Supercond. Sci. Technol. 28(10), 104001 (2015). https://doi.org/10.1088/0953-2048/28/10/104001
J.I. Cirac, P. Zoller, H.J. Kimble, H. Mabuchi, Quantum state transfer and entanglement distribution among distant nodes in a quantum network. Phys. Rev. Lett. 78, 3221–3224 (1997). https://doi.org/10.1103/PhysRevLett.78.3221
H.-J. Briegel, W. Dür, J.I. Cirac, P. Zoller, Quantum repeaters: The role of imperfect local operations in quantum communication. Phys. Rev. Lett. 81, 5932–5935 (1998). https://doi.org/10.1103/PhysRevLett.81.5932
J. Borregaard, H. Pichler, T. Schröder, M.D. Lukin, P. Lodahl, A.S. Sørensen, One-way quantum repeater based on near-deterministic photon-emitter interfaces. Phys. Rev. X 10, 021071 (2020). https://doi.org/10.1103/PhysRevX.10.021071
Y.-A. Chen, Q. Zhang, T.-Y. Chen, W.-Q. Cai, S.-K. Liao, J. Zhang, K. Chen, J. Yin, J.-G. Ren, Z. Chen, S.-L. Han, Q. Yu, K. Liang, F. Zhou, X. Yuan, M.-S. Zhao, T.-Y. Wang, X. Jiang, L. Zhang, W.-Y. Liu, Y. Li, Q. Shen, Y. Cao, C.-Y. Lu, R. Shu, J.-Y. Wang, L. Li, N.-L. Liu, F. Xu, X.-B. Wang, C.-Z. Peng, J.-W. Pan, An integrated space-to-ground quantum communication network over 4,600 kilometres. Nature 589(7841), 214–219 (2021). https://doi.org/10.1038/s41586-020-03093-8
B.C. Jacobs, T.B. Pittman, J.D. Franson, Quantum relays and noise suppression using linear optics. Phys. Rev. A 66, 052307 (2002). https://doi.org/10.1103/PhysRevA.66.052307
E. Knill, R. Laflamme, G.J. Milburn, A scheme for efficient quantum computation with linear optics. Nature 409(6816), 46–52 (2001). https://doi.org/10.1038/35051009
V. Scarani, H. Bechmann-Pasquinucci, N.J. Cerf, M. Dušek, N. Lütkenhaus, M. Peev, The security of practical quantum key distribution. Rev. Mod. Phys. 81, 1301–1350 (2009). https://doi.org/10.1103/RevModPhys.81.1301
C. Portmann, R. Renner, Security in quantum cryptography. Rev. Mod. Phys. 94, 025008 (2022). https://doi.org/10.1103/RevModPhys.94.025008
T. Roger, T. Paraiso, I.D. Marco, D.G. Marangon, Z. Yuan, A.J. Shields, Real-time interferometric quantum random number generation on chip. J. Opt. Soc. Am. B 36(3), 137–142 (2019). https://doi.org/10.1364/JOSAB.36.00B137
A. Prokhodtsov, V. Kovalyuk, P. An, A. Golikov, R. Shakhovoy, V. Sharoglazova, A. Udaltsov, Y. Kurochkin, G. Goltsman, Silicon nitride mach-zehnder interferometer for on-chip quantum random number generation. J. Phys: Conf. Ser. 1695(1), 012118 (2020). https://doi.org/10.1088/1742-6596/1695/1/012118
F. Regazzoni, E. Amri, S. Burri, D. Rusca, H. Zbinden, E. Charbon, A High Speed Integrated Quantum Random Number Generator with on-Chip Real-Time Randomness Extraction (2021). arXiv:abs/2102.06238
B. Bai, J. Huang, G.-R. Qiao, Y.-Q. Nie, W. Tang, T. Chu, J. Zhang, J.-W. Pan, 18.8 gbps real-time quantum random number generator with a photonic integrated chip. Appl. Phys. Lett. 118(26), 264001 (2021). https://doi.org/10.1063/5.0056027
F.B. Basset, M. Valeri, E. Roccia, V. Muredda, D. Poderini, J. Neuwirth, N. Spagnolo, M.B. Rota, G. Carvacho, F. Sciarrino, R. Trotta, Quantum key distribution with entangled photons generated on demand by a quantum dot. Sci. Adv. 7(12), 6379 (2021). https://doi.org/10.1126/sciadv.abe6379
F.B. Basset, M. Valeri, J. Neuwirth, E. Polino, M.B. Rota, D. Poderini, C. Pardo, G. Rodari, E. Roccia, S.F.C. da Silva, G. Ronco, N. Spagnolo, A. Rastelli, G. Carvacho, F. Sciarrino, R. Trotta, Daylight entanglement-based quantum key distribution with a quantum dot source. Quantum Science and Technology 8, 025002 (2023). https://doi.org/10.1088/2058-9565/acae3d
T.K. Paraïso, I. De Marco, T. Roger, D.G. Marangon, J.F. Dynes, M. Lucamarini, Z. Yuan, A.J. Shields, A modulator-free quantum key distribution transmitter chip. npj Quantum Information 5(1), 42 (2019). https://doi.org/10.1038/s41534-019-0158-7
G. Zhang, J.Y. Haw, H. Cai, F. Xu, S.M. Assad, J.F. Fitzsimons, X. Zhou, Y. Zhang, S. Yu, J. Wu, W. Ser, L.C. Kwek, A.Q. Liu, An integrated silicon photonic chip platform for continuous-variable quantum key distribution. Nat. Photonics 13(12), 839–842 (2019). https://doi.org/10.1038/s41566-019-0504-5
H. Semenenko, P. Sibson, A. Hart, M.G. Thompson, J.G. Rarity, C. Erven, Chip-based measurement-device-independent quantum key distribution. Optica 7(3), 238–242 (2020). https://doi.org/10.1364/OPTICA.379679
K. Wei, W. Li, H. Tan, Y. Li, H. Min, W.-J. Zhang, H. Li, L. You, Z. Wang, X. Jiang, T.-Y. Chen, S.-K. Liao, C.-Z. Peng, F. Xu, J.-W. Pan, High-speed measurement-device-independent quantum key distribution with integrated silicon photonics. Phys. Rev. X 10, 031030 (2020). https://doi.org/10.1103/PhysRevX.10.031030
R. Raussendorf, H.J. Briegel, A one-way quantum computer. Phys. Rev. Lett. 86, 5188–5191 (2001). https://doi.org/10.1103/PhysRevLett.86.5188
R. Raussendorf, D.E. Browne, H.J. Briegel, Measurement-based quantum computation on cluster states. Phys. Rev. A 68, 022312 (2003). https://doi.org/10.1103/PhysRevA.68.022312
H.J. Briegel, D.E. Browne, W. Dür, R. Raussendorf, M. Van den Nest, Measurement-based quantum computation. Nat. Phys. 5(1), 19–26 (2009). https://doi.org/10.1038/nphys1157
A. Broadbent, J. Fitzsimons, E. Kashefi, Universal blind quantum computation. In: 2009 50th Annual IEEE Symposium on Foundations of Computer Science, pp. 517–526 (2009). https://doi.org/10.1109/FOCS.2009.36
M. Gimeno-Segovia, H. Cable, G.J. Mendoza, P. Shadbolt, J.W. Silverstone, J. Carolan, M.G. Thompson, J.L. O’Brien, T. Rudolph, Relative multiplexing for minimising switching in linear-optical quantum computing. New J. Phys. 19(6), 063013 (2017). https://doi.org/10.1088/1367-2630/aa7095
T. Rudolph, Why i am optimistic about the silicon-photonic route to quantum computing. APL Photonics 2(3), 030901 (2017). https://doi.org/10.1063/1.4976737
J.E. Bourassa, R.N. Alexander, M. Vasmer, A. Patil, I. Tzitrin, T. Matsuura, D. Su, B.Q. Baragiola, S. Guha, G. Dauphinais, K.K. Sabapathy, N.C. Menicucci, I. Dhand, Blueprint for a Scalable Photonic Fault-Tolerant Quantum Computer. Quantum 5, 392 (2021). https://doi.org/10.22331/q-2021-02-04-392
M.A. Ciampini, A. Orieux, S. Paesani, F. Sciarrino, G. Corrielli, A. Crespi, R. Ramponi, R. Osellame, P. Mataloni, Path-polarization hyperentangled and cluster states of photons on a chip. Light: Science & Applications 5(4), 16064 (2016). https://doi.org/10.1038/lsa.2016.64
J. Zeuner, I. Pitsios, S.-H. Tan, A.N. Sharma, J.F. Fitzsimons, R. Osellame, P. Walther, Experimental quantum homomorphic encryption. npj Quantum Information 7(1), 25 (2021). https://doi.org/10.1038/s41534-020-00340-8
W.-T. Fang, Y.-H. Li, Z.-Y. Zhou, L.-X. Xu, G.-C. Guo, B.-S. Shi, On-chip generation of time-and wavelength-division multiplexed multiple time-bin entanglement. Opt. Express 26(10), 12912–12921 (2018). https://doi.org/10.1364/OE.26.012912
S. Barz, E. Kashefi, A. Broadbent, J.F. Fitzsimons, A. Zeilinger, P. Walther, Demonstration of blind quantum computing. Science 335(6066), 303–308 (2012). https://doi.org/10.1126/science.1214707
P.P. Rohde, J.F. Fitzsimons, A. Gilchrist, Quantum walks with encrypted data. Phys. Rev. Lett. 109, 150501 (2012). https://doi.org/10.1103/PhysRevLett.109.150501
A. Aspuru-Guzik, P. Walther, Photonic quantum simulators. Nat. Phys. 8, 285 (2012). https://doi.org/10.1038/nphys2253
J. Huh, G.G. Guerreschi, B. Peropadre, J.R. McClean, A. Aspuru-Guzik, Boson sampling for molecular vibronic spectra. Nat. Photonics 9(9), 615–620 (2015). https://doi.org/10.1038/nphoton.2015.153
L. Banchi, M. Fingerhuth, T. Babej, C. Ing, J.M. Arrazola, Molecular docking with gaussian boson sampling. Science Advances 6(23), (2020). https://doi.org/10.1126/sciadv.aax1950
K. Bradler, P.-L. Dallaire-Demers, P. Rebentrost, D. Su, C. Weedbrook, Gaussian boson sampling for perfect matchings of arbitrary graphs. Phys. Rev. A 98, 98 (2018). https://doi.org/10.1103/PhysRevA.98.032310
J.M. Arrazola, T.R. Bromley, Using gaussian boson sampling to find dense subgraphs. Phys. Rev. Lett. 121, 030503 (2018). https://doi.org/10.1103/PhysRevLett.121.030503
M. Schuld, K. Brádler, R. Israel, D. Su, B. Gupt, Measuring the similarity of graphs with a gaussian boson sampler. Phys. Rev. A 101, 032314 (2020). https://doi.org/10.1103/PhysRevA.101.032314
J. Biamonte, P. Wittek, N. Pancotti, P. Rebentrost, N. Wiebe, S. Lloyd, Quantum machine learning. Nature 549(7671), 195–202 (2017). https://doi.org/10.1038/nature23474
N.C. Harris, G.R. Steinbrecher, M. Prabhu, Y. Lahini, J. Mower, D. Bunandar, C. Chen, F.N.C. Wong, T. Baehr-Jones, M. Hochberg, S. Lloyd, D. Englund, Quantum transport simulations in a programmable nanophotonic processor. Nat. Photonics 11(7), 447–452 (2017). https://doi.org/10.1038/nphoton.2017.95
C. Sparrow, E. Martín-López, N. Maraviglia, A. Neville, C. Harrold, J. Carolan, Y.N. Joglekar, T. Hashimoto, N. Matsuda, J.L. O’Brien, D.P. Tew, A. Laing, Simulating the vibrational quantum dynamics of molecules using photonics. Nature 557(7707), 660–667 (2018). https://doi.org/10.1038/s41586-018-0152-9
A. Crespi, L. Sansoni, G. Della Valle, A. Ciamei, R. Ramponi, F. Sciarrino, P. Mataloni, S. Longhi, R. Osellame, Particle statistics affects quantum decay and fano interference. Phys. Rev. Lett. 114, 090201 (2015). https://doi.org/10.1103/PhysRevLett.114.090201
H. Tang, C. Di Franco, Z.-Y. Shi, T.-S. He, Z. Feng, J. Gao, K. Sun, Z.-M. Li, Z.-Q. Jiao, T.-Y. Wang, M.S. Kim, X.-M. Jin, Experimental quantum fast hitting on hexagonal graphs. Nat. Photonics 12(12), 754–758 (2018). https://doi.org/10.1038/s41566-018-0282-5
V. Saggio, B.E. Asenbeck, A. Hamann, T. Strömberg, P. Schiansky, V. Dunjko, N. Friis, N.C. Harris, M. Hochberg, D. Englund, S. Wölk, H.J. Briegel, P. Walther, Experimental quantum speed-up in reinforcement learning agents. Nature 591(7849), 229–233 (2021). https://doi.org/10.1038/s41586-021-03242-7
M. Spagnolo, J. Morris, S. Piacentini, M. Antesberger, F. Massa, A. Crespi, F. Ceccarelli, R. Osellame, P. Walther, Experimental photonic quantum memristor. Nat. Photonics 16(4), 318–323 (2022). https://doi.org/10.1038/s41566-022-00973-5
D.J. Brod, E.F. Galvão, A. Crespi, R. Osellame, N. Spagnolo, F. Sciarrino, Photonic implementation of boson sampling: a review. Advanced Photonics 1(3), 1–14 (2019)
M.A. Broome, A. Fedrizzi, S. Rahimi-Keshari, J. Dove, S. Aaronson, T.C. Ralph, A.G. White, Photonic boson sampling in a tunable circuit. Science 339(6121), 794–798 (2013). https://doi.org/10.1126/science.1231440
N. Spagnolo, C. Vitelli, L. Sansoni, E. Maiorino, P. Mataloni, F. Sciarrino, D.J. Brod, E.F. Galvão, A. Crespi, R. Ramponi, R. Osellame, General rules for bosonic bunching in multimode interferometers. Phys. Rev. Lett. 111(13), 130503 (2013). https://doi.org/10.1103/PhysRevLett.111.130503
N. Spagnolo, C. Vitelli, M. Bentivegna, D.J. Brod, A. Crespi, F. Flamini, S. Giacomini, G. Milani, R. Ramponi, P. Mataloni, R. Osellame, E.F. Galvão, F. Sciarrino, Experimental validation of photonic boson sampling. Nature Photon. 8(8), 615–620 (2014). https://doi.org/10.1038/nphoton.2014.135
J. Carolan, J.D. Meinecke, P.J. Shadbolt, N.J. Russell, N. Ismail, K. Wörhoff, T. Rudolph, M.G. Thompson, J.L. O’Brien, J.C. Matthews, A. Laing, On the experimental verification of quantum complexity in linear optics. Nature Photon. 8(8), 621–626 (2014). https://doi.org/10.1038/nphoton.2014.152
T. Giordani, F. Flamini, M. Pompili, N. Viggianiello, N. Spagnolo, A. Crespi, R. Osellame, N. Wiebe, M. Walschaers, A. Buchleitner, F. Sciarrino, Experimental statistical signature of many-body quantum interference. Nat. Photonics 12(3), 173–178 (2018). https://doi.org/10.1038/s41566-018-0097-4
J. Loredo, M. Broome, P. Hilaire, O. Gazzano, I. Sagnes, A. Lemaitre, M. Almeida, P. Senellart, A. White, Boson sampling with single-photon fock states from a bright solid-state source. Phys. Rev. Lett. 118(13), 130503 (2017). https://doi.org/10.1103/PhysRevLett.118.130503
Y. He, X. Ding, Z.-E. Su, H.-L. Huang, J. Qin, C. Wang, S. Unsleber, C. Chen, H. Wang, Y.-M. He, X.-L. Wang, W.-J. Zhang, S.-J. Chen, C. Schneider, M. Kamp, L.-X. You, Z. Wang, S. Höfling, C.-Y. Lu, J.-W. Pan, Time-bin-encoded boson sampling with a single-photon device. Phys. Rev. Lett. 118(19), 190501 (2017). https://doi.org/10.1103/PhysRevLett.118.190501
H. Wang, Y. He, Y.-H. Li, Z.-E. Su, B. Li, H.-L. Huang, X. Ding, M.-C. Chen, C. Liu, J. Qin, J.-P. Li, Y.-M. He, C. Schneider, M. Kamp, C.-Z. Peng, S. Höfling, C.-Y. Lu, J.-W. Pan, High-efficiency multiphoton boson sampling. Nature Photon. 11(6), 361–365 (2017). https://doi.org/10.1038/nphoton.2017.63
D. Istrati, Y. Pilnyak, J.C. Loredo, C. Antón, N. Somaschi, P. Hilaire, H. Ollivier, M. Esmann, L. Cohen, L. Vidro, C. Millet, A. Lemaître, I. Sagnes, A. Harouri, L. Lanco, P. Senellart, H.S. Eisenberg, Sequential generation of linear cluster states from a single photon emitter. Nat. Commun. 11(1), 5501 (2020). https://doi.org/10.1038/s41467-020-19341-4
Funding
Open access funding provided by Università degli Studi di Roma La Sapienza within the CRUI-CARE Agreement. This work is supported by the ERC Advanced grant QU-BOSS (Grant Agreement No. 884676) and by the PNRR MUR project PE0000023-NQSTI.
Author information
Authors and Affiliations
Contributions
All authors contributed equally to the review.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare they have no competing interests.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Giordani, T., Hoch, F., Carvacho, G. et al. Integrated photonics in quantum technologies. Riv. Nuovo Cim. 46, 71–103 (2023). https://doi.org/10.1007/s40766-023-00040-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40766-023-00040-x