Abstract
Ultrastable glasses (mostly prepared from the vapor phase under optimized deposition conditions) represent a unique class of materials with low enthalpies and high kinetic stabilities. These highly stable and dense glasses show unique physicochemical properties, such as high thermal stability, improved mechanical properties or anomalous transitions into the supercooled liquid, offering unprecedented opportunities to understand many aspects of the glassy state. Their improved properties with respect to liquid-cooled glasses also open new prospects to their use in applications where liquid-cooled glasses failed or where not considered as usable materials. In this review article we summarize the state of the art of vapor-deposited (and other) ultrastable glasses with a focus on the mechanism of equilibration, the transformation to the liquid state and the low temperature properties. The review contains information on organic, metallic, polymeric and chalcogenide glasses and an updated list with relevant properties of all materials known today to form a stable glass.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Since their discovery in 2007 by Mark Ediger and his group at the university of Wisconsin [1], Madison, vapor-deposited stable glasses have become an important area of research within the glass community due to their remarkable properties that facilitate new approaches to the exploration of some long-standing problems in glass science, such as the glass transition phenomenology and the existence or not of an ideal glass that is hidden by the kinetic glass transition observed in the laboratory. At the same time, vapor-deposition offers a versatile route to produce organic thin film glasses with enhanced kinetic and thermodynamic stability, as well as tailored molecular orientation, opening new possibilities to improve the efficiency and lifetime of organic optoelectronic devices [2]. While much research has focused on organic glasses, a new burst of activity is related now to ultrastability in metallic glasses and polymers, two families of materials with many relevant industrial applications. We note that several excellent reviews have been recently published covering aspects related to the origin of ultrastability, their packing anisotropy and tuning of the molecular orientation, as well as structure–property relationships of stable organic glasses [3,4,5]. Here, we intend to give a broader description that provides updated information on the different materials that have been grown from the vapor as ultrastable glasses including metallic, organic, polymeric, and chalcogenides. Although during the 14 years of activity in this field most of the work has involved organic glasses, we incorporate whenever possible data from metallic glasses and polymers. From this diverse perspective we focus on the mechanism of formation of stable glasses and on their low-temperature properties, their transformation into the supercooled liquid, the role of fragility in stable glass formation and some potential applications of these materials. The review is organized as follows. The first section provides a general introduction of the main characteristics of stable glasses and some common properties and distinctions between stable glasses of different families and prepared by different routes. It includes organic, metallic, polymer and chalcogenide glasses and a comprehensive up-to-date list/table of most materials prepared from the vapor as stable glasses. The second section covers the mechanism of formation of low enthalpy glasses by vapor deposition. Section 3 deals with the transformation mechanism of organic stable glasses into the supercooled liquid. It covers two scenarios: in very thin films propagation fronts parallel to the film surface (or interfaces) dominate the transformation and, in much thicker films, the transformation proceeds through a bulk process that resembles nucleation and growth in the melting of polycrystalline solids. Section 4 describes some of the remarkable features of the low-temperature properties of glasses and the exceptional properties of vapor-deposited stable glasses. Finally, Sect. 5 summarizes some interesting (opto)electronic and thermal transport properties of vapor-deposited stable glasses in relation to present or potential applications.
1 Introduction
Glasses can be broadly defined as non-equilibrium solids lacking long-range order. The absence of periodicity provides exceptional attributes to these materials. In particular, they can be made more homogeneous on larger scales than crystals due to the absence of grain boundaries and there is a large flexibility in tuning their composition and properties without entering well-defined thermodynamic states. They exhibit a reversible transition between the glass and the supercooled liquid that is termed glass transition. Consequently, a good understanding of the dynamical behavior of supercooled liquids is crucial for a precise knowledge of the formation of the glass. The reader is referred to several reviews covering the supercooled liquid state [6, 7], here we briefly introduce some ideas that we consider relevant for the discussion below. The glass is usually obtained by cooling the liquid from above the melting temperature of the material, bypassing crystallization, to low temperature regions where viscosity is high enough to consider the material a solid in observational time scales.Footnote 1 In the glass state, molecular motion almost ceases, except for thermal vibrations. A similar statement can be formulated in terms of the structural relaxation time, τ (also called alpha relaxation), considering the Maxwell equation [8] that relates the relaxation time of the supercooled liquid and the shear viscosity through \(\tau ={G}_{\infty }\cdot \eta \), where \({G}_{\infty }\) is the shear modulus measured at high frequency. The relaxation time of the liquid is proportional to the viscosity and roughly follows its same temperature dependence, since the variation of \({G}_{\infty }\) with temperature is much less dramatic than that of the viscosity. Therefore, similarly to viscosity, \(\tau \) of the supercooled liquid grows abruptly close to the glass transition, although this dynamical change is not associated to a structural variation. The relaxation time can be considered as a characteristic time associated to the rearrangement of a system once it has been externally altered and moved out from equilibrium. It can also be associated to the dissipation of spontaneous density fluctuations occurring in the liquid structure. Both characteristic times are related by the fluctuation–dissipation theorem. For example, when reducing the temperature of a liquid by a small value, its volume (or enthalpy) does not change immediately, but the process requires a certain amount of time to reach equilibrium. This equilibration time (or relaxation time), which is temperature dependent, governs the dynamics of such a change. The temperature at which the relaxation time of the material exceeds standard laboratory time scales (by convention chosen at around 100 s) is considered as the standard glass transition temperature, Tg, (Fig. 1a). This temperature marks the transition from the supercooled liquid to the glass state [6]. The glass transition temperature can be defined in many other alternative ways: for instance, in calorimetry experiments, its value for a given substance is defined by a finite discontinuity of the heat capacity when cooling from the liquid at − 10 K/min [9] (see Fig. 2). Throughout this review, we will refer to a conventional glass as one that has been cooled from the liquid at − 10 K/min, and its Tg is measured on cooling or at the subsequent heating at + 10 K/min. However, the temperature associated to the atomic/molecular arrest depends on the thermal history of the material, that is, for instance, on its cooling rate. The lower the cooling rate, the lower the glass transition temperature, if crystallization can be avoided. In other words, the glass can be made more stable (lower Tg on cooling) by simply decreasing the cooling rate. Of course, besides the risk of crystallization that is a handicap for many families of glasses, there is a practical obstacle to this processing route since, roughly speaking, temperature excursions of tens/hundreds of degrees from the liquid state are typically required to produce a glass. That is, cooling at 0.01 K/min for 100 K will require around 10 days. Further lowering two orders of magnitude, the cooling rate to obtain a glass with higher thermodynamic stability (lower Tg) will raise this number to 3 years. The amount of stability enhancement upon lowering the cooling rate will ultimately depend on the fragility of the supercooled liquid. The kinetic fragility is a measure of the non-Arrhenius character of the change of viscosity (or relaxation time) of the supercooled liquid when approaching the glass transition temperature. Strong liquids display an Arrhenius temperature dependence, while fragile liquids are highly non-Arrhenius [10, 11]. The larger the deviation from Arrhenius, the higher the fragility, as schematically shown in Fig. 1b. An indicator of the kinetic fragility of the liquid is the parameter m, that is obtained through the Angell plot [12] (log (η) vs Tg/T, as in Fig. 1b), using the following expression, \(m={\left.\frac{d\mathrm{log}\left[\tau \left(T\right)\right]}{d\left(\frac{{T}_{\mathrm{g}}}{T}\right)}\right]}_{T={T}_{\mathrm{g}}}\). Low and large m values mean strong and fragile liquids, respectively.
Representation of the dynamics of typical glass-forming liquids: a logarithm of the structural (alpha) relaxation time of glycerol as a function of 1000/T, showing the exponential growth of relaxation dynamics as the temperature is lowered, and b logarithm of the viscosity as a function of the normalized inverse of temperature for materials with different fragility. Strong materials, such as silicon dioxide, follow an Arrhenius expression, while fragile glass formers, such as o-terphenyl, follow a super Arrhenius expression. Data obtained from [13, 14]
Representation of the typical specific heat trace of a glass transition during cooling (dashed red line) and the subsequent heating, at a faster pace than the previous cooling (blue line). The beginning of the glass transition peak on heating corresponds to the onset temperature (Ton). The integration of the specific heat trace yields the enthalpy curve. The limiting fictive temperature can be calculated as the intersection between the enthalpy curve and the extrapolation of the supercooled liquid enthalpy line
The stability of a glass can also be improved by annealing the glass below the glass transition temperature, a process often termed aging. Aging, in a structural sense, is a very slow relaxation process because it relies on the bulk structural relaxation, that has a sharp exponential behavior below Tg (see Fig. 1a). Therefore, unreachable time scales are often needed to prepare a glass with very high thermal stability. This is the main drawback of liquid-cooled glasses, because if the glass is not stable enough at the working temperatures it may undergo changes during its lifetime operation in many practical applications.
One of the most relevant attributes of vapor-deposited stable glasses is that they can be prepared in thermodynamic states comparable to glasses that have been cooled (or equivalently aged) for hundreds/thousands of years. This property brings unusual opportunities to prepare, in just a few hours, glasses that may take unattainable waiting times by conventional liquid-cooled protocols. This correspondence between vapor-deposited and conventional glasses is always established upon extrapolation of the properties of the liquid-cooled glass towards extremely low cooling rates or geological timescales of aging. In addition, vapor-deposited glasses often exhibit molecular packing anisotropy [15, 16] which adds another degree of freedom to tune the properties of the material, but at the same time hinders a direct correlation of some of their properties with respect to isotropic liquid-cooled glasses. Therefore, one of the relevant questions in the field of vapor-deposited stable glasses is whether they would be comparable to glasses prepared by conventional means in unreachable timescales, or they correspond to unique configurations that are a particularity of the preparation method.
Probably, the most prominent characteristics of vapor-deposited glasses are related to their kinetic and thermodynamic stabilities. The kinetic stability is typically measured through the shift of the onset of devitrification (Ton), defined as the temperature at which the glass starts to transform into the supercooled liquid on heating. Since stable glasses are prepared from the vapor as films, the variation of Ton is typically measured either with calorimetry (by standard calorimetry for micron-thick films or chip-based calorimetry for thinner ones) or with ellipsometry, measuring the thickness change as a function of temperature. Ton is evaluated at the crossing point between the heat capacity of the glass and the rapidly increasing heat capacity line. This temperature coincides with the inflection point of the Cp line during cooling when \(\left|{q}_{\mathrm{c}}\right|=\left|{q}_{\mathrm{h}}\right|\). If heating is faster than cooling, Ton is right shifted compared to the inflection point of the heat capacity on cooling (Tg), as shown in Fig. 2. This is the situation for vapor-deposited glasses: since they are in thermodynamic states equivalent to glasses cooled at extremely small cooling rates, but Ton is measured on heating at rates around 10 K/min. Therefore, Ton is shifted to high temperatures with respect to Tg, the larger the shift the higher the kinetic stability of the glass. An alternative (but closely related) quantification of the kinetic stability can be obtained by comparing the time needed to transform a material to its supercooled liquid state during an isotherm at T > Tg with the alpha relaxation time at that temperature. This time is referred to as transformation time. For instance, if a glass takes 1000 s to become a liquid at T1 > Tg and τα is 0.1 s at T1, then the ratio ttrans/τα is 104. Another signature of the high stability of ultrastable glasses is the thermodynamic stability, which is measured by the decrease of a state variable (enthalpy, volume) with respect to the liquid-cooled glass. Enthalpy reductions around 5–10 J/g are typically reached in ultrastable glasses (Table I). The thermodynamic stability is described through the concept of the fictive temperature (Tf), defined as the temperature at which the state variable (enthalpy or density) has the same value for the glass and for the extrapolated equilibrium liquid [9, 17] (see Fig. 2). While it has been recognized that glasses do not show a unique, macroscopic, Tf, but rather a microscopic dispersion of fictive temperatures [18], it is a useful parameter to globally define the stability of a glass and we will use it this way throughout this review. The evaluation of Tf can be done in several ways: using calorimetric data, the integration of heat capacity yields the enthalpy as a function of temperature and the extrapolation of the enthalpy of the supercooled liquid line to low temperatures provides Tf at the crossing point between the liquid and the glass lines (see Fig. 2).
Tf can also be evaluated from the specific heat data using the area matching method of Moynihan et al. [17]. A different approach is to use ellipsometric data and extract Tf as the intersection between the thickness of the glass and the extrapolation to lower temperatures of the thickness of the liquid. In view of the above, though ultrastability is a tunable quantity, an ultrastable glass could be defined as a glass that simultaneously exhibits: (i) transformation times when annealed above Tg that are orders of magnitude larger than the alpha relaxation times at that temperature (typical values in organic glasses are 103–106) or equivalently shifts in Ton (during a heating scan) by some important fraction (around 5% or more) relative to Tg. ΔTon (%) is defined as ((Ton(stable)-Tg(conventional))/Tg(conventional)) × 100, and (ii) a fictive temperature evaluated through any relevant macroscopic property (enthalpy, density, hardness) that approaches the ideal glass state beyond what can be achieved by cooling the liquid in reasonable time scales. As will be shown below, not all materials termed ultrastable glasses in the literature comply with the same characteristics. Organic glasses show low enthalpic fictive temperatures while in metallic glasses, due to the difficulty of measuring in a sufficiently large temperature interval the heat capacity of the liquid because of crystallization, it is best to correlate the stability with respect to the mechanical properties.
At this point, we introduce the potential energy landscape (PEL) paradigm, which is so widely employed to visualize and discuss the dynamic and thermodynamic behavior of glasses and viscous liquids. As depicted in Fig. 3, the PEL of an ensemble of N particles is essentially a topographic view of the (3N + 1) potential-energy hypersurface of any glass-forming substance [19,20,21], though it is schematically projected on two dimensions for sake of convenience. Even a small portion of this energy diagram is plenty of local minima and saddle points for thermal energies below kBTm (where Tm stands for the melting temperature of the stable crystalline state, when it exists). When a liquid is supercooled bypassing the crystallization down to the glass-transition temperature Tg, it becomes a glass getting trapped in one of the many possible local minima or metastable states, depending on the thermal history followed. Furthermore, many authors have speculated on the possible existence of an “ideal glass” which should correspond to the best and most stable possible glass achievable, associated with the lowest relative minimum. This ideal glass would have zero configurational entropy, equal to that of crystals, and has been associated to the possible existence of an underlying, likely second order, thermodynamic glass transition occurring at the so-called Kauzmann temperature TK [22].
Schematic potential energy landscape (PEL) for supercooled liquids and glasses, including the hypothetical absolute minimum for a glass state. An ideal glass would be obtained after an infinitely long aging at the Kauzmann temperature TK. Double-well (DWP) and single-well (SWP) potentials are also suggested (see Sect. 4 for a detailed discussion). A glass could evolve by aging, exploring lower energy states, or by rejuvenation, moving towards higher energy states. A vapor deposited ultrastable glass can access low energy states, close to the ideal glass
Interestingly, a few experiments in the last decade have addressed more directly this question, by trying to get very deep in the energy landscape, approaching the ideal glass state, as illustrated in Fig. 3. The recent emergence of highly stable glasses has opened an appealing and timely window to investigate these issues in a real, not speculative way [23,24,25]. In a PEL view the kinetic stability can be seen as the height of the barriers that need to be overcome to attain another, more equilibrated, metastable state. Hence the thermodynamic stability is pictured by a deep position in the PEL. The lower the value of Tf, the higher is the stability of the glass or, to put it another way, the lower is the position of the glass in the PEL.
1.1 Organic glasses
Most of the work on ultrastable glasses has involved molecular glasses. Since the first measurements in 2007 [1] with 1,3-bis-(1-naphthyl)-5-(2-naphthyl)benzene (TNB) (Tg = 347 K) and indomethacin (IMC) (Tg = 315 K), more than 45 different organic molecules, ranging from small molecules such as toluene [26,27,28] and ethylbenzene [28] to pharmaceuticals such as IMC and TNB and more recently to organic semiconductors like TPD [29, 30], NPD [31, 32] and TPBi [2], have shown their ability to form highly stable glasses upon growth by physical vapor deposition at the right processing conditions. Table 1 shows a comprehensive list of molecules and some of the outstanding properties of the vapor-deposited thin film ultrastable glasses obtained from them. As a general trend, vapor-deposited organic glasses show a substantial increase of Ton compared to a conventional glass prepared by cooling the liquid at − 10 K/min. ΔTon roughly varies from 2 to 10% (see Table 1) depending on the molecular system and growth conditions.
The two most relevant external parameters influencing the kinetic and thermodynamic stability of vapor-deposited organic glasses are the substrate temperature during growth from the vapor, Tsub, and the growth rate, g [33,34,35]. In most cases, stable organic glasses are deposited using g values around 0.1–1 nm/s. Lower (higher) rates can be used to prepare glasses with higher(lower) stability. The influence of these parameters on glass stability can be understood through the concept of surface equilibration and will be deeply discussed in Sect. 2. Figure 4 shows typical trends for Ton and Tf as a function of the substrate temperature (for g ≈ 0.1–1 nm/s). The region of maximum stability (both kinetic and thermodynamic) is broadly located between 0.8 and 0.9 Tg, being Tg the glass transition temperature of the conventional glass. In the region close to Tg the glass can be grown in equilibrium with the liquid at the deposition temperature if the growth rate is low enough [36]. That is, in these conditions, a glass grown at a substrate temperature of, for example, 0.95 Tg, will have a fictive temperature that equals 0.95 Tg. Figure 4 also shows that as we lower Tsub we get to a temperature at which the glass falls out of equilibrium, i.e. does not follow the extrapolation line of the supercooled liquid. This has been explored in detail by Beasley et al. [25] and brings the interesting issue as to how low can we reduce the substrate temperature (and, concomitantly, the growth rate) to obtain glasses in equilibrium with the supercooled liquid. The fundamental and relevant question would be: How far an ultrastable glass can go down in the energy landscape? That is, can we reach an enthalpy state close to the one theoretically predicted for the ideal glass? This relevant issue is further discussed in Sect. 2.5.
Onset temperature of devitrification (bottom) and fictive temperature (top) of several organic thin films: a Toluene; b Tris(4-carbazoyl-9-ylphenyl)amine (TCTA), c Celecoxib. Lines are a guide to the eye. The devitrification was measured by quasi-adiabatic membrane-based nanocalorimetry, at heating rates of the order of 3 × 104 K/s for films of equal thickness. Data extracted from different sources [37,38,39]
In practical experiments, lowering the value of g even further is experimentally challenging, and at some point when the substrate temperature decreases the vapor-deposited glass will fall out of equilibrium, i.e. its average fictive temperature will be higher than Tsub. This is the shadow region in Fig. 4a. The properties of vapor-deposited glasses grown at low substrate temperatures, below 0.75 Tg, have not been explored in detail and it is too early to draw conclusions about the mechanism of stabilization in this temperature regime, at least for organic glasses. Recent experiments from Fakhraai and coworkers [40] show that at temperatures around and below 0.85 Tg it is possible to access to a different phase in TPD vapor deposited glasses but only for very thin films, below 70 nm. This is a clear example showing how complex can become the relaxation mechanisms that take place during the deposition process.
The role other external variables can play in the properties of the glass is much less explored compared to temperature and growth rate. Below, we describe several ways one could think to modify the energy of the incoming molecules or their arrangement/packing within a glass. For instance, ion-beam-assisted deposition (IBAD) irradiating the substrate surface with a low-energy ion beam during growth could be used to enhance surface diffusion. If crystals can be avoided during thin film growth, this deposition technique may enable highly stable glasses at lower deposition temperatures compared to standard physical vapor deposition. Other external variables such as electric/magnetic fields or light during thin film growth may have some impact on the formation of stable glasses depending on the nature of the organic molecule. For example, organic molecules with large intrinsic electric dipolar moments could be orientationally tuned by high external electric fields while keeping a high thermodynamic stability. The presence of magnetic fields during deposition may also play a role in molecules containing magnetic atoms. Or illumination of the substrate during growth may affect the formation of semiconductor molecules with homo–lumo levels lower than the energy of the incident light [41].
Another property that is very useful in understanding some of the unusual properties of stable organic glasses is density. Ellipsometry data are employed to infer the density of the films and highly stable organic glasses are consistently more dense than conventional liquid-cooled glasses by around 1–2% depending on the organic molecule and the deposition conditions (see Table 1). The increased density of the glass correlates relatively well with the enhanced thermodynamic stability, i.e. fictive temperature [37, 38]. The high packing density of stable glasses is often invoked to explain the heterogenous nature of the transformation of the stable glass into the supercooled liquid, that starts in regions of high mobility at the surface of the glass, where mobility is orders of magnitude higher than in the bulk. The observation of propagation fronts that start at surfaces/interfaces has already been observed and analyzed in many organic glasses. Section 3 gives a detailed overview of this mechanism.
A remarkable characteristic of many vapor-deposited glasses is the existence of molecular anisotropy. An excellent review on this topic has appeared recently [5] and here we only give a short summary. While conventional glasses, those prepared by cooling from the melt, are completely isotropic, glasses prepared by physical deposition exhibit a particular molecular arrangement whose magnitude depends on deposition conditions (Tsub and growth rate) and on molecular shape. In general, glasses deposited below, and close to, Tg, exhibit an isotropic structure comparable to conventional glasses. Decreasing Tsub, the grown glass has an increasing tendency towards end-on packing (i.e. long axis of the molecule perpendicular to the substrate). Eventually, upon further decreasing of Tsub, the orientation of the molecule becomes more planar (parallel to the substrate), see Fig. 5. These observations have been experimentally determined using variable angle spectroscopic ellipsometry, X-ray diffraction, infrared/UV spectroscopy or absorption [3, 5, 42,43,44,45] and supported by a number of simulation works[29, 46]. The relation of molecular anisotropy with the mode of growth is described in Sect. 2 and the impact on the electronic and other properties considered in Sect. 5. To what extent molecular ordering and thermal stability are related is not well known, but several experiments point out that both properties are not correlated (see Sect. 2.5).
(Left) GIWAXS scattering patterns obtained from TPD glasses vapor deposited at substrate temperatures of 260 K and 315 K. The concentration of intensity observed along qz and qxy indicates anisotropic packing. These scattering patterns were obtained at an incidence angle of 0.14° and represent scattering from the entire thickness of the film. (Right) Schematic representing the microstructures of TPD glasses with the highest magnitude positive and negative order parameters in this study corresponding to sample prepared at 260 K and 315 K. For illustrative purposes, the degree of order has been enhanced in the schematics. Reprinted with permission from A. Gujral et al. Chem. Mater. 2015, 27, 9, 3341–3348 [47].
1.2 Metallic glasses
Metallic glasses, MG, are a family of remarkably important materials that share the properties of both metals and glasses giving rise to unique mechanical and functional properties, key to their use in many applications, such as computer memories and magnetic resistance sensors in electronics, surgical tools in the bio-medical industry, nuclear waste disposal reservoirs due to their resistance to irradiation or as the core of high-power transformers based on the soft magnetic properties of some metallic alloys [48]. However, their applicability is often limited by their tendency to exhibit low thermal stability and crystallization. Therefore, one of the main goals in the metallic glass community over the years has been to enhance the glass forming ability and to improve the thermal stability and mechanical strength of glasses.
While most of the studies are devoted to bulk metallic glasses (BMG) and the emphasis is placed on obtaining large-size disordered materials from the liquid using low cooling rates avoiding crystallization, recent efforts are also directed towards the preparation of thin film metallic glasses (TFMG) because of their potential use in specific areas such as biomedical and optical components [49]. Recent work on thin film metallic glasses prepared by magnetron sputtering has shown the feasibility of obtaining ultrastable metallic glasses in a broader range of deposition conditions (Tsub and g) compared to organic glasses [35, 50, 51].
In contrast to the behavior of organic vapor-deposited glasses where both kinetic and thermodynamic stability appear to be correlated and are always enhanced in highly stable glassy materials, the observation of high kinetic stability in TFMG, typically identified by a shift in Ton to higher temperatures during heating, has not always been accompanied by an enhancement of the thermodynamic stability (we note that in the metallic glass community Tg refers to the onset of the devitrification temperature measured by calorimetry at heating rates of around 10 to 20 K/min). That is, some stable MG exhibit simultaneously a higher onset of devitrification temperature and, apparently, a high position in the potential energy landscape, quantified through enthalpy plots or through the enthalpic fictive temperature. It seems that in metallic glasses the presence of large energy barriers to change the inner energy of the system also appear in states that are located high in the potential energy landscape, i.e. states with low thermodynamic stability. This is a distinct, and still not well understood, variation between vapor-deposited metallic and organic glasses. We note, however, that it is often difficult to evaluate with enough accuracy the enthalpic fictive temperature in thin film metallic glasses because of the presence of crystallization close to the glass transition.
Two reports in 2013 [50, 51] were the first observation of ultrastability in metallic glasses and since then many others have been published, most of them within the Zr-based family [35, 52,53,54,55,56,57,58,59]. Aji et al. reported ultrahigh stability in a multicomponent metallic alloy of composition Zr55Cu30Ni5Al10 (at %) [50]. They vapor-deposited the material using magnetron sputtering with a single sputtering target at a substrate temperature of 0.8 Tg (573 K) and a growth rate of 0.2 nm/s. The calorimetric curves of the vapor-deposited film showed an increase of the onset temperature of devitrification by 51 K with respect to the liquid-quenched glass of the same composition measured on heating at 10 K/min, ∆Ton = 7.1%, as shown in Fig. 6A. The crystallization temperature (Tx) also increased by 207 K. In addition, the hardness and elastic modulus were also improved by ~ 30% with respect to the bulk metallic glass.
DSC scans at heating rate of 20 K/min of Zr55Cu30Ni5Al10 glass samples: (a) bulk glass produced by copper-mold-casting (black); ultrastable glass produced by RF sputtering deposited at 573 K (green); bulk glass annealed at 683 K for 60 (red) and 360 min (blue). (b) Enthalpy of Zr55Cu30Ni5Al10 glass samples derived by integrating the curves shown in (a). Reprinted with permission from Aji et al. [50]
The thermodynamic stability in metallic glasses is difficult to quantify from calorimetric data since crystallization frequently occurs not far from the glass transition temperature, although these authors reported an apparent decrease of the fictive temperature in the stable glass (Fig. 6b). In parallel with the previous work, Yu et al. [51] reported ultrastability in the ternary Zr65Cu27.5Al7.5 glass vapor-deposited at 0.8 Tg (Tg = 676 K) using a higher growth rate of 1.4 nm/s. The as-grown glass had an 11 K increase in Ton (∆Ton = 1.6%), but an enthalpy higher than the liquid-cooled or annealed glasses. Another option to quantify stability is using the relaxation time. Ruta et al. [52] used X-ray photon correlation spectroscopy on Cu50Zr50 thin film MGs prepared by magnetron sputtering at different conditions to find that glasses prepared at 0.89Tg have higher structural relaxation times than fast quenched MGs, a factor 2–3 slower. Moreover, when taken to temperatures close to Tg, this vapor deposited MGs relax into a less stable configuration, with a higher relaxation time, in a similar way to hyperaged geological amber when taken to temperatures above its Tf [51].
In general, as it occurs in organic glasses, the deposition temperature and the growth rate are very influential parameters to obtain stable metallic glasses. However, some reports also point out that the specific technique used for deposition can also have a significant impact on the growth conditions to achieve high stability [55]. In fact, while most thin film ultrastable MGs are grown by magnetron sputtering in the temperature window between 0.7 and 0.85 Tg, some other approaches have shown the feasibility to obtain stable glasses at even lower temperatures. Ion beam assisted deposition (IBAD) has been used by Bai and coworkers [56] to obtain stable glassy materials of CuZr (Cu50Zr50) using very low deposition rates (down to 0.06 nm/s) at room temperature. Although these materials do not show a well-defined devitrification process in calorimetry scans, the increase of the crystallization temperature and the enhancement of the mechanical properties suggest that they are in a more stable state compared to liquid-quenched MGs. Very recently, the work of Luo et al. [35] has challenged the view that ultrastable vapor-deposited glasses need to be grown at temperatures in the vicinity of 0.8–0.85 Tg. By using ion beam assisted deposition (IBAD) and reducing the growth rate to 0.017 nm/s these authors demonstrate ultrastability in a Zr-based (Zr46Cu46Al8 (at.%)) MG at deposition temperatures as low as 0.43 Tg, (Fig. 7). As a cautionary note, in the technique used by this group the ions were used to sputter the atoms from the target to the surface of the substrate. This is in contrast to what is commonly referred to as IBAD, in which ions are used to bombard the substrate surface during deposition with the aim to increase the density of the thin films or to enhance adhesion [60]. The onset of devitrification of the vapor-deposited ultrastable glass increases by ∼60 K (∆Ton = 8.5%) and displays a better glass forming ability that the liquid-quenched glass. They also report and enhancement of Tx, so higher annealing temperatures are necessary to initiate crystallization. Remarkably, the crystalline phases obtained by annealing this Zr-based vapor-deposited ultrastable glass are different from the ones obtained by annealing a conventional MG. That may be due to different local atomic arrangements in both materials. Analogous conclusions are reached in the work of Ferry and coworkers [55] who observed an increase in the onset temperature of devitrification by ∼ 70–75 K (∆Ton = 10.5%) compared to bulk MGs by reducing the deposition rate a factor of 50 from ∼ 4 nm/s to ∼ 0.08 nm/s at 0.43 Tg for glasses of Zr50Cu44.5Al5.5 and Zr50Cu41.5Al5.5Mo3. Interestingly, using magnetron sputtering they achieved similar degree of kinetic stability than the work of Luo et al. [35] but with 10 times faster growth rates (∼ 0.17 nm/s versus ∼ 0.017 nm/s), which illustrates that the impact of the growth rate on glass stability may depend on the specificities of the technique used for deposition, among them on the energetics of the atomic species when they reach the substrate surface. These works [35, 54] clearly exemplify the influence of the deposition rate in attaining very high stability at a given deposition temperature. There is a minimum growth rate (whose value depends on Tsub for each deposition technique) beyond which no further enhancement of stability is achieved. Figure 7 illustrates the impact of reducing the growth rate on enhancing Tx. The role of oxygen or other impurities at this very low growth rates (or at higher temperatures) should be properly addressed, as their presence may substantially impact the physic-chemical and mechanical properties of the glass. It is remarkable that the influence of the growth rate on the degree of stability is much stronger in metallic glasses than in the case of organic molecules. As an example, Luo et al. achieved a variation of onset temperature with respect to Tg (ΔTon/Tg) of 7.1% over one order of magnitude change of growth rate between 1 and 10 nm/min, while in the case of the organic semiconductor TPD, Kearns et al. reached a lower ΔTon/Tg of 3% over more than two orders of magnitude variation in growth rate, from 0.3 to 70 nm/s [61]. This difference could be related to the fragility of the glass-forming systems [62]. A recent work by Muley et al. [62] investigated the stability, mechanical properties and structure of vapor-deposited glasses of Zr65Cu27.5Al7.5 with the same composition as those reported previously by Yu et al. [51]. While the general features of both studies are similar, the most stable glasses of Muley’s work were achieved at different conditions and with a different degree of stability compared to Yu’s work. And, in fact, growing above 0.707 Ton and at any deposition rate, the samples in Muley’s work were crystalline while in that by Yu et al. were amorphous. This points to the influence of uncontrolled processing parameters that may play a significant role in the properties of the material. Interestingly, the icosahedral order in these CuZrAl MG seems to improve for the kinetically more stable glasses grown at the slowest deposition rates. This in agreement with the earlier report by Aji et al. [50] in which atomic ordering analysis revealed that the stable MG had a higher medium range order (MRO) compared to liquid-cooled or annealed glasses. The changes in MRO may originate from enhanced surface mobility during vapor deposition at temperatures close to Tg that enable atoms to find more energetically favorable positions.
a Representative DSC curves at a heating rate of 20 K min−1 for Zr46Cu46Al8 MGs grown by IBAD technique. Ordinary glass produced by melt-spinning technique; vapor-deposited glass films produced at different growth rates as denoted below each curve. Tg and Tx are defined from the onset of the transformation as indicated by the intersection of the black lines. b Tg vs. deposition rate. For comparison, the Tg and Tx with their variation ranges for the ordinary glass are presented by the shaded magenta areas. Reprinted with permission from Luo et al., Nat Comm. 9, 1389 (2018) [35]
We also note on the existence of conflicting results in which increased deposition temperature produced metallic glasses with enhanced density and mechanical properties but with lower thermal stability, i.e. lower temperatures of crystallization. This was the case for MG of composition ≈ Zr60Cu8Ni25Al4Hf1Ti2[63]. Chu et al. observed no modification of the thermal stability (Tg = 400 °C and Tx = 500 °C) in sputter-deposited Zr51.4Cu29.5Ni12.3Al6.8 thin film metallic glasses prepared at different temperatures ranging from RT to 400 °C [59]. On the contrary, hardness and elastic modulus increased by 30% and 20%, respectively, in films grown at 400 °C with respect to those grown at room temperature.
The enhancement in mechanical properties is a common feature of most vapor-deposited metallic glasses and some authors consider them ultrastable because of this improvement [53]. Gianola and coworkers [64] investigated the mechanical properties of Pd77.5Cu6Si16.5 MG by nanoindentation. Maximum values of hardness were achieved in samples grown at 0.73Tg with values 33% higher (hardness = 9.7 GPa) than for the glass grown at room temperature (0.52Tg, hardness = 7.3 GPa). At this temperature shear banding was also enhanced in the more stable MGs. Dziuba et al. [53] related the enhanced mechanical properties of a Cu50Zr50 ultrastable glass to a low position in the potential energy landscape. Following this trend, Muley et al. [62] used a relation already established [65] to relate deformation energy and fictive temperature to quantify the improvement in thermodynamic stability of their vapor deposited glasses. Nevertheless, some vapor deposited metallic glasses show the opposite behavior, an improvement of the mechanical properties together with an apparent decrease of thermodynamic stability [51]. This uncorrelation could be a signature that in metallic glasses other parameters, such as local structure, should be considered to get the full picture when considering the characteristics of vapor deposited glasses.
A different approach towards ultrastability was adopted by Bai et al. [66] using high pressure in a PdNiCuP (Pd40.16Ni9.64Cu30.12P20.08) MG. Interestingly, they found that those glasses, after being held at approximately 15 GPa for 1 h, exhibit similar properties to vapor-deposited metallic glasses (at least to those reported previously by Luo et al. [35] and somehow to those reported by Aji et al. [50]), namely higher Tg by 8–11 K, higher density by up to 1%, higher hardness by up to 8%, higher glass forming ability (GFA: ΔT = Tx − Tg) up to 10 K at 18 GPa. Similar to Samwer’s glasses [51] these pressurized glasses do not have low enthalpy. They are located up in the potential energy landscape (PEL), but with high barriers (higher Tg) indicating that a lot of energy is needed to take them out from the energy minima where they are located. In the same manuscript they also reported that pressure induces changes in the local atomic order with respect to ‘normal’ liquid-quenched glasses. The effect of pressure-induced structural changes has also been explored in organic glass formers. Rams-Baron et al. showed that a liquid-cooled glass of etoricoxib formed at high pressure exhibited, when measured at ambient pressure, an increased devitrification temperature and higher density [67]. On the other hand, Rodriguez-Tinoco et al. investigated the effect of pressure on IMC glasses, both vapor-deposited and rejuvenated. Both exhibited an increase on the onset of devitrification with increasing pressure, though at a different pace. However, the rejuvenated glass submitted to high pressure and subsequently depressurized exhibited the same devitrification temperature that a glass formed at ambient temperature [68].
1.3 Polymer glasses
While there are many examples of reported ultrastable organic glasses made out from small molecules, the production of ultrastable polymers from the vapor is far more problematic. Because of the strong intermolecular forces between polymer chains, the polymer can thermally degrade rather than vaporize, manifested in some cases as a reduction of molecular weight or decomposition of some components [69]. Despite this difficulty, there are a few works reporting on the production of ultrastable polymer glasses from the vapor-phase, though most of them cannot be considered exactly equivalent to the physical vapor deposition, PVD, of molecular glasses.
Yoon et al. [70] described the preparation of vapor-deposited ultrastable polymer glasses of Teflon AF 1600, known to have weak molecular interactions and a low dielectric constant, by vacuum pyrolysis technique, i.e., pyrolysis of the target material and subsequent repolymerization on the substrate. Because of the pyrolysis process, they observe some chain scission, but they argue that the resulting thin film is still polymeric with an equivalent chemical state as the precursor. By tuning the substrate temperature during the deposition, they obtained glasses exhibiting large enthalpy overshoots and higher devitrification temperatures upon heating in a Flash DSC®. Glasses deposited at around 0.85Tg exhibit the largest devitrification temperatures but an increase in fictive temperature of 14% with respect to the rejuvenated glass, obtained by slowly cooling from the supercooled liquid.
With the aim of fully avoiding changes in the polymer nature, Guo et al. used matrix assisted pulsed laser deposition (MAPLE) to prepare thin films of PMMA glasses [71]. As opposed to other evaporation routes, MAPLE provides a gentle and non-destructive means for the deposition of polymer films. By controlling the substrate temperature during deposition and setting a growth rate of 0.25 nm/s, they were able to form glassy polymer films with higher devitrification temperature, up to 40 K, and lower specific heat (a reduction of up to 20%), with respect to ordinary glasses prepared from the melt. Furthermore, the kinetic stability in the glassy state (transformation time at Tg) could be enhanced by two orders of magnitude. However, contrary to stable organic molecular glasses, which show an increase in density and a lower enthalpy, the stable polymer glasses exhibited a reduction in density of 40% (glass grown at 0.86Tg) and a higher enthalpy (up to 60 J/g higher for Tsub = 0.84Tg). The calculated Tf for these glasses was up to 24% higher. According to the authors, the origin of this unique combination of properties was related to the growth mechanism, different to the surface facilitation mechanism responsible for the formation of stable vapor deposited glasses of small molecules. In MAPLE, film formation proceeds by the assembly of nearly spherical polymer nano-globules. According to the authors, solvent evaporation of the globules in their path from the target to the substrate induce their collapse into stable globules. In parallel, limiting coalescence of each of these globules would result in a poorly packed structure. The combination of the two phenomena would give rise to a glass with higher devitrification temperature (due to the stability of the globules) but with lower overall density (due to limited coalescence).
A simpler approach, but reliable in the sense that the structure of the material is preserved, and similar to those of small-molecular glasses, was followed by Forrest and co-workers [72]. To obtain appreciable deposition rates at temperatures below those at which thermal degradation occurs, they used near-oligomeric (N ≃ 6–12) polystyrene and polymethyl methacrylate. By characterizing the properties of the resulting thin layer by ellipsometry, they found an increase in devitrification temperature of 6%, as well as an increase in density of about 1.6% and 25 K decrease in limiting fictive temperature, for layers deposited at 0.89 Tg. It should be noted that the Tg of the material is affected by the deposition conditions, since the molecular weight of the material changes due to temperature changes or time after the deposition has started (the smaller oligomers are evaporated first and then the largest ones). These glasses exhibit an (extrapolated) transformation time of up to 3 million years.
A very different kind of highly stable polymer glass, not prepared from the vapor phase but by chemical vitrification, is that of geological glasses such as amber. Amber is a fossilized tree resin which has undergone a maturation and stabilization process for tens or even hundreds of millions of years. This is another route to go very deep in the PEL (Fig. 3), which will be described more in detail in Sect. 4 in the framework of low-temperature properties of ultrastable glasses. Another potential route to stabilization has been demonstrated by aging below Tg ultrathin polymer films and spherical nanoparticles [73, 74].
1.4 Chalcogenide glasses
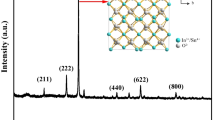
Amorphous chalcogenides are useful for applications ranging from phase change memory materials for random access memory applications to photovoltaics. Zhang et al. have prepared thin film glasses of Sb2Se3 by vapor deposition in the temperature window where glass stability could be present [75]. Although they could not clearly identify the glass transition signature by DSC, they report an enhanced crystallization temperature, lower surface roughness and high refractive index for glasses grown at 373 K as an indication of enhanced thermal (kinetic) stability of the material. In particular, the crystallization temperature increased by 17 K with respect to a glass grown at room temperature. Interestingly, this work reports a distinct (and surprisingly smaller) coordination number for the stable glass with respect to the ordinary amorphous material, but close, at the same time, to the one of the crystal. Stable glasses are also less dense, implying that there is not always a direct correlation between stability and density. In the case of chalcogenides, this could be due to the large number of intramolecular interactions, which can result in strong repulsive forces in a dense molecular packing.
Amorphous selenium has also been grown as a thin film from the vapor in the range of temperatures and growth rates that could lead to high stability [41]. In addition, since a-Se is very sensitive to above-band gap visible light, white illumination was used during growth to investigate the effect of this parameter. Glasses grown in the dark and under white-light illumination showed signs of high stability, both in terms of kinetic and thermodynamic stability, an indirect indication that the surface mobility is enhanced compared to the bulk dynamics. However, films prepared under white light exhibited lower density, but higher kinetic stability (higher onset of devitrification) when directly compared to films grown in the dark, providing access to a different local minimum on the potential energy landscape, not accessible by any other means. Apparently, light would induce the formation of a chain structure that lowers density but increases kinetic stability due to the difficulty of breaking these extra bonds. Since the formation of these networks is induced by light, it is exclusively a surface effect and therefore, the propagation of these networks throughout the film is only achievable because of the illumination of the sample during the PVD deposition. As happened with the stable chalcogenide glass and some metallic glasses, amorphous selenium shows that density (or thermodynamic stability) does not necessarily correlate always with kinetic stability.
2 Mechanism of formation of low enthalpy glasses by vapor deposition
A priori, one would think that molecules landing onto the substrate during vapor deposition would be submitted to extremely fast cooling rates, from the high temperatures at which they are ejected from the source (typically around the Tm of the material) to the low temperatures of the substrate (around or below Tg). Consequently, without invoking any equilibration mechanism, glasses produced by PVD should vitrify at higher temperatures due to the arrest of the structural relaxation and, therefore, would be less stable (lower density) than those prepared by controlled cooling from the melt. This intuitive description does not match with reality, it is just the opposite, since highly stable glasses are nowadays routinely produced in this way [1]. Therefore, a particular molecular mechanism that allows equilibration of the molecules during the deposition process must exist and, in fact, decreasing the growth rate at a fixed substrate temperature leads to more equilibrated glasses [25, 35, 61]. In the following we describe several alternative views that may explain the enhanced stability of vapor-deposited organic glasses, though this subject is still under intense investigation. Although this section mainly deals with molecular glasses where most of the research has been done, several very recent works on metallic glasses are also included.
2.1 Is surface diffusion responsible for ultrastable glass formation?
Surface diffusion seems to be a relevant quantity and only recently sensitive approaches have been devised to infer its value over extended temperature intervals. Enhanced molecular diffusion at the surface is responsible for fast surface crystal growth in many organic glasses as crystal growth rate is nearly proportional to the surface diffusion coefficient, Ds [130]. One way to measure surface diffusion is by the embossing of surface gratings onto glassy surfaces and subsequent measurement by diffraction of the decay of the grating pattern [89, 131]. Surface diffusion can also be accessed by measuring the evolution of the response when a probe is placed on the surface, inducing the formation of a meniscus due to surface-mediated flow. Fakhraai and coworkers, for instance, used the tobacco mosaic virus to investigate surface diffusion in molecular glasses of TPD [100, 122]. In general, measured Ds values on organic glasses range from 10–11 to 10–16 m2/s at Tg, 4 to 8 orders of magnitude larger than the bulk counterpart, as shown in Fig. 8 [89, 100].

Copyright 2017 American Chemical Society. TPD data obtained from [100]
This eightfold enhancement of surface diffusion with respect to bulk diffusion [131] allows to circumvent the restrictions to molecular rearrangement imposed by the slow bulk dynamics. Indeed, at the surface layer, molecules exhibit diffusion levels that allow them to reach stable packing arrangements in timescales comparable to the residence time of these molecules on the surface. This time is determined by the growth rate. For a given deposition rate g, the mobile surface layer of depth ξ will be equilibrated on a time scale ξ/g. If the surface layer is considered to have 1 nm and the growth rate is 0.1 nm/s, then the residence time of each molecule is 10 s. If surface diffusion is high enough, the residence time may be enough for the molecules to efficiently sample the energy landscape and find close to equilibrium configurations before being buried by other incoming molecules. Surface diffusion typically follows an Arrhenius dependence with temperature with activation energies around 100 kJ/mol (Table I and Fig. 8). This behavior is in contrast to bulk diffusion, which follows a super-Arrhenius dependence with temperature, inducing a more abrupt kinetic arrest as temperature is decreased.
The relevance of surface diffusion as an indicator of the formation of stable glasses has been analyzed in detail in several reports involving organic molecules with different degrees of hydrogen bonding (HB) and/or variations of molecular size [131]. HB reduces surface diffusion due to their robustness at surface layers, which makes the barrier for diffusion approximately the same on the surface as in the bulk. As an example, the surface diffusion coefficient of o-terphenyl (OTP), a non HB-molecule, and sorbitol (HB molecule), two molecules with similar sizes, differ by 105 at Tg [132]. In the same reasoning line, it was shown that molecules forming extensive intermolecular HB, such as polyalcohols, produced glasses of lower kinetic stability compared to non-hydrogen-bonding molecules at the same deposition rate [88, 91, 93, 132].
Molecular size also plays a role in surface diffusion. In non-HB molecules, such as OTP, TNB or IMC, it has been shown a decrease in surface diffusion as the size of the molecules increases (five orders of magnitude increase of DS per decreasing 1 nm in size, as seen in Fig. 9a) [133, 134]. This behavior is attributed to a steep gradient of mobility beyond the free surface and the penetration of large molecules into areas with lower mobility. This anchoring effect leads to slower diffusion of the hole molecule (understanding the movement of the molecule as the movement of its center-of-mass) even though the top part of the molecule is in a more mobile environment [135].
Representation of a measured surface diffusion values and b transformation time (as a measurement of kinetic stability of the vapor deposited glass) with respect to the size of the molecule. Symbols with the text “ub” indicate the upper bound for the surface diffusion in these materials. The left figure shows a good correlation of the surface diffusion in non-HB systems within an extended range of molecular sizes, d. Reprinted with permission from Yinshan Chen et al., J. Chem. Phys. 150, 024,502 (2019), AIP publishing [131]
While the decrease of glass stability correlates well with the increase of hydrogen bonding and the reduction of surface diffusion, glass stability seems to be less affected by molecular size, at least for d < 1 nm, as seen in Fig. 9b. A possible explanation for this uncorrelation is that stable glass formation does not show a simple relationship with the translational molecular motion due to surface diffusion. Since glass stabilization relies on the improvement of local packing arrangement, other processes involving a reduced amount of translational movement may be responsible for the high stability attained during growth [131].
The influence of other mechanisms beyond surface diffusion on the stability of the glass is illustrated in the experimental work of Samanta et al. [122] They analyzed ultrastable glass formation of two molecular glass formers, TNB and 9-(3,5-di(naphthalen-1-yl)phenyl)anthracene (α,α-A), with very different values of surface diffusion. While TNB exhibits measurable enhanced surface diffusion compared to bulk, α,α-A does not, due to pairing or aggregation of anthracenyl substituents on the free surface. Remarkably, they observe that both systems can be prepared in similar stability states. Moreover, they infer enhanced dynamics by dewetting experiments. Their conclusion is clear: enhanced surface diffusion is not a requisite for enhanced dynamics and, hence, for the formation of highly stable glasses by PVD [122]. The decoupling between DS and τs (surface relaxation time) has also been observed in polymers, where surface diffusion is avoided by the large degree of entanglement between polymeric chains. Notwithstanding, enhanced surface relaxation time has been measured [136, 137]. All these observations point towards a complex scenario, where surface equilibration to reach ultrastability cannot be explained by surface diffusion alone.
2.2 Surface relaxation
As discussed above, the crucial factor that seems to allow the formation of ultrastable glasses is a surface equilibration mechanism that operates fast enough to enable the equilibration of molecules in timescales comparable to the residence time of the adsorbed molecules before they are buried by other molecules during growth. A process that may not be related to translational molecular movements, but to a local relaxation mechanism, thus decoupling surface diffusion and mobility. In the previously mentioned experiment, Samanta et al. investigated thin film dynamics (10 nm) of TNB and α,α-A by measuring the dewetting dynamics as a proxy to surface relaxation time [122]. As-deposited thin films showed evidence of dewetting on a silicon substrate, even at a Tsub which yielded stable glasses, an indication of a reduced relaxation time at the surface. This is not the only evidence of fast dynamics at the surface. Very recently, fast surface dynamics has been directly probed by Thoms et al. [138] through the recording of the dielectric relaxation spectra during film growth of a molecular glass former (2-methyltetrahydrofuran, MTHF) at Tsub = 0.82 Tg and at g = 0.2 nm/s onto interdigitated electrodes (IDE). This work provides direct evidence of the existence of a mobile surface layer, 2.5 nm thick, with an average relaxation time of 0.1 s, orders of magnitude faster than the bulk, that grows with a high kinetic stability. Higher deposition rates, to the point that the residence time of the molecules at the surface is below \({\tau }_{\mathrm{s}}\), may result in films with lower stability because equilibration is restricted.
It is often argued that the structural relaxation of a free-standing thin-layer or a supported ultrathin layer speeds-up. However, there is a strong debate on that topic, extensively studied in polymers, mainly due to the sensitivity of the dynamics to many factors, especially the sample boundary conditions [136, 139]. In the limit of a monolayer, the structural relaxation time of this nanoconfined layer would correspond to the surface dynamics that controls the stability of a glass growing from the vapor. In this sense, Zhang et al. using dewetting as a proxy for relaxation time for TPD thin layers, observed that, as the thickness decreases, molecular motion speeds up [140]. Interestingly, in a subsequent work, Zhang [141] compared the evolution of these relaxation times with that of the surface diffusion. They observed that, by reducing the thickness, the later stays invariant while the former increases, supporting the uncorrelation between surface mobility and diffusion, discussed above.
The role of surfaces on the relaxation dynamics of a structure, and how the cooperative structural relaxation speeds up at the free interface, is explained in a simple way by the random first-order transition theory (RFOT). In this framework, the vitrification of glasses is due to the cage effect, i.e., the constraining of a particle because it is surrounded by its neighbors. In mean field theory this leads to a friction crisis at the mode coupling theory (MCT) critical temperature (TC), below which any large-scale motions require cooperativity and the definition of a cooperative length-scale. Since surface particles feel a weaker structural cage, they would undergo dynamic arrest at a lower temperature and remain more mobile below the bulk glass transition temperature [142]. Under this framework, hence, the acceleration of the surface relaxation is related to the effect of free surfaces on the bulk relaxation process, and this surface relaxation time can be expressed as \({\tau }_{\mathrm{s}}\propto \sqrt{{\tau }_{\mathrm{bulk}}}\).
Some molecular dynamics simulations have also pointed in a similar direction. Kuon et al. [143] investigated the emerging heterogeneous dynamics at the surface of a supported supercooled liquid film in comparison with the dynamics of a bulk-like region of the film. The dynamics at the surface turns out to be almost three orders of magnitude faster than the dynamics within the bulk. Note that the reported difference in surface and bulk dynamics is much lower than the experimentally determined difference in diffusion coefficients (up to 8 orders of magnitude). In another work, Berthier and co-workers were able to computationally reproduce a vapor deposited glass, equilibrated at low temperatures, by using a swap Monte Carlo algorithm [144]. This study provides a quantitative test of the role of surface mobility in the creation of vapor deposited glasses. From the decay of a self-intermediate scattering function, they extract the relaxation times of the different particles of the simulated system. At high temperature there is a population of fast particles across all the sample, but at low temperature fast particles are concentrated on the surface of the material. The surface relaxation time follows a super-Arrhenius dependence with temperature, like the one followed by bulk dynamics, but with lower values and lower divergence temperature (see Fig. 10). They argue that this faster surface relaxation process is at the origin of the ultrastability of vapor deposited glasses and conclude that the surface relaxation time and deposition rate determine the distance to equilibrium for vapor-deposited films in the exact same way that bulk relaxation time and cooling rate control the distance from equilibrium for liquid-cooled films.

copyright 2017 American Physical Society [144]
Examples of the variation of bulk and surface structural relaxation processes as a function of the inverse of the temperature. In a, the overall relaxation time in two different simulations (constant volume (NVT, canonical ensemble) and constant pressure (NPT, Isothermal–isobaric ensemble)) is represented together with the bulk and surface contributions. In b, the surface relaxation time is fitted in a short temperature range with an Arrhenius curve. The bulk relaxation time is fitted, in all cases, with a VFT curve. Reprinted with permission from (a) J. Chem. Phys. 149, 074501 (2018), AIP publishing [143] and (b) Phys. Rev. Lett. 119, 188002 (2017),
When discussing about any property “at the surface”, it is fundamental to consider the length scale across which this property propagates into the bulk. By measuring the relaxation dynamics of thin glassy TNB and α,α-A films, Samanta et al. concluded that while the bulk of the glass is in a deeply quenched glassy state, the molecules within 10 nm from the surface can have a faster dynamics and are able to equilibrate before becoming part of the bulk [122]. Similar conclusions are obtained by More et al. [145]. They used molecular dynamics simulations to study empirical coarse-grained models of organic molecules containing model fluorocarbon tails of increasing length: zero, one, four, and eight fluorocarbons, with a structure composed of a phenyl “body” and a fluorocarbon “tail”, to simulate the formation of a vapor deposited glass. They observe that longer molecules tend to become trapped locally during deposition reaching less optimized packing. They also observe that films show a tail-enriched surface due to the migration of tails towards the surface. Very interestingly, this tail enrichment is progressively erased during deposition, i.e., during growth, the film reconfigures towards a more homogeneous structure. This means that the more mobile surface layer extends beyond the length of the molecule. They conclude that significant rearrangement could occur in layers below the immediate free surface, even for molecules that do not show significantly enhanced surface diffusion (molecules with long tails). Early evidence for enhanced mobility below the surface, based on the breadth of the interfaces determined by neutron scattering, was already presented by Swallen et al. in 2007 [1]. In the same direction, Wolynes stated that the enhanced mobility of the surface would penetrate the bulk at least on the cooperative length-scale, of few intermolecular spaces. This intense mobility gradient is relaxed, diffusing the excess mobility towards the bulk. At the end, the distance the excess mobility penetrates is calculated as 20 times the correlation length, i.e., 20 nm for Indomethacin, one of the most studied ultrastable glasses, an amount significantly larger than “just the surface” [142].
2.3 Ultrastability and fragility
There have been several attempts to correlate glass stability and fragility with distinct and uncertain success. Here we briefly outline some of the most relevant works. If the enhanced surface mobility is a consequence of a different molecular arrangement around the molecules at the surface with respect to the more crowded environment in the bulk, as proposed by most of the above-mentioned interpretations, it is reasonable to think that the fragility of the glass-former may play a role on ultrastable glass formation. As described in Sect. 1, the fragility is defined as the degree to which the relaxation time increases when approaching Tg and is often considered as a deviation of the Arrhenius dependence between relaxation time and temperature [12]. Several works have shown a moderate positive correlation between fragility and ultrastability. Yu and Samwer [51] reported a mild correlation between the onset temperature of the transformation of vapor-deposited organic and metallic glasses (Ton) and the kinetic fragility index m of the corresponding supercooled liquid. Tylinski et al. [93] thoroughly analyzed the potential role of fragility in the formation of ultrastable glasses by considering additional measures of fragility and increasing the number of explored systems. As an indicator of the stability achieved for each material, they use the transformation time needed to transform the glass into the supercooled liquid at a temperature above Tg. By analyzing data corresponding to 14 systems, they observe a slight positive correlation between fragility and the transformation time. The correlation is especially good when using log(τα) at 1.25Tg as proxy for fragility. It is noted that log(η) (an equivalent parameter to log(τ)) was previously successfully correlated with the surface diffusion [132], Fig. 11. There are several empirical arguments to support the positive correlation between stability and fragility. Chen and co-workers argue that the loss of neighbors at the surface can be compared to an “excitation”, similar to a temperature increase [132]. Since strong systems follow an Arrhenius behavior, energy barriers do not increase significantly upon cooling and one might think that strong systems are “easier” to equilibrate even by cooling from the liquid and, therefore, also by vapor deposition. The advantage of fast surface dynamics would not provide then any significant enhancement. In other words, fragile glass-forming liquids should lead to highly stable vapor-deposited glasses and stronger liquids may fail to reach high stability in the glassy state [93, 146]. This view was supported by early experiments on molecular [147] and metallic glasses [51], but contradicts more recent data on organic (methyl-m-toluate and ethylcyclohexane) and metallic glasses (ZrCuAl family) with strong character that have been grown as highly stable glasses [51, 94] (see Table 1 for values of m and associated indicators of stability). Therefore, there are also arguments and experimental data to justify the opposite conclusion. Larger fragilities, i.e., more abrupt slowing down of structural relaxation dynamics upon cooling, is related to larger cooperative rearranging regions: since more molecules should cooperatively relax to reach equilibrium, the process becomes slower. Therefore, one would assume that, if more fragile materials indeed have longer co-operative length scales, the size of cooperatively rearranging regions might grow sufficiently, so the ability to relax via the surface, crucial for ultrastable glasses, would be lost. Conversely, for strong glass formers, with small co-operative length scales, the ability of the surface to enable relaxation may be retained at much deeper supercooling. Royall and co-workers tested this hypothesis by plotting the parameter θ0 = (Teq − T0)/(Tg − T0), with respect to the inverse fragility D found after Vogel–Fulcher–Tammann fitting of the liquid by equation \({\tau }_{\alpha }={\tau }_{0}\times \mathrm{exp}\left(\frac{D{T}_{0}}{T-{T}_{0}}\right)\) [148]. T0 is the Vogel–Fulcher–Tammann divergence temperature and Teq is equivalent to Tf. They observe a negative correlation between both parameters, indicating that stronger glass formers should yield more stable glasses (Fig. 11).
Relationship between thermodynamic stability and fragility for different glass-formers, following two alternative approaches. (Left) The transformation time of the ultrastable glass measured above Tg is used as a signature of the thermodynamic stability (longer transformation times are related to higher stability), while the value of the structural relaxation time of the corresponding supercooled liquid at 1.25Tg is used as a measurement of fragility (lower values of log(τ) imply larger fragility values, note the inverted horizontal axis). (Right) The stability parameter ϑ0 is used as a measurement of thermodynamic stability (lower ϑ0 means larger stability) while the parameter D obtained from the VFT fitting of log(τ) vs 1000/T is used as an indicator of fragility (larger D means lower fragility). Colors and symbols match in both figures and the legend. Reprinted with permission from Tylinski M et al., J Chem Phys 145, 174506 (2016), AIP publishing, and Royall CP et al., J Phys Condens Matter 30, 363001 (2018), IOP Science [93, 148].
The lack of clear correlation between fragility and ultrastable glass formation may undermine a direct connection between structural relaxation (and its faster counterpart at the surface) and ultrastable glass formation. In this direction, Mangalara et al. proposed a new model [149] based on the well-known mismatch between variations in structural relaxation time (and, hence, Tg) and density near free surfaces: while the former is affected along a length scale of 10 nm, gradients in density exhibit much shorter length scales, of about 1 nm [150]. In their model, they introduce an intermediate layer in the growing glass with mixed properties: it exhibits bulk like liquid density (like in the inner layers of the glass) and nearly suppressed Tg (like in the very surface layer), i.e., with decoupled density and structural relaxation. Because of the lower Tg, vitrification of the intermediate layer occurs at lower temperature, allowing the formation of a lower enthalpy glass. A similar conclusion is reached by Sussman and co-workers in a molecular dynamics study of thin film glasses [151]. In that work, the authors invoked the concept of softness, related to local structure around a particle, to decouple changes in local structure to changes in dynamics at different points of a thin film. In bulk, there is a direct connection between the local structural environment of a particle and its easiness to rearrange [152, 153], however, near free surfaces, relaxation is dominated by mechanisms that are independent of the local structure. In other words, the faster equilibration process that brings to the formation of an ultrastable glass may not be uniquely linked to the change in local structure at the very surface. And they go further in their interpretation of the simulation results: the relaxation dynamics in glassy thin films is characterized by two independent processes, one that depends on local structure, active at the surface of the film, and another one that is purely Arrhenius and depends on the position in the film but not on local structure.
2.4 Alternative explanations for enhanced surface mobility
Different authors have explored the hypothesis that fast surface mobility is a consequence of the change in structure at the surface layer and have proposed alternative ideas to explain the formation of stable glasses by vapor deposition. We briefly summarize some of them: Ngai and coworkers, in the frame of the Ngai’s coupling model, relate surface diffusion to the secondary Johari-Goldstein (JG) relaxation found in many glass formers [154]. In this context, JG-beta relaxation has been linked to the surface mobility in analogy to the role of structural relaxation in bulk dynamics. They have compared the range of deposition temperatures at which a physical vapor deposited glass exhibits enhanced stability in relation to the liquid quenched counterpart, with the temperature range where the JG-beta relaxation is allowed to relax during the experimental timescale (i.e., lower than 100 s) (see Fig. 12). The two ranges matched fairly, suggesting that the activity of the secondary mode was connected to the enhancement of stability observed in vapor deposited glasses.
Relaxation dynamics of supercooled celecoxib (top) and stability of the vapor-deposited glass measured through their onset of devitrification in heating scans (bottom). In the indicated temperature range, beta relaxation time is lower than 100 s, and the vapor deposited glass shows enhanced kinetic stability with respect to the ordinary glass. Reprinted with permission from K. L. Ngai et al., J. Phys. Chem. Lett. 8, 2739–2744 (2017) [154].
A related explanation involving the beta relaxation is also provided by Schick and co-workers to interpret their experimental data [94]. They explored the role of the growth rate in the formation of stable glasses of ethylcyclohexane at different substrate temperatures, to determine the time required to equilibrate the glass at that temperature, maximizing its kinetic stability. The equilibration time of vapor deposited glasses across a wide temperature range, spanning near 100 K below Tg, followed a much weaker temperature dependence than the structural relaxation. Their measure of equilibration time is within two orders of magnitude of the beta relaxation, even though the authors remark that the temperature dependence is not the same (Fig. 13), and they argue that the β process is just a speed limit for surface relaxation.
Timescales of different dynamic processes in ethylcyclohexane. Red stars correspond to the frequency dependence of dynamic glass transition temperatures from AC calorimetry. The required surface equilibration times (τsurface = 10 τKWW) at each substrate temperature are shown as solid blue triangles. Solid black squares and circles correspond to the α- and β-relaxations of ethylcyclohexane. T0 and TK are shown as a reference. Reprinted with permission from Y. Z. Chua et al., J. Chem. Phys. 142, 054506 (2015), AIP publishing [94]
Another hypothesis about the stabilization of vapor deposited glasses can be extracted from the recent study of aging in polymer systems performed by Cangialosi et al. [73, 155, 156]. Enthalpy recovery experiments of polymer thin films and spheres aged for different times and at different temperatures show the presence of a two-step enthalpy recovery with two different enthalpy plateaus that could be associated to two equilibration time scales. The faster one exhibits an activation energy significantly smaller than that of the structural relaxation process at Tg, whereas the slower time scale is compatible with the bulk structural relaxation. These observations are compatible with the theoretical predictions made by Sussman et al. [151]. According to their analysis, the relaxation dynamics in glassy thin films are characterized by two independent processes, one super Arrhenius that depends on local structure but remains unchanged regardless of the distance from the surface, and another one that is purely Arrhenius and depends on the distance from the surface but not on local structure [151]. Cangialosi and coworkers, using this fast relaxation process at free surfaces, dramatically reduce the time to equilibration in thin films of PS and small PtBS spheres reaching a near ideal glass state in experimentally accessible timescales, with Tf values down to 70–80 K below the Tg of the bulk material, close to the Kauzmann temperature [73, 74, 157]. These results are consistent with the accelerated aging observed by Sepulveda et al. on ultrathin films of liquid-cooled toluene glasses [158]. In these fast equilibration experiments, the existence of large surface/bulk ratios is fundamental. Indeed, models based on the diffusion of free volume holes [159] from the bulk to the surface have been used to explain the efficiency of nanosized systems to reach equilibrium. This fast equilibration mechanism would be responsible for the translation of these free volume holes to the surface. While it would be tempting to ascribe this first fast equilibration mechanism to the secondary relaxation, as discussed above, the real nature of that process is still unknown, even though Ngai has ascribed the nature of this fast equilibration mechanism in some polymers to the JG-β relaxation [160]. In a very recent work, Low et al. prepare vapor deposited ZrCuAl metallic glasses deposited below Tg at different growth rates to explore the effect of the surface residence time on stability and microstructure [161]. For all investigated rates, they obtain glasses with enhanced kinetic stability (as measured through Ton on heating). However, the microstructure of the fast-deposited MG exhibits a nanoscale compositional segregation more accentuated than in the conventional glass, while in the case of the slow-deposited glass, they observe a remarkable homogeneity. They attribute these differences to two different surface phenomena: at high rates, high-energy molecules diffuse on the surface developing this nanoscale heterogeneity, while at low deposition rates, long residence times allows for the removal of these heterogeneities and the growth of a homogeneous metallic glass. Whether these two mechanisms could be compared to the two equilibration mechanisms discussed in polymer systems is not clear. Importantly, in this picture, the authors incorporate an element often not considered in the context of organic glasses: the high kinetic energy of the atoms that land on the substrate.
2.5 Towards what state?
We have discussed about different alternative views to explain the mechanism responsible for the formation of ultrastable glasses from the vapor phase, but are these glasses equivalent to glasses produced by cooling from the melt, if sufficiently time would be provided to the liquid-cooled glass? As commented in Sect. 1, glasses grown below, but close to, Tg exhibit a value of Tf that closely matches Tsub if the growth rate is low enough. By decreasing the growth rate, one could virtually follow this equilibrium line down to the Kauzmann temperature, TK. This idea was explored by Beasley et al. who were able to obtain ethylbenzene glasses with Tf only 2 K above TK [25] (Fig. 14). The main uncertainty in this evaluation comes from the exact value of TK, which is prone to some considerations. The readers are recommended to consult references [22, 162] for more information on the evaluation of TK. Following this idea, one would expect that the lower the equilibration temperature, the higher the kinetic and thermodynamic stability of the glass if it has been equilibrated (since the enthalpy of the supercooled liquid continuously decreases with decreasing temperature).
Fictive temperature as a function of substrate temperature and deposition rate for vapor deposited ethylbenzene glasses. Values calculated from thickness change (red symbols), changes in index of refraction (teal symbols) and from enthalpy measurements (black squares). Glasses grown at the minimum growth rate follow the extrapolated equilibrium liquid line to within 2 K of TK. Gray solid lines are guides to the eye. Reprinted with permission from M. S. Beasley et al., J. Phys. Chem. Lett. 2019, 10, 4069–4075 [25].
However, the experiment of Chua et al. shows that the apparent equilibrium state reached by a vapor deposited glass grown at sufficiently low Tsub exhibits shorter transformation times that one grown at higher Tsub, i.e. with lower kinetic stability[94]. One could not discard, though, that this state may correspond to the first plateau of the two-steps equilibration mechanism discussed above and, in that case, further lowering the growth rate would allow to obtain glasses whose properties would match the ones expected from the equilibrium liquid.
As described in Sect. 2.4 systems with large free interfacial areas such as ultrathin films, free-standing ultrathin membranes or (micro)nanoparticles undergo a rapid reduction of the time scale to reach equilibrium. Using this approach, it has been shown that polymer microspheres (Tg = 415 K) can be equilibrated by mild aging at 260 K into the ideal glass state (Tf = 330 K) [73]. This state is characterized by a kink in the enthalpy, that the authors identify with a transition to the ideal glass. This highly aged glass shows no Boson peak (see also Sect. 4). Remarkably, these ‘highly-aged’ polymer glasses do not exhibit high kinetic stability, i.e. Ton does not increase with a reduction of Tf. A different behavior with respect to vapor-deposited ultrastable glasses.
Another ingredient that originates certain controversy to the similarity between liquid-cooled and vapor-deposited glasses is the existence of molecular anisotropy. At this point, it is fundamental to remark, as already briefly introduced in Sect. 1, that vapor deposited glasses often exhibit anisotropy in the molecular arrangement. Since the surface is highly anisotropic and surface equilibration is the mechanism of formation of vapor-deposited films, at least at temperatures close or below Tg, molecules in vapor-deposited thin film glasses are often arranged with different orientation patterns depending on the growth conditions. This is remarkably different to liquid-cooled glasses that are highly isotropic with a molecular structure equivalent to the liquid state. A very recent review [5] describes the influence of the surface equilibration mechanism on the molecular orientation. Anisotropic packing is therefore almost ubiquitous in vapor-deposited glasses [29, 43,44,45, 163]. This fact automatically poses the question whether vapor deposited glasses are equivalent to ordinary isotropic glasses prepared from the liquid, and if the equilibration state reached in this way, could lead to a true equilibrium state. Considerable progress has been made recently in understanding what controls the anisotropy of organic glasses prepared by vapor deposition. According to the current view, molecular anisotropy in vapor deposited glasses can be rationalized in the context of the discussed surface equilibration mechanism. But one extra ingredient is required: the molecular anisotropy at the surface of liquids in equilibrium, theoretically observed in computer simulations, and depicted in Fig. 15. While the bulk of the liquid is completely isotropic, on the very surface molecular layer, even though early work pointed to a universal pattern for rod-shaped molecules [29], a range of patterns have been observed in subsequent work, depending upon molecular shape and interactions [164].
(Left) Schematic showing the different molecular packing that can be found in the film as a function of thickness when changing the preparation conditions of the thin film organic glass (based on computer simulations). The lozenge shapes illustrate the orientation of a rod-molecule such as TPD. (Right) Order parameter, Sz, for glassy thin films of three organic molecules as a function of substrate temperature. According to the definition of Sz, a value of Sz = − 0.5 corresponds to a completely horizontal orientation of the molecules (parallel to the substrate), while Sz = 1 would be obtained when molecules are perpendicular to the substrate. Reprinted with permission from M.D. Ediger, J. Chem. Phys. 147, 210901 (2017), AIP Publishing; and M.D. Ediger et al., Acc. Chem. Res. 2019, 52, 407 − 414 (2019),
During deposition and depending on the time during which the landing molecule is sufficiently mobile (which depends, at least, on Tsub and growth rate), landing molecules will be able to equilibrate into one of these equilibrium arrangements. Therefore, at low Tsub, only the top layer equilibrates, and this leads to a glass in which horizontal orientation is trapped. At a higher Tsub, the top two layers manage to equilibrate during deposition; further deposition then leads to a glass in which vertical orientation is trapped [4]. As a result, it exhibits a particular value of molecular orientation, from glasses with molecules predominantly laying on the substrate to glasses where the molecules are, on average, with the axis perpendicular to the substrate (on-face vs on-edge, respectively) (Fig. 15).
In addition of the in-plane molecular orientation, some molecular layering has also been observed. While molecular orientation is often identified by X-Ray diffraction techniques from the relative intensity along the amorphous halo observed in organic glasses at 1.4 A−1 (distance between carbon atoms), molecular layering is identified from a peak in the diffraction pattern at shorter wavevectors. Contrary to the molecular orientation, which deviates from the ordinary isotropic arrangement almost across the whole deposition temperature range, molecular layering is only observed relatively close (and below) Tg, with a maximum around 0.85Tg [88, 126, 165]. Interestingly, some vapor deposited glasses can exhibit molecular layering (diffraction peak related to molecular size) with negligible molecular orientation, such as Alq3. The origin of this molecular layering has also been ascribed to the equilibrium conformations at the surface layer in bulk liquids [16]. According to these observations, the nature of molecular orientation in vapor deposited glasses is linked to an equilibration process, which is intrinsically different to the one we may observe in glasses formed from the melt. It is natural to ask whether this equilibration process is the same as the mechanism responsible for fast enthalpy relaxation or if it is a different and independent molecular process. In fact, it is possible to produce ultrastable glasses in systems without intrinsic anisotropy, as has been demonstrated in metallic glasses and in some organic glasses. Vapor-deposited glasses of a spherical molecule such as tetrachloromethane that, in principle, are isotropic, exhibit high kinetic stability (high-onset temperatures) relative to the conventional liquid-cooled glass [90]. This is another evidence that molecular anisotropy is a feature of the vapor-deposition process in the organic materials but not required to achieve ultrastability. Also, Fakhraai and coworkers prepared ultrastable glasses from α,α-A, that retains nearly isotropic shape. Indeed, as measured by photoluminescence, they conclude that the vapor deposited glasses show no molecular orientation, while forming a highly stable glass [123]. However, to fully discard this hypothesis, one should be able to independently tune molecular orientation and enthalpy in glasses formed by physical vapor deposition. While more experimental data is needed to confirm this view, simulated vapor-deposited glasses made of hard spheres [166, 167] do show enhanced stability with similar structural order as in the liquid state. In a recent work on the liquid crystal itraconazole, Bishop and co-workers [33] investigated the effect of Tsub and growth rate on the structural anisotropy and the layering structure of the glass former and estimated the time required for surface molecules to reach the equilibrium state, shown in Fig. 16, in an analogous way as Schick and co-workers did to estimate the equilibration time of vapor deposited glasses of ethylcyclohexane in terms of transformation time [94]. A comparison between orientation (and layering) and enthalpy equilibration times would be very tempting to determine whether the same molecular mechanism is responsible for the two main characteristics of vapor deposited stable glasses. Unfortunately, up to the date, there is no available data for the two magnitudes in the same system. We note that, even though itraconazole is a liquid crystal and, contrary to other molecular glass formers, shows orientation already in the conventional state, the equilibration of the orientation with time could be used as a representation of the mechanism active on the surface layers of all vapor deposited organic glasses.
Relaxation map of itraconazole. Bulk processes are shown in grayscale (squares: structural relaxation, upward triangles: secondary relaxation, downward triangles: equilibration of orientation in bulk glasses). The timescale of surface order relaxation processes (orientation and layering) is shown in blue. The fit to the experimental data is also shown. The vertical dashed line indicates the standard Tg of Itraconazole. Reprinted with permission from C. Bishop et al., J. Phys. Chem. Lett., 10, 3536−3542 (2019), AIP publishing
It is also interesting to note the similitude in activation energies of the orientation equilibration time and the delta secondary relaxation measured in bulk itraconazole (see in Fig. 16, downward and upward triangles, respectively), attributed to reorientation of the molecules [168], indicating, as discussed previously for the enthalpy relaxation, that the molecular mechanism responsible for orientation does also exist in bulk material. In relation to that, a recent work by Cassidy et al. [169] shows the relaxation of the spontaneous polarization formed in vapor deposited films of cis-methyl formate during growth. They relate this relaxation time to the time taken before the first molecules begin to rotate away from a dipole-oriented conformation. At low temperatures, they observe the decay of the induced electric field after times much shorter than the timescale of structural reorganization related to diffusion. They relate the depolarization mechanism to a secondary relaxation, much faster than the structural relaxation.
As mentioned above, the origin of the molecular arrangement of vapor deposited glasses is the equilibrium configuration of the topmost liquid layers during glass formation. It is natural to think, hence, if the substrate may influence the molecular configuration, as it happens in crystal or polymer growth. Yokoyama et al. [44] claimed that the molecular structure of 100 nm glassy films deposited on different substrates (ITO, sapphire or fused silica) was different. A similar effect was observed by Yoshizaki et al. [170] measuring the polar order of 200 nm thin film glasses deposited on gold or aluminum. On the other hand, in a recent work by Bagchi et al. the authors measure the GIWAXS order parameter of thin glassy films of DSA-Ph with thicknesses ranging from 10 to 600 nm [171]. They observe that molecular orientation tends to be vanished when the thickness of the layer goes below 20 nm. The authors, supported by both experiments and simulations, conclude that a 3–8 nm isotropic layer is formed at the interface with the substrate, both for gold or native silicon oxide. The authors attribute the formation of such an isotropic layer to the interaction with the substrate. However, they mention, as a possible partial source of isotropicity, at the very beginning of the deposition process, the existence of an isotropic dewetted layer.
3 Mechanisms of transformation into supercooled liquid
One of the most intriguing characteristics of vapor-deposited stable glasses is related to their transformation into the supercooled liquid and to the fact that stable glasses transform with characteristic times much longer than those of the structural alpha relaxation at a given temperature [172]. This very slow kinetics is one of the essential signatures of stable glasses and yields a differentiated transformation mechanism compared to liquid-cooled glasses. So, a relevant question here is: how does an ultrastable thin film glass transits from the glassy to the liquid state? There is significant evidence, from theory, simulations and experiments, which show that the transformation behavior of ultrastable glasses is more similar to crystals than to conventional liquid-cooled glasses, resembling a melting process, far from the cooperative rearrangement expected for a glass [18, 173, 174]. For very thin films, the transition takes place via a liquid parallel front that forms at free surfaces and mobile interfaces [175] and proceeds until consuming all the glass (see Fig. 17). This is the dominating mechanism when the thickness is lower than a certain characteristic length, the cross-over length. This magnitude is defined as the distance that the parallel front has travelled when the transformation of the bulk glass dominates the transition and its value depends on the material, the stability of the glass and the temperature as explained further below [98, 173]. However, films thicker than this cross-over length transform into the supercooled liquid mainly via the growth of patches of liquid distributed all over the bulk of the glass [176], as schematically shown in Fig. 17. The basic requirement for these types of transitions to take place is basically a big contrast between the mobilities of the actual glass and the new phase to form, i.e. the equilibrated supercooled liquid [18]. This contrast can easily be achieved when working with ultrastable glasses [112]. At the end, and in agreement with random first-order transition theory, it seems that both mechanisms (front and bulk) may originate from the same physical mechanism but at different locations in the sample, due to the existence of nearby regions with high mobility contrast [177].
Cartoon showing the different regions where the melting of ultrastable glasses can originate. a Thin film, with a transformation mechanism that consists predominantly of a parallel liquid front that grows parallel to the surfaces and interfaces with higher mobility. Even if there are some nuclei forming in the bulk of the film, those are so dispersed that the fraction of glass transformed via a growth of the liquid phase inside the film is negligible in comparison to the fraction transformed via the parallel front. b When the film is much thicker, although the nuclei are dispersed in the film, the fraction of glass transformed via the growth of these nuclei becomes more significant the thicker the film when compared to the one corresponding to the liquid front. These nuclei are identified as regions of higher mobility than the surrounding glass. When submitting the glass to an up-jump of temperature, the surrounding glass would remain frozen in the initial conditions while these regions could be in equilibrium with the external temperature. c When the thin film is capped with a less mobile material (higher Tg), the mobility at the surface and interfaces is arrested and there is no propagation front, so the only transformation mechanism originates in the liquid regions formed in the bulk. The ratio between thickness and width is not at scale with real samples
3.1 Front melting
The presence of this transformation mechanism in thin film ultrastable glasses was first suggested by Swallen et al. in 2008 [178] after carrying out isothermal treatments above Tg on isotopically labeled ultrastable multilayer films of tris_naphthylbenzene (TNB) and measuring the translational motion using neutron reflectivity. One year later, the same group directly observed by secondary ion mass spectrometry [179] that the transformation was spatially inhomogeneous with sharp fronts originating at surfaces/interfaces. From that moment, many other techniques have been used to identify and investigate the dynamics of the liquid front. In all cases, results were consistent, showing as solid observations the non-dependence of front velocity with film thickness, for films thinner than the cross-over length, and a strong dependence of this velocity with temperature [30, 99, 106, 117, 173, 175, 179,180,181]. An empirical relation between velocity and temperature was suggested, where the relaxation time of the equilibrated super-cooled liquid is invoked to introduce the temperature dependence of the propagation front [120]:
where \(\tau \) is the alpha relaxation time of the supercooled liquid, C is a constant and \(\gamma \) is constant and below 1. The value of gamma depends exclusively on the material and for the organic glasses measured so far has been found to be in the range of 0.7–0.95 [104, 180]. An Arrhenius relation for the front velocity and the temperature has also been satisfactorily used to fit the experimental data [99] in limited temperature intervals, as shown in Fig. 18.
a Propagation velocity of the supercooled liquid parallel front as a function of the alpha-relaxation time for IMC samples grown at different deposition temperatures (indicated in the legend). The fitting of the data has been done using Eq. 1, which yields an exponent γ of 0.78 for all glasses, regardless the deposition temperature. b Same representation than in a including data measured at lower temperature. The figure shows how Eq. 1 can fit the data for an extended range in relaxation time, while an Arrhenius function does not fit the high and low temperature data. The low temperature data of Tsub = 220 K sample has been extracted from [34]. Reproduced from C. Rodríguez-Tinoco et al., Phys. Chem. Chem. Phys, 17, 31,195–31,201 (2015) with permission from Royal Society of Chemistry.
Equation 1 shows that the temperature dependence of the front velocity is inversely proportional to the alpha relaxation time softened by an exponent close to one. In other words, the velocity at which the supercooled liquid front propagates into the glass is strongly dependent on the mobility of the equilibrated supercooled liquid at that temperature. Calculations by Wolynes in the frame of random first order theory (RFOT) already predicted this result, showing that the velocity of a transforming front depends mainly on the mobility of the most mobile region which in this case is clearly the newly formed liquid front [18]. In particular, the relation between front velocity and temperature of Eq. 1 was reproduced by Wisitsorasak and Wolynes using numerical methods and linearized inhomogeneous mode coupling theory (Li-IMCT) [177]. Equation 1 has been found to be valid to describe the velocity of the front for a large range of temperatures, as shown in Fig. 18b (from Tg up to Tg + 75 K for the case of indomethacin glasses) or equivalently spanning 12 orders of magnitude in \({\tau }_{\alpha }\). The exploration of the velocity dependence in this large temperature interval was possible thanks to the combination of conventional calorimetry (DSC at 10 K/min) and fast-scanning nanocalorimetry (3.5 × 104 K/s) that due to its fast heating rates shifts the onset temperature of devitrification to even higher temperatures [112]. Interestingly, the relationship described by Eq. 1 also holds for glasses with lower stability [38]. In this case, the velocity of the front is faster but the dependence of the velocity with temperature remains the same (see Fig. 18a). The effect of the lower stability of the glass or other characteristics such as the preferential orientation of the molecules, heavily linked to the deposition conditions, are introduced in the model via the parameter C of Eq. 1. To date, the exact effect of each one of these different parameters on C is not yet well established [38, 180]. What is beyond doubt is that the velocity of the front, and therefore the transformation time is much slower in ultrastable thin film glasses. Just for the sake of giving some context, a glass obtained by cooling down the melt at 10 K/min would take around 100 s to transform into the SCL at Tg, while an ultrastable thin film glass (of IMC in this case, although there is not much difference between molecules) would transform at a rate of 0.003 nm/s, i.e., a 1 µm film would take around 3 × 105 s to transform and, theoretically, one would need to go below nm thickness to transform in the same time as the conventional glass.
If glasses with lower stability also transform by a propagation front that propagates faster than in ultrastable glasses one can wonder, why this mechanism was not previously observed in liquid-cooled glasses. The answer is probably related to the value of the cross-over length. The lower the stability of the glass, the smaller is the cross-over length [38, 98], to the point that a conventional glass can have a cross-over length of few nanometers, making it very challenging to identify this mechanism for the transition into the liquid of a standard liquid-cooled glass. However, the crossover length depends on the temperature at which the transition is taking place and being the glass transition a dynamic transformation, the crossover must depend also on the heating rate to the point that if a conventional glass is heated at very high heating rates (105 K/s) it is possible to identify the propagating front of the SCL as the main transformation mechanism, as previously shown by Sadtchenko and coworkers [98, 182]. On the opposite side it would be interesting to understand if a liquid-cooled glass substantially aged at Taging < Tg to attain a limiting fictive temperature of Taging, will transform into the SCL via propagation fronts similarly to a vapor-deposited glass grown in equilibrium at the same temperature.
The existence of the supercooled liquid propagation front as the main transforming mechanism of thin film stable glasses plus the crossover to a bulk transition for thicker films has also been observed in simulations [177, 183,184,185,186,187]. For instance, de Pablo et al. [183] used molecular dynamics and a simulation procedure that imitates the physical deposition process but of a mixture of Lennard–Jones binary particles for producing thin film glasses of different stabilities. A parallel front is the only transformation mechanism in very stable samples, which remain frozen when the mobility of the surface layer is restrained. Léonard and Harrowell [184] used a facilitated kinetic Ising model, generally used for modelling the collective relaxation in a glass forming liquid, to mimic the transition of an ultrastable thin film glass. Without the involvement of an equilibrium phase transition, this simple spin model can reproduce the features of the heterogeneous front-like transition mechanism observed experimentally, i.e. the presence of a liquid front that starts at the surface and progresses transforming the glass at a velocity that changes with temperature according to the empirical relation of Eq. 1.
3.2 Cross-over length
As stated above the cross-over length, \(\xi ,\) can be understood as the thickness transformed into liquid by the propagating front before the bulk mechanism sets in and dominates the transformation. The cross-over length can be determined by measuring the transformation time of a thin film glass as a function of its thickness at constant temperature [104, 173]. For films thinner than the crossover length, the transformation time increases linearly with thickness in agreement with the propagation of a liquid front at constant velocity. Thicker films, however, always take the same time to fully transform into the liquid irrespective of the thickness of the film, since the transformation occurs simultaneously in the whole sample volume. The value of the cross-over length spans from few nanometers to several microns [38, 98, 104, 173] depending on the material, the deposition conditions (which determine stability, density, and molecular orientation) and the temperature. To understand this dependence, we must include the interplay between the dynamics of glass and liquid during the transformation process. Several works have contemplated the necessity of considering extra transition layers to describe the interface between the glass and a more mobile region [98, 149, 182, 188]. Rodriguez-Tinoco et al. considered the transformation front as a progression of transforming intermediate layers that would take a time \({t}_{i}=d/{v}_{\mathrm{F}}\) to transform into the liquid state where d is the thickness of the intermediate layer and \({v}_{\mathrm{F}}\) is the velocity of the front. One would expect the properties of the intermediate layer to be some kind of average of the properties of the two adjacent states, the supercooled liquid, and the glass [98]. According to this assumption, the velocity of the front at a specific temperature is expressed as:
where tbulk is the transformation time of the bulk, which depends on the temperature and the properties of the glass [112], and \({\tau }_{\alpha }\) is the alpha-relaxation time of the liquid. Equation 2 assumes the lifetime of this intermediate layer associated with the moving front as the geometric mean between the bulk transformation time and the alpha relaxation time (see Fig. 19).
Characteristic times for Indomethacin (a), toluene (b) and TPD (c). In orange, alpha-relaxation time for each material. In black, transformation time for a bulk ultrastable glass [112]. In blue, transformation time for an intermediate layer, ti, according to Eq. 2 calculated from experimental data of the front velocity considering a thickness of the intermediate layer of d = 2 nm (open squares) and directly from the tbulk and \({\tau }_{\alpha }\) data (stars). Lines are fittings performed with the corresponding models: VFT for τα, modified VFT for tbulk [112] and Eq. 2 for ti, considering d = 2 nm
According to this definition \(\xi \) can be redefined as the thickness corresponding to the number of intermediate layers (each of them of thickness d and taking ti to transform) that transform during tbulk:
This expression for the cross-over length would explain the dependence of this parameter with the properties of the glass, via the transformation time of the bulk, which is expected to be shorter as the stability of the glass decreases, decreasing the crossover length and making it more difficult to be observed experimentally. Although not explicitly, Eq. 3 also contains information about the dependence of the crossover length with temperature. Since \({\tau }_{\alpha }\) decreases faster than tbulk as a function of temperature [112], the crossover length will increase for higher temperatures.
A similar expression to Eq. 3 was obtained by Wolynes [18] by combining mode coupling theory (MCT) with the mosaic distribution of relaxation times of RFOT to study the expansion dynamics of a mobile region of the glass during the transformation of the glass into the supercooled liquid when there is a big contrast in mobility between the mobile region and the surrounding glassy matrix. In that work a more general expression was obtained for a 3D scenario and a distribution of relaxation times via the β stretched exponential of the KWW distribution of relaxation times:
where \({t}_{\mathrm{R}}\) is the rejuvenation time, \(\widehat{\tau }\) is the harmonic mean relaxation time at the final fictive temperature \({T}_{\mathrm{F}}^{\mathrm{fin}} \sim T\), \(\tau \) is the mean relaxation time of the rejuvenating regions, and \(\xi \) and \({\xi }_{\mathrm{o}}\) are, respectively, the correlation length and the size of the initial equilibrated region, with \({\xi \sim \xi }_{\mathrm{o}}\) [18]. Equation 4 reduces to the expression for \({t}_{\mathrm{i}}\) of Eq. 3 when considering a propagation of the fast region in one-dimension, as it is the case of the parallel front, an equivalency between \({t}_{\mathrm{R}}\) and \({t}_{i}\), \(\widehat{\tau }({T}_{\mathrm{F}}^{\mathrm{fin}},T)\) and \(\tau \), \(\tau ({T}_{\mathrm{F}}^{\mathrm{in}},T)\) and \({t}_{\mathrm{bulk}}\), and a beta close to one, implying a relatively sharp distribution of relaxation times in the glass, as is expected for ultrastable glasses [106] (An estimation of the dispersion in front velocity, and therefore in relaxation time according to Eq. 4, in ultrastable glasses yields distributions with a full-width half-maximum lower than a 25% of total deviation [106]).
This critical length scale has also been explored in silico using quite diverse approaches. Reichman et al. [187] recreated glasses of different stabilities using random pinning of a certain fraction of particles, f, from an equilibrated supercooled liquid sample. After a sudden temperature jump, the mechanism for the system returning to equilibrium depends on the fraction of pinned particles, showing a competition between front and bulk transformation and the appearance of a characteristic length determining the dominance of one of the two mechanisms depending on f. Gutiérrez and Garrahan [185] used a kinetically constrained model, a three-dimensional East model with soft constraints, to reproduce the transition of thin film glasses. In their work, they reproduce the crossover between the two transformation mechanisms, front and bulk, as a function of film thickness. Fullerton et al. [186] used a combination of swap Monte Carlo and molecular dynamics to prepare glasses of size polydisperse Lennard–Jones particles of different stabilities, achieving glasses of unprecedently high kinetic stability. This allows them to study the front and bulk transitions and the crossover between them as a function of different parameters such as melting temperature but also glass stability. The crossover length arises naturally from their simulations, with a similar trend as has been observed experimentally, with a decrease both for lower stability glasses and for lower melting temperatures. The way in which the authors of this study prepare their samples results always in isotropic, equilibrium glasses. The fact that they observe a front-mediated transformation in all cases, lets the authors conclude that this transformation mechanism results from the inherent kinetic stability of the glass, independently of the preparation process or the anisotropy of the glass. It should, therefore, be observed also in liquid-cooled glasses under proper melting conditions.
3.3 Bulk melting
If the ultrastable glass film is thicker than the crossover length, then a bulk transformation mechanism dominates the transition of the glass into the liquid state, as schematically shown in Fig. 17b. In this section we highlight experimental and simulation evidence pointing out that the bulk transformation of highly stable glasses bears a close resemblance with a melting process in crystals.
The first experimental work addressing the anomalies of the bulk mechanism for stable glasses with respect to conventional liquid-cooled glasses was published by Kearns et al. back in 2009 [173]. This work already identified the kinetics of the bulk process as an Avrami-type kinetics [189]. Subsequently, many theoretical and simulation studies have worked on the transformation of low-temperature equilibrated glasses which are exposed to a temperature jump above Tg [18, 174, 185, 187, 190, 191], to find that the equilibration to this new temperature takes place via the expansion of high temperature equilibrated regions into the immobile glass matrix. The requirement for this process to dominate the transition is the presence of large mobility contrasts between both regions, which can be achieved either by a big temperature jump or by a very low-temperature equilibrated glass as a starting configuration. These high mobility regions are the result of fluctuations in the system, as in the case of the entropy drops of the model based on RFOT developed by Wolynes [18], the inherent dynamic heterogeneities as in the facilitated kinetic Ising model of Douglass and Harrowell [191], the local excitations as in the kinetically constrained model used by Gutiérrez and Garrahan for simulating ultrastable glasses [185], or higher temperature regions as in the simulations by Lulli et al. based on a distinguishable-particle lattice model, where the authors followed the spatial profiles of particle displacement and their interactions [190], as shown in Fig. 20. Jack and Berthier reproduced the same transformation mechanism using the triangular plaquette model, which is defined in terms of spin variables with simple interactions. In that study, they reproduced not only the nucleation and growth mechanism for equilibration to higher temperatures of very stable glasses which is successfully characterized using the Avrami formalism, but also the transition into the homogeneous relaxation with a broad range of relaxation times expected for low stability glasses when the starting configuration corresponded to a glass equilibrated at higher temperatures [174]. More recently, Fullerton and Berthier [167] used the Swap Monte Carlo approach to generate in-silico glasses of ultra-high stability, with transformation times five orders of magnitude slower than the equilibrated liquid. When analyzing the transition of these glasses into the liquid state, they found out that again it took place via the formation of liquid patches that grow until consuming the static glass matrix, following an Avrami-like kinetics. The reason behind this behavior, was attributed to the big contrast between the density of the glass and that of the new-formed liquid.
Snapshots of structural temperature \({T}_{\mathrm{S}}\left(\overrightarrow{x},t\right)\) and particle displacement \(d\left(\overrightarrow{x},t\right)\) for a temperature up jump. Different columns refer to average overlap q between the actual and the initial configuration, corresponding to increasing time from left to right. \({T}_{\mathrm{S}}\left(\overrightarrow{x},t\right)\) and \(d\left(\overrightarrow{x},t\right)\) show heterogneous evolution with large domains for the up jump. Immobile domains coincide with low structural temperature (i.e. low limiting fictive temperature) domains. Reprinted with permission from Lulli et al. 124, 095501 (2020) [190].
Since the cross-over length for highly stable organic glasses is typically larger than one micron, one needs to produce thick glasses to engage in such a study, which is time demanding given the fact that highly stable glasses are typically grown with growth rates around 0.1 nm/s. This limitation can be overcome by arresting the mobile regions that would initiate the liquid front. By capping the stable film with a layer of an organic molecule with higher Tg, one can inhibit the formation of the front [30, 175] at the interfaces forcing the stable glass to transform through a bulk process. In a recent study from Vila-Costa et al. [176], capped ultrastable thin films were isothermally annealed at temperatures above the glass transition temperature and their transformation kinetics extracted from the calorimetric trace of partially transformed glasses. A schematic of the thermal treatment together with an example of the resulting curves is reproduced in Fig. 21.
Results of the study of bulk glass transition of TPD thin and thick ultrastable film glasses. a Thermal protocol to measure the amount of liquid formed during an isothermal treatment. The samples are deposited at Tsub. Afterwards, samples are hold at Tiso for a specific time. After the isotherm, samples are cooled down at 10 K/min in the case of the thick films (30 μm) and at 500 K/s in the case of the thin films (around 80 nm). Samples are then heated at 10 K/min in the case of thick films and at 3 × 104 K/s in the case of thin films. b Mass fraction of liquid formed during the isotherm at Tiso = Tg + 14 K as a function of annealing time for thin and thick films. The fraction is extracted from the specific heat data, evaluating the amount of fast-cooled glass from the growth of the first calorimetric peak. The lines are fits of the data performed using the Avrami model, which yields exponents close to 2 for the thin films and close to 3 for the thick films. c, d Resulting specific heat curves (last step of the thermal protocol) after different times (indicated in the legend) at Tiso = Tg + 14 K for thin (c) and thick films (d). The inset in fig. d is a magnification of the low temperature peak region. The first calorimetric peak can be identified with the liquid regions formed during the isotherm, that become a fast- cooled glass when cooling down the sample after the isotherm. The second peak corresponds to the glass transition of the remaining glass. Reprinted with the permission of A. Vila-Costa et al., Phys. Rev. Lett. 124, 076002 (2020) [176].
The first calorimetric peak in Fig. 21c,d corresponds to the glass transition of a fast-cooled glass, which is the result of the formation of regions of supercooled liquid during the isothermal treatment. The fast cooling of the sample at around − 500 K/s after the isotherm transforms these liquid regions into a fast-cooled glass, which has a lower glass transition temperature with respect to the vapor-deposited stable glass, as shown in the final up scan. During an isotherm at T > Tg, the progress of the transformation, i.e. the development of these liquid regions for different times, can be followed from the evolution of the calorimetric peak of the fast-cooled glass [176]. This analysis yields curves of transformed fraction as a function of time providing information on the transformation mechanism (Fig. 21b). The fitting of these curves using the Kolmogorov–Johnson–Mehl–Avrami–Erofeev, KJMAE [189], formalism corroborates that the transformation of the highly stable glass into the supercooled liquid takes place by a nucleation and growth process in agreement with theoretical predictions and previous work [18, 190, 191]. The KJMAE formalism describes the occupation of space by the transformed phase during a transformation based on statistical considerations. This model is widely used for phase transitions which take place via a nucleation and growth of the new phase, such as a crystallization from an amorphous phase or melting. Non-random nucleation, non-isotropic growth and finite size effects are not properly described by KJMAE [189]. However, it is compatible with homogeneous, time, temperature o pressure dependent nucleation rates and also with interface, diffusion and time, temperature and pressure dependent growth rates.
In the case of an ultrastable organic thin film glass capped with a higher Tg material, the fitting of the transformed fraction data, during an isotherm above Tg, using the KJMAE formalism yields Avrami exponents of the order of two. Considering that these are thin film glasses (around 70–80 nm thick), it is an indication that the transformation into the supercooled liquid takes place by 2D growth from pre-existing nuclei. When measuring much thicker films (more than 10 \(\upmu \)m thick) the Avrami exponent takes values around n = 3, compatible with a 3D growth of pre-existing nuclei, consistent with the results obtained for thinner films (see Fig. 21). However, identifying the transformation mechanism using the Avrami exponent alone is not conclusive since the same exponent is compatible with different transformation mechanisms and geometries. Extra information about the characteristics of the sample, i.e. some independent measurements of the nucleation sites or about the growth front velocity of the SCL, would be very useful to confirm the precise mechanism of the transformation.
However, the nature of these pre-existing nuclei is difficult to identify experimentally. As mentioned above, many simulations predict the existence of dynamic heterogeneities that would act as seeds for the initiation of the transformation. These heterogeneities could be viewed as intrinsic dynamic fluctuations of the system [18, 190], to the point to assert that if there were none of these heterogeneities, the equilibration of the glass at that temperature would never take place [191]. This view would agree with the existence of pre-existing nuclei, as the analysis of the experimental data suggests. Another possibility, described in some simulations, invoke a rate of formation of high fictive temperature regions [174, 185]. Although this approximation is not consistent with the treatment of the experimental data so far, the formation of new liquid regions during the isothermal treatment cannot be fully discarded. In any case, there seems to be a relation between the stability (volume density) of the glass and the number density of these dynamic homogeneities, with a decreasing number of defects the higher the stability of the glass [192].
The average distance between the initiation sites is difficult to discern from the fitting of the transformed fraction since this parameter and the growth front velocity are both correlated in the equation leading to the transformed fraction. Therefore, similar fittings to the experimental data could be achieved with a lower density of nuclei and larger growth-front velocity or, oppositely, using a much higher density of nuclei with a slower propagation front velocity. As a first assumption, the work of Vila-Costa el al. [176] uses the velocity obtained for the propagation front during the surface transformation of very thin films at each temperature. In this case, the obtained average distance between nuclei of few microns roughly coincides with the cross-over length [104, 173, 176] yielding a consistent result. Assuming that the growth of the liquid phase is 2D (Avrami exponent close to 2) a lower limit of the growth front velocity can be estimated. Since the films under study were 80 nm thick, the distance between nuclei must be at least around twice this thickness for the growth to be considered 2D [193], that is around 200 nm. In this extreme case, the nuclei density would be around two orders of magnitude higher compared to the one obtained using the front velocity as liquid growth rate [176]. Since the transformation rate depends on the product \(N{v}^{2}\), with \(N\) the density of initial nuclei and \(v\) the growth rate, a higher nuclei density would yield a lower growth rate. If \(N\) changes by two orders of magnitude the velocity of the liquid regions in the bulk would be one order of magnitude slower than the velocity of the surface propagation front. In this scenario, the difference in propagation velocity of the liquid between the front and the bulk could be due to a pressure increase arising from the difference in density of 1.7% between the glass and the liquid at the same temperature [40]. However, a study of the transformation of very thick films of an organic glass by means of dielectric spectroscopy showed that the relaxation time of the liquid surface propagation front and of the liquid formed in the bulk was not only the same, but equal to the alpha-relaxation time expected for an equilibrium supercooled liquid at that temperature [104]. Still, even if the liquid is completely equivalent, the propagation velocity could be different. Clearly, a precise determination of the density of nuclei is necessary to get a better insight into the transformation mechanism.
In the case of bulk transition in ultrastable thin film glasses, the second peak of the calorimetric traces shown in Fig. 21 corresponds to the glass transition of the remaining glass, which has not experimented a remarkable softening during the isotherm, considering that its position shifts only slightly to lower temperatures when increasing the isothermal time. The shift is more significant however, in the thicker films. Whether this difference is related to the thickness of the films or to the fact that the heating ramp after the isothermal treatment is performed five orders of magnitude slower in the case of the thick films, it is still not known. In fact, a very interesting question is which is the mechanism behind the transition of the ultrastable glass when submitted to a continuous heating treatment. Is it the same nucleation and growth mechanism obtained for the isothermal treatment? Is it a homogenous softening as in the case of conventional glasses? Or is it a mixture of both mechanisms?
Back to the theoretical models and simulations, a common feature is that the existence of these melting-like transitions into the supercooled liquid requires a large mobility contrast or difference in the equilibration temperature, between the immobile glass and the high temperature equilibrated nuclei. Following this argument, it should be possible therefore to observe this transformation mechanism in conventional glasses. The only requirement would be to measure the transition at temperatures far above the glass transition of the glass, so the above-mentioned condition would be fulfilled. The realization of such an experiment is challenging due to the short transformation times for such glasses when getting far above Tg. On the opposite side, one would expect that the equilibration of an ultrastable glass, which has been driven above its equilibration temperature just a few degrees, would take place following the dynamics of a cooperative rearrangement. Again, the experimental realization of such an experiment would require extremely long measuring times.
4 Low-temperature properties: two-level systems and boson peak
Non-crystalline solids, whether glasses or other amorphous solids, and even some glass-like disordered crystals, are well known to exhibit thermal, acoustic and dielectric properties at low temperatures clearly different from those found in textbook crystalline solids [194,195,196]. Furthermore, these low-temperature glassy “anomalies” show a remarkable degree of universality for any type of glass, qualitatively and, in many respects, even quantitatively. Specifically, below about 1 or 2 K the specific heat of non-crystalline solids is much larger than that of their crystalline counterparts and depends roughly linearly on temperature, Cp ∝ T, whereas the thermal conductivity is orders of magnitude lower and varies almost quadratically, κ ∝ T2. Both power laws are in clear contrast with the cubic dependences observed in crystalline solids, which are successfully explained by Debye’s theory. Acoustic properties also dramatically differ from those found in crystals, the attenuation being much stronger—as may be expected—, but with a rich and peculiar phenomenology of frequency and temperature behavior, including sign-changing logarithmic temperature variations of sound velocity. Dielectric properties exhibit a similar behavior [194].
Most of those low-temperature properties of glasses below 1 K have been successfully explained by the Standard Tunneling Model (STM) since long [197,198,199]. The essential hypothesis of the STM is the ubiquitous existence of atoms (or, more likely, groups of atoms) in amorphous solids, which can sit almost equally well in two different configurations of similar energy. Hence, there will be a vast, random distribution of low-energy anharmonic excitations via quantum tunneling at low temperature between the two lowest energy levels of such atomic groups, what will work as two-level systems (TLS) in asymmetric double-well potentials.
To calculate the specific heat of that random distribution of tunneling states within the STM, it is a good and usual approximation to simply take a constant density of TLS, i.e. n(E) ≈ nTLS. Then, CV = (π2/6) nTLS kB2T is readily obtained, which accounts for the experimentally observed quasilinear dependence of the specific heat in glasses. Typical values nTLS ~ 1046 J−1 m−3 have been so found for many different materials, within one order of magnitude, though the dispersion could be much stronger [200]. A corresponding STM expression accounts for the thermal conductivity and its quadratic dependence on temperature, governed by the TLS resonantly scattering off thermal phonons [194, 197,198,199]. Also, acoustic and dielectric properties at low temperature can be reasonably explained by the STM.
Despite the apparent success of this 50-year-old model, the structural origin and the very microscopic nature of the TLS remain unclear indeed. Although single-molecule spectroscopy experiments [201, 202] have provided some experimental evidence for their existence in particular cases, a few authors [196, 203,204,205] have seriously questioned the STM and the very idea of a random ensemble of independent tunneling states as the cause of the universal behavior of every glass at low temperatures.
Furthermore, the thermal behavior of glasses above 1–2 K presents other features beyond the reach of the tunneling model and its TLS. A broad maximum in Cp/T3 is observed in most glasses at typically 3–10 K, which is associated with the so-called “boson peak” [194, 206], observed by Raman scattering, inelastic neutron scattering and other spectroscopic techniques, arising from an unexpected and controversial excess in the Debye-reduced vibrational density of states g(ω)/ω2 at around 1 THz. In the same temperature range of the Cp/T3 peak, the thermal conductivity levels off to a plateau region. Astonishingly, the thermal conductivity coefficient of all non-crystalline solids is ~ 10−3 W cm−1 K−1, irrespective of the type of material. This is probably the most universal glass anomaly, together with a related feature in the acoustic properties, namely another universal plateau Q−1 ~ 5 × 10−4 in the internal friction [194, 196, 207].
An open question for decades has been whether these universal “anomalies” of glasses at low temperature could be eventually suppressed by strong or long enough annealing (or aging) stabilization processes near or below the glass transition temperature Tg. In fact, many different experiments have been long reported about these issues, though with unclear or contradictory conclusions (see a more detailed discussion about it in ref. [208]).
For decades, rare exceptions to the general picture described above had been observed only for the internal friction in amorphous films of covalently bonded, fourfold-coordinated elements, namely Si, Ge, and C [207, 209, 210], presumably because of the rigid and stable character of their network. In addition, an absence of the characteristic far-infrared resonant absorption ascribed to TLS was reported [211] for a “tetrahedral liquid” such as low-density amorphous (LDA) water.
The case of amorphous silicon (a-Si) is particularly interesting and has been thoroughly addressed. After earlier acoustic experiments in a-Si showed a depletion of the TLS plateau in the internal friction (see left panel in Fig. 22), low-temperature specific heat and thermal conductivity measurements in evaporated thin films confirmed such depletion of glassy low-energy excitations in a-Si [212]. As depicted in the right panel of Fig. 22, studied a-Si thin films exhibited a simple Debye behavior at least down to 2 K, apparently without a linear term nor a boson peak (only a typical van Hove peak above 30 K). Nonetheless, more recent experiments performed by the same group have shown that changing the preparation conditions of the a-Si thin films determined the occurrence or not of typical low-energy glassy excitations at low temperature [213,214,215].
Data on amorphous silicon. Left panel: Internal friction of as-sputtered and annealed thin films of a-Si. The solid line shows the internal friction of bulk a-SiO2, and the double arrow indicates the glassy range observed in typical amorphous solids (after Ref. [212]). Right panel: Specific heat of a-Si, including earlier data and crystalline Si as a reference (after Ref [210].). Reprinted with permission from X. Liu et al., Phys. Rev. B 58, 9067 (1998) and Zink et al. Phys. Rev. Lett. 96, 055902 (2006) [210, 212].
We make use again of the potential energy landscape to point out there the existence of tunneling TLS in double-well potentials (DWP) and low-frequency vibrational excitations in single-well potentials (SWP), visualized as local minima in the rugged potential landscape (see Fig. 3 in Sect. 1). The interest in the preparation of glasses with low-enthalpy is twofold. First, it could provide a definite answer to the fundamental question of whether or not ideal glasses would contain such excess of “glassy” low-energy excitations, since we would be measuring ideal or almost ideal glasses, not just extrapolating or inferring results. Second, the presence of TLS excitations in non-crystalline solids is the main difficulty hampering, for example, an efficient use of superconducting circuits for quantum computation [216, 217], which seems to be mainly limited by TLS losses. Specifically, tunneling TLS present in amorphous parts of the devices are thought to be the major source of noise and decoherence in superconducting quantum circuits [218].
In Fig. 23 we show specific-heat measurements [219] at low temperature performed on several physical vapor deposited (PVD) thin films of indomethacin (IMC), one of the first and most studied ultrastable glasses up to date. The left panel (a) shows the data in the whole temperature range using the typical Debye-reduced cp/T3: T plot, whereas the right panel (b) amplifies the lowest temperature region to determine the linear and cubic coefficients. Two samples, prepared under slightly different deposition conditions as ultrastable glasses (labeled USG-1 and USG-2), exhibited a full suppression of the linear contribution ascribed to TLS. On the contrary, another similar sample but prepared under non-ideal deposition conditions (conventional glass) presented the usual glassy behavior with a significant linear term. Moreover, one of the USG samples was stored in poor vacuum and temperature conditions for months (labeled as degraded USG). Then, it was measured again and showed a recovery of its glassy features. Also, a similarly prepared sample was led to crystallization and was measured as a reference.
Specific-heat data for different PVD thin films of indomethacin, including one conventional glass, two ultrastable glasses—USG-1 is 50 μm-thick and USG-2 is 80 μm-thick—, another standard glass formed by degradation of the latter, and a film in crystalline state (Debye extrapolated at lower temperatures). a Debye-reduced cp/T3: T plot; b cp/T: T 2 plot at very low temperatures to determine the TLS (linear) and the Debye (cubic) coefficients. Dashed lines show the corresponding linear fits for experimental data below 2 K
In summary, USGs of IMC lack the universal linear term coefficient in CP, in clear contrast with samples of the same substance prepared as standard glasses. Therefore, it is tempting to associate the found depletion of TLS for the USG of IMC to the extraordinary structural and thermodynamic stability of this kind of glasses. Another possibility pointed out in Ref. [219] would be, however, that the special growing conditions and the corresponding anisotropic character of these PVD highly-stable glasses hindered the appearance of TLS. The latter option was suggested also because of the results obtained in a different type of highly-stable glasses, namely hyperaged geological glasses of amber [208, 220].
Amber is a polymeric glass that has been aging below Tg for millions of years. In contrast to standard annealing processes, in the case of amber the pristine sample is the highly-stable glass. Subsequently, after performing the desired measurements, the very same sample is annealed and thus partially or totally rejuvenated. Oppositely to the case of PVD ultrastable glasses of IMC, stable amber glasses of 110 Myears (from El Soplao, Spain) [208] were undoubtedly found to exhibit a linear term in the specific heat, which is, qualitatively, and even quantitatively, identical to that seen in its state as rejuvenated or standard glass. Also, the presence of a glassy “boson peak” persists in ancient amber (in comparison to rejuvenated samples), though in this case the strength of the peak increased with rejuvenation. This observation in Cp/T3 was later confirmed by measuring the low-frequency vibrational density of states by means of inelastic X-ray scattering (IXS), as shown in the left panel of Fig. 24 [221]. The persistence of these glassy thermal properties at low temperatures in highly-stable glasses was also observed in Dominican amber glass [220, 222], again in clear contrast with the case of IMC (Fig. 23).
Specific heat of 110-Myear-old Spanish amber [209]. (Left): Typical cp/T 3: T representation showing the boson peak for the pristine amber and for the same sample after fully rejuvenation. Solid lines are curves calculated from the vibrational density of states obtained from IXS data [221]. (Right): same cp data plotted as cp/T: T2 at the lowest temperatures to show the invariant linear coefficient (the intercept with the ordinate axis), also including the sample in an intermediate partially-rejuvenated state
Most recent advances in computational studies can shed light on this issue. By using a new Monte Carlo algorithm (swap), a strong depletion of TLS when increasing the stability in computer-generated glasses has been recently found [223], apparently supporting the abovementioned results obtained in PVD ultrastable glasses of IMC [208]. The question of why amber glasses behave so differently is left aside.
More experiments are needed to answer the question of whether the persistence or suppression of TLS in stable glasses could depend on the kind of glass-forming material and is not a universal property, or if the anisotropy may play a role. Specifically, further specific-heat measurements in other glasses able to be prepared with a high kinetic and thermodynamic stability would be most interesting, as well as more simulations on computer glasses of different kind, including polymeric-like or anisotropic systems.
Finally, we could mention a possible new kind of highly-stable glasses recently introduced by Cangialosi and coworkers [73]. They prepared glasses out of polymer spheres with large interfacial area, which appeared to attain the ideal glass state in time scales of about one day. By employing inelastic neutron scattering they observed a suppression of the boson peak in the Debye-reduced vibrational density of states for the stabilized glasses. Certainly, it would be most desirable to explore the existence or absence of TLS by specific-heat measurements or other properties at very low temperatures in this new system.
5 Opto-electronic properties and thermal transport in organic vapor-deposited glasses
5.1 Electronic transport
Small organic semiconductor molecules are key to develop organic based electronic and optoelectronic devices, such as organic field effect transistors (OFETs), organic light emitting devices (OLEDs) and organic photovoltaics (OPVs) with higher performance than their inorganic counterparts. Electronic applications, in which carrier transport is the key parameter, often involve crystalline layers due to their superior carrier mobilities in comparison to structurally disordered organic glasses. Over the years, there has been an intense effort to prepare single crystalline organic layers with high carrier mobilities enabling high electronic conductivity. Yet, it is extremely challenging to obtain large area single crystals and typically, OFETs are made of polycrystalline layers. However, the presence of grain boundaries is detrimental to carrier transport and therefore highly-dense amorphous layers with improved air and thermal stability and better electrical properties could have some advantages over their polycrystalline counterparts. Many of the prominent small organic molecules with high mobilities are based on acenes and fused heteroacenes, i.e. pentacene, tetracene. The key of their success is linked both to their molecular structure and to the intermolecular packing that determine the energetic disorder of the energy levels and the charge transfer integral between adjacent molecules. However, these materials have a high tendency for crystallization during vapor-deposition and are extremely challenging to grow as glasses within the correct temperature window to form stable glasses. Other more-complex, organic semiconductors, such as those used in OLEDs, are easier to grow from the vapor as glasses [2, 45]. One of the main limitations of organic glasses is their low carrier mobility compared to other inorganic materials. Most disordered organic semiconductors operate in the hopping regime in which carriers hop from one molecule to another under the influence of an external electric field. The disordered structure and the weakly van der Waals forces between molecules give rise, therefore, to low mobility hopping transport [224]. However, during the last 25 years mobility has raised from 10–4 to 10–3 cm2/Vs to values exceeding 1–10 cm2/Vs, same order of magnitude as those characteristic of thin film amorphous Si (0.5–1 cm2/Vs) [224]. One possibility to further enhance mobility is through increasing the density and molecular alignment of the molecules conforming the glass. The higher density and tunable molecular orientation of glasses grown under appropriate conditions may also facilitate charge hopping through the enhancement of the charge transfer integral between adjacent molecules. Density enhancement may also lead to other beneficial effects such as lower vapor uptake to improve the air stability [119] and device performance [31] and higher photostability under light irradiation [111].
To improve the efficiency of organic devices, it is mandatory to control the properties of the semiconductor glass by tuning molecular orientation, increasing kinetic and thermal stability and glass density as to achieve the highest efficiency through enlargement of the π–π interactions.
There have been quite a few studies devoted to understanding the effect of deposition temperature on the charge transport properties of thin film glasses of organic semiconductors. Yokoyama et al. [15, 43, 44] have already shown that molecular orientation modifies charge transport in anisotropic glasses and that substrate temperature could be used to tune the molecular orientation of linear-shaped molecules from horizontally-aligned at low temperature to a more isotropic distribution at higher temperatures, below the glass transition temperature (see Sect. 2). Ellipsometry (not shown) indicates OXD7 films are optically isotropic whereas the Bpy-OXD film exhibits a very large optical anisotropy. A horizontal orientation with respect to the substrate strongly increases electrical conductivity in the perpendicular direction, as shown in Fig. 25. The effect is by no means small and tenfold improvements or more in mobility can be reached, as shown in Bpy-OXD or for the linear-shaped BSB-Cz molecule [15]. The enhancement is related to the increase in carrier mobility attributed to an improved π–π stacking that result in better overlap of the HOMO–LUMO orbitals of adjacent molecules. These earlier studies were not aware of the increased density and enhanced thermal stability of the thin film glasses grown below Tg and therefore, could not disentangle the separate role of density and molecular orientation on carrier mobility. More recently, Adachi and coworkers have studied the influence of molecular orientation and density on the transport properties of alpha-NPD thin film glasses. Interestingly, they observed that a density increase of 1–2%, reached at Tsub = 0.7–0.8 Tg, was the main reason for the increase of the current density and that molecular orientation had a minor contribution [31]. The increased density of the stable films was also responsible for the larger operational lifetime of the devices. This was preliminary ascribed to a better thermal stability related to the lower water vapor uptake of denser films [119].
Variation of electron mobility as a function of the electric field for OXD7 (blue) and Bpy-OXD (red) films determined using two devices each (circles and triangles). Reprinted with permission from D. Yokoyama et al., Appl. Phys. Lett. 95, 243303 (2009), AIP publishing [15]
In glasses, there is an energetic and structural disorder in the alignment of the energy levels compared to crystals. In amorphous solids, the energy levels are shifted and broadened with respect to the corresponding HOMO and LUMO levels of the isolated molecules. In general, the HOMO–LUMO gap shrinks, and the density of states becomes a Gaussian distribution. Typically, the energetic disorder is bound to have a significant impact in the mobility, since a broad distribution of energy levels is synonymous of larger average hopping barriers between adjacent molecules. In this sense, it would be highly desirable to understand the role of the deposition conditions on the energetic disorder of the HOMO–LUMO distributions. It is to be expected that a higher density and a better molecular alignment may also modify the energetic distribution resulting in a narrower density of states, DOS. A narrow DOS will result in improved hopping due to the lower energy barrier for states at the center of the DOS distribution. In fact, in a recent work, Adachi and coworkers [32], carried out thermally stimulated current (TSC) measurements to unveil the reason for the change in the hole current density in amorphous (bulk-like, thickness 300 nm) films of alpha-NPD, a hole-transporting material, deposited at various substrate temperatures below the glass transition temperature (Tg = 362 K). The highest value of the hole current was found at Tsub = 0.75 Tg. The analysis of the TSC measurements led the authors to conclude that hole traps were uniformly distributed across the films for all substrate temperatures, but the hole trap energy was the smallest for the films grown at 0.75 Tg, Fig. 26. However, the hole trap density decreased linearly as temperature was increased from 240 to 330 K (0.65–0.90 Tg), as shown in Fig. 26. At present, there is not a clear correlation between increased density, trap energy, trap density and molecular orientation, so further studies are mandatory to better understand structure–property indicators that allow for proper tuning of the electronic properties of vapor-deposited organic semiconductor glasses.
a Orientational order parameter S and b relative density ρrel as a function of substrate temperature during vacuum deposition, Tsub. The chemical structure of α-NPD is shown in the inset of panel a. c Plot of current density J at E = 1.0 × 105 V/cm versus Tsub. d dependence of hole trap density on Tsub. e Trap depth versus Tsub. Lines are guides to the eye. Reprinted with permission from Esaki Y et al., J. Phys. Chem. Lett. 8, 23, 5891–5897 (2017). Copyright {2017} by American Chemical Society and Esaki Y et al., Appl Phys Lett 114, 173301 (2019), AIP Publishing [31, 32]
Atomistic studies of charge transport in simulated vapor-deposited glasses also highlight the benefits of structural ordering on enhancing the rate of hopping of charge carriers through the glass. De Pablo and coworkers [225] used simulated ethylbenzene glasses as a simple example to understand other, more complex, molecular semiconductor glasses. Interestingly, the transfer integral between neighbor molecules was enhanced by 10% and the energetic disorder of the anisotropic and more stable vapor-deposited glass was 10% lower relative to the conventional glass. While more work needs to be done on larger molecules used in practical applications, this tendency supports the still scarce experimental evidence discussed above.
5.2 Organic light emitting devices
Organic light emitting devices (OLEDs) are composed of a series of stacks of organic materials to enable injection of charge carriers (electrons and holes) when a voltage is applied to the electrodes and their recombination within the emissive layer. A simplified stack including contacts, electron transport layer (ETL), hole transport layer (HTL), hole and electron blocking layers (HBL and EBL, not shown) and the emissive layer (EML) at the center is shown in Fig. 27. It is important to realize that the organic layers conforming the OLED structure are disordered and often grown by vapor deposition at room temperature irrespective of the glass transition of the glassy films. The reader is referred to more specialized reviews for details of this large field of research [226]. Although in use in applications such as mobile displays and TVs, there are still challenges OLEDs must overcome for a more diverse deployment. Long-term stability is one of the main issues in relation to high-brightness applications (> 1000 cdm−2) and here the high thermal stability attained by ultrastable glass can be an added value. However, the OLED community has not yet paid much attention to the implications to use high dense low enthalpy ultrastable glasses as part of the OLED stack and, in fact, all materials are grown at room temperature regardless the Tg of each material evaporated.
(Left) OLED device working principle. The electroluminescence is achieved when a voltage is applied across the electrodes allowing the injection of holes and electrons to the HOMO and LUMO levels of the respective organic layers. Those form an exciton that recombines radiatively. (Right) OLED light outcoupling. Sketch of the different light losses mechanism that can occur within an OLED device. Total internal reflection will be produced for emission at higher angles than the critical angle. Adapted from [37]
Recent studies have analyzed how vapor deposition affects molecular alignment in single layers of organic semiconductors [29] and the impact of orientation on transport properties [44], as discussed in Sect. 5.1. Mu et al. [227] studied the effect of the deposition temperature on the performance of a highly simplified OLED based on a CBP:Ir(ppy)3 [CBP = 4′-bis(carbazol-9-yl)biphenyl emission layer (EML). They assigned a Tg for CBP of 60 °C and according to this value the best devices were grown at temperatures above the glass transition temperature of the ETL and HTL, therefore outside the window of formation of highly stable glasses. However, recent measurements have shown the Tg for CBP is about 110 °C, using two different techniques [228]. Based upon the revised Tg value, the best devices in the work of Mu et al. were produced at 0.87 Tg.
Here we briefly outline recent efforts to incorporate ultrastable glasses into OLEDs and the main achievements so far. There are different aspects to consider building up an efficient OLED. High charge injection and electrical conductivity within the electron and hole transport layers is a first requirement to generate a high number of photons in the emissive layer. Other factors are essential to extract all these photons as useful light outside the device. Among them the most relevant are, the radiative efficiency of the decay process, the photon emission direction achieved through an adequate molecular orientation (preferentially with the emitter parallel to the substrate) and the refractive index of the layers to improve light-output. The first attempt to study the impact of the growth conditions of the organic layers during vapor deposition on the performance of state-of-the-art OLEDs was carried out several years ago by Rafols-Ribé et al. [2]. They used the simplified three-layer Meyer stack outlined in Fig. 28 to test the influence of the deposition temperature on the efficiency and lifetime of a monochrome phosphorescent light-emitting diode. The hole transport layer (HTL) is TCTA (Tg = 151 °C) whereas TPBi (Tg = 122 °C) is used both as emitter matrix for the emission layer (EML) and electron transport layer (ETL). This study showed significant improvements of the external quantum efficiency EQE and luminous efficiency LE (up to 24% and 30%, respectively) and device lifetime (by up to 4 times) for the green emitter, Ir(ppy)2(acac)) by heating the glass substrate to 0.85 Tg during evaporation of the ETL and EML (Fig. 28) Other phosphorescent emitters such as Ir(MDQ)2(acac), Ir(ppy)3, and FIrpic were also tested with EQE enhancements by 15%, 22% and 163%, respectively at Tsub = 0.85 Tg.
(Left) Schematic device structure of the studied device. As a first study, and single OLED run was prepared using the green emitter Ir(ppy)2(acac) (8 wt%) and evaporating the EML and ETL layers at six different substrate temperatures. The rest of the layers were deposited at room temperature. A second run, explained later in the text, consisted in using the same stack but with three different emitters and just two substrate temperatures for each emitter. (Right) Devices performance versus deposition temperature. External quantum efficiency (EQE) (red, left-axis) and luminous efficacy (LE) (blue, right-axis) at 100 cdm−2 as a function of the deposition temperature. The error bars are the standard deviation at the 95% confidence interval and weighted with the t-student factor for small samples sizes (between 2 and 6 samples for each temperature). Lines are a guide-to-the-eyes. Reprinted with permission from J. Ràfols-Ribé, Science Advances 4, eaar8332 (2018) [2]
These improvements were attributed to a superior radiative efficiency due to observed changes of the excited state lifetime. The reduced non-radiative decay rate of the emitter was probably related to a denser packaging of the molecules. This view was supported by a previous study by Qiu et al. [92] that showed the enhanced resistance to light irradiation (photostability) achieved in ultrastable glasses of DO37 (3-[[4-(2,6-dichloro-4-nitrophenyl)azo]-N-ethylanilino]-pro-pionitrile or Dispersive Orange 37). The high density of the films formed as ultrastable glasses is likely to suppress coupling to generally accessible decay states present in OLEDs. The influence of other potentially relevant parameters such as charge transport, radiative rate and emitter orientation were ruled out as the main sources of improvement of device performance after detailed characterization. In the case of charge transport current–voltage characteristics were minimally affected by substrate temperature. Emitter orientation was also shown not to influence light-output since a detailed investigation of the transition dipole moment of the emitter Ir(ppy)2(acac) clearly showed that a change of dipole orientation was not the origin for the enhancement. In another work, Bangsund et al. [229] link the observed increased of the EQE efficiency in the Meyer stack comprising ultrastable glasses to the reduction of spontaneous oriented polarization (SOP)-induced exciton quenching. SOP leads to the accumulation of charge carriers, typically holes, at the interface that are effective in exciton quenching. Thus, according to these authors heating the substrate is effective to reduce SOP and increase the efficiency. Another recent study with the green thermally activated delayed fluorescent (TADF) emitter (4CzIPN) in a similar stack as that used by Rafols-Ribé et al. [2] was carried out by Will et al. [230] using a similar strategy of growing the ETL and EML at different temperatures. The EQE shows little sensitivity to changes of the substrate temperature. The efficiency of the stack did not reach the one of state-of-the-art devices that used other emitters probably because of insufficient energy transfer to the 4CzIPN emitter used in this study.
These studies show that layer deposition at the right deposition conditions (mainly at the appropriate temperature) may be a useful route to improve the efficiency and lifetime of OLEDs. However, it is still too early to draw general conclusions since the underlying processes are still not well understood and more research efforts are needed to elucidate the physics behind the observed improvements and if this methodology can be extended to other emitters, materials and stacks.
5.3 Thermal transport
While many previous studies have focused on the electronic transport properties of small molecule organic glasses, thermal transport in thin film organic glasses remains largely unexplored and only few studies are reported to date [101, 176, 231,232,233,234]. The van der Waals interaction between adjacent or next-neighbor molecules has a profound effect on heat propagation and disorder seems to play a minor effect on the thermal conductivity compared to organic crystals. Therefore, the changes of thermal conductivity between glassy and crystalline organic materials are much lower than the ones observed in inorganic solids. One illustrative example is Si, for which the thermal conductivity, k, ranges from 150 Wm−1 K−1 at room temperature in the single crystal to 1.5 Wm−1 K−1 in the amorphous material. In contrast, thermal transport in poly- or single-crystals of small organic molecules (rubrene, pentacene, Alq3, TIPS-pentacene, DNTT, C60) [233, 235,236,237] already lie in the low k range 0.1–1 Wm−1 K−1.
The limited thermal conductivity in organic semiconductors is often described through localization of lattice vibrations where heat is transferred by random walk motion through the lattice. However, our current understanding of heat conduction in organic glasses is limited by the largely incomplete knowledge about the actual mechanisms ruling over thermal energy exchange in these systems and how the glass atomic scale morphology affects transport.
Cross-plane and in-plane thermal transport measurements of vapor-deposited thin film glasses of TPD [101] and α-NPD [37] indicate molecular orientation plays a pivotal role in the value of the thermal conductivity. Rafols-Ribé et al. [101] have shown that by changing the deposition temperature, the thermal anisotropy ratio, defined as the relative difference between in-plane \({k}_{\parallel }\) and through-plane \({k}_{\perp }\) conductivity, (\({k}_{\parallel }-{k}_{\perp })/{k}_{\perp }\), can be modified to nearly 40%. As described in Sect. 2, molecular orientation in vapor-deposited TPD or α-NPD glasses is dominated by surface equilibration at each deposition temperature and it is well stablished that the lower the substrate temperature during growth, the higher is the tendency towards horizontal orientation. That is, films grown at around 0.7 Tg are mostly face-on oriented, while films grown around 0.9 Tg have a small degree of vertical alignment and those grown above 0.95 Tg are mostly isotropic, as shown by the order parameter, Sz, in Fig. 29 for TPD. Figure 29 also shows the relative variation of \({k}_{\parallel }\)(blue squares, left-axis) normalized to the 325 K value, 0.152 ± 0.004 Wm−1 K−1.
Correlation between thermal conductivity and molecular orientation. The left vertical axis shows the relative variation of the in-plane thermal conductivity with respect to its value a substrate temperature of 325 K, \({k}_{\parallel }=0.152 \) Wm−1 K−1 and the right axis the order parameter obtained from Dalal et al. Both quantities are plotted against the substrate temperature scaled by Tg. Reprinted with permission from J. Ràfols-Ribé et al., Phys. Rev. Materials 2, 035603 (2018) [101].
Interestingly, the role of the anisotropic molecular packing in thermal transport is anticorrelated with respect to electronic transport. That is, thermal transport is favored along the direction of the long-axis of the TPD molecule while electronic transport favors propagation along the perpendicular direction to the long axis of the molecule provided there is sufficient π–π interaction. This is supported by molecular dynamic all-atom simulations that identify the variation of thermal transport with changes in the strengths of the molecular interaction. Stronger molecular interactions along the backbone of the molecule favor the propagation of microscopic heat carriers along this direction [101]. The decoupling of electrical and thermal transport provides an interesting avenue to further explore the thermoelectric properties of small molecule thin films, since the efficiency of a thermoelectric material is evaluated through the dimensionless figure of merit, \(zT={S}^{2}\sigma /k\), where S is the Seebeck coefficient, \(\sigma \) the electrical conductivity and \(k\) the thermal conductivity due to charge carriers and lattice vibrations, being T[K] the average temperature between the hot and cold regions. So, \(zT\) is high in materials that simultaneously exhibit high electrical conductivity and low thermal conductivity.
6 Conclusions
Ultrastable glasses have become an opportunity for new discoveries in the areas of glass physics and chemistry, and represent one of the major cornerstones of the glass community in recent years. Here we have intended to provide a broad vision of the different aspects that encompass the research of stable glasses, highlighting and discussing different views offered by scientists in the area along their 14 years of existence. While most of the work on stable glasses has revolved around organic glasses, the increasingly important contribution of metallic and polymer glasses is also included in this review. The most significant properties are compiled in a table that contains 57 different glassy systems prepared by PVD in the range of substrate temperatures close to Tg. Most of them formed stable glasses under suitable growth conditions.
Central to the debate of ultrastable glasses is their mechanism of equilibration. It is highly recognized today that the extraordinary properties of vapor-deposited glasses are linked to the enhanced mobility of the surface layer leading to a very fast equilibration under appropriate deposition conditions, where molecules or atoms have enough time to reach equilibrium before being buried by other atoms/molecules. We also offer some alternative views invoking the influence of beta relaxation or other equilibration mechanisms to explain the formation of stable glasses. With high densities and low enthalpies approaching the ‘ideal glass’, highly stable glasses show unique features in their transformation to the liquid state, such as the existence of front melting in very thin films, starting at regions of high mobility located at surfaces/interfaces. Very thick (bulk-like) films have a glass transition that resembles melting or crystallization by nucleation and growth. In this respect, there is still a lack of understanding about the influence of the stability in the mechanism of transformation. Moreover, there are no detailed investigations of the mechanism behind the glass transition in ultrastable polymer and metallic glasses. The universality of the low-temperature glassy properties (in particular, the existence of two-level systems) seems to be broken by this family of highly-stable vapor deposited glasses. However, the research in this area is still scarce and more data is needed before reaching sound conclusions. For instance, we are not aware of any measurements of thermal conductivity in the low-temperature region to ascertain whether stable glasses show the thermal conductivity plateau often observed in conventional glasses.
The enhanced mechanical properties, thermal stability and resistance against degradation and crystallization of highly stable glasses, bring great opportunities for their use in applications where conventional liquid-cooled glasses fail. In addition, the simultaneous tunability of the molecular orientation in vapor-deposited organic glasses and their higher density reached under appropriate deposition conditions, is of relevance to prepare (opto)electronic devices with higher efficiencies and lifetimes. Some preliminary activities in organic light emitting diodes and organic field effect transistors have shown promising results, but the field is still largely unexplored.
Notes
The glass state is said to be reached when the viscosity attains 1012 Pa·s (1013 poise)[238].
References
S.F. Swallen, K.L. Kearns, M.K. Mapes et al., Organic glasses with exceptional thermodynamic and kinetic stability. Science 315, 353–356 (2007). https://doi.org/10.1126/science.1135795
J. Ràfols-Ribé, P.-A. Will, C. Hänisch et al., High-performance organic light-emitting diodes comprising ultrastable glass layers. Sci Adv 4, aar8332 (2018). https://doi.org/10.1126/sciadv.aar8332
M.D. Ediger, J. De Pablo, L. Yu, Anisotropic vapor-deposited glasses: hybrid organic solids. Acc. Chem. Res. 52, 407–414 (2019). https://doi.org/10.1021/acs.accounts.8b00513
M.D. Ediger, Perspective: highly stable vapor-deposited glasses. J. Chem. Phys. 147, 210901 (2017). https://doi.org/10.1063/1.5006265
K. Bagchi, M.D. Ediger, Controlling structure and properties of vapor-deposited glasses of organic semiconductors: recent advances and challenges. J. Phys. Chem. Lett. 11, 6935–6945 (2020)
A. Cavagna, Supercooled liquids for pedestrians. Phys. Rep. 476, 51–124 (2009). https://doi.org/10.1016/j.physrep.2009.03.003
M.D. Ediger, C.A. Angell, S.R. Nagel, Supercooled liquids and glasses. J. Phys. Chem. 100, 13200–13212 (1996). https://doi.org/10.1021/jp953538d
J.C. Maxwell, IV. On the dynamical theory of gases. Philos Trans R Soc London 157, 49–88 (1867). https://doi.org/10.1098/rstl.1867.0004
P. Badrinarayanan, W. Zheng, Q. Li, S.L. Simon, The glass transition temperature versus the fictive temperature. J Non Cryst Solids 353, 2603–2612 (2007). https://doi.org/10.1016/j.jnoncrysol.2007.04.025
L.-M. Martinez, C.A. Angell, A thermodynamic connection to the fragility of glass-forming liquids. Nature 410, 663–667 (2001). https://doi.org/10.1038/35070517
N.A. Mauro, M. Blodgett, M.L. Johnson et al., A structural signature of liquid fragility. Nat. Commun. 5, 4616 (2014). https://doi.org/10.1038/ncomms5616
L.L.-M. Wang, V. Velikov, C.A.C. Angell, Direct determination of kinetic fragility indices of glassforming liquids by differential scanning calorimetry: kinetic versus thermodynamic fragilities. J. Chem. Phys. 117, 10184 (2002). https://doi.org/10.1063/1.1517607
K.L. Ngai, P. Lunkenheimer, C. León et al., Nature and properties of the Johari-Goldstein β-relaxation in the equilibrium liquid state of a class of glass-formers. J Chem Phys 115, 1405–1413 (2001). https://doi.org/10.1063/1.1381054
L. Comez, C. Masciovecchio, G. Monaco, D. Fioretto, Progress in liquid and glass physics by Brillouin scattering spectroscopy, in Solid State Physics. ed. by S. Sps (Elsevier, Amsterdam, 2012), pp. 1–77
D. Yokoyama, A. Sakaguchi, M. Suzuki, C. Adachi, Enhancement of electron transport by horizontal molecular orientation of oxadiazole planar molecules in organic amorphous films. Appl Phys Lett 95, 243303 (2009). https://doi.org/10.1063/1.3274135
K. Bagchi, N.E. Jackson, A. Gujral et al., Origin of anisotropic molecular packing in vapor-deposited Alq3 glasses. J. Phys. Chem. Lett. 10, 164–170 (2018). https://doi.org/10.1021/ACS.JPCLETT.8B03582
C.T. Moynihan, S.-K. Lee, M. Tatsumisago, T. Minami, Estimation of activation energies for structural relaxation and viscous flow from DTA and DSC experiments. Thermochim Acta 280–281, 153–162 (1996). https://doi.org/10.1016/0040-6031(95)02781-5
P.G. Wolynes, Spatiotemporal structures in aging and rejuvenating glasses. Proc Natl Acad Sci USA 106, 1353–1358 (2009). https://doi.org/10.1073/pnas.0812418106
M. Goldstein, Viscous liquids and the glass transition: a potential energy barrier picture. J. Chem. Phys. 51, 3728 (2003). https://doi.org/10.1063/1.1672587
F.H. Stillinger, A topographic view of supercooled liquids and glass formation. Science (80-) 267, 1935–1939 (1995). https://doi.org/10.1126/SCIENCE.267.5206.1935
P.G. Debenedetti, F.H. Stillinger, Supercooled liquids and the glass transition. Nat 410, 259–267 (2001). https://doi.org/10.1038/35065704
W. Kauzmann, The nature of the glassy state and the behavior of liquids at low temperatures. Chem. Rev. 43, 219–256 (1948). https://doi.org/10.1021/CR60135A002
E.A.A. Pogna, C. Rodríguez-Tinoco, G. Cerullo et al., Probing equilibrium glass flow up to exapoise viscosities. Proc Natl Acad Sci USA 112, 2331–2336 (2015). https://doi.org/10.1073/pnas.1423435112
J. Zhao, S.L. Simon, G.B. McKenna, Using 20-million-year-old amber to test the super-Arrhenius behaviour of glass-forming systems. Nat. Commun. 4, 1783 (2013). https://doi.org/10.1038/ncomms2809
M.S. Beasley, C. Bishop, B.J. Kasting, M.D. Ediger, Vapor-deposited ethylbenzene glasses approach “ideal glass” density. J. Phys. Chem. Lett. 10, 4069–4075 (2019). https://doi.org/10.1021/acs.jpclett.9b01508
E. Leon-Gutierrez, A. Sepúlveda, G. Garcia et al., Stability of thin film glasses of toluene and ethylbenzene formed by vapor deposition: an in situ nanocalorimetric study. Phys. Chem. Chem. Phys. 12, 14693–14698 (2010). https://doi.org/10.1039/c0cp00208a
E. Leon-Gutierrez, A. Sepúlveda, G. Garcia et al., Correction: stability of thin film glasses of toluene and ethylbenzene formed by vapor deposition: an in situ nanocalorimetric study. Phys. Chem. Chem. Phys. 18, 8244–8245 (2016). https://doi.org/10.1039/C6CP90023B
S.L.L.M. Ramos, M. Oguni, K. Ishii, H. Nakayama, Character of devitrification, viewed from enthalpic paths, of the vapor-deposited ethylbenzene glasses. J. Phys. Chem. B 115, 14327–14332 (2011). https://doi.org/10.1021/jp203612s
S.S. Dalal, D.M. Walters, I. Lyubimov et al., Tunable molecular orientation and elevated thermal stability of vapor-deposited organic semiconductors. Proc. Natl. Acad. Sci. 112, 4227–4232 (2015). https://doi.org/10.1073/pnas.1421042112
J. Ràfols-Ribé, A. Vila-Costa, C. Rodríguez-Tinoco et al., Kinetic arrest of front transformation to gain access to the bulk glass transition in ultrathin films of vapour-deposited glasses. Phys. Chem. Chem. Phys. 20, 29989–29995 (2018). https://doi.org/10.1039/c8cp06264a
Y. Esaki, T. Komino, T. Matsushima, C. Adachi, Enhanced electrical properties and air stability of amorphous organic thin films by engineering film density. J. Phys. Chem. Lett. 8, 5891–5897 (2017). https://doi.org/10.1021/acs.jpclett.7b02808
Y. Esaki, T. Matsushima, C. Adachi, Discussion on hole traps of amorphous films of N, N ′-di(1-naphthyl)- N, N ′-diphenyl-(1,1′-biphenyl)-4,4′-diamine (α-NPD) deposited at different substrate temperatures. Appl. Phys. Lett. 114, 173301 (2019). https://doi.org/10.1063/1.5089269
C. Bishop, A. Gujral, M.F. Toney et al., Vapor-deposited glass structure determined by deposition rate-substrate temperature superposition principle. J. Phys. Chem. Lett. 10, 3536–3542 (2019). https://doi.org/10.1021/acs.jpclett.9b01377
K.L. Kearns, S.F. Swallen, M.D. Ediger et al., Influence of substrate temperature on the stability of glasses prepared by vapor deposition. J. Chem. Phys. 127, 154702 (2007). https://doi.org/10.1063/1.2789438
P. Luo, C.R. Cao, F. Zhu et al., Ultrastable metallic glasses formed on cold substrates. Nat. Commun. 9, 1389 (2018). https://doi.org/10.1038/s41467-018-03656-4
K.L. Kearns, S.F. Swallen, M.D. Ediger et al., Hiking down the energy landscape: progress toward the Kauzmann temperature via vapor deposition. J. Phys. Chem. B 112, 4934–4942 (2008). https://doi.org/10.1021/jp7113384
Ràfols Ribé J, Organic vapour-deposited stable glasses: from fundamental thermal properties to high-performance organic light-emitting diodes. PhD thesis Univ Autònoma Barcelona http//hdl.handle.net/10803/457956 (2017)
J. Ràfols-Ribé, M. Gonzalez-Silveira, C. Rodríguez-Tinoco, J. Rodríguez-Viejo, The role of thermodynamic stability in the characteristics of the devitrification front of vapour-deposited glasses of toluene. Phys. Chem. Chem. Phys. 19, 11089–11097 (2017). https://doi.org/10.1039/c7cp00741h
C. Rodríguez-Tinoco, M. Gonzalez-Silveira, J. Ràfols-Ribé et al., Highly stable glasses of celecoxib: influence on thermo-kinetic properties, microstructure and response towards crystal growth. J. Non Cryst. Solids 407, 256–261 (2015). https://doi.org/10.1016/j.jnoncrysol.2014.07.031
Y. Jin, A. Zhang, S.E. Wolf et al., Glasses denser than the supercooled liquid. Proc Natl Acad Sci USA 118, 1–7 (2021). https://doi.org/10.1073/pnas.2100738118
A. Zhang, Y. Jin, T. Liu et al., Polyamorphism of vapor-deposited amorphous selenium in response to light. PNAS 117, 24076–24081 (2020). https://doi.org/10.1073/pnas.2009852117/-/DCSupplemental.y
A. Gujral, L. Yu, M.D. Ediger, Anisotropic organic glasses. Curr. Opin. Solid State Mater. Sci. 22, 49–57 (2018). https://doi.org/10.1016/j.cossms.2017.11.001
D. Yokoyama, Molecular orientation in small-molecule organic light-emitting diodes. J. Mater. Chem. 21, 19187 (2011). https://doi.org/10.1039/c1jm13417e
D. Yokoyama, Y. Setoguchi, A. Sakaguchi et al., Orientation control of linear-shaped molecules in vacuum-deposited organic amorphous films and its effect on carrier mobilities. Adv Funct Mater 20, 386–391 (2010). https://doi.org/10.1002/adfm.200901684
M. Shibata, Y. Sakai, D. Yokoyama, Advantages and disadvantages of vacuum-deposited and spin-coated amorphous organic semiconductor films for organic light-emitting diodes. J. Mater. Chem. C 3, 11178–11191 (2015). https://doi.org/10.1039/C5TC01911G
I. Lyubimov, L. Antony, D.M. Walters et al., Orientational anisotropy in simulated vapor-deposited molecular glasses. J. Chem. Phys. 143, 094502 (2015). https://doi.org/10.1063/1.4928523
A. Gujral, K.A. O’Hara, M.F. Toney et al., Structural characterization of vapor-deposited glasses of an organic hole transport material with X-ray scattering. Chem. Mater. 27, 3341–3348 (2015). https://doi.org/10.1021/acs.chemmater.5b00583
E. Axinte, Metallic glasses from “alchemy” to pure science: present and future of design, processing and applications of glassy metals. Mater. Des. 35, 518–556 (2012). https://doi.org/10.1016/j.matdes.2011.09.028
S. Liu, Q. Cao, D. Zhang, J.Z. Jiang, Metallic glassy thin films: perspective on mechanical, magnetic, biomedical, and optical properties. Adv. Eng. Mater. 21, 1900046 (2019)
Aji DPB, Hirata A, Zhu F, et al., Ultrastrong and ultrastable metallic glass. Arxive http://arxiv.org/abs/1306.1575 (2013)
Y.-B. Bin, Y. Luo, K. Samwer, Ultrastable metallic glass. Adv. Mater. 25, 5904–5908 (2013). https://doi.org/10.1002/adma.201302700
M. Lüttich, V.M. Giordano, S. Le Floch et al., Anti-aging in ultrastable metallic glasses. Phys. Rev. Lett. 120, 135504 (2018). https://doi.org/10.1103/PhysRevLett.120.135504
T. Dziuba, Y. Luo, K. Samwer, Local mechanical properties of an ultrastable metallic glass. J. Phys. Condens. Matter 32, 345101 (2020). https://doi.org/10.1088/1361-648X/ab8aa2
Q. Sun, D.M. Miskovic, M. Ferry, Film thickness effect on formation of ultrastable metallic glasses. Mater. Today Phys. 18, 100370 (2021). https://doi.org/10.1016/j.mtphys.2021.100370
Q. Sun, D.M. Miskovic, K. Laws et al., Transition towards ultrastable metallic glasses in Zr-based thin films. Appl. Surf. Sci. 533, 147453 (2020). https://doi.org/10.1016/j.apsusc.2020.147453
M. Liu, C.R. Cao, Y.M. Lu et al., Flexible amorphous metal films with high stability. Appl. Phys. Lett. 110, 031901 (2017). https://doi.org/10.1063/1.4974153
A.D.S. Parmar, M. Ozawa, L. Berthier, Ultrastable metallic glasses in silico. Phys. Rev. Lett. 125, 085505 (2020). https://doi.org/10.1103/PhysRevLett.125.085505
G.B. Bokas, L. Zhao, D. Morgan, I. Szlufarska, Increased stability of CuZrAl metallic glasses prepared by physical vapor deposition. J. Alloys. Compd. 728, 1110–1115 (2017). https://doi.org/10.1016/j.jallcom.2017.09.068
J.-H. Chu, H.-W. Chen, Y.-C. Chan et al., Modification of structure and property in Zr-based thin film metallic glass via processing temperature control. Thin Solid Films 561, 38–42 (2014). https://doi.org/10.1016/j.tsf.2013.05.179
J.K. Hirvonen, Ion beam assisted thin film deposition. Mater. Sci. Rep. 6, 215–274 (1991). https://doi.org/10.1016/0920-2307(91)90008-B
K.L. Kearns, P. Krzyskowski, Z. Devereaux, Using deposition rate to increase the thermal and kinetic stability of vapor-deposited hole transport layer glasses via a simple sublimation apparatus. J. Chem. Phys. 146, 203328 (2017). https://doi.org/10.1063/1.4979814
S.V. Muley, C. Cao, D. Chatterjee et al., Varying kinetic stability, icosahedral ordering, and mechanical properties of a model Zr-Cu-Al metallic glass by sputtering. Phys. Rev. Mater. 5, 033602 (2021). https://doi.org/10.1103/physrevmaterials.5.033602
S.Y. Liu, Q.P. Cao, X. Qian et al., Effects of substrate temperature on structure, thermal stability and mechanical property of a Zr-based metallic glass thin film. Thin Solid Films 595, 17–24 (2015). https://doi.org/10.1016/j.tsf.2015.10.049
D.J. Magagnosc, G. Feng, L. Yu et al., Isochemical control over structural state and mechanical properties in Pd-based metallic glass by sputter deposition at elevated temperatures. APL Mater. 4, 086104 (2016). https://doi.org/10.1063/1.4960388
B. Yang, C.T. Liu, T.G. Nieh, Unified equation for the strength of bulk metallic glasses. Appl. Phys. Lett. 88, 7–9 (2006). https://doi.org/10.1063/1.2206099
R.J. Xue, L.Z. Zhao, C.L. Shi et al., Enhanced kinetic stability of a bulk metallic glass by high pressure. Appl. Phys. Lett. 109, 221904 (2016). https://doi.org/10.1063/1.4968834
M. Rams-Baron, Z. Wojnarowska, J. Knapik-Kowalczuk et al., The dielectric signature of glass density. Appl. Phys. Lett. 111, 121902 (2017). https://doi.org/10.1063/1.4990411
C. Rodríguez-Tinoco, M. González-Silveira, M. Barrio et al., Ultrastable glasses portray similar behaviour to ordinary glasses at high pressure. Sci. Rep. 6, 34296 (2016). https://doi.org/10.1038/srep34296
H. Usui, Preparation of polymer thin films by physical vapor deposition. Funct. Polym. Film 1, 287–318 (2011). https://doi.org/10.1002/9783527638482.CH9
H. Yoon, Y.P. Koh, S.L. Simon, G.B. McKenna, An ultrastable polymeric glass: amorphous fluoropolymer with extreme fictive temperature reduction by vacuum pyrolysis. Macromolecules 50, 4562–4574 (2017). https://doi.org/10.1021/acs.macromol.7b00623
Y. Guo, A. Morozov, D. Schneider et al., Ultrastable nanostructured polymer glasses. Nat. Mater. 11, 337–343 (2012). https://doi.org/10.1038/nmat3234
A.N. Raegen, J. Yin, Q. Zhou, J.A. Forrest, Ultrastable monodisperse polymer glass formed by physical vapour deposition. Nat. Mater. 19, 1110–1113 (2020). https://doi.org/10.1038/s41563-020-0723-7
X. Monnier, J. Colmenero, M. Wolf, D. Cangialosi, Reaching the ideal glass in polymer spheres: thermodynamics and vibrational density of states. Phys. Rev. Lett. 126, 118004 (2021). https://doi.org/10.1103/PhysRevLett.126.118004
X. Monnier, D. Cangialosi, Thermodynamic ultrastability of a polymer glass confined at the micrometer length scale. Phys. Rev. Lett. 121, 137801 (2018). https://doi.org/10.1103/PhysRevLett.121.137801
K. Zhang, Y. Li, Q. Huang et al., Ultrastable amorphous Sb2Se3 Film. J. Phys. Chem. B 121, 8188–8194 (2017). https://doi.org/10.1021/acs.jpcb.7b03408
A. Vila-Costa, J. Ràfols-Ribé, M. Gonzalez-Silveira et al., Multiple glass transitions in vapor-deposited orientational glasses of the most fragile plastic crystal Freon 113. Phys. Chem. Chem. Phys. 21, 10436–10441 (2019). https://doi.org/10.1039/c9cp00976k
K. Kaminski, S. Pawlus, K. Adrjanowicz et al., The importance of the activation volume for the description of the molecular dynamics of glass-forming liquids. J. Phys. Condens. Matter 24, 065105 (2012). https://doi.org/10.1088/0953-8984/24/6/065105
C. Rodríguez-Tinoco, K.L. Ngai, M. Rams-Baron et al., Distinguishing different classes of secondary relaxations from vapour deposited ultrastable glasses. Phys. Chem. Chem. Phys. 20, 21925–21933 (2018). https://doi.org/10.1039/c8cp02341g
M.T. Viciosa, J.J. Moura Ramos, H.P. Diogo, Thermal behavior and molecular mobility studies in the supercooled liquid and glassy states of carvedilol and loratadine. Int. J. Pharm. 584, 119410 (2020). https://doi.org/10.1016/j.ijpharm.2020.119410
K. Adrjanowicz, Z. Wojnarowska, P. Wlodarczyk et al., Molecular mobility in liquid and glassy states of Telmisartan (TEL) studied by Broadband Dielectric Spectroscopy. Eur. J. Pharm. Sci. 38, 395–404 (2009). https://doi.org/10.1016/j.ejps.2009.09.009
M. Rams-Baron, J. Pacult, A. Jedrzejowska et al., Changes in physical stability of supercooled etoricoxib after compression. Mol. Pharm. 15, 3969–3978 (2018). https://doi.org/10.1021/acs.molpharmaceut.8b00428
C. Rodríguez-Tinoco, M. Rams-Baron, K.L. Ngai et al., Secondary relaxation in ultrastable etoricoxib: evidence of correlation with structural relaxation. Phys. Chem. Chem. Phys. 20, 3939–3945 (2018). https://doi.org/10.1039/C7CP06445D
L.M. Wang, C.A. Angell, R. Richert, Fragility and thermodynamics in nonpolymeric glass-forming liquids. J. Chem. Phys. 125, 074505-1-074505–6 (2006). https://doi.org/10.1063/1.2244551
B. Riechers, A. Guiseppi-Elie, M.D. Ediger, R. Richert, Dielectric properties of vapor-deposited propylbenzenes. J. Chem. Phys. 151, 174503 (2019). https://doi.org/10.1063/1.5125138
Z. Chen, R. Richert, Dynamics of glass-forming liquids. XV. Dynamical features of molecular liquids that form ultra-stable glasses by vapor deposition. J. Chem. Phys. 135, 124515 (2011). https://doi.org/10.1063/1.3643332
M.S. Beasley, B.J. Kasting, M.E. Tracy et al., Physical vapor deposition of a polyamorphic system: Triphenyl phosphite. J. Chem. Phys. 153, 124511 (2020). https://doi.org/10.1063/5.0019872
M.S. Beasley, M. Tylinski, Y.Z. Chua et al., Glasses of three alkyl phosphates show a range of kinetic stabilities when prepared by physical vapor deposition. J. Chem. Phys. 148, 174503 (2018). https://doi.org/10.1063/1.5026505
A. Laventure, A. Gujral, O. Lebel et al., Influence of hydrogen bonding on the kinetic stability of vapor-deposited glasses of triazine derivatives. J. Phys. Chem. B 121, 2350–2358 (2017). https://doi.org/10.1021/ACS.JPCB.6B12676
Y. Chen, M. Zhu, A. Laventure et al., Influence of hydrogen bonding on the surface diffusion of molecular glasses: comparison of three triazines. J. Phys. Chem. B 121, 7221–7227 (2017). https://doi.org/10.1021/acs.jpcb.7b05333
Y.Z. Chua, M. Tylinski, S. Tatsumi et al., Glass transition and stable glass formation of tetrachloromethane. J. Chem. Phys. 144, 244503-1-244503–9 (2016). https://doi.org/10.1063/1.4954665
M. Tylinski, M.S. Beasley, Y.Z. Chua et al., Limited surface mobility inhibits stable glass formation for 2-ethyl-1-hexanol. J. Chem. Phys. 146, 203317 (2017). https://doi.org/10.1063/1.4977787
Y. Qiu, L.W. Antony, J.J. De Pablo, M.D. Ediger, Photostability can be significantly modulated by molecular packing in glasses. J. Am. Chem. Soc. 138, 11282–11289 (2016). https://doi.org/10.1021/jacs.6b06372
M. Tylinski, Y.Z. Chua, M.S. Beasley et al., Vapor-deposited alcohol glasses reveal a wide range of kinetic stability. J. Chem. Phys. 145, 174506 (2016). https://doi.org/10.1063/1.4966582
Y.Z. Chua, M. Ahrenberg, M. Tylinski et al., How much time is needed to form a kinetically stable glass? AC calorimetric study of vapor-deposited glasses of ethylcyclohexane. J. Chem. Phys. 142, 1–12 (2015). https://doi.org/10.1063/1.4906806
D.M. Walters, L. Antony, J.J. De Pablo, M.D. Ediger, Influence of molecular shape on the thermal stability and molecular orientation of vapor-deposited organic semiconductors. J. Phys. Chem. Lett. 8, 3380–3386 (2017). https://doi.org/10.1021/acs.jpclett.7b01097
K. Bagchi, A. Gujral, M.F. Toney, M.D. Ediger, Generic packing motifs in vapor-deposited glasses of organic semiconductors. Soft Matter 15, 7590–7595 (2019). https://doi.org/10.1039/c9sm01155b
J. Jiang, D.M. Walters, D. Zhou, M.D. Ediger, Substrate temperature controls molecular orientation in two-component vapor-deposited glasses. Soft Matter 12, 3265–3270 (2016). https://doi.org/10.1039/c6sm00262e
C. Rodríguez-Tinoco, M. Gonzalez-Silveira, J. Ràfols-Ribé et al., Surface-bulk interplay in vapor-deposited glasses: crossover length and the origin of front transformation. Phys. Rev. Lett. 123, 155501 (2019). https://doi.org/10.1103/PhysRevLett.123.155501
D.M. Walters, R. Richert, M.D. Ediger, Thermal stability of vapor-deposited stable glasses of an organic semiconductor. J. Chem. Phys. 142, 134504 (2015). https://doi.org/10.1063/1.4916649
Y. Zhang, R. Potter, W. Zhang, Z. Fakhraai, Using tobacco mosaic virus to probe enhanced surface diffusion of molecular glasses. Soft Matter 12, 9115–9120 (2016). https://doi.org/10.1039/c6sm01566b
J. Ràfols-Ribé, R. Dettori, P. Ferrando-Villalba et al., Evidence of thermal transport anisotropy in stable glasses of vapor deposited organic molecules. Phys. Rev. Mater 2, 035603 (2018). https://doi.org/10.1103/PhysRevMaterials.2.035603
M.D. Ediger, P. Harrowell, L. Yu, Crystal growth kinetics exhibit a fragility-dependent decoupling from viscosity. J. Chem. Phys. 128, 214504 (2008). https://doi.org/10.1063/1.2815325
K.R. Whitaker, M. Tylinski, M. Ahrenberg et al., Kinetic stability and heat capacity of vapor-deposited glasses of o-terphenyl. J. Chem. Phys. 143, 084511 (2015). https://doi.org/10.1063/1.4929511
A. Sepúlveda, M. Tylinski, A. Guiseppi-Elie et al., Role of fragility in the formation of highly stable organic glasses. Phys. Rev. Lett. 113, 1–5 (2014). https://doi.org/10.1103/PhysRevLett.113.045901
B.J. Kasting, M.S. Beasley, A. Guiseppi-Elie et al., Relationship between aged and vapor-deposited organic glasses: secondary relaxations in methyl- m -toluate. J. Chem. Phys. 151, 144502 (2019). https://doi.org/10.1063/1.5123305
M. Tylinski, A. Sepúlveda, D.M. Walters et al., Vapor-deposited glasses of methyl- m -toluate: how uniform is stable glass transformation? J. Chem. Phys. 143, 244509 (2015). https://doi.org/10.1063/1.4938420
M. Ahrenberg, Y.Z. Chua, K.R. Whitaker et al., In situ investigation of vapor-deposited glasses of toluene and ethylbenzene via alternating current chip-nanocalorimetry. J. Chem. Phys. 138, 024501 (2013). https://doi.org/10.1063/1.4773354
H.B. Yu, M. Tylinski, A. Guiseppi-Elie et al., Suppression of β relaxation in vapor-deposited ultrastable glasses. Phys. Rev. Lett. 115, 185501 (2015). https://doi.org/10.1103/PhysRevLett.115.185501
E. León-Gutierrez, G. Garcia, A.F. Lopeandía et al., In situ nanocalorimetry of thin glassy organic films. J. Chem. Phys. 129, 181101 (2008). https://doi.org/10.1063/1.3009766
K.R. Whitaker, D.J. Scifo, M.D. Ediger et al., Highly stable glasses of cis-decalin and cis/trans-decalin mixtures. J. Phys. Chem. B 117, 12724–12733 (2013). https://doi.org/10.1021/jp400960g
Y. Qiu, L.W. Antony, J.M. Torkelson et al., Tenfold increase in the photostability of an azobenzene guest in vapor-deposited glass mixtures. J. Chem. Phys. 149, 204503 (2018). https://doi.org/10.1063/1.5052003
C. Rodríguez-Tinoco, J. Ràfols-Ribé, M. González-Silveira, J. Rodríguez-Viejo, Relaxation dynamics of glasses along a wide stability and temperature range. Sci. Rep. 6, 35607 (2016). https://doi.org/10.1038/srep35607
L. Zhu, C.W. Brian, S.F. Swallen et al., Surface self-diffusion of an organic glass. Phys. Rev. Lett. 106, 256103 (2011). https://doi.org/10.1103/PhysRevLett.106.256103
C. Rodríguez-Tinoco, M. Gonzalez-Silveira, J. Ràfols-Ribé et al., Evaluation of growth front velocity in ultrastable glasses of indomethacin over a wide temperature interval. J. Phys. Chem. B 118, 10795–10801 (2014). https://doi.org/10.1021/jp506782d
K.L. Kearns, K.R. Whitaker, M.D. Ediger et al., Observation of low heat capacities for vapor-deposited glasses of indomethacin as determined by AC nanocalorimetry. J. Chem. Phys. 133, 014702 (2010). https://doi.org/10.1063/1.3442416
S.S. Dalal, Z. Fakhraai, M.D. Ediger, High-throughput ellipsometric characterization of vapor-deposited indomethacin glasses. J. Phys. Chem. B 117, 15415–15425 (2013). https://doi.org/10.1021/jp405005n
Z. Chen, A. Sepúlveda, M.D. Ediger, R. Richert, Dynamics of glass-forming liquids. XVI. Observation of ultrastable glass transformation via dielectric spectroscopy. J. Chem. Phys. 138, 12A519 (2013). https://doi.org/10.1063/1.4771695
Z. Fakhraai, T. Still, G. Fytas, M.D. Ediger, Structural variations of an organic glassformer vapor-deposited onto a temperature gradient stage. J. Phys. Chem. Lett. 2, 423–427 (2011)
K.J. Dawson, K.L. Kearns, M.D. Ediger et al., Highly stable indomethacin glasses resist uptake of water vapor. J. Phys. Chem. B 113, 2422–2427 (2009). https://doi.org/10.1021/jp808838t
A. Sepúlveda, S.F. Swallen, L. Kopff, a, et al., Stable glasses of indomethacin and α, α, β-tris-naphthylbenzene transform into ordinary supercooled liquids. J. Chem. Phys. 137, 204508 (2012). https://doi.org/10.1063/1.4768168
T. Liu, K. Cheng, E. Salami-Ranjbaran et al., The effect of chemical structure on the stability of physical vapor deposited glasses of 1,3,5-triarylbenzene. J. Chem. Phys. 143, 84506 (2015). https://doi.org/10.1063/1.4928521
S. Samanta, G. Huang, G. Gao et al., Exploring the importance of surface diffusion in stability of vapor-deposited organic glasses. J. Phys. Chem. B 123, 4108–4117 (2019). https://doi.org/10.1021/acs.jpcb.9b01012
T. Liu, A.L. Exarhos, E.C. Alguire et al., Birefringent stable glass with predominantly isotropic molecular orientation. Phys. Rev. Lett. 119, 095502 (2017). https://doi.org/10.1103/PhysRevLett.119.095502
K.R. Whitaker, M. Ahrenberg, C. Schick, M.D. Ediger, Vapor-deposited α, α, β-tris-naphthylbenzene glasses with low heat capacity and high kinetic stability. J. Chem. Phys. 137, 154502 (2012). https://doi.org/10.1063/1.4758807
S.S. Dalal, A. Sepúlveda, G.K. Pribil et al., Density and birefringence of a highly stable α, α, β- trisnaphthylbenzene glass. J. Chem. Phys. 136, 204501 (2012). https://doi.org/10.1063/1.4719532
K. Dawson, L.A. Kopff, L. Zhu et al., Molecular packing in highly stable glasses of vapor-deposited tris-naphthylbenzene isomers. J. Chem. Phys. 136, 094505 (2012). https://doi.org/10.1063/1.3686801
K.L. Kearns, T. Still, G. Fytas, M.D. Ediger, High-modulus organic classes prepared by physical vapor deposition. Adv. Mater. 22, 39–42 (2010). https://doi.org/10.1002/adma.200901673
C. Bishop, K. Bagchi, M.F. Toney F, M.D. Ediger, Vapor deposition rate modifies anisotropic glassy structure of an anthracene-based organic semiconductor. http://arxiv.org/abs/211006747 (2021)
H. Yoon, G.B. McKenna, Testing the paradigm of an ideal glass transition: dynamics of an ultrastable polymeric glass. Sci. Adv. 4, 5423 (2018). https://doi.org/10.1126/SCIADV.AAU5423
C. Huang, S. Ruan, T. Cai, L. Yu, Fast surface diffusion and crystallization of amorphous griseofulvin. J. Phys. Chem. B 121, 9463–9468 (2017). https://doi.org/10.1021/acs.jpcb.7b07319
Y. Chen, Z. Chen, M. Tylinski et al., Effect of molecular size and hydrogen bonding on three surface-facilitated processes in molecular glasses: surface diffusion, surface crystal growth, and formation of stable glasses by vapor deposition. J. Chem. Phys. 150, 024502 (2019). https://doi.org/10.1063/1.5079441
Y. Chen, W. Zhang, L. Yu, Hydrogen bonding slows down surface diffusion of molecular glasses. J. Phys. Chem. B 120, 8007–8015 (2016). https://doi.org/10.1021/ACS.JPCB.6B05658
S. Ruan, W. Zhang, Y. Sun et al., Surface diffusion and surface crystal growth of tris -naphthyl benzene glasses. J. Chem. Phys. 145, 064503 (2016). https://doi.org/10.1063/1.4960301
W. Zhang, C.W. Brian, L. Yu, Fast surface diffusion of amorphous o-terphenyl and its competition with viscous flow in surface evolution. J. Phys. Chem. B 119, 5071–5078 (2015). https://doi.org/10.1021/jp5127464
W. Zhang, L. Yu, Surface diffusion of polymer glasses. Macromolecules 49, 731–735 (2016). https://doi.org/10.1021/ACS.MACROMOL.5B02294
Y. Chai, T. Salez, J.D. McGraw et al., A direct quantitative measure of surface mobility in a glassy polymer. Science 343, 994–999 (2014). https://doi.org/10.1126/SCIENCE.1244845
Z. Fakhraai, J.A. Forrest, Measuring the surface dynamics of glassy polymers. Science (80-) 319, 600–604 (2008). https://doi.org/10.1126/SCIENCE.1151205
E. Thoms, J.P. Gabriel, A. Guiseppi-Elie et al., In situ observation of fast surface dynamics during the vapor-deposition of a stable organic glass. Soft Matter 16, 10860–10864 (2020). https://doi.org/10.1039/D0SM01916J
K. Paeng, S.F. Swallen, M.D. Ediger, Direct measurement of molecular motion in freestanding polystyrene thin films. J. Am. Chem. Soc. 133, 8444–8447 (2011). https://doi.org/10.1021/JA2022834
Y. Zhang, E.C. Glor, M. Li et al., Long-range correlated dynamics in ultra-thin molecular glass films. J. Chem. Phys. 145, 114502 (2016). https://doi.org/10.1063/1.4962734
Y. Zhang, Z. Fakhraai, Decoupling of surface diffusion and relaxation dynamics of molecular glasses. Proc. Natl. Acad. Sci. USA 114, 4915–4919 (2017). https://doi.org/10.1073/pnas.1701400114
J.D. Stevenson, P.G. Wolynes, On the surface of glasses. J. Chem. Phys. 129, 234514 (2008). https://doi.org/10.1063/1.3041651
N. Kuon, E. Flenner, G. Szamel, Comparison of single particle dynamics at the center and on the surface of equilibrium glassy films. J. Chem. Phys. 149, 074501 (2018). https://doi.org/10.1063/1.5039505
L. Berthier, P. Charbonneau, E. Flenner, F. Zamponi, Origin of ultrastability in vapor-deposited glasses. Phys. Rev. Lett. 119, 188002 (2017). https://doi.org/10.1103/PhysRevLett.119.188002
A.R. Moore, G. Huang, S. Wolf et al., Effects of microstructure formation on the stability of vapor-deposited glasses. Proc. Natl. Acad. Sci. USA 116, 5937–5942 (2019). https://doi.org/10.1073/pnas.1821761116
C.A. Angell, On the uncertain distinction between fast landscape exploration and second amorphous phase (ideal glass) interpretations of the ultrastable glass phenomenon. J. Non Cryst. Solids 407, 246–255 (2015). https://doi.org/10.1016/j.jnoncrysol.2014.08.044
H. Nakayama, K. Omori, K. Ino-u-e, K. Ishii, Molar volumes of ethylcyclohexane and butyronitrile glasses resulting from vapor deposition: dependence on deposition temperature and comparison to alkylbenzenes. J. Phys. Chem. B 117, 10311–10319 (2013). https://doi.org/10.1021/JP404256R
C.P. Royall, F. Turci, S. Tatsumi et al., The race to the bottom: approaching the ideal glass? J. Phys. Condens. Matter 30, 363001 (2018). https://doi.org/10.1088/1361-648x/aad10a
J.H. Mangalara, M.D. Marvin, D.S. Simmons, Three-layer model for the emergence of ultrastable glasses from the surfaces of supercooled liquids. J. Phys. Chem. B 120, 4861–4865 (2016). https://doi.org/10.1021/acs.jpcb.6b04736
R.J. Lang, D.S. Simmons, Interfacial dynamic length scales in the glass transition of a model freestanding polymer film and their connection to cooperative motion. Macromolecules 46, 9818–9825 (2013). https://doi.org/10.1021/MA401525Q
D.M. Sussman, S.S. Schoenholz, E.D. Cubuk, A.J. Liu, Disconnecting structure and dynamics in glassy thin films. Proc. Natl. Acad. Sci. USA 114, 10601–10605 (2017). https://doi.org/10.1073/pnas.1703927114
A. Widmer-Cooper, H. Perry, P. Harrowell, D.R. Reichman, Irreversible reorganization in a supercooled liquid originates from localized soft modes. Nat. Phys. 49(4), 711–715 (2008). https://doi.org/10.1038/nphys1025
C.P. Royall, S.R. Williams, T. Ohtsuka, H. Tanaka, Direct observation of a local structural mechanism for dynamic arrest. Nat. Mater. 77(7), 556–561 (2008). https://doi.org/10.1038/nmat2219
K.L. Ngai, L.M. Wang, H.B. Yu, Relating ultrastable glass formation to enhanced surface diffusion via the Johari-Goldstein β-relaxation in molecular glasses. J. Phys. Chem. Lett. 8, 2739–2744 (2017). https://doi.org/10.1021/acs.jpclett.7b01192
D. Cangialosi, V.M. Boucher, A. Alegría, J. Colmenero, Direct evidence of two equilibration mechanisms in glassy polymers. Phys. Rev. Lett. 111, 095701 (2013). https://doi.org/10.1103/PhysRevLett.111.095701
N.G.P.-D. Eulate, D. Cangialosi, The very long-term physical aging of glassy polymers. Phys. Chem. Chem. Phys. 20, 12356–12361 (2018). https://doi.org/10.1039/C8CP01940A
V.M. Boucher, D. Cangialosi, A. Alegría et al., Reaching the ideal glass transition by aging polymer films. Phys. Chem. Chem. Phys. 19, 961–965 (2017). https://doi.org/10.1039/C6CP07139B
A. Sepúlveda, E. Leon-Gutierrez, M. Gonzalez-Silveira et al., Accelerated aging in ultrathin films of a molecular glass former. Phys. Rev. Lett. 107, 025901 (2011). https://doi.org/10.1103/PhysRevLett.107.025901
Q. Tang, W. Hu, Molecular simulation of structural relaxation in ultrathin polymer films. Phys. Chem. Chem. Phys. 15, 20679–20690 (2013). https://doi.org/10.1039/C3CP53555J
K.L. Ngai, The origin of the faster mechanism of partial enthalpy recovery deep in the glassy state of polymers. Phys. Chem. Chem. Phys. 23, 13468–13472 (2021). https://doi.org/10.1039/D1CP01445E
P. Luo, F. Zhu, Y.-M. Lv et al., Microscopic structural evolution during ultrastable metallic glass formation. ACS Appl. Mater Interfaces 13(33), 40098–40105 (2021). https://doi.org/10.1021/ACSAMI.1C10716
F.H. Stillinger, P.G. Debenedetti, T.M. Truskett, The Kauzmann paradox revisited. J. Phys. Chem. B 105(47), 11809–11816 (2001). https://doi.org/10.1021/jp011840i
S.S. Dalal, M.D. Ediger, Molecular orientation in stable glasses of indomethacin. J. Phys. Chem. Lett. 3, 1229–1233 (2012). https://doi.org/10.1021/jz3003266
C. Bishop, J.L. Thelen, E. Gann et al., Vapor deposition of a nonmesogen prepares highly structured organic glasses. Proc. Natl. Acad. Sci. 116, 21421–21426 (2019). https://doi.org/10.1073/pnas.1908445116
K. Dawson, L. Zhu, L. Yu, M.D. Ediger, Anisotropic structure and transformation kinetics of vapor-deposited indomethacin glasses. J. Phys. Chem. B 115, 455–463 (2011)
D.R. Reid, I. Lyubimov, M.D. Ediger, J.J. De Pablo, Age and structure of a model vapour-deposited glass. Nat. Commun. 7, 13062 (2016). https://doi.org/10.1038/ncomms13062
C.J. Fullerton, L. Berthier, Density controls the kinetic stability of ultrastable glasses. EPL 119, 36003 (2017). https://doi.org/10.1209/0295-5075/119/36003
M. Tarnacka, K. Adrjanowicz, E. Kaminska et al., Molecular dynamics of itraconazole at ambient and high pressure. Phys. Chem. Chem. Phys. 15, 20742–20752 (2013). https://doi.org/10.1039/C3CP52643G
A. Cassidy, M.R.V. Jørgensen, A. Glavic et al., A mechanism for ageing in a deeply supercooled molecular glass. Chem. Commun. 57, 6368–6371 (2021). https://doi.org/10.1039/D1CC01639C
K. Yoshizaki, T. Manaka, M. Iwamoto, Large surface potential of Alq3 film and its decay. J. Appl. Phys. 97, 023703 (2004). https://doi.org/10.1063/1.1835543
K. Bagchi, C. Deng, C. Bishop et al., Over what length scale does an inorganic substrate perturb the structure of a glassy organic semiconductor? ACS Appl. Mater. Interfaces 12, 26717–26726 (2020). https://doi.org/10.1021/ACSAMI.0C06428
L. Berthier, M.D. Ediger, How to “measure” a structural relaxation time that is too long to be measured? J. Chem. Phys. 153, 044501 (2020). https://doi.org/10.1063/5.0015227
K.L. Kearns, M.D. Ediger, H. Huth, C. Schick, One micrometer length scale controls kinetic stability of low-energy glasses. J. Phys. Chem. Lett. 1, 388–392 (2010). https://doi.org/10.1021/jz9002179
R.L. Jack, L. Berthier, The melting of stable glasses is governed by nucleation-and-growth dynamics. J. Chem. Phys. 144, 244506 (2016). https://doi.org/10.1063/1.4954327
A. Sepúlveda, S.F. Swallen, M.D. Ediger, Manipulating the properties of stable organic glasses using kinetic facilitation. J. Chem. Phys. 138, 12A517 (2013). https://doi.org/10.1063/1.4772594
A. Vila-Costa, J. Ràfols-Ribé, M. González-Silveira et al., Nucleation and growth of the supercooled liquid phase control glass transition in bulk ultrastable glasses. Phys. Rev. Lett. 124, 076002 (2020). https://doi.org/10.1103/PhysRevLett.124.076002
A. Wisitsorasak, P. Wolynes, Fluctuating mobility generation and transport in glasses. Phys. Rev. E 88, 022308 (2013). https://doi.org/10.1103/PhysRevE.88.022308
S.F. Swallen, K.L. Kearns, S. Satija et al., Molecular view of the isothermal transformation of a stable glass to a liquid. J. Chem. Phys. 128, 214514 (2008). https://doi.org/10.1063/1.2919570
S.F. Swallen, K. Traynor, R.J. McMahon, M.D. Ediger, Stable glass transformation to supercooled liquid via surface-initiated growth front. Phys. Rev. Lett. 102, 065503 (2009). https://doi.org/10.1103/PhysRevLett.102.065503
C. Rodríguez-Tinoco, M. Gonzalez-Silveira, J. Ràfols-Ribé et al., Transformation kinetics of vapor-deposited thin film organic glasses: the role of stability and molecular packing anisotropy. Phys. Chem. Chem. Phys. 17, 31195–31201 (2015). https://doi.org/10.1039/c5cp04692k
D. Bhattacharya, V. Sadtchenko, Enthalpy and high temperature relaxation kinetics of stable vapor-deposited glasses of toluene. J. Chem. Phys. 141, 094502 (2014). https://doi.org/10.1063/1.4893716
U.S. Cubeta, V. Sadtchenko, Glass softening kinetics in the limit of high heating rates. J. Chem. Phys. 150, 094508 (2019). https://doi.org/10.1063/1.5046304
I. Lyubimov, M.D. Ediger, J.J. de Pablo, Model vapor-deposited glasses: growth front and composition effects. J. Chem. Phys. 139, 144505 (2013). https://doi.org/10.1063/1.4823769
S. Léonard, P. Harrowell, Macroscopic facilitation of glassy relaxation kinetics: ultrastable glass films with frontlike thermal response. J. Chem. Phys. 133, 244502 (2010). https://doi.org/10.1063/1.3511721
R. Gutiérrez, J.P. Garrahan, Front propagation versus bulk relaxation in the annealing dynamics of a kinetically constrained model of ultrastable glasses. J. Stat. Mech. Theory Exp. 2016, 074005 (2016). https://doi.org/10.1088/1742-5468/2016/07/074005
E. Flenner, L. Berthier, P. Charbonneau, C.J. Fullerton, Front-mediated melting of isotropic ultrastable glasses. Phys. Rev. Lett. (2019). https://doi.org/10.1103/PhysRevLett.123.175501
G.M. Hocky, L. Berthier, D.R. Reichman, Equilibrium ultrastable glasses produced by random pinning. J. Chem. Phys. 141, 224503 (2014). https://doi.org/10.1063/1.4903200
W. Ogieglo, K. Tempelman, S. Napolitano, N.E. Benes, Evidence of a transition layer between the free surface and the bulk. J. Phys. Chem. Lett. 9, 1195–1199 (2018). https://doi.org/10.1021/acs.jpclett.8b00076
M.T. Clavaguera-Mora, N. Clavaguera, D. Crespo, T. Pradell, Crystallisation kinetics and microstructure development in metallic systems. Prog. Mater. Sci. 47, 559–619 (2002). https://doi.org/10.1016/S0079-6425(00)00021-9
M. Lulli, C.S. Lee, H.Y. Deng et al., Spatial Heterogeneities in structural temperature cause Kovacs’ expansion gap paradox in aging of glasses. Phys. Rev. Lett. 124, 095501 (2020). https://doi.org/10.1103/PhysRevLett.124.095501
I. Douglass, P. Harrowell, Can a stable glass be superheated modelling the kinetic stability of coated glassy films. J. Chem. Phys. 138, 12A516 (2013). https://doi.org/10.1063/1.4772480
C. Scalliet, L. Berthier, F. Zamponi, Nature of excitations and defects in structural glasses. Nat. Commun. 10, 5102 (2019). https://doi.org/10.1038/s41467-019-13010-x
J. Očenášek, P. Novák, S. Agbo, Finite-thickness effect on crystallization kinetics in thin films and its adaptation in the Johnson–Mehl–Avrami–Kolmogorov model. J. Appl. Phys. 115, 043505 (2014). https://doi.org/10.1063/1.4862858
W.A. Phillips, Amorphous Solids: Low-Temperature Properties (Springer, Berlin, 1981)
S.R. Elliott, Physics of Amorphous Materials, 2nd edn. (Longman, Essex, 1990)
P. Esquinazi, Tunneling Systems in Amorphous Ans Crystalline Solids (Springer, New York, 1998)
W.A. Phillips, Tunneling states in Amorphous And Crystalline. J. Low. Temp. Phys. 7, 351–360 (1972)
P.W. Anderson, B.I. Halperin, C.M. Varma, Anomalous low-temperature thermal properties of glasses and spin glasses. Philos. Mag. 25, 1–9 (1972). https://doi.org/10.1080/14786437208229210
W.A. Phillips, Two-level states in glasses. Rep. Prog. Phys. 50, 1657 (1987). https://doi.org/10.1088/0034-4885/50/12/003
M.A. Ramos, Are universal “anomalous” properties of glasses at low temperatures truly universal? Low Temp. Phys. 46, 104 (2020). https://doi.org/10.1063/10.0000527
A.V. Naumov, Y.G. Vainer, L. Kador, Does the standard model of low-temperature glass dynamics describe a real glass? Phys. Rev. Lett. 98, 145501 (2007). https://doi.org/10.1103/PhysRevLett.98.145501
I.Y. Eremchev, Y.G. Vainer, A.V. Naumov, L. Kador, Low-temperature dynamics in amorphous polymers and low-molecular-weight glasses—what is the difference? Phys. Chem. Chem. Phys. 13, 1843–1848 (2011). https://doi.org/10.1039/C0CP01690J
C.C. Yu, A.J. Leggett, Low temperature properties of amorphous materials: through a glass darkly. Comments Condes. Mat. Phys. 14, 231 (1988)
A.J. Leggett, Amorphous materials at low temperatures: why are they so similar? Phys. B Condens. Matter 169, 322–327 (1991). https://doi.org/10.1016/0921-4526(91)90246-B
M. Baggioli, R. Milkus, A. Zaccone, Vibrational density of states and specific heat in glasses from random matrix theory. Phys. Rev. E 100, 062131 (2019). https://doi.org/10.1103/PhysRevE.100.062131
R. Zorn, The boson peak demystified? Physics. 4, 44 (2011)
R.O. Pohl, X. Liu X, E. Thompson, Low-temperature thermal conductivity and acoustic attenuation in amorphous solids, Rev. Mod. Phys. 74, 991–1013 (2002). https://doi.org/10.1103/RevModPhys.74.991
T. Pérez-Castañeda, R.J. Jiménez-Riobóo, M.A. Ramos, Two-level systems and boson peak remain stable in 110-million-year-old amber glass. Phys. Rev. Lett. 112, 165901 (2014). https://doi.org/10.1103/PhysRevLett.112.165901
X. Liu, B.E. White Jr., R.O. Pohl et al., Amorphous solid without low energy excitations. Phys. Rev. Lett. 78, 4418–4421 (1997). https://doi.org/10.1103/PhysRevLett.78.4418
X. Liu, R.O. Pohl, Low-energy excitations in amorphous films of silicon and germanium. Phys. Rev. B 58, 9067–9081 (1998). https://doi.org/10.1103/PhysRevB.58.9067
N.I. Agladze, A.J. Sievers, Absence of an isotope effect in the two level spectrum of amorphous ice. Phys. Rev. Lett. 80, 4209–4212 (1998). https://doi.org/10.1103/PhysRevLett.80.4209
B.L. Zink, R. Pietri, F. Hellman, Thermal conductivity and specific heat of thin-film amorphous silicon. Phys. Rev. Lett. 96, 055902 (2006). https://doi.org/10.1103/PhysRevLett.96.055902
D.R. Queen, X. Liu, J. Karel et al., Excess specific heat in evaporated amorphous silicon. Phys. Rev. Lett. 110, 135901 (2013). https://doi.org/10.1103/PhysRevLett.110.135901
X. Liu, D.R. Queen, T.H. Metcalf et al., Hydrogen-free amorphous silicon with no tunneling states. Phys. Rev. Lett. 113, 025503 (2014). https://doi.org/10.1103/PhysRevLett.113.025503
M. Molina-Ruiz, H.C. Jacks, D.R. Queen et al., Two-level systems and growth-induced metastability in hydrogenated amorphous silicon. Mater. Res. Express 7, 095201 (2020). https://doi.org/10.1088/2053-1591/ABB498
J. Clarke, F.K. Wilhelm, Superconducting quantum bits. Nature 453, 1031–1042 (2008). https://doi.org/10.1038/NATURE07128
M.H. Devoret, R.J. Schoelkopf, Superconducting Circuits for quantum information: an outlook. Science 339, 1169–1174 (2013). https://doi.org/10.1126/science.1231930
C. Müller, J.H. Cole, J. Lisenfeld, Towards understanding two-level-systems in amorphous solids: insights from quantum circuits. Rep. Prog. Phys. 82, 124501 (2019). https://doi.org/10.1088/1361-6633/AB3A7E
T. Pérez-Castañeda, C. Rodríguez-Tinoco, J. Rodríguez-Viejo, M.A. Ramos, Suppression of tunneling two-level systems in ultrastable glasses of indomethacin. Proc. Natl. Acad. Sci. 111, 11275–11280 (2014). https://doi.org/10.1073/PNAS.1405545111
T. Pérez-Castañeda, R.J.J. Riobóo, M.A. Ramos, Low-temperature thermal properties of a hyperaged geological glass. J. Phys. Condens. Matter 25, 295402 (2013). https://doi.org/10.1088/0953-8984/25/29/295402
E.A.A. Pogna, A.I. Chumakov, C. Ferrante et al., Tracking the connection between disorder and energy landscape in glasses using geologically hyperaged amber. J. Phys. Chem. Lett. 10, 427–432 (2019). https://doi.org/10.1021/ACS.JPCLETT.9B00003
T. Pérez-Castañeda, R.J. Jiménez-Riobóo, M.A. Ramos, Do two-level systems and boson peak persist or vanish in hyperaged geological glasses of amber? Philos. Mag. 96, 774–787 (2015). https://doi.org/10.1080/14786435.2015.1111530
D. Khomenko, C. Scalliet, L. Berthier et al., Depletion of two-level systems in ultrastable computer-generated glasses. Phys. Rev. Lett. 124, 225901 (2020). https://doi.org/10.1103/PhysRevLett.124.225901
H. Sirringhaus, 25th Anniversary Article: organic field-effect transistors: the path beyond amorphous silicon. Adv. Mater. 26, 1319–1335 (2014). https://doi.org/10.1002/adma.201304346
L.W. Antony, N.E. Jackson, I. Lyubimov et al., Influence of vapor deposition on structural and charge transport properties of ethylbenzene films. ACS Cent. Sci. 3, 415–424 (2017). https://doi.org/10.1021/acscentsci.7b00041
M.C. Gather, S. Reineke, Recent advances in light outcoupling from white organic light-emitting diodes. J. Photonics Energy 5, 057607 (2015). https://doi.org/10.1117/1.JPE.5.057607
H. Mu, L. Rao, W. Li et al., Electroluminescence dependence of the simplified green light organic light emitting diodes on in situ thermal treatment. Appl. Surf. Sci. 357, 2241–2247 (2015). https://doi.org/10.1016/J.APSUSC.2015.09.217
N. Van den Brande, A. Gujral, C. Huang et al., Glass structure controls crystal polymorph selection in vapor-deposited films of 4,4′-Bis(N-carbazolyl)-1,1′-biphenyl. Cryst. Growth Des. 18, 5800–5807 (2018). https://doi.org/10.1021/acs.cgd.8b00329
J.S. Bangsund, J.R. Van Sambeek, N.M. Concannon, R.J. Holmes, Sub–turn-on exciton quenching due to molecular orientation and polarization in organic light-emitting devices. Sci Adv 6, eabb659 (2020). https://doi.org/10.1126/sciadv.abb2659
P.-A. Will, S. Lenk, S. Reineke, 26–1: Invited paper: thermally activated delayed fluorescence organic light-emitting diodes comprising ultrastable glass layers. SID Symp. Dig. Tech. Pap. 50, 356–359 (2019). https://doi.org/10.1002/SDTP.12930
N. Kim, B. Domercq, S. Yoo et al., Thermal transport properties of thin films of small molecule organic semiconductors. Appl. Phys. Lett. 87, 241908 (2005). https://doi.org/10.1063/1.2140478
N. Lu, L. Li, N. Gao, M. Liu, A unified description of thermal transport performance in disordered organic semiconductors. Org. Electron. 41, 294–300 (2017). https://doi.org/10.1016/j.orgel.2016.11.019
E. Selezneva, A. Vercouter, G. Schweicher et al., Strong suppression of thermal conductivity in the presence of long terminal alkyl chains in low-disorder molecular semiconductors. Adv. Mater. 33(37), 2008708 (2021). https://doi.org/10.1002/adma.202008708
X. Wang, K.D. Parrish, J.A. Malen, P.K.L. Chan, Modifying the thermal conductivity of small molecule organic semiconductor thin films with metal nanoparticles. Sci. Rep. 5, 16095 (2015). https://doi.org/10.1038/srep16095
R.C. Yu, N. Tea, M.B. Salamon et al., Thermal conductivity of single crystal C60. Phys. Rev. Lett. 68, 2050–2053 (1992). https://doi.org/10.1103/PhysRevLett.68.2050
M. Shahi, J.W. Brill, Frequency-dependent photothermal measurement of thermal diffusivity for opaque and non-opaque materials: application to crystals of TIPS-pentacene. J. Appl. Phys. 124, 155104 (2018). https://doi.org/10.1063/1.5050189
Y. Okada, M. Uno, Y. Nakazawa et al., Low-temperature thermal conductivity of bulk and film-like rubrene single crystals. Phys. Rev. B 83, 113305 (2011). https://doi.org/10.1103/PhysRevB.83.113305
C. Angell, Relaxation in liquids, polymers and plastic crystals—strong/fragile patterns and problems. J. Non Cryst. Solids 131–133, 13–31 (1991). https://doi.org/10.1016/0022-3093(91)90266-9
Acknowledgements
JRV and MGS acknowledge Grant MAT2016-79759-R funded by MCIN/AEI/ 10.13039/501100011033 and “ERDF A way of making Europe”, and Grant PID2020-117409RB-I00 funded by MCIN/AEI/ 10.13039/501100011033. CRT is a Serra Húnter Fellow. M.A.R. acknowledges financial support from MCIN/AEI/ 10.13039/501100011033, through the “María de Maeztu” Programme for Units of Excellence in R&D (CEX2018-000805-M), as well as from the Autonomous Community of Madrid through program S2018/NMT-4321 (NANOMAGCOST-CM). We also thank the BBVA Foundation for its financial support to the “Nicolás Cabrera” International Summer School on “Ultrastable Glasses: new perspectives for an old problem”. The ICN2 was funded by the CERCA programme / Generalitat de Catalunya. The ICN2 was supported by the Severo Ochoa Centres of Excellence Programme, funded by the Spanish Research Agency (AEI, Grant no. SEV-2017-0706).
Funding
JRV and MGS acknowledge Grant MAT2016-79759-R funded by MCIN/AEI/10.13039/501100011033 and “ERDFAway ofmakingEurope”, and Grant PID2020-117409RB-I00 funded by MCIN/AEI/ 10.13039/501100011033. CRT is a Serra Húnter Fellow. M.A.R. acknowledges financial support from MCIN/AEI/ 10.13039/501100011033, through the “María de Maeztu” Programme for Units of Excellence in R&D (CEX2018-000805-M), as well as from the Autonomous Community of Madrid through program S2018/NMT-4321 (NANOMAGCOST-CM). The ICN2 was funded by the CERCA programme / Generalitat de Catalunya. The ICN2 was supported by the Severo Ochoa Centres of Excellence Programme, funded by the Spanish Research Agency (AEI, Grant no. SEV-2017-0706). We also thank the BBVA Foundation for its financial support to the “Nicolás Cabrera” International Summer School on “Ultrastable Glasses: new perspectives for an old problem”.
Author information
Authors and Affiliations
Contributions
All authors have contributed to the different sections of this review and have contributed to the writing of the manuscript. All authors read and approved the final manuscript.
Corresponding authors
Ethics declarations
Conflict of interest
The authors declare no competing financial interests.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Rodriguez-Tinoco, C., Gonzalez-Silveira, M., Ramos, M.A. et al. Ultrastable glasses: new perspectives for an old problem. Riv. Nuovo Cim. 45, 325–406 (2022). https://doi.org/10.1007/s40766-022-00029-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40766-022-00029-y