Coursework in advanced mathematics topics such as abstract algebra is required in virtually all secondary mathematics certification programs for teachers. This requirement is justifiable on many grounds, including the existence of deep connections between concepts in abstract algebra and the school mathematics curriculum (Conference Board of the Mathematical Sciences 2001). However, recent trends in educational research suggest that we must study how prospective secondary mathematics teachers (henceforth: prospective teachers) establish and employ these connections. Early studies such as those by Begle (1979) and Monk (1994) examined the effect of subject matter knowledge on teaching indirectly by comparing the number of mathematics content courses taken by teachers to measures of student mathematics achievement. Not surprisingly, the results were complicated and mixed. Though Monk found that the first few undergraduate mathematics courses taken by prospective secondary teachers modestly improved their students’ subsequent performance, simply requiring prospective teachers to take additional advanced mathematics courses did not continue to improve student achievement.

Looking more closely at teachers’ subject matter knowledge, Shulman (1986) described an absence of focus on subject matter among the research paradigms for the study of teaching. He noted that research missed questions such as, “How does the successful college student transform his or her expertise in the subject matter into a form that high school students can comprehend?”, “How does he or she employ content expertise to generate new explanations, representations, or clarifications?”, “What are the sources of analogies, metaphors, examples, demonstrations and rephrasings?”, and “How does the novice teacher (or even the seasoned veteran) draw on expertise in the subject matter in the process of teaching?” (p. 8). In order to begin addressing Schulman’s questions, researchers moved away from equating subject matter knowledge with the number of college courses taken by a teacher in a subject area (as in Begle (1979) and Monk (1994)). As an alternative, researchers began developing a definition of subject matter knowledge for teaching that is informed by evidence on ways in which teachers use mathematics in their work with students.

The National Research Council (2001) gave a compelling summary of the justifications for the development of a new perspective on teachers’ subject matter knowledge and its implications for the mathematical education of prospective teachers. Their report, “Adding It Up: Helping Children Learn Mathematics,” states that prospective teachers who take advanced mathematics coursework have “only a cursory understanding of the concepts underlying elementary mathematics” (National Research Council 2001). Additionally:

They may have learned mathematics that is not well connected to what they teach or may not know how to connect it. … [Moreover,] courses that reflect a serious examination of the nature of the mathematics that teachers use in the practice of teaching do have some promise of improving student performance. (p. 373–375)

This conception of the mathematical knowledge employed by teachers in their practice is referred to as mathematical knowledge for teaching (MKT). There are two predominant and complementary conceptualizations of MKT. One has a focus on mathematical knowledge visible during instructional activities such as, “explaining terms and concepts to students, interpreting students’ statements and solutions, judging and correcting textbook treatments of particular topics, using representations accurately in the classroom, and providing students with examples of mathematical concepts, algorithms, or proofs” (Hill et al. 2005, p.373). Reliable multiple-choice items have been developed to test for these teaching-related mathematical skills at the elementary level. These test items have been shown to be valid measures of mathematical knowledge for teaching (Hill et al. 2004). Moreover, Hill et al. (2005) showed that teachers’ scores on these items were a predictor of elementary students’ gains in mathematics achievement.

A second characterization of MKT, formulated originally by Silverman and Thompson (2008), builds upon the notion of key developmental understandings (KDUs). A KDU is a “conceptual advance that is important to the development of a concept” (Simon 2006 , p.363). With this perspective, a teacher has developed MKT of a topic if they have achieved a KDU encompassing the topic along with an understanding of how the topic may evolve instructionally in support of students’ reasoning. This paper reports on preliminary research into the nature of prospective teachers’ explanations of concepts after taking an advanced mathematics course (performance). The study design and analysis are focused primarily on the first conceptualization of MKT characterized by Ball and her colleagues. Henceforth, MKT will refer to this conceptualization unless otherwise indicated.

Progress in defining and quantifying MKT has given teacher educators a promising new perspective on the learning of mathematics by prospective teachers. It has begun to close the gap in our understanding of how teacher knowledge is related to student achievement that was first highlighted several decades ago. It also has implications for the design and teaching of university mathematics courses for teachers. However, most of the research on mathematical knowledge for teaching has focused on the learning of mathematics by elementary school teachers (e.g., Hill et al. 2008a, b; Izsak 2008; Morris et al. 2009; Hill 2010).

Secondary mathematics is the capstone of the school mathematics education experience and the bridge to higher mathematics. Due to the level of mathematical complexity in the secondary curriculum, prospective teachers are required to complete coursework in advanced and theoretical mathematical topics. However, only a few studies on mathematical knowledge for teaching have addressed the ways in which we expect prospective teachers to integrate this knowledge into their practice. In one relevant study, Even (1993) found prospective secondary teachers to have a limited concept image of “function” that influenced their pedagogical thinking. In another study, Knuth (2002) found that the teachers in his study “[held] limited views of the nature of proof in mathematics and demonstrated inadequate understandings of what constitutes proof,” (p.379) an obstacle to reform efforts pushing the study of proof in the secondary school mathematics curriculum.

If mathematical knowledge for teaching is characterized, in part, by a teacher’s ability to explain concepts to students and to use mathematical representations accurately, then we must study how prospective teachers integrate their knowledge of abstract mathematical concepts and formal mathematical argument learned in college into their explanations of school mathematics concepts. For example, one might ask how knowledge about the abstract concepts of inverse and identity underscore a prospective teacher’s understanding of high-school level algebra.Footnote 1 This study focuses on the links between abstract algebra concepts and school mathematics because (a) abstract algebra is a course requirement for most prospective secondary mathematics teachers and (b) abstract algebra is generally the first undergraduate course that requires students to grapple with concepts presented structurally (Dubinsky et al. 1994).

While a great deal of research has been conducted on (a) justification and argumentation (e.g., Harel and Sowder 2007; Weber and Alcock 2004) and on (b) the learning and understanding of abstract algebra (e.g., Dubinsky et al. 1994; Findell 2001; Hazzan 1999; Leron et al. 1995), most of the relevant research focused on students’ conceptions of and production of proofs and on difficulties students have with particular concepts in group theory. Thus, research offers some understanding of the acquisition of abstract algebra knowledge but offers little regarding prospective teachers’ transfer of this knowledge to secondary school teaching. This study begins to fill this void in research. It explores the question: What is the nature of the gap between (a) knowing abstract algebra well enough to pass the course and (b) being able to effectively use that knowledge to explain a concept or property to secondary school students? In particular, how do prospective teachers integrate their knowledge of abstract algebra into their explanations of mathematical concepts that they deem appropriate for their students?

Before teachers can integrate their knowledge of abstract algebra into their teaching practice, they must develop proficiency in understanding and constructing proofs. Many students have trouble achieving this proficiency, and a great deal of research has been done to identify reasons why. This research has demonstrated that the problem is large and complex. Some studies begin by dissecting proof types and then addressing how these types may be related to true conceptual knowledge (e.g., Weber and Alcock 2004). Other studies investigate students’ difficulties in producing and assessing the validity of proofs (e.g., Martin and Guershon 1989; Weber 2001). Harel and Sowder (2007) argue for a conceptual framework to study students’ notion of proof that addresses its cognitive, mathematical, epistemological-historical, and social aspects. This need is due, in part, to the obvious differences in the notion of proof held by different contemporary communities (high school students vs. college students vs. mathematicians, for example) and to the change in the notion of proof over time.

Prospective teachers must move beyond proficiency in proof, however. They must be able to make use of proof in their own secondary classrooms, even though proofs are not typically the primary method for communicating mathematical concepts in this context. Teachers struggle to make use of what they have learned about proofs, in part, because they do not see proofs as evidence or as “convincing arguments” (Harel and Sowder 1998 ,p.237; Knuth 2002 ,p.385). In explaining mathematical concepts to their students, prospective teachers must establish truths for themselves based on arguments that are convincing to them. When prospective teachers do not value mathematical proof as a means of establishing truth, then their teaching practices drift free from their moorings in actual mathematics. Given the widespread efforts to convert the school mathematics learning environment into one that resembles that of the research mathematics community (e.g., Ball and Bass 2000; Boaler 2002; Lampert 1990), this problem has serious consequences. To address this problem, more research is needed on the particular ways in which prospective teachers view, produce, and use formal mathematical argument.

This study focuses on the strategies employed by prospective teachers when asked to explain mathematical concepts that they have studied recently from a theoretical perspective and that are also integral to the school mathematics curriculum. For example, starting with a concept such as division by zero, how do prospective teachers integrate (if at all) a theoretical understanding of the concept with a simple explanation that is suitable for secondary students? The Principles and Standards for School Mathematics (2000) states that, “By the end of secondary school, students should be able to understand and produce mathematical proofs—arguments consisting of logically rigorous deductions of conclusions from hypotheses—and should appreciate the value of such arguments” (p. 56). This end cannot be achieved unless prospective teachers, themselves, are able to produce such proofs and arguments (as they relate to the secondary curriculum), and, just as importantly, place value on such arguments. Ideally, prospective teachers should be able to: (a) reason logically and produce proofs about concepts related to the secondary mathematics curriculum, (b) value the truths deduced from such reasoning and arguments, and (c) use this ability to ground and inform the related conceptual representations used in their practice. Indeed, any characterization of mathematical knowledge for teaching at the secondary level should encompass proficiency in, valuing of, and ability to translate a rigorous proof in abstract algebra into an explanation that is suitable for secondary students.

Method

Participants

Five upper division university students in the United States participated in this study. These participants completed an abstract algebra course taught by the author of this study in the fall of 2005. Participants were chosen based on: (a) their willingness to participate in such an interview, as indicated on their signed consent form, and (b) their availability during the interview scheduling period. Interviews were conducted during the spring 2006 semester, after the abstract algebra course was completed. Subject names used in this paper are pseudonyms: Arbella, Diego, Frank, Jake, and Lilly.

Arbella, Diego, Jake and Lilly were mathematics majors in the Mathematics for Secondary Education program. All completed their student teaching experiences following the fall 2005 algebra course. (For several participants, student teaching overlapped with the interview period for this project.) Frank was a practicing middle school teacher in a post-baccalaureate program seeking secondary mathematics certification. His teaching experience was limited to the elementary and middle grades. Arbella and Diego are not native English speakers.

The fall 2005 section of abstract algebra taken by participants was a typical first-semester majors’ course covering algebraic systems, with an emphasis on group theory. Topics included: groups, subgroups, the classification of finite cyclic groups, permutations, homomorphism, isomorphism, and Lagrange’s Theorem. Rings and fields were addressed to a lesser extent. In order to earn a passing grade, students were required to demonstrate acceptable proficiency in writing algebraic proofs. In addition to the typical aspects of an abstract algebra course, the students in the fall 2005 course were asked to think about ways in which the course concepts connected to topics from the school mathematics curriculum. The time spent on these connections was minimal given the amount of time required to cover the material in a typical first-semester algebra course.

The prerequisites for the abstract algebra course are (1) an introduction to proofs course and (2) a course in linear algebra. Both of these prerequisites have a prerequisite of Calculus I. Table 1 below shows the mathematics courses taken by the participants before they completed the fall 2005 abstract algebra course and their course grade for abstract algebra. Table 2 shows the mathematics courses taken concurrently with the abstract algebra course.

Table 1 Courses taken prior to the fall 2005 abstract algebra course and course grade in abstract algebra
Full size table
Table 2 Courses taken concurrently with the fall 2005 abstract algebra course
Full size table

Data Collection and Instrumentation

Rationale and Procedure

The exploratory study reported in this article reflects data collected from interviews conducted in March and April of 2006. The goal of the interviews was to explore the responses given by prospective teachers when asked to explain connected concepts. A concept in abstract algebra is considered “connected” if it also exists explicitly in the K-12 mathematics curriculum.

Abstract algebra is a course whose subject matter encompasses the mathematical structure and properties of number systems. As such, concepts studied as part of this course are often connected to basic arithmetic and, thus, to the number system properties underpinning school algebra. Many concepts that directly connect school mathematics to abstract algebra topics may fundamentally belong at the elementary school level. Examples include “evenness” (parity/equivalence relations), “division by zero” (derived properties of the additive identity in a field), and clock arithmetic (modular rings). The relevance of these concepts to secondary teachers is that (1) proficiency in algebra directly extends proficiency in arithmetic and (2) secondary teachers must frequently address elementary concepts in their support of students’ learning of more advanced topics.

All interview items were mathematical questions related to connected concepts. Interviews were conducted and audiotaped several months after the participants had completed the fall 2005 abstract algebra course. Each participant was interviewed once. All subjects were asked all questions. During the interviews, participants were not allowed any resources. They were provided with a pen and blank paper if they desired to write as they responded to interview questions. Each interview lasted approximately 30 minutes.

Interview Items

Interviews provided the opportunity to explore participants’ abilities to connect concepts in abstract algebra to school mathematics. In response to interview questions, participants often employed several methods of explanation. When this did not occur naturally, participants were probed with questions such as, “How would you explain this to a high school student?”, “How would you explain this to a peer?” or “How does this question relate to what you learned in abstract algebra?” The complete list of interview questions is given below. The questions were purposely vague in order to see what conditions students would supply to make them more precise.

  1. 1.

    What is an even number?

  2. 2.

    Can you give me several alternative definitions of even?

  3. 3.

    What kinds of numbers can be even?

  4. 4.

    Is 0 even, odd, or neither? Why?

  5. 5.

    Which topics from abstract algebra connect to the concept of even?

  6. 6.

    What about division by 0? Can you make meaning of 1/0? Why or why not?

  7. 7.

    Which topics from abstract algebra connect to the concept division by 0?

Data Analysis

The audiotaped interviews were analyzed, annotated, and summarized by the author; emergent themes were identified and recorded. Special attention was given to the type of explanation given, the appropriateness of the answer, the use of multiple explanations (if given), mistakes, and the use of abstract and theoretical concepts.

Upon analysis of the data, it became evident that all prospective teachers’ responses could be classified into one of three distinct, encompassing, and recognizable categories: Abstract Mathematical Argument (AMA), Analogy, and Rules. These categories emerged from the data. Additionally, analysis occasionally uncovered interesting insights into the way the participants thought about mathematics and their views of the mathematics that is important for students to learn.

Description of Explanatory Strategies

Mathematical truths are established through the construction of valid mathematical proofs. However, mathematical explanations are not always given in the form of formal proofs, especially in the school mathematics environment. Abstract Mathematical Argument, Analogy, and Rules (described below) are strategies employed by the participants in this study to explain mathematical concepts. They do not necessarily represent conventional mathematical reasoning.

Abstract Mathematical Argument (AMA) encompasses any attempt to use abstract mathematical reasoning and justification techniques to provide an explanation. Undergraduate mathematics theory courses such as discrete mathematics, abstract algebra, and analysis expose prospective teachers to the formal justification and explanatory techniques characteristic of mathematics. In these courses, students are taught to classify mathematical objects by formulating and applying mathematical definitions, to establish truths (theorems) deductively by appealing to definitions, axioms, and previously-proved theorems, and to falsify conjectures by providing counter-examples. Essentially, AMA captures the influence of a student’s theoretical mathematics experience on their explanation of fundamental concepts. Any conceptual and abstract explanation that might be given by a professor or student in a mathematics theory class is AMA.

If an interview response is not AMA, then the response falls into two possible categories: explanation or non-explanation. If an explanation is not abstract, then it has some concrete aspect. That is, it employs a concrete context to build a justification. This context may be a physical representation (such as the use of apples shared among baskets to describe division) or it may be an explanation that depends entirely and fundamentally on a specific mathematical context or representation (such as giving an answer that relies on properties of a specific algebraic system or grounding an argument on properties of the number line). This type of concrete explanation is termed Analogy.

If an answer to an interview question is not AMA and not an explanation, then it is some sort of proclamation of truth. This could be of the form “because the textbooks say so” or “because you just can’t” or “because that’s the definition.” It could also take the form of an alternative rule or “trick” (e.g., “The product of two negatives is positive because two negative signs cancel.”) Any non-explanation of this type is termed a Rule. This classification scheme is coarse; however, the categories covered all explanations given as part of this study.

All data collected for this study were categorized according to the three explanatory strategies. This categorization was then used to analyze student responses and to gain insight into their understanding of mathematics and how this understanding is activated in the context of answering mathematical questions.

Results and Analysis

In this section, various instances of explanatory strategies and explanatory strategies in competition are presented, along with an instance of strategy integration. Interpretations are also provided. Additionally, some indications of a link between the development of correct, coherent, and integrated explanations and the development of MKT in the sense of Silverman and Thompson (2008) are reported.

Categories of Explanatory Strategies

In the sections that follow, each explanatory strategy is elaborated. Excerpts of interviews with participants are given to illustrate the use of each of the three types of explanatory strategies. Interpretations and analyses are provided for each excerpt.

Abstract Mathematical Argument

Abstract Mathematical Argument is an explanatory strategy that is characterized by the attempted use of abstract mathematical reasoning and justification. Excerpt 1 exemplifies one student’s use of AMA.Footnote 2

Excerpt 1: “R” stands for “Researcher”; “F” stands for “Frank.”

1. R: What’s an even number?

2. F: (Laughs) Which definition do you want?

3. R: Oh, any. Whatever.

4. F: OK, I’ll give you the one that we, uh … It’s a number that is divisible by two without a remainder. That would be, probably, the simplest way to put it … including zero: zero divided by two is zero, there’s no remainder.

5. R: OK. And so, what class of numbers does that pertain to?

6. F: That would … That’s another good question, too! We could argue about it all day. Personally, I believe it includes integers, both positive and negative.

In this example, Frank classified the set of even numbers in a mathematically general way. He stated that an integer is a member of the set of even numbers provided it satisfies the property: integer division by two yields a remainder of zero. In his response, he invoked the division algorithm and he gave the usual domain of the definition: the set of integers. Frank also illustrated his definition by applying it to show that the integer zero is even according to his definition. Since Frank’s response incorporates abstract and theoretical mathematical techniques, it is classified as AMA. In this case, AMA also coincides with conventional and appropriate mathematical reasoning. Excerpt 2 is Lilly’s response to the same question.

Excerpt 2: “R” stands for “Researcher”; “L” stands for “Lilly.”

1. R: Could you tell me what an even number is?

2. L: An even number is a number that is two k [meaning 2 k]

3. R: OK. And what can k be?

4. L: k can be any real number.

5. R: Any real number? So, like, two times point one is OK?

6. L: Oh, boy. Two times point one? Sure. Would that be an even number or would that be integers? Right. Um. Boy. I would have to say it would be OK. I would say point two would be OK.

Lilly stated that a real number is even if it can be written as two times a real number k. However, unlike Frank’s characterization of even numbers, Lilly’s formulation was mathematically unconventional. She failed to recognize that “evenness” is a concept customarily associated with integer division. Real number division, by contrast, does not produce a remainder in the sense that dividing any real number by two yields a real number. All real numbers can be written as 2 k for some real number k, including all odd integers. Thus, using Lilly’s definition, all real numbers are even. However, since Lilly set up a mathematically general characterization of evenness, as she might in the context of a university mathematics class, her response to the question is categorized as AMA.

The following excerpt is illustrative of an AMA that is grounded in conventional mathematical reasoning. In this excerpt, AMA was used by Jake to deduce an implication of a definition.

Excerpt 3: “R” stands for “Researcher”; “J” stands for “Jake.”

1. R: […] can you use that language um just to bring in that word inverse here to talk about the symbol one over zero?

2. J: Well. If you’re talking about multiplication, then zero doesn’t have an inverse. ‘Cause nothing times zero is going to give you one.

When Jake stated “zero doesn’t have an inverse,” he correctly interpreted the symbol 1/0 to mean the multiplicative inverse of zero. He then applied the mathematical definition of multiplicative inverse appropriately in the setting of real numbers: A real number a has multiplicative inverse b (a real number which can be denoted by 1/a or a −1) provided a * b = 1. Zero has no multiplicative inverse because there is no real number b so that 0 * b = 1. Jake’s explanation was deductive. Thus, his response is classified as AMA.

Analogy

When participants offered reasonably detailed mathematical explanations that involved the use of concrete contexts or tangible objects, their strategy was categorized as Analogy. When explanations accurately reflect conventional mathematical reasoning, Analogies might be called concrete mathematical representations. However, in this study, the use of Analogy was often disconnected from valid mathematical reasoning and was influenced by the physical attributes of the chosen concrete context. Participants often remarked that they would appeal to the use of Analogy when explaining concepts to students. The following excerpts were classified as Analogy.

Excerpt 4: “R” stands for “Researcher”; “A” stands for “Arbella.”

1. R: So when you talk about the nothing given to nothing. Like I said

A over B. If you just wrote A over B. And you said this “giving nothing to no one.” Could you tell me in general what that rule is that you’re using?

2. A: So, I’m taking A stuff and I’m splitting it to B people. For example, to B elements or locations. To B receivers. So, if B was five, for example, and A was 10, for example, the five receivers would each receive two of ten. Let’s say the A were apples and the B were baskets. Each basket would have two apples in it.

Arbella used a concrete context involving apples and baskets to explain division. The domain of this Analogy (the set of numbers for which the Analogy is an accurate representation of the underlying formal mathematics) is inherently limited. For example, it is not appropriate to use the Analogy to explain π/(−2). However, the Analogy is a mathematical representation of division in a limited context. As discussed in the following section (Explanatory Strategies in Competition), problems with Analogy arise when the explainer derives conclusions by inappropriately attaching mathematical meaning to aspects of the concrete context—that is, when Analogy is used independently of conventional mathematical reasoning.

In the following excerpt, Diego gave an initial answer to the question, “What is an even number?” by referring to divisibility. After probing, he then attempted to represent the concept of even numbers using a concrete context.

Excerpt 5: “R” stands for “Researcher”; “D” stands for “Diego.”

1. R: What is an even number?

2. D: I think an even number is uh…when you pair numbers there is certain characteristics about a number if it can be divisible by any other number…by two… I think it is a even number. If it cannot be divided by two then it shouldn’t be an even number. […] I unfortunately don’t have the answer right now how to use a high school level to describe what an even number is other than using the divisible rule that we learned in…I think we learned in elementary school.

3. R: Well, uh, divisibility by two is probably appropriate for high school students, but, um, what if you were going to try to show a young kid that four was even? And you said that they may need visual representations or something physical. What would you do with …

4. D: (interrupts) See if I … I don’t remember how the way I learned numbers.

5. R: That’s OK …

6. D: (interrupts) (unintelligible) They just gives [sic] us the number then we used them but I think I have no … no answers to … to describe visually how a number … how an even number looks like, but if we just use symbols, we can use two sticks and … and try to make a pattern. What are even numbers, for example if we have two sticks and then we have one stick, and then … I mean three sticks so you always have the number one. If you pair them and using two sticks, you always have one … one remaining which is … we come back to the divisibility rules or number theory.

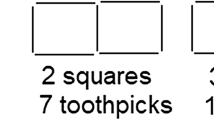
Diego struggled to represent, in a concrete way, integer division by two. As Diego discussed sticks (paragraph 6, lines 3–7), he also drew the sticks roughly uniformly and indicated, by underlining, that he was attending to the number of sticks rather than their length. (See Fig. 1 below.) Though his response was tentative and incomplete, he began to paint a picture of sticks bundled into groups of two. There were two possibilities: no remaining sticks or “one remaining.” Thus, at least in the limited case of positive integers, Diego built an Analogy that accurately reflected the application of the division algorithm in the case of integer division by two.

Fig. 1
figure 1

Diego’s sticks. Diego shows sticks bundled in groups of two with zero or one remaining stick

Full size image

Rules

In mathematics, rules are statements of mathematical theorems or definitions which carry mathematical meaning. When rules are statements of theorems, they have been established through mathematical proof. When rules are mathematical definitions, they are not arbitrary. Mathematical definitions are made because they (a) describe a meaningful mathematical concept and (b) are consistent with other, established mathematical concepts. For example, given a positive real number a, defining a 0 to be 1 is consistent with the limit calculation lim n→∞ a 1/n = 1 and makes the exponential function y = a x continuous at x = 0. Rules as an explanatory strategy is characterized by reference to (what the explainer believes to be) a mathematical “fact” that is to be accepted and remembered. The following interview responses were classified as Rules:

Excerpt 6 (Jake explaining division by zero): “R” stands for “Researcher”; “J” stands for “Jake.”

1. R: Can we make meaning of the symbol one over zero?

2. J: Um. Well. We know it’s undefined. Just from what we learned in grade school and high school.

Excerpt 7 (Frank explaining division by zero): “R” stands for “Researcher”; “F” stands for “Frank.”

1. R: Um … Talking about zero, but maybe taking a little bit of a detour, what about: Can we make meaning of the symbol one over zero?

2. F: OK. That’s a great question. Now we’re saying one over zero as division?

3. R: Uh, yeah, well, actually, I didn’t want to say that. I guess I said it as a symbol because I want you to just tell me whatever you think. So, it may just be a formal symbol, or it may be division. That division may happen wherever you tell me it happens.

4. F: […] Uh, you are taught very early on… uh… that you cannot divide by zero. You’re taught… I don’t even know what grade that is, but it’s when you first teach division! Kids are told, “You can’t divide by zero.” So, you can never have a zero in the denominator.

Excerpt 8 (Arbella explaining division by zero): “A” stands for “Arbella.”

A: […] So, I mean, that’s why they call this no number. It’s an error.[….] It’s not accepted! ‘Cause that’s what I try to explain. My students say, “Why can’t I divide one by zero?” And I say … Because I even check myself, “Zero divide by zero is error again!” It’s not true. It’s amazing.

All three of the above examples are responses to the same question posed by the researcher: Can you make meaning (or sense) of the symbol “one over zero”? The use of Rules in each case is reflective of students’ (apparent and sometimes local) lack of sense-making in response to the question.

Explanatory Strategies in Competition

During interviews, when asked to explain a connected concept such as division by zero or even numbers, participants tended to incorporate multiple explanatory strategies into their responses. Frequently, these strategies were in direct competition with one another. In some cases, different strategies yielded competing conclusions. In other cases, certain strategies were abandoned before they were fully realized. In either situation, participants were compelled to choose a strategy and the conclusion derived from applying that strategy, regardless of sense-making. In some cases, participants settled upon unconventional conclusions drawn from the use of Analogy or Rules even when confronted with their own conventional mathematical reasoning.

Competition Among Strategies

In the following interview excerpt, we see three different explanatory strategies in competition as Diego attempts to explain division by zero (1/0).

Excerpt 9: “R” stands for “Researcher”; “D” stands for “Diego.”

1. R: What about division by zero? So, can you make sense of the symbol one divided by zero?

2. D: If we have one divided by zero, we consider it as uh, an undefined term … See, if we have the zero backwards, we can write zero times one, right? […] But, if we flip this, we can say that … n equals zero times one … or I can’t remember exactly how the rule goes, but uh, supposedly we cannot have uh, … The other way around we cannot have this operation because if we look at it as an elementary way, what can you divide by zero? ‘Cause if zero represents nothing … If you take five dollars, how can you divide five dollars into zeros? You can always have that idea that, using the number or any other manipulatives to break down another number. So, how can we break down a number five using a zero? Is it possible to break it down? I don’t think it’s possible at this point ‘cause this idea of undefined …

Note that Diego stated, “if we have the zero backwards…” (paragraph 2, line 2) meaning 0/1 = 0 because 0 = 0 * 1, but then interpreted 1/0 = n multiplicatively as n = 0 * 1 instead of 1 = 0 * n. Even though Diego’s explanation was incomplete, his attempt is categorized as AMA because Diego attempted to use the properties of inverse and the definition: for all integers a, b, and c, a/b = c if and only if a = b * c. However, he could not apply this definition in the case of 1/0. As a consequence, he abandoned this strategy in favor of a different type of explanation: “…because if we look at it in an elementary way, what can you divide by zero?… If you take five dollars, how can you divide [partition] five dollars into zeros?” (paragraph 2, lines 5 though 7).

Diego moved from AMA into Analogy. He did this by introducing the concrete context of money and a measurement model for division. (By specifying the size of the group to be zero he asked: How many groups of size zero are there in five?) As with his attempt at AMA, Diego wasn’t able to make his Analogy work when the size of the group is zero. In the end, Diego settled upon the Rule that division by zero is “undefined”: “I don’t think it’s possible at this point ‘cause this idea of undefined…” (paragraph 2, lines 9-11).

It seems that Diego had some understanding of what the “correct” conclusion should be: Division by zero is undefined. In his attempts to support this conclusion, Diego appealed to AMA and Analogy. However, when he was unable to reconcile competing strategies, he settled on a Rule as his ultimate justification.

Another participant also used competing strategies to explain the meaning of division. Arbella used an Analogy (“apples and baskets”) to explain division partitively. That is, a/b = c meant a apples are shared among b baskets. The result (c) is the number of apples per basket. In Excerpt 10, we see that Arbella used this analogy to explain several division problems. In Excerpt 11, we see her Analogy strategy in competition with her AMA.

Excerpt 10: “R” stands for “Researcher”; “A” stands for “Arbella.”

1. A: So, I’m taking a stuff and I’m splitting it to b people. For example, to b elements or locations. To b receivers. So, if b was five, for example, and a was 10, for example, the five receivers would each receive two of ten. Let’s say the a’s were apples and the b’s were baskets. Each basket would have two apples in it. […]

2. R: Let’s do one divided by zero maybe.

3. A: One divide by zero.

4. R: And you had one apple and you have …

5. A: No baskets. What am I going to put in my basket? Where am I going to put my apples? Sorry.

6. R: So, can you do the other ones for me now like zero over one?

7. A: So, if I have no apple and I have one basket, I could say, “Well, my basket’s empty. I have nothing in it.” But if I have one apple and I have no basket … uh, there’s something wrong here! How am I going to say I have no basket? But I’m dividing … I’m giving the apple. There should be a receiving side!

8. R: OK. Combining that to the zero over zero. Then what’s the statement?

9. A: Honestly, I think zero divided by zero should be zero. But, again …

10. R: But with the apples and the baskets, what do you say there?

11. A: So, I have no apples and I have no baskets. I have nothing! It should be nothing, right? […]

12. R: What if you have the numerator smaller than the denominator? So, instead of…

13. A: The numerator smaller?

14. R: Like five over ten. Then how does your apples and baskets thing work there?

15. A: So, each basket will get half of an apple!

Arbella used her Analogy appropriately to explain division in several cases. However, in the case of zero divided by zero, her use of Analogy no longer worked. At that point, she verbalized her belief that 0/0 = 0. After a brief return to the problem of 1/0, the conversation came back to a discussion of 0/0.

Excerpt 11: “R” stands for “Researcher”; “A” stands for “Arbella.”

1. R: Say zero divided by zero is something.

2. A: Equal n, right?

3. R: Could you write that…

4. A: (interrupts) As a multiplication? Zero equals zero times n. And, although it is true, but it’s not. Because you simply cannot divide by zero. […] Take an example, if you want to split an apple and give it to no one, who’s taking this piece of apple?

Arbella wrote the statement “0/0 = n” and then the statement “0 = 0 * n” as she spoke (Fig. 2), and realized that “0 = 0 * n” is true for all values of n. However, she rejected this idea because it conflicted with the conclusions she had drawn from her use of Analogy—that 0/0 = 0. Her use of Analogy in this case was similar to her use of Analogy to explain why 1/0 is undefined. In the end, she accepted the coexistence of two competing mathematical ideas: an invalid conclusion that 0/0 = 0 and a valid conclusion that 0/0 = n is true for any (real number) n.

Fig. 2
figure 2

Arbella’s division by zero AMA. Arbella frames the problem of 0/0 multiplicatively

Full size image

Note that it would have been possible for Arbella to integrate her Analogy and her AMA strategies for explaining why 0/0 is undefined, but to do so would have taken: (a) faith in and understanding of the valid mathematical argument that 0/0 is undefined because there is no single number n that makes 0 = 0*n a true statement, and (b) the ability to creatively stretch the Analogy to address the case of 0/0. For example, we could say that when you take the number of baskets (0) times the number of apples per basket (anything), you get back the original amount (0). Put another way: Add up all the apples in each basket. You must get zero. Since there are no baskets, it doesn’t matter how many apples are in them.

Competition Within Strategies

In some cases, students created competition within a category of explanatory strategies. During his interview, Frank struggled with two different rules and two different conclusions to the problem of potential meanings of 0/0.

Excerpt 12: “F” stands for “Frank.”

1. F: OK. Here’s our three problems: one over zero, zero over one, and zero over zero. Alright. Here is… here is… Wherein lies the crux of the problem for everybody.

2. Uh, you are taught very early on… uh… that you cannot divide by zero. You’re taught… I don’t even know what grade that is, but it’s when you first teach division! Kids are told, “You can’t divide by zero.” So, you can never have a zero in the denominator. You look at algebra books, you know, like you always get…what… A cannot be equal to zero because we can’t have zero in the denominator. So with one over zero, I think, for me personally, just because this is what we’ve been told for years and years, that that has no solution. It can’t even… it can’t even exist.

3. Zero over one is equal to zero. Divide zero by any number and you’re going to get zero.

4. The problem arises with zero over zero. And here…and here is the reason why. Three divided by… anything divided by itself is one. It doesn’t make any difference: algebraically A divided by A is one. You know, just use numbers: negative three divided by negative three or three divided by three is one. With that thinking, zero divided by zero should be equal to one! However, this is kind of like the chicken and the egg. Which rule supersedes which rule? That we can’t have zero in the denominator? Or…And if that’s the case, then there’s no solution to zero over zero. Or is anything divided by itself equal to one? I don’t know. I think that’s a mathematical theory question that probably… you could probably argue about all day.

5. I think it’s real easy to just stick to the first rule and just say that that has no solution as well. But I kind of think it’s…uh…it’s a little more romantic if you will, to think that that should be one.

In this excerpt, Frank gave three rules: “You cannot divide by zero” (paragraph 2, lines 1-3), “Divide zero by any number and you’re going to get zero” (paragraph 3), and “Anything divided by itself is one” (paragraph 4, lines 2–3). When he applied these rules to the problems 1/0 and 0/1, Frank arrived at mathematically conventional conclusions: (1) that 1/0 “has no solution. […] it can’t even exist” (paragraph 2 lines 6–7) and (2) that “zero over one is equal to zero” (paragraph 3). In these cases, Frank’s Rules were not in competition. However, when faced with the problem of 0/0, two of Frank’s rules competed. From his rule, “Anything divided by itself is one,” Frank concluded that “zero divided by zero should be equal to one” (paragraph 4, lines 4–5). From his rule “You cannot divide by zero,” Frank concluded that “there’s no solution to zero over zero” (paragraph 4, line 5). It is worth noting that we could adopt the convention that 0/0 = 1 to be consistent with the fact that, \( \underset{x\to 0}{ \lim}\frac{x}{x}=1 \) much as we might define 00 = 1 to be consistent with the fact that \( \underset{x\to {0}^{+}}{ \lim }{x}^x=1 \).

In Excerpts 9, 10, and 11 it is clear that both Diego and Arbella had a single conclusion to the problem proposed in mind. Diego first attempted to explain (using AMA and Analogy) that 1/0 is undefined before he settled on a Rule as his ultimate justification. Arbella dismissed her conclusion, drawn from AMA, that 0/0 = n does not have a single solution in favor of her conclusion that 0/0 = 0, drawn from her Analogy. In Excerpt 12, Frank’s choice of conclusion appears to be arbitrary. He was faced with an “easy” conclusion that 0/0 is undefined and a “romantic” one that 0/0 = 1 (Excerpt 12, paragraph 5, lines 1–3).

After Frank gave his response (Excerpt 12) to the question, “Can you make meaning of the symbol 1/0?” he was asked, explicitly, for an explanation of his Rule: “Can you… can I ask you to tell me more about this if you can? Like why might that rule hold? Why is it that we can’t divide by zero?” Frank responded by digressing. He commented that, historically, there wasn’t the concept of a zero, then there was, and it represented “nothing” and that’s “possibly why” division by zero is not allowed.

An Integration of Strategies

Interview data yielded instances of explanatory strategy integration based on proper mathematical reasoning, as in the following case of Jake exploring the concept of division by zero. Notice that in his first response, he began with a Rule (“[0/1] is undefined”) but quickly moved on to reference a “proof” that shows that if we allow division by zero, then 1 = 2. Jake’s Rule was supported by a mathematically correct AMA strategy. His concept explanation was constructed to be appropriate for the level of the secondary student, but it was grounded in and informed by correct and general mathematical reasoning.

Excerpt 13: “R” stands for “Researcher”; “J” stands for “Jake.”

1. R: Can we make meaning of the symbol one over zero?

2. J: Um Well. We know it’s undefined. Just from what we learned in grade school and high school. And there was a proof that that one guest speaker actually put on the board that I never saw until that day and I wrote it down. And I think that will be something that I actually share in my class when I do say why you can’ t… well if they’re ready for equations at that point. I’ll say, “This is why you can’t divide by zero.” And I’ll show them the proof. It’s just x and y and it turns out that what you get at the end can’t be true and zero messes up the system. So we just don’t divide by it. And that’s kind of the explanation I was given, so it’s pretty much as far … you know it’s as deep as I have an understanding of is that it messes up the group or the system so we took it out.

When prompted, Jake was also able to couch his answer in terms of the general algebraic concept of “inverse.”

Excerpt 14: “R” stands for “Researcher”; “J” stands for “Jake.”

1. R: […] can you use that language um just to bring in that word inverse here to talk about the symbol one over zero?

2. J: Well. If you’re talking about multiplication, then zero doesn’t have an inverse. ‘Cause nothing times zero is going to give you one. So I think that’s possibly why we can’t do that. If we’re talking about addition but we’re not in that case, but if you were then zero is its own inverse. But with the multiplication like we said it’s not going to work.

Jake then reflected on his instinct to incorrectly apply a Rule in response to a question about 0/0. He moved first to a correctly applied Rule and then, ultimately, to a correct and convincing AMA. As with Diego and Arbella (Excerpts 9, 10, and 11), Jake seemed to have a single conclusion in mind. He was convinced that that 0/0 is undefined. However, in this case, it appeared that Jake saw the need to justify his use of a Rule with a correct and appropriately rigorous mathematical argument. Thus, AMA was his ultimate justification.

Excerpt 15: “R” stands for “Researcher”; “J” stands for “Jake.”

1. R: Right. So you just said um “there’s nothing that you can multiply by zero to get one.” Um. So that’s sort of looking at that multiplicatively. What about that zero over zero that you brought up before?

2. J: That was a tricky question just because you were taught that anything divided by itself is one. And when I first saw that, that’s how I wanted to answer the question—just say well, it has to be one. But you’re still dividing by zero. And if we allow it in just that one case, then why can’t you allow it in more? It’s just… it still throws off the system to me. And the same thing is going to happen. I mean. Zero multiplied by anything is going to give you zero. You’re not going to get one.

Explanatory Strategies from a Cognitive Perspective

The design of this study was grounded in the performance-based conceptualization of MKT (Hill et al. 2004). Explanations that the participants provided as part of this study were regarded as indicators of what they know, but the initial analysis of the data did not focus on their thinking or their views on the mathematics that it is important for students to learn. The complementary characterization of MKT developed by Silverman and Thompson (2008) focuses on the mathematical understandings of teachers that might impact their students’ ability to develop a rich understanding of mathematical concepts. Viewing MKT from this perspective requires attending to teachers’ thinking in order to understand their conceptual structures.

Despite this study’s focus on performance, there were opportunities to gain insight into the participants’ thinking with regard to the mathematics they were explaining. In analyzing the relevant excerpts, we can see how participants’ understandings of mathematical concepts influenced strategy integration. This leads to a natural connection between strategy integration and coherence of mathematical meanings (Thompson et al. 2007).

A Closer Look: Why Integration Fails

In Excerpts 9, 10, and 11, Diego and Arbella were unable to integrate their strategies when explaining division by zero. Further analysis reveals that Diego and Arbella held different understandings of the mathematical concepts involved, and these understandings caused their strategy integrations to fail in different ways. In the following excerpt, we also see that Diego’s failure to integrate strategies was connected to the mathematics that he felt was important for his students to learn.

Excerpt 16: “D” stands for “Diego.”

D: See, we see the abstract thinking in college. Going back to high school it’s not always the case. Actually, my [student teaching] supervisor, he mentioned it last time that if we see students as… psychologically… they don’t think the same way as adults think. Their brain is not developed to the full amount of percentage that they should be to be understanding the concepts. For me, I see that a number-- you cannot break it down into zeros. But the zero, it’s the opposite. Actually I still don’t understand why zero divided by a number is always zero. So, maybe it’s the identity. We use it as the identity of the real numbers. One is the… or… is it one? I don’t remember if it’s one or zero, but we’re using real numbers in here as well.

In this instance, it is clear that Diego was unable to formulate an explanation of 1/0 and 0/1 due, in part, to his lack of understanding of identity element in the context of real numbers (Excerpt 16 lines 6–9). This observation explains why Diego could not construct a conventional AMA (Excerpt 9, paragraph 2, lines 1–3): he did not see that 1/0 could be interpreted as “the number you multiply zero by to get one.” The potential impact of Diego’s limited understanding of identity on his ability to support student thinking is underscored by his statement that students’ “brain[s] [are] not developed to the full amount […] they should be to be understanding the concepts” (Excerpt 16 lines 4–5). Diego goes on to offer an explanation of identity element that he felt was appropriate for students. In the following excerpt, Diego created an Analogy by connecting the notion of identity in the context of real number arithmetic to an example of an identity element in a specific context outside of the usual number systems.

Excerpt 17: “R” stands for “Researcher”; “D” stands for “Diego.”

1. D: It will be helpful with the students. At least to understand how… what’s the identity. ‘Cause I have no idea, when they say, “1 is the identity, but I never understand why 1 is the identity.”

2. R: When they say that to you?

3. D: Yeah. When I was in the high school or in elementary. “Why is it the identity?” Then I explain, “Well, the identity is something that doesn’t do anything. It just keeps yourself motionless in a place.” Now I can … at least I can see it geometrically, and that, you know, 1, it could be the identity because you don’t move. If you use a group actions, I mean if you use a group, like the military group, we use the identity, well you don’t move! So those things, they will be helpful to the students.

Note that the “military group” referred to by Diego is the set of parade commands: left face (L), right face (R), about face (A), and stand as you were (S) together with the operation “followed by.” It was defined for the students enrolled in the fall 2005 section of abstract algebra in the first week of classes to help them begin to think about groups and group properties before they reviewed the formal definition of a group. Diego evidently missed the point of this example. In the example, the objects of interest are transformations of the formation, not the formation. S is an identity under the operation: composition of transformations. It leaves unchanged the transformation with which it is composed. For example, S ∘ L = L ∘ S = L means that the formation was effected as if the L was given by itself. Diego did not realize that an element is an identify element relative to an operation on a set of elements. It is not an identify element in and of itself. He seemed to think that S was an identity element because it left the formation unchanged, irrespective of composition as an operation.

In Excerpt 17, Diego’s limited understanding of identity was evident when he failed to specify the set or operation in his statement that “one is the identity,” (paragraph 1 lines 2–3 and paragraph 3 line 4). Having failed to achieve (or, at least, having failed to sustain) a structural understanding of identity, Diego gave an explanation drawn from his experience with abstract algebra that was entirely metaphorical: “the identity is something that doesn’t do anything. It just keeps yourself motionless in a place.” (paragraph 3 lines 2–3). Taken together, Excerpts 9, 16 and 17 show that, rather than “comprising a web of mathematical ideas and compatible ways of thinking,” (Thompson et al. 2007, p.416) Diego’s conceptual understanding of division involving zero and identity appeared to be a set of disconnected ideas. Diego’s explanations were not organized around properties of an operation on a set as a “big idea.”

In the following excerpt, we see that Arbella had a way of thinking about identity that differed from Diego’s.

Excerpt 18: “R” stands for “Researcher”; “A” stands for “Arbella.”

1. A: Um, well zero under addition then is the identity. But under multiplication it’s not. It’s that one number that you cannot use at all. ‘Cause it destroys your group, kind of […] So, under multiplication, it’s not honored, I guess.

2. R: It’s not honored?

3. A: […] Because, like what we did in [the abstract algebra course], we always took zero out because it didn’t allow… under multiplication, it ruined our group so we had to throw it out all the time.[…]

4. R: When we made our multiplicative groups?

5. A: Tables.

6. R: What happened in the table when you left zero in there?

7. A: Well, it destroys, kind of, when we start… For example, let’s say zero, one two, three, and we did zero one two and three. And instead of giving me the identity, you know when you multiply something by an identity, you get the same thing, right? Instead, it gave me everything zero! It gave me… It changed everything to itself! […] But under addition it works fine I guess. So, instead you’ve got all zeros here and it ruined you’re… ‘cause now it’s… one times one, and you get one times two, and […] And the identity you kind of lose here. Let me see… two and three. And then two times two you get four, which is not even in the group.

8. R: Could you make it in the group? What kind of multiplication are you doing here?

9. A: Um. Oh yeah. This is a kind of regular multiplication, let’s say. It’s kind of including zero. But then, um, we can divide by four. […] Isn’t that mod 4? […]

10. R: How can you recognize that [a table is] a group? Just out of curiosity.

11. Cause you have, like the diagonal thing. When we said like you can pick this and you have all the elements… First of all you have all the elements zero one two zero one two, and, uh.... And like whatever you’re doing […] you’re getting the same numbers that you have in your set.

In Excerpt 18, Arbella, built an Analogy to contrast the properties of the additive and multiplicative identity elements and to explain the multiplicative property of zero in a context outside of our usual number systems: in the ring of remainders modulo four. During this discussion (paragraph 7), Arbella produced the operation table in Fig. 3. We see here that Arbella, unlike Diego (Excerpt 16), remembered that zero is the additive identity element (Excerpt 18 paragraph 1, line 1). She justified her claim that “under multiplication, [zero] ruined our group” (paragraph 3) by referring to table properties. Arbella created the row and column of zeros in her table first before completing the table. She then stopped to point out that, “instead of giving me the identity, you know when you multiply something by an identity, you get the same thing, right? Instead, it gave me everything zero!” (paragraph 7, lines 2–4). She later stated why this is a problem: In a group table, “you have all the elements” (paragraph 11 lines 1–2) and “you’re getting the same numbers that you have in your set” (paragraph 11 lines 3–4). Arbella appeared to be recalling a theorem that was assigned and proved in her fall 2005 algebra course: Every group table is a Latin square. She recognized that, if her table were a group, every row and column would contain all of the elements in her set.

Fig. 3
figure 3

Arbella’s operation table. Arbella demonstrates the multiplicative property of zero in the ring of remainders modulo four

Full size image

Arbella’s Analogy was primarily rooted in group table properties. Even so, she laid out enough information to connect her Analogy to the problem of division by zero if it had occurred to her to do so: The lack of a “1” in the row and column for zero in the table means that there is no remainder a modulo four such that a*0 = 1. Thus, zero has no inverse in this setting. (1/0 is undefined.) Ideally, such an observation would be authentically connected to the arithmetic context: Any multiple of four times any integer is always a multiple of four, and, thus, is never an integer congruent to one modulo four. Therefore, there is no multiplicative inverse of zero in the ring of remainders modulo four.

For Arbella’s limited purpose of illustrating that zero is not the multiplicative identity, her Analogy was appropriately applied. However, as noted above, Arbella did not connect her Analogy to the problem of division by zero. We also recall that Arbella employed a Rule (“error!” Excerpt 8) and an Analogy (“I have no apples and I have no baskets. I have nothing!” Excerpt 10, paragraph 11) to explain division by zero. Thus, we see that her understanding of identity did not inform her understanding of division by zero. Arbella’s failure to express the fundamental nature of the problem of division by zero across her explanatory strategies signifies that her understanding was not key and did not support her mathematical knowledge for teaching the concept.

Silverman and Thompson (2008) argue that MKT is “grounded in a personally powerful understanding of particular mathematical concepts” and is “created through the transformation of those concepts from an understanding having pedagogical potential to an understanding having pedagogical power” (p.502). In exploring why Diego’s and Arbella’s explanatory strategy integrations fail, we saw that both participants lacked a well-developed personal understanding of the concepts involved in their explanations. (Their understandings were not “personally powerful.”)

To illustrate the pedagogical potential of an algebraic understanding of division, we note that a key understanding in support of MKT might be exhibited as follows: When explaining division by zero to a student, a teacher could take the opportunity to reinforce the relationship between division and multiplication (by a multiplicative inverse), highlighting the properties of inverse and identity. From this perspective, students learn to understand that in order to find an inverse (if one exists), one must attend to the universe of discourse as well as the operation under consideration. (Does the integer 2 have a multiplicative inverse within the set of integers?) Framing of the problem of division by zero multiplicatively (What times zero gives you one?) connects the problem to the multiplicative property of zero, which is readily explained in elementary terms.Footnote 3 There are additional benefits to thinking of division as “multiplying by the inverse.” For example, it helps students see that there is a distributive property for division over addition which is simply a restatement of the usual distributive property for multiplication over addition. This property can be stated as: Given real numbers and c with \( c\ne 0,\frac{a+b}{c}=\frac{1}{c}\left(a+b\right)=\frac{1}{c}a+\frac{1}{c}b=\frac{a}{c}+\frac{b}{c} \). This may help students avoid the common error of equating \( \frac{a}{b+c} \) with \( {\scriptscriptstyle \frac{a}{b}}+{\scriptscriptstyle \frac{a}{c}} \).

Integration, Coherence, and Key Developmental Understandings

Lack of strategy integration (as in Excerpts 9 through 12 and 17) suggests a lack of coherence of mathematical understanding among the participants in this study. That is, the participants’ conceptual structures did not “comprise a web of mathematical ideas and compatible ways of thinking” (Thompson et al. 2007, p.502), nor did they “serve as a conceptual anchor for mathematics curricula and instruction” (Silverman and Clay 2009, p.1353). In some cases, such as Diego’s explanation of division by zero (Excerpt 9), it is clear that the participant did not have complete metaphors or conventional structural understandings of the concepts involved in a particular problem. Diego’s strategies failed to cohere because they were incomplete. In other cases (such as Arbella and Frank’s explanations of division by zero in Excerpts 10, 11, and 12), the participants had complete yet contradictory explanatory strategies. Arbella had conventional knowledge sufficient to explain division by zero by reframing the problem multiplicatively (Excerpt 11, paragraph 4, line 1). However, her metaphorical understanding involving apples and baskets conflicted with her structural understanding, creating a dissonance that she resolved by making a choice of strategy (Excerpt 11, paragraph 4, lines 2–4). Additionally, Arbella could not leverage her understanding of identity to gain insight in to the problem of division by zero. Thus, Arbella’s strategies failed to cohere because they were limited and contradictory and because she saw no reason to reconcile them. Regarding division by zero, only in the case of Jake’s explanation (Excerpts 13 and 14) do we see complete, complementary, and connected strategies.

Simon (2006) suggests that “one way to identify KDUs is to observe students engaged in mathematical tasks to specify understandings that can account for differences in the actions of different students in response to the same task” (p.363). When explaining the concept of division by zero, most participants in this study were unable to frame the problem generally and provide explanations in algebraic terms (such as identity and inverse). We might view these participants as engaged in a task (employing explanatory strategies) in which one participant was able to integrate his strategies (Excerpts 13–15), while the others could not. Given the relationship between the ability to integrate explanatory strategies and the development of coherent mathematical understandings that support the teaching of school mathematics concepts, it can be argued that the integration of explanatory strategies in response to a mathematical question is evidence of the development of an important KDU for prospective teachers.

The table below summarizes the number and type of distinct explanatory strategies used by the participants when responding to interview questions. The interview questions asked of all participants fell into two main categories: questions about even numbers and questions about division by zero. In all cases, more than one strategy was used. For each topic and each participant, it is noted whether or not their strategies were integrated Table 3.

Table 3 Strategies employed and integration by topic and participant
Full size table

Future studies from a cognitive perspective, such as the “teaching experiments” described by Thompson and Thompson (1994, 1996), may help support the analysis above. Such studies may also point to ways in which the issues that arose in this study may be addressed instructionally (such as by the development of tasks for prospective teachers aimed at the development of the strategy integration KDU). It is hoped that future studies will lead to a better understanding of how to support prospective teachers’ development of MKT and, ultimately, to a better understanding of the role that advanced coursework can play in the mathematical preparation of teachers.

Conclusion

Students (including prospective teachers) in an abstract algebra course study the structural underpinnings of school algebra. They spend time grappling with concepts such as identity and inverse in a variety of algebraic settings that are different from their familiar number systems. They learn to prove theorems about abstract algebraic concepts.

Certainly, students enter such a course with a set of algebraic concept images that they have developed from their prior mathematical experiences (Vinner and Tall 1981). In this study, we saw that participants clearly held idiosyncratic concept images of identity and highly metaphoric meanings of division. The abstract algebra course taken by the participants should have served as an opportunity to narrow the gap between their algebraic concept images and the actual concept definitions. However, the data show that most participants did not recall much about abstract algebraic concepts they had studied only a few months earlier and that their course experience did not transform their algebraic concept images in ways that could support their teaching practice.

The categorization of explanatory strategies proposed and employed in this study elucidates the consequences of prospective teachers holding incomplete and incoherent concept images: multiple strategies are brought to bear on a problem, sometimes the multiple strategies are in conflict, and often one strategy ends up being valued over others. In the case of unconventional explanations involving the Analogy strategy, we see inappropriate reasoning influenced by the physical attributes of the chosen concrete context (“I have no apples and I have no baskets. I have nothing!” Excerpt 10, paragraph 11). In the case of unconventional explanations involving the Rules strategy, we see inappropriate conclusions drawn on the basis of gut feeling, intuition, or idealism (“I kind of think it’s a little romantic to think that that [0/0] should be one” Excerpt 12, paragraph 5). Most of the prospective teachers in this study failed to develop Abstract Mathematical Arguments or failed to integrate these strategies with their Analogies and Rules.

Confronting novel approaches to a problem and judging the validity of students’ approaches in the secondary classroom require correct and appropriate mathematical reasoning by the teacher paired with the development of explanatory strategies that are coherent and integrated. The role of advanced coursework for teachers is centered, in part, on “framing mathematical concepts and relationships in clear language” and “constructing and analyzing proofs” (Conference Board of the Mathematical Sciences 2001, p.141). However, the results here suggest that performing well on typical assessments in an abstract algebra course is not sufficient for the development of effective explanatory strategies and KDUs in support of mathematical knowledge for teaching. Evidence points to the need for teachers to develop the ability to formulate and integrate pedagogically compelling and appropriate explanations (Analogies and Rules) in ways that reflect a structural understanding of algebraic concepts. Continued research from a cognitive perspective is indicated to better explain the role of explanatory strategy use and integration in the development of MKT anchored in formal mathematical structure.

There are essentially two implications of students’ failure to connect the principles of abstract algebra and school mathematics. One is that instruction in abstract algebra might be modified so that students see such connections more clearly. The other is that university students’ understandings of grade school mathematics (e.g., multiplication and division) is so incoherent that they cannot make a connection between their existing ways of thinking about numbers and operations and any treatment of abstract algebra that retains fidelity to the subject as a university course.

The author’s position is that the field of mathematics education must take seriously both implications. Doing so would involve efforts (1) to rethink the way that abstract algebra is taught to prospective teachers, and (2) to improve school mathematics instruction with regard to meanings that students construct. It would simultaneously involve efforts to help university students re-learn numbers and operations meaningfully in order to prepare them to make sense of abstract algebra concepts in ways that support their instructional practices.