It is now well known that digital tools provide relative affordances in comparison with those provided by physical tools, such as paper-and-pencil environments and concrete manipulatives. Yet, there is a dearth of research regarding the inter-related roles played by these two types of tools. This gap in the extant research is highlighted as a problem by Maschietto and Soury-Lavergne (2013), who state that “very little research focuses on the combined use of the two kinds of resource, physical and digital, in the learning process” (p. 959).When incorporating digital tools into classroom practice, it is likely that students also have notebooks and worksheets on which they can perform complementary actions such as writing down what they have noticed on the computer screen, as well as drawing diagrams and building on mathematical expressions to help their thinking about how to solve problems. Thus, investigating the interplay between students’ digital tool use and their paper-and-pencil activity is important to gain insight into classroom practices. Such insight could provide directions for better integration of digital tools into classrooms.

In this article, we focus on this issue of the combined use of digital and physical tools within the area of conjecturing and proving, tools which are at the core of mathematical practice (Stylianides et al. 2017) and, in line with this, are emphasised in curriculum documents in a range of countries, including Japan and England. For example, the current version of England’s national curriculum “aims to ensure that all pupils […] reason mathematically by following a line of enquiry, conjecturing relationships and generalisations, and developing an argument, justification or proof using mathematical language” (DfE 2013, p. 2).

One of the most extensively used digital tools for conjecturing and proving is dynamic geometry environments (DGEs). Many studies have investigated the affordances of DGEs, which include dragging and measuring modalities that lead to the production and testing of conjectures by generating various diagrams (Arzarello et al. 2002; Olivero and Robutti 2007). Some researchers argue that bridging what can appear to students as a ‘gap’ between argumentation and proving (especially the ‘gap’ between empirical investigation/conjecturing and deductive proving) is helped if students experience ‘cognitive unity’ between conjecturing and proving (Boero et al. 1996; Fiallo and Gutiérrez 2017).

Meanwhile, research on diagrammatic reasoning shows the importance of paper-and-pencil drawing in the development of concepts, involving the construction of diagrams, experimentation with them and reflection on the experimentation results (Bakker and Hoffmann 2005). Students often produce valid arguments through introducing the visual images of concepts and connecting them with their formal definitions (Alcock and Simpson 2004). Working on diagrams is especially helpful for solving proving tasks in geometry, because students can relate such tasks with known results by adding auxiliary lines and marks to the diagrams given in the tasks (Palatnik and Dreyfus 2019).

Given the affordances of DGEs and paper-and-pencil environments, a question of particular interest is how students engage in conjecturing and proving using both tools. Indeed, some studies have reported that, when using DGEs, students also generate material products such as written proofs and diagrams (Baccaglini-Frank et al. 2018; Healy and Hoyles 2001). A case study by Prusak et al. (2012) showed that a pair of pre-service teachers engaged in productive argumentation through an iterative combination of DGE use and paper-and-pencil work accompanied with paper folding. Meanwhile, Koyuncu et al. (2015) showed differences between prospective teachers’ problem-solving strategies in a DGE and in a paper-and-pencil environment.

While these studies have provided insight into the proving behaviour of students in DGEs, in-depth attention has not been paid to the interplay between students’ paper-and-pencil activity and DGE use. Looking into this interplay is especially important given that, as stated above, in many classroom situations students have notebooks and worksheets on which they can carry out actions complementary to their DGE use. The aforementioned research gap is addressed in this article by focusing on one aspect of geometric proof, specifically in the context in which students generalise a statement after proving it (we clarify this further below). Thus, the research question for this article is: What is the interplay between paper-and-pencil activity and DGE use when students are engaged in producing and proving a generalisation of a mathematical statement?

In what follows, we first review the relevant literature in order to propose a framework for the interplay between physical and digital activity, and explicate a characteristic of geometric proof in order to frame our focus about proof-related activity. We then examine a series of classroom lessons involving Japanese secondary school students (aged 14–15, grade 9) using a DGE. These lessons are analysed in terms of the interplay between the students’ paper-and-pencil activity and DGE use, as well as the roles taken by the teacher in supporting their work.

Framework

A small number of studies have investigated the interplay between students’ physical and digital activity. For example, Maschietto and Soury-Lavergne (2013) examined the duo of a material and a digital artefact through the arithmetic machine (Pascaline) and its digital counterpart (e-Pascaline). Their purpose in designing e-Pascaline was not to replicate Pascaline with digital technology, but rather to enhance students’ understanding of the decimal number system and arithmetic operations such as addition and subtraction. To this end, e-Pascaline was designed in a way that was complementary to Pascaline; while several features were added to e-Pascaline that Pascaline did not have, some features of Pascaline were also not included in e-Pascaline. Subsequently, Maschietto and Soury-Lavergne (2017) conducted a study involving primary school students and reported that, because of a certain design feature of e-Pascaline that constrained the students’ actions (the number of possible rotations of gears was restricted), the students, with their teacher’s intervention, developed their own addition strategies from the iterative procedure to the decomposition procedure based on the place-value system.

A more back-and-forth interplay between physical and digital activity was observed in the study by Voltolini (2018), which also addressed the duo of a material and a digital artefact. On the topic of the geometric construction of triangles, a learning sequence was designed that consisted of a spiral process of ruler-and-compass construction and preceding e-book activity intended to provide groundwork for the ruler-and-compass construction. The e-book used a DGE and included a specific design feature whereby a line segment could be rotated around one end-point by dragging the other. The learning sequence was implemented with primary school students and it was found that they developed a new conception of a triangle (as a closed, broken line) and a new way to use a compass (as a tool to rotate segments) through the successive interplay between ruler-and-compass construction and its preceding e-book activity.

Faggiano et al. (2018) examined the benefits of synergy between a manipulative and a digital artefact. They designed and implemented a learning sequence where primary school students first drew line-symmetrical figures by folding a sheet of paper and using a pin. The students then extended their experience of manipulation by producing a line-symmetric point in a DGE and dragging the original point, the given axis and the line-symmetric point. The students also interpreted the dynamic behaviour of each figure by using the paper and pin once again. Faggiano and colleagues concluded that this synergy between manipulative and digital activity helped the students understand the functional dependency of symmetrical figures (i.e. that line-symmetric points are dependent on the original points and given axes).

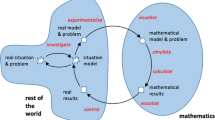
Based on the above literature review, we propose a framework (shown in Fig. 1) to analyse the interplay between physical and digital activity. Student activity in general is usually initiated by the provision of tasks. From an educational point of view, it could be assumed that certain learning objectives, such as acquiring mathematical knowledge and engaging in mathematical practice, are embedded in the given tasks (Maschietto and Soury-Lavergne 2013).

Fig. 1
figure 1

A model of the interplay between physical and digital activity

Full size image

On one hand, this framework is intended to be sufficiently simple and general to warrant its application to a wider context; it is not restricted to paper-and-pencil activity, DGE use, and conjecturing and proving. On the other hand, when applying the framework to individual cases, it is crucial to examine the details of each element to ensure a fine-grained analysis. These details include the types of physical activity (e.g. paper-and-pencil work and the use of concrete manipulatives and machines) and of digital activity (e.g. the use of DGE, virtual manipulatives and the computer algebra system) in Fig. 1.

A detailed examination is required specifically for the element interplay; it is essential to examine not just whether the interplay occurs or not, but also what kinds of interplay arise in relation to the intended learning objective. In terms of the theory of semiotic mediation (Bartolini-Bussi and Mariotti 2008), it is crucial to analyse the types of combined physical and digital tool use that mediate the achievement of the learning objective. This idea was emphasised in the existing studies reviewed above. Said studies did not merely iterate physical activity with digital technology; rather, they aimed to mediate certain learning goals, such as the place value system (Maschietto and Soury-Lavergne 2013) and geometric construction (Voltolini 2018), through the stimulation of the interplay between physical and digital activity that was relevant to these goals.

The model depicted in Fig. 1 is employed in this article within the context of proving in geometry, where the element physical activity involves paper-and-pencil work and the element digital activity involves the use of DGEs. The element interplay is not specified here a priori, but rather the details of interplay actually occurring between students’ paper-and-pencil work and DGE use are examined by analysing a classroom episode in the subsequent analysis and discussion sections. This study focuses on a particular aspect of proving in geometry, which is clarified by elaborating on the characteristics of geometric proof.

Proving and Generalisation in Geometry

In secondary school geometry, a mathematical statement to be proved is often described with reference to a particular diagram representing a certain general class (Otten et al. 2014). It is necessary to consider this diagram as a generic example and construct deductive arguments using geometrical relationships suggested in the statement. However, the diagram may represent only a certain single case and, thus, may not capture all the configurations to which the statement can possibly refer. Hence, when transforming the diagram, various diagram types may be obtained, some of which show significant differences even within the identical problem. To address this generalisation, the statement must be revised and/or new proofs must be constructed for different configurations (Komatsu 2017; Komatsu, Jones, Ikeda & Narazaki, 2017).

In this sense, geometric proof differs from proof in other domains such as number theory. For the latter, arguments based on generic examples usually lead to the production of proofs for general cases (e.g. Rowland 2002). In contrast, a geometric statement can possibly refer to multiple configurations that are sometimes not captured by a single, seemingly generic, diagram. A deductive proof based on the generic diagram may be valid only within a certain case, and different proofs may be required for different configurations. It is within this type of generalisation that DGEs can play a key role, because the dragging function of DGEs allows for relatively easy access to multiple diagrams, while keeping certain the geometrical relationships imposed on the diagrams. The successive transformation of diagrams can highlight continuity and discontinuity between different configurations within an identical statement (Komatsu and Jones 2019).

The literature regarding the use of DGEs in proof-related activity has paid attention to conjecture generation and the transition from conjecture generation to proof production (e.g. Baccaglini-Frank and Mariotti 2010; Baccaglini-Frank et al. 2018). Our study aims to complement the existing studies by focusing on the subsequent process described above, namely the generalisation after proving a statement through transforming the diagram given in the statement. This type of generalisation is significant from an educational point of view, because student mathematical activity does not finish in the production of proofs; it continues to develop through revising statements and proofs by experimentation involving the examination of diagrams. This process is relevant to the growth of mathematical knowledge illustrated by Lakatos (1976) and, thus, integrating experimentation and proof in such a way can provide students with an insight into the nature of mathematics (de Villiers 2004; Komatsu 2017).

In sum, the current article investigates the interplay that arises between students’ paper-and-pencil activity and their use of DGE during the producing and proving of a generalisation of a statement.

Methods

In this article, we present an analysis of a series of mathematics lessons conducted as part of our three-year research project entitled Proofs and Refutations in Dynamic Geometry Environments (PRinDGE). The project’s objective is to find ways to engage students in mathematical activity with DGE that is consonant with the process described by Lakatos (1976) (though the purpose of this article is not to evaluate the effect of our study on supporting students in this activity). In the first year, we focused on task design and conducted task-based interviews with Japanese secondary school students and undergraduates to examine the advantages of the designed tasks (Komatsu and Jones 2019). In the second and third years of the project, we extended this study to classroom-based interventions by collaborating with teachers of six classes in Japanese lower secondary schools. All the classes were Grade 9 and all students were aged 14–15 years.

In this article, we describe and analyse a series of lessons from one class. These lessons were carried out in the second year of our project in a school affiliated with a Japanese national university. We selected this class for the current article because the students’ motion between paper-and-pencil work and DGE use was observed multiple times during the lessons. The teacher who implemented the lessons in his class had extensive experience over eighteen years. Below, we examine work across four lessons, with each one lasting fifty minutes (note that the first half of lesson 1 was unrelated to our study, thus meaning that the number of relevant lessons was, in effect, 3.5).

In the intervention study, we, as researchers, designed the tasks to be implemented and roughly drafted a set of lesson plans. Following this, the teacher devised the lesson plans based on our rough draft and discussed these with the first author of this article prior to teaching. The teacher conducted the lessons and the first author observed as a non-participant.

There were thirty-eight students in the class. Each participated in the lessons using one of the school’s tablet computers equipped with GeoGebra as a DGE. The teacher often taught lessons using tablet computers, meaning that the students were comfortable using the computers and, in particular, could use the DGE flexibly. As such, the students knew how to construct geometric figures, transform figures by dragging, and measure the length of segments and the size of angles. However, the students were not familiar with the GeoGebra angle/segment marking tool, text tool or pen tool, as the teacher had not mentioned these tools in his lessons.

The students had studied Euclidean-type geometry in Grades 8 and 9, and they had had considerable experience with proofs involving congruent and similar triangles. They were also familiar with some basic geometry theorems with proofs, including the triangle interior angle sum theorem, the triangle exterior angle theorem and the inscribed angle theorem. Yet, the students were not familiar either with the cyclic quadrilateral theorem (that the sum of opposite angles of a cyclic quadrilateral is 180 degrees, and that an interior angle of a cyclic quadrilateral is equivalent to the exterior angle of the opposite angle) or with the alternate segment theorem (that the angle between a tangent and a chord is equal to the angle in the alternate segment).

Data Collection and Analysis

Three video-cameras were used to record the lessons. Two were placed at the front and back of the classroom and, when the students were working, the first author moved around the classroom with a third video-camera to observe and record their work and their interactions with classmates. The data used for analysis in this study thus included video recordings, the transcripts made from the recordings, the students’ worksheets and notebooks, photographs of the blackboard and field notes taken by the first author.

Because the focus of this article is on a specific aspect of geometric proof as mentioned above, we analysed the data with a particular focus on the students’ activity when generalising the statement rather than the students’ initial proving of the statement. Thus, we concentrated on how the students generalised the statement and addressed the generalisation. We also examined how they made use of the DGE, or their worksheets and notebooks, or both in combination. Additionally, we considered the roles performed by the teacher in the lessons.

All the students’ names used here are pseudonyms. The task sentences, the students’ proofs, and the students’ and teacher’s utterances have been translated into English from the original Japanese. Words in square brackets are added to the transcripts to aid clarification.

Analysis of the Lessons

The focus of the analysis presented here is the interplay between the student’s pencil-and-paper activity and their DGE use. We begin by summarising their work on the original statement shown in Fig. 2. We do this briefly because, as previously mentioned, the focus of this article is on the students’ activity after proof construction. We then analyse the students’ generalisation of the original statement and the series of moves they subsequently made between their DGE use and pencil-and-paper activity.

Fig. 2
figure 2

Original statement

Full size image

Proof of the Original Statement

In lesson 1, after solving several problems to find unknown angles using the inscribed angle theorem, the students tackled the task shown in Fig. 2.

The students produced two proofs for the statement. One of these proofs (hereafter referred to as proof X) is presented belowFootnote 1:

Proof X:

In ∆PAB and ∆PDC, since the inscribed angles corresponding to the arc AD are equal,

$$ \angle \mathrm{ABP}=\angle \mathrm{DCP} $$
(1)

Since vertical angles are equal,

$$ \angle \mathrm{APB}=\angle \mathrm{DPC} $$
(2)

From (1) and (2), since the two pairs of angles are equal, ∆PAB ~ ∆PDC.

Generalisation of the Original Statement

Lesson 2 began with the students’ construction of the diagram presented in Fig. 2 using the DGE. The teacher then posed the following question, which encouraged the students to investigate whether proof X was more widely applicable to the cases where points A–D were on different places on circle O:

Teacher: Well, drag and move one point [among the four points A–D]. When moving [the points], can you still show that [triangles] PAB and PDC are similar by this proof [pointing to proof X written on the blackboard]?

The students found that point P disappeared when it was not inside circle O, as illustrated in Fig. 3a. One student, Daiki, said, “Well, [point P is] from A on the extended lines of AC and BD”. The students reconstructed the diagram by replacing segments AC and BD with lines AC and BD, as shown in Fig. 3b.

Fig. 3
figure 3

Extension of segments AC and BD

Full size image

The teacher then presented another task:

Task 2. Put four points A, B, C and D on circle O, and let point P be the intersection point of line AC and line BD. Can we say that ∆PAB and ∆PDC, which can be made by respectively connecting A and B, and C and D, are similar, even if the points A, B, C, and D are positioned anywhere on the circle?

The conjecture suggested in this task is a generalisation of the original statement. The students worked on the conjecture individually and by discussing it with their neighbours for some seventeen minutes using the DGE. Figure 4 illustrates some of the cases discovered by the students.

Fig. 4
figure 4

Different locations of points A–D

Full size image

During their work, they found some degenerate cases where ∆PAB or ∆PDC did not appear at all. For example, one student, Shota, discovered the case shown in Fig. 4a, where AC // BD. He shared his thoughts about this case during the whole-class discussion: “Because point P is the intersection point of line AC and line BD, the intersection point is not made if [lines] AC and BD are parallel, so it is not necessary to consider whether [∆PAB and ∆PDC are] similar.”

The case represented by Fig. 4b was not complicated for the students. Although the aforementioned proof X cannot be directly employed for this case (because ∠ABP and ∠DCP are not inscribed angles), the students were sure that the conjecture, ∆PAB ~ ∆PDC, was still true. They rapidly completed the proof, showing that ∠APB = ∠DPC (common angles) and ∠PAB = ∠PDC (inscribed angles corresponding to arc BC).

Attempt with DGE

While the students straightforwardly managed the case of Fig. 4b, they struggled to deal with the case represented in Fig. 4c using the DGE. Again, the aforementioned proof X is not applicable to this case because ∠ABP = ∠DCP cannot be directly derived from the inscribed angle theorem.This case was extremely challenging for the students, as they had not yet studied the cyclic quadrilateral theorem.

Our analysis found that the students’ responses to Fig. 4c during their use of the DGE in their individual or small-group work can be categorised in two ways. First, some students either judged that the conjecture, ∆PAB ~ ∆PDC, was not true in this case, or they were not sure whether the conjecture was true. This means that the students considered this case to be, or possibly be, a counterexample to the conjecture. Below is a representative response from a student (recorded from the class discussion):

Misaki: Well, point P is the connection of extended lines AC and BD. If [lines] AB and CD are parallel, then [∆PAB and ∆PDC are] similar. But, when [lines] AB and CD are not parallel, [∆PAB and ∆PDC are] not similar.

Misaki found that the conjecture was true in a particular case where segments AB and CD were parallel. At the same time, she also recognised that these two segments were not necessarily parallel and, thus, considered the conjecture not to be generally true.

Second, contrary to the first category of responses, the students in this category anticipated that the conjecture would remain true in the case of Fig. 4c. However, they got stuck in proving the conjecture. This is well-illustrated in the exchange that took place between students Kaito and Daiki during their individual work (see below). As they already understood that one pair of angles, ∠APB and ∠DPC, were equal, the students paid particular attention to another pair of angles:

Kaito: Well, [∆PAB and ∆PDC] look similar, but how, how, how do we prove it?

Daiki: Let’s measure the angles ... the angles.

Kaito: Probably this, probably so [he anticipates the similarity of the two triangles].

Daiki: Let’s measure the angles [He activates the measuring function of the DGE and measures ∠PAB and ∠PDC]. Oh, same [he finds that ∠PAB = ∠PDC on the tablet screen].

Kaito: Same.

Daiki: Same.

Kaito: As I thought, this is [∆PAB and ∆PDC are] similar, similar. But, how do we do [prove it]?

Daiki: Well, how can I prove [it]? Frustrated [with eagerness as he wants to prove the conjecture].

Kaito: I’m also, I’m also frustrated [in the same tone as Daiki]. How can I do [prove it]?

Daiki: Frustrated. I can’t do [prove it].

As shown by this conversation, the students conjectured that ∆PAB and ∆PDC would be similar. To verify this, they used the DGE and empirically checked that ∠PAB = ∠PDC by measuring these angles in degrees. However, they were not able to show deductively that ∠PAB = ∠PDC using the DGE.

Paper-and-Pencil Work

In lesson 3, the students continued to examine the case shown in Fig. 4c. At the beginning of the lesson, the teacher held a classroom discussion where he encouraged the students to think about their plans for addressing the case. Since some students had tackled the case in lesson 2 by drawing auxiliary lines, the teacher asked what kinds of auxiliary lines the students had drawn thus far in other circle-related tasks. The students suggested the use of auxiliary lines making right-angled triangles and isosceles triangles, and the teacher added the possibility of auxiliary lines making inscribed angles. Student Ryota then stated that ∠APB and ∠DPC were common and, thus, clearly equal, while Tomoya added that it was therefore sufficient to show that ∠PAB = ∠PDC or ∠PBA = ∠PCD. Following these ideas, the teacher suggested focusing on ∠PAB and ∠PDC.

Following this, the students worked for some twenty-four minutes individually and through discussions with their neighbours. During their work, the students had both the DGE and worksheets to work from. Initially, several students used the DGE to transform their diagrams by dragging and, by measuring ∠PAB and ∠PDC, found that these angles were always equal. However, they did not advance their work any further and fewer students used the DGE as time passed. Most students worked with the worksheets by drawing auxiliary lines, adding signs indicative of equal angles, and employing mathematical expressions and sentences (as seen in Figures 5 and 6). Meanwhile, the teacher drew attention to ∠PDC and ∠PAB being, respectively, an interior angle and an exterior angle of the quadrilateral ABDC, and asked whether the students remembered anything about the relationship between interior angles and exterior angles.

The students eventually succeeded in proving that ∠PAB = ∠PDC in various ways. Across the class, they constructed what we categorised as five types of proofs, two of which are roughly illustrated in Fig. 5 (taken from the students’ worksheets). The circles, the points, lines AC and BD, and segments AB and CD had been printed on the worksheets, but all the other things, such as auxiliary lines, marks and mathematical expressions, were added by the students themselves while examining how to prove that ∠PAB = ∠PDC.

Fig. 5
figure 5

The students’ rough proofs (taken from their worksheets)

Full size image

Kazuki shared his proof with the whole class (Fig. 5a), adding auxiliary lines that allowed him to identify the pairs of equal angles (indicated with the marks and letters in the diagram) and then using the triangle exterior angle theorem in triangle ABC. Ayano shared another proof (Fig. 5b), where she used the symbol x to represent ∠BOC and other angles, including ∠PAB = 180 – (360 – x)/2. She then performed algebraic calculations to show the requested conclusion.

A more complete proof by Nanami is shown in Fig. 6. She represented several geometrical relationships of the angles using mathematical language and expressions. She then integrated these expressions to show that ∠PAB = ∠PDC. Thus, on their worksheets the students managed to prove that ∆PAB ~ ∆PDC in the case represented in Fig. 4c.

Fig. 6
figure 6

Nanami’s proof (English translations added by us)

Full size image

Another Move between DGE Use and Paper-and-Pencil Work

In lesson 4, the class used the DGE to revisit the unaddressed case represented in Fig. 4d. First, the teacher shared with the class an issue raised by student Takumi who said that, when points A and C coincided, it could be possible that line AC was not uniquely determined because there were infinite lines passing through one point. To respond to this comment, the teacher constructed a circle, placed points A and B on the circle, and drew line AB on the DGE (Fig. 7a). He gradually positioned point B closer to point A with the zoom-in tool of the DGE (Fig. 7b). He then used the zoom-out tool to show the diagram displayed in Fig. 7c. The students noted that line AB was tangent to the circle, a point justified by one student as follows, “The definition of a tangent line is a line tangent to a circle at only one point, so I think when the two points get closer, the two points are getting convergent to one point”. Thus, the students considered the line passing through point A or C in Fig. 4d to be a line tangent to the circle.Footnote 2

Fig. 7
figure 7

Examination of the tangent case

Full size image

The students conjectured that ∆PAB ~ ∆PDC in the case of Fig. 4d. Similar to lesson 3, the teacher held a whole-class discussion so that students could share ideas about how to prove the conjecture. One student noted that ∠BPA = ∠CPD since they were common angles. The teacher reminded the students of the property – which they had learned in Grade 7 – that a line tangent to a circle is perpendicular to the radius that passes through the tangent point. Takumi mentioned another property that an inscribed angle corresponding to a semicircle arc is a right angle. The teacher then suggested focusing on the proving of ∠PAB = ∠PDC.

The students tackled this proof for seventeen minutes using their notebooks, where they added auxiliary lines, marks and mathematical expressions. Yuka completed the proof shown in Fig. 8, where she used the symbol a to represent ∠PDC and other related angles, such as ∠OCB = (180 – 2a)/2. She subsequently performed algebraic calculations to show that ∠PAB = ∠PDC. Kaito provided another rough proof and shared it with the whole class on the blackboard (Fig. 9). He introduced mathematical expressions to represent several geometrical relationships among the angles, and then combined these expressions to show the requested conclusion. Thus, the students proved that ∆PAB ~ ∆PDC in the case represented in Fig. 4d using their notebooks.

Fig. 8
figure 8

Yuka’s proof (English translations added by us)

Full size image
Fig. 9
figure 9

Kaito’s rough proof (written on the blackboard)

Full size image

Discussion

The mathematical activity of the class is represented in Fig. 10 using our model (see Fig. 1) of the interplay between physical and digital activity. Two tasks (#1 and #2) aimed at generalisation with proving were implemented in the lessons. The students’ activity began with their paper-and-pencil work where they constructed proof X for task 1. In lesson 2, the class engaged with task 2 using the DGE and generalised the statement through producing different diagrams. However, the students were not able to determine the truth of the conjecture in the case of Fig. 4c with the DGE. In lesson 3, the students addressed this case on their worksheets and their paper-and-pencil activity, along with the teacher’s support, led to their success in proving the truth of the conjecture. Another shift between paper-and-pencil activity and DGE use was observed in lesson 4, where the class considered the case of Fig. 4d (which had remained without being addressed in the generalisation) using the DGE and then proved the conjecture in their notebooks.

Fig. 10
figure 10

The interplay between paper-and-pencil activity and DGE use in the lessons

Full size image

Although this article reports on the student activity of a single class, a similar process was observed in other lessons implemented as part of our research project. It was generally found that through the students’ intensive paper-and-pencil activity on their worksheets, they succeeded in showing that ∠PAB = ∠PDC for the case presented in Fig. 4c. Thus, the model in Fig. 10 has some degree of generality beyond the single case described in this article.

Existing studies have tended to emphasise the relative affordances of DGEs in comparison with those of paper-and-pencil environments. The dragging function of DGEs, leading to a variety of diagrams, enables students to engage in dynamic mathematical activity where they can produce conjectures by themselves, discover counterexamples and come up with ideas regarding how to prove conjectures (Baccaglini-Frank and Mariotti 2010; Baccaglini-Frank et al. 2018; Komatsu and Jones 2019). This is partly the case with the lessons described in this article, as the students discovered the existence of different cases through dragging and investigated a conjecture generalising the original statement. In particular, the successive transformation of the diagrams using the DGE allowed the students to consider the particular case of Fig. 4d in conjunction with other cases (see Fig. 7).

Beyond such anticipated results, this article reveals the complementary roles played by paper-and-pencil activity and the use of DGE, and their interplay. It was found that paper-and-pencil work was needed if tasks were challenging and the sole use of DGE did not necessarily lead students to make progress with their activity (Hoyles and Jones 1998). Given that multiple diagrams produced by a DGE could potentially distract students (de Villiers 2007; Goldenberg 1995), concentrated work on a single static diagram on paper may be helpful. This may specifically be the case when students cannot see a way to advance their activity from their DGE diagrams. In such a case, it can be helpful (and perhaps, sometimes, indispensable) to add auxiliary lines and marks indicating congruent segments and angles to the diagrams, and also to employ symbolic representations (Palatnik and Dreyfus 2019; Herbst 2004). While DGEs also allow for these actions, it may be easier for students to do this on worksheets if, at the moment, they are typically more accustomed to doing such things on paper.

In this sense, the benefit of the paper-and-pencil environment observed in this study is not in its physical nature itself, but rather in its affordance to support students in working on representation processes, which is important in terms of Duval’s (2006, 2017) research on the register of representation. According to Duval, mathematical processing requires the transformation of representations that consists of treatment and conversion: treatment refers to manipulating representations within the same register, while conversion refers to translating representations in one register to those in another.

In the case reported in this article, these transformations of representation were facilitated by the ‘writing tool’ provided by the paper-and-pencil environment (see Figs. 5, 6, 8 and 9). The students performed the treatment in the visual register where they drew auxiliary lines and added marks indicating geometrical relationships (i.e. equal angles). They then converted the geometrical relationships they noticed in the visual register into the symbolic register using mathematical expressions. This conversion of representations allowed another treatment in the symbolic register, one where the requested conclusion was shown by integrating multiple mathematical expressions (Figs. 6 and 9) and performing algebraic calculations (Figs. 5b and 8). This combined transformation of the visual and the symbolic register was derived from the students’ familiarity with the writing tool that helped them represent, and build on, complex geometrical relationships. They were not able to manage the geometrical relationships completely and effectively through mental control of the visual representation provided by the DGE alone.

We do not intend to argue that paper-and-pencil activity is always needed. Students could manage the cases shown in Fig. 4c and 4d solely with a DGE, were they familiar with additional geometric theorems (i.e. the cyclic quadrilateral theorem and the alternate segment theorem) and certain DGE tools (e.g. angle marking tool, text tool and pen tool). Based on the results of this study, our intention is to offer the conjecture that paper-and-pencil work would be helpful if tasks are demanding and thus require solvers to convert and treat representations. This conjecture depends on student knowledge and skill, as well as their familiarity with DGE, and thus needs to be examined further in future studies.

The Teacher’s Roles

In the implemented lessons, the interplay between students’ paper-and pencil activity and their DGE use did not occur spontaneously. Rather, the teacher’s role was key in stimulating this interplay and can be explained in terms of the theory of instrumental orchestration (Trouche 2004). Drijvers et al. (2010) differentiate three elements within an instrumental orchestration. The first is a didactical configuration, which refers to an arrangement of tools (the DGE and worksheets in our study) in the classroom, and the second is an exploitation mode, which refers to the teacher’s decision regarding the use of the tools to achieve the learning objective. The exploitation mode is also related to the teacher’s decision on how to introduce a task and his/her expectation on the roles of the tools to be played in the students’ work on the task.

One objective of lesson 2 was generalisation where the students examined the truth of the original statement in diagrams different from the one given in the statement. For this purpose, it was necessary to produce various diagrams that still satisfied the premises of the statement, but this was not easy for students in paper-and-pencil environments (Komatsu et al. 2017). The teacher supported the students in this aspect through a didactical configuration of the DGE and worksheets, and by adopting an exploitation mode where he introduced task 2 in the DGE. This mode stimulated the students’ move from the paper-and-pencil environment to the DGE, and the role of the DGE (i.e. the dragging function) enabled the students to produce and examine different cases shown in Fig. 4.

At the same time, the DGE was not helpful to the students in achieving the subsequent goal (i.e. proving that ∠PAB = ∠PDC in the case shown in Fig. 4c). In lesson 3, the teacher set up a didactical configuration where he arranged both the DGE and worksheets, and enacted an exploitation mode where the students were allowed to tackle the task not necessarily using the DGE (Tabach 2011). These aspects of the teacher’s instrumental orchestration helped the students prove the conjecture by means of going back to the paper-and-pencil environment and capitalising on its affordances discussed in the previous section. In summary, the teacher exploited the affordances of both the DGE and the paper-and-pencil environment.

The teacher supported the students in another aspect, in particular when proving the conjecture using the paper-and-pencil environment. In lesson 3, the teacher held a whole-class discussion where the students had an opportunity to share their ideas on how to approach the task before actually tackling it. Through eliciting students’ responses, the teacher implied the possibility of introducing several auxiliary lines and drew the students’ attention to one pair of angles (∠PAB and ∠PDC). In addition, the teacher reminded the students about what they had studied regarding interior and exterior angles, since the targeted angles ∠PDC and ∠PAB were, respectively, an interior angle and an exterior angle of quadrilateral ABDC in Fig. 4c. Sharing problem-solving plans in this way is helpful, especially because students often face difficulties in finding how to get started on proving and difficulties in invoking the knowledge they have (e.g. facts and theorems) to prove the target statements (Moore 1994; Weber 2001).

While the teacher facilitated the students’ activity in these ways, he deliberately maintained a space into which the students could venture by taking the initiative to explore the task by themselves. If the interaction and guidance of a teacher is too excessive, it can considerably narrow the scope of the students’ engagement and have them simply follow the path predetermined by the teacher (Bauersfeld 1988). The teacher in the current study focused the students’ attention on particular aspects of the task by, for example, implying the use of a specific theorem (i.e. the triangle exterior angle theorem). However, this teacher’s action did not restrict the students’ engagement, as was evident in their subsequent activity, where they constructed multiple kinds of proofs by themselves. The teacher ensured that the students could engage actively in proving that ∠PAB = ∠PDC. Although the entire discussion here is related to lesson 3, similar teacher roles were observed in lesson 4.

In summary, our analysis underscores the importance of interplay between paper-and-pencil activity and the use of a DGE when tackling challenging geometric tasks. This interplay does not arise spontaneously, and teachers’ roles are essential in supporting students’ active and successful engagement.

Conclusion

In this article, we have analysed a series of secondary school lessons to investigate the interplay between students’ paper-and-pencil activity and their use of a DGE in conjecturing and proving. In the lessons, while DGE use supported the students in generalising a statement, they were initially not able to prove the generalisation solely through use of the DGE. However, they did eventually succeed in constructing proofs through combining their DGE work with paper-and-pencil activity. This finding provides a new insight into students’ proving activity with a DGE, given that existing studies have emphasised the advantages of DGEs in comparison with paper-and-pencil environments.

Our analysis shows how these two environments can play a complementary role to one another in mathematical learning according to the distinctive affordances of each environment. In particular, paper-and-pencil environments can afford students the tools for representing and building on different representations. Since our study has several limitations (e.g. the number of lessons analysed and the particularity of tasks used), it is necessary to examine our findings further by involving more students and using different tasks.

Despite the limitations of this study, one implication of our research in relation to teaching is that teachers may encourage students to capitalise on each affordance of a digital and a physical tool rather than using one tool in isolation, such as simply considering a DGE as solely a substitute for paper-and-pencil work (Højsted 2020). For instance, after using a DGE for conjecture generation, teachers may invite students to engage in paper-and-pencil work should the students face difficulties in proving their conjectures. This is because, as shown in this article, concentrating on a single static diagram on paper with adding auxiliary lines and marks to the said diagram, as well as employing symbolic representations, may be as helpful as, or more helpful than, considering multiple diagrams using DGE in order to come up with ideas for proof construction.

Our results highlight the need for further research into the back-and-forth use of digital and physical tools. Given our specific focus (i.e. proof-related activity with a DGE and on paper), it would be worthwhile to consider different digital and physical tools in relation to different mathematical activity. There are several directions for future research, even within the area of conjecturing and proving. One possible direction is a focus on the aspects of proving activity that were not examined in this article. We examined a particular case where the students already had the statement to be proved (task 1), proved it (proof X) and then engaged in the generalisation of the statement. Future work should examine its preceding process (i.e. the process from conjecture generation to proof construction), as this process is generally difficult for students.

We surmise that similar findings may be obtained – namely, that the use of a DGE would facilitate the production of conjectures (as has been shown in many articles) and that paper-and-pencil work may be helpful, particularly if additional diagrammatic and symbolic work is indispensable for proving the conjectures. It would also be worthwhile to consider different types of proofs, such as proofs by contradiction, as well as refutations by counterexamples involving the revision of conjectures and proofs. The model proposed in this article (Fig. 1) can be employed to analyse such proving activity in particular, and the interplay between students’ physical and digital activity in general.