Bi-HS-RRT$^\text {X}$: an efficient sampling-based motion planning algorithm for unknown dynamic environments

Abstract

In the field of autonomous mobile robots, sampling-based motion planning methods have demonstrated their efficiency in complex environments. Although the Rapidly-exploring Random Tree (RRT) algorithm and its variants have achieved significant success in known static environment, it is still challenging in achieving optimal motion planning in unknown dynamic environments. To address this issue, this paper proposes a novel motion planning algorithm Bi-HS-RRT$^\text {X}$, which facilitates asymptotically optimal real-time planning in continuously changing unknown environments. The algorithm swiftly determines an initial feasible path by employing the bidirectional search. When dynamic obstacles render the planned path infeasible, the bidirectional search is reactivated promptly to reconstruct the search tree in a local area, thereby significantly reducing the search planning time. Additionally, this paper adopts a hybrid heuristic sampling strategy to optimize the planned path quality and search efficiency. The convergence of the proposed algorithm is accelerated by merging local biased sampling with nominal path and global heuristic sampling in hyper-ellipsoid region. To verify the effectiveness and efficiency of the proposed algorithm in unknown dynamic environments, numerous comparative experiments with existing algorithms were conducted. The experimental results indicate that the proposed planning algorithm has significant advantages in planned path length and planning time.

Introduction

Currently, the exponential growth of unmanned autonomous systems, such as robots and autonomous vehicles, is increasingly permeating and playing a pivotal role in the transformation of societal and industrial ecosystems. Specifically, autonomous robots have demonstrated immense application potential in areas such as emergency response [1], logistics transportation [2], and smart manufacturing [3], attracting widespread attention from researchers. It is well-acknowledged that perception, localization, motion planning, and control are indispensable modules for autonomous navigation in robotics, with motion planning playing a critical role in the reliable and efficient execution of tasks by mobile robots. Particularly, real-time, efficient, and reliable motion planning in unknown dynamic environments remains an unresolved open challenge.

At present, motion planning algorithms for robots can generally be categorized into three types: methods based on artificial potential fields, grid-based methods, and sampling-based methods. Although these published algorithms have advanced the field to some extent, most are predicated on the assumption of static environments, leading to poor environmental adaptability and computational complexity. Specifically, grid-based methods like A* [4] and D* [5] face exponential growth in computational complexity in high-dimensional environments. Methods based on artificial potential fields, such as those described in [6] and [7], are prone to entrapment in local minima during motion planning, resulting in the termination or failure of the plan. Benefitting from their efficiency in search and low memory usage, sampling-based methods have become the mainstream choice for robotic motion planning. Representative of these, the RRT [8] algorithm, while efficient and suitable for high-dimensional spaces, does not consider path quality and lacks re-planning capabilities, rendering it unsuitable for unknown dynamic environments.

Addressing these gaps, researchers have proposed a series of improved algorithms. Typically, RRT-connect [9] shortens planning time through a bidirectional search strategy. RRT* [10] reduces path length through rewiring processes. Informed-RRT* [11] further accelerates convergence by focusing sampling on key regions of the state space. ERRT [12] can store waypoints from previous plans to guide tree growth during replanning but is time-consuming. Additionally, RRT$^\text {X}$ [13], as the first asymptotically optimal single-query sampling-based replanning algorithm, is particularly noteworthy. By continuously optimizing the same search tree and maintaining $\mathrm {\epsilon }$-consistent graphs at each node, combined with a reconnection mechanism, RRT$^\text {X}$ effectively addresses the impact of dynamic obstacles. However, when encountering the challenge of search tree interruption caused by unknown obstacles, RRT$^\text {X}$ needs to regrow on the existing tree to establish new connective paths, significantly increasing planning time. Likewise, RRT$^\text {X}$ still does not adequately address the challenges posed by sampling strategies.

In response to the long planning time and path length in unknown dynamic environments of existing methods, this paper proposes a novel motion planning algorithm driven by a synergy of hybrid heuristic sampling and bidirectional search, named Bi-HS-RRT$^\text {X}$. Specifically, the algorithm employs a bidirectional search strategy to identify an initial feasible path, which is subsequently merged with a reverse search tree for backward searching. In situations where the established path is blocked by dynamic obstacles, the algorithm leverages the robot’s current position and the existing valid nodes on the reverse tree to reinitiate the bidirectional search in a local area. The replanning phase can effectively reduce the planning time. Moreover, the algorithm adopts a hybrid sampling strategy that combines local biased sampling based on nominal paths with global sampling in elliptical heuristic regions, and the adaptive techniques are introduced into the algorithm to enable dynamic switching between global and local sampling. Thus, the path length and planning time are further optimized. The contributions of this paper include:

• Aiming at effectively improving planning time and path length in unknown dynamic environments, a bidirectional search strategy leveraging the robot’s position and valid nodes is proposed for cost-effective planning. Besides, the path length is optimized through a hybrid heuristic sampling strategy that combines local biased sampling and global sampling based on an n-dimensional ellipsoid. The planning time can be further reduced.

• Comprehensive experiments in environments with unknown dynamic obstacles were conducted for validation. Experimental results demonstrate that the Bi-HS-RRT$^\text {X}$ can significantly reduce planning time and path length compared to RT-RRT*, RRT$^\text {X}$ and DRRT. Besides, the analysis of the bidirectional search and hybrid sampling strategies within Bi-HS-RRT$^\text {X}$ confirms its feasibility and effectiveness in unknown dynamic environments.

Related work

Autonomous mobile robot motion planning, which entails devising viable paths for robotic systems, has attracted considerable interest, particularly in dynamic environments. To tackle the challenges associated with motion planning, a diverse array of algorithms has been developed.

Ferguson et al. [14] proposed the DRRT algorithm, which starts from the goal point as the root and grows inversely to the starting point, allowing the same search tree to be reused after environmental changes. This algorithm efficiently eliminates invalid paths caused by obstacles. However, this can lead to increased overall planning time, as new paths must be generated after paths are removed due to obstacles. Building on DRRT, Otte et al. [13] used a rapid re-wiring operation to repair damaged branches, thereby reconstructing the tree structure to speed up the search process. In [15], Zucker et al. introduced an innovative re-planning algorithm, MP-RRT, which achieves real-time planning in dynamic environments by biasing the sampling distribution and reusing branches from previous planning iterations. Kuwata et al. [16] presented CL-RRT for motion planning in complex environments. This method leverages the input space of closed-loop controllers for sample selection and combines efficient techniques to reduce the computational complexity of constructing the state space. Fulgenzi et al. [17] proposed Risk-RRT, based on a probabilistic collision risk function, actively predicting the trajectories of moving obstacles and samples. Naderi et al. [18] designed the RT-RRT* algorithm, intertwining motion planning with tree growth and avoiding waiting for the complete construction of the tree by moving the tree root through a proxy. To further enhance the planning efficiency of Risk-RRT and RT-RRT*, Bi-Risk-RRT [19] and Bi-AM-RRT* [20] respectively adopted bidirectional search strategies to reduce planning time.

Additionally, to simultaneously maintain the speed of the planner and obtain optimal paths, ensuring the quality of planning, numerous algorithms have been proposed and improved. Karaman et al. [10] introduced RRT*, the first incrementally optimal sample-based motion planning algorithm, which ensures incremental optimality by reconnecting neighboring vertices using newly generated nodes, albeit with a slow convergence rate. To accelerate convergence, Arslan et al. [21] proposed RRT$^{\#}$, based on RRT, ensuring that after each iteration, all samples are connected to the search tree in an optimal manner, mainly by adopting cost heuristics to update suboptimal connection samples in cost order. Further, Quick-RRT* [22] significantly improved optimization speed and path quality by tracking the parent nodes within and utilizing the triangle inequality. Moreover, based on path optimization and intelligent sampling techniques, Islam et al. [23] proposed RRT*-Smart, introducing an intelligent sampling method to obtain optimal or near-optimal solutions. Informed-RRT* introduced a direct sampling method by defining the acceptance region as a hyper-ellipsoid, thereby eliminating the need for iteration until a satisfactory state is found. In [24], Faroni et al. enhanced the performance of sample-based motion planning like RRT* by combining acceptable informed sampling with local sampling. Enevoldsen et al. [25] introduced a class of informed subsets composed of unions of ellipsoids formed by designated nominal paths, ensuring current safety in the face of potential collisions. However, these methods face challenges in motion planning efficiency in dynamic environments.

In this paper, a proactive planning approach based on RRT$^\text {X}$ is adopted, integrating a bidirectional search strategy for shorter planning time. This approach is enhanced by a local biased sampling strategy based on nominal paths and a global sampling strategy utilizing symmetric ellipses for direct sampling, aiming to accelerate the convergence of the algorithm and shorten the path lengths.

The remainder of this paper is structured as follows: “Preliminaries” outlines the problem and introduces RRT$^\text {X}$. “Algorithms” provides a detailed description of the algorithm. “Theoretical analysis” analyzes the algorithm’s probabilistic completeness, asymptotic optimality, and complexity. “Experiments and Results” reports and analyzes experimental results. Additionally, the practicality of the bidirectional search hybrid sampling strategies, along with their impact on the algorithm, are discussed. The paper concludes with “Conclusion”, summarizing the findings, implications of the research, and directions for future work.

Preliminaries

Motion planning problem definition

Let $X \in {\mathbb {R}}^n$ be the state space for a robotic system, with x denoting all possible states. The obstacle space, denoted by $X \subseteq X_{obs}$, represents the regions where the robot is “in collision” with obstacles or itself, while the complementary closed subset $X_{free} = X / X_{obs}$ constitutes the free space, encompassing all states that are accessible to the robot and align with the system’s and environment’s constraints.

The initial and target positions of the robot are denoted as $x_{start}$ and $x_{goal}$, respectively. The robot’s location at any given moment t is represented by $x_{robot}(t)$, mapping the robot’s journey from its commencement at $t_0$ to the present moment $t_{cur}$ within the state-space X. This path is undefined beyond $t_{cur}$. Both the obstacle space and the free space are subject to change over time or depending on the robot’s current position, as described by $\Delta X_{obs} = f(t, x_{robot})$. Changes in these spaces could result from factors like unpredictable movement of obstacles, errors in the initial understanding of $X_{obs}$, or the need for the robot to detect portions of $X_{free}$ using its sensors.

Fig. 1

The four stages of proposed algorithm: a initial feasible solution search, b path optimization, c reconnection upon path invalidation by dynamic obstacles, and d bidirectional search re-initiation to repair the reverse tree after reconnection failure. Green, orange, and blue lines represent the forward, reverse, and local reverse tree edges, respectively. Corresponding solid circles indicate the robot’s position, the target, and the root of the local reverse tree. Obstacles are shown in dark gray, and gray lines indicate invalidated paths

Define $\sigma : [0, 1] \rightarrow X_{free}$ as a path within the free state space, where $\sigma (0)$ corresponds to the initial state $x_{start}$ and $\sigma (1)$ corresponds to the final state $x_{goal}$. Let $\Sigma$ denote the set comprising all feasible and significant paths, including $\sigma$. The path’s length is denoted by $d(\sigma )$, which is a function of the path itself. In scenarios involving the state space X, a dynamic obstacle space characterized by $\Delta X_{obs} = f(t, x_{robot})$, and the robot’s initial and desired final states, the goal is to determine the optimal path, $\sigma ^*$. The criterion for optimality of $\sigma ^*$ is the minimization of the path length, formally given by

$$\begin{aligned} \sigma ^* = \arg \min _{\sigma \in \Sigma } d(\sigma ) \end{aligned}$$

(1)

subject to the condition that the path $\sigma$ is within the free space $X_{free}$ and avoids collision with obstacles. As the robot navigates and as the obstacle configuration changes over time, the optimal path may be recomputed to ensure it reflects the latest information, adhering to the evolving environmental dynamics and constraints.

RRT$^\text {X}$

RRT$^\text {X}$ is recognized as the pioneering sampling-based replanning algorithm that achieves asymptotic optimality, specifically crafted for offline computation within unknown environments. Notably, RRT$^\text {X}$ commences by searching for an initial path and then performs iterative optimizations in real-time when new obstacles emerge, thus enabling the dynamic repair of its graph/tree structure. A distinctive characteristic of the algorithm is its capability to swiftly rebuild and mend its graph/tree when modifications in obstacles are detected, as opposed to merely pruning the affected branches. Moreover, positioned at the goal state, the root of the tree facilitates the efficient reutilization of prior information.

Asymptotic optimality, a salient feature of RRT$^\text {X}$, is realized through the implementation of two innovative graph rewiring strategies. These strategies ensure the same iterated amortized runtime complexity of $\Theta \left( \log n \right)$ as RRT and RRT$^*$, where n denotes the count of vertices. This efficiency is achieved by first terminating cascade rewiring when the graph becomes $\mathrm {\epsilon }$-consistent, with $\mathrm {\epsilon }$ being a positive constant, and secondly by maintaining connectivity information in local neighbor sets at each node. This approach allows for asymmetric edges where the connection between nodes (u, v) may ultimately be disregarded as detailed in [13].

Particularly, a node v invariably retains the memory of its original neighbors as they were initially integrated into the search graph. Nevertheless, once these original neighbors no longer fall within an RRT$^*$-like shrinking ball of radius D centered at v, except for those on the shortest path subtree, the connections to v will be effectively dismissed.

Algorithms

This paper introduces Bi-HS-RRT$^\text {X}$, an algorithm designed for real-time optimal motion planning of mobile robots in unknown dynamic environments. The proposed algorithm distinguishes itself from RRT$^\text {X}$ by: (1) employing a bidirectional search strategy that quickly finds feasible path and integrates them into the reverse search tree for backward searching; (2) reactivating the bidirectional search during the replanning phase using the robot’s current position and the valid nodes on the reverse tree when the current path is invalidated by dynamic obstacles, thus reducing the planning time for replanning; (3) adopting a hybrid heuristic sampling strategy that samples the state space, using nominal path to guide the local sampling process and accelerate path optimization. Figure 1 illustrates the intuition of our method. The organization of this section is as follows. “Overall framework” describes the overall process of Bi-HS-RRT$^\text {X}$. “Connection radius” discusses the selection of the connection radius. “Bidirectional search” describes the process of reinitiating the bidirectional search, and “Hybrid heuristic sampling explains the hybrid heuristic sampling strategy.

Overall framework

Algorithm 1 details the implementation specifics of the Bi-HS-RRT$^\text {X}$ algorithm. The algorithm commences with the initialization of relevant variables, selecting the start point $x_{start}$ as the robot’s current position node $x_{robot}$ and loading map information (lines 1–3). Subsequently, it enters the main control loop (lines 4–24), which persists until the robot reaches the target area, thereby concluding the loop. At the start of each iteration, like RRT$^\text {X}$, the algorithm considers the impact of changes in obstacles on the planning. When the current path is detected to remain valid, the algorithm updates the robot’s position. If the path is found to be invalid, the robot’s movement is halted, and the replanning process begins, attempting to reconnect the robot with the reverse search tree. Should reconnection fail, the flag for activating the bidirectional search strategy is set (lines 7–13). The reconnection operation involves checking the reverse tree for any valid nodes that can directly connect to the nodes in the isolated node set.

Subsequently, the algorithm updates the RRT*-like connection radius and advances to sample using the hybrid heuristic sampling strategy. The tree growth strategy is selected based on whether $x_{robot}$ lies within the isolated node set $V_{{\mathcal {T}}}^{c}$. If so, $x_{closest}$, the nearest valid node on the reverse tree, is chosen as the root of the local reverse tree for bidirectional growth. Otherwise, the algorithm proceeds with the standard bidirectional search with $x_{robot}$ and $x_{goal}$ as the root nodes of the forward and reverse trees, respectively. The reverse growth process parallels the RRT$^\text {X}$ algorithm but incorporates additional constraints in the extend function. A node is considered promising if the following condition is met: if the parent(x) is not null and $\text {Key}(parent(x)) < \text {Key}(x_{robot})$ Essentially, a new node is added to the search tree only if its parent node is deemed promising. The condition $\text {Key}(parent(x)) < \text {Key}(x_{robot})$ implies that the heuristic function $h(x_{robot})=0$ [26], and g(x) is the ($\mathrm {\epsilon }$-consistent) cost-to-goal of reaching $x_{goal}$ from x through ${\mathcal {T}}$. The look-ahead estimate of cost-to-goal is $\text {lmc}(x)$. Finally, the guess probability is updated.

Algorithm 1

$\text {Bi-HS-RRT}^{\text {X}}$

Connection radius

Adjustments to the connection radius are crucial for achieving asymptotically optimal solutions and enhancing the algorithm’s operational efficiency. Typically, a larger connection radius $r$ accelerates the attainment of asymptotically optimal solutions, while a smaller $r$ boosts the algorithm’s execution efficiency. Karaman, in reference [10], proposed a formula for the lower bound of the connection radius, based on the metric of the problem space and the number of nodes in the graph. Building on Karaman’s research, Solovey provided a mathematically robust demonstration of asymptotic optimality in [27], indicating the necessity for an increased connection radius for the RRT* algorithm from: $\gamma \left( \frac{\log |V|}{|V|}\right) ^{1/d}$ to $\gamma ^{\prime }\left( \frac{\log |V|}{|V|}\right) ^{1/(d+1)}$, where d represents the system’s dimension, $\left| \cdot \right|$ is the cardinality of the set, and $\gamma$, $\gamma ^{\prime }$ are scenario-specific percolation theory parameters, expressed as:

$$\begin{aligned}{} & {} \gamma \ge \Bigg (2\Bigg (1+\frac{1}{d}\Bigg )\Bigg (\frac{\left| {\mathcal {F}}\right| }{\zeta _d}\Bigg )\Bigg )^{1/d}, \end{aligned}$$

(2)

$$\begin{aligned}{} & {} \gamma '\ge \left( 2+\theta \right) \Bigg (\frac{\left( 1+\varepsilon /4\right) c^*}{\left( d+1\right) \theta \left( 1-\mu \right) }\cdot \frac{\left| {\mathcal {F}}\right| }{\zeta _d}\Bigg )^{1/\left( d+1\right) }, \end{aligned}$$

(3)

where $\zeta _{d}$ denotes the Lebesgue measure of the d-dimensional unit sphere, defined as:

$$\begin{aligned} \zeta _d=\frac{\pi ^{\frac{d}{2}}}{\Gamma \left( \frac{d}{2}+1\right) }. \end{aligned}$$

(4)

$\varepsilon \in \begin{pmatrix}0,1\end{pmatrix}, \theta \in \begin{pmatrix}1,1/4\end{pmatrix}, \mu >0$, $c^*$ denotes the asymptotically optimal path’s convergence length. ${\mathcal {F}}$ represents the free space.

The bounds of $\gamma$ carry significant theoretical relevance, rather than constituting obligatory parameters. Owing to the common challenge of precisely ascertaining the specific values of ${\mathcal {F}}$ or $c^*$, despite potential approximations, the practical selection of $\gamma$ is generally based on reasoned conjectures, subject to modification as necessary. Nonetheless, empirical evidence indicates a broad efficacy range for $\gamma$ values [28]. To facilitate more effective solutions in motion planning, this study employs the connection radius outlined in [27], applied for exploitation search and the updating of neighboring nodes.

Bidirectional search

For motion planning based on RRT, employing a bidirectional search strategy facilitates faster feasible motion planning than a unidirectional approach. Algorithm 2 encapsulates the bidirectional search mechanism of Bi-HS-RRT$^\text {X}$. It begins with the initialization of forward and reverse trees, reassessing the root nodes of both. The algorithm then promotes tree growth using standard sampling-based motion planning operations. In each iteration, a new node, $x_{new}$, is grown from $x_{nearest}$ towards $x_{rand}$ within ${\mathcal {T}}_r$, using the steer function, and if no collision occurs between the new and the nearest node, the new node is incorporated into ${\mathcal {T}}_r$. Subsequently, the algorithm identifies the node $x_{nearest}$ in ${\mathcal {T}}_f$ closest to $x_{new}$ and attempts growth in that direction, generating another new node $x'_{new}$. If this node is also collision-free, it is added to ${\mathcal {T}}_f$.

The bidirectional growth process is carried out iteratively until predetermined conditions are met. The algorithm terminates the bidirectional search when the newly generated node $x'_{new}$ is less than 0.5 units away from $x_{new}$ and when $x_{goal}$ is within the tree ${\mathcal {T}}_r$, thus ensuring that subsequent expansion originates from the reverse tree. At this point, a feasible path is deduced that bridges the two trees, and this path is then assimilated into the reverse tree, a step that is essential for the swift rectification of the tree. Should ${\mathcal {T}}_f$ be smaller in size compared to ${\mathcal {T}}_r$, a swap of the trees is performed to initiate the following iteration with the smaller tree, enhancing the growth efficiency. This methodical approach is intended to balance the expansion of the two trees, thereby accelerating the discovery of a viable path linking the start and endpoint.

Algorithm 2

$\text {bidirectionalGrow}$

Hybrid heuristic sampling

In this subsection, Algorithm 3 presents a hybrid heuristic sampling process that supersedes the previously inefficient uniform sampling strategy. Uniform sampling is only effective until a feasible path is discovered, after which a non-uniform, hybrid heuristic sampling strategy is employed. The overall sampling is divided into three stages. In the first stage, uniform sampling is conducted across the map:

$$\begin{aligned} x_{rand}\thicksim {\mathcal {U}}(Map), \end{aligned}$$

(5)

where $x_{\text {rand}}$ denotes the sampling point and ${\mathcal {U}}$ indicates a uniform distribution, the second phase involves selecting an adaptive sampling probability $p$, based on the improvement of the current solution. The evolution of $p$ is described as:

$$\begin{aligned} p_{k+1} = {\left\{ \begin{array}{ll} v p_k + (1-v) \frac{c_{k-1} - c_k}{c_{k-1} - u}, &{} \text {if } c_{k-1} > c_k, \\ v p_k, &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

(6)

where $k$ signifies the $k$-th iteration, $v$ is the forgetting factor used to smooth the evolution of probability $p$, $c$ represents the path length, and $u$ denotes an acceptable path length, selecting the appropriate $p$ value becomes crucial. It plays a key role in achieving global asymptotic optimality and rapid convergence to local optima, as well as in mitigating slow convergence rates and stagnation at local minima.

Algorithm 3

$\text {hybridHeuristicSample}$

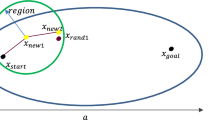
During the local biased sampling phase, a nominal path is introduced to guide the local sampling, as illustrated in Fig. 2. Initially, the current path is simplified using the Ramer–Douglas–Peucker (RDP) algorithm [29], with the simplified path serving as the nominal path $\sigma ^*$. The simplification disregards potential collisions with obstacles, and the parameter $\epsilon$ is empirically set to 5. Subsequently, the path cost of the nominal path is calculated to determine the sampling radius for biased sampling. The function biasSampling starts by uniformly sampling a point $b$ within a unit $n$-dimensional sphere centered at the origin, denoted as $x_{\text {ball}} \sim {\mathcal {U}}(X_{\text {ball}})$. This sample is then scaled and transformed to obtain a sample within a sphere of radius $R$ centered at $\sigma (s)$:

$$\begin{aligned} x_{rand}\leftarrow \sigma (s)+Rb, \end{aligned}$$

(7)

where $s \sim {\mathcal {U}}(0,\text {len}(\sigma ))$, and $\sigma (s)$ signifies a random path point on the current path.

The method for global sampling aligns with that of Informed-RRT*. An informed subset was formulated as an ellipsoid, and was given by

$$\begin{aligned} X_f=\{x\in X|\left\| x_{start}-x\right\| _2+\left\| x-x_{goal}\right\| _2\le c_k\}, \end{aligned}$$

(8)

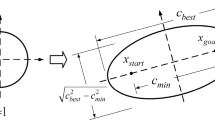
where $c_k$ denotes the cost associated with the best solution, $c_{best}$, obtained in the $k$-th iteration, and this informed set represents the intersection of $X_{free}$ with an $n$-dimensional hyper-ellipsoid centered on the line segment from $x_{start}$ to $x_{goal}$, with its primary diameter being $c_k$ and orthogonal diameters being $\sqrt{c_k^2 - c_{min}^2}$, where $\Vert x_{goal} - x_{robot} \Vert _2 \ge c_{min}$. The parameters $c_{best}$ and $c_{min}$, as well as the depiction of the informed subset, are illustrated in Fig. 3. For comprehensive details on the informed subset, refer to [11] and [30].

Fig. 2

The orange line segments represent the nominal paths, and the red lines indicate the current feasible paths

Fig. 3

As proposed in [11], the sampling area is confined to an ellipsoid, increasing the chances of improving the current path

Theoretical analysis

Probabilistic completeness

In robustly feasible path planning scenarios, a viable trajectory necessitates a path that ensures a clearance greater than a specified positive value $\delta$ from any obstacles [10]. An algorithm that addresses the robustly feasible trajectory determination challenge in the $X_{free}, x_{init}, X_{goal}$ configuration space achieves probabilistic completeness when the following condition is satisfied:

$$\begin{aligned}{} & {} \lim _{n\longrightarrow \infty } \textrm{inf} {\mathbb {P}} \left( \left\{ \exists x_{goal}\in V\cap {\mathcal {X}} _{goal}\,\,such\,\,that\,\,x_{init}\right. \right. \nonumber \\{} & {} \left. \left. \quad is\,\,connected\,\,to\,\,x_{goal}\,\,in\,\,G_n \right\} \right) =1, \end{aligned}$$

(9)

where $G_n$ signifies the generated graph on the $n$-th iteration of planning and ${\mathbb {P}}(\cdot )$ represents the probability measure [10]. This denotes that the algorithm is deemed probabilistically complete if it is capable of invariably identifying a solution to the planning problem, provided that there are adequate temporal resources available.

Rooted in Rapidly-exploring Random Trees principles, the Bi-HS-RRT$^\text {X}$ algorithm’s bidirectional search alternates between two independent trees to fulfill criterion (9). Moreover, it employs a heuristic connection strategy that enhances the identification of viable paths by expanding the target region [31], thereby refining the efficiency of connectivity between $x_{robot}$ and $x_{goal}$.

Asymptotic optimality

Sampling-based path planning algorithms are generally considered to exhibit almost-sure asymptotic optimality, which indicates that as the number of samples approaches infinity, the solution obtained by the algorithm converges to the optimal solution with probability 1 [10]. The hybrid heuristic sampling strategy proposed in this study employs a local sampling strategy with probability $\phi$ and a global sampling strategy with probability $1 - \phi$, and utilizes a non-uniform probability density $d$ to sample the free space $X_{free}$. When $\phi$ is less than 1, the probability density $d$ can be regarded as a mixture of probability densities over $X_{free}$, which is expressed as

$$\begin{aligned} d=\left( 1-\varphi \right) d_1+\varphi d_2 \end{aligned}$$

(10)

where $d_1$ represents a strictly positive uniform probability density across $X_free$ and

$$\begin{aligned} d_2=\frac{d\lambda (X_{free})-1+\phi }{\phi \lambda (X_{free})}. \end{aligned}$$

(11)

Based on this, the proof of the planner’s asymptotic optimality can be traced back to the demonstration of non-uniform sampling’s asymptotic optimality as presented in [32].

As shown in Eq. (6), consider $p_k \in [0, 1]$ as the estimate of approaching the local optimal solution in the $k$-th iteration. If there is an improvement in cost (i.e., $c_k < c_{k-1}$), then $p_{k+1}$ is rewarded proportionally to the relative improvement in cost and scaled by the distance between the actual cost and the estimated acceptable cost $u$. This allows the algorithm to adjust the proportion of local and global sampling as it continually improves the solution, thereby increasing the convergence speed without sacrificing asymptotic optimality.

Since local biased sampling does not uniformly sample near the nominal path, but instead over-samples within a tube centered on points along the nominal path with a radius of R, this may help reduce the path length [24].

Complexity

The space and time complexity of RRT$^\text {X}$ as demonstrated in [13] is given by $O\left( n\log n \right)$ and $\Theta \left( n\log n \right)$. Mathematical analysis reveals that Bi-HS-RRT$^\text {X}$ retains the space and time complexity of RRT$^\text {X}$, while achieving similar optimality with a significantly reduced n, thereby enhancing performance compared to RRT$^\text {X}$.

Space complexity

Space complexity is a measure of the memory needed for an algorithm’s execution. The Bi-HS-RRT$^\text {X}$ algorithm, which integrates bidirectional search and hybrid heuristic sampling strategies, does not increase memory demands beyond those of the original RRT$^\text {X}$ algorithm. Similar to RRT$^\text {X}$, each node in Bi-HS-RRT$^\text {X}$ is associated with a data structure holding $O(\log n)$ neighboring nodes. As a result, its space complexity remains $O(n \log n)$, mirroring that of RRT$^\text {X}$ and exhibiting linear growth in memory use.

Fig. 4

a–c show three distinct simulation scenarios during a single experimental trial. Lime and magenta stars mark the start and target points, respectively. Blue, red, green and orange lines trace paths by Bi-HS-RRT$^\text {X}$, RT-RRT*, RRT$^\text {X}$ and DRRT

Fig. 5

Three stages of navigation using Bi-HS-RRT$^\text {X}$ in unknown environments: the initial phase (t = start), the mid-point (t = 30 s), and the completion (t = end). Green and red circles denote start and target points, respectively. Grey lines show the algorithm’s exploration, red indicates chosen paths, and bold green traces the robot’s actual route. Orange circles represent emerging obstacles

Table 1 Performance metrics of three algorithms in unknown obstacle scenarios T denotes the planning time consumed; L refers to the path length; and ST signifies the search time to find a feasible path

Time complexity

Time complexity typically measures the amount of time needed to solve a problem of size $n$. According to [13], the RRT$^\text {X}$ algorithm exhibits a time complexity of $\Theta (n \log n)$. In contrast, the Bi-HS-RRT$^\text {X}$ algorithm, attributable to its bidirectional search approach, conducts a neighbor search within each of the two trees during every iteration. Giving

$$\begin{aligned} \Theta (n_f\log n_f)+\Theta (n_r\log n_r)\le & {} 2\Theta (n\log n)\nonumber \\= & {} \Theta (n\log n), \end{aligned}$$

(12)

where $n_f$ is the number of vertices in the forward tree ${\mathcal {T}}_f$, $n_r$ is the number of vertices in the reverse tree ${\mathcal {T}}_r$, and $n = \max (n_f, n_r)$. Since the search time for both trees does not exceed $\Theta (n \log n)$, the overall time complexity of the Bi-HS-RRT$^\text {X}$ algorithm is considered to be $\Theta (n \log n)$. The hybrid heuristic strategy merely enhances sampling efficiency by restricting the sampling area, without increasing computational load.

When new obstacle information is discovered, it must be propagated through the reverse tree ${\mathcal {T}}_r$ to remove the affected edges. Assuming the set of vertices with trajectories conflicting with the obstacle information is denoted as $V_{obs}$ and their descendant set as $D(V_{obs})$, this propagation process can be completed in $O(|D(V_{obs})| \log (n))$ time, facilitated by the efficiency of heap operations.

Experiments and results

To effectively demonstrate the efficacy of the proposed method, comprehensive experiments are outlined in “Performance evaluation of the proposed algorithm” through “Ablation study”. “Performance evaluation of the proposed algorithm” compares the algorithm with established methods such as RT-RRT*, RRT$^\text {X}$, and DRRT in four different environments, employing multiple iterations to account for the randomness inherent in sampling algorithms. “Impact of connection radius” explores the impact of connection radius parameters on the algorithm, while “Impact of nominal path parameter” investigates the influence of parameters within the RDP algorithm. “Ablation study” is dedicated to further validating the effectiveness and efficiency of the proposed bidirectional search strategy and hybrid heuristic sampling strategy, through a comprehensive set of comparative experiments involving Bi-HS-RRT$^\text {X}$, Bi-RRT$^\text {X}$, HS-RRT$^\text {X}$, and RRT$^\text {X}$ planners in two sets of scenarios. All simulations are conducted using PyCharm 2023 on a Lenovo ThinkBook 16 laptop equipped with an AMD Ryzen${\hbox {TM}}$ 7 6800 H processor at 3.2 GHz, and 16 GB RAM, running under the Windows system. The results and visualizations of these experiments are thoroughly presented in “Performance evaluation of the proposed algorithm” to “Ablation study”.

Performance evaluation of the proposed algorithm

Scenario with unknown obstacles: To test the obstacle-avoidance capabilities of the proposed method and its rapid convergence to an optimal path when confronted with sudden obstacles, the performance of Bi-HS-RRT$^\text {X}$, RT-RRT*, RRT$^\text {X}$ and DRRT is compared in three different scenarios, as depicted in Fig. 4. Each algorithm is run 25 times per scenario, comparing their average planning time, average path length, and average search time for a feasible path.

In these experiments, the planning time taken refers to the overall time cost for the robot to move from the start to the target point, including planning and execution time, starting from the moment the robot identifies a path. The path length is the cumulative Euclidean distance of waypoints from the start to the target. The three simulation scenarios used are shown in Fig. 4, with each map measuring 30 m by 50 m. The target area radius and the bidirectional search connection threshold are both set at 0.5 m. Emergent obstacles are simulated by gray solid circles with a radius of 1 m, which can appear at any location at any time to obstruct the robot’s path. To ensure fairness in experimentation, these circles are added 10 m ahead of the current path and 30 s after the robot begins moving, with results shown in Fig. 5.

Fig. 6

Box plot comparison of path lengths for Bi-HS-RRT$^\text {X}$, RT-RRT*, RRT$^\text {X}$ and DRRT across various scenarios

Fig. 7

The robot conducts navigation planning with Bi-HS-RRT$^\text {X}$ in an environment with five obstacles, depicted by dark grey shapes. The executed path is a black dashed line, while the colored segments show the planned position of the robot and the estimated positions of the obstacles with respect to the robot’s time-to-goal

Table 2 Performance metrics of three algorithms in moving obstacle scenarios T denotes the planning time consumed; L refers to the path length

Table 1 compiles the average total duration, path length, and time to first identify a feasible path across all simulations conducted in three distinct scenarios. The Bi-HS-RRT$^\text {X}$ algorithm surpasses RT-RRT*, RRT$^\text {X}$, and DRRT in all metrics. Against RT-RRT*, it shows path length reductions of 3.98$\%$, 4.18$\%$, and 1.40$\%$, and against RRT$^\text {X}$, reductions of 18.31$\%$, 9.93$\%$, and 7.79$\%$. When compared to DRRT, Bi-HS-RRT$^\text {X}$ further reduces path lengths by 20.46$\%$, 18.14$\%$, and 11.26$\%$, respectively, while decreasing planning time by 87.88$\%$, 85.52$\%$, and 76.70$\%$. These results emphasize Bi-HS-RRT$^\text {X}$’s marked efficiency in motion planning across varied test environments. Moreover, the Bi-HS-RRT$^\text {X}$’s adeptness at handling dynamic environments is underscored by its rapid response to unexpected obstacles, which are methodically recorded as 0.004, 0.089, and 0.1113 s for the respective scenarios previously described. These findings attest to the algorithm’s swift adaptability and robust performance, reaffirming its potential for real-world applications in motion planning.

The box plots in Fig. 6 illustrate the cost distribution of Bi-HS-RRT$^\text {X}$ relative to RT-RRT*, RRT$^\text {X}$ and DRRT across three different map environments. The consistently lower median costs and tighter distributions for Bi-HS-RRT$^\text {X}$ indicate its faster convergence and greater stability in motion planning. The notable cost-benefit advantages of Bi-HS-RRT$^\text {X}$ suggest its capability to discover more optimal paths under similar conditions. Hence, this method not only effectively reduces planning time but also provides higher-quality path options when navigating complex environments.

Scenario with moving obstacles: To further evaluate the obstacle avoidance performance of the proposed algorithm in dynamic environments, a series of experiments were conducted in scenarios with varying numbers of moving obstacles. In these experiments, the robot radius was set to 1.5 m, with a maximum speed of 15 m/s, in an experimental environment measuring 100 m by 100 m. The dynamic obstacles, comprising circles of two different radii (5 m and 10 m respectively), moved in random directions uniformly chosen from 0 to 2$\pi$ and traveled a random distance uniformly selected within 0 to 50 m. Upon contacting the environment boundary, these obstacles would rebound and continue moving in a new direction. To simulate real-world conditions in the simulations, the obstacles were set not to collide with the robot. If an obstacle blocked the robot’s current feasible path, the robot would stop and search for a new path. The results of these experiments are depicted in Fig. 7.

Fig. 8

Trend of path length variations for different connection radii across three scenarios

Fig. 9

Trend of path length variations for different $\epsilon$ values across three scenarios

Table 2 compares the Bi-HS-RRT$^\text {X}$ algorithm against RT-RRT*, RRT$^\text {X}$, and DRRT through 30 iterations across scenarios with 1 to 7 dynamic obstacles, confirming result stability and validity. Bi-HS-RRT$^\text {X}$ maintained strong performance, with average planning times of 33.89 s and path lengths of 128.75 m. Efficiency comparisons show Bi-HS-RRT$^\text {X}$ saving 9.77s over RT-RRT*, 5.42 s over RRT$^\text {X}$, and 10.62 s over DRRT. It also generated shorter paths by 14.04 m, 7.92 m, and 18.11 m, respectively. Despite performance dips with more dynamic obstacles, Bi-HS-RRT$^\text {X}$ demonstrated greater resilience and consistency, particularly in higher density scenarios (6 and 7 obstacles), with less time and path length increase compared to counterparts, indicating its adaptability and effectiveness in dynamic settings.

Impact of connection radius

To rigorously examine the impact of connection radius on the performance of the Bi-HS-RRT$^\text {X}$, this study conducted a series of simulation experiments within the same scenarios described in “Probabilistic completeness”. The experimental conditions were meticulously controlled, varying only the connection radius parameter, while all other conditions, such as the scenario configurations and other algorithmic parameters, remained constant. To ensure the stability and reliability of the experimental outcomes, all simulations were carried out in a static environment and were repeated 20 times for each scenario, with a fixed experimental runtime of 60 s.

The experimental results depicted in Fig. 8 clearly demonstrate that, across three distinct testing scenarios, employing a larger connection radius significantly enhances the speed of path convergence. Specifically, in Scenario 1, a simple environment, the selection of connection radius $R^{\prime } = \gamma ^{\prime }\left( \frac{\log \mid V\mid }{\mid V\mid }\right) ^{1/(d+1)}$ resulted in a notable decrease in path length by the 250th iteration, approaching the optimal solution more rapidly compared to radius $R = \gamma \left( \frac{\log \mid V\mid }{\mid V\mid }\right) ^{1/d}$. Despite the presence of sharp turns in Scenario 3, the speed of path length convergence remained impressive when using connection radius $R^{\prime }$. In Scenario 2, which features dense obstacles, although the convergence speed was reduced for both radii, choosing radius $R^{\prime }$ ultimately proved significantly better than radius R, yielding shorter path lengths. These experimental findings profoundly reveal that in the application of the Bi-HS-RRT$^\text {X}$ algorithm, selecting a larger connection radius can significantly improve the efficiency and quality of path planning, indicating that appropriate adjustment of the connection radius is a key factor in optimizing algorithm performance.

Fig. 10

Each row illustrates a complete navigation process within a scenario. The starting point is located at the bottom of the map and the destination at the top, both marked by white squares. The colors represent the goal cost for the current node of the robot. The dark grey lines indicate feasible paths, while the red paths show the executed trajectory. Obstacles composed of black circles and squares appear and disappear randomly over time

Fig. 11

The dual line chart for Scenario 1 displays the planning time consumption and corresponding path length for twenty-five repeated experiments of each of the four algorithms

Fig. 12

The dual line chart for Scenario 2 displays the planning time consumption and corresponding path length for twenty-five repeated experiments of each of the four algorithms

Fig. 13

The dual line chart for Scenario 2 displays the planning time consumption and corresponding path length for twenty-five repeated experiments of each of the four algorithms

Fig. 14

The dual line chart for Scenario 2 displays the planning time consumption and corresponding path length for twenty-five repeated experiments of each of the four algorithms

Impact of nominal path parameter

This section discusses the impact of the parameter $\epsilon$ in the RDP algorithm on the efficiency of the Bi-HS-RRT$^\text {X}$ algorithm. Repeated planning tasks were conducted on three different maps, each with 10 distinct values of $\epsilon$, and with each task running for 60 s. The path lengths corresponding to the same number of iterations for different values of $\epsilon$ were evaluated. Figure 9 illustrates the influence of $\epsilon$ on path lengths across three distinct scenarios. The results indicate that in simple scenarios, where the paths have fewer turns, the impact of $\epsilon$ is not significant. However, in the second scenario, characterized by dense obstacles, the shortest path length is achieved when $\epsilon =9$. As the value of $\epsilon$ increases, the path length decreases, and the number of iterations within the same time frame also reduces. Notably, the most rapid decline in path length occurs at $\epsilon =5$. This phenomenon suggests that in complex scenarios, where initial paths typically contain multiple turns, the RDP algorithm should be used to generate nominal paths that closely follow the shape of the original path, but without excessive adherence to avoid unnecessary sampling. In the third scenario, the experimental results still favor $\epsilon =9$ as the optimal value, suggesting that when selecting RDP parameters, values that are too low, which may result in nominal paths that do not conform to the shape of the original path, should be avoided; similarly, values that are too high should be avoided to prevent the nominal path from overly conforming to the original path, thereby wasting sampling points.

Ablation study

In this subsection, a series of ablation studies were conducted to understand the individual contributions of the proposed bidirectional search and hybrid heuristic sampling strategies to the performance of the algorithm. These experiments were designed to isolate each strategy, thereby assessing their separate impacts on the efficiency and robustness of the algorithm. By comparing the Bi-HS-RRT$^\text {X}$ algorithm with its variant versions-Bi-RRT$^\text {X}$, which excludes the hybrid heuristic sampling strategy, and HS-RRT$^\text {X}$, which omits the bidirectional search strategy-against the original RRT$^\text {X}$ algorithm, this study seeks to validate the effectiveness and necessity of the proposed strategies.

The study’s experimental design features two $100 \times 100$ scenarios with unknown obstacles, detailed in Fig. 10. Initially, robots receive a partial map, updated via remote sensor feedback. Post a 5-s warm-up, they navigate at 5 m/s, halting and replanning when encountering unexpected obstacles. Scenario 1 mimics a dense forest with small obstacles, while Scenario 2 represents an indoor setting with larger obstructions.

Figures 11 and 12 further elucidate the performance of the proposed algorithm and its ablated versions across these scenarios, repeatedly substantiating the relationship between planning time consumption and path length through multiple experiments. The analysis reveals that within the Bi-RRT$^\text {X}$ algorithm, there is a proportional relationship between to planning time and path length, highlighting the efficiency of the bidirectional search strategy when confronting emergent obstacles-swiftly identifying new feasible routes and thus reducing the robot’s idle time. In contrast, the HS-RRT$^\text {X}$ algorithm demonstrates significant fluctuations between time consumption and path length when facing larger obstructions, which may be attributed to the computational overhead imposed by the constraints of the hybrid heuristic sampling strategy on the selection of sampling points.

In the forest scene simulations (refer to Fig. 13), the Bi-HS-RRT$^\text {X}$ algorithm demonstrates marked superiority over Bi-RRT$^\text {X}$, HS-RRT$^\text {X}$, and RRT$^\text {X}$, enhancing planning time by 8.0$\%$, 12.6$\%$, and 22.6$\%$, respectively, and reducing path length by 6.6$\%$, 8.2$\%$, and 23.5$\%$. These results underscore Bi-HS-RRT$^\text {X}$’s enhanced efficiency and path optimization in complex, unknown environments. In indoor scenarios (as shown in Fig. 14), Bi-HS-RRT$^\text {X}$ continues to excel, reducing path length by 19.60$\%$ and 16.76$\%$ compared to Bi-RRT$^\text {X}$ and HS-RRT$^\text {X}$, respectively, and by 10.71$\%$ compared to RRT$^\text {X}$. Moreover, it outperforms these algorithms in planning time by 13.87$\%$, 154.71$\%$, and 61.32$\%$, respectively, highlighting its rapid response and path optimization capabilities in dynamic and unknown settings. Overall, Bi-HS-RRT$^\text {X}$, as proposed in this study, exhibits outstanding practicality, robustness, and efficiency, significantly outperforming the conventional RRT$^\text {X}$ algorithm.

Conclusion

This paper introduces a novel motion planning method, Bi-HS-RRT$^\text {X}$, which employs a bidirectional search strategy and a hybrid heuristic sampling approach to reduce planning time and path lengths. The algorithm is designed to optimize these metrics, especially during the initial planning stages and the replanning process in complex unknown dynamic environments. By utilizing a bidirectional search mechanism in the early stages of planning, the method allows for the parallel expansion of two search trees when the target is not yet included in the reverse tree, merging the paths upon successful connection and halting further growth of the forward tree. During the replanning phase, the algorithm rapidly reinitiates the bidirectional search using the robot’s current position and existing reverse tree information after simple reconnection attempts fail, thus reducing the necessary planning time.

The hybrid heuristic sampling strategy introduced in this paper utilizes an elliptical region for global heuristic sampling and a local sampling process guided by nominal path to accelerate the algorithm’s convergence, effectively shortening both the planning time and path length. Simulation evaluations across four different environments have thoroughly demonstrated the significant efficiency and practical advantages of Bi-HS-RRT$^\text {X}$. Moreover, the paper delves into the specific impacts of the proposed strategies on the algorithm’s performance, validating their feasibility and robustness in practical applications. Future work will focus on deploying Bi-HS-RRT$^\text {X}$ on actual platforms and conducting detailed parameter studies to ensure its suitability for real-world applications, thereby enhancing its practical deployment potential.