Introduction

Practical control problems often involve the inability to connect state variables directly to the problem or lack of suitable sensing devices or transducers, many of which are expensive. These issues recur in numerous practical control problems. To generate estimations of states in such situations, observer–based control schemes must be developed. This has resulted in considerable activity for observer design in recent years, as it has been more challenging than controlling systems. There is no need to coordinate the design of state observers and controllers [1, 2]. Studies on fuzzy logic systems, which are capable of universal approximation, have been undertaken for decades on modeling and identification. One tool available to design and analyze fuzzy control systems is Takagi–Sugeno’s (T–S) fuzzy system [3, 4], which linearly combines state variables from input state variables. T–S fuzzy systems can then be applied to nonlinear systems ranging from stochastic stability and neural networks [5, 6] through to fuzzy plants with both fuzzy and non–fuzzy plants being addressed in [7, 8]. T–S models can effectively represent nonlinear systems. Fuzzy observers designed on T–S fuzzy models represent nonlinear systems.

The design of the T–S fuzzy controller requires two steps. A local linear model must first be identified, followed by the development of a global controller in step two. Fuzzy neural networks were applied with input–output data sets to identify parameters of local models found in published literature [9]. Stabilizing a system requires combining multiple local linear controllers in order to stabilize it—this is at the core of controller design problems. This paper introduces an innovative method for designing nonlinear controllers by employing T–S fuzzy models inspired by the adaptive control theory of linear systems. A system is initially identified using a model with parameters aligned with the T–S fuzzy model. Assuming a linear state feedback controller with initial gains for each local linear model, the global linear model can be conceptualized as the convex combination of all local linear models. To achieve convergence of tracking and identification errors, adaptively tuned local controller gains are adaptively adjusted. Unlike other approaches, our method does not necessitate the identification of T–S model parameters prior to implementation. Asymptotically approaching their ideal values is ensured through a single adaptation mechanism, as opposed to existing multi–model adaptive control techniques for nonlinear systems, which require switching laws. Furthermore, an adaptive control law removes all constraints associated with existing T–S model control techniques.

Another significant approach involves using fuzzy systems to approximate the unknown nonlinear dynamics of a system. Despite the fact that many control methods for nonlinear descriptor systems assume an understanding of plant dynamics, practical systems often lack a complete understanding of these dynamics. It is in situations characterized by uncertainty or unknown dynamics that fuzzy systems can be effective, as they have universal approximation capabilities [10]. By using an adapting law, it is possible to update the parameters of the approximators fuzzy system according to the system response. Nonlinear systems with uncertainty or limited information have benefited greatly from adaptive fuzzy control, recently gaining considerable attention in the field of ordinary systems [11,12,13]. Controllers can be classified as direct or indirect adaptive controllers. To meet the desired control objectives, direct adaptive fuzzy control (DAFC) adjusts the parameters of the fuzzy system using a fuzzy system as the basis for the control action. A fuzzy system is used in indirect adaptive fuzzy control (IAFC) to identify plant dynamics, and a suitable controller is then developed based on that identification. There are many approaches to solving problems, each with its own advantages and disadvantages. As a result of its simpler structure, DAFC has several advantages. The number of fuzzy systems required by DAFC is directly proportional to the number of inputs, regardless of how many unknown functions are used in the model. There are some restrictions in the design process of DAFC, despite the fact that prior knowledge of model functions may not be required. The advantage of IAFC, however, is that controller design is separated from model adaptation. The convergence of models and parameters can thus be analyzed independently of control stability and performance. Moreover, since IAFC employs fuzzy rules, the controller can be tuned without altering the fuzzy model or its parameters. It is noteworthy that the model of the plant does not need to be modified due to changes in the controller.

A fuzzy system is designed to operate in situations where plant parameters and structures may vary significantly with uncertainty. A system’s performance is intended to remain consistent even when uncertain conditions exist. As a result, advanced fuzzy systems need to be able to adapt to changing conditions. As a result of implementing a training algorithm in a fuzzy logic system with an observer, it is called an adaptive fuzzy observer. Conventional adaptive schemes cannot incorporate linguistic fuzzy information provided by human operators, which is the main advantage of adaptive fuzzy schemes [14,15,16]. As adaptive schemes for nonlinear systems have become more popular, fuzzy systems are increasingly being integrated into them. The feedback linearization method is used to implement several indirect adaptive fuzzy control algorithms [17, 18]. The inverse dynamics of plants with singularities cannot be linearized using the feedback linearization method. An adaptive fuzzy control algorithm based on feedback linearization must take into account infinite control inputs in cases in which the inverse dynamics is at the singularity or the parameter approximation error diverges to infinity. As for sampled–data control, this statistical technique is utilized to monitor and control processes using samples of measurements or observations taken at different time intervals. The process periodically collects data that are then matched to pre–defined control limits to determine whether the process is in control or if an out-of-control signal indicates a potential problem. Recent efforts include even–trigged schemes for example even–trigged scheme [19] and two self–trigger methods are currently examined in [20] and emphasis–dynamic triggering method [21]. Other previous research considered an adaptive indirect control input done by an alternate strategy based on the no existence of the parametric uncertainties in the state.

The observer–based fuzzy system is essential part for adaptive controllers since it allows for modeling and control of uncertain and complex systems with more accurately. They keep modifying their system parameters and revising their controller’s action; they allow their action to adjust according to the observer’s feedback. The behaviour of controller in a stability region works smoothly while retaining a stable and the desired performance can still be achieved with a seamless system running with this actual adaptive controller. The use of observer–based fuzzy systems as adaptive controllers allows systems with various complexities to be better operated in dynamic conditions by instantly adapting. They manage uncertainties and nonlinearities that can limit system conduct, permitting a more vigorous and adaptable adaptive control. Observer–based fuzzy systems dramatically expand the new modeling strategies, control behaviour, and adaptation capabilities of adaptive controllers. One such adaptive control problem was examined using a state observer in this research paper [22]. For measuring system states that cannot be directly measured, they developed a high–gain fuzzy based on state observer and discussed adaptable neural network for the output feedback control with nonlinear systems in [23]. Keep in mind that time delays frequently arise in real–world applications and that this can have serious repercussions for performance and cause instability. Therefore, adaptive control of nonlinear systems for the time delays has received exponential attention in recent times. Scholars have employed a Lyapunov–Krasovskii functional to counteract the time–varying state delays effect using Lyapunov–Krasovskii functional, alongside an auxiliary system cited [24,25,26,27] to address both input delays and delays due to inputs. [28, 29] examined how nonlinear systems with uncertainties present adaptive control challenges that must be overcome to be successfully managed; unfortunately however this issue of adaptive control for T–S fuzzy systems with unknown measurements remains unanswered.

Related work

Over the last several decades, nonlinear models have played a pivotal role in many areas of application, from mobile robots and Energy Internet networks to unmanned helicopters and more [31, 32]. Tracking control is one of the main topics to be researched for fuzzy systems. The goal of tracking control is to find an appropriate control strategy based on state information and interactive control protocols to achieve the desired trajectory. An indirect adaptive controller plays an integral part in reaching this target. Nonlinearity often affects industrial systems’ control performance. However, only very few papers directly deal with practical applications for their research [33,34,35,36,37], and [38]. Researchers developed the [33] system with greater accuracy at reduced energy use for application across industries and rehabilitation systems. Furthermore, an indirect adaptive control scheme for fixed–wing aircraft was developed using Recursive Least Squares (RLS) with Purple Citation of [34]. Task space tracking control of industrial robot manipulators powered by brushless DC (BLDC) motors was introduced in [35] while consensus problems of multiple random mechanical systems were addressed in [36]. In the power sector, investigators compared an adaptive controller applying to an active magnetic bearing for position constraint control with prescriptive tracking performance [37] and feedback controller for backside weld width achieved in [38]. Therefore, designing a controller with nonlinear functions whose task is to maintain performance under nonlinearities is a significant issue. Is it possible to solve adaptive control problems using nonlinear functions under one umbrella framework? One purpose of this paper is to answer in favor.

As the following discussion, the authors describe some of the major achievements of their research.

  1. (1)

    This research paper presents an indirect adaptive fuzzy controller (I–AFO) and observer using a T–S fuzzy model. To analyze the dynamics of an observational system, this approach allows researchers to estimate unmeasurable states within nonlinear systems that cannot be observed directly.

  2. (2)

    Based on the T–S fuzzy model, the authors developed an indirect adaptive fuzzy observer (I–AFO) in an unified frame work. This indirect adaptive fuzzy observer (I-AFO) can handle unknown states and parameters.

  3. (3)

    The proposed controller includes a feedback method to avoid singularity issues that arise in linearization methods for inverse dynamics without needing additional algorithms.

  4. (4)

    Fuzzy models that represent observation systems can be estimated using an adaptive fuzzy scheme, using Lyapunov theory and Lipschitz condition to derive its adaptive law.

Following is the sequence of this research: Sect. 2’s purpose is to give an introduction to fuzzy systems and identify any arising problems; Sect. 3 constructs the proposed observer while the derivation of the output feedback controller is presented in Sect. 4. An example along with computer simulations is presented in Sect. 5 to illustrate how the proposed controller is designed and how it can be applied. Several conclusions are drawn at the end of Sect. 6.

Brief description of the problem

T–S fuzzy systems serve an integral role in nonlinear systems as both model and control frameworks, with this approach capable of representing and analyzing complex nonlinear relationships to identify systems, control nonlinearly, recognize patterns, as well as deal effectively with uncertainty and disturbances allowing the systems to perform reliably under real–world scenario.

Takagi–Sugeno (T–S) fuzzy model

It is possible to derive a highly nonlinear functional relationship using the T–S fuzzy model even though many of its rules have a small number of implications [30]. Following is a brief description of the T–S fuzzy model in the form of IF–THEN.

Plant Rule i: IF s(t) is \(\emptyset _{i}^{1}\) and \(\dot{s}(t)\) is \(\emptyset _{i}^{2}\) and ...and \(s(t)^{(n-1)}\) is \(\emptyset _{i}^{n}\), THEN

$$\begin{aligned} s(t)^{(n)}=\mathcal {A}_{i}^{T} s(t)+\mathcal {B}_{i} u(t), \quad i=1,2, \ldots , r \end{aligned}$$
(1)

where

$$\begin{aligned}{} & {} s(t)=\left[ \begin{array}{llll} s(t) \quad \dot{s}(t) \quad \cdots \quad s(t)^{(n-1)} \end{array}\right] ^{T} \in \mathbb {R}^{n},\\{} & {} \quad \mathcal {A}_{i} \in \mathbb {R}^{n}, \quad \mathcal {B}_{i} \in \mathbb {R} \\ \end{aligned}$$

\(\emptyset _{i}^{j}\) is the fuzzy set and r is the number of rules.

$$ \begin{aligned} s(t)^{(n)}&=\frac{\sum _{i=1}^{r} \nu _{i}(s)\left\{ \mathcal {A}_{i}^{T} s(t)+\mathcal {B}_{i} u(t)\right\} }{\sum _{i=1}^{r} \nu _{i}(x)} \\&=\sum _{i=1}^{r} \lambda _{i}(s(t))\left\{ \mathcal {A}_{i}^{T} s(t)+\mathcal {B}_{i} u(t)\right\} \end{aligned} $$

where

$$\begin{aligned} \nu _{i}(s(t))= & {} \prod _{j=1}^{n} \emptyset _{i j}\left( s(t)^{(j-1)}\right) \\ \lambda _{i}(s(t))= & {} \frac{\nu _{i}(s(t))}{\sum _{i=1}^{r} \nu _{i}(s(t))} \end{aligned}$$

Based on this assumption,

$$ \begin{array}{l} \nu _{i}(s(t)) \ge 0, \quad \displaystyle \sum _{i=1}^{r} \nu _{i}(s(t))>0, \quad i=1,2,3, \ldots , r \end{array} $$

Hence,

$$\lambda _{i}(s) \ge 0, \quad \sum _{i=1}^{r} \lambda _{i}(s)=1 $$

Problem specification

The following nonlinear SISO system has a regulation problem of \(n^{th}\) order.

$$\begin{aligned} \begin{array}{l} \dot{s}(t)=\displaystyle \sum _{i=1}^{r} \lambda _{i}(s(t))\left\{ \mathcal {A}_{i} s(t)+\mathcal {B}_{i}(\zeta _{f}(s)+\zeta _{g}(s) u(t))\right\} \\ y(t)=\displaystyle \sum _{i=1}^{r} \lambda _{i}(s(t))\mathcal {C}_{i} s(t) \\ s(t)= \phi (t), \end{array} \end{aligned}$$
(2)

where,

$$ \mathcal {A}_{i}=\left[ \begin{array}{ccccc} 0 \quad 1 \quad 0 \quad \cdots \quad 0 \\ 0 \quad 0 \quad 1 \quad \cdots \quad 0 \\ \vdots \quad \vdots \quad \vdots \quad \ddots \quad \vdots \\ 0 \quad 0 \quad 0 \quad \cdots \quad 1 \\ 0 \quad 0 \quad 0 \quad \cdots \quad 0 \end{array}\right] , \mathcal {B}_{i}=\left[ \begin{array}{c} 0 \\ 0 \\ \vdots \\ 0 \\ 1 \end{array}\right] , \mathcal {C}_{i}=[1\quad 0 \cdots 0 \quad 0] $$

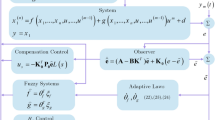
\(\phi (t)\) presents the initial conditions; u(t) presents the control input and \(\zeta _{f}(s)\), and \(\zeta _{g}(s)\) are unknown but bounded continuous nonlinear functions. Let \(s(t)=\big [s(t) \dot{s}(t) \cdots s(t)^{(n-1)}\big ]^{T}=\big [s_{1}(t)s_{2}(t) \cdots s_{n}(t)\big ]^{T} \in \mathbb {R}^{n}\) be the state vector of the model which is supposed to be unmeasurable. Here, unknown parameters and states are estimated and output is regulated. In this case, a fuzzy T–S model is used in conjunction with an indirect adaptive scheme. The authors develop an observer structure based on the T–S fuzzy model and estimate the unknown parameters by using the derived adaptive laws. An overview of the proposed scheme can be seen in Fig. 1. The T–S fuzzy model can be used to express the nonlinear function.

$$\begin{aligned} \begin{array}{l} \zeta _{f}(s)=\displaystyle \sum _{i=1}^{r} \lambda _{i}(s) \alpha _{i}^{T} s(t) \\ \zeta _{g}(s)=\displaystyle \sum _{i=1}^{r} \lambda _{i}(s) \beta _{i} \end{array} \end{aligned}$$
(3)

In order to describe the original system using the T–S fuzzy model, we can use the following data:

$$\begin{aligned} \begin{array}{l} \dot{s}(t)=\displaystyle \sum _{i=1}^{r} \lambda _{i}(s(t))\left\{ \mathcal {A}_{i} s(t)+\mathcal {B}_{i}(\alpha _{i}^{T} s(t)+ \beta _{i} u(t))\right\} \\ y(t)=\displaystyle \sum _{i=1}^{r} \lambda _{i}(s(t))\mathcal {C}_{i} s(t) \end{array} \end{aligned}$$
(4)

It is assumed that \(\alpha _{i}^{T} \) and \(\beta _{i}\) are unknown system parameters. The authors will describe in the next section how the proposed observation structure is based on a T–S fuzzy model.

Fig. 1
figure 1

Proposed methodology for adaptive controller

Full size image

Indirect adaptive fuzzy observer

In this section, a fuzzy observer is constructed to accurately estimate system states. The design procedure begins with a T–S fuzzy–model–based representation of the observer system—where \(\hat{s}(t)\) and \(\hat{y}(t)\) represent the estimated state vector and output vector for the augmented observer system.

$$\begin{aligned}{} & {} \hat{s}(t)= \left[ \begin{array}{ccccc} \hat{s}(t) \quad \dot{\hat{s}}(t) \quad \cdots \quad \hat{s}(t)^{(n-1)}\end{array} \right] ^{T}\nonumber \\{} & {} = \left[ \begin{array}{ccccc} \hat{s}_{1}(t) \quad \hat{s}_{2}(t) \quad \hat{s}_{n}(t) \quad \cdots \quad \hat{s}_{n}(t) \end{array}\right] \in \mathbb {R}^{n} \end{aligned}$$
(5)

An observer system is proposed such as:

$$\begin{aligned} \dot{\hat{s}}(t)= & {} \mathcal {A}_{i} \hat{s}(t)+\mathcal {B}_{i}\left[ \sum _{i=1}^{r} \lambda _{i}(\hat{s}) \hat{\alpha }_{i}^{T} \hat{s}(t)+\sum _{i=1}^{r} \lambda _{i}(\hat{s}) \hat{\beta }_{i} u(t)\right] \nonumber \\{} & {} \quad +\mathcal {L}_{i}(y(t)-\hat{y}(t)) \nonumber \\ \hat{y}(t)= & {} \hat{s}(t)\nonumber \\ \hat{s}(t)= & {} \hat{\phi }(t) \end{aligned}$$
(6)

\(\hat{\phi }(t)\) presents the initial conditions for the observer–based system. In this case, \(\hat{\alpha }_{i}\) and \(\hat{\beta }_{i}\) are adaptive parameters. An estimation error equals the difference between the original state and the estimated state, which is calculated as follows:

$$\begin{aligned} e(t){:}{=}s(t)-\hat{s}(t) \end{aligned}$$
(7)

To obtain an error dynamic equation, the authors must differentiate e(t) and substitute the original system and observer system into it.

$$\begin{aligned} \dot{e}(t)= & {} (\mathcal {A}_{i}-\mathcal {L}_{i} \mathcal {C}_{i}) e(t) +\mathcal {B}_{i}\left[ \sum _{i=1}^{r} \lambda _{i}(\hat{s})\left( \alpha _{i}^{T} s(t)\right. \right. \nonumber \\{} & {} \left. \left. \quad -\hat{\alpha }_{i}^{T} \hat{s}(t)\right) +\sum _{i=1}^{r} \lambda _{i}(\hat{s})\left( \beta _{i}-\hat{\beta }_{i}\right) u(t) \right] \end{aligned}$$
(8)

It can be observed that \(\lambda _{i}(\hat{s})\) should be used as the membership function for both s(t) and \(\hat{s}(t)\) since only \(\hat{s}(t)\)is measurable. It follows that e(t) approaches zero if all \((\mathcal {A}_{i}-\mathcal {L}_{i} \mathcal {C}_{i})\) eigenvalues are negative, and if the original parameters are estimated as well. The adaptive law can therefore be derived by following the next steps.

Assumption 1

The resultant model (1)can only be controlled if their rank \([\mathcal {C}] = n\).

Assumption 2

The nonlinear continuous term g(s, t) is assumed to be known and Lipschitz about the state s(t) uniformly, i.e.,

$$ \Vert g(s,t)-g(\hat{s},t)\Vert \le \mathcal {\mathbb {L}}_{f}, \forall \quad s(t),\ \hat{s}(t) \in \mathbb {R}^{n} $$

where \(\mathcal {\mathbb {L}}_{f}\) is the known Lipschitz constant.

Stability analysis

In T–S fuzzy systems, adaptive control is crucial for maintaining stability because it allows the system’s parameters to be adjusted and modified in real–time to take account of changing conditions and uncertainties.

Formulation of the adaptive law

In this section, the authors derive adaptive laws based on Lyapunov theory and Lipschitz conditions for parameter estimations.

$$\begin{aligned} \begin{array}{c} \mathcal {V}(t)=e^{T}(t) \mathbb {P} e(t)+\frac{1}{\Xi _{1}} \displaystyle \sum _{i=1}^{r} \tilde{\alpha }_{i} \tilde{\alpha }_{i}^{T}+\frac{1}{\Xi _{2}} \sum _{i=1}^{r} \tilde{\beta }_{i} \tilde{\beta }_{i}^{T} \end{array} \end{aligned}$$
(9)

with

$$\begin{aligned} \begin{array}{c} \tilde{\alpha }_{i}=\alpha _{i}-\hat{\alpha }_{i}, \\ \tilde{\beta }_{i} =\beta _{i} -\hat{\beta }_{i} \end{array} \end{aligned}$$
(10)

where,

  1. (a)

    The function \(\mathcal {V}(t)\) is radially unbounded and positive definite.

  2. (b)

    Positive definite matrices have the symbol \(\mathbb {P}\).

  3. (c)

    \(\Xi _{1}\) and \(\Xi _{2}\) represent the positive adaptation constant gains.

By differentiating \(\mathcal {V}(t)\) we are able to construct the adaptive law that will make \(\dot{\mathcal {V}}(t) \le 0\) (negative semi–definite). As a result of the following derivation, we have \(\mathcal {V}(t)\).

$$\begin{aligned} \dot{\mathcal {V}}(t){} & {} \le \dot{e}^{T}(t) \mathbb {P} e(t)+e^{T}(t) \mathbb {P} \dot{e}(t) +\frac{2}{\Xi _{1}} \sum _{i=1}^{r} \dot{\tilde{\alpha }} \tilde{\alpha }_{i}^{T}\nonumber \\{} & {} \quad +\frac{2}{\Xi _{2}} \sum _{i=1}^{r} \dot{\tilde{\beta }} \tilde{\beta }_{i}^{T} \end{aligned}$$
(11)

This expression for \(\dot{\mathcal {V}}(t)\) can be obtained by substituting (8) for (11).

$$\begin{aligned} \dot{\mathcal {V}}(t) \le{} & {} e^{T}(t)(\mathcal {A}_{i}-\mathcal {L}_{i} \mathcal {C}_{i})^{T} \mathbb {P} e(t)+e^{T}(t) \mathbb {P}(\mathcal {A}_{i}-\mathcal {L}_{i} \mathcal {C}_{i}) e(t) \nonumber \\{} & {} \quad +2 e^{T}\mathbb {P} \mathcal {B}_{i}\left[ \sum _{i=1}^{r} \lambda _{i}(\hat{s})\left( \alpha _{i}^{T} s(t)-\hat{\alpha }_{i}^{T} \hat{s}(t)\right) \right. \nonumber \\{} & {} \quad \left. +\sum _{i=1}^{r} \lambda _{i}(\hat{s})\left( \beta _{i}-\hat{\beta }_{i}\right) u(t)\right] +\bigsqcup _{i} \nonumber \\ \le{} & {} -e^{T}(t) \mathbb {Q} e(t)+2 e^{T}(t) \mathbb {P} \mathcal {B}_{i}\left[ \sum _{i=1}^{r} \lambda _{i}(\hat{s})\left( \alpha _{i}^{T} s(t)\right. \right. \nonumber \\{} & {} \left. \quad +\alpha _{i}^{T} \hat{s}(t)-\hat{\alpha }_{i}^{T} \hat{s}(t)-\alpha _{i}^{T} \hat{s}(t)\right) \nonumber \\{} & {} \left. \left. \right. \quad +\sum _{i=1}^{r} \lambda _{i}(\hat{s})\left( \beta _{i}-\hat{\beta }_{i}\right) u(t)\right] +\bigsqcup _{i} \nonumber \\ \le{} & {} -e^{T} \mathbb {Q} e(t)+2 e^{T} \mathbb {P} \mathcal {B}_{i} \sum _{i=1}^{r} \lambda _{i}(\hat{s}) \alpha _{i}^{T} e(t)\nonumber \\{} & {} \quad +2 e^{T}(t) \mathbb {P} \mathcal {B}_{i}\left[ \sum _{i=1}^{r} \lambda _{i}(\hat{s}) \tilde{\alpha }_{i}^{T} \hat{s}(t)\right. \nonumber \\{} & {} \quad \left. +\sum _{i=1}^{r} \lambda _{i}(\hat{s}) \tilde{\beta _{i}} u(t)\right] +\bigsqcup _{i} \end{aligned}$$
(12)

where

$$ \bigsqcup _{i} = \frac{2}{\Xi _{1}} \sum _{i=1}^{r} \dot{\tilde{\alpha }}_{i} \tilde{\alpha }_{i}+\frac{2}{\Xi _{2}} \sum _{i=1}^{r} \dot{\tilde{\beta }}_{i} \tilde{\beta }_{i}^{T} $$

In order to make \(\dot{\mathcal {V}}(t)\) negative definite, the adaptive law would require e(t) to approach zero over time from the equation (12). According to the following Theorem, some definitions and conditions are required to obtain the adaptive law.

Theorem 1

Let \(\lambda _{\min }(\mathbb {Z})\) represent the minimum eigenvalue of \(\mathbb {Z}\) and \(\lambda _{\max }(\mathbb {Z})\) the maximum eigenvalue. Consequently, it can be deduced from \(\mathbb {Z}=\mathbb {G} ^{T} \Lambda \mathbb {G} \) that

$$\begin{aligned} \lambda _{\min }(\mathbb {Z})\left\| s(t) \right\| ^{2} \le s^{T}(t) \mathbb {Z} s(t) \le \lambda _{\max }(\mathbb {Z})\Vert s (t)\Vert ^{2} \end{aligned}$$
(13)

where \(\mathbb {Z}\) represents a matrix that is positive definite, \(\mathbb {G} ^{T} \mathbb {G} =I\) denotes the identity matrix, and \(\Lambda \) is a diagonal matrix that comprises the eigenvalues of the matrix \(\mathbb {Z}\).

Proof

Using Lipschitz condition [39], the following condition is applicable to (12).

$$\begin{aligned} \sum _{i=1}^{r} \lambda _{i}(\hat{s})\left( \alpha _{i}^{T} s(t)-\alpha _{i}^{T} \hat{s}(t)\right) \le \mathbb {L}_{f}\Vert s(t)-\hat{s}(t)\Vert \end{aligned}$$

the Lipschitz constant, denoted as \(\mathbb {L}_{f}\), is present. Furthermore, Theorem 1 establishes that the subsequent inequality is satisfied.

$$\begin{aligned}{} & {} \dot{\mathcal {V}}(t)\le -e(t)^{T} \mathbb {Q} e(t)+2 e^{T}(t) \mathbb {P} \mathcal {B}_{i} \sum _{i=1}^{T} \lambda _{i}(\hat{s}) \alpha _{i}^{T} e(t) \nonumber \\{} & {} \qquad +2 e^{T}(t) \mathbb {P} \mathcal {B}_{i}\left[ \sum _{i=1}^{r} \lambda _{i}(\hat{s}) \tilde{\alpha }_{i} \hat{s}(t)+\sum _{i=1}^{r} \lambda _{i}(\hat{s}) \tilde{\beta }_{i} u(t)\right] +\bigsqcup _{i} \nonumber \\{} & {} \quad \le -e^{T}(t) \mathbb {Q} e(t)+2 \mathbb {L}_{f}\Vert \mathcal {B}_{i}\Vert \lambda _{\max }(\mathbb {P})\Vert e(t)\Vert ^{2}\nonumber \\{} & {} \qquad +2 e^{T}(t) \mathbb {P} \mathcal {B}_{i}\left[ \sum _{i=1}^{r} \lambda _{i}(\hat{s}) \tilde{\alpha }_{i}^{T} \hat{s}(t)+\sum _{i=1}^{r} \lambda _{i}(\hat{s}) \tilde{\beta }_{i} u(t)\right] +\bigsqcup _{i} \nonumber \\{} & {} \quad \le -\lambda _{\min }(\mathbb {Q})\Vert e(t)\Vert ^{2}+2 \mathbb {L}_{f}\Vert \mathcal {B}_{i}\Vert \lambda _{\max }(\mathbb {P})\Vert e(t)\Vert ^{2}\nonumber \\{} & {} \quad +2 e^{T}(t) \mathbb {P} \mathcal {B}_{i}\left[ \sum _{i=1}^{r} \lambda _{i}(\hat{s}) \tilde{\alpha }_{i}^{T} \hat{s}(t)+\sum _{i=1}^{r} \lambda _{i}(\hat{s}) \tilde{\beta _{i}} u(t)\right] v +\bigsqcup _{i} \nonumber \\{} & {} \quad \le -\left[ \lambda _{\min }(\mathbb {Q})-2 \mathbb {L}_{f}\Vert \mathcal {B}_{i}\Vert \lambda _{\max }(\mathbb {P})\right] \Vert e(t)\Vert ^{2}\nonumber \\{} & {} \qquad +2 e^{T}(t) \mathbb {P} \mathcal {B}_{i}\left[ \sum _{i=1}^{r} \lambda _{i}(\hat{s}) \tilde{\alpha }_{i}^{T} \hat{s}(t)+\sum _{i=1}^{r} \lambda _{i}(\hat{s}) \tilde{\beta _{i}} u(t)\right] +\bigsqcup _{i}\nonumber \\ \end{aligned}$$
(14)

In order to make \(\dot{\mathcal {V}}(t)\) negative definite in (14), we have to not only find suitable \(\mathbb {P}\) and \(\mathbb {Q}\) but also derive the adaptive law of \(\dot{\hat{\alpha }}_{i}\) and \(\dot{\hat{\beta }}_{i}\). The matrices \(\mathbb {P}\) and \( \mathbb {Q}\) can be easily chosen, which satisfy (15).

$$\begin{aligned} \mathbb {L}_{f}\Vert \mathcal {B}_{i}\Vert< & {} \frac{\lambda _{\min }(\mathbb {Q})}{2 \lambda _{\max }(\mathbb {P})}\end{aligned}$$
(15)
$$\begin{aligned} \mathcal {B}_{i}^{T} \mathbb {P}= & {} \mathcal {C}_{i} \end{aligned}$$
(16)

From equation (15), it can be inferred that the negative definite value of \(-\left[ \lambda _{\min }(\mathbb {Q})-2 \mathbb {L}_{f}\Vert \mathcal {B}_{i}\Vert \lambda _{\max }(\mathbb {P})\right] \Vert e(t)\Vert ^{2}\) in (14) is evident. Our sole objective becomes the convergence of the remaining portion of (14) to zero, for instance.

$$\begin{aligned} 2 e^{T}(t) \mathbb {P} \mathcal {B}_{i}\left[ \sum _{i=1}^{r} \lambda _{i}(\hat{s}) \tilde{\alpha }_{i}^{T} \hat{s}(t)+\sum _{i=1}^{r} \lambda _{i}(\hat{s}) \tilde{\beta }_{i} u(t)\right] +\bigsqcup _{i} =0\nonumber \\ \end{aligned}$$
(17)

Let us consider the assumption that \(\mathbb {S}=2 e^{T}(t) \mathbb {P} \mathcal {B}_{i}\left[ \sum _{i=1}^{r} \lambda _{i}(s) \tilde{\alpha }_{i}^{T} \tilde{s}(t)+\sum _{i=1}^{r} \lambda _{i}(s) \tilde{\beta }_{i} u(t)\right] \). Consequently, \(\mathbb {S}\) can be equated to \(\mathbb {S}=\mathbb {S}^{T}\) due to the fact that \(\mathbb {S}\) possesses a scalar value. Consequently, the authors can conclude that.

$$\begin{aligned} \begin{array}{l} 2 e^{T}(t) \mathbb {P} \mathcal {B}_{i}\displaystyle \left[ \sum _{i=1}^{r} \lambda _{i}(\hat{s}) \tilde{\alpha }_{i}^{T} \hat{s}(t)+\sum _{i=1}^{r} \lambda _{i}(\hat{s}) \tilde{\beta }_{i} u(t)\right] \\ \quad =2\displaystyle \left[ \sum _{i=1}^{r} \lambda _{i}(\hat{s}) \tilde{\alpha }_{i}^{T} \hat{s}(t)+\sum _{i=1}^{r} \lambda _{i}(\hat{s}) \tilde{\beta }_{i} u(t)\right] ^{T}(y(t)-\hat{y}(t)) \end{array} \nonumber \\ \end{aligned}$$
(18)

It can be observed that \(\mathcal {B}_{i}^{T} \mathbb {P}^{T} e(t)\) is equivalent to \((y(t)-\hat{y}(t))\) due to the presence of a symmetric positive definite matrix \(\mathbb {P}\), and equation (15). By utilizing equation (18), we can express the equation (17) in the following manner.

$$\begin{aligned}{} & {} 2\left[ \sum _{i=1}^{r} \lambda _{i}(\hat{s}) \tilde{\alpha }_{i}^{T} \hat{s}(t) +\sum _{i=1}^{r} \lambda _{i}(\hat{s}) \tilde{\beta _{i}} u(t)\right] ^{T}\nonumber \\{} & {} (y(t)-\hat{y}(t)) +\frac{2}{\Xi _{1}} \sum _{i=1}^{r} \dot{\tilde{\alpha }}_{i} \tilde{\alpha }_{i}^{T} +\frac{2}{\Xi _{2}} \sum _{i=1}^{r} \dot{\tilde{\beta }}_{i} \tilde{\beta }_{i}^{T}=0 \end{aligned}$$
(19)

with respect to \(\alpha \),

$$\begin{aligned}{} & {} 2 \sum _{i=1}^{r} \lambda _{i}(\hat{s}) \hat{s}^{T}(t) \hat{\alpha }_{i}(y(t)-\hat{y}(t))+\frac{2}{\Xi _{1}} \sum _{i=1}^{r} \dot{\tilde{\alpha }}\tilde{\alpha }_{i}^{T} \nonumber \\{} & {} \sum _{i=1}^{r} \dot{\tilde{\alpha }}_{i} \tilde{\alpha }_{i}^{T}=-\Xi _{1} \sum _{i=1}^{r} \lambda _{i}(\hat{s}) \dot{\tilde{s}}^{T}(t) \hat{\alpha }_{i}(y(t)-\tilde{y}(t)) \nonumber \\= & {} -\Xi _{1}(y(t)-\tilde{y}(t)) \sum _{i=1}^{r} \lambda _{i}(\hat{s}) \hat{s}^{T}(t) \hat{\alpha }_{i} \end{aligned}$$
(20)

with respect to \(\beta \),

$$\begin{aligned}{} & {} 2 \sum _{i=1}^{T} \lambda _{i}(\hat{s}) u^{T}(t) \tilde{\beta }_{i}^{T}(y(t)-\hat{y}(t))+\frac{2}{\Xi _{2}} \sum _{i=1}^{r} \dot{\tilde{\beta }}_{i} \tilde{\beta }_{i}^{T}=0 \nonumber \\{} & {} \sum _{i=1}^{r} \dot{\tilde{\beta }}_{i} \tilde{\beta }_{i}^{T} =-\Xi _{2} \sum _{i=1}^{r} \lambda _{i}(\hat{s}) u^{T}(t) \tilde{\beta }_{i}^{T}(y(t)-\hat{y}(t)) \nonumber \\{} & {} =-\Xi _{2}(y(t)-\hat{y}(t)) \sum _{i=1}^{r} \lambda _{i}(\hat{s}) u^{T}(t) \tilde{\beta }_{i}^{T} \end{aligned}$$
(21)

From the equation (10),

$$\begin{aligned} \left\{ \begin{array}{ccl} \dot{\tilde{\alpha }}_{i}&{}=&{}-\dot{\hat{\alpha }}_{i} \\ \dot{\tilde{\beta }}_{i}&{}=&{}-\dot{\hat{\beta }}_{i} \end{array}\right. \end{aligned}$$

From equations (20) and (21), the values of \(\dot{\hat{\alpha }}_{i}\) and \(\dot{\hat{\beta }}_{i}\) can be derived through a series of calculations.

$$\begin{aligned} \left\{ \begin{array}{ccl} \dot{\hat{\alpha }}^{T}&{}=&{}\Xi _{1}(y(t)-\hat{y}(t)) \lambda _{i}(\hat{s}) \hat{s}^{T}(t) \\ \dot{\hat{\beta }}_{i} &{}=&{}\Xi _{2}(y(t)-\hat{y}(t)) \lambda _{i}(\hat{s}) u^{T}(t) \end{array}\right. \end{aligned}$$

\(\square \)

Output feedback controller

In this section, the authors will present the some basic steps for the Controller structure in nonlinear systems. Firstly, identify the plant model and its nonlinearities. Then, design a suitable controller that can handle the nonlinearities and uncertainties in the system. Secondly, implement the designed controller into the system and ensure its stability and performance. Furthermore, update the parameters of the adaptive controller and adjust the control strategy based on system feedback and analysis. In the last, validate the performance and stability of the controller through simulation.

Controller structure

The controller that is being suggested exhibits a straightforward configuration for the output feedback.

$$\begin{aligned} u(t)={\mathcal {K}}_{i}^{T} {\hat{s}}(t) \end{aligned}$$
(22)

by employing the adaptive state feedback gain vector \(\mathcal {K}_{i} \in \mathcal {R}^{n}\), which belongs to the n–dimensional Euclidean space \(\mathcal {R}^{n}\), we can substitute equation (22) into equations (4) and (6). This substitution allows us to obtain the closed loop system for each equation and subsequently proceed with the same methodology employed in the design of the indirect adaptive fuzzy observer as discussed in Sect. 2. This methodology involves organizing an error dynamics and deriving an adaptive law. Upon completion of this process, we arrive at the following composed error dynamic equation.

$$\begin{aligned} \dot{e}(t)= & {} (\mathcal {A}_{i}-\mathcal {L}_{i} \mathcal {C}_{i}) e(t)+\mathcal {B}_{i}\left[ \sum _{i=i}^{r} \lambda _{i}(\hat{s})\left( \alpha _{i}^{T} s(t)-\hat{\alpha }_{i}^{T} \hat{s}(t)\right) \right. \nonumber \\{} & {} \quad \left. +\sum _{i=i}^{r} \lambda _{i}(\hat{s})\left( \beta _{i}-\hat{\beta _{i}}\right) \mathcal {K}_{i}^{T} \hat{s}(t)\right] \end{aligned}$$
(23)

Following is a selection of a Lyapunov function.

$$\begin{aligned} \mathcal {V}_{1}(t)= & {} s^{T}(t) \mathbb {P} s(t)+e^{T}(t) \mathbb {P} e(t)+\mathcal {K}_{i}^{T} \Lambda ^{-1} \mathcal {K}_{i} \nonumber \\{} & {} \quad +\frac{1}{\Xi _{1}} \sum _{i=1}^{r} \tilde{\alpha }_{i} \tilde{\alpha }_{i}^{T}+\frac{1}{\Xi _{2}} \sum _{i=1}^{r} \tilde{\beta }_{i} \tilde{\beta }_{i}^{T} \end{aligned}$$
(24)

In controller design, states should be taken into account, so (24) differs from (9). The following is the construction of \(\mathcal {V}_{1}(t)\) according to Lyapunov theory.

$$\begin{aligned} \mathcal {V}_{1}(t)\le & {} \displaystyle s^{T}(t)\left( \mathcal {A}_{i}^{T} \mathbb {P}+\mathbb {P} \mathcal {A}_{i}\right) s(t) \nonumber \\{} & {} +2 s^{T}(t) \mathbb {P} \mathcal {B}_{i}\left[ \displaystyle \sum _{i=1}^{r} \lambda _{i}(\hat{s}) \alpha _{i}^{T}+\sum _{i=1}^{r} \lambda _{i}(\hat{s}) \beta _{i} \mathcal {K}_{i}^{T} \hat{s}(t)\right] \nonumber \\{} & {} \displaystyle +e^{T}(t)\left[ (\mathcal {A}_{i}-\mathcal {L}_{i} \mathcal {C}_{i})^{T} \mathbb {P}+\mathbb {P}(A_{i}-\mathcal {L}_{i} \mathcal {C}_{i})\right] e(t) \nonumber \\{} & {} \displaystyle +2 e^{T}(t) \mathbb {P} \mathcal {B}_{i}\left[ \sum _{i=1}^{r} \lambda _{i}(\hat{s})\left( \alpha _{i}^{T} s(t)-\hat{\alpha }_{i}^{T} \hat{s}(t)\right) \right. \nonumber \\{} & {} \displaystyle \left. +\sum _{i=1}^{r} \lambda _{i}(\hat{s})\left( \beta _{i}-\hat{\beta }_{i}\right) \mathcal {K}_{i}^{T} \hat{s}(t)\right] +2 \dot{\mathcal {K}}_{i}^{T} \Lambda ^{-1} \mathcal {K}_{i}+\bigsqcup _{i}\nonumber \\ \end{aligned}$$
(25)

From the equation (25) can also be presented as follows using (7).

$$\begin{aligned} \mathcal {V}_{1}(t)\le & {} s^{T}(t) \mathbb {Q}_{1} s(t)\nonumber \\{} & {} \quad +2 s^{T}(t) \mathbb {P} \mathcal {B}_{i}\left[ \sum _{i=1}^{r} \lambda _{i}(\hat{s}) \alpha _{i}^{T}+\sum _{i=1}^{r} \lambda _{i}(\hat{s}) \beta _{i} \mathcal {K}_{i}^{T} \hat{s}(t)\right] \nonumber \\{} & {} \quad + e^{T}(t) \mathbb {Q}_{2} e(t)+2 e^{T}(t) \mathbb {P} \mathcal {B}_{i}\left[ \sum _{i=1}^{r} \lambda _{i}(\hat{s})\left( \alpha _{i}^{T} s(t)-\hat{\alpha }_{i}^{T} \hat{s}(t)\right) \right. \nonumber \\{} & {} \left. +\sum _{i=1}^{r} \lambda _{i}(\hat{s})\left( \beta _{i}-\hat{\beta _{i}}\right) \mathcal {K}_{i}^{T} s(t)\right] +2 \dot{\mathcal {K}}_{i}^{T} \Lambda ^{-1} \mathcal {K}_{i}+\bigsqcup _{i} \nonumber \\\le & {} -s^{T}(t) \mathbb {Q}_{1} s(t)+2 s^{T}(t) \mathbb {P} \mathcal {B}_{i} \sum _{i=1}^{r} \lambda _{i}(\hat{s}) \alpha _{i}^{T} s(t) \nonumber \\{} & {} \quad -e^{T}(t) \mathbb {Q}_{2} e(t)+2 e^{T}(t) \mathbb {P} \mathcal {B}_{i} \sum _{i=1}^{r} \lambda _{i}(\hat{s}) \alpha _{i}^{T} e(t) \nonumber \\{} & {} \quad +2 s^{T}(t) \mathbb {P} \mathcal {B}_{i} \sum _{i=1}^{r} \lambda _{i}(\hat{s}) \tilde{\beta }_{i} \mathcal {K}_{i}^{T} \hat{s}(t) \nonumber \\{} & {} +2 s^{T}(t) \mathbb {P} \mathcal {B}_{i} \sum _{i=1}^{r} \lambda _{i}(\hat{s}) \hat{\beta }_{i} \mathcal {K}_{i}^{T} \hat{s}(t) \nonumber \\{} & {} \quad +2 e^{T}(t) \mathbb {P} \mathcal {B}_{i} \sum _{i=1}^{r} \lambda _{i}(\hat{s}) \tilde{\alpha }_{i}^{T} \hat{s}(t) +2 e^{T}(t) \mathbb {P} \mathcal {B}_{i} \nonumber \\{} & {} \quad \sum _{i=1}^{r} \lambda _{i}(\hat{s}) \tilde{\beta }_{i} \mathcal {K}_{i}^{T} \hat{s}(t)+2 \dot{\mathcal {K}}_{i}^{T} \Lambda ^{-1} \mathcal {K}_{i}+\bigsqcup _{i} \end{aligned}$$
(26)

Since \(s^{T}(t)\mathbb {P}\mathcal {B}_{i}\), \(\mathcal {C}_{i} s(t)\) and \(\alpha _{i}^{T} s(t)\) are scalars, their transpose also has a scalar value; therefore, the inequality (26) can be expressed as follows, and it is verified that this match is in fact true, as shown in (28).

$$\begin{aligned} \begin{aligned}&2 s^{T}(t) \mathbb {P} \mathcal {B}_{i} \sum _{i=1}^{r} \lambda _{i}(\hat{s}) \alpha _{i}^{T} s(t) =2 \mathcal {B}_{i}^{T} \mathbb {P} s(t) \sum _{i=1}^{r} \lambda _{i}(\hat{s}) \alpha _{i}^{T} s(t)\\&\quad = 2 \mathcal {C}_{i} s(t) \sum _{i=1}^{r} \lambda _{i}(\hat{s}) \alpha _{i}^{T} s(t) =2 \sum _{i=1}^{r} \lambda _{i}(\hat{s})\left( \mathcal {C}_{i} s(t)s^{T}(t) \alpha _{i}\right) \end{aligned} \nonumber \\ \end{aligned}$$
(27)

Furthermore,

$$\begin{aligned} 2 s^{T}(t) \mathbb {P} \mathcal {B}_{i} \sum _{i=1}^{r} \lambda _{i}(\hat{s}) \alpha _{i}^{T} s(t){} & {} \le 2 \sum _{i=1}^{r} \lambda _{i}(\hat{s})\left\| \alpha _{i}^{T}\right\| \Vert s(t)\Vert ^{2}, \nonumber \\ {}{} & {} \quad with \quad \Vert \mathcal {C}_{_{i}}\Vert =1 \end{aligned}$$
(28)

From (13) and (26), (28) satisfies the following inequality.

$$\begin{aligned} \begin{aligned} \mathcal {V}_{1}(t)&\le -\left( \lambda _{\min }\left( \mathbb {Q}_{1}\right) -2 \sum _{i=1}^{r} \lambda _{i}(\hat{s})\left\| \alpha _{i}^{T}\right\| \right) \Vert s(t)\Vert ^{2} \\&\quad -\lambda _{\min }\left( \mathbb {Q}_{2}\right) \Vert e(t)\Vert ^{2}+2 \mathbb {L}_{f}\Vert \mathcal {B}_{i}\Vert \lambda _{\max }(\mathbb {P})\Vert e(t)\Vert ^{2} \\&\quad +2 s^{T}(t) \mathbb {P} \mathcal {B}_{i} \sum _{i=1}^{r} \lambda _{i}(\hat{s}) \tilde{\beta }_{i} \mathcal {K}_{i}^{T} \hat{s}(t) \\&\quad +2 s^{T}(t) \mathbb {P} \mathcal {B}_{i} \sum _{i=1}^{r} \lambda _{i}(\hat{s}) \hat{\beta }_{i} \mathcal {K}_{i}^{T} \hat{s}(t)\\&\quad +2 e^{T}(t) \mathbb {P} \mathcal {B}_{i} \sum _{i=1}^{r} \lambda _{i}(\hat{s}) \tilde{\alpha }_{i}^{T} \hat{s}(t)\\&\quad +2 e^{T}(t) \mathbb {P} \mathcal {B}_{i} \sum _{i=1}^{r} \lambda _{i}(\hat{s}) \hat{\beta }_{i} \mathcal {K}_{i}^{T} \hat{s}(t) +2 \dot{\mathcal {K}}_{i}^{T} \Lambda ^{-1} \mathcal {K}_{i}+\bigsqcup _{i} \end{aligned} \end{aligned}$$
(29)

Remark 1

Several factors contribute to the difficulty of designing adaptive control for T–S fuzzy systems. There are several factors to consider here, including the complexity of the system, modeling uncertainties, parameter variations, and the need for online learning and adaptation. An additional challenge lies in maintaining system stability, robustness, and satisfactory performance despite nonlinear dynamics and disturbances by effectively tuning adaptive control parameters. When designing adaptive control systems for T–S fuzzy systems, key decisions include choosing fuzzy sets and rule bases as well as their number/structure/rule bases to consider for their design as these decisions will have significant effects. When considering the computational complexity of real–time implementation of adaptive control algorithms as well as tradeoffs between adaptation speed and accuracy it is also crucial.

Theorem 2

If, we choose the matrices \(\mathbb {Q}_{1}\) in a way that \(\lambda _{\min }(\mathbb {Q})-2 \mathbb {Z}_{i} \ge \mu >0 \) for some non–negative constant, we get the non–positive definite values from \(\mathcal {V}_{1}(t)\). Based on Theorem Theorem 2 and (15), any underlined portion of (29) always has a negative value. As a result, other than the underlined part, the rest of (29) must be zero for \(\mathcal {V}_{1}(t)\) to be negative definite. Based on this Theorem, the adaptive control law parameters are as follow:

$$\begin{aligned} \dot{\hat{\alpha }}_{i}^{T}= & {} \Xi _{1}(y(t)-\hat{y}(t)) \lambda _{i}(\hat{s}) \hat{s}^{T}(t) \nonumber \\ \dot{\hat{\beta }}_{i}= & {} \Xi _{2}( y(t)-\hat{y}(t)) \lambda _{i}(\hat{s}) \hat{s}^{T}(t) \mathcal {K}_{i} \nonumber \\ \dot{\mathcal {K}}_{i}^{T}= & {} -y(t) \sum _{i=1}^{r} \lambda _{i}(\hat{s}) \hat{\beta }_{i} \hat{s}^{T}(t) \Lambda \end{aligned}$$
(30)

Proof

To derive the adaptive control law, let’s let the rest part of (29) be zero, and then we get equation (31).

$$\begin{aligned}{} & {} 2 s^{T}(t) \mathbb {P} \mathcal {B}_{i} \sum _{i=1}^{T} \lambda _{i}(\hat{s}) \tilde{\beta }_{i} \mathcal {K}_{i}^{T} \hat{s}(t) \nonumber \\{} & {} \qquad +2 s^{T}(t) \mathbb {P} \mathcal {B}_{i} \sum _{i=1}^{r} \lambda _{i}(\hat{s}) \hat{\beta }_{i} \mathcal {K}_{i}^{T} \hat{s}(t) \nonumber \\{} & {} \qquad +2 e^{T}(t) \mathbb {P} \mathcal {B}_{i} \sum _{i=1}^{r} \lambda _{i}(\hat{s}) \tilde{\alpha }_{i}^{T} \hat{s}(t) \nonumber \\{} & {} \qquad +2 e^{T}(t) \mathbb {P} \mathcal {B}_{i} \sum _{i=1}^{r} \lambda _{i}(\hat{s}) \tilde{\beta }_{i} \mathcal {K}_{i}^{T} \hat{s}(t) \nonumber \\{} & {} \qquad +2 \dot{\mathcal {K}}_{i}^{T} \Lambda ^{-1} \mathcal {K}_{i}+\bigsqcup _{i}=0 \end{aligned}$$
(31)

Further computing for the derivation of adaptive control law:

$$\begin{aligned}{} & {} 2 s^{T}(t) \mathbb {P} \mathcal {B}_{i} \sum _{i=1}^{r} \lambda _{i}(\hat{s}) \tilde{\beta }_{i} \mathcal {K}_{i}^{T} \hat{s}(t)\nonumber \\{} & {} \quad +2 s^{T}(t) \mathbb {P} \mathcal {B}_{i} \sum _{i=1}^{r} \lambda _{i}(\hat{s}) \hat{\beta }_{i} \mathcal {K}_{i}^{T^{T}} \hat{s}(t)\nonumber \\{} & {} \quad +2 e^{T}(t) \mathbb {P} \mathcal {B}_{i} \sum _{i=1}^{r} \lambda _{i}(\hat{s}) \tilde{\alpha }_{i}^{T} \hat{s}(t) \nonumber \\{} & {} \quad +2 e^{T}(t)\mathbb {P} \mathcal {B}_{i} \sum _{i=1}^{r} \lambda _{i}(\hat{s}) \tilde{\beta }_{i} \mathcal {K}_{i}^{T} \hat{s}(t) +2 \mathcal {\dot{K}}_{i}^{T} \Lambda ^{-1} \mathcal {K}_{i}\nonumber \\{} & {} \quad +\bigsqcup _{i}=0 \end{aligned}$$
(32)

Now suppose that

$$\begin{aligned} \gamma _{1}= & {} 2 e^{T}(t) \mathbb {P} \mathcal {B}_{i} \sum _{i=1}^{r} \lambda _{i}(\hat{s}) \tilde{\alpha }_{i}^{T} \hat{s}(t) \nonumber \\ \gamma _{2}= & {} 2 e^{T}(t) \mathbb {P} \mathcal {B}_{i} \sum _{i=1}^{r} \lambda _{i}(\hat{s}) \tilde{\beta }_{i} \mathcal {K}_{i}^{T} \tilde{s}(t) \nonumber \\ \gamma _{3}= & {} 2 s^{T}(t) \mathbb {P} \mathcal {B}_{i} \sum _{i=1}^{r} \lambda _{i}(\hat{s}) \tilde{\beta }_{i} \mathcal {K}_{i}^{T} \hat{s}(t) \end{aligned}$$
(33)

Since each \(\gamma _{\ell }\), \(\ell =1,2,3.\) have a scalar value, it satisfies that \(\gamma _{1}^{T}=\gamma _{1}\), \(\gamma _{2}^{T}=\gamma _{2}\) and \(\gamma _{3}^{T}=\gamma _{3}\) and they can be represented as follows.

$$\begin{aligned} \begin{array}{l} \gamma _{1}=\gamma _{1}^{T}=2\displaystyle \left[ \sum _{i=1}^{r} \lambda _{i}(\hat{s}) \tilde{\alpha }_{i}^{T} \hat{s}\right] ^{T}(y(t)-\hat{y}(t)) \\ \gamma _{2}=\gamma _{2}^{T}=2\displaystyle \left[ \sum _{i=1}^{r} \lambda _{i}(\hat{s}) \tilde{\beta }_{i} \mathcal {K}_{i}^{T} \hat{s}\right] ^{T}(y(t)-\hat{y}(t)) \\ \gamma _{3}=\gamma _{3}^{T}=2\displaystyle \left[ \sum _{i=1}^{r} \lambda _{i}(\hat{s}) \tilde{\beta }_{i} \mathcal {K}_{i}^{T} \hat{s}\right] ^{T} y(t) \end{array} \end{aligned}$$
(34)

where

$$\begin{aligned} \left\{ \begin{array}{ccl} e(t)&{}{:}{=}&{}s(t)-\hat{s}(t), \qquad \mathcal {B}_{i}^{T} \mathbb {P}=\mathcal {C}_{i} \\ \mathcal {C}_{i}(s(t)-\hat{s}(t))&{}=&{}y(t)-\hat{y}(t) \end{array}\right. \end{aligned}$$

After substituting the values of equation (34) into (26), we divide (33) into three parts with respect to \(\alpha _{i}\), \(\beta _{i}\) and \( \mathcal {K}_{i} \) in order to obtain adaptive control law. \(\square \)

Calculation of adaptive parameter with respect to \(\alpha _{i}\):

In this section, the authors will present some basic steps to calculate the unknown parameter \(\alpha _{i}\):

$$\begin{aligned}{} & {} 2\left[ \sum _{i=1}^{r} \lambda _{i}(\hat{s}) \tilde{\alpha }_{i}^{T} \hat{s}(t)\right] ^{T}(y(t)-\hat{y}(t))+\frac{2}{\Xi _{1}} \sum _{i=1}^{r} \dot{\tilde{\alpha }}_{i} \tilde{\alpha }_{i}^{T}=0 \nonumber \\\end{aligned}$$
(35)
$$\begin{aligned}{} & {} \frac{2}{\Xi _{1}} \sum _{i=1}^{r} \dot{\tilde{\alpha }}_{i} \tilde{\alpha }_{i}^{T}=-2\left[ \sum _{i=1}^{r} \lambda _{i}(\hat{s}) \tilde{\alpha }_{i}^{T} \hat{s}(t)\right] ^{T}(y(t)-\hat{y}(t)) \nonumber \\\end{aligned}$$
(36)
$$\begin{aligned}{} & {} \sum _{i=1}^{r} \dot{\tilde{\alpha }} \tilde{\alpha }_{i}^{T}=-\Xi _{1}(y(t)-\hat{y}(t)) \sum _{i=1}^{r} \lambda _{i}(\hat{s}) \hat{s}^{T}(t) \tilde{\alpha }_{i} \nonumber \\\end{aligned}$$
(37)
$$\begin{aligned}{} & {} \tilde{\alpha }_{i}^{T}=-\Xi _{1}(y(t)-\hat{y}(t)) \lambda _{i}(\hat{s}) \hat{s}^{T}(t)\nonumber \\ \end{aligned}$$
(38)

Calculation of adaptive parameter with respect to \(\beta _{i}\):

A simple method for calculating the unknown parameter \(\beta _{i}\) is presented in this section:

$$\begin{aligned}{} & {} 2\left[ \sum _{i=1}^{r} \lambda _{i}(\hat{s}) \tilde{\beta }_{i} ^{T}\mathcal {K}_{i}^{T} \hat{s}(t)\right] ^{T} y(t)\nonumber \\{} & {} \quad +2\left[ \sum _{i=1}^{r} \lambda _{i}(\hat{s}) \tilde{\beta } \mathcal {K}_{i}^{T} \hat{s}(t)\right] ^{T}(y(t)-\hat{y}(t))\nonumber \\{} & {} \quad +\frac{2}{\Xi _{2}} \sum _{i=1}^{r} \dot{\tilde{\beta }}_{i} \tilde{\beta }_{i}^{T}=0\end{aligned}$$
(39)
$$\begin{aligned}{} & {} \frac{2}{\Xi _{2}} \sum _{i=1}^{r} \dot{\tilde{\beta }}_{i} \tilde{\beta }_{i}^{T}=-2\left[ \sum _{i=1}^{r} \lambda _{i}(\hat{s}) \tilde{\beta }_{i} \mathcal {K}_{i}^{T} \hat{s}(t)\right] ^{T} y(t) \quad \nonumber \\{} & {} \quad -2\left[ \sum _{i=1}^{r} \lambda _{i}(\hat{s}) \tilde{\beta }_{i} \mathcal {K}_{i}^{T} \hat{s}(t)\right] ^{T}(y(t)-\hat{y}(t)) \end{aligned}$$
(40)
$$\begin{aligned}{} & {} \sum _{i=1}^{r} \dot{\tilde{\beta }} \tilde{\beta }_{i}^{T}=-\Xi _{2}( y(t)-\hat{y}(t)) \sum _{i=1}^{r} \lambda _{i}(\hat{s}) \hat{s}^{T}(t) \mathcal {K}_{i} \tilde{\beta }_{i}^{T}\end{aligned}$$
(41)
$$\begin{aligned}{} & {} \dot{\tilde{\beta }}_{i}=-\Xi _{2}(y(t)-\hat{y}(t)) \lambda _{i}(\hat{s}) \hat{s}^{T}(t) \mathcal {K}_{i} \end{aligned}$$
(42)

Calculation of adaptive parameter with respect to \(\mathcal {K}_{i}\):

This section presents a simple method for calculating the controller parameter \(\mathcal {K}_{i}\):

$$\begin{aligned} 2 s^{T}(t) \mathbb {P} \mathcal {B}_{i} \sum _{i=1}^{r} \lambda _{i}(\hat{s}) \hat{\beta }_{i} \mathcal {K}_{i}^{T} \hat{s}(t) +2\dot{ \mathcal {K}}_{i}^{T} \Lambda ^{-1} \mathcal {K}_{i}=0 \end{aligned}$$
(43)

After this

$$\begin{aligned} \begin{aligned} 2 \dot{\mathcal {K}}_{i}^{T} \Lambda ^{-1} \mathcal {K}_{i}=&-2 s^{T}(t) \mathbb {P} \mathcal {B}_{i} \sum _{i=1}^{r} \lambda _{i}(\hat{s}) \hat{\beta }_{i} \mathcal {K}_{i}^{T} \hat{s}(t)\\ =&-2\left[ \sum _{i=1}^{r} \lambda _{i}(\hat{s}) \hat{\beta }_{i} \mathcal {K}_{i}^{T} \hat{s}(t)\right] ^{T} \mathcal {B}_{i}^{T} \mathbb {P} s(t)\\ =&-2\left[ \sum _{i=1}^{r} \lambda _{i}(\hat{s}) \hat{\beta }_{i} \mathcal {K}_{i}^{T} \hat{s}\right] ^{T} y(t) \\ \end{aligned} \nonumber \\ \end{aligned}$$
(44)
Fig. 2
figure 2

Structure of truck–trailer system [40]

Full size image
Table 1 Truck trailer system model parameters
Full size table
Fig. 3
figure 3

State trajectories of truck–trailer model

Full size image

In addition

$$\begin{aligned} \dot{ \mathcal {K}_{i}}^{T} \Lambda ^{-1} \mathcal {K}_{i}= & {} -y(t) \sum _{i=1}^{r} \lambda _{i}(\hat{s}) \hat{\beta }_{i} \mathcal {K}_{i}^{T} \hat{s}(t) \nonumber \\= & {} -y(t) \sum _{i=1}^{r} \lambda _{i}(\hat{x}) \hat{\beta }_{i} \hat{s}^{T}(t) \mathcal {K}_{i} \nonumber \\ \dot{ \mathcal {K}_{i}}^{T}= & {} -y(t) \sum _{i=1}^{r} \lambda _{i}(\hat{s}) \hat{\beta }_{i} \hat{s}^{T}(t) \Lambda \end{aligned}$$
(45)

Since from equation (10)

$$\begin{aligned} \dot{\tilde{\alpha }}_{i}= & {} -\dot{\hat{\alpha }}_{i} \nonumber \\ \dot{\tilde{\beta }}_{i}= & {} -\dot{\hat{\beta }}_{i} \end{aligned}$$
(46)

and only \(\hat{\alpha }_{i}\) and \(\hat{\beta }_{i}\) are available, (35), (39), and (45), should be modified into the following equations and they are the adaptive control law.

$$\begin{aligned} \dot{\hat{\alpha }}_{i}^{T}=\Xi _{1}(y(t)-\hat{y}(t)) \lambda _{i}(\hat{s}) \hat{s}^{T} (t) \end{aligned}$$
(47)
$$\begin{aligned} \dot{\hat{\beta }}_{i}=\Xi _{2}(y(t)-\hat{y}(t)) \lambda _{i}(\hat{s}) \hat{s}^{T} (t) \end{aligned}$$
(48)
$$\begin{aligned} \dot{\mathcal {K}_{i}}^{T}=-y(t) \sum _{i=1}^{r} \lambda _{i}(\hat{s}) \hat{\beta }_{i} \hat{s}^{T}(t) \Lambda \end{aligned}$$
(49)
Fig. 4
figure 4

Tracking trajectories of \(s_1(t)\) and \(\hat{s}_1(t)\)

Full size image
Fig. 5
figure 5

Tracking trajectories of \(s_2(t)\) and \(\hat{s}_2(t)\)

Full size image

Remark 2

Designing adaptive control for T–S fuzzy systems is made more complex by various factors, including the complexity of the plant, parameter variations, modeling uncertainties, The necessity for online learning, and the ability to adapt [41, 42]. Another key challenge lies in robustness, maintaining system stability, and desired performance index with adaptive control parameters that can be effectively tuned to manage nonlinear dynamics and disturbances. Decisions related to determining the number of new fuzzy rules with the proper selection of adjustable fuzzy sets and rule bases are paramount when establishing an adaptive control model based on T–S fuzzy systems. Furthermore, when developing these adaptive control algorithms it’s crucial to keep in mind both the computational complexity of real–time implementation of adaptive control algorithms as well as the adaptation speed vs accuracy tradeoff when creating them.

Fig. 6
figure 6

Tracking trajectories of \(s_3(t)\) and \(\hat{s}_3(t)\)

Full size image
Fig. 7
figure 7

Output response of y(t)

Full size image
Fig. 8
figure 8

Control input response of u(t)

Full size image
Fig. 9
figure 9

The membership functions \(\lambda _{1}(s(t))\) and \(\lambda _{2}(s(t))\)

Full size image
Table 2 Comparison of the computational complexity of recent studies
Full size table

Remark 3

The achieved results in this research paper can be attributed to several key elements. One such factor is the indirect adaptive fuzzy controller’s efficiency in managing nonlinear systems with low–pass filters—this factor alone plays an integral role in producing such results. Transforming a complex system into two unknown nonlinear functions plays a pivotal role in improving controller performance, making it simpler to estimate system states and estimate their levels more accurately. Utilizing a state observer to estimate difficult–to–calculate states of a converted system improves its adaptability and robustness, leading to more effective control outcomes. Furthermore, designing new control laws with adaptive laws for parameter estimation and fuzzy systems for nonlinear function approximation further bolsters a controller’s ability to effectively regulate system dynamics.

Numerical example

Our proposed algorithms are demonstrated in this section with an example of a truck–trailer system. According to Fig. 2, the truck–trailer system is denoted by [40]. Its dynamic equation is as follows:

$$\begin{aligned} \dot{s}_{1}(t)= & {} -\Gamma _{a}\frac{\Gamma _{v}\bar{t}}{\Gamma _{\mathcal {L}}t_{0}} s_{1}(t)-(1-\Gamma _{a})\frac{\Gamma _{v}\bar{t}}{\Gamma _{\mathcal {L}}t_{0}}s_{1}(t-\tau (t))\nonumber \\{} & {} +\frac{\Gamma _{v}\bar{t}}{\Gamma _{\mathcal {L}}t_{0}} u(t) \nonumber \\ \dot{s}_{2}(t)= & {} \Gamma _{a}\frac{\Gamma _{v}\bar{t}}{\Gamma _{\mathcal {L}}t_{0}} s_{1}(t)+(1-\Gamma _{a})\frac{\Gamma _{v}\bar{t}}{\Gamma _{\mathcal {L}}t_{0}}s_{1}(t-\tau (t)) \nonumber \\ \dot{s}_{3}(t)= & {} \frac{\Gamma _{v}\bar{t}}{t_{0}}\sin \left[ s_{2}(t)+\Gamma _{a}\frac{v\bar{t}}{2\Gamma _{\mathcal {L}}}s_{1}(t)+(1-\Gamma _{a})\frac{\Gamma _{v}\bar{t}}{2\Gamma _{\mathcal {L}}}s_{1}(t-\tau (t))\right] \nonumber \\ \end{aligned}$$
(50)
Fig. 10
figure 10

Tracking trajectories of s(t) and \(\hat{s}(t)\) with Type-I nonlinear function

Full size image
Fig. 11
figure 11

Tracking trajectories errors and disturbance performance of nonlinear function (Type-I)

Full size image

where

  • \(s_{1}(t)\) presented the angle difference between trailer and truck.

  • \(s_{2}(t)\), denoted the angle of trailer position.

  • \(s_{3}(t)\), exhibited the angle of vertical position.

  • u(t) represented the steering angle.

There are coefficients for the truck–trailer system in Table 1. Using the membership functions in (2) to model the truck–trailer system in (50), the reference [40] represents the truck–trailer system under consideration as a T–S fuzzy system.

$$\begin{aligned} \lambda _{1}(t)= & {} \left\{ \begin{array}{l} \displaystyle \frac{\sin (\digamma (t))-\bar{g}\digamma (t)}{\digamma (t)(1-\bar{g})}, \quad \digamma (t)\ne 0 \\ 1, \quad \quad \quad \quad \quad \quad \quad \quad \digamma (t)=0\\ \end{array}\right. \end{aligned}$$
$$\begin{aligned} \lambda _{2}(t)= & {} \left\{ \begin{array}{l} \displaystyle \frac{\digamma (t)-\sin (\digamma (t))}{\digamma (t)(1-\bar{g})}, \quad \digamma (t)\ne 0 \\ 0, \quad \quad \quad \quad \quad \quad \quad \quad \digamma (t)=0\\ \end{array}\right. \end{aligned}$$

where

$$\begin{aligned} \digamma (t)=s_{2}(t)+\lambda \frac{\Gamma _{v}\bar{t}}{2\Gamma _{\mathcal {L}}}s_{1}(t)+(1-\lambda )\frac{\Gamma _{v}\bar{t}}{2\Gamma _{\mathcal {L}}}s_{1}(t-\tau (t)) \end{aligned}$$

Based on the numerical values in Table 1, we can obtain the system matrices as follows:

Fig. 12
figure 12

Tracking trajectories of s(t) and \(\hat{s}(t)\) with Type-I nonlinear function. (a) \(s_1(t)\) and \(\hat{s}_1(t)\) trajectories. (b) \(s_2(t)\) and \(\hat{s}_2(t)\) trajectories. (c) \(s_3(t)\) and \(\hat{s}_3(t)\) trajectories

Full size image
Fig. 13
figure 13

Tracking trajectories errors and disturbance performance of nonlinear function (Type-I). (a) Tracking trajectories errors. (b) Tracking disturbance performance

Full size image

The remaining parameters possess a value of zero. Within this section, we shall advance with this particular exemplification under two circumstances. In the initial circumstance, the authors shall deliberate upon the nominal system, whereas in the subsequent circumstance, the authors shall elucidate the system featuring a nonlinear function, correspondingly. The authors set for the initial functions \(\phi (t)= \left[ \begin{array}{c} 10 \\ -10\\ 15 \end{array}\right] \) and \(\hat{\phi }(t)= \left[ \begin{array}{c} -10 \\ 10\\ -15 \end{array}\right] \). Trajectories of the various states or variables within the truck trailer system refer to their paths or movements over time. The truck and trailer may show different positions, speeds, accelerations, and orientations at different times. Scientists and engineers can optimize the performance and safety of truck trailer systems by analyzing state trajectories, which helps them understand dynamic behavior. Figure 3 shows the state response of the truck–trailer model.

In the subsequent pair of scenarios, the authors will examine the configuration of an adaptive controller. In regard to the standard system, the controller and observer gains with adaptive gain \((\Xi _{1},\Xi _{2})=(0.85,0.93)\) are as stated below:

$$\begin{aligned} \left[ \begin{array}{c|c} \mathbb {Q}_{1} &{} \mathbb {Q}_{2} \\ \end{array} \right]= & {} \left[ \begin{array}{ccc|ccc} 3.6598 &{} -5.6691&{} \quad 1.4644&{} \quad 3.6598&{} \quad -5.6691&{} \quad 1.4644 \\ 5.1470 &{} -7.3429&{} \quad 2.0139&{} \quad 5.1470&{} \quad -7.3429&{} \quad 2.0139 \\ 5.1470 &{} -7.3429&{} \quad 2.0139&{} \quad 5.1470&{} \quad -7.3429&{} \quad 2.0139 \end{array} \right] \\ \mathbb {P}= & {} \left[ \begin{array}{ccc} 3.6598\quad -5.6691 \quad 1.4644 \\ 5.1470 \quad -7.3429 \quad 2.0139 \\ 5.1470 \quad -7.3429 \quad 2.0139 \end{array} \right] \\ \left[ \begin{array}{c} \mathcal {K}_{1} \\ \mathcal {K}_{2} \\ \end{array} \right]= & {} \left[ \begin{array}{ccc} 3.6598 \quad -5.6691 \quad 1.4644 \\ \hline 5.1470 \quad -7.3429 \quad 2.0139\\ \end{array} \right] ,\quad \left[ \begin{array}{c} \mathcal {L}_{1} \\ \mathcal {L}_{2} \\ \end{array} \right] = \left[ \begin{array}{ccc} 0.2409 \quad \\ 0.3605 \\ -0.0476 \quad \\ \hline -0.0150 \\ 0.4094 \quad \\ 0.5948 \end{array} \right] \end{aligned}$$
Fig. 14
figure 14

Tracking trajectories of \(s_1(t)\) and \(\hat{s}_1(t)\) with nonlinear function (Type-II)

Full size image
Fig. 15
figure 15

Tracking trajectories of \(s_2(t)\) and \(\hat{s}_2(t)\) with nonlinear function (Type-II)

Full size image
Fig. 16
figure 16

Tracking trajectories of \(s_3(t)\) and \(\hat{s}_3(t)\) with nonlinear function (Type-II)

Full size image

The T–S fuzzy controllers rely on states and their estimation for real–time information about the dynamics of their systems. As a result of this information, the fuzzy controller constantly makes adjustments to its parameters, adapting and optimizing its performance accordingly. Tracking errors can introduce oscillations or instability in the system, leading to poor performance and even system failure. For this, the authors present some pictorial view for the tracking path in the figures. In Fig. 4, the authors present the angle difference between the trailer and the truck \(s_{2}(t)\) and its estimation, while in Fig. 5, we present the angle of the trailer position \(s_{2}(t)\) and its estimation. Additionally, Fig. 6 presents \(s_{3}(t)\) and its estimation for the angle of vertical position. The output response y(t) and steering angle u(t) behavior are presented in Figs. 7 and 8, respectively. Tracking problems will be further improved by using adaptive neural networks.

An input variable’s membership function in a fuzzy system refers to a mathematical representation that defines its participation in a fuzzy set. A membership function is a mathematical representation that determines whether an input variable fits into a particular fuzzy set based on its degree of membership or likelihood. As a result of this membership function, each input variable’s weight or contribution to the overall fuzzy system’s decision–making is determined. A fuzzy set’s strength can be measured by its membership to an input value. The T–S fuzzy systems use the membership function to determine what proportion of each input value belongs to each fuzzy set. It indicates the degree of membership or involvement of an input value in a particular fuzzy set within a T–S fuzzy system by assigning values between 0 and 1. Membership functions in T–S fuzzy systems provide information about the influence of each input variable on the system, or in other words, how much each input variable influences the system. Figure 9 presents the membership function of the truck trailer model.

Remark 4

Indirect adaptive control systems provide a control mechanism designed to address unknown nonlinear functions in systems, but even though these indirect adaptive systems offer many potential benefits, some drawbacks should also be considered when applying such controls with unknown nonlinear functions. One difficulty lies in accurately modeling and identifying unknown nonlinear functions, leading to inaccurate estimations of system dynamics that ultimately lead to suboptimal control performance. Another limitation stems from using predetermined reference models. Reference models do not always accurately represent system dynamics in the presence of unknown nonlinearities. Furthermore, indirect adaptive control systems with nonlinear functions that have yet to be compensated can suffer from issues related to stability and convergence; their adaptive control algorithm may struggle to converge or maintain stability as it attempts to accommodate unknown nonlinear functions.

Table 2 details the computational complexity of Theorem 2’s LMI–based conditions compared with those proposed in References [45,46,47] and [48], providing information such as LMI row size \(\mathcal {S}_{\ell r}\) and conditions totaling \(\mathcal {N}_{c}\) as well as decision variables required (\(\mathcal {N}_{d}\)). This shows that Theorem 2 requires fewer decision variables and LMI conditions compared with References [47] and [48], yet remains reasonable and above all acceptable in terms of computational complexity compared with References [45,46,47], and [48].

Performance analysis with different nonlinear functions

In T–S fuzzy systems, nonlinear functions are crucial to capture the complex relationship between inputs and outputs. The T–S fuzzy systems are highly effective in a number of applications, such as control systems and pattern recognition, because these functions make it possible to model and represent intricate and dynamic systems accurately. Real–world T–S fuzzy systems leverage nonlinearity in real–time, leading to more robust and accurate predictions and control decisions. Nonlinear functions also play an integral role in reducing T–S fuzzy system complexity. Fuzzy membership functions offer tremendous versatility due to their adaptability; thus enabling improved system performance and adaptability by adapting to shifting conditions and accommodating uncertainty. For our proposed algorithm to be effective, its authors have implemented various nonlinear functions for the T–S fuzzy system and compared and analyzed their performance under different scenarios– providing compelling evidence of its efficacy. According to their analysis, the algorithm demonstrates the potential for improving prediction accuracy and reliability. In our research, the authors implement two different kinds of nonlinear functions to check the robustness of the proposed methodology.

Type-I Nonlinear function:

$$\begin{aligned} \zeta _{f}(s)=\left\{ \begin{array}{ccl} 5.8 (\sin (2(t-4\pi )))^{2}&{}&{} \qquad 15\le t \le 25 \ \sec . \\ 0;&{}&{} \qquad else \qquad 0 \quad \sec . \end{array}\right. \nonumber \\ \end{aligned}$$
(51)
$$\begin{aligned} \zeta _{g}(s)=\left\{ \begin{array}{ccl} 4.5 (\cos (4(t-6\pi )))^{2}&{}&{} \qquad 8 \le t \le 22 \ \sec . \\ 0;&{}&{} \qquad else \qquad 0 \quad \sec . \end{array}\right. \nonumber \\ \end{aligned}$$
(52)

In Type–I nonlinear functions (\(\zeta _{f}(s)\)), the authors present the explicit function in equation (51). This behavior can be observed in Figs. 10 and 11. Our nonlinear function appeared over the time span between 15 s and 25 s, while nonlinear function performance tracking can be observed in Fig. 11 for Type–I. From this analysis, one can see that our suggested algorithm has efficient performance against the nonlinear function (\(\zeta _{f}(s)\)). In the domain of Type–I nonlinear functions (\(\zeta _{g}(s)\)), the authors put forth the explicit function delineated by equation (52). This particular behavior is visually evident in Fig. 10 as well as Fig. 11. The presence of our nonlinear function was detected within the time interval spanning from 8 s to 22 s, where as the tracking of nonlinear function performance for Type–I can be observed in Figs. 10, 11, 12, 13. Based on this analysis, it becomes evident that our proposed algorithm exhibits commendable efficiency when dealing with the nonlinear function (\(\zeta _{g}(s)\)) and further can be improved by implementing the new technique as mentioned in [43].

Fig. 17
figure 17

Tracking trajectories error of e(t) with nonlinear function (Type-II)

Full size image
Fig. 18
figure 18

Tracking trajectories of nonlinear function \(\zeta _{f}(s)\) and \(\hat{\zeta }_{f}(s)\)

Full size image
Fig. 19
figure 19

Adaption of parameters and its estimation. (a) Adaption of parameters of \(\alpha _{1,2}\) and \(\hat{\alpha }_{1,2}\). (b) Adaption of parameters of \(\beta _{1,2}\) and \(\hat{\beta }_{1,2}\)

Full size image

Type-II nonlinear function:

In Type–II nonlinear functions \((\zeta _{f}(s))\), the authors present the explicit function in equation (53), which is given below.

$$\begin{aligned} \zeta _{f}(s)=\left\{ \begin{array}{ccl} 5.8 (\sin (2(t-4\pi )))^{2}&{}&{} \qquad t \le 25 \ \sec . \\ 0;&{}&{} \qquad else \ 0 \ \sec . \end{array}\right. \end{aligned}$$
(53)

Nonlinear function impact behavior can be observed in Figs. 14 and 15 as well as in Fig. 16. Our nonlinear function appeared over the time span between 25 s and 50 s, while nonlinear function behaviour of resultant error system and performance tracking can be observed in Figs. 17 and 18, respectively for Type–II. From this analysis, one can see that our suggested algorithm has efficient performance against the nonlinear function \((\zeta _{f}(s))\). Based on this analysis, it becomes evident that our proposed algorithm exhibits commendable efficiency when dealing with the nonlinear function \((\zeta _{f}(s))\). Optimizing the performance of T–S fuzzy adaptive controllers requires accurate estimation and adaptation of parameters. On the basis of real-time system response and input–output data, algorithms, and techniques are implemented to continuously update membership functions, rule bases, and consequent parameters. Adapting to Difficulties, Disturbances, and Uncertainties allows the T–S fuzzy adaptive controller to maintain robust and accurate control. An adaptive T–S fuzzy controller can be configured to respond effectively to changing conditions and provide optimal performance in real–time by adapting its parameters. The adaption of parameters and its estimation is presented in Fig. 19. In addition, in Fig. 19a, the authors presented the \(\alpha _{1,2}\) and \(\hat{\alpha }_{1,2}\), while other adaption parameter and its estimation is investigated in Fig.19b.

Fig. 20
figure 20

A schematic of the assembly of a supercritical water gasification reactor [44]

Full size image

Conclusions

Utilizing the T–S fuzzy model as its fundamental, this paper proposes an indirect adaptive fuzzy observer and controller design scheme using indirect adaptive fuzzy observer methodology. Based on the structure of the proposed system, the T–S fuzzy model was adopted. System parameters were estimated using indirect adaptive laws. Self–tuning was also performed on the control gain. The Lipschitz conditions and Lyapunov functions are used in adaptive law. As a result, both unknown and known states could be handled by the proposed observer system. As a result of using the state–feedback method, all inverses exhibited inverse dynamics that disappeared with the solution to the singularity problem. A simulation study showed that it was possible to solve the problem of observing unknown states and estimating unknown parameters using the proposed algorithm.

In the process of producing bio–diesel through transesterification, a large amount of crude glycerol is produced as a byproduct, which poses a technical and economic challenge to utilize. To produce hydrogen–rich syn–gas from crude glycerol, supercritical water gasification (SCWGs) will be considered in future studies, where our proposed algorithm will be implemented for a biogas plant. In Fig. 20, a pressure gauge, gas–liquid point, and temperature control will be adopted according to the working conditions. These points are very critical for the biogas industry. SCWGs will be composed of crude glycerol and then will be tested for crude glycerol, which will be more beneficial for the environment than crude glycerol alone.