Introduction

Classification of imbalanced data has become an important research topic in machine learning [1]. Imbalanced data indicate a skewed distribution; namely, the number of instances in the minority class is much less than that of instances in the majority class. This situation often occurs in many applications, such as medical diagnosis [2], credit risk evaluation [3], and behavioral analysis [4]. Standard classifiers will produce an inductive bias toward the majority class because the minority class contributes less to the minimization of the objective function. From a learning point of view, however, the minority class represents a more important pattern that deserves more attention. It also implies a higher cost when the minority is not well classified. For example, the cost of misdiagnosing a healthy patient is quite different from that of misdiagnosing a patient [5]. Therefore, improving minority class prediction is a key problem for imbalanced classification.

Many methods have been proposed to solve the aforementioned problem. These methods can be roughly categorized into three groups: data-level groups, algorithm-level groups, and hybrid-based groups [6, 7]. The data-level group uses resampling techniques to achieve data rebalancing [8]. It involves oversampling the minority class, undersampling the majority class, and hybrid sampling. The algorithm-level group places more emphasis on the minority class by modifying existing algorithms. It mainly includes cost-sensitive learning and ensemble methods. Cost-sensitive learning improves performance by penalizing the misclassification of the minority class. The ensemble method splits the majority class into several subsets with a size equal to the number of instances in the minority class [9]. The hybrid-based group combines data-level methods and algorithm-level methods. For example, the hybrid classifier ensemble [10] not only assigns higher weights to misclassified instances, but also performs density-based undersampling to obtain multiple subsets following a balanced distribution between classes.

Among these methods, algorithm-level methods refer to the modification of existing algorithms to adapt them to imbalanced data, which require a deep understanding of the specific algorithms and cost functions [11]. In contrast, data-level methods, also called resampling methods, are widely considered and most commonly used in imbalanced classification because they can be regarded as preprocessing steps and are always classifier independent [12, 16]. This advantage makes them very flexible and enables them to be applied to any classification algorithm [13]. In resampling, undersampling changes the class distribution by reducing the majority instances, which may lead to the loss of useful information. In [14, 15], the authors have also shown that undersampling is less effective than oversampling, especially in cases where the dataset is small. Therefore, this paper focuses on oversampling strategies.

Oversampling provides an effective solution to imbalanced classification by compensating for the insufficiency of minority class information. The synthetic minority oversampling technique (SMOTE) is the most well-known oversampling method [17], where the new instances are generated by linearly interpolating between a selected minority instance and one of its k-nearest minority neighbors [16]. In recent decades, SMOTE has been greatly developed and has derived many variants [18].

Although SMOTE can achieve a better balance in the number of instances between classes, when used in isolation, it may obtain results that are not as good as they could be [19]. This is because SMOTE ignores the natural distribution of instances due to its equal oversampling. Most of the classifiers attempt to learn the borderline of classes as exactly as possible in the training process. The borderline instances are more apt to be misclassified than those far from the borderline, and thus deserve more attention [19,20,21,22].

Borderline-SMOTE determines the borderline instances by the k-nearest neighbors (KNNs) rule [20]. It divides the minority instances into three categories: safe, danger and noise. A noise indicates that its KNNs are all majority instances, a safe instance indicates that more than half of its KNNs are minority instances, and a danger instance indicates that more than half of its KNNs are majority instances. Only the danger instances are treated as borderline instances and are oversampled. ADASYN adopts a similar strategy as Borderline-SMOTE to identify the borderline instances, where the minority instances with more majority neighbors in their KNNs are assigned higher weights to have greater chances to be oversampled [14, 16].

However, both Borderline-SMOTE and ADASYN fail to find all the borderline instances due to the ill-posed parameter k [23]. Figure 1 gives an example involving only Borderline-SMOTE. When \(k=3\), the minority instance P is identified as noise; when \(k=5\), P is a danger instance; and when \(k=7\), P is a safe instance. From Fig. 1, it can be seen that the setting of different k values significantly affects the determination of the borderline instances. An inappropriate k value can also degrade the quality of newly synthesized instances. Therefore, establishing a more effective determination mechanism for borderline instances has become a key issue in oversampling methods.

Fig. 1
figure 1

Influence of parameter k on Borderline-SMOTE. The markers “” and “” represent a minority instance and a majority instance, respectively

Full size image

The Tomek link is an enhancement of the KNN rule and is defined as a pair of minimally distant nearest neighbors of opposite classes [24]. If two instances form a Tomek link, then either one of them is noise or both are near the borderline [40]. According to Batista et al. [25], the Tomek link can be used as an undersampling technique or as a postprocessing cleaning step. If used as an undersampling technique, only the instances from the majority class are removed. If used as a postprocessing cleaning step, both instances are removed.

In this paper, the use of the Tomek link will be extended in dealing with the class imbalance problem. A refined method called oversampling borderline minority instances (OBMI) is proposed. It consists of two stages. In the first stage, the borderline minority instances are located and oversampled via a Tomek link-finding procedure. In the second stage, Tomek links are employed again for overlap reduction. The merits of the proposed method are as follows:

  • It can determine informative borderline instances and avoid the difficulty involving the choice of parameter k, unlike Borderline-SMOTE or ADASYN. Additionally, it is wellposed. Once the distance function is selected, the result obtained is unique.

  • It is lightweight and simple to implement. There is no complicated iteration; it can be easily implemented by its definition. In some real-time scenarios, the simpler model should be preferred (Occam’s razor).

  • Experimental evaluation with ten well-known oversampling methods (i.e., SMOTE [17], Borderline-SMOTE [20], ADASYN [14], SMOTE-TL [25], SMOTE-IPF [19], kmeans-SMOTE [50], NaNSMOTE [51], RBO [52], SyMProD [54], and NaNBDOS [55]) demonstrates its effectiveness and competitiveness.

The rest of the paper is organized as follows. “Related works” section reviews the related work. “The proposed method” section presents the proposed OBMI in two separate stages: the oversampling stage and the cleaning stage. The corresponding algorithms are also described in detail. In “Experiment on 2D toy datasets” and “Experiment on benchmark datasets” sections, OBMI is evaluated by experiments both on synthetic datasets and on benchmark datasets. Furthermore, nonparametric statistical tests are also performed. “Conclusion” section gives the concluding remarks with a brief discussion.

Related works

There have been extensive studies on oversampling methods [18, 26, 27]. Each of them has its specific capabilities. This section will summarize those related to this work from three aspects: oversampling for borderline instances, oversampling with postprocessing cleaning, and several other well-known methods.

Oversampling for borderline instances

Chawla et al. [17] proposed the classical SMOTE as an alternative to random oversampling. SMOTE generates new synthetic instances by linear interpolations instead of random duplications, which can improve the quality of data fed to subsequent classifiers. Recently, many different extensions have been proposed with the objective of improving some of the capabilities of SMOTE [28]. One common idea is to calculate which minority instances are the best candidates for oversampling.

Borderline-SMOTE was proposed as an enhancement of SMOTE, in which only the borderline minority instances are oversampled [20]. It builds on the premise that the instances near the borderline are more apt to be misclassified than those far from the borderline and, thus, more important for classification. To obtain the borderline instances, the ratio of the majority instances in the neighbors of each minority instance is calculated. Similar to Borderline-SMOTE, the essential idea of ADASYN is to use a weighted distribution for different minority instances according to their level of difficulty in learning [14]. More synthetic instances are generated for minority instances that are harder to learn compared to those that are easier to learn.

Nguyen et al. [22] presented a novel method to achieve borderline oversampling. The borderline region is approximated by the support vectors obtained after training a standard support vector machine (SVM) classifier. New instances are created along the lines joining each support vector of the minority class with a number of its KNNs using interpolation or extrapolation. Tian et al. [29] adopted a similar strategy to oversample minority instances identified as support vectors. For the majority class instances, middle score k-means (MSK) is presented to decompose them into serval clusters. Subsequently, these clusters are used to build an SVM ensemble with the oversampled minority instances. Wang et al. [31] proposed another ensemble method called bagging of extrapolation Borderline-SMOTE SVM (BEBS) for addressing the class imbalance problem. BEBS screens the informative borderline instances by SVM in advance, and then the bagging mechanism is applied to promote the generalization.

Zhu et al. [30] proposed a position characteristic-aware interpolation oversampling algorithm (PAIO). In PAIO, the minority instances are divided into three groups: the inland group, the borderline group, and the trapped group with different position characteristics, by using NBDOS clustering. Then, the different oversampling strategies are applied to these groups to alleviate the overfitting. Tao et al. [16] proposed adaptive weighted oversampling based on density peak clustering with heuristic filtering. The size of each identified subcluster is adaptively determined according to its own size and density. The minority instances within each subcluster are oversampled based on their probabilities inversely proportional to their distances to the majority class and their densities to generate more synthetic minority instances for borderline and sparser instances.

Wang et al. [15] proposed a local distribution-based adaptive minority oversampling method (LAMO) to address the class imbalance problem. LAMO identifies the informative borderline minority instances as sampling seeds according to the neighbor relations and class distribution. Next, LAMO generates synthetic instances around seeds via a Gaussian mixture model. Revathi et al. [32] combined noise reduction with oversampling to emphasize the importance of borderline instances. For noise reduction, it decides whether one instance should be kept or removed by a calculated propensity score. For oversampling, only the borderline instances located in the danger region are selected as sampling seeds. Chen et al. [33] introduced the relative density to measure the local density of each minority instance. A self-adaptive robust SMOTE (RSMOTE) was further proposed, which distinguishes the borderline instances and the safe instances by the relative density. The number of synthetic instances for each base instance is reweighed according to its chaotic level. Leng et al. [55] proposed NaNBDOS (short for borderline oversampling via natural neighbor search) to improve class-imbalance learning. It adaptively assigns dynamic sampling weights to the base instances. More synthetic instances will be generated around the base instances with more minority natural neighbors. This strategy is closely related to the data complexity and can maintain the original distribution to a certain extent.

Oversampling with postprocessing cleaning

Data cleaning after oversampling is considered a good strategy. There are several early methods, including SMOTE-TL [25], SMOTE-ENN [49], and SMOTE-RSB [35]. SMOTE-TL [25] removes the Tomek links from the balanced dataset to alleviate overlap. SMOTE-ENN [49] employs the edited nearest neighbor (ENN) rule to remove noisy instances. It can extend the limitation of defining noises to some extent, and further provides more in-depth cleaning of data compared to SMOTE-TL. Based on rough set theory, SMOTE-RSB [35] eliminates any synthetic instance that does not belong to the lower approximation of the minority class, considering these instances in the borderline region as noisy and not useful for classification.

Sáez et al. [19] proposed an extension of SMOTE through an iterative-partitioning filter (IPF). SMOTE-IPF has the ability to control the noise introduced by the balancing between classes produced by SMOTE and to make the class boundaries more regular. Tao et al. [16] proposed a novel adaptive weighted oversampling method based on density peak clustering. It can simultaneously address between-class and within-class imbalances. Moreover, a heuristic filtering strategy is developed inspired by PSO evolution, in which the position updating mechanism is used to iteratively move the possibly overlapping minority instances away from the majority class. Koziarski et al. [35] proposed a multiclass combined cleaning and resampling (MC-CCR) algorithm. MC-CCR utilizes an energy-based approach to model the regions suitable for oversampling and combines it with a simultaneous cleaning operation. It is less affected by interclass relationship information loss than the traditional multiclass decomposition strategies.

Li et al. [21] proposed a filtering-based oversampling method called SMOTE-NaN-DE. Minority instances are first generated to balance the datasets, and then the natural neighbor is applied to detect noisy and borderline instances. Furthermore, differential evolution is used to optimize and change the positions of found instances instead of eliminating them. Tao et al. [36] proposed SVDDDPCO for handling imbalanced and overlapped data, which combines SVDD (support vector data description) and DPC (density peak clustering). It first utilizes SVDD to generate the class boundary and clean up the potential overlapped or noisy instances. Then, DPC is used to cluster the minority instances to address the within-class imbalance. Zhang et al. [37] proposed a SMOTE variant with reverse KNNs. After oversampling, the noisy instances are identified based on probability density but not local neighborhood information. Finally, these training instances with relevant probability densities higher than a given threshold are removed.

Other well-known oversampling methods

Douzas et al. [50] developed a simple and effective oversampling method called kmeans-SMOTE, which is based on k-means clustering and SMOTE. It can avoid noise generation and can overcome imbalances between and within classes. In kmeans-SMOTE, a high ratio of minority instances is used as an indicator that a cluster is a safe area. Furthermore, the average distance among a cluster’s minority instances is used to identify sparse areas. In general, those sparse clusters are assigned higher sampling weights. Koziarski et al. [52] introduced a new algorithm called radial-based oversampling (RBO) for imbalanced and noisy data. Instead of relying on neighborhood search, RBO uses radial-based functions to determine local distributions of both minority and majority instances. Moreover, calculating joint potentials is employed to calibrate classification difficulty in a specific area. Thus, the oversampling process is guided so that it can better allocate synthetic instances without increasing overlap. Kunakorntum et al. [54] presented a new oversampling technique, namely synthetic minority based on probabilistic distribution (SyMProD), to handle class-imbalance datasets. SyMProD normalizes data using a Z-score and creates synthetic instances that cover the minority class distribution, avoiding the noise generation. Additionally, it reduces the possibilities of overlapping classes and overgeneralization problems.

In SMOTE and its extensions, the choice of the neighbor parameter k is challenging. To address this issue, Li et al. [51] proposed a novel approach by embedding natural neighbors in SMOTE (NaNSMOTE). The random difference between a selected base instance and one of its natural neighbors is used to generate new synthetic instances. NaNSMOTE has an adaptive k value related to the data complexity. The instances closer to class centers have more neighbors to improve the generalization of oversampling results. In contrast, the borderline instances have fewer neighbors to reduce the error of newly generated instances. In a recent practical application, Jovanovic et al. [53] combined the firefly algorithm with SMOTE to detect credit card fraud. This new strategy was named the group search firefly algorithm (GSFA), and its effectiveness was confirmed in comparative experiments with other competitors.

The proposed method

There is one common concern when oversampling, and the instances far from the borderline may not provide a substantial contribution to the classification ability of the model [28]. This paper proposes oversampling borderline minority instances (OBMI) to improve oversampling effectiveness. The OBMI consists of two stages: the oversampling stage and the cleaning stage. Next, the details of the two-stage procedure will be explained, and the corresponding algorithms will be described.

Notations and terms

Several notations and terms used in this paper are as follows.

  • |S| represents the cardinality of set S.

  • \({ S min}=\{u_1, u_2, \ldots , u_i, \ldots , u_{|{ S min}|}\}\) is a minority dataset.

  • \({ S maj}=\{v_1, v_2, \ldots , v_j, \ldots , v_{|{ S maj}|}\}\) is a majority dataset.

  • \(\textrm{dist}(u_i, v_j)=||u_i-v_j||_2\) stands for the Euclidean distance between \(u_i\) and \(v_j\).

  • A base instance indicates a sampling seed selected from the minority class.

  • K is a KNN parameter used for generating new instances, generally in the oversampling process.

  • k is a kNN parameter used for the calculation of local density, specifically in Borderline-SMOTE and ADASYN.

Tomek link

Given two instances \(u_i \in { S min}\) and \(v_j \in { S maj}\), a pair \((u_i, v_j)\) is called a Tomek link if there is no other instance \(w_t\), such that \(\textrm{dist}(u_i, w_t)<\textrm{dist}(u_i, v_j)\) or \(\textrm{dist}(w_t, v_j)<\textrm{dist}(u_i, v_j)\) [38], i.e.,

$$\begin{aligned} \textrm{dist}\left( {{u_i},{v_j}} \right) = \mathop {\min }\limits _{{w_t} \in { S min}} \textrm{dist}\left( {{w_t},{v_j}} \right) = \mathop {\min }\limits _{{w_t} \in { S maj}} \textrm{dist}\left( {{u_i},{w_t}} \right) . \end{aligned}$$
(1)

A procedure for finding Tomek links was developed straightforwardly from its definition [39]. Step 1: For each \(u_i \in { S min}\), find the nearest instance \(v_p \in { S maj}\). The link set \(L_{12}=\{(u_i, v_p)|u_i \in { S min}, v_p \in { S maj}\}\) is saved. Step 2: For each \(v_j \in { S maj}\), find the nearest instance \(u_q \in { S min}\). The link set \(L_{21}=\{(u_q, v_j)|u_q\in { S min}, v_j \in { S maj}\}\) is saved. Step 3: A set of Tomek links \(T=\{L_{12} \cap L_{21}\}\) is finally obtained.

Actually, the above procedure can be simplified. In Step 2, it can start from only the instances in \(L_{12}\) instead of all the instances in \({ S maj}\). As shown in Fig. 2, for four instances \(u_1, u_2, u_3, u_4 \in { S min}\), two instances \(v_1, v_2 \in { S maj}\) nearest to them are first found separately. Then, starting from \(v_1\) and \(v_2\), \(u_2\) and \(u_3\) are found, and two Tomek links \((u_2, v_1)\) and \((u_3, v_2)\) are obtained.

Fig. 2
figure 2

Two Tomek links \((u_2, v_1)\) and \((u_3, v_2)\)

Full size image
Algorithm 1
figure c

*    Find-TLs

Full size image

The algorithm for finding Tomek links (Find-TLs for short) is depicted in Algorithm 1. If two instances can form a Tomek link, then they are near the borderline with a high probability [40]. Taking advantage of the ability to locate borderline instances, the Tomek links are employed to oversample the borderline minority instances in “Oversampling stage” section and then perform a postprocessing cleaning step in “Cleaning stage” section.

Fig. 3
figure 3

An illustrative example of Oversample-BMIs. The marker “” represents a synthetic instance

Full size image

Oversampling stage

In the OBMI oversampling stage, a Tomek link-finding procedure is first employed to identify the borderline instances. Then, oversampling is performed on the identified minority instances, and new instances are generated near the borderline. As a result, a balance between classes is achieved.

Given a minority dataset \({ S min}\) and a majority dataset \({ S maj}\), a set T of Tomek links is obtained by the Find-TLs algorithm (Algorithm 1). Furthermore, the borderline minority instances are extracted from T and placed into a candidate set \(R^{'}\) of base instances. Thus, an oversampling factor \(\delta \) can be calculated as follows:

$$\begin{aligned} \delta \mathrm{{ = }}\frac{{\left| { Smaj } \right| \mathrm{{ - }}\left| { Smin } \right| }}{{\left| {{R^{'}}} \right| }}. \end{aligned}$$
(2)

If \(\delta < 1\), it is clear that the number of instances in \(R^{'}\) is greater than the difference between the numbers of instances in \( Smaj \) and \( Smin \). In this case, only a part of the instances from \(R^{'}\) are selected as the base instances. These base instances are then stored into a set R for generating new instances. Notably, there is a one-to-one correspondence between the new instances and the base instances.

Fig. 4
figure 4

A post-process cleaning using Tomek links

Full size image
Fig. 5
figure 5

Comparison of OBMI with Borderline-SMOTE on the wave dataset

Full size image

Otherwise, all instances in \(R^{'}\) will be stored in the base instance set R. A synthesis coefficient \(\gamma \) is calculated as follows:

$$\begin{aligned} \gamma \mathrm{{ = }}\left[ {\frac{{\left| { Smaj } \right| \mathrm{{ - }}\left| { Smin } \right| }}{{\left| R \right| }}} \right] , \end{aligned}$$
(3)

where \(\gamma \) is an integer and "[]" represents the rounding operation. The synthesis coefficient \(\gamma \) indicates the number of new instances to be generated for each base instance. It should be noted that Eq. (3) is not simply obtained by rounding Eq. (2) since \(R^{'}\) is a proper subset of R when \(\delta < 1\).

For each base instance \(u_i \in R\), its KNNs in \( Smin \) are calculated. Then, one (\(\delta <1\)) or \(\gamma \) (\(\delta \ge 1\)) of KNNs is selected to generate one or \(\gamma \) new synthetic instances. Assuming that one nearest neighbor \(u_t\) is selected, a new instance \(u_{new}\) can be generated by linear interpolation:

$$\begin{aligned} {u_{new}} = {u_i} + \textrm{random}(0,1) \times \left( {{u_t} - {u_i}} \right) , \end{aligned}$$
(4)

where \(\textrm{random}(0, 1)\) denotes a random number between 0 and 1.

An informal description of the oversampling stage is depicted in Algorithm 2 (Oversample-BMIs for short). To make it easier to follow, the algorithm is expressed in a high-level pseudocode, with detailed comments.

Algorithm 2
figure e

*   Oversample-BMIs

Full size image

Figure 3 shows an illustrative example of oversampling BMIs. The original dataset consists of eight minority instances and 17 majority instances (Fig. 3a). Using the Find-TLs algorithm, four Tomek links, \((u_1, v_1)\), \((u_2, v_2)\), \((u_3, v_3)\), and \((u_4, v_4)\), are obtained (Fig. 3b). Then, a base instance set \(R=\{u_1, u_2, u_3, u_4\}\) is constructed by extracting the minority instances from the obtained Tomek links. Subsequently, the number of synthetic instances for each base instance is calculated by Eq. (3). Finally, eight new minority instances are generated, two for each base instance (Fig. 3c).

Cleaning stage

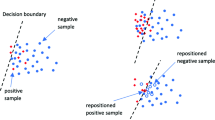
After the oversampling stage, a balanced dataset is obtained. New synthetic instances are generated near the borderline with a high probability. It is also a re-emphasis on the claim that the borderline instances are critical for estimating the optimal decision boundary [22]. However, one problem with oversampling is that the degree of overlap between classes increases, since the synthetic minority instances might invade the majority class space [41].

Fig. 6
figure 6

Comparison of OBMI with Borderline-SMOTE on the circle dataset

Full size image
Fig. 7
figure 7

Classification boundaries of SVM and MLP on the oversampled datasets by Scikit-learn [43]

Full size image

To alleviate the overlap, in the second stage of OBMI, a postprocessing cleaning step is performed. The Find-TLs algorithm is called again. Both instances in the obtained Tomek links are removed. It is worth noting that the Tomek links obtained in this stage and those obtained in the oversampling stage are very different because of the participation of newly generated instances. In the oversampling stage (Fig. 3b), four Tomek links are identified and used to generate new instances. In the cleaning stage (Fig. 4a), five Tomek links are found: \((u_1, v_1)\), \((u_{11}, v_5)\), \((u_{13}, v_2)\), \((u_3, v_3)\), and \((u_{16}, v_4)\). A total of ten instances will be removed from the balanced dataset. In particular, the majority instance \(v_4\) will be regarded as noise. The treatment using Tomek links for cleaning can play a role in noise reduction to a certain extent. Due to pairwise deletion, the cleaned dataset is still balanced. Moreover, the overlap between classes is significantly alleviated (Fig. 4b), which helps the classifier learn an optimized classification model.

Table 1 Benchmark datasets used in this experiment
Full size table

Experiment on 2D toy datasets

In determining borderline instances, Borderline-SMOTE does not perform well due to the choice of the value of neighbor parameter k used for calculating local density (see Fig. 1), while the proposed OBMI is expected to provide a stable solution. In this section, a comparative experiment is conducted to intuitively illustrate the difference between them. Two 2D toy datasets, Wave and Circle, are created with 214 minority instances and 586 majority instances and 162 minority instances and 638 majority instances, respectively. Figures 5 and 6 show the experimental results on Wave and Circle.

The Borderline-SMOTE determines different minority instances as borderline instances as the value of k changes (Figs. 5b–e and 6b–e). Correspondingly, it can be seen that oversampling occurs in different borderline regions. For OBMI, it can obtain unique oversampling results (Figs. 5f, 6f). Additionally, the oversampled instances spread over the entire borderline region, unlike Borderline-SMOTE with multiple separate clusters. In Wave, 368 new instances are generated, and 18 Tomek links are identified (Fig. 5g). On Circle, 484 new instances are generated, and 23 Tomek links are identified (Fig. 6g). It can be seen that these instances cleaned by Tomek links only account for a small proportion of the oversampled instances, which does not cause excessive computing resource waste. Figures 5h and 6h show the final results.

This section also provides a visualization of the classification boundaries by using the Scikit-learn toolkit [43], as shown in Fig. 7. Four oversampled datasets are used: Wave1 to Fig. 5c, Circle1 to Fig. 6c, Wave2 to Fig. 5h, and Circle2 to Fig. 6h. Support vector machine (SVM) and multilayer perceptron (MLP) are employed as the classification algorithms, with default settings. As Fig. 7 shows, one dataset oversampled by Borderline-SMOTE and that by OBMI induces very different classification models, even though they are from the same original dataset.

Experiment on benchmark datasets

In this section, the performance of the proposed OBMI is evaluated on 17 benchmark datasets by comparing it with ten well-known methods.

Datasets and metrics

Seventeen binary-class imbalanced datasets are selected from the KEEL repository [44]. Detailed information about these datasets can be found in Table 1. n is the number of total instances (from 129 to 5472), D is the number of features (from 3 to 18), and \(\textrm{IR} = \frac{{{n^ - }}}{{{n^ + }}}\) is the imbalanced ratio varying from 1.82 to 32.78. For convenience, a key is used to abbreviate the name of one dataset.

Table 2 Confusion matrix
Full size table
Table 3 Oversampling methods used for comparison
Full size table

In a confusion matrix (Table 2), FP is the number of negative (majority) instances that are predicted to be positive (minority), and the rest can be understood similarly. Based on the confusion matrix, several metrics are given to assess the class imbalance problem.

$$\begin{aligned}{} & {} \textrm{Precision} = \frac{\textrm{TP}}{\textrm{TP}+\textrm{FP}}, \end{aligned}$$
(5)
$$\begin{aligned}{} & {} \textrm{Recall} = \frac{\textrm{TP}}{\textrm{TP}+\textrm{FN}}, \end{aligned}$$
(6)
$$\begin{aligned}{} & {} \textrm{Specificity} = \frac{\textrm{TN}}{\textrm{FP}+\textrm{TN}}, \end{aligned}$$
(7)
$$\begin{aligned}{} & {} F1\mathrm{-score} = \frac{{{2 \times \textrm{precision} \times \textrm{recall}}}}{{{\textrm{precision}+\textrm{recall}}}}, \end{aligned}$$
(8)
$$\begin{aligned}{} & {} G\mathrm{-mean} = \sqrt{\textrm{recall} \times \textrm{specificity}}. \end{aligned}$$
(9)

The F1-score is the harmonic mean of precision and recall, mainly involving the positive instances. The G-mean is the geometric mean of recall and specificity, involving both positive and negative instances. They have the property of better characterizing quality when data are imbalanced. They are used as assessment metrics in this experiment.

Methods used for comparison

Three classical oversampling methods, i.e., SMOTE [17], Borderline-SMOTE [20], and ADASYN [14] are used as baselines. Since the proposed OBMI has a postprocessing cleaning step, it is also compared with two other methods with cleaning steps, SMOTE-TL [25] and SMOTE-IPF [19]. Five recent methods (kmeans-SMOTE [50], RBO [51], NaNSMOTE [52], SyMProD [54], and NaNBDOS [55]) are state-of-the-art references. The parameters of these methods are listed in Table 3.

Table 4 Experimental results in terms of F1-score (%) with SVM as post classifier
Full size table
Table 5 Experimental results in terms of G-mean (%) with SVM as post-classifier
Full size table
Table 6 Experimental results in terms of F1-score (%) with MLP as post-classifier
Full size table
Table 7 Experimental results in terms of G-mean (%) with MLP as post-classifier
Full size table

In parameter settings, \(K=5\) denotes that in the synthesis phase, five nearest neighbors are considered and some of them are used for linear interpolation with the base instance, while \(k=5\) means that in the calculation phase of local density, five nearest neighbors are employed to determine whether one minority instance is a "danger" instance (for Borderline-SMOTE) or how many new instances should be generated around a base instance (for ADASYN). In ADASYN, \(\beta \in [0, 1]\) is used to specify the desired balance level, and \(d_{th}\) is a preset threshold for the maximum tolerated degree of imbalance ratio. In SMOTE-IPF, \({ i ters}\) is the number of consecutive iterations for the stop criterion, p represents the number of subsets obtained by splitting the current training dataset, and r is the proportion of removing noise instances in each iteration. In kmeans-SMOTE, the number of nearest neighbors is selected from \(\{3, 6\}\), and an exponent de used for computation of density is set to the number of features. In NaNSMOTE, the number of nearest neighbors is set to five, the same as in SMOTE. In RBO, a parameter selection for \(\gamma \) is performed, considering the values in \(\{0.001, 0.01 \ldots , 10.0\}\). Furthermore, the probability of early stopping (pes) is set to 0.001, the number of iterations to 5,000, and the step size to 0.0001. In SyMProD, NT is the noise threshold to detect and remove noisy data, CT is the cutoff threshold to filter minority instances out of majority region, K1 is the number of nearest neighbors to compare the closeness factor between groups, and M is the number of nearest neighbors to generate synthetic instances. The values of all SyMProD parameters are set by default.

Although the proposed method also has a parameter K that is commonly used for linear interpolation in the oversampling methods, a fact needs to be emphasized. OBMI does not require any parameters in the process of determining the borderline instances, which is essentially different from Borderline-SMOTE and ADASYN. In addition, SVM with RBF kernel (\(C=1000, \gamma =0.001\)) and MLP with conjugate gradient are employed as the postclassifiers.

Results and discussion

By adopting fivefold cross-validation [45], each dataset used in this experiment is first randomly divided into 5 disjoint folds that have approximately the same number of instances. Then, every fold plays a role in testing the model induced by the other fourfold. The average results with standard deviations are reported in Tables 4, 5, 6 and 7, where the highest scores are marked in bold, the symbol "+" denotes that OBMI outperforms the comparison method, "=" indicates that both obtain the same score, and "-" indicates that OBMI performs worse than the comparison method.

From Tables 4, 5, 6 and 7, the following observations can be made:

  1. (1)

    In terms of the F1-score with SVM, OBMI achieves the highest score on four datasets, i.e., iri0, pbl0, s2v4, and gla5. Specifically, compared with SMOTE, Borderline-SMOTE, ADASYN, SMOTE-TL, SMOTE-IPF, kmeans-SMOTE, NaNSMOTE, RBO, NaNBDOS, and SyMProD, it wins on 12, 11, 14, 11, 10, 12, 10, 8, 10, and 11 datasets, respectively. Especially on the "gla5" dataset, OBMI has an average testing F1-score of 89.33%, which is much higher than that obtained by the other nine methods (NaNBDOS excepted).

  2. (2)

    In terms of G-mean with SVM, OBMI obtains the best results on six datasets, i.e., iri0, hab, nth2, gla4, gla5, and yea5. It performs better than SMOTE, Borderline-SMOTE, ADASYN, SMOTE-TL, kmeans-SMOTE, NaNSMOTE, RBO, NaNBDOS, and SyMProD on 10, 12, 13, 9, 12, 12, 10, 11, and 14 datasets, respectively. Compared with SMOTE-IPF, OBMI wins on eight datasets with a win–loss ratio of 50%. It is also comparable to other methods on these datasets where OBMI does not achieve the highest scores.

  3. (3)

    In terms of the F1-score with MLP, OBMI achieves the highest score on seven datasets, i.e., gla1, iri0, gla0, g03v46, nth2, s2v4, and yea5. It outperforms SMOTE, Borderline-SMOTE, ADASYN, SMOTE-TL, SMOTE-IPF, kmeans-SMOTE, NaNSMOTE, RBO, NaNBDOS, and SyMProD on 14, 10, 15, 11, 11, 10, 10, 8, 12, and 10 datasets, respectively. More remarkably, on the "g03v46" dataset, OBMI obtained an average F1-score of 90.05%, much higher than the result obtained by the other ten methods.

  4. (4)

    In terms of G-mean with MLP, OBMI obtains the best results on six datasets, i.e., gla1, iri0, gla0, veh1, g03v46, and s2v4. In pairwise comparisons, it performs better than SMOTE, Borderline-SMOTE, ADASYN, SMOTE-TL, kmeans-SMOTE, NaNSMOTE, RBO, NaNBDOS, and SyMProD on 12, 13, 10, 9, 10, 10, 9, 15, and 13 datasets, respectively. SMOTE-IPF obtains the best results on eight datasets, two more than OBMI. Nevertheless, it still has a 7:8 win-loss ratio in a one-to-one comparison with OBMI.

Experimental results on benchmark datasets show that OBMI is generally better than SMOTE, Borderline-SMOTE, ADASYN, SMOTE-TL, kmeans-SMOTE, NaNSMOTE, RBO, NaNBDOS, and SyMProD in terms of both F1-score and G-mean. Additionally, compared with SMOTE-IPF, OBMI achieves similar or better performance on most of the selected datasets. Overall, OBMI shows a promising ability to improve imbalanced classification.

Table 8 Friedman ranking and mean (%) on different metrics
Full size table
Fig. 8
figure 8

A combination of boxplots and swarmplots for statistical analysis

Full size image

Nonparametric statistical test and analysis

To present a thorough comparison among these methods, a nonparametric statistical test is also conducted. The Friedman test and Bonferroni–Dunn post hoc procedure [46,47,48] are employed to differentiate the performance of the comparative methods on 17 datasets. The proposed OBMI is used as the control method and compared with other methods by multiple comparison tests. The test results are listed in Table 8, along with the mean scores of each method on different metrics.

Table 8 shows that OBMI achieves the top Friedman ranking on the first three metrics (F1-score with SVM, G-mean with SVM, and F1-score with MLP). On the last metric (G-mean with MLP), OBMI takes second place, just behind SMOTE-IPF. Remarkably, in terms of mean scores, it outperforms other methods used for comparison.

Figure 8 is the visualization result of the metric scores by a combination of boxplots and swarmplots. It displays the distribution of scores based on a five-number summary, i.e., minimum, first quartile, median, third quartile, and maximum. It can be observed that OBMI is robust because of the degree of dispersion. Overall, OBMI can effectively improve the oversampling method, which aims to synthesize high-quality new instances to better assist the classifier.

Conclusion

Inspired by the critical importance of borderline instances in classification, OBMI is proposed to oversample the borderline minority instances for the class imbalance problem. OBMI is essentially a two-stage Tomek link-finding procedure. In the oversampling stage, the minority instances in the Tomek links are used as sampling seeds to balance the dataset. In the cleaning stage, both instances in the Tomek links are removed for overlap reduction between classes. Unlike classic Borderline-SMOTE and ADASYN, OBMI is well-posed and parameter-free in determining the borderline instances.

The experimental results show that OBMI has clear superiority over the remaining methods in terms of the F1-score. It obtains similar or better G-means on most of the selected benchmark datasets. This indicates that OBMI not only emphasizes the importance of the minority instances, but also takes the majority instances into account. The statistical test also confirms its higher-level Friedman ranking.

Despite the promising performance, the proposed OBMI also has some limitations. The Tomek link represents a rigid rule, and oversampling with it will focus on considering the borderline instances. The overall data distribution may be ignored. In addition, the neighbor parameter K involved in linear interpolation is still inherent (the same as other SMOTE extensions), which will restrict the oversamplers from finding natural neighbors.

In future work, a fuzzy rule that extends the Tomek link to k-nearest-opposed pairs will be employed to improve the selection of borderline instances. Moreover, the theory of natural neighbors will be introduced to enhance the neighbor relationship. Correspondingly, linear interpolation will be achieved between the base instance and one of its natural neighbors so that the data distribution is considered. The proposed method can also be extended to multiclass problems. However, an ingenious decomposition strategy is needed. In-depth research on these issues should be regarded as an attractive advancement for class imbalance learning.