Complex fuzzy intelligent decision modeling for optimizing economic sustainability in transportation sector

Abstract

This paper introduces the concept of complex quadratic Diophantine fuzzy sets (CQDFS) which serves as a robust framework for effectively dealing with uncertainty within decision-making challenges. The study comprehensively explores the properties and characteristics of CQDFS by conducting a systematic comparative analysis to demonstrate its superiority over existing techniques in managing complex fuzzy information. This foundation contributes to the theoretical understanding of CQDFS and also provides valuable practical insights into a wide range of transportation strategies and economic efficiency. These insights offer practical solutions to enhance decision-making within these important and interconnected domains. The proposed complex information system serves as a versatile and adaptive tool, significantly strengthening the flexibility available for addressing complex decision-making challenges, particularly in contexts such as the management of GPS-enabled cargo vehicles and cargo loading operations, where precision and efficiency are of great importance.

Introduction

In the field of decision-making and data analysis, uncertainty and imprecision are extensive challenges that can significantly impact the quality of decisions. Traditional approaches that rely on crisp sets and binary logic often struggle to adequately address these challenges, as they are ill-equipped to handle the inherent ambiguity and vagueness present in real-world scenarios. The fuzzy set (FS) [39] offers a mathematical framework that allows us to represent and reason with uncertain and imprecise information in a more realistic way by introducing the notion of membership degrees that represent the uncertain nature of human perception and reasoning. Decision-makers can indicate the extent to which an element belongs to a given set by assigning membership degrees to elements, offering a more precise representation of available information. Elements can be assigned membership degrees depending on the decision-maker’s knowledge, experience, and confidence in their evaluations. This enables a more flexible and fine-grained depiction of uncertainty, which is particularly useful when dealing with imprecise and ambiguous data. FS allows decision-makers to capture the lack of exact boundaries, allowing for more robust decision-making procedures that are more matched with the complexity of real-world problems. In the context of multi-criteria decision analysis, the fuzzy set theory provides a natural framework for representing and evaluating preferences and trade-offs across various criteria. Traditional decision models often struggle to handle multiple criteria and their associated uncertainties, leading to oversimplified and biased decisions. This theory offers a comprehensive strategy that helps decision-makers to successfully handle and balance various factors at the same time. Decision-makers are enabled to make well-rounded and informed judgments that reflect the inherent ambiguity and imprecision within the decision-making environment by including fuzzy sets and fuzzy logic in multi-criteria decision models.

Over the years, fuzzy set theory has witnessed several developments and extensions to address specific challenges and application domains to other branches of mathematics such as fuzzy ordinary differential equations [33], fuzzy partial differential equations [1, 30, 32, 41], fuzzy numerical analysis [2, 9].

For instance, the intuitionistic fuzzy set (IFS) introduced by Atanassov in [5] extended fuzzy sets by incorporating the concept of non-membership, capturing uncertainty and hesitancy in decision-making. Cuong [8] introduced the concept of a picture fuzzy set (PFS), a novel paradigm characterized by three functions assigning positive membership, neutral, and negative membership functions to individual objects or alternatives. In [35], Yager introduced the Pythagorean fuzzy set (PyFS), which encompasses both membership and non-membership degrees. These degrees satisfy the condition that the sum of their squares is less than or equal to 1. Applications of PyFS in decision-making can be found, e.g., in [18]. Atanassov [6] also referred to the PyFS as the interval-valued fuzzy set (IFS) of type 2. Scholars have since focused their research on exploring the q-rung orthopair fuzzy set (q-ROFS) as an additional model to expand the possibilities offered by IFS and PFS [22]. Riaz introduced the concept of linear Diophantine fuzzy set (LDFS) in [27]. This extension provides a novel approach to expressing uncertainty and offers increased versatility and reliability compared to existing notions such as IFS, PyFS, and q-ROFS. This is primarily due to the incorporation of reference or control factors along with membership and non-membership functions. More recently, Zia et al. [42] proposed the concept of a quadratic Diophantine fuzzy set (QDFS). This extension of LDFS introduces a third reference parameter, enabling the handling of uncertain scenarios involving ignorance or hesitation.

In practical scenarios, data often exhibits fluctuating cycles, encompassing periodicity, along with inherent ambiguity and uncertainty. Existing theories and approaches, however, frequently struggle to successfully analyze and capture the complexity involved with such data, sometimes resulting in data loss throughout the analysis process. Ramot et al. [26] presented a new notion called the complex fuzzy set (CFS) to address this problem. Unlike regular fuzzy sets, the CFS includes a unit disc on a complex plane rather than the conventional interval of [0, 1]. This addition gives a more thorough representation of the data, allowing for a broader range of values and reflecting the subtle relationships and patterns seen in complex data sets. The advent of the CFS has sparked significant interest in the subject of fuzzy set theory, providing a useful tool for dealing with data with periodic changes and intrinsic uncertainty.

Alkouri and Salleh [4] extended the concept of CFS and developed the notion of a complex intuitionistic fuzzy set (CIFS). This generalized version includes complex-valued membership and non-membership functions in polar coordinates. This representation allows decision-makers to capture and depict ambiguity and uncertainty in a more nuanced and adaptable way, taking into account the complicated relationship between both members and non-members in complex decision-making contexts. Furthermore, Akram et al. [3] presented the complex picture fuzzy set (CPFS), which includes hesitation-type fuzzy information. To broaden the use and applicability of CIFS, Ullah et al. [34] created the concept of a complex Pythagorean fuzzy set (CPyFS). This enhancement enhances the decision-making process by allowing complicated uncertainties to be considered. Liu et al. [21] established the notion of the Cq-ROFS in the pursuit of constructing effective decision models, which enables decision-makers to negotiate the presence of uncertainty and imprecision inherent in complex data sets. It is worth noting that existing ideas and methodologies for complex fuzzy information frequently place tight requirements on complex membership and non-membership functions, restricting their capacity to handle functions from anywhere in the space. Kamacı [14], Yousafzai et al. [38] (alternate definition) and Zia et al. [44], on the other hand, offered the notion of the complex linear Diophantine fuzzy set (CLDFS) as a more straightforward, valid, and adaptable technique that can be used to a broad variety of options and attributes.

A brief literature review will now be presented, highlighting innovative methods that have surfaced in recent academic research about the application of fuzzy decision-making in transportation planning. In a study by Zhang et al. [40], they addressed the complex challenge of public transportation development decision-making by actively involving the public using a large-scale group decision-making method rooted in fuzzy preference relations. In another study by Mohammadi et al. [23], the researchers devised a multi-objective reliable optimization model. This model incorporated various aspects, such as reliable facility location-allocation, equitable distribution of relief items, victim assignment, and truck routing by utilizing robust optimization and the neutrosophic fuzzy set to overcome uncertainties inherent in catastrophe situations. On the sustainable front, Seker and Aydin [28] introduced a novel two-stage hybrid method, IVIF-AHP and CODAS, for evaluating public transportation system sustainability. This approach considers disparate stakeholder viewpoints, ensuring a holistic evaluation process. Sensitivity analyses were performed to validate the method’s robustness, highlighting its reliability and suitability for real-world applications. In urban traffic congestion, Hartanti et al. [12] focused on optimizing traffic light settings using fuzzy logic. By employing the fuzzy Mamdani method, they created an intelligent traffic management system capable of real-time predictions and adjustments. By averting unnecessary green signals through predictive intelligence, this approach aimed to substantially reduce congestion, offering potential solutions for urban traffic management challenges. Lian et al. [20] presented a novel solution via fuzzy modeling for nonlinear autonomous vehicles to smoothly follow the planned path under external disturbances and network-induced issues, such as cyber-attacks, time delays, and limited bandwidths. These studies emphasize the significance of fuzzy decision-making in enhancing the efficiency, resilience, and sustainability of transportation systems. Furthermore, these methods offer adaptable, data-driven solutions, underscoring the crucial role of advanced computational techniques in shaping the future of transportation planning and management. By utilizing the neuro-inference fuzzy system, Zivkovic et al. [43] improved the current time-series prediction (forecasting) algorithms based on hybrids between machine learning and nature-inspired algorithms for COVID-19 case prediction.

Fuzzy set theory has various diverse applications in different branches of science for example in a study by Korenevskiy et al. [19] they investigated predicting the severity of end-organ damage of the anatomical zones of the lower extremities. Azizpour et al. [7] simulated the time series of groundwater parameters using fuzzy models. Parsajoo et al. [25] developed artificial bee colony techniques for the assessment of rock brittleness index by applying fuzzy model.

Various types of fuzzy sets, such as CFSs, CIFSs, CPyFSs, and Cq-ROFSs, have been extensively examined and implemented in practical applications. However, these sets impose stringent constraints on both membership and nonmembership grades. In response to these limitations, CLDFS introduces reference parameters for membership and nonmembership grades, thereby broadening the applicability of these sets. Nevertheless, CLDFS still incorporates acceptance- and rejection-type parameters, which may not comprehensively capture fuzzy information about denial, ignorance, or confusion.

To bridge this research gap, there is a need for a specialized fuzzy set that not only effectively handles ignorance or confusion, as observed in CPFS, but also extends the feasible space by introducing parameters akin to CLDFS. Hence, CQDFS emerges as a motivating solution in this context. Consequently, the current study aims to leverage the concept of CQDFS, which includes a third parameter to address scenarios involving denial, ignorance, or confusion. The objectives of this paper are outlined as follows:

• To utilize the CQDFS in real-life decision-making scenarios and explain its characteristics and comparison method.

• To compare CQDFS with existing CFS, such as CIFS, CPyFS, Cq-ROFS, CLDFS, and CPFS, and demonstrate its superiority over them.

• To address decision-making challenges within the transportation sector by integrating inverse discrete Fourier transform principles and abstract algebraic notions.

The structure of this paper is as follows. In “Preliminaries”, an introduction is presented, explaining key fuzzy sets such as CFS, CIFS, CPFS, CPyFS, Cq-ROFS, and CLDFS. Furthermore, the concept of CQDFS is introduced, and a comparative analysis is conducted with established fuzzy sets. Moving on to “Smart transportation decisions with CQDFS”, the application of CQDFS in addressing a decision-making problem associated with the transportation of goods using GPS-equipped vehicles is proposed. A novel methodology is provided, entailing the integration of CQDFS with discrete Fourier transform to derive a comprehensive solution. “Optimizing cargo loading with CQDF-congruences” extends the discussion to utilizing CQDF congruences in decision-making processes about cargo loading operations. In “Comparative analysis”, a comparative analysis is presented, contrasting the attributes of CQDFS with those of existing fuzzy sets. Finally, “Conclusion” summarises the paper with a thorough conclusion, providing a comprehensive synthesis of the study’s findings.

Preliminaries

In this section, the core concepts of CFS, CIFS, CPyFS, CPFS, Cq-ROFS, and CLDFS are explored. This exploration is vital as it equips readers with the fundamental knowledge necessary to shape and define the CQDFS, setting the stage for a deeper understanding of this innovative concept in the realm of fuzzy sets. This will establish a foundation upon which the superior performance of the proposed CQDFS can be assessed when compared to the aforementioned complex fuzzy systems. This investigation aims to highlight the innovative advancements introduced to the field of fuzzy systems and their potential implications for various applications.

Definition 1

[26] A complex fuzzy set (CFS) ${\mathbb {C}}_F$ over the non-empty reference set $\Omega$, is an object of the form:

$$\begin{aligned} {\mathbb {C}}_F=\left\{ \left( \lambda ,f_{{\mathbb {C}}_F}(\lambda )\text {e}^{ i\theta _{{\mathbb {C}}_F}(\lambda )}\right) :\lambda \in \Omega \right\} , \end{aligned}$$

where $f_{{\mathbb {C}}_F}(\lambda )\text {e}^{i\theta _{{\mathbb {C}}_F}(\lambda )}$ is the membership function, which lies within a unit disk in a complex plane with $f_{{\mathbb {C}}_F}( \lambda )$ and $\theta _{{\mathbb {C}}_F}(\lambda )$ being real-valued functions satisfying the condition

$$\begin{aligned} 0\le f_{{\mathbb {C}}_F}(\lambda ),\theta _{{\mathbb {C}}_F}(\lambda )\le 1. \end{aligned}$$

Definition 2

[11] Let $\Omega$ be the non-empty reference set. A complex intuitionistic fuzzy set (CIFS) ${\mathbb {C}}_I$ is an object of the form:

$$\begin{aligned} {\mathbb {C}}_I=\left\{ \left( \lambda ,f_{{\mathbb {C}}_I}(\lambda )\text {e}^{ i\theta _{{\mathbb {C}}_I}(\lambda )},g_{{\mathbb {C}}_I}(\lambda )\text {e}^{ i\phi _{{\mathbb {C}}_I}(\lambda )}\right) :\lambda \in \Omega \right\} , \end{aligned}$$

where the membership function and non-membership function are:

$$\begin{aligned} f_{{\mathbb {C}}_I}(\lambda )\text {e}^{ i\theta _{{\mathbb {C}}_I}(\lambda )}\quad \text {and}\quad g_{{\mathbb {C}}_I}(\lambda )\text {e}^{ i\phi _{{\mathbb {C}}_I}(\lambda )}. \end{aligned}$$

which lie within a unit disk in complex plane with $f_{{\mathbb {C}}_I}( \lambda ),g_{{\mathbb {C}}_I}(\lambda ),\theta _{{\mathbb {C}}_I}(\lambda )$ and $\phi _{{\mathbb {C}}_I}(\lambda )$ being real-valued functions satisfying the conditions

$$\begin{aligned} 0\le f_{{\mathbb {C}}_I}(\lambda )+g_{{\mathbb {C}}_I}(\lambda )\le 1\quad \text {and}\quad 0\le \theta _{{\mathbb {C}}_I}(\lambda )+\phi _{{\mathbb {C}}_I}(\lambda )\le 1. \end{aligned}$$

Definition 3

[3] A complex picture fuzzy set (CPFS) ${\mathbb {C}}_{P}$ on a universal set $\Omega$ is defined as:

$$\begin{aligned} {\mathbb {C}}_{P}= & {} \left\{ \left( \lambda ,\left( f_{{\mathbb {C}}_{P}} (\lambda )\text {e}^{i\theta _{{\mathbb {C}}_{P}}(\lambda )},h_{{\mathbb {C}}_{P}} (\lambda )\text {e}^{i\phi _{{\mathbb {C}}_{P}}(\lambda )},\right. \right. \right. \\{} & {} \left. \left. \left. g_{{\mathbb {C}}_{P}} (\lambda )\text {e}^{i\psi _{{\mathbb {C}}_{P}}(\lambda )}\right) \right) :\lambda \in \Omega \right\} \end{aligned}$$

here $f(\lambda )$ is called membership function, $h(\lambda )$ is called neutral membership function and $g(\lambda )$ is called non-membership function with $f_{{\mathbb {C}}_{P}},h_{{\mathbb {C}}_{P}}(\lambda ),g_{{\mathbb {C}}_{P}}(\lambda ),\theta _{{\mathbb {C}}_{P}}(\lambda ),$ $\phi _{{\mathbb {C}}_{P}}(\lambda ),\psi _{{\mathbb {C}}_{P}}(\lambda )\in [0,1]$, satisfying $0\le f_{{\mathbb {C}}_{P}}+h_{{\mathbb {C}}_{P}}(\lambda )+g_{{\mathbb {C}}_{P}}(\lambda ),\le 1$ and $0\le \theta _{{\mathbb {C}}_{P}}+\phi _{{\mathbb {C}}_{P}}(\lambda )+\psi _{{\mathbb {C}}_{P}}(\lambda ),\le 1$.

Definition 4

[34] For a non-empty reference set $\Omega$. The complex Pythagorean fuzzy set (CPyFS) ${\mathbb {C}}_{Py}$ is defined as

$$\begin{aligned} {{\mathbb {C}}_{Py}}=\left\{ \left( \lambda ,f_{{\mathbb {C}}_{Py}}(\lambda )\text {e}^{ i\theta _{{\mathbb {C}}_{Py}}(\lambda )},g_{{\mathbb {C}}_{Py}}(\lambda )\text {e}^{ i\phi _{{\mathbb {C}}_{Py}}(\lambda )}\right) :\lambda \in \Omega \right\} , \end{aligned}$$

where

$$\begin{aligned} f_{{\mathbb {C}}_{Py}}(\lambda )\text {e}^{ i\theta _{{\mathbb {C}}_{Py}}(\lambda )}\quad \text {and}\quad g_{ {\mathbb {C}}_{Py}}(\lambda )\text {e}^{ i\phi _{{\mathbb {C}}_{Py}}(\lambda )}, \end{aligned}$$

denote the complex-valued membership and non-membership functions respectively, satisfying the conditions

$$\begin{aligned} 0\le f_{{\mathbb {C}}_{Py}}^{2}(\lambda )+g_{{\mathbb {C}}_{Py}}^{2}(\lambda )\quad \text {and}\quad 0\le \theta _{{\mathbb {C}}_{Py}}^{2}(\lambda )+\phi _{{\mathbb {C}}_{Py}}^{2}(\lambda )\le 1. \end{aligned}$$

Definition 5

[21] Let $\Omega$ be the non-empty reference set. The complex q-rung orthopair fuzzy set (Cq-ROFS) ${\mathbb {C}}_{qR}$ is given by

$$\begin{aligned} {\mathbb {C}}_{qR}=\left\{ \left( \lambda _{{\mathbb {C}}_{qR}}(\lambda )\text {e}^{ i\theta _{{\mathbb {C}}_{qR}}(\lambda )},g_{{\mathbb {C}}_{qR}}(\lambda )\text {e}^{ i\phi _{{\mathbb {C}}_{qR}}\lambda )}(\right) :\lambda \in \Omega \right\} , \end{aligned}$$

where

$$\begin{aligned} f_{{\mathbb {C}}_{qR}}(\lambda )\text {e}^{ i\theta _{{\mathbb {C}}_{qR}}(\lambda )}\quad \text {and}\quad g_{ {\mathbb {C}}_{qR}}(\lambda )\text {e}^{ i\phi _{{\mathbb {C}}_{qR}}(\lambda )}, \end{aligned}$$

denote the complex-valued membership and non-membership functions respectively, satisfying the conditions

$$\begin{aligned}{} & {} 0\le f_{{\mathbb {C}}_{qR}}^{q}(\lambda )+g_{{\mathbb {C}}_{qR}}^{q}(\lambda )\le 1\nonumber \\{} & {} \quad \text {and}\quad 0\le \theta _{{\mathbb {C}}_{qR}}^{q}(\lambda )+\phi _{{\mathbb {C}}_{qR}}^{q}(\lambda )\le 1,(q\ge 1). \end{aligned}$$

Definition 2.1

[14] Let $\Omega$ be a non-empty universal set. A CLDFS ${\mathbb {C}}_L$ on $\Omega$ is an object of the form

$$\begin{aligned} {\mathbb {C}}_L= \left\{ \left( \lambda ,\left( f_{ {\mathbb {C}}_L }(\lambda )\text {e}^{i\theta _{ {\mathbb {C}}_L }(\lambda )},g_{ {\mathbb {C}}_L }(\lambda )\text {e}^{i\phi _{ {\mathbb {C}}_L }(\lambda )}\right) ,\left( \alpha ,\beta \right) \right) :\lambda \in \Omega \right\} , \end{aligned}$$

where $f_{ {\mathbb {C}}_L }(\lambda )\text {e}^{i\theta _{ {\mathbb {C}}_L }(\lambda )},g_{ {\mathbb {C}}_L }(\lambda )\text {e}^{i\phi _{ {\mathbb {C}}_L }(\lambda )}$ are respectively the complex membership and non-membership functions, and $\alpha ,\beta$ are reference parameters such that

$$\begin{aligned} f_{ {\mathbb {C}}_L }(\lambda ),g_{ {\mathbb {C}}_L }(\lambda ),\theta _{ {\mathbb {C}}_L }(\lambda ),\phi _{ {\mathbb {C}}_L }(\lambda ),\alpha ,\beta \in [0,1], \end{aligned}$$

which satisfies the following conditions : 

• (i) $0\le \alpha f_{ {\mathbb {C}}_L }(\lambda )+\beta g_{ {\mathbb {C}}_L }(\lambda )\le 1;$

• (ii) $0\le \alpha \theta _{ {\mathbb {C}}_L }(\lambda )+\beta \phi _{ {\mathbb {C}}_L }(\lambda )\le 1;$

• (iii) $0\le \alpha +\beta \le 1.$

Complex quadratic Diophantine fuzzy set

The concept of a CQDFS is introduced in this section. The proposed idea is motivated by the concept of a general quadratic Diophantine equation in two variables x and y of the form:

$$\begin{aligned} \alpha x^{2}+\beta xy+\gamma y^{2}=k. \end{aligned}$$

Considering this equation, the introduction of the concept of CQDFS is now presented as follows:

Let $\Omega$ be a non-empty universal set. A CQDFS ${\mathbb {C}}_Q$ on $\Omega$ is an object of the form

$$\begin{aligned} {\mathbb {C}}_Q= \left\{ \left( \lambda ,\left( f_{ {\mathbb {C}}_Q }(\lambda )\text {e}^{i\theta _{ {\mathbb {C}}_Q }(\lambda )},g_{ {\mathbb {C}}_Q }(\lambda )\text {e}^{i\phi _{ {\mathbb {C}}_Q }(\lambda )}\right) ,\left( \alpha ,\beta ,\gamma \right) \right) :\lambda \in \Omega \right\} , \end{aligned}$$

where $f_{ {\mathbb {C}}_Q }(\lambda )\text {e}^{i\theta _{ {\mathbb {C}}_Q }(\lambda )},g_{ {\mathbb {C}}_Q }(\lambda )\text {e}^{i\phi _{ {\mathbb {C}}_Q }(\lambda )}$ are respectively the complex membership and non-membership functions, and $\alpha ,\beta ,\gamma$ are reference parameters such that

$$\begin{aligned} f_{ {\mathbb {C}}_Q }(\lambda ),g_{ {\mathbb {C}}_Q }(\lambda ),\theta _{ {\mathbb {C}}_Q }(\lambda ),\phi _{ {\mathbb {C}}_Q }(\lambda ),\alpha ,\beta ,\gamma \in [0,1], \end{aligned}$$

which satisfies the following conditions:

• (i) $0\le \alpha f_{ {\mathbb {C}}_Q }^{2}(\lambda )+\beta f_{ {\mathbb {C}}_Q }(\lambda )g_{ {\mathbb {C}}_Q }(\lambda )+\gamma g_{ {\mathbb {C}}_Q }^{2}(\lambda )\le 1;$

• (ii) $0\le \alpha \theta _{ {\mathbb {C}}_Q }^{2}(\lambda )+\beta \theta _{ {\mathbb {C}}_Q }(\lambda )\phi _{ {\mathbb {C}}_Q }(\lambda )+\gamma \phi _{ {\mathbb {C}}_Q }^{2}(\lambda )\le 1;$

• (iii) $0\le \alpha +\beta +\gamma \le 1.$

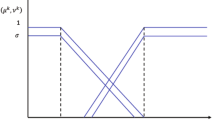
For convenience, let ${\mathbb {C}}_Q=\vartheta =\left( \left( f_{ {\mathbb {C}}_Q }\text {e}^{i\theta _{ {\mathbb {C}}_Q }},g_{ {\mathbb {C}}_Q }\text {e}^{i\phi _{ {\mathbb {C}}_Q }}\right) ,\right. \left. \left( \alpha ,\beta ,\gamma \right) \right)$ be a complex quadratic Diophantine fuzzy number (CQDFN). Figure 1 above represents the illustration of feasible spaces for membership and non-membership functions for various choices of reference parameters.

Now, the objective is to emphasize the advantages and broader applicability of CQDFS by conducting a comparison with various other fuzzy number systems. Through the examination of these comparisons, a deeper understanding of the unique features and benefits offered by CQDFS can be obtained.

Fig. 1

Complex quadratic Diophantine fuzzy sets with different reference parameters

CQDFS against CIFS, CPyFS and Cq-ROFS

Now, it is demonstrated that in CQDFS, there is a greater feasible space available for selecting membership and non-membership values. In this context, the following theorem is presented.

Theorem 2.2

The space of CQDFNs is larger than that of CIFNs,  CPyFNs,  and Cq-ROFNs.

Proof

Let $\left( \left( f\text {e}^{i\theta },g\text {e}^{i\phi }\right) ,\left( \alpha ,\beta ,\gamma \right) \right)$ be a CQDFN then the inequalities

$$\begin{aligned}&0\le \alpha f^2+\beta fg+\gamma g^2\le 1,0\le \alpha \theta ^2+\beta \theta \phi +\gamma \phi ^2\le 1\\&\quad \text {and}\quad 0\le \alpha +\beta +\gamma \le 1. \end{aligned}$$

for $\beta =0$ and arbitrary choice of $\alpha$ and $\gamma$ holds for every CIFN, CPyFN. Hence every CIFN and CPyFN is also a CQDFN. A CQDFN with a given set of parameters may not necessarily be a CIFN or CPyFN.

For example, let $f\text {e}^{i\theta }=0.63\text {e}^{i0.89}$ and $g\text {e}^{i\phi }=0.94\text {e}^{i0.89}$, then

$$\begin{aligned} f+g=1.56>1\quad \text {and}\quad \theta +\phi =1.78 >1, \end{aligned}$$

and

$$\begin{aligned} f^2+g^2=1.27>1\quad \text {and}\quad \theta ^2+\phi ^2=1.58 >1. \end{aligned}$$

However, when $\alpha =0.51$, $\beta =0.11$ and $\gamma =0.04$. the expressions are as follows:

$$\begin{aligned}&\alpha f^2+\beta fg+\gamma g^2=0.30<1\\&\quad \text {and}\quad \alpha \theta ^2+\beta \theta \phi +\gamma \phi ^2=0.52<1. \end{aligned}$$

Similarly, it is easy to check that for a Cq-ROFS, whenever $f\text {e}^{i\theta }\approx g\text {e}^{i\phi }\rightarrow \text {e}^i$, then $q\rightarrow \infty$.

For a special case $f\text {e}^{i\theta }=g\text {e}^{i\phi }=\text {e}^i$, there does not exist any specific q. In this particular instance, there is no existence of a Cq-ROFN. However, for any chosen values of $\alpha$, $\beta$, and $\gamma$ such that $0 \le \alpha + \beta + \gamma \le 1$, the following inequalities hold:

$$\begin{aligned} \alpha f^2{+}\beta fg{+}\gamma g^2{=}\alpha \theta ^2+\beta \theta \phi {+}\gamma \phi ^2=\alpha +\beta +\gamma \le 1. \end{aligned}$$

So, it concludes that the space of CQDFN consists of more points than the spaces of CIFN, CPyFN, and Cq-ROFN, providing more freedom to assign values to f and g. $\square$

CQDFS against CPFS

The complex picture fuzzy set imposes a limitation on membership, neutral, and non-membership functions that their sum must not exceed 1, as a result, the feasible space of CPFS gets restricted. For example, let $\left( \left( f\text {e}^{i\theta },h\text {e}^{i\psi },g\text {e}^{i\phi }\right) \right)$ be a CPFN such that $f_{{\mathbb {C}}_{P}}=0.43$, $h_{{\mathbb {C}}_{P}}=0.52$ and $g_{{\mathbb {C}}_{P}}=0.21.$ Then,

$$\begin{aligned} f+h+g=0.43+0.52+0.21=1.16>1. \end{aligned}$$

Hence, such f, g, and h do not represent the CPFN. Now in CQDFN for $\alpha =0.43$, $\beta =0.52$ and $\gamma =0.21$ and the pair $f=0.62$ and $g=0.51$, the following inequality holds:

$$\begin{aligned} \alpha f^{2}(x)+\beta fg+\gamma g^{2}(x)=0.38<1. \end{aligned}$$

Thus, there exist numbers that are not CPFNs but are CQDFNs. By following the same arguments as in Theorem 2.2, it is easy to show that every CPFN is, in fact, a CQDFN.

CQDFS against CLDFS

In this section, it is discussed why CQDFS is advantageous over CLDFS despite having the same space. Since CLDFS involves two parameters, $\alpha$ for acceptance type and $\beta$ for rejection type, CQDFS consists of three parameters. The third additional parameter $\gamma$ is of the hesitating kind, allowing a phenomenon to be ignored. In real-life situations, decision-makers often come across scenarios where they feel unsure or uncertain about making a choice. Let’s consider the context of investing in the stock market. When an investor is considering buying stocks, there are different possibilities they might encounter. For instance, they could choose to invest in the stocks of a specific company, believing it to be a good opportunity (acceptance type). On the other hand, they might decide to reject that particular company’s stocks and instead invest in stocks of a different company that they perceive to have more potential (rejection type). Lastly, they may feel hesitant or unsure about investing in stocks and choose to keep their funds in safer options like bonds or savings accounts (ignorance type). In such situations, utilizing CQDFS as an analytical tool can provide valuable insights for decision-making in the complex world of stock market investments.

Based on the comparisons above, it becomes apparent that the newly introduced CQDFS represents a unique hybrid form of fuzzy set, combining the distinctive characteristics of both CLDFS and CPFS. This combination of features creates a novel and versatile fuzzy set, thereby extending the scope and capabilities of fuzzy systems in various decision-making applications. In the following sections, an exploration will be conducted to uncover the advantages of CQDFS, emphasizing its potential to address complex problems with enhanced efficacy and precision.

Fig. 2

Hierarchical representation of fuzzy sets

Figure 2 represents the hierarchical generalization from the most simple complex fuzzy set to the most advanced complex quadratic Diophantine fuzzy set.

Smart transportation decisions with CQDFS

Transportation plays a crucial role in global economies, enabling the movement of goods, services, and people. Decisions made in transportation have a profound impact on economic development, affecting market access, supply chains, production costs, and consumer behavior. Therefore, strategic decision-making in transportation is vital for economic growth and stability. Various factors influence transportation decisions, including market demand, infrastructure development, technology, environmental concerns, and regulations. Understanding consumer demand patterns is especially important. It helps optimize transportation routes, ensure timely deliveries, and enhance market responsiveness and competitiveness. In the modern era, data and technology have transformed transportation decision-making. Tools like data analytic, predictive modeling, and real-time monitoring offer valuable insights into transportation patterns. These insights help stakeholders make informed decisions, using CQDFS to navigate transportation complexities. The use of CQDFS can better shape transportation decision-making by incorporating membership, hesitancy, and non-membership values, providing a comprehensive tool for addressing transportation problems. The interaction between data, technology, and CQDFS capabilities leads to a future where transportation systems are efficient, environmentally, and economically sustainable. Within this section, an examination will be undertaken to address a decision-making problem concerning the transportation of goods using GPS-equipped vehicles, with the aim of enhancing cargo operations. Prior to delving into this specific problem, crucial definitions will be introduced to incorporate CQDFS and formulate a comprehensive methodology. This methodology aims to address the challenge of economic efficiency within the transportation sector that relies on GPS-enabled vehicles for goods transportation.

Definition 6

[29] A sequence $\{d(q)\}$ of length $\Gamma$ has the following definition for the qth inverse discrete Fourier transform coefficient:

$$\begin{aligned} d(q)=\frac{1}{\Gamma }\sum _{p=0}^{\Gamma -1}d^{\prime }(p)\text {cis}{\frac{2\pi }{ \Gamma }pq},\quad p\in {0,1,2,\ldots ,\Gamma -1}, \end{aligned}$$

where $d(\Gamma )$ has different values.

In the analysis, a specific case is considered, where a function is defined as $d^{\prime }(q)= S[q] (\alpha [q] +\beta [q]) \in [0,1]$. Here, S[q] represents the measured signal, $\alpha [q]$ represents the level of certainty, and $\beta [q]$ represents the measure of confusion associated with the measurement of S[q].

Definition 7

[29] The matrix product form provides the representation of the discrete Fourier transform (DFT) for the sequence ${d^{\prime }(q):0\le q\le \Gamma -1}$.

$$\begin{aligned}{} & {} \begin{pmatrix} d^{\prime }(0) \\ d^{\prime }(1) \\ \vdots \\ d^{\prime }(\Gamma -1) \end{pmatrix}\\{} & {} \quad =\begin{pmatrix} 1 &{} 1 &{} 1 &{} \ldots &{} 1 \\ 1 &{} \text {cis}{\left( -\frac{2\pi }{\Gamma }(1)\right) } &{} \text {cis}{\left( -\frac{2\pi }{\Gamma }(2)\right) } &{} \ldots &{} \text {cis}{\left( -\frac{2\pi }{\Gamma }(\Gamma -1)\right) } \\ \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots \\ 1 &{} \text {cis}{\left( -\frac{2\pi }{\Gamma }(\Gamma -1)\right) } &{} \text {cis}{\left( -\frac{2\pi }{\Gamma } (\Gamma -1)\right) } &{} \ldots &{} \text {cis}{\left( -\frac{2\pi }{\Gamma }(\Gamma -1)^{2}\right) } \end{pmatrix}\\{} & {} \qquad \times \begin{pmatrix} d(0) \\ d(1) \\ \vdots \\ d(\Gamma -1) \end{pmatrix}, \end{aligned}$$

the inverse discrete Fourier transform is given by:

$$\begin{aligned}{} & {} \begin{pmatrix} d(0) \\ d(1) \\ \vdots \\ d(\Gamma -1) \end{pmatrix}\\{} & {} \quad =\frac{1}{\Gamma }\begin{pmatrix} 1 &{} 1 &{} 1 &{} \ldots &{} 1 \\ 1 &{} \text {cis}{\left( \frac{2\pi }{\Gamma }(1)\right) } &{} \text {cis}{\left( \frac{2\pi }{\Gamma }(2)\right) } &{} \ldots &{} \text {cis}{\left( \frac{2\pi }{\Gamma }(\Gamma -1)\right) } \\ 1 &{} \text {cis}{\left( \frac{2\pi }{\Gamma }(2)\right) } &{} \text {cis}{\left( \frac{2\pi }{\Gamma }(4)\right) } &{} \ldots &{} \text {cis}{\left( \frac{2\pi }{\Gamma }2(\Gamma -1)\right) } \\ \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots \\ 1 &{} \text {cis}{\left( \frac{2\pi }{\Gamma }(\Gamma -1)\right) } &{} \text {cis}{\left( \frac{2\pi }{\Gamma } (\Gamma -1)\right) } &{} \ldots &{} \text {cis}{\left( \frac{2\pi }{\Gamma }(\Gamma -1)^{2}\right) } \end{pmatrix}\\{} & {} \qquad \times \begin{pmatrix} d^{\prime }(0) \\ d^{\prime }(1) \\ \vdots \\ d^{\prime }(\Gamma -1) \end{pmatrix}. \end{aligned}$$

By studying these equations, it can be seen that the first matrix on the right-hand side concentrates on the signal’s time, while the second matrix deals with its amplitude.

In the forthcoming section, an algorithm will be delineated for the implementation of CQDFS in the domain of signals and systems. The primary objective is to identify a particular signal within the presence of noise.

Let $\Gamma$ represent the number of distinct signals, and let $s_1(q), s_2(q), s_3(q), \ldots , s_m(q)$ denote these signals, accompanied by their respective noise components $n_1(q), n_2(q),$ $n_3(q), \ldots , n_m(q)$. Each signal is recorded at $\Gamma$ different time instances, with q ranging from 0 to $\Gamma -1$. Precisely, the signal denoted as $s_m(q)$ and its corresponding noise, referred to as $n_m(q)$, are specifically associated with the $\Gamma$-th signal. Moreover, $\alpha _m(q)$ and $\gamma _m(q)$ represent measures of certainty associated with the signal and noise measurements, while $\beta _m(q)$ quantifies the level of ambiguity encountered during signal processing. It is essential to acknowledge that the certainty measure can be subjective, reflecting the receiver’s personal opinion, or it can serve as an indicator of the accuracy of the signal-measuring device. The discrete Fourier transform of this $\Gamma$-th signal can be mathematically expressed as:

$$\begin{aligned} s_m(q)= & {} \frac{1}{\Gamma }\sum _{p=0}^{\Gamma -1} S[p] (\alpha [p]+\beta [p]) \nonumber \\{} & {} \text {cis}{\ \frac{2\pi }{\Gamma } pq},\quad q, p \in {0,1,2, \ldots , \Gamma -1}. \end{aligned}$$

(3.1)

Similarly, the discrete Fourier transform of the $\Gamma$-th noise is

$$\begin{aligned} n_m(q)= & {} \frac{1}{\Gamma }\sum _{p=0}^{\Gamma -1} N[p] (\gamma [p]+\beta [p]) \text {cis}{\ \frac{2\pi }{\Gamma } pq},\nonumber \\{} & {} q, p \in {0,1,2, \ldots , \Gamma -1}. \end{aligned}$$

(3.2)

In representing a signal affected by noise, Eqs. (3.1) and (3.2) are utilized as a model, incorporating CQDFS for the representation process.

CQDFS is used in signal analysis to identify a specific signal from a group of signals collected by a receiver. To achieve this, a reference signal is established as an initial point. This reference signal indicated as Phi, is captured many times, exactly Gamma times. This reference signal’s discrete Fourier transform (DFT) is stated as:

$$\begin{aligned} \Phi (q)=\frac{1}{\Gamma }\sum _{p=0}^{\Gamma -1} \Phi ^{\prime }(p) \text {cis}{\ \frac{ 2\pi }{\Gamma } pq},\quad q, p \in {0,1,2, \ldots , \Gamma -1}, \end{aligned}$$

where $\Phi ^{\prime }(p) \in [0,1]$ and $0 \le p \le \Gamma -1$.

Algorithm

For comparing signals, the following method will be employed, comprising the subsequent steps:

Step 1: By expanding $s_{\Gamma }(q)$ and $n_{\Gamma }(q)$, following expressions are obtained:

$$\begin{aligned} s_{\Gamma }(q)=\frac{1}{\Gamma }\left[ \begin{array}{lll} S[0](\alpha [0]+\beta [0])\text {cis}{\frac{2\pi }{\Gamma }q(0)}\\ \quad +S[1](\alpha [1]+\beta [1])\text {cis}{\frac{2\pi }{\Gamma }q(1)} \\ \quad +S[2](\alpha [2]+\beta [2])\text {cis}{\frac{2\pi }{\Gamma }q(2)} +\cdots \\ \quad +S[\Gamma -1](\alpha [\Gamma -1] \\ \quad +\beta [\Gamma -1])\text {cis}{\frac{2\pi }{\Gamma }q(\Gamma -1)} \end{array} \right] , \end{aligned}$$

and

$$\begin{aligned} n_{\Gamma }(q)=\frac{1}{\Gamma }\left[ \begin{array}{l} N[0]\gamma [0]\text {cis}{\frac{2\pi }{\Gamma }q(0)}+N[1]\gamma [1]\text {cis}{ \frac{2\pi }{\Gamma }q(1)} \\ \quad +N[2]\gamma [2]\text {cis}{\frac{2\pi }{\Gamma }q(2)}+\cdots \\ \quad +N[\Gamma -1]\gamma [\Gamma -1]\text {cis}{\frac{2\pi }{\Gamma }q(\Gamma -1)} \end{array} \right] . \end{aligned}$$

By substituting $q=0,1,2,3,\ldots ,\Gamma -1$ into the above, the following expressions are derived for $s_{\Gamma }(q)$. Specifically, when $q=0$, the equation becomes:

$$\begin{aligned} s_{\Gamma }(0)=\frac{1}{\Gamma }\left[ \begin{array}{l} S[0](\alpha [0]+\beta [0])\cdot 1+S[1]\alpha [1]\cdot 1\\ \quad +S[2](\alpha [2]+\beta [2])\cdot 1 +\ldots \\ \quad +S[\Gamma -1](\alpha [\Gamma -1]+\beta [\Gamma -1])\cdot 1 \end{array} \right] . \end{aligned}$$

For $q=1$:

$$\begin{aligned} s_{\Gamma }(1)=\frac{1}{\Gamma }\left[ \begin{array}{l} S[0](\alpha [0]+\beta [0])\cdot 1+S[1](\alpha [1]+\beta [1])\\ \quad \text {cis}{\frac{2\pi }{\Gamma }(1)} +S[2](\alpha [2]+\beta [2])\\ \quad \text {cis}{\frac{2\pi }{\Gamma }(2)} +\cdots +S[\Gamma -1](\alpha [\Gamma -1] \\ \quad +\beta [\Gamma -1])\text {cis}{\frac{2\pi }{\Gamma }(\Gamma -1)} \end{array} \right] . \end{aligned}$$

Continuing with the same approach, when $q=\Gamma -1$, the following equation is obtained:

$$\begin{aligned} s_{\Gamma }(\Gamma -1)=\frac{1}{\Gamma }\left[ \begin{array}{l} S[0](\alpha [0]+\beta [0])\cdot 1+S[1]\alpha [1]\\ \quad \text {cis}{ \frac{2\pi }{\Gamma }(\Gamma -1)} +S[2](\alpha [2]+\beta [2])\\ \quad \text {cis}{\frac{2\pi }{\Gamma }2(\Gamma -1)}+\cdots \\ \quad +S[\Gamma -1](\alpha [\Gamma -1] \\ \quad +\beta [\Gamma -1])\text {cis}{\frac{2\pi }{\Gamma }(\Gamma -1)^{2}} \end{array} \right] . \end{aligned}$$

Follow a similar process for $n_{\Gamma }(q)$ and the reference signal $\Phi (q)$.

Step 2: In the subsequent step, transform these $\Gamma$ samples of $s_{\Gamma }(q)$ and $n_{\Gamma }(q)$ into matrix form. In addition, compute the discrete Fourier transform (DFT) for $\Phi (q)$. Employing the Definition 7, obtain:

$$\begin{aligned}{} & {} \begin{pmatrix} s_{\Gamma }(0) \\ s_{\Gamma }(1) \\ \vdots \\ s_{\Gamma }(\Gamma -1) \end{pmatrix}\\{} & {} \quad =\frac{1}{\Gamma } \begin{pmatrix} 1 &{} 1 &{} 1 &{} \ldots &{} 1 \\ 1 &{} \text {cis}{\left( \frac{2\pi }{\Gamma }(1)\right) } &{} \text {cis}{\left( \frac{2\pi }{\Gamma }(2)\right) } &{} \ldots &{} \text {cis}{\left( \frac{2\pi }{\Gamma }(\Gamma -1)\right) } \\ 1 &{} \text {cis}{\left( \frac{2\pi }{\Gamma }(2)\right) } &{} \text {cis}{\left( \frac{2\pi }{\Gamma }(4)\right) } &{} \ldots &{} \text {cis}{\left( \frac{2\pi }{\Gamma }2(\Gamma -1)\right) } \\ \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots \\ 1 &{} \text {cis}{\left( \frac{2\pi }{\Gamma }(\Gamma -1)\right) } &{} \text {cis}{\left( \frac{2\pi }{\Gamma } 2(\Gamma -1)\right) } &{} \ldots &{} \text {cis}{\left( \frac{2\pi }{\Gamma }(\Gamma -1)^{2}\right) } \end{pmatrix}\\{} & {} \qquad \times \begin{pmatrix} S[0](\alpha [0]+\beta [0]) \\ S[1](\alpha [1]+\beta [1]) \\ \vdots \\ S[\Gamma -1](\alpha [\Gamma -1]+\beta [\Gamma -1]) \end{pmatrix},\\{} & {} \begin{pmatrix} n_{\Gamma }(0) \\ n_{\Gamma }(1) \\ \vdots \\ n_{\Gamma }(\Gamma -1) \end{pmatrix}\\{} & {} \quad =\frac{1}{\Gamma } \begin{pmatrix} 1 &{} 1 &{} 1 &{} \ldots &{} 1 \\ 1 &{} \text {cis}{\left( \frac{2\pi }{\Gamma }(1)\right) } &{} \text {cis}{\left( \frac{2\pi }{\Gamma }(2)\right) } &{} \ldots &{} \text {cis}{\left( \frac{2\pi }{\Gamma }(\Gamma -1)\right) } \\ 1 &{} \text {cis}{\left( \frac{2\pi }{\Gamma }(2)\right) } &{} \text {cis}{\left( \frac{2\pi }{\Gamma }(4)\right) } &{} \ldots &{} \text {cis}{\left( \frac{2\pi }{\Gamma }2(\Gamma -1)\right) } \\ \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots \\ 1 &{} \text {cis}{\left( \frac{2\pi }{\Gamma }(\Gamma -1)\right) } &{} \text {cis}{\left( \frac{2\pi }{\Gamma } (\Gamma -1)\right) } &{} \ldots &{} \text {cis}{\left( \frac{2\pi }{\Gamma }(\Gamma -1)^{2}\right) } \end{pmatrix}\\{} & {} \qquad \times \begin{pmatrix} N[0](\gamma [0]+\beta [0]) \\ N[1](\gamma [1]+\beta [1]) \\ \vdots \\ N[\Gamma -1](\gamma [\Gamma -1]+\beta [\Gamma -1]) \end{pmatrix}, \end{aligned}$$

and

$$\begin{aligned}{} & {} \begin{pmatrix} \Phi (0) \\ \Phi (1) \\ \vdots \\ \Phi (\Gamma -1) \end{pmatrix}\\{} & {} \quad = \frac{1}{\Gamma } \begin{pmatrix} 1 &{} 1 &{} 1 &{} \ldots &{} 1 \\ 1 &{} \text {cis}{ \left( \frac{2\pi }{\Gamma }(1)\right) } &{} \text {cis}{\ \left( \frac{2\pi }{\Gamma }(2)\right) } &{} \ldots &{} \text {cis}{ \left( \frac{2\pi }{\Gamma }(\Gamma -1)\right) } \\ 1 &{} \text {cis}{ \left( \frac{2\pi }{\Gamma }(2)\right) } &{} \text {cis}{\ \left( \frac{2\pi }{\Gamma }(4)\right) } &{} \ldots &{} \text {cis}{ \left( \frac{2\pi }{\Gamma }2(\Gamma -1)\right) } \\ \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots \\ 1 &{} \text {cis}{ \left( \frac{2\pi }{\Gamma }(\Gamma -1)\right) } &{} \text {cis}{ \left( \frac{2\pi }{\Gamma } 2(\Gamma -1)\right) } &{} \ldots &{} \text {cis}{\ \left( \frac{2\pi }{\Gamma }(\Gamma -1)^2\right) } \end{pmatrix}\\{} & {} \qquad \times \begin{pmatrix} \Phi ^{\prime }[0] \\ \Phi ^{\prime }[1] \\ \vdots \\ \Phi ^{\prime }[\Gamma -1] \end{pmatrix}. \end{aligned}$$

Step 3: Upon computing the matrices above, values within the unit circle in a complex plane are obtained. Given that the order of complex numbers is not crucial, the absolute values of the $\Gamma$ samples for the signal $s_{\Gamma }(q)$, noise $n_{\Gamma }(q)$, and the reference signal $\Phi (q)$ are calculated. This leads to the following:

$$\begin{aligned} \begin{pmatrix} \left| s_{\Gamma }(0)\right| \\ \left| s_{\Gamma }(1)\right| \\ \vdots \\ \left| s_{\Gamma }(\Gamma -1)\right| \end{pmatrix} , \begin{pmatrix} \left| n_{\Gamma }(0)\right| \\ \left| n_{\Gamma }(1)\right| \\ \vdots \\ \left| n_{\Gamma }(\Gamma -1)\right| \end{pmatrix} \text { and } \begin{pmatrix} \left| \Phi (0)\right| \\ \left| \Phi (1)\right| \\ \vdots \\ \left| \Phi (\Gamma -1)\right| \end{pmatrix}. \end{aligned}$$

These matrices are commonly referred to as absolute matrices.

Step 4: In the subsequent step, a comparison is made between the largest entry derived from the absolute matrix of $s_{\Gamma }(q)$ and the largest entry in $n_{\Gamma }(q)$. If the signal entry is determined to be lower than the noise value, it is excluded from further comparison. Conversely, if the signal entry surpasses the noise entry, a comparison is then made between the difference of these entries and the reference signal.

Optimizing vehicle position estimate in a noisy GPS

In this scenario, let’s consider a transportation company managing a fleet of vehicles that transport goods between different locations. Each vehicle is equipped with GPS and communication systems to track its position and communicate with the central control system. However, the GPS signals received, denoted as $s_1(q)$, $s_2(q)$, and $s_3(q)$, representing the positions of vehicles, are corrupted by noise, denoted as $n_1(q)$, $n_2(q)$, and $n_3(q)$.

To accurately estimate the positions of vehicles, data from each vehicle is recorded multiple times. In addition, the transportation company has a reference signal $\Phi (q)$, representing a known signal, which serves as a reference for position estimation. The reconstruction of the positions of vehicles can be formulated as follows:

$$\begin{aligned} s_{m}(q)= & {} \frac{1}{4}\sum _{p=0}^{3}S_{m}[p](\alpha _{m}[p]+\beta _{m}[p])\nonumber \\{} & {} \text {cis}{ \frac{2\pi }{4}pq};\quad q,p=0,1,2,3, \end{aligned}$$

(3.3)

$$\begin{aligned} n_{m}(q)= & {} \frac{1}{4}\sum _{p=0}^{3}N_{m}[p](\gamma _{m}[p]+\beta _{m}[p])\nonumber \\{} & {} \text {cis}{ \frac{2\pi }{4}pq};\quad q,p=0,1,2,3, \end{aligned}$$

(3.4)

where $S_{m}[q](\alpha _{m}[q]+\beta _{m}[q]),N_{m}[q](\gamma _{m}[q]+\beta _{m}[q])\in [0,1]$. Also

$$\begin{aligned} \Phi _{m}(q)=\frac{1}{4}\sum _{p=0}^{3}\Phi ^{\prime }[p]\text {cis}{\frac{2\pi }{4}pq };\quad q,p=0,1,2,3. \end{aligned}$$

(3.5)

Expanding (3.3):

$$\begin{aligned} s_{m}(q)=\frac{1}{4}\left[ \begin{array}{lll} S_{m}[0](\alpha _{m}[0]+\beta _{m}[0])\text {cis}({\frac{2\pi }{4}q(0)})\\ \quad +S_{m}[1](\alpha _{m}[1]+\beta _{m}[1])\text {cis}({\frac{2\pi }{4}q(1)}) \\ \quad +S_{m}[2](\alpha _{m}[2]+\beta _{m}[2])\text {cis}({\frac{2\pi }{4}q(2)})\\ \quad +S_{m}[3](\alpha _{m}[3]+\beta _{m}[3])\text {cis}({\frac{2\pi }{4}q(3)}) \end{array} \right] . \end{aligned}$$

In this context, the received signals $s_1(q)$, $s_2(q)$, and $s_3(q)$ represent the vehicles’ positions, which are essential economic indicators for the transportation company. The noise $n_1(q)$, $n_2(q)$, and $n_3(q)$ represent uncertainties or disruptions in the GPS signals, while the reference signal $\Phi (q)$ provides a stable point of comparison. By employing the given formulas, the transportation company can reconstruct accurate vehicle positions, crucial for optimizing routes, ensuring timely deliveries, and ultimately enhancing their economic efficiency and customer satisfaction.

Substituting $q=0,1,2,3$ in Eq. 3.3,

$$\begin{aligned} s_{m}(0)= & {} \frac{1}{4}\left[ \begin{array}{lll} S_{m}[0](\alpha _{m}[0]+\beta _{m}[0])\cdot 1\\ \quad +S_{m}[1](\alpha _{m}[1]+\beta _{m}[1])\cdot 1 \\ \quad +S_{m}[2](\alpha _{m}[2]+\beta _{m}[2])\cdot 1\\ \quad +S_{m}[3](\alpha _{m}[3]+\beta _{m}[3])\cdot 1 \end{array}\right] ,\\ s_{m}(1)= & {} \frac{1}{4}\left[ \begin{array}{lll} S_{m}[0](\alpha _{m}[0]+\beta _{m}[0])\cdot 1+S_{m}[1](\alpha _{m}[1]\\ \quad +\beta _{m}[1])\text {cis}\left( {\frac{2\pi }{4}(1)}\right) \\ \quad +S_{m}[2](\alpha _{m}[2]+\beta _{m}[2])\text {cis}\left( {\frac{2\pi }{4}(2)} \right) \\ \quad +S_{m}[3](\alpha _{m}[3]+\beta _{m}[3])\text {cis}\left( {\frac{2\pi }{4}(3)}\right) \end{array}\right] ,\\ s_{m}(2)= & {} \frac{1}{4}\left[ \begin{array}{l} S_{m}[0](\alpha _{m}[0]+\beta _{m}[0])\cdot 1+S_{m}[1](\alpha _{m}[1]\\ \quad +\beta _{m}[1])\text {cis}\left( {\frac{2\pi }{4}(2)}\right) \\ \quad +S_{m}[2](\alpha _{m}[2]+\beta _{m}[2])\text {cis}\left( {\frac{2\pi }{4}(4)} \right) \\ \quad +S_{m}[3](\alpha _{m}[3]+\beta _{m}[3])\text {cis}\left( {\frac{2\pi }{4}(6)}\right) \end{array}\right] , \end{aligned}$$

and

$$\begin{aligned} s_{m}(3)=\frac{1}{4}\left[ \begin{array}{llll} S_{m}[0](\alpha _{m}[0]+\beta _{m}[0])\cdot 1+S_{m}[1](\alpha _{m}[1]\\ \quad +\beta _{m}[1])\text {cis}\left( {\frac{2\pi }{4}(3)}\right) \\ \quad +S_{m}[2](\alpha _{m}[2]+\beta _{m}[2])\text {cis}\left( {\frac{2\pi }{4}(6)}\right) \\ \quad +S_{m}[3](\alpha _{m}[3]+\beta _{m}[3])\text {cis}\left( {\frac{2\pi }{4}(9)}\right) \end{array} \right] . \end{aligned}$$

Writing (3.3.1), (3.3.2), (3.3.3) and (3.3.4) in matrix form:

$$\begin{aligned} \begin{pmatrix} s_{m}(0) \\ s_{m}(1) \\ s_{m}(2) \\ s_{m}(3) \end{pmatrix}= & {} \frac{1}{4} \begin{pmatrix} 1 &{} 1 &{} 1 &{} 1 \\ 1 &{} \text {cis}{\frac{2\pi }{4}(1)} &{} \text {cis}{\frac{2\pi }{4}(2)} &{} \text {cis}{\frac{2\pi }{4} (3)} \\ 1 &{} \text {cis}{\frac{2\pi }{4}(2)} &{} \text {cis}{\frac{2\pi }{4}(4)} &{} \text {cis}{\frac{2\pi }{4} (6)} \\ 1 &{} \text {cis}{\frac{2\pi }{4}(3)} &{} \text {cis}{\frac{2\pi }{4}(6)} &{} \text {cis}{\frac{2\pi }{4} (9)} \end{pmatrix}\\{} & {} \times \begin{pmatrix} S_{m}[0](\alpha _{m}[0]+\beta _{m}[0]) \\ S_{m}[1](\alpha _{m}[1]+\beta _{m}[1]) \\ S_{m}[2](\alpha _{m}[2]+\beta _{m}[2]) \\ S_{m}[3](\alpha _{m}[3]+\beta _{m}[3]) \end{pmatrix}. \end{aligned}$$

In a similar way, (3.4) and (3.5) can be written. This gives

$$\begin{aligned} \begin{pmatrix} n_{m}(0) \\ n_{m}(1) \\ n_{m}(2) \\ n_{m}(3) \end{pmatrix}= & {} \frac{1}{4} \begin{pmatrix} 1 &{} 1 &{} 1 &{} 1 \\ 1 &{} \text {cis}{\frac{2\pi }{4}(1)} &{} \text {cis}{\frac{2\pi }{4}(2)} &{} \text {cis}{\frac{2\pi }{4} (3)} \\ 1 &{} \text {cis}{\frac{2\pi }{4}(2)} &{} \text {cis}{\frac{2\pi }{4}(4)} &{} \text {cis}{\frac{2\pi }{4} (6)} \\ 1 &{} \text {cis}{\frac{2\pi }{4}(3)} &{} \text {cis}{\frac{2\pi }{4}(6)} &{} \text {cis}{\frac{2\pi }{4} (9)} \end{pmatrix}\\{} & {} \times \begin{pmatrix} N_{m}[0](\gamma _{m}[0]+\beta _{m}[0]) \\ N_{m}[1](\gamma _{m}[1]+\beta _{m}[1]) \\ N_{m}[2](\gamma _{m}[2]+\beta _{m}[2]) \\ N_{m}[3](\gamma _{m}[3]+\beta _{m}[3]) \end{pmatrix}, \end{aligned}$$

and

$$\begin{aligned} \begin{pmatrix} \Phi (0) \\ \Phi (1) \\ \Phi (2) \\ \Phi (3) \end{pmatrix} {=}\frac{1}{4} \begin{pmatrix} 1 &{} 1 &{} 1 &{} 1 \\ 1 &{} \text {cis}{\frac{2\pi }{4}(1)} &{} \text {cis}{\frac{2\pi }{4}(2)} &{} \text {cis}{\frac{2\pi }{4} (3)} \\ 1 &{} \text {cis}{\frac{2\pi }{4}(2)} &{} \text {cis}{\frac{2\pi }{4}(4)} &{} \text {cis}{\frac{2\pi }{4} (6)} \\ 1 &{} \text {cis}{\frac{2\pi }{4}(3)} &{} \text {cis}{\frac{2\pi }{4}(6)} &{} \text {cis}{\frac{2\pi }{4} (9)} \end{pmatrix} \begin{pmatrix} \Phi ^{\prime }[0] \\ \Phi ^{\prime }[1] \\ \Phi ^{\prime }[2] \\ \Phi ^{\prime }[3] \end{pmatrix}. \end{aligned}$$

Now compute reference signal $\Phi (q)$. For this:

$$\begin{aligned} \Phi ^{\prime }[p]= {\left\{ \begin{array}{ll} 0.07; &{} \quad p=0 \\ 0.1; &{} \quad p=1 \\ 0.2; &{} \quad p=2 \\ 0.12; &{} \quad p=3 \end{array}\right. } . \end{aligned}$$

Using these values of $\Phi [p]$,obtain

$$\begin{aligned} \begin{pmatrix} \Phi (0) \\ \Phi (1) \\ \Phi (2) \\ \Phi (3) \end{pmatrix} =\frac{1}{4} \begin{pmatrix} 1 &{} 1 &{} 1 &{} 1 \\ 1 &{} i &{} -1 &{} -i \\ 1 &{} -1 &{} 1 &{} -1 \\ 1 &{} -i &{} -1 &{} i \end{pmatrix} \begin{pmatrix} 0.07 \\ 0.1 \\ 0.2 \\ 0.12 \end{pmatrix} = \begin{pmatrix} 0.12 \\ -0.03-0.01i \\ 0.01 \\ -0.03+0.01i \end{pmatrix}. \end{aligned}$$

The absolute value matrix of the reference signal is then:

$$\begin{aligned} \begin{pmatrix} \left| \Phi (0)\right| \\ \left| \Phi (1)\right| \\ \left| \Phi (2)\right| \\ \left| \Phi (3)\right| \end{pmatrix} = \begin{pmatrix} 0.12 \\ 0.03 \\ 0.01 \\ 0.03 \end{pmatrix} . \end{aligned}$$

From here, it is seen that the maximum value is 0.12.

Next, for the signal $s_{1}(q)$; $q=0,1,2,3$:

$$\begin{aligned} S_{1}[p]= & {} {\left\{ \begin{array}{ll} 3; &{} \quad p=0 \\ 1; &{} \quad p=1 \\ 1; &{} \quad p=2 \\ 10; &{} \quad p=3 \end{array}\right. },\quad \alpha _{1}[p]= {\left\{ \begin{array}{ll} 0.14; &{} \quad p=0 \\ 0.12; &{} \quad p=1 \\ 0.02; &{} \quad p=2 \\ 0.04; &{} \quad p=3 \end{array}\right. },\\ \quad \beta _{1}[p]= & {} {\left\{ \begin{array}{ll} 0.08; &{} \quad p=0 \\ 0.09; &{} \quad p=1 \\ 0.35; &{} \quad p=2 \\ 0.01; &{} \quad p=3 \end{array}\right. }. \end{aligned}$$

This gives us

$$\begin{aligned} \begin{pmatrix} s_{1}(0) \\ s_{1}(1) \\ s_{1}(2) \\ s_{1}(3) \end{pmatrix}= & {} \begin{pmatrix} 1 &{} 1 &{} 1 &{} 1 \\ 1 &{} i &{} -1 &{} -i \\ 1 &{} -1 &{} 1 &{} -1 \\ 1 &{} -i &{} -1 &{} i \end{pmatrix} \begin{pmatrix} (3)\cdot (0.22) \\ (1)\cdot (0.21) \\ (1)\cdot (0.37) \\ (10)\cdot (0.5) \end{pmatrix}\\= & {} \begin{pmatrix} 0.44 \\ 0.07-0.07i \\ 0.08 \\ 0.07+0.07i \end{pmatrix}. \end{aligned}$$

The absolute value matrix then becomes

$$\begin{aligned} \begin{pmatrix} \left| s_{1}(0)\right| \\ \left| s_{1}(1)\right| \\ \left| s_{1}(2)\right| \\ \left| s_{1}(3)\right| \end{pmatrix} =\begin{pmatrix} 0.44 \\ 0.1 \\ 0.08 \\ 0.1 \end{pmatrix}. \end{aligned}$$

Along the same lines, for the noise profile $n_{1}(q)$, Let

$$\begin{aligned} N_{1}[p]= & {} {\left\{ \begin{array}{ll} 1; &{} \quad p=0 \\ 1; &{} \quad p=1 \\ 2; &{} \quad p=2 \\ 4; &{} \quad p=3 \end{array}\right. },\quad \gamma _{1}[p]= {\left\{ \begin{array}{ll} 0.39; &{} \quad p=0 \\ 0.52; &{} \quad p=1 \\ 0.12; &{} \quad p=2 \\ 0.07; &{} \quad p=3 \end{array}\right. },\\ \quad \beta _{1}[p]= & {} {\left\{ \begin{array}{ll} 0.08; &{} \quad p=0 \\ 0.09; &{} \quad p=1 \\ 0.35; &{} \quad p=2 \\ 0.01; &{} \quad p=3 \end{array}\right. }. \end{aligned}$$

Putting these values in the matrix form, to get

$$\begin{aligned} \begin{pmatrix} n_{1}(0) \\ n_{1}(1) \\ n_{1}(2) \\ n_{1}(3) \end{pmatrix}= & {} \begin{pmatrix} 1 &{} 1 &{} 1 &{} 1 \\ 1 &{} i &{} -1 &{} -i \\ 1 &{} -1 &{} 1 &{} -1 \\ 1 &{} -i &{} -1 &{} i \end{pmatrix} \begin{pmatrix} (1)\cdot (0.47) \\ (1)\cdot (0.61) \\ (2)\cdot (0.47) \\ (4)\cdot (0.08) \end{pmatrix}\\= & {} \begin{pmatrix} 0.59 \\ -0.12+0.07i \\ 0.12 \\ -0.12-0.07i \end{pmatrix}. \end{aligned}$$

The absolute value matrix is

$$\begin{aligned} \begin{pmatrix} \left| n_{1}(0)\right| \\ \left| n_{1}(1)\right| \\ \left| n_{1}(2)\right| \\ \left| n_{1}(3)\right| \end{pmatrix} = \begin{pmatrix} 0.59 \\ 0.14 \\ 0.12 \\ 0.14 \end{pmatrix} . \end{aligned}$$

According to the previous two absolute value matrices for $s_1(q)$ and $n_1(q)$, the greatest value is 0.44, with a noise maximum of 0.59. As a result, the $s_1(q)$ is discarded.

For $s_{2}(q)$:

$$\begin{aligned} S_{2}[p]= & {} {\left\{ \begin{array}{ll} 1; &{} \quad p=0 \\ 2; &{} \quad p=1 \\ 5; &{} \quad p=2 \\ 8; &{} \quad p=3 \end{array}\right. },\quad \alpha _{2}[p]= {\left\{ \begin{array}{ll} 0.56; &{} \quad p=0 \\ 0.03; &{} \quad p=1 \\ 0.09; &{} \quad p=2 \\ 0.06; &{} \quad p=3 \end{array}\right. },\\ \quad \beta _{2}[p]= & {} {\left\{ \begin{array}{ll} 0.12; &{} \quad p=0 \\ 0.42; &{} \quad p=1 \\ 0.06; &{} \quad p=2 \\ 0.01; &{} \quad p=3 \end{array}\right. }. \end{aligned}$$

Proceeding in the same way as before, the following matrix is obtained

$$\begin{aligned} \begin{pmatrix} \left| s_{2}(0)\right| \\ \left| s_{2}(1)\right| \\ \left| s_{2}(2)\right| \\ \left| s_{2}(3)\right| \end{pmatrix} =\begin{pmatrix} 0.72 \\ 0.09 \\ 0.01 \\ 0.09 \end{pmatrix} , \end{aligned}$$

so, the max value is 0.72.

For $n_{2}(q)$, Let

$$\begin{aligned} N_{2}[p]= & {} {\left\{ \begin{array}{ll} 2; &{} \quad p=0 \\ 0; &{} \quad p=1 \\ 3; &{} \quad p=2 \\ 11; &{} \quad p=3 \end{array}\right. },\quad \gamma _{2}[p]= {\left\{ \begin{array}{ll} 0.18; &{} \quad p=0 \\ 0.38; &{} \quad p=1 \\ 0.25; &{} \quad p=2 \\ 0.07; &{} \quad p=3 \end{array}\right. },\\ \beta _{2}[p]= & {} {\left\{ \begin{array}{ll} 0.12; &{} \quad p=0 \\ 0.42; &{} \quad p=1 \\ 0.06; &{} \quad p=2 \\ 0.01; &{} \quad p=3 \end{array}\right. }. \end{aligned}$$

Solving it the same way as was done for $n_{1}(\Gamma )$:

$$\begin{aligned} \begin{pmatrix} \left| n_{2}(0)\right| \\ \left| n_{2}(1)\right| \\ \left| n_{2}(2)\right| \\ \left| n_{2}(3)\right| \end{pmatrix} =\begin{pmatrix} 0.6 \\ 0.23 \\ 0.16 \\ 0.23 \end{pmatrix} . \end{aligned}$$

Here, max value of $s_{2}(q)$ is 0.72 with max value of $n_{2}(q)$ 0.6. Therefore, the difference between signal and noise is 0.12.

Now, in respect of signal $s_{3}(q)$, let

$$\begin{aligned} S_{3}[p]= & {} {\left\{ \begin{array}{ll} 6; &{} \quad p=0 \\ 1; &{} \quad p=1 \\ 6; &{} \quad p=2 \\ 4; &{} \quad p=3 \end{array}\right. },\quad \alpha _{3}[p]= {\left\{ \begin{array}{ll} 0.02; &{} \quad p=0 \\ 0.14; &{} \quad p=1 \\ 0.03; &{} \quad p=2 \\ 0.16; &{} \quad p=3 \end{array}\right. },\\ \quad \beta _{3}[p]= & {} {\left\{ \begin{array}{ll} 0.08; &{} \quad p=0 \\ 0.14; &{} \quad p=1 \\ 0.01; &{} \quad p=2 \\ 0.07; &{} \quad p=3 \end{array}\right. }. \end{aligned}$$

It is seen that the absolute value matrix is

$$\begin{aligned} \begin{pmatrix} \left| s_{3}(0)\right| \\ \left| s_{3}(1)\right| \\ \left| s_{3}(2)\right| \\ \left| s_{3}(3)\right| \end{pmatrix} =\begin{pmatrix} 0.51 \\ 0.18 \\ 0.09 \\ 0.18 \end{pmatrix}. \end{aligned}$$

For the noise profile $n_{3}(q)$, let

$$\begin{aligned} N_{3}[p]= & {} {\left\{ \begin{array}{ll} 0; &{} \quad p=0 \\ 1; &{} \quad p=1 \\ 8; &{} \quad p=2 \\ 1; &{} \quad p=3 \end{array}\right. }.\quad \gamma _{3}[p]= {\left\{ \begin{array}{ll} 0.94; &{} \quad p=0 \\ 0.74; &{} \quad p=1 \\ 0.02; &{} \quad p=2 \\ 0.74; &{} \quad p=3 \end{array}\right. },\\ \quad \beta _{3}[p]= & {} {\left\{ \begin{array}{ll} 0.08; &{} \quad p=0 \\ 0.14; &{} \quad p=1 \\ 0.01; &{} \quad p=2 \\ 0.07; &{} \quad p=3 \end{array}\right. }. \end{aligned}$$

Solving similarly, the following matrix is obtained:

$$\begin{aligned} \begin{pmatrix} \left| n_{3}(0)\right| \\ \left| n_{3}(1)\right| \\ \left| n_{3}(2)\right| \\ \left| n_{3}(3)\right| \end{pmatrix} =\begin{pmatrix} 0.48 \\ 0.06 \\ 0.36 \\ 0.06 \end{pmatrix}. \end{aligned}$$

Hence, the max value is 0.51 with a corresponding noise value of 0.48 and the difference is 0.03. From the above calculations, it is evident that the signal $s_2(k)$ resembles the most with the reference signal.

Fig. 3

Visual representation of GPS signal disparities

In Fig. 3, the signals under consideration are denoted as $s_1$, $s_2$, and $s_3$. The graphical representation divides the region into two distinct sections: the upper portion, situated above the horizontal axis, corresponds to signal strength, while the lower section, located below the horizontal axis, represents noise. The ultimate magnitudes of the signals are visually depicted using white circles featuring a black center. Notably, the yellow dashed line serves as a benchmark delineating the criteria necessary for signal acceptance.

Optimizing cargo loading with CQDF-congruences

The efficient transfer of goods from ships to trucks plays a pivotal role in the transportation sector, impacting various stakeholders, including businesses, consumers, and the economy as a whole with a particular focus on its contribution to economic efficiency in the transportation sector. This process directly supports the expansion of international trade, which is a critical driver of economic growth. Efficiency in goods transfer leads to cost savings in the transportation sector. Optimizing the transition from ships to trucks maintains competitive prices for goods and services in the market. Efficient goods transfer also plays a role in reducing the environmental impact of the transportation sector. It encourages the adoption of cleaner and more sustainable transportation methods, such as electrified trucks and renewable energy sources for port operations. Ports and transportation hubs that efficiently handle cargo attract more shipping traffic and investment. As a result, these areas become key players in global trade networks, leading to increased economic activity and international competitiveness.

In this section, the main objective is to investigate the application of CQDF-congruences within the context of a decision-making framework based on AG-groupoids. The aim is to explore how this decision-making process plays a key role in cargo loading operations, with a specific emphasis on enhancing the efficiency of goods transfer from ships to trucks. Before exploring the problem at hand, it is important to provide an introductory foundation containing the fundamental structure and essential definitions that will serve as the basis for formulating a methodology. This methodology will be specifically designed to address the inherent uncertainties within cargo loading operations, particularly when employing various loading methods.

In the context of ternary operations, the commutative law states that $abc=cba$. By placing brackets on the left side of this equation, specifically $(ab)c=(cb)a$, a new algebraic structure called a left almost semigroup (LA-semigroup), was introduced by Kazim and Naseeruddin [16]. This identity is commonly known as the left invertive law. The alternative name for this structure is Abel-Grassmann’s groupoid (AG-groupoid), as referred to by Stevanovic and Protic in [31]. An AG-groupoid is a non-associative and non-commutative algebraic structure that falls between a groupoid and a commutative semigroup [24]. If an AG-groupoid with a left identity has inverses, it is called an AG-group [15]. It has been shown in [16] that an AG-groupoid S satisfies the medial law, which states that $(ab)(cd)=(ac)(bd)$ for all $a,b,c,d\in S$. The existence of a left identity in an AG-groupoid may vary. However, if a left identity exists in an AG-groupoid, it is unique [24]. Moreover, in an AG-groupoid S with a left identity, the paramedial law $(ab)(cd)=(dc)(ba)$ holds for all $a,b,c,d\in S$. By applying the medial law with a left identity, the equation $a(bc)=b(ac)$ for all $a,b,c\in S$ can be obtained.

To explore the latest applications of AG-groupoids in decision-making, it is suggested to refer to the following sources: [10, 17, 36,37,38]. These references offer insightful examples demonstrating how AG-groupoids have been effectively employed in this domain, highlighting their relevance and potential impact.

Score and accuracy functions

In this section, the score and accuracy functions will be introduced, playing a crucial role in determining the ranking of CQDFNs. The score function of a CQDFN can be defined as follows:

Definition 8

Let $\vartheta =\left( \left( f_{ {\mathbb {C}}_Q }\text {e}^{i\theta _{ {\mathbb {C}}_Q }},g_{ {\mathbb {C}}_Q }\text {e}^{i\phi _{ {\mathbb {C}}_Q }}\right) ,\left( \alpha ,\beta ,\gamma \right) \right)$ be a CQDFN, then the score function on $\vartheta$ can be defined by the mapping $\Psi _{ {\mathbb {C}}_Q }\rightarrow [-1,1]$ as follows : 

$$\begin{aligned} \Psi _{ {\mathbb {C}}_Q }(\vartheta )=\frac{(f_{ {\mathbb {C}}_Q }+\alpha +\theta _{ {\mathbb {C}}_Q }+\beta )-(g_{ {\mathbb {C}}_Q }+\phi _{ {\mathbb {C}}_Q }+\gamma )}{3}, \end{aligned}$$

where $\Psi _{ {\mathbb {C}}_Q }(\vartheta )$ is the score of a CQDFN $\vartheta .$

In particular,  if $\Psi _{{\mathbb {C}}_Q}(\vartheta )=1,$ then $(f_{{\mathbb {C}}_Q }+\alpha +\theta _{{\mathbb {C}}_Q}+\beta )-(g_{{\mathbb {C}}_Q}+\phi _{{\mathbb {C}}_Q }+\gamma )=3$.

Rearranging the terms, it is seen that $(f_{{\mathbb {C}}_Q}+\theta _{{\mathbb {C}}_Q })-(g_{{\mathbb {C}}_Q}+\phi _{{\mathbb {C}}_Q})+(\alpha +\beta -\gamma )=3$. Since the largest possible value of $\alpha +\beta +\gamma =1$, it can easily infer that the largest value of $\alpha +\beta -\gamma =1$. This is only possible when $\alpha +\beta =1$ and $\gamma =0$. Along with this, for the above equation to attain a value of 3, the term $(f_{{\mathbb {C}}_Q}+\theta _{{\mathbb {C}}_Q })-(g_{{\mathbb {C}}_Q}+\phi _{{\mathbb {C}}_Q})$ must be 2. If the term $g_{{\mathbb {C}}_Q} + \phi {{\mathbb {C}}_Q} \ne 0$, considering the fact that $0 \le f{{\mathbb {C}}_Q}, \theta {{\mathbb {C}}_Q} \le 1$, it follows that $f{{\mathbb {C}}_Q} + \theta {{\mathbb {C}}_Q} \le 2$. Even when the maximum value is considered, i.e., $f{{\mathbb {C}}_Q} + \theta {{\mathbb {C}}_Q} = 2$, the expression $(f{{\mathbb {C}}_Q} + \theta {{\mathbb {C}}_Q}) - (g{{\mathbb {C}}_Q} + \phi {{\mathbb {C}}_Q})$ cannot be justified since $g{{\mathbb {C}}_Q} + \phi {{\mathbb {C}}_Q} \ne 0$. It can easily be seen that a value of 2 for this expression is only possible when $f_{{\mathbb {C}}_Q}+\theta _{{\mathbb {C}}_Q}=2$ and $g_{{\mathbb {C}}_Q}+\phi _{{\mathbb {C}}_Q }=0$. From here, $f_{{\mathbb {C}}_Q}=\theta _{{\mathbb {C}}_Q}=1$ and $g_{ {\mathbb {C}}_Q}=\phi _{{\mathbb {C}}_Q}=0$. A similar argument ensures that $\Psi _{{\mathbb {C}}_Q}(\vartheta )=-1$ is possible only when $f_{{\mathbb {C}}_Q}=\theta _{{\mathbb {C}}_Q}=0$, $g_{{\mathbb {C}}_Q }=\phi _{{\mathbb {C}}_Q}=1$, $\alpha =\beta =0$, and $\gamma =1$.

Let

$$\begin{aligned} \vartheta _{1}=\left( \left( 0.8\text {e}^{i(0.5)},0.9\text {e}^{i(0.3)}\right) ,\left( 0.3,0.4,0.2\right) \right) , \end{aligned}$$

and

$$\begin{aligned} \vartheta _{2}=\left( \left( 0.2\text {e}^{i(0.6)},0.7\text {e}^{i(0.2)}\right) ,\left( 0.1,0.5,0.2\right) \right) , \end{aligned}$$

then $\Psi _{{\mathbb {C}}_Q}(\vartheta _{1})=0.2,$ and $\Psi _{{\mathbb {C}}_Q }(\vartheta _{2})=0.1$. Since $\Psi _{{\mathbb {C}}_Q}(\vartheta _{1})>\Psi _{ {\mathbb {C}}_Q}(\vartheta _{2})$, the score function of CQDFN $\vartheta _{1}$ is higher than $\vartheta _{2}$.

However if $\vartheta _{3}=(\left( 0.6\text {e}^{i(0.3)},0.7\text {e}^{i(0.1)}\right) ,\left( 0.3,0.3,0.1\right) )$, then $\Psi _{{\mathbb {C}}_Q}(\vartheta _{3})=0.2$. From here, it can be seen that $\Psi _{{\mathbb {C}}_{Q1}}$= $\Psi _{{\mathbb {C}}_{Q3}}$. In this case, the score function can not distinguish between CQDFNs $\Psi _{ {\mathbb {C}}_{Q1}}$ and $\Psi _{{\mathbb {C}}_{Q3}}$. To address this issue, consider the following definition of an accuracy function as follows:

Definition 9

The accuracy function on $\vartheta$ can be defined by the mapping $\psi _{ {\mathbb {C}}_Q }\rightarrow [0,1]$ as follows : 

$$\begin{aligned} \psi _{ {\mathbb {C}}_Q }(\vartheta )=\frac{f_{ {\mathbb {C}}_Q }+g_{ {\mathbb {C}}_Q }+\theta _{ {\mathbb {C}}_Q }+\phi _{ {\mathbb {C}}_Q }+\alpha +\beta +\gamma }{5}, \end{aligned}$$

where $\psi _{ {\mathbb {C}}_Q }(\vartheta )$ is the accuracy of a CQDFN $\vartheta .$

From above CQDFNs $\vartheta _{1}$ and $\vartheta _{3}$, now calculate that $\psi _{{\mathbb {C}}_Q}(\vartheta _{1})=0.68$ and $\psi _{{\mathbb {C}}_Q}(\vartheta _{3})=0.48$, that is, the accuracy of $\vartheta _{1}$ is greater than that of $\vartheta _{3}$.

The relationship between the score function and the accuracy function has been noted to exhibit similarities to the statistical relationship between the mean and variance [13]. In statistics, a proficient estimator is characterized by a smaller variance in its sampling distribution, indicating superior performance. Likewise, it is justifiable to argue that a higher degree of accuracy in a CQDFN corresponds to its enhanced quality.

When comparing two CQDFNs, specifically $\vartheta _1$ and $\vartheta _2$, the score and accuracy function could be employed based on the following criteria:

• if $\Psi _{ {\mathbb {C}}_{Q1} }\le \Psi _{ {\mathbb {C}}_{Q2} }$ then $\vartheta _{1}\le \vartheta _{2}$.

• if $\Psi _{ {\mathbb {C}}_{Q1}} \ge \Psi _{ {\mathbb {C}}_{Q2} }$ then $\vartheta _{1}\ge \vartheta _{2}$.

• if $\Psi _{ {\mathbb {C}}_{Q1} }=\Psi _{ {\mathbb {C}}_{Q2} }$ then

  . if $\psi _{ {\mathbb {C}}_{Q1} }\le \psi _{ {\mathbb {C}}_{Q2} }$ then $\vartheta _{1}\le \vartheta _{2}$.

  . if $\psi _{ {\mathbb {C}}_{Q1} }\ge \psi _{ {\mathbb {C}}_{Q2} }$ then $\vartheta _{1}\ge \vartheta _{2}$.

  . if $\psi _{ {\mathbb {C}}_{Q1} }=\psi _{ {\mathbb {C}}_{Q2} }$ then $\vartheta _{1}=\vartheta _{2}$.

On CQDF-congruences

This section introduces the concept of congruences in an AG-groupoid, employing the notions of CQDFS and the score function. Through the introduction of these congruences, the goal is to enhance the comprehensive understanding of an AG-groupoid, particularly in the context of decision-making problems related to transportation.

For simplicity, in the rest of the article $\Psi$ refers to $\Psi _{{\mathbb {C}}_Q}.$

Let S be an AG-groupoid. A mapping $\Psi :S\times S\rightarrow [0,1]$ is called a CQDF-relation on S,  where $\Psi$ is a score function. Let $\Psi _{1},$ $\Psi _{2}$ be two CQDF-relations on S. The product $\Psi _{1}\circ \Psi _{2}$ is defined by

$$\begin{aligned} (\Psi _{1}\circ \Psi _{2})(a,b)=\bigvee \limits _{x\in S}\left\{ \Psi _{1}(a,x)\wedge \Psi _{2}(x,b)\right\} \quad \text {for all }x\in S. \end{aligned}$$

A CQDF-relation $\Psi$ on S is called equivalence relation if

• (i) $\Psi (a,a)=1$ for all $a\in S$ (reflexive); 

• (ii) $\Psi (a,b)=\Psi (b,a)$ for all $a,b\in S$ (symmetric); 

• (iii) $\Psi \circ \Psi \le \Psi$ (transitive), and it is called left (right) compatible if for all $a,b\in S,$

  $$\begin{aligned} \Psi (xa,xb)\ge \Psi (a,b)\ (\Psi (ax,bx)\ge \Psi (a,b)). \end{aligned}$$

Compatible if,

$$\begin{aligned} \Psi (a,b)\wedge \Psi (c,d)\le \Psi (ab,cd)\quad \text {for all } a,b,c,d\in S. \end{aligned}$$

A CQDF-equivalence relation on S is called congruence if it is compatible.

Optimizing the transportation of agricultural products

In the heart of agricultural regions, the challenge of transporting fresh produce from farms to bustling marketplaces is of supreme importance. The loading methods employed in this crucial process significantly influence not only delivery schedules but also the financial viability of the entire agricultural sector. Choosing the appropriate loading method is a complex decision, dependent on factors such as crop type, vehicle capacity, and accessibility. To have an overview of this, three loading methods are currently being explored, each demonstrating distinct advantages and limitations.

• Method A: Precision Loading with Automation

  Consider a scenario where a farm harvests delicate fruits such as strawberries. Precision Loading with Automation proves invaluable here. Advanced sensors and precision controls meticulously load these fragile fruits onto vehicles. For instance, automated arms gently pick strawberries one by one, ensuring minimal bruising and damage during loading. While this method excels in delicate handling, achieving this precision demands meticulous alignment between the vehicle and the loading system. Consequently, the process can be time-consuming, particularly for large-scale shipments.

• Method B: Conveyor Belt System

  In the context of transporting bulk items like potatoes, the Conveyor Belt System showcases its efficiency. Conveyor belts, seamlessly integrated into the infrastructure of a farm, steadily move the potatoes from storage to awaiting trucks. This continuous loading method ensures a swift and continuous flow of produce, optimizing the loading time significantly. However, the automated nature of the process might not be suitable for fragile crops such as tomatoes, as the rapid movement might cause damage during transit.

• Method C: Forklift-Based Loading

  Imagine a farm where a diverse array of produce, including crates of vegetables and bulk items like pumpkins, need to be loaded. Forklift-Based Loading proves indispensable in this scenario. Forklift operators skillfully maneuver through tight spaces, swiftly loading crates onto trucks. The flexibility of forklifts enables the efficient handling of various agricultural products, making them suitable for farms and marketplaces with limited accessibility. However, this method, reliant on manual labor, might require more time and effort, potentially impacting the overall loading duration.

In addressing this decision-making challenge, the goal is to explore the interactions between these loading methods in terms of sequences and combinations, employing an abstract algebraic approach incorporating CQDFS. For example, the order of loading methods, such as starting with precision loading with automation followed by forklift-based loading, may yield different outcomes compared to the reverse sequence or incorporating the conveyor belt system. This analysis results in a total of nine distinct combinations. Utilizing a thorough evaluation approach, the aim is to enable informed decision-making, ensuring that the chosen methods precisely align with the distinct requirements and constraints associated with each cargo shipment. This strategic alignment ultimately contributes to enhanced operational outcomes within the agricultural transportation sector.

An evaluation matrix is created, denoted as a, b, and c, representing Methods A, B, and C, respectively. The aim is to establish a specialized loading structure that ensures chaining interactions between these methods in the framework of CQDF-congruences induced by AG-groupoids. This chaining is crucial as the efficiency of loading operations varies depending on the sequence in which methods are employed.

Let us consider a set $S=\{a,b,c\}$ under a binary operation “$\cdot$” given as follows:

Define a function $\vartheta$ that takes two methods as inputs and produces a complex number along with a probability distribution. The complex number represents the observed performance of different loading method pairs. They assign specific values to $\vartheta$ for each pair of methods based on their observations and measurements. Let us define $\vartheta :S\times S\rightarrow [0,1]$ as follows.

$$\begin{aligned}{} & {} \vartheta (x,y)\\{} & {} \quad =\left\{ \begin{array}{llll} ( ( 1\text {e}^{i(1)},0\text {e}^{i(0)}) ,(0.6,0.4,0) ) :(x,y)=(a,a) \\ ( ( 1\text {e}^{i(1)},0.2\text {e}^{i(0.5)}) ,(0.6,0.3,0.1) ) :(x,y)=(a,b) \\ ( ( 0.8\text {e}^{i(0.7)},0.6\text {e}^{i(0.1)}) , ((0.5,0.2,0.3) ) :(x,y)=(a,c) \\ ( (0.9\text {e}^{i(0.7)},0.1\text {e}^{i(0.2)}) , ( 0.3,0.6,0.1) ) :(x,y)=(b,a) \\ ( (1\text {e}^{i(1)},0\text {e}^{i(0)}) ,( 0.5,0.5,0) ) :(x,y)=(b,b) \\ ( ( 0.4\text {e}^{i(0.6)},0.7\text {e}^{i(0.6)}) , ( 0.1,0.2,0.6) ) :(x,y)=(b,c) \\ ( ( 0.9\text {e}^{i(0.6)},0.4\text {e}^{i(0.3)}) , ( 0.2,0.5,0.3) ) :(x,y)=(c,a) \\ ( ( 0.5\text {e}^{i(0.5)},0.8\text {e}^{i(0.4)}) , ( 0.2,0.1,0.7) ) :(x,y)=(c,b) \\ ( ( 1\text {e}^{i(1)},0\text {e}^{i(0)}) ,( 0.2,0.8,0) ) :(x,y)=(c,c). \end{array}\right. \end{aligned}$$

It can be easily verified that $\vartheta$ is CQDFS. Now, the engineers can calculate the score for each alternative based on the given parameters. The score ranges from $-1$ to 1, with 1 indicating the highest score. The score function of $\vartheta$, given by $\Psi$ is given as follows:

$$\begin{aligned} \Psi (a,b)=\left\{ \begin{array}{ll} 1&{}\quad \text {if }(x,y)=(a,a) \\ 0.7&{}\quad \text {if }(x,y)=(a,b) \\ 0.4&{}\quad \text {if }(x,y)=(a,c) \\ 0.7&{}\quad \text {if }(x,y)=(b,a) \\ 1&{}\quad \text {if }(x,y)=(b,b) \\ -0.2&{}\quad \text {if }(x,y)=(b,c) \\ 0.4&{}\quad \text {if }(x,y)=(c,a) \\ -0.2&{}\quad \text {if }(x,y)=(c,b) \\ 1&{}\quad \text {if }(x,y)=(c,c). \end{array} \right. \end{aligned}$$

It can be verified that $\Psi$ is a congruence relation on S.

Based on the scores (accuracies), the engineers rank the alternatives in order of preference. The alternative with the highest score (accuracy) is considered the most favorable, followed by the alternatives with lower scores (accuracies). The following table will give us the score (accuracy) for each alternative based on the given parameters:

The positions of the alternatives based on the above score (accuracy) can be seen as follows:

The loading approach, wherein the same method is applied repeatedly, is considered trivial due to its inherent property within CQDF-congruences, which does not offer substantial information for ranking purposes. Consequently, the focus lies in exploring combinations of methods where each method employed is distinct, avoiding repetitions, to gain meaningful insights. It is found that the alternatives are ranked as follows (also see Fig. 4) for loading operations:

• 1st: with method a first and then with method b.

• 2nd: with method b first and then with method a.

• 3rd: with method a first and then with method c and vice versa.

• 4th: with method b first and then with method c and vice versa.

Fig. 4

Visualization for loading methods rankings

The scoring system $\Psi$ takes these interactions into account, providing insights into the effectiveness of different loading method pairs based on real-world observations. This evaluation ensures that the harbor’s cargo loading operations are optimized, contributing to economic efficiency and the smooth flow of goods in and out of the harbor. Based on these rankings, one can make an informed decision about which method(s) to choose for loading operations based on performance measurements provided by the function $\vartheta$. Figure 5 displays a heat map illustrating the rankings of different methods. The color spectrum used in this representation spans from blue, representing a zero ranking, to yellow, signifying a fourth ranking. This graphical representation provides a visually intuitive way to understand the hierarchical placement of the methods being examined, with each color indicating a distinct level of ranking achievement.

Fig. 5

Heat map of loading methods rankings

The aforementioned decision-making problem provides a clear and well-structured set of preferences for loading cargo using various methods. These preferences play a crucial role in guiding the choices and ensuring efficiency in cargo loading operations. At the highest level of priority is “Method A” followed by “Method B”. The 1st priority preference (a, b) signifies that these methods are the top choices for loading cargo. This preference emphasizes their superior efficiency, reliability, or other advantages, making them the primary options to consider. The preference hierarchy outlined in this decision-making problem provides valuable guidance for cargo loading operations. It allows decision-makers to make informed choices based on the specific circumstances and constraints of each situation, ensuring the most efficient and effective approach to cargo handling.

Comparative analysis

In this section, a comprehensive comparative analysis is undertaken to assess the advantages and characteristics of the CQDFS model, as introduced within this research, in contrast to established techniques. The resulting comparative assessment is outlined in Fig. 6, where a thorough investigation is carried out to clarify the features of the CQDFS model with various extensions of complex fuzzy sets. The complex quadratic Diophantine fuzzy set’s superiority lies in its ability to handle a wide range of uncertain information by considering the simultaneous consideration of hesitancy and parameters. This makes it a valuable tool across multiple domains where the management of imprecise and uncertain data constitutes a common challenge.

Fig. 6

Comparison of CQDFS with existing extensions of fuzzy sets

Figure 6 presents a detailed illustration that highlights the distinctive attributes of various fuzzy sets. The chosen color scheme serves to differentiate the presence and absence of characteristics, with green indicating the presence and red signifying the absence of these attributes. The observed patterns underscore the diverse capabilities inherent in different extensions of fuzzy sets, particularly in their ability to manage various types of information.

Specifically, it is evident that CFS exclusively handles information categorized as acceptance type. In contrast, CIFS, CPyFS, and Cq-ROFS demonstrate a more encompassing nature, allowing them to consider both acceptance and rejection types of information. CPFS further extends its applicability by accommodating information characterized by an ignorance type. Despite these advancements, it is noteworthy that all these extensions introduce certain constraints on membership and non-membership functions. An exception to this general trend is CLDFS, which distinguishes itself by eliminating these restrictions through the imposition of parameterization. However, it is essential to acknowledge that while CLDFS exhibits this enhanced flexibility, it faces limitations in effectively handling information characterized by ignorance types. This nuanced analysis underscores the intricate trade-offs and capabilities associated with each fuzzy set extension, providing insights into their respective strengths and limitations in processing diverse forms of information.

The CQDFS method proposed in this study provides a higher degree of flexibility and autonomy in handling fuzzy information.

The provided table offers a comprehensive overview of the ranking comparisons involving the proposed CQDFS. A notable observation is that CFS shares the same ranking as CQDFS, indicating a degree of similarity in their performance. Interestingly, CLDFS exhibits identical rankings at both the first and last positions when compared to CQDFS, suggesting some congruence in their outcomes.

However, the ranking comparisons for CIFS, CPyFS, and Cq-ROFS are not feasible due to their limited feasible space. Specifically, the given preference $(a,b) = (1\text {e}^{i(1)},0.2\text {e}^{i(0.5)}),(0.6,0.3,0.1)$ falls outside the domains of these methods. Consequently, a direct comparison of rankings cannot be conducted for these fuzzy set extensions, highlighting a constraint in their applicability to the specified preference values.

Conclusion

This study introduces the concept of CQDFS with a specific focus on addressing challenges related to uncertainty and ambiguity in decision-making. CQDFS incorporates membership, non-membership, and hesitating values innovatively, establishing a flexible framework for decision-makers to effectively navigate complex and uncertain scenarios. The versatility of CQDFS becomes apparent through its comprehensive consideration of various aspects of uncertainty, providing decision-makers with a robust tool for managing complexity. Through a detailed comparative analysis, the study demonstrates the superior flexibility and autonomy of CQDFS compared to existing fuzzy set extensions. This comparative assessment underscores the unique capabilities of CQDFS, positioning it as an advanced and reliable solution for decision-makers dealing with intricate decision environments. It is crucial to note certain limitations within the algorithm. The potential for extension to consider big data enhances its applicability to large-scale data sets. Moreover, the algorithm’s adaptability to attributes through the incorporation of weights contributes to enhanced precision in decision-making scenarios. The practical implications of these findings extend beyond theoretical advancements, especially in the context of enhancing economic sustainability within the transportation industry. Looking ahead, there is promising potential for further exploration of CQDFS applications and a comprehensive evaluation of its effectiveness across diverse domains. Future research endeavors could delve into its utility in analyzing extensive data sets in finance and economics, as well as in assessing the capabilities of large language models in artificial intelligence. Furthermore, the integration of modern algebra within the CQDFS framework presents exciting possibilities for expanding research scope and facilitating practical implementations in these evolving fields.