The fuzzy support vector data description based on tightness for noisy label detection

Abstract

Machine learning (ML) is an approach driven by data, and as research in machine learning progresses, the issue of noisy labels has garnered widespread attention. Noisy labels can significantly reduce the accuracy of supervised classification models, making it important to address this problem. Therefore, it is a very meaningful task to detect as many noisy labels as possible from the big data. In this study, a new method is proposed for detecting noisy labels in datasets. This method leverages a deep pre-trained network to extract a feature set from the image data first which can extract more accurate data features. Then, a membership degree based on tightness into the support vector data description (SVDD) model named TF-SVDD is introduced to detect noisy data in the dataset. In order to simulate different types of label noise more accurately, we first assumed that the labels of the datasets used were all correct, and in addition constructed the noise set using two method: the density peak noise set and the random noise set. Experimental results demonstrate that the TF-SVDD can effectively detect noisy label data, surpassing traditional support vector data description algorithms and other methods in terms of outlier detection accuracy, with the average accuracy mostly exceeding 50$\%$, and even reaching 80$\%$. Furthermore, one novel measure called ‘confidence’ is employed to rectify noisy labels in the data. Following the correction of noisy labels, the accuracy of image classification experiences a significant improvement, with the average promotion ratio mostly exceeding 10$\%$, and reaching 30$\%$.

Introduction

In real-world applications, the existence of noisy labels can present a significant challenge to achieving accurate supervised classification [1,2,3]. Noisy supervision may arise from multiple sources, including non-expert annotators or automatic labeling, collecting accurate datasets is time consuming and expensive. However, the success of deep neural networks in recent years is partly attributed to their capacity to leverage clean and extensive dataset [4]. To address this challenge, detecting noisy labels is crucial in Supervised Learning (SL) [5]. During model training, some critical labels, specifically noisy labels, significantly impact the model’s performance [6], while others may not. One approach to mitigate the adverse impact of these disruptive labels is noise modeling, which involves representing the fundamental noise process. In Ref [7], the expected error of a noise model estimated from pairs of clean and noisy labels was derived, highlighting factors such as noise distribution and sampling technique.

With the rapid development of deep learning, researchers have proposed different techniques to tackle the problem of noisy labels in training samples. For instance, Fazekax et al. [8] utilized ensembles of established noise correction methods to pre-process the training set. Zheng et al. [9] provided a theoretical explanation for data-re-calibrating methods and propose a label-correction algorithm. This is especially significant as deep neural networks have a propensity for strong memorization power [10, 11].

Various methods have been proposed to address noisy labels in training samples, some of these methods aim to improve the quality of the dataset by removing noisy labels to obtain a cleaner dataset. For instance, Wu et al. [12] proposed the topofilter method to delete noise data in the largest connected component of each class, where data is filtered by flapping features, and a label-correction model is further proposed to correct misclassified labels. Moreover, the nearest neighbor-based filtering method is a prevalent approach for noise reduction, typically implemented through the K-NN classifier. However, in contrast to noise filtering techniques, our method is designed to identify as many instances of noisy labeled data as feasible, rather than eliminating all anomalous data. This approach avoids the deletion of potentially important data. Tu et al. [13,14,15,16] combined superpixel-to-pixel weighting distance and density peak clustering to detect and remove noisy labels in the training set before classification. Noisy label detection often involves the use of multi-class classification algorithms [17, 18]. However, when the dataset is unbalanced, One-Class Classification (OCC) becomes particularly important [19, 20]. In this investigation, the utilization of SVDD as a data descriptor is employed to identify outliers within the dataset. The applications of SVDD are diverse and extensive, for example, anomaly detection [21], image classification [22], and fault diagnosis [23]. Although the SVDD model can find the description boundary that suits the dataset [24], it ignores the distribution of data. Several improved SVDD methods have been proposed that focus on disregarding data structure using different concepts. For instance, Wu et al. [25] introduced MR-SVDD, which combines the SVDD model with manifold regularization to detect noisy labels. Furthermore, DW-SVDD [26] is an improved SVDD method that utilizes a density weight based on k-NN to enhance the penalty for misclassifying dense data. In addition, Jiang et al. [27] presented a second map support vector data description (SM-SVDD) method, utilizing an anomalous and close surface instead of a hypesphere to describe the target data. Despite its widespread use for outlier detection, the SVDD model has a major drawback in that it disregards the data’s distribution, which can lead to inaccuracy in outlier detection. To address this limitation, we propose a novel method to enhance SVDD by incorporating a fuzzy membership degree as a weight, which considers the distribution of data. By integrating the fuzzy membership degree, the proposed method can more effectively differentiate noisy label from data, leading to more accurate noisy detection.

Another approach for addressing noisy labels involves using a noise classifier to predict data labels, followed by label correction [32]. In addition, some studies have combined the use of fuzzy membership degree as a weight to identify noise data [33, 34]. When training samples contain noisy labels, these samples often contain “abnormal” information that resides near the classification surface in the feature space. Consequently, the resulting classification surface may not represent the optimal classification boundary. Color image possess intricate and diverse characteristics, making them susceptible to noise influence and non-uniformity. To solve this problem, numerous researchers have dedicated themselves to integrating fuzzy set theory into image processing and recognition technology. Lin et al. [35] proposed the Fuzzy Support Vector Machine (FSVM) method, leveraging fuzzy technology to analyze different samples. The application of fuzzy rough set techniques is widespread. For instance, Kaminska et al. [36] applied fuzzy rough nearest neighbor methods for detecting emotions, hate speech, and irony. In addition, Qi et al. [37] proposed the fuzzy covering-based rough set for decision-making. Fuzzy theory has yielded significant achievements in the realm of machine learning. For instance, in chaotic time series prediction, the fuzzy neural network is employed to capture the dynamic behavior of chaotic time series and forecast long-term values [28]. Moreover, following the recent COVID-19 outbreak, the fuzzy neural network has been utilized to predict the number of cases [29]. In addition, the T-S fuzzy neural network finds widespread application in various domains, such as short-term traffic flow [30] and water quality assessment [31].

Fig. 1

The detailed process of TF-SVDD. After extracting the image features through the ResNet-18 network, the two noise sets are added to the dataset separately to be detected using the TF-SVDD algorithm and finally corrected using the confidence function

Recently, a variety of methodologies are available for the construction of membership functions, although there is no universally accepted standard to follow. Numerous researchers have delved into this field, primarily concentrating on quantifying membership extent through the assessment of the distance between the sample and the class. Assessing the degree of membership for a sample solely based on distance poses a challenge in distinguishing samples with noise or outliers from the valid sample set. This challenge stems from the oversight of considering the interrelationship between samples when determining membership solely on the basis distance from the class center. Consequently, only the distance itself is taken into consideration. Hence, in determining the membership degree of a sample, it is crucial to consider not only the distance between the sample and the class center but also the cohesion among the samples within the class. In light of this, a method of fuzzy support vector data description based on cohesion is formulated.

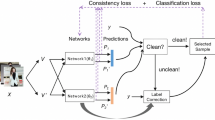
In order to implement our proposed method, a pre-trained network is utilized to extract the features from the color image dataset. There are various methods for feature extraction from images, including the method proposed by Kumar et al. [38, 39], which employed GPS for reconstructing 3D models to acquire more accurate city structure data, specifically for 3D data. However, for the purpose of label noise detection in this study, only images are utilized, hence the ResNet-18 network is utilized for feature extraction. Subsequently, the density peak algorithm is applied to identify nodes with higher density to establish the initial noise set. Finally, the tightness membership degree is introduced as the weight and integrated into the SVDD algorithm, resulting in the development of the fuzzy SVDD algorithm, which is employed for detecting noise labels in the dataset. The tightness among samples is assessed by measuring the minimum spherical radius surrounding samples within the same class. The detailed process is depicted in Fig. 1.

Contributions The main achievements of this study can be summarized as

• (1) We first adopted the traditional density peak clustering algorithm to construct the initial noise set.

• (2) We introduced a new method that fuzzy SVDD model based on tightness to distinguish noisy samples more accurately.

• (3) New confidence level is proposed to correct the noisy labels.

The rest of this paper is provided as follows. “Related work” describes the traditional SVDD model and SVM model. “Proposed method” introduces the method of fuzzy SVDD based on the membership degree of tightness to detect noisy labels of dataset. “Experimental results” compares traditional algorithms for noisy labels detection and visualization results. In addition, we correct the noise data detected by the proposed method. “Conclusions” concludes the paper.

Related work

In this section, some relevant knowledge about SVM model and SVDD model are introduced briefly.

Kernel-based one-class classification

Given a training sample set $D = (x_1, y_1), (x_2, y_2), \cdots , (x_m, y_m)$ where $y_i \in \{-1, +1\}$, the fundamental concept of classification learning is to find a partition hyperplane in the sample space based on the training set D and divide samples of different classes. In the sample space, the partition hyperplane can be described by the following linear equation:

$$\begin{aligned} \varvec{\omega ^T}x + b = 0, \end{aligned}$$

(1)

where $\varvec{\omega } = ( \omega _1, \omega _2, \cdots , \omega _d)$ is the normal vector, b is the displacement term. One of the most well-known kernel-based methods for one-class classification is the One-Class SVM (OC-SVM) [43]. The primary goal of OC-SVM is to identify a hyperplane with the maximum margin in the feature space. The optimization problem of OC-SVM is formulated as

$$\begin{aligned} \begin{aligned} {Min}&\quad \frac{\left\| \varvec{\omega }\right\| }{2}^{2} +C \sum _{i=1}^{l} \xi _{i}\\ s.t.&\quad y_i(\varvec{\omega ^T}x_i + b )\ge 1- \xi _i, \\&\quad \xi _i \ge 0, i=1,2 \cdots l. \end{aligned} \end{aligned}$$

(2)

where C is penalty parameter and $\xi _i$ are slack variables to relax the constraints.

The SVDD model was initially proposed by Tax [44] in 1999. SVDD is a minimum enclosing ball optimization problem. To describe data ($x_{i}$, $y_{i}$), a hyper sphere with Radius R and Center a encloses the interested class. Due to the presence of non-linearly divisible data, certain targets are excluded when forming a small hypersphere. The optimization problem is formulated as

$$\begin{aligned} \begin{aligned} \quad {Min}&\quad R^{2}+C \sum _{i=1}^{l} \xi _{i} \\ s.t.&\quad \left\| \Phi \left( x_{i}\right) -a\right\| ^{2} \le R^{2}+\xi _{i},\\&\quad \xi _{i} \ge 0, i=1,2 \ldots l, \end{aligned} \end{aligned}$$

(3)

where $\left\| \cdot \right\|$ means Euclidean norm, $\Phi (x_i)$ maps point $x_i$ from data space into the kernel space, R is the radius of the hypersphere, and a is the center of the hypersphere.

Both OC-SVM and SVDD are one-class classifiers and are very related. Both methods can be employed to detect outliers. While SVM distinguishes between positive and negative examples by finding the hyperplane with the maximum margin, SVDD trains a hypersphere to encapsulate the dataset. SVDD can be utilized to encapsulate multiple categories of data by category with hypersphere, which can more accurately detect outliers of each class of data. In this paper, the application of the SVDD model is utilized for identifying noisy labels and add membership degrees based on the tightness of the hypersphere, facilitating more accurate detection of outliers for each class of data.

Fuzzy SVM

Lin et al. [35] proposed a fuzzy support vector machine (FSVM) method to enhance the SVM by reducing the impact of outliers and noise in data.

Given a set of labeled training points with associated fuzzy membership

$$\begin{aligned} (y_1, x_1, s_1),(y_2, x_2, s_2),\ldots , (y_l, x_l, s_l) \end{aligned}$$

(4)

where $x_i\in R^N$, $y_i\in \{-1, 1\}$, $s_i$ is fuzzy membership and $\sigma \le s_i \le 1$ with $\sigma \ge 0$. The optimization problem is constructed as

$$\begin{aligned} \begin{aligned} {Min}&\quad \frac{\left\| \varvec{\omega }\right\| }{2}^{2} +C \sum _{i=1}^{l} s_i\xi _{i}\\ s.t.&\quad y_i(\varvec{\omega ^T}x_i + b )\ge 1- \xi _i, \\&\quad \xi _i \ge 0, i=1,2 \cdots l. \end{aligned} \end{aligned}$$

(5)

The FSVM method applies fuzzy membership into each input point of SVM, utilizing distinct penalty weight coefficients for different samples to construct the objective function. By assigning smaller weights to samples containing noise or outliers, their influence can be eliminated. This strategy permits varying samples to make differing contributions, thus enhancing the precision the SVM.

Proposed method

Motivations

In the support vector data description model, the optimal classification surface is mainly determined by support vectors, which are located at the edge of the class. Outlier or noisy samples often reside near the edge of the class, potentially impacting the precision of sample membership determination. Failure to differentiate normal samples from outliers or noisy samples may lead to a suboptimal classification surface. To tackle this challenge, various SVDD variants have been developed, such as density-weighted [26] and automatic support vector data description (ASVDD) based on validation degree [33]. However, the fuzzy support vector data description method introduces a membership function that can objectively and accurately reflect the uncertainty of the system. The design of the membership function is crucial and should consider both the distance between the sample and the class center, and the closeness between the samples in the class. Furthermore, the training data collected by the neural network is enclosed within a sphere or hypersphere using the SVDD model, enabling more accurate detection of noisy data. In contrast to the noise filtering method [12], identifying noisy label data allows for the retention of as many instances of label noise as possible, thus averting inadvertent removal potentially significant data.

Initial training set generation

In this section, two methods are introduced for constructing noise sets. Due to the various types of noise, a range of methods is employed to simulate as many noise types as possible. Considering the random occurrence of noise labels, the first method involves randomly selecting a portion of the data as noise. In addition, considering the label noise of some important and difficult noisy labels, the second method is based on the density peak algorithm, which is a clustering algorithm proposed in Science in 2014 [45]. This algorithm can automatically discover cluster centers and efficiently cluster data of arbitrary shapes. Inspired by the density peak clustering algorithm [45,46,47], we contemplate its use in constructing the initial noise set. The instance density, as defined in Ref. [45], is used to determine the initial noise set:

$$\begin{aligned} \rho (x_{i}) = \sum _{j\in [1..n],i\ne j} e^{-(dist(x_{i},x_{j}))^2/d_c}, \end{aligned}$$

(6)

where $d_c$ is the cutoff distance. Then, $\delta (x_i)$ is measured by computing the minimum distance

$$\begin{aligned} \delta (x_i)=\left\{ \begin{array}{cc} max_{j\in [1, \dots ,n]} dist(x_{i},x_{j}),~~~~\rho (x_{i})\quad \textrm{is}\quad \textrm{maximal}~~\\ min_{j: \rho (x_{i})>\rho (x_{j})} dist(x_{i},x_{j}), ~ \textrm{otherwise}.~~~~~~~~~~~~~~ \end{array} \right. \end{aligned}$$

(7)

The instance significance is given by [47]

$$\begin{aligned} \gamma (x_i) = \rho (x_i) \cdot \delta (x_i). \end{aligned}$$

(8)

Fig. 2

The illustration of distance between points

Feature selection

In this paper, the ResNet-18 network is utilized to extract image features. ResNet is renowned for its efficacy in image feature extraction. Currently, there are many feature acquisition methods based on deep learning. For example, in Ref. [40], Juan et al. uses MResNet modules to extract input features, yielding commendable outcomes. In Ref. [41], deep learning can be considered a promising method for accelerating and automating the modeling of climate functions. In addition, Ahmed Ali et al. [42] investigated DeepHAR-Net, through a strategic fusion of convolutional neural networks and Long Short-Term Memory networks, coupled with tailored data augmentation. The comprehensive exploration of benchmark datasets showcased DeepHAR-Net’s prowess in capturing intricate spatial and temporal patterns inherent in diverse human activities. However, deeper is not always better. Experiments have shown that the model’s accuracy initially increases and then decreases with the increase in network depth. Therefore, employing ResNet-18 proves to be advantageous. The convolution layer at the beginning of the network captures local and detailed information of the image and has a relatively small receptive field. Progressing deeper into the network, the convolutional layers boast a larger receptive field, enabling the capture of more intricate and abstract image information. Iteratively passing the image through these convolutional layers yields abstract representations of the image at varying scales. Consequently, leveraging convolutional neural networks for image feature extraction facilitates the acquisition of precise data information.

Fuzzy membership

In the SVDD method, the optimal classification surface is primarily determined by the support vector, which is situated at the class boundary. However, samples with noise are often located near the edge of the class. If effective samples are treated identically to noisy samples when determining the membership of the samples, the resultant classification surface is not optimal. Therefore, in the construction of the fuzzy SVDD method, the design of the membership function is crucial. The membership function must objectively and accurately reflect the uncertainty of the system. Generally, the fundamental principle underlying the determination of membership size is founded on the significance of the sample’s class or its contribution to the corresponding class. One of the criteria for evaluating a sample’s contribution to a class is by measuring its distance from the class center.

Currently, there are numerous approaches to constructing membership functions. In this paper, the membership function is utilized to represent the distance between a sample point and its corresponding class center, as shown in Fig. 2. In both Fig. 2a and b, the distances between the sample x and their respective class centers are equivalent. If membership is solely predicated on distance, then both samples would possess identical membership within their respective classes. However, this does not consider the fact that in (a), the distance between sample x and other samples in the class is much smaller compared to (b), where the distance between sample x and other samples in the class is larger. This situation suggests that sample x in (a) is likely to be a valid sample, while sample x in (b) is highly likely to be an outlier. In fact, the membership of sample x in its respective class should be higher in (a) than in (b). Therefore, when determining the membership of a sample, we need to consider not only the distance between the sample and the class center, but also the distance between the sample and other samples in the class. The distance between the sample and other samples in the class can reflect the compactness of the samples in the class.

Let $O_p$ and $O_n$ denote the centers of the positive sample group $G_p$ and negative sample group $G_n$, respectively. The distance between a sample point and its respective class center is given by

$$\begin{aligned} \left\{ \begin{array}{cc} d_p = max \left\| o_p - x_i \right\| , \quad x_i\in G_p; \\ d_n = max \left\| o_n - x_i \right\| , \quad x_i\in G_n. \end{array} \right. \end{aligned}$$

(9)

The distance fuzzy membership degree is defined as [48]

$$\begin{aligned} s_i =\left\{ \begin{array}{cc} &{} 1-\frac{\left\| o_p - x_i \right\| }{d_p+\delta };\\ &{} 1-\frac{\left\| o_n - x_i \right\| }{d_n+\delta }, \end{array} \right. \end{aligned}$$

(10)

where $\delta$ is an arbitrarily small positive number. The distance between points is determined using the k-nearest neighbor approach, which serves as the basis for our methodology [49]

$$\begin{aligned} \left\{ \begin{array}{cc} \begin{aligned} d_{ij}&{}=\frac{1}{k}\sum _{j=1, \dots , l}\left\| x_i - x_j \right\| , \\ d_{i1}&{}\le d_{i2} \dots \le d_{i(l-2)} \le d_{i(l-1)}. \end{aligned} \end{array} \right. \end{aligned}$$

(11)

The tightness of the sample is given by

$$\begin{aligned} \left\{ \begin{array}{cc} \begin{aligned} b_{i}&{}=\frac{1}{d_{ij}} \\ B &{}= max \{b_1, b_2, \cdots , b_l\} \end{aligned} \end{array} \right. \end{aligned}$$

(12)

The fuzzy membership degree is defined as

$$\begin{aligned} \mu _i =\left\{ \begin{array}{cc} 1-\alpha \frac{\left\| o_p - x_i \right\| }{d_p+\delta }-(1-\alpha )\frac{D_p}{B+\delta };\\ 1-\alpha \frac{\left\| o_n - x_i \right\| }{d_n+\delta }-(1-\alpha )\frac{D_n}{B+\delta }, \end{array} \right. \end{aligned}$$

(13)

where $\alpha \in [0,1]$.

Fuzzy SVDD based on the membership degree of tightness

Since the membership degree represents the degree of certainty that a sample belongs to a particular class, the classification error term in the objective function of the support vector machine is penalized. The optimal solution for the objective function below gives the optimal classification surface for the compact-based fuzzy support vector machine:

$$\begin{aligned} \begin{aligned} {Min}&\quad R^{2}+C \sum _{i=1}^{l}\mu _i\xi _{i}\\ s.t.&\quad \left\| \Phi \left( x_{i}; \varvec{\omega }\right) -a\right\| ^{2} \le R^{2}+\xi _{i}, \\&\quad \xi _{i} \ge 0, i=1,2 \cdots l. \end{aligned} \end{aligned}$$

(14)

The optimization function used in this paper is the fuzzy SVDD model, where $\mu _i$ represents the membership degree function.

For Eq. (14), we have

$$\begin{aligned} max(0, \left\| \Phi \left( x_{i}; \varvec{\omega }\right) -a\right\| ^{2}-R^{2}) = \xi _{i}, \end{aligned}$$

(15)

Obviously, $\xi _{i} \ge 0$. When $\left\| \Phi \left( x_{i}; \varvec{\omega }\right) -a\right\| ^{2}-R^{2} \ge 0$, we have

$$\begin{aligned} \left\| \Phi \left( x_{i}; \varvec{\omega }\right) -a\right\| ^{2}-R^{2} = \xi _{i}, \end{aligned}$$

(16)

When $\left\| \Phi \left( x_{i}; \varvec{\omega }\right) -a\right\| ^{2}-R^{2} \le 0$, we have

$$\begin{aligned} \xi _{i} = 0, \end{aligned}$$

(17)

Therefore, $\left\| \Phi \left( x_{i}; \varvec{\omega }\right) -a\right\| ^{2} \le R^{2}+\xi _{i}.$

The kernel matrix, denoted by ${\mathcal {K}}$, is calculated based on the Gaussian kernel function as follows:

$$\begin{aligned} {\mathcal {K}}\left( x_{i}, \textrm{x}\right) =\exp \left( -\frac{\left\| x_{i}-x\right\| ^{2}}{2 \sigma ^{2}}\right) , \end{aligned}$$

(18)

where the constant parameter $\sigma$ that determines its strength.

Equation (14) is a non-convex function. To address this issue, a strategy is suggested that we know $\left\| \Phi \left( x_{i}; \varvec{\omega }\right) -a\right\| ^{2} - R^{2} - \xi _{i}$ is a convex function for R. Therefore, we replace $R^{2}$ with $R^{'}$, transform Problem Eq. (14) into a convex function, and construct a Lagrange function shown as follows:

$$\begin{aligned} {\mathcal {L}}= & {} R^{'}+C \sum _{i=1}^{l+u}\mu _i \xi _{i} -\sum _{i=1}^{l+u} \alpha _{i}\left( R^{2}+\xi _{i}\right. \nonumber \\{} & {} \left. -\left\| \Phi \left( x_{i}; \varvec{\omega }\right) -a\right\| ^{2}\right) -\sum _{i=1}^{l+u} \beta _{i} \xi _{i}, \end{aligned}$$

(19)

Then, Eq. (19) is converted to

$$\begin{aligned} \begin{aligned} \frac{\partial {\mathcal {L}}}{\partial R}&=0 \rightarrow \sum _{i=1}^{l+u} \alpha _{i}=1,\\ \frac{\partial {\mathcal {L}}}{\partial a}&=0 \rightarrow a=\sum _{i=1}^{l+u} \alpha _{i} \Phi \left( x_{i}\right) , \\ \frac{\partial {\mathcal {L}}}{\partial \xi _{i}}&=0 \rightarrow \mu _i\textrm{C}=\sum _{i=1}^{l+u} \alpha _{i}+\sum _{i=1}^{l+u} \beta _{i}, \end{aligned} \end{aligned}$$

(20)

By replacing of Eq. (20), a form of Eq. (14) is constructed in the form of Eq. (21):

$$\begin{aligned} \begin{aligned} Max&\quad \sum _{i=1}^{l} \alpha _{i} {\mathcal {K}}\left( x_{i}, x_{i}\right) -\sum _{i=1}^{l} \sum _{j=1}^{l} \alpha _{i} \alpha _{j} {\mathcal {K}}\left( x_{i}, x_{j}\right) , \\ s.t.&\quad \sum _{i=1}^{l} \alpha _{i}=1,\\&\quad 0 < \alpha _{i}\le C\cdot \mu _i. \end{aligned} \end{aligned}$$

(21)

According to Eq. (21), two categories of support vectors exist: those satisfying $0< \alpha _{i} < C\cdot \mu _i$ lie near the spherical classification surface; The other satisfies $\alpha _i = C\cdot \mu _i$ support vector for misclassified samples.

Noisy label corrections with confidence degree

In the previous section, SVDD with fuzzy membership was utilized to detect label noise in the data. In this section, the task is to ascertain the appropriate label when a detected label is erroneous. Taking inspiration from [50], it is proposed to correct the noisy label based on the confidence level. First, the average value $e_i$ of all features of $x_{i}$ is calculated. Next, the expectation $\mu _j$ of all data for each class is calculated, and finally, the mean value of the detected noise data is compared with the expectation of all other classes. When $x_i$ has high confidence in the label $y_i$, there is a greater likelihood that $y_i$ is correct. As a result, a ‘confidence’ metric is introduced to evaluate the probability of any data being associated with the corresponding class:

$$\begin{aligned} e_i - \mu _j \ge \delta \sigma _j. \end{aligned}$$

(22)

where $\sigma _j$, for $j=1,\ldots , n$, is the standard deviation of all the values $e_i$, for $i=1,\ldots , l$, see Sec. 4.3.3 for choosing the proper parameter $\delta$ for experiments in this work.

Algorithm1 shows the details of TF-SVDD.

Experimental results

Datasets descriptions

Three color image datasets, namely cats and dogs, fruits, and dishware, were selected to evaluate the proposed algorithm. To identify outliers, one class from each dataset was designated as the target class, and data points from the other class were considered potential outliers. For the cats and dogs datasets, 80$\%$ of each class was allocated as training data and 20$\%$ as test data. as show in Table 1. For the Fruits dataset, 207 instances of each class of data were used as training data and 23 as test data, as show in Table 1. Finally, 20$\%$, 40$\%$, and 60$\%$ random noise and density noise were added to each class in the dataset.

Table 1 The employed three experiment datasets

Experiment setup

In this experiment, two types of noise sets are utilized to evaluate the proposed algorithm. Initially, the training dataset is divided into distinct subsets based on different categories, and noise sets of 20$\%$, 40$\%$, and 60$\%$ are subsequently introduced. The proposed algorithm is then applied to detect noisy labels from the training labels. Following this, the Average Accuracy of SVDD, ASVDD [33], SM-SVDD [27], and our method is calculated using the color image set. Furthermore, the confidence function is employed to rectify the noise labels detected by the algorithm, and SVM is used to assess the classification accuracy of different categories within the datasets.

Parameters’ settings

We set the gamma and cost parameters at 0.00001 and 0.3, respectively. The experimental environment of this paper is Intel(R) Core(TM) i5-10400 CPU @ 2.90 GHz 8 GB, Windows 11 system. The algorithm is implemented in Matlab language.

Table 2 Detection accuracy of cats and dogs (I)

Table 3 Detection accuracy of cats and dogs (II)

Evaluation criterion

We evaluated the effectiveness of our noisy label detection method by calculating the number of correctly noisy labels that detected by model (FM) and all noise labels that artificially added (AN). Finally, calculate the average accuracy (AA) of each category. Furthermore, partial noise labels are corrected according to Eq. (22) and classified by SVM.

Table 4 Detection accuracy of cats and dogs

Table 5 Detection accuracy of dishware(I)

Noisy label detection

In this section, an empirical evaluation of our proposed method with various datasets is conducted. The accuracy of our proposed method and SVDD in detecting noisy labels is evaluated using an unbalanced dataset of cats and dogs. A noise dataset was created by random selection (Tables 2, 4) and density peak (Table 3). The average accuracy of each class was then compared and the results are presented in Tables 2, 4 and 3.

Then, we evaluated the noisy label detection accuracy of both SVDD and our proposed method using dishware dataset. To create the noisy dataset, we randomly selected (Tables 5, 7) and added density peaks (Table 6). We compare the average accuracy of each class between the two methods, as shown in Tables 5, 6, and 7.

Table 6 Detection accuracy of dishware (II)

We also evaluated the performance of SVDD and our proposed method in detecting noisy labels in the fruits dataset. To introduce noise, we randomly selected Table 8 and added density peaks Table 9. Tabular comparison of the average accuracy for each class is presented in Tables 8 and 9.

Noisy label corrections

In this experiment, we correct the noise data detected in the previous section by Eq. (22). By comparing the expected of $x_i$ with the expectations of other class, we classify the data above $2\sigma$ as other class, the data below $2\sigma$ as the original class. Then, we use SVM to classify and compare, the accuracy as show in Tables 10, 11, 12.

Table 7 Detection accuracy of dishware

Table 8 Detection accuracy of Fruits(I)

Algorithm analysis

With the aim of resolving the issue of noise sensitivity in machine learning, this paper proposes a fuzzy SVDD method based on tightness, termed TF-SVDD. TF-SVDD not only effectively distinguish outlier or noisy samples from valid samples in the dataset, but also assigns their respective membership degrees according to different rules, thereby better reflecting the role of samples in the objective function of fuzzy support vector data description based on tightness. Experimental results show that our algorithm achieves performs well in most cases, and the average detection accuracy is generally above 40$\%$. In addition, after correcting the detected label noise by the novel measure ‘confidence’, the classification accuracy obtained using SVM method is greatly improved. Compared with other traditional fuzzy support vector data description methods, the TF-SVDD method proposed in this paper has better anti-noise performance and classification ability.

The algorithm performs well and has been validated across various datasets. However, our algorithm primarily focuses on noisy labels, and the partitioning of multi-label data restricts the comprehensive identification of noisy nodes. Given that every multi-labeled data point may be identified as a noise node, our algorithm should be better suited for single-labeled data partitioning. In future work, we plan to enhance the algorithm by leveraging deep SVDD. In addition, the algorithm’s limited robustness may be attributed to the composition of the dataset. Moving forward, we aim to explore methods to improve the coherence and reliability of the sampled data.

Table 9 Detection accuracy of Fruits(II)

Table 10 Classification accuracy of cats and dogs

Table 11 Classification accuracy of dishware

Table 12 Classification accuracy of fruits

AUC accuracy comparison

This section shows the Area under the ROC curve(AUC) variation curves of TF-SVDD method and SVDD method respectively after adding 20$\%$, 40$\%$ and 60$\%$ noise labels, as show in Figs. 3, 4, 5. The results indicate that the TF-SVDD method generally outperforms the SVDD method in terms of AUC value.

Results analysis

In our experiment, we evaluated the effectiveness of the proposed algorithm in comparison to SVDD, ASVDD, and SM-SVDD by examining their respective accuracy in detecting noisy labels. Two distinct categories of noise sets, random noise and density peak noise, were added to different classes within each dataset. The results demonstrate the outstanding performance of our proposed algorithm in terms of average detection accuracy. For the cats and dogs dataset, we observed a decline in noise detection accuracy as the ratio of random noise increased. However, the overall accuracy remained above 60$\%$, as shown in Fig. 6a. Conversely, when noise was introduced using density peaks, the detection accuracy decreased rapidly, dropping below 50$\%$ at a noise ratio of 60$\%$. Moreover, we present the spherical center distance plot of the density peak noise set, as shown in Fig. 7. For the dishware data set, we also observed a reduction in noise detection accuracy as the ratio of random and density peak noise increased. However, the overall accuracy remained above 40$\%$, as shown in Fig. 6b. For the fruits dataset, the average detection accuracy on the random noise set basically remained above 50$\%$, and we analyzed a single category due to the large number of categories, as shown in Fig. 8. Due to the poor robustness of the algorithm, the accuracy of the detection results is slightly unstable, and this problem will be further explored in future research. Furthermore, experimental findings indicate that due to the significant impact of noise labels derived from the density peak algorithm, random noise is more readily detected compared to density peak noise. Since our algorithm is designed to target the detection of individual categories within the dataset, it is less affected by data imbalance.

Furthermore, this study employed SVM to classify datasets with varying ratios of noise labels. As the noise ratio increased, the classification accuracy of SVM showed a significant decline. However, following the application of confidence correction, the classification accuracy showed a significant improvement. The classification accuracy of the cats and dogs dataset and the fruits dataset after correction exceeded 90$\%$. Across the three datasets, the classification accuracy improved by an average of 20$\%$, with some even reaching 30$\%$. However, due to the imbalance of the dishware dataset, the improvement in classification accuracy after correction is unstable. Therefore, a relatively large amount of data is required when using the proposed method for label correction. In situations where the dataset is too small, it may be challenging to identify suitable reference values, leading to inaccurate label correction. In our future research, we plan to explore the application of different forms of transformation to address class imbalances in order to create a balanced dataset, thereby minimizing the impact of imbalance.

Fig. 3

The above AUC diagram with 20$\%$ density peak noise set added to the dishware dataset. a The class of cup with TF-SVDD; b the class of cup with SVDD; c the class of bowl with TF-SVDD; d the class of bowl with SVDD; e the class of plate with TF-SVDD; f the class of plate with SVDD

Fig. 4

The above AUC diagram with 40$\%$ density peak noise set added to the dishware dataset. a The class of cup with TF-SVDD; b the class of cup with SVDD; c the class of bowl with TF-SVDD; d the class of bowl with SVDD; e the class of plate with TF-SVDD; f the class of plate with SVDD

Fig. 5

The above AUC diagram with 60$\%$ density peak noise set added to the dishware dataset. a The class of cup with TF-SVDD; b the class of cup with SVDD; c the class of bowl with TF-SVDD; d the class of bowl with SVDD; e the class of plate with TF-SVDD; f the class of plate with SVDD

Fig. 6

The detection accuracy of random noise. a The average detection accuracy of cats and dogs; b the average detection accuracy of dishware

Fig. 7

Spherical centroid distance plot for the cats and dogs dataset. a The spherical center distance plot of the noise set of 20$\%$ density peaks was added to the cat dataset; b the spherical center distance plot of the noise set of 40$\%$ density peaks was added to the cat dataset; c the spherical center distance plot of the noise set of 60$\%$ density peaks was added to the cat dataset

Fig. 8

The detection accuracy of fruits on 10-class fruit dataset for different algorithms. a 0$\%$ random noise; b 20$\%$ random noise; c 40$\%$ random noise; d 60$\%$ random noise

Conclusions

This paper introduces an innovative approach, TF-SVDD, for detecting noisy labels within a given dataset by utilizing the concept of tightness-based membership. The proposed method employs a compact hypersphere to surround the sample set and calculates the membership degree of each sample using two different methods for samples within and outside the radius, respectively. This closeness-based approach effectively distinguishes outlier or noisy samples from valid samples in the dataset compared to the distance-based method. Moreover, we introduce two techniques for constructing the initial noise set. The experimental findings indicate that our proposed method outperforms SVDD in terms of average accuracy.

In the future, we aim to enhance the algorithm and intend to employ deep neural networks to characterize the decision boundary, enabling the detection of noisy labels in more complex datasets. Furthermore, we are keen on exploring the realm of multi-label learning, which holds significant practical applications, especially in constructing a multi-label classification model with a large volume of data in the of prior supervision.