Hamacher interaction aggregation operators for complex intuitionistic fuzzy sets and their applications in green supply chain management

Abstract

A complex intuitionistic fuzzy (CIF) set contains the membership and non-membership in the shape of a complex number whose amplitude term and phase term are covered in the unit interval. Moreover, Hamacher interaction aggregation operators are the combination of two major operators, called Hamacher aggregation operators and interaction aggregation operators, and they are used to aggregate the collection of information into one value. In this manuscript, we present the concept of Hamacher interaction operational laws for CIF sets (CIFSs). Further, we develop the CIF Hamacher interaction weighted averaging (CIFHIWA) operator, CIF Hamacher interaction ordered weighted averaging (CIFHIOWA) operator, CIF Hamacher interaction weighted geometric (CIFHIWG) operator, and CIF Hamacher interaction ordered weighted geometric (CIFHIOWG) operator. For these operators, we also discuss some basic properties, such as idempotency, monotonicity, and boundedness. Additionally, we develop a MADM method based on the developed operators and apply it to solve the green supply chain management problems, which can implement environmentally friendly practices to minimize carbon emissions, resource consumption, and waste generation while promoting long-term sustainability. Finally, we verify the superiority and effectiveness of the proposed method based on a comparative analysis between the proposed techniques and existing methods.

Introduction

Green supply chain management (GSCM) [1] is used in many fields. The main goal of the GSCM procedure is to reduce the environmental impact of the supply chain process, such as manufacturing transportation, distribution, and encompassing of raw materials [2]. Furthermore, the multi-attribute decision-making (MADM) procedure [3, 4] is also used to select the best one from the collection of solutions by aggregating the finite collection of information into one value, and the MADM technique [5] has been used to classical information which is expressed by classical set, only with zero or one, which is very limited or restricted for experts [6, 7]. For this, Zadeh [8] developed the fuzzy set (FS) which contains the grade of membership “${\varpi }_{at}\left({\psi }_{\Finv }\right)$” where it is defined by ${\varpi }_{at}:\psi \to \left[\mathrm{0,1}\right]$, called membership or truth or supporting or satisfactory grade. Furthermore, Mahmood and Ali [9] developed the fuzzy superior Mandelbrot sets, which is the combination of FS and superior Mandelbrot set. Additionally, in FS, the expert shows only the positive aspects, but not the negative, where negative information plays a valuable and dominant role in many real problems. Therefore, Atanassov [10, 11] developed the intuitionistic FS (IFS), which covers the grades of membership “${\varpi }_{at}\left({\psi }_{\Finv }\right)$” and non-membership “${\Xi }_{at}\left({\psi }_{\Finv }\right)$” with a condition: $0\le {\varpi }_{at}\left({\psi }_{\Finv }\right)+{\Xi }_{{\text{at}}}\left({\psi }_{\Finv }\right)\le 1$. Furthermore, FS is a special case of IFS, if ${\Xi }_{at}\left({\psi }_{\Finv }\right)=0$. Further, Gohain et al. [12] proposed the distance measures for interval-valued IFSs, Ejegwa and Ahemen [13] presented similarity measures for enhanced IFSs, Davoudabadi et al. [14] derived the simulation approaches for IFSs, Ejegwa and Agbetayo [15] introduced the similarity-distance measures for IFSs, Salimian and Mousavi [16] presented the MADM technique based on IFSs, Mahmood et al. [17] proposed the TOPSIS method and Hamacher Choquet integral operators for IFSs, Shi et al. [18] developed the power operators for interval-valued IFSs, Garg et al. [19] gave the Schweizer–Sklar prioritized operators for IFSs, Albaity et al. [20] presented Aczel–Alsina operators for intuitionistic fuzzy soft set (IFSS). Ecer [21] derived the modified MAIRCA technique for IFSSs, Garg and Rani [22] presented the distance measures for IFSs, Khan et al. [23] proposed the divergence measures for IFSs, and Gohain et al. [24] discussed the distance measures for IFS and their applications in decision-making, pattern recognition, and clustering analysis.

The above different FSs have achieved great applications in real problems; however, they cannot express some complex decision problems, for example, to purchase any type of software from a software house, the owner of the software house might give two types of information regarding each software, called the name and version of the software. Here, the name and version are shown as the amplitude and phase terms of the complex number, but in the case of the above different FSs, we have only the real number. Therefore, to construct the membership grade in the shape of a complex number, the complex FS (CFS) was proposed by Ramot et al. [25]. The membership grade in CFS is expressed by polar coordinates whose amplitude term and phase term are contained in the unit interval. Further, Liu et al. [26] presented the distance measures for CFSs, and Mahmood et al. [27] developed the neighborhood operators based on CFSs. Additionally, Alkouri and Salleh [28] proposed the complex IFS (CIFS), where the complex-valued membership grade “${\varpi }_{at}\left({\psi }_{\Finv }\right){e}^{i2\pi \left({\varpi }_{\mathfrak{H}t}\left({\psi }_{\Finv }\right)\right)}$” and non-membership grade “${\Xi }_{at}\left({\psi }_{\Finv }\right){e}^{i2\pi \left({\Xi }_{\mathfrak{H}t}\left({\psi }_{\Finv }\right)\right)}$” are the part of CIFS with $0\le {\varpi }_{at}\left({\psi }_{\Finv }\right)+{\Xi }_{at}\left({\psi }_{\Finv }\right)\le 1$ and $0\le {\varpi }_{\mathfrak{H}t}\left({\psi }_{\Finv }\right)+{\Xi }_{\mathfrak{H}t}\left({\psi }_{\Finv }\right)\le 1$. Moreover, Rani and Garg [29] developed the distance measures for CIFSs, Garg and Rani [30] derived the information measures for CIFSs, Ke et al. [31] developed the distance measures for IFSs, and finally, Garg and Rani [32] derived the correlation co-efficient measures for CIFSs.

After successfully achieving different types of extensions of FSs to express complex information, another problem is how to aggregate the collection of information into one value; for this, Xu [33] proposed the aggregation operators (AOs) based on IFS by the algebraic t-norm (TN) and t-conorm (TCN). Furthermore, Hamacher [34] developed the Hamacher TN and TCN in 1978. These norms are modified versions of the algebraic norms. Moreover, Wang and Liu [35] derived the Einstein operators based on Einstein TN and TCN for IFSs, and He et al. [36] presented the geometric interaction operators based on interaction TN and TCN for IFSs. Furthermore, Yu and Xu [37] developed the prioritized AOs for IFSs, Akram et al. [38] proposed the Hamacher AOs for CIFSs, Garg and Rani [39] derived the generalized AOs for CIFSs, Garg and Rani [40] introduced the generalized geometric AOs for CIFSs, Mahmood et al. [41] presented the Aczel–Alsina AOs for CIFSs, Mahmood and Ali [42] derived the Aczel–Alsina power AOs for CIFSs, Azeem et al. [43] pioneered the Einstein AOs for CIFSs, Liu et al. [44] presented the prioritized AOs for CIFSs based on Aczel–Alsina TN and TCN, and Yang et al. [45] developed the Frank AOs for CIFSs. From the above analysis, we observed that all experts have the following major problems:

• (1) How to prepare new operational laws based on CIFSs?

• (2) How to develop new operators based on two old techniques?

• (3) How to rank all the alternatives based on the developed operators?

For solving the above problems, we combine the old technique of Hamacher operators and interaction aggregation operators to address the above complication problems. Furthermore, we also observed that the Hamacher AOs and Einstein AOs have been developed by many scholars and applied to many real problems, but the interaction AOs for CIFSs are not proposed because of some complications; furthermore, to combine the Hamacher AOs and interaction AOs based on CIFSs is also a very difficult and changing task. Further, it is also clear that the Hamacher AOs, interaction AOs, averaging AOs, and geometric AOs for FSs, IFSs, CFSs, and CIFSs are the special cases of the Hamacher interaction AOs for CIFSs. The advantages of the proposed operators are listed below:

• (1) Averaging/geometric aggregation operators for FSs, IFSs, CFSs, and CIFSs are specific cases of the developed operators.

• (2) Interaction averaging/geometric aggregation operators for FSs, IFSs, CFSs, and CIFSs are specific cases of the developed operators.

• (3) Hamacher averaging/geometric aggregation operators for FSs, IFSs, CFSs, and CIFSs are specific cases of the developed operators.

• (4) Hamacher interaction averaging/geometric aggregation operators for FSs, IFSs, CFSs, and CIFSs are specific cases of the developed operators.

The geometrical representation of the proposed works is shown in Fig. 1.

Fig. 1

Geometrical representation of the proposed works

The advantages of the proposed operators are listed below:

• (1) To propose the Hamacher interaction operational laws for CIFSs.

• (2) To develop the CIFHIWA operator, CIFHIOWA operator, CIFHIWG operator, and CIFHIOWG operator.

• (3) To discuss some basic properties, such as idempotency, monotonicity, and boundedness.

• (4) To develop a MADM method based on the developed operators to find the best type of green supply chain management among the five green supply chain management.

• (5) To verify the superiority and effectiveness of the proposed method based on a comparative analysis between proposed techniques and existing methods.

The summary of this manuscript is shown as follows. In "Preliminaries", we introduced the CIFSs and their operational laws. In "Hamacher interaction weighted aggregation operators for CIFSs", we developed the concept of Hamacher interaction operational laws for CIFSs. Further, we proposed the CIFHIWA operator, CIFHIOWA operator, CIFHIWG operator, and CIFHIOWG operator. Further, we also discussed some basic properties, such as idempotency, monotonicity, and boundedness. In "MADM method based on presented operators", we developed a MADM method and used it to find the best type of green supply chain management among the five green supply chain management, and did a comparative analysis between proposed techniques and existing methods. Some concluding information is shown in "Conclusion".

Preliminaries

In this section, we introduced the CIFSs and their operational laws based on a universal set ${\Sigma }_{u}$. Furthermore, we used the following symbols, such as ${\varpi }_{at}\left({\psi }_{\Finv }\right){e}^{i2\pi \left({\varpi }_{\mathfrak{H}t}\left({\psi }_{\Finv }\right)\right)},{\Xi }_{at}\left({\psi }_{\Finv }\right){e}^{i2\pi \left({\Xi }_{\mathfrak{H}t}\left({\psi }_{\Finv }\right)\right)},{\psi }_{\Finv },\psi ,$ and ${\mu }^{s}$ represent the complex-valued positive, complex-valued negative, element of universal sets, universal sets, and scaler element, respectively.

Definition 1

[28] A CIFS ${\zeta }_{II}$ in a finite universe of discourse $\psi =\left\{{\psi }_{1},{\psi }_{2},\dots ,{\psi }_{\mathfrak{H}}\right\}$ is defined by

$${\zeta }_{II}=\left\{\left({\varpi }_{at}\left({\psi }_{\Finv }\right){e}^{i2\pi \left({\varpi }_{\mathfrak{H}t}\left({\psi }_{\Finv }\right)\right)},{\Xi }_{at}\left({\psi }_{\Finv }\right){e}^{i2\pi \left({\Xi }_{\mathfrak{H}t}\left({\psi }_{\Finv }\right)\right)}\right):{\psi }_{\Finv }\in \psi \right\},$$

where ${\varpi }_{at}\left({\psi }_{\Finv }\right),{\Xi }_{at}\left({\psi }_{\Finv }\right)$ and ${\varpi }_{\mathfrak{H}t}\left({\psi }_{\Finv }\right),{\Xi }_{\mathfrak{H}t}\left({\psi }_{\Finv }\right)$ show the amplitude term and phase term of the membership and non-membership grade with two strong conditions $0\le {\varpi }_{at}\left({\psi }_{\Finv }\right)+{\Xi }_{at}\left({\psi }_{\Finv }\right)\le 1$ and $0\le {\varpi }_{\mathfrak{H}t}\left({\psi }_{\Finv }\right)+{\Xi }_{\mathfrak{H}t}\left({\psi }_{\Finv }\right)\le 1$. Moreover, we also gave the neutral grade in the form: ${\omega }_{at}\left({\psi }_{\Finv }\right){e}^{i2\pi \left({\omega }_{\mathfrak{H}t}\left({\psi }_{\Finv }\right)\right)}=\left(1-{\varpi }_{at}\left({\psi }_{\Finv }\right)-{\Xi }_{at}\left({\psi }_{\Finv }\right)\right){e}^{i2\pi \left(1-{\varpi }_{\mathfrak{H}t}\left({\psi }_{\Finv }\right)-{\Xi }_{\mathfrak{H}t}\left({\psi }_{\Finv }\right)\right)}$. Finally, we gave the simple form of CIFN, such as ${\zeta }_{II}^{\Finv }=\left({\varpi }_{at}^{\Finv }{e}^{i2\pi \left({\varpi }_{\mathfrak{H}t}^{\Finv }\right)},{\Xi }_{at}^{\Finv }{e}^{i2\pi \left({\Xi }_{\mathfrak{H}t}^{\Finv }\right)}\right),\Finv =\mathrm{1,2},\dots ,\mathfrak{H}$.

Definition 2

[39] Consider any two CIFSs ${\zeta }_{II}^{\Finv }=\left({\varpi }_{at}^{\Finv }{e}^{i2\pi \left({\varpi }_{\mathfrak{H}t}^{\Finv }\right)},{\Xi }_{at}^{\Finv }{e}^{i2\pi \left({\Xi }_{\mathfrak{H}t}^{\Finv }\right)}\right), \Finv =\mathrm{1,2};$ some algebraic operational laws are presented as

$${\zeta }_{II}^{1}\oplus {\zeta }_{II}^{2}=\left(\left({\varpi }_{at}^{1}+{\varpi }_{at}^{2}-{\varpi }_{at}^{1}{\varpi }_{at}^{2}\right){e}^{i2\pi \left({\varpi }_{\mathfrak{H}t}^{1}+{\varpi }_{\mathfrak{H}t}^{2}-{\varpi }_{\mathfrak{H}t}^{1}{\varpi }_{\mathfrak{H}t}^{2}\right)},\left({\Xi }_{at}^{1}{\Xi }_{at}^{2}\right){e}^{i2\pi \left({\Xi }_{\mathfrak{H}t}^{1}{\Xi }_{\mathfrak{H}t}^{2}\right)}\right),$$

$${\zeta }_{II}^{1}\otimes {\zeta }_{II}^{2}=\left(\left({\varpi }_{at}^{1}{\varpi }_{at}^{2}\right){e}^{i2\pi \left({\varpi }_{\mathfrak{H}t}^{1}{\varpi }_{\mathfrak{H}t}^{2}\right)},\left({\Xi }_{at}^{1}+{\Xi }_{at}^{2}-{\Xi }_{at}^{1}{\Xi }_{at}^{2}\right){e}^{i2\pi \left({\Xi }_{\mathfrak{H}t}^{1}+{\Xi }_{\mathfrak{H}t}^{2}-{\Xi }_{\mathfrak{H}t}^{1}{\Xi }_{\mathfrak{H}t}^{2}\right)}\right),$$

$${\mu }^{s}{\zeta }_{II}^{1}=\left(\left(1-{\left(1-{\varpi }_{at}^{1}\right)}^{{\mu }^{s}}\right){e}^{i2\pi \left(1-{\left(1-{\varpi }_{\mathfrak{H}t}^{1}\right)}^{{\mu }^{s}}\right)},{\left({\Xi }_{at}^{1}\right)}^{{\mu }^{s}}{e}^{i2\pi \left({\left({\Xi }_{\mathfrak{H}t}^{1}\right)}^{{\mu }^{s}}\right)}\right),$$

$${\left({\zeta }_{II}^{1}\right)}^{{\mu }^{s}}=\left({\left({\varpi }_{at}^{1}\right)}^{{\mu }^{s}}{e}^{i2\pi \left({\left({\varpi }_{\mathfrak{H}t}^{1}\right)}^{{\mu }^{s}}\right)},\left(1-{\left(1-{\Xi }_{at}^{1}\right)}^{{\mu }^{s}}\right){e}^{i2\pi \left(1-{\left(1-{\Xi }_{\mathfrak{H}t}^{1}\right)}^{{\mu }^{s}}\right)}\right).$$

Definition 3

[39] Consider any two CIFSs ${\zeta }_{II}^{\Finv }=\left({\varpi }_{at}^{\Finv }{e}^{i2\pi \left({\varpi }_{\mathfrak{H}t}^{\Finv }\right)},{\Xi }_{at}^{\Finv }{e}^{i2\pi \left({\Xi }_{\mathfrak{H}t}^{\Finv }\right)}\right), \Finv =\mathrm{1,2}$; the score function and the accuracy function are defined as

$${\rm SC}\left({\zeta }_{II}^{\Finv }\right)=\frac{1}{2}\left({\varpi }_{at}^{\Finv }+{\varpi }_{\mathfrak{H}t}^{\Finv }-{\Xi }_{at}^{\Finv }-{\Xi }_{\mathfrak{H}t}^{\Finv }\right)\in \left[-\mathrm{1,1}\right],$$

$${\rm AC}\left({\zeta }_{II}^{\Finv }\right)=\frac{1}{2}\left({\varpi }_{at}^{\Finv }+{\varpi }_{\mathfrak{H}t}^{\Finv }+{\Xi }_{at}^{\Finv }+{\Xi }_{\mathfrak{H}t}^{\Finv }\right)\in \left[\mathrm{0,1}\right].$$

Based on the score value and accuracy value, we give the comparison rules, such as if ${\rm SC}\left({\zeta }_{II}^{1}\right)>{\rm SC}\left({\zeta }_{II}^{2}\right)\Rightarrow {\zeta }_{II}^{1}>{\zeta }_{II}^{2}$, if ${\rm SC}\left({\zeta }_{II}^{1}\right)={\rm SC}\left({\zeta }_{II}^{2}\right)$, then if ${\rm AC}\left({\zeta }_{II}^{1}\right)>{\rm AC}\left({\zeta }_{II}^{2}\right)\Rightarrow {\zeta }_{II}^{1}>{\zeta }_{II}^{2}$.

Definition 4

[43] Consider any two CIFSs ${\zeta }_{II}^{\Finv }=\left({\varpi }_{at}^{\Finv }{e}^{i2\pi \left({\varpi }_{\mathfrak{H}t}^{\Finv }\right)},{\Xi }_{at}^{\Finv }{e}^{i2\pi \left({\Xi }_{\mathfrak{H}t}^{\Finv }\right)}\right), \Finv =\mathrm{1,2}$; some Einstein operational laws are proposed as

$${\zeta }_{II}^{1}\oplus {\zeta }_{II}^{2}=\left(\left(\frac{{\varpi }_{at}^{1}{\varpi }_{at}^{2}}{1+\left(1-{\varpi }_{at}^{1}\right)\left(1-{\varpi }_{at}^{2}\right)}\right){e}^{i2\pi \left(\frac{{\varpi }_{\mathfrak{H}t}^{1}{\varpi }_{\mathfrak{H}t}^{2}}{1+\left(1-{\varpi }_{\mathfrak{H}t}^{1}\right)\left(1-{\varpi }_{\mathfrak{H}t}^{2}\right)}\right)},\left(\frac{{\Xi }_{at}^{1}+{\Xi }_{at}^{2}}{1-{\Xi }_{at}^{1}{\Xi }_{at}^{2}}\right){e}^{i2\pi \left(\frac{{\Xi }_{\mathfrak{H}t}^{1}+{\Xi }_{\mathfrak{H}t}^{2}}{1-{\Xi }_{\mathfrak{H}t}^{1}{\Xi }_{\mathfrak{H}t}^{2}}\right)}\right),$$

$${\zeta }_{II}^{1}\otimes {\zeta }_{II}^{2}=\left(\left(\frac{{\varpi }_{at}^{1}+{\varpi }_{at}^{2}}{1-{\varpi }_{at}^{1}{\varpi }_{at}^{2}}\right){e}^{i2\pi \left(\frac{{\varpi }_{\mathfrak{H}t}^{1}+{\varpi }_{\mathfrak{H}t}^{2}}{1-{\varpi }_{\mathfrak{H}t}^{1}{\varpi }_{\mathfrak{H}t}^{2}}\right)},\left(\frac{{\Xi }_{at}^{1}{\Xi }_{at}^{2}}{1+\left(1-{\Xi }_{at}^{1}\right)\left(1-{\Xi }_{at}^{2}\right)}\right){e}^{i2\pi \left(\frac{{\Xi }_{\mathfrak{H}t}^{1}{\Xi }_{\mathfrak{H}t}^{2}}{1+\left(1-{\Xi }_{\mathfrak{H}t}^{1}\right)\left(1-{\Xi }_{\mathfrak{H}t}^{2}\right)}\right)}\right),$$

$${\mu }^{s}{\zeta }_{II}^{1}=\left(\begin{array}{c}\left(\frac{{\left(1+{\varpi }_{at}^{1}\right)}^{{\mu }^{s}}-{\left(1-{\varpi }_{at}^{1}\right)}^{{\mu }^{s}}}{{\left(1+{\varpi }_{at}^{1}\right)}^{{\mu }^{s}}+{\left(1-{\varpi }_{at}^{1}\right)}^{{\mu }^{s}}}\right){e}^{i2\pi \left(\frac{{\left(1+{\varpi }_{\mathfrak{H}t}^{1}\right)}^{{\mu }^{s}}-{\left(1-{\varpi }_{\mathfrak{H}t}^{1}\right)}^{{\mu }^{s}}}{{\left(1+{\varpi }_{\mathfrak{H}t}^{1}\right)}^{{\mu }^{s}}+{\left(1-{\varpi }_{\mathfrak{H}t}^{1}\right)}^{{\mu }^{s}}}\right)},\\ \left(\frac{2{\left({\Xi }_{at}^{1}\right)}^{{\mu }^{s}}}{{\left(2-{\Xi }_{at}^{1}\right)}^{{\mu }^{s}}+{\left({\Xi }_{at}^{1}\right)}^{{\mu }^{s}}}\right){e}^{i2\pi \left(\frac{2{\left({\Xi }_{\mathfrak{H}t}^{1}\right)}^{{\mu }^{s}}}{{\left(2-{\Xi }_{\mathfrak{H}t}^{1}\right)}^{{\mu }^{s}}+{\left({\Xi }_{\mathfrak{H}t}^{1}\right)}^{{\mu }^{s}}}\right)}\end{array}\right),$$

$${\left({\zeta }_{II}^{1}\right)}^{{\mu }^{s}}=\left(\begin{array}{c}\left(\frac{2{\left({\varpi }_{at}^{1}\right)}^{{\mu }^{s}}}{{\left(2-{\varpi }_{at}^{1}\right)}^{{\mu }^{s}}+{\left({\varpi }_{at}^{1}\right)}^{{\mu }^{s}}}\right){e}^{i2\pi \left(\frac{2{\left({\varpi }_{\mathfrak{H}t}^{1}\right)}^{{\mu }^{s}}}{{\left(2-{\varpi }_{\mathfrak{H}t}^{1}\right)}^{{\mu }^{s}}+{\left({\varpi }_{\mathfrak{H}t}^{1}\right)}^{{\mu }^{s}}}\right)},\\ \left(\frac{{\left(1+{\Xi }_{at}^{1}\right)}^{{\mu }^{s}}-{\left(1-{\Xi }_{at}^{1}\right)}^{{\mu }^{s}}}{{\left(1+{\Xi }_{at}^{1}\right)}^{{\mu }^{s}}+{\left(1-{\Xi }_{at}^{1}\right)}^{{\mu }^{s}}}\right){e}^{i2\pi \left(\frac{{\left(1+{\Xi }_{\mathfrak{H}t}^{1}\right)}^{{\mu }^{s}}-{\left(1-{\Xi }_{\mathfrak{H}t}^{1}\right)}^{{\mu }^{s}}}{{\left(1+{\Xi }_{\mathfrak{H}t}^{1}\right)}^{{\mu }^{s}}+{\left(1-{\Xi }_{\mathfrak{H}t}^{1}\right)}^{{\mu }^{s}}}\right)}\end{array}\right).$$

Definition 5

[38] Consider any two CIFSs ${\zeta }_{II}^{\Finv }=\left({\varpi }_{at}^{\Finv }{e}^{i2\pi \left({\varpi }_{\mathfrak{H}t}^{\Finv }\right)},{\Xi }_{at}^{\Finv }{e}^{i2\pi \left({\Xi }_{\mathfrak{H}t}^{\Finv }\right)}\right), \Finv =\mathrm{1,2};$ some Hamacher operational laws are defined as

$${\zeta }_{II}^{1}\oplus {\zeta }_{II}^{2}=\left(\begin{array}{c}\left(\frac{{\varpi }_{at}^{1}+{\varpi }_{at}^{2}-{\varpi }_{at}^{1}{\varpi }_{at}^{2}-\left(1-{\dddot{\beth}}\right){\varpi }_{at}^{1}{\varpi }_{at}^{2}}{1-\left(1-{\dddot{\beth}}\right){\varpi }_{at}^{1}{\varpi }_{at}^{2}}\right){e}^{i2\pi \left(\frac{{\varpi }_{\mathfrak{H}t}^{1}+{\varpi }_{\mathfrak{H}t}^{2}-{\varpi }_{\mathfrak{H}t}^{1}{\varpi }_{\mathfrak{H}t}^{2}-\left(1-{\dddot{\beth}}\right){\varpi }_{\mathfrak{H}t}^{1}{\varpi }_{\mathfrak{H}t}^{2}}{1-\left(1-{\dddot{\beth}}\right){\varpi }_{\mathfrak{H}t}^{1}{\varpi }_{\mathfrak{H}t}^{2}}\right)},\\ \left(\frac{{\Xi }_{at}^{1}{\Xi }_{at}^{2}}{{\dddot{\beth}}+\left(1-{\dddot{\beth}}\right)\left({\Xi }_{at}^{1}+{\Xi }_{at}^{2}-{\Xi }_{at}^{1}{\Xi }_{at}^{2}\right)}\right){e}^{i2\pi \left(\frac{{\Xi }_{\mathfrak{H}t}^{1}{\Xi }_{\mathfrak{H}t}^{2}}{{\dddot{\beth}}+\left(1-{\dddot{\beth}}\right)\left({\Xi }_{\mathfrak{H}t}^{1}+{\Xi }_{\mathfrak{H}t}^{2}-{\Xi }_{\mathfrak{H}t}^{1}{\Xi }_{\mathfrak{H}t}^{2}\right)}\right)}\end{array}\right),$$

$${\zeta }_{II}^{1}\otimes {\zeta }_{II}^{2}=\left(\begin{array}{c}\left(\frac{{\varpi }_{at}^{1}{\varpi }_{at}^{2}}{{\dddot{\beth}}+\left(1-{\dddot{\beth}}\right)\left({\varpi }_{at}^{1}+{\varpi }_{at}^{2}-{\varpi }_{at}^{1}{\varpi }_{at}^{2}\right)}\right){e}^{i2\pi \left(\frac{{\varpi }_{\mathfrak{H}t}^{1}{\varpi }_{\mathfrak{H}t}^{2}}{{\dddot{\beth}}+\left(1-{\dddot{\beth}}\right)\left({\varpi }_{\mathfrak{H}t}^{1}+{\varpi }_{\mathfrak{H}t}^{2}-{\varpi }_{\mathfrak{H}t}^{1}{\varpi }_{\mathfrak{H}t}^{2}\right)}\right)},\\ \left(\frac{{\Xi }_{at}^{1}+{\Xi }_{at}^{2}-{\Xi }_{at}^{1}{\Xi }_{at}^{2}-\left(1-{\dddot{\beth}}\right){\Xi }_{at}^{1}{\Xi }_{at}^{2}}{1-\left(1-{\dddot{\beth}}\right){\Xi }_{at}^{1}{\Xi }_{at}^{2}}\right){e}^{i2\pi \left(\frac{{\Xi }_{\mathfrak{H}t}^{1}+{\Xi }_{\mathfrak{H}t}^{2}-{\Xi }_{\mathfrak{H}t}^{1}{\Xi }_{\mathfrak{H}t}^{2}-\left(1-{\dddot{\beth}}\right){\Xi }_{\mathfrak{H}t}^{1}{\Xi }_{\mathfrak{H}t}^{2}}{1-\left(1-{\dddot{\beth}}\right){\Xi }_{\mathfrak{H}t}^{1}{\Xi }_{\mathfrak{H}t}^{2}}\right)}\end{array}\right),$$

$${\mu }^{s}{\zeta }_{II}^{1}=\left(\begin{array}{c}\left(\frac{{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{at}^{1}\right)}^{{\mu }^{s}}-{\left(1-{\varpi }_{at}^{1}\right)}^{{\mu }^{s}}}{{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{at}^{1}\right)}^{{\mu }^{s}}+\left({\dddot{\beth}}-1\right){\left(1-{\varpi }_{at}^{1}\right)}^{{\mu }^{s}}}\right){e}^{i2\pi \left(\frac{{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{\mathfrak{H}t}^{1}\right)}^{{\mu }^{s}}-{\left(1-{\varpi }_{\mathfrak{H}t}^{1}\right)}^{{\mu }^{s}}}{{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{\mathfrak{H}t}^{1}\right)}^{{\mu }^{s}}+\left({\dddot{\beth}}-1\right){\left(1-{\varpi }_{\mathfrak{H}t}^{1}\right)}^{{\mu }^{s}}}\right)},\\ \left(\frac{{\dddot{\beth}}{\left({\Xi }_{at}^{1}\right)}^{{\mu }^{s}}}{{\left(1+\left({\dddot{\beth}}-1\right)\left(1-{\Xi }_{at}^{1}\right)\right)}^{{\mu }^{s}}+\left({\dddot{\beth}}-1\right){\left({\Xi }_{at}^{1}\right)}^{{\mu }^{s}}}\right){e}^{i2\pi \left(\frac{{\dddot{\beth}}{\left({\Xi }_{\mathfrak{H}t}^{1}\right)}^{{\mu }^{s}}}{{\left(1+\left({\dddot{\beth}}-1\right)\left(1-{\Xi }_{\mathfrak{H}t}^{1}\right)\right)}^{{\mu }^{s}}+\left({\dddot{\beth}}-1\right){\left({\Xi }_{\mathfrak{H}t}^{1}\right)}^{{\mu }^{s}}}\right)}\end{array}\right),$$

$${\left({\zeta }_{II}^{1}\right)}^{{\mu }^{s}}=\left(\begin{array}{c}\left(\frac{{\dddot{\beth}}{\left({\varpi }_{at}^{1}\right)}^{{\mu }^{s}}}{{\left(1+\left({\dddot{\beth}}-1\right)\left(1-{\varpi }_{at}^{1}\right)\right)}^{{\mu }^{s}}+\left({\dddot{\beth}}-1\right){\left({\varpi }_{at}^{1}\right)}^{{\mu }^{s}}}\right){e}^{i2\pi \left(\frac{{\dddot{\beth}}{\left({\varpi }_{\mathfrak{H}t}^{1}\right)}^{{\mu }^{s}}}{{\left(1+\left({\dddot{\beth}}-1\right)\left(1-{\varpi }_{\mathfrak{H}t}^{1}\right)\right)}^{{\mu }^{s}}+\left({\dddot{\beth}}-1\right){\left({\varpi }_{\mathfrak{H}t}^{1}\right)}^{{\mu }^{s}}}\right)},\\ \left(\frac{{\left(1+\left({\dddot{\beth}}-1\right){\Xi }_{at}^{1}\right)}^{{\mu }^{s}}-{\left(1-{\Xi }_{at}^{1}\right)}^{{\mu }^{s}}}{{\left(1+\left({\dddot{\beth}}-1\right){\Xi }_{at}^{1}\right)}^{{\mu }^{s}}+\left({\dddot{\beth}}-1\right){\left(1-{\Xi }_{at}^{1}\right)}^{{\mu }^{s}}}\right){e}^{i2\pi \left(\frac{{\left(1+\left({\dddot{\beth}}-1\right){\Xi }_{\mathfrak{H}t}^{1}\right)}^{{\mu }^{s}}-{\left(1-{\Xi }_{\mathfrak{H}t}^{1}\right)}^{{\mu }^{s}}}{{\left(1+\left({\dddot{\beth}}-1\right){\Xi }_{\mathfrak{H}t}^{1}\right)}^{{\mu }^{s}}+\left({\dddot{\beth}}-1\right){\left(1-{\Xi }_{\mathfrak{H}t}^{1}\right)}^{{\mu }^{s}}}\right)}\end{array}\right).$$

Hamacher interaction weighted aggregation operators for CIFSs

In this section, we propose the Hamacher interaction operational laws based on CIFSs. Moreover, we develop the CIFHIWA operator, CIFHIOWA operator, CIFHIWG operator, and CIFHIOWG operator. Some fundamental properties are also discussed.

Definition 6

Consider any two CIFSs ${\zeta }_{II}^{\Finv }=\left({\varpi }_{at}^{\Finv }{e}^{i2\pi \left({\varpi }_{\mathfrak{H}t}^{\Finv }\right)},{\Xi }_{at}^{\Finv }{e}^{i2\pi \left({\Xi }_{\mathfrak{H}t}^{\Finv }\right)}\right), \Finv =\mathrm{1,2}$; some improved Hamacher interaction operational laws are proposed as

$${\zeta }_{II}^{1}\oplus {\zeta }_{II}^{2}=\left(\begin{array}{c}\left(\frac{\prod_{\Finv =1}^{2}\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{at}^{\Finv }\right)-\prod_{\Finv =1}^{2}\left(1-{\varpi }_{at}^{\Finv }\right)}{\prod_{\Finv =1}^{2}\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{at}^{\Finv }\right)+\left({\dddot{\beth}}-1\right)\prod_{\Finv =1}^{2}\left(1-{\varpi }_{at}^{\Finv }\right)}\right){e}^{i2\pi \left(\frac{\prod_{\Finv =1}^{2}\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{\mathfrak{H}t}^{\Finv }\right)-\prod_{\Finv =1}^{2}\left(1-{\varpi }_{\mathfrak{H}t}^{\Finv }\right)}{\prod_{\Finv =1}^{2}\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{\mathfrak{H}t}^{\Finv }\right)+\left({\dddot{\beth}}-1\right)\prod_{\Finv =1}^{2}\left(1-{\varpi }_{\mathfrak{H}t}^{\Finv }\right)}\right)},\\ \left(\frac{{\dddot{\beth}}\prod_{\Finv =1}^{2}\left(1-{\varpi }_{at}^{\Finv }\right)-{\dddot{\beth}}\prod_{\Finv =1}^{2}\left(1-{\varpi }_{at}^{\Finv }-{\Xi }_{at}^{\Finv }\right)}{\prod_{\Finv =1}^{2}\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{at}^{\Finv }\right)+\left({\dddot{\beth}}-1\right)\prod_{\Finv =1}^{2}\left(1-{\varpi }_{at}^{\Finv }\right)}\right){e}^{i2\pi \left(\frac{{\dddot{\beth}}\prod_{\Finv =1}^{2}\left(1-{\varpi }_{\mathfrak{H}t}^{\Finv }\right)-{\dddot{\beth}}\prod_{\Finv =1}^{2}\left(1-{\varpi }_{\mathfrak{H}t}^{\Finv }-{\Xi }_{\mathfrak{H}t}^{\Finv }\right)}{\prod_{\Finv =1}^{2}\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{\mathfrak{H}t}^{\Finv }\right)+\left({\dddot{\beth}}-1\right)\prod_{\Finv =1}^{2}\left(1-{\varpi }_{\mathfrak{H}t}^{\Finv }\right)}\right)}\end{array}\right),$$

$${\zeta }_{II}^{1}\otimes {\zeta }_{II}^{2}=\left(\begin{array}{c}\left(\frac{{\dddot{\beth}}\prod_{\Finv =1}^{2}\left(1-{\Xi }_{at}^{\Finv }\right)-{\dddot{\beth}}\prod_{\Finv =1}^{2}\left(1-{\varpi }_{at}^{\Finv }-{\Xi }_{at}^{\Finv }\right)}{\prod_{\Finv =1}^{2}\left(1+\left({\dddot{\beth}}-1\right){\Xi }_{at}^{\Finv }\right)+\left({\dddot{\beth}}-1\right)\prod_{\Finv =1}^{2}\left(1-{\Xi }_{at}^{\Finv }\right)}\right){e}^{i2\pi \left(\frac{{\dddot{\beth}}\prod_{\Finv =1}^{2}\left(1-{\Xi }_{\mathfrak{H}t}^{\Finv }\right)-{\dddot{\beth}}\prod_{\Finv =1}^{2}\left(1-{\varpi }_{\mathfrak{H}t}^{\Finv }-{\Xi }_{\mathfrak{H}t}^{\Finv }\right)}{\prod_{\Finv =1}^{2}\left(1+\left({\dddot{\beth}}-1\right){\Xi }_{\mathfrak{H}t}^{\Finv }\right)+\left({\dddot{\beth}}-1\right)\prod_{\Finv =1}^{2}\left(1-{\Xi }_{\mathfrak{H}t}^{\Finv }\right)}\right)},\\ \left(\frac{\prod_{\Finv =1}^{2}\left(1+\left({\dddot{\beth}}-1\right){\Xi }_{at}^{\Finv }\right)-\prod_{\Finv =1}^{2}\left(1-{\Xi }_{at}^{\Finv }\right)}{\prod_{\Finv =1}^{2}\left(1+\left({\dddot{\beth}}-1\right){\Xi }_{at}^{\Finv }\right)+\left({\dddot{\beth}}-1\right)\prod_{\Finv =1}^{2}\left(1-{\Xi }_{at}^{\Finv }\right)}\right){e}^{i2\pi \left(\frac{\prod_{\Finv =1}^{2}\left(1+\left({\dddot{\beth}}-1\right){\Xi }_{\mathfrak{H}t}^{\Finv }\right)-\prod_{\Finv =1}^{2}\left(1-{\Xi }_{\mathfrak{H}t}^{\Finv }\right)}{\prod_{\Finv =1}^{2}\left(1+\left({\dddot{\beth}}-1\right){\Xi }_{\mathfrak{H}t}^{\Finv }\right)+\left({\dddot{\beth}}-1\right)\prod_{\Finv =1}^{2}\left(1-{\Xi }_{\mathfrak{H}t}^{\Finv }\right)}\right)}\end{array}\right),$$

$${\mu }^{s}{\zeta }_{II}^{1}=\left(\begin{array}{c}\left(\frac{{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{at}^{1}\right)}^{{\mu }^{s}}-{\left(1-{\varpi }_{at}^{1}\right)}^{{\mu }^{s}}}{{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{at}^{1}\right)}^{{\mu }^{s}}+\left({\dddot{\beth}}-1\right){\left(1-{\varpi }_{at}^{1}\right)}^{{\mu }^{s}}}\right){e}^{i2\pi \left(\frac{{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{\mathfrak{H}t}^{1}\right)}^{{\mu }^{s}}-{\left(1-{\varpi }_{\mathfrak{H}t}^{1}\right)}^{{\mu }^{s}}}{{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{\mathfrak{H}t}^{1}\right)}^{{\mu }^{s}}+\left({\dddot{\beth}}-1\right){\left(1-{\varpi }_{\mathfrak{H}t}^{1}\right)}^{{\mu }^{s}}}\right)},\\ \left(\frac{{\dddot{\beth}}{\left(1-{\varpi }_{at}^{1}\right)}^{{\mu }^{s}}-{\dddot{\beth}}{\left(1-{\varpi }_{at}^{1}-{\Xi }_{at}^{1}\right)}^{{\mu }^{s}}}{{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{at}^{1}\right)}^{{\mu }^{s}}+\left({\dddot{\beth}}-1\right){\left(1-{\varpi }_{at}^{1}\right)}^{{\mu }^{s}}}\right){e}^{i2\pi \left(\frac{{\dddot{\beth}}{\left(1-{\varpi }_{\mathfrak{H}t}^{1}\right)}^{{\mu }^{s}}-{\dddot{\beth}}{\left(1-{\varpi }_{\mathfrak{H}t}^{1}-{\Xi }_{\mathfrak{H}t}^{1}\right)}^{{\mu }^{s}}}{{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{\mathfrak{H}t}^{1}\right)}^{{\mu }^{s}}+\left({\dddot{\beth}}-1\right){\left(1-{\varpi }_{\mathfrak{H}t}^{1}\right)}^{{\mu }^{s}}}\right)}\end{array}\right),$$

$${\left({\zeta }_{II}^{1}\right)}^{{\mu }^{s}}=\left(\begin{array}{c}\left(\frac{{\dddot{\beth}}{\left(1-{\Xi }_{at}^{1}\right)}^{{\mu }^{s}}-{\dddot{\beth}}{\left(1-{\varpi }_{at}^{1}-{\Xi }_{at}^{1}\right)}^{{\mu }^{s}}}{{\left(1+\left({\dddot{\beth}}-1\right){\Xi }_{at}^{1}\right)}^{{\mu }^{s}}+\left({\dddot{\beth}}-1\right){\left(1-{\Xi }_{at}^{1}\right)}^{{\mu }^{s}}}\right){e}^{i2\pi \left(\frac{{\dddot{\beth}}{\left(1-{\Xi }_{\mathfrak{H}t}^{1}\right)}^{{\mu }^{s}}-{\dddot{\beth}}{\left(1-{\varpi }_{\mathfrak{H}t}^{1}-{\Xi }_{\mathfrak{H}t}^{1}\right)}^{{\mu }^{s}}}{{\left(1+\left({\dddot{\beth}}-1\right){\Xi }_{\mathfrak{H}t}^{1}\right)}^{{\mu }^{s}}+\left({\dddot{\beth}}-1\right){\left(1-{\Xi }_{\mathfrak{H}t}^{1}\right)}^{{\mu }^{s}}}\right)},\\ \left(\frac{{\left(1+\left({\dddot{\beth}}-1\right){\Xi }_{at}^{1}\right)}^{{\mu }^{s}}-{\left(1-{\Xi }_{at}^{1}\right)}^{{\mu }^{s}}}{{\left(1+\left({\dddot{\beth}}-1\right){\Xi }_{at}^{1}\right)}^{{\mu }^{s}}+\left({\dddot{\beth}}-1\right){\left(1-{\Xi }_{at}^{1}\right)}^{{\mu }^{s}}}\right){e}^{i2\pi \left(\frac{{\left(1+\left({\dddot{\beth}}-1\right){\Xi }_{\mathfrak{H}t}^{1}\right)}^{{\mu }^{s}}-{\left(1-{\Xi }_{\mathfrak{H}t}^{1}\right)}^{{\mu }^{s}}}{{\left(1+\left({\dddot{\beth}}-1\right){\Xi }_{\mathfrak{H}t}^{1}\right)}^{{\mu }^{s}}+\left({\dddot{\beth}}-1\right){\left(1-{\Xi }_{\mathfrak{H}t}^{1}\right)}^{{\mu }^{s}}}\right)}\end{array}\right).$$

Definition 7

Consider any finite collection of CIFSs ${\zeta }_{II}^{\Finv }=\left({\varpi }_{at}^{\Finv }{e}^{i2\pi \left({\varpi }_{\mathfrak{H}t}^{\Finv }\right)},{\Xi }_{at}^{\Finv }{e}^{i2\pi \left({\Xi }_{\mathfrak{H}t}^{\Finv }\right)}\right), \Finv =\mathrm{1,2},\dots , \mathfrak{H}$; then the CIF Hamacher interaction weighted averaging (CIFHIWA) operator is defined as

$${\text{CIIFHIIWA}}\left({\zeta }_{II}^{1},{\zeta }_{II}^{2},\dots ,{\zeta }_{II}^{\mathfrak{H}}\right)={\equiv }_{II}^{1}{\zeta }_{II}^{1}\oplus {\equiv }_{II}^{2}{\zeta }_{II}^{2}\oplus \dots \oplus {\equiv }_{II}^{\mathfrak{H}}{\zeta }_{II}^{\mathfrak{H}}={\oplus }_{{\Finv }=1}^{\mathfrak{H}}\left({\equiv }_{II}^{{\Finv }}{\zeta }_{II}^{{\Finv }}\right)$$

(1)

where the weight vector is represented by ${\equiv }_{II}^{\Finv }\in \left[\mathrm{0,1}\right]$ with $\sum_{\Finv =1}^{\mathfrak{H}}{\equiv }_{II}^{\Finv }=1$.

Theorem 1

Consider any finite collection of CIFSs ${\zeta }_{II}^{\Finv }=\left({\varpi }_{at}^{\Finv }{e}^{i2\pi \left({\varpi }_{\mathfrak{H}t}^{\Finv }\right)},{\Xi }_{at}^{\Finv }{e}^{i2\pi \left({\Xi }_{\mathfrak{H}t}^{\Finv }\right)}\right),\Finv =\mathrm{1,2},\dots ,\mathfrak{H}$. Then we prove that the result in Eq. (1) is also a CIFN, such as

$$\begin{aligned}&{\text{CIIFHIIWA}}\left({\zeta }_{II}^{1},{\zeta }_{II}^{2},\dots ,{\zeta }_{II}^{\mathfrak{H}}\right)\\ &\quad=\left(\begin{array}{c}\left(\frac{\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{at}^{{\Finv }}\right)}^{{\equiv }_{II}^{{\Finv }}}-\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1-{\varpi }_{at}^{{\Finv }}\right)}^{{\equiv }_{II}^{{\Finv }}}}{\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{at}^{{\Finv }}\right)}^{{\equiv }_{II}^{{\Finv }}}+\left({\dddot{\beth}}-1\right)\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1-{\varpi }_{at}^{{\Finv }}\right)}^{{\equiv }_{II}^{{\Finv }}}}\right){e}^{i2\pi \left(\frac{\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{\mathfrak{H}t}^{{\Finv }}\right)}^{{\equiv }_{II}^{{\Finv }}}-\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1-{\varpi }_{\mathfrak{H}t}^{{\Finv }}\right)}^{{\equiv }_{II}^{{\Finv }}}}{\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{\mathfrak{H}t}^{{\Finv }}\right)}^{{\equiv }_{II}^{{\Finv }}}+\left({\dddot{\beth}}-1\right)\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1-{\varpi }_{\mathfrak{H}t}^{{\Finv }}\right)}^{{\equiv }_{II}^{{\Finv }}}}\right)},\\ \left(\frac{{\dddot{\beth}}\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1-{\varpi }_{at}^{{\Finv }}\right)}^{{\equiv }_{II}^{{\Finv }}}-{\dddot{\beth}}\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1-{\varpi }_{at}^{{\Finv }}-{\Xi }_{at}^{{\Finv }}\right)}^{{\equiv }_{II}^{{\Finv }}}}{\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{at}^{{\Finv }}\right)}^{{\equiv }_{II}^{{\Finv }}}+\left({\dddot{\beth}}-1\right)\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1-{\varpi }_{at}^{{\Finv }}\right)}^{{\equiv }_{II}^{{\Finv }}}}\right){e}^{i2\pi \left(\frac{{\dddot{\beth}}\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1-{\varpi }_{\mathfrak{H}t}^{{\Finv }}\right)}^{{\equiv }_{II}^{{\Finv }}}-{\dddot{\beth}}\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1-{\varpi }_{\mathfrak{H}t}^{{\Finv }}-{\Xi }_{\mathfrak{H}t}^{{\Finv }}\right)}^{{\equiv }_{II}^{{\Finv }}}}{\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{\mathfrak{H}t}^{{\Finv }}\right)}^{{\equiv }_{II}^{{\Finv }}}+\left({\dddot{\beth}}-1\right)\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1-{\varpi }_{\mathfrak{H}t}^{{\Finv }}\right)}^{{\equiv }_{II}^{{\Finv }}}}\right)}\end{array}\right).\end{aligned}$$

(2)

Proof

We use mathematical induction to prove it. Firstly, we consider the value of $\mathfrak{H}=2$ in Eq. (2); then we have

$${\equiv }_{II}^{1}{\zeta }_{II}^{1}=\left(\begin{array}{c}\left(\frac{{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{at}^{1}\right)}^{{\equiv }_{II}^{1}}-{\left(1-{\varpi }_{at}^{1}\right)}^{{\equiv }_{II}^{1}}}{{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{at}^{1}\right)}^{{\equiv }_{II}^{1}}+\left({\dddot{\beth}}-1\right){\left(1-{\varpi }_{at}^{1}\right)}^{{\equiv }_{II}^{1}}}\right){e}^{i2\pi \left(\frac{{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{\mathfrak{H}t}^{1}\right)}^{{\equiv }_{II}^{1}}-{\left(1-{\varpi }_{\mathfrak{H}t}^{1}\right)}^{{\equiv }_{II}^{1}}}{{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{\mathfrak{H}t}^{1}\right)}^{{\equiv }_{II}^{1}}+\left({\dddot{\beth}}-1\right){\left(1-{\varpi }_{\mathfrak{H}t}^{1}\right)}^{{\equiv }_{II}^{1}}}\right)},\\ \left(\frac{{\dddot{\beth}}{\left(1-{\varpi }_{at}^{1}\right)}^{{\equiv }_{II}^{1}}-{\dddot{\beth}}{\left(1-{\varpi }_{at}^{1}-{\Xi }_{at}^{1}\right)}^{{\equiv }_{II}^{1}}}{{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{at}^{1}\right)}^{{\equiv }_{II}^{1}}+\left({\dddot{\beth}}-1\right){\left(1-{\varpi }_{at}^{1}\right)}^{{\equiv }_{II}^{1}}}\right){e}^{i2\pi \left(\frac{{\dddot{\beth}}{\left(1-{\varpi }_{\mathfrak{H}t}^{1}\right)}^{{\equiv }_{II}^{1}}-{\dddot{\beth}}{\left(1-{\varpi }_{\mathfrak{H}t}^{1}-{\Xi }_{\mathfrak{H}t}^{1}\right)}^{{\equiv }_{II}^{1}}}{{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{\mathfrak{H}t}^{1}\right)}^{{\equiv }_{II}^{1}}+\left({\dddot{\beth}}-1\right){\left(1-{\varpi }_{\mathfrak{H}t}^{1}\right)}^{{\equiv }_{II}^{1}}}\right)}\end{array}\right)$$

$${\equiv }_{II}^{2}{\zeta }_{II}^{2}=\left(\begin{array}{c}\left(\frac{{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{at}^{2}\right)}^{{\equiv }_{II}^{2}}-{\left(1-{\varpi }_{at}^{2}\right)}^{{\equiv }_{II}^{2}}}{{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{at}^{2}\right)}^{{\equiv }_{II}^{2}}+\left({\dddot{\beth}}-1\right){\left(1-{\varpi }_{at}^{2}\right)}^{{\equiv }_{II}^{2}}}\right){e}^{i2\pi \left(\frac{{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{\mathfrak{H}t}^{2}\right)}^{{\equiv }_{II}^{2}}-{\left(1-{\varpi }_{\mathfrak{H}t}^{2}\right)}^{{\equiv }_{II}^{2}}}{{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{\mathfrak{H}t}^{2}\right)}^{{\equiv }_{II}^{2}}+\left({\dddot{\beth}}-1\right){\left(1-{\varpi }_{\mathfrak{H}t}^{2}\right)}^{{\equiv }_{II}^{2}}}\right)},\\ \left(\frac{{\dddot{\beth}}{\left(1-{\varpi }_{at}^{2}\right)}^{{\equiv }_{II}^{2}}-{\dddot{\beth}}{\left(1-{\varpi }_{at}^{2}-{\Xi }_{at}^{2}\right)}^{{\equiv }_{II}^{2}}}{{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{at}^{2}\right)}^{{\equiv }_{II}^{2}}+\left({\dddot{\beth}}-1\right){\left(1-{\varpi }_{at}^{2}\right)}^{{\equiv }_{II}^{2}}}\right){e}^{i2\pi \left(\frac{{\dddot{\beth}}{\left(1-{\varpi }_{\mathfrak{H}t}^{2}\right)}^{{\equiv }_{II}^{2}}-{\dddot{\beth}}{\left(1-{\varpi }_{\mathfrak{H}t}^{2}-{\Xi }_{\mathfrak{H}t}^{2}\right)}^{{\equiv }_{II}^{2}}}{{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{\mathfrak{H}t}^{2}\right)}^{{\equiv }_{II}^{2}}+\left({\dddot{\beth}}-1\right){\left(1-{\varpi }_{\mathfrak{H}t}^{2}\right)}^{{\equiv }_{II}^{2}}}\right)}\end{array}\right).$$

Thus,

$$ \begin{aligned} & {\text{CIIFHIIWA}}\left({\zeta }_{II}^{1},{\zeta }_{II}^{2}\right)={\equiv }_{II}^{1}{\zeta }_{II}^{1}\oplus {\equiv }_{II}^{2}{\zeta }_{II}^{2} \\ & \quad =\left(\begin{array}{c}\left(\frac{{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{at}^{1}\right)}^{{\equiv }_{II}^{1}}-{\left(1-{\varpi }_{at}^{1}\right)}^{{\equiv }_{II}^{1}}}{{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{at}^{1}\right)}^{{\equiv }_{II}^{1}}+\left({\dddot{\beth}}-1\right){\left(1-{\varpi }_{at}^{1}\right)}^{{\equiv }_{II}^{1}}}\right){e}^{i2\pi \left(\frac{{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{\mathfrak{H}t}^{1}\right)}^{{\equiv }_{II}^{1}}-{\left(1-{\varpi }_{\mathfrak{H}t}^{1}\right)}^{{\equiv }_{II}^{1}}}{{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{\mathfrak{H}t}^{1}\right)}^{{\equiv }_{II}^{1}}+\left({\dddot{\beth}}-1\right){\left(1-{\varpi }_{\mathfrak{H}t}^{1}\right)}^{{\equiv }_{II}^{1}}}\right)},\\ \left(\frac{{\dddot{\beth}}{\left(1-{\varpi }_{at}^{1}\right)}^{{\equiv }_{II}^{1}}-{\dddot{\beth}}{\left(1-{\varpi }_{at}^{1}-{\Xi }_{at}^{1}\right)}^{{\equiv }_{II}^{1}}}{{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{at}^{1}\right)}^{{\equiv }_{II}^{1}}+\left({\dddot{\beth}}-1\right){\left(1-{\varpi }_{at}^{1}\right)}^{{\equiv }_{II}^{1}}}\right){e}^{i2\pi \left(\frac{{\dddot{\beth}}{\left(1-{\varpi }_{\mathfrak{H}t}^{1}\right)}^{{\equiv }_{II}^{1}}-{\dddot{\beth}}{\left(1-{\varpi }_{\mathfrak{H}t}^{1}-{\Xi }_{\mathfrak{H}t}^{1}\right)}^{{\equiv }_{II}^{1}}}{{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{\mathfrak{H}t}^{1}\right)}^{{\equiv }_{II}^{1}}+\left({\dddot{\beth}}-1\right){\left(1-{\varpi }_{\mathfrak{H}t}^{1}\right)}^{{\equiv }_{II}^{1}}}\right)}\end{array}\right)\\ &\quad\oplus \left(\begin{array}{c}\left(\frac{{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{at}^{2}\right)}^{{\equiv }_{II}^{2}}-{\left(1-{\varpi }_{at}^{2}\right)}^{{\equiv }_{II}^{2}}}{{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{at}^{2}\right)}^{{\equiv }_{II}^{2}}+\left({\dddot{\beth}}-1\right){\left(1-{\varpi }_{at}^{2}\right)}^{{\equiv }_{II}^{2}}}\right){e}^{i2\pi \left(\frac{{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{\mathfrak{H}t}^{2}\right)}^{{\equiv }_{II}^{2}}-{\left(1-{\varpi }_{\mathfrak{H}t}^{2}\right)}^{{\equiv }_{II}^{2}}}{{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{\mathfrak{H}t}^{2}\right)}^{{\equiv }_{II}^{2}}+\left({\dddot{\beth}}-1\right){\left(1-{\varpi }_{\mathfrak{H}t}^{2}\right)}^{{\equiv }_{II}^{2}}}\right)},\\ \left(\frac{{\dddot{\beth}}{\left(1-{\varpi }_{at}^{2}\right)}^{{\equiv }_{II}^{2}}-{\dddot{\beth}}{\left(1-{\varpi }_{at}^{2}-{\Xi }_{at}^{2}\right)}^{{\equiv }_{II}^{2}}}{{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{at}^{2}\right)}^{{\equiv }_{II}^{2}}+\left({\dddot{\beth}}-1\right){\left(1-{\varpi }_{at}^{2}\right)}^{{\equiv }_{II}^{2}}}\right){e}^{i2\pi \left(\frac{{\dddot{\beth}}{\left(1-{\varpi }_{\mathfrak{H}t}^{2}\right)}^{{\equiv }_{II}^{2}}-{\dddot{\beth}}{\left(1-{\varpi }_{\mathfrak{H}t}^{2}-{\Xi }_{\mathfrak{H}t}^{2}\right)}^{{\equiv }_{II}^{2}}}{{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{\mathfrak{H}t}^{2}\right)}^{{\equiv }_{II}^{2}}+\left({\dddot{\beth}}-1\right){\left(1-{\varpi }_{\mathfrak{H}t}^{2}\right)}^{{\equiv }_{II}^{2}}}\right)}\end{array}\right) \\ & \quad =\left(\begin{array}{c}\left(\frac{\prod_{\Finv =1}^{2}{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}-\prod_{\Finv =1}^{2}{\left(1-{\varpi }_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}}{\prod_{\Finv =1}^{2}{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}+\left({\dddot{\beth}}-1\right)\prod_{\Finv =1}^{2}{\left(1-{\varpi }_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}}\right){e}^{i2\pi \left(\frac{\prod_{\Finv =1}^{2}{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{\mathfrak{H}t}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}-\prod_{\Finv =1}^{2}{\left(1-{\varpi }_{\mathfrak{H}t}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}}{\prod_{\Finv =1}^{2}{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{\mathfrak{H}t}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}+\left({\dddot{\beth}}-1\right)\prod_{\Finv =1}^{2}{\left(1-{\varpi }_{\mathfrak{H}t}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}}\right)},\\ \left(\frac{{\dddot{\beth}}\prod_{\Finv =1}^{2}{\left(1-{\varpi }_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}-{\dddot{\beth}}\prod_{\Finv =1}^{2}{\left(1-{\varpi }_{at}^{\Finv }-{\Xi }_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}}{\prod_{\Finv =1}^{2}{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}+\left({\dddot{\beth}}-1\right)\prod_{\Finv =1}^{2}{\left(1-{\varpi }_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}}\right){e}^{i2\pi \left(\frac{{\dddot{\beth}}\prod_{\Finv =1}^{2}{\left(1-{\varpi }_{\mathfrak{H}t}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}-{\dddot{\beth}}\prod_{\Finv =1}^{2}{\left(1-{\varpi }_{\mathfrak{H}t}^{\Finv }-{\Xi }_{\mathfrak{H}t}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}}{\prod_{\Finv =1}^{2}{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{\mathfrak{H}t}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}+\left({\dddot{\beth}}-1\right)\prod_{\Finv =1}^{2}{\left(1-{\varpi }_{\mathfrak{H}t}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}}\right)}\end{array}\right). \end{aligned} $$

So Eq. (2) is held for $\mathfrak{H}=2$; furthermore, we consider that Eq. (2) is also held for $\mathfrak{H}=q$; then

$$\begin{aligned}&{\text{CIIFHIIWA}}\left({\zeta }_{II}^{1},{\zeta }_{II}^{2},\dots ,{\zeta }_{II}^{q}\right)\\ &\quad=\left(\begin{array}{c}\left(\frac{\prod_{\Finv =1}^{q}{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}-\prod_{\Finv =1}^{q}{\left(1-{\varpi }_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}}{\prod_{\Finv =1}^{q}{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}+\left({\dddot{\beth}}-1\right)\prod_{\Finv =1}^{q}{\left(1-{\varpi }_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}}\right){e}^{i2\pi \left(\frac{\prod_{\Finv =1}^{q}{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{\mathfrak{H}t}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}-\prod_{\Finv =1}^{q}{\left(1-{\varpi }_{\mathfrak{H}t}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}}{\prod_{\Finv =1}^{q}{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{\mathfrak{H}t}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}+\left({\dddot{\beth}}-1\right)\prod_{\Finv =1}^{q}{\left(1-{\varpi }_{\mathfrak{H}t}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}}\right)},\\ \left(\frac{{\dddot{\beth}}\prod_{\Finv =1}^{q}{\left(1-{\varpi }_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}-{\dddot{\beth}}\prod_{\Finv =1}^{q}{\left(1-{\varpi }_{at}^{\Finv }-{\Xi }_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}}{\prod_{\Finv =1}^{q}{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}+\left({\dddot{\beth}}-1\right)\prod_{\Finv =1}^{q}{\left(1-{\varpi }_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}}\right){e}^{i2\pi \left(\frac{{\dddot{\beth}}\prod_{\Finv =1}^{q}{\left(1-{\varpi }_{\mathfrak{H}t}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}-{\dddot{\beth}}\prod_{\Finv =1}^{q}{\left(1-{\varpi }_{\mathfrak{H}t}^{\Finv }-{\Xi }_{\mathfrak{H}t}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}}{\prod_{\Finv =1}^{q}{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{\mathfrak{H}t}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}+\left({\dddot{\beth}}-1\right)\prod_{\Finv =1}^{q}{\left(1-{\varpi }_{\mathfrak{H}t}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}}\right)}\end{array}\right);\end{aligned}$$

thus, we prove that the Eq. (2) is also held for $\mathfrak{H}=q+1$, such as

$$ \begin{aligned} & {\text{CIIFHIIWA}}\left({\zeta }_{II}^{1},{\zeta }_{II}^{2},\dots ,{\zeta }_{II}^{q+1}\right)={\oplus }_{\Finv =1}^{q}\left({\equiv }_{II}^{\Finv }{\zeta }_{II}^{\Finv }\right)\oplus {\equiv }_{II}^{q+1}{\zeta }_{II}^{q+1} \\ & \quad =\left(\begin{array}{c}\left(\frac{\prod_{\Finv =1}^{q}{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}-\prod_{\Finv =1}^{q}{\left(1-{\varpi }_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}}{\prod_{\Finv =1}^{q}{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}+\left({\dddot{\beth}}-1\right)\prod_{\Finv =1}^{q}{\left(1-{\varpi }_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}}\right){e}^{i2\pi \left(\frac{\prod_{\Finv =1}^{q}{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{\mathfrak{H}t}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}-\prod_{\Finv =1}^{q}{\left(1-{\varpi }_{\mathfrak{H}t}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}}{\prod_{\Finv =1}^{q}{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{\mathfrak{H}t}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}+\left({\dddot{\beth}}-1\right)\prod_{\Finv =1}^{q}{\left(1-{\varpi }_{\mathfrak{H}t}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}}\right)},\\ \left(\frac{{\dddot{\beth}}\prod_{\Finv =1}^{q}{\left(1-{\varpi }_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}-{\dddot{\beth}}\prod_{\Finv =1}^{q}{\left(1-{\varpi }_{at}^{\Finv }-{\Xi }_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}}{\prod_{\Finv =1}^{q}{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}+\left({\dddot{\beth}}-1\right)\prod_{\Finv =1}^{q}{\left(1-{\varpi }_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}}\right){e}^{i2\pi \left(\frac{{\dddot{\beth}}\prod_{\Finv =1}^{q}{\left(1-{\varpi }_{\mathfrak{H}t}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}-{\dddot{\beth}}\prod_{\Finv =1}^{q}{\left(1-{\varpi }_{\mathfrak{H}t}^{\Finv }-{\Xi }_{\mathfrak{H}t}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}}{\prod_{\Finv =1}^{q}{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{\mathfrak{H}t}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}+\left({\dddot{\beth}}-1\right)\prod_{\Finv =1}^{q}{\left(1-{\varpi }_{\mathfrak{H}t}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}}\right)}\end{array}\right)\oplus {\equiv }_{II}^{q+1}{\zeta }_{II}^{q+1} \\ & \quad =\left(\begin{array}{c}\left(\frac{\prod_{\Finv =1}^{q}{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}-\prod_{\Finv =1}^{q}{\left(1-{\varpi }_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}}{\prod_{\Finv =1}^{q}{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}+\left({\dddot{\beth}}-1\right)\prod_{\Finv =1}^{q}{\left(1-{\varpi }_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}}\right){e}^{i2\pi \left(\frac{\prod_{\Finv =1}^{q}{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{\mathfrak{H}t}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}-\prod_{\Finv =1}^{q}{\left(1-{\varpi }_{\mathfrak{H}t}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}}{\prod_{\Finv =1}^{q}{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{\mathfrak{H}t}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}+\left({\dddot{\beth}}-1\right)\prod_{\Finv =1}^{q}{\left(1-{\varpi }_{\mathfrak{H}t}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}}\right)},\\ \left(\frac{{\dddot{\beth}}\prod_{\Finv =1}^{q}{\left(1-{\varpi }_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}-{\dddot{\beth}}\prod_{\Finv =1}^{q}{\left(1-{\varpi }_{at}^{\Finv }-{\Xi }_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}}{\prod_{\Finv =1}^{q}{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}+\left({\dddot{\beth}}-1\right)\prod_{\Finv =1}^{q}{\left(1-{\varpi }_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}}\right){e}^{i2\pi \left(\frac{{\dddot{\beth}}\prod_{\Finv =1}^{q}{\left(1-{\varpi }_{\mathfrak{H}t}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}-{\dddot{\beth}}\prod_{\Finv =1}^{q}{\left(1-{\varpi }_{\mathfrak{H}t}^{\Finv }-{\Xi }_{\mathfrak{H}t}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}}{\prod_{\Finv =1}^{q}{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{\mathfrak{H}t}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}+\left({\dddot{\beth}}-1\right)\prod_{\Finv =1}^{q}{\left(1-{\varpi }_{\mathfrak{H}t}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}}\right)}\end{array}\right)\\ &\quad\quad\oplus \left(\begin{array}{c}\left(\frac{{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{at}^{q+1}\right)}^{{\equiv }_{II}^{q+1}}-{\left(1-{\varpi }_{at}^{q+1}\right)}^{{\equiv }_{II}^{q+1}}}{{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{at}^{q+1}\right)}^{{\equiv }_{II}^{q+1}}+\left({\dddot{\beth}}-1\right){\left(1-{\varpi }_{at}^{q+1}\right)}^{{\equiv }_{II}^{q+1}}}\right){e}^{i2\pi \left(\frac{{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{\mathfrak{H}t}^{q+1}\right)}^{{\equiv }_{II}^{q+1}}-{\left(1-{\varpi }_{\mathfrak{H}t}^{q+1}\right)}^{{\equiv }_{II}^{q+1}}}{{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{\mathfrak{H}t}^{q+1}\right)}^{{\equiv }_{II}^{q+1}}+\left({\dddot{\beth}}-1\right){\left(1-{\varpi }_{\mathfrak{H}t}^{q+1}\right)}^{{\equiv }_{II}^{q+1}}}\right)},\\ \left(\frac{{\dddot{\beth}}{\left(1-{\varpi }_{at}^{q+1}\right)}^{{\equiv }_{II}^{q+1}}-{\dddot{\beth}}{\left(1-{\varpi }_{at}^{q+1}-{\Xi }_{at}^{q+1}\right)}^{{\equiv }_{II}^{q+1}}}{{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{at}^{q+1}\right)}^{{\equiv }_{II}^{q+1}}+\left({\dddot{\beth}}-1\right){\left(1-{\varpi }_{at}^{q+1}\right)}^{{\equiv }_{II}^{q+1}}}\right){e}^{i2\pi \left(\frac{{\dddot{\beth}}{\left(1-{\varpi }_{\mathfrak{H}t}^{q+1}\right)}^{{\equiv }_{II}^{q+1}}-{\dddot{\beth}}{\left(1-{\varpi }_{\mathfrak{H}t}^{q+1}-{\Xi }_{\mathfrak{H}t}^{q+1}\right)}^{{\equiv }_{II}^{q+1}}}{{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{\mathfrak{H}t}^{q+1}\right)}^{{\equiv }_{II}^{q+1}}+\left({\dddot{\beth}}-1\right){\left(1-{\varpi }_{\mathfrak{H}t}^{q+1}\right)}^{{\equiv }_{II}^{q+1}}}\right)}\end{array}\right) \\ & \quad =\left(\begin{array}{c}\left(\frac{\prod_{\Finv =1}^{q+1}{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}-\prod_{\Finv =1}^{q+1}{\left(1-{\varpi }_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}}{\prod_{\Finv =1}^{q+1}{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}+\left({\dddot{\beth}}-1\right)\prod_{\Finv =1}^{q+1}{\left(1-{\varpi }_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}}\right){e}^{i2\pi \left(\frac{\prod_{\Finv =1}^{q+1}{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{\mathfrak{H}t}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}-\prod_{\Finv =1}^{q+1}{\left(1-{\varpi }_{\mathfrak{H}t}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}}{\prod_{\Finv =1}^{q+1}{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{\mathfrak{H}t}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}+\left({\dddot{\beth}}-1\right)\prod_{\Finv =1}^{q+1}{\left(1-{\varpi }_{\mathfrak{H}t}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}}\right)},\\ \left(\frac{{\dddot{\beth}}\prod_{\Finv =1}^{q+1}{\left(1-{\varpi }_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}-{\dddot{\beth}}\prod_{\Finv =1}^{q+1}{\left(1-{\varpi }_{at}^{\Finv }-{\Xi }_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}}{\prod_{\Finv =1}^{q+1}{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}+\left({\dddot{\beth}}-1\right)\prod_{\Finv =1}^{q+1}{\left(1-{\varpi }_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}}\right){e}^{i2\pi \left(\frac{{\dddot{\beth}}\prod_{\Finv =1}^{q+1}{\left(1-{\varpi }_{\mathfrak{H}t}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}-{\dddot{\beth}}\prod_{\Finv =1}^{q+1}{\left(1-{\varpi }_{\mathfrak{H}t}^{\Finv }-{\Xi }_{\mathfrak{H}t}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}}{\prod_{\Finv =1}^{q+1}{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{\mathfrak{H}t}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}+\left({\dddot{\beth}}-1\right)\prod_{\Finv =1}^{q+1}{\left(1-{\varpi }_{\mathfrak{H}t}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}}\right)}\end{array}\right). \end{aligned} $$

Hence, the Eq. (2) is held for all possible positive values of $\mathfrak{H}$. Moreover, we verify the idempotency, monotonicity, and boundedness of this operator.

Property 1

Consider any finite collection of CIFSs ${\zeta }_{II}^{\Finv }=\left({\varpi }_{at}^{\Finv }{e}^{i2\pi \left({\varpi }_{\mathfrak{H}t}^{\Finv }\right)},{\Xi }_{at}^{\Finv }{e}^{i2\pi \left({\Xi }_{\mathfrak{H}t}^{\Finv }\right)}\right),\Finv =\mathrm{1,2},\dots ,\mathfrak{H}$. If ${\zeta }_{II}^{\Finv }={\zeta }_{II}=\left({\varpi }_{at}{e}^{i2\pi \left({\varpi }_{\mathfrak{H}t}\right)},{\Xi }_{at}{e}^{i2\pi \left({\Xi }_{\mathfrak{H}t}\right)}\right)$, then

$${\text{CIIFHIIWA}}\left({\zeta }_{II}^{1},{\zeta }_{II}^{2},\dots ,{\zeta }_{II}^{\mathfrak{H}}\right)={\zeta }_{II}.$$

Proof

If ${\zeta }_{II}^{\Finv }={\zeta }_{II}=\left({\varpi }_{at}{e}^{i2\pi \left({\varpi }_{\mathfrak{H}t}\right)},{\Xi }_{at}{e}^{i2\pi \left({\Xi }_{\mathfrak{H}t}\right)}\right)$, then

$$ \begin{aligned}&{\text{CIIFHIIWA}}\left({\zeta }_{II}^{1},{\zeta }_{II}^{2},\dots ,{\zeta }_{II}^{\mathfrak{H}}\right)\\ &\quad=\left(\begin{array}{c}\left(\frac{\prod_{\Finv =1}^{\mathfrak{H}}{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{at}\right)}^{{\equiv }_{II}^{\Finv }}-\prod_{\Finv =1}^{\mathfrak{H}}{\left(1-{\varpi }_{at}\right)}^{{\equiv }_{II}^{\Finv }}}{\prod_{\Finv =1}^{\mathfrak{H}}{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{at}\right)}^{{\equiv }_{II}^{\Finv }}+\left({\dddot{\beth}}-1\right)\prod_{\Finv =1}^{\mathfrak{H}}{\left(1-{\varpi }_{at}\right)}^{{\equiv }_{II}^{\Finv }}}\right){e}^{i2\pi \left(\frac{\prod_{\Finv =1}^{\mathfrak{H}}{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{\mathfrak{H}t}\right)}^{{\equiv }_{II}^{\Finv }}-\prod_{\Finv =1}^{\mathfrak{H}}{\left(1-{\varpi }_{\mathfrak{H}t}\right)}^{{\equiv }_{II}^{\Finv }}}{\prod_{\Finv =1}^{\mathfrak{H}}{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{\mathfrak{H}t}\right)}^{{\equiv }_{II}^{\Finv }}+\left({\dddot{\beth}}-1\right)\prod_{\Finv =1}^{\mathfrak{H}}{\left(1-{\varpi }_{\mathfrak{H}t}\right)}^{{\equiv }_{II}^{\Finv }}}\right)},\\ \left(\frac{{\dddot{\beth}}\prod_{\Finv =1}^{\mathfrak{H}}{\left(1-{\varpi }_{at}\right)}^{{\equiv }_{II}^{\Finv }}-{\dddot{\beth}}\prod_{\Finv =1}^{\mathfrak{H}}{\left(1-{\varpi }_{at}-{\Xi }_{at}\right)}^{{\equiv }_{II}^{\Finv }}}{\prod_{\Finv =1}^{\mathfrak{H}}{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{at}\right)}^{{\equiv }_{II}^{\Finv }}+\left({\dddot{\beth}}-1\right)\prod_{\Finv =1}^{\mathfrak{H}}{\left(1-{\varpi }_{at}\right)}^{{\equiv }_{II}^{\Finv }}}\right){e}^{i2\pi \left(\frac{{\dddot{\beth}}\prod_{\Finv =1}^{\mathfrak{H}}{\left(1-{\varpi }_{\mathfrak{H}t}\right)}^{{\equiv }_{II}^{\Finv }}-{\dddot{\beth}}\prod_{\Finv =1}^{\mathfrak{H}}{\left(1-{\varpi }_{\mathfrak{H}t}-{\Xi }_{\mathfrak{H}t}\right)}^{{\equiv }_{II}^{\Finv }}}{\prod_{\Finv =1}^{\mathfrak{H}}{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{\mathfrak{H}t}\right)}^{{\equiv }_{II}^{\Finv }}+\left({\dddot{\beth}}-1\right)\prod_{\Finv =1}^{\mathfrak{H}}{\left(1-{\varpi }_{\mathfrak{H}t}\right)}^{{\equiv }_{II}^{\Finv }}}\right)}\end{array}\right)\\ &\quad=\left(\begin{array}{c}\left(\frac{{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{at}\right)}^{\sum_{\Finv =1}^{\mathfrak{H}}{\equiv }_{II}^{\Finv }}-{\left(1-{\varpi }_{at}\right)}^{\sum_{\Finv =1}^{\mathfrak{H}}{\equiv }_{II}^{\Finv }}}{{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{at}\right)}^{\sum_{\Finv =1}^{\mathfrak{H}}{\equiv }_{II}^{\Finv }}+\left({\dddot{\beth}}-1\right){\left(1-{\varpi }_{at}\right)}^{\sum_{\Finv =1}^{\mathfrak{H}}{\equiv }_{II}^{\Finv }}}\right){e}^{i2\pi \left(\frac{{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{\mathfrak{H}t}\right)}^{\sum_{\Finv =1}^{\mathfrak{H}}{\equiv }_{II}^{\Finv }}-{\left(1-{\varpi }_{\mathfrak{H}t}\right)}^{\sum_{\Finv =1}^{\mathfrak{H}}{\equiv }_{II}^{\Finv }}}{{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{\mathfrak{H}t}\right)}^{\sum_{\Finv =1}^{\mathfrak{H}}{\equiv }_{II}^{\Finv }}+\left({\dddot{\beth}}-1\right){\left(1-{\varpi }_{\mathfrak{H}t}\right)}^{\sum_{\Finv =1}^{\mathfrak{H}}{\equiv }_{II}^{\Finv }}}\right)},\\ \left(\frac{{\dddot{\beth}}{\left(1-{\varpi }_{at}\right)}^{\sum_{\Finv =1}^{\mathfrak{H}}{\equiv }_{II}^{\Finv }}-{\dddot{\beth}}{\left(1-{\varpi }_{at}-{\Xi }_{at}\right)}^{\sum_{\Finv =1}^{\mathfrak{H}}{\equiv }_{II}^{\Finv }}}{{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{at}\right)}^{\sum_{\Finv =1}^{\mathfrak{H}}{\equiv }_{II}^{\Finv }}+\left({\dddot{\beth}}-1\right){\left(1-{\varpi }_{at}\right)}^{\sum_{\Finv =1}^{\mathfrak{H}}{\equiv }_{II}^{\Finv }}}\right){e}^{i2\pi \left(\frac{{\dddot{\beth}}{\left(1-{\varpi }_{\mathfrak{H}t}\right)}^{\sum_{\Finv =1}^{\mathfrak{H}}{\equiv }_{II}^{\Finv }}-{\dddot{\beth}}{\left(1-{\varpi }_{\mathfrak{H}t}-{\Xi }_{\mathfrak{H}t}\right)}^{\sum_{\Finv =1}^{\mathfrak{H}}{\equiv }_{II}^{\Finv }}}{{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{\mathfrak{H}t}\right)}^{\sum_{\Finv =1}^{\mathfrak{H}}{\equiv }_{II}^{\Finv }}+\left({\dddot{\beth}}-1\right){\left(1-{\varpi }_{\mathfrak{H}t}\right)}^{\sum_{\Finv =1}^{\mathfrak{H}}{\equiv }_{II}^{\Finv }}}\right)}\end{array}\right)\\ &\quad=\left(\begin{array}{c}\left(\frac{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{at}\right)-\left(1-{\varpi }_{at}\right)}{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{at}\right)+\left({\dddot{\beth}}-1\right)\left(1-{\varpi }_{at}\right)}\right){e}^{i2\pi \left(\frac{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{\mathfrak{H}t}\right)-\left(1-{\varpi }_{\mathfrak{H}t}\right)}{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{\mathfrak{H}t}\right)+\left({\dddot{\beth}}-1\right)\left(1-{\varpi }_{\mathfrak{H}t}\right)}\right)},\\ \left(\frac{{\dddot{\beth}}\left(1-{\varpi }_{at}\right)-{\dddot{\beth}}\left(1-{\varpi }_{at}-{\Xi }_{at}\right)}{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{at}\right)+\left({\dddot{\beth}}-1\right)\left(1-{\varpi }_{at}\right)}\right){e}^{i2\pi \left(\frac{{\dddot{\beth}}\left(1-{\varpi }_{\mathfrak{H}t}\right)-{\dddot{\beth}}\left(1-{\varpi }_{\mathfrak{H}t}-{\Xi }_{\mathfrak{H}t}\right)}{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{\mathfrak{H}t}\right)+\left({\dddot{\beth}}-1\right)\left(1-{\varpi }_{\mathfrak{H}t}\right)}\right)}\end{array}\right)\\ &\quad=\left(\begin{array}{c}\left(\frac{\left(1+{\dddot{\beth}}{\varpi }_{at}-{\varpi }_{at}-1+{\varpi }_{at}\right)}{\left(1+{\dddot{\beth}}{\varpi }_{at}-{\varpi }_{at}\right)+\left({\dddot{\beth}}\left(1-{\varpi }_{at}\right)-\left(1-{\varpi }_{at}\right)\right)}\right){e}^{i2\pi \left(\frac{\left(1+{\dddot{\beth}}{\varpi }_{\mathfrak{H}t}-{\varpi }_{\mathfrak{H}t}-1+{\varpi }_{\mathfrak{H}t}\right)}{\left(1+{\dddot{\beth}}{\varpi }_{\mathfrak{H}t}-{\varpi }_{\mathfrak{H}t}\right)+\left({\dddot{\beth}}\left(1-{\varpi }_{\mathfrak{H}t}\right)-\left(1-{\varpi }_{\mathfrak{H}t}\right)\right)}\right)},\\ \left(\frac{\left({\dddot{\beth}}-{\dddot{\beth}}{\varpi }_{at}-{\dddot{\beth}}+{\dddot{\beth}}{\varpi }_{at}+{\dddot{\beth}}{\Xi }_{at}\right)}{\left(1+\left({\dddot{\beth}}{\varpi }_{at}-{\varpi }_{at}\right)\right)+\left({\dddot{\beth}}\left(1-{\varpi }_{at}\right)-\left(1-{\varpi }_{at}\right)\right)}\right){e}^{i2\pi \left(\frac{\left({\dddot{\beth}}-{\dddot{\beth}}{\varpi }_{\mathfrak{H}t}-{\dddot{\beth}}+{\dddot{\beth}}{\varpi }_{\mathfrak{H}t}+{\dddot{\beth}}{\Xi }_{\mathfrak{H}t}\right)}{\left(1+\left({\dddot{\beth}}{\varpi }_{\mathfrak{H}t}-{\varpi }_{\mathfrak{H}t}\right)\right)+\left({\dddot{\beth}}\left(1-{\varpi }_{\mathfrak{H}t}\right)-\left(1-{\varpi }_{\mathfrak{H}t}\right)\right)}\right)}\end{array}\right)\\ &\quad=\left({\varpi }_{at}{e}^{i2\pi \left({\varpi }_{\mathfrak{H}t}\right)},{\Xi }_{at}{e}^{i2\pi \left({\Xi }_{\mathfrak{H}t}\right)}\right)={\zeta }_{II}.\end{aligned}$$

Property 2

Consider any finite collection of CIFSs ${\zeta }_{II}^{\Finv }=\left({\varpi }_{at}^{\Finv }{e}^{i2\pi \left({\varpi }_{\mathfrak{H}t}^{\Finv }\right)},{\Xi }_{at}^{\Finv }{e}^{i2\pi \left({\Xi }_{\mathfrak{H}t}^{\Finv }\right)}\right),\Finv =\mathrm{1,2},\dots ,\mathfrak{H}$. If ${\zeta }_{II}^{\Finv }\le {{\zeta }^{\#}}_{II}^{\Finv }$, then

$${\text{CIIFHIIWA}}\left({\zeta }_{II}^{1},{\zeta }_{II}^{2},\dots ,{\zeta }_{II}^{\mathfrak{H}}\right)\le {\text{CIIFHIIWA}}\left({{\zeta }^{\#}}_{II}^{1},{{\zeta }^{\#}}_{II}^{2},\dots ,{{\zeta }^{\#}}_{II}^{\mathfrak{H}}\right).$$

Proof

If ${\zeta }_{II}^{\Finv }\le {{\zeta }^{\#}}_{II}^{\Finv }$, then ${\varpi }_{at}^{\Finv }\le {{\varpi }^{\#}}_{at}^{\Finv },{\varpi }_{\mathfrak{H}t}^{\Finv }\le {{\varpi }^{\#}}_{\mathfrak{H}t}^{\Finv }$ and ${\Xi }_{at}^{\Finv }\ge {{\Xi }^{\#}}_{at}^{\Finv },{\Xi }_{\mathfrak{H}t}^{\Finv }\ge {{\Xi }^{\#}}_{\mathfrak{H}t}^{\Finv }$; thus,

$$ \begin{aligned} & {\varpi }_{at}^{\Finv }\le {{\varpi }^{\#}}_{at}^{\Finv }\Rightarrow 1-{\varpi }_{at}^{\Finv }\ge 1-{{\varpi }^{\#}}_{at}^{\Finv } \\ & \quad \Rightarrow {\left(1-{\varpi }_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}\ge {\left(1-{{\varpi }^{\#}}_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}\Rightarrow \prod_{\Finv =1}^{\mathfrak{H}}{\left(1-{\varpi }_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}\ge \prod_{\Finv =1}^{\mathfrak{H}}{\left(1-{{\varpi }^{\#}}_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }} \Rightarrow -\prod_{\Finv =1}^{\mathfrak{H}}{\left(1-{\varpi }_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}\le -\prod_{\Finv =1}^{\mathfrak{H}}{\left(1-{{\varpi }^{\#}}_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }} \\& \quad \Rightarrow \prod_{\Finv =1}^{\mathfrak{H}}{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}-\prod_{\Finv =1}^{\mathfrak{H}}{\left(1-{\varpi }_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}\le \prod_{\Finv =1}^{\mathfrak{H}}{\left(1+\left({\dddot{\beth}}-1\right){{\varpi }^{\#}}_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}-\prod_{\Finv =1}^{\mathfrak{H}}{\left(1-{{\varpi }^{\#}}_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }} \\ & \quad \Rightarrow \frac{\prod_{\Finv =1}^{\mathfrak{H}}{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}-\prod_{\Finv =1}^{\mathfrak{H}}{\left(1-{\varpi }_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}}{\prod_{\Finv =1}^{\mathfrak{H}}{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}+\left({\dddot{\beth}}-1\right)\prod_{\Finv =1}^{\mathfrak{H}}{\left(1-{\varpi }_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}}\le \frac{\prod_{\Finv =1}^{\mathfrak{H}}{\left(1+\left({\dddot{\beth}}-1\right){{\varpi }^{\#}}_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}-\prod_{\Finv =1}^{\mathfrak{H}}{\left(1-{{\varpi }^{\#}}_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}}{\prod_{\Finv =1}^{\mathfrak{H}}{\left(1+\left({\dddot{\beth}}-1\right){{\varpi }^{\#}}_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}+\left({\dddot{\beth}}-1\right)\prod_{\Finv =1}^{\mathfrak{H}}{\left(1-{{\varpi }^{\#}}_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}}. \end{aligned} $$

Similarly, we discuss the phase term for truth grade, such as

$$\begin{aligned}{\varpi }_{\mathfrak{H}t}^{\Finv }&\le {{\varpi }^{\#}}_{\mathfrak{H}t}^{\Finv }\Rightarrow \frac{\prod_{\Finv =1}^{\mathfrak{H}}{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{\mathfrak{H}t}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}-\prod_{\Finv =1}^{\mathfrak{H}}{\left(1-{\varpi }_{\mathfrak{H}t}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}}{\prod_{\Finv =1}^{\mathfrak{H}}{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{\mathfrak{H}t}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}+\left({\dddot{\beth}}-1\right)\prod_{\Finv =1}^{\mathfrak{H}}{\left(1-{\varpi }_{\mathfrak{H}t}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}}\\ &\le \frac{\prod_{\Finv =1}^{\mathfrak{H}}{\left(1+\left({\dddot{\beth}}-1\right){{\varpi }^{\#}}_{\mathfrak{H}t}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}-\prod_{\Finv =1}^{\mathfrak{H}}{\left(1-{{\varpi }^{\#}}_{\mathfrak{H}t}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}}{\prod_{\Finv =1}^{\mathfrak{H}}{\left(1+\left({\dddot{\beth}}-1\right){{\varpi }^{\#}}_{\mathfrak{H}t}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}+\left({\dddot{\beth}}-1\right)\prod_{\Finv =1}^{\mathfrak{H}}{\left(1-{{\varpi }^{\#}}_{\mathfrak{H}t}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}}.\end{aligned}$$

Furthermore, we discuss it for amplitude for non-membership grades, such as

$$ \begin{aligned} {\Xi }_{at}^{\Finv }&\ge {{\Xi }^{\#}}_{at}^{\Finv }\Rightarrow \left(1-{\Xi }_{at}^{\Finv }\right)\le \left(1-{{\Xi }^{\#}}_{at}^{\Finv }\right) \\ & \Rightarrow \left(1-{\varpi }_{at}^{\Finv }-{\Xi }_{at}^{\Finv }\right)\ge \left(1-{{\varpi }^{\#}}_{at}^{\Finv }-{{\Xi }^{\#}}_{at}^{\Finv }\right)\Rightarrow {\left(1-{\varpi }_{at}^{\Finv }-{\Xi }_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}\ge {\left(1-{{\varpi }^{\#}}_{at}^{\Finv }-{{\Xi }^{\#}}_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }} \\ & \Rightarrow \prod_{\Finv =1}^{\mathfrak{H}}{\left(1-{\varpi }_{at}^{\Finv }-{\Xi }_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}\ge \prod_{\Finv =1}^{\mathfrak{H}}{\left(1-{{\varpi }^{\#}}_{at}^{\Finv }-{{\Xi }^{\#}}_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }} \\ & \Rightarrow -{\dddot{\beth}}\prod_{\Finv =1}^{\mathfrak{H}}{\left(1-{\varpi }_{at}^{\Finv }-{\Xi }_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}\ge -{\dddot{\beth}}\prod_{\Finv =1}^{\mathfrak{H}}{\left(1-{{\varpi }^{\#}}_{at}^{\Finv }-{{\Xi }^{\#}}_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }} \\ & \Rightarrow {\dddot{\beth}}\prod_{\Finv =1}^{\mathfrak{H}}{\left(1-{\varpi }_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}-{\dddot{\beth}}\prod_{\Finv =1}^{\mathfrak{H}}{\left(1-{\varpi }_{at}^{\Finv }-{\Xi }_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}\ge {\dddot{\beth}}\prod_{\Finv =1}^{\mathfrak{H}}{\left(1-{{\varpi }^{\#}}_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}-{\dddot{\beth}}\prod_{\Finv =1}^{\mathfrak{H}}{\left(1-{{\varpi }^{\#}}_{at}^{\Finv }-{{\Xi }^{\#}}_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }} \\ & \Rightarrow \frac{{\dddot{\beth}}\prod_{\Finv =1}^{\mathfrak{H}}{\left(1-{\varpi }_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}-{\dddot{\beth}}\prod_{\Finv =1}^{\mathfrak{H}}{\left(1-{\varpi }_{at}^{\Finv }-{\Xi }_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}}{\prod_{\Finv =1}^{\mathfrak{H}}{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}+\left({\dddot{\beth}}-1\right)\prod_{\Finv =1}^{\mathfrak{H}}{\left(1-{\varpi }_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}} \\ & \ge \frac{{\dddot{\beth}}\prod_{\Finv =1}^{\mathfrak{H}}{\left(1-{{\varpi }^{\#}}_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}-{\dddot{\beth}}\prod_{\Finv =1}^{\mathfrak{H}}{\left(1-{{\varpi }^{\#}}_{at}^{\Finv }-{{\Xi }^{\#}}_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}}{\prod_{\Finv =1}^{\mathfrak{H}}{\left(1+\left({\dddot{\beth}}-1\right){{\varpi }^{\#}}_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}+\left({\dddot{\beth}}-1\right)\prod_{\Finv =1}^{\mathfrak{H}}{\left(1-{{\varpi }^{\#}}_{at}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}}. \end{aligned} $$

Similarly, we discuss the phase term for truth grade, such as

$$ \begin{aligned} {\Xi }_{\mathfrak{H}t}^{\Finv } & \ge {{\Xi }^{\#}}_{\mathfrak{H}t}^{\Finv }\Rightarrow \frac{{\dddot{\beth}}\prod_{\Finv =1}^{\mathfrak{H}}{\left(1-{\varpi }_{\mathfrak{H}t}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}-{\dddot{\beth}}\prod_{\Finv =1}^{\mathfrak{H}}{\left(1-{\varpi }_{\mathfrak{H}t}^{\Finv }-{\Xi }_{\mathfrak{H}t}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}}{\prod_{\Finv =1}^{\mathfrak{H}}{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{\mathfrak{H}t}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}+\left({\dddot{\beth}}-1\right)\prod_{\Finv =1}^{\mathfrak{H}}{\left(1-{\varpi }_{\mathfrak{H}t}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}} \\ & \ge \frac{{\dddot{\beth}}\prod_{\Finv =1}^{\mathfrak{H}}{\left(1-{{\varpi }^{\#}}_{\mathfrak{H}t}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}-{\dddot{\beth}}\prod_{\Finv =1}^{\mathfrak{H}}{\left(1-{{\varpi }^{\#}}_{\mathfrak{H}t}^{\Finv }-{{\Xi }^{\#}}_{\mathfrak{H}t}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}}{\prod_{\Finv =1}^{\mathfrak{H}}{\left(1+\left({\dddot{\beth}}-1\right){{\varpi }^{\#}}_{\mathfrak{H}t}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}+\left({\dddot{\beth}}-1\right)\prod_{\Finv =1}^{\mathfrak{H}}{\left(1-{{\varpi }^{\#}}_{\mathfrak{H}t}^{\Finv }\right)}^{{\equiv }_{II}^{\Finv }}}. \end{aligned} $$

Thus, based on the score value and accuracy value, we can easily get the result, such as

$${\text{CIIFHIIWA}}\left({\zeta }_{II}^{1},{\zeta }_{II}^{2},\dots ,{\zeta }_{II}^{\mathfrak{H}}\right)\le {\text{CIIFHIIWA}}\left({{\zeta }^{\#}}_{II}^{1},{{\zeta }^{\#}}_{II}^{2},\dots ,{{\zeta }^{\#}}_{II}^{\mathfrak{H}}\right).$$

Property 3

Consider any finite collection of CIFSs ${\zeta }_{II}^{\Finv }=\left({\varpi }_{at}^{\Finv }{e}^{i2\pi \left({\varpi }_{\mathfrak{H}t}^{\Finv }\right)},{\Xi }_{at}^{\Finv }{e}^{i2\pi \left({\Xi }_{\mathfrak{H}t}^{\Finv }\right)}\right),\Finv =\mathrm{1,2},\dots ,\mathfrak{H}$. If ${\zeta }_{II}^{-}=\left(\underset{\Finv }{{\text{min}}}{\varpi }_{at}^{\Finv }{e}^{i2\pi \left(\underset{\Finv }{{\text{min}}}{\varpi }_{\mathfrak{H}t}^{\Finv }\right)},\underset{\Finv }{{\text{max}}}{\Xi }_{at}^{\Finv }{e}^{i2\pi \left(\underset{\Finv }{{\text{max}}}{\Xi }_{\mathfrak{H}t}^{\Finv }\right)}\right)$ and ${\zeta }_{II}^{+}=\left(\underset{\Finv }{{\text{max}}}{\varpi }_{at}^{\Finv }{e}^{i2\pi \left(\underset{\Finv }{{\text{max}}}{\varpi }_{\mathfrak{H}t}^{\Finv }\right)},\underset{\Finv }{{\text{min}}}{\Xi }_{at}^{\Finv }{e}^{i2\pi \left(\underset{\Finv }{{\text{min}}}{\Xi }_{\mathfrak{H}t}^{\Finv }\right)}\right)$, then

$${\zeta }_{II}^{-}\le {\text{CIIFHIIWA}}\left({\zeta }_{II}^{1},{\zeta }_{II}^{2},\dots ,{\zeta }_{II}^{\mathfrak{H}}\right)\le {\zeta }_{II}^{+}.$$

Proof

Using property 1 and property 2, we have

$${\text{CIIFHIIWA}}\left({\zeta }_{II}^{1},{\zeta }_{II}^{2},\dots ,{\zeta }_{II}^{\mathfrak{H}}\right)\le {\text{CIIFHIIWA}}\left({{\zeta }^{+}}_{II}^{1},{{\zeta }^{+}}_{II}^{2},\dots ,{{\zeta }^{+}}_{II}^{\mathfrak{H}}\right)={\zeta }_{II}^{+},$$

$${\text{CIIFHIIWA}}\left({\zeta }_{II}^{1},{\zeta }_{II}^{2},\dots ,{\zeta }_{II}^{\mathfrak{H}}\right)\ge {\text{CIIFHIIWA}}\left({{\zeta }^{-}}_{II}^{1},{{\zeta }^{-}}_{II}^{2},\dots ,{{\zeta }^{-}}_{II}^{\mathfrak{H}}\right)={\zeta }_{II}^{-}.$$

Thus,

$${\zeta }_{II}^{-}\le {\text{CIIFHIIWA}}\left({\zeta }_{II}^{1},{\zeta }_{II}^{2},\dots ,{\zeta }_{II}^{\mathfrak{H}}\right)\le {\zeta }_{II}^{+}.$$

Definition 8

Consider any finite collection of CIFSs ${\zeta }_{II}^{\Finv }=\left({\varpi }_{at}^{\Finv }{e}^{i2\pi \left({\varpi }_{\mathfrak{H}t}^{\Finv }\right)},{\Xi }_{at}^{\Finv }{e}^{i2\pi \left({\Xi }_{\mathfrak{H}t}^{\Finv }\right)}\right), \Finv =\mathrm{1,2},\dots , \mathfrak{H}$; then the CIF Hamacher interaction ordered weighted averaging (CIFHIOWA) operator is proposed as

$${\text{CIIFHIIOWA}}\left({\zeta }_{II}^{1},{\zeta }_{II}^{2},\dots ,{\zeta }_{II}^{\mathfrak{H}}\right)={\equiv }_{II}^{1}{\zeta }_{0\left(II\right)}^{1}\oplus {\equiv }_{II}^{2}{\zeta }_{0\left(II\right)}^{2}\oplus \dots \oplus {\equiv }_{II}^{\mathfrak{H}}{\zeta }_{0\left(II\right)}^{\mathfrak{H}}={\oplus }_{{\Finv }=1}^{\mathfrak{H}}\left({\equiv }_{II}^{{\Finv }}{\zeta }_{0\left(II\right)}^{{\Finv }}\right)$$

(3)

where the weight vector is represented by ${\equiv }_{II}^{\Finv }\in \left[\mathrm{0,1}\right]$ with $\sum_{\Finv =1}^{\mathfrak{H}}{\equiv }_{II}^{\Finv }=1$ and ${\zeta }_{0\left(II\right)}^{\Finv }\le {\zeta }_{0\left(II-1\right)}^{\Finv }$.

Theorem 2

Consider any finite collection of CIFSs ${\zeta }_{II}^{\Finv }=\left({\varpi }_{at}^{\Finv }{e}^{i2\pi \left({\varpi }_{\mathfrak{H}t}^{\Finv }\right)},{\Xi }_{at}^{\Finv }{e}^{i2\pi \left({\Xi }_{\mathfrak{H}t}^{\Finv }\right)}\right),\Finv =\mathrm{1,2},\dots ,\mathfrak{H}$. Then we prove that the result in Eq. (3) is also a CIFN, such as

$$\begin{aligned}&{\text{CIIFHIIOWA}}\left({\zeta }_{II}^{1},{\zeta }_{II}^{2},\dots ,{\zeta }_{II}^{\mathfrak{H}}\right)\\ &\quad=\left(\begin{array}{c}\left(\frac{\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{at}^{0\left({\Finv }\right)}\right)}^{{\equiv }_{II}^{{\Finv }}}-\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1-{\varpi }_{at}^{0\left({\Finv }\right)}\right)}^{{\equiv }_{II}^{{\Finv }}}}{\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{at}^{0\left({\Finv }\right)}\right)}^{{\equiv }_{II}^{{\Finv }}}+\left({\dddot{\beth}}-1\right)\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1-{\varpi }_{at}^{0\left({\Finv }\right)}\right)}^{{\equiv }_{II}^{{\Finv }}}}\right){e}^{i2\pi \left(\frac{\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{\mathfrak{H}t}^{0\left({\Finv }\right)}\right)}^{{\equiv }_{II}^{{\Finv }}}-\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1-{\varpi }_{\mathfrak{H}t}^{0\left({\Finv }\right)}\right)}^{{\equiv }_{II}^{{\Finv }}}}{\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{\mathfrak{H}t}^{0\left({\Finv }\right)}\right)}^{{\equiv }_{II}^{{\Finv }}}+\left({\dddot{\beth}}-1\right)\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1-{\varpi }_{\mathfrak{H}t}^{0\left({\Finv }\right)}\right)}^{{\equiv }_{II}^{{\Finv }}}}\right)},\\ \left(\frac{{\dddot{\beth}}\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1-{\varpi }_{at}^{0\left({\Finv }\right)}\right)}^{{\equiv }_{II}^{{\Finv }}}-{\dddot{\beth}}\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1-{\varpi }_{at}^{0\left({\Finv }\right)}-{\Xi }_{at}^{0\left({\Finv }\right)}\right)}^{{\equiv }_{II}^{{\Finv }}}}{\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{at}^{0\left({\Finv }\right)}\right)}^{{\equiv }_{II}^{{\Finv }}}+\left({\dddot{\beth}}-1\right)\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1-{\varpi }_{at}^{0\left({\Finv }\right)}\right)}^{{\equiv }_{II}^{{\Finv }}}}\right){e}^{i2\pi \left(\frac{{\dddot{\beth}}\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1-{\varpi }_{\mathfrak{H}t}^{0\left({\Finv }\right)}\right)}^{{\equiv }_{II}^{{\Finv }}}-{\dddot{\beth}}\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1-{\varpi }_{\mathfrak{H}t}^{0\left({\Finv }\right)}-{\Xi }_{\mathfrak{H}t}^{0\left({\Finv }\right)}\right)}^{{\equiv }_{II}^{{\Finv }}}}{\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1+\left({\dddot{\beth}}-1\right){\varpi }_{\mathfrak{H}t}^{0\left({\Finv }\right)}\right)}^{{\equiv }_{II}^{{\Finv }}}+\left({\dddot{\beth}}-1\right)\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1-{\varpi }_{\mathfrak{H}t}^{0\left({\Finv }\right)}\right)}^{{\equiv }_{II}^{{\Finv }}}}\right)}\end{array}\right).\end{aligned}$$

(4)

Moreover, we give the idempotency, monotonicity, and boundedness of this operator.

Property 3

Consider any finite collection of CIFSs ${\zeta }_{II}^{\Finv }=\left({\varpi }_{at}^{\Finv }{e}^{i2\pi \left({\varpi }_{\mathfrak{H}t}^{\Finv }\right)},{\Xi }_{at}^{\Finv }{e}^{i2\pi \left({\Xi }_{\mathfrak{H}t}^{\Finv }\right)}\right),\Finv =\mathrm{1,2},\dots ,\mathfrak{H}$. Then

• 1. If ${\zeta }_{II}^{{\Finv }}={\zeta }_{II}=\left({\varpi }_{at}{e}^{i2\pi \left({\varpi }_{\mathfrak{H}t}\right)},{\Xi }_{at}{e}^{i2\pi \left({\Xi }_{\mathfrak{H}t}\right)}\right)$, then

  $${\text{CIIFHIIOWA}}\left({\zeta }_{II}^{1},{\zeta }_{II}^{2},\dots ,{\zeta }_{II}^{\mathfrak{H}}\right)={\zeta }_{II}.$$

• 2. If ${\zeta }_{II}^{\Finv }\le {{\zeta }^{\#}}_{II}^{\Finv }$, then

  $${\text{CIIFHIIWA}}\left({\zeta }_{II}^{1},{\zeta }_{II}^{2},\dots ,{\zeta }_{II}^{\mathfrak{H}}\right)\le {\text{CIIFHIIWA}}\left({{\zeta }^{\#}}_{II}^{1},{{\zeta }^{\#}}_{II}^{2},\dots ,{{\zeta }^{\#}}_{II}^{\mathfrak{H}}\right).$$

• 3. If $\small{\zeta }_{II}^{-}{=}\left(\underset{{\Finv }}{{\text{min}}}{\varpi }_{at}^{{\Finv }}{e}^{i2\pi \left(\underset{{\Finv }}{{\text{min}}}{\varpi }_{\mathfrak{H}t}^{{\Finv }}\right)},\underset{{\Finv }}{{\text{max}}}{\Xi }_{at}^{{\Finv }}{e}^{i2\pi \left(\underset{{\Finv }}{{\text{max}}}{\Xi }_{\mathfrak{H}t}^{{\Finv }}\right)}\right)$ and $\tiny{\zeta }_{II}^{+}\!{=}\!\left(\underset{{\Finv }}{{\text{max}}}{\varpi }_{at}^{{\Finv }}{e}^{i2\pi \left(\underset{{\Finv }}{{\text{max}}}{\varpi }_{\mathfrak{H}t}^{{\Finv }}\right)},\underset{{\Finv }}{{\text{min}}}{\Xi }_{at}^{{\Finv }}{e}^{i2\pi \left(\underset{{\Finv }}{{\text{min}}}{\Xi }_{\mathfrak{H}t}^{{\Finv }}\right)}\right)$, then

  $${\zeta }_{II}^{-}\le {\text{CIIFHIIWA}}\left({\zeta }_{II}^{1},{\zeta }_{II}^{2},\dots ,{\zeta }_{II}^{\mathfrak{H}}\right)\le {\zeta }_{II}^{+}.$$

Definition 9

Consider any finite collection of CIFSs ${\zeta }_{II}^{\Finv }=\left({\varpi }_{at}^{\Finv }{e}^{i2\pi \left({\varpi }_{\mathfrak{H}t}^{\Finv }\right)},{\Xi }_{at}^{\Finv }{e}^{i2\pi \left({\Xi }_{\mathfrak{H}t}^{\Finv }\right)}\right), \Finv =\mathrm{1,2},\dots , \mathfrak{H}$; then we develop the CIF Hamacher interaction weighted geometric (CIFHIWG) operator, such as

$${\text{CIIFHIIWG}}\left({\zeta }_{II}^{1},{\zeta }_{II}^{2},\dots ,{\zeta }_{II}^{\mathfrak{H}}\right)={\left({\zeta }_{II}^{1}\right)}^{{\equiv }_{II}^{1}}\otimes {\left({\zeta }_{II}^{2}\right)}^{{\equiv }_{II}^{2}}\otimes \dots \otimes {\left({\zeta }_{II}^{\mathfrak{H}}\right)}^{{\equiv }_{II}^{\mathfrak{H}}}={\otimes }_{{\Finv }=1}^{\mathfrak{H}}{\left({\zeta }_{II}^{{\Finv }}\right)}^{{\equiv }_{II}^{{\Finv }}},$$

(5)

where the weight vector is represented by ${\equiv }_{II}^{\Finv }\in \left[\mathrm{0,1}\right]$ with $\sum_{\Finv =1}^{\mathfrak{H}}{\equiv }_{II}^{\Finv }=1$.

Theorem 3

Consider any finite collection of CIFSs ${\zeta }_{II}^{\Finv }=\left({\varpi }_{at}^{\Finv }{e}^{i2\pi \left({\varpi }_{\mathfrak{H}t}^{\Finv }\right)},{\Xi }_{at}^{\Finv }{e}^{i2\pi \left({\Xi }_{\mathfrak{H}t}^{\Finv }\right)}\right),\Finv =\mathrm{1,2},\dots ,\mathfrak{H}$. Then we prove that the result in Eq. (5) is also a CIFN, such as

$$\begin{aligned}&{\text{CIIFHIIWG}}\left({\zeta }_{II}^{1},{\zeta }_{II}^{2},\dots ,{\zeta }_{II}^{\mathfrak{H}}\right)\\ &\quad=\left(\begin{array}{c}\left(\frac{{\dddot{\beth}}\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1-{\Xi }_{at}^{{\Finv }}\right)}^{{\equiv }_{II}^{{\Finv }}}-{\dddot{\beth}}\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1-{\Xi }_{at}^{{\Finv }}-{\varpi }_{at}^{{\Finv }}\right)}^{{\equiv }_{II}^{{\Finv }}}}{\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1+\left({\dddot{\beth}}-1\right){\Xi }_{at}^{{\Finv }}\right)}^{{\equiv }_{II}^{{\Finv }}}+\left({\dddot{\beth}}-1\right)\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1-{\Xi }_{at}^{{\Finv }}\right)}^{{\equiv }_{II}^{{\Finv }}}}\right){e}^{i2\pi \left(\frac{{\dddot{\beth}}\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1-{\Xi }_{\mathfrak{H}t}^{{\Finv }}\right)}^{{\equiv }_{II}^{{\Finv }}}-{\dddot{\beth}}\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1-{\Xi }_{\mathfrak{H}t}^{{\Finv }}-{\varpi }_{\mathfrak{H}t}^{{\Finv }}\right)}^{{\equiv }_{II}^{{\Finv }}}}{\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1+\left({\dddot{\beth}}-1\right){\Xi }_{\mathfrak{H}t}^{{\Finv }}\right)}^{{\equiv }_{II}^{{\Finv }}}+\left({\dddot{\beth}}-1\right)\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1-{\Xi }_{\mathfrak{H}t}^{{\Finv }}\right)}^{{\equiv }_{II}^{{\Finv }}}}\right)},\\ \left(\frac{\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1+\left({\dddot{\beth}}-1\right){\Xi }_{at}^{{\Finv }}\right)}^{{\equiv }_{II}^{{\Finv }}}-\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1-{\Xi }_{at}^{{\Finv }}\right)}^{{\equiv }_{II}^{{\Finv }}}}{\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1+\left({\dddot{\beth}}-1\right){\Xi }_{at}^{{\Finv }}\right)}^{{\equiv }_{II}^{{\Finv }}}+\left({\dddot{\beth}}-1\right)\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1-{\Xi }_{at}^{{\Finv }}\right)}^{{\equiv }_{II}^{{\Finv }}}}\right){e}^{i2\pi \left(\frac{\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1+\left({\dddot{\beth}}-1\right){\Xi }_{\mathfrak{H}t}^{{\Finv }}\right)}^{{\equiv }_{II}^{{\Finv }}}-\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1-{\Xi }_{\mathfrak{H}t}^{{\Finv }}\right)}^{{\equiv }_{II}^{{\Finv }}}}{\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1+\left({\dddot{\beth}}-1\right){\Xi }_{\mathfrak{H}t}^{{\Finv }}\right)}^{{\equiv }_{II}^{{\Finv }}}+\left({\dddot{\beth}}-1\right)\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1-{\Xi }_{\mathfrak{H}t}^{{\Finv }}\right)}^{{\equiv }_{II}^{{\Finv }}}}\right)}\end{array}\right).\end{aligned}$$

(6)

Moreover, we verify the idempotency, monotonicity, and boundedness of this operator.

Property 5

Consider any finite collection of CIFSs ${\zeta }_{II}^{\Finv }=\left({\varpi }_{at}^{\Finv }{e}^{i2\pi \left({\varpi }_{\mathfrak{H}t}^{\Finv }\right)},{\Xi }_{at}^{\Finv }{e}^{i2\pi \left({\Xi }_{\mathfrak{H}t}^{\Finv }\right)}\right),\Finv =\mathrm{1,2},\dots ,\mathfrak{H}$.

• 1. If ${\zeta }_{II}^{{\Finv }}={\zeta }_{II}=\left({\varpi }_{at}{e}^{i2\pi \left({\varpi }_{\mathfrak{H}t}\right)},{\Xi }_{at}{e}^{i2\pi \left({\Xi }_{\mathfrak{H}t}\right)}\right)$, then

  $${\text{CIIFHIIWG}}\left({\zeta }_{II}^{1},{\zeta }_{II}^{2},\dots ,{\zeta }_{II}^{\mathfrak{H}}\right)={\zeta }_{II}.$$

• 2. If ${\zeta }_{II}^{\Finv }\le {{\zeta }^{\#}}_{II}^{\Finv }$, then

  $${\text{CIIFHIIWG}}\left({\zeta }_{II}^{1},{\zeta }_{II}^{2},\dots ,{\zeta }_{II}^{\mathfrak{H}}\right)\le {\text{CIIFHIIWG}}\left({{\zeta }^{\#}}_{II}^{1},{{\zeta }^{\#}}_{II}^{2},\dots ,{{\zeta }^{\#}}_{II}^{\mathfrak{H}}\right).$$

• 3. If $\tiny{\zeta }_{II}^{-}=\left(\underset{{\Finv }}{{\text{min}}}{\varpi }_{at}^{{\Finv }}{e}^{i2\pi \left(\underset{{\Finv }}{{\text{min}}}{\varpi }_{\mathfrak{H}t}^{{\Finv }}\right)},\underset{{\Finv }}{{\text{max}}}{\Xi }_{at}^{{\Finv }}{e}^{i2\pi \left(\underset{{\Finv }}{{\text{max}}}{\Xi }_{\mathfrak{H}t}^{{\Finv }}\right)}\right)$ and $\tiny{\zeta }_{II}^{+}=\left(\underset{{\Finv }}{{\text{max}}}{\varpi }_{at}^{{\Finv }}{e}^{i2\pi \left(\underset{{\Finv }}{{\text{max}}}{\varpi }_{\mathfrak{H}t}^{{\Finv }}\right)},\underset{{\Finv }}{{\text{min}}}{\Xi }_{at}^{{\Finv }}{e}^{i2\pi \left(\underset{{\Finv }}{{\text{min}}}{\Xi }_{\mathfrak{H}t}^{{\Finv }}\right)}\right)$, then

  $${\zeta }_{II}^{-}\le {\text{CIIFHIIWG}}\left({\zeta }_{II}^{1},{\zeta }_{II}^{2},\dots ,{\zeta }_{II}^{\mathfrak{H}}\right)\le {\zeta }_{II}^{+}.$$

Definition 10

Consider any finite collection of CIFSs ${\zeta }_{II}^{\Finv }=\left({\varpi }_{at}^{\Finv }{e}^{i2\pi \left({\varpi }_{\mathfrak{H}t}^{\Finv }\right)},{\Xi }_{at}^{\Finv }{e}^{i2\pi \left({\Xi }_{\mathfrak{H}t}^{\Finv }\right)}\right), \Finv =\mathrm{1,2},\dots , \mathfrak{H}$; then we develop the CIF Hamacher interaction ordered weighted geometric (CIFHIOWG) operator, such as

$${\text{CIIFHIIOWG}}\left({\zeta }_{II}^{1},{\zeta }_{II}^{2},\dots ,{\zeta }_{II}^{\mathfrak{H}}\right)={\left({\zeta }_{0\left(II\right)}^{1}\right)}^{{\equiv }_{II}^{1}}\otimes {\left({\zeta }_{0\left(II\right)}^{2}\right)}^{{\equiv }_{II}^{2}}\otimes \dots \otimes {\left({\zeta }_{0\left(II\right)}^{\mathfrak{H}}\right)}^{{\equiv }_{II}^{\mathfrak{H}}}={\otimes }_{{\Finv }=1}^{\mathfrak{H}}{\left({\zeta }_{0\left(II\right)}^{{\Finv }}\right)}^{{\equiv }_{II}^{{\Finv }}},$$

(7)

where the weight vector is represented by ${\equiv }_{II}^{\Finv }\in \left[\mathrm{0,1}\right]$ with $\sum_{\Finv =1}^{\mathfrak{H}}{\equiv }_{II}^{\Finv }=1$ and ${\zeta }_{0\left(II\right)}^{\Finv }\le {\zeta }_{0\left(II-1\right)}^{\Finv }$.

Theorem 4

Consider any finite collection of CIFSs ${\zeta }_{II}^{\Finv }=\left({\varpi }_{at}^{\Finv }{e}^{i2\pi \left({\varpi }_{\mathfrak{H}t}^{\Finv }\right)},{\Xi }_{at}^{\Finv }{e}^{i2\pi \left({\Xi }_{\mathfrak{H}t}^{\Finv }\right)}\right),\Finv =\mathrm{1,2},\dots ,\mathfrak{H}$. Then we prove that the result in Eq. (7) is also a CIFN, such as

$$\begin{aligned}&{\text{CIIFHIIOWG}}\left({\zeta }_{II}^{1},{\zeta }_{II}^{2},\dots ,{\zeta }_{II}^{\mathfrak{H}}\right)\\ &\quad=\left(\begin{array}{c}\left(\frac{{\dddot{\beth}}\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1-{\Xi }_{at}^{0\left({\Finv }\right)}\right)}^{{\equiv }_{II}^{{\Finv }}}-{\dddot{\beth}}\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1-{\Xi }_{at}^{0\left({\Finv }\right)}-{\varpi }_{at}^{0\left({\Finv }\right)}\right)}^{{\equiv }_{II}^{{\Finv }}}}{\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1+\left({\dddot{\beth}}-1\right){\Xi }_{at}^{0\left({\Finv }\right)}\right)}^{{\equiv }_{II}^{{\Finv }}}+\left({\dddot{\beth}}-1\right)\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1-{\Xi }_{at}^{0\left({\Finv }\right)}\right)}^{{\equiv }_{II}^{{\Finv }}}}\right){e}^{i2\pi \left(\frac{{\dddot{\beth}}\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1-{\Xi }_{\mathfrak{H}t}^{0\left({\Finv }\right)}\right)}^{{\equiv }_{II}^{{\Finv }}}-{\dddot{\beth}}\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1-{\Xi }_{\mathfrak{H}t}^{0\left({\Finv }\right)}-{\varpi }_{\mathfrak{H}t}^{0\left({\Finv }\right)}\right)}^{{\equiv }_{II}^{{\Finv }}}}{\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1+\left({\dddot{\beth}}-1\right){\Xi }_{\mathfrak{H}t}^{0\left({\Finv }\right)}\right)}^{{\equiv }_{II}^{{\Finv }}}+\left({\dddot{\beth}}-1\right)\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1-{\Xi }_{\mathfrak{H}t}^{0\left({\Finv }\right)}\right)}^{{\equiv }_{II}^{{\Finv }}}}\right)},\\ \left(\frac{\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1+\left({\dddot{\beth}}-1\right){\Xi }_{at}^{0\left({\Finv }\right)}\right)}^{{\equiv }_{II}^{{\Finv }}}-\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1-{\Xi }_{at}^{0\left({\Finv }\right)}\right)}^{{\equiv }_{II}^{{\Finv }}}}{\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1+\left({\dddot{\beth}}-1\right){\Xi }_{at}^{0\left({\Finv }\right)}\right)}^{{\equiv }_{II}^{{\Finv }}}+\left({\dddot{\beth}}-1\right)\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1-{\Xi }_{at}^{0\left({\Finv }\right)}\right)}^{{\equiv }_{II}^{{\Finv }}}}\right){e}^{i2\pi \left(\frac{\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1+\left({\dddot{\beth}}-1\right){\Xi }_{\mathfrak{H}t}^{0\left({\Finv }\right)}\right)}^{{\equiv }_{II}^{{\Finv }}}-\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1-{\Xi }_{\mathfrak{H}t}^{0\left({\Finv }\right)}\right)}^{{\equiv }_{II}^{{\Finv }}}}{\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1+\left({\dddot{\beth}}-1\right){\Xi }_{\mathfrak{H}t}^{0\left({\Finv }\right)}\right)}^{{\equiv }_{II}^{{\Finv }}}+\left({\dddot{\beth}}-1\right)\prod_{{\Finv }=1}^{\mathfrak{H}}{\left(1-{\Xi }_{\mathfrak{H}t}^{0\left({\Finv }\right)}\right)}^{{\equiv }_{II}^{{\Finv }}}}\right)}\end{array}\right).\end{aligned}$$

(8)

Moreover, we give its idempotency, monotonicity, and boundedness.

Property 6

Consider any finite collection of CIFSs ${\zeta }_{II}^{\Finv }=\left({\varpi }_{at}^{\Finv }{e}^{i2\pi \left({\varpi }_{\mathfrak{H}t}^{\Finv }\right)},{\Xi }_{at}^{\Finv }{e}^{i2\pi \left({\Xi }_{\mathfrak{H}t}^{\Finv }\right)}\right),\Finv =\mathrm{1,2},\dots ,\mathfrak{H}$.

• 1. If ${\zeta }_{II}^{{\Finv }}={\zeta }_{II}=\left({\varpi }_{at}{e}^{i2\pi \left({\varpi }_{\mathfrak{H}t}\right)},{\Xi }_{at}{e}^{i2\pi \left({\Xi }_{\mathfrak{H}t}\right)}\right)$, then

  $${\text{CIIFHIIOWG}}\left({\zeta }_{II}^{1},{\zeta }_{II}^{2},\dots ,{\zeta }_{II}^{\mathfrak{H}}\right)={\zeta }_{II}.$$

• 2. If ${\zeta }_{II}^{\Finv }\le {{\zeta }^{\#}}_{II}^{\Finv }$, then

  $${\text{CIIFHIIOWG}}\left({\zeta }_{II}^{1},{\zeta }_{II}^{2},\dots ,{\zeta }_{II}^{\mathfrak{H}}\right)\le {\text{CIIFHIIOWG}}\left({{\zeta }^{\#}}_{II}^{1},{{\zeta }^{\#}}_{II}^{2},\dots ,{{\zeta }^{\#}}_{II}^{\mathfrak{H}}\right).$$

• 3. If $\tiny{\zeta }_{II}^{-}=\left(\underset{{\Finv }}{{\text{min}}}{\varpi }_{at}^{{\Finv }}{e}^{i2\pi \left(\underset{{\Finv }}{{\text{min}}}{\varpi }_{\mathfrak{H}t}^{{\Finv }}\right)},\underset{{\Finv }}{{\text{max}}}{\Xi }_{at}^{{\Finv }}{e}^{i2\pi \left(\underset{{\Finv }}{{\text{max}}}{\Xi }_{\mathfrak{H}t}^{{\Finv }}\right)}\right)$ and $\tiny{\zeta }_{II}^{+}=\left(\underset{{\Finv }}{{\text{max}}}{\varpi }_{at}^{{\Finv }}{e}^{i2\pi \left(\underset{{\Finv }}{{\text{max}}}{\varpi }_{\mathfrak{H}t}^{{\Finv }}\right)},\underset{{\Finv }}{{\text{min}}}{\Xi }_{at}^{{\Finv }}{e}^{i2\pi \left(\underset{{\Finv }}{{\text{min}}}{\Xi }_{\mathfrak{H}t}^{{\Finv }}\right)}\right)$, then

  $${\zeta }_{II}^{-}\le {\text{CIIFHIIOWG}}\left({\zeta }_{II}^{1},{\zeta }_{II}^{2},\dots ,{\zeta }_{II}^{\mathfrak{H}}\right)\le {\zeta }_{II}^{+}.$$

MADM method based on presented operators

The MADM technique is to select the best optimal from the collection of finite alternatives. In this section, we develop the MADM method based on the proposed CIFHIWA operator and CIFHIWG operator and then use it to solve the problem of green supply chain management.

For this, we consider ${\zeta }_{II}^{1},{\zeta }_{II}^{2},\dots ,{\zeta }_{II}^{\mathfrak{H}}$, represent the collection of alternatives, and for each alternative, we consider some finite attributes, such as ${\zeta }_{At}^{1},{\zeta }_{At}^{2},\dots ,{\zeta }_{At}^{q}$. Furthermore, we consider some weight vectors of the attributes ${\equiv }_{II}^{\Finv }\in \left[\mathrm{0,1}\right]$ with the condition $\sum_{\Finv =1}^{\mathfrak{H}}{\equiv }_{II}^{\Finv }=1$. Moreover, we aim to construct the decision matrix by using the CIFSs, where ${\varpi }_{at}\left({\psi }_{\Finv }\right),{\Xi }_{at}\left({\psi }_{\Finv }\right)$ and ${\varpi }_{\mathfrak{H}t}\left({\psi }_{\Finv }\right),{\Xi }_{\mathfrak{H}t}\left({\psi }_{\Finv }\right)$ show the amplitude term and phase term of the membership and non-membership grade with two conditions $0\le {\varpi }_{at}\left({\psi }_{\Finv }\right)+{\Xi }_{at}\left({\psi }_{\Finv }\right)\le 1$ and $0\le {\varpi }_{\mathfrak{H}t}\left({\psi }_{\Finv }\right)+{\Xi }_{\mathfrak{H}t}\left({\psi }_{\Finv }\right)\le 1$. Moreover, we also gave the neutral grade in the form: ${\omega }_{at}\left({\psi }_{\Finv }\right){e}^{i2\pi \left({\omega }_{\mathfrak{H}t}\left({\psi }_{\Finv }\right)\right)}=\left(1-{\varpi }_{at}\left({\psi }_{\Finv }\right)-{\Xi }_{at}\left({\psi }_{\Finv }\right)\right){e}^{i2\pi \left(1-{\varpi }_{\mathfrak{H}t}\left({\psi }_{\Finv }\right)-{\Xi }_{\mathfrak{H}t}\left({\psi }_{\Finv }\right)\right)}$. For convenience, we use the simple form of CIFN ${\zeta }_{II}^{\Finv }=\left({\varpi }_{at}^{\Finv }{e}^{i2\pi \left({\varpi }_{\mathfrak{H}t}^{\Finv }\right)},{\Xi }_{at}^{\Finv }{e}^{i2\pi \left({\Xi }_{\mathfrak{H}t}^{\Finv }\right)}\right),\Finv =\mathrm{1,2},\dots ,\mathfrak{H}$. Finally, we use the MADM method to solve this problem, and the steps are as follows:

Step 1: Construct the decision matrix based on the CIF information.

Step 2: Normalize the matrix, if we have the cost of data, such as

$$N=\left\{\begin{array}{cc}\left({\varpi }_{at}^{\Finv }{e}^{i2\pi \left({\varpi }_{\mathfrak{H}t}^{\Finv }\right)},{\Xi }_{at}^{\Finv }{e}^{i2\pi \left({\Xi }_{\mathfrak{H}t}^{\Finv }\right)}\right)& \mathrm{for \; benefit}\\ \left({\Xi }_{at}^{\Finv }{e}^{i2\pi \left({\Xi }_{\mathfrak{H}t}^{\Finv }\right)},,{\varpi }_{at}^{\Finv }{e}^{i2\pi \left({\varpi }_{\mathfrak{H}t}^{\Finv }\right)}\right)& \mathrm{for \; cost}\end{array}.\right.$$

But in the case of benefit types of data, we do not need to normalize the data.

Step 3: Aggregate the decision matrix by the CIFHIWA operator and CIFHIWG operator, and get aggregated values.

Step 4: Calculate the score or accuracy values of each aggregated value.

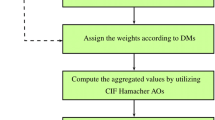
Step 5: Rank all the considered alternatives according to their score or accuracy values and select the best optimal. The geometrical representation of the proposed algorithm is listed in Fig. 2.

Fig. 2

Geometrical representation of the proposed algorithm

In the following, we use the proposed decision method to solve the selection problem of green supply chain management problem.

Green supply chain management

A supply chain describes the flow of services from the first step of production to the last step of delivering to the end of the customer. In general, a straightforward supply chain includes the following major features:

• (1) Suppliers.

• (2) Manufacturing or production.

• (3) Distribution.

• (4) Retailers.

• (5) End consumers.

In this example, we consider the five types of green supplier chain management and then find the best one by the developed method. For this, we consider five alternatives which are briefly discussed below:

• (1) Sustainable sourcing “${\zeta }_{II}^{1}$”: The practice of prioritizing the acquisition of raw materials and components from vendors that follow sustainable and environmentally friendly methods, such as the use of renewable resources, the reduction of waste, and the mitigation of carbon emissions.

• (2) Energy efficiency “${\zeta }_{II}^{2}$”: Energy efficiency is the practice of putting policies in place to reduce energy use in processes such as manufacturing, shipping, and storage. To decrease carbon footprint and reduce greenhouse gas emissions, this includes using energy-efficient technology and procedures.

• (3) Waste reduction and recycling “${\zeta }_{II}^{3}$”: Implementing measures to decrease waste generation during manufacturing and distribution, and encouraging recycling of materials and products to extend their life cycle and reduce landfill trash are two aspects of waste reduction and recycling.

• (4) Green transportation “${\zeta }_{II}^{4}$”: Green transportation is the use of environmentally friendly transportation strategies to minimize emissions and air pollution during product delivery, such as hybrid or electric cars.

• (5) Sustainable packing “${\zeta }_{II}^{5}$”: Using recyclable and environmentally acceptable materials for packaging reduces.

To choose the best one, we use the following features as an attribute, such as ${\zeta }_{At}^{1}$: risk analysis, ${\zeta }_{At}^{2}$: growth analysis, ${\zeta }_{At}^{3}$: political impact, and ${\zeta }_{At}^{4}$: environmental impact with weight vectors 0.2,0.3,0.3, and 0.2 for the above four attributes in each alternative. Then to find the best one, we use the above MADM technique to solve this problem, and the steps are shown as follows:

Step 1: Construct the decision matrix based on the CIF information, which is listed in Table 1.

Table 1 CIF information matrix

Step 2: Normalize the matrix in Table 1. Because attribute one for each alternative is risk type, we need to normalize it, and the result is shown in Table 2.

Table 2 Normalized CIF information matrix

Step 3: Aggregate the decision matrix by the CIFHIWA operator and CIFHIWG operator, and get the aggregated result shown in Table 3.

Table 3 Aggregated results

Step 4: Calculate the score values of each aggregated value, see Table 4.

Table 4 The score values

Step 5: Rank all the alternatives according to their score values and get the best optimal, see Table 5.

Table 5 Ranking values and the best decision

From the ranking results in Table 5, we observed that the best optimal is ${\zeta }_{II}^{3}$ based on the CIFHIWA operator and CIFHIWG operator for the value of the scaler ${\dddot{\beth}}=2$.

Furthermore, we check the stability or influence of the parameter ${\dddot{\beth}}$ for different values. Firstly, for the CIFHIWA operator, for different values of ${\dddot{\beth}}$, the ranking results are shown in Table 6.

Table 6 Ranking values for different values of parameters based on the CIFHIWA operator

From Table 6, we observed that the best optimal is ${\zeta }_{II}^{3}$ according to the CIFHIWA operator for different values ${\dddot{\beth}}$. Furthermore, for the CIFHIWG operator, for different values of ${\dddot{\beth}}$, the ranking results are listed in Table 7.

Table 7 Ranking values for different values of parameters based on the CIFHIWG operator

From Table 7, we observed that the best optimal is ${\zeta }_{II}^{3}$ based on the CIFHIWG operator for different values of a scaler ${\dddot{\beth}}$.

Furthermore, we do a comparative analysis of our method with some existing methods based on the data in Table 2.

Comparative analysis

In this subsection, we compare the proposed method with some existing techniques. For this, we select some prevailing operators, such as Wang and Liu [35] presented the Einstein operators based on Einstein TN and TCN for IFSs, and He et al. [36] developed the geometric interaction operators based on interaction TN and TCN for IFSs. Furthermore, Yu and Xu [37] proposed the prioritized AOs for IFSs, Akram et al. [38] gave the Hamacher AOs for CIFSs, Garg and Rani [39] developed the generalized AOs for CIFSs, Garg and Rani [40] proposed the generalized geometric AOs for CIFSs, Mahmood et al. [41] developed the Aczel–Alsina AOs for CIFSs, Mahmood and Ali [42] derived the Aczel–Alsina power AOs for CIFSs, and Liu et al. [44] presented the prioritized AOs for CIFSs based on Aczel–Alsina TN and TCN. By using the data in Table 2, the comparison results are shown in Table 8.

Table 8 Comparative analysis (proposed operators and existing operators)

From Table 8, we observed that the best optimal is ${\zeta }_{II}^{3}$ based on the Akram et al. [38], Garg and Rani [39, 40], Mahmood et al. [41], Mahmood and Ali [42], Liu et al. [43], CIFHIWA operator and CIFHIWG operator for the value of scaler ${\dddot{\beth}}=2$. But the presented operators by Wang and Liu [35], He et al. [36], and Yu and Xu [37] failed to solve this problem properly because these operators are presented based on IFSs which are special cases of the proposed operators.

Based on the above analyses, the proposed operators are very reliable and dominant for depicting awkward and unreliable information in real-life problems.

Conclusion

Hamacher AOs and interaction AOs are very valuable techniques for aggregating the collection of information. Furthermore, the CIFS is also a good tool to describe uncertain and awkward information in real-life problems, which is modified by many prevailing techniques, such as FSs, IFSs, and CFSs. Based on the above advantages, our main contributions are shown below:

• (1) Presented the Hamacher interaction operational laws for CIFSs.

• (2) Developed the CIFHIWA operator, CIFHIOWA operator, CIFHIWG operator, and CIFHIOWG operator.

• (3) Discussed some basic properties of the presented operators, such as idempotency, monotonicity, and boundedness.

• (4) Developed a MADM method based on the developed operators to find the best type of green supply chain management among the five green supply chain management.

• (5) Verified the superiority and effectiveness of the proposed method based on a comparative analysis between proposed techniques and existing methods.

The above operators based on the CIFSs are very reliable but in many situations it is not working effectively, because the CIFSs have some limitations, such as during election we have faced many kind of opinions such as yes, no, abstinence, and refusal, but the CIFSs has deal only with yes and no, but not with abstinence; therefore, we needed to use the complex picture fuzzy sets and their generalizations for coping with unreliable vague information.

In the future, we will use the proposed method to evaluate the smart systems in hydroponic vertical farming [46], the metaverse integration [47], finite-interval-valued type-2 Gaussian fuzzy number [48], and portfolio allocation with the TODIM technique [49]. Furthermore, we will also develop some aggregation operators, similarity measures, and different types of methods for some new uncertain information to enhance the worth of the proposed approaches.