Introduction

Rotating machinery is one critical component in many mechanical systems. It contains a large number of bearings and gear structures that are highly susceptible to damage. Prognostics and Health Management (PHM) is an essential tool for maintaining the reliability of rotating machinery and reducing maintenance costs [1]. PHM has been applied for much fields, such as the unmanned air vehicles [2], vehicles [3], and wind turbine system [4]. Development of fault diagnosis methods has a positive impact on the PHM.

With the continuous exploration and research of scholars, data-driven intelligent fault diagnosis methods have achieved great success, which rely on large amounts of labeled data. The data-driven intelligent fault diagnosis methods based on the deep neural network have the ability of extracting deeper features [5]. Therefore, we can obtain better fault features of rotating machinery. First, the vibration signal of the rotating machinery is obtained through the vibration sensor. Then, the feature extractor based on deep neural network is used to extract the features of the vibration signal. Finally, the mechanical fault type is predicted based on the probability value given by the classifier. The accuracy of fault diagnosis largely depends on the quality of the features extracted from the vibration signal [6]. Namely, the feature extractor is the key of the machinery fault diagnosis. Feature extraction methods have lots of base models including convolutional neural network (CNN) [7], residual neural network (ResNet) [8], deep belief network [9], transformer [10], comparative learning [11], and so on. Paper [12,13,14] do the feature extraction using multilayer CNN. Paper [15, 16], first, use Short-time Fourier Transform and wavelet packet transformation to process the original signal, respectively. Then, the ResNet is used for further feature extraction. Paper [17] proposes one extended deep belief network to fully exploit useful information in the raw vibration signal. Paper [18] uses continuous wavelet transform to construct raw vibration signal into time–frequency images. Then use the optimized SequeezeNet model, which has been integrated one base transformer, to extract the features. Paper [19] constructs the positive samples pair by same labels with different working condition and negative samples by different labels. Then the Contrastive Learning is used for extracting features. Despite the great accuracy achieved by the above model, the above model lacks an insight into the intrinsic properties of the signals for which it is intended.

Furthermore, the state of the operation of rotating machinery is not static. When the state of operation of the machinery changes, the accuracy of model will decrease. If the model can be retrained by the labeled data obtained in the new state of operation, the performance of the model will increase again [20]. The fact is that the labeled data is hard to get obtained in the actual industrial environment. In response to this issue, scholars have proposed a variety of unsupervised domain adaptation methods. The methods of unsupervised domain adaptation are pseudo-labeling, generative adversarial, Wasserstein distance, MMD, etc. The paper [21] proposes a domain adaptation strategy that leverages the pseudo-labels technique to compute conditional probability loss jointly with source domain loss. This approach enables the realistic migration of the model from the source domain to the target domain. Paper [22] distinguishes source and target domain data using generative adversarial networks, and aligns the distribution of source and target domain data using maximum mean difference. Paper [23] aligns source and target domain distributions using Wasserstein distance to achieve label-free migration of target domains. Paper [24] uses the MMD algorithm to align the source and target domains distributions and classifies the target domain using a source domain classifier. Paper [25] propose an unsupervised cross-domain fault diagnosis method based on time–frequency information fusion, which uses the pseudo-labels to reduce data distribution differences. All of the above methods map the source and target domains into the specified space so that the source and target domain data distributions are aligned. However, they overlook the fact that even if the data distributions of the source and target domains are aligned, there is still a possibility that the classifier may not achieve better diagnostic accuracy. This can be attributed to the inconsistency of the value ranges present in the source and target domain data. In addition, during the process of aligning the distributions, it is possible that the inherent distribution of the data may be disrupted.

Therefore, in this paper, we propose a novel unsupervised domain adaptation framework based on multi-kernel maximum mean discrepancy (M-Net) for fault diagnosis of rotating machinery. The main contributions of this paper can be summarized as follows.

  1. (1)

    Generate the domain-invariant features: We propose a multi-scale feature extractor based on the residual neural network (ResNet) and multi-head self-attention. The feature extractor is capable of extracting and fusing multi-scale features, thereby generating the domain-invariant features.

  2. (2)

    Transfer the model using unlabeled data: We propose a generator based on multi-kernel maximum mean discrepancy (MK-MMD). The generator aims to minimize the distance between the source and target features, effectively mapping them into the same latent space. This allows us to transfer the model from the labeled domain to the unlabeled domain.

  3. (3)

    Verify the M-Net on two data sets: We assess the performance of the M-Net on both the source and target domains, demonstrating its effectiveness in diagnostic and transfer tasks. Additionally, we provide visual explanations to illustrate why the M-Net is successful.

The remaining sections of this paper are structured as follows: “Preliminary” provides an overview of the preliminary aspects, including the problem formulation and the maximum mean discrepancy. “Proposed method” offers a detailed illustration of the M-Net for fault diagnosis. In “Experimental verification”, we present experimental results on two different data sets to validate the performance of the M-Net. Finally, “Conclusion” provides concluding remarks for this paper.

Preliminary

Problem formulation

We formulate the process of transferring the model from the source domain to the target domain to provide a more precise definition of the problem.

We denote the source domain as \(\mathcal {D}^s\), which consists of data \(\mathcal {X}^s\) and labels \(\mathcal {Y}^s\). The data \(\mathcal {X}^s\) follows the distribution \(\mathcal {P}^s\), as shown in Eq. 1:

$$\begin{aligned} \mathcal {D}^s = \{(\mathcal {X}^s, \mathcal {Y}^s) \ \vert \ \mathcal {X}^s \sim \mathcal {P}^s \}. \end{aligned}$$
(1)

We denote the fe ature extractor as \(\mathcal {F}_f\) and the fault predictor as \(\mathcal {F}_c\). These components are responsible for extracting domain-invariant fault characteristics from vibration signals and predicting the health status of rotating machinery. The source domain \(\mathcal {D}^s\) can be processed using \(\mathcal {F}_f\) and \(\mathcal {F}_c\), as shown in Eqs. 2 and 3:

$$\begin{aligned} f_s= & {} \mathcal {F}_f(\mathcal {X}^s), \end{aligned}$$
(2)
$$\begin{aligned} \mathcal {\hat{Y}}^s= & {} \mathcal {F}_c(f_s). \end{aligned}$$
(3)

First, the data is fed into \(\mathcal {F}_f\) and \(\mathcal {F}_c\) for forward propagation. The objective function is defined as the cross-entropy loss, as shown in Eq. 4. Then, during the backward propagation, the optimal parameters \(\theta _f\) and \(\theta _c\) of \(\mathcal {F}_f\) and \(\mathcal {F}_c\) are updated, as shown in Eq. 5:

$$\begin{aligned}{} & {} \mathcal {L}^s_{(\theta _f,\theta _c)} = \sum \mathcal {L}_{cross-entropy}(\mathcal {Y}^s,\mathcal {\hat{Y}}^s), \end{aligned}$$
(4)
$$\begin{aligned}{} & {} \theta _f,\theta _c = \arg \min \mathcal {L}^s_{(\theta _f,\theta _c)} . \end{aligned}$$
(5)

We denote the target domain as \(\mathcal {D}^t\), which consists only of the data \(\mathcal {X}^t\), as shown in Eq. 6. The data \(\mathcal {X}^t\) follows the distribution \(\mathcal {P}^t\), and it is important to note that \(\mathcal {P}^s\) (the distribution of the source domain) and \(\mathcal {P}^t\) (the distribution of the target domain) are different, but they are similar, as indicated in Eq. 7:

$$\begin{aligned}{} & {} \mathcal {D}^t = \{\mathcal {X}^t \ \vert \ \mathcal {X}^t \sim \mathcal {P}^t \}, \end{aligned}$$
(6)
$$\begin{aligned}{} & {} \mathcal {P}^s \ne \mathcal {P}^t,\ and \ \mathcal {P}^s \approx \mathcal {P}^t. \end{aligned}$$
(7)

We denote the generator \(\mathcal {F}_g\), which addresses the problem that the distribution of \(\mathcal {D}^s\) differs from that of \(\mathcal {D}^t\). We can obtain the features \(\varvec{f}_s\) of \(\mathcal {D}^s\) and the features \(\varvec{f}_t\) of \(\mathcal {D}^t\), shown as Eqs. 8, 9, 10, and 11:

$$\begin{aligned} \varvec{f}_s= & {} \mathcal {F}_f(\mathcal {X}^s), \end{aligned}$$
(8)
$$\begin{aligned} \varvec{f}_s^{\prime }= & {} \mathcal {F}_g(\varvec{f}_s), \end{aligned}$$
(9)
$$\begin{aligned} \varvec{f}_t= & {} \mathcal {F}_f(\mathcal {X}^t), \end{aligned}$$
(10)
$$\begin{aligned} \varvec{f}_t^{\prime }= & {} \mathcal {F}_g(\varvec{f}_t). \end{aligned}$$
(11)

To reduce the discrepancy between \(\varvec{f}_s^{\prime }\) and \(\varvec{f}_t^{\prime }\), we will compute the distance between them as the objective function \(\mathcal {L}^{t}_{(\theta _g)}\), shown in Eq. 12. Then, we will use backward propagation to update the parameters \(\theta _g\) of \(\mathcal {F}_g\), as shown in Eq. 13:

$$\begin{aligned}{} & {} \mathcal {L}^{t}_{(\theta _g)} = \sum \mathcal {L}_{MMD}, \end{aligned}$$
(12)
$$\begin{aligned}{} & {} \theta _g = \arg \min \mathcal {L}^{t}_{(\theta _g)}. \end{aligned}$$
(13)

We will fine-tune the \(\theta _c\) of \(\mathcal {F}_c\) when \(\mathcal {L}^{t}_{(\theta _g)}\) converges, as shown in Eq. 14. We will continue to use cross-entropy loss as the objective function, shown in Eq. 15. Then, we will use backward propagation to obtain the optimized parameters \(\theta _c^{\prime }\) of \(\mathcal {F}_c\), as shown in Eq. 16:

$$\begin{aligned}{} & {} \mathcal {\hat{Y}}^{s^{\prime }} = \mathcal {F}_c(\mathcal {F}_{g_{\theta _g}}(\mathcal {F}_{f_{\theta _f}}(\mathcal {X}^s))), \end{aligned}$$
(14)
$$\begin{aligned}{} & {} \mathcal {L}^t_{(\theta _{c^{\prime }})} = \sum \mathcal {L}_{cross-entropy}(\mathcal {Y}^s,\mathcal {\hat{Y}}^{s^{\prime }}), \end{aligned}$$
(15)
$$\begin{aligned}{} & {} \theta _{c^{\prime }} = \arg \min \mathcal {L}^t_{(\theta _{c^{\prime }})}. \end{aligned}$$
(16)

As of now, we can perform fault diagnosis in \(\mathcal {D}^t\) using \(\mathcal {F}_{f_{\theta _f}}\), \(\mathcal {F}_{g_{\theta _g}}\), and \(\mathcal {F}_{c_{\theta _{c^{\prime }}}}\).

Fig. 1
figure 1

Structure of the M-Net

Full size image

MMD

The maximum mean discrepancy (MMD) is used to measure the distance between the distributions of two different but related random variables. The MMD for \(\mathcal {D}^s\) and \(\mathcal {D}^t\) can be defined as exemplified in Eq. 17:

$$\begin{aligned} \textrm{MMD} [\mathcal {F}, \mathcal {P}^s, \mathcal {P}^t]= & {} \textrm{sup}_{f \in \mathcal {F}}\{E_{x^s \sim \mathcal {P}^s}[f(x^s)]\nonumber \\{} & {} -E_{x^t \sim \mathcal {P}^t}[f(x^t)]\} , \end{aligned}$$
(17)

The purpose of this equation is to find a mapping function \(\mathcal {F}\) that can map the variables to a higher dimensional space. The Mean Discrepancy is then computed to quantify the difference between the expectations of the two distributed random variables after undergoing the mapping process. The Maximum Mean Discrepancy (MMD) is obtained by finding the upper bound of this Mean Discrepancy. If the moments of any order of two random variables are the same, it indicates that the distributions of the two random variables are also the same. Conversely, if the distributions of the two random variables are not the same, the moment that exhibits the greatest difference between the two distributions is utilized as a measure of the distance between the two random variables.

Proposed method

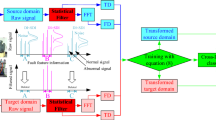
In actual industrial environments, it is challenging to obtain a sufficient amount of labeled fault data. Additionally, due to the differences in distribution between the source and target domains, models trained on the source domain cannot be directly applied to the unlabeled target domain. To address this issue, we propose a novel unsupervised domain adaptation framework based on multi-kernel maximum mean discrepancy for fault diagnosis of rotating machinery, referred to as M-Net. The structure of M-Net is illustrated in Fig. 1. It consists of three main components: (1) Feature extractor: This component is responsible for extracting domain-invariant representations from the input data. (2) Classifier: The classifier utilizes the extracted representations to predict the fault types. (3) Generator: The generator aims to minimize the distribution gap between the source and target domains, facilitating effective knowledge transfer. We will delve into a detailed explanation of each section.

Feature extractor

The feature extractor, denoted as \(\mathcal {F}_f(\cdot )\), is responsible for extracting the domain-invariant representation. The structure of the feature extractor is illustrated in Fig. 2.

Fig. 2
figure 2

Structure of feature extractor: it has two identical extraction unit

Full size image

From Fig. 2, it can be observed that the feature extractor can be divided into two extraction units, both designed to extract the domain-invariant representation. These two extraction units share the same structure. We consider one of the structures of the extraction unit as an example, illustrated in Fig. 3.

Figure 3 consists of a scale-extraction unit and a scale-fusion unit, which are employed to extract representations at different scales and fuse them together. The scale-extraction unit consists of three pathway. Each pathway has same structure, as shown in Fig. 4. However, three pathways have different convolution kernel size. To achieve this, we set the convolution kernel sizes to 3, 7, and 17, enabling the extraction of features in three different sizes. Residual learning, inspired by the ability to address vanishing/exploding gradients [26], is utilized as the backbone network. Convolutional layers are employed for extracting features, while batch normalization (BN) is applied to stabilize the distribution of data features. This helps eliminate the distribution differences caused by different working conditions and assists in extracting domain-invariant features. The Wavelet pooling (WPl) layer is incorporated to decrease dimensionality by preserving low-frequency features while discarding high-frequency noise [27]. For the activation function, scaled exponential linear units (SELU) [28] are employed to enhance the model’s capability for non-linear expression.

The structure of the scale-fusion unit is illustrated in Fig. 5. Three types of scale representations, namely \(f_{s_1}\), \(f_{m_1}\), and \(f_{l_1}\), are denoted as \(x_{s_1}\), \(x_{m_1}\), and \(x_{l_1}\), respectively, with shapes of (B, C, L). In step 1, 2, and 3, \(x_{s_1}\), \(x_{m_1}\), and \(x_{l_1}\) are obtained to form \(x_{s_{1}-m_{1}-l_1}\), which has a shape of (B, 3, C). Subsequently, \(x_{s_1}\), \(x_{m_1}\), and \(x_{l_1}\) from step 4 and 5 are used to generate \(x_{s_{1}-m_{1}-l_1}^v\), with a shape of \((B,3,C*L)\). \(x_{s_{1}-m_{1}-l_1}^v\) serves as the value (V), while \(x_{s_{1}-m_{1}-l_1}\) is assigned to the query (Q) and key (K). By applying \(\textrm{Softmax}(\frac{QK^T}{\sqrt{d_k}})V\) to Q, K, V, the resulting output is \(x_{attn}\). Through steps 6 and 7, \(x_{attn}\) completes the fusion of representations across different scales. After these steps, the representations of different scales are fused, while the noise component is discarded.

Fig. 3
figure 3

Structure of extraction unit: it includes a scale-extraction unit and a scale-fusion unit

Full size image
Fig. 4
figure 4

Structure of pathway

Full size image
Fig. 5
figure 5

Structure of scale-fusion unit

Full size image

Classifier

The classifier \(\mathcal {F}_c(\cdot )\) is responsible for predicting the health status and is composed of a multi-layer perceptron, as illustrated in Fig. 6.

The fault representations extracted by the feature extractor are mapped into the sample space using fully connected (FC) layers. The dropout operation is applied to enhance the generalization ability of the classifier. SELU is utilized as the activation function to enhance the model’s capability for nonlinear expression. In the last layer, softmax operation is employed to predict the fault types. The objective function used is cross-entropy, which aims to optimize the parameters.

Fig. 6
figure 6

Structure of the classifier

Full size image

Generator

The generator \(\mathcal {F}_g(\cdot )\) is employed to align the feature space of the source and target domains. The structure of the generator is illustrated in Fig. 7.

FC layers are utilized to reduce the distribution gap between the source and target domains. Batch normalization (BN) is employed to stabilize the distribution of features and eliminate the distribution differences between the two domains. SELU is chosen as the activation function to enhance the model’s ability for nonlinear expression. To address the challenge of aligning the feature distributions between the source and target domains, we adopt the Maximum Mean Discrepancy (MMD) as our objective function. However, if we only input the target domain features \(f_T\) into the generator while keeping the source domain features \(f_S\) unchanged, it becomes difficult to align the distribution of \(f_T\) with that of \(f_S\) due to the range of values being altered by the generator. Therefore, both \(f_S\) and \(f_T\) are fed into the generator. However, it is important to minimize the distribution adjustment of both \(f_S\) and \(f_T\) to avoid disrupting the intra-class distribution. To achieve this, we compute three types of losses and sum them together, as shown in Eq. 18:

$$\begin{aligned} \mathcal {L}_T = \mathcal {L}(f_{S^{'}},f_{T^{'}}) + \mathcal {L}(f_{S},f_{T^{'}}) + \mathcal {L}(f_{S},f_{S^{'}}) \end{aligned}$$
(18)

The calculation of \(\mathcal {L}(\cdot )\) is performed using Maximum Mean Discrepancy (MMD), as indicated in Eq. 17. The Gaussian kernel, defined in Eq. 19, is utilized as the kernel function for MMD:

$$\begin{aligned} k(x^s,x^t) = e^{-\frac{{\Vert x^s-x^t \Vert }^2}{2\sigma ^2}} = e^{-\frac{\sum _{i=1}^{N}{( x_i^s-x_i^t )}^2}{2\sigma ^2}} \end{aligned}$$
(19)
Fig. 7
figure 7

Structure of the generator

Full size image

Training procedure

The M-Net is initially pretrained on the source domain. After the pretraining phase is completed, the M-Net is then transferred to the target domain.

Pretraining in the source domain

We utilize the source domain to pretrain \(\mathcal {F}_f(\cdot )\). We feed the source domain into \(\mathcal {F}_f(\cdot )\) and \(\mathcal {F}_c(\cdot )\), as depicted in Eqs. 2 and 3. The cross-entropy loss is employed as the objective function, represented by Eq. 4. The pseudo code for this process is outlined in Algorithm 1.

Algorithm 1
figure a

Pretrain the M-Net in \(\mathcal {D}^s\)

Full size image

Training in the target domain

Once \(\mathcal {F}_f\) is well pretrained on the source domain, we transfer the learned representations from \(\mathcal {F}_f\) with fixed parameters \(\theta ^{}_{f}\) to the target domain. We then fix \(\theta ^{}_{f}\) in \(\mathcal {F}_f\). The source domain \(\mathcal {D}^s\) and target domain \(\mathcal {D}^t\) are fed into \(\mathcal {F}_{f_{\theta ^{}_{f}}}\) and \(\mathcal {F}_g\), as described in Eqs. 8, 9, 10, and 11. Backward propagation is performed based on Eq. 18. Once \(\mathcal {F}_g\) converges, both \(\mathcal {F}_f\) and \(\mathcal {F}_g\) are fixed. Subsequently, we fine-tune \(\mathcal {F}_c\) according to Eqs. 14 and 15. The pseudo code for this process is illustrated in Algorithm 2.

Algorithm 2
figure b

Train the M-Net in \(\mathcal {D}^t\)

Full size image

Experimental verification

We investigate the M-Net in two cases: transferring diagnosis knowledge across different working conditions and transferring diagnostic knowledge across different bearings. We compare the performance of the M-Net with other methods, namely MSTLN [29], DADAN [30], DCTLN [31], and RTDGN [32] on both the source and target domains. Additionally, we provide a visual interpretation of the M-Net. The optimal parameters for the M-Net are determined using grid search. The models are implemented in the PyTorch framework with 200 epochs, a batch size of 128, and a learning rate of 0.001. To ensure the robustness of our experiments, we employ tenfold cross-validation for all trials. The model accuracy is calculated by averaging the results of the ten folds, while the standard deviation (STD) is used to assess the stability of the model.

Case I: transferring diagnosis knowledge across different working conditions

Description of data set \(\mathcal {D}^1\)

The \(\mathcal {D}^1\) bearing data set has been sourced from Case Western Reserve University. The test stand used to collect the data is depicted in Fig. 8.

Fig. 8
figure 8

Test stand of \(\mathcal {D}^1\)

Full size image

Electro-discharge machining has been employed to introduce single-point faults of diameters measuring 7 mils, 14 mils, and 21 mils into the test bearing. Data is recorded at a sampling rate of 12000 samples per second. The types of faults include inner race, ball, and outer race defects.

Comparing with other methods on the source domain

We evaluate the effectiveness of M-Net by comparing its accuracy and STD with MSTLN, DADAN, DCTLN, and RTDGN on \(\mathcal {D}^1\), as illustrated in Table 1.

Table 1 Accuracy ± STD of models on \(\mathcal {D}^1\)
Full size table

The MSTLN and DCTLN models exhibit the best fault diagnosis performance with an accuracy of 100.0% and STD of 0.0%. The RTDGN model achieves an accuracy of 96.700% with an STD of 0.446%, which indicates worse performance compared to the other four models. Our proposed model, M-Net, achieves an accuracy of 99.986% ± 0.011%, which while high, is not the most optimal for fault diagnosis. We incorporate label smoothing technology into the cross-entropy loss function during the training of M-Net. This is done to extract more general features that are less susceptible to overfitting. This approach reduces the model’s confidence, enabling it to capture more general features for the purpose of model transferring. We will provide evidence to support this point in “Comparing with other methods on the target domain”. Furthermore, an accuracy of 99.986% and an STD of 0.011% for M-Net are acceptable values for fault diagnosis.

Comparing with other methods on the target domain

We divide \(\mathcal {D}^1\) into subsets \(\mathcal {D}^1_1\), \(\mathcal {D}^1_2\), \(\mathcal {D}^1_3\), and \(\mathcal {D}^1_4\), based on motor load. The models are initially trained in the source domain (\(\mathcal {S}\)). Subsequently, we apply the models trained in \(\mathcal {S}\) to the target domains (\(\mathcal {T}_1\), \(\mathcal {T}_2\), and \(\mathcal {T}_3\)) without any further fine-tuning. The results are depicted in Fig. 9.

Fig. 9
figure 9

Transfer accuracy without fine-tuning on the \(\mathcal {D}^1\)

Full size image

In Fig. 9a, the results for \(\mathcal {D}^1_1\) show that \(\mathcal {D}_1^1\) is utilized as the source domain (\(\mathcal {S}\)), while \(\mathcal {D}_2^1\), \(\mathcal {D}_3^1\), and \(\mathcal {D}_4^1\) are considered the target domains (\(\mathcal {T}_1\), \(\mathcal {T}_2\), and \(\mathcal {T}_3\), respectively). On the source domain \(\mathcal {S}\), all the models achieve commendable accuracy, especially MSTLN, DADAN, and DCTLN with accuracy of 100.0% ± 0.0%. Our proposed model, M-Net, achieves an accuracy of 99.988% ± 0.015%, which, while not the highest, still demonstrates strong performance. We believe M-Net’s slightly lower accuracy indicates it has learned more general features compared to other models. In the target domains \(\mathcal {T}_1\), \(\mathcal {T}_2\), and \(\mathcal {T}_3\), the M-Net demonstrates outstanding performance. In \(\mathcal {T}_1\), M-Net achieves the highest accuracy of 96.572% ± 1.329% among the three transfer cases. Even in the case of \(\mathcal {T}_3\), where the accuracy is lowest, it still achieves 81.747% ± 4.813%. Similar situations can be observed in Fig. 9b, c, and d. While M-Net might not achieve the highest accuracy on the source domain \(\mathcal {S}\), its exceptional transfer accuracy on \(\mathcal {T}_1\), \(\mathcal {T}_2\), and \(\mathcal {T}_3\) highlights its ability to learn more general features and exhibit superior transfer performance.

We transfer the M-Net trained in \(\mathcal {S}\) into the target domains (\(\mathcal {T}_1\), \(\mathcal {T}_2\), and \(\mathcal {T}_3\)). This transfer involves aligning the distribution of \(\mathcal {S}\) with that of \(\mathcal {T}_1\), \(\mathcal {T}_2\), and \(\mathcal {T}_3\) respectively. The results of this transfer process are depicted in Fig. 10.

Fig. 10
figure 10

Transfer accuracy of M-Net on the \(\mathcal {D}^1\)

Full size image

Figure 10a illustrates the transfer accuracy of M-Net on \(\mathcal {D}^1_1\). The term “Source” refers to accuracy on the source domain, while “Target” denotes accuracy on the target domain without fine-tuning. “Target-FT” represents accuracy on the target domain with fine-tuning. In all cases, various degrees of improvement are observed. For instance, in Fig. 10a, accuracy on \(\mathcal {T}_3\) improves by up to 6.567% after fine-tuning the M-Net. Similar patterns of improvement are shown in Fig. 10b, c, and d. These results provide evidence of the effectiveness of the M-Net model.

Visual interpretation of the model

To elucidate the effectiveness of the M-Net on \(\mathcal {D}^1\), we offer visual interpretations of the model from two perspectives: high-level feature visualization and vibration signal visualization.

We extract the input features from the last layer of the M-Net and employ the t-Distributed Stochastic Neighbor Embedding (t-SNE) algorithm [33] to project the 128-dimensional features into two-dimensional vectors. The outcomes are visualized in Fig. 11a.

Fig. 11
figure 11

Visual interpretation of M-Net on the \(\mathcal {D}^1\)

Full size image

The visualization demonstrates that each class is distinct from the others and, at the same time, each class is internally cohesive. This alignment with the actual class distribution serves as evidence of the effectiveness of the M-Net model.

We initiate this process by capturing the output of the feature extractor. Subsequently, we leverage the eigenvector-based class activation map (Eigen-CAM) technique [34] to derive the attention sequence from the M-Net. This attention sequence is then mapped onto the vibration signal, as demonstrated in Fig. 11b and c. In these figures, the vertical axis represents the amplitude of the time-domain vibration signal, while the horizontal axis corresponds to the sampling points. The color bar indicates the extent of attention allocated by the M-Net, with green signifying higher attention and red denoting lower attention. We’ve outlined the vibration signal portions that receive greater attention from the M-Net with blue ovals. Upon examining Fig. 11b and c, it’s evident that the M-Net places more attention on the peaks of the vibration signals. This observation indicates that the M-Net adeptly extracts relevant features from the vibration signals at appropriate points.

Case II: transferring diagnostic knowledge across different bearings

Description of data set \(\mathcal {D}^2\)

The \(\mathcal {D}^2\) bearing data set is provided by Paderborn University. The test stand used for data collection is depicted in Fig. 12.

Fig. 12
figure 12

Test stand of \(\mathcal {D}^2\)

Full size image

The data set encompasses ten categories of bearings, incorporating two speed types, two load torque types, and two radial force types.

Comparing with other methods on the source domain

The accuracy and standard deviation (STD) are depicted in Table 2. These metrics have been evaluated using M-Net, MSTLN, DADAN, DCTLN, and RTDGN on \(\mathcal {D}^2\).

Table 2 Accuracy ± STD of models on \(\mathcal {D}^2\)
Full size table

The M-Net achieves a notably higher accuracy of 99.131% and a comparatively lower STD of 0.138%. Conversely, the RTDGN model performs less effectively with an accuracy of 79.234% and a higher STD of 1.312%. The remaining models, namely MSTLN, DADAN, and DCTLN, exhibit commendable performance, though not as exceptional as M-Net. Given that \(\mathcal {D}^2\) possesses a more intricate distribution than \(\mathcal {D}^1\), it’s evident that the accuracy of all models experiences a decline compared to \(\mathcal {D}^1\). Nonetheless, the M-Net still maintains a strong accuracy, which underscores its robust non-linear expression capabilities.

Comparing with other methods on the target domain

To assess the transfer performance on \(\mathcal {D}^2\), we divide it into four distinct subdata sets: \(\mathcal {D}^2_1\) with 1500 rpm, 0.7 Nm, and 1000N; \(\mathcal {D}^2_2\) with 900 rpm, 0.7 Nm, and 1000N; \(\mathcal {D}^2_3\) with 1500 rpm, 0.1 Nm, and 1000N; and \(\mathcal {D}^2_4\) with 1500 rpm, 0.7 Nm, and 400N. Subsequently, we transfer the models trained in the source domain (\(\mathcal {S}\)) to the target domains (\(\mathcal {T}_1\), \(\mathcal {T}_2\), and \(\mathcal {T}_3\)). The results of this transfer process are depicted in Fig. 13.

Fig. 13
figure 13

Transfer accuracy without fine-tuning on the \(\mathcal {D}^2\)

Full size image

In Fig. 13a, we observe the results on \(\mathcal {D}^2_1\), where \(\mathcal {D}^2_1\) serves as the source domain (\(\mathcal {S}\)), and \(\mathcal {D}^2_2\), \(\mathcal {D}^2_3\), and \(\mathcal {D}^2_4\) are the respective target domains (\(\mathcal {T}_1\), \(\mathcal {T}_2\), and \(\mathcal {T}_3\)). On the source domain \(\mathcal {S}\), the M-Net achieves the highest accuracy of 99.993% ± 0.003%. In contrast, the RTDGN exhibits a lower accuracy of 91.530% ± 0.928%. On the target domains \(\mathcal {T}_1\), \(\mathcal {T}_2\), and \(\mathcal {T}_3\), the M-Net achieves remarkable accuracy of 41.622% ± 1.917%, 98.973% ± 0.404%, and 75.615% ± 3.581% respectively. The other models experience varying degrees of accuracy decrease on these target domains, with none surpassing the M-Net’s performance. Similar patterns are observed in Fig. 13b and d. In Fig. 13c, there is an exception where, on the source domain \(\mathcal {S}\), MSTLN exhibits slightly higher accuracy of 99.874% ± 0.031% compared to M-Net’s accuracy of 99.787% ± 0.051%. However, in the transfer cases, M-Net demonstrates superior transfer accuracy. Even though M-Net is not the top performer in the source domain \(\mathcal {S}\), the small accuracy difference between M-Net and MSTLN is overshadowed by M-Net’s superior transfer performance on \(\mathcal {T}_1\), \(\mathcal {T}_2\), and \(\mathcal {T}_3\). Overall, the results in Fig. 13 reinforce the notion that M-Net excels at learning more general features and exhibiting better transfer performance.

To assess the transfer performance of M-Net, we conduct 12 transfer experiments. In each experiment, we transfer the M-Net trained in the source domain (\(\mathcal {S}\)) into the target domains (\(\mathcal {T}_1\), \(\mathcal {T}_2\), and \(\mathcal {T}_3\)). The outcomes of these experiments are displayed in Fig. 14.

Fig. 14
figure 14

Transfer accuracy of M-Net on the \(\mathcal {D}^2\)

Full size image

Figure 14a examines the scenario where \(\mathcal {D}^2_1\) is taken as the source domain (\(\mathcal {S}\)), and \(\mathcal {D}^2_2\), \(\mathcal {D}^2_3\), and \(\mathcal {D}^2_4\) are treated as \(\mathcal {T}_1\), \(\mathcal {T}_2\), and \(\mathcal {T}_3\) respectively. In this case, we transfer the M-Net trained on \(\mathcal {D}^2_1\) into the target domains. Notably, the accuracy of M-Net experiences varying degrees of improvement after fine-tuning. Particularly in \(\mathcal {T}_3\), there is a significant increase in accuracy. Similar patterns are observed in Fig. 14b, c, and d. In summary, M-Net demonstrates remarkable transfer performance across all cases.

Visual interpretation of the model

Similar to \(\mathcal {D}^1\), for \(\mathcal {D}^2\), we provide visual interpretations of the M-Net’s efficacy from two perspectives: high-level feature visualization and vibration signal visualization.

The input features from the last layer of the M-Net are extracted and processed. To condense the 128-dimensional features, we utilize the t-Distributed Stochastic Neighbor Embedding (t-SNE) technique, which transforms them into two-dimensional vectors. The resulting visualization is presented in Fig. 15a.

The visualization shows clear separation between different classes, with data points tightly clustered within each class. This evident distinction and cohesion among classes provide strong evidence of the M-Net’s effective functioning.

Fig. 15
figure 15

Visual interpretation of M-Net on the \(\mathcal {D}^2\)

Full size image

The process begins with capturing the output of the feature extractor. Subsequently, we employ the Eigen-CAM method to generate the attention sequence of the M-Net. This attention sequence is then mapped onto the vibration signal, as illustrated in Fig. 15b and c. In these figures, the vertical axis represents the amplitude of the time-domain vibration signal, while the horizontal axis corresponds to the sampling points. The color bar indicates the intensity of attention assigned by the M-Net, with green signifying higher attention and red indicating lower attention. The areas of the vibration signal that receive more attention from the M-Net are marked with blue ovals. Upon examining Fig. 15b and c, it’s evident that the M-Net assigns heightened attention to the peaks of the vibration signals. This observation reinforces the conclusion that the M-Net effectively extracts pertinent features from the vibration signal, contributing to accurate identification.

Conclusion

To tackle the challenge of limited labeled data availability, we propose a novel unsupervised domain adaptation framework based on multi-kernel maximum mean discrepancy (M-Net) for intelligent fault diagnosis of rotating machinery. First, we propose a multi-scale feature extractor to extract and fuse multi-scale features, which will be trained in the source domain with a sufficient amount of labeled data. Second, we propose a generator model that leverages unlabeled data to reduce the distribution distance between the source and target features. This allows us to transfer the M-Net from the source domain to the target domain. Our experiments are conducted on two publicly available data sets. We compare the performance of M-Net with other methods in the source domain. Our results indicate that M-Net can achieve perfect performance in the source domain. Then, we evaluate the ability of M-Net to extract domain-invariant features and its transfer performance to the target domain. Finally, we provide a visual interpretation of why M-Net works. All experiments can prove that M-Net can diagnose faults even without labeled data. Although M-Net has great performance, in this paper, one assumption acts as a premise: the source and target domains have the same set of faults. Therefore, future research should aim to disturb this assumption.