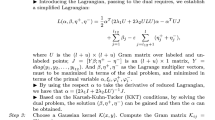A meta-learning network method for few-shot multi-class classification problems with numerical data

Abstract

The support vector machine (SVM) method is an important basis of the current popular multi-class classification (MCC) methods and requires a sufficient number of samples. In the case of a limited number of samples, the problem of over-learning easily occurs, resulting in unsatisfactory classification. Therefore, this work investigates an MCC method that requires only a small number of samples. During model construction, raw data are converted into two-dimensional form via preprocessing. Via feature extraction, the learning network is measured and the loss function minimization principle is considered to better solve the problem of learning based on a small sample. Finally, three examples are provided to illustrate the feasibility and effectiveness of the proposed method.

Introduction

While two categories of classification problems are frequently discussed, in actuality, there are many multi-class or multi-objective classification problems [1]. In general, the mathematical language of multi-class classification (MCC) problems is described as follows. Given a data set T containing n independent identically distributed samples,

$$T=\left\{\left({x}_{1},{y}_{1}\right),\left({x}_{2},{y}_{2}\right),\cdots ,\left({x}_{n},{y}_{n}\right)\right\},$$

(1.1)

where ${x}_{i}\in R,{y}_{i}\in \left\{\mathrm{1,2},\cdots ,M\right\}, M>2,i =\mathrm{1,2},\cdots ,n$.

The support vector machine (SVM) is a learning method developed based on statistical learning theory [2, 3]. SVMs adopt the kernel function idea [4] to transform a nonlinear space into a linear space, which reduces the algorithm complexity. Therefore, this method has good classification capability and high computational efficiency. In addition, the SVM method can achieve satisfactory results without preprocessing the original data; thus, it is suitable for MCC problems. SVMs can be used to solve MCC problems only when they are properly treated. Because each SVM can only provide a "yes" or "no" answer to one question, it can only determine whether a test sample is in a category set. To determine the category of the test sample, other categories must be excluded. Therefore, when SVMs deal with an MCC problem, multiple categories must be combined, and the output results of each SVM are integrated to determine the final category of the test object. The existing programs include the following.

One against rest: The concept of this program is to construct multiple binary classifiers, each of which divides one class of sample data from all other classes. Vapnik proposed the "one against rest" algorithm, in which a classification function is constructed between each category and all other classes, and, during the classification process, the category with the largest output value of the classification function is the prediction category [5, 6]. Therefore, the training time of this algorithm is directly proportional to the number of categories. As relevant considerations are not involved in the impact of multiple classifiers on the test misclassification rate, it is difficult to train on a large training sample, and misclassification and indivisible regions inevitably exist. Platt et al. proposed the decision directed acyclic graph (DDAG) algorithm [7,8,9], which was developed based on the “one against rest” algorithm. In this method, it is not necessary to use all SVMs to determine the category of the unknown category samples, as long as a node with a zero entry degree goes to a node with a zero exit degree. In addition, because of its special structure, this method has certain fault tolerance. However, the phenomenon of error accumulation also exists in a directed acyclic graph. Therefore, the closer the classification error occurs to the zero entry node, the worse will be the classification performance due to the cumulative effect of the errors.

One-against-one: The "one-against-one" algorithm, also known as the "voting method," constructs a classification model in pairs among various categories, detects the pending samples in turn and obtains corresponding results, and then provides statistics on the output results. The category to which the pending samples belong is the category with the most votes. The disadvantage of this method is that the classification function increases rapidly with the increase of the number of categories, which slows down the prediction process [10, 11].

Many-to-many: The basic idea of this program is to use a binary tree to organize multiple SVMs [12, 13]. This algorithm not only uses SVMs to ensure classification accuracy, but also adopts a tree structure to improve the calculation speed. In the case of similar classification accuracies, the amount of calculation is greatly reduced. The disadvantage of this method is that it is possible to produce an error accumulation phenomenon; if a classification error occurs on a node, the error will be continued, and the classification of that node on subsequent nodes will be meaningless.

Other SVM methods: The M-ARY classification method proposed by Sebald et al. [14] makes full use of the binary classification characteristics of the SVM and recombines various categories of MCC to form an SVM sub-classifier. Hence, the M-ARY classification method subtly transforms the MCC problem into a small number of two-class SVM classifiers, which significantly reduces the amounts of training and test calculation. Therefore, it is a favorable MCC method. The fuzzy membership algorithm [15] solves the non-separable region of the SVM by introducing the fuzzy membership function. The basic idea is to calculate the fuzzy membership degree of the sample to be classified for each candidate category. The candidate category with the highest fuzzy membership degree becomes the category of the sample. Fuzzy membership algorithms can be either all one-to-many or all one-to-one SVMs. Moreover, the definition of the fuzzy membership degree is different for different SVMs.

Other MCC algorithms include pairwise coupling [16], which presents two approaches to obtaining class probabilities. Each method can be reduced to linear systems and is easy to implement. Pairwise coupling is popular, and combines all comparisons for each pair of classes. However, Li [17] built multi-class classifiers for tissue classification based on gene expression. A fusion approach has also been proposed to produce a weighted and compatible multi-criteria decision-making ranking for MCC algorithms [18]. In another study, a class of SVMs was combined with discriminant functions to solve the MCC problem [19]. Moreover, an MCC algorithm based on a sequential regression machine has been proposed [20]; while it is similar to the support vector classification–regression algorithm, it contains fewer parameters. Polat and Gunes [21] proposed a new intelligent classifier based on a mixture of the C4.5 classification tree and the "one-to-many" method to solve MCC problems [21]. After a discussion on the multinomial probit regression model with Bayesian gene selection, [22] proposed two Bayesian gene selection schemes, namely, (1) employing different strongest genes for different probit regressions and (2) employing the same strongest genes for all regressions. Compared with existing multi-class cancer classification methods, these two methods can identify which genes are the most important and affect which kinds of cancer. In addition, competitive neural networks with the learning vector quantization (LVQ) algorithm have been used for the classification of electrocardiogram signals [23].

The present work mainly investigates the MCC method of numerical data, where $\left({x}_{i},{y}_{i}\right),\left(i=1,\cdots, n\right)$ is the numerical data. Focus is placed on the traditional MCC problem when the sample size tends to infinity, which is also the assumption on which existing MCC methods are based. However, in some practical problems, many traditional MCC methods perform poorly due to the limited sample size. In view of the shortcomings of traditional methods, some new MCC methods with good performance should be explored. Therefore, this work primarily investigates a method for the solution of numerical few-shot MCC problems.

At present, meta-learning, as the key to achieving general artificial intelligence, has been widely applied in few-shot problems [23,24,25]. Meta-learning [26,27,28] can be applied to the few-shot classification problem because its training process can be decomposed into different training tasks (batches or tasks). During each training task, the generalization ability of the model under the category change is learned. During the testing task, faced with new categories and only a small amount of data for each category, classification can be completed without changing existing models [29,30,31]. Moreover, during the training process, each round of training includes different samples; thus, each round of training contains a different category combination. This mechanism enables the model to learn the common parts of different samples, and the model through this learning mechanism can be better classified in the face of new and unseen samples [32,33,34,35].

The particularities of the MCC problem and the few-shot problem are comprehensively considered. This paper proposes an MCC method, but, different from previous studies [5, 20], neither an ordinal regression machine nor an SVM is used. Instead, meta-learning and the network model are used to solve the MCC and few-shot problems. One of the strengths of this method is that it is suitable for MCC problems with a small sample size for each category. To carry out MCC with a small sample size, useful information related to the sample should first be input into the computer. Then, the sample should be scientifically abstracted and its mathematical model should be established to describe and replace the original numerical sample. A simple and accurate method is used to improve the representation of raw data in a form that can be processed by computers. Thus, the classification effect of small-sample MCC problems can be improved. So, the major contributions of the paper are summarized as follows.

• 1. By using preprocessing models, CNNs, metric networks, and meta-learning algorithms, a new classification model was proposed to solve MCC problems with few samples per category.

• 2. The proposed model improves the classification accuracy of MCC problems.

• 3. The proposed method has universal applicability.

The remainder of this paper is organized as follows. The proposed method for solving the few-shot MCC problem is presented in Sect. “Few-shot multi-class classification network algorithm”, and the MCC algorithm is illustrated in Sect. “Experiments”. The numerical results are reported in Sect. “Conclusion”. Finally, the conclusions are drawn in Sect. “Conclusion”.

Few-shot multi-class classification network algorithm

Deep learning has been widely applied in a variety of fields to solve problems in image recognition and natural language processing. However, deep learning requires a large number of annotated samples. The acquisition of large-scale annotated data samples is the key to training a model with high accuracy. However, due to the large number of unlabeled samples in real life and the high cost incurred by obtaining labeled samples, the use of a small number of samples to train effective models has become an issue of substantial concern in the field of deep learning. In particular, when the few-shot problem and the MCC problem are encountered simultaneously, it is more difficult to solve the combined problem. Determining how to maintain the excellent performance of the classification algorithm in few-shot MCC problems has become a popular topic investigated by many scholars.

Description of few-shot multi-class classification problems

A classification method for MCC problems with few-shot numerical samples is constructed. The goal is to find a high-precision classification method for MCC problems with a small number of numerical samples in each category. For this purpose, the few-shot MCC problem with numerical data is defined as follows.

Definition 1

(few-shot MCC problem with numerical data): Given a data set $T$ containing $n$ independent identically distributed samples, $T=\left({x}_{1},{y}_{1}\right),\left({x}_{2},{y}_{2}\right),\cdots ,\left({x}_{n},{y}_{n}\right)$, where ${x}_{i}\in R,{y}_{i}\in \mathrm{1,2},\cdots ,M,M>2,i=\mathrm{1,2},\cdots ,n$, and ∆ < 40. ∆ is the number of samples per category.

Construction of the meta-learning network algorithm

For a complex numerical few-shot MCC problem, it is difficult for traditional methods to achieve satisfactory recognition performance. Therefore, the few-shot MCC problem is solved based on meta-learning, and a model for use in various learning tasks is obtained as ${\tau }_{l}\left(l=\mathrm{1,2},\cdots ,N\right)$. In this sense, only a small number of samples can be used to solve some new learning tasks with a learning ability. Each iteration of this model uses a different meta-learning task ${\tau }_{l}$. During the training process, each training task has a different sample. Therefore, each training task contains a different combination of categories, and tasks with open categories can also be better classified. In general, the previous task learned during meta-learning is called meta-training, and the new task encountered is called meta-testing. Because each task has its own training and test sets, the training and test sets within the meta-task are, respectively, called the support set and query set to avoid confusion.

Therefore, meta-training and meta-testing are two stages of MCC model construction based on meta-learning. Meta-learning is used to generate a classifier for MCC on the training data set. Each training sample in the training data set contains category attributes. The MCC algorithm constructs classifiers by learning the attribute categories and features of these samples. The meta-testing stage is the process of classifying the query set by using the model and determining the class label of the unknown data, thus allowing for the evaluation of the classification accuracy of the classifier. The samples in the query set are randomly selected and independent of the samples in the support set. If the measured accuracy is considered acceptable, the model can be used to classify other unknown data or objects. Figure 1 presents the framework of the method for solving the few-shot MCC problem.

Fig. 1

Framework of the method for the few-shot multi-classification problem

Meta-training and meta-testing can be decomposed according to different tasks ${\tau }_{l}$, but it is not common for the sample data set to be used in these stages. To strictly meet the conditions of few-shot problems, the classifier includes the feature extraction model of the dimension reduction model to measure the learning model and conduct loss function analysis.

Pretreatment model

Humans ####are capable of identifying new objects from a few samples. For instance, a child can recognize a “zebra” or “rhinoceros” by looking at a few pictures in a book. This is primarily due to the accumulation of knowledge in life and the innate ability to think (e.g., analogy). The human brain can quickly compare a never-before-seen image with previously acquired knowledge (there may be some other mental activities), which enables the achievement of rapid learning. Inspired by this ability, after learning a large amount of data in a certain category, the meta-learning model is posited to quickly learn a new category with only a small number of samples. Therefore, to imitate the ability of humans to quickly identify images, feature coding is first carried out for samples and data are obtained in the form of image representation. In other words, one-dimensional numerical data are converted into two-dimensional data via data re-coding. The basic idea is to represent all possible values of each feature with vectors.

First, each feature of the sample must be reanalyzed and mapped to a new space. Sample $X=\left\{{x}_{1},{x}_{2},\cdots ,{x}_{n}\right\}$ has $G$ features, which can be expressed as ${X}_{j},j=\mathrm{1,2},\cdots ,G$. To map each feature ${X}_{j}$ to the new space, all values of each feature are one-hot encoded. Each possible value is mapped to a vector, and different values of each feature correspond to different vectors. Let the number of values of each feature be ${P}_{j},j=\mathrm{1,2},\cdots ,G$. For any sample, according to the corresponding vector of each feature, it is regrouped into a new feature matrix. The length of each vector is different considering the different numbers of possible values of each feature, which will make it impossible to combine the new feature matrix by one-hot coding. Therefore, the dimension of each vector is set as $Q$, $Q\ge \left(\mathrm{max}\left({P}_{1},{P}_{2},\cdots ,{P}_{G}\right)\right)$, and the other dimensions are represented by 0. Then, after mapping $g$ and one-hot encoding, ${x}_{i}$ can be represented by a new eigenmatrix corresponding to any sample ${X}_{i}^{\prime}$.

$$g\left({X}_{i}\right)\to {X}_{i}^{\prime}.$$

(2.1)

In other words, for a sample, each feature is re-encoded and a two-dimensional array is used to store multiple possible values of each feature. The possible values of each feature are represented by the two-dimensional array, only one of which is valid at any time. For feature $i$, assuming that there are $q$ possible values, the space of all the values of the $i-th$ feature can be expressed as follows.

$${x}_{i1} \to \left[1 \quad 0 \quad \cdots \quad 0\right]$$

$${x}_{i2} \to \left[0 \quad 1 \quad \cdots\quad 0\right]$$

(2.2)

$$\cdots $$

$${x}_{iq} \to \left[0\quad 0 \quad \cdots \quad 1\right]$$

Algorithm 1

Pretreatment model

In addition to transforming one-dimensional numerical data into two-dimensional data, Algorithm 1 is adopted to solve the problem of feature coding. Quantized numbers can be defined freely, and the values serve only for identification. Moreover, Algorithm 1 plays a role in feature expansion. The method is easy to understand and the corresponding code is simple to write.

However, the feature space will be large if the category of the sample data is complex, which can easily lead to a dimensional disaster. In addition, the interpretability of data worsens with this feature coding, and the eigenmatrix is discrete and sparse with a large number of zero components. Therefore, the classification difficulties caused by the occurrence of these two situations should be avoided when constructing MCC models.

Feature selection model

The preprocessed data set is mainly composed of a large number of two-dimensional arrays with zero components. As the sample data category becomes complex, there will exist a lot of information irrelevant to the MCC task of classifying small samples in the data set, which will introduce great difficulties. Therefore, it is imperative to filter these characteristics according to certain rules. In other words, it is necessary to screen out features with a good classification ability from a large number of original feature sets. This can not only reduce the computational complexity of the algorithm, but can also effectively improve the classification accuracy. In this way, the set of features with good classification ability should meet the following characteristics:

• (1) The occurrence frequency of each value of the selected feature in the category to which it belongs should be high;

• (2) Each value of the selected feature should be evenly distributed and can represent most samples of this class;

• (3) The feature set should identify a large number of meta-testing samples.

Mapping all samples to a new space can help to screen out features with good classification ability. In terms of the two-dimensional array obtained after pretreatment, the convolutional neural network (CNN) has advantages for the considered method, as it has a strong nonlinear expression ability. In essence, a CNN is a mapping between an input and an output, and it can learn a large number of mapping relationships between the input and output without any precise mathematical expressions. As long as it is trained with known patterns, the network has the ability to map input and output pairs. In this study, the CNN block consists of a data input layer, a convolutional computation layer, a ReLU excitation layer, a pooling layer, and a fully connected layer, which are defined as follows.

• Input layer ${\varvec{I}}$: Data are processed by the preprocessed model${X}_{i}^{\prime}$.

• Convolutional layer ${\varvec{C}}$: After the calculation of the convolutional layer, the information irrelevant to the few-shot MCC task can be greatly reduced, and the information of the data set can be saved to a certain extent. In addition, a critical feature of the CNN is that it is top-heavy (the lower the input weight, the higher the output weight), and can be represented as an inverted triangle, which can sufficiently avoid the fast gradient loss during backpropagation (BP).

• Normalization layer ${\varvec{B}}$: BatchNorm2d is added after the convolutional layer of the CNN to normalize the data. The network performance will not be unstable due to the large data before the ReLU activation function.

• Excitation layer ${\varvec{\sigma}}$: The output results of the convolutional layer are nonlinearly mapped. The classical ReLU function is adopted in this study, which contributes to fast convergence. As its partial derivative is 1 on the right side of the origin, it is easy to take the derivative; thus, the BP speed is relatively fast.

• Pooling layer ${\varvec{M}}$: The sample feature space obtained by preprocessing via Algorithm 1 is large due to the complex sample data categories. Although some irrelevant information is removed after processing, the features that can best express the sample are retained. However, the pooling layer is adopted here to avoid excessive network parameters and the increased difficulty of calculation due to the large matrix generated later. Furthermore, it can, to some extent, prevent over-fitting, which is common in small-sample problems. Therefore, the pooling layer can compress the amount of data and parameters and reduce the occurrence of overfitting.

The structure of the CNN in this study is presented in Fig. 2.

Fig. 2

The framework of the feature extraction model

The mathematical formula of the feature extraction model is as follows:

$${f}_{\mu }\left({X}_{i}^{\mathrm{^{\prime}}}\right)={M}^{L}(\sigma ({B}^{L}{C}^{L})\cdots {M}^{1}(\sigma \left({B}^{1}{C}^{1}\left({X}_{i}^{{{\prime}}}\right)\right),$$

(2.3)

where ${f}_{\mu }\left({X}_{i}^{\prime}\right)$ is the feature extraction network mapping model, and $L$ is the number of convolution blocks. Each CNN contains a convolutional layer, a normalization layer, an activation function layer, and a maximum pooling layer. When the problem is complex and there are few data features, more convolution blocks are used to extract the sample features.

The CNN was selected because the convolutional neurons on the surface of the same feature map neural network weight values are the same, with the special structure of local weights of sharing. The CNN is more similar to real biological neural networks. Via the CNN, the complexity of network weight-sharing is reduced, and the pretreatment of the two-dimensional network input vector data can be directly input. The high complexity caused by the two-dimensional data output by the preprocessing module is reduced. In addition, after the preprocessing model, the sample is transformed into two-dimensional data. Hence, the features of the sample must be extracted by the CNN sharing the convolution kernel. In this way, features do not need to be manually selected; the weight must only be trained to obtain features that have a strong impact on the classification effect. In addition, the CNN can avoid gradient loss too fast during BP in the BP neural network, and can avoid the occurrence of the zero-gradient phenomenon, as well as the over-fitting problem that commonly occurs in few-shot problems.

In addition, when constructing the network, the multi-layer convolutional computing layer is selected for normalization. The excitation layer is then used, and the pooling layer is used for training. Because the data are sparse after being converted into two-dimensional data, a multi-layer CNN is used to learn the features of samples. The purpose of using the multi-layer CNN is that the features learned by one-layer convolution are often local. The higher the number of layers, the more global the learned features, and the more representative the meaning of the data. Networks with deeper layers can achieve the same level of performance or higher with fewer parameters. Moreover, the expressiveness of the network is improved via the ReLU activation function because the "nonlinear" expressiveness based on the activation function is added to the network. Via the superposition of nonlinear functions, more complex things can be expressed. By deepening the network, problems that must be learned can be hierarchically broken down into simpler problems.

Classification model

After dimensionality reduction, the features ${f}_{\mu }\left({X}_{s}^{\prime}\right)\mathrm{ and }{f}_{\mu }\left({X}_{q}^{\prime}\right)$ of the support set and query set are superimposed to form a group of large features. The combined features are then input into the metric learning model for recognition and classification. In other words, various feature vectors of the two samples are combined to form a group of larger feature vectors, which are then input into a model for recognition and classification. This method can prevent the loss of input information before feature combination. The expression of the connection model [31] is.

$$C\left({f}_{\mu }\left({X}_{s}^{\prime}\right)\bullet {f}_{\mu }\left({X}_{q}^{\prime}\right)\right)=\phi \left(\upsilon \right),$$

(2.4)

where, $\phi (\upsilon )$ represents the data obtained after being connected to the model.

From a mathematical perspective, the classification of few-shot MCC problems by the metric learning model is a process of mapping ${g}_{\varphi }$. The probability of unlabeled samples is mapped to existing categories in the classification system, which is a one-to-many mapping problem. Each mapping value represents the probability that the sample belongs to each category. The last category of the sample is determined according to the probability value ${g}_{\varphi }:\upsilon \to {X}_{sq}^{\prime}$. The metric learning model includes multiple convolution blocks and a fully connected layer. Each convolution block also includes an input layer, a convolution computation layer ${C}^{\prime}$, a normalization layer ${B}^{\prime}$, a ReLU excitation layer $\sigma$, and a pooling layer ${M}^{\prime}$. However, considering the characteristics of over-fitting in few-shot learning, the network parameters of this model should be compressed to the greatest possible extent. Via this principle, the network ${g}_{\varphi }$ can be expressed as.

$${g}_{\varphi }\left({X}_{sq}^{\prime}\right)=\underset{C}{\mathrm{max}}{g}_{\mathit{\varphi out}}\left(\left(\prod {\left(h=1\right)}^{N}{\omega }_{h}\psi \left(\upsilon \right)\right)\right),$$

(2.5)

where

$$\psi \left(\upsilon \right)={M}^{\prime}\left(\sigma \left({B}^{\prime}{C}^{\prime}\left(\phi \left(\upsilon \right)\right)\right)\right),$$

(2.6)

Via the numerical few-shot multi-class classifier constructed by the previously described learning method, the probability of incorrect category classification should be as low as possible, while the probability of correct category classification should be as high as possible. The unknown samples should meet the relevant requirements of few-shot MCC problems. In fact, model (2.1) can be interpreted as follows: $C$ probability values are obtained for classifier $C$. For the samples from class $i$, there exists a unique probability among these probability values that meets the following conditions:

• 1. The probability of category $i$ samples belonging to this category is greater than 0.5;

• 2. A sample from class $i$ has the highest probability of being in this category.

The purpose of this study is to estimate the dependence between the input and output of a system based on a given training sample to make accurate predictions about an unknown output. Multi-class data can be perfectly labeled according to the rules provided by Eq. (2.5), and the empirical risk is approximately zero.

$${}{R_{emp}} = 1/\tau \mathop \sum \limits_\tau \mathop \sum \limits_i \mathop \sum \limits_j \left( {{{\mathcal L}_\tau }\left( {{x_i},{y_i},{\omega _h}} \right)} \right).$$

(2.7)

Because the CNN is used to fit a method to measure unknown categories, it can be regarded as a regression problem to be solved. Therefore, the mean square error is used to train the model, and the function ${\mathcal{L}}_{\tau }$ can be expressed as follows.

$${\mathcal{L}}_{\tau }=\mathop {\sum }\limits_{s=1}^{k}\mathop {\sum }\limits_{q=1}^{k}\frac{1}{k}\frac{1}{k}{\bigg({g}_{\varphi }\left({X}_{sq}^{\prime}\right)-y\bigg)}^{2}.$$

(2.8)

Consider all models parameterized by $\theta$. The initial parameter $\theta$ is determined for task-specific learning, and the model parameter $\theta$ is updated by the gradient descent method:

$${\theta }^{(\tau +1)}={\theta }^{(\tau )}-\alpha \frac{1}{k}\frac{1}{k}\mathop {\sum }\limits_{k}\mathop {\sum }\limits_{k}{\nabla }_{{\theta }^{\left(\tau \right)}}{\mathcal{L}}_{\tau }(\upsilon ,{X}^{\prime}),$$

(2.9)

where $\alpha$ is the learning rate. In particular, the weight $\omega$ of the fully connected layer is updated as follows.

$$\prod_{h=1}^{N}{\omega }_{h}^{(\tau +1)}=\prod_{h=1}^{N}({\omega }_{h}^{(\tau )}-\alpha \frac{1}{k}\frac{1}{k}\mathop {\sum }\limits_{k}\mathop {\sum }\limits_{k}{\nabla }_{{\omega }_{h}^{(\tau )}}{\mathcal{L}}_{\tau }(\upsilon ,{X}^{\prime})),$$

(2.10)

$\nabla {\mathcal{L}}_{\tau }\left(\upsilon ,{X}^{\prime}\right)=e\left({X}^{\prime},y\right)$ is then set.

$$\begin{aligned}&\mathop {\prod }\limits_{h=1}^{N}{\omega }_{h}^{(\tau )}-\frac{\alpha }{k}\frac{1}{k}\sum\limits_{k}\sum\limits_{k}\sum\limits_{h=1}^{N} \bigg(\mathop {\prod }\limits_{i=1}^{h-1}{\omega }_{i}^{(\tau )}\bigg){\left(\mathop {\prod }\limits_{i=1}^{h-1}{\omega }_{i}^{\left(\tau \right)}\right)}^{T}\\ &\qquad\,e({X}^{{{\prime}}},y)\left(\mathop {\prod }\limits_{i=h+1}^{N}{\omega }_{i}^{\left(\tau \right)}\right){\left(\mathop {\prod }\limits_{i=h+1}^{N}{\omega }_{i}^{\left(\tau \right)}\right)}^{T}-o({\alpha }^{2})\end{aligned}.$$

Both sides of the equation are multiplied by an arbitrary value $\psi \left({X}_{test}^{*},\theta \right)$, which can be obtained by the previous equation, namely,

$$\begin{aligned} & \mathop {\prod }\limits_{h=1}^{N}{\omega }_{h}^{(\tau )}\psi \left({X}_{test}^{*},\theta \right)\\&\quad-\frac{\alpha }{k}\frac{1}{k}\mathop {\sum }\limits_{k}\mathop {\sum }\limits_{k}\mathop {\sum }\limits_{h=1}^{N}\left(\mathop {\prod }\limits_{i=1}^{h-1}{\omega }_{i}^{(\tau )}\right){\left(\mathop {\prod }\limits_{i=1}^{h-1}{\omega }_{i}^{\left(\tau \right)}\right)}^{T}e({X}^{\prime},y)\\&\quad\left(\mathop {\prod }\limits_{i=h+1}^{N}{\omega }_{i}^{\left(\tau \right)}\right){\left(\mathop {\prod }\limits_{i=h+1}^{N}{\omega }_{i}^{\left(\tau \right)}\right)}^{T}\psi \left({X}_{test}^{*},\theta \right)\end{aligned}$$

$$\quad=\mathop {\prod }\limits_{j=1}^{N}{\omega }_{j}^{(\tau +1)}\psi \left({X}_{test}^{*},\theta \right).$$

(2.11)

Then, the following equation can be obtained.

$${g}_{\varphi }^{\left(\tau \right)}-\alpha \frac{1}{k}\frac{1}{k}\mathop {\sum }\limits_{k}\mathop {\sum }\limits_{k}{\nabla }_{{g}^{\left(\tau \right)}}{\mathcal{L}}_{\tau }\left(\upsilon ,{X}^{\prime}\right)={g}_{\varphi }^{\left(\tau +1\right)}.$$

(2.12)

The universal applicability of the proposed method can be proved.

Summary of the few-shot MCC meta-learning network algorithm

Given a sample $x$ in the meta-training stage, the output of the classifier is the vector about the probability that the sample belongs to each category, among which the category corresponding to the maximum probability is selected as the category of the sample. The whole classifier is described as follows.

Algorithm 2

Meta-learning network algorithm

Theorem 1

(Universality theorem). For an arbitrary ${x}_{i}$, the meta-learning network method (Algorithm 2) is used to attain the function ${g}_{\varphi }$, which can be updated by the loss function ${\nabla }_{{g}^{\left(\tau \right)}}{\mathcal{L}}_{\tau }\left(\upsilon ,{X}^{\prime}\right)$ in task $\tau$ with learning rate $\alpha$, namely,

$${g}_{\varphi }^{(\tau +1)}={g}_{\varphi }^{\left(\tau \right)}--\alpha \frac{1}{k}\frac{1}{k}\mathop{\sum}\limits_{k}\mathop{\sum}\limits_{k}{\nabla }_{{g}^{\left(\tau \right)}}{\mathcal{L}}_{\tau }(\upsilon ,{X}^{\prime}).$$

(2.13)

The category of the arbitrary ${x}_{i}$ is obtained by this equation.

Proof

Please see the Appendix.

Experiments

The data from a data set in a public database were used to test the validity of the proposed method. First, the data were prepared. Preliminary screening was carried out on all the data, after which multiple classes were obtained, each of which had a small amount of valid data. Then, meta-training and meta-testing were conducted. The performance of the algorithm was tested in the meta-learning training mode. In this mode, one or five samples from $C$ categories were taken as support set samples, and meta-training was repeated to completion. Then, in the meta-testing stage, evaluation indicators were used to test the MCC effect of the constructed model. To reflect the performance of the prediction model for few-shot MCC problems, the model prediction effect for the data set was evaluated by the calculation accuracy. In addition, the accuracy of the proposed method was compared with that of other methods to reflect its effectiveness. Furthermore, to maintain structural integrity, it is not feasible to directly delete a module in the algorithm. However, to demonstrate the effectiveness of the proposed method, an ablation setting was designed to remove the meta-learning process to verify that it is an indispensable part of the network that greatly improves the algorithm performance.

Experimental precision analysis

Experiment 1 (Classification of credit card overdue time)

During credit card use, users should not be overdue in credit repayment. An overdue payment may have adverse impacts on the personal credit of the cardholder and can sometimes cause the holder to undertake criminal responsibilities. Hence, overdue credit payment was selected as the first case.

Given that credit cards have long been used in countries worldwide, in-depth analyses of credit card risk have been conducted. Both theoretical and practical investigations have been carried out from all dimensions of credit card risk, and researchers have analyzed the penalty after a credit card payment is overdue. It has been posited that although charging the corresponding penalty interest after the due date may increase the bank’s income to a certain extent, it imposes a heavier burden on customers and becomes a reason for which customers refuse to make a payment. Credit risk is generated primarily due to the failure of banks to understand their clients, their ill judgment of the risking-taking ability and reimbursement capacity of clients, and their problematic procedures and management. Moreover, during the use of a credit card, a variety of factors affect repayment and may cause a default. Therefore, in the case of limited tagging samples, if a bank or enterprise can accurately predict whether or when clients will be overdue in repayment based on their accounts, it is possible to conduct corresponding measures to cope with this risk and reduce the losses of both banks and clients.

This analysis was based on a data set of credit card users from the UCI public database. One of the 1000 samples were selected. The data collected from each sample contained 14 features. All the features were numerical data, including data on credit cards, gender, education, marital status, age, overdue monthly bills over the past six months, and the payment condition of the client over the past three months as the dependent variables. Thus, the target was to predict the recent monthly payment based on the customer's information. In addition, the dependent variable contained seven categories indicating that the customer paid on time, one month late, two months late, and more than six months late. Four experimental methods were designed, namely (1) $C=3,k=1$, (2) $C=3,k=5$, (3) $C=5,k=1$, and (4) $C=5,k=5$. Table 1 displays the final classification results with $L=6$ and $\tau =50{,}000$ based on the proposed method. The results of the Model-Agnostic Meta-Learning (MAML), Matching Network (MN), the proposed meta-learning network method (MLNM), and ablation test are presented. However, MAML and MN methods should also consider the pretreatment model (PRE) when dealing with numerical data. Meanwhile, an ablation setting without meta-learning is designed [36] to verify that the meta-learning process is a key part of the network and it induces great improvement in the algorithm performance. In other words, the proposed method directly gets to the meta-test stage where the single classification task of all training data points is tested on the query set after updating the entire model on the support set.

Table 1 The results of Experiment 1

Table 1 reports the classification results of the credit card data set based on training by the four models. According to the results, the accuracy of the proposed method was better than that of the traditional machine learning and deep learning algorithms. Therefore, the proposed method is suitable for the few-shot MCC problem, and lays a foundation for research on the credit card MCC problem.

Experiment 2 (Classification of coupon types)

With the development of the market economics, competition among commercial enterprises has been fiercely increasing. Promotions are essential tools for sales growth, and coupons are a promotional tool frequently adopted by commercial enterprises. Coupons attract the attention of customers when they buy products and drive product marketing. In essence, product purchasing will increase if coupons are used to promote products. Moreover, via the use of coupons, customers are highly likely to acquire quality commodities at lower costs; thus, they develop loyalty toward the enterprises that sell these commodities. Furthermore, the use of coupons makes consumers revisit the business and increases customer stickiness. Coupons can therefore act as a guide to consumers and are an important asset and source of profit for companies and businesses competing with others. Therefore, data related to coupons were selected as a second case study to demonstrate the ability of the proposed method to solve the few-shot MCC problem. To achieve better coupon distribution during a campaign, enterprises can use coupons to track and analyze the purchasing behavior of customers together with the preferences and purchasing habits of previous coupon recipients, thus allowing them to obtain the history of consumers' use of coupons. User groups are who are using the coupon.

This experiment was based on data from a survey conducted by Amazon Turkish Machinery, and the data were also collected from the UCI public database. The data set contains different driving scenarios, including the destination, current time, weather, and passengers. The types of coupons accepted, including five types of coupons for restaurants (< $20), cafes, takeout, bars, and restaurants ($20–50), were classified in the experiments. Four experimental methods were designed, namely (1) $C=3,k=1$, (2) $C=3,k=5$, (3) $C=5,k=1$, and (4) $C=5,k=5$, respectively. The final classification results with $L=4S$ and $\tau =50{,}000$ based on the proposed method are displayed in Table 2. The results of the PRE + MAML, PRE + MN, and MLNM are presented. Meanwhile, an ablation setting without meta-learning is designed to verify that the meta-learning process is a key part of the network.

Table 2 The results of Experiment 2

Table 2 shows the classification results of the coupon data set based on model training. According to the results, the accuracy of the proposed method was 98%, while the accuracy of the traditional machine learning and deep learning methods was less than 70%. Therefore, the proposed method is more suitable for few-shot MCC problems.

Experiment 3 (Classification of customer regions for online shopping)

The emergence of business-to-consumer (B2C) e-commerce, such as eBay and Amazon, marked the birth of the e-commerce model. Subsequently, each country developed its own e-commerce channel and became a major player in the e-commerce retail market. With the rapid growth of Internet users and the spread of online payment and logistics information technology, the online retail market has grown rapidly and is now dominated by B2C and consumer-to-consumer (C2C) e-commerce platforms. In the last decade, the online-to-offline (O2O) model has emerged and matured with the advancement of technology, changes in people's lifestyles, and the improvement of instant delivery capabilities. In the future, with the gradual development of the online and instant consumption habits of consumers and the integration of online and offline omni-channel retailing, O2O e-commerce will become one of the key models in the online retail market. In addition, the development of the e-commerce market has continued to improve in recent years. The year 2020 witnessed the steady growth of the online sales market and new heights reached by the market scale in the face of the huge impact of the COVID-19 pandemic.

Even if the online retail business model solves the sorting and distribution of products, it still faces the problems of market and customer demand. Therefore, it is important for the online shopping industry to study customer behavior for the development of the market and marketing strategies, and thus to expand online sales. Therefore, data related to e-commerce customers were selected as the third case study to prove the ability of the proposed few-shot MCC method.

The data on online shopping transactions were also collected from the UCI public database. This data set contains the following variables: Administrative, Informational, ProductRelated BounceRates, ExitRates, PageValues, SpecialDay, Month, OperatingSystems, Browser, VisitorType, Weekend, Revenue, TrafficType, and Region. Region is a multi-category variable; therefore, the classification ability of the proposed method for this feature was investigated.

Four experimental methods were designed, namely (1) $C=3,k=1$, (2) $C=3,k=5$, (3) $C=5,k=1$, and (4) $C=5,k=5$, respectively. The final classification results with $L=8$ and $\tau =50{,}000$ based on the proposed method are displayed in Table 3. The results of the PRE + MAML, PRE + MN, MLNM, and ablation test are presented.

Table 3 The results of Experiment 3

As can be seen from Table 3, compared with the classical numerical data classification algorithm, the proposed meta-learning network method achieved the highest accuracy. Therefore, as compared with other methods, the meta-learning network method is more suitable for few-shot MCC problems.

The statistical analysis of the experimental results

The Chi-square test

The characterization of a statistical test of the classification data is an important modeling factor. In this study, the sum of Chi-square test was mainly considered. As a nonparametric test where both independent and dependent variables are classification data, Chi-square test evaluates the differences between the practical and the theoretical values of the statistical samples: a large Chi-square value indicates a large difference and low consistency between practical and theoretical values. However, a small Chi-square value indicates a tiny difference and a high consistency of practical and theoretical values. Moreover, a null Chi-square value indicates that practical and theoretical values coincide with each other, suggesting that the theoretical value is perfectly correct. First, two hypotheses were proposed:

${H}_{0}$: the practical and the predicted values are independent;

${H}_{1}$: the practical and predicted values have dependency;

According to the calculation results, the p-values of Chi-square tests of Experiments 1, 2, and 3 were null (< 0.05). Hence, ${H}_{0}$ was rejected, meaning that the practical and the predicted values have a negligible difference.

The likelihood ratio test is also an authenticity indicator reflecting both sensitivity and specificity. This test can also serve as an integrated index evaluating the difference between practical and expected frequencies. The likelihood ratio varies between 0 and 1: a value approaching 1 signifies that the original hypothesis of the problem is verified whereas a value approaching 0 means that the original hypothesis of the problem is rejected. To start with, the two proposed hypotheses were the followings:

${H}_{0}$: practical frequency is not consistent with expected frequency;

${H}_{1}$: practical frequency is consistent with expected frequency;

According to the calculation results, the p-values of Chi-square tests of Experiments 1, 2, and 3 were 0 (< 0.05). Hence, ${H}_{0}$ was rejected; therefore, the practical frequency and expected frequency have a negligible difference.

The Wilcoxon rank sum test

The Wilcoxon rank sum test is a nonparametric hypothesis test used to test whether two data sets come from the same distributed population. In the rank sum test, we do not require the two sets of data to be tested to contain the same number of elements, in other words, the rank sum test is more suitable for the difference detection between unpaired data. So, the two hypotheses about the predicted values of the PRE + MAML and MLNM were proposed:

${H}_{0}$: the predicted values of the PRE + MAML and MLNM are independent;

${H}_{1}$: the predicted values of the PRE + MAML and MLNM are non-independent;

According to the calculation results, the $p$-values of Wilcoxon rank sum test of Experiments 1, 2, and 3 were greater than 0.05. Hence, ${H}_{0}$ was accepted, it meaning that the predicted values of the PRE + MAML and MLNM have a statistically significant difference.

According to the accuracy and the statistical results, the proposed method can effectively solve the MCC problems for numerical small-amount samples in the field of economics. Therefore, the proposed network model can more effectively handle harsh sample conditions in the field of the economics with fewer numerical data samples, suggesting that the proposed method can more effectively solve the MCC problems.

Conclusion

This paper presented a detailed classification model suitable for the solution of small-sample MCC problems with few-shot learning. There are many existing methods for the solution of MCC problems, most of which require large amounts of data to train high-precision models. By using preprocessing models, CNNs, metric networks, and meta-learning algorithms, a new classification model was proposed to solve MCC problems with few samples per category. This research not only proposes a new concept for the solution of few-shot MCC problems, but also improves the classification accuracy of MCC problems. The work and research results of this paper are summarized as follows.

• (1) A neural network model for few-shot MCC problems based on meta-learning was proposed. The basic modules are composed of a preprocessing module, feature extraction module, metric network module, and loss function module. Each basic module is trained by the meta-learning training model. The model improves the accuracy of MCC problems with a small number of samples.

• (2) The proposed method was tested on the UCI public database. The experimental results show that, compared with other classical integration algorithms, the proposed model has the advantage of high classification accuracy when dealing with few-shot MCC problems.

Appendices

In this section, we prove the following theorem 1.

Theorem 1 (Universality theorem).

For an arbitrary ${x}_{i}$, the meta-learning network method (Algorithm 2) is used to attain the function ${g}_{\varphi }$, which can be updated by the loss function ${\nabla }_{{g}^{\left(\tau \right)}}{\mathcal{L}}_{\tau }\left(\upsilon ,{X}^{\prime}\right)$ in task $\tau$ with learning rate $\alpha$, namely,

$${g}_{\varphi }^{(\tau +1)}={g}_{\varphi }^{\left(\tau \right)}--\alpha \frac{1}{k}\frac{1}{k}\mathop{\sum}\limits_{k}\mathop{\sum}\limits_{k}{\nabla }_{{g}^{\left(\tau \right)}}{\mathcal{L}}_{\tau }\left(\upsilon ,{X}^{\prime}\right),$$

(2.14)

to get the category of arbitrary ${x}_{i}$.

Proof

This paper uses mean square error to train the model, and the ${\mathcal{L}}_{\tau }$ function can be expressed as:

$${\mathcal{L}}_{\tau }=\mathop{\sum}\limits_{s=1}^{k} \mathop{\sum}\limits_{q=1}^{k}\frac{1}{k}\frac{1}{k}{({g}_{\varphi }\left({X}_{sq}^{\prime}\right)-y)}^{2}.$$

(2.15)

In this paper, the weight $\omega$ of the full connection layer is updated by gradient descent in the task $\tau +1$

$$\prod_{h=1}^{N}{\omega }_{h}^{(\tau +1)}=\prod_{h=1}^{N}({\omega }_{h}^{(\tau )}-\alpha \frac{1}{k}\frac{1}{k}\mathop\sum\limits_{k}\mathop\sum\limits_{k}{\nabla }_{{\omega }_{h}^{(\tau )}}{\mathcal{L}}_{\tau }(\upsilon ,{X}^{\prime})),$$

(2.16)

where α is the learning rate. We set $\nabla {\mathcal{L}}_{\tau }\left(\upsilon ,{X}^{\prime}\right)=e\left({X}^{\prime},y\right)$, then we have:

$$\begin{aligned} & \mathop{\prod }\limits_{h=1}^{N}{\omega }_{h}^{(\tau )}-\frac{\alpha }{k}\frac{1}{k}\mathop\sum\limits_{k}\mathop\sum\limits_{k}\mathop\sum\limits_{h=1}^{N} \left(\mathop\prod\limits_{i=1}^{h-1}{\omega }_{i}^{(\tau )}\right)\\ &\quad{\left(\mathop{\prod }\limits_{i=1}^{h-1}{\omega }_{i}^{\left(\tau \right)}\right)}^{T}e({X}^{\prime},y) \left(\mathop{\prod }\limits_{i=h+1}^{N}{\omega }_{i}^{\left(\tau \right)}\right)\\ &\quad{\left(\mathop{\prod }\limits_{i=h+1}^{N}{\omega }_{i}^{\left(\tau \right)}\right)}^{T}-o\left({\alpha }^{2}\right).\end{aligned}$$

Let us multiply both sides by arbitrary $\psi \left({X}_{test}^{*},\theta \right)$, which can be attained by the above equation, namely,

$$\begin{aligned} & \mathop{\prod }\limits_{h=1}^{N}{\omega }_{h}^{(\tau )}\psi \left({X}_{test}^{*},\theta \right)\\ &\quad-\frac{\alpha }{k}\frac{1}{k}\mathop\sum\limits_{k}\mathop\sum\limits _{k}\mathop\sum\limits _{h=1}^{N}\left(\mathop{\prod }\limits_{i=1}^{h-1}{\omega }_{i}^{(\tau )}\right){\bigg(\mathop{\prod }\limits_{i=1}^{h-1}{\omega }_{i}^{\left(\tau \right)}\bigg)}^{T}e({X}^{\prime},y)\\ &\quad \left(\mathop{\prod }\limits_{i=h+1}^{N}{\omega }_{i}^{\left(\tau \right)}\right){\left(\mathop{\prod }\limits_{i=h+1}^{N}{\omega }_{i}^{\left(\tau \right)}\right)}^{T}\psi \left({X}_{test}^{*},\theta \right)\end{aligned}$$

$$\quad=\mathop{\prod }\limits_{j=1}^{N}{\omega }_{j}^{(\tau +1)}\psi \left({X}_{test}^{*},\theta \right),$$

(2.17)

then the following equation can be obtained:

$${g}_{\varphi }^{(\tau +1)}={g}_{\varphi }^{\left(\tau \right)}--\alpha \frac{1}{k}\frac{1}{k}\mathop\sum\limits _{k}\mathop\sum\limits _{k}{\nabla }_{{g}^{\left(\tau \right)}}{\mathcal{L}}_{\tau }\left(\upsilon ,{X}^{\prime}\right).$$

(2.18)

The universal applicability of the proposed method can be proved.