A novel fuzzy TOPSIS method based on T-spherical fuzzy Aczel–Alsina power Heronian mean operators with applications in pharmaceutical enterprises’ selection

Abstract

One of the most significant and complete approaches to accommodate greater uncertainty than current fuzzy structures is the T-Spherical Fuzzy Set (T^SPFS). The primary benefit of T^SPFS is that current fuzzy structures are special cases of it. Firstly, some novel T^SPF power Heronian mean (T^SPFPHM) operators are initiated based on Aczel–Alsina operational laws. These aggregation operators (AOs) have the capacity to eliminate the impact of uncomfortable data and can simultaneously consider the relationships between any two input arguments. Secondly, some elementary properties and core cases with respect to parameters are investigated and found that some of the existing AOs are special cases of the newly initiated aggregation operators. Thirdly, based on these AOs and Aczel–Alsina operational laws a newly advanced technique for order of preference by similarity to ideal solution (TOPSIS)-based method for dealing with multi-attribute group decision-making (MAGDM) problems in a T-Spherical fuzzy framework is established, where the weights of both the decision makers (DMs) and the criteria are completely unknowable. Finally, an illustrative example is provided to evaluate and choose the pharmaceutical firms with the capacity for high-quality, sustainable development in the T^SPF environment to demonstrate the usefulness and efficacy. After that, the comparison analysis with other techniques is utilized to demonstrate the coherence and superiority of the recommended approach.

Introduction

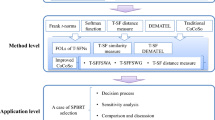
Multi-attribute group decision-making (MAGDM)/multiple attribute decision making (MADM) has been increasingly important in recent research environments for decision support systems [1,2,3,4,5,6,7]. The international economy has grown quickly with the emergence and strengthening of global economic integration. However, fast economic expansion has also brought forth several issues with social stability, ecological governance, and environmental conservation. The preservation of a beautiful environment and ecological balance is a crucial assurance for the growth of the green economy at the same time as rapid economic development. To enhance the quality of economic growth, it is crucial to examine businesses from the standpoint of sustainable and high-quality development ability [8]. The assessment of firms with sustainable and high-quality development ability may be viewed as a multi-criteria group decision-making (MCGDM) problem since the process of assessment incorporates criteria for assessment of several aspects and experts and academics in various domains. Although researchers have proposed numerous models to address these issues, the results above seldom take into account elements like expert judgement and the unpredictability and incompleteness of the decision environment. Therefore, to offer assessment specialists with rational, empirical decision assistance, it is important to develop a model for assessment in a fuzzy uncertainty environment (Fig. 1).

Fig. 1

Graphical abstract of the proposed research work

It might be challenging for specialists to convey their preferences through precise values in the analysis of practical choice difficulties when dealing with complicated and unclear decision-making challenges. A novel mathematical technique known as the fuzzy set (FS) [9] is proposed to use membership degree (MD) to represent uncertain information, but it is constrained by the objective complexity of decision-making issues and the constraints of decision makers' subjective comprehension. The intuitionistic fuzzy set (IFS) [10] theory is created to more properly express unreliable data by adding non-membership degree (N-MD) and hesitation degree (HD) on the framework of FS, which addresses the impediment that FS only employs MD for expressing fuzzy information. Currently, intuitionistic fuzziness research has produced useful discoveries and has been utilized extensively in several disciplines [11,12,13,14,15,16]. Despite extensive research and solutions to several uncertain decision and assessment problems, IFSs are unable to represent ambiguous and contradictory information. Then, Yager [17] introduced the Pythagorean fuzzy (PyF) set, which is distinguished by the positive and negative membership grades, and which meets the requirement that the square sum of the specified functions is less than or equal to one. PyFS fuzzy fails in some instances, when the total of squares of both positive and negative membership grades is larger than 1. To overawe, this imperfection of PyFS, Yager [18] proposed a new concept called q-rung orthopair fuzzy set (Q-ROFS), which is characterized by positive and negative MDs, that satisfy the requirement that the qth (q > 0) power sum of the specified functions be less than or equal to one. Researchers from several fields were drawn to the use of Q-ROFS in different fields [19,20,21,22,23].

Yet, there are still instances when human opinions have several consequences, such as in electoral systems where there are four options: vote for, abstain, and refuse. Cuong and Kreinovich [24] presented picture fuzzy sets (PFSs) as a solution to this sort of issue, where the total of the MD, abstinence degree (AD), and N-MD is less than or equal to 1. The PFSs were further developed by Ashraf et al. [25], Gündoğdu et al. [26], and Mahmood et al. [27] to include spherical fuzzy sets (SPFSs) and T-spherical fuzzy sets (T^SPFSs). The square sum of MD, AD, and N-MD does not exceed one in SPFSs, while the qth power sum of MD, AD, and N-MD does not exceed one in T^SPFSs. T^SPFSs, that have a wider viable domain than conventional FSs, can be utilized to describe unreliable and ambiguous information more correctly and effectively. Since its introduction, T^SPFS have already seen significant expansion. Garg et al. [28] proposed some power aggregation operators and apply them to solve MADM problems. Wu et al. [29] introduced some cosine similarity measures and applied them to pattern recognition. Mahnaz et al. [30] proposed some entropy measures and Frank aggregation operators and applied them to solve MADM problems. Garg et al. [31] proposed some interactive aggregation operators and apply them to solve MADM problems. Ullah et al. [32] introduced some Hamacher aggregation operators and are utilized to evaluate the effectiveness of search and rescue robots utilizing a MAD technique because of how well they perform under pressure. Khan et al. [33] proposed some Schweizer–Sklar power Heronian mean operators for T^SPFS and applied them to solve MAGDM problems. Numerous scholars have recently progressed in distance and similarity measures [6, 34,35,36,37] and developed various techniques [38,39,40,41,42] for different fuzzy structures and applied them to solve MADM/MAGDM in various fields. Recently, Hussain et al. [43] initiated some Aczel–Alsina operational laws for T^SPFS, based on these operational laws various Aczel–Alsina aggregation operators are developed and applied them to solve MADM problems.

The development of decision analysis using various decision techniques is the most significant MCGDM process. Numerous approaches for making decisions have been developed in the literature throughout the years, with Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) being one of the most well-known and widely employed. TOPSIS was introduced by Hwang and Yoon [44] to deal with MADM problems. The optimal alternative in MADM problems is the one where the distance between it and the positive ideal solution (POIS) is the shortest and the distance between it and the negative ideal solution (NOIS) is the greatest. The TOPSIS employing the FS environment to solve the MADM problems was presented by Chen in [45]. Numerous academics have recently developed an interest in TOPSIS and used it to actual MADM/MAGDM problems under various extended FS structures [5, 46,47,48,49] in the decision sciences. It should also be noted that the current TOPSIS algorithms have the limitation that to solve MADM problems, either DMs weights [50] or criteria weights [51, 52] are known, or both [53, 54]. Some researchers assigned unknown weight information to DMs [55, 56] with known criterion weights. Instead, other researchers solved MCGDM difficulties using DMs with known weights to manage uncertain criterion weights.

As a result of the above-mentioned discussion, to provide a new enlarged TOPSIS technique in a T^SPF environment, allowing us to take advantages of the TOPSIS method, T^SPFS and T^SPF power Heronian mean operators. As the T^SPFS is the generalized version of the current different structures of FS, including IF sets, PyF sets, and PF sets, T^SP-SF sets may handle more uncertainty than FS, IF sets, PyF sets, and PF sets. To deal with such conditions of unknown weight information for both DMs and criterion weights and to solve the MAGDM problems after computing all the weights, a unique enhanced TOPSIS-based algorithm is created in this study. Selecting the optimum viewpoint that is better related to each DMs matrix is crucial for solving the MADM/MAGDM problems. In the approach shown, the ideal opinion is selected using the T^SPF Aczel–Alsina power Heronian mean operators/geometric Heronian mean operators. The distance measures and entropy measure are also utilized in the proposed T-spherical fuzzy TOPSIS (T^SPF TOPSIS) for addressing MAGDM problems to determine the criterion weights under the T^SPF information.

The rest of the article is arranged as follows. In “Preliminaries”, some basic definitions and results related to our work are given. In “T-spherical fuzzy Aczel–Alsina power Heronian mean operators”, T^SPFAAPHM operator and T^SPFAAPGHM operator, core properties and some special cases with respect to the parameters are initiated. In “The TSFAAWPHM operator and TSFAAWPGHM operators”, the weighted forms of the said aggregation operators are given. In “T-Spherical Fuzzy MAGDM Model Based on Improved T-Spherical Fuzzy TOPSIS”, MAGDM model and T^SPF TOPSIS approach is initiated based on these aggregation operators. In “Illustrative example”, an illustrative example is given to show the effectiveness and practicality of the proposed approach. In “TSPF TOPSIS approached based on TSPFAAPWGHM operators”, the same example is solved with the same technique, instead of using the T^SPFAAWPHM operator, the T^SPFAAWPGHM operator is used. In Effect of the parameters N,$Q,{\mathbb{R}}$ and q on final ranking results, comparisons with some existing approaches are investigated. Finally, conclusion and future work and references are given.

Preliminaries

In this portion, some core definitions, and results about T^SPFSs, Aczel–Alsina TN and TC-N have been discussed.

TSPFS and their operational laws

Definition 1

[27] Suppose that the universe of discourse is symbolized by $\mathfrak{B}$ and $\mathfrak{E} \in {\mathbb{A}}$ be any element. Then, a T^SPFS $\widetilde{TS}$ in the universe of discourse is symbolized by.

$$ \widetilde{TS} = \left\{ {\left\langle {\mathfrak{E},A_{{\widetilde{TS}}} (\mathfrak{E}),I_{{\widetilde{TS}}} (\mathfrak{E}),F_{{\widetilde{TS}}} (\mathfrak{E})} \right\rangle |\mathfrak{E} \in {\mathbb{A}}} \right\}, $$

(1)

where $A_{{\widetilde{TS}}} ,I_{{\widetilde{TS}}}$ and $F_{{\widetilde{TS}}}$ respectively, articulated the membership grade, indeterminacy grade and the non-membership grade of $\mathfrak{E}$ in the T^SPFS $\widetilde{TS}$ such that $0 \le A_{{\widetilde{TS}}} (\mathfrak{E}),I_{{\widetilde{TS}}} (\mathfrak{E}),F_{{\widetilde{TS}}} (\mathfrak{E}) \le 1$ with the condition $0 \le \left( {A_{{\widetilde{TS}}} (\mathfrak{E})} \right)^{q} + \left( {I_{{\widetilde{TS}}} (\mathfrak{E})} \right)^{q} + \left( {F_{{\widetilde{TS}}} (\mathfrak{E})} \right)^{q} \le 1\left( {q > 0} \right)$. The hesitancy grade $\widetilde{E}_{{\widetilde{TS}}} (\oe )$ of the member $\oe$ in the T^SPFS $\widetilde{TS}$ is demarcated by $\widetilde{E}_{{\widetilde{TS}}} (\mathfrak{E}) = \left( {1 - \left( {A_{{\widetilde{TS}}} (\mathfrak{E})} \right)^{q} - \left( {I_{{\widetilde{TS}}} (\mathfrak{E})} \right)^{q} - \left( {F_{{\widetilde{TS}}} (\mathfrak{E})} \right)^{q} } \right)$, satisfying $0 \le \widetilde{E}_{{\widetilde{TS}}} (\mathfrak{E}) \le 1$ and $\mathfrak{E} \in {\mathbb{A}}$.

The pair $\left\langle {A_{{\widetilde{TS}}} (\mathfrak{E}),I_{{\widetilde{TS}}} (\mathfrak{E}),F_{{\widetilde{TS}}} (\mathfrak{E})} \right\rangle$ was named T^SPFN by Mahmood et al. [27] and is denoted $S = \left\langle {A,I,F} \right\rangle$ satisfying the condition $0 \le A,I,F \le 1$ with the axiom $0 \le \left( A \right)^{q} + \left( I \right)^{q} + \left( F \right)^{q} \le 1\left( {q > 0} \right).$

To compare two T^SPFNs, the score function and accuracy function are determined as:

Definition 2

[27] The score function $\overline{\overline{SC}} \left( S \right)$ and accuracy function $\overline{\overline{AY}} \left( S \right)$ of a T^SPFN $S = \left\langle {A,I,F} \right\rangle$ can be emitted as.

$$ \begin{gathered} \overline{\overline{SC}} \left( S \right) = A_{S}^{q} - I_{S}^{q} - F_{S}^{q} , \,\,\,{\text{Where}}\,\,\,\overline{\overline{SC}} \left( S \right) \in \left[ { - 1,1} \right]; \hfill \\ \overline{\overline{AY}} \left( S \right) = A_{S}^{q} + F_{S}^{q} ,\,\,\,\,\,{\text{Where}}\,\,\overline{\overline{AY}} \left( S \right) \in \left[ {0,1} \right]. \hfill \\ \end{gathered} $$

(2)

For rating the T^SPFNs, Liu and Wang [27] devised a comparative approach based on the score and exactness function, which is expressed as:

Definition 3

[27] Suppose that the two T^SPFNS are $S_{1} = \left\langle {A_{1} ,I_{1} ,F_{1} } \right\rangle$ and $S_{2} = \left\langle {A_{2} ,I_{2} ,F_{2} } \right\rangle$. Let $\overline{\overline{SC}} \left( {S_{1} } \right)$,$\overline{\overline{SC}} \left( {S_{2} } \right)$ be the score functions and $\overline{\overline{AY}} \left( {S_{1} } \right),\overline{\overline{AY}} \left( {S_{2} } \right)$ be the accuracy functions of $S_{i} \,\,\left( {i = 1,2} \right)$ respectively. Then.

(1) $\overline{\overline{SC}} \left( {S_{1} } \right)$ < $\overline{\overline{SC}} \left( {{S}_{2} } \right)$, then $S_{1} < S_{2}$;

(2) $\overline{\overline{SC}} \left( {S_{1} } \right)$ > $\overline{\overline{SC}} \left( {S_{2} } \right)$, then $S_{1} > S_{2}$;

(3) $\overline{\overline{SC}} \left( {S_{1} } \right)$ = $\overline{\overline{SC}} \left( {S_{2} } \right)$, then;

(i) $\overline{\overline{AY}} \left( {S_{1} } \right)$ < $\overline{\overline{AY}} \left( {S_{2} } \right)$, then $S_{1} < S_{2}$;

(ii) $\overline{\overline{AY}} \left( {S_{1} } \right)$ > $\overline{\overline{AY}} \left( {S_{2} } \right)$, then $S_{1} > S_{2}$;

(iii) $\overline{\overline{AY}} \left( {S_{1} } \right)$ = $\overline{\overline{AY}} \left( {S_{2} } \right)$, then $S_{1} = S_{2}$.

Definition 4

[27] Let $S = \left\langle {A,I,F} \right\rangle ,S_{1} = \left\langle {A_{1} ,I_{1} ,F_{1} } \right\rangle$ and $S_{2} = \left\langle {A_{2} ,I_{2} ,F_{2} } \right\rangle$.be any three T^SPFNs. The following describes the basic interactions between them.

$$ (1)\;S_{1} \vee S_{2} = \left\langle {\max \left( {A_{{S_{1} }} ,A_{{S_{2} }} } \right),\min \left( {I_{{S_{1} }} ,I_{{S_{2} }} } \right),\min \left( {F_{{S_{1} }} ,F_{{S_{2} }} } \right)} \right\rangle ; $$

(3)

$$ (2)\;S_{1} \wedge S_{2} = \left\langle {\min \left( {A_{{S_{1} }} ,A_{{S_{2} }} } \right),\max \left( {I_{{S_{1} }} ,I_{{S_{2} }} } \right),\max \left( {F_{{S_{1} }} ,F_{{S_{2} }} } \right)} \right\rangle ; $$

(4)

$$ (3)\;S_{1} \oplus S_{2} = \left\langle {\sqrt[q]{{1 - A_{{S_{1} }}^{q} - A_{{S_{2} }}^{q} }},I_{{S_{1} }} I_{{S_{2} }} ,F_{{S_{1} }} F_{{S_{2} }} } \right\rangle ; $$

(5)

$$ (4)\;S_{1} \otimes S_{2} = \left\langle {A_{{S_{1} }} A_{{S_{2} }} ,\sqrt[q]{{1 - I_{{S_{1} }}^{q} - I_{{S_{2} }}^{q} }},\sqrt[q]{{1 - F_{{S_{1} }}^{q} - F_{{S_{2} }}^{q} }}} \right\rangle ; $$

(6)

$$ (5)\;\zeta S = \left\langle {\sqrt[q]{{1 - \left( {1 - A_{S}^{q} } \right)^{\zeta } }},I_{S}^{\zeta } ,F_{S}^{\zeta } } \right\rangle ,\quad \zeta > 0; $$

(7)

$$ (6)\;S^{\zeta } = \left\langle {A_{S}^{\zeta } ,\sqrt[q]{{1 - \left( {1 - I_{S}^{q} } \right)^{\zeta } }},\sqrt[q]{{1 - \left( {1 - G_{S}^{q} } \right)^{\zeta } }}} \right\rangle ,\quad \zeta > 0; $$

(8)

$$ (7)\;S^{c} = \left\langle {F,I,A} \right\rangle . $$

(9)

Considering the Aczel–Alsina (AA) t-norm and t-conorm, we conferred how Aczel–Alsina operations relate to T^SPFNs (Table 1).

Table 1 Key words used in this paper

Defiition 5

[34] Let $S = \left\langle {A,I,F} \right\rangle ,S_{1} = \left\langle {A_{1} ,I_{1} ,F_{1} } \right\rangle$ and $S_{2} = \left\langle {A_{2} ,I_{2} ,F_{2} } \right\rangle$ be any three T^SPFNs. The following describes the AA interactions between them.

$$\begin{aligned} (1)\;S_{1} \oplus S_{2} &= \Bigg\langle \sqrt[q]{{1 - e^{{ - \left( {\left( { - \ln \left( {1 - A_{{S_{1} }}^{q} } \right)} \right)^{N} + \left( { - \ln \left( {1 - A_{{S_{2} }}^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} }},\\ & \quad \sqrt[q]{{e^{{ - \left( {\left( { - \ln I_{{S_{1} }}^{q} } \right)^{N} + \left( { - \ln I_{{S_{2} }}^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} }},\\ & \quad \sqrt[q]{{e^{{ - \left( {\left( { - \ln F_{{S_{1} }}^{q} } \right)^{N} + \left( { - \ln F_{{S_{2} }}^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} }} \Bigg\rangle ; \end{aligned}$$

(10)

$$\begin{aligned} (2)\;S_{1} \otimes S_{2} &= \Bigg\langle \sqrt[q]{{e^{{ - \left( {\left( { - \ln A_{{S_{1} }}^{q} } \right)^{N} + \left( { - \ln A_{{S_{2} }}^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} }},\\ & \quad \sqrt[q]{{1 - e^{{ - \left( {\left( { - \ln \left( {1 - I_{{S_{1} }}^{q} } \right)} \right)^{N} + \left( { - \ln \left( {1 - I_{{S_{2} }}^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} }},\\ & \quad \sqrt[q]{{1 - e^{{ - \left( {\left( { - \ln \left( {1 - F_{{S_{1} }}^{q} } \right)} \right)^{N} + \left( { - \ln \left( {1 - F_{{S_{2} }}^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} }} \Bigg\rangle ; \end{aligned}$$

(11)

$$\begin{aligned} (3)\;\zeta S &= \Bigg\langle \sqrt[q]{{1 - e^{{ - \left( {\zeta \left( { - \ln \left( {1 - A_{S}^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} }},\\ & \quad \sqrt[q]{{e^{{ - \left( {\zeta \left( { - \ln I_{{S_{1} }}^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} }},\\ & \quad \sqrt[q]{{e^{{ - \left( {\zeta \left( { - \ln F_{{S_{1} }}^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} }} \Bigg\rangle ,\quad \zeta > 0; \end{aligned}$$

(12)

$$\begin{aligned} (4)\;S^{\zeta } &= \Bigg\langle \sqrt[q]{{e^{{ - \left( {\zeta \left( { - \ln A_{{S_{1} }}^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} }},\\ & \quad \sqrt[q]{{1 - e^{{ - \left( {\zeta \left( { - \ln \left( {1 - I_{S}^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} }},\\ & \quad \sqrt[q]{{1 - e^{{ - \left( {\zeta \left( { - \ln \left( {1 - F_{S}^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} }} \Bigg\rangle ,\quad \zeta > 0. \end{aligned}$$

(13)

Theorem 1

[34] Let $S = \left\langle {A,I,F} \right\rangle ,S_{1} = \left\langle {A_{1} ,I_{1} ,F_{1} } \right\rangle$ and $S_{2} = \left\langle {A_{2} ,I_{2} ,F_{2} } \right\rangle$ be any three T^SPFNs. Then, we have.

• 1. $S_{1} \oplus S_{2} = S_{2} \oplus S_{1} ;$

• 2. $S_{1} \otimes S_{2} = S_{2} \otimes S_{1} ;$

• 3. ${\mathbb{B}}\left( {S_{1} \oplus S_{2} } \right) = {\mathbb{B}}S_{1} \oplus {\mathbb{B}}S_{2} ,\,\,\,\,\,\,\,\,\,\,{\mathbb{B}} > 0;$

• 4. $\left( {{\mathbb{B}}_{1} + {\mathbb{B}}_{2} } \right)S = {\mathbb{B}}_{1} S \oplus {\mathbb{B}}_{2} S,\,\,\,\,\,\,\,\,\,\,{\mathbb{B}}_{1} ,{\mathbb{B}}_{2} > 0;$

• 5. $\left( {S_{1} \otimes S_{2} } \right)^{\mathbb{B}} = S_{1}^{\mathbb{B}} \otimes S_{2}^{\mathbb{B}} ,\,\,\,\,\,\,\,\,\,\,{\mathbb{B}} > 0;$

• 6. $S^{{\left( {{\mathbb{B}}_{1} + {\mathbb{B}}_{2} } \right)}} = S^{{{\mathbb{B}}_{1} }} \otimes S^{{{\mathbb{B}}_{2} }} ,\,\,\,\,\,\,\,\,\,\,{\mathbb{B}}_{1} ,{\mathbb{B}}_{2} > 0.$

Definition 6

[30] Let $S$ be a T^SPFS. Then, the entropy measure of $S$ is defined as:

$$ \overline{\overline{EN}} T\left( S \right) = \frac{1}{n}\sum\limits_{z = 1}^{n} {\left( {1 - \frac{4}{5}\left[ {\left| {A^{q} \left( {S_{z} } \right) - F^{q} \left( {S_{z} } \right)} \right| + \left| {I^{q} \left( {S_{z} } \right) - 0.25} \right|} \right]} \right)} . $$

(14)

Definition 7

[28] Let $S_{1} = \left\langle {A_{1} ,I_{1} ,F_{1} } \right\rangle$ and $S_{2} = \left\langle {A_{2} ,I_{2} ,F_{2} } \right\rangle$ be any two T^SPFNs. Then, the distance measure among $S_{1}$ and $S_{2}$ is defined as:

$$ \overline{\overline{DIS}} \left( {S_{1} ,S_{2} } \right) = \left( {\left| {A_{1}^{q} - A_{2}^{q} } \right|^{2} + \left| {I_{1}^{q} - I_{2}^{q} } \right|^{2} + \left| {F_{1}^{q} - F_{2}^{q} } \right|^{2} } \right)^{\frac{1}{2}} $$

(15)

PA operator

For aggregation, the PA [48] operator is another important AO that may be used to reduce the negative effects of uncomfortable data on the outcomes of the final ranking process. It is defined as:

Definition 8

[48] Let $\overline{\overline{\wp }}_{l} \left( {l = 1,2,...,g} \right)$ be a group of positive crisp numbers. Then, the PA operator is quantified as.

$$ PA\left( {\overline{\overline{\wp }}_{1} ,\overline{\overline{\wp }}_{2} ,....,\overline{\overline{\wp }}_{g} } \right) = \frac{{\mathop \oplus \nolimits_{l = 1}^{g} \left( {1 + T\left( {\overline{\overline{\wp }}_{l} } \right)} \right)\overline{\overline{\wp }}_{l} }}{{\mathop \oplus \nolimits_{l = 1}^{g} \left( {1 + T\left( {\overline{\overline{\wp }}_{l} } \right)} \right)}}, $$

(16)

where $T\left( {\overline{\overline{\wp }}_{l} } \right) = \mathop \oplus \nolimits_{m = 1,l \ne m}^{g} {\text{Spt}}\left( {\overline{\overline{\wp }}_{l} ,\overline{\overline{\wp }}_{m} } \right)$,${\text{Sprt}}\left( {\overline{\overline{\wp }}_{l} ,\overline{\overline{\wp }}_{m} } \right)$ indicates the support for $\overline{\overline{\wp }}_{l}$ from $\overline{\overline{\wp }}_{m}$ executing the axioms:

• 1. $0 \le {\text{Sprt}}\left( {\overline{\overline{\wp }}_{l} ,\overline{\overline{\wp }}_{m} } \right) \le 1$,

• 2. ${\text{Sprt}}\left( {\overline{\overline{\wp }}_{l} ,\overline{\overline{\wp }}_{m} } \right) = {\text{Sprt}}\left( {\overline{\overline{\wp }}_{m} ,\overline{\overline{\wp }}_{l} } \right)$ and

• 3. ${\text{Sprt}}\left( {\overline{\overline{\wp }}_{j} ,\overline{\overline{\wp }}_{h} } \right) \le {\text{Sprt}}\left( {\overline{\overline{\wp }}_{l} ,\overline{\overline{\wp }}_{m} } \right),$ if $\left| {\overline{\overline{\wp }}_{l} ,\overline{\overline{\wp }}_{m} } \right| \ge \left| {\overline{\overline{\wp }}_{j} ,\overline{\overline{\wp }}_{h} } \right|.$

The HM operators

For aggregation, The HM [49] operator, which may represent the relationships between the input attributes, is another important AO, and is perceived as:

Definition 9

[49] Let $\overline{\overline{\mathbb{G}}} = \left[ {0,1} \right],Q,{\mathbb{R}} \ge 0,HM^{p,r} :\overline{\overline{\mathbb{G}}}^{Z} \to \overline{\overline{\mathbb{G}}} ,$ if $HM^{{Q,{\mathbb{R}}}}$ satisfies.

$$ HM^{{Q,{\mathbb{R}}}} \left( {{\mathbb{G}}_{1} ,{\mathbb{G}}_{2} ,...,{\mathbb{G}}_{z} } \right) = \left( {\frac{2}{{z^{2} + z}}\sum\limits_{i = 1}^{z} {\sum\limits_{j = i}^{z} {{\mathbb{G}}_{i}^{Q} {\mathbb{G}}_{j}^{\mathbb{R}} } } } \right)^{{\frac{1}{{Q + {\mathbb{R}}}}}} . $$

(17)

Then, the function $HM^{{Q,{\mathbb{R}}}}$ is assumed to be HM operator with parameters $Q,{\mathbb{R}}$. The HM operator must confirm the characteristics of idempotency, boundedness and monotonicity.

T-spherical fuzzy Aczel–Alsina power Heronian mean operators

In this part, based on the Aczel–Alsina operational laws, several aggregation operators, such as T-Spherical fuzzy Aczel–Alsina power Heronian mean, T-Spherical fuzzy Aczel–Alsina power geometric Heronian mean operators are introduced and several core properties and special cases with respect to the parameters are investigated.

The T-spherical fuzzy Aczel–Alsina power Heronian mean operators

In this subpart, T-Spherical fuzzy Aczel–Alsina power Heronian mean (TSPFAAPHM) operators are introduced, some properties and special cases about generalized parameters are investigated.

Definition 10

Let $S_{i} = \left\langle {A_{i} ,I_{i} ,F_{i} } \right\rangle \,\,\left( {i = 1,2,...,{\mathbb{V}}} \right)$ be a class of T^SPFNs, and $Q, {\mathbb{R}} \ge 0$. Then, the T^SPFAAPHM operator is defined as:

$$ \begin{aligned}&{\text{T}}^{{\text{S}}} {\text{PFAAPHM}}^{{Q, {\mathbb{R}}}} \left( {S_{1} ,S_{2} ,...,S_{\mathbb{V}} } \right) \\ & = \Bigg( \frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}\sum\limits_{i = 1}^{\mathbb{V}} \sum\limits_{j = i}^{\mathbb{V}} \left( {\frac{{{\mathbb{V}}\left( {1 + T\left( {S_{i} } \right)} \right)}}{{\sum\limits_{p = 1}^{\mathbb{V}} {\left( {1 + T\left( {S_{i} } \right)} \right)} }}S_{i} } \right)^{Q} \otimes_{AA} \left( {\frac{{{\mathbb{V}}\left( {1 + T\left( {S_{j} } \right)} \right)}}{{\sum\limits_{p = 1}^{\mathbb{V}} {\left( {1 + T\left( {S_{j} } \right)} \right)} }}S_{j} \Bigg)^{\mathbb{R}} } \right)^{{\frac{1}{{Q + {\mathbb{R}}}}}} ,\end{aligned} $$

(18)

where $T\left( {S_{i} } \right) = \sum\nolimits_{i = 1,j \ne i}^{\mathbb{V}} {\text{sprt}}\left( {S_{j} ,S_{i} } \right),\,\,{\text{sprt}}\left( {S_{j} ,S_{i} } \right) = 1 - \overline{\overline{{{\text{DIS}}}}} \left( {S_{j} ,S_{i} } \right)$ is the support degree for $S_{j}$ from $S_{i}$ sustaining the following requirements:

• (1) ${\text{sprt}}\left( {S_{i} ,S_{j} } \right) \in \left[ {0,1} \right]$;

• (2) ${\text{sprt}}\left( {S_{j} ,S_{i} } \right) = {\text{sprt}}\left( {S_{i} ,S_{j} } \right)$;

• (3) ${\text{sprt}}\left( {S_{i } ,S_{j} } \right) \ge {\text{sprt}}\left( {S_{k} ,S_{l} } \right)$, if $\overline{\overline{{{\text{DIS}}}}} \left( {S_{i } ,S_{j} } \right) < \overline{\overline{{{\text{DIS}}}}} \left( {S_{k} ,S_{l} } \right)$ in which $\overline{\overline{{{\text{DIS}}}}} \left( {S_{i } ,S_{j} } \right)$ is the distance measure between two T^SPFNs.

To write Eq. (18), in a simplified form, we can denote,

$$ \Im_{i} = \frac{{\left( {1 + T\left( {S_{i } } \right)} \right)}}{{\sum\nolimits_{l = 1}^{\mathbb{V}} {\left( {1 + T\left( {S_{i } } \right)} \right)} }}. $$

(19)

By utilizing Eq. (19), Eq. (18) becomes

$$ {\text{T}}^{{\text{S}}} {\text{PFAAPHM}}^{{Q,{\mathbb{R}}}} \left( {S_{1} ,S_{2} ,...,S_{\mathbb{V}} } \right) = \left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {{\mathbb{V}}\Im_{i } S_{i } } \right)^{Q} \otimes_{AA} \left( {{\mathbb{V}}\Im_{j} S_{j} } \right)^{\mathbb{R}} } } } \right)^{{\frac{1}{{Q + {\mathbb{R}}}}}} . $$

(20)

Theorem 2

Let $S_{i} = \left\langle {A_{i} ,I_{i} ,F_{i} } \right\rangle \,\,\left( {i = 1,2,...,{\mathbb{V}}} \right)$ be a group of an T^SPFNs. Then, the result obtained by using Eq. (20) is still TSFNs, and.

$$ \begin{aligned} & {\text{T}}^{{\text{S}}} {\text{PFAAPHM}}^{{Q,{\mathbb{R}}}} \left( {S_{1} ,S_{2} ,...,S_{\mathbb{V}} } \right) = \Bigg\langle {\left( {e^{{ - \left( {\left( {\frac{1}{{Q + {\mathbb{R}}}}} \right)\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}} \right)\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i} \left( { - \ln \left( {1 - A_{i}^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln \left( {1 - A_{j}^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)} ^{\frac{1}{q}} , \hfill \\ & \qquad\qquad\qquad\qquad\qquad \left( {1 - e^{{ - \left( {\left( {\frac{1}{{Q + {\mathbb{R}}}}} \right)\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}} \right)\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln I_{i }^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln I_{j}^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} , \hfill \\ &\qquad\qquad\qquad\qquad {\left( {1 - e^{{ - \left( {\left( {\frac{1}{{Q + {\mathbb{R}}}}} \right)\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}} \right)\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln F_{i }^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln F_{j}^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} } \Bigg\rangle . \hfill \\ \end{aligned} $$

(21)

Proof

Based on Aczel–Alsina operational laws for T^SPFNs, we have.

$$ {\mathbb{V}}\Im_{i} S_{i} = \left\langle {\left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i} \left( { - \ln \left( {1 - A_{i}^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} ,\left( {e^{{ - \left( {{\mathbb{V}}\Im_{i} \left( { - \ln I_{i}^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} ,\left( {e^{{ - \left( {{\mathbb{V}}\Im_{i} \left( { - \ln F_{i}^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} } \right\rangle ; $$

and

$$ \begin{aligned}& \left( {{\mathbb{V}}\Im_{i} S_{i} } \right)^{Q} = \left\langle {\left( {e^{{ - \left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i} \left( { - \ln \left( {1 - A_{i}^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} ,\left( {1 - e^{{ - \left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i} \left( { - \ln I_{i}^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} } \right., \hfill \\ & \qquad \left. {\left( {1 - e^{{ - \left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i} \left( { - \ln F_{i}^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} } \right\rangle . \hfill \\ \end{aligned} $$

Similarly,

$$ \begin{aligned}& \left( {{\mathbb{V}}\Im_{j} S_{j} } \right)^{\mathbb{R}} = \left\langle {\left( {e^{{ - \left( {{\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln \left( {1 - A_{j}^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} ,\left( {1 - e^{{ - \left( {{\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln I_{j}^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} ,} \right. \hfill \\ & \qquad\left. {\left( {1 - e^{{ - \left( {{\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln F_{j}^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} } \right\rangle ; \hfill \\ \end{aligned} $$

So,

$$ \begin{aligned} & \left( {{\mathbb{V}}\Im_{i} S_{i} } \right)^{Q} \otimes_{AA} \left( {{\mathbb{V}}\Im_{i} S_{i} } \right)^{\mathbb{R}} = \left\langle {\left( {e^{{ - \left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i} \left( { - \ln \left( {1 - A_{i}^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln \left( {1 - A_{j}^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right.^{\frac{1}{q}} , \hfill \\ & \qquad \left. \left( {1 - e^{{ - \left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i} \left( { - \ln I_{i} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln I_{j} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} ,\right.\\ & \qquad \left.\left( {1 - e^{{ - \left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i} \left( { - \ln F_{i} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln F_{j} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} \right\rangle \hfill \\ \end{aligned} $$

Let ${\ddot{Y}} = 1 - e^{{ - \left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln \left( {1 - A_{i }^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln \left( {1 - A_{j}^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} ,$ then $\ln \left( {1 - {\ddot{Y}} } \right) = - \left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i} \left( { - \ln \left( {1 - A_{i}^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln \left( {1 - A_{j}^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)^{\frac{1}{N}}$.

Utilizing this, we have

$$ \begin{aligned} &\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {{\mathbb{V}}\Im_{i } S_{i } } \right)^{Q} \otimes_{AA} \left( {{\mathbb{V}}\Im_{j} S_{j} } \right)^{\mathbb{R}} } } \\ &\quad = \left\langle {\left( {1 - e^{{ - \left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i} \left( { - \ln \left( {1 - A_{i}^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln \left( {1 - A_{j}^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)^{\frac{1}{N}} }} } \right)} \right.^{\frac{1}{q}} , \hfill \\ & \quad \left( {e^{{ - \left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln I_{i }^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln I_{j}^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} ,\\ &\qquad \left. {\left( {e^{{ - \left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln F_{i }^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln F_{j}^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} } \right\rangle . \hfill \\ \end{aligned}$$

Therefore,

$$ \begin{aligned} &\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {{\mathbb{V}}\Im_{i} S_{i} } \right)^{Q} \otimes_{AA} \left( {{\mathbb{V}}\Im_{j} S_{j} } \right)^{\mathbb{R}} } } } \right) \\ &\quad = \left\langle {\left( {1 - e^{{ - \left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln \left( {1 - A_{i }^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln \left( {1 - A_{j}^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)} \right.^{q} , \hfill \\ &\quad \left( {e^{{ - \left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {,\Im_{i } \left( { - \ln I_{i }^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln I_{j}^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} ,\\ & \quad \left. {\left( {e^{{ - \left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {,\Im_{i } \left( { - \ln F_{i }^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln F_{j}^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} } \right\rangle . \hfill \\ \end{aligned}$$

Hence,

$$ \begin{aligned} &\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {{\mathbb{V}}\Im_{i} S_{i} } \right)^{Q} \otimes_{AA} \left( {{\mathbb{V}}\Im_{j} S_{j} } \right)^{\mathbb{R}} } } } \right)^{{\frac{1}{{Q + {\mathbb{R}}}}}} \\ &\quad = \left\langle {\left( {e^{{ - \left( {\left( {\frac{1}{{Q + {\mathbb{R}}}}} \right)\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}} \right)\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln \left( {1 - A_{i }^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln \left( {1 - A_{j}^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)} \right.^{\frac{1}{q}} , \hfill \\ & \quad \left( {1 - e^{{ - \left( {\left( {\frac{1}{{Q + {\mathbb{R}}}}} \right)\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}} \right)\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln I_{i }^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln I_{j}^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} ,\\ & \quad \left. {\left( {1 - e^{{ - \left( {\left( {\frac{1}{{Q + {\mathbb{R}}}}} \right)\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}} \right)\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln F_{i }^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln F_{j}^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} } \right\rangle . \hfill \\ \end{aligned} $$

$$ \begin{gathered} {\text{TSFAAPHM}}^{{Q,{\mathbb{R}}}} \left( {S_{1} ,S_{2} ,...,S_{\mathbb{V}} } \right) = \left\langle {\left( {e^{{ - \left( {\left( {\frac{1}{{Q + {\mathbb{R}}}}} \right)\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}} \right)\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln \left( {1 - A_{i }^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln \left( {1 - A_{j}^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)} \right.^{\frac{1}{q}} , \hfill \\ \quad \quad \quad \quad \quad \left( {1 - e^{{ - \left( {\left( {\frac{1}{{Q + {\mathbb{R}}}}} \right)\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}} \right)\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln I_{i }^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln I_{j}^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} , \hfill \\ \quad \quad \quad \quad \quad \left. {\left( {1 - e^{{ - \left( {\left( {\frac{1}{{Q + {\mathbb{R}}}}} \right)\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}} \right)\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln F_{i }^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln F_{j}^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} } \right\rangle . \hfill \\ . \hfill \\ \end{gathered} $$

Theorem 3

(Idempotency) Let $Q \ge 0,{\mathbb{R}} \ge 0$, and $Q,{\mathbb{R}}$ can only accept one 0 value at a time, $S_{i } = \left\langle {A_{i } ,I_{i } ,F_{i } } \right\rangle \left( {i = 1,2,....,{\mathbb{V}}} \right)$ be a group of T^SPFNs and $S_{i } = \left\langle {A_{i } ,I_{i } ,F_{i } } \right\rangle = S = \left\langle {A,I,F} \right\rangle \left( {i = 1,2,...,{\mathbb{V}}} \right)$. Then

$$ T^{S} PFAAPHM^{{Q,{\mathbb{R}}}} \left( {S_{1} ,S_{2} ,...,S_{\mathbb{V}} } \right) = S = \left\langle {A,I,F} \right\rangle $$

(22)

Proof

Since $S_{i } = \left\langle {A_{i } ,I_{i } ,F_{i } } \right\rangle = S = \left\langle {A,I,F} \right\rangle \left( {i = 1,2,...,{\mathbb{V}}} \right)$, we have.

${\text{Sprt}}\left( {S_{i } ,S_{j} } \right) = 1\left( {\forall i,j = 1,2,...,{\mathbb{V}}} \right)$, so $\Im_{i } = 1\left( {\forall i = 1,2,...,{\mathbb{V}}} \right)$ and ${\mathbb{V}}\Im_{i } = {\mathbb{V}}\frac{1}{\mathbb{V}} = 1\left( {\forall i = 1,2,...,{\mathbb{V}}} \right)$. Then

$$ \begin{gathered} {\text{T}}^{{\text{S}}} {\text{PFAAPHM}}^{{Q,{\mathbb{R}}}} \left( {S_{1} ,S_{2} ,...,S_{\mathbb{V}} } \right) = {\text{T}}^{{\text{S}}} {\text{PFAAPHM}}^{{Q,{\mathbb{R}}}} \left( {S,S,...,S} \right)\\ = \left\langle {\left( {e^{{ - \left( {\left( {\frac{1}{{Q + {\mathbb{R}}}}} \right)\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}} \right)\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln \left( {1 - A^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln \left( {1 - A^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} } \right., \hfill \\ \,\,\,\,\,\,\,\,\,\left( {1 - e^{{ - \left( {\left( {\frac{1}{{Q + {\mathbb{R}}}}} \right)\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}} \right)\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln I^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln I^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} , \hfill \\ \left. {\,\,\,\,\,\,\,\,\left( {1 - e^{{ - \left( {\left( {\frac{1}{{Q + {\mathbb{R}}}}} \right)\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}} \right)\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln F^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln F^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} } \right\rangle ; \hfill \\ \end{gathered} $$

$$ \begin{gathered} = \left\langle {\left( {e^{{ - \left( {\left( {\frac{1}{{Q + {\mathbb{R}}}}} \right)\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}} \right)\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {\left( { - \ln \left( {1 - A^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {\left( { - \ln \left( {1 - A^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} } \right., \hfill \\ \left( {1 - e^{{ - \left( {\left( {\frac{1}{{Q + {\mathbb{R}}}}} \right)\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}} \right)\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {\left( { - \ln I^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {\left( { - \ln I^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} , \hfill \\ \left. {\left( {1 - e^{{ - \left( {\left( {\frac{1}{{Q + {\mathbb{R}}}}} \right)\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}} \right)\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {\left( { - \ln F^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {\left( { - \ln F^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} } \right\rangle . \hfill \\ \end{gathered} $$

$$ \begin{gathered} = \left\langle {\left( {e^{{ - \left( {\left( {\frac{1}{{Q + {\mathbb{R}}}}} \right)\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}} \right)\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {Q\left( { - \ln A^{q} } \right)^{N} + {\mathbb{R}}\left( { - \ln A^{q} } \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} } \right.,\left( {1 - e^{{ - \left( {\left( {\frac{1}{{Q + {\mathbb{R}}}}} \right)\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}} \right)\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {Q\left( { - \ln \left( {1 - I^{q} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - I^{q} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} , \hfill \\ \left. {\left( {1 - e^{{ - \left( {\left( {\frac{1}{{Q + {\mathbb{R}}}}} \right)\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}} \right)\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {Q\left( { - \ln \left( {1 - F^{q} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - F^{q} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} } \right\rangle ; \hfill \\ \end{gathered} $$

$$ = \left\langle {\left( {e^{{ - \left( {\left( {\frac{1}{{Q + {\mathbb{R}}}}} \right)\left( {Q + {\mathbb{R}}} \right)\left( { - \ln A^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} ,\left( {1 - e^{{ - \left( {\left( {\frac{1}{{Q + {\mathbb{R}}}}} \right)\left( {Q + {\mathbb{R}}} \right)\left( { - \ln \left( {1 - I^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} ,\left( {1 - e^{{ - \left( {\left( {\frac{1}{{Q + {\mathbb{R}}}}} \right)\left( {Q + {\mathbb{R}}} \right)\left( { - \ln \left( {1 - F^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} } \right\rangle ; $$

$$\begin{gathered} = \left\langle {\left( {e^{{ - \left( {\left( { - \ln A^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} ,\left( {1 - e^{{ - \left( {\left( { - \ln \left( {1 - I^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} ,\left( {1 - e^{{ - \left( {\left( { - \ln \left( {1 - F^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} } \right\rangle \hfill \\ = \left\langle {\left( {e^{{\ln A^{q} }} } \right)^{\frac{1}{q}} ,\left( {1 - e^{{\ln \left( {1 - I^{q} } \right)}} } \right)^{\frac{1}{q}} ,\left( {1 - e^{{\ln \left( {1 - F^{q} } \right)}} } \right)^{\frac{1}{q}} } \right\rangle = \left\langle {A,I,F} \right\rangle \hfill \\ \end{gathered}$$

.

Theorem 4

(Commutativity) Let $\left( {S^{\prime}_{1} ,S_{2}^{\prime } ,...,S_{\mathbb{V}}^{\prime } } \right)$ be any permutation of $\left( {S_{1} ,S_{2} ,...,S_{\mathbb{V}} } \right)$. Then

$$ {\text{T}}^{{\text{S}}} {\text{PFAAPHM}}^{{Q,{\mathbb{R}}}} \left( {S^{\prime}_{1} ,S_{2}^{\prime } ,...,S_{\mathbb{V}}^{\prime } } \right) = {\text{T}}^{{\text{S}}} {\text{PFAAPHM}}^{{Q,{\mathbb{R}}}} \left( {S_{1} ,S_{2} ,...,S_{\mathbb{V}} } \right). $$

(23)

Proof

Since $\left( {S^{\prime}_{1} ,S_{2}^{\prime } ,...,S_{\mathbb{V}}^{\prime } } \right)$ is any permutation of $\left( {S_{1} ,S_{2} ,...,S_{\mathbb{V}} } \right)$. So,

$$ {\text{T}}^{{\text{S}}} {\text{FAAPHM}}^{{Q,{\mathbb{R}}}} \left( {S_{1} ,S_{2} ,...,S_{\mathbb{V}} } \right) = \left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {{\mathbb{V}}\Im_{i } S_{i } } \right)^{Q} \otimes_{AA} \left( {{\mathbb{V}}\Im_{j} S_{j} } \right)^{\mathbb{R}} } } } \right)^{{\frac{1}{{Q + {\mathbb{R}}}}}} ; $$

$$ \begin{gathered} = \left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {{\mathbb{V}}\Im_{i } S^{\prime}_{i } } \right)^{Q} \otimes_{AA} \left( {{\mathbb{V}}\Im_{j} S^{\prime}_{j} } \right)^{\mathbb{R}} } } } \right)^{{\frac{1}{{Q + {\mathbb{R}}}}}} \hfill \\ = {\text{TSFAAPHM}}^{{Q,{\mathbb{R}}}} \left( {S^{\prime}_{1} ,S^{\prime}_{2} ,...,S_{\mathbb{V}}^{\prime } } \right) \hfill \\ \end{gathered} $$

Theorem 5

(Boundedness) Let $S_{i} = \left\langle {A_{i} ,I_{i} ,F_{i} } \right\rangle \left( {i = 1,2,...,{\mathbb{V}}} \right)$ be a group of T^SPFNs, $S^{ - } = \left\langle {\min A_{i} ,\max I_{i} ,\max F_{i} } \right\rangle$ and $S^{ + } = \left\langle {\max A_{i} ,\min I_{i} ,\min F_{i} } \right\rangle$. Then

$$ S^{ - } \le {\text{T}}^{{\text{S}}} {\text{PFAAPHM}}^{{Q,{\mathbb{R}}}} \left( {S_{1} ,S_{2} ,...,S_{\mathbb{V}} } \right) \le S^{ + } . $$

(24)

Proof

By the comparison rules defined in Definition 3, then utilizing on Theorems 3 and 4, we have

$$ T^{S} PFAAPHM^{{Q,{\mathbb{R}}}} \left( {S_{1} ,S_{2} ,...,S_{\mathbb{V}} } \right) \ge T^{S} PFAAPHM^{{Q,{\mathbb{R}}}} \left( {S_{1}^{ - } ,S_{2}^{ - } ,...,S_{\mathbb{V}}^{ - } } \right) = S^{ - } . $$

Similarly, we can have

$$ T^{S} PFAAPHM^{{Q,{\mathbb{R}}}} \left( {S_{1} ,S_{2} ,...,S_{\mathbb{V}} } \right) \le T^{S} PFAAPHM^{{Q,{\mathbb{R}}}} \left( {S_{1}^{ + } ,S_{2}^{ + } ,...,S_{\mathbb{V}}^{ + } } \right) = S^{ + } $$

Therefore, we can have.

$$ T^{S} PFAAPHM^{{Q,{\mathbb{R}}}} \left( {S_{1}^{ - } ,S_{2}^{ - } ,...,S_{\mathbb{V}}^{ - } } \right) \le T^{S} PFAAPHM^{{Q,{\mathbb{R}}}} \left( {S_{1} ,S_{2} ,...,S_{\mathbb{V}} } \right) \le T^{S} PFAAPHM^{{Q,{\mathbb{R}}}} \left( {S_{1}^{ + } ,S_{2}^{ + } ,...,S_{\mathbb{V}}^{ + } } \right) $$

Hence, we can get.

$$ S^{ - } \le T^{S} PFAAPHM^{{Q,{\mathbb{R}}}} \left( {S_{1} ,S_{2} ,...,S_{\mathbb{V}} } \right) \le S^{ + } . $$

By allocating distinct values to the parameters $q,Q,{\mathbb{R}}$ various aggregation operators are obtained as a special case of the initiated aggregation operators.

1. If $q = 1,$ then the TSPFAAPHM operators degenerates to the picture FAAPHM operators which can be expressed as follows:

$$ \begin{gathered} T^{S} PFAAPHM^{{Q,{\mathbb{R}}}} \left( {S_{1} ,S_{2} ,...,S_{\mathbb{V}} } \right) = \left\langle {\left( {e^{{ - \left( {\left( {\frac{1}{{Q + {\mathbb{R}}}}} \right)\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}} \right)\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln \left( {1 - A_{i} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln \left( {1 - A_{j} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)} \right., \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {1 - e^{{ - \left( {\left( {\frac{1}{{Q + {\mathbb{R}}}}} \right)\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}} \right)\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln I_{i } } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln I_{j} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right), \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left. {\left( {1 - e^{{ - \left( {\left( {\frac{1}{{Q + {\mathbb{R}}}}} \right)\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}} \right)\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln F_{i } } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln F_{j} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)} \right\rangle . \hfill \\ . \hfill \\ \end{gathered} $$

(25)

2. If $q = 2$, then the TSPFAAPHM operators degenerates to the SFAAPHM operators which can be expressed as follows:

$$ \begin{gathered} T^{S} PFAAPHM^{{Q,{\mathbb{R}}}} \left( {S_{1} ,S_{2} ,...,S_{\mathbb{V}} } \right)\hfill\\ \quad = \left\langle {\left( {e^{{ - \left( {\left( {\frac{1}{{Q + {\mathbb{R}}}}} \right)\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}} \right)\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln \left( {1 - A_{i}^{2} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln \left( {1 - A_{j}^{2} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)} \right.^{\frac{1}{2}} , \hfill \\ \qquad \left( {1 - e^{{ - \left( {\left( {\frac{1}{{Q + {\mathbb{R}}}}} \right)\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}} \right)\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln I_{i }^{2} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln I_{j}^{2} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{2}} , \hfill \\ \qquad \left. {\left( {1 - e^{{ - \left( {\left( {\frac{1}{{Q + {\mathbb{R}}}}} \right)\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}} \right)\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln I_{i }^{2} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln I_{j}^{2} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{2}} } \right\rangle . \hfill \\ \end{gathered} $$

(26)

3. If ${\mathbb{R}} \to 0,$ then the TSPFAAPHM operator degenerates to the TSFAA descending power average operator, which can be expressed as follows:

$$ \begin{gathered} T^{S} PFAAPHM^{{Q,{\mathbb{R}}}} \left( {S_{1} ,S_{2} ,...,S_{\mathbb{V}} } \right)\hfill \\ \quad = \mathop {\lim }\limits_{{{\mathbb{R}} \to 0}} \left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {{\mathbb{V}}\Im_{i } S_{i } } \right)^{Q} \otimes_{AA} \left( {{\mathbb{V}}\Im_{j} S_{j} } \right)^{\mathbb{R}} } } } \right)^{{\frac{1}{{Q + {\mathbb{R}}}}}}= \left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}\sum\limits_{i = 1}^{\mathbb{V}} {\left( {{\mathbb{V}} + 1 - i } \right)\left( {{\mathbb{V}}\Im_{i } S_{i } } \right)^{Q} } } \right)^{\frac{1}{Q}} \hfill \\ \quad = \left\langle {\left( {e^{{ - \left( {\frac{1}{Q}\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\left( {{\mathbb{V}} + 1 - i } \right)\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln \left( {1 - A_{i }^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } \right)} \right)} \right)^{\frac{1}{N}} }} } \right)} \right.^{\frac{1}{q}} , \hfill \\ \left. {\left( {1 - e^{{ - \left( {\frac{1}{Q}\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\left( {{\mathbb{V}} + 1 - i } \right)\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln I_{i }^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } \right)} \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} ,\left( {1 - e^{{ - \left( {\frac{1}{Q}\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\left( {{\mathbb{V}} + 1 - i } \right)\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln F_{i }^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } \right)} \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} } \right\rangle \hfill \\ \end{gathered} $$

(27)

4. If $Q \to 0,$ then the TSPFAAPHM operator degenerates to the TSFAA ascending power average operator, which can be expressed as follows:

$$ \begin{gathered} T^{S} PFAAPHM^{{0,{\mathbb{R}}}} \left( {S_{1} ,S_{2} ,...,S_{\mathbb{V}} } \right) = \mathop {\lim }\limits_{Q \to 0} \left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {{\mathbb{V}}\Im_{i } S_{i} } \right)^{Q} \otimes_{AA} \left( {{\mathbb{V}}\Im_{j} S_{j} } \right)^{\mathbb{R}} } } } \right)^{{\frac{1}{{Q + {\mathbb{R}}}}}} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\, = \left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}\sum\limits_{i = 1}^{\mathbb{V}} {i \left( {{\mathbb{V}}\Im_{i } S_{i } } \right)^{\mathbb{R}} } } \right)^{{\frac{1}{\mathbb{R}}}} = \left\langle {\left( {e^{{ - \left( {\frac{1}{\mathbb{R}}\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}\left( {\sum\limits_{i = 1}^{\text{\aa}} {\left( i \right)\left( {{\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln \left( {1 - A_{i }^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } \right)} \right)} \right)^{\frac{1}{N}} }} } \right)} \right.^{\frac{1}{q}} , \hfill \\ \left( {1 - e^{{ - \left( {\frac{1}{\mathbb{R}}\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\left( i \right)\left( {{\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln I_{i }^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } \right)} \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} ,\left. {\left( {1 - e^{{ - \left( {\frac{1}{\mathbb{R}}\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\left( i \right)\left( {{\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln F_{i }^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } \right)} \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} } \right\rangle . \hfill \\ \end{gathered} $$

(28)

5. If ${\mathbb{R}} \to 0,$ and $sprt\left( {S_{i} ,S_{j} } \right) = u\left( {u \in \left[ {0,1} \right]} \right)\left( {\forall i \ne j} \right),$ then the TSPFAAPHM operator degenerates to the TSPFAA linear descending WA operator, which can be defined as follows:

$$ \begin{gathered} T^{S} PFAAPHM^{Q,0} \left( {S_{1} ,S_{2} ,...,S_{\mathbb{V}} } \right) = \mathop {\lim }\limits_{{{\mathbb{R}} \to 0}} \left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {{\mathbb{V}}\Im_{i } S_{i } } \right)^{Q} \otimes_{AA} \left( {{\mathbb{V}}\Im_{j} S_{j} } \right)^{\mathbb{R}} } } } \right)^{{\frac{1}{{Q + {\mathbb{R}}}}}} \hfill \\ \, = \left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}\sum\limits_{i = 1}^{\mathbb{V}} {\left( {{\mathbb{V}} + 1 - i } \right)\left( {S_{i } } \right)^{Q} } } \right)^{\frac{1}{Q}} = \left\langle {\left( {e^{{ - \left( {\frac{1}{Q}\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\left( {{\mathbb{V}} + 1 - i } \right)\left( {\left( { - \ln \left( {1 - e^{{ - \left( {Q\left( { - \ln \left( {1 - A_{i }^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } \right)} \right)} \right)^{\frac{1}{N}} }} } \right)} \right.^{\frac{1}{q}} , \hfill \\ \left( {1 - e^{{ - \left( {\frac{1}{Q}\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\left( {{\mathbb{V}} + 1 - i } \right)\left( {\left( { - \ln \left( {1 - e^{{ - \left( {Q\left( { - \ln I_{i }^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } \right)} \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} ,\left. {\left( {1 - e^{{ - \left( {\frac{1}{Q}\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\left( {{\mathbb{V}} + 1 - i } \right)\left( {\left( { - \ln \left( {1 - e^{{ - \left( {Q\left( { - \ln F_{i }^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } \right)} \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} } \right\rangle . \hfill \\ \end{gathered} $$

(29)

6. If ¥ → 0, and ${\text{Sprt}}\left( {S_{i} ,S_{j} } \right) = c\left( {c \in \left[ {0,1} \right]} \right)\left( {\forall i \ne j} \right),$ then the TSPFAAPHM operator degenerates to the TSFAA linear Ascending WA operator, which can be defined as follows:

$$ \begin{gathered} T^{S} PFAAPHM^{{0,{\mathbb{R}}}} \left( {S_{1} ,S_{2} ,...,S_{\mathbb{V}} } \right) = \mathop {\lim }\limits_{Q \to 0} \left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {{\mathbb{V}}\Im_{i } S_{i } } \right)^{Q} \otimes_{AA} \left( {{\mathbb{V}}\Im_{j} S_{j} } \right)^{\mathbb{R}} } } } \right)^{{\frac{1}{{Q + {\mathbb{R}}}}}} \hfill \\ \, = \left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}\sum\limits_{i = 1}^{\mathbb{V}} {\left( i \right)\left( {S_{i } } \right)^{\mathbb{R}} } } \right)^{{\frac{1}{\mathbb{R}}}} = \left\langle {\left( {e^{{ - \left( {\frac{1}{\mathbb{R}}\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\left( i \right)\left( {\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{R}}\left( { - \ln \left( {1 - A_{i }^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } \right)} \right)} \right)^{\frac{1}{N}} }} } \right)} \right.^{\frac{1}{q}} , \hfill \\ \left( {1 - e^{{ - \left( {\frac{1}{\mathbb{R}}\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\left( i \right)\left( {\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{R}}\left( { - \ln I_{i }^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } \right)} \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} ,\left. {\left( {1 - e^{{ - \left( {\frac{1}{\mathbb{R}}\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\left( i \right)\left( {\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{R}}\left( { - \ln F_{i }^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } \right)} \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} } \right\rangle . \hfill \\ \end{gathered} $$

(30)

7. If $Q = {\mathbb{R}} = \frac{1}{2},$ and $Sprt\left( {S_{i} ,S_{j} } \right) = u\left( {u \in \left[ {0,1} \right]} \right)\left( {\forall i \ne j} \right),$ then the TSPFAAPHM operator degenerates to the TSFAA basic HM operator, which can be defined as follows:

$$ \begin{gathered} T^{S} PFAAPHM^{{\frac{1}{2},\frac{1}{2}}} \left( {S_{1} ,S_{2} ,...,S_{\mathbb{V}} } \right) = \left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {{\mathbb{V}}\Im_{i } S_{i } } \right)^{\frac{1}{2}} \otimes_{AA} \left( {{\mathbb{V}}\Im_{j} S_{j} } \right)^{\frac{1}{2}} } } } \right) \hfill \\ = \left\langle {\left( {1 - e^{{ - \left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln \left( {1 - A_{i }^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln \left( {1 - A_{j}^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)} \right.^{\frac{1}{q}} , \hfill \\ \,\,\,\,\,\,\,\left( {e^{{ - \left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln I_{i }^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln I_{j}^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} \hfill \\ \left. {\left( {e^{{ - \left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln F_{i }^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln F_{j}^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} } \right\rangle \hfill \\ \end{gathered} $$

(31)

8. If $Q = {\mathbb{R}} = 1,$ and $Sprt\left( {S_{i} ,S_{j} } \right) = u\left( {u \in \left[ {0,1} \right]} \right)\left( {\forall i \ne j} \right),$ then the TSPFAAPHM operator degenerates to the TSPFAA linear HM operator, which can be defined as follows:

$$ \begin{gathered} T^{S} PFAAPHM^{1,1} \left( {S_{1} ,S_{2} ,...,S_{\mathbb{V}} } \right) = \left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {{\mathbb{V}}\Im_{i } S_{i } } \right)^{1} \otimes_{AA} \left( {{\mathbb{V}}\Im_{j} S_{j} } \right)^{1} } } } \right)^{\frac{1}{2}} \hfill \\ = \left\langle {\left( {e^{{ - \left( {\left( \frac{1}{2} \right)\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}} \right)\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln \left( {1 - A_{i }^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + \left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln \left( {1 - A_{j}^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)} \right.^{\frac{1}{q}} , \hfill \\ \left( {1 - e^{{ - \left( {\left( \frac{1}{2} \right)\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}} \right)\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln I_{i }^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + \left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln I_{j}^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} , \hfill \\ \left. {\left( {1 - e^{{ - \left( {\left( \frac{1}{2} \right)\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}} \right)\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln F_{i }^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + \left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln F_{j}^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} } \right\rangle . \hfill \\ \end{gathered} $$

(32)

The T-spherical fuzzy Aczel–Alsina power geometric Heronian mean operators

In this subpart, T-Spherical fuzzy Aczel–Alsina power Heronian mean (T^SPFAAPGHM) operators are introduced, some properties and special cases about generalized parameters are investigated.

Definition 11.

Let $S_{i} = \left\langle {A_{i} ,I_{i} ,F_{i} } \right\rangle \,\,\left( {i = 1,2,...,{\mathbb{V}}} \right)$ be a group of an TSFNs, and $Q, {\mathbb{R}} \ge 0$. Then, the T^SFAAPGHM is defined as:

$$ T^{S} PFAAPGHM^{{Q, {\mathbb{R}}}} \left( {S_{1} ,S_{2} ,...,S_{\mathbb{V}} } \right) = \frac{1}{{Q + {\mathbb{R}}}}\left( {\prod\limits_{i = 1}^{\mathbb{V}} {\prod\limits_{j = i}^{\mathbb{V}} {\left( {QS_{i }^{{\frac{{{\mathbb{V}}\left( {1 + T\left( {S_{i } } \right)} \right)}}{{\sum\nolimits_{p = 1}^{\mathbb{V}} {\left( {1 + T\left( {S_{i } } \right)} \right)} }}}} \oplus_{AA} {\mathbb{R}}S_{j}^{{\frac{{{\mathbb{V}}\left( {1 + T\left( {S_{j} } \right)} \right)}}{{\sum\nolimits_{p = 1}^{\mathbb{V}} {\left( {1 + T\left( {S_{j} } \right)} \right)} }}}} } \right)} } } \right)^{{\frac{2}{{{\text{\aa}}\left( {{\text{\aa}} + 1} \right)}}}} $$

(33)

where $T( {S_{i} }) = \sum\nolimits_{i = 1,j \ne i}^{\mathbb{V}} {\text{Sprt}}\left( {S_{j} ,S_{i} } \right),\,\,{\text{Sprt}}\left( {S_{j} ,S_{i} } \right) = 1 - \overline{\overline{{{\text{DIS}}}}} (S_{j}, S_{i})$ is the support degree for $S_{j}$ from $S_{i }$ sustaining the following requirements:

• (1) ${\text{Sprt}}\left( {S_{i} ,S_{j} } \right) \in \left[ {0,1} \right]$;

• (2) ${\text{Sprt}}\left( {S_{j} ,S_{i} } \right) = {\text{Sprt}}\left( {S_{i} ,S_{j} } \right)$;

• (3) ${\text{Sprt}}\left( {S_{i} ,S_{j} } \right) \ge {\text{Sprt}}\left( {S_{k} ,S_{l} } \right)$, if $\overline{\overline{{{\text{DIS}}}}} \left( {S_{i} ,S_{j} } \right) < \overline{\overline{{{\text{DIS}}}}} \left( {S_{k} ,S_{l} } \right)$ in which $\overline{\overline{{{\text{DIS}}}}} \left( {S_{i} ,S_{j} } \right)$ is the distance measure between two TSFNs.

To write Eq. (33), in a simplified form, we can denote,

$$ \Im_{i } = \frac{{\left( {1 + T\left( {S_{i } } \right)} \right)}}{{\sum\nolimits_{i = 1}^{\mathbb{V}} {\left( {1 + T\left( {S_{i } } \right)} \right)} }}. $$

(34)

By Utilizing Eq. (34), Eq. (33) becomes

$$ T^{S} PFAAPGHM^{{Q,{\mathbb{R}}}} \left( {S_{1} ,S_{2} ,...,S_{\mathbb{V}} } \right) = \frac{1}{{Q + {\mathbb{R}}}}\left( {\prod\limits_{i = 1}^{\mathbb{V}} {\prod\limits_{j = i}^{\mathbb{V}} {\left( {QS_{i }^{{{\mathbb{V}}\Im_{i } }} \oplus_{AA} {\mathbb{R}}S_{j}^{{{\mathbb{V}}\Im_{j} }} } \right)} } } \right)^{{\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}}} $$

(35)

Theorem 6

Let $S_{i} = \left\langle {A_{i} ,I_{i} ,F_{i} } \right\rangle \,\,\left( {i = 1,2,...,{\mathbb{V}}} \right)$ be a group of an T^SPFNs. Then, the result obtained by using Eq. (35) is still TSFNs, and.

$$ \begin{gathered} T^{S} PFAAPGHM^{{Q,{\mathbb{R}}}} \left( {S_{1} ,S_{2} ,...,S_{\mathbb{V}} } \right) \hfill \\ = \left\langle {\left( {1 - e^{{ - \left( {\left( {\frac{1}{{Q + {\mathbb{R}}}}} \right)\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}} \right)\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln A_{i }^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + \left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln A_{j}^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} ,} \right. \hfill \\ \left( {e^{{ - \left( {\left( {\frac{1}{{Q + {\mathbb{R}}}}} \right)\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}} \right)\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln \left( {1 - I_{i }^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln \left( {1 - I_{j}^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} \hfill \\ \left. {\left( {e^{{ - \left( {\left( {\frac{1}{{Q + {\mathbb{R}}}}} \right)\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}} \right)\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln \left( {1 - F_{i }^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln \left( {1 - F_{j}^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} } \right\rangle . \hfill \\ \end{gathered} $$

(36)

Proof

Based on Aczel–Alsina operational laws for T^SPFNs, we have

$$S_{i }^{{{\mathbb{V}}\Im_{i } }} = \left\langle {\left( {e^{{ - \left( {{\mathbb{V}}\Im_{i} \left( { - \ln A_{i}^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}},\break \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i} \left( { - \ln \left( {1 - I_{i}^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} ,\left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i} \left( { - \ln \left( {1 - F_{i}^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} } \right\rangle ;$$

and

$$\begin{gathered} Q\left( {S_{i }^{{{\mathbb{V}}\Im_{i } }} } \right) = \left\langle {\left( {1 - e^{{ - \left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln A_{i}^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right.^{\frac{1}{q}} ,\left( {e^{{ - \left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i} \left( { - \ln \left( {1 - I_{i}^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} , \hfill \\ \left. {\left( {e^{{ - \left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i} \left( { - \ln \left( {1 - F_{i}^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} } \right\rangle . \hfill \\ \end{gathered}.$$

Similarly,

$$\begin{gathered} {\mathbb{R}}\left( {S_{j}^{{{\mathbb{V}}\Im_{j} }} } \right) = \left\langle {\left( {1 - e^{{ - \left( {{\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln A_{j}^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} } \right., \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {e^{{ - \left( {{\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln \left( {1 - I_{j}^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} ,\left. {\left( {e^{{ - \left( {{\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln \left( {1 - F_{j}^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} } \right\rangle . \hfill \\ \end{gathered}.$$

So,

$$ \begin{gathered} Q\left( {S_{i}^{{{\mathbb{V}}\Im_{i } }} } \right) \oplus_{AA} {\mathbb{R}}\left( {S_{j}^{{{\mathbb{V}}\Im_{j} }} } \right) = \left\langle {\left( {1 - e^{{ - \left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln A_{i }^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln A_{j}^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right.^{\frac{1}{q}} , \hfill \\ \left( {e^{{ - \left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln \left( {1 - I_{i }^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln \left( {1 - I_{j}^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}},\\ \qquad\qquad\qquad \left. {\left( {e^{{ - \left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln \left( {1 - F_{i }^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln \left( {1 - F_{j}^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} } \right\rangle . \hfill \\ \end{gathered} $$

Let ${\ddot{Y}} = 1 - e^{{ - \left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln \left( {1 - A_{i }^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln \left( {1 - A_{j}^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} ,$ then $\ln \left( {1 - \ddot{Y}} \right) = - \left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {\mathbb{V}\Im _{i} \left( { - \ln \left( {1 - A_{i} ^{q} } \right)} \right)^{N} } \right)^{{\frac{1}{N}}} }} } \right)} \right)^{N} + \mathbb{R}\left( { - \ln \left( {1 - e^{{ - \left( {\mathbb{V}\Im _{j} \left( { - \ln \left( {1 - A_{j} ^{q} } \right)} \right)^{N} } \right)^{{\frac{1}{N}}} }} } \right)} \right)^{N} } \right)^{{\frac{1}{N}}}$. Utilizing this, we have

$$\begin{gathered} \prod\limits_{i = 1}^{\mathbb{V}} {\prod\limits_{j = i}^{\mathbb{V}} {Q\left( {S^{{{\mathbb{V}}\Im_{i } }}_{i} } \right) \oplus_{AA} {\mathbb{R}}\left( {S_{j}^{{{\mathbb{V}}\Im_{j} }} } \right)} } = \left\langle {\left( {e^{{ - \left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln A_{i }^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln A_{j}^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)^{\frac{1}{N}} }} } \right)} \right.^{\frac{1}{q}} , \hfill \\ \left( {1 - e^{{ - \left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln \left( {1 - I_{i }^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln \left( {1 - I_{j}^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} ,\\ \qquad\qquad\qquad \left. {\left( {1 - e^{{ - \left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln \left( {1 - F_{i }^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln \left( {1 - F_{j}^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} } \right\rangle . \hfill \\ \end{gathered}$$

Therefore,

$$ \begin{aligned} & \left( {\prod\limits_{i = 1}^{\mathbb{V}} {\prod\limits_{j = i}^{\mathbb{V}} {Q\left( {S_{i }^{{{\mathbb{V}}\Im_{i } }} } \right) \oplus_{AA} {\mathbb{R}}\left( {S_{j}^{{{\mathbb{V}}\Im_{j} }} } \right)} } } \right)^{{\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}}} \\ &\quad = \left( {e^{{ - \left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln A_{i }^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln A_{j}^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} , \hfill \\ &\quad \left( {1 - e^{{ - \left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln \left( {1 - I_{i }^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln \left( {1 - I_{j}^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} ,\\ &\quad \left. {\left( {1 - e^{{ - \left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln \left( {1 - F_{i }^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln \left( {1 - F_{j}^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} } \right\rangle . \hfill \\ \end{aligned}$$

Hence,

$$ \begin{aligned} &\frac{1}{{Q + {\mathbb{R}}}}\left( {\prod\limits_{i = 1}^{\mathbb{V}} {\prod\limits_{j = i}^{\mathbb{V}} {Q\left( {S_{i }^{{{\mathbb{V}}\Im_{i } }} } \right) \oplus_{AA} {\mathbb{R}}\left( {S_{j}^{{{\mathbb{V}}\Im_{j} }} } \right)} } } \right)^{{\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}}} \\ &\quad = \left\langle {\left( {1 - e^{{ - \left( {\left( {\frac{1}{{Q + {\mathbb{R}}}}} \right)\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}} \right)\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln A_{i }^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln A_{j}^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} } \right., \hfill \\ &\quad \left( {e^{{ - \left( {\left( {\frac{1}{{Q + {\mathbb{R}}}}} \right)\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}} \right)\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln \left( {1 - I_{i }^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln \left( {1 - I_{j}^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} ,\\ &\quad \left. {\left( {e^{{ - \left( {\left( {\frac{1}{{Q + {\mathbb{R}}}}} \right)\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}} \right)\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln \left( {1 - F_{i }^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln \left( {1 - F_{j}^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} } \right\rangle . \hfill \\ \end{aligned} $$

$$ \begin{aligned} & {\text{T}}^{{\text{S}}} {\text{PFAAPGHM}}^{{Q,\mathbb{R}}} \left( {S_{1} ,S_{2} ,...,S_{\mathbb{V}} } \right) \\ & \quad = \left\langle {\left( {1 - e^{{ - \left( {\left( {\frac{1}{{Q + \mathbb{R}}}} \right)\left( {\frac{2}{{\mathbb{V}\left( {\mathbb{V} + 1} \right)}}} \right)\left( {\sum\limits_{{i = 1}}^{\mathbb{V}} {\sum\limits_{{j = i}}^{\mathbb{V}} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {\mathbb{V}\Im _{i } \left( { - \ln A_{i } ^{q} } \right)^{N} } \right)^{{\frac{1}{N}}} }} } \right)} \right)^{N} + \mathbb{R}\left( { - \ln \left( {1 - e^{{ - \left( {\mathbb{V}\Im _{j} \left( { - \ln A_{j} ^{q} } \right)^{N} } \right)^{{\frac{1}{N}}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{{\frac{1}{N}}} }} } \right)^{{\frac{1}{q}}} } \right., \\ & \left( {e^{{ - \left( {\left( {\frac{1}{{Q + \mathbb{R}}}} \right)\left( {\frac{2}{{\mathbb{V}\left( {\mathbb{V} + 1} \right)}}} \right)\left( {\sum\limits_{{i = 1}}^{\mathbb{V}} {\sum\limits_{{j = i}}^{\mathbb{V}} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {\mathbb{V}\Im _{i } \left( { - \ln \left( {1 - I_{i } ^{q} } \right)} \right)^{N} } \right)^{{\frac{1}{N}}} }} } \right)} \right)^{N} + \mathbb{R}\left( { - \ln \left( {1 - e^{{ - \left( {\mathbb{V}\Im _{j} \left( { - \ln \left( {1 - I_{j} ^{q} } \right)} \right)^{N} } \right)^{{\frac{1}{N}}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{{\frac{1}{N}}} }} } \right)^{{\frac{1}{q}}} , \\ & \left. {\left( {e^{{ - \left( {\left( {\frac{1}{{Q + \mathbb{R}}}} \right)\left( {\frac{2}{{\mathbb{V}\left( {\mathbb{V} + 1} \right)}}} \right)\left( {\sum\limits_{{i = 1}}^{\mathbb{V}} {\sum\limits_{{j = i}}^{\mathbb{V}} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {\mathbb{V}\Im _{i } \left( { - \ln \left( {1 - F_{i } ^{q} } \right)} \right)^{N} } \right)^{{\frac{1}{N}}} }} } \right)} \right)^{N} + \mathbb{R}\left( { - \ln \left( {1 - e^{{ - \left( {\mathbb{V}\Im _{j} \left( { - \ln \left( {1 - F_{j} ^{q} } \right)} \right)^{N} } \right)^{{\frac{1}{N}}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{{\frac{1}{N}}} }} } \right)^{{\frac{1}{q}}} } \right\rangle . \\ \end{aligned} $$

.

Theorem 7

(Idempotency) Let $Q \ge 0,{\mathbb{R}} \ge 0$, and $Q,{\mathbb{R}}$ can only accept one 0 value at a time, $S_{i } = \left\langle {A_{i } ,I_{i } ,F_{i } } \right\rangle \left( {i = 1,2,....,{\mathbb{V}}} \right)$ be a group of T^SPFNs and $S_{i } = \left\langle {A_{i } ,I_{i } ,F_{i } } \right\rangle = S = \left\langle {A,I,F} \right\rangle \left( {i = 1,2,...,{\mathbb{V}}} \right)$. Then

$$ T^{S} PFAAPGHM^{{Q,{\mathbb{R}}}} \left( {S_{1} ,S_{2} ,...,S_{\mathbb{V}} } \right) = S = \left\langle {A,I,F} \right\rangle . $$

(37)

Theorem 8

(Commutativity) Let $\left( {S^{\prime}_{1} ,S_{2}^{\prime } ,...,S_{\mathbb{V}}^{\prime } } \right)$ be any permutation of $\left( {S_{1} ,S_{2} ,...,S_{\mathbb{V}} } \right)$. Then

$$ T^{S} PFAAPGHM^{{Q,{\mathbb{R}}}} \left( {S^{\prime}_{1} ,S_{2}^{\prime } ,...,S_{\mathbb{V}}^{\prime } } \right) = T^{S} PFAAPGHM^{{Q,{\mathbb{R}}}} \left( {S_{1} ,S_{2} ,...,S_{\mathbb{V}} } \right). $$

(38)

Theorem 9

(Boundedness) Let $S_{i } = \left\langle {A_{i } ,I_{i } ,F_{i } } \right\rangle \left( {i = 1,2,....,{\mathbb{V}}} \right)$ be a collection of T^SPFNs, $S^{ - } = \left\langle {\min A_{i} ,\max I_{i} ,\max F_{i} } \right\rangle$ and $S^{ + } = \left\langle {\max A_{i} ,\min I_{i} ,\max F_{i} } \right\rangle$. Then

$$ S^{ - } \le T^{S} PFAAPGHM^{{Q,{\mathbb{R}}}} \left( {S_{1} ,S_{2} ,...,S_{\mathbb{V}} } \right) \le S^{ + } . $$

(39)

By allocating distinct values to the parameters $q,Q\,\,and\,\,{\mathbb{R}}$ various aggregation operators are obtained as a special case of the initiated aggregation operators.

1. If $q = 1,$ then the TSPFAAPGHM operators degenerates to the picture FAAPGHM operators which can be expressed as follows:

$$ \begin{aligned}& T^{S} PFAAPGHM^{{Q,{\mathbb{R}}}} \left( {S_{1} ,S_{2} ,...,S_{\mathbb{V}} } \right) \\ &\quad = \left\langle {\left( {1 - e^{{ - \left( {\left( {\frac{1}{{Q + {\mathbb{R}}}}} \right)\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}} \right)\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln A_{i } } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln A_{j} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)} \right., \hfill \\ &\quad \left( {e^{{ - \left( {\left( {\frac{1}{{Q + {\mathbb{R}}}}} \right)\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}} \right)\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln \left( {1 - I_{i } } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln \left( {1 - I_{j} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right), \hfill \\ & \quad \left. {\left( {e^{{ - \left( {\left( {\frac{1}{{Q + {\mathbb{R}}}}} \right)\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}} \right)\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln \left( {1 - F_{i } } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln \left( {1 - F_{j} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)} \right\rangle . \hfill \\ \hfill \\ \end{aligned}$$

(40)

2. If $q = 2$, then the TSPFAAPGHM operators degenerates to the SFAAPGHM operators which can be expressed as follows:

$$ \begin{gathered} T^{S} PFAAPGHM^{{Q,{\mathbb{R}}}} \left( {S_{1} ,S_{2} ,...,S_{\mathbb{V}} } \right) \hfill \\ = \left\langle {\left( {1 - e^{{ - \left( {\left( {\frac{1}{{Q + {\mathbb{R}}}}} \right)\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}} \right)\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln A_{i }^{2} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln A_{j}^{2} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{2}} } \right., \hfill \\ \left( {e^{{ - \left( {\left( {\frac{1}{{Q + {\mathbb{R}}}}} \right)\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}} \right)\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i} \left( { - \ln \left( {1 - I_{i}^{2} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln \left( {1 - I_{j}^{2} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{2}} , \hfill \\ \left. {\left( {e^{{ - \left( {\left( {\frac{1}{{Q + {\mathbb{R}}}}} \right)\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}} \right)\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i} \left( { - \ln \left( {1 - F_{i}^{2} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln \left( {1 - F_{j}^{2} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{2}} } \right\rangle . \hfill \\ \end{gathered} $$

(41)

3. If ${\mathbb{R}} \to 0,$ then the TSPFAAPGHM operator degenerates to the TSFAA descending power geometric average operator, which can be expressed as follows:

$$ \begin{gathered} T^{S} PFAAPGHM^{Q,0} \left( {S_{1} ,S_{2} ,...,S_{\mathbb{V}} } \right) = \mathop {lim}\limits_{{{\mathbb{R}} \to 0}} \left( {\frac{1}{{Q + {\mathbb{R}}}}\left( {\prod\limits_{i = 1}^{\mathbb{V}} {\prod\limits_{j = i}^{\mathbb{V}} {\left( {QS_{i }^{{{\mathbb{V}}\Im_{i } }} \oplus_{AA} {\mathbb{R}}S_{j}^{{{\mathbb{V}}{\mathbb{R}}_{j} }} } \right)} } } \right)^{{\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}}} } \right) \hfill \\ \,\,\, = \frac{1}{Q}\left( {\prod\limits_{i = 1}^{\mathbb{V}} {Q\left( {S_{i }^{{{\mathbb{V}}\Im_{i } }} } \right)^{{\left( {{\mathbb{V}} - i + 1} \right)}} } } \right)^{{\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}}} = \left\langle {\left( {1 - e^{{ - \left( {\frac{1}{Q}\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\left( {{\mathbb{V}} + 1 - i } \right)\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln A_{i }^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } \right)} \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} } \right., \hfill \\ \left. {\left( {e^{{ - \left( {\frac{1}{Q}\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\left( {{\mathbb{V}} + 1 - i } \right)\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln \left( {1 - I_{i }^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } \right)} \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} ,\left( {e^{{ - \left( {\frac{1}{Q}\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\left( {{\mathbb{V}} + 1 - i } \right)\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln \left( {1 - F_{i }^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } \right)} \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} } \right\rangle . \hfill \\ \end{gathered} $$

(42)

4. If $Q \to 0,$ then the TSPFAAPHM operator degenerates to the TSPFAA ascending power average operator, which can be expressed as follows:

$$ \begin{gathered} T^{S} PFAAPGHM^{{0,{\mathbb{R}}}} \left( {S_{1} ,S_{2} ,...,S_{\mathbb{V}} } \right) = \mathop {Lim}\limits_{Q \to 0} \left( {\frac{1}{{Q + {\mathbb{R}}}}\left( {\prod\limits_{i = 1}^{\mathbb{V}} {\prod\limits_{j = i}^{\mathbb{V}} {\left( {QS_{i }^{{{\mathbb{V}}\Im_{i } }} \oplus_{AA} {\mathbb{R}}S_{j}^{{{\mathbb{V}}\Im_{j} }} } \right)} } } \right)^{{\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}}} } \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{1}{\mathbb{R}}\left( {\prod\limits_{i = 1}^{\mathbb{V}} {\left( {{\mathbb{R}}S_{i }^{{{\mathbb{V}}\Im_{i } }} } \right)^{i } } } \right)^{{\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}}} = \left\langle {\left( {1 - e^{{ - \left( {\frac{1}{\mathbb{R}}\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\left( i \right)\left( {{\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln A_{i }^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } \right)} \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} } \right., \hfill \\ \left( {e^{{ - \left( {\frac{1}{\mathbb{R}}\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\left( i \right)\left( {{\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln \left( {1 - I_{i }^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } \right)} \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} ,\left. {\left( {e^{{ - \left( {\frac{1}{\mathbb{R}}\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\left( i \right)\left( {{\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln \left( {1 - F_{i }^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } \right)} \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} } \right\rangle . \hfill \\ \end{gathered} $$

(43)

5. If ${\mathbb{R}} \to 0,$ and $Sprt\left( {S_{i } ,S_{j} } \right) = u\left( {u \in \left[ {0,1} \right]} \right)\left( {\forall i \ne j} \right),$ then the TSPFAAPGHM operator degenerates to the TSPFAA linear descending WGA operator, which can be defined as follows:

$$ \begin{gathered} T^{S} PFAAPGHM^{Q,0} \left( {S_{1} ,S_{2} ,...,S_{\mathbb{V}} } \right) = \mathop {\lim }\limits_{{{\mathbb{R}} \to 0}} \left( {\frac{1}{{Q + {\mathbb{R}}}}\left( {\prod\limits_{i = 1}^{\mathbb{V}} {\prod\limits_{j = i}^{\mathbb{V}} {\left( {QS_{i }^{{{\mathbb{V}}\Im_{i } }} \oplus_{AA} {\mathbb{R}}S_{j}^{{{\mathbb{V}}\Im_{j} }} } \right)} } } \right)^{{\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}}} } \right) \hfill \\ \, = \frac{1}{Q}\left( {\prod\limits_{i = 1}^{\mathbb{V}} {\prod\limits_{j = i }^{\mathbb{V}} {\left( {QS_{i } } \right)^{{\left( {{\mathbb{V}} + 1 - i } \right)}} } } } \right)^{{\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}}} = \left\langle {\left( {1 - e^{{ - \left( {\frac{1}{Q}\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\left( {{\mathbb{V}} + 1 - i } \right)\left( {\left( { - \ln \left( {1 - e^{{ - \left( {Q\left( { - \ln A_{i }^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } \right)} \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} } \right., \hfill \\ \left( {e^{{ - \left( {\frac{1}{Q}\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\left( {{\mathbb{V}} + 1 - i } \right)\left( {\left( { - \ln \left( {1 - e^{{ - \left( {Q\left( { - \ln \left( {1 - I_{i }^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } \right)} \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} ,\left. {\left( {e^{{ - \left( {\frac{1}{Q}\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\left( {{\mathbb{V}} + 1 - i } \right)\left( {\left( { - \ln \left( {1 - e^{{ - \left( {Q\left( { - \ln \left( {1 - F_{i }^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } \right)} \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} } \right\rangle . \hfill \\ \end{gathered} $$

(44)

6. If $Q \to 0,$ and $Sprt\left( {S_{i } ,S_{j} } \right) = u\left( {u \in \left[ {0,1} \right]} \right)\left( {\forall i \ne j} \right),$ then the TSPFAAPGHM operator degenerates to the TSPFAA linear Ascending WGA operator, which can be defined as follows:

$$ \begin{gathered} T^{S} FAAPGHM^{{0,{\mathbb{R}}}} \left( {S_{1} ,S_{2} ,...,S_{\mathbb{V}} } \right) = \mathop {\lim }\limits_{Q \to 0} \frac{1}{{Q + {\mathbb{R}}}}\left( {\prod\limits_{i = 1}^{\mathbb{V}} {\prod\limits_{j = i}^{\mathbb{V}} {\left( {QS_{i }^{{{\mathbb{V}}\Im_{i } }} \oplus_{AA} {\mathbb{R}}S_{j}^{{{\mathbb{V}}\Im_{j} }} } \right)} } } \right)^{{\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}}} \hfill \\ \, = \frac{1}{\mathbb{R}}\left( {\prod\limits_{i = 1}^{\mathbb{V}} {\left( {{\mathbb{R}}S_{i } } \right)^{\left( i \right)} } } \right)^{{\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}}} = \left\langle {\left( {1 - e^{{ - \left( {\frac{1}{\mathbb{R}}\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\left( i \right)\left( {\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{R}}\left( { - \ln A_{i }^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } \right)} \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} } \right., \hfill \\ \left( {e^{{ - \left( {\frac{1}{\mathbb{R}}\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\left( i \right)\left( {\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{R}}\left( { - \ln \left( {1 - I_{i }^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } \right)} \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} ,\left. {\left( {e^{{ - \left( {\frac{1}{\mathbb{R}}\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\left( i \right)\left( {\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{R}}\left( { - \ln \left( {1 - F_{i }^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } \right)} \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} } \right\rangle . \hfill \\ \end{gathered} $$

(45)

7. If $Q = {\mathbb{R}} = \frac{1}{2},$ and $Sprt\left( {S_{i } ,S_{j} } \right) = u\left( {u \in \left[ {0,1} \right]} \right)\left( {\forall i \ne j} \right),$ then the TSPFAAPGHM operator degenerates to the TSPFAA basic GHM operator, which can be defined as follows:

$$ \begin{gathered} T^{S} PFAAPGHM^{{\frac{1}{2},\frac{1}{2}}} \left( {S_{1} ,S_{2} ,...,S_{\mathbb{V}} } \right) = \left( {\prod\limits_{i = 1}^{\mathbb{V}} {\prod\limits_{j = i}^{\mathbb{V}} {\left( {\frac{1}{2}S_{i }^{{{\mathbb{V}}\Im_{i } }} \oplus_{AA} \frac{1}{2}S_{j}^{{{\mathbb{V}}\Im_{j} }} } \right)} } } \right)^{{\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}}} \hfill \\ = \left\langle {\left( {e^{{ - \left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {\frac{1}{2}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln A_{i }^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + \frac{1}{2}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln A_{j}^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} } \right., \hfill \\ \left( {1 - e^{{ - \left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {\frac{1}{2}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln \left( {1 - I_{i }^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + \frac{1}{2}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln \left( {1 - I_{j}^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} , \hfill \\ \left. {\left( {1 - e^{{ - \left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {\frac{1}{2}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln \left( {1 - F_{i }^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + \frac{1}{2}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln \left( {1 - F_{j}^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} } \right\rangle . \hfill \\ \end{gathered} $$

(46)

8. If $Q = {\mathbb{R}} = 1,$ and $Sprt\left( {S_{i } ,S_{j} } \right) = u\left( {u \in \left[ {0,1} \right]} \right)\left( {\forall i \ne j} \right),$ then the TSPFAAPGHM operator degenerates to the TSPFAA linear GHM operator, which can be defined as follows:

$$ \begin{gathered} T^{S} PFAAPGHM^{1,1} \left( {S_{1} ,S_{2} ,...,S_{\mathbb{V}} } \right) = \frac{1}{{Q + {\mathbb{R}}}}\left( {\prod\limits_{i = 1}^{\mathbb{V}} {\prod\limits_{j = i}^{\mathbb{V}} {\left( {QS_{i }^{{{\mathbb{V}}\Im_{i } }} \oplus_{AA} {\mathbb{R}}S_{j}^{{{\mathbb{V}}\Im_{j} }} } \right)} } } \right)^{{\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}}} \hfill \\ = \left\langle {\left( {1 - e^{{ - \left( {\left( \frac{1}{2} \right)\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}} \right)\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln A_{i }^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + \left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln A_{j}^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} } \right., \hfill \\ \left( {e^{{ - \left( {\left( \frac{1}{2} \right)\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}} \right)\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln \left( {1 - I_{i }^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + \left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln \left( {1 - I_{j}^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} , \hfill \\ \left. {\left( {e^{{ - \left( {\left( \frac{1}{2} \right)\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}} \right)\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{i } \left( { - \ln \left( {1 - F_{i }^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + \left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}\Im_{j} \left( { - \ln \left( {1 - F_{j}^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} } \right\rangle . \hfill \\ \end{gathered} $$

(47)

The TSFAAWPHM operator and TSFAAWPGHM operators

In this portion, the weighted forms of the initiated aggregation operators are introduced by considering the weights of the attributes.

Definition 12

Let $S_{i } = \left\langle {A_{i } ,I_{i } ,F_{i } } \right\rangle \,\,\left( {i = 1,2,...,{\mathbb{V}}} \right)$ be a class of an T^SPFNs,$Q,{\mathbb{R}} \ge 0$ and ${\mathbb{N}} = \left( {{\mathbb{N}}_{1} ,{\mathbb{N}}_{2} ,...,{\mathbb{N}}_{\mathbb{V}} } \right)^{T}$ be the importance degree of $S_{i } \left( {i = 1,2,...,{\mathbb{V}}} \right),$ where ${\mathbb{N}}_{i} \ge 0\,\,\,and\,\,\,\sum\nolimits_{i = 1}^{\mathbb{V}} {{\mathbb{N}}_{i} = 1}$. Then, the T^SPFAAWPHM is defined as:

$$ T^{S} PFAAWPHM^{{Q,\mathbb{R}}} \left( {S_{1} ,S_{2} ,...,S_{\mathbb{V}} } \right) = \left( {\frac{2}{{\mathbb{V}\left( {\mathbb{V} + 1} \right)}}\sum\limits_{{i = 1}}^{\mathbb{V}} {\sum\limits_{{j = i}}^{\mathbb{V}} {\left( {\frac{{\mathbb{V}\mathbb{N}_{i } \left( {1 + T\left( {S_{i } } \right)} \right)}}{{\sum\limits_{{p = 1}}^{\beta } {\mathbb{N}_{i } \left( {1 + T\left( {S_{i } } \right)} \right)} }}S_{i } } \right)^{Q} \otimes _{{AA}} \left( {\frac{{\mathbb{V}\mathbb{N}_{j} \left( {1 + T\left( {S_{j} } \right)} \right)}}{{\sum\limits_{{p = 1}}^{\beta } {\mathbb{N}_{j} \left( {1 + T\left( {S_{j} } \right)} \right)} }}S_{j} } \right)^{\mathbb{R}} } } } \right)^{{\frac{1}{{Q + \mathbb{R}}}}}, $$

(48)

where $T\left( {S_{i } } \right) = \sum\nolimits_{i = 1,j \ne i}^{\mathbb{V}} {Sprt\left( {S_{j} ,S_{i} } \right),\,\,Sprt\left( {S_{j} ,S_{i} } \right) = 1 - \overline{\overline{DIS}} \left( {S_{j} ,S_{i} } \right)}$ is the support degree for $S_{j}$ from $S_{i }$ sustaining the following requirements:

• (1) $Sprt\left( {S_{i} ,S_{j} } \right) \in \left[ {0,1} \right]$;

• (2) $Sprt\left( {S_{j} ,S_{i} } \right) = Sprt\left( {S_{i} ,S_{j} } \right)$;

• (3) $Sprt\left( {S_{i} ,S_{j} } \right) \ge Sprt\left( {S_{k} ,S_{l} } \right)$, if $\overline{\overline{DIS}} \left( {S_{i} ,S_{j} } \right) < \overline{\overline{DIS}} \left( {S_{k} ,S_{l} } \right)$ in which $\overline{\overline{DIS}} \left( {S_{i} ,S_{j} } \right)$ is the distance measure between two T^SPFNs.

To write Eq. (48), in a simplified form, we can denote,

$$ \Im_{i } = \frac{{\left( {1 + T\left( {S_{i } } \right)} \right)}}{{\sum\nolimits_{l = 1}^{\mathbb{V}} {\left( {1 + T\left( {S_{i } } \right)} \right)} }} $$

(49)

By utilizing Eq. (49), Eq. (48) becomes

$$ T^{S} PFAAWPHM^{{Q, {\mathbb{R}}}} \left( {S_{1} ,S_{2} ,...,S_{\mathbb{V}} } \right) = \left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {{\mathbb{V}}{\mathbb{N}}_{i } \Im_{i } S_{i } } \right)^{Q} \otimes_{AA} \left( {{\mathbb{V}}{\mathbb{N}}_{j} \Im_{j} S_{j} } \right)^{\mathbb{R}} } } } \right)^{{\frac{1}{{Q + {\mathbb{R}}}}}} $$

(50)

Theorem 10

Let $S_{i } = \left\langle {A_{i } ,I_{i } ,F_{i } } \right\rangle \,\,\left( {i = 1,2,...,{\mathbb{V}}} \right)$ be a group of an T^SPFNs. Then, the result obtained by using Eq. (50) is still TSFNs, and.

$$ \begin{gathered} T^{S} PFAAWPHM^{{Q,{\mathbb{R}}}} \left( {S_{1} ,S_{2} ,...,S_{\mathbb{V}} } \right) \hfill \\ = \left\langle {\left( {e^{{ - \left( {\left( {\frac{1}{{Q + {\mathbb{R}}}}} \right)\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}} \right)\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}{\mathbb{N}}_{i } \Im_{i } \left( { - \ln \left( {1 - A_{i }^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}{\mathbb{N}}_{j} \Im_{j} \left( { - \ln \left( {1 - A_{j}^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} ,} \right. \hfill \\ \left( {1 - e^{{ - \left( {\left( {\frac{1}{{Q + {\mathbb{R}}}}} \right)\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}} \right)\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}{\mathbb{N}}_{i } \Im_{i } \left( { - \ln I_{i }^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}{\mathbb{N}}_{j} \Im_{j} \left( { - \ln I_{j}^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} , \hfill \\ \left. {\left( {1 - e^{{ - \left( {\left( {\frac{1}{{Q + {\mathbb{R}}}}} \right)\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}} \right)\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}{\mathbb{N}}_{i } \Im_{i } \left( { - \ln F_{i }^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}{\mathbb{N}}_{j} \Im_{j} \left( { - \ln F_{j}^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} } \right\rangle . \hfill \\ \end{gathered} $$

(51)

Definition 13

Let $S_{i } = \left\langle {A_{i } ,I_{i } ,F_{i } } \right\rangle \,\,\left( {i = 1,2,...,{\mathbb{V}}} \right)$ be a class of an T^SPFNs,$Q,{\mathbb{R}} \ge 0$ and ${\mathbb{N}} = \left( {{\mathbb{N}}_{1} ,{\mathbb{N}}_{2} ,...,{\mathbb{N}}_{\mathbb{V}} } \right)^{T}$ be the importance degree of $S_{i } \left( {i = 1,2,...,{\mathbb{V}}} \right),$ where ${\mathbb{N}}_{i} \ge 0\,\,\,and\,\,\,\sum\nolimits_{i = 1}^{\mathbb{V}} {{\mathbb{N}}_{i} = 1}$. Then, the T^SFAAWPGHM is defined as:

$$ T^{S} PFAAWPGHM^{{Q,{\mathbb{R}}}} \left( {S_{1} ,S_{2} ,...,S_{\mathbb{V}} } \right) = \frac{1}{{Q + {\mathbb{R}}}}\left( {\prod\limits_{i = 1}^{\mathbb{V}} {\prod\limits_{j = i}^{\mathbb{V}} {\left( {QS_{i}^{{\frac{{{\mathbb{V}}{\mathbb{N}}_{i } \left( {1 + T\left( {S_{i } } \right)} \right)}}{{\sum\limits_{p = 1}^{\text{\aa}} {{\mathbb{N}}_{i } \left( {1 + T\left( {S_{i } } \right)} \right)} }}}} \oplus_{AA} {\mathbb{R}}S_{j}^{{\frac{{{\mathbb{V}}{\mathbb{N}}_{j} \left( {1 + T\left( {S_{j} } \right)} \right)}}{{\sum\limits_{p = 1}^{\text{\aa}} {{\mathbb{N}}_{j} \left( {1 + T\left( {S_{j} } \right)} \right)} }}}} } \right)} } } \right)^{{\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}}} $$

(52)

where $T\left( {S_{i } } \right) = \sum\limits_{i = 1,j \ne i}^{\mathbb{V}} {Sprt\left( {S_{j} ,S_{i} } \right),\,\,Sprt\left( {S_{j} ,S_{i} } \right) = 1 - \overline{\overline{DIS}} \left( {S_{j} ,S_{i} } \right)}$ is the support degree for $S_{j}$ from $S_{i }$ sustaining the following requirements:

• (4) $Sprt\left( {S_{i} ,S_{j} } \right) \in \left[ {0,1} \right]$;

• (5) $Sprt\left( {S_{j} ,S_{i} } \right) = Sprt\left( {S_{i} ,S_{j} } \right)$;

• (6) $Sprt\left( {S_{i} ,S_{j} } \right) \ge Sprt\left( {S_{k} ,S_{l} } \right)$, if $\overline{\overline{DIS}} \left( {S_{i} ,S_{j} } \right) < \overline{\overline{DIS}} \left( {S_{k} ,S_{l} } \right)$ in which $\overline{\overline{DIS}} \left( {S_{i} ,S_{j} } \right)$ is the distance measure between two T^SPFNs.

To write Eq. (52), in a simplified form, we can denote,

$$ \Im_{i } = \frac{{\left( {1 + T\left( {S_{i } } \right)} \right)}}{{\sum\nolimits_{l = 1}^{\mathbb{V}} {\left( {1 + T\left( {S_{i } } \right)} \right)} }} $$

(53)

By utilizing Eq. (53), Eq. (52) becomes

$$ T^{S} PFAAWPGHM^{{Q,{\mathbb{R}}}} \left( {S_{1} ,S_{2} ,...,S_{\mathbb{V}} } \right) = \frac{1}{{Q + {\mathbb{R}}}}\left( {\prod\limits_{i = 1}^{\mathbb{V}} {\prod\limits_{j = i}^{\mathbb{V}} {\left( {QS_{i }^{{{\mathbb{V}}{\mathbb{N}}_{i } \Im_{i } }} \oplus_{AA} {\mathbb{R}}S_{j}^{{{\mathbb{V}}{\mathbb{N}}_{j} \Im_{j} }} } \right)} } } \right)^{{\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}}} $$

(54)

Theorem 11

Let $S_{i } = \left\langle {A_{i } ,I_{i } ,F_{i } } \right\rangle \,\,\left( {i = 1,2,...,{\mathbb{V}}} \right)$ be a group of an T^SPFNs. Then, the result obtained by using Eq. (54) is still TSFNs, and.

$$ \begin{gathered} T^{S} PFAAWPGHM^{{Q,{\mathbb{R}}}} \left( {S_{1} ,S_{2} ,...,S_{\mathbb{V}} } \right) \hfill \\ = \left\langle {\left( {1 - e^{{ - \left( {\left( {\frac{1}{{Q + {\mathbb{R}}}}} \right)\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}} \right)\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}{\mathbb{N}}_{i } \Im_{i } \left( { - \ln A_{i }^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}{\mathbb{N}}_{j} \Im_{j} \left( { - \ln A_{j}^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)} \right.^{\frac{1}{q}} , \hfill \\ \left( {e^{{ - \left( {\left( {\frac{1}{{Q + {\mathbb{R}}}}} \right)\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}} \right)\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}{\mathbb{N}}_{i } \Im_{i } \left( { - \ln \left( {1 - I_{i }^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}{\mathbb{N}}_{j} \Im_{j} \left( { - \ln \left( {1 - I_{j}^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} , \hfill \\ \left. {\left( {e^{{ - \left( {\left( {\frac{1}{{Q + {\mathbb{R}}}}} \right)\left( {\frac{2}{{{\mathbb{V}}\left( {{\mathbb{V}} + 1} \right)}}} \right)\left( {\sum\limits_{i = 1}^{\mathbb{V}} {\sum\limits_{j = i}^{\mathbb{V}} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}{\mathbb{N}}_{i } \Im_{i } \left( { - \ln \left( {1 - F_{i }^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {{\mathbb{V}}{\mathbb{N}}_{j} \Im_{j} \left( { - \ln \left( {1 - F_{j}^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} } \right\rangle . \hfill \\ \end{gathered} $$

(55)

T-Spherical Fuzzy MAGDM Model Based on Improved T-Spherical Fuzzy TOPSIS

The applications of these operators in the MAGDM will be covered in this section.

T-Spherical Fuzzy MAGDM problem

In this sub-portion, a model is initiated to handle MAGDM problems under T-SPF information. The MAGDM problems can be resolved using a decision matrix, in which the rows denote choices/alternatives, and the columns denote a group of attributes/criteria. Thus for the decision matrix ${\mathbb{M}}_{n \times m}$ assume a group of $n$ choices $\left\{ {'\!\gamma_{1} ,'\!\gamma_{2} ,'\!\gamma_{3} ,...,'\!\gamma_{n} } \right\}$ and $m$ attributes/criteria $\left\{ {'\!O_{1} ,'\!O_{2} ,'\!O_{3} ,...,'\!O_{m} } \right\}.$ The importance degrees of decision makers and that of attributes/criteria are unknown and are symbolized by ${\mathbb{W}} = \left\{ {{\mathbb{W}}_{1} ,{\mathbb{W}}_{2} ,...,{\mathbb{W}}_{c} } \right\}$ and ${\mathbb{Z}} = \left\{ {{\mathbb{Z}}_{1} ,{\mathbb{Z}}_{2} ,{\mathbb{Z}}_{3} ,...,{\mathbb{Z}}_{m} } \right\}$ respectively, subject to the constrains ${\mathbb{W}}_{g} ,{\mathbb{Z}}_{z} \in \left[ {0,1} \right],\left( {g = 1,2,...,c,z = 1,2...,m} \right)$ with $\sum\nolimits_{g = 1}^{c} {{\mathbb{W}}_{g} = 1} ,\sum\nolimits_{z = 1}^{m} {{\mathbb{Z}}_{z} = 1}$. Assumed that the T-SPF decision matrix is symbolized by ${\mathbb{M}}^{\zeta } = \left[ {\varsigma_{i j}^{\zeta } } \right]_{n \times m} = \left\langle {A_{i j}^{\zeta } ,I_{i j}^{\zeta } ,F_{i j}^{\zeta } } \right\rangle$, where $A_{i j}$ epitomizes the degree of the choice/alternative $'\!\gamma_{i }$ indulges the attribute/criteria $'\!O_{j}$ judged by the decision makers (DMs), $I_{i j}$ epitomizes the degree of the choice/alternative $'\!\gamma_{i }$ is neutral for the attribute/criteria $'\!O_{j}$ judged by the DMs and $F_{i j}$ epitomizes the degree of the choice/alternative $'\!\gamma_{i }$ does not indulge the attribute/criteria $'\!O_{j}$ judged by the DMs.

$$ {\mathbb{M}}_{n \times m}^{\zeta } = \begin{array}{*{20}l} {\begin{array}{*{20}l} {'\!\gamma_{1} } \\ {\begin{array}{*{20}l} {'\!\gamma_{2} } \\ \vdots \\ \end{array} } \\ {'\!\gamma_{n} } \\ \end{array} } & {\left( {\begin{array}{*{20}l} {'\!O_{1} } & {'\!O_{2} } & \cdots & {'\!O_{m} } \\ {\left\langle {A_{{\varsigma_{11} }}^{\zeta } ,I_{{\varsigma_{11} }}^{\zeta } ,F_{{\varsigma_{11} }}^{\zeta } } \right\rangle } & {\left\langle {A_{{\varsigma_{12} }}^{\zeta } ,I_{{\varsigma_{12} }}^{\zeta } ,F_{{\varsigma_{12} }}^{\zeta } } \right\rangle } & \cdots & {\left\langle {A_{{\varsigma_{1m} }}^{\zeta } ,I_{{\varsigma_{1m} }}^{\zeta } ,F_{{\varsigma_{1m} }}^{\zeta } } \right\rangle } \\ {\begin{array}{*{20}l} {\left\langle {A_{{\varsigma_{21} }}^{\zeta } ,I_{{\varsigma_{21} }}^{\zeta } ,F_{{\varsigma_{21} }}^{\zeta } } \right\rangle } \\ \vdots \\ \end{array} } & {\begin{array}{*{20}l} {\left\langle {A_{{\varsigma_{22} }}^{\zeta } ,I_{{\varsigma_{22} }}^{\zeta } ,F_{{\varsigma_{22} }}^{\zeta } } \right\rangle } \\ \vdots \\ \end{array} } & {\begin{array}{*{20}l} \cdots \\ \ddots \\ \end{array} } & {\begin{array}{*{20}l} {\left\langle {A_{{\varsigma_{2m} }}^{\zeta } ,I_{{\varsigma_{2m} }}^{\zeta } ,F_{{\varsigma_{2m} }}^{\zeta } } \right\rangle } \\ \vdots \\ \end{array} } \\ {\left\langle {A_{{\varsigma_{n1} }}^{\zeta } ,I_{{\varsigma_{n1} }}^{\zeta } ,F_{{\varsigma_{n1} }}^{\zeta } } \right\rangle } & {\left\langle {A_{{\varsigma_{n2} }}^{\zeta } ,I_{{\varsigma_{n2} }}^{\zeta } ,F_{{\varsigma_{n2} }}^{\zeta } } \right\rangle } & \cdots & {\left\langle {A_{{\varsigma_{nm} }}^{\zeta } ,I_{{\varsigma_{nm} }}^{\zeta } ,F_{nm}^{\zeta } } \right\rangle } \\ \end{array} } \right)} \\ \end{array} .$$

(56)

Note that none of the information on the DM weights and attribute values is known in the context of decision-making.

Obtaining the T-SPF information

We initially established the expert assessment committee by inviting specialists and intellectuals from related fields to select the most satisfying proposal from the group of proposals. An expert assessment committee is given a translation relation from linguistic concepts to TSPFN mentioned in Table 2, so they may choose the identified strategy according to multiple considerations. Following that, the cognitive preference capability and knowledge background of the specialists are used to obtain the linguistic assessment information of alternatives.

Table 2 Assessments of pharmaceutical companies in view of linguistic terms

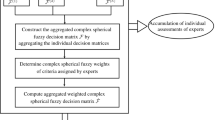
After obtaining the linguistic evaluation data for alternatives, we change the expert committee's recommended preferences to get the TSPF evaluation matrices ${\mathbb{M}}^{\zeta } = \left[ {\varsigma_{i j}^{\zeta } } \right]_{n \times m} = \left\langle {A_{i j}^{\zeta } ,I_{i j}^{\zeta } ,F_{i j}^{\zeta } } \right\rangle$ (Fig. 2).

Fig. 2

Flowchart of the proposed MAGDM process

The T-SPF-TOPSIS methodology

There are three basic components to the approach. Using the suggested aggregation operators, we determine the decision makers' weights in the first section. In the second section, the suggested aggregation operators and entropy measure are addressed in relation to computing the weights of the criterion. The last section uses a rating system based on how closely each solution matches the ideal one in terms of PIS and NIS.

The following procedures are provided to solve the T-Spherical fuzzy MAGDM issue utilizing a TOPSIS-based methodology.

Step 1. The decision matrices ${\mathbb{M}}_{n \times m}^{\zeta }$ should be normalized. In a MAGDM issue, the benefit type criterion and the cost type criteria are typically the two types of characteristics. The following equation converts the cost type criteria to benefit type criteria to harmonies the criterion:

$$ \Xi_{i j}^{(\zeta )} = \left\{ \begin{gathered} \left\langle {A_{i j}^{\zeta } ,I_{i j}^{\zeta } ,F_{i j}^{\zeta } } \right\rangle \quad {\text{if}}\quad C_{B} \hfill \\ \left\langle {F_{i j}^{\zeta } ,I_{i j}^{\zeta } ,A_{i j}^{\zeta } } \right\rangle \quad {\text{if}}\quad C_{Co} , \hfill \\ \end{gathered} \right. $$

(57)

where $C_{B}$ represent benefit type criteria and $C_{Co}$ represent cost type criteria.

Step 2. Generate the supports.

$$ {\text{Sprt}}\left( {'\!\gamma_{i j}^{\zeta } ,'\!\gamma_{i j}^{h} } \right) = 1 - \overline{\overline{\text{DIS}}} \left( {'\!\gamma_{i j}^{\zeta } ,'\!\gamma_{i j}^{h} } \right),\,\,\left( {\zeta ,h = 1,2,...,t,i = 1,2,.,,,n,j = 1,2,3,...,m} \right) $$

(58)

where $\overline{\overline{DIS}} \left( {'\!\gamma_{i j}^{\zeta } ,'\!\gamma_{i j}^{h} } \right)$ is the distance measure given in Definition (7).

Step 3. Generate $T\left( {'\!\gamma_{i j}^{\zeta } } \right)$

$$ T\left( {'\!\gamma_{i j}^{\zeta } } \right) = \sum\limits_{\begin{subarray}{l} h = 1 \\ {\AE} \ne h \end{subarray} }^{t} {\left( {'\!\gamma_{i j}^{\zeta } ,'\!\gamma_{i j}^{h} } \right)} ,\,\,\left( {\zeta ,h = 1,2,...,t,i = 1,2,.,,,n,j = 1,2,3,...,m} \right) $$

(59)

Step 4. Generate the weight vector ${\mathbb{W}}_{i j}^{\zeta }$ of power operator associated with the T^SPFN $'\!\gamma_{i j}^{\zeta }$,

$$ \Im_{i j}^{\zeta } = \frac{{\left( {1 + T\left( {'\!\gamma_{i j}^{\zeta } } \right)} \right)}}{{\sum\nolimits_{\zeta = 1}^{t} {\left( {1 + T\left( {'\!\gamma_{i j}^{\zeta } } \right)} \right)} }},\,\,\,\left( {\zeta = 1,2,3,...,t,i = 1,2,3,...,n,j = 1,2,3,...,m} \right) $$

(60)

Step 5 (a). The optimal group decision ideal solution (GDEIS) should be calculated by taking the average of all the opinions of each individual DMs, since it is closer to the GDEIS than any one DM's opinions. Therefore, in this stage, instead of taking average of all opinions, we compute the GDEIS by using the T-SPFWPHM values of alternatives that meet the criteria provided by decision makers and considering the same weighting of the DM's values as follows.

$$ GDEIS = \left( {\begin{array}{*{20}l} {EIS_{11} } & \ldots & {EIS_{1n} } \\ \vdots & \ddots & \vdots \\ {EIS_{m1} } & \cdots & {EIS_{mn} } \\ \end{array} } \right) $$

(61)

where ${\mathbb{W}}_{i } = \frac{1}{t}$ and

$$ \begin{gathered} EIS = \left( {\frac{2}{{t\left( {t + 1} \right)}}\sum\limits_{i = 1}^{t} {\sum\limits_{j = i }^{t} {\left( {\frac{{t{\mathbb{W}}_{i } \left( {1 + T\left( {'\!\gamma_{i } } \right)} \right)}}{{\sum\limits_{p = 1}^{t} {{\mathbb{W}}_{i } \left( {1 + T\left( {'\!\gamma_{i } } \right)} \right)} }}_{i } } \right)^{Q} \otimes_{AA} \left( {\frac{{t{\mathbb{W}}_{j} \left( {1 + T\left( {'\!\gamma_{j} } \right)} \right)}}{{\sum\limits_{p = 1}^{t} {{\mathbb{W}}_{j} \left( {1 + T\left( {'\!\gamma_{j} } \right)} \right)} }}_{j} } \right)^{\mathbb{R}} } } } \right)^{{\frac{1}{{Q + {\mathbb{R}}}}}} \hfill \\ = \left\langle {\left( {e^{{ - \left( {\left( {\frac{1}{{Q + {\mathbb{R}}}}} \right)\left( {\frac{2}{{t\left( {t + 1} \right)}}} \right)\left( {\sum\limits_{i = 1}^{t} {\sum\limits_{j = i }^{t} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {t{\mathbb{W}}_{i } \Im_{i } \left( { - \ln \left( {1 - A_{i }^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {t{\mathbb{W}}_{j} \Im_{j} \left( { - \ln \left( {1 - A_{j}^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} ,} \right. \hfill \\ \left( {1 - e^{{ - \left( {\left( {\frac{1}{{Q + {\mathbb{R}}}}} \right)\left( {\frac{2}{{t\left( {t + 1} \right)}}} \right)\left( {\sum\limits_{i = 1}^{t} {\sum\limits_{j = i }^{t} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {t{\mathbb{W}}_{i } \Im_{i } \left( { - \ln I_{i }^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {t{\mathbb{W}}_{j} \Im_{j} \left( { - \ln I_{j}^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} , \hfill \\ \left. {\left( {1 - e^{{ - \left( {\left( {\frac{1}{{Q + {\mathbb{R}}}}} \right)\left( {\frac{2}{{t\left( {t + 1} \right)}}} \right)\left( {\sum\limits_{i = 1}^{t} {\sum\limits_{j = i }^{t} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {t{\mathbb{W}}_{i } \Im_{i } \left( { - \ln F_{i }^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {t{\mathbb{W}}_{j} \Im_{j} \left( { - \ln F_{j}^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} } \right\rangle . \hfill \\ \end{gathered} $$

(62)

Step 5 (b). Do the following computations to determine the group right optimal decision (GROD) and group left optimal decision (GLOD):

$$ \begin{gathered} GROD = \left( {\begin{array}{*{20}l} {ROD_{11} } & {ROD_{12} } & \cdots & {ROD_{1n} } \\ {ROD_{21} } & {ROD_{22} } & \cdots & {ROD_{2n} } \\ \vdots & \vdots & \ddots & \vdots \\ {ROD_{m1} } & {ROD_{m2} } & \cdots & {ROD_{mn} } \\ \end{array} } \right) \hfill \\ {\text{where}} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,ROD_{i j} = \left\{ {'\!\gamma_{i j}^{\zeta } :\mathop {\max }\limits_{\zeta } \left\{ {\Xi_{i j}^{(\zeta )} } \right\}} \right\} \hfill \\ \end{gathered} $$

(63)

$$ \begin{gathered} GLOD = \left( {\begin{array}{*{20}l} {LOD_{11} } & {LOD_{12} } & \cdots & {LOD_{1n} } \\ {LOD_{21} } & {LOD_{22} } & \cdots & {LOD_{2n} } \\ \vdots & \vdots & \ddots & \vdots \\ {LOD_{m1} } & {LOD_{m2} } & \cdots & {LOD_{mn} } \\ \end{array} } \right) \hfill \\ where \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,LOD_{i j} = \left\{ {'\!\gamma_{i j}^{\zeta } :\mathop {\min }\limits_{\zeta } \left\{ {\Xi_{i j}^{(\zeta )} } \right\}} \right\}. \hfill \\ \end{gathered} $$

(64)

Step 5 (c). This stage involves determining the decision matrices distances from GDEIS, GROD, and GLOD using Definition 10. The distances are represented symbolically by the inscriptions DGDEIS, DGROD, and DGLOD. Where

$$ DGDOS_{i }^{\zeta } = \left\{ {\frac{1}{2t}\sum\limits_{i = 1}^{t} {\left| {\left( {A_{{\Xi_{i j} }}^{\zeta } } \right)^{q} - \left( {A_{{OS_{i j} }}^{\zeta } } \right)^{q} } \right|^{'\!\!A} + \left| {\left( {I_{{\Xi_{i j} }}^{\zeta } } \right)^{q} - \left( {I_{{OS_{i j} }}^{\zeta } } \right)^{q} } \right|^{'\!\!A} + \left| {\left( {F_{{\Xi_{i j} }}^{\zeta } } \right)^{q} - \left( {F_{{OS_{i j} }}^{\zeta } } \right)^{q} } \right|^{'\!\!A} } } \right\}^{{\frac{1}{'\!\!A}}} $$

(65)

$$ DGROS_{i }^{\zeta } = \left\{ {\frac{1}{2t}\sum\limits_{i = 1}^{t} {\left| {\left( {A_{{\Xi_{i j} }}^{\zeta } } \right)^{q} - \left( {A_{{ROS_{i j} }}^{\zeta } } \right)^{q} } \right|^{'\!\!A} + \left| {\left( {I_{{\Xi_{i j} }}^{\zeta } } \right)^{q} - \left( {I_{{ROS_{i j} }}^{\zeta } } \right)^{q} } \right|^{'\!\!A} + \left| {\left( {F_{{\Xi_{i j} }}^{\zeta } } \right)^{q} - \left( {F_{{ROS_{i j} }}^{\zeta } } \right)^{q} } \right| } } \right\}^{{\frac{1}{'\!\!A}}} ; $$

(66)

$$ DGLOS_{i }^{\zeta } = \left\{ {\frac{1}{2t}\sum\limits_{i = 1}^{t} {\left| {\left( {A_{{\Xi_{i j} }}^{\zeta } } \right)^{q} - \left( {A_{{LOS_{i j} }}^{\zeta } } \right)^{q} } \right|^{'\!\!A} + \left| {\left( {I_{{\Xi_{i j} }}^{\zeta } } \right)^{q} - \left( {I_{{LOS_{i j} }}^{\zeta } } \right)^{q} } \right|^{'\!\!A} + \left| {\left( {F_{{\Xi_{i j} }}^{\zeta } } \right)^{q} - \left( {F_{{LOS_{i j} }}^{\zeta } } \right)^{q} } \right| } } \right\}^{{\frac{1}{'\!\!A}}} $$

(67)

where $i = 1,2,...,m,\,\,\zeta = 1,2,3,...,t$ and ${'\!\!A}$ is generalized parameter.

Step 5 (d). In this stage, we compute the closeness indicators (CIs) using the Yue model [46] in the manner described below.

$$ CI^{\left( \zeta \right)} = \frac{{\sum\nolimits_{i = 1}^{m} {DROD_{i }^{(\zeta )} } + \sum\limits_{i = 1}^{m} {DLOD_{i }^{(\zeta )} } }}{{\sum\nolimits_{i = 1}^{m} {DGROD_{i }^{{(\zeta ) + \sum\nolimits_{i = 1}^{m} {DROD_{i }^{(\zeta )} } + \sum\nolimits_{i = 1}^{m} {DLOD_{i }^{(\zeta )} } }} } }}, $$

(68)

for $\zeta = 1,2,3,...,t$.

Step 5 (e). In this stage, the weights of DMs are computed as follows:

$$ {\mathbb{W}}^{(\zeta )} = \frac{{CI^{\zeta } }}{{\sum\nolimits_{i = 1}^{t} {CI^{\zeta } } }} $$

(69)

Step 6 (a). Generate the weight vector $'\Omega_{i j}^{\zeta }$ of power operator associated with the T^SPFN $'\!\gamma_{i j}^{\zeta }$,

$$ '\Omega_{i j}^{\zeta } = \frac{{t{\mathbb{W}}_{i j}^{\zeta } \left( {1 + T\left( {'\!\gamma_{i j}^{\zeta } } \right)} \right)}}{{\sum\nolimits_{\zeta = 1}^{t} {{\mathbb{W}}_{i j}^{\zeta } \left( {1 + T\left( {'\!\gamma_{i j}^{\zeta } } \right)} \right)} }},\,\,\,\left( {\zeta = 1,2,3,...,t,i = 1,2,3,...,n,j = 1,2,3,...,m} \right) $$

(70)

Step 6 (b). In this stage, with the TSPF entropy measure, compute the updated group decision (UGDOS) as follows to get the weights of the attributes. (${\mathbb{W}}_{i }^{\zeta } ='\Omega{i j}^{\zeta }$)

$$ \begin{gathered} ROS = \left( {\frac{2}{t(t + 1)}\sum\limits_{i = 1}^{t} {\sum\limits_{j = i }^{t} {\left( {\frac{{t{\mathbb{W}}_{i } \left( {1 + T\left( {'\!\gamma_{i } } \right)} \right)}}{{\sum\limits_{p = 1}^{t} {{\mathbb{W}}_{i } \left( {1 + T\left( {'\!\gamma_{i } } \right)} \right)} }}_{i } } \right)^{Q} \otimes_{AA} \left( {\frac{{t{\mathbb{W}}_{j} \left( {1 + T\left( {'\!\gamma_{j} } \right)} \right)}}{{\sum\limits_{p = 1}^{t} {{\mathbb{W}}_{j} \left( {1 + T\left( {'\!\gamma_{j} } \right)} \right)} }}_{j} } \right)^{\mathbb{R}} } } } \right)^{{\frac{1}{{Q + {\mathbb{R}}}}}} \hfill \\ = \left\langle {\left( {e^{{ - \left( {\left( {\frac{1}{{Q + {\mathbb{R}}}}} \right)\left( {\frac{2}{{t\left( {t + 1} \right)}}} \right)\left( {\sum\limits_{i = 1}^{t} {\sum\limits_{j = i }^{t} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {t{\mathbb{W}}_{i } \Im_{i } \left( { - \ln \left( {1 - A_{i }^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {t{\mathbb{W}}_{j} \Im_{j} \left( { - \ln \left( {1 - A_{j}^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} ,} \right. \hfill \\ \left( {1 - e^{{ - \left( {\left( {\frac{1}{{Q + {\mathbb{R}}}}} \right)\left( {\frac{2}{{t\left( {t + 1} \right)}}} \right)\left( {\sum\limits_{i = 1}^{t} {\sum\limits_{j = i }^{t} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {t{\mathbb{W}}_{i } \Im_{i } \left( { - \ln I_{i }^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {t{\mathbb{W}}_{j} \Im_{j} \left( { - \ln I_{j}^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} , \hfill \\ \left. {\left( {1 - e^{{ - \left( {\left( {\frac{1}{{Q + {\mathbb{R}}}}} \right)\left( {\frac{2}{{t\left( {t + 1} \right)}}} \right)\left( {\sum\limits_{i = 1}^{t} {\sum\limits_{j = i }^{t} {\left( {Q\left( { - \ln \left( {1 - e^{{ - \left( {t{\mathbb{W}}_{i } \Im_{i } \left( { - \ln F_{i }^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} + {\mathbb{R}}\left( { - \ln \left( {1 - e^{{ - \left( {t{\mathbb{W}}_{j} \Im_{j} \left( { - \ln F_{j}^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)} \right)^{N} } \right)} } } \right)} \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} } \right\rangle . \hfill \\ \end{gathered} $$

(71)

Step 6(c). Utilizing Definition 6, to compute the T-SPF entropy measure of each attribute as follows:

$$ \overline{\overline{ENT}}_{j} = \overline{\overline{ENT}} \left( {ROS_{1j} ,ROS_{2j} ,.....,ROS_{mj} } \right),\,\,j = 1,2,3,.....,m. $$

(72)

Step 6 (d). Attributes weights are computed as follows:

$$ {\mathbb{Z}}_{j} = \frac{{\overline{\overline{ENT}}_{j} }}{{\sum\nolimits_{j = 1}^{m} {\overline{\overline{ENT}}_{j} } }} $$

(73)

Step 7 (a). Utilizing the weights of the attributes, compute the weighted normalized decision matrices by the following formula:

$$ \begin{gathered} \overline{\overline{NWDM}} \left( {\Xi_{i j}^{\zeta } } \right) = \sum\limits_{{{\AE} = 1}}^{t} {{\mathbb{Z}}_{j} } \Xi_{i j}^{\zeta } \hfill \\ = \left\langle \left( {1 - e^{{ - \left( {{\mathbb{Z}}_{j} \left( { - \ln \left( {1 - \left( {A_{i j}^{\left( \zeta \right)} } \right)^{q} } \right)} \right)^{N} } \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} ,\right.\\ \left. \left( {e^{{ - \left( {{\mathbb{Z}}_{j} \left( { - \ln \left( {I_{i j}^{\left( \zeta \right)} } \right)^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} ,\right.\\ \left.\left( {e^{{ - \left( {{\mathbb{Z}}_{j} \left( { - \ln \left( {F_{i j}^{\left( \zeta \right)} } \right)^{q} } \right)^{N} } \right)^{\frac{1}{N}} }} } \right)^{\frac{1}{q}} \right\rangle \hfill \\ \end{gathered} $$

(74)

Step 7 (b). Utilizing NWD matrices $\overline{\overline{NWDM}} \left( {\Xi_{i j}^{\zeta } } \right)$, calculate the positive optimal matrix (POM) and negative optimal matrix (NOS) for decision matrices by the following formula:

$$ \begin{gathered} POM^{\zeta } = \left\{ {\overline{\overline{NWDM}} \left( {\Xi_{i j}^{\zeta } } \right):\mathop {\max }\limits_{i } \left[ {\Xi_{i j}^{\zeta } } \right]} \right\},j = 1,2,3...,m; \hfill \\ and \hfill \\ NOM^{\zeta } = \left\{ {\overline{\overline{NWDM}} \left( {\Xi_{i j}^{\zeta } } \right):\mathop {mi n}\limits_{i } \left[ {\Xi_{i j}^{\zeta } } \right]} \right\},j = 1,2,3...,m. \hfill \\ \end{gathered} $$

(75)

Step 8. Utilizing Definition 7 to calculate the distances of NWD matrices to POS and NOS by the following formula:

$$ \begin{gathered} DIS_{i }^{ + \zeta } = \left\{ {\frac{1}{2t}\sum\limits_{j = 1}^{t} {{\mathbb{Z}}_{j} \left( {\left| {\left( {A_{{\overline{\overline{NWDM}} \left( {\Xi^{\zeta } } \right)}} } \right)^{q} - \left( {A_{{POM^{\zeta } }} } \right)^{q} } \right|^{'\!\!A} + \left| {\left( {I_{{\overline{\overline{NWDM}} \left( {\Xi^{\zeta } } \right)}} } \right)^{q} - \left( {I_{{POM^{\zeta } }} } \right)^{q} } \right|^{'\!\!A} + \left| {\left( {F_{{\overline{\overline{NWDM}} \left( {\Xi^{\zeta } } \right)}} } \right)^{q} - \left( {F_{{POM^{\zeta } }} } \right)^{q} } \right| } \right)} } \right\}^{{\frac{1}{}}} , \hfill \\ DIS_{i }^{ - \zeta } = \left\{ {\frac{1}{2t}\sum\limits_{j = 1}^{t} {{\mathbb{Z}}_{j} \left( {\left| {\left( {A_{{\overline{\overline{NWDM}} \left( {\Xi^{\zeta } } \right)}} } \right)^{q} - \left( {A_{{NOM^{\zeta } }} } \right)^{q} } \right| + \left| {\left( {I_{{\overline{\overline{NWDM}} \left( {\Xi^{\zeta } } \right)}} } \right)^{q} - \left( {I_{{NOM^{\zeta } }} } \right)^{q} } \right|^{'\!\!A} + \left| {\left( {F_{{\overline{\overline{NWDM}} \left( {\Xi^{\zeta } } \right)}} } \right)^{q} - \left( {F_{{NOM^{\zeta } }} } \right)^{q} } \right|^{'\!\!A} } \right)} } \right\}^{{\frac{1}{'\!\!A}}} \hfill \\ \end{gathered} $$

(76)

Step 9. In this stage, we compute the revised closeness indicators (CIs) the following formula:

$$ RCI^{\left( \zeta \right)} = \frac{{\sum\nolimits_{i = 1}^{m} {DIS_{i }^{ - (\zeta )} } }}{{\sum\nolimits_{i = 1}^{m} {DIS_{i }^{ + (\zeta )} } + \sum\nolimits_{i = 1}^{m} {DIS_{i }^{ - (\zeta )} } }} $$

(77)

Step 10. In this stage, the final FCIs are computed by the following formula follows:

$$ FRCI_{i } = \sum\limits_{i = 1}^{t} {'\!E^{(\zeta )} RCI^{\zeta } } . $$

(78)

Sort the computed FRCI values in descending order; the option with the highest value is the best option.

Illustrative example

To confirm the viability and applicability of the suggested group decision framework, this section makes use of the newly introduced TSPF TOPSIS group decision method based on TSPFAAPWHM operators for evaluating and selecting a suitable pharmaceutical enterprise, who have a sustainable and high-quality development capability. To demonstrate the reliability and dominance on their own, sensitivity analysis and contrast research are also used.

Numerous difficulties have been brought about by the rapid spread of COVID-19 for public health defense, fiscal growth, and human production life. Currently, scientists both locally and internationally are working hard to create new medicines to treat crown pneumonia, and they have made some substantial progress. Selecting pharmaceutical companies with sustainable and high-quality development capacity for drug manufacturing and environmental protection is crucial for further mitigating the pandemic. Considering sustainable and high-quality growth, a city's pharmaceutical management agency will select pharmaceutical companies to make medicines. Six regional businesses identified as $\left\{ {'\!\gamma_{1} ,'\!\gamma_{2} ,...,'\!\gamma_{6} } \right\}$ are chosen as candidate businesses for the assessment committee to choose the best pharmaceutical companies based on several evaluation criteria after undergoing preliminary qualification test and screening. To start, the Pharmaceutical Administration Department formed an assessment committee by inviting four specialists $\left\{ {EX_{1} ,EX_{2} ,EX_{2} ,EX_{2} } \right\}$ from the disciplines of medication research and development, production management, and sustainable economic growth. Second, seven assessment criteria $\left\{ {'\!O_{1} ,'\!O_{2} ,'\!O_{3} ,...,'\!O_{7} } \right\}$ are chosen as the comprehensive evaluation criteria following a debate among the rating committee members and a review of the body of literature [2, 7]. The descriptions of the criteria are, $'\!O_{1}$ represents effective supply ability, $'\!O_{2}$ represents scientific and technological innovation ability, $'\!O_{3}$ transnational cooperation ability,$'\!O_{4}$ efficient operation ability, $'\!O_{5}$ represents market improvement ability, $'\!O_{6}$ represents green improvement ability, and $'\!O_{7}$ social contribute ability. The expert weight and criterion weight in the assessment process are entirely unknown due to the ambiguity and complexity of the assessment environment, thus experts must offer comparison preferences between the criteria in order to ascertain the subjective weight of the criteria. This part uses the suggested group decision-making technique to rate the six pharmaceutical firms in the area and choose the top six based on the assessment data given by experts. To solve such a decision-making problem, the following steps are to be followed using the proposed approach.

Four experts provide their opinions and assessments of the pharmaceutical companies using the linguistic terms mentioned in Table 2 and the criteria listed above. The linguist term assessment of the experts $EX_{h} = (h = 1,...,4)$ is given in Tables 3, 4, 5 and 6 below.

Table 3 Linguistic term evaluation provided by expert $EX_{1}$

Table 4 Linguistic term evaluation provided by expert $EX_{2}$

Table 5 Linguistic term evaluation provided by expert $EX_{3}$

Table 6 Linguistic term evaluation provided by expert $EX_{4}$

Utilizing Table 2, the linguistic term evaluation Tables 3, 4, 5 and 6 are converted to TSPF environment which are listed in Tables 7, 8, 9 and 10 given below.

Table 7 TSPF evaluation matrix ${\mathbb{M}}_{1}$

Table 8 TSPF evaluation matrix ${\mathbb{M}}_{2}$

Table 9 TSPF evaluation matrix ${\mathbb{M}}_{3}$

Table 10 TSPF evaluation matrix ${\mathbb{M}}_{4}$

Step 1. Utilize formula (57), to normalize the cost type attribute. Since all the attributes are of benefit type, there is no need to normalize it.

Step 2. Utilize formula (58), to generate the supports ${\text{Sprt}}\left( {'\!\gamma_{i j}^{gh} ,'\!\gamma_{i j}^{gl} } \right) \quad \left( {g,h,l = 1,...,4,i = 1,2,.,,,7,j = 1,2,...,6} \right)$. Instead of writing $Sprt\left( {'\!\gamma_{i j}^{gh} ,'\!\gamma_{i j}^{gl} } \right)$, we denote it by $S_{i j}^{gl}$ which are listed below.

$$\begin{gathered} S_{11}^{12} = S_{11}^{21} = 0.7833,S_{11}^{13} = S_{11}^{31} = 0.7024,S_{11}^{14} = S_{11}^{41} = 0.7833,S_{11}^{23} = S_{11}^{32} = 0.9113,S_{11}^{24} = S_{11}^{42} = 1.0000,S_{11}^{34} = S_{11}^{34} = 0.9113, \hfill \\ S_{12}^{12} = S_{12}^{21} = 0.9029,S_{12}^{13} = S_{12}^{31} = 0.8173,S_{12}^{14} = S_{12}^{41} = 0.8173,S_{12}^{23} = S_{12}^{32} = 0.9113,S_{12}^{24} = S_{12}^{42} = 0.9113,S_{12}^{34} = S_{12}^{43} = 1.0000, \hfill \\ S_{13}^{12} = S_{13}^{21} = 1.0000,S_{13}^{13} = S_{13}^{31} = 0.7833,S_{13}^{14} = S_{13}^{41} = 0.5830,S_{13}^{23} = S_{13}^{32} = 0.7833,S_{13}^{24} = S_{13}^{42} = 0.5830,S_{13}^{34} = S_{13}^{43} = 0.7603, \hfill \\ S_{14}^{12} = S_{14}^{21} = 1.0000,S_{14}^{13} = S_{14}^{31} = 0.6485,S_{14}^{14} = S_{14}^{41} = 0.8790,S_{14}^{23} = S_{14}^{32} = 0.6485,S_{14}^{24} = S_{14}^{42} = 0.8790,S_{14}^{34} = S_{14}^{43} = 0.7603, \hfill \\ S_{15}^{12} = S_{15}^{21} = 1.0000,S_{15}^{13} = S_{15}^{31} = 0.5830,S_{15}^{14} = S_{15}^{41} = 0.8790,S_{15}^{23} = S_{15}^{23} = 0.5830,S_{15}^{24} = S_{15}^{42} = 0.8790,S_{15}^{34} = S_{15}^{43} = 0.6840, \hfill \\ S_{16}^{12} = S_{16}^{21} = 0.9113,S_{16}^{13} = S_{16}^{31} = 1.0000,S_{16}^{14} = S_{16}^{41} = 0.7024,S_{16}^{23} = S_{16}^{32} = 0.9113,S_{16}^{24} = S_{16}^{42} = 0.7833,S_{16}^{34} = S_{16}^{43} = 0.7024, \hfill \\ S_{17}^{12} = S_{17}^{21} = 1.0000,S_{17}^{13} = S_{17}^{31} = 0.6485,S_{17}^{14} = S_{17}^{41} = 0.7833,S_{17}^{23} = S_{17}^{32} = 0.6485,S_{17}^{24} = S_{17}^{42} = 0.7833,S_{17}^{34} = S_{17}^{43} = 0.4960, \hfill \\ \end{gathered}$$

$$ \begin{gathered} S_{21}^{12} = S_{21}^{21} = 1.0000,S_{21}^{13} = S_{21}^{31} = 1.0000,S_{21}^{14} = S_{21}^{41} = 0.9029,S_{21}^{23} = S_{21}^{32} = 1.0000,S_{21}^{24} = S_{21}^{42} = 0.9029,S_{21}^{34} = S_{21}^{43} = 0.9029, \hfill \\ S_{22}^{12} = S_{22}^{21} = 0.5830,S_{22}^{13} = S_{22}^{31} = 0.5830,S_{22}^{14} = S_{22}^{41} = 0.7833,S_{22}^{23} = S_{22}^{32} = 1.0000,S_{22}^{24} = S_{22}^{42} = 0.7603,S_{22}^{34} = S_{22}^{43} = 0.7603, \hfill \\ S_{23}^{12} = S_{23}^{21} = 1.0000,S_{23}^{13} = S_{23}^{31} = 0.7024,S_{23}^{14} = S_{23}^{41} = 0.6485,S_{23}^{23} = S_{23}^{32} = 0.7024,S_{23}^{24} = S_{23}^{42} = 0.6485,S_{23}^{34} = S_{23}^{43} = 0.9113, \hfill \\ S_{24}^{12} = S_{24}^{21} = 1.0000,S_{24}^{13} = S_{24}^{31} = 0.9113,S_{24}^{14} = S_{24}^{41} = 1.0000,S_{24}^{23} = S_{24}^{32} = 0.9113,S_{24}^{24} = S_{24}^{42} = 1.0000,S_{24}^{34} = S_{24}^{43} = 0.9113, \hfill \\ S_{25}^{12} = S_{25}^{21} = 0.7833,S_{25}^{13} = S_{25}^{31} = 1.0000,S_{25}^{14} = S_{25}^{41} = 0.7833,S_{25}^{23} = S_{25}^{32} = 0.7833,S_{25}^{24} = S_{25}^{42} = 1.0000,S_{25}^{34} = S_{25}^{43} = 0.7833, \hfill \\ S_{26}^{12} = S_{26}^{21} = 1.0000,S_{26}^{13} = S_{26}^{31} = 0.7603,S_{26}^{14} = S_{26}^{41} = 0.8790,S_{26}^{23} = S_{26}^{32} = 0.7603,S_{26}^{24} = S_{26}^{42} = 0.8790,S_{26}^{34} = S_{26}^{43} = 0.6485, \hfill \\ S_{27}^{12} = S_{27}^{21} = 0.8480,S_{27}^{13} = S_{27}^{31} = 0.9113,S_{27}^{14} = S_{27}^{41} = 1.0000,S_{27}^{23} = S_{27}^{32} = 0.9113,S_{27}^{24} = S_{27}^{42} = 0.8480,S_{27}^{34} = S_{27}^{43} = 0.9113, \hfill \\ \end{gathered} $$

Step 3. Utilize formula (59), to generate $T\left( {'\!\gamma_{i j}^{g} } \right)\,\,(g = 1,...,4,i = 1,...,6,j = 1,...,7)$. Instead of writing $T\left( {'\!\gamma_{i j}^{g} } \right)$, we will simply denote it by $T_{i j}^{g}$ which are listed below.

$$ \begin{gathered} T_{11}^{1} = 2.2691,T_{11}^{2} = 2.6947,T_{11}^{3} = 2.5251,T_{11}^{4} = 2.6947,T_{12}^{1} = 2.5375,T_{12}^{2} = 2.7255,T_{12}^{3} = 2.7287,T_{12}^{4} = 2.7287, \hfill \\ T_{13}^{1} = 2.3663,T_{13}^{2} = 2.3663,T_{13}^{3} = 2.3269,T_{13}^{4} = 1.9262,T_{14}^{1} = 2.5275,T_{14}^{2} = 2.5275,T_{14}^{3} = {\kern 1pt} 2.0573,T_{14}^{4} = 2.5183, \hfill \\ T_{15}^{1} = 2.4620,T_{15}^{2} = 2.4620,T_{15}^{3} = 1.8500,T_{15}^{4} = 2.4420,T_{16}^{1} = 2.6137,T_{16}^{2} = 2.6060,T_{16}^{3} = 2.6137,T_{16}^{4} = 2.1881, \hfill \\ T_{17}^{1} = 2.4318,T_{17}^{2} = 2.4318,T_{17}^{3} = 1.7930,T_{17}^{4} = 2.0627,T_{21}^{1} = 2.9029,T_{21}^{2} = 2.9029,T_{21}^{3} = 2.9029,T_{21}^{4} = 2.7086, \hfill \\ T_{22}^{1} = 1.9493,T_{22}^{2} = 2.3433,T_{22}^{3} = 2.3433,T_{22}^{4} = 2.3039,T_{23}^{1} = 2.3509,T_{23}^{2} = 2.3509,T_{23}^{3} = 2.3161,T_{23}^{4} = 2.2083, \hfill \\ T_{24}^{1} = 2.9113,T_{24}^{2} = 2.9113,T_{24}^{3} = 2.7340,T_{24}^{4} = 2.9113,T_{25}^{1} = 2.5667,T_{25}^{2} = 2.5667,T_{25}^{3} = 2.5667,T_{25}^{4} = 2.5667, \hfill \\ T_{26}^{1} = 2.6393,T_{26}^{2} = 2.6393,T_{26}^{3} = 2.1691,T_{26}^{4} = 2.4065,T_{27}^{1} = 2.7593,T_{27}^{2} = 2.6073,T_{27}^{3} = 2.7340,T_{27}^{4} = 2.7593, \hfill \\ \end{gathered} $$

$$ \begin{gathered} T_{31}^{1} = 2.5137,T_{31}^{2} = 2.5197,T_{31}^{3} = 2.5197,T_{31}^{4} = 2.2838,T_{32}^{1} = 2.4542,T_{31}^{2} = 2.4859,T_{31}^{3} = 1.8145,T_{31}^{4} = 2.4859, \hfill \\ T_{33}^{1} = 2.4030,T_{33}^{2} = 2.1534,T_{33}^{3} = 2.1011,T_{33}^{4} = 2.3539,T_{34}^{1} = 2.0573,T_{34}^{2} = 2.5275,T_{34}^{3} = 2.5183,T_{34}^{4} = 2.5275, \hfill \\ T_{35}^{1} = 1.9895,T_{35}^{2} = 2.5347,T_{35}^{3} = 2.5316,T_{35}^{4} = 2.5347,T_{36}^{1} = 2.6847,T_{36}^{2} = 2.6862,T_{36}^{3} = 2.6862,T_{36}^{4} = 2.4457, \hfill \\ {\kern 1pt} T_{37}^{1} = 2.6707,T_{37}^{2} = 2.8227,T_{37}^{3} = 2.6707,T_{37}^{4} = 2.8227,T_{41}^{1} = 2.4838,T_{41}^{2} = 2.7254,T_{41}^{3} = 2.4186,T_{41}^{4} = 2.7254, \hfill \\ T_{42}^{1} = 2.0774,T_{42}^{2} = 1.7814,T_{42}^{3} = 2.2793,T_{42}^{4} = 2.2221,T_{43}^{1} = 2.8227,T_{43}^{2} = 2.6707,T_{43}^{3} = 2.8227,T_{43}^{4} = 2.6707, \hfill \\ T_{44}^{1} = 2.5077,T_{44}^{2} = 2.2040,T_{44}^{3} = 2.5087,T_{44}^{4} = 2.3180,T_{45}^{1} = 2.5488,T_{45}^{2} = 1.9600,T_{45}^{3} = 2.5488,T_{45}^{4} = 2.2481, \hfill \\ {\kern 1pt} T_{46}^{1} = 2.4666,T_{46}^{2} = 1.7424,T_{46}^{3} = 2.4666,T_{46}^{1} = 2.4545,T_{47}^{1} = 2.6073,T_{47}^{2} = 2.7593,T_{47}^{3} = 2.7593,T_{47}^{4} = 2.7340, \hfill \\ \end{gathered} $$

$$ \begin{gathered} T_{51}^{1} = 2.6137,T_{51}^{2} = 2.1881,T_{51}^{3} = 2.6137,T_{51}^{4} = 2.6060,T_{52}^{1} = 2.5342,T_{52}^{2} = 2.5422,T_{52}^{3} = 2.3108,T_{52}^{4} = 2.2568, \hfill \\ {\kern 1pt} T_{53}^{1} = 2.4965,T_{53}^{2} = 2.0803,T_{53}^{3} = 2.4965,T_{53}^{4} = 2.4793,T_{54}^{1} = 2.2040,T_{54}^{2} = 2.5077,T_{54}^{3} = 2.3180,T_{54}^{4} = 2.5087, \hfill \\ T_{55}^{1} = 2.6862,T_{55}^{2} = 2.6862,T_{55}^{3} = 2.6847,T_{55}^{4} = 2.4457,T_{56}^{1} = 2.2481,T_{56}^{2} = 2.5488,T_{56}^{3} = 2.5488,T_{56}^{4} = 1.9600, \hfill \\ T_{57}^{1} = 2.6137,T_{57}^{2} = 2.6137,T_{57}^{3} = 2.6060,T_{57}^{4} = 2.1881,T_{61}^{1} = 2.9029,T_{61}^{2} = 2.7086,T_{61}^{3} = 2.9029,T_{61}^{4} = 2.9029, \hfill \\ T_{62}^{1} = 2.5197,T_{62}^{2} = 2.2838,T_{62}^{3} = 2.5137,T_{62}^{4} = 2.5197,T_{63}^{1} = 2.6060,T_{63}^{2} = 2.6137,T_{63}^{3} = 2.1881,T_{63}^{4} = 2.6137, \hfill \\ T_{64}^{1} = 2.5722,T_{64}^{2} = 2.5718,T_{64}^{3} = 2.3306,T_{64}^{4} = 2.5722,T_{65}^{1} = 2.5488,T_{65}^{2} = 2.2481,T_{65}^{3} = 1.9600,T_{65}^{4} = 2.5488, \hfill \\ {\kern 1pt} T_{66}^{1} = 2.8790,T_{66}^{2} = 2.8790,T_{66}^{3} = 2.6370,T_{66}^{4} = 2.8790,T_{67}^{1} = 2.2631,T_{67}^{2} = 2.3912,T_{67}^{3} = 2.3779,T_{67}^{4} = 1.6909. \hfill \\ \end{gathered} $$

Step 4. Utilize formula (60), to generate the weight vector $'\!E_{i j}^{g}$ of power operator associated with the T^SPFN $'\!\gamma_{i j}^{g}$,

$$ \begin{gathered}'\!E_{11}^{1} = 0.2305,'\!E_{11}^{2} = 0.2605,'\!E_{11}^{3} = 0.2485,'\!E_{11}^{4} = 0.2605,'\!E_{12}^{1} = 0.2403,'\!E_{12}^{2} = 0.2531,'\!E_{12}^{3} = 0.2533,'\!E_{12}^{4} = 0.2533, \hfill \\'\!E_{13}^{1} = 0.2592,'\!E_{13}^{2} = 0.2592,'\!E_{13}^{3} = 0.2562,'\!E_{13}^{4} = 0.2253,'\!E_{14}^{1} = 0.2588,'\!E_{14}^{2} = 0.2588,'\!E_{14}^{3} = 0.2243,'\!E_{14}^{4} = 0.2581, \hfill \\'\!E_{15}^{1} = 0.2620,'\!E_{15}^{2} = 0.2620,'\!E_{15}^{3} = 0.2156,'\!E_{15}^{4} = 0.2604,'\!E_{16}^{1} = 0.2577,'\!E_{16}^{2} = 0.2572,'\!E_{16}^{3} = 0.2577,'\!E_{16}^{4} = 0.2274, \hfill \\'\!E_{17}^{1} = 0.2698,'\!E_{17}^{2} = 0.2698,'\!E_{17}^{3} = 0.2196,'\!E_{17}^{4} = 0.2408,'\!E_{21}^{1} = 0.2531,'\!E_{21}^{2} = 0.2531,'\!E_{21}^{3} = 0.2531,'\!E_{21}^{4} = 0.2406, \hfill \\'\!E_{22}^{1} = 0.2279,'\!E_{22}^{2} = 0.2584,'\!E_{22}^{3} = 0.2584,'\!E_{22}^{4} = 0.2553,'\!E_{23}^{1} = 0.2534,'\!E_{23}^{2} = 0.2534,'\!E_{23}^{3} = 0.2507,'\!E_{23}^{4} = 0.2426, \hfill \\'\!E_{24}^{1} = 0.2529,'\!E_{24}^{2} = 0.2529,'\!E_{24}^{3} = 0.2414,'\!E_{24}^{4} = 0.2529,'\!E_{25}^{1} = 0.2500,'\!E_{25}^{2} = 0.2500,'\!E_{25}^{3} = 0.2500,'\!E_{25}^{4} = 0.2500, \hfill \\'\!E_{26}^{1} = 0.2627,'\!E_{26}^{2} = 0.2627,'\!E_{26}^{3} = 0.2287,'\!E_{26}^{4} = 0.2459,'\!E_{27}^{1} = 0.2530,'\!E_{27}^{2} = 0.2428,'\!E_{27}^{3} = 0.2513,'\!E_{27}^{4} = 0.2530, \hfill \\ \end{gathered} $$

Step 5 (a). Utilize formulas (61) and (62), to compute the GDEIS by using the T-SPFWPHM values of alternatives that meet the criteria provided by decision makers and considering the same weighting of the DM's values which is listed in Table 11 below (Table 12).

$$ \begin{gathered}'\!E_{31}^{1} = 0.2539,'\!E_{31}^{2} = 0.2544,'\!E_{31}^{3} = 0.2544,'\!E_{31}^{4} = 0.2373,'\!E_{32}^{1} = 0.2609,'\!E_{32}^{2} = 0.2633,'\!E_{32}^{3} = 0.2126,'\!E_{32}^{4} = 0.2633, \hfill \\'\!E_{33}^{1} = 0.2615,'\!E_{33}^{2} = 0.2424,'\!E_{33}^{3} = 0.2383,'\!E_{33}^{4} = 0.2578,'\!E_{34}^{1} = 0.2243,'\!E_{34}^{2} = 0.2588,'\!E_{34}^{3} = 0.2581,'\!E_{34}^{4} = 0.2588, \hfill \\'\!E_{35}^{1} = 0.2200,'\!E_{35}^{2} = 0.2601,'\!E_{35}^{3} = 0.2599,'\!E_{35}^{4} = 0.2601,'\!E_{36}^{1} = 0.2541,'\!E_{36}^{2} = 0.2542,'\!E_{36}^{3} = 0.2542,'\!E_{36}^{4} = 0.2376, \hfill \\'\!E_{37}^{1} = 0.2449,'\!E_{37}^{2} = 0.2551,'\!E_{37}^{3} = 0.2449,'\!E_{37}^{4} = 0.2551,'\!E_{41}^{1} = 0.2427,'\!E_{41}^{2} = 0.2596,'\!E_{41}^{3} = 0.2382,'\!E_{41}^{4} = 0.2596, \hfill \\'\!E_{42}^{1} = 0.2490,'\!E_{42}^{2} = 0.2250,'\!E_{42}^{3} = 0.2653,'\!E_{42}^{4} = 0.2607,'\!E_{43}^{1} = 0.2551,'\!E_{43}^{2} = 0.2449,'\!E_{43}^{3} = 0.2551,'\!E_{43}^{4} = 0.2449, \hfill \\'\!E_{44}^{1} = 0.2591,'\!E_{44}^{2} = 0.2367,'\!E_{44}^{3} = 0.2592,'\!E_{44}^{4} = 0.2451,'\!E_{45}^{1} = 0.2667,'\!E_{45}^{2} = 0.2225,'\!E_{45}^{3} = 0.2667,'\!E_{45}^{4} = 0.2441, \hfill \\ \end{gathered} $$

$\begin{gathered}'\!E_{46}^{1} = 0.2640,'\!E_{46}^{2} = 0.2089,'\!E_{46}^{3} = 0.2640,'\!E_{46}^{4} = 0.2631,'\!E_{47}^{1} = 0.2428,'\!E_{47}^{2} = 0.2530,'\!E_{47}^{3} = 0.2530,'\!E_{47}^{4} = 0.2513, \hfill \\'\!E_{51}^{1} = 0.2577,'\!E_{51}^{2} = 0.2274,'\!E_{51}^{3} = 0.2577,'\!E_{51}^{4} = 0.2572,'\!E_{52}^{1} = 0.2590,'\!E_{52}^{2} = 0.2596,'\!E_{52}^{3} = 0.2427,'\!E_{52}^{4} = 0.2387, \hfill \\'\!E_{53}^{1} = 0.2580,'\!E_{53}^{2} = 0.2273,'\!E_{53}^{3} = 0.2580,'\!E_{53}^{4} = 0.2567,'\!E_{54}^{1} = 0.2367,'\!E_{54}^{2} = 0.2591,'\!E_{54}^{3} = 0.2451,'\!E_{54}^{4} = 0.2592, \hfill \\'\!E_{55}^{1} = 0.2542,'\!E_{55}^{2} = 0.2542,'\!E_{55}^{3} = 0.2541,'\!E_{55}^{4} = 0.2376,'\!E_{56}^{1} = 0.2441,'\!E_{56}^{2} = 0.2667,'\!E_{56}^{3} = 0.2667,'\!E_{56}^{4} = 0.2225, \hfill \\'\!E_{57}^{1} = 0.2577,'\!E_{57}^{2} = 0.2577,'\!E_{57}^{3} = 0.2572,'\!E_{57}^{4} = 0.2274,'\!E_{61}^{1} = 0.2531,'\!E_{61}^{2} = 0.2406,'\!E_{61}^{3} = 0.2531,'\!E_{61}^{4} = 0.2531, \hfill \\'\!E_{62}^{1} = 0.2544,'\!E_{62}^{2} = 0.2373,'\!E_{62}^{3} = 0.2539,'\!E_{62}^{4} = 0.2544,'\!E_{63}^{1} = 0.2572,'\!E_{63}^{2} = 0.2577,'\!E_{63}^{3} = 0.2274,'\!E_{63}^{4} = 0.2577, \hfill \\'\!E_{64}^{1} = 0.2543,'\!E_{64}^{2} = 0.2543,'\!E_{64}^{3} = 0.2371,'\!E_{64}^{4} = 0.2543,'\!E_{65}^{1} = 0.2667,'\!E_{65}^{2} = 0.2441,'\!E_{65}^{3} = 0.2225,'\!E_{65}^{4} = 0.2667, \hfill \\'\!E_{66}^{1} = 0.2540,'\!E_{66}^{2} = 0.2540,'\!E_{66}^{3} = 0.2381,'\!E_{66}^{4} = 0.2540,'\!E_{67}^{1} = 0.2565,'\!E_{67}^{2} = 0.2665,'\!E_{67}^{3} = 0.2655,'\!E_{67}^{4} = 0.2115. \hfill \\ \end{gathered}$

Table 11 GDEIS matrix

Table 12 GDRIS matrix

Step 5 (b). Utilize formulas (63) and (64), to determine the GROD and GLOD matrices which are listed in Tables 13 and 14 below.

Table 13 GLOD matrix

Table 14 GLOD matrix

Step 5 (c). Utilize formulas (65), (66) and (67), to determine distances from GDEIS, GROD, and GLOD which are listed in Tables 15, 16 and 17.

Table 15 DGDEIS matrix

Table 16 GROD matrix

Table 17 GLOD matrix

Step 5 (d). Utilize formula (68), to compute the CIs which is listed below.

$$ CI^{1} = 0.6937,CI^{2} = 0.6744,CI^{3} = 0.7262,CI^{4} = 0.6964. $$

Step 5 (e). Utilize formula (69), to determine the weights of DMs which are listed below.

$$ {\mathbb{W}}_{1} = 0.2486,{\mathbb{W}}_{2} = 0.2417,{\mathbb{W}}_{3} = 0.2602,{\mathbb{W}}_{4} = 0.2496. $$

Step 6 (a). Utilize formula (70), to generate the weight vector $\mathcal{J}_{i j}^{g}$ of power operator associated with the T^SPFN $'\!\gamma_{i j}^{g}$ which are listed below.

$$ \begin{gathered} \mathcal{J}_{11}^{1} = 0.9169,\mathcal{J}_{11}^{2} = 1.0075,\mathcal{J}_{11}^{3} = 1.0351,\mathcal{J}_{11}^{4} = 1.0405,\mathcal{J}_{12}^{1} = 0.9557,\mathcal{J}_{12}^{2} = 0.9785,\mathcal{J}_{12}^{3} = 1.0545,\mathcal{J}_{12}^{4} = 1.0113,\mathcal{J}_{13}^{1} = 1.0310,\mathcal{J}_{13}^{2} = 1.0024,\mathcal{J}_{13}^{3} = 1.0667,\mathcal{J}_{13}^{4} = 0.8998, \hfill \\ \mathcal{J}_{14}^{1} = 1.0307,\mathcal{J}_{14}^{2} = 1.0021,\mathcal{J}_{14}^{3} = 1.0790,\mathcal{J}_{14}^{4} = 1.0348,\mathcal{J}_{15}^{1} = 1.0478,\mathcal{J}_{15}^{2} = 1.0148,\mathcal{J}_{15}^{3} = 0.8995,\mathcal{J}_{15}^{4} = 1.0419,\mathcal{J}_{16}^{1} = 1.0249,\mathcal{J}_{16}^{2} = 0.9943,\mathcal{J}_{16}^{3} = 1.0729,\mathcal{J}_{16}^{1} = 0.9078, \hfill \\ \mathcal{J}_{17}^{1} = 1.0752,\mathcal{J}_{17}^{2} = 1.0454,\mathcal{J}_{17}^{3} = 0.9161,\mathcal{J}_{17}^{4} = 0.9634,\mathcal{J}_{21}^{1} = 1.0068,\mathcal{J}_{21}^{2} = 0.9788,\mathcal{J}_{21}^{3} = 1.0539,\mathcal{J}_{21}^{4} = 0.9605,\mathcal{J}_{22}^{1} = 0.9063,\mathcal{J}_{22}^{2} = 0.9989,\mathcal{J}_{22}^{3} = 1.0755,\mathcal{J}_{22}^{4} = 1.0193, \hfill \\ \mathcal{J}_{23}^{1} = 1.0077,\mathcal{J}_{23}^{2} = 0.9797,\mathcal{J}_{23}^{3} = 1.0439,\mathcal{J}_{23}^{4} = 0.9648,\mathcal{J}_{24}^{1} = 1.0061,\mathcal{J}_{24}^{2} = 0.9782,\mathcal{J}_{24}^{3} = 1.0533,\mathcal{J}_{24}^{4} = 1.0102,\mathcal{J}_{25}^{1} = 0.9943,\mathcal{J}_{25}^{2} = 0.9667,\mathcal{J}_{25}^{3} = 1.0408,\mathcal{J}_{25}^{4} = 0.9982, \hfill \\ \mathcal{J}_{26}^{1} = 1.0461,\mathcal{J}_{26}^{2} = 1.0171,\mathcal{J}_{26}^{3} = 0.9536,\mathcal{J}_{26}^{4} = 0.9831,\mathcal{J}_{27}^{1} = 1.0058,\mathcal{J}_{27}^{2} = 0.9384,\mathcal{J}_{27}^{3} = 1.0459,\mathcal{J}_{27}^{4} = 1.0099,\mathcal{J}_{31}^{1} = 1.0099,\mathcal{J}_{31}^{2} = 0.9835,\mathcal{J}_{31}^{3} = 1.0590,\mathcal{J}_{31}^{4} = 0.9476, \hfill \\ \mathcal{J}_{32}^{1} = 1.0397,\mathcal{J}_{32}^{2} = 1.0201,\mathcal{J}_{32}^{3} = 0.8868,\mathcal{J}_{32}^{4} = 1.0534,\mathcal{J}_{33}^{1} = 1.0405,\mathcal{J}_{33}^{2} = 0.9374,\mathcal{J}_{33}^{3} = 0.9926,\mathcal{J}_{33}^{4} = 1.0255,\mathcal{J}_{34}^{1} = 0.8919,\mathcal{J}_{34}^{2} = 0.8671,\mathcal{J}_{34}^{3} = 0.9337,\mathcal{J}_{34}^{4} = 0.8955, \hfill \\ \mathcal{J}_{35}^{1} = 0.8746,\mathcal{J}_{35}^{2} = 1.0054,\mathcal{J}_{35}^{3} = 1.0816,\mathcal{J}_{35}^{4} = 1.0383,\mathcal{J}_{36}^{1} = 1.0104,\mathcal{J}_{36}^{2} = 0.9828,\mathcal{J}_{36}^{3} = 1.0582,\mathcal{J}_{36}^{4} = 0.9486,\mathcal{J}_{37}^{1} = 0.9744,\mathcal{J}_{37}^{2} = 0.9866,\mathcal{J}_{37}^{3} = 1.0201,\mathcal{J}_{37}^{4} = 1.0189, \hfill \\ \end{gathered} $$

$$ \begin{gathered} \mathcal{J}_{41}^{1} = 0.9661,\mathcal{J}_{41}^{2} = 1.0044,\mathcal{J}_{41}^{3} = 0.9924,\mathcal{J}_{41}^{4} = 1.0372,\mathcal{J}_{42}^{1} = 0.9888,\mathcal{J}_{42}^{2} = 0.8688,\mathcal{J}_{42}^{3} = 1.1030,\mathcal{J}_{42}^{4} = 1.0394,\mathcal{J}_{43}^{1} = 1.0141,\mathcal{J}_{43}^{2} = 0.9467,\mathcal{J}_{43}^{3} = 1.0616,\mathcal{J}_{43}^{4} = 0.9737, \hfill \\ \mathcal{J}_{44}^{1} = 1.0296,\mathcal{J}_{44}^{2} = 1.0010,\mathcal{J}_{44}^{3} = 1.0779,\mathcal{J}_{44}^{4} = 1.0337,\mathcal{J}_{45}^{1} = 1.0591,\mathcal{J}_{45}^{2} = 0.8589,\mathcal{J}_{45}^{3} = 1.1087,\mathcal{J}_{45}^{4} = 0.9733,\mathcal{J}_{46}^{1} = 1.0481,\mathcal{J}_{46}^{2} = 0.8061,\mathcal{J}_{46}^{3} = 1.0972,\mathcal{J}_{46}^{4} = 1.0486, \hfill \\ \mathcal{J}_{47}^{1} = 0.9654,\mathcal{J}_{47}^{2} = 0.9781,\mathcal{J}_{47}^{3} = 1.0532,\mathcal{J}_{47}^{4} = 1.0033,\mathcal{J}_{51}^{1} = 1.0239,\mathcal{J}_{51}^{2} = 0.8783,\mathcal{J}_{51}^{3} = 1.0719,\mathcal{J}_{51}^{4} = 1.0259,\mathcal{J}_{52}^{1} = 1.0308,\mathcal{J}_{52}^{2} = 1.0045,\mathcal{J}_{52}^{3} = 1.0109,\mathcal{J}_{52}^{4} = 0.9537, \hfill \\ \mathcal{J}_{53}^{1} = 1.0250,\mathcal{J}_{53}^{2} = 0.8779,\mathcal{J}_{53}^{3} = 1.0730,\mathcal{J}_{53}^{4} = 1.0200,\mathcal{J}_{54}^{1} = 0.9416,\mathcal{J}_{54}^{2} = 0.9155,\mathcal{J}_{54}^{3} = 0.9857,\mathcal{J}_{54}^{4} = 0.9454,\mathcal{J}_{55}^{1} = 1.0108,\mathcal{J}_{55}^{2} = 0.9828,\mathcal{J}_{55}^{3} = 1.0578,\mathcal{J}_{55}^{4} = 0.9486, \hfill \\ \mathcal{J}_{56}^{1} = 0.9706,\mathcal{J}_{56}^{2} = 1.0311,\mathcal{J}_{56}^{3} = 1.1102,\mathcal{J}_{56}^{4} = 0.8881,\mathcal{J}_{57}^{1} = 1.0250,\mathcal{J}_{57}^{2} = 0.9965,\mathcal{J}_{57}^{3} = 1.0707,\mathcal{J}_{57}^{4} = 0.9079,\mathcal{J}_{61}^{1} = 1.0064,\mathcal{J}_{61}^{2} = 0.9297,\mathcal{J}_{61}^{3} = 1.0535,\mathcal{J}_{61}^{4} = 1.0104, \hfill \\ \mathcal{J}_{62}^{1} = 1.0111,\mathcal{J}_{62}^{2} = 0.9171,\mathcal{J}_{62}^{3} = 1.0566,\mathcal{J}_{62}^{4} = 1.0151,\mathcal{J}_{63}^{1} = 1.0241,\mathcal{J}_{63}^{2} = 0.9978,\mathcal{J}_{63}^{3} = 0.9478,\mathcal{J}_{63}^{4} = 1.0263,\mathcal{J}_{64}^{1} = 1.0121,\mathcal{J}_{64}^{2} = 0.9840,\mathcal{J}_{64}^{3} = 1.0595,\mathcal{J}_{64}^{4} = 1.0162, \hfill \\ \mathcal{J}_{65}^{1} = 1.0618,\mathcal{J}_{65}^{2} = 0.9449,\mathcal{J}_{65}^{3} = 0.9272,\mathcal{J}_{65}^{4} = 1.0661,\mathcal{J}_{66}^{1} = 1.0107,\mathcal{J}_{66}^{2} = 0.9826,\mathcal{J}_{66}^{3} = 0.9920,\mathcal{J}_{66}^{4} = 1.0147,\mathcal{J}_{67}^{1} = 1.0199,\mathcal{J}_{67}^{2} = 1.0305,\mathcal{J}_{67}^{3} = 1.1052,\mathcal{J}_{67}^{4} = 0.8444. \hfill \\ \end{gathered} $$

Step 6 (b). Utilize formula (71) to compute the UGDOS which is give in Table 18 below.

Table 18 UGDOS matrix

Step 6(c). Utilize formula (72), to compute the T-SPF entropy measure of each attribute which is listed below.

$$ \overline{\overline{ENT}}_{1} = 0.7106,\overline{\overline{ENT}}_{2} = 0.7262,\overline{\overline{ENT}}_{3} = 0.7928,\overline{\overline{ENT}}_{4} = 0.6768,\overline{\overline{ENT}}_{5} = 0.6901,\overline{\overline{ENT}}_{6} = 0.7233,\overline{\overline{ENT}}_{7} = 0.7920. $$

Step 6 (d). Utilize formula (73), to compute the attributes weights which is listed below.

$$ {\mathbb{Z}}_{1} = 0.1390,{\mathbb{Z}}_{2} = 0.1421,{\mathbb{Z}}_{3} = 0.1551,{\mathbb{Z}}_{4} = 0.1324,{\mathbb{Z}}_{5} = 0.1350,{\mathbb{Z}}_{6} = 0.1415,{\mathbb{Z}}_{7} = 0.1549. $$

Step 7 (a). Utilize formula (74), and the weights of the attributes, to compute the weighted normalized decision matrices which are listed in Tables 19, 20, 21 and 22.

Table 19 Revised decision matrix $\overline{\overline{NWDM}}^{1}$

Table 20 Revised decision matrix $\overline{\overline{NWDM}}^{2}$

Table 21 Revised decision matrix $\overline{\overline{NWDM}}^{3}$

Table 22 Revised decision matrix $\overline{\overline{NWDM}}^{4}$

Step 7 (b). Utilize Formula (75), and NWD matrices, to calculate the POIM and NOIM which are listed in Tables 23 and 24.

Table 23 POI matrix

Table 24 NOI matrix

Step 8. Utilize formula (76), to calculate the distances of NWD matrices to POS and NOS which are listed in Tables 25 and 26.

Table 25 Distance from POIM

Table 26 Distance from NOIM

Step 9. Utilize formula (77), to compute the revised closeness indicators (RCIs) which is listed in Table 27.

Table 27 RCIs matrix

Step 10. Use formula (78), to determine the final CIs which is given below.

$$ '\!\gamma_{1} = 1.1623,'\!\gamma_{2} = 0.9008,'\!\gamma_{3} = 0.9596,'\!\gamma_{4} = 1.0902,'\!\gamma_{5} = 1.2465,'\!\gamma_{6} = 1.3701. $$

From the FRCIs values, the best is $'\!\gamma_{6}$, while the worst on is $'\!\gamma_{2}$.

TSPF TOPSIS approached based on TSPFAAPWGHM operators

In this part, we will utilize the same approach to solve the above example. In the above approach, the TSPF-TOPSIS is based on TSPFAAWPHM operators. Here, we will utilize TSPFAAWPGHM operator instead of TSPFAAWPHM operator. The same steps should be followed to solve the above MAGDM problem.

Steps 1 to 4 are the same.

Step 5 (a). The GDEIS should be calculated by taking the average of all the opinions of each individual DMs, since it is closer to the GDEIS than any one DM's opinions. Therefore, in this stage, instead of taking average of all opinions, we compute the GDEIS by using the T-SPFWPGHM values of alternatives that meet the criteria provided by DMs and considering the same weighting of the DM's values as follows which is listed in Table 28.

Table 28 GDEIS matrix

Step 5 (b). The GROD matrix and the GLOD matrix is given Tables 13 and 14 respectively.

Step 5 (c). Utilize formulas (65), (66) and (67) to compute the decision matrices distances from GDEIS, GROD, and GLOD. The distances are represented symbolically by the inscriptions DGDEIS, DGROD, and DGLOD and are listed in Tables 29, 30, and 31, respectively.

Table 29 DGDEIS matrix

Table 30 DGROD matrix

Table 31 DGLOD matrix

Step 5 (d). Utilize formula (68), to compute the CIs which is listed below.

$$ CI^{1} = 0.7307,CI^{2} = 0.7486,CI^{3} = 0.6904,CI^{4} = 0.7283. $$

Step 5 (e). Utilize formula (69), to determine the weights of DMs which are listed below.

$$ {\mathbb{W}}_{1} = 0.2521,{\mathbb{W}}_{2} = 0.2583,{\mathbb{W}}_{3} = 0.2382,{\mathbb{W}}_{4} = 0.2513. $$

Step 6 (a). Utilize formula (70), to generate the weight vector $\mathcal{J}_{i j}^{g}$ of power operator associated with the T^SPFN $'\!\gamma_{i j}^{g}$. Which are listed below:

$$ \begin{gathered} \mathcal{J}_{{11}}^{1} = 0.9295,\mathcal{J}_{{11}}^{2} = 1.0763,\mathcal{J}_{{11}}^{3} = 0.9471,\mathcal{J}_{{11}}^{4} = 1.0471,\mathcal{J}_{{12}}^{1} = 0.9696,\mathcal{J}_{{12}}^{2} = 1.0461,\mathcal{J}_{{12}}^{3} = 0.9656,\mathcal{J}_{{12}}^{4} = 1.0186,\mathcal{J}_{{13}}^{1} = 1.0458,\mathcal{J}_{{13}}^{2} = 1.0714,\mathcal{J}_{{13}}^{3} = 0.9766,\mathcal{J}_{{13}}^{4} = 0.9061, \hfill \\ \mathcal{J}_{{14}}^{1} = 1.0423,\mathcal{J}_{{14}}^{2} = 1.0678,\mathcal{J}_{{14}}^{3} = 0.8536,\mathcal{J}_{{14}}^{4} = 1.0362,\mathcal{J}_{{15}}^{1} = 1.0545,\mathcal{J}_{{15}}^{2} = 1.0803,\mathcal{J}_{{15}}^{3} = 0.8202,\mathcal{J}_{{15}}^{4} = 1.0450,\mathcal{J}_{{16}}^{1} = 1.0399,\mathcal{J}_{{16}}^{2} = 1.0631,\mathcal{J}_{{16}}^{3} = 0.9826,\mathcal{J}_{{16}}^{4} = 0.9144, \hfill \\ \mathcal{J}_{{17}}^{1} = 1.0861,\mathcal{J}_{{17}}^{2} = 1.1127,\mathcal{J}_{{17}}^{3} = 0.8352,\mathcal{J}_{{17}}^{4} = 0.9661,\mathcal{J}_{{21}}^{1} = 1.0213,\mathcal{J}_{{21}}^{2} = 1.0463,\mathcal{J}_{{21}}^{3} = 0.9650,\mathcal{J}_{{21}}^{4} = 0.9673,\mathcal{J}_{{22}}^{1} = 0.9198,\mathcal{J}_{{22}}^{2} = 1.0681,\mathcal{J}_{{22}}^{3} = 0.9851,\mathcal{J}_{{22}}^{4} = 1.0270, \hfill \\ \mathcal{J}_{{23}}^{1} = 1.0220,\mathcal{J}_{{23}}^{2} = 1.0470,\mathcal{J}_{{23}}^{3} = 0.9556,\mathcal{J}_{{23}}^{4} = 0.9753,\mathcal{J}_{{24}}^{1} = 1.0196,\mathcal{J}_{{24}}^{2} = 1.0445,\mathcal{J}_{{24}}^{3} = 0.9197,\mathcal{J}_{{24}}^{4} = 1.0162,\mathcal{J}_{{25}}^{1} = 1.0086,\mathcal{J}_{{25}}^{2} = 1.0332,\mathcal{J}_{{25}}^{3} = 0.9530,\mathcal{J}_{{25}}^{4} = 1.0052, \hfill \\ \mathcal{J}_{{26}}^{1} = 1.0581,\mathcal{J}_{{26}}^{2} = 1.0840,\mathcal{J}_{{26}}^{3} = 0.8706,\mathcal{J}_{{26}}^{4} = 0.9872,\mathcal{J}_{{27}}^{1} = 1.0209,\mathcal{J}_{{27}}^{2} = 1.0035,\mathcal{J}_{{27}}^{3} = 0.9581,\mathcal{J}_{{27}}^{4} = 1.0175,\mathcal{J}_{{31}}^{1} = 1.0245,\mathcal{J}_{{31}}^{2} = 1.0514,\mathcal{J}_{{31}}^{3} = 0.9697,\mathcal{J}_{{31}}^{4} = 0.9544, \hfill \\ \mathcal{J}_{{32}}^{1} = 1.0500,\mathcal{J}_{{32}}^{2} = 1.0855,\mathcal{J}_{{32}}^{3} = 0.8084,\mathcal{J}_{{32}}^{4} = 1.0561,\mathcal{J}_{{33}}^{1} = 1.0547,\mathcal{J}_{{33}}^{2} = 1.0012,\mathcal{J}_{{33}}^{3} = 0.9081,\mathcal{J}_{{33}}^{4} = 1.0360,\mathcal{J}_{{34}}^{1} = 0.9051,\mathcal{J}_{{34}}^{2} = 1.0699,\mathcal{J}_{{34}}^{3} = 0.9842,\mathcal{J}_{{34}}^{4} = 1.0409, \hfill \\ \mathcal{J}_{{35}}^{1} = 0.8877,\mathcal{J}_{{35}}^{2} = 1.0753,\mathcal{J}_{{35}}^{3} = 0.9909,\mathcal{J}_{{35}}^{4} = 1.0462,\mathcal{J}_{{36}}^{1} = 1.0251,\mathcal{J}_{{36}}^{2} = 1.0506,\mathcal{J}_{{36}}^{3} = 0.9689,\mathcal{J}_{{36}}^{4} = 0.9554,\mathcal{J}_{{37}}^{1} = 0.9877,\mathcal{J}_{{37}}^{2} = 1.0538,\mathcal{J}_{{37}}^{3} = 0.9333,\mathcal{J}_{{37}}^{4} = 1.0252, \hfill \\ \mathcal{J}_{{41}}^{1} = 0.9784,\mathcal{J}_{{41}}^{2} = 1.0718,\mathcal{J}_{{41}}^{3} = 0.9071,\mathcal{J}_{{41}}^{4} = 1.0428,\mathcal{J}_{{42}}^{1} = 1.0059,\mathcal{J}_{{42}}^{2} = 0.9314,\mathcal{J}_{{42}}^{3} = 1.0128,\mathcal{J}_{{42}}^{4} = 1.0498,\mathcal{J}_{{43}}^{1} = 1.029,\mathcal{J}_{{43}}^{2} = 1.0127,\mathcal{J}_{{43}}^{3} = 0.9727,\mathcal{J}_{{43}}^{4} = 0.9852, \hfill \\ \mathcal{J}_{{44}}^{1} = 1.0461,\mathcal{J}_{{44}}^{2} = 0.9789,\mathcal{J}_{{44}}^{3} = 0.9887,\mathcal{J}_{{44}}^{4} = 0.9863,\mathcal{J}_{{45}}^{1} = 1.0777,\mathcal{J}_{{45}}^{2} = 0.9209,\mathcal{J}_{{45}}^{3} = 1.0183,\mathcal{J}_{{45}}^{4} = 0.9831,\mathcal{J}_{{46}}^{1} = 1.0671,\mathcal{J}_{{46}}^{2} = 0.8648,\mathcal{J}_{{46}}^{3} = 1.0083,\mathcal{J}_{{46}}^{4} = 1.0599, \hfill \\ \mathcal{J}_{{47}}^{1} = 0.9794,\mathcal{J}_{{47}}^{2} = 1.0457,\mathcal{J}_{{47}}^{3} = 0.9644,\mathcal{J}_{{47}}^{4} = 1.0105,\mathcal{J}_{{51}}^{1} = 1.0408,\mathcal{J}_{{51}}^{2} = 0.9407,\mathcal{J}_{{51}}^{3} = 0.9834,\mathcal{J}_{{51}}^{4} = 1.0351,\mathcal{J}_{{52}}^{1} = 1.0443,\mathcal{J}_{{52}}^{2} = 1.0722,\mathcal{J}_{{52}}^{3} = 0.9243,\mathcal{J}_{{52}}^{4} = 0.9591, \hfill \\ \mathcal{J}_{{53}}^{1} = 1.0419,\mathcal{J}_{{53}}^{2} = 0.9403,\mathcal{J}_{{53}}^{3} = 0.9844,\mathcal{J}_{{53}}^{4} = 1.0334,\mathcal{J}_{{54}}^{1} = 0.9543,\mathcal{J}_{{54}}^{2} = 1.0703,\mathcal{J}_{{54}}^{3} = 0.9338,\mathcal{J}_{{54}}^{4} = 1.0416,\mathcal{J}_{{55}}^{1} = 1.0255,\mathcal{J}_{{55}}^{2} = 1.0506,\mathcal{J}_{{55}}^{3} = 0.9686,\mathcal{J}_{{55}}^{4} = 0.9554, \hfill \\ \mathcal{J}_{{56}}^{1} = 0.9852,\mathcal{J}_{{56}}^{2} = 1.1028,\mathcal{J}_{{56}}^{3} = 1.0171,\mathcal{J}_{{56}}^{4} = 0.8949,\mathcal{J}_{{57}}^{1} = 1.0399,\mathcal{J}_{{56}}^{2} = 1.0653,\mathcal{J}_{{56}}^{3} = 0.9804,\mathcal{J}_{{56}}^{4} = 0.9144,\mathcal{J}_{{61}}^{1} = 1.0217,\mathcal{J}_{{61}}^{2} = 0.9946,\mathcal{J}_{{61}}^{3} = 0.9654,\mathcal{J}_{{61}}^{4} = 1.0183, \hfill \\ \mathcal{J}_{{62}}^{1} = 1.0268,\mathcal{J}_{{62}}^{2} = 0.9814,\mathcal{J}_{{62}}^{3} = 0.9685,\mathcal{J}_{{62}}^{4} = 1.0234,\mathcal{J}_{{63}}^{1} = 1.0367,\mathcal{J}_{{63}}^{2} = 1.0637,\mathcal{J}_{{63}}^{3} = 0.8655,\mathcal{J}_{{63}}^{4} = 1.0348,\mathcal{J}_{{64}}^{1} = 1.0251,\mathcal{J}_{{64}}^{2} = 1.0501,\mathcal{J}_{{64}}^{3} = 0.9031,\mathcal{J}_{{64}}^{4} = 1.0217, \hfill \\ \mathcal{J}_{{65}}^{1} = 1.0746,\mathcal{J}_{{65}}^{2} = 1.0076,\mathcal{J}_{{65}}^{3} = 0.8469,\mathcal{J}_{{65}}^{4} = 1.0710,\mathcal{J}_{{66}}^{1} = 1.0238,\mathcal{J}_{{66}}^{2} = 1.0488,\mathcal{J}_{{66}}^{3} = 0.9070,\mathcal{J}_{{66}}^{4} = 1.0204,\mathcal{J}_{{67}}^{1} = 1.0350,\mathcal{J}_{{67}}^{2} = 1.1019,\mathcal{J}_{{67}}^{3} = 1.0124,\mathcal{J}_{{67}}^{4} = 0.8507. \hfill \\ \end{gathered} $$

Step 6 (b). Utilize TSPAAWPGHM operators, with the TSPF entropy measure, to compute the UGDOS which is listed in Table 32.

Table 32 UGDOS matrix

Step 6(c). Utilize formula (72), to compute the T-SPF entropy measure of each attribute which is listed below.

$$ \overline{\overline{ENT}}_{1} = 0.5500,\overline{\overline{ENT}}_{2} = 0.5833,\overline{\overline{ENT}}_{3} = 0.5804,\overline{\overline{ENT}}_{4} = 0.4481,\overline{\overline{ENT}}_{5} = 0.4176,\overline{\overline{ENT}}_{6} = 0.4374,\overline{\overline{ENT}}_{7} = 0.6461. $$

Step 6 (d). Utilize formula (73), to compute the attributes weights which is listed below.

$$ {\mathbb{Z}}_{1} = 0.1501,{\mathbb{Z}}_{2} = 0.1592,{\mathbb{Z}}_{3} = 0.1584,{\mathbb{Z}}_{4} = 0.1223,{\mathbb{Z}}_{5} = 0.1140,{\mathbb{Z}}_{6} = 0.1194,{\mathbb{Z}}_{7} = 0.1764. $$

Step 7 (a). Utilize formula (74), and the weights of the attributes, to compute the weighted normalized decision matrices which are listed in Tables 33,34, 35 and 36.

Table 33 Revised decision matrix ${\mathbb{M}}^{1}$

Table 34 Revised decision matrix ${\mathbb{M}}^{2}$

Table 35 Revised decision matrix ${\mathbb{M}}^{3}$

Table 36 Revised decision matrix ${\mathbb{M}}^{4}$

Step 7 (b). Utilize Formula (75), and NWD matrices, to calculate the POIM and NOIM which are listed in Tables 37 and 38.

Table 37 POI matrix

Table 38 NOI matrix

Step 8. Utilize formula (76), to calculate the distances of NWD matrices to POS and NOS which are listed in Tables 39 and 40.

Table 39 Distance from POIM

Table 40 Distance from NOIM

Step 9. Utilize formula (77), to compute the revised closeness indicators (RCIs) which is listed in Table 41.

Table 41 RCIs matrix

Step 10. Use formula (78), to determine the final CIs which is given below.

$$ '\!\gamma_{1} = 1.4544,'\!\gamma_{2} = 1.2937,'\!\gamma_{3} = 1.4370,'\!\gamma_{4} = 1.0902,'\!\gamma_{5} = 1.5967,'\!\gamma_{6} = 1.7882. $$

From the FRCIs values, the best is $'\!\gamma_{6}$, while the worst on is $'\!\gamma_{2}$.

Effect of the parameters $N$,$Q,{\mathbb{R}}$ and $q$ on final ranking results

In this part, effect of different values of the parameters $N$,$Q,{\mathbb{R}}$ and $q$ are investigated utilizing TSPFAAWPHM/TSPFAAWPGHM operators.

Effect of the parameter $N$ on final ranking results

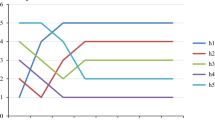
In this subpart, effect of the parameter $N$ is investigated utilizing T^SPFAAWPHM/T^SPFPAAWPGHM operators, while the values of the parameter ${\mathbb{Q}},{\mathbb{R}}$ and $q$ are fixed. That is $\left( {q = 3,\,\,{\mathbb{Q}} = 2,\,\,\,{\mathbb{R}} = 3} \right)$ and the alternatives/choices are, respectively, represented by $'\!\gamma_{1} =_{1}$,$'\!\gamma_{2} =_{2}$,$'\!\gamma_{3} =_{3}$,$'\!\gamma_{4} =_{4}$,$'\!\gamma_{5} =_{5}$ and $'\!\gamma_{6} =_{6}$ in the below figures.

From Fig. 3, one can see that the score values obtained for different values of the parameter $N$ while utilizing T^SPFAAWPHM operators are different, but the ranking order remain the same. That is the best alternative is Ђ₆ while the worst on is Ђ₂. Similarly, from Fig. 4, one can observe that the score values obtained for different values of the parameter $N$ while utilizing T^SPFAAWPGHM operators are different, but the ranking order remain the same. That is the best alternative is Ђ₆ while the worst on is Ђ₃. One can also noticed that when the values of the parameter $N$ increases the score values decreases while utilizing T^SPFAAWPHM/T^SPFPAAWPGHM operators.

Fig. 3

Effect of parameter N on final ranking results utilizing TSPFAAWPHM operator

Fig. 4

Effect of the parameter N on final ranking results utilizing TSPFAAWPGHM operator

Effect of the parameter $q$ on final ranking results

In this subpart, effect of the parameter $q$ is investigated utilizing T^SPFAAWPHM/T^SPFPAAWPGHM operators, while the values of the parameter ${\mathbb{Q}}\ominus \,,{\mathbb{R}}$ and $N$ are fixed. That is $\left( {N = 3,\,\,{\mathbb{Q}} = 2,\,\,\,{\mathbb{R}} = 3} \right)$.

From Fig. 5, one can see that the score values obtained for different values of the parameter $q$ while utilizing T^SPFAAWPHM operators are different, but the ranking order remain the same. That is the best alternative is Ђ₆ while the worst on is Ђ₂. Similarly, from Fig. 6, one can observe that the score values obtained for different values of the parameter $q$ while utilizing T^SPFAAWPGHM operators are different, and the ranking orders are also different. That is the best alternative is Ђ₆ while the worst on is Ђ₃ when the value of the parameter $q = 4$. When the values of the parameter $q = 7$ and greater than 7 the worst alternative becomes Ђ₂, while the best on remain the same. One can also notice that when the values of the parameter $N$ increases, the score values decreases while utilizing T^SPFAAWPHM/T^SPFPAAWPGHM operators.

Fig. 5

Effect of the parameter q on final ranking result utilizing TSPAAWPHM operators

Fig. 6

Effect of the parameter q on final ranking results utilizing TSPFAAWPGHM operator

Effect of the parameter $Q,{\mathbb{R}}$ on final ranking results

In this subpart, the effect of the parameters $Q,{\mathbb{R}}$ are investigated utilizing T^SPFAAWPHM/T^SPFPAAWPGHM operators, while the values of the parameter $q$ and $N$ are fixed. That is $\left( {N = 3,\,\,q = 3} \right)$.

From Fig. 7, one can see that the score values obtained for different values of the parameters ${\mathbb{Q}}\,,{\mathbb{R}}$ while utilizing T^SPFAAWPHM operators are different, but the ranking order remain the same. That is the best alternative is Ђ₆ while the worst on is Ђ₂. Similarly, from Fig. 8, one can observe that the score values obtained for different values of the parameter $Q,{\mathbb{R}}$ while utilizing T^SPFAAWPGHM operators are different, but the ranking order remain the same. That is the best alternative is Ђ₆ while the worst on is Ђ₃. One can also noticed that when the values of the parameters $Q,{\mathbb{R}}$ increases the score values increases while utilizing T^SPFAAWPHM/T^SPFPAAWPGHM operators.

Fig. 7

Effect of the parameters Q, R on final ranking results utilizing TSPFAAWPHM operators

Fig. 8

Effect of the parameters Q, R on final ranking results utilizing TSPFAAWPGHM operators

This makes the developed TOPSIS method more flexible. Since the existing TOPSIS methods for different fuzzy structure is mainly based on weighted/geometric averaging operators. But the developed TOPSIS method is based on T^SPFAAWPHM/T^SPFAAWGHM operator, which have the capability of taking interrelationship among input arguments and also vanish the influence unreliable data from the final ranking results. Hence, the proposed TOPSIS method is more reasonable to be utilized to solve more complex MAGDM problems.

Comparison of the proposed TOPSIS method with existing approaches

In this subpart, the proposed approach is compared with different approaches.

As from Fig. 9, one can see that utilizing the TSPFAAWA/TSPFAAWG [34] operators the best alternative is Ђ₆ while the worst on is Ђ₂ and Ђ₃. Similarly, Figure 9 shows that when the TSPFEWA/TSPFEWG [31] operators are utilized the best alternative is Ђ₆ while the worst on is Ђ₂ and Ђ₆, and when SPF TOPSIS [23] method is utilized the best alternative is Ђ₅ while the worst on is Ђ₃. The ranking order obtained from the TSPFAAWA/TSPFAAWG [34] and TSPFEWA/TSPFEWG [31] are the same as obtained from developed approach but the ranking order obtained from SPF TOPSIS method [23] is different from the proposed approach, although the worst alternative is the same. The main reason behind this different ranking order is that the developed TOPSIS approach is based on TSPAAWPHM/TSPAAWPGHM operators while the SPF TOPSIS approach is simply based on SPWA operators. The developed TSPF TOPSIS method has some advantages over the existing approaches. The developed T^SPF TOPSIS approach is based TSPFAAWPHM/TSPFAAWPGHM operators, which consist of four parameters, remove the effect of unreliable data and can consider the interrelationship among input arguments. Due to these characteristics, the developed approach is more flexible and can be utilized to solve more complex MADM/MAGDM problems.

Fig. 9

Comparison of the proposed approach with different approaches

Advantages and disadvantages of the developed approach

In this subpart, advantages and disadvantages of the developed approaches are investigated.

The initiated MAGDM approach-based TSPF TOPSIS methods have some advantages over the existing approaches. Firstly, the initiated T^SPF TOPSIS method is based T^SPFAAWPHM/T^SPFAAWPGHM operators. The, T^SPFAAWPHM/T^SPFAAWPGHM is hybrid structure, that is T^SPFAAWPHM/T^SPFAAWPGHM operators are combination of PA/PG operator and HM/GHM operator. The T^SPFAAWPHM/T^SPFAAWPGHM operators have both the characteristics PA/PG and HM/GHM operators. Secondly, these aggregation operators are initiated utilizing Aczel–Alsina operational laws, which consist of generalized parameter. Thirdly, some of the existing aggregation operators are obtained by giving specific values to the parameters. The disadvantage of the initiated aggregation operators is that it can consider the interrelationship among any two input arguments and unable to consider the interrelationship among any number of input arguments. Due to above-defined characteristics, the developed approach is more flexible and can be utilized to solve more complex MADM/MAGDM problems.

Conclusion

One of the key indicators for pharmaceutical companies to prove their fundamental competence against the backdrop of green economic growth is their capacity for sustainable and high-quality development. When creating growth strategies and correcting pharmaceutical companies, pharmaceutical management departments may benefit greatly from using the evaluation of pharmaceutical companies from a standpoint of sustainable and high-quality development. In this article, some novel T^SPF power Heronian mean operators are initiated based on Aczel–Alsina operational laws such as TSPFAAPHM and TSPFAAGHM operators. Some core properties and special cases with respect to generalized parameters are also investigated and found that some of the existing aggregation operators are special cases of it. The weighted forms of the said aggregation operators are also developed. As these aggregation operators have the capability of removing the effect of awkward data and can consider the interrelationship among any two input arguments at the same time. Further, based on these aggregation operators and Aczel–Alsina operational laws a newly advanced TOPSIS-based method for dealing with MAGDM problems in a T-Spherical fuzzy framework is established, where the weights of both the DMs and the criteria are completely unknowable. Finally, an illustrative example is provided to evaluate and choose the pharmaceutical firms with the capacity for high-quality, sustainable development in the T^SPF environment to show the effectiveness and practicality. Following that, the comparison analysis with existing methods is used to support the suggested method's coherence and supremacy.

In future, we will try to extend the proposed aggregation operators to some advanced fuzzy structure such as, Py m-polar FS [2], complex IFS [11], linguistic IFS [38], q-rung orthopair fuzzy soft sets [40] and apply them to solve MADM/MAGDM problems in different fields.