Introduction

Mobile robots are increasingly being utilized in various engineering systems across a wide range of fields. These include industries, such as agriculture, forestry, mining, and healthcare, as well as applications in search and rescue, rehabilitation, and even entertainment. They are particularly useful in dangerous and remote locations where human intervention may be difficult or impossible. Therefore, the modeling and controlling of these MRs have been the focus of many researchers, in the past few decades. Wheeled mobile robots (MRs) are an example of systems that are subject to nonholonomic constraints due to the contact of their wheels with the ground. These constraints arise from the fact that the wheels can only move forward or backward without slipping in the direction of motion, limiting the robot’s ability to change direction or position in a smooth and unconstrained way. Numerous control concerns have been taken into consideration in the realm of motion control of these systems for the automated operation of wheeled robots. These problems include time-varying path following, stability around desirable scenarios, and path following [1,2,3].

In the last few decades, extensive research has been conducted in the field of mobile robot control and many studies have been reported in this regard. It can be said that a major part of this research has focused on the problem of tracking the path by the robot in the presence of uncertainties. There are many problems in implementing model-based controllers on real systems such as robots. One of the most important reasons is the inability to accurately model real systems. Furthermore, even in a few case studies, if this capability exists, the resulting model is so complex that makes controller design difficult. Inaccuracy in modeling is caused by two primary sources: 1—uncertainty in model parameters and 2—unmodeled dynamics. A considerable number of standard control methods to deal with these uncertainties are seen in the literature [4]. Many of the methods that were originally proposed for the control of the MRs, without considering the dynamics of the robot, were designed for the tracking control problem using only the kinematic mode of the robot [5]. Backstepping is one of the most commonly employed stabilizing control methods for kinematic control [6]. The sliding-mode controller (SMC) is another method that is widely employed for the control of MRs [7, 8]. Designing this controller is simple and it results in a relatively good response, but this controller has some problems such as control input chattering. The chattering issue of SMC is investigated in [9], and a self-organizing approach is suggested. By experimental studies on a robot, it is shown that the suggested controller is applicable, and the chattering is decreased. In [10], an adaptive controller is suggested, and an event-triggered scheme is developed for patrolling MRs. In [11], the slip effects are taken into account, and a mathematical model is developed for MRs in the presence of the slip effect. The stability of MR in the designed path is investigated using the Lyapunov approach. In [12], the aperiodic sampling is studied, and a cooperative controller is designed. A simple observer is also designed to estimate the disturbances.

Adaptive control and robust control are two important and complementary methods that have been proposed to overcome uncertainties and perturbations [13]. Adaptive control can adequately address this issue by adapting to the changing dynamics and canceling the effect from uncertainties and disturbances in a systematic manner, as suggested in [14, 15]. One of the simplest approaches in robust controller design is SMC. The high frequency of the control signal causes activation of unmodeled dynamics of MR. In addition to the difficulty of implementation, vibration caused by control signal fluctuations causes damage to mechanical parts. To solve the issues of traditional controllers, some intelligent neuro-fuzzy controllers have been studied. For instance, in [16], an FLS-based controller is developed, and it is tested on a surgery robot. Similarly, an SMC is developed in [17] using FLSs, and a Kalman filter is suggested for learning FLS. Finally, the effectiveness of the developed FLSs is evaluated by applying them to a 6-DOF robot. In [18], a fractional controller is suggested for MRs, and FLS is employed to handle the effect of disturbances. In [19], the terminal SMC is studied for MRs, and FLS is utilized for the estimation of uncertainties in MR dynamics. In some simulations, the validity of the controller is examined. The chattering problem of SMC is studied in [20] using FLSs, and by implementing it on a robot, the better accuracy of FLS-based SMC is demonstrated. In [21], mooring is developed, and FLS are used to dampen the undesired forces. In various sea conditions, the designed controller is examined, and the effectiveness of FLSs is shown. The effect of the overturning angle is studied in [22], and the feasibility of the controller is demonstrated using an eight-wheeled prototype. Also, it is verified that FLSs are effective in accuracy improvement. In [23], an FLS-based controller is suggested for navigation of MRs, and by Kinect sensors, the effectiveness is examined on an experimental setup.

One of the important applications of MR is to follow a path, in a secure scheme. Many approaches have been suggested for secure path planning. One of the fundamental approaches is chaotic systems. The main foundation of chaos theory is the idea that order and chaos are not always opposites. The fusion of order and chaos in chaotic systems is remarkable. Although these systems appear chaotic and operate in an unpredictable manner when viewed from the outside, they really include a set of deterministic equations that function with the order. Chaos is a name that is often applied to a non-linear dynamic. This expression is used to explain the complex behavior of the so-called simple, linear, and well-behaved systems. Chaotic behavior appears irregular and often random, similar to the behavior of a system strongly affected by random external noise. Chaos is described mathematically as the long-term, unexpected behavior of a deterministic dynamical system that is sensitive to the beginning circumstances [24]. Chaos theory is the in-depth analysis of unstable periodic behavior in deterministic non-linear dynamical systems. The origins of chaos theory go back to Henry Poincaré, who tried to solve an unsolved problem of Newtonian Laplacian celestial mechanics (the three-body problem). Poincaré realized that it is possible for there to be orbits that are acyclic and are not constantly increasing or converging to a fixed point. During this research, Poincaré realized that in non-linear systems, there may be infinitely complex behavior. Chaos theory has fascinated scientists and engineers for two reasons: (1) Chaos theory provides theoretical and empirical tools to categorize and understand complex behavior in which other theories fail. (2) Chaos is universal; that is, it is used in mechanical oscillators, electrical circuits, chemical reactions, optical systems, nerve cells, lasers, etc. Universality means that what we learn from studying the chaotic behavior of a mechanical oscillator, we can quickly apply it to understand the chaotic behavior of other systems. The chaos theory in MR has been studied in a few papers. For example, in [25], Hénon chaotic map is used for generating paths for MRs, and it is evaluated using multi-robots. In [26], the chaos theory is combined with the ant colony algorithm to design a path for MRs. The control of MR in a chaotic path is studied in [27]. In [28], a chaotic map is designed for vacuum cleaning MRs, and it is shown that by the chaotic path, the number of collisions and motion commands is decreased while covering the working space more effectively. In [29], the robot’s chaotic beginning state parameters and initial coordinates are used to generate the moving route points. The mobile space of the robot meshes, and the dynamic mesh activity value is computed in accordance with the excitation, taking into account the local optimum path planning solution. The mobile route planning is divided using the mesh activity, and the local path and angular displacement changes are then determined. To correct the planning outcomes, the relevant index assessment is also created for local path planning. The secure communication system for MR is studied in [30]. The transmission of images between MRs is encrypted by chaotic systems. In [31], a random bit generator is initially created using the dynamic equations of two straightforward chaotic systems. Autonomous robots use this as a source to develop a set of navigational instructions that it uses to explore space while maintaining unexpected and random mobility. This navigational method covers a large region, but it also results in many trips back to earlier cells. In this paper, a memory approach is used to restrict the robot’s chaotic navigation that has received the fewest visits, improving performance all around. In [32], a coupled-oscillator particle model is examined with an emphasis on the special scenario of agents forming symmetric clusters while traveling in a circular motion. The findings in this paper show that some areas of the parameter are conducive to the emergence of these clusters. In [33], the real output trajectory-tracking performance of an MR is improved using an intelligent controller and offline and online tuning back-propagation methods. The objectives of this approach are to construct a trajectory-tracking controller and identify the best path to direct the movement of the non-linear kinematics MR system. Since the route should prevent colliding with barriers and must have the shortest possible length, a chaotic-based swarm optimization technique is employed to solve these two challenges of path design.

More recently, type-3 FLSs have been introduced in a wide range of practical problems, such as forecasting [34], industrial controllers [35], chaotic financial system [36], robotic applications [27], optimization [37], among many others. However, the stable fractional-order T3-FLS-based controllers with stable learning schemes have not been studied. Regarding the literature review, the research gap is summarized as:

  • In most studies, the suggested approach can be applied just to a specific robot task.

  • The complicated path for secure applications has been quite rarely studied. In most studies, the simple path is considered for tracking.

  • The robot dynamics are derived with simplifications on nonholonomic constraints and lack of kinetodynamics considerations of the robot.

  • There is little known about the type-3 FLS-based controllers for MRs that can potentially yield better performance.

  • The stability under complicated references and perturbations is neglected in most of the above-investigated studies.

  • A few of the studies in the literature have incorporated the experimental tests of the proposed control scheme.

Regarding the above discussion, the main motivation is to design a new predictive control scheme using T3-FLSs and fractional-order calculus with a stable learning scheme, such that the controller to be applicable in real-world environments. The main contributions are as follows:

  • A new fractional-order fuzzy predictive controller with an online stable learning scheme is introduced.

  • Type-3 FLSs are used for online estimation and prediction.

  • A new strong secure path planning scheme is introduced for MRs.

  • The feasibility of the suggested controller is examined by a real-world setup.

  • The robustness is analyzed under unknown dynamics of MR, chaotic reference, and sudden changes of path based on a chaotic scheme.

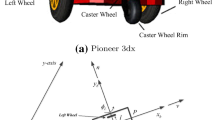
System description

Kinematic model

The linear and angular velocities are given as

$$\begin{aligned} \begin{array}{ll} {v = r\left( {{{{{\dot{\theta }}} }_r} + {{{{\dot{\theta }}} }_l}} \right) /2}\\ {w = r\left( {{{{{\dot{\theta }}} }_r} - {{{{\dot{\theta }}} }_l}} \right) /2l}, \end{array} \end{aligned}$$
(1)

where r/l denotes the radius/distance of wheels. Then, it can be written

$$\begin{aligned} \left[ {\begin{array}{ll} {\dot{x}}\\ {\dot{y}}\\ {{{\dot{\varphi }}} } \end{array}} \right] = \left[ {\begin{array}{ll} {\frac{r}{2}}&{}\quad {\frac{r}{2}}\\ 0&{}\quad 0\\ {\frac{r}{{2l}}}&{}\quad { - \frac{r}{{2l}}} \end{array}} \right] \left[ {\begin{array}{ll} {{{{{\dot{\theta }}} }_r}}\\ {{{{{\dot{\theta }}} }_l}} \end{array}} \right] . \end{aligned}$$
(2)

In (X,Y) coordination, it can be written

$$\begin{aligned} \left[ {\begin{array}{ll} {\dot{X}}\\ {\dot{Y}}\\ {{{\dot{\varphi }}} } \end{array}} \right] = \left[ {\begin{array}{ll} {\frac{r}{2}\cos \left( \varphi \right) }&{}\quad {\frac{r}{2}\cos \left( \varphi \right) }\\ {\frac{r}{2}\sin \left( \varphi \right) }&{}\quad {\frac{r}{2}\sin \left( \varphi \right) }\\ {\frac{r}{{2l}}}&{}\quad { - \frac{r}{{2l}}} \end{array}} \right] \left[ {\begin{array}{ll} {{{{{\dot{\theta }}} }_R}}\\ {{{{{\dot{\theta }}} }_L}} \end{array}} \right] . \end{aligned}$$
(3)

Dynamic model

The general dynamics of MRs are written as

$$\begin{aligned}{} & {} {\Psi \left( \xi \right) \ddot{\xi }+ V\left( {\xi ,{{\dot{\xi }}} } \right) {{\dot{\xi }}} + G\left( \xi \right) + {\tau _d} }\nonumber \\{} & {} \quad ={B\left( \xi \right) \tau - {A^T}\varsigma }, \end{aligned}$$
(4)

where \(\Psi \) and V are inertia and Coriolis matrices. G denotes the gravitational effects. \(\tau _d\) is disturbance. B is a constant matrix. \(\tau \) and \(\varsigma \) are kinematic terms and Lagrange vector. \(\xi \), \({{\dot{\xi }}}\), and \(\ddot{\xi }\) are position, velocity, and acceleration. From \(G=0\), we write

$$\begin{aligned}{} & {} \Psi \left( \xi \right) = \left[ {\begin{array}{lllll} m&{}\quad 0&{}\quad { - md\sin \left( \varphi \right) }&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad {md\cos \left( \varphi \right) }&{}\quad 0&{}\quad 0\\ { - md\sin \left( \varphi \right) }&{}\quad {md\cos \left( \varphi \right) }&{}\quad I&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad {{I_w}}&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad {{I_w}} \end{array}} \right] \nonumber \\ \end{aligned}$$
(5)
$$\begin{aligned}{} & {} V\left( \xi \right) = \left[ {\begin{array}{lllll} 0&{}\quad { - md{{\dot{\varphi }}} \cos \left( \varphi \right) }&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad { - md{{\dot{\varphi }}} \sin \left( \varphi \right) }&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0 \end{array}} \right] \end{aligned}$$
(6)
$$\begin{aligned}{} & {} {A^T} = \left[ {\begin{array}{lll} { - \sin \left( \varphi \right) }&{}\quad {\cos \left( \varphi \right) }&{}\quad {\cos \left( \varphi \right) }\\ {\cos \left( \varphi \right) }&{}\quad {\sin \left( \varphi \right) }&{}\quad {\sin \left( \varphi \right) }\\ { - d}&{}\quad l&{}\quad { - l}\\ 0&{}\quad { - r}&{}\quad 0\\ 0&{}\quad 0&{}\quad { - r} \end{array}} \right] . \end{aligned}$$
(7)

Considering a transformation Z, such that \({{\dot{\xi }}} = Z\left( \xi \right) \eta \), \(\eta = {\left[ {\begin{array}{ll} {{{\dot{\theta }}_r}}&{{{{{\dot{\theta }}} }_l}} \end{array}} \right] ^T}\), \(\ddot{\xi }= \dot{Z}\left( \xi \right) \eta + Z\left( \xi \right) {{\dot{\eta }}} \), and \({Z^T}{A^T} = 0\), we obtain

$$\begin{aligned}{} & {} \left[ {\begin{array}{ll} {\dot{x}}\\ {\dot{y}}\\ {{{\dot{\varphi }}} }\\ {{{{{\dot{\theta }}} }_r}}\\ {{{{{\dot{\theta }}} }_l}} \end{array}} \right] = \left[ {\begin{array}{ll} {\frac{r}{2}\cos \left( \varphi \right) }&{}\quad {\frac{r}{2}\cos \left( \varphi \right) }\\ {\frac{r}{2}\sin \left( \varphi \right) }&{}\quad {\frac{r}{2}\sin \left( \varphi \right) }\\ {\frac{r}{{2l}}}&{}\quad { - \frac{r}{{2l}}}\\ 1&{}\quad 0\\ 0&{}\quad 1 \end{array}} \right] \left[ {\begin{array}{ll} {{{{{\dot{\theta }}} }_r}}\\ {{{{{\dot{\theta }}} }_l}} \end{array}} \right] \end{aligned}$$
(8)
$$\begin{aligned}{} & {} {\Psi \left( \xi \right) \left( {\dot{Z}\left( \xi \right) \eta + Z\left( \xi \right) {{\dot{\eta }}} } \right) + V\left( {\xi ,{{\dot{\xi }}} } \right) Z\left( \xi \right) }\nonumber \\{} & {} \quad =B\left( \xi \right) \tau - {A^T}\varsigma . \end{aligned}$$
(9)

From (9), we have

$$\begin{aligned} {{\bar{\Psi }}} \left( \xi \right) {{\dot{\eta }}} + {{\bar{V}}}\left( {\xi ,\dot{\xi }} \right) \eta = {{\bar{B}}}\left( \xi \right) \tau , \end{aligned}$$
(10)

where

$$\begin{aligned}{} & {} {{{\bar{\Psi }}} \left( \xi \right) }\nonumber \\{} & {} \quad {=\left[ {\begin{array}{ll} {\frac{{{r^2}}}{{4{l^2}}}\left( {m{l^2} + I} \right) + {I_w}}&{}\quad {\frac{{{r^2}}}{{4{l^2}}}\left( {m{l^2} - I} \right) }\\ {\frac{{{r^2}}}{{4{l^2}}}\left( {m{l^2} - I} \right) }&{}\quad {\frac{{{r^2}}}{{4{l^2}}}\left( {m{l^2} + I} \right) + {I_w}} \end{array}} \right] } \end{aligned}$$
(11)
$$\begin{aligned}{} & {} {{{\bar{V}}}\left( \xi \right) } = {\left[ {\begin{array}{ll} 0&{}\quad {\frac{{{m_c}d{{\dot{\varphi }}} {r^2}}}{{2{l^2}}}}\\ { - \frac{{{m_c}d{{\dot{\varphi }}} {r^2}}}{{2{l^2}}}}&{}\quad 0 \end{array}} \right] } \end{aligned}$$
(12)
$$\begin{aligned}{} & {} {{\bar{B}}}\left( \xi \right) = \left[ {\begin{array}{ll} 1&{}\quad 0\\ 0&{}\quad 1 \end{array}} \right] \end{aligned}$$
(13)
$$\begin{aligned}{} & {} \begin{array}{ll} {m = {m_c} + 2{m_w}}\\ {I = {I_c} + {m_c}{d^2} + 2{m_w}{l^2} + 2{I_m}}. \end{array} \end{aligned}$$
(14)

The linear/angular velocities from (4) and (10) are written as

$$\begin{aligned}{} & {} {\left[ {\begin{array}{ll} {\frac{{2{I_w}}}{{{r^2}}} + m}&{}\quad 0\\ 0&{}\quad {\frac{{2{I_w}}}{{{r^2}}} + m} \end{array}} \right] \left( {\begin{array}{ll} {\dot{v}}\\ {\dot{w}} \end{array}} \right) }\nonumber \\{} & {} \quad + {\left[ {\begin{array}{ll} 0&{}\quad { - {m_c}dw}\\ {{m_c}dw}&{}\quad 0 \end{array}} \right] \left( {\begin{array}{ll} v\\ w \end{array}} \right) = \left[ {\begin{array}{ll} {\frac{1}{r}}&{}\quad 0\\ 0&{}\quad {\frac{1}{r}} \end{array}} \right] \left( {\begin{array}{ll} {{u_v}}\\ {{u_w}} \end{array}} \right) }.\nonumber \\ \end{aligned}$$
(15)

Multi-switching path

The path of MR is planned by the M chaotic systems

$$\begin{aligned} \begin{array}{ll} {{\textrm{Master }}\,{\textrm{system}}\# 1:\,\,\,{{{{\dot{\zeta }}} }_1} = {F_1}\left( {{\zeta _1}} \right) }\\ {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \vdots }\\ {{\textrm{Master }}\,{\textrm{system}}\# 1:{{{{\dot{\zeta }}} }_m} = {F_m}\left( {{\zeta _m}} \right) }. \end{array} \end{aligned}$$
(16)

The controller u should be designed, such that the error (17) is approached zero

$$\begin{aligned} \left\{ \begin{array}{l} Mode\# 1:\,\,\,\,\,\,\,{e_1}(t) = {\zeta _1}(t) - \xi (t)\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \vdots \\ Mode\# m:{e_m}(t) = {\zeta _m}(t) - \xi (t), \end{array} \right. \end{aligned}$$
(17)

where \(\xi \) denotes robot x-axis position. The switching scheme is given in Fig. 1. The key idea is that the switching is also managed by a chaotic system.

Fig. 1
figure 1

Switching modes

Full size image

It should be noted that the reference path is generated using some chaotic signals. In other words, the reference path is switched between some chaotic signals. To enhance the security of the path, the switching mechanism is also controlled by a chaotic signal. The idea is that the time switching is constant, but the target of switching is determined by a chaotic signal. For example, suppose that we have five chaotic signals. The first signal is used for the switching mechanism, and four others are used for path generation. The switching period is constant, and suppose it is 5 s. Therefore, after every 5 s, the value of the first signal determines which of the four chaotic signals should be used to generate the path. For example, if the value of the first signal is between a and b, the reference is switched to signal 3; if it is between b and c, the reference is switched to signal 2, and so on.

General view

A general view of the schemed controller is depicted in Fig. 2.

Fig. 2
figure 2

Control scheme

Full size image

For the described MR, a T3-FLS-based model estimator is suggested

$$\begin{aligned} D_t^q{{\hat{\xi }}} (t) = f\left[ {{X_f}(t),{\vartheta _f}(t)} \right] + u(t)/U, \end{aligned}$$
(18)

where \({{{\hat{\xi }}}}\) is the estimation of \({ \xi }\), \(f\left[ {X_f(t),\vartheta _f (t)} \right] \) represents a T3-FLS, \({{\vartheta _f}}\) denotes a vector that includes the parameters of f, U is the upper bound of u, and \(X_f\) includes the inputs of f. Therefore, \(X_f\) is defined as

$$\begin{aligned} X_f(t) = {\left[ {{{\hat{\xi }}} (t),{{\hat{\xi }}} \left( {t - \tau } \right) ,{{\hat{\xi }}} \left( {t - 2\tau } \right) ,\hat{\xi }\left( {t - 3\tau } \right) } \right] ^T}, \end{aligned}$$
(19)

where \(\tau \) is specified delay, and \(D_t^q{{\hat{\xi }}}(t)\) denotes the Caputo fractional derivative. \(D_t^q{{\hat{\xi }}}(t)\) is written as

$$\begin{aligned} D_t^q{{\hat{\xi }}} (t) = \frac{1}{{\Gamma (1 - q)}}\int _0^t {{{(t - x)}^{ - q}}\frac{d}{{dt}}{{\hat{\xi }}} (x)\textrm{d}x}, \end{aligned}$$
(20)

where \(0< q < 1\), and \(\Gamma ( \cdot )\) is Gamma function. T3-FLSs are learned by the tuning laws, extracted from a fractional-order stability analysis. From (18), the estimation error (\({{\hat{e}}} = \xi -{{\hat{\xi }}}\)) dynamics are written as

$$\begin{aligned} D_t^q{{\hat{e}}}(t) = f\left[ {{X_f}(t),\vartheta _f^*(t)} \right] - f\left[ {{X_f}(t),{\vartheta _f}(t)} \right] + \delta (t), \nonumber \\ \end{aligned}$$
(21)

where \(f\left[ {X_f(t),{\vartheta _f ^*}(t)} \right] \) is a T3-FLS with optimal \(\vartheta _f ^*\), and \({\delta }\) denotes the approximation error. The suggested controller is generally written as

$$\begin{aligned} u(t) = {u_p}(t) + {u_c}(t), \end{aligned}$$
(22)

where \({u_{c}}(t)\) and \({u_p}(t)\) are predictive controller and compensator. The predictive controller is a T3-FLS and is denoted as \(g\left[ {{X_g}(t),{\vartheta _g}(t)} \right] \). \({X_g}\) and \({{\vartheta _g}}\) are the input and rule vectors of \(g\left[ {{X_g}(t),{\vartheta _g}(t)} \right] \). The predictive controller is tuned in the direction of minimizing of (23)

$$\begin{aligned} J = \int _t^{t + \pi } {\left( {{{\hat{\xi }}} \left( x \right) - {\xi _d}\left( x \right) } \right) } \textrm{d}x, \end{aligned}$$
(23)

where \(\pi \) denotes a prediction horizon, and \({\xi }_d\) is the reference signal.

Type-3 FLSs

The MR dynamics are considered entirely unknown. The T3-FLS is used for online dynamic identifying and trajectory prediction. T3-FLSs have been successfully used for estimations and prediction applications. In this paper, new fractional-order learning laws are presented for T3-FLSs [38]. Also, a predictive controller is designed on the basis of the T3-FLS model of MR. In this section, the T3-FLS is illustrated.

  1. (1)

    The input variables for T3-FLS (\({{x _i}}, \,i=1,\ldots ,4\)) in modeling part are \( {{\hat{\xi }}} (t)\), \({{\hat{\xi }}} \left( {t - \tau } \right) \), \({{\hat{\xi }}} \left( {t - 2\tau } \right) \), and \({\hat{\xi }} \left( {t - 3\tau } \right) \). \(\tau \) denotes a delay. In the predictive control part, the input variables for T3-FLS are \(\xi \), e, \(D_t^qe\), and \(D_t^{ - q}e\).

  2. (2)

    Regarding the upper and lower bounds of input signals, just two membership functions are considered for input signals (\(\tilde{\Omega }_i^j\), \(i=1,..,4\), \(j=1,2\)). The memberships of \({\tilde{\Omega }_i^j}\) at horizontal slice levels \({ {{{{\underline{\alpha }}}}_i}}\) and \({ {{{{\bar{\alpha }}} }_i}}\) are given as [39] (see Fig. 3)

    $$\begin{aligned}{} & {} {{{\bar{H}} }_{{{\tilde{\Omega }}}_{i\,\,| {{{{\bar{\alpha }}} }_i}}^j}} = \left\{ {\begin{array}{ll} {1 - {{\left( {\frac{{\left| {x_i - {C_{{{\tilde{\Omega }}}_i^j}}} \right| }}{{{{{\underline{s}} }_{{{\tilde{\Omega }}}_i^j}}}}} \right) }^{{\bar{\alpha }_i}}}\,if\,{C_{{{\tilde{\Omega }}}_i^j}} - {{{\underline{s}} }_{{{\tilde{\Omega }}}_i^j}}< x_i \le {C_{{{\tilde{\Omega }}}_i^j}}}\\ {1 - {{\left( {\frac{{\left| {x_i - {C_{{{\tilde{\Omega }}}_i^j}}} \right| }}{{{{{{\bar{s}}}}_{{{\tilde{\Omega }}}_i^j}}}}} \right) }^{{{{{\bar{\alpha }}} }_i}}}\,if\,{C_{{{\tilde{\Omega }}}_i^j}} < x_i \le {C_{\tilde{\Omega }_i^j}} + {{{{\bar{s}}}}_{{{\tilde{\Omega }}}_i^j}}}\\ {0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,if\,x_i > {C_{{{\tilde{\Omega }}}_i^j}} + {{{{\bar{s}}}}_{{{\tilde{\Omega }}}_i^j}}\,or\,x_i \le {C_{{{\tilde{\Omega }}}_i^j}} - {{{\underline{s}} }_{{{\tilde{\Omega }}}_i^j}}} \end{array}} \right. \nonumber \\ \end{aligned}$$
    (24)
    $$\begin{aligned}{} & {} {{{\bar{H}} }_{{{\tilde{\Omega }}}_{i\,\,| {{{{\underline{\alpha }}} }_i}}^j}} = \left\{ {\begin{array}{ll} {1 - {{\left( {\frac{{\left| {x_i - {C_{{{\tilde{\Omega }}}_i^j}}} \right| }}{{{{{\underline{s}} }_{{{\tilde{\Omega }}}_i^j}}}}} \right) }^{{{{{\underline{\alpha }}} }_i}}}\,if\,{C_{{{\tilde{\Omega }}}_i^j}} - {{{\underline{s}} }_{{{\tilde{\Omega }}}_i^j}}< x_i \le {C_{\tilde{\Omega }_i^j}}}\\ {1 - {{\left( {\frac{{\left| {x_i - {C_{{{\tilde{\Omega }}}_i^j}}} \right| }}{{{{{{\bar{s}}}}_{{{\tilde{\Omega }}}_i^j}}}}} \right) }^{{{\underline{\alpha }}_i}}}\,if\,{C_{{{\tilde{\Omega }}}_i^j}} < x_i \le {C_{\tilde{\Omega }_i^j}} + {{{{\bar{s}}}}_{{{\tilde{\Omega }}}_i^j}}}\\ {0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,if\,x_i > {C_{{{\tilde{\Omega }}}_i^j}} + {{{{\bar{s}}}}_{{{\tilde{\Omega }}}_i^j}}\,or\,x_i \le {C_{{{\tilde{\Omega }}}_i^j}} - {{{\underline{s}} }_{{{\tilde{\Omega }}}_i^j}}} \end{array}} \right. \nonumber \\ \end{aligned}$$
    (25)
    $$\begin{aligned}{} & {} {{\underline{H}} _{{{\tilde{\Omega }}}_{i\,\,| {{{{\bar{\alpha }}} }_i}}^j}} = \left\{ {\begin{array}{ll} {1 - {{\left( {\frac{{\left| {x_i - {C_{{{\tilde{\Omega }}}_i^j}}} \right| }}{{{{{\underline{s}} }_{{{\tilde{\Omega }}}_i^j}}}}} \right) }^{\frac{1}{{{{{{\bar{\alpha }}} }_i}}}}}\,if\, {C_{\tilde{\Omega }_i^j}} - {{{\underline{s}} }_{{{\tilde{\Omega }}}_i^j}}< x_i \le {C_{{{\tilde{\Omega }}}_i^j}}}\\ {1 - {{\left( {\frac{{\left| {x_i - {C_{{{\tilde{\Omega }}}_i^j}}} \right| }}{{{{{{\bar{s}}}}_{{{\tilde{\Omega }}}_i^j}}}}} \right) }^{\frac{1}{{{{{{\bar{\alpha }}} }_i}}}}}\,if\, {C_{\tilde{\Omega }_i^j}} < x_i \le {C_{{{\tilde{\Omega }}}_i^j}} + {{{{\bar{s}}}}_{\tilde{\Omega }_i^j}}}\\ {0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,if\,x_i > {C_{{{\tilde{\Omega }}}_i^j}} + {{{{\bar{s}}}}_{{{\tilde{\Omega }}}_i^j}}\,or\,x_i \le {C_{{{\tilde{\Omega }}}_i^j}} - {{{\underline{s}} }_{{{\tilde{\Omega }}}_i^j}}} \end{array}} \right. \nonumber \\ \end{aligned}$$
    (26)
    $$\begin{aligned}{} & {} {{\underline{H}} _{{{\tilde{\Omega }}}_{i\,\,| {{{{\underline{\alpha }}} }_i}}^j}} = \left\{ {\begin{array}{ll} {1 - {{\left( {\frac{{\left| {x_i - {C_{{{\tilde{\Omega }}}_i^j}}} \right| }}{{{{{\underline{s}} }_{{{\tilde{\Omega }}}_i^j}}}}} \right) }^{\frac{1}{{{{{{\underline{\alpha }}} }_i}}}}}\, if\,{C_{\tilde{\Omega }_i^j}} - {{{\underline{s}} }_{{{\tilde{\Omega }}}_i^j}}< x_i \le {C_{{{\tilde{\Omega }}}_i^j}}}\\ {1 - {{\left( {\frac{{\left| {x_i - {C_{{{\tilde{\Omega }}}_i^j}}} \right| }}{{{{{{\bar{s}}}}_{{{\tilde{\Omega }}}_i^j}}}}} \right) }^{\frac{1}{{{{{{\underline{\alpha }}} }_i}}}}}\, if\,{C_{\tilde{\Omega }_i^j}} < x_i\le {C_{{{\tilde{\Omega }}}_i^j}} + {{{{\bar{s}}}}_{\tilde{\Omega }_i^j}}}\\ {0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,if\,x_i > {C_{{{\tilde{\Omega }}}_i^j}} + {{{{\bar{s}}}}_{{{\tilde{\Omega }}}_i^j}}\,\,or\,\,x_i \le {C_{\tilde{\Omega }_i^j}} - {{{\underline{s}} }_{{{\tilde{\Omega }}}_i^j}}}, \end{array}} \right. \nonumber \\ \end{aligned}$$
    (27)

    where \({{{\bar{H}} }_{{{\tilde{\Omega }}}_{i| {{{{\bar{\alpha }}} }_i}}^j}}\)/\({{{\bar{H}} }_{{{\tilde{\Omega }}}_{i| {{\underline{\alpha }}_i}}^j}}\) and \({{\underline{H}} _{{{\tilde{\Omega }}}_{i| {{{{\bar{\alpha }}} }_i}}^j}}\)/\({{\underline{H}} _{{{\tilde{\Omega }}}_{i | {{{{\underline{\alpha }}} }_i}}^j}}\) are the upper/lower memberships for \({{{\tilde{\Omega }}}_i^j}\) at \({ {{{{\underline{\alpha }}} }_i}}\) and \({ {{{{\bar{\alpha }}} }_i}}\). \({{C_{{{\tilde{\Omega }}}_i^j}}}\) are the center of \({{C_{{{\tilde{\Omega }}}_i^j}}}\) and \({{{{\underline{s}} }_{\tilde{\Omega }_i^j}}}\) and \({{{{{\bar{s}}}}_{{{\tilde{\Omega }}}_i^j}}}\) are the distances of \({{C_{{{\tilde{\Omega }}}_i^j}}}\) to the beginning/last points of \({{{\tilde{\Omega }}}_i^j}\) (see Fig. 3).

  3. (3)

    The upper rule firings \({{\bar{\mu }}} _{{{{{\bar{\alpha }}} }_i}}^l\), \(\bar{\mu }_{{{{{\underline{\alpha }}} }_i}}^l\), and lower firings \(\underline{\mu }_{{{{{\bar{\alpha }}} }_i}}^l\) and \({{\underline{\mu }}} _{{{\underline{\alpha }}_i}}^l\) are written as

    $$\begin{aligned}{} & {} {{\bar{\mu }}} _{{{{{\bar{\alpha }}} }_i}}^l = {{{\bar{H}} }_{\tilde{\Omega }_{1\,\,\,\,|\, {{{{\bar{\alpha }}} }_i}}^{{p_1}}}} \cdot {{{\bar{H}} }_{{{\tilde{\Omega }}}_{1\,\,\,\,|\, {{{{\bar{\alpha }}} }_i}}^{{p_2}}}} \cdots {{{\bar{H}} }_{{{\tilde{\Omega }}}_{1\, \, \,\,|\, {{{{\bar{\alpha }}} }_i}}^{{p_n}}}} \end{aligned}$$
    (28)
    $$\begin{aligned}{} & {} {{\bar{\mu }}} _{{{{{\underline{\alpha }}} }_i}}^l = {{{\bar{H}} }_{\tilde{\Omega }_{1\,\,\,\,|\, {{{{\underline{\alpha }}} }_i}}^{{p_1}}}} \cdot {{{\bar{H}} }_{{{\tilde{\Omega }}}_{1\,\,\,\,|\, {{{{\underline{\alpha }}} }_i}}^{{p_2}}}} \cdots {{{\bar{H}} }_{{{\tilde{\Omega }}}_{1\,\,\,\,|\, {{{{\underline{\alpha }}} }_i}}^{{p_n}}}} \end{aligned}$$
    (29)
    $$\begin{aligned}{} & {} {{\underline{\mu }}} _{{{{{\bar{\alpha }}} }_i}}^l = {{\underline{H}} _{\tilde{\Omega }_{1\,\,\,\,|\, {{{{\bar{\alpha }}} }_i}}^{{p_1}}}} \cdot {\underline{H} _{{{\tilde{\Omega }}}_{1\,\,\,\,|\, {{{{\bar{\alpha }}} }_i}}^{{p_2}}}} \cdots {{\underline{H}} _{{{\tilde{\Omega }}}_{1\,\,\,\,|\, {{{{\bar{\alpha }}} }_i}}^{{p_n}}}} \end{aligned}$$
    (30)
    $$\begin{aligned}{} & {} {{\underline{\mu }}} _{{{{{\underline{\alpha }}} }_i}}^l = {{\underline{H}} _{{{\tilde{\Omega }}}_{1\,\,\,\,|\, {{{{\underline{\alpha }}} }_i}}^{{p_1}}}} \cdot {{\underline{H}} _{{{\tilde{\Omega }}}_{1\,\,\,\,|\, {{\underline{\alpha }}_i}}^{{p_2}}}} \cdots {{\underline{H}} _{\tilde{\Omega }_{1\,\,\,\, |\, {{{{\underline{\alpha }}} }_i}}^{{p_n}}}}, \end{aligned}$$
    (31)

    where form of \(l-th\) rule is given as

    $$\begin{aligned}{} & {} {l - th\,Rule:}\nonumber \\{} & {} if\,{{\hat{\xi }}} \,is\,\,{{\tilde{\Omega }}} _{1\,\,\,\,}^{{p_1}}\,and\,\xi \left( {t - \tau } \right) \,is\,\,{{\tilde{\Omega }}} _2^{{p_2}}\,and\, \nonumber \\{} & {} \quad \cdots \,\,\xi \left( {t - 3\tau }\right) \,\,is\,\,{{\tilde{\Omega }}} _n^{{p_n}}\nonumber \\{} & {} Then\,f \in \left[ {{{{{\underline{\vartheta }}} }_l},{{\bar{\vartheta }}_l}} \right] ,l = 1,\ldots ,M, \end{aligned}$$
    (32)

    where \({{{\underline{\vartheta }}} _l} \in \left[ {{{{{\underline{\vartheta }}} }_{l,{{\underline{\alpha }}} }},{{{{\underline{\vartheta }}} }_{l,{{\bar{\alpha }}} }}} \right] \), \({{{{\bar{\vartheta }}} }_l} \in \left[ {{{{{\bar{\vartheta }}} }_{l,{{\underline{\alpha }}} }},{{{{\bar{\vartheta }}} }_{l,{{\bar{\alpha }}} }}} \right] \), \({{\tilde{\Omega }}}_i^{{p_j}}\) denotes the MF for input \(x_i\), and \({{{{\underline{\vartheta }}} }_l}\) and \({{{\bar{\vartheta }}} }_l\) denote the rule parameters.

  4. (4)

    The output signal f is

    $$\begin{aligned} f = \frac{{\sum \nolimits _{i = 1}^{{n_\alpha }} {\left( {{{\underline{\alpha }}_i}{{{{\underline{\ell }}} }_i} + {{{{\bar{\alpha }}} }_i}{{{{\bar{\ell }}} }_i}} \right) } }}{{\sum \nolimits _{i = 1}^{{n_\alpha }} {\left( {{{{{\underline{\alpha }}} }_i} + {{{{\bar{\alpha }}} }_i}} \right) } }}{\mathrm{}}, \end{aligned}$$
    (33)

    where

    $$\begin{aligned}{} & {} {{{{\bar{\ell }}} }_i} = \frac{{\sum \nolimits _{l = 1}^{{n_r}} {\left( {\bar{\mu }_{{{{{\bar{\alpha }}} }_i}}^l{{{{\bar{\vartheta }}} }_{l,{{{{\bar{\alpha }}} }_i}}} + {{\underline{\mu }}} _{{{{{\bar{\alpha }}} }_i}}^l{{\underline{\vartheta }}_{l,{{{{\bar{\alpha }}} }_i}}}} \right) } }}{{\sum \nolimits _{l = 1}^{{n_r}} {\left( {{{\bar{\mu }}} _{{{{{\bar{\alpha }}} }_i}}^l + \underline{\mu }_{{{{{\bar{\alpha }}} }_i}}^l} \right) } }} \end{aligned}$$
    (34)
    $$\begin{aligned}{} & {} {{{\underline{\ell }}} _i} = \frac{{\sum \nolimits _{l = 1}^{{n_r}} {\left( {{{\bar{\mu }}} _{{{{{\underline{\alpha }}} }_i}}^l{{{{\bar{\vartheta }}} }_{l,{{{{\underline{\alpha }}} }_i}}} + {{\underline{\mu }}} _{{{\underline{\alpha }}_i}}^l{{{{\underline{\vartheta }}} }_{l,{{{{\underline{\alpha }}} }_i}}}} \right) } }}{{\sum \nolimits _{l = 1}^{{n_r}} {\left( {{{\bar{\mu }}} _{{{{{\underline{\alpha }}} }_i}}^l + {{\underline{\mu }}} _{{{\underline{\alpha }}_i}}^l} \right) } }}. \end{aligned}$$
    (35)
Fig. 3
figure 3

Type-3 MF

Full size image

The output is rewritten as

$$\begin{aligned} f\left( {X,\vartheta } \right) = {\vartheta ^T}\beta , \end{aligned}$$
(36)

where

$$\begin{aligned} {\beta ^T}= & {} \left[ {{{{{\underline{\beta }}} }_{1,{{{{\underline{\alpha }}} }_i}}},\ldots ,{{{{\underline{\beta }}} }_{{n_r},{{{{\underline{\alpha }}} }_i}}},} \quad {{{\underline{\beta }}} _{1,{{{{\bar{\alpha }}} }_i}}},\ldots ,{{{\underline{\beta }}} _{{n_r},{{{{\bar{\alpha }}} }_i}}}, \right. \nonumber \\{} & {} \left. {{{{\bar{\beta }}} }_{1,{{{{\underline{\alpha }}} }_i}}},\ldots ,{{{{\bar{\beta }}} }_{{n_r},{{{{\underline{\alpha }}} }_i}}},\quad {{{{\bar{\beta }}} }_{1,{{\bar{\alpha }}_i}}},\ldots ,{{{{\bar{\beta }}} }_{{n_r},{{{{\bar{\alpha }}} }_i}}} \right] \end{aligned}$$
(37)
$$\begin{aligned} {\vartheta ^T}= & {} \left[ {{{{{\underline{\vartheta }}} }_{1,{{\underline{\alpha }}_i}}},\ldots ,{{{{\underline{\vartheta }}} }_{{n_r},{{\underline{\alpha }}_i}}}} , \quad {{{\underline{\vartheta }}} _{1,{{\bar{\alpha }}_i}}},\ldots ,{{{\underline{\vartheta }}} _{{n_r},{{{{\bar{\alpha }}} }_i}}},\right. \nonumber \\{} & {} \left. {{{{\bar{\vartheta }}} }_{1,{{\underline{\alpha }}_i}}},\ldots ,{{{{\bar{\vartheta }}} }_{{n_r},{{{{\underline{\alpha }}} }_i}}},\quad {{{{\bar{\vartheta }}} }_{1,{{\bar{\alpha }}_i}}},\ldots ,{{{{\bar{\vartheta }}} }_{{n_r},{{{{\bar{\alpha }}} }_i}}} \right] \end{aligned}$$
(38)
$$\begin{aligned} {{{\underline{\beta }}} _{l,{{{{\underline{\alpha }}} }_i}}}= & {} \frac{{\sum \nolimits _{i = 1}^{{n_\alpha }} {{{{{\underline{\alpha }}} }_i}{{\underline{\mu }}} _{{{{{\underline{\alpha }}} }_i}}^l} }}{{\sum \nolimits _{i = 1}^{{n_\alpha }} {\left( {{{{{\underline{\alpha }}} }_i} + {{{{\bar{\alpha }}} }_i}} \right) } \sum \nolimits _{l = 1}^{{n_r}} {\left( {{{\bar{\mu }}} _{{{{{\underline{\alpha }}} }_i}}^l + {{\underline{\mu }}} _{{{{{\underline{\alpha }}} }_i}}^l} \right) } }} \end{aligned}$$
(39)
$$\begin{aligned} {{{{\bar{\beta }}} }_{l,{{{{\underline{\alpha }}} }_i}}}= & {} \frac{{\sum \nolimits _{i = 1}^{{n_\alpha }} {{{{{\underline{\alpha }}} }_i}{{\bar{\mu }}} _{{{{{\underline{\alpha }}} }_i}}^l} }}{{\sum \nolimits _{i = 1}^{{n_\alpha }} {\left( {{{{{\underline{\alpha }}} }_i} + {{{{\bar{\alpha }}} }_i}} \right) } \sum \nolimits _{l = 1}^{{n_r}} {\left( {{{\bar{\mu }}} _{{{{{\underline{\alpha }}} }_i}}^l + {{\underline{\mu }}} _{{{\underline{\alpha }}_i}}^l} \right) } }} \end{aligned}$$
(40)
$$\begin{aligned} {{{{\underline{\beta }}} }_{l,{{\bar{\alpha }}} }}= & {} \frac{{\sum \nolimits _{i = 1}^{{n_\alpha }} {{{{{\bar{\alpha }}} }_i}{{\underline{\mu }}} _{{{\bar{\alpha }}} }^l} }}{{\sum \nolimits _{i = 1}^{{n_\alpha }} {\left( {{{\underline{\alpha }}_i} + {{{{\bar{\alpha }}} }_i}} \right) } \sum \nolimits _{l = 1}^{{n_r}} {\left( {{{\bar{\mu }}} _{{{\bar{\alpha }}} }^l + {{\underline{\mu }}} _{{{\bar{\alpha }}} }^l} \right) } }} \end{aligned}$$
(41)
$$\begin{aligned} {{{{\bar{\beta }}} }_{l,{{\bar{\alpha }}} }}= & {} \frac{{\sum \nolimits _{i = 1}^{{n_\alpha }} {{{{{\bar{\alpha }}} }_i}{{\bar{\mu }}} _{{{\bar{\alpha }}} }^l} }}{{\sum \nolimits _{i = 1}^{{n_\alpha }} {\left( {{{{{\underline{\alpha }}} }_i} + {{{{\bar{\alpha }}} }_i}} \right) } \sum \nolimits _{l = 1}^{{n_r}} {\left( {{{\bar{\mu }}} _{{{\bar{\alpha }}} }^l + {{\underline{\mu }}} _{{{\bar{\alpha }}} }^l} \right) } }}. \end{aligned}$$
(42)

Predictive T3-FLS leaning

The BBO algorithm is formulated to optimize the predictive controller \(g\left[ {{X_g}(t),{\vartheta _g}(t)} \right] \). The parameter vector \({\vartheta _g}(t) \) is adjusted, such that (43) is minimized

$$\begin{aligned} J = \int _t^{t + \pi } {\left( {{{\hat{\xi }}} \left( x \right) - {\xi _d}\left( x \right) } \right) } \textrm{d}x, \end{aligned}$$
(43)

where \({{\hat{\xi }}}(t)\) is the estimated position of MR, \(\pi \) denotes the prediction horizon, and \(\xi _d(t)\) is the expected path of MR. The cost function J is defined as

$$\begin{aligned} J = \sum \nolimits _{x = 1}^\rho {{{\left( {{{\hat{\xi }}} \left( {t + x} \right) - {\xi _d}\left( {t + x} \right) } \right) }^2}} ,\quad x = 1,\ldots ,\rho .\nonumber \\ \end{aligned}$$
(44)

The optimization procedure is described as

  1. (1)

    Consider a set of possible vectors \({{\vartheta _g}}\) as an initial population \(P_{N \times \left( {\kappa + 4K} \right) }\). \(\kappa \) is the rule numbers, N denotes the number \({{\vartheta _g}}\) in P, and K represents the \(\alpha \)-cut numbers.

  2. (2)

    For each row of P, as \(P_j,\,j=1,\ldots ,N\), the immigration/emigration rates \({\lambda _j}\)/\(\gamma _j\) are defined as

    $$\begin{aligned}{} & {} {\lambda _j} = \frac{1}{N}\left( {j - 1} \right) \end{aligned}$$
    (45)
    $$\begin{aligned}{} & {} {\gamma _j} = - \frac{1}{N}\left( {j - 1} \right) + 1. \end{aligned}$$
    (46)
  3. (3)

    For each row of P, do:

    1. (3.a)

      Obtain the output of T3-FLS as

      $$\begin{aligned} {u_{{p_j}}}(t) =g\left( {{X_g}|{P_j}} \right) , \end{aligned}$$
      (47)

      where \({u_{{p_j}}}(t)\) represents the jth predictive control signal based on the jth row of P.

    2. (3.b)

      Construct \({X_f}\) as \({X_f} = \big [{{\hat{\xi }}} (t),{{\hat{\xi }}} \left( {t - \tau } \right) , {{\hat{\xi }}} \left( {t - 2\tau } \right) ,{{\hat{\xi }}} \left( {t - 3\tau } \right) \big ]^T\), the control signal becomes \({u_j}(t) = {u_{{p_j}}}(t) + {u_c}(t)\).

    3. (3.c)

      For \({u_j}(t)\) that was obtained in the previous step, calculate \({{\hat{\xi }}} \left( {t + x} \right) \) for \(x = 1,\ldots ,\rho \) as follows: Using the Adams–Bashforth approach, we have

      $$\begin{aligned}{} & {} {{\hat{\xi }}} \left( {t + x} \right) = {{\hat{\xi }}} (t) + \frac{{{j^q}}}{{\Gamma \left( {q + 2} \right) }}\left[ {f\left[ {{X_f}(t),{\vartheta _f}(t)} \right] } \right. \nonumber \\{} & {} \quad + \frac{{{u_j}(t)}}{U}\left( {{{\left( {x - 1} \right) }^{q + 1}} - \left( {x - 1 - q} \right) {x^q}} \right) \nonumber \\{} & {} \quad \left( {f\left[ {{X_f}(t),{\vartheta _f}(t)} \right] + \frac{{{u_j}(t)}}{U}} \right) + \mathop {\sum }\limits _{i = 0}^{x - 1}\nonumber \\{} & {} \quad \left. \times { {\left( {f\left[ {{X_f}\left( {t + i} \right) ,{\vartheta _f}(t)} \right] + \frac{{{u_j}(t)}}{U}} \right) a\left( {x,i} \right) } } \right] , \nonumber \\ \end{aligned}$$
      (48)

      where \({X_f}\left( {t + x} \right) \), \({X_f}\left( {t + i } \right) \) and \({{{{{\hat{\xi }}}}_p}\left( {t + x } \right) }\), are

      $$\begin{aligned}{} & {} {X_f}\left( {t + x} \right) = \,\,\left[ {{{{{\hat{\xi }}} }_p}\left( {t + x} \right) ,{{{{\hat{\xi }}} }_p}\left( {t + x - \tau } \right) } \right. ,\nonumber \\{} & {} \left. {{{{{\hat{\xi }}} }_p}\left( {t + x - 2\tau } \right) ,{{{{\hat{\xi }}} }_p}\left( {t + x - 3\tau } \right) } \right] \end{aligned}$$
      (49)
      $$\begin{aligned}{} & {} {X_f}\left( {t + i} \right) = \,\,\,\,\left[ {{{\hat{\xi }}} \left( {t + i} \right) ,{{\hat{\xi }}} \left( {t + i - \tau } \right) } \right. ,\nonumber \\{} & {} {{\hat{\xi }}} \left. {\left( {t + i - 2\tau } \right) ,{{\hat{\xi }}} \left( {t + i - 3\tau } \right) } \right] \end{aligned}$$
      (50)
      $$\begin{aligned}{} & {} {{{{\hat{\xi }}} }_p}\left( {t + x} \right) = {{\hat{\xi }}} (t) \nonumber \\{} & {} \quad + \frac{{{j^q}}}{{\Gamma \left( {q + 1} \right) }}\mathop {\sum }\limits _{i = 0}^{x - 1} \nonumber \\{} & {} \quad {\left[ {f\left[ {{X_f}\left( {t + i} \right) ,{\vartheta _f}(t)} \right] + \frac{{{u_j}(t)}}{U}} \right] b\left( {x,i} \right) }, \end{aligned}$$
      (51)

      where

      $$\begin{aligned} b\left( {x,i} \right)= & {} {\left( {x - i} \right) ^q} - {\left( {x - i - 1} \right) ^q} \end{aligned}$$
      (52)
      $$\begin{aligned} a\left( {x,i} \right)= & {} {\left( {x - i + 1} \right) ^{q + 1}} - 2{\left( {x - i} \right) ^{q + 1}} \nonumber \\{} & {} + {\left( {x - i - 1} \right) ^{q + 1}}. \end{aligned}$$
      (53)
    4. (3.d)

      Examine (44) and calculate the value of cost function.

  4. (4)

    Sort the rows of P from the best to worst fitness.

  5. (5)

    For each row of \(P_j,\,h=1,\ldots ,N\), the mutation is applied as follows. If the randomly produced number is less than \({\lambda _h}\), then the jth row participates in a mutation operation. To apply mutation, another \({P_{j'}}\) is randomly selected, and \(P_j\) is updated as

    $$\begin{aligned} {{P'}_j} = {P_j} + \eta \left( {{P_{j'}} - {P_j}} \right) , \end{aligned}$$
    (54)

    where \(0<\eta \le 1\).

  6. (6)

    The new generated \({{P'}_j}\) is evaluated on the basis of fitness function.

  7. (7)

    The new population \(P_{new}\) is constructed by the use new generated solutions \({{P'}_j}\) and old matrix P. If new generated \({{P'}_j}\) is better than old, a row of matrix P is replaced with that row.

  8. (8)

    By the use od best of row of P, the predictive control signal \({u_p} = g\left( {{X_g}|{P_{best}}} \right) \) is generated.

Stability analysis

To analyze the stability, a Lyapunov function is considered, and tuning rules are extracted for \(f\left[ {{X_f}(t),{\vartheta _f}(t)} \right] \).

Theorem 1

The MR system is asymptotically stable by adaptation law (55) and compensator (56)

$$\begin{aligned} D_t^q(t){\vartheta _f}(t){} & {} \!= \mu {{\hat{e}}}(t){\beta _f}(t) \end{aligned}$$
(55)
$$\begin{aligned} {u_c}(t){} & {} \!= {{{{\bar{u}}}}_p}\tanh \left[ {e(t)} \right] \nonumber \\{} & {} \quad + \frac{{U\left| {{{\hat{e}}}(t)} \right| {{\bar{\delta }}} \tanh \left[ {e(t)} \right] + \tanh \left[ {e(t)} \right] {{\bar{\xi }}} + \tanh \left[ {e(t)} \right] {{\bar{f}}}}}{{\left| {e(t)} \right| + \varepsilon }},\nonumber \\ \end{aligned}$$
(56)

where \(0 < \mu \le 1\), \({{\hat{e}}} = \xi - {{\hat{\xi }}}\), \(\xi _f\) includes the rule parameters of \({f\left[ {{X_f}\left( {t } \right) ,{\vartheta _f}(t)} \right] }\), \(e = {\xi y_d} - {{\hat{\xi }}}\), \(\varepsilon \) is a small constant, and U, \({{{\bar{u}}_p}}\), \({{{{{\bar{f}}}}}}\), \({{\bar{\delta }}} \) and \({{{\bar{\xi }}} }\) denote upper bounds of u , \({{{ u}_p}}\) , \({f\left[ {{X_f}\left( {t } \right) ,{\vartheta _f}(t)} \right] }\), \(\delta (t)\), and \(D_t^q{\xi _d}(t)\), respectively.

Fig. 4
figure 4

Fabricated MR for the experimental tests of the proposed control scheme

Full size image

Proof

The Lyapunov function is given as

$$\begin{aligned} V(t) = \frac{1}{2}{{{{\hat{e}}}}^2}(t) + \frac{1}{2}{e^2}(t) + \frac{1}{{2\mu }}{{\tilde{\vartheta }}} _f^T(t){{\tilde{\vartheta }}} _f^{}(t), \end{aligned}$$
(57)

where

$$\begin{aligned}{} & {} {{\hat{e}}}(t) = \xi (t) - {{\hat{\xi }}} (t)\nonumber \\ {}{} & {} e(t) = {\xi _d}(t) - {{\hat{\xi }}} (t)\nonumber \\ {}{} & {} {{\tilde{\vartheta }}} _f^{}(t) = \vartheta _f^*(t) - \vartheta _f^{}(t), \end{aligned}$$
(58)

where \({{\tilde{\vartheta }}} _f^{} = \vartheta _f^* - \vartheta _f^{}\). Considering the inequality \(D_t^q\left( {\frac{1}{2}{x^2}} \right) \le xD_t^qx\), from (57), we can write

$$\begin{aligned} D_t^qV(t) \le {{\hat{e}}}(t)D_t^q{{\hat{e}}}(t) + e(t)D_t^qe(t)- \frac{1}{\mu }{{\tilde{\vartheta }}} _f^T(t)D_t^q{\vartheta _f}(t).\nonumber \\ \end{aligned}$$
(59)

The estimation error in (21) can be rewritten as

$$\begin{aligned} D_t^q{{\hat{e}}}(t) = {{\tilde{\vartheta }}} _f^T(t){\beta _f}(t) + \delta (t). \end{aligned}$$
(60)

By substituting (60) into (59), we can obtain

$$\begin{aligned} D_t^qV(t)\le & {} {{\hat{e}}}(t){{\tilde{\vartheta }}} _f^T(t){\beta _f}(t) + e(t)D_t^qe(t)\nonumber \\{} & {} - \frac{1}{\mu }{{\tilde{\vartheta }}} _f^T(t)D_t^q{\vartheta _f}(t) + {{\hat{e}}}(t)\delta (t). \end{aligned}$$
(61)

From (61), we can write

$$\begin{aligned} D_t^qV(t)\le & {} {{\tilde{\vartheta }}} _f^T(t)\left( {{{\hat{e}}}(t){\beta _f}(t) - \frac{1}{\mu }D_t^q(t){\vartheta _f}(t)} \right) \nonumber \\{} & {} + e(t)D_t^qe(t) + {{\hat{e}}}(t)\delta (t). \end{aligned}$$
(62)

Substituting the adaptation law (55) into (62) yields

$$\begin{aligned} D_t^qV \le eD_t^qe + {{\hat{e}}}{E_m}. \end{aligned}$$
(63)

From (18), (58), and (63), one has

$$\begin{aligned} D_t^qV(t)\le & {} D_t^q{\xi _d}(t) - e(t)f\left[ {{X_f}(t),{\vartheta _f}(t)} \right] \nonumber \\{} & {} + {{\hat{e}}}(t)\delta (t) - e(t)u(t)/U, \end{aligned}$$
(64)

where \(f\left[ {{X_f}(t),{\vartheta _f}(t)} \right] \) is a T3-FLS, and \(\delta (t)\) and U denote the estimation error and upper bound of u. From compensator (22), the inequality (64) becomes

$$\begin{aligned} D_t^qV(t)\le & {} \,{{{{\bar{\xi }}} }_d} + \left| {e(t)} \right| \left| {f\left[ {{X_f}(t),{\vartheta _f}(t)} \right] } \right| + \left| {{{\hat{e}}}(t)} \right| \left| {\delta (t)} \right| \nonumber \\{} & {} + \left| {e(t)} \right| \left| {{u_p}(t)} \right| /U - e(t){u_c}(t)/U. \end{aligned}$$
(65)

From compensator (56), the inequality (65) becomes

$$\begin{aligned} D_t^qV(t)\le & {} {{{{\bar{\xi }}} }_d} + \left| {e(t)} \right| \left| {f\left[ {{X_f}(t),{\vartheta _f}(t)} \right] } \right| \nonumber \\{} & {} + \left| {{{\hat{e}}}(t)} \right| \left| {\delta (t)} \right| + \left| {e(t)} \right| \left| {{u_p}(t)} \right| /U- e(t)/U\nonumber \\{} & {} \times \left\{ \begin{array}{l} {{{{\bar{u}}}}_p}\tanh \left[ {e(t)} \right] + \\ \,\,\,\,\,\frac{{U\left| {{{\hat{e}}}(t)} \right| {{\bar{\delta }}} \tanh \left[ {e(t)} \right] + \tanh \left[ {e(t)} \right] {{\bar{\xi }}} + \tanh \left[ {e(t)} \right] {{\bar{f}}}}}{{\left| {e(t)} \right| + \varepsilon }}. \end{array} \right\} \nonumber \\ \end{aligned}$$
(66)

Inequality (66) is rewritten as

$$\begin{aligned} D_t^qV(t)\le & {} {{{{\bar{\xi }}} }_d} - \frac{{e(t)\tanh \left[ {e(t)} \right] {{\bar{\xi }}} }}{{\left| {e(t)} \right| + \varepsilon }} \nonumber \\{} & {} + \left| {e(t)} \right| \left| {f\left[ {{X_f}(t),{\vartheta _f}(t)} \right] } \right| \nonumber \\{} & {} - \frac{{e(t)\tanh \left[ {e(t)} \right] \bar{f}}}{{\left| {e(t)} \right| + \varepsilon }}\nonumber \\{} & {} \left| {{{\hat{e}}}(t)} \right| \left| {\delta (t)} \right| - \frac{{\left| {{{\hat{e}}}(t)} \right| \tanh \left[ {e(t)} \right] {{\bar{\delta }}} }}{{\left| {e(t)} \right| + \varepsilon }}\nonumber \\{} & {} \left| {e(t)} \right| \left| {{u_p}(t)} \right| /U\nonumber \\{} & {} - \frac{{\left| {{{\hat{e}}}(t)} \right| \tanh \left[ {e(t)} \right] {{{{\bar{u}}}}_p}}}{{\left| {e(t)} \right| + \varepsilon }}/U. \end{aligned}$$
(67)

Consider the inequalities

$$\begin{aligned}{} & {} {{{{\bar{\xi }}} }_d} - \frac{{e(t)\tanh \left[ {e(t)} \right] {{\bar{\xi }}} }}{{\left| {e(t)} \right| + \varepsilon }} \le 0 \end{aligned}$$
(68)
$$\begin{aligned}{} & {} \left| {e(t)} \right| \left| {f\left[ {{X_f}(t),{\vartheta _f}(t)} \right] } \right| - \frac{{e(t)\tanh \left[ {e(t)} \right] \bar{f}}}{{\left| {e(t)} \right| + \varepsilon }} \le 0 \end{aligned}$$
(69)
$$\begin{aligned}{} & {} \left| {{{\hat{e}}}(t)} \right| \left| {\delta (t)} \right| - \frac{{\left| {{{\hat{e}}}(t)} \right| \tanh \left[ {e(t)} \right] {{\bar{\delta }}} }}{{\left| {e(t)} \right| + \varepsilon }} \le 0 \end{aligned}$$
(70)
$$\begin{aligned}{} & {} \left| {e(t)} \right| \left| {{u_p}(t)} \right| /U - \frac{{\left| {{{\hat{e}}}(t)} \right| \tanh \left[ {e(t)} \right] {{{{\bar{u}}}}_p}}}{{\left| {e(t)} \right| + \varepsilon }}/U \le 0; \end{aligned}$$
(71)

we can conclude that \(D_t^qV(t) \le 0\). Since \(\ddot{V}(t)\) is bounded, then considering Barbalat’s lemma, the proof is complete. For some related Lemmas, see [40]. \(\square \)

Fig. 5
figure 5

Implemented result: planned path 1

Full size image

Simulations and experimental examination

Implementation

The robot is designed with Solid software. A series of parts of the robot were made using a 3D printer, which includes the base of the motors and four columns that were placed on the four sides of the robot to connect the Sharp sensors, so that the sensors could be placed at a suitable angle and height on the four sides of the robot. MR has two regular wheels, which are connected to two stepper motors with high precision, and two idler pins to maintain the balance of the robot. MR has eight Sharp sensors and one Angular acceleration sensor. The two-phase stepper motors have an accuracy of 1.8 degrees per step. Using four 7 cm spacers, the chassis surface is raised to place the PCB on it (see Fig. 4). The communication between the robot and the laptop is through the NRF24L01 radio transceiver module, the communication modulation of this module is GFSK and the communication frequency of this chip is 2.4 GHz, which is much easier to pass through the wall or other objects due to its high frequency. The maximum data rate of this chip is 2 MB per second, which can be used to transmit heavy data, such as audio or even video. The receiver that is connected to the laptop is connected to a microcontroller with the SPI protocol, and on the other hand, this microcontroller is connected to the laptop with a USB to serial converter, which is connected to the MATLAB software through a virtual serial port with 9600 baud rate. In the robot, this module is connected to one of the microcontrollers using the SPI protocol, the same microcontroller that controls the Sharp sensors, and this wireless module. This microcontroller is connected to the microcontroller that controls the motors using UART serial communication. The angular acceleration sensor is also connected to the microcontroller that controls the motors using the I2C protocol. The baud rate of these two microcontrollers on the board is considered to be 250,000. Motor drivers have three control pins, including the EN pin, which is the activator, the direction pin, and the pulse or step pin, which rotates the motor one step for each pulse received.

The results for experimental examination are given in Fig. 5. Two distinct chaotic systems are selected to generate the reference path. The aim is to assess the performance of a robot that is programmed to follow the generated chaotic path. Through conducting experiments, the results obtained demonstrate the practicality and effectiveness of the strategy that has been designed. Even in the face of having no prior knowledge about the dynamics of the MR, as well as various experimental limitations, it is observed that the MR successfully and accurately traces the intended chaotic path. This finding highlights the robustness and adaptability of the implemented approach, further emphasizing its potential for real-world applications.

Simulations

Example 1

The reference signal is generated using the states of (72). The first signal is used for switching control. After each 5s if \(\zeta _{11}>0\), the reference signal is switched (see Fig. 6). The MR should track the chaotic path under chaotic switching. The MR parameters are provided in Table 1. Output trajectory is given in Fig. 7. The output signal well tracks the chaotic path. The reference is changed four times between \(\zeta _{13}\) and \(\zeta _{14}\). The switching mechanism is controlled by the first date \(\zeta _{11}\). In spite of the hard path and unknown dynamics, MR well follows the designed route. The associated control signal is depicted in Fig. 8. The estimation accuracy is examined in Fig. 9. The good convergence in Fig. 9 demonstrates the good estimation ability of T3-FLSs with the suggested fractional-order learning technique

$$\begin{aligned} \left\{ {\begin{array}{ll} {D_t^{0.97}{\zeta _{11}} = 35{\zeta _{12}}{\zeta _{13}} + 35\left( {{\zeta _{12}} - {\zeta _{11}}} \right) }\\ {D_t^{0.97}{\zeta _{12}} = - 5{\zeta _{11}}{\zeta _{13}}25{\zeta _{11}} + {\zeta _{12}} + {\zeta _{14}}}\\ {D_t^{0.97}{\zeta _{13}} = {\zeta _{11}}{\zeta _{12}} - 4{\zeta _{13}}}\\ {D_t^{0.97}{\zeta _{14}} = - 100{\zeta _{12}}}. \end{array}} \right. \end{aligned}$$
(72)
Fig. 6
figure 6

Example 1: switching modes

Full size image
Table 1 Simulation conditions
Full size table
Fig. 7
figure 7

Example 1: output signal

Full size image
Fig. 8
figure 8

Example 1: control signal

Full size image
Fig. 9
figure 9

Example 1: estimation performance

Full size image
Fig. 10
figure 10

Example 2: switching modes

Full size image
Fig. 11
figure 11

Example 2: output signal

Full size image
Fig. 12
figure 12

Example 2: control trajectory

Full size image
Fig. 13
figure 13

Example 2: estimation performance

Full size image

Example 2

In this example, two hyperchaotic systems are considered to produce the reference signal. The master systems are given in (73). Similar to the first example, the first signal is used for switching control. After each 5s, if \(\zeta _{11}>10\), then the reference signal is switched to \(\zeta _{21}\); if \(\zeta _{11}<10\) and \(\zeta _{11}>0\), the reference signal is switched to \(\zeta _{22}\); if \(\zeta _{11}<0\) and \(\zeta _{11}>-10\), the reference signal is switched to \(\zeta _{23}\); if \(\zeta _{11}<-10\), the reference signal is switched to \(\zeta _{14}\) (see Fig. 10). The output trajectory is shown in Fig. 11. The reference is changed four times between \(\zeta _{14}\), \(\zeta _{21}\), \(\zeta _{22}\), and \(\zeta _{23}\). The switching mechanism similar to the previous example is controlled by the first date \(\zeta _{11}\). It is evident that MR well follows the designed trajectory, under the difficult defined scenarios. The associated control signal is depicted in Fig. 8. The estimated signal is depicted in Fig. 9. The good accuracy in Fig. 9 demonstrates a good estimation scheme with a good fractional-order learning technique. It should be noted that the small difference in tracking accuracy of various modes is because of the big difference in the dynamics behavior of different chaotic systems in different modes

$$\begin{aligned} Master\# 1:\left\{ {\begin{array}{ll} {D_t^{0.97}{\zeta _{11}} = 35{\zeta _{12}}{\zeta _{13}} + 35\left( {{\zeta _{12}} - {\zeta _{11}}} \right) }\\ {D_t^{0.97}{\zeta _{12}} = - 5{\zeta _{11}}{\zeta _{13}}25{\zeta _{11}} + {\zeta _{12}} + {\zeta _{14}}}\\ {D_t^{0.97}{\zeta _{13}} = {\zeta _{11}}{\zeta _{12}} - 4{\zeta _{13}}}\\ {D_t^{0.97}{\zeta _{14}} = - 100{\zeta _{12}}} \end{array}} \right. \end{aligned}$$
$$\begin{aligned} Master\# 2:\left\{ {\begin{array}{ll} {D_t^{0.97}{\zeta _{21}} = {\zeta _{24}}35\left( {{\zeta _{22}} - {\zeta _{21}}} \right) }\\ {D_t^{0.97}{\zeta _{22}} = - {\zeta _{21}}{\zeta _{23}}7{\zeta _{21}} + 12{\zeta _{22}}}\\ {D_t^{0.97}{\zeta _{23}} = {\zeta _{21}}{\zeta _{22}} - 3{\zeta _{23}}}\\ {D_t^{0.97}{\zeta _{24}} = {\zeta _{22}}{\zeta _{23}} + 0.3{\zeta _{24}}}. \end{array}} \right. \end{aligned}$$
(73)

Example 3

In this example, the performance of the MR robot in accurately tracking the intended chaotic path is compared with other related controllers, namely, type-2 FLS-based controller (T2FPC) [41], and non-linear predictive controller (NPC) [42]. To assess the tracking accuracy, an additional perturbation in the form of Gaussian noise is introduced. The root-mean-square errors obtained from the experiments are presented in Table 2. The results indicate that the proposed predictive scheme exhibits better accuracy compared to the other controllers. Particularly, when subjected to higher noise conditions, the suggested type-3 FLS-based controller demonstrates superior resistance in accurately tracking the chaotic path. This further highlights the effectiveness and robustness of the implemented approach, making it highly suitable for real-world applications.

Table 2 Example 3: comparison of RMSE
Full size table

Conclusion

In this study, a new secure path planning and tracking scheme are developed for MRs with nonholonomic constraints and unknown dynamics. Multiple chaotic systems and a chaotic switching mechanism generate the reference trajectory. A strong controller is suggested that the robot well tracks the designed path, despite uncertain dynamics of MR, complicated chaotic reference path, and sudden changing of the reference. A new fuzzy controller based on fractional-order calculus is proposed. The suggested controller uses T3-FLSs to estimate the dynamics and predict the output. Also, an adaptive compensator is suggested to work in parallel with the main controller to guarantee stability.

The designed controller is experimentally applied on a real-world MR. The results confirm the feasibility of the suggested approach; it is shown that MR well follows the planned complicated path. Also, in two simulation examples, the controller’s accuracy is tested. In the first one, a hyperchaotic system with four states is considered the reference system. The first state is used for managing the switching mechanism, and the reference is chaotically switched between the other states. The simulation results demonstrate that the suggested controller results in the desired accuracy. In the second example, two hyperchaotic systems are considered, and the reference signal is switched between five signals, in a chaotic scheme. The MR well follows the designed path, and the results show good accuracy. Finally, a comparison with other related controllers is presented to show the superiority of the T3-FLS-based controller. It can be seen that under high-noisy conditions, the suggested technique has a much stable response.

The main limitation is that the controller does not support the resiliency of system against faults and cyber attacks. In future, the control of MR for resilience as well as fault tolerance will be studied. The concept of resilience along with its related concepts is referred to the literature [43, 44]. Also, the suggested controller can be improved by new prediction models [45], multi-agent task planning [46], and new optimization techniques [47]. Financial systems are another case of complicated systems that suggested method can be applied for. In our future studies, the suggested multi-switching chaotic systems and type-3 fuzzy control method are extended for modeling and analyzing of financial chaotic systems. We will use the suggested method for forecasting and controlling the chaotic behavior of financial problems.