Introduction

In real decision-making issues, the decision data are normally inaccurate, uncertain, or incomplete. Therefore, it is becoming more and more difficult to make scientific and reasonable decisions. Thus, to put it succinctly, Zadeh’s [59] concept of fuzzy set (FS) has played an important role in decision-making issues by allowing each element to have a membership degree. Later on, Atanassov [5] prolongs the FSs to intuitionistic FSs (IFSs) by adding nonmembership degrees along with MDs, such that their sum can’t pass one. In the contemporary world, the interconnected structure involves vulnerabilities in acquaintance with indeterminacy, and consequently, the existing FS or IFS are unable to manage the data effectively. In light of the deficiency in managing fragmented data, Smarandache [52] initiated the neutrosophic set (NS) by including the three individual mappings, in particular “truth”, “indeterminacy” and “falsity”, which are real or non-real subsets of \(]^{-}0, 1^{+}[\). A year later, NSs were extended to SVNSs on the basis of the standard real interval [0, 1] to facilitate their use in genuine logical and designing regions [54]. Because of its significance, a few specialists have implemented their attempts to enhance the idea of SVNSs in the decision-making approach.

Motivation of the study

Ye [58] primarily defined the functional laws for SVNSs and initiated the idea of weighted averaging/geometric operators. Peng et al. [38] noticed that several SVNS operations ascertained by Ye [57] were often incorrect, and they characterized new functional rules and AOs and utilized them to similarity measure issues. Peng et al. [37] characterized the score function in order to organize SVNSs. Later, Nancy and Garg [35] exhibited a further developed score function. Garai et al. [10] exhibited first time probability hypothesis of SVNNs and implemented it in decision-making issue. Mondal et al. [33] formulated a model, which is dependent on hybrid weighted score-accuracy functions and utilized it in the recruitment of teachers in educational institutions. Liu et al. [29] defined the operators on the basis of Hamacher norm. Nancy and Garg [36] developed Frank t-NM-based AOs for decision-making issues. In recent times, Tian et al. [53] and Zhao et al. [60] offered a few novel SVN Heronian power AOs and recommended new decision-making techniques utilizing the advanced operators. Wei and Zhang [55] defined some Bonferroni mean AOs. Yang and Li [56] presented power AOs for SVNS. Liu and Wang [30] outlined a weighted normalised Bonferroni mean AO of SVNS. Garg and Nancy [12] presented the power AOs for the linguistic SVNSs. Ji et al. [23] developed the frank prioritized BM operators for solving DMPs. Garg [13] defined the concept of neutrality functional rules and the AOs that are based on them for resolving decision-making concerns. Sahin et al. [41] considered the notion of subsethood as a measure for SVNSs. By analyzing Choquet integral, Heronian mean and Frank t-NM, Garg et al. [14] expanded the Heronian hybrid mean AOs for linguistic SVNSs. Majumdar et al. [31] and Qin et al. [39] calculated similarity measures, Hausdorff distances, cardinality, weights and entropy of SVNSs. Karaaslan and Hunu [24] presented Type-2 SVNSs and their utilization in MCGDM on the basis of TOPSIS method. Karaaslan [26] defined similarity measures for SVNSs under refined situations. Karaaslan and Hayat [25] defined a few novel operations for SVNSs and applied them to MCGDM concerns. Nabeeh et al. [34] consolidated AHP strategies with neutrosophic procedures to adequately introduce the models identified with powerful factors for a fruitful IoT venture. Basset et al. [7] recommended an approach that joins bipolar neutrosophic numbers with TOPSIS under GDM. By joining TOPSIS techniques and type-2 neutrosophic numbers, Basset et al. [6] recommended a novel T2NN-TOPSIS technique for retailer selection. Additional information on related operators and concepts can be found at [11, 15,16,17,18,19, 22].

Fig. 1
figure 1

Framework of the study

Full size image

Menger [32] introduced the tought of “triangular norms” in his concept of stochastic euclidean space, which was the starting point for the concept. In the early 2000s, Klement et al. [27] did a lot of good work on the features and parts of “triangular norms,” and their observations have been broadly accepted. AA [3] introduced two novel operations in 1982, which are referred to as AA t-NM and AA t-CNM, and they have a big effect on how parameters are used. Using the AA t-NMs, Senapati and his collaborators have just recently opened up new perspectives in the realm of decision-making arrangements. They had been using AA t-NMs to solve problems with making decisions in IFS [46, 47], interval-valued IFS [48, 49], hesitant fuzzy [50], Pythagorean fuzzy [51], environments. Motivated by these novel concepts, we developed an SVN MADM strategy focused on the AA AOs for managing SVN MADM within SVNSs. Figure 1 depicts the implications of our methodological approach.

Contributions of this study

The purpose of this investigation is to develop a strategic and insightful recommendation technique that will enable the choice of the alternative approach that represents the most appropriate alternative among a repository of alternatives. Using the AA t-NMs and t-CNMs, we have developed a new type of SVN AOs. Consequently, the primary objective of this research is to define the concepts of SVN AA weighted average AOs within the framework of SVNS. In addition, we show the effectiveness of various AOs. Ultimately, the following are the principal accomplishments of this paper:

  1. 1.

    To develop new AOs, such as the SVN Aczel-Alsina weighted average (SVNAAWA) operator, the SVN Aczel-Alsina order weighted average (SVNAAOWA) operator and the SVN Aczel-Alsina hybrid average (SVNAAHA) operator in the framework of SVNSs, it is necessary to investigate the basic operations of t-NMs and t-CNMs.

  2. 2.

    Investigate the properties of such novel operators, as well as specific examples of their use.

  3. 3.

    Construct an algorithm that can deal with MADM issues while also making use of SVN data.

  4. 4.

    Some computational results based on SVN data are discussed to figure out how reliable and useful the suggested method is.

  5. 5.

    In a comparison analysis, we contrast pre-existing AOs with those that we suggest. These comparison outcomes demonstrating the efficacy of the suggested AOs are exhaustively summarised.

  6. 6.

    To show that the presented method is both reliable and strong, sensitivity analyses are done.

Structure of this study

The sections of this paper are set up like this: “Preliminaries” presents fundamental notions related to t-NMs, t-CNMs, AA t-NMs, SVNs, and many operational rules in the context of SVNNs. In “AA operations of SVNNs”, we talk about the AA working rules and the properties of SVNNs. We outline several SVN AA AOs in “SVN AA average aggregation operators”. Additionally, we look at plenty of desired characteristics. “Method for MADM issues based on SVNAAWA operator” addresses the MADM concern through the use of SVN AA aggregated techniques. “Numerical example” contains an exemplary example. In “Evaluation of the influence of the operational parameter E on decision-making consequences”, we assess the influence of a parameter on the outcomes of decision-making. In “Sensitivity analysis (SA) of criteria weights”, we examine the impact of weighted criteria on ranking results. In “Comparative analysis”, the proposed AOs are compared to the dominant AOs. “Conclusions” summarizes the work and discusses potential future research.

Preliminaries

To begin, we will cover some fundamental aspects of t-NMs, t-CNMs, AA t-NMs, and SVNSs.

t-NMs, t-CNMs, AA t-NMs

A t-NM is a non-decreasing, symmetric, associative operation \(T:[0,1] \times [0,1] \rightarrow [0,1]\) with neutral element 1. The immediate consequences of this definition are the boundary conditions:

$$\begin{aligned} T(f, 1)= & {} T(1,f)=f, \end{aligned}$$
(1)
$$\begin{aligned} T(f,0)= & {} T(0,f)=0, \end{aligned}$$
(2)

for this reason, all t-NMs coincide on the boundary of the unit square \([0,1] \times [0,1]\).

Some examples of t-NMs are the product \(T_P\), the minimum \(T_M\), the Lukasiewicz t-NM \(T_L\), and the Drastic t-NM \(T_D\) given, respectively, by

$$\begin{aligned} T_{P}(f,z)= & {} f.z \end{aligned}$$
(3)
$$\begin{aligned} T_{M}(f,z)= & {} \min (f,z) \end{aligned}$$
(4)
$$\begin{aligned} T_{L}(f,z)= & {} \max (f + z-1, 0)\end{aligned}$$
(5)
$$\begin{aligned} T_D(f,z)= & {} \left\{ \begin{array}{ll} f, &{} \text{ if } z=1\\ z, &{} \text{ if } f=1\\ 0, &{} \text{ otherwise } \end{array}\right. , \end{aligned}$$
(6)

for all \(f, z \in [0, 1]\).

A t-CNM is a symmetric, associative, non-decreasing operation \(S:[0,1] \times [0,1]\rightarrow [0,1]\) with \(S(f,0) =f\) for all \(f \in [0, 1]\).

The distinction between t-NMs and t-CNMs is self-evident. Let \(N:[0, 1] \rightarrow [0, 1]\) be a strong (fuzzy) negation, i.e., an involution that reverses the order. The mapping \(S_{T, N}:[0, 1] \times [0,1] \rightarrow [0, 1]\) described by

$$\begin{aligned} S_{T, N}(f, z)=N(T(N(f),N(z))) \end{aligned}$$
(7)

is a t-CNM, also known as the N-dual of T, for a t-NM T. In addition, for a t-CNM S, the mapping \(T_{S,N}:[0, 1] \times [0,1] \rightarrow [0,1]\) provided by

$$\begin{aligned} T_{S,N}(f,z)=N(S(N(f),N(z))) \end{aligned}$$
(8)

is a t-NM, known as the N-dual of the t-CNM S.

The duals of the four t-NMs are the probabilistic sum \(S_P\), the maximum \(S_M\), the Lukasiewicz t-CNM \(S_L\), and the Drastic t-CNM \(S_D\) given, respectively, by

$$\begin{aligned} S_{P}(f,z)= & {} f+z-f.z \end{aligned}$$
(9)
$$\begin{aligned} S_{M}(f,z)= & {} \max (f,z) \end{aligned}$$
(10)
$$\begin{aligned} S_{L}(f,z)= & {} \min (f + z, 1)\end{aligned}$$
(11)
$$\begin{aligned} S_D(f,z)= & {} \left\{ \begin{array}{ll} f, &{} \text{ if } z=0\\ z, &{} \text{ if } f=0\\ 1, &{} \text{ otherwise } \end{array}\right. \end{aligned}$$
(12)

for every \(f, z \in [0, 1]\).

Definition 1

[3, 4](AA t-NM) AA introduced this category of t-NM in the early 1980s, for \(0 \le \varrho \le + \infty \), in terms of functional equations, and it has been in use ever since.

The category \((T_{A}^{\varrho })_{\varrho \in [0,\infty ]}\) of AA t-NMs are constructed as

$$\begin{aligned} T_{A}^{\varrho }(f,z)=\left\{ \begin{array}{ll} T_D(f,z), &{} \textrm{if} \,\, \varrho =0\\ \min (f,z), &{} \textrm{if} \,\, \varrho =+ \infty \\ e^{-((-\ln f)^\varrho +(-\ln z)^\varrho )^{1/\varrho }}, &{} \textrm{if} \,\, 0<\varrho < +\infty \end{array}\right. \end{aligned}$$
(13)

The category \((S_{A}^{\varrho })_{\varrho \in [0,\infty ]}\) of AA t-CNMs are constructed as

$$\begin{aligned}{} & {} S_{A}^{\varrho }(f,z)\nonumber \\{} & {} =\left\{ \begin{array}{ll} S_D(f,z), &{} \textrm{if} \,\, \varrho =0\\ \max (f,z), &{} \textrm{if} \,\, \varrho =+ \infty \\ 1-e^{-((-\ln (1- f))^\varrho +(-\ln (1-z))^\varrho )^{1/\varrho }}, &{} \textrm{if} \,\, 0<\varrho < +\infty \end{array}\right. \nonumber \\ \end{aligned}$$
(14)

Limiting values: \(T_{A}^{0}=T_D\), \(T_{A}^{\infty }=\min \), \(T_{A}^{1}=T_P\), \(S_{A}^{0}=S_D\), \(S_{A}^{\infty }=\max \), \(S_{A}^{1}=S_P\).

The t-NM \(T_{A}^{\varrho }\) and t-CNM \(S_{A}^{\varrho }\) are dual to one another for each \(\varrho \in [0,\infty ]\). The class of AA t-NMs is strictly increasing, and the class of AA t-CNMs is strictly decreasing.

SVNSs

SVNS is a particular type of neutrosophic set. It tends to be utilized in engineering and real-world scientific problems. In these subsections, we give a few basic definitions, SVN operations, and information about how they work with SVNSs [54].

Definition 2

[54] Let \(\varPhi \) be defined as a set of objects (points), with a conventional component in \(\varPhi \) indicated by \(\phi \). A SVNS E in \(\varPhi \) is portrayed by three membership functions (MFs): a truth-MF \(\hat{\eta }_E\), an indeterminacy-MF \(\hat{\gamma }_E\), and a falsity-MF \(\hat{\wp }_E\). If the functions \(\hat{\eta }_E\), \(\hat{\gamma }_E\) and \(\hat{\wp }_E\) are defined in terms of singleton subintervals or subsets in the real standard [0, 1] (i.e., \(\hat{\eta }_E: \varPhi \rightarrow [0, 1]\), \(\hat{\gamma }_E: \varPhi \rightarrow [0, 1]\) and \(\hat{\wp }_E: \varPhi \rightarrow [0, 1]\), respectively), then the sum of \(\hat{\eta }_E(\phi )\), \(\hat{\gamma }_E(\phi )\), and \(\hat{\wp }_E(\phi )\) fulfills the condition:

$$\begin{aligned} 0 \le \hat{\eta }_E(\phi )+\hat{\gamma }_E(\phi )+\hat{\wp }_E(\phi )\le 3 \end{aligned}$$
(15)

for any \(\phi \in \varPhi \). Then, an SVNS E is denoted in the following manner:

$$\begin{aligned} E=\{\phi , \langle \hat{\eta }_E(\phi ), \hat{\gamma }_E(\phi ), \hat{\wp }_E(\phi )\rangle |\phi \in \varPhi \}, \end{aligned}$$
(16)

is referred to as a “single-valued neutrosophic set (SVNS)”.

For simplification purposes, the ordered triple component \((\hat{\eta }_E(\phi ),\hat{\gamma }_E(\phi ),\) \(\hat{\wp }_E(\phi ) )\), which is the core of SVNS, may be referred to as a “single-valued neutrosophic number (SVNN)”.

Definition 3

[30, 37] If \(E=(\hat{\eta }_{E}, \hat{\gamma }_{E}, \hat{\wp }_{E})\), \(E_1=(\hat{\eta }_{E_1}, \hat{\gamma }_{E_1}, \hat{\wp }_{E_1})\) and \(E_2=(\hat{\eta }_{E_2}, \hat{\gamma }_{E_2},\) \(\hat{\wp }_{E_2})\) are three SVNNs in the universe \(\varPhi \), then the following operations are generally expressed as follows:

$$\begin{aligned}{} & {} E_1\subseteq E_2, \quad \text{ if } \hat{\eta }_{E_1}(\phi )\le \hat{\eta }_{E_2}(\phi ), \hat{\gamma }_{E_1}(\phi )\le \hat{\gamma }_{E_2}(\phi ) \text{ and } \nonumber \\{} & {} \hat{\wp }_{E_1}(\phi )\ge \hat{\wp }_{E_2}(\phi ); \end{aligned}$$
(17)
$$\begin{aligned}{} & {} E_1=E_2 \quad \text{ iff } E_1 \subseteq E_2 \text{ and } E_2 \subseteq E_1; \end{aligned}$$
(18)
$$\begin{aligned}{} & {} E_1 \cup E_2 = \langle \max \{\hat{\eta }_{E_1}(\phi ),\hat{\eta }_{E_2}(\phi )\}, \min \{\hat{\gamma }_{E_1}(\phi ),\hat{\gamma }_{E_2}(\phi )\}, \nonumber \\{} & {} \qquad \qquad \qquad \quad \min \{\hat{\wp }_{E_1}(\phi ),\hat{\wp }_{E_2} (\phi )\}\rangle ; \end{aligned}$$
(19)
$$\begin{aligned}{} & {} E_1 \cap E_2 = \langle \min \{\hat{\eta }_{E_1}(\phi ),\hat{\eta }_{E_2}(\phi )\}, \max \{\hat{\gamma }_{E_1}(\phi ),\hat{\gamma }_{E_2}(\phi )\}, \nonumber \\{} & {} \qquad \qquad \qquad \quad \max \{\hat{\wp }_{E_1}(\phi ),\hat{\wp }_{E_2}\}\rangle ; \end{aligned}$$
(20)
$$\begin{aligned}{} & {} \overline{E} = \langle \hat{\wp }_E(\phi ), 1-\hat{\gamma }_E(\phi ), \hat{\eta }_E(\phi )\rangle ; \end{aligned}$$
(21)
$$\begin{aligned}{} & {} E_1 \bigoplus E_2 = \big \langle \hat{\eta }_{E_1}(\phi )+\hat{\eta }_{E_2}(\phi )-\hat{\eta }_{E_1}(\phi )\hat{\eta }_{E_2}(\phi ),\nonumber \\{} & {} \hat{\gamma }_{E_1}(\phi )\hat{\gamma }_{E_2}(\phi ), \hat{\wp }_{E_1}(\phi )\hat{\wp }_{E_2}(\phi )\big \rangle ; \end{aligned}$$
(22)
$$\begin{aligned}{} & {} E_1 \bigotimes E_2 = \big \langle \hat{\eta }_{E_1}(\phi )\hat{\eta }_{E_2}(\phi ),\hat{\gamma }_{E_1}(\phi )+\hat{\gamma }_{E_2}(\phi )-\hat{\gamma }_{E_1}(\phi )\nonumber \\{} & {} \qquad \times \hat{\gamma }_{E_2}(\phi ),\hat{\wp }_{E_1}(\phi )+\hat{\wp }_{E_2}(\phi ) -\hat{\wp }_{E_1}(\phi )\hat{\wp }_{E_2}(\phi )\big \rangle ; \end{aligned}$$
(23)
$$\begin{aligned}{} & {} \delta E = \big \langle 1-(1-\hat{\eta }_E(\phi ))^{\delta }, \hat{\gamma }^{\delta }_E(\phi ), \hat{\wp }^{\delta }_E(\phi )\big \rangle ; \end{aligned}$$
(24)
$$\begin{aligned}{} & {} E^{\delta } = \big \langle \hat{\eta }_E^{\delta }(\phi ), 1-(1-\hat{\gamma }_E(\phi ))^{\delta }, 1-(1-\hat{\wp }_E(\phi ))^{\delta }\big \rangle . \end{aligned}$$
(25)

Definition 4

[54] Let \(E=(\hat{\eta }_{E}, \hat{\gamma }_{E}, \hat{\wp }_{E})\), \(E_1=(\hat{\eta }_{E_1}, \hat{\gamma }_{E_1}, \hat{\wp }_{E_1})\) and \(E_2=(\hat{\eta }_{E_2}, \hat{\gamma }_{E_2},\) \(\hat{\wp }_{E_2})\) be three SVNNs over the universe \(\varPhi \) and \(\delta ,\delta _1,\delta _2>0\), then

$$\begin{aligned}{} & {} E_1 \bigoplus E_2= E_2 \bigoplus E_1, \end{aligned}$$
(26)
$$\begin{aligned}{} & {} E_1 \bigotimes E_2= E_2 \bigotimes E_1,\end{aligned}$$
(27)
$$\begin{aligned}{} & {} \delta (E_1 \bigoplus E_2)=\delta E_1 \bigoplus \delta E_2, \end{aligned}$$
(28)
$$\begin{aligned}{} & {} (E_1 \bigotimes E_2)^{\delta }=E_{1}^{\delta }\bigotimes E_{2}^{\delta }, \end{aligned}$$
(29)
$$\begin{aligned}{} & {} \delta _1E \bigoplus \delta _2 E=(\delta _1+\delta _2)E, \end{aligned}$$
(30)
$$\begin{aligned}{} & {} E^{\delta _1}\bigotimes E^{\delta _2}=E^{(\delta _1+\delta _2)}, \end{aligned}$$
(31)
$$\begin{aligned}{} & {} (E^{\delta _1})^{\delta _2}=E^{\delta _1\delta _2}. \end{aligned}$$
(32)

Definition 5

[37] Let \(E_1=(\hat{\eta }_{E_1}, \hat{\gamma }_{E_1}, \hat{\wp }_{E_1})\) and \(E_2=(\hat{\eta }_{E_2}, \hat{\gamma }_{E_2}, \hat{\wp }_{E_2})\) be two SVNNs, and the comparison methodology for SVNNs would be like this:

  1. (1)

    If \(\hat{Y}(E_1)> \hat{Y}(E_2)\) or \(\hat{Y}(E_1)= \hat{Y}(E_2)\) and \(\hat{K}(E_1) > \hat{K}(E_2)\), then \(E_1 \succ E_2\);

  2. (2)

    If \(\hat{Y}(E_1)< \hat{Y}(E_2)\) or \(\hat{Y}(E_1)= \hat{Y}(E_2)\) and \(\hat{K}(E_1) < \hat{K}(E_2)\), then \(E_1 \prec E_2\);

  3. (3)

    If \(\hat{Y}(E_1)= \hat{Y}(E_2)\) and \(\hat{K}(E_1) =\hat{K}(E_2)\), then \(E_1=E_2\);

where

$$\begin{aligned} \hat{Y}(E_i)= & {} \frac{1}{3}(\hat{\eta }_{E_i}+1-\hat{\gamma }_{E_i}+1-\hat{\wp }_{E_i}),\nonumber \\ \hat{Y}(E_i)\in & {} [0,1], \end{aligned}$$
(33)
$$\begin{aligned} \hat{K}(E_i)= & {} \hat{\eta }_{E_i}- \hat{\wp }_{E_i}, \hat{K}(E_i)\in [-1,1] \end{aligned}$$
(34)

\((i=1,2)\), respectively, denote the scoring and accuracy functions.

The weighted averaging AOs are described this way for a set of SVNNs:

Definition 6

[37] Let \(\tilde{\mathfrak {U}}_\varphi =(\hat{\eta }_\varphi ,\hat{\gamma }_\varphi ,\hat{\wp }_\varphi )\) \((\varphi =1,2,\ldots ,\rho )\) represent a set of SVNNs. A SVN weighted averaging (SVNWA) operator of dimension \(\rho \) is a mapping \(\tilde{P}^{\rho }\rightarrow \tilde{P}\) that is closely correlated with a weight vector \(\mathfrak {F}=(\mathfrak {F}_1,\mathfrak {F}_2,\ldots ,\mathfrak {F}_\rho )^{T}\) such that \(\mathfrak {F}> 0\) and \(\sum ^{\rho }\nolimits _{\varphi =1} \mathfrak {F}_\varphi =1\), as

$$\begin{aligned}{} & {} SVNWA_{\mathfrak {F}}(\tilde{\mathfrak {U}}_1,\tilde{\mathfrak {U}}_2,\ldots , \tilde{\mathfrak {U}}_\rho )=\bigoplus ^{\rho }\limits _{\varphi =1}(\mathfrak {F}_\varphi \tilde{\mathfrak {U}}_\varphi )\nonumber \\{} & {} \quad =\left( 1-\prod ^{\rho }\limits _{\varphi =1}{(1-\hat{\eta }_\varphi )}^{\mathfrak {F}_\varphi }, \prod ^{\rho }\limits _{\varphi =1}{\hat{\gamma }_\varphi }^{\mathfrak {F}_\varphi }, \prod ^{\rho }\limits _{\varphi =1}{\hat{\wp }_\varphi }^{\mathfrak {F}_\varphi }\right) . \end{aligned}$$
(35)

Definition 7

[37] Let \(\tilde{\mathfrak {U}}_\varphi =(\hat{\eta }_\varphi ,\hat{\gamma }_\varphi ,\hat{\wp }_\varphi )\) \((\varphi =1,2,\ldots ,\rho )\) represent a collection of SVNNs. A SVN ordered weighted averaging (SVNOWA) operator of dimension \(\rho \) is a function \(\tilde{P}^{\rho }\rightarrow \tilde{P}\) that is closely correlated with weight vector \(\mathfrak {F}=(\mathfrak {F}_1,\mathfrak {F}_2,\ldots ,\mathfrak {F}_\rho )^{T}\) including \(\mathfrak {F}> 0\) and \(\sum ^{\rho }\nolimits _{\varphi =1} \mathfrak {F}_\varphi =1\), as

$$\begin{aligned}{} & {} SVNOWA_{\mathfrak {F}}(\tilde{\mathfrak {U}}_1,\tilde{\mathfrak {U}}_2,\ldots , \tilde{\mathfrak {U}}_\rho )=\bigoplus ^{\rho }\limits _{\varphi =1}\Big (\mathfrak {F}_\varphi \tilde{\mathfrak {U}}_{(\mathfrak {T}_\varphi )}\Big )\nonumber \\{} & {} \quad =\left( 1-\prod ^{\rho }\limits _{\varphi =1}{\Big (1-\hat{\eta }_{\mathfrak {T}(\varphi )}\Big )}^{\mathfrak {F}_\varphi },\prod ^{\rho }\limits _{\varphi =1}{\hat{\gamma }^{\mathfrak {F}_\varphi }_{\mathfrak {T}(\varphi )}}, \prod ^{\rho }\limits _{\varphi =1}{\hat{\wp }^{\mathfrak {F}_\varphi }_{\mathfrak {T}(\varphi )}}\right) ,\nonumber \\ \end{aligned}$$
(36)

where \((\mathfrak {T}(1),\mathfrak {T}(2),\ldots ,\mathfrak {T}(\rho ))\) is a permutation of \((1,2,\ldots ,\rho )\), including \(\tilde{\mathfrak {U}}_{\mathfrak {T}(\varphi -1)}\ge \tilde{\mathfrak {U}}_{\mathfrak {T}(\varphi )}\) for each \(\varphi =1,2,\ldots ,\rho \).

AA operations of SVNNs

In light of AA t-NM and AA t-CNM, we explained AA operations concerning SVNNs.

Definition 8

Let \(\tilde{\mathfrak {U}}=(\hat{\eta }, \hat{\gamma }, \hat{\wp })\), \(\tilde{\mathfrak {U}}_1=(\hat{\eta }_1, \hat{\gamma }_1, \hat{\wp }_1)\) and \(\tilde{\mathfrak {U}}_2=(\hat{\eta }_2, \hat{\gamma }_2, \hat{\wp }_2)\) be three SVNNs, \(\mathfrak {E} \ge 1\) and a constant \(\delta >0\). Hence, the AA t-NM and AA t-CNM operations of SVNNs are formulated as having

  1. (i)
    $$\begin{aligned}{} & {} \tilde{\mathfrak {U}}_1 \oplus \tilde{\mathfrak {U}}_2= \Big \langle 1-e^{-((-\ln (1- \hat{\eta }_1))^\mathfrak {E}+(-\ln (1-\hat{\eta }_2))^\mathfrak {E})^{1/\mathfrak {E}}},\\{} & {} e^{-((-\ln \hat{\gamma }_1)^\mathfrak {E}+(-\ln \hat{\gamma }_2)^\mathfrak {E})^{1/\mathfrak {E}}}, e^{-((-\ln \hat{\wp }_1)^\mathfrak {E}+(-\ln \hat{\wp }_2)^\mathfrak {E})^{1/\mathfrak {E}}}\Big \rangle ; \end{aligned}$$
  2. (ii)
    $$\begin{aligned}{} & {} \tilde{\mathfrak {U}}_1 \otimes \tilde{\mathfrak {U}}_2= \Big \langle e^{-((-\ln \hat{\eta }_1)^\mathfrak {E}+(-\ln \hat{\eta }_2)^\mathfrak {E})^{1/\mathfrak {E}}},\\{} & {} 1- e^{-((-\ln (1- \hat{\gamma }_1))^\mathfrak {E}+(-\ln (1-\hat{\gamma }_2))^\mathfrak {E})^{1/\mathfrak {E}}},\\{} & {} 1-e^{-((-\ln (1- \hat{\wp }_1))^\mathfrak {E}+(-\ln (1-\hat{\wp }_2))^\mathfrak {E})^{1/\mathfrak {E}}} \Big \rangle ; \end{aligned}$$
  3. (iii)
    $$\begin{aligned}{} & {} \delta .\; \tilde{\mathfrak {U}} =\Big \langle 1-e^{-(\delta (-\ln (1- \hat{\eta }))^\mathfrak {E})^{1/\mathfrak {E}}},\\{} & {} e^{-(\delta (-\ln \hat{\gamma })^\mathfrak {E})^{1/\mathfrak {E}}}, e^{-(\delta (-\ln \hat{\wp })^\mathfrak {E})^{1/\mathfrak {E}}} \Big \rangle ; \end{aligned}$$
  4. (iv)
    $$\begin{aligned}{} & {} \tilde{\mathfrak {U}}^{\delta }=\Big \langle e^{-(\delta (-\ln \hat{\eta })^\mathfrak {E})^{1/\mathfrak {E}}},\\{} & {} 1-e^{-(\delta (-\ln (1- \hat{\gamma }))^\mathfrak {E})^{1/\mathfrak {E}}}, 1-e^{-(\delta (-\ln (1- \hat{\wp }))^\mathfrak {E})^{1/\mathfrak {E}}}\Big \rangle . \end{aligned}$$

Example 1

Let \(\tilde{\mathfrak {U}}{=}0.58, 0.82,0.33)\), \(\tilde{\mathfrak {U}}_1{=}(0.78, 0.23,0.41)\) and \(\tilde{\mathfrak {U}}_2=(0.34,\) 0.62, 0.38) be three SVNNs. Using the AA operation on SVNNs as specified in Definition 8 for \(\mathfrak {E}=3\) and \(\delta =6\), we can get

  1. (i)

       

    $$\begin{aligned}{} & {} \tilde{\mathfrak {U}}_1 \oplus \tilde{\mathfrak {U}}_2 =\Big \langle 1-e^{-((-\ln (1- 0.78))^3+(-\ln (1-0.34))^3)^{1/3}},\\{} & {} \qquad e^{-((-\ln 0.23)^3+(-\ln 0.62)^3)^{1/3}},\\{} & {} \quad e^{-((-\ln 0.41)^3+(-\ln 0.38)^3)^{1/3}}\Big \rangle \\{} & {} \quad =\langle 0.782267369, 0.226197985, 0.309386337 \rangle . \end{aligned}$$
  2. (ii)

       

    $$\begin{aligned}{} & {} \tilde{\mathfrak {U}}_1\otimes \tilde{\mathfrak {U}}_2= \Big \langle e^{-((-\ln 0.78)^3+(-\ln 0.34)^3)^{1/3}},\\{} & {} \qquad 1- e^{-((-\ln (1- 0.23))^3+(-\ln (1-0.62))^3)^{1/3}},\\{} & {} \qquad 1-e^{-((-\ln (1- 0.41))^3+(-\ln (1-0.38))^3)^{1/3}}\Big \rangle \\{} & {} \quad =\langle 0.338515656 0.622392345 0.470100879 \rangle . \end{aligned}$$
  3. (iii)
    $$\begin{aligned} \quad 6.\; \tilde{\mathfrak {U}}= & {} \Big \langle 1-e^{-(6(-\ln (1- 0.58))^3)^{1/3}}, e^{-(6(-\ln 0.82)^3)^{1/3}},\\{} & {} \quad e^{-(6(-\ln 0.33)^3)^{1/3}}\Big \rangle \\= & {} \langle 0.793272369, 0.69725137, 0.133377252 \rangle . \end{aligned}$$
  4. (iv)
    $$\begin{aligned} \quad \tilde{\mathfrak {U}}^{6}= & {} \Big \langle e^{-(6(-\ln 0.58)^3)^{1/3}}, 1-e^{-(6(-\ln (1- 0.82))^3)^{1/3}},\\{} & {} 1-e^{-(6(-\ln (1- 0.33))^3)^{1/3}} \Big \rangle \\= & {} \langle 0.371638018, 0.955665651, 0.516989088 \rangle . \end{aligned}$$

Theorem 1

Let \(\tilde{\mathfrak {U}}=(\hat{\eta }, \hat{\gamma }, \hat{\wp })\), \(\tilde{\mathfrak {U}}_1=(\hat{\eta }_1, \hat{\gamma }_1, \hat{\wp }_1)\), \(\tilde{\mathfrak {U}}_2=(\hat{\eta }_2, \hat{\gamma }_2, \hat{\wp }_2)\) be three SVNNs, and \(\delta , \delta _1, \delta _2\) be three constants \(>0\), then we obtain

  1. (i)

    \(\tilde{\mathfrak {U}}_1 \oplus \tilde{\mathfrak {U}}_2=\tilde{\mathfrak {U}}_2 \oplus \tilde{\mathfrak {U}}_1\),

  2. (ii)

    \(\tilde{\mathfrak {U}}_1 \otimes \tilde{\mathfrak {U}}_2=\tilde{\mathfrak {U}}_2 \otimes \tilde{\mathfrak {U}}_1\),

  3. (iii)

    \(\delta (\tilde{\mathfrak {U}}_1 \oplus \tilde{\mathfrak {U}}_2)=\delta \tilde{\mathfrak {U}}_1 \oplus \delta \tilde{\mathfrak {U}}_2\), \(\delta >0\),

  4. (iv)

    \((\delta _1+\delta _2 )\tilde{\mathfrak {U}}=\delta _1 \tilde{\mathfrak {U}} \oplus \delta _2 \tilde{\mathfrak {U}}\), \(\delta _1, \delta _2 >0\),

  5. (v)

    \( (\tilde{\mathfrak {U}}_1 \otimes \tilde{\mathfrak {U}}_2)^\delta =\tilde{\mathfrak {U}}_1^\delta \otimes \tilde{\mathfrak {U}}_2^\delta \), \(\delta >0\),

  6. (vi)

    \(\tilde{\mathfrak {U}}^{\delta _1} \otimes \tilde{\mathfrak {U}}^{\delta _2}=\tilde{\mathfrak {U}}^{(\delta _1+\delta _2 )}\), \(\delta _1, \delta _2 >0\).

Proof

In accordance with Definition 8, we may obtain the following for the three SVNNs \(\tilde{\mathfrak {U}}\), \(\tilde{\mathfrak {U}}_1\) and \(\tilde{\mathfrak {U}}_2\), and \(\delta , \delta _1, \delta _2 > 0\).

  1. (i)
    $$\begin{aligned}{} & {} \tilde{\mathfrak {U}}_1\oplus \tilde{\mathfrak {U}}_2= \Big \langle 1-e^{-((-\ln (1- \hat{\eta }_1))^\mathfrak {E}+(-\ln (1-\hat{\eta }_2))^\mathfrak {E})^{1/\mathfrak {E}}},\\{} & {} \quad e^{{-}(({-}\ln \hat{\gamma }_1)^\mathfrak {E}{+}({-}\ln \hat{\gamma }_2)^\mathfrak {E})^{1/\mathfrak {E}}}, e^{{-}(({-}\ln \hat{\wp }_1)^\mathfrak {E}{+}({-}\ln \hat{\wp }_2)^\mathfrak {E})^{1/\mathfrak {E}}}\Big \rangle \\{} & {} \quad =\Big \langle 1-e^{-((-\ln (1- \hat{\eta }_2))^\mathfrak {E}+(-\ln (1-\hat{\eta }_1))^\mathfrak {E})^{1/\mathfrak {E}}},\\{} & {} \qquad e^{-((-\ln \hat{\gamma }_2)^\mathfrak {E}+(-\ln \hat{\gamma }_1)^\mathfrak {E})^{1/\mathfrak {E}}}, \\{} & {} \qquad e^{-((-\ln \hat{\wp }_2)^\mathfrak {E}+(-\ln \hat{\wp }_1)^\mathfrak {E})^{1/\mathfrak {E}}}\Big \rangle =\tilde{\mathfrak {U}}_2 \oplus \tilde{\mathfrak {U}}_1. \end{aligned}$$
  2. (ii)

    It is straightforward.

  3. (iii)

    Assume \(t= 1-e^{-((-\ln (1- \hat{\eta }_1))^\mathfrak {E}+(-\ln (1-\hat{\eta }_2))^\mathfrak {E})^{1/\mathfrak {E}}}\).

    Therefore \(\ln (1-t)=-((-\ln (1- \hat{\eta }_1))^\mathfrak {E}+(-\ln (1-\hat{\eta }_2))^\mathfrak {E})^{1/\mathfrak {E}}\).

    This gives us

    $$\begin{aligned}{} & {} \delta (\tilde{\mathfrak {U}}_1 \oplus \tilde{\mathfrak {U}}_2)=\delta \Big \langle 1-e^{-((-\ln (1- \hat{\eta }_1))^\mathfrak {E}+(-\ln (1-\hat{\eta }_2))^\mathfrak {E})^{1/\mathfrak {E}}},\\{} & {} \quad e^{-((-\ln \hat{\gamma }_1)^\mathfrak {E}+(-\ln \hat{\gamma }_2)^\mathfrak {E})^{1/\mathfrak {E}}}, e^{-((-\ln \hat{\wp }_1)^\mathfrak {E}+(-\ln \hat{\wp }_2)^\mathfrak {E})^{1/\mathfrak {E}}}\Big \rangle \\{} & {} \quad =\Big \langle 1- e^{-(\delta ((-\ln (1- \hat{\eta }_1))^\mathfrak {E}+(-\ln (1-\hat{\eta }_2))^\mathfrak {E})^{1/\mathfrak {E}}},\\{} & {} \qquad e^{-(\delta ((-\ln \hat{\gamma }_1)^\mathfrak {E}+(-\ln \hat{\gamma }_2)^\mathfrak {E}))^{1/\mathfrak {E}}},\\{} & {} \quad e^{-(\delta ((-\ln \hat{\wp }_1)^\mathfrak {E}+(-\ln \hat{\wp }_2)^\mathfrak {E}))^{1/\mathfrak {E}}}\Big \rangle \\{} & {} \quad =\Big \langle 1-e^{-(\delta (-\ln (1- \hat{\eta }_1))^\mathfrak {E})^{1/\mathfrak {E}}}, e^{-(\delta (-\ln \hat{\gamma }_1)^\mathfrak {E})^{1/\mathfrak {E}}},\\{} & {} \qquad e^{-(\delta (-\ln \hat{\wp }_1)^\mathfrak {E})^{1/\mathfrak {E}}}\Big \rangle \\{} & {} \qquad \oplus \Big \langle 1-e^{-(\delta (-\ln (1- \hat{\eta }_2))^\mathfrak {E})^{1/\mathfrak {E}}}, e^{-(\delta (-\ln \hat{\gamma }_2)^\mathfrak {E})^{1/\mathfrak {E}}}, \\{} & {} \quad e^{-(\delta (-\ln \hat{\wp }_2)^\mathfrak {E})^{1/\mathfrak {E}}}\Big \rangle \\{} & {} \quad =\delta \tilde{\mathfrak {U}}_1 \oplus \delta \tilde{\mathfrak {U}}_2. \end{aligned}$$
  4. (iv)
    $$\begin{aligned}{} & {} \delta _1 \tilde{\mathfrak {U}} \oplus \delta _2 \tilde{\mathfrak {U}}=\Big \langle 1-e^{-(\delta _1(-\ln (1- \hat{\eta }))^\mathfrak {E})^{1/\mathfrak {E}}}, e^{-(\delta _1(-\ln \hat{\gamma })^\mathfrak {E})^{1/\mathfrak {E}}}, \\{} & {} \qquad e^{-(\delta _1(-\ln \hat{\wp })^\mathfrak {E})^{1/\mathfrak {E}}}\Big \rangle \\{} & {} \quad \oplus \Big \langle 1-e^{-(\delta _2(-\ln (1- \hat{\eta }))^\mathfrak {E})^{1/\mathfrak {E}}}, e^{-(\delta _2(-\ln \hat{\gamma })^\mathfrak {E})^{1/\mathfrak {E}}}, \\{} & {} \qquad e^{-(\delta _2(-\ln \hat{\wp })^\mathfrak {E})^{1/\mathfrak {E}}}\Big \rangle \\{} & {} \qquad =\Big \langle 1-e^{-((\delta _1+\delta _2)(-\ln (1- \hat{\eta }))^\mathfrak {E})^{1/\mathfrak {E}}}, \\{} & {} \quad e^{-((\delta _1+\delta _2)(-\ln \hat{\gamma })^\mathfrak {E})^{1/\mathfrak {E}}}, e^{-((\delta _1+\delta _2)(-\ln \hat{\wp })^\mathfrak {E})^{1/\mathfrak {E}}}\Big \rangle \\{} & {} \quad =(\delta _1+\delta _2 )\tilde{\mathfrak {U}}. \end{aligned}$$
  5. (v)
    $$\begin{aligned}{} & {} (\tilde{\mathfrak {U}}_1 \otimes \tilde{\mathfrak {U}}_2)^\delta = \Big \langle e^{-((-\ln \hat{\eta }_1)^\mathfrak {E}+(-\ln \hat{\eta }_2)^\mathfrak {E})^{1/\mathfrak {E}}},\\{} & {} \qquad 1- e^{-((-\ln (1- \hat{\gamma }_1))^\mathfrak {E}+(-\ln (1-\hat{\gamma }_2))^\mathfrak {E})^{1/\mathfrak {E}}},\\{} & {} \qquad 1-e^{-((-\ln (1- \hat{\wp }_1))^\mathfrak {E}+(-\ln (1-\hat{\wp }_2))^\mathfrak {E})^{1/\mathfrak {E}}} \Big \rangle ^\delta \\{} & {} \quad =\Big \langle e^{-(\delta ((-\ln \hat{\eta }_1)^\mathfrak {E}+(-\ln \hat{\eta }_2)^\mathfrak {E}))^{1/\mathfrak {E}}},\\{} & {} \qquad 1-e^{-(\delta ((-\ln (1- \hat{\gamma }_1))^\mathfrak {E}+(-\ln (1-\hat{\gamma }_2))^\mathfrak {E})^{1/\mathfrak {E}}},\\{} & {} \qquad 1-e^{-(\delta ((-\ln (1- \hat{\wp }_1))^\mathfrak {E}+(-\ln (1-\hat{\wp }_2))^\mathfrak {E})^{1/\mathfrak {E}}}\Big \rangle \\{} & {} \quad =\Big \langle e^{-(\delta (-\ln \hat{\eta }_1)^\mathfrak {E})^{1/\mathfrak {E}}}, 1- e^{-(\delta (-\ln (1- \hat{\gamma }_1))^\mathfrak {E})^{1/\mathfrak {E}}},\\{} & {} \qquad 1-e^{-(\delta (-\ln (1- \hat{\wp }_1))^\mathfrak {E})^{1/\mathfrak {E}}}\Big \rangle \oplus \Big \langle e^{-(\delta (-\ln \hat{\eta }_2)^\mathfrak {E})^{1/\mathfrak {E}}},\\{} & {} \qquad 1-e^{-(\delta (-\ln (1- \hat{\gamma }_2))^\mathfrak {E})^{1/\mathfrak {E}}}, 1-e^{-(\delta (-\ln (1- \hat{\wp }_2))^\mathfrak {E})^{1/\mathfrak {E}}}\Big \rangle \\{} & {} \quad =\tilde{\mathfrak {U}}_1^\delta \otimes \tilde{\mathfrak {U}}_2^\delta . \end{aligned}$$
  6. (vi)
    $$\begin{aligned}{} & {} \tilde{\mathfrak {U}}^{\delta _1} \otimes \tilde{\mathfrak {U}}^{\delta _2} =\Big \langle e^{-(\delta _1(-\ln \hat{\eta })^\mathfrak {E})^{1/\mathfrak {E}}}, 1-e^{-(\delta _1(-\ln (1- \hat{\gamma }))^\mathfrak {E})^{1/\mathfrak {E}}},\\{} & {} \qquad 1-e^{-(\delta _1(-\ln (1- \hat{\wp }))^\mathfrak {E})^{1/\mathfrak {E}}} \Big \rangle \\{} & {} \quad \otimes \Big \langle e^{-(\delta _2(-\ln \hat{\eta })^\mathfrak {E})^{1/\mathfrak {E}}}, 1-e^{-(\delta _2(-\ln (1- \hat{\gamma }))^\mathfrak {E})^{1/\mathfrak {E}}}, \\{} & {} \qquad 1-e^{-(\delta _2(-\ln (1- \hat{\wp }))^\mathfrak {E})^{1/\mathfrak {E}}} \Big \rangle =\Big \langle e^{-((\delta _1+\delta _2)(-\ln \hat{\eta })^\mathfrak {E})^{1/\mathfrak {E}}}, \\{} & {} \qquad 1- e^{-((\delta _1+\delta _2)(-\ln (1- \hat{\gamma }))^\mathfrak {E})^{1/\mathfrak {E}}},\\{} & {} \qquad -e^{-((\delta _1+\delta _2)(-\ln (1- \hat{\wp }))^\mathfrak {E})^{1/\mathfrak {E}}}\Big \rangle \\{} & {} \quad =\tilde{\mathfrak {U}}^{(\delta _1+\delta _2 )}. \end{aligned}$$

\(\square \)

SVN AA average aggregation operators

We furnish lot of SVN average AOs in this section employing the AA operations.

Definition 9

Let \(\tilde{\mathfrak {U}}_\varphi =(\hat{\eta }_\varphi ,\hat{\gamma }_\varphi ,\hat{\wp }_\varphi )\) (\(\varphi =1,2,\ldots ,\rho )\) be a set of SVNNs. Then, the SVN AA weighted average (SVNAAWA) operator is a function \(P^{\rho }\rightarrow P\), so that

$$\begin{aligned}{} & {} \textrm{SVNAAWA}_{\mathfrak {F}}(\tilde{\mathfrak {U}}_1,\tilde{\mathfrak {U}}_2,\ldots ,\tilde{\mathfrak {U}}_\rho )=\bigoplus ^{\rho }\limits _{\varphi =1}\mathfrak {F}_\varphi \tilde{\mathfrak {U}}_\varphi \nonumber \\{} & {} \quad =\mathfrak {F}_1 \tilde{\mathfrak {U}}_1 \bigoplus \mathfrak {F}_2 \tilde{\mathfrak {U}}_2 \bigoplus \cdots \bigoplus \eta _\rho \tilde{\mathfrak {U}}_\rho \end{aligned}$$
(37)

in which \(\mathfrak {F}=(\mathfrak {F}_1,\mathfrak {F}_2,\ldots ,\mathfrak {F}_\rho )^{T}\) is the weighted vector of \(\tilde{\mathfrak {U}}_\varphi \) \((\varphi =1,2,\ldots ,\rho )\) with \(\mathfrak {F}_\varphi > 0\) and \(\sum ^{\rho }\nolimits _{\varphi =1}\mathfrak {F}_\varphi =1\).

As a result, we find the underlying result, which is consistent with the AA operations on SVNNs.

Theorem 2

Let \(\tilde{\mathfrak {U}}_\varphi =(\hat{\eta }_\varphi ,\hat{\gamma }_\varphi ,\hat{\wp }_\varphi )\) (\(\varphi =1,2,\ldots ,\rho )\) be a set of SVNNs, then aggregated value of them utilizing the SVNAAWA operation is additionally SVNNs, and

$$\begin{aligned}{} & {} \textrm{SVNAAWA}_{\mathfrak {F}} (\tilde{\mathfrak {U}}_1,\tilde{\mathfrak {U}}_2,\ldots ,\tilde{\mathfrak {U}}_\rho ) {=} \bigoplus ^{\rho }\limits _{\varphi =1}(\mathfrak {F}_\varphi \tilde{\mathfrak {U}}_\varphi )\nonumber \\{} & {} \quad {=} \,\left\langle 1{-}e^{{-}\Big (\sum ^{\rho }\limits _{\varphi {=}1}\mathfrak {F}_\varphi (-\ln (1{-} \hat{\eta }_\varphi ))^\mathfrak {E}\Big )^{1/\mathfrak {E}}}, e^{{-}\Big (\sum ^{\rho }\limits _{\varphi =1}\mathfrak {F}_\varphi (-\ln \hat{\gamma }_\varphi )^\mathfrak {E} \Big )^{1/\mathfrak {E}}}, \right. \nonumber \\{} & {} \qquad \left. e^{-\Big (\sum ^{\rho }\limits _{\varphi =1}\mathfrak {F}_\varphi (-\ln \hat{\wp }_\varphi )^\mathfrak {E} \Big )^{1/\mathfrak {E}}}\right\rangle \end{aligned}$$
(38)

where \(\mathfrak {F}=(\mathfrak {F}_1,\mathfrak {F}_2,\ldots ,\mathfrak {F}_\rho )\) is the weight vector of \(\tilde{\mathfrak {U}}_\varphi \) \((\varphi =1,2,\ldots ,\rho )\) including \(\mathfrak {F}_\varphi > 0\) and \(\sum ^{\rho }\nolimits _{\varphi =1}\mathfrak {F}_\varphi =1\).

Proof

We employed mathematical induction to prove Theorem 2 as follows:

(i) When \(\rho =2\), in light of AA operations of SVNNs, we obtain

$$\begin{aligned} \mathfrak {F}_1 \tilde{\mathfrak {U}}= & {} \Big \langle 1-e^{-(\mathfrak {F}_1(-\ln (1- \hat{\eta _1}))^\mathfrak {E})^{1/\mathfrak {E}}}, e^{-(\mathfrak {F}_1(-\ln \hat{\gamma _1})^\mathfrak {E})^{1/\mathfrak {E}}},\\{} & {} \quad e^{-(\mathfrak {F}_1(-\ln \hat{\wp _1})^\mathfrak {E})^{1/\mathfrak {E}}} \Big \rangle ,\\ \mathfrak {F}_2 \tilde{\mathfrak {U}}= & {} \Big \langle 1-e^{-(\mathfrak {F}_2(-\ln (1- \hat{\eta _2}))^\mathfrak {E})^{1/\mathfrak {E}}}, e^{-(\mathfrak {F}_2(-\ln \hat{\gamma _2})^\mathfrak {E})^{1/\mathfrak {E}}},\\{} & {} \quad e^{-(\mathfrak {F}_2(-\ln \hat{\wp _2})^\mathfrak {E})^{1/\mathfrak {E}}} \Big \rangle . \end{aligned}$$

Based on Definition 8, we obtain

$$\begin{aligned}{} & {} \textrm{SVNAAWA}_{\mathfrak {F}}(\tilde{\mathfrak {U}}_1,\tilde{\mathfrak {U}}_2)=\mathfrak {F}_1 \tilde{\mathfrak {U}}_1 \bigoplus \mathfrak {F}_2 \tilde{\mathfrak {U}}_2 \\{} & {} \quad =\Big \langle 1-e^{-(\mathfrak {F}_1(-\ln (1- \hat{\eta _1}))^\mathfrak {E})^{1/\mathfrak {E}}}, e^{-(\mathfrak {F}_1(-\ln \hat{\gamma _1})^\mathfrak {E})^{1/\mathfrak {E}}},\\{} & {} \quad e^{-(\mathfrak {F}_1(-\ln \hat{\wp _1})^\mathfrak {E})^{1/\mathfrak {E}}} \Big \rangle \\{} & {} \quad \bigoplus \Big \langle 1-e^{-(\mathfrak {F}_2(-\ln (1- \hat{\eta _2}))^\mathfrak {E})^{1/\mathfrak {E}}}, e^{-(\mathfrak {F}_2(-\ln \hat{\gamma _2})^\mathfrak {E})^{1/\mathfrak {E}}},\\{} & {} \quad e^{-(\mathfrak {F}_2(-\ln \hat{\wp _2})^\mathfrak {E})^{1/\mathfrak {E}}} \Big \rangle \\{} & {} \quad =\left\langle 1-e^{-\Big (\mathfrak {F}_1(-\ln (1- \hat{\eta }_1))^\mathfrak {E}+\mathfrak {F}_2(-\ln (1- \hat{\eta }_2))^\mathfrak {E}\Big )^{1/\mathfrak {E}}},\right. \\{} & {} \qquad e^{-\Big (\mathfrak {F}_1(-\ln \hat{\gamma }_1)^\mathfrak {E}+\mathfrak {F}_2(-\ln \hat{\gamma }_2)^\mathfrak {E} \Big )^{1/\mathfrak {E}}}, \\{} & {} \qquad \left. e^{-\Big (\mathfrak {F}_1(-\ln \hat{\wp }_1)^\mathfrak {E}+\mathfrak {F}_2(-\ln \hat{\wp }_2)^\mathfrak {E} \Big )^{1/\mathfrak {E}}}\right\rangle \\{} & {} =\left\langle 1-e^{-\Big (\sum ^{2}\limits _{\varphi =1}\mathfrak {F}_\varphi (-\ln (1- \hat{\eta }_\varphi ))^\mathfrak {E}\Big )^{1/\mathfrak {E}}}, \right. \\{} & {} \qquad \left. e^{-\Big (\sum ^{2}\limits _{\varphi =1}\mathfrak {F}_\varphi (-\ln \hat{\gamma }_\varphi )^\mathfrak {E} \Big )^{1/\mathfrak {E}}}, e^{-\Big (\sum ^{2}\limits _{\varphi =1}\mathfrak {F}_\varphi (-\ln \hat{\wp }_\varphi )^\mathfrak {E} \Big )^{1/\mathfrak {E}}}\right\rangle . \end{aligned}$$

Thus, (38) holds true when \(\rho =2\).

(ii) Considering that (38) is true for \(\rho =k\), we derive

$$\begin{aligned}{} & {} \textrm{SVNAAWA}_{\mathfrak {F}}(\tilde{\mathfrak {U}}_1,\tilde{\mathfrak {U}}_2,\ldots , \tilde{\mathfrak {U}}_k) =\bigoplus ^{k}\limits _{\varphi =1}(\mathfrak {F}_\varphi \tilde{\mathfrak {U}}_\varphi ) \\{} & {} \quad =\left\langle 1- e^{-\Big (\sum ^{k}\limits _{\varphi =1}\mathfrak {F}_\varphi (-\ln (1- \hat{\eta }_\varphi ))^\mathfrak {E}\Big )^{1/\mathfrak {E}}}, \right. \\{} & {} \qquad \left. e^{-\Big (\sum ^{k}\limits _{\varphi =1}\mathfrak {F}_\varphi (-\ln \hat{\gamma }_\varphi )^\mathfrak {E} \Big )^{1/\mathfrak {E}}}, e^{-\Big (\sum ^{k}\limits _{\varphi =1}\mathfrak {F}_\varphi (-\ln \hat{\wp }_\varphi )^\mathfrak {E} \Big )^{1/\mathfrak {E}}}\right\rangle . \end{aligned}$$

Now, for \(\rho =k+1\), then

$$\begin{aligned}{} & {} \textrm{SVNAAWA}_{\mathfrak {F}}(\tilde{\mathfrak {U}}_1, \tilde{\mathfrak {U}}_2,\ldots , \tilde{\mathfrak {U}}_k, \tilde{\mathfrak {U}}_{k+1}) =\bigoplus ^{k}\limits _{\varphi =1}(\mathfrak {F}_\varphi \tilde{\mathfrak {U}}_\varphi )\\{} & {} \quad \bigoplus (\mathfrak {F}_{k+1} \tilde{\mathfrak {U}}_{k+1})\\{} & {} \quad =\left\langle 1-e^{-\Big (\sum ^{k}\limits _{\varphi =1}\mathfrak {F}_\varphi (-\ln (1- \hat{\eta }_\varphi ))^\mathfrak {E}\Big )^{1/\mathfrak {E}}}, e^{-\Big (\sum ^{k}\limits _{\varphi =1}\mathfrak {F}_\varphi (-\ln \hat{\gamma }_\varphi )^\mathfrak {E} \Big )^{1/\mathfrak {E}}},\right. \\{} & {} \qquad \left. e^{-\Big (\sum ^{k}\limits _{\varphi =1}\mathfrak {F}_\varphi (-\ln \hat{\wp }_\varphi )^\mathfrak {E} \Big )^{1/\mathfrak {E}}}\right\rangle \\{} & {} \quad \bigoplus \left\langle 1-e^{-\Big (\mathfrak {F}_{k+1}(-\ln (1- \hat{\eta }_{k+1}))^\mathfrak {E}\Big )^{1/\mathfrak {E}}}, e^{-\Big (\mathfrak {F}_{k+1}(-\ln \hat{\gamma }_{k+1})^\mathfrak {E} \Big )^{1/\mathfrak {E}}},\right. \\{} & {} \quad \left. e^{-\Big (\mathfrak {F}_{k+1}(-\ln \hat{\wp }_{k+1})^\mathfrak {E} \Big )^{1/\mathfrak {E}}} \right\rangle =\left\langle 1-e^{-\Big (\sum ^{k+1}\limits _{\varphi =1}\mathfrak {F}_\varphi (-\ln (1- \hat{\eta }_\varphi ))^\mathfrak {E}\Big )^{1/\mathfrak {E}}}, \right. \\{} & {} \qquad \left. e^{-\Big (\sum ^{k+1}\limits _{\varphi =1}\mathfrak {F}_\varphi (-\ln \hat{\gamma }_\varphi )^\mathfrak {E} \Big )^{1/\mathfrak {E}}}, e^{-\Big (\sum ^{k+1}\limits _{\varphi =1}\mathfrak {F}_\varphi (-\ln \hat{\wp }_\varphi )^\mathfrak {E} \Big )^{1/\mathfrak {E}}}\right\rangle . \end{aligned}$$

Consequently, if \(\rho =k+1\), (38) is accurate.

We draw the conclusion from (i) and (ii) that (38) is valid for every \(\rho \). \(\square \)

By applying the SVNAAWA operator, we can successfully exhibit the pursuing features.

Theorem 3

(Idempotency) In the event that \(\tilde{\mathfrak {U}}_\varphi =(\hat{\eta }_\varphi ,\hat{\gamma }_\varphi ,\hat{\wp }_\varphi )\) \((\varphi =1,2,\ldots ,\) \(\rho )\) be a set of entirely equal SVNNs, i.e., \(\tilde{\mathfrak {U}}_\varphi =\tilde{\mathfrak {U}}\) for all \(\varphi \), then \(\textrm{SVNAAWA}_{\mathfrak {F}}\) \((\tilde{\mathfrak {U}}_1,\tilde{\mathfrak {U}}_2,\ldots ,\tilde{\mathfrak {U}}_\rho )=\tilde{\mathfrak {U}}.\)

Proof

Since \(\tilde{\mathfrak {U}}_\varphi =(\hat{\eta }_\varphi ,\hat{\gamma }_\varphi ,\hat{\wp }_\varphi )=\tilde{\mathfrak {U}}\) \((\varphi =1,2,\ldots ,\rho )\). Then, we have by Eq. (38),

$$\begin{aligned}{} & {} \textrm{SVNAAWA}_{\mathfrak {F}}(\tilde{\mathfrak {U}}_1,\tilde{\mathfrak {U}}_2,\ldots , \tilde{\mathfrak {U}}_\rho )=\bigoplus ^{\rho }\limits _{\varphi =1}(\mathfrak {F}_\varphi \tilde{\mathfrak {U}}_\varphi )\\{} & {} \quad =\left\langle 1-e^{-\Big (\sum ^{\rho }\limits _{\varphi =1}\mathfrak {F}_\varphi (-\ln (1- \hat{\eta }_\varphi ))^\mathfrak {E}\Big )^{1/\mathfrak {E}}}, \right. \\{} & {} \qquad \left. e^{-\Big (\sum ^{\rho }\limits _{\varphi =1}\mathfrak {F}_\varphi (-\ln \hat{\gamma }_\varphi )^\mathfrak {E} \Big )^{1/\mathfrak {E}}}, e^{-\Big (\sum ^{\rho }\limits _{\varphi =1}\mathfrak {F}_\varphi (-\ln \hat{\wp }_\varphi )^\mathfrak {E} \Big )^{1/\mathfrak {E}}} \right\rangle \\{} & {} \quad =\left\langle 1-e^{-\Big ((-\ln (1- \hat{\eta }))^\mathfrak {E}\Big )^{1/\mathfrak {E}}}, e^{-\Big ((-\ln \hat{\gamma })^\mathfrak {E} \Big )^{1/\mathfrak {E}}}, \right. \\{} & {} \quad \left. e^{-\Big ((-\ln \hat{\wp })^\mathfrak {E} \Big )^{1/\mathfrak {E}}}\right\rangle \\{} & {} \quad =\Bigg \langle 1-e^{\ln (1- \hat{\eta })}, e^{\ln \hat{\gamma }}, e^{\ln \hat{\wp }}\Bigg \rangle =(\hat{\eta },\hat{\gamma },\hat{\wp })=\tilde{\mathfrak {U}}. \end{aligned}$$

Thus, \(\textrm{SVNAAWA}_{\mathfrak {F}}(\tilde{\mathfrak {U}}_1,\tilde{\mathfrak {U}}_2,\ldots ,\tilde{\mathfrak {U}}_\rho )=\tilde{\mathfrak {U}}\) holds. \(\square \)

Theorem 4

(Boundedness) Let \(\tilde{\mathfrak {U}}_\varphi =(\hat{\eta }_\varphi ,\hat{\gamma }_\varphi ,\hat{\wp }_\varphi )\) \((\varphi =1,2,\ldots ,\rho )\) be an accumulation of SVNNs. Let \(\tilde{\mathfrak {U}}^{-}=\min (\tilde{\mathfrak {U}}_1,\tilde{\mathfrak {U}}_2,\ldots , \tilde{\mathfrak {U}}_\rho )\) and \(\tilde{\mathfrak {U}}^{+}=\max (\tilde{\mathfrak {U}}_1,\) \(\tilde{\mathfrak {U}}_2,\ldots ,\) \( \tilde{\mathfrak {U}}_\rho )\). Then, \(\tilde{\mathfrak {U}}^{-}\le \textrm{SVNAAWA}_{\mathfrak {F}}(\tilde{\mathfrak {U}}_1,\tilde{\mathfrak {U}}_2,\ldots ,\tilde{\mathfrak {U}}_\rho )\le \tilde{\mathfrak {U}}^{+}.\)

Proof

Let \(\tilde{\mathfrak {U}}_\varphi =(\hat{\eta }_\varphi ,\hat{\gamma }_\varphi ,\hat{\wp }_\varphi )\) \((\varphi =1,2,\ldots ,\rho )\) be several SVNNs. Let \(\tilde{\mathfrak {U}}^{-}=\min (\tilde{\mathfrak {U}}_1,\tilde{\mathfrak {U}}_2,\ldots , \tilde{\mathfrak {U}}_\rho )=\langle \hat{\eta }^{-},\hat{\gamma }^{-},\hat{\wp }^{-}\rangle \) and \(\tilde{\mathfrak {U}}^{+}=\max (\tilde{\mathfrak {U}}_1,\tilde{\mathfrak {U}}_2,\ldots , \tilde{\mathfrak {U}}_\rho )=\langle \hat{\eta }^{+},\hat{\gamma }^{+},\) \(\hat{\wp }^{+}\rangle \). We have, \(\hat{\eta }^{-}=\min \limits _{\varphi }\{\hat{\eta }_\varphi \}\), \(\hat{\gamma }^{-}=\max \limits _{\varphi }\{\hat{\gamma }_\varphi \}\), \(\hat{\wp }^{-}=\max \limits _{\varphi }\{\hat{\wp }_\varphi \}\), \(\hat{\eta }^{+}=\max \limits _{\varphi }\{\hat{\eta }_\varphi \}\), \(\hat{\gamma }^{+}=\min \limits _{\varphi }\{\hat{\gamma }_\varphi \}\) and \(\hat{\wp }^{+}=\min \limits _{\varphi }\{\hat{\wp }_\varphi \}\). Hence, there have the subsequent inequalities,

$$\begin{aligned}{} & {} 1{-}e^{{-}\Big (\sum ^{\rho }\limits _{\varphi {=}1}\mathfrak {F}_\varphi ({-}\ln (1{-} \hat{\eta }^{-}))^\mathfrak {E}\Big )^{1/\mathfrak {E}}} {\le } 1{-}e^{{-}\Big (\sum ^{\rho }\limits _{\varphi {=}1}\mathfrak {F}_\varphi ({-}\ln (1{-} \hat{\eta }_\varphi ))^\mathfrak {E}\Big )^{1/\mathfrak {E}}}\\{} & {} \quad \le 1-e^{-\Big (\sum ^{\rho }\limits _{\varphi =1}\mathfrak {F}_\varphi (-\ln (1- \hat{\eta }^{+}))^\mathfrak {E}\Big )^{1/\mathfrak {E}}},\\{} & {} \qquad e^{-\Big (\sum ^{\rho }\limits _{\varphi =1}\mathfrak {F}_\varphi (-\ln \hat{\gamma }^{+})^\mathfrak {E} \Big )^{1/\mathfrak {E}}} \le e^{-\Big (\sum ^{\rho }\limits _{\varphi =1}\mathfrak {F}_\varphi (-\ln \hat{\gamma }_\varphi )^\mathfrak {E} \Big )^{1/\mathfrak {E}}} \\{} & {} \quad \le e^{-\Big (\sum ^{\rho }\limits _{\varphi =1}\mathfrak {F}_\varphi (-\ln \hat{\gamma }^{-})^\mathfrak {E} \Big )^{1/\mathfrak {E}}},\\{} & {} \qquad e^{-\Big (\sum ^{\rho }\limits _{\varphi =1}\mathfrak {F}_\varphi (-\ln \hat{\wp }^{+})^\mathfrak {E} \Big )^{1/\mathfrak {E}}} \le e^{-\Big (\sum ^{\rho }\limits _{\varphi =1}\mathfrak {F}_\varphi (-\ln \hat{\wp }_\varphi )^\mathfrak {E} \Big )^{1/\mathfrak {E}}} \\{} & {} \quad \le e^{-\Big (\sum ^{\rho }\limits _{\varphi =1}\mathfrak {F}_\varphi (-\ln \hat{\wp }^{-})^\mathfrak {E} \Big )^{1/\mathfrak {E}}}. \end{aligned}$$

Therefore, \(\tilde{\mathfrak {U}}^{-}\le \textrm{SVNAAWA}_{\mathfrak {F}}(\tilde{\mathfrak {U}}_1,\tilde{\mathfrak {U}}_2,\ldots ,\tilde{\mathfrak {U}}_\rho )\le \tilde{\mathfrak {U}}^{+}.\) \(\square \)

Theorem 5

(Monotonicity) Let \(\tilde{\mathfrak {U}}_\varphi \) and \(\tilde{\mathfrak {U}}^{'}_\varphi \) \((\varphi =1,2,\ldots ,\rho )\) be a couple of SVNNs, if \(\tilde{\mathfrak {U}}_\varphi \le \tilde{\mathfrak {U}}^{'}_\varphi \) for all \(\varphi \), then

$$\begin{aligned}{} & {} \textrm{SVNAAWA}_{\mathfrak {F}}(\tilde{\mathfrak {U}}_1,\tilde{\mathfrak {U}}_2,\ldots ,\tilde{\mathfrak {U}}_\rho )\\{} & {} \le \textrm{SVNAAWA}_{\mathfrak {F}}(\tilde{\mathfrak {U}}^{'}_1,\tilde{\mathfrak {U}}^{'}_2,\ldots ,\tilde{\mathfrak {U}}^{'}_\rho ). \end{aligned}$$

We would now like to introduce the SVN AA ordered weighted averaging (SVNAAOWA) operator.

Definition 10

Let \(\tilde{\mathfrak {U}}_\varphi =(\hat{\eta }_\varphi ,\hat{\gamma }_\varphi ,\hat{\wp }_\varphi )\) \((\varphi =1,2,\ldots ,\rho )\) be a set of SVNNs. A SVNAAOWA operator with a dimension of \(\rho \) is a function \(SVNAAOWA: \tilde{P}^{\rho }\rightarrow \tilde{P}\) with the affiliated vector \(\varPsi =(\varPsi _1,\varPsi _2,\ldots ,\varPsi _\rho )^{T}\) including \(\varPsi _\varphi >0\) and \(\sum ^{\rho }\limits _{\varphi =1}\varPsi _\varphi =1\), as

$$\begin{aligned}{} & {} \textrm{SVNAAOWA}_{\varPsi }(\tilde{\mathfrak {U}}_1,\tilde{\mathfrak {U}}_2,\ldots ,\tilde{\mathfrak {U}}_\rho )=\bigoplus ^{\rho }\limits _{\varphi =1}\varPsi _\varphi \tilde{\mathfrak {U}}_{\mathfrak {T}(\varphi )}\nonumber \\{} & {} \quad =\varPsi _1\tilde{\mathfrak {U}}_{\mathfrak {T}(1)}\bigoplus \varPsi _2\tilde{\mathfrak {U}}_{\mathfrak {T}(2)} \bigoplus \cdots \bigoplus \varPsi _\rho \tilde{\mathfrak {U}}_{\mathfrak {T}(\rho )} \end{aligned}$$
(39)

where \((\mathfrak {T}(1),\mathfrak {T}(2),\ldots ,\mathfrak {T}(\rho ))\) are the permutation of \((\varphi =1,2,\ldots ,\rho )\), in a manner that \(\tilde{\mathfrak {U}}_{\mathfrak {T}(\varphi -1)}\ge \tilde{\mathfrak {U}}_{\mathfrak {T}(\varphi )}\) for all \(\varphi =1,2,\ldots ,\rho \).

On the basis of AA product operation on SVNNs, the accompanying hypothesis is created.

Theorem 6

Assume that \(\tilde{\mathfrak {U}}_\varphi {=}(\hat{\eta }_\varphi ,\hat{\gamma }_\varphi ,\hat{\wp }_\varphi )\) \((\varphi {=}1,2,\ldots ,\rho )\) be a set of SVNNs. A SVN AA ordered weighted average (SVNAAOWA) operator of dimension \(\rho \) is a function \(SVNAAOWA: \tilde{P}^{\rho }\rightarrow \tilde{P}\) with the corresponding vector \(\varPsi =(\varPsi _1,\varPsi _2,\ldots ,\varPsi _\rho )^{T}\) so that \(\varPsi _\varphi >0\) and \(\sum ^{\rho }\nolimits _{\varphi =1}\varPsi _\varphi =1\). Then

$$\begin{aligned}{} & {} \textrm{SVNAAOWA}_{\varPsi }(\tilde{\mathfrak {U}}_1,\tilde{\mathfrak {U}}_2, \ldots , \tilde{\mathfrak {U}}_\rho )= \bigoplus ^{\rho }\limits _{\varphi =1}(\varPsi _\varphi \tilde{\mathfrak {U}}_{\mathfrak {T}(\varphi )})\nonumber \\{} & {} \quad = \left\langle 1-e^{-\Big (\sum ^{\rho }\limits _{\varphi =1}\varPsi _\varphi \big (-\ln \big (1- \hat{\eta }_{\mathfrak {T}(\varphi )}\big )\big )^\mathfrak {E}\Big )^{1/\mathfrak {E}}}, \right. \nonumber \\{} & {} \quad e^{-\Big (\sum ^{\rho }\limits _{\varphi =1}\varPsi _\varphi \big (-\ln \hat{\gamma }_{\mathfrak {T}(\varphi )}\big )^\mathfrak {E} \Big )^{1/\mathfrak {E}}}, \nonumber \\{} & {} \qquad \left. e^{-\Big (\sum ^{\rho }\limits _{\varphi =1}\varPsi _\varphi \big (-\ln \hat{\wp }_{\mathfrak {T}(\varphi )}\big )^\mathfrak {E} \Big )^{1/\mathfrak {E}}} \right\rangle , \end{aligned}$$
(40)

where \((\mathfrak {T}(1),\mathfrak {T}(2),\ldots ,\mathfrak {T}(\rho ))\) are the permutation of \((\varphi =1,2,\ldots ,\rho )\), in a manner that \(\tilde{\mathfrak {U}}_{\mathfrak {T}(\varphi -1)}\ge \tilde{\mathfrak {U}}_{\mathfrak {T}(\varphi )}\) for any \(\varphi =1,2,\ldots ,\rho \).

By applying the SVNAAOWA operator, it is possible to efficiently show the properties listed below.

Theorem 7

(Idempotency) Assuming that \(\tilde{\mathfrak {U}}_\varphi \) \((\varphi {=}1,2,\ldots ,\rho )\) are totally equivalent, i.e., \(\tilde{\mathfrak {U}}_\varphi {=}\tilde{\mathfrak {U}}\) for all \(\varphi \), then

$$\begin{aligned} \textrm{SVNAAOWA}_{\varPsi }(\tilde{\mathfrak {U}}_1,\tilde{\mathfrak {U}}_2,\ldots ,\tilde{\mathfrak {U}}_\rho )=\tilde{\mathfrak {U}}. \end{aligned}$$
(41)

Theorem 8

(Boundedness) Assuming \(\tilde{\mathfrak {U}}_\varphi \) \((\varphi =1,2,\ldots ,\rho )\) be a set of SVNNs, and \(\tilde{\mathfrak {U}}^{-}=\min \limits _{\varphi }\tilde{\mathfrak {U}}_\varphi \), \(\tilde{\mathfrak {U}}^{+}=\max \limits _{\varphi }\tilde{\mathfrak {U}}_\varphi .\) Then

$$\begin{aligned} \tilde{\mathfrak {U}}^{-}\le \textrm{SVNAAOWA}_{\varPsi }(\tilde{\mathfrak {U}}_1,\tilde{\mathfrak {U}}_2,\ldots ,\tilde{\mathfrak {U}}_\rho )\le \tilde{\mathfrak {U}}^{+}. \end{aligned}$$
(42)

Theorem 9

(Monotonicity) Let \(\tilde{\mathfrak {U}}_\varphi \) and \(\tilde{\mathfrak {U}}^{'}_\varphi \) \((\varphi =1,2,\ldots ,\rho )\) be a couple of SVNNs, if \(\tilde{\mathfrak {U}}_\varphi \le \tilde{\mathfrak {U}}^{'}_\varphi \) for all \(\varphi \), then

$$\begin{aligned}{} & {} \textrm{SVNAAOWA}_{\varPsi }(\tilde{\mathfrak {U}}_1,\tilde{\mathfrak {U}}_2,\ldots ,\tilde{\mathfrak {U}}_\rho )\nonumber \\{} & {} \quad \le \textrm{SVNAAOWA}_{\varPsi }(\tilde{\mathfrak {U}}^{'}_1,\tilde{\mathfrak {U}}^{'}_2,\ldots ,\tilde{\mathfrak {U}}^{'}_\rho ). \end{aligned}$$
(43)

Theorem 10

(Commutativity) Let \(\tilde{\mathfrak {U}}_\varphi \) and \(\tilde{\mathfrak {U}}^{'}_\varphi \) \((\varphi {=}1,2,\ldots ,\rho )\) be a couple of SVNNs, then

$$\begin{aligned}{} & {} \textrm{SVNAAOWA}_{\varPsi }(\tilde{\mathfrak {U}}_1,\tilde{\mathfrak {U}}_2,\ldots ,\tilde{\mathfrak {U}}_\rho )\nonumber \\{} & {} \quad = \textrm{SVNAAOWA}_{\varPsi }(\tilde{\mathfrak {U}}^{'}_1,\tilde{\mathfrak {U}}^{'}_2,\ldots , \tilde{\mathfrak {U}}^{'}_\rho ) \end{aligned}$$
(44)

where \(\tilde{\mathfrak {U}}^{'}_\varphi \) \((\varphi =1,2,\ldots ,\rho )\) is any permutation of \(\tilde{\mathfrak {U}}_\varphi \) \((\varphi =1,2,\ldots ,\rho )\).

According to Definition 9, SVNAAWA operator rates are the most basic form of SVNN, and according to Definition 10, SVNAAOWA operator values are the form of weights that are used to arrange the SVNNs. As a result, the weights, which are specified in operators SVNAAWA and SVNAAOWA, give a variety of scenarios that are antagonistic to one another. However, in terms of the general approach, these viewpoints are considered equal to one another. In order to alleviate this discomfort, we will now propose the SVN AA hybrid averaging (SVNAAHA) operator in the following paragraph.

Definition 11

Suppose \(\tilde{\mathfrak {U}}_\varphi \) \((\varphi =1,2,\ldots ,\rho )\) be a set of SVNNs. A \(\rho \)-dimensional SVNAAHA operator is a mapping \(\textrm{SVNAAHA}: \tilde{P}^{\rho }\rightarrow \tilde{P}\), so that

$$\begin{aligned}{} & {} \textrm{SVNAAHA}_{\mathfrak {F},\varPsi }(\tilde{\mathfrak {U}}_1, \tilde{\mathfrak {U}}_2, \ldots , \tilde{\mathfrak {U}}_\rho )= \bigoplus ^{\rho }_{\varphi =1}(\varPsi _\varphi \dot{\tilde{\mathfrak {U}}}_{\mathfrak {T}(\varphi )})\nonumber \\{} & {} \quad = \varPsi _1 \dot{\tilde{\mathfrak {U}}}_{\mathfrak {T}(1)} \bigoplus \varPsi _2 \dot{\tilde{\mathfrak {U}}}_{\mathfrak {T}(2)} \bigoplus \cdots \bigoplus \varPsi _\rho \dot{\tilde{\mathfrak {U}}}_{\mathfrak {T}(\rho )} \end{aligned}$$
(45)

where \(\varPsi =(\varPsi _1, \varPsi _2, \ldots , \varPsi _\rho )^T\) is the weighted vector involved in dealing with the SVNAAHA operator, with \(\varPsi _\varphi \in [0, 1]\) \((\varphi =1,2,\ldots ,\rho )\) and \(\sum \nolimits _{\varphi =1}^{\rho }\varPsi _\varphi =1\); \(\dot{\tilde{\mathfrak {U}}}_\varphi = h \mathfrak {F}_\varphi \tilde{\mathfrak {U}}_\varphi \), \(\varphi =1,2,\ldots ,\rho \), \((\dot{\tilde{\mathfrak {U}}}_{\mathfrak {T}(1)}, \dot{\tilde{\mathfrak {U}}}_{\mathfrak {T}(2)}, \ldots , \dot{\tilde{\mathfrak {U}}}_{\mathfrak {T}(\rho )})\) is any permutations of the collections of the weighted SVNNs \((\dot{\tilde{\mathfrak {U}}}_1, \dot{\tilde{\mathfrak {U}}}_2, \ldots , \dot{\tilde{\mathfrak {U}}}_\rho )\), so that \(\dot{\tilde{\mathfrak {U}}}_{\mathfrak {T}(\varphi -1)} \ge \dot{\tilde{\mathfrak {U}}}_{\mathfrak {T}(\varphi )}\) \((\varphi =1,2,\ldots ,\rho )\); \(\mathfrak {F} = (\mathfrak {F}_1, \mathfrak {F}_2, \ldots , \eta _\rho )^T\) is the weighted vector of \(\tilde{\mathfrak {U}}_\varphi \) \((\varphi =1,2,\ldots ,\rho )\), with \(\mathfrak {F}_\varphi \in [0, 1]\) \((\varphi =1,2,\ldots ,\rho )\) and \(\sum \nolimits _{\varphi =1}^{\rho } \mathfrak {F}_\varphi = 1\), and \(\rho \) is the balance coefficient, that performs a function in sustaining stability.

The underlying theorem may be proven using AA operations on SVNNs data.

Theorem 11

Let \(\tilde{\mathfrak {U}}_\varphi \) \((\varphi =1,2,\ldots ,\rho )\) be a set of SVNNs. Their accumulated value as determined by the SVNAAHA operator remains an SVNN, and

$$\begin{aligned}{} & {} \textrm{SVNAAHA}_{\mathfrak {F},\varPsi }(\tilde{\mathfrak {U}}_1,\tilde{\mathfrak {U}}_2,\ldots , \tilde{\mathfrak {U}}_\rho )=\bigoplus ^{\rho }\limits _{\varphi =1}(\varPsi _\varphi \dot{\tilde{\mathfrak {U}}}_{\mathfrak {T}(\varphi )})\nonumber \\{} & {} \quad = \left\langle 1{-}e^{{-}\Big (\sum ^{\rho }\limits _{\varphi {=}1}\varPsi _\varphi \big ({-}\ln \big (1{-} \dot{\hat{\eta }}_{\mathfrak {T}(\varphi )}\big )\big )^\mathfrak {E}\Big )^{1/\mathfrak {E}}}, \right. \nonumber \\{} & {} \qquad e^{{-}\Big (\sum ^{\rho }\limits _{\varphi {=}1}\varPsi _\varphi \big ({-}\ln \dot{\hat{\gamma }}_{\mathfrak {T}(\varphi )}\big )^\mathfrak {E} \Big )^{1/\mathfrak {E}}}, \nonumber \\{} & {} \qquad \left. e^{-\Big (\sum ^{\rho }\limits _{\varphi =1}\varPsi _\varphi \big (-\ln \dot{\hat{\wp }}_{\mathfrak {T}(\varphi )}\big )^\mathfrak {E} \Big )^{1/\mathfrak {E}}}\right\rangle . \end{aligned}$$
(46)

Proof

We can acquire Theorem 11 in a manner similar to that of Theorem 2. \(\square \)

Theorem 12

The SVNAAWA and SVNAAOWA operators are special cases of the SVNAAHA operator.

Proof

(1) Let \(\varPsi =(1/\rho , 1/\rho , \ldots , 1/\rho )^T\). Then

$$\begin{aligned}{} & {} \textrm{SVNAAHA}_{\mathfrak {F},\varPsi }(\tilde{\mathfrak {U}}_1, \tilde{\mathfrak {U}}_2, \ldots , \tilde{\mathfrak {U}}_\rho )\\{} & {} \quad = \varPsi _1 \dot{\tilde{\mathfrak {U}}}_{\mathfrak {T}(1)} \bigoplus \varPsi _2 \dot{\tilde{\mathfrak {U}}}_{\mathfrak {T}(2)} \bigoplus \cdots \bigoplus \varPsi _\rho \dot{\tilde{\mathfrak {U}}}_{\mathfrak {T}(\rho )}\\{} & {} \quad =\frac{1}{\rho }(\dot{\tilde{\mathfrak {U}}}_{\mathfrak {T}(1)} \bigoplus \dot{\tilde{\mathfrak {U}}}_{\mathfrak {T}(2)} \bigoplus \cdots \bigoplus \dot{\tilde{\mathfrak {U}}}_{\mathfrak {T}(\rho )})\\{} & {} \quad =\mathfrak {F}_1 \tilde{\mathfrak {U}}_1 \bigoplus \mathfrak {F}_2 \tilde{\mathfrak {U}}_2 \bigoplus \cdots \bigoplus \eta _\rho \tilde{\mathfrak {U}}_\rho \\{} & {} \quad = \textrm{SVNAAWA}_{\mathfrak {F}}(\tilde{\mathfrak {U}}_1, \tilde{\mathfrak {U}}_2, \ldots , \tilde{\mathfrak {U}}_\rho ), \end{aligned}$$

(2) Let \(\mathfrak {F}=(1/\rho , 1/\rho , \ldots , 1/\rho )^T\). Then, \(\dot{\tilde{\mathfrak {U}}}_\varphi =\tilde{\mathfrak {U}}_\varphi \) \((\varphi =1,2,\ldots ,\rho )\) and

$$\begin{aligned}{} & {} \textrm{SVNAAHA}_{\mathfrak {F},\varPsi }(\tilde{\mathfrak {U}}_1, \tilde{\mathfrak {U}}_2, \ldots , \tilde{\mathfrak {U}}_\rho )\\{} & {} \quad = \varPsi _1 \dot{\tilde{\mathfrak {U}}}_{\mathfrak {T}(1)} \bigoplus \varPsi _2 \dot{\tilde{\mathfrak {U}}}_{\mathfrak {T}(2)} \bigoplus \cdots \bigoplus \varPsi _\rho \dot{\tilde{\mathfrak {U}}}_{\mathfrak {T}(\rho )}\\{} & {} \quad = \varPsi _1 \tilde{\mathfrak {U}}_{\mathfrak {T}(1)} \bigoplus \varPsi _2 \tilde{\mathfrak {U}}_{\mathfrak {T}(2)} \bigoplus \cdots \bigoplus \varPsi _\rho \tilde{\mathfrak {U}}_{\mathfrak {T}(\rho )}\\{} & {} \quad = \textrm{SVNAAOWA}_{\varPsi }(\tilde{\mathfrak {U}}_1, \tilde{\mathfrak {U}}_2, \ldots , \tilde{\mathfrak {U}}_\rho ), \end{aligned}$$

this leads to the result. \(\square \)

Method for MADM issues based on SVNAAWA operator

To do this, we might offer a MADM strategy that has SVN AOs, uses SVNNs as attribute values, and uses real numbers as attribute weights. Assume \(\partial =\{\partial _1, \partial _2,\ldots , \partial _g\}\) is a set of options, \(\hslash =\{\hslash _1, \hslash _2, \ldots ,\) \( \hslash _\rho \}\) is a set of attributes, \(\mathfrak {F}=(\mathfrak {F}_1,\mathfrak {F}_2,\ldots ,\mathfrak {F}_\rho )\) is a weight vector of the attribute \(\mathfrak {F}_\varphi \) \((\varphi =1,2,\ldots ,\rho )\) so that \(\mathfrak {F}_\varphi >0\) and \(\sum ^{\rho }\nolimits _{\varphi =1}\mathfrak {F}_\varphi =1\). The provisional of the option \(\partial _\eth \) \((\eth =1,2,\ldots ,g)\) in terms of the criterion \(\hslash _\varphi \) \((\varphi =1,2,\ldots ,\rho )\) is expressed explicitly by \(\zeta _{g \rho } =(\hat{\eta }_{g \rho },\hat{\gamma }_{g \rho },\hat{\wp }_{g \rho })\). Assume that \(R =\big (\zeta _{g \rho }\big )_{g \times \rho }\) is the SVN decision matrix, where \(\hat{\eta }_{g \rho }\) denotes the positive membership degree such that choice \(\partial _\varphi \) fulfills the attribute \(\hslash _\varphi \) specified by the decision maker, \(\hat{\gamma }_{g \rho }\) signifies the neutral membership degree such that choice \(\partial _\eth \) does not fulfill the attribute \(\hslash _\varphi \), and \(\hat{\wp }_{g \rho }\) signifies the degree to which choice \(\partial _\eth \) does not address the attribute \(\hslash _\varphi \) specified by decision maker, where \(\hat{\eta }_{g \rho }\), \(\hat{\gamma }_{g \rho }\), \(\hat{\wp }_{g \rho }\subset [0,1]\) allowing

$$\begin{aligned} 0\le \hat{\eta }_{g \rho }+\hat{\gamma }_{g \rho }+\hat{\wp }_{g \rho }\le 3, (\eth =1,2,\ldots ,g). \end{aligned}$$
(47)

In the next algorithm, we use the SVNAAWA operator to try to solve the MADM problem with this kind of SVN data.

Step 1. Transform the decision matrix \(R =\big (\zeta _{g \rho }\big )_{g \times \rho }\) into the normalization matrix \(\overline{R} =\big (\overline{\zeta }_{g \rho } \big )_{g \times \rho }\).

$$\begin{aligned} \overline{\zeta }_{g \rho }=\left\{ \begin{array}{ll} \zeta _{g \rho } \text{ for } \text{ benefit } \text{ attribute }\, \hslash _\varphi \\ (\zeta _{g \rho })^c \text{ for } \text{ cost } \text{ attribute }\, \hslash _\varphi , \end{array}\right. \end{aligned}$$
(48)

where \((\zeta _{g \rho })^c\) is the complement of \(\zeta _{g \rho }\) and \((\zeta _{g \rho })^c=(\hat{\wp }_{g \rho },\hat{\gamma }_{g \rho },\hat{\eta }_{g \rho })\).

If all of the attributes \(\hslash _\varphi \) \((\varphi =1,2,\ldots ,\rho )\) are of the same type, it is not necessary to normalise the values of the attributes; however, if there are cost and benefit attributes in MADM concerns, we can change the cost type rating values into the benefit type rating values. Consequently, \(R =\big (\zeta _{g \rho }\big )_{g \times \rho }\) can be turned into an SVN decision matrix \(\overline{R} =\big (\overline{\zeta }_{g \rho } \big )_{g \times \rho }\).

Step 2. We take into account the collected data mentioned in matrix \(\overline{R}\), along with the operator SVNAAWA:

$$\begin{aligned} \zeta _\eth= & {} \textrm{SVNAAWA}(\zeta _{t1},\zeta _{t2},\ldots ,\zeta _{tn})=\bigoplus ^{\rho }\limits _{\varphi =1}(\mathfrak {F}_\varphi \zeta _{g \rho })\nonumber \\= & {} \left\langle 1-e^{-\Big (\sum ^{\rho }\limits _{\varphi =1}\mathfrak {F}_\varphi (-\ln (1-\hat{\eta }_\varphi ))^\mathfrak {E}\Big )^{1/\mathfrak {E}}}, e^{-\Big (\sum ^{\rho }\limits _{\varphi =1}\mathfrak {F}_\varphi (-\ln \hat{\gamma }_\varphi )^\mathfrak {E} \Big )^{1/\mathfrak {E}}},\right. \nonumber \\{} & {} \left. e^{-\Big (\sum ^{\rho }\limits _{\varphi =1}\mathfrak {F}_\varphi (-\ln \hat{\wp }_\varphi )^\mathfrak {E} \Big )^{1/\mathfrak {E}}} \right\rangle \end{aligned}$$
(49)

to derive the standardized desired values \(\zeta _\eth \) \((\eth =1,2,\ldots ,g)\) of the options \(\partial _\eth \).

Step 3. We calculate the score value \(\hat{Y}(\zeta _\eth )\) \((\eth =1,2,\ldots , g)\) depending on generalized SVN data \(\zeta _\eth \) \((\eth =1,2,\ldots ,g)\) in ranking all the options \(\partial _\eth \) \((\eth =1,2,\ldots ,g)\) in step is to select the better option \(\partial _\eth \). When there is no distinction to be made between the score functions \(\hat{Y}(\zeta _\eth )\) and \(\hat{Y}(\zeta _\varphi )\), we proceed to calculate the accuracy degrees of \(\hat{K}(\zeta _\eth )\) and \(\hat{K}(\zeta _\varphi )\) anticipated on conventional SVN data for \(\zeta _\eth \) and \(\zeta _\varphi \), and we rank the alternatives \(\partial _\eth \) in relation to the accuracy degrees of \(\hat{K}(\zeta _\eth )\) and \(\hat{K}(\zeta _\varphi )\).

Step 4. We rank all of the options \(\partial _\eth \) \((\eth =1,2,\ldots ,g)\) to choose the best one(s) based on \(\hat{Y}(\zeta _\eth )\) \((\eth =1,2,\ldots ,g)\).

Step 5. End.

Numerical example

To demonstrate the technique’s utility, we’ll consider a situation in which a financial company needs to invest a large sum of money in the best option. There is indeed a committee containing five different investment opportunities: \(\partial _1\) represents a passenger vehicle industry; \(\partial _2\) represents a supermarket chain; \(\partial _3\) represents a technology company; \(\partial _4\) represents a weapons industry; and \(\partial _5\) represents a broadcasting corporation. The corporation limited must make a judgment in accordance with the four characteristics listed below:

\(\hslash _1\):

: Vulnerability assessment.

\(\hslash _2\):

: Developmental assessment.

\(\hslash _3\):

: Social-political effect assessment.

\(\hslash _4\):

: Environmental and sustainability assessment.

The decision-maker is to evaluate the five feasible options \(\partial _\eth \) \((\eth =1,2,\ldots , 5)\) utilising SVN data for the four above-mentioned attributes (for whom the weighted vector \(\mathfrak {F}=(0.30, 0.40, 0.20, 0.10)^T\)), as indicated in the following matrix (Table 1).

Table 1 SVN decision matrix
Full size table
Table 2 Priority ranking for various values of the operational parameters in the aggregating process
Full size table

To identify the most advantageous company \(\partial _\eth \) \((\eth =1,2,\ldots , 5)\), we employ the SVNAAWA operator to construct a MADM approach using SVN data, which can be determined by measuring:

  • Step 1. Taking the assumption that \(\mathfrak {E}=1\), we can use the SVNAAWA operator to compute the conventional desired values \(\zeta _\eth \) of the companies \(\partial _\eth \) \((\eth =1,2,\ldots ,5)\). Specifically

    Company

    Desired value

    \(\zeta _1\)

    (0.526189, 0.303500, 0.514930)

    \(\zeta _2\)

    (0.409656, 0.353031, 0.307311)

    \(\zeta _3\)

    (0.347555, 0.535247, 0.289129)

    \(\zeta _4\)

    (0.593350, 0.332730, 0.338323)

    \(\zeta _5\)

    (0.579400, 0.251404, 0.510950)

  • Step 2. We evaluate the score values \(\hat{Y}(\zeta _\eth )\) \((\eth =1,2,\ldots ,5)\) of SVNNs \(\zeta _\eth \) employing Definition 5. The score values are as follows: \(\hat{Y}(\zeta _1)=0.569253\), \(\hat{Y}(\zeta _2)=0.583105\), \(\hat{Y}(\zeta _3)=0.507727\), \(\hat{Y}(\zeta _4)=0.640765\), \(\hat{Y}(\zeta _5)=0.605683\).

  • Step 3. Order all of the companies \(\partial _\eth \) \((\eth =1,2,\ldots ,5)\) based on the score values \(\hat{Y}(\zeta _\eth )\) \((\eth =1,2,\ldots ,5)\) of the overall SVNNs as \(\partial _4\succ \partial _5\succ \partial _2\succ \partial _1\succ \partial _3\).

  • Step 4. \(\partial _4\) is selected as the optimal alternative.

Evaluation of the influence of the operational parameter \(\mathfrak {E}\) on decision-making consequences

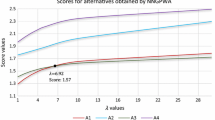
For the purpose of demonstrating the influence of the operational parameters \(\mathfrak {E}\) on MADM findings, we will use a variety of estimates of \(\mathfrak {E}\) that are ranked in conformity with the alternatives. On the basis of score values, the consequences of ordering the choices \(\partial _\eth \) \((\eth =1,2,\ldots ,5)\) from the perspective of the said SVNAAWA operator are furnished in Table 2 and illustrated visually in Fig. 2.

It has become obvious that as the amplitude of \(\mathfrak {E}\) intensifies for such an SVNAAWA operator, its score values for the options keep increasing, but still, the corresponding ranking stays the same \(\partial _4\succ \partial _5\succ \partial _2\succ \partial _1\succ \partial _3\), indicating that the improvement methodologies generally have the isotonic property, permitting the decision-maker to provide an acceptable value in light of their tendencies.

In addition, as illustrated in Fig. 2, the results derived for the alternatives are identical when the value of \(\mathfrak {E}\) is varied in the example, demonstrating the consistency of the recommended SVNAAWA operators.

Sensitivity analysis (SA) of criteria weights

We look at how weighted criteria affect the order of preference using a sensitivity analysis. This is done with 24 distinct weight sets, notably \(S1, S2,\ldots , S24\) (Table 3), which are made by looking at all possible ways to combine the weights for the criteria \(\psi _1=0.3\), \(\psi _2=0.4\), \(\psi _3=0.2\) and \(\psi _4=0.1\). This is especially important for getting a greater variety of criterion weights when figuring out how much the built model matters. Figure 3 shows a total of how the different options were rated, and Table 4 shows how they were ranked. When the SVNAAWA operator (with \(\mathfrak {E}=10\)) is employed and the ranking order of options is examined, it is discovered that \(\partial _4\) ranks first in 83.33\(\%\) of situations. Accordingly, the ranking of options obtained using our technique is realistic.

Comparative analysis

In this section, we compare our proposed methodologies to existing models, including the “SVN weighted averaging (SVNWA) operator” [37], the “SVN Einstein weighted averaging (SVNEWA) operator” [28], the “SVN Hamacher weighted averaging (SVNHWA) operator” [29], and the “SVN Dombi weighted averaging (SVNDWA) operator” [8]. Table 5 contains the results of the comparison studies, and Fig. 4 depicts the results in graphical form. As shown in Tables 2 and 5, the SVNWA operator is a specific instance of our recommended SVNAAWA operator and it takes place when \(\mathfrak {E}=1\).

As a result, our theories and methods are typically more comprehensive and versatile than certain commonly used techniques for managing SVN MADM difficulties.

Fig. 2
figure 2

Score values of the alternatives for various values \(\mathfrak {E}\) by SVNAAWA operator

Full size image
Fig. 3
figure 3

Final utility values of options for different sorts of criteria weights

Full size image

Limitations of our study:

  1. 1.

    One of the biggest problems with the way we suggest doing things is that it relies only on the knowledge and experience of people.

  2. 2.

    The reliability of these systems is greatly affected by the fact that they use a lot of unclear information and inputs.

  3. 3.

    This techniques are incapable of identifying machine learning or neural networks.

Table 3 Various weight sets of criteria
Full size table
Table 4 Priority ranking of options for various weight sets
Full size table
Table 5 Comparative analyses using a selection of presently available methodologies
Full size table
Fig. 4
figure 4

Comparative assessment using several popular approaches

Full size image

Conclusions

Our research has focused on expanding the AA t-NM and AA t-CNM to account for SVN circumstances, developing several innovative operational rules concerning SVNNs, and investigating their characteristics and interconnections. Next, based on these innovative operational rules, several novel AOs, such as the SVNAAWA operator, the SVNAAOWA operator, and the SVNAAHA operator, have been created to suit circumstances in which the provided arguments are SVNNs. Many appealing features and specific examples of such operators are now being investigated in considerable detail, as are the interconnections between these operators. The suggested operators have been placed on MADM difficulties together with SVN information, and a mathematical framework is being provided to illustrate the decision-making processes. A mathematical instance has been presented to highlight the validity and dependability of the technique. Ongoing research looks into the impact of criteria weights on ranking order. The influence of parameter \(\mathfrak {E}\) on decision-making consequences has been investigated. The proposed work is judged by comparing the number of options that can be done with new and old aggregation operators to show how important it is.

Following the construction of this paper, it focuses on the theoretical aspect of the problem. We will continue to study the application of the new method in some other fields, such as fuzzy dynamical systems, hypothesis testing, logistics solutions, and optimization approaches. Incredibly powerful computing and decision frameworks built on the SVN framework remain limited. It is noticeable that all decision-making problems with SVNSs can be addressed in a similar way to the offered case study. Furthermore, we will continue to research decision making with SVN information and introduce more simple and applicable decision-making methods. Artificial intelligence, data extraction, pattern recognition, computer vision, visual analytics, and maybe even more fields with unpredictable results [1, 2, 9, 20, 21, 40, 42,43,44,45, 61] are all interesting new areas of study.

Furthermore, it might be helpful to build consensus approaches for the SVN MADM difficulties that are based on AA t-NMs and AA t-CNMs and then use the results of these approaches to solve realistic problems. Another possibility is granular computing, which makes it possible to construct many SVN aggregation operators. The way of determining which is the advantageous parameter for AA aggregation is an important one; hence, the appropriate exploitation of data precision will be an effective approach to identify a solution to this primary problem. In subsequent studies, attention will be paid to the aforementioned concerns.