Evolutionary generative design of supercritical airfoils: an automated approach driven by small data

Abstract

Supercritical airfoils are critical components in the design of commercial wide-body aircraft wings due to their ability to enhance aerodynamic performance in transonic flow regimes. However, traditional design methods for supercritical airfoils can be time-consuming and require significant manual effort, not to mention the high cost associated with computational fluid dynamics analysis. To address these challenges, this paper introduces a highly automated approach for supercritical airfoil design, called Evolutionary Generative Design (EvoGD). The EvoGD approach is based on the framework of Evolutionary Computation and employs a series of sophisticated data-driven generative models incorporated with physical information to iteratively refine initial airfoil shapes, resulting in improved aerodynamic performances and reduced constraint violations. Moreover, to speed up the evaluation of the generated airfoils, a series of accurate and efficient data-driven predictors are utilized. The efficacy of the EvoGD approach was demonstrated through experiments on a dataset of 501 supercritical airfoils, including one baseline design and 500 randomly perturbed airfoils. On average, the generated airfoils showed improved performance in terms of buffet lift coefficient, cruise lift-to-drag ratio, and thickness by 5%, 4%, and 1%, respectively. The best generated airfoil outperformed the baseline design in terms of critical buffet lift coefficient and cruise lift-to-drag ratio by 7.1% and 6.4%, respectively. The entire design process was completed in less than an hour on a personal computer, highlighting the high efficiency and scalability of the EvoGD approach.

Introduction

Modern commercial wide-body aircrafts often operate at relatively high speeds, typically exceeding 0.8 Mach or 980 km/h. The presence of high-speed transonic air flows in certain regions around the aircraft, particularly above the wings, requires mitigation. Supercritical airfoils are utilized as cross sections in the design of commercial wide-body aircraft wings to decrease drag, improve lift, and increase stability and comfort. Given the growing importance of environmental and economic efficiency in commercial wide-body aircraft design, well-designed supercritical airfoils are crucial for success.

However, the design of supercritical airfoils presents a number of challenges, particularly the requirement for precise determination of shape parameters as aerodynamic performance is extremely sensitive to small geometric variations. This design process often necessitates the involvement of experienced professionals and multiple rounds of design iterations, simulations, and real-world testing.

In recent years, the rapid advancement of Artificial Intelligence (AI) has led to an increase in attention towards AI-assisted positive [1,2,3,4,5,6] and inverse [7, 8] supercritical airfoil design. Despite the notable progress made in the field, its development is still in its infancy and several critical open challenges remain to be addressed.

❶ Costly datasets. Existing AI-assisted supercritical airfoil design methods often require a significant number of samples for effective functioning. However, the collection of large-scale datasets through computationally costly and sometimes labor-intensive Computational Fluid Dynamics (CFD) analyses can be prohibitively expensive.

❷ Complicated physical constraints. Existing AI-assisted supercritical airfoil design approaches commonly use supercritical airfoil parametrization methods such as sampled coordinates or plain images. However, these approaches do not effectively encode the rigid and complex physical constraints of supercritical airfoils, resulting in potentially unstable design outcomes.

❸ Inefficient design generation. Existing AI-assisted supercritical airfoil design methods frequently rely on random or stochastic sampling for the generation of new airfoils. However, due to the highly sensitive nature of aerodynamic performance to design variables, these conventional AI methods can be inefficient in producing high-quality designs.

❹ Imbalanced diversity and reliability. Existing AI-assisted supercritical airfoil design methods either directly optimize a limited number of designs or do not incorporate local search operations. However, given the complex nature of supercritical airfoil design, these AI approaches may only produce airfoils that are either diverse or reliable, but not both.

The Evolutionary Computation (EC) paradigm has been widely recognized for its power in solving optimization problems [9]. In recent years, the application of data-driven EC has shown promise in optimizing real-world problems [10]. However, despite efforts to apply data-driven EC to airfoil design [11,12,13], the precision of the designs remains subpar, particularly in the case of supercritical airfoils, which require higher precision as their aerodynamic performance is more sensitive than that of subcritical airfoils.

The limitations in precision of data-driven EC can be attributed mainly to the fact that previous studies have primarily focused on surrogate modeling of evaluators, leaving the EC framework underutilized in terms of fully exploiting the potential of data for solution generation. Although recent research has investigated the use of generative learning in EC for efficient solution generation [14], its low precision remains a challenge to its practical application in tasks such as airfoil design.

Therefore, to address the challenges faced by existing AI-assisted supercritical airfoil design methods by fully leveraging the potential of EC, this work proposes an Evolutionary Generative Design (EvoGD) approach. On the one hand, the framework of EC provides an optimal platform for the generation of diverse and innovative supercritical airfoils. On the other hand, filled by carefully designed data-drive evaluators and generators, the proposed EvoGD approach is able to generate and identify high-performing supercritical airfoils with a high degree of accuracy and efficiency. The main contributions of this work are:

• The proposed approach in this work offers a departure from the traditional supercritical airfoil design process, which often involves the expertise of experienced professionals and multiple rounds of design iterations, simulations, and real-world testing. In contrast, the proposed approach is purely data-driven, offering the potential to significantly reduce the human effort and computational costs involved in supercritical airfoil design.

• To address challenge ❶, the proposed approach in this work leverages the EC framework and integrates it with a unique type of generative models for accommodating unpaired inputs, thus allowing for effective operation even on small datasets.

• To address challenge ❷, the proposed approach in this work conducts an empirical comparison of various parameterization methods for supercritical airfoils. Based on the comparison, a suitable parameterization method is selected that is capable of effectively capturing most of the physical constraints of supercritical airfoils.

• To address challenge ❸, the proposed approach incorporates an AI generative model that is capable of directly generating high-performing supercritical airfoils with improved aerodynamic and geometric characteristics. Additionally, the approach minimizes the number of designs that violate physical constraints, ensuring a robust design solution.

• To address challenge ❹, the proposed approach in this work employs a multi-objective EC framework integrated with fast and accurate data-driven supercritical airfoil generators and performance predictors. This allows for the inherent consideration of both design diversity and design reliability in the proposed approach.

• To accommodate the proposed approach with small data, this work introduces a new generative model training method. First, it incorporates physics information into the training process to boost the accuracy and efficiency. Second, it employs a combination of multiple generative models rather than a single one, to enhance robustness at the system level.

The remainder of this paper is organized as follows. In “Related work” section, we provide a comprehensive overview of previous studies on the application of AI to airfoil design. In “Problem formulation” section, we justify our choice of parameterization method and formulate the optimization problem for supercritical airfoil design. In “Method” section, we elaborate our proposed EvoGD approach and provide a thorough description of its implementation. In “Experimental study” section, we demonstrate the comprehensive experimental results. In “Conclusion” section, we conclude this paper with a summary of our findings and future directions for research.

Related work

In recent years, the application of AI to airfoil design, particularly supercritical airfoils, has become a topic of increasing interest due to the prohibitive computational expense of traditional CFD solvers. Early work by Yilmaz and German [15] utilized Convolutional Neural Networks (CNNs) to predict subcritical airfoil performance, which was later modified by Hui et al. [16] to include wall pressure coefficients. In addition to the use of data-driven surrogate models as performance predictors, there has also been a growing body of research on data-driven airfoil shape generation models. For instance, Sekar et al. [17] used CNNs for inverse airfoil design, where a subcritical airfoil was generated from a given wall pressure distribution. On the other hand, direct airfoil generation models have been explored, such as the use of Generative Adversarial Networks (GANs) by Chen et al. [18] and the use of Conditional Generative Adversarial Networks (CGANs) by Yilmaz [19] for the generation of subcritical airfoils with desired aerodynamic performance. Despite the ease of generalization to different airfoil design problems offered by these methods, which often adopt plain images as representations for airfoil shapes and prediction results, they may not be directly applicable to supercritical airfoil design due to the highly sensitive nature of aerodynamic performance to small changes in supercritical airfoil shape.

The application of AI-assisted approaches towards supercritical airfoil design has received growing attention in recent years. A number of studies have proposed utilizing AI optimization methods and/or AI predictors to address the challenges in this field. For example, Wang et al. [1] used a modified Particle Swarm Optimization (PSO) method and a simple back-propagation neural network as the performance predictor. Liu et al. [2] adopted a hybrid of Differential Evolution (DE) and Invasive Weed Optimization (IWO) methods combined with a Gaussian Process (GP) as the predictor. The rapid advancements in AI techniques, particularly deep learning, have also shown promising potential in this field. For example, Bouhlel et al. [4] employed a CFD-enhanced Artificial Neural Network (ANN) to achieve a prediction error of 0.48%. Wu et al. [20] combined CNN and (GAN) to establish a mapping between supercritical airfoils and transonic flow fields. Wang et al. [8] employed a Conditional Variational Autoencoder with Generative Adversarial Network (CVAE-GAN) to generate supercritical airfoils’ wall Mach number distributions and a Deep Neural Network (DNN) to map them back to supercritical airfoils. These works have demonstrated the potential of utilizing AI techniques in supercritical airfoil design.

Despite the recent progress in AI-assisted supercritical airfoil design, the development of the filed is still in its infancy, and there remain several technical details that require further investigation. For example, the precision of existing data-driven predictors can be limited when working with a small dataset, and the combination of high-performing predictors with simple, non-explorative AI optimization methods may not yield optimal results. Furthermore, the sophisticated AI generators currently in use do not guarantee the generation of supercritical airfoils with improved performance compared to existing designs. These limitations have underscored the ongoing need for further research and advancements in AI-assisted supercritical airfoil design.

Problem formulation

In this section, we will first introduce the NURBS as the method for parameterizing the supercritical airfoils. Then, the problem of supercritical airfoil design optimization will be mathematically formulated by defining its optimization objectives and constraints.

Table 1 Summarized features of several commonly adopted parametrization methods for supercritical airfoils

Parametrization method

Since we are considering supercritical airfoils whose aerodynamic performances are highly sensitive to shape modifications and defects, the reasonable design variables shall be the parameterized ones that perfectly describe supercritical airfoil shapes. Apparently, the design variables of plain images are impractical due to the relatively low precision and too much redundant variables. As summarized in Table 1, although there are also other specified parameterization methods for supercritical airfoil design, not all of them are suitable in our case. For example, a commonly adopted method was proposed by Kulfan et al. [21], where class and shape functions are used to represent geometric Class Shape Transformations (CSTs) and fitted to many supercritical airfoils with an experienced Bernstein Polynomial Order (BPO) as shape functions. However, one defect of this method is that their parameters are not quite physically meaningful. Another commonly used method is the Parametric Section (PARSEC) method proposed by Sobieczky [22]. This method has all physically meaningful parameters that correspond only to smooth airfoils with high robustness, but it cannot precisely control supercritical airfoil shapes.

Out of comprehensive considerations, we have chosen the Non-Uniform Rational B Spline (NURBS) curve [23] as our parametrization method in this work. Below are detailed justifications.

First, sampled coordinates can be converted to a NURBS curve easily. The general form of a NURBS curve, $\vec {C}(u) \equiv \left[ C_{x}(u),C_{y}(u) \right]$, is given by:

$$\begin{aligned} \vec {C}(u) = \sum _{i = 1}^{m}{\frac{N_{i,o}(u)w_{i}}{\sum _{j = 1}^{m}{N_{j,o}(u)w_{i}}}{\vec {P}}_{i}}, \end{aligned}$$

(1)

where $u \in [0,1]$ signifies the parameter of the function $\vec {C}(u)$, while $\vec {P}_{i} \equiv \left[P_{i,x},P_{i,y} \right]$ denotes the ith control point. The array $\varvec{P} = \big [\vec {P}_{1},\ldots ,\vec {P}_{m} \big ]^{T}$ represents the collective set of all control points. Further, $w_{i}$ refers to the weight of $\vec {P}_{i}$, and $N_{i,o}(u)$ is the ith basis function of a Non-Uniform Rational B-Spline (NURBS) curve of order o. Notably, the vector notation corresponds to either a vector or a point in a two-dimensional Cartesian coordinate system. It can be shown that it is simple to fit a NURBS curve to a set of coordinates $\varvec{X} = \left[{\vec {x}}_{1},\ldots ,{\vec {x}}_{n} \right]^{T}$, which is equivalent to solving for $\varvec{P}$ in the least-squares solution of the system of equations:

$$\begin{aligned} \varvec{NP} = \varvec{X}, \end{aligned}$$

(2)

where

$$\begin{aligned} \varvec{N}_{i,j} = N_{j,o}\left( \frac{\sum _{l = 1}^{i - 1}\left\| {\vec {x}}_{l + 1} - {\vec {x}}_{l} \right\| }{\sum _{l = 1}^{n - 1}\left\| {\vec {x}}_{l + 1} - {\vec {x}}_{l} \right\| } \right) \end{aligned}$$

(3)

is the basis matrix.

Second, NURBS can achieve high representation accuracy with a relatively small number of control points (i.e., design variables). For example, in our study, a NURBS curve can achieve a maximum relative error deviation of $10^{- 5}$ with only 18 control points of order 3. By further removing redundant variables, the actual number of design variables can be even reduced to 16 real values, represented by the vector $\varvec{q}$, i.e., all the y-coordinates except the first and last control points. The control points $\varvec{P}$ can then be reconstructed using a simple function $\varvec{P}(\varvec{q})$, where $\varvec{P}:\mathcal {Q} \rightarrow \mathcal {P}$ and $\varvec{q} \in \mathcal {Q}$, $\varvec{P}(\varvec{q}) \in \mathcal {P}$.

Third, the relative geometric flexibility of NURBS makes it desirable for use in our EvoGD approach. This feature provides us with an enhanced level of control over the details of supercritical airfoil shapes, making it possible to generate novel and diverse supercritical airfoils that are distinct from those in the dataset.

Additionally, the use of the Cartesian coordinate system for the design variables makes it easier for our AI generators and predictors to model and calculate the validity of designs. Furthermore, the actual supercritical airfoil shape depends almost linearly and locally on the NURBS control points, which helps to avoid the issue of generating designs with small non-smoothness or fluctuations that can occur in Proper Orthogonal Decomposition (POD) [24] and sampled coordinate methods.

Optimization objectives and constraints

For our proposed EvoGD approach to be practical and applicable in real-world scenarios, we consider several optimization objectives, including: (1) aerodynamic performance, (2) geometric performance, and (3) a series of aerodynamic and geometric constraints. In particular, we take the following geometric and aerodynamic performances of supercritical airfoils into consideration:

• h: Thickness. This is the maximum distance between the upper and lower surfaces of the supercritical airfoil, as illustrated in Fig. 1.

• K(u): Convex metric. A smooth supercritical airfoil implies that its convex metric has one and only one zero point on the lower surface.

• $\alpha _{0}$: Cruise angle of attack. This is the angle at which the supercritical airfoil produces a lift coefficient of $C_{L,0}$, which is 0.8 in this work, as shown in Fig. 2.

• $C_{LD}$: Cruise lift-to-drag ratio. This is defined as ${C_{L,0}}/C_{D}\left( \alpha _{0} \right)$, where $C_{D}$ is the drag coefficient; it is depicted in Fig. 2 as well.

• $C_{L}$: Buffet lift coefficient. This is the lift coefficient at the buffet angle of attack, which is defined as

  $$\begin{aligned} \alpha _1 = {(C'_L)}^{(-1)}\left\{ C'_L\left[ \underset{\alpha _l \le \alpha \le \alpha _h}{{\text {argmax}}}{\left| C''_L(\alpha )\right| } \right] - k_\text {diff} \right\} , \end{aligned}$$

  where $\alpha _l = -2$, $\alpha _h = 1$ and $k_\text {diff} = 0.1$ for this work. The buffet lift coefficient is also shown in Fig. 2.

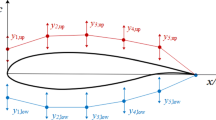
• $\varvec{C}_{P}\left( \alpha _{0} \right)$: Wall pressure coefficients at cruise angle of attack. In practice, the suction peak point $F_\textrm{sp}$ is the highest value of the wall pressure coefficients before maximum thickness, while the shock wave point $F_\textrm{sw}$ is the wall pressure coefficient at the wall Mach number of 1. An acceptable wall pressure coefficient should have limited decrease from $F_\textrm{sp}$ to $F_\textrm{sw}$ and contain exactly one $F_\textrm{sw}$. This is plotted in Fig. 3.

Fig. 1

The shape of NASA SC(2)-0410 supercritical airfoil. The digits “04” represent the theoretical optimal lift coefficient; the digits “10” represent that the maximum thickness is 10% of its total width or chord length c

Fig. 2

The curves of lift coefficients and lift-to-drag ratios vs. the angles of attack for the baseline supercritical airfoil. The physical meanings of $\alpha _{0}$, $C_{LD}$ and $C_{L}$ are depicted: at the cruise angle of attack $\alpha _0$, the lift coefficient is exactly $C_{L,0}$; at the same angle, the lift-to-drag ratio is the $C_{LD}$

Fig. 3

The curve of wall pressure coefficients ($\varvec{C}_P$) vs. the horizontal coordinates (x/c). The chord length c is set to 1 throughout this work. The suction peak point $F_\textrm{sp}$ and the shock wave point $F_\textrm{sw}$ are the key features. The suction peak point $F_\textrm{sp}$ is the highest value of the wall pressure coefficients before the maximum thickness, while the shock wave point $F_\textrm{sw}$ is the wall pressure coefficient at the wall Mach number of 1

In this work, we select $C_{L}$, $C_{LD}$ and h as our optimization objectives, and $\alpha _{0}$, $\varvec{C}_{P}\left( \alpha _{0} \right)$, h and K(u) as our constraints. These values are functions of the NURBS control points, represented by the design variables $\varvec{q}$. For the rest of the paper, these values will be written as $C_{L}\left( \varvec{q} \right)$ and so on.

The cruise angle of attack $\alpha _{0}\left( \varvec{q} \right)$ must lie within a specified range, such as:

$$\begin{aligned} \alpha _{\textrm{min}} \le \alpha _{0}\left( \varvec{q} \right) \le \alpha _{\textrm{max}}, \end{aligned}$$

(4)

where $\alpha _{\textrm{min}} = 1^{\circ }$ and $\alpha _{\textrm{max}} = 2^{\circ }$ are commonly used.

Additionally, the suction peak $F_{\textrm{sp}}\left( \varvec{q},\alpha _0\left( \varvec{q}\right) \right)$ should not exceed $F_{\textrm{sp,0}} \approx - 1.2$ to avoid sharp leading edges. Similarly, the difference between the absolute values of $F_{\textrm{sw}}\left( \varvec{q},\alpha _0\left( \varvec{q}\right) \right)$ and $F_{\textrm{sp}}\left( \varvec{q},\alpha _0\left( \varvec{q}\right) \right)$ must lie in a certain range, typically 0.05:

$$\begin{aligned} \left\{ \begin{aligned}&F_{\textrm{sp}}\left( \varvec{q},\alpha _0\left( \varvec{q}\right) \right) \ge F_{\textrm{sp,0}} \\&0.05 \le F_{\textrm{sw}}\left( \alpha _{0} \right) - F_{\textrm{sp}}\left( \alpha _{0} \right) \le 0.05 \end{aligned}\right. . \end{aligned}$$

(5)

Moreover, the convex metric of the supercritical airfoil must satisfy the following conditions:

$$\begin{aligned} \begin{aligned} K(u)&\equiv x'(u)y''(u) - x''(u)y'(u) \\&\left\{ \begin{aligned} \ge 0,\ \&u \in \left[ 0,{1}/{2} \right) \cup \left( u_{c},1 \right] \\ \le 0,\ \&\text {otherwise}, \\ \end{aligned} \right. \end{aligned} \end{aligned}$$

(6)

where $\left[x(u),y(u) \right]\equiv {\vec {N}}_{o}^{T}(u)\varvec{P}\left( \varvec{q} \right)$ is the parametric representation of the supercritical airfoil defined by the design variables $\varvec{q}$ in terms of the NURBS basis functions $\vec {N}_{o}^{T}(u)$ and the control points $\varvec{P}(\varvec{q})$, and $\left[x\left( u_{c} \right) ,y\left( u_{c} \right) \right]$ is the point on the lower surface of the supercritical airfoil where the curve changes from convex upward to concave upward.

Finally, to prevent extrapolation outside the range of our prediction models, we also consider the maximum values of $C_{L}\left( \varvec{q} \right)$ and $C_{LD}\left( \varvec{q} \right)$ among the given dataset $\mathcal {D}$:

$$\begin{aligned} \left\{ \begin{aligned}&C_{L}\left( \varvec{q} \right)< (1 + \varepsilon )\max _{\varvec{q}\in \mathcal {D}}{C_{L}\left( \varvec{q} \right) }\\&C_{LD}\left( \varvec{q} \right) < (1 + \varepsilon )\max _{\varvec{q}\in \mathcal {D}}{C_{LD}\left( \varvec{q} \right) } \end{aligned}\right. , \end{aligned}$$

(7)

where $\varepsilon$ is a small number that has been validated to be safe for prediction extrapolation.

Table 2 The optimization objectives and constraints of the supercritical airfoil design in this work. d is short for dimension

Based on the above, problem formulation of the supercritical airfoil design is summarized in Table 2. In general, the optimization objectives are highly conflicting, particularly between h and $C_{L}$, $C_{LD}$. Hence, h is not only a constraint but also an optimization objective in this work. This modification may make the design process more challenging, but it can also result in improved outcomes for supercritical airfoil design.

Method

The proposed EvoGD approach for supercritical airfoil design consists of four components in its main iterative loop: Generator, Evaluator, Selector, and Interactor, as illustrated in Fig. 4. In each iteration, first, the Generator generates a new batch of supercritical airfoils based on the information obtained from the previous iteration, with the goal of improving the design diversity and performance of the existing supercritical airfoils; the Evaluator is then utilized to assess the aerodynamic performances and constraint violations of the new batch of airfoils; afterwards, the Selector selects high-quality airfoils by ranking with optimization objectives of $C_{L}$, $C_{LD}$ and $h$, as well as constraints of $\alpha _{0}$, $C_{L}$, $C_{LD}$, $\varvec{C}_{P}\left( \alpha _{0} \right)$ and $h$; finally, the designer has the option to interact with the process via Interactor before the next iteration begins.

Fig. 4

Main loop of the proposed EvoGD approach. There are four main components—Generator, Evaluator, Selector, and Interactor. In the case of supercritical airfoil design, both Generator and Evaluator are purely data-driven ones, where Selector and Interactor are not

In the case of supercritical airfoil design, the Selector is not data-driven since all optimization objectives and constraints are deterministic and well-defined, and thus it is not imminent to supply Selector with data. Hence, we adopt the selection method of [25] as our Selector. However, in other cases where selection process is nondeterministic or ill-defined, the proposed EvoGD can still be applied with an implementation of data-driven selector(s). Moreover, even though the Interactor in this work is merely used to display the results to the designer, it can also show the selected supercritical airfoils to designers and asking for new information such as aerodynamic performances to update data-driven models on the fly. Specifically, the data-driven Generator and Evaluator are further elaborated in the following subsections.

Generator

Our Generator component further encompasses several data-driven generators, which offer a more efficient alternative to manual supercritical airfoil design. The generators previously adopted in AI-assisted supercritical airfoil design are instances of the conditional probability

(8)

where $T \equiv T(\alpha _{0},C_{L},C_{LD},C_{P},h)$ represents the joint distribution of target performances, t represents an arbitrary instance of T, and $\varvec{Q}$ represents the joint distribution of design variables $\varvec{q}$. Various generators, such as Variational Autoencoders (VAEs) [26], Generative Adversarial Networks (GANs) [27] Conditional Generative Adversarial Networks (CGANs) [28], and SoloGAN [29], have been introduced in previous studies to model this Probability Density Function (PDF).

However, the target aerodynamic performance space spanned by $T$ in the training dataset for this model is often limited and discrete, leading to an uneven distribution. This can result in generators’ failure in accurately modeling the target performance space and the generated supercritical airfoils may even be infeasible. To address the issue of uneven distribution of the target aerodynamic performance space, in this work, we adopt the following model:

(9)

where and represent two conditional probabilities in a traditional generator, and $t' \preccurlyeq t$ indicates that the target performances of $t'$ are generally worse than t’s.

The adopted model in this work can be considered as a redesign/refine model that generates a new supercritical airfoil based on learned dominance relations between the aerodynamic performances. Local and global search operators for optimization objectives such as $C_{L}$, $C_{LD}$, and h, as well as their combination, are examples of such generators. To implement these search operators, Artificial Neural Networks (ANNs) are commonly utilized. Specifically, in this work, we use the generators in the Cycle Generative Adversarial Networks (Cycle GANs) [30].

Notably, the model described in Eq. (9) can be viewed as a generative model that integrates physics information, resulting in the inherent consideration of physical performance and constraints during the training of our Cycle GANs. This integration of physics information enhances the stability of the training process, while the use of multiple generators for each physical performance improves the robustness of the entire Generator. Further details of the training process can be found in “Model training” section.

As illustrated in Fig. 5, the Cycle GAN is originally designed to find a pair of generators mapping between two domains, $\mathcal {X}$ and $\mathcal {Y}$, using two generator-discriminator pairs: $G:\mathcal {X \rightarrow Y}$ with $D_{G}$ and $F:\mathcal {Y \rightarrow X}$ with $D_{F}$. The discriminators, $D_G$ and $D_F$, aim to minimize the classification error rates between real and generated fake inputs, while the generators, G and F, aim to maximize the discriminators’ classification error rates for fake inputs. Additionally, the Cycle GAN minimizes the cyclic consistency losses, $\left\| F\left( G\left( \varvec{x} \right) \right) - \varvec{x} \right\|$ and $\left\| G\left( F\left( \varvec{y} \right) \right) - \varvec{y} \right\|$, where $\varvec{x}\in \mathcal {X}$ and $\varvec{y}\in \mathcal {Y}$ are samples from the two domains.

Fig. 5

Structure of a Cycle GAN. The input samples from domain $\mathcal {X}$ are input as x and the samples from domain $\mathcal {Y}$ are input as y. The generator G maps the samples from domain $\mathcal {X}$ to domain $\mathcal {Y}$, generating the fake 2 output Y. Likewise, the generator F, maps the samples from domain $\mathcal {Y}$ to domain $\mathcal {X}$, generating the fake 1 output X. The discriminators $D_F$, $D_G$ receive x and X, y and Y, respectively, and output cross-entropy losses $\mathcal {L}_{D_F}$ and $\mathcal {L}_{D_G}$, respectively, for classifying real and fake supercritical airfoils. The fake outputs X and Y are also sent to their corresponding generators G and F, respectively, to produce the reconstructed supercritical airfoils $y'$ and $x'$. The cyclic consistency losses $\mathcal {L}_{GF}$ and $\mathcal {L}_{FG}$ of the Cycle GAN is the difference between x, $x'$ and y, $y'$, respectively. The model minimizes the $\mathcal {L}_{GF}$ and $\mathcal {L}_{FG}$ with respect to both generators G and F. In the mean time, it also minimizes the $\mathcal {L}_{D_G}$ and $\mathcal {L}_{D_F}$ with respect to the $D_G$ and $D_F$, respectively. Additionally, like in a traditional GAN, the classification errors for Y and X are inverted to train G and F, respectively

Specifically, there are four different loss functions in training the Cycle GAN:

$$\begin{aligned} \mathcal {L}_{GF},\quad \mathcal {L}_{FG},\quad \mathcal {L}_{D_G}\quad \text {and}\quad \mathcal {L}_{D_F}. \end{aligned}$$

(10)

They can be written as

$$\begin{aligned} \begin{aligned}&\mathcal {L}_{GF} = \left\| F\left( G\left( \varvec{x} \right) \right) - \varvec{x} \right\| ,\\&\mathcal {L}_{FG} = \left\| G\left( F\left( \varvec{y} \right) \right) - \varvec{y} \right\| ,\\&\mathcal {L}_{D_G} = \log {D_{G}\left( \varvec{y} \right) } + \log \left[1 - D_{G}\left( G\left( \varvec{x} \right) \right) \right],\\ \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \mathcal {L}_{D_F} = \log {D_{F}\left( \varvec{x} \right) } + \log \left[1 - D_{F}\left( F\left( \varvec{y} \right) \right) \right]. \end{aligned}$$

To train the discriminators $D_G$ and $D_F$, the loss functions $\mathcal {L}_{D_G}$ and $\mathcal {L}_{D_F}$ are minimized with respect to the parameters of $D_{G}$ and $D_{F}$, respectively. Since the data never flows between the discriminators, it is equivalent to minimize

$$\begin{aligned} \begin{aligned} \mathcal {L}_{\text {discriminator}}&= \log {D_{G}\left( \varvec{y} \right) } + \log \left[1 - D_{G}\left( G\left( \varvec{x} \right) \right) \right]\\&\quad + \log {D_{F}\left( \varvec{x} \right) } + \log \left[1 - D_{F}\left( F\left( \varvec{y} \right) \right) \right]\end{aligned} \end{aligned}$$

(11)

with respect to the parameters of $D_{G}$ and $D_{F}$ combined.

To train the generators G and F, the loss function $\mathcal {L}_{\text {generator}}$ is minimized with respect to the parameters of G and F combined:

$$\begin{aligned} \begin{aligned} \mathcal {L}_{\text {generator}}&= \lambda \left( \mathcal {L}_{GF} + \mathcal {L}_{FG}\right) - \log \left[1 - D_{G}\left( G\left( \varvec{x} \right) \right) \right]\\&\quad - \log \left[1 - D_{F}\left( F\left( \varvec{y} \right) \right) \right], \end{aligned} \end{aligned}$$

(12)

where $\lambda$ is the coefficient that characterizes the importance of cyclic consistency losses in training.

When adopting Cycle GAN in the proposed EvoGD approach, the input datasets are carefully divided based on the aerodynamic and geometric performance objectives $C_{L}$, $C_{LD}$, and $h$. The original dataset consists of design variables of supercritical airfoils (NURBS control points) and their respective performance objectives, defined as:

$$\begin{aligned} \begin{aligned} \mathcal {D}&= \left\{ \left( \varvec{q}_{1},C_{L,1},C_{LD,1},h_{1} \right) ,\ldots , \right. \\&\quad \quad \quad \left. \left( \varvec{q}_{501},C_{L,501},C_{LD,501},h_{501} \right) \right\} . \end{aligned} \end{aligned}$$

(13)

It is then divided into three pairs of input datasets:

(14)

where $C_{L,\epsilon }$, $C_{LD,\epsilon }$ and $h_{\epsilon }$ are the tunable separation thresholds of three targets. Specifically, multiple thresholds are used for each target $t_{i}$ to train different generators. To further enhance the performances of our generators, another pair of input dataset is also provided:

(15)

which are divided by Pareto dominance relations of all objectives.

As mentioned earlier, our generators can be represented as

(16)

where $\mathbb {E}\left( t_{i} \right) > \mathbb {E}\left( t_{i}' \right)$. The generator $G_{i}$ maps the supercritical airfoil design variable space with lower target performance $t_{i}'$ to the one with higher target performance $t_{i}$. In our implementation, the generator $G_{i}$ is the generator G of the ith Cycle GAN, trained by providing samples to y and x inputs with $\mathcal {Q}_{i,1}$ and $\mathcal {Q}_{i,2}$, respectively. Upon convergence, the generators will possess the ability to refine the given supercritical airfoils to produce new ones with better optimization objectives at high probabilities. In addition, the use of random divisions to separate median samples from the original dataset increases the diversity of generated supercritical airfoils.

Evaluator

Our Evaluator is also composed of data-driven predictors, which serve as computationally inexpensive surrogates for estimating the aerodynamic performances of supercritical airfoils, rather than relying on computationally intensive CFD simulations.

In general, a predictor is an instance of the discriminative/regression model—a model of conditional probability

(17)

where $\varvec{q}$ is the given supercritical airfoil’s design variables (obtained from NURBS curve control points) and $T \equiv T\left( \alpha _{0},C_{L},C_{LD},C_{P} \right)$ is the target aerodynamic performances’ joint distribution. To optimize both buffet and cruise performance of a supercritical airfoil, we need to model and predict its cruise angle of attack

(18)

its buffet lift coefficient

(19)

its cruise lift-to-drag ratio

(20)

and its cruise surface pressure coefficients

(21)

where the vector notation of $\varvec{C}_{P}$ indicates that it is a vector representation of curve at any given angle of attack and supercritical airfoil. It can be noticed that the angle of attack is not a condition variable for the first three predictors, but we directly target the aerodynamic performances at cruise and buffet angles of attack. This is crucial for these predictors to work properly on a dataset with an unprecedented small size of 501.

Specifically, each predictor is a Multi-Layer Perceptron (MLP) [31] composed of an input layer, two–three hidden full-connection layers, and an output layer. The adopted MLP is simple and efficient, with input layers consisting of the 16 design variables of the supercritical airfoil, output layers being the corresponding prediction values of size 1 or 30, and hidden layers of size 60–100. The hidden layer configurations vary between different predictors due to differences in purposes and complexities. All predictive models use Mean Squared Error (MSE) as the loss function $\mathcal {L}$:

$$\begin{aligned} \mathcal {L} = \left\| \varvec{n}_{\text {last}} - \varvec{n}_{\text {real}} \right\| ^{2}, \end{aligned}$$

(22)

where $\varvec{n}_{\text {last}}$ are the output values of the last layer of the MLP and $\varvec{n}_{\text {real}}$ are the actual values to predict.

For each predictor for cruise angle of attack ($\alpha _{0}(\varvec{q})$), buffet lift coefficient ($C_{L}(\varvec{q})$), and cruise lift-to-drag ratio ($C_{LD}(\varvec{q})$), a MLP with two hidden layers and hyperbolic tangent activation function is employed. To ensure proper performance, the $\alpha _{0}$, $C_{L}$, and $C_{LD}$ values in the dataset are first normalized and any anomalies are removed. After this preprocessing, the three MLPs are trained, one for each value to be predicted.

For the predictor of cruise surface pressure coefficients $\varvec{C}_{P}(\varvec{q})$, the Proper Orthogonal Decomposition (POD) method is utilized. The POD method transforms the original data points of $\varvec{C}_{P}$ and extracts the first few modes for prediction. In this case, only 30 modes are required for the decomposition for achieve a high prediction accuracy. To further improve the overall performance of the predictive model of $\varvec{C}_{P}(\varvec{q})$, the $\varvec{C}_{P}(\alpha ;\varvec{q})$ of all provided $\alpha$ values are included in the dataset, using the regression model:

(23)

where $\varvec{c}$ is the POD modes’ singular values. The MLP structure for this predictor is compact, consisting of only three hidden layers of size 100–200, with a hyperbolic tangent activation function.

Selector

As articulated above, in the context of supercritical airfoil design, all optimization objectives and constraints are deterministic. Consequently, our Selector does not rely on a data-driven approach. The general process of the Selector can be summarized as follows:

• 1. Compute all objectives and violations of constraints for the current population;

• 2. Determine the Pareto rank r utilizing the fast non-dominant sort method as proposed in NSGA-II [25];

• 3. Compute the shared fitness values by

  $$\begin{aligned} f_i = \frac{1}{r_i\cdot \sum _{j=1}^{N}\max \{1 - [\Vert \varvec{F}_i - \varvec{F}_j\Vert ], 0\}}, \end{aligned}$$

  where $\varvec{F}_i$ is the rescaled objectives of individual i and N is the number of individuals in the population;

• 4. Adjust their shared fitness $f_i$ by subtracting their constraint violations;

• 5. The subsequent generation is selected randomly by weights $w_i = {e^{f_i}}/{\sum _{j=1}^N{e^{f_j}}}$.

Experimental study

In this section, we present the details of the experimental study conducted to validate the proposed EvoGD approach. First, we introduce the dataset used in the experiment and present the design results. Then, we delve deeper into the key components of EvoGD: Evaluator and Generator, respectively.

Dataset

The dataset is an essential component for data-driven models to achieve better training and testing performance. Therefore, an adaptive sampling strategy was applied to generate a diverse range of supercritical airfoil shapes, ensuring the diversity of the dataset. To ensure its practicality, constraints such as a leading-edge radius of less than 0.007 and a thickness ranging from 0.113 to 0.123 were imposed. In this paper, the dataset consists of 501 supercritical airfoils in total, including one baseline plus 500 randomly perturbed variants. The aerodynamic performance of each airfoil was calculated using high-fidelity CFD simulations.

For the CFD simulations, a structured O-grid with a radius of 30c was adopted, where $c=1$ is the chord length of all the supercritical airfoils. The grid sizes along the normal direction to the surface were kept relatively small to take the thickness of the boundary layer into account. After grid independence verification, the adopted grid consisted of 385 points along the circumference of the supercritical airfoil and 193 points along the normal direction. The Reynolds Average Navier–Stokes (RANS) equations with the Shear Stress Transport (SST) turbulence model were used, and the solutions were calculated using the open-source code CFL3D.¹ The MUSCL scheme was used for state-variable interpolation at the cell interfaces, the Roe scheme was used for spatial discretization, and the lower-upper symmetric Gaussian–Seidel method was used for time advancement.

As an overview, the shapes and performances of the supercritical airfoils in the dataset are depicted in Fig. 6.

Fig. 6

The stacked plot of the baseline and dataset supercritical airfoils (a), and the parallel axis plot of the aerodynamic and geometric performances ($C_{L}$, $C_{LD}$ and h) of the baseline and dataset supercritical airfoils (b). In the parallel axis plot, each vertical axis represents a performance of supercritical airfoils. The orange and blue lines in each plot represent the baseline supercritical airfoil and its 500 randomly perturbed variants respectively

General design results

With the above dataset, we ran the proposed EvoGD for 100 iterations and obtained a new set of 240 airfoils, where 95% meet all design constraints and 75% (i.e., 180 elite airfoils) successfully achieved the basic design goals as shown in Table 3. Notably, it only took less than a hour on a PC with i7 CPU to complete the entire design process, including the training of the Generator and Evaluator.

Table 3 The basic design goals of the supercritical airfoil optimization design problem

Fig. 7

The histograms of the improvements on aerodynamic and geometric performances ($C_{L}$, $C_{LD}$ and h) of the generated elite supercritical airfoils compared to the baseline supercritical airfoil

As summarized in in Fig. 7, generally, our EvoGD managed to improve the buffet lift coefficient $C_{L}$ by at most 9%, the cruise lift-to-drag ratio $C_{LD}$ by at most 9%, and the thickness h by at most 4%, as shown in Fig. 7. Out of the 180 elite airfoils as obtained, there are 120 that fully dominate the baseline airfoil in all optimization objectives. It can also be seen from the Fig. 7 that the distributions of improved $C_{L}$, $C_{LD}$, and h all have mean values that are significantly greater than 0. Furthermore, on average, $C_{L}$ and $C_{LD}$ were significantly improved by 5–6%, much more than the design goals of them. From the distribution of improved h in Fig. 7, it can be implied that our approach did not compromise geometric performance for better aerodynamics. Besides, from the parallel axis plot in Fig. 8b, one can also notice such implication. Moreover, the diversity of the generated supercritical airfoils was well preserved, as demonstrated by the stacked plot in Fig. 8a. By contrast, none of the 500 randomly perturbed airfoils in the dataset can achieve the results stated above.

Fig. 8

The stacked plot of the baseline and the generated elite supercritical airfoils (a) and the parallel axis plot of the aerodynamic and geometric performances ($C_{L}$, $C_{LD}$ and h) of the baseline and the generated elite supercritical airfoils (b). Each vertical axis in the parallel axis plot represents a supercritical airfoil’s performance. The orange and blue lines represent and the baseline supercritical airfoil and the ones generated by EvoGD, respectively

Assessment of generator

In this subsection, we will conduct the experiment for assessing the performance of Generator in the proposed EvoGD approach, including model training and model testing.

Model training

With the fully dataset consisting of 501 supercritical airfoils

$$\begin{aligned} \mathcal {Q} = \left\{ \varvec{q}^{1},\ldots ,\varvec{q}^{501} \right\} , \end{aligned}$$

(24)

we adopt distinct separation criteria with different thresholds to separate the original dataset into 20 pairs of training datasets to train four different types of generators. Specifically, as shown in Eq. (14), the tunable separation thresholds $C_{L,\epsilon }$, $C_{LD,\epsilon }$, and $h_{\epsilon }$ are randomly selected to ensure diversity. Each separation thresholds are five samples from distribution $\mathcal {N}\left( m_{t},{\sigma _{t}}/{10} \right)$, where t represents each optimization objective and $m_{t}$ and $\sigma _{t}$ are the median and standard deviation of t in the original dataset, respectively. As for the separation of all objectives $C_{L}$, $C_{LD}$, and h, it is performed using Pareto dominance sorting. The first Pareto optimal set of the original supercritical airfoils is defined as

(25)

Then, the set $\mathcal {Q}^{1}$ is removed from $\mathcal {Q}$ to find the next Pareto optimal set $\mathcal {Q}^{2}$. This process is repeated until $\left| \mathcal {Q}^{1} \cup \cdots \cup \mathcal {Q}^{r} \right| > {501}/{2}$. The median group $\mathcal {Q}^{r}$ is then divided into 5 different datasets by random choices to form the datasets for the last type of generators.

To increase diversity in generating supercritical airfoil search directions and steps, our proposed Generator includes 20 generators (from 20 Cycle GANs), each trained on a different pair of datasets. During the training for each generator, the $\lambda$ in Eq. (12) is set to 10, the batch size is fixed to 64 and it is stopped when training time exceeds 100 s. Moreover, the sum of all losses in Eq. (10),

$$\begin{aligned} \mathcal {L} = \lambda (\mathcal {L}_{GF} + \mathcal {L}_{FG}) + \mathcal {L}_{D_G} + \mathcal {L}_{D_F}, \end{aligned}$$

(26)

is used for model preservation: $\mathcal {L}$ is calculated for each epoch and the epoch with lowest $\mathcal {L}$ is selected as the final generator.

Model testing

After applying all the generators to the design variables of the original supercritical airfoils, their modifications (i.e., search steps) can be partially characterized by their marginal probability density function (PDF), as shown in Fig. 9. The decomposition of this PDF into Gaussian mixture models is also depicted. It is noticeable that our generators provide both large and small search steps: since the range of the original supercritical airfoil design variables is only 0.02, the mean values of the left or right Gaussian mixtures (around 0.002) correspond to an average search step size of around 10%, while the main Gaussian mixture corresponds to an average step size of around 1.5%.

Fig. 9

The probability density function (PDF) of all generators’ modifications to the original supercritical airfoil design variables. The solid line represents the overall PDF, while the horizontal axis represents the search steps of the generators and the vertical axis represents the probability densities of the corresponding search steps. The dashed lines are the Gaussian mixture model fittings of three Gaussians with different means and variances. It is notable that the areas of these components are equal, implying that the generators have modeled both small and large search steps in a balanced manner

Since the PDFs shown in Fig. 9 are only marginal PDFs that flattens all the modifications of different supercritical airfoil design variables, it is necessary to view the covariance matrices of such modifications to verify that our generators do models the performance improvement mapping Eq. (9). For example, the covariance matrices of the $C_{LD}$ generators’ modifications to original supercritical airfoils are shown in Fig. 10. Their relatively stable mean values $\mu$ and covariance matrices $\Sigma$ imply that the generators have learned certain modification directions from the given datasets. However, it does not imply that our generators are randomly perturbing the design variables (i.e., $\varvec{p}$) by $\mathcal {N}(\mu ,\Sigma )$. For example, Fig. 11 depicts the side-by-side comparison of the objective improvements between randomly perturbed $\varvec{p}$ with covariance matrix the same as Fig. 10 and modified $\varvec{p}$ via $C_{LD}$ generators. It shows that our generators are inherently different from high-dimensional Gaussian distributions.

Fig. 10

The plot of the covariance matrix of the $C_{LD}$ generators’ modifications to original supercritical airfoils. The $C_{LD}$ generators are the ones trained with $\mathcal {Q}_{2,1}$ and $\mathcal {Q}_{2,2}$ in Eq. (14). Hence, it is aimed to improve the $C_{LD}$ objective of the given supercritical airfoils. Since the differences between the covariance matrices of different generators are marginal, they are not shown and the mean value of the matrices are plotted instead

Fig. 11

A comparison of the probability distribution functions (PDFs) of the objective improvements between randomly perturbed $\varvec{p}$ following $\mathcal {N}(\mu ,\Sigma )$ with the same $\Sigma$ as in Fig. 10a and modified $\varvec{p}$ via the $C_{LD}$ generators (b). The comparison reveals that random perturbations are more likely to alter $C_{L}$ than the generators, which is undesirable since our goal is to improve $C_{LD}$. Additionally, the random perturbations tend to reduce the thickness more significantly than the generators. Furthermore, the random perturbations’ $C_{LD}$ improvements are evenly distributed around 0, indicating that they are not as effective in improving $C_{LD}$ as the generators

Moreover, the autocorrelation function (ACF) of our generators’ modifications is distinct from that obtained from randomly perturbing design variables, as shown in Fig. 12. Specifically, the ACF we adopt is calculated as follows:

$$\begin{aligned} \text {ACF}\left[C_{y},u_{l} \right]= \frac{\left( C_{y}(u) - \mathbb {E}\left[C_{y} \right]\right) *\left( C_{y}\left( u + u_{l} \right) - \mathbb {E}\left[C_{y} \right]\right) }{\mathbb {V}\left[C_{y} \right]},\nonumber \\ \end{aligned}$$

(27)

where $C_{y}$ represents the y coordinate of the modification curve, u is its parameter, and $C_{y}(u + 1) = C_{y}(u)$. The operator $*$ represents the convolution with respect to u, $\mathbb {E}\left[C_{y} \right]$ is the expectation of $C_{y}$, and $\mathbb {V}\left[C_{y} \right]$ is the variance of $C_{y}$. Empirically, the ACF at $u_{l}$ indicates the average relationship between all point pairs separated by a distance of $u_{l}$ on $C_{y}$: values close to 1 imply that most point pairs are positively related; values close to $- 1$ imply that most are negatively related; while values close to 0 imply that they are on average not related.

Fig. 12

The average autocorrelation function (ACF) of modifications to all original supercritical airfoil curves. The blue line represents the average ACF of modifications made by all generators, while the orange line represents the average ACF of random perturbations. The horizontal axis (distance on curve) indicates the distances between the pairs of points on the parametric modification curves being considered. The vertical axis indicates the average correlation between the point pairs of the corresponding distance. It is observed that the ACF of the random perturbations rapidly decreases to near 0, while the ACF of our generators has much longer tails. This difference implies that our generators tend to globally modify the shape of the supercritical airfoils with dedicated correlations

Compared to random perturbation of the original supercritical airfoils’ design variables, our generators generate or redesign supercritical airfoils in a more global manner in their geometries, as demonstrated in Fig. 12. In addition, Fig. 13 shows that our generators generally produce supercritical airfoils with better aerodynamic performance compared to the input ones. 43% of the generated supercritical airfoils show dominant performance over the input ones, while 40.5% exhibit trade-off between the two aerodynamic performances. Only 16.5% of the generated supercritical airfoils are dominated by the input ones, with the majority clustered around the origin. This further supports that our generators correctly model the performance improvement mapping as described in Eq. (9).

Fig. 13

The improvements in aerodynamic performance of all the generators applied to all supercritical airfoils in the dataset. The four numbers in the figure indicate the percentages of supercritical airfoils in each region. It is evident that our generators can generate supercritical airfoils with superior performance compared to the input ones

In conclusion, our proposed Generator has been shown to be an effective approximation of both local and global search operators in the supercritical airfoil design space. Through training on a dataset, the generators have acquired the ability to learn the natural constraints and generate reasonable modifications to supercritical airfoils by refining them globally with both small and large steps, while maintaining their geometric constraints.

Fig. 14

The actual vs. predicted plots for $C_{L}$, $C_{LD}$, and $\alpha _{0}$ predictors in the testing dataset. The orange dots represent the predicted normalized performances and the actual normalized performances, respectively, with the horizontal positions indicating the predicted values and the vertical positions indicating the actual values. The dashed lines represent the ideal predictions

Assessment of evaluator

In this subsection, we will conduct the experiment for assessing the performance of Evaluator in the proposed EvoGD approach, including model training and model testing.

Model training

With the full dataset consisting of 501 supercritical airfoils, the following datasets are used for training the $C_{L}$, $C_{LD}$, $\alpha _{0}$, and $\varvec{C}_{P}$ predictors, respectively:

$$\begin{aligned}{} & {} \mathcal {D} = \left\{ \left( \varvec{q}^{1},C_{L}^{1} \right) ,\ldots ,\left( \varvec{q}^{501},C_{L}^{501} \right) \right\} , \nonumber \\{} & {} \mathcal {D} = \left\{ \left( \varvec{q}^{1},C_{LD}^{1} \right) ,\ldots ,\left( \varvec{q}^{501},C_{LD}^{501} \right) \right\} , \nonumber \\{} & {} \mathcal {D} = \left\{ \left( \varvec{q}^{1},\alpha _{0}^{1} \right) ,\ldots ,\left( \varvec{q}^{501},\alpha _{0}^{501} \right) \right\} \quad \text {and} \nonumber \\{} & {} \mathcal {D} = \left\{ \left( \varvec{q}^{1}, \alpha ^{1,1},\varvec{C}_{P}^{1,1} \right) ,\ldots ,\left( \varvec{q}^{501}, \alpha ^{501,57}, \varvec{C}_{P}^{501,57} \right) \right\} . \nonumber \\ \end{aligned}$$

(28)

The superscripts of $\varvec{q}$ indicate the index of the supercritical airfoil, while the other superscripts indicate the sample index.

For the predictors of $C_L$, $C_{LD}$, and $\alpha _0$, the aerodynamic performances are first normalized:

$$\begin{aligned} {\tilde{t}}^{i} = \frac{t^{i} - \min \left\{ t \right\} }{\max \left\{ t \right\} - \min \left\{ t \right\} }, \end{aligned}$$

(29)

where t is the aerodynamic performance. This normalization ensures that the error $\varepsilon ^{i} = {\tilde{t}}_{\text {predict}}^{i} - {\tilde{t}}_{\text {real}}^{i}$ is inherently normalized. The datasets are then randomly divided into training sets of size 450 and testing sets of size 51.

For the $\varvec{C}_{P}$ predictor, the angle of attacks are first normalized with same extreme values of $\alpha _{0}$ as above:

$$\begin{aligned} {\tilde{\alpha }}^{k,i} = \frac{\alpha ^{k,i} - \min \left\{ \alpha _{0} \right\} }{\max \left\{ \alpha _{0} \right\} - \min \left\{ \alpha _{0} \right\} }, \end{aligned}$$

(30)

which ensures that the predictor models no additional normalization. Then, proper orthogonal decomposition (POD) is applied to $\varvec{C}_{P}^{k,i}$ through the following procedure: first, all $\varvec{C}_{P}^{k,i}$ are combined into a matrix

$$\begin{aligned} \varvec{M}_{C_{P}}:= \left[\varvec{C}_{P}^{1,1},\ldots ,\varvec{C}_{P}^{1,i_{\text {max}}^{1}},\varvec{C}_{P}^{2,1},\ldots ,\varvec{C}_{P}^{501,i_{\text {max}}^{501}} \right], \end{aligned}$$

(31)

where $\varvec{M}_{C_{P}} \in \mathbb {R}^{353 \times 27,514}$ for our dataset; second, Singular Value Decomposition (SVD) is applied to $\varvec{M}_{C_{P}}$ to obtain $\varvec{M}_{C_{P}} \rightarrow \varvec{US}\varvec{V}^{T}$, where $\varvec{S} = \textrm{diag}\left\{ s_{1},\ldots ,s_{353} \right\}$; finally, the first 30 columns of the left singular vectors $\varvec{U}$ and the entries of the mode amplitudes $\varvec{S}$ are retained to achieve the desired decomposition accuracy as shown in Fig. 16. In this way, the dataset is transformed into

$$\begin{aligned} \tilde{\mathcal {D}} ={} & {} \Big \{ \left\{ \varvec{q}^{1},{\tilde{\alpha }}^{1,1} \right\} \rightarrow \left\{ s_{1}^{1,1},\ldots ,s_{30}^{1,1} \right\} , \nonumber \\{} & {} \left\{ \varvec{q}^{1},{\tilde{\alpha }}^{1,2} \right\} \rightarrow \left\{ s_{1}^{1,2},\ldots ,s_{30}^{1,2} \right\} ,\ldots , \nonumber \\{} & {} \left. \left\{ \varvec{q}^{501},{\tilde{\alpha }}^{501,i_{\text {max}}^{501}}\right\} \rightarrow \left\{ s_{1}^{501,i_{\text {max}}^{501}},\ldots ,s_{30}^{501,i_{\text {max}}^{501}} \right\} \right\} . \nonumber \\ \end{aligned}$$

(32)

The training and testing sets for the $\varvec{C}_{P}$ predictor are randomly divided into 90% and 10%, respectively, prior to training the model.

In the training process of each predictor, the batch size is set to the maximum possible value (24,762 for the $\varvec{C}_{P}$ predictor and 450 for the others) and training is stopped if it exceeds 200 s. The loss function in Eq. (22) is used to evaluate the performance of each predictor, and the epoch with the lowest loss on the testing set is selected as the final predictor.

Model testing

For the $C_L$, $C_{LD}$ and $\alpha _0$ predictors, the actual vs. predicted plots of the testing set are shown in Fig. 14. In addition, the prediction errors on the whole datasets are depicted in Fig. 15.

Overall, our predictive models for $C_L$, $C_{LD}$, and $\alpha _0$ show high accuracy, with normalized mean absolute errors of 0.44%, 0.45%, and 0.47%, respectively. The probability density functions of the prediction errors are all close to each other, and the probabilities of predicting absolute normalized errors beyond 1% are small. Null hypothesis tests of $H_{0}:\mathbb {P}(\varepsilon )\not \sim \mathcal {N}(\mu ,\sigma )$ can all be rejected at a confidence level of 95%, indicating that our predictive models are unbiased in this confidence level (Fig. 15).

The $\varvec{C}_P$ predictor achieved a prediction error of only 0.33% for mode amplitudes $\varvec{s}$ on the testing dataset. The PDF of the prediction error is not significantly degraded compared to the POD result, as shown in Fig. 16

Fig. 15

The normalized error probability density functions (PDFs) for the $C_L$, $C_{LD}$ and $\alpha _0$ predictors on combined dataset (training and testing). Due to the limited amount of original supercritical airfoils, no meaningful figure can be made if we only plot the PDF of normalized error on testing dataset. Generally, the predictors are of high accuracy, with maximum relative errors less than 3%. The errors are evenly distributed around zero, indicating that the predictors are unbiased

Fig. 16

The normalized error probability density functions (PDFs) of proper orthogonal decomposition (POD) alone and POD with $\varvec{C}_P$ predictor on combined dataset (training and testing). Due to the limited amount of original supercritical airfoils, no meaningful figure can be made if we only plot the PDF of normalized error on testing dataset. It can be noticed that the POD accuracy is high: its maximum relative error is less than 0.3%. Moreover, the prediction error is quite similar to the POD error, proving that our $\varvec{C}_P$ predictor is accurate enough

In conclusion, our proposed Predictor has demonstrated its ability to efficiently and accurately evaluate aerodynamic performance for both optimization objectives and constraints, even with a limited dataset of 501 supercritical airfoils. The results show great potential for improvement, and these models could be further enhanced with a larger dataset.

CFD assessment

As the evaluations previously discussed were all performed using the provided dataset and Multi-Layer Perceptron (MLP) evaluators, the Computational Fluid Dynamics (CFD) results for the initial batch of generated supercritical airfoils were calculated to confirm that we have attained the improvement goals as detailed in Table 3. These results are presented in Table 4. Due to the high computational burden of CFD, only the first 28 supercritical airfoils were processed.

Table 4 The CFD results for the initial 28 generated supercritical airfoils. The zeroth row represents the CFD outcome for the baseline supercritical airfoil. It can be seen that over half (16 out of 28) of the generated supercritical airfoils achieved the design goal, while none of the original dataset did

Conclusion

In this work, we proposed a highly efficient and accurate data-driven evolutionary generative design (EvoGD) approach based on AI for supercritical airfoil design. The approach consisted of an evolutionary computational framework combined with data-driven generators and predictors. The results of this approach were highly impressive, producing 180 diverse supercritical airfoils within an hour on a personal computer while improving the design optimization objectives $C_{L}$, $C_{LD}$, and h by 2–9%, 1–9%, and up to 4% compared to the baseline, respectively.

The study on supercritical airfoil parametrization methods showed that the NURBS curve was a balanced choice and was especially suitable for the proposed AI-assisted design approach. The data-driven generators, consisting of a series of Cycle GANs incorporated with physics information, were able to refine the given airfoils towards better-performing ones while maintaining the geometric constraints. Moreover, the data-driven predictors were able to accurately estimate the aerodynamic performances of the airfoils, reducing the need for computationally expensive CFD simulations.

However, there are a few limitations associated with the proposed EvoGD approach. First, to bolster the Generator’s performance, a suite of generative models is trained during the process, which inevitably contributes to a significant startup time for the algorithm. Second, according to the CFD result, the current $C_{LD}$ MLP model does not extrapolate effectively, as it fails to accurately predict some generated $C_{LD}$ values. Lastly, the proposed EvoGD approach has not been tested on other problems, and hence, further adjustments may be required when comprehensive experiments are conducted.

Nonetheless, the proposed EvoGD approach was purely data driven and could work with a small dataset, making it highly efficient and effective. This approach has great potential to be generalized to other industrial design processes, reducing costs and increasing the diversity and performance of the design outcomes.