Introduction

In the modern society, the complexity of the communication system increases exponentially as the number of cellular users (CU), demand for quality of service (QoS) and the service data volume keep growing all the time. In order to overcome this problem and improve spectrum efficiency, the device-to-device (D2D) communication technique is considered one of the most important approach in IMT-2020(5G) system [1]. The D2D communication implies that the user equipment (UE) nearby can communicate with each other by directly connecting or through the enhanced-Node B (eNB) [2, 3]. Instead of the traditional cellular connections, the UE in D2D communication system can be connected with another adjacent equipment using direct links, which brings a considerable offloading potential. In addition, the D2D communication paradigm also provides significant performance gains in terms of spectral efficiency, energy efficiency and system capacity due to the physical proximity [4].

Due to the aforementioned advantages, the D2D communication technique has attracted the attention of scholars worldwide in recent years. In order to verify the efficiency and potential benefits of D2D communication technique, extensive studies have been carried out in the literature [5,6,7]. Among the existing studies, the research contributions concerning D2D communications mainly include the resource allocation [8], mode selection [9], interference management [10], power control [11] and so on.

This study mainly focuses on the resource allocation problem of large-scale D2D communication for maximizing the system energy efficiency. Specifically, the D2D-pair users (DP) can reuse certain CU uplink resources under the control of eNB to provide communication service. However, when the communication links are established, the transmission of DP transmitter (DT) will cause interference to eNB, and the transmission of CU may also interfere the DP receiver (DR). As a result, the detailed resource allocation strategy for CUs and DPs significantly affects the system spectrum efficiency and QoS. In order to solve this problem, some advanced resource allocation methodologies are widely developed. For example, Jiang et al. investigated the clustering and resource allocation problem in D2D multicast transmission underlay cellular networks, and a hybrid intelligent clustering strategy and joint resource allocation scheme were developed by considering the QoS constraints [12]. In Jiang’s study, the numbers of CUs and DPs included in the evaluated system were all less than 50. Xu et al. focused on the unfair resource usage and limited energy storage problems in D2D communications, and a multi-objective resource allocation method was developed for maximizing the security-aware efficiency and optimizing the transmit power [13]. However, the system scale of Xu’s study was very small, in which only 3 CUs and 3pairs of DPs were included in their case study. Pawar et al. developed a joint uplink-downlink resource allocation approach for maximizing the network throughput while guaranteeing the QoS for both CUs and DPs [14]. In addition, a mixed-integer nonlinear programming-based resource allocation model was established, and a two-stage (i.e., sub-channel assignment stage and power allocation stage) allocation methodology was also developed for optimizing the aforementioned model. In Pawar’s study, the evaluated system was also in normal scale, in which the numbers of CUs and DPs were all less than 50. Sultana et al. introduced the sparse code multiple access (SCMA) method to a D2D-enabled cellular network, in order to utilize the overloading feature of SCMA to support a massive device connectivity while enhancing the overall network performance [15]. According to the simulation parameter settings in Sultana’s study, the total number of DPs was 5–40, and the total number of CUs was 12–24. Mohamad et al. proposed a dynamic sectorization method for effectively allocating the resource block to D2D users (DU). In their developed method, eNB can vary the number of sectors dynamically. According to the experimental results provided in Mohamad’s study, the signal-to-interference-noise-ratio (SINR) and overall allocation performance were significantly improved [16]. However, the evaluated system in Mohamad’s study was also in normal scale. Specifically, the number of CUs included in the system was 50 and the number of DPs was 20.

With the fast development of artificial intelligence (AI) in recent years, the AI-based methodologies are also widely employed for solving the resource allocation problem in D2D communications, e.g. the machine learning (ML) based algorithms [17] and the meta-heuristic algorithms [18]. Based on the Q-learning theory, Amin et al. developed a ML-based resource allocation algorithm, in which the multi-agent learners from multiple DU were created, and the system throughput was determined by the state-learning of Q value list [19]. Sun et al. developed a resource allocation strategy by using differential evolution (DE) algorithm, in order to balance the energy efficiency and system throughput [20]. Gu et al. employed the particle swarm optimization (PSO) to optimally allocate the DU power by introducing a set of penalty functions. In addition, the optimal relationships of CU and DP were matched by proposing the Kuhn–Munkres algorithm [21]. Kuang et al. employed PSO algorithm to optimize the resource allocation model of D2D communications, which was proved to be a non-convex and mixed-integer optimization problem. In Kuang’s study, the total transmission power of DU equipment, as well as the load balance of base station was considered as the model constraints. Experimental results showed that the system energy efficiency was significantly improved by employing the developed algorithm [22].

As discussed above, in most of the existing studies, the resource allocation problem of D2D communications is always solved by using traditional methods. Although the intelligent approaches, e.g., the ML or meta-heuristic algorithms have been already introduced into the D2D communications, the existing studies mainly focus on D2D communication system with normal size. Specifically, the resource allocation problem with normal size means the model dimensionality is less than 100. When the model dimensionality increases to more than 100, the problem is always called the high dimensional resource allocation problem. Moreover, when the model dimensionality further increases to 1000, the problem is called the ultra-high dimensional or large-scale resource allocation problem. Obviously, the model complexity increases exponentially with the system size (i.e., model dimensionality) due the “curse of dimensionality”, and performance of the existing PSO or DE based algorithms will deteriorate rapidly.

Considering the aforementioned research gap, the resource allocation for large D2D communication system is established as a constrained large-scale optimization problem (LSOP) in this study. Then, on one hand, the variable-coupling relationship of the developed model is analysed and the mathematical proof is firstly provided. On the other hand, a novel meta-heuristic algorithm namely multi-modal mutation cooperatively coevolving particle swarm optimization (MMCC-PSO) is developed for effectively optimize the LSOP-based resource allocation model.

The rest of this study is organized as follows. In “Constrained LSOP-based resource allocation model in D2D communications”, the resource allocation problem in D2D communications is comprehensively discussed, and the LSOP-based resource allocation model is developed. In “Variable-coupling analysis and mathematical proof”, the variable-coupling relationship of the developed model is analysed and proved in detail. Then, the novel MMCC-PSO algorithm for optimizing LSOP is proposed in “A novel MMCC-PSO algorithm”. The detailed simulation experiments and analysis are conducted in “Simulation experiments and analysis”. Finally, this paper is concluded in “Conclusion”.

Constrained LSOP-based resource allocation model in D2D communications

Resource allocation in D2D communications

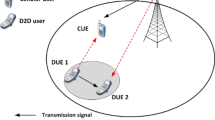
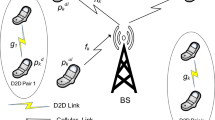
In this study, a cellular network of LTE-Advance systems is employed. In the evaluated system, the eNB locates at the center of a hexagonal region, and all the CUs and DPs are randomly distributed within the hexagonal region. Denote C = {CUn | n = 1, 2, …, N} and D = {DPm | m = 1, 2, …, M} as the sets of CU and DP, in which N and M represent the numbers of CU and DP in the evaluated system. Structure of the evaluated D2D communication system can be illustrated as Fig. 1, in which DTm and DRm represent the transmitter and receiver of DPm, respectively.

Fig. 1
figure 1

Structure of the evaluated D2D communication system

Full size image

As shown in Fig. 1, the transmission of DT will cause interference to eNB, and the transmission of CU will also interfere DR. In the resource allocation of D2D communications, the entire energy efficiency of the system should be maximized by satisfying certain constraints like QoS. According to reference [23], the system energy efficiency SEE to be maximized can be formulized as

$$ SEE = \frac{{\sum\nolimits_{m = 1}^{M} {\sum\nolimits_{n = 1}^{N} {k_{m,n} \cdot \log_{2} \left( {1 + \frac{{TP_{m,n} \cdot G_{m} }}{{TP_{n} \cdot G_{m,n} + n_{0} }}} \right)} } }}{{\sum\nolimits_{m = 1}^{M} {\sum\nolimits_{n = 1}^{N} {k_{m,n} \cdot TP_{m,n} + PC_{m} } } }} $$
(1)

where TPm,n denotes the transmission power of DPm when the uplink resource of CUn is reused; Gm denotes the channel gain from DTm to DRm; TPn denotes the transmission power of CUn; Gm,n denotes the channel gain from DTm to CUn; n0 denotes the channel noise power under the effect of white Gaussian noise; PCm denotes the circuit power consumption of DPm; km,n is a binary variable, which denotes whether the uplink resource of CUn is reused by DPm. The detailed definition for km,n can be formulized as

$$ k_{m,n} { = }\left\{ {\begin{array}{*{20}l} {1,} & {if\;{\text{the}}\;{\text{uplink}}\;{\text{resource}}\;{\text{of}}\;CU_{n} \;{\text{is}}\;{\text{reused}}\;{\text{by}}\;DP_{m} } \\ {0,} & {otherwise} \\ \end{array} } \right. $$
(2)

Considering that the uplink resource of each CU can be reused by at most one DP, and each DP can reuse one or more CU uplink resources, the constraints formulized in Eq. (3) should be included into the resource allocation model.

$$ s.t.\;\;\left\{ {\begin{array}{*{20}c} {\;\sum\limits_{m = 1}^{M} {k_{m,n} \le 1} \;\;(n = 1,\;2,\;...,\;N)\;} \\ {\;\sum\limits_{n = 1}^{N} {k_{m,n} \ge 1} \;\;(m = 1,\;2,\;...,\;M)} \\ \end{array} } \right.\; $$
(3)

Encoding and decoding schemes

In order to effectively optimize the resource allocation model described in “Resource allocation in D2D communications”, an efficient encoding scheme is required. As discussed in “Resource allocation in D2D communications”, the uplink resource of each CU can be reused by at most one DP. As a result, the variable xn which indicates the relationship between a certain CUn and each DPm (m = 1, 2, …, M) is employed to form the optimization vector. Specifically, the encoding scheme for optimization vector \(\vec{x}\) is defined as

$$ {\vec{x}} = (x_{1} ,\;x_{2} ,\;...,\;x_{N} ),\quad x_{n} \in [0.5,\;M + 0.5]\;\;(n = 1,\;2,\;...,\;N) $$
(4)

As shown in Eq. (4), each optimization variable xn is defined to describe the reuse relationship between the nth CU and each DP. For example, the nth CU will be reused by the mth DP if the optimization variable \(x_{n} \in [m - 0.5,\;m + 0.5]\). Obviously, the lower boundary for xn is 0.5, which indicates the minimum value corresponding to DP1. In addition, the upper boundary for xn is M + 0.5, which indicates the maximum value corresponding to DPM. As a result, the lower and upper boundaries for each optimization variable are set to 0.5 and M + 0.5, respectively.

According to Eq. (4), the encoding scheme for optimization variable xn is defined as

$$ CU_{n} \;{\text{is reused by}}\;\left\{ {\begin{array}{*{20}l} {DP_{1} ,} & {if\;x_{n} \in [0.5,\;1.5)} \\ {DP_{2} ,} & {if\;x_{n} \in [1.5,\;2.5)} \\ {} & {...} \\ {DP_{M} ,\;} & {if\;x_{n} \in [M - 0.5,\;M + 0.5)} \\ \end{array} } \right.(n = 1,\;2,\;...,\;N) $$
(5)

For example, if the optimization vector \(\vec{x}\) is equal to {2.85, 4.12, 4.96, 3.09, 2.43, 1.35, 1.65, 2.11, 1.39}, the detailed relationships between each CUn and DPm can be decoded as Table 1.

Table 1 Decoding scheme for \(\vec{x}\) = {2.85, 4.12, 4.96, 3.09, 2.43, 1.35, 1.65, 2.11, 1.39}
Full size table

Fitness function

As discussed in “Resource allocation in D2D communications”, target of the resource allocation in D2D communications is to maximize the system energy efficiency SEE as shown in Eq. (1). According to reference [23], the maximization of Eq. (1) is equal to minimize the following equation

$$ f_{SEE} = \sum\limits_{m = 1}^{M} {\sum\limits_{n = 1}^{N} {k_{m,n} \cdot \frac{{G_{n,m} \cdot G_{m,n} }}{{G_{m} \cdot G_{n} }}} } $$
(6)

where Gn denotes the channel gain from CUn to eNB; Gm denotes the channel gain from DTm to DRm; Gn,m denotes the channel gain from CUn to DRm; Gm,n denotes the channel gain from DTm to CUn. The channel gains Gn, Gm, Gn,m and Gm,n are calculated using the following equation

$$ G = 10^{{( - P_{L} - L_{f} )/10}} $$
(7)

where PL denotes the pathloss; Lf denotes the lognormal fading between the corresponding transmitter and receiver.

In order to ensure that each DP should be allocated with at least one CU uplink resource, this constraint is satisfied by introducing the following penalty function

$$ \left\{ {\begin{array}{*{20}c} {\;f_{p} = \lambda \cdot \sum\limits_{m = 1}^{M} {(f_{judge} \cdot } f_{guide} )} \\ {f_{judge} = \prod\limits_{n = 1}^{N} {\sqrt[{10}]{{\left| {m - y_{n} } \right|}}} \;\;\;} \\ {f_{guide} = \prod\limits_{n = 1}^{N} {\sqrt[{10}]{{\left| {m - x_{n} } \right|}}} \;\;\;} \\ \end{array} } \right. $$
(8)

where \(\lambda\) is the penalty factor which is used for controlling the punishment intensity; xn and yn denotes the continuous and discrete optimization variables, respectively (i.e., before and after decoding by using Eq. (5)).

As shown in Eq. (8), definition of the penalty function mainly contains the following two items:

  1. 1.

    fjudge is the judging item used to judge whether the solution \(\vec{x}{\text{ = \{ }}x_{1} {,}\;x_{2} {,}\;...{,}\;x_{N} {\text{\} }}\) can satisfy the constraint. By introducing fjudge, the punish function fp is equal to 0 only if for each m (m = 1, 2, …, M), there is at least one value in yn (n = 1, 2, …, N) is equal to m. In another word, fp = 0 only if each DPm is allocated with at least one CU uplink resource. Otherwise, the solution will be punished by Eq. (8).

  2. 2.

    fguide is the guiding item used to guide the individuals to converge to the potential optimum. As xn in fguide is the continuous variable before decoding, the difference between m and xn is defined as the “penalty gradient” to accelerate the convergence speed for satisfying the constraint.

As a result, the entire fitness function for the resource allocation problem is the summary of system energy efficiency fSEE and the penalty function fp. Then, the overall resource allocation model can be formulized as

$$ \min \;f = f_{SEE} + f_{p} $$
(9)

As shown in Eq. (9), the penalty function fp is directly added to the fitness function f. That is to say, if a solution is not feasible, a large penalty value will be directly added to the fitness function f. Obviously, in the minimization problem, this large penalty value will make the solution poor enough to be eliminated by the algorithmic mechanism.

Variable-coupling analysis and mathematical proof

As discussed in “Constrained LSOP-based resource allocation model in D2D communications”, dimensionality of the developed resource allocation model is equal to N. Obviously, for a large-scale D2D communication system, the model complexity will increase exponentially with the total number of CUs within the system. Although a lot of intelligent methods are widely developed for solving the complex engineering problems [24,25,26,27,28], performance of the existing optimization algorithms will deteriorate rapidly due to the “curse of dimensionality”.

Based on the philosophy of “divide and conquer”, the cooperatively coevolving (CC) framework is developed to effectively optimize the high-dimensional problems [29]. According to the basic theory of CC, the CC framework performs efficiently when solving the separable problem, which means there is no coupling-relationship between each of the optimization variables. However, for the partial-separable or non-separable problems, most of the basic CC based algorithms will also lose their efficacies.

Definitions for separable variable and component

In this study, before employing the CC framework to solve the aforementioned resource allocation problem, the variable-coupling relationships of the developed model are comprehensively analysed. First of all, the definition for separable variable is given as

Definition 1

The optimization variable xi is separable for fitness function f, if satisfying

$$ \forall \;\vec{x}_{a} = (x_{a1} ,\;x_{a2} ,\;...,\;x_{aD} ) \in S^{D} ,\;\;\;if\;\exists \;x_{bi} \;\;\;s.t.\;\;f(x_{bi} |\vec{x}_{a} ) < f(\vec{x}_{a} )\;\; \Rightarrow \;\forall \;\vec{x}_{c} = (x_{c1} ,\;x_{c2} ,\;...,\;x_{cD} ) \in S^{D} ,\;\;f(x_{bi} |\vec{x}_{c} ) < f(x_{ai} |\vec{x}_{c} ) $$
(10)

where SD denotes the D-dimensional solution space;\({\vec{\text{x}}} = x_{bi} |\vec{x}_{a}\) denotes the values for optimization vector \({\vec{\text{x}}}\) in which all the variables are set the same with \(\vec{x}_{a}\) except that the ith variable is replaced by xbi. That is to say, \(f(x_{bi} |\vec{x}_{a} )\), \(f(x_{bi} |\vec{x}_{c} )\) and \(f(x_{ai} |\vec{x}_{c} )\) in Eq. (10) are defined as

$$ \left\{ {\begin{array}{*{20}c} {f(x_{bi} |\vec{x}_{a} ) = f(x_{a1} ,\;...,\;x_{a(i - 1)} ,\;x_{bi} ,\;x_{a(i + 1)} ,\;...,\;x_{aD} )} \\ {f(x_{bi} |\vec{x}_{c} ) = f(x_{c1} ,\;...,\;x_{c(i - 1)} ,\;x_{bi} ,\;x_{c(i + 1)} ,\;...,\;x_{cD} )} \\ {f(x_{ai} |\vec{x}_{c} ) = f(x_{c1} ,\;...,\;x_{c(i - 1)} ,\;x_{ai} ,\;x_{c(i + 1)} ,\;...,\;x_{cD} )} \\ \end{array} } \right. $$
(11)

According to Definition 1, the “divide and conquer” philosophy proposed in basic CC framework can be expressed as Remark 1 [29].

Remark 1

For the fitness function f, the minimization for all the variables \({\vec{\text{x}}}\) is equivalent to the minimization for each separable component (i.e., the collection of several separable variables). This can be formulized as

$$ \arg \;\mathop {\min }\limits_{{{\vec{\text{x}}}}} \;f\; = \;\bigg(\arg \;\mathop {\min }\limits_{{{\vec{\text{x}}}_{1} }} \;f,\;\arg \;\mathop {\min }\limits_{{{\vec{\text{x}}}_{2} }} \;f,\;..,\;\arg \;\mathop {\min }\limits_{{{\vec{\text{x}}}_{C} }} \;f\bigg) $$
(12)

where \({\vec{\text{x}}}\) denotes the entire D-dimensional optimization vector; \({\vec{\text{x}}}_{1}\), \({\vec{\text{x}}}_{2}\), …, \({\vec{\text{x}}}_{C}\) denote each of the separable components in \({\vec{\text{x}}}\).

Mathematical proof for variable-coupling relationships in resource allocation model

As shown in Remark 1, in order to decrease the dimensionality of the aforementioned resource allocation model, the separable components within the model can be decomposed into different groups and coevolved separately.

  1. 1.

    Variable-coupling relationship for fSEE

Actually, all the continuous variables xi (i = 1, 2, …, N) are separable for the system energy efficiency fSEE. This can be described as Lemma 1.

Lemma 1

Each of the optimization variables xi (i = 1, 2, …, N) is separable for the fitness function fSEE in Eq. (6).

Lemma 1 can be proved in detail as follows:

Proof

For the each of the variable, say the ith xi (i = 1, 2, …, N), satisfying

$$ \forall \;\vec{x}_{a} = (x_{a1} ,\;x_{a2} ,\;...,\;x_{aN} ) \in S^{N} ,\;\;\;\;if\;\;\exists \;\;{\text{a}} \;value\;of\;\;x_{i} = \;x_{bi} \;\;\;\;s.t.\;\;f_{SEE} (x_{bi} |\vec{x}_{a} ) < f_{SEE} (\vec{x}_{a} ) $$
(13)

That is

$$ f_{SEE} (x_{a1} ,\;...,\;x_{a(i - 1)} ,\;x_{bi} ,\;x_{a(i + 1)} ,...,\;x_{aN} ) < f_{SEE} (x_{a1} ,\;...,\;x_{a(i - 1)} ,\;x_{ai} ,\;x_{a(i + 1)} ,...,\;x_{aN} ) $$
(14)

Put Eq. (6) into Eq. (14), then Eq. (14) can be rewritten as

$$ \begin{aligned} &\sum\limits_{m = 1}^{M} \left( \sum\limits_{n = 1}^{i} {k_{m,n} \cdot \frac{{G_{n,m} \cdot G_{m,n} }}{{G_{m} \cdot G_{n} }}} + k_{{x_{bi} ,i}} \cdot \frac{{G_{{i,x_{bi} }} \cdot G_{{x_{bi} ,i}} }}{{G_{{x_{bi} }} \cdot G_{i} }} \right.\\ &\left. \qquad + \sum\limits_{n = i + 1}^{N} {k_{m,n} \cdot \frac{{G_{n,m} \cdot G_{m,n} }}{{G_{m} \cdot G_{n} }}} \right) \\ &\quad < \sum\limits_{m = 1}^{M} \left( \sum\limits_{n = 1}^{i} {k_{m,n} \cdot \frac{{G_{n,m} \cdot G_{m,n} }}{{G_{m} \cdot G_{n} }}} + k_{{x_{ai} ,i}} \cdot \frac{{G_{{i,x_{ai} }} \cdot G_{{x_{ai} ,i}} }}{{G_{{x_{ai} }} \cdot G_{i} }} \right.\\ &\qquad \left.+ \sum\limits_{n = i + 1}^{N} {k_{m,n} \cdot \frac{{G_{n,m} \cdot G_{m,n} }}{{G_{m} \cdot G_{n} }}} \right) \end{aligned} $$
(15)

As the ith CU is allocated to the xaith DP in solution \(\vec{x}_{a}\), and allocated to the xbith DP in solution \(\vec{x}_{b}\), then \(k_{{x_{ai} ,i}} = k_{{x_{bi} ,i}} = 1\). Obviously, Eq. (15) can be further simplified as

$$ \frac{{G_{{i,x_{bi} }} \cdot G_{{x_{bi} ,i}} }}{{G_{{x_{bi} }} }} < \frac{{G_{{i,x_{ai} }} \cdot G_{{x_{ai} ,i}} }}{{G_{{x_{ai} }} }} $$
(16)

Then, \(\forall \;\vec{x}_{c} = (x_{c1} ,\;x_{c2} ,\;...,\;x_{cN} ) \in S^{N}\), according to Eq. (16), the following equation can be easily derived

$$ \begin{aligned} f_{SEE} (x_{bi} |\vec{x}_{c} ) &= \sum\limits_{m = 1}^{M} \left( \sum\limits_{n = 1}^{i} {k_{m,n}^{c} \cdot \frac{{G_{n,m}^{c} \cdot G_{m,n}^{c} }}{{G_{m}^{c} \cdot G_{n}^{c} }}} + k_{{x_{bi} ,i}} \cdot \right.\\ & \qquad \left.\frac{{G_{{i,x_{bi} }} \cdot G_{{x_{bi} ,i}} }}{{G_{{x_{bi} }} \cdot G_{i} }} + \sum\limits_{n = i + 1}^{N} {k_{m,n}^{c} \cdot \frac{{G_{n,m}^{c} \cdot G_{m,n}^{c} }}{{G_{m}^{c} \cdot G_{n}^{c} }}} \right) \\ & < \sum\limits_{m = 1}^{M} \left( \sum\limits_{n = 1}^{i} {k_{m,n}^{c} \cdot \frac{{G_{n,m}^{c} \cdot G_{m,n}^{c} }}{{G_{m}^{c} \cdot G_{n}^{c} }}} + k_{{x_{ai} ,i}} \cdot \right.\\ &\qquad \left.\frac{{G_{{i,x_{ai} }} \cdot G_{{x_{ai} ,i}} }}{{G_{{x_{ai} }} \cdot G_{i} }} + \sum\limits_{n = i + 1}^{N} {k_{m,n}^{c} \cdot \frac{{G_{n,m}^{c} \cdot G_{m,n}^{c} }}{{G_{m}^{c} \cdot G_{n}^{c} }}} \right) \\ &= f_{SEE} (x_{ai} |\vec{x}_{c} ) \end{aligned} $$
(17)

Obviously, according to Definition 1, the variable xi is separable for the fitness function fSEE. Lemma 1 is proved.

  1. 2.

    Variable-coupling relationship for fp

For the penalty function fp, all the continuous variables xi (i = 1, 2, …, N) are non-separable. This can be described as Lemma 2.

Lemma 2

Each of the optimization variables xi (i = 1, 2, …, N) is non-separable for the penalty function fp in Eq. (8).

For the each of the variable, say the ith xi (i = 1, 2, …, N), satisfying

$$ \forall \;\vec{x}_{a} = (x_{a1} ,\;x_{a2} ,\;...,\;x_{aN} ) \in S^{N} ,\;\;\;\;if\;\;\exists \;\;{\text{a}} \;value\;of\;\;x_{i} = \;x_{bi} \;\;\;\;s.t.\;\;f_{p} (x_{bi} |\vec{x}_{a} ) < f_{p} (\vec{x}_{a} ) $$
(18)

Equation (18) can be illustrated as Fig. 2.

Fig. 2
figure 2

Illustration for Eq. (18)

Full size image

However, a counter-example for supporting that xi is separable can be provide as

$$ \exists \;\;\vec{x}_{c} = (x_{c1} ,\;x_{c2} ,\;...,\;x_{cN} ) \in S^{N} ,\;\;\;s.t.\;\;f_{p} (x_{bi} |\vec{x}_{c} ) > f_{p} (\vec{x}_{c} ) $$
(19)

Equation (19) can be illustrated as Fig. 3.

Fig. 3
figure 3

A counter-example for supporting that xi is separable

Full size image

Obviously, according to Definition 1, the variable xi is not separable for the penalty function fp. Lemma 2 is proved.

A novel MMCC-PSO algorithm

In order to effectively optimize the resource allocation model, a novel MMCC-PSO algorithm is developed based on the result of variable-coupling analysis.

Particle swarm optimization

PSO is one of the most widely used optimization algorithms proposed originally by Kennedy and Eberhart, which exploits the concepts of the social behavior of animals like fish schooling and bird flocking [30]. In recent years, a lot of PSO-variants are developed and successfully employed to solve real-world optimization problems [31,32,33].

In classical PSO algorithm, a population with Np particles is randomly initialized within a certain search space. Then, the personal best position for each particle and the global best position found so far are initialized. After that, each of the particles evolves using the following equations

$$ v_{i} (t + 1) = \omega \cdot v_{i} (t) + \alpha_{l} (t) \cdot [\hat{x}_{i} (t) - x_{i} (t)] + \alpha_{g} (t) \cdot [\hat{x}_{g} (t) - x_{i} (t)] $$
(20)
$$ x_{i} (t + 1) = x_{i} (t) + v_{i} (t + 1) $$
(21)

where vi(t + 1) and xi(t + 1) represent the velocity and position of the ith particle in the (t + 1)th iteration; \(\hat{x}_{i} (t)\) represents the personal best position for the ith particle in the tth iteration; \(\hat{x}_{g} (t)\) represents the global best position in the tth iteration; \(\omega\) is the inertia weight; \(\alpha_{l} (t)\) and \(\alpha_{g} {(}t{)}\) are independent random numbers uniquely generated at every iteration.

At the end of the iteration, compare and update each personal best position \(\hat{x}_{i} (t)\) and the global best position \(\hat{x}_{g} (t)\). Then, start another iteration till the stopping criteria are satisfied.

Cooperatively coevolving framework

As most of the existing meta-heuristic algorithms will lose their efficacies when optimizing high-dimensional problems, the cooperatively coevolving (CC) framework is developed to improve the ability for overcoming the so-called “curse of dimensionality” [29].

According to the basic principle of CC framework, the high-dimensional problem is decomposed into several low-dimensional subproblems to be optimized one-by-one. In addition, the context vector with entire dimensionalities is introduced to provide reference when calculating the fitness function value of each subproblem. That is because each of the subproblem only contains a certain part of the variables in the original problem, and the fitness function value cannot be calculated without a reference of the other dimensionalities.

The basic principle of CC framework can be summarized as follows.

  1. 1.

    Initialize the population with a certain number of D-dimensional individuals. Initialize the context vector using the global best individual within the current population.

  2. 2.

    Decompose the original D-dimensional problem into K subproblems, and each subproblem represents certain d dimensionalities of the original problem. Obviously, d = D/K.

  3. 3.

    Evolve each subproblem using a certain evolutionary algorithm principle (e.g., PSO, DE and so on). When compute the fitness function value of a certain subproblem, the dimensionalities corresponding to the other subproblems are kept the same with context vector.

  4. 4.

    Proceed another cycle if the stopping criteria are not satisfied. Otherwise, stop the evolution process.

Multi-modal mutation strategy for context vector

As discussed in “Fitness function”, most of the solutions within the solution space are infeasible solutions because of the introduced penalty function as listed in Eq. (8). That is to say, the continuous solution space is seriously destroyed by the penalty function, and the feasible solutions are only distributed in the dispersed feasible sub-spaces. This can be illustrated as Fig. 4.

Fig. 4
figure 4

Solution space of the resource allocation problem with penalty function

Full size image

As shown in Fig. 4, the feasible solutions only locate in the sub-spaces which are not punished by the penalty function, and these sub-spaces widely distribute within the original solution space because of the introducing of penalty function. As a result, in order to obtain accurate optimization performance and fast convergence speed, the population should have the global and local exploring abilities. On one hand, each of the individual should avoid the infeasible sub-spaces, on the other hand, all the individuals should not gather within a single feasible sub-space to avoid the prematurity.

As discussed above, in order to improve the performance of CC-based algorithms on optimizing the resource allocation model, a novel multi-modal mutation (MM) strategy is developed. The detailed principles of MM strategy can be illustrated as the following steps.

Step 1: Randomly generate a mutation-selection factor Fms within the interval (0, 1). Then, go to Step 2 to execute mutation modal I (MM-I) if 0 < Fms < 1/3. Go to Step 3 to execute mutation modal II (MM-II) if 1/3 < Fms < 2/3; Otherwise, go to Step 4 to execute mutation modal III (MM-III).

Step 2: Execute MM-I (namely self-mutation). For each context vector, say the ith context vector (denote as CVi), randomly exchange a certain proportion (denote as pI%, \(p_{I} {\text{\% }} \in [0\% ,\;100\% ]\)) dimensionalities of CVi itself. The self-mutation for context vector (i.e., MM-I) can be formulized as

$$ {\text{exchange}}\;\;CV_{i} (x_{k1} ) \Leftrightarrow CV_{i} (x_{k2} )\;\;{\text{for}}\;\;(p_{I} {\text{\% }} \cdot D)\;\;{\text{times}} $$
(22)

where CVi(xk1) and CVi(xk2) denote two randomly selected variables of CVi.

Step 3: Execute MM-II (namely cross-mutation). Randomly select two context vectors, say the CVi and CVj, then randomly exchange a certain proportion (denote as pII%, \(p_{II} {\text{\% }} \in [0\% ,\;100\% ]\)) dimensionalities of CVi and CVj. The cross-mutation for context vector (i.e., MM-II) can be formulized as

$$ {\text{exchange}}\;\;CV_{i} (x_{k1} ) \Leftrightarrow CV_{j} (x_{k2} )\;\;{\text{for}}\;\;(p_{II} {\text{\% }} \cdot D)\;\;{\text{times}} $$
(23)

where CVi(xk1) and CVj(xk2) denote two randomly selected variables of CVi and CVj, respectively.

Step 4: Execute MM-III (namely individual-mutation). Randomly select a context vector, say the ith CVi, then randomly select an individual within the current population, say the jth individual (denote as INj). Randomly exchange a certain proportion (denote as pIII%, \(p_{III} {\text{\% }} \in [0\% ,\;100\% ]\)) dimensionalities of CVi and INj. The individual-mutation for context vector (i.e., MM-III) can be formulized as

$$ {\text{exchange}}\;\;CV_{i} (x_{k1} ) \Leftrightarrow IN_{j} (x_{k2} )\;\;{\text{for}}\;\;(p_{III} {\text{\% }} \cdot D)\;\;{\text{times}} $$
(24)

where CVi(xk1) and INj(xk2) denote two randomly selected variables of CVi and INj, respectively.

Step 5: Compare the newly mutated context vector (denote as CVmut) and the original context vector (denote as CVorg) before mutation, update CVmut using CVorg if better.

Evolution principle for MMCC-PSO

In this study, a novel evolution principle is developed for effectively optimize the resource allocation model. Specifically, in the developed evolution principle, the position for each individual is updated using the following four “best positions”.

  1. 1.

    The global best individual within the current population, i.e., Xbest-I(t) = \(\hat{X}_{g} (t)\), in which Xbest-I(t) represents the first best-position employed for evolution at the tth iteration; \(\hat{X}_{g} (t)\) represents the global best individual at the tth iteration.

  2. 2.

    The personal best position for the target individual, i.e., Xbest-II(t) = \(\hat{X}_{i} (t)\), in which Xbest-II(t) represents the second best-position employed for evolution at the tth iteration; \(\hat{X}_{i} (t)\) represents the personal best position of the ith individual at the tth iteration.

  3. 3.

    The randomly selected context vector, i.e., Xbest-III(t) = CVrand(t), in which Xbest-III(t) represents the third best-position employed for evolution at the tth iteration; CVrand-i(t) represents the randomly selected context vector for the ith individual at the tth iteration.

  4. 4.

    The best individual within the neighbor sub-population, i.e., Xbest-IV(t) = XN-i(t), in which Xbest-IV(t) represents the fourth best-position employed for evolution at the tth iteration; XN-i(t) represents the neighbor best position of the ith individual at the tth iteration. Note that in order to obtain XN-i(t), the original population should be divided into several sub-populations with a certain topology, e.g., the ring-topology. Then, the neighbor best of the ith individual is randomly generated from the best individual of the connected sub-populations. The generation of neighbor best position can be illustrated as Fig. 5.

Fig. 5
figure 5

Generation of neighbour best position based on ring-topology

Full size image

As shown in Fig. 5, the neighbour best of xi(t) is randomly generated from the best individuals of sub-population 2 and sub-population 4 as these sub-populations are connected with xi(t).

Based on the definitions of Xbest-I(t) to Xbest-IV(t), the evolution principle employed in MMCC-PSO is developed as

$$ \left\{ {\begin{array}{*{20}l} {x_{i} (t + 1) = \frac{1}{2} \cdot [A(t + 1) + B(t + 1)] + N(0,1) \cdot \left| {A(t + 1) - B(t + 1)} \right|\;\;\;\;\;\;\;\;\;} \\ {\;A(t + 1) = \frac{1}{2} \cdot [X_{best - I} (t) + X_{best - II} (t)] + N(0,1) \cdot \left| {X_{best - I} (t) - X_{best - II} (t)} \right|\;\;\;} \\ {\;\;B(t + 1) = \frac{1}{2} \cdot [X_{best - III} (t) + X_{best - IV} (t)] + N(0,1) \cdot \left| {X_{best - III} (t) - X_{best - IV} (t)} \right|} \\ \end{array} } \right. $$
(25)

Note that in Eq. (25), N(0,1) denotes a randomly generated value which follows the Gaussian distribution. As shown in Eq. (25), A(t + 1) denotes the newly generated position between Xbest-I(t) and Xbest-II(t), and the distance between A(t + 1) and the midpoint of Xbest-I(t) and Xbest-II(t) follows Gaussian distribution. Similarly, B(t + 1) denotes the newly generated position between Xbest-III(t) and Xbest-IV(t), and the distance between B(t + 1) and the midpoint of Xbest-III(t) and Xbest-IV(t) also follows Gaussian distribution. Equation (25) can be further illustrated as Fig. 6.

Fig. 6
figure 6

Schematic of the evolution principle in Eq. (25)

Full size image

In addition, as discussed in “Encoding and decoding schemes”, the lower and upper boundaries for each optimization variable are 0.5 and M + 0.5, respectively. That is to say, the solution space of the developed model is [0.5, M + 0.5]N. In order to avoid the exceeding of solution space, each of the xi(t + 1) computed by Eq. (25) will be checked using Eq. (26).

$$ x_{{i{ - }update}} (t + 1){ = }\left\{ {\begin{array}{*{20}c} {x_{i} (t + 1),} & {if\;x_{i} (t + 1) \in [0.5,\;M + 0.5]} \\ {\frac{{x_{i} (t) + 0.5}}{2},} & {if\;x_{i} (t + 1) < 0.5} \\ {\frac{{x_{i} (t) + [M + 0.5]}}{2},} & {if\;x_{i} (t + 1) > M + 0.5} \\ \end{array} } \right. $$
(26)

where xi-update(t + 1) denotes xi(t + 1) after boundary checking. As shown in Eq. (26), the computed xi(t + 1) is directly used to update the particle position if it is within the solution space. However, if the computed xi(t + 1) exceeds the lower boundary, the particle will move to the midpoint of the current position xi(t) and the lower boundary 0.5. Similarly, if the computed xi(t + 1) exceeds the upper boundary, the particle will move to the midpoint of the current position xi(t) and the upper boundary M + 0.5.

The MMCC-PSO algorithm

Based on the multi-modal mutation strategy described in “Multi-modal mutation strategy for context vector” and the evolution principle described in “The MMCC-PSO algorithm”, the MMCC-PSO algorithm is developed in this section. Procedure of the MMCC-PSO algorithm can be illustrated as Table 2.

Table 2 Pseudo code of MMCC-PSO
Full size table

Simulation experiments and analysis

Parameter setting and tuning

  1. 1.

    Parameter setting

In this section, the developed MMCC-PSO algorithm is tested by a comprehensive set of simulation experiments. On one hand, efficiencies of the developed multi-modal mutation strategy and evolution principle are verified. On the other hand, the overall MMCC-PSO algorithm is compared with some famous algorithms for different dimensional cases. In the following experiments, the detailed parameter settings for MMCC-PSO are listed in Table 3.

Table 3 Parameter settings for the developed MMCC-PSO algorithm
Full size table
  1. 2.

    Parameter tuning.

In order to verify the effect of algorithm parameters on the final optimization performance, the parameter tuning experiments are conducted in this section. Specifically, the MMCC-PSO algorithm with different parameter values are compared in detail, and the parameters to be tuned include pI, pII, pIII, Nsp and S.

In the following experiments, the assumption of communication scenario is based on the common practices in most of the existing studies. Specifically, in the evaluated D2D communication system, the numbers of CU and DP are set to 200 and 50, respectively. All the users are assumed to be randomly distributed within a square region with a side-length of 500 m. The distributions of these 250 users are shown as Fig. 7. The average result for 30 independent runs is recorded. The final optimization results of MMCC-PSO with different pI, pII and pIII values are compared in Table 4. Note that the values of the other parameters are kept the same with Table 3.

Fig. 7
figure 7

Distributions of CU and DP within the D2D communication system

Full size image
Table 4 Experimental results of MMCC-PSO with different pI, pII and pIII values for 30 independent runs
Full size table

As shown in Table 4, performance of the MMCC-PSO is not very sensitive to the parameters pI, pII and pIII. Specifically, when these parameters are set to 0.1, 0.5 and 0.8, the average performance for 30 independent runs is almost the same. However, when pI, pII and pIII are set too small (e.g., pI = pII = pIII = 0.01 or pI = pII = pIII = 0.05), the performance of MMCC-PSO will deteriorate to different degrees. That is because the developed multi-modal mutation mechanism will lose its efficacy if the exchange proportions are too small.

The final optimization results of MMCC-PSO with different Nsp values are compared in Table 5. As shown in the table, the effect of the parameter Nsp is significant. Specifically, the best choice for the number of sub-populations is Nsp = 5, and the average optimization result is 41.2454. The performance of Nsp = 10 is slightly worse than that of Nsp = 5. However, when the values of Nsp are set too small (e.g., Nsp = 1, which means the population contains only 1 sub-population), the final optimization performance deteriorate significantly. Similarly, when the values of Nsp are set too large (e.g., Nsp = 50, which means the population contains 50 sub-populations but each with only 1 particle), the final optimization performance is also very poor. Actually, for the original population with 50 particles, the better decomposition strategy is to divide it into five sub-populations and each with ten particles, or to divide it into ten sub-populations and each with five particles.

Table 5 Experimental results of MMCC-PSO with different Nsp values for 30 independent runs
Full size table

Finally, the optimization results of MMCC-PSO with different S values are compared in Table 6. As shown in the table, performance of MMCC-PSO becomes poor when S is set too small or too large. For example, the population cannot obtain enough iterations when S = {1, 2, 3, 5}, so the average optimization result is 88.0918, which is significantly worse than S = {5, 10, 20, 30, 40, 50}. However, for S = {50, 100, 150, 200}, although the population can obtain enough iterations, the sub-problem is still too complex to be optimized efficiently, and the average optimization performance is still worse than S = {5, 10, 20, 30, 40, 50}.

Table 6 Experimental results of MMCC-PSO with different S values for 30 independent runs
Full size table

As discussed above, the developed MMCC-PSO is not very sensitive to the exchange proportions pI, pII and pIII. In addition, for the number of sub-populations Nsp, a good choice is to use 5–10 sub-populations and each with 10–5 particles. Moreover, the set of group-size S should contain a wide range to effectively balance the number of iterations and the complexity of each sub-problem. Although the settings of Nsp and S can affect the performance of MMCC-PSO, the fault tolerance intervals are still large.

Verification for the multi-modal mutation strategy

In this section, the MMCC-PSO with and without the developed multi-modal mutation strategy (described in “Multi-modal mutation strategy for context vector”) are compared. Parameter settings for the evaluated D2D communication system are the same with “Parameter setting and tuning”. The average result for 30 independent runs is recorded. The final optimization results of MMCC-PSO with and without the developed multi-modal mutation strategy are compared in Table 7, in which MMCC-PSO denotes the algorithm integrated with mutation strategy and MMCC-PSOwithoutMM denotes the opposite. In addition, the convergence graphs obtained by MMCC-PSO and MMCC-PSOwithoutMM are compared in Fig. 8.

Table 7 Experimental results of MMCC-PSO and MMCC-PSOwithoutMM for 30 independent runs
Full size table
Fig. 8
figure 8

Average convergence graphs of MMCC-PSO and MMCC-PSOwithoutMM

Full size image

As shown in Table 7, with the integration of multi-modal mutation strategy, the MMCC-PSO significantly outperforms MMCC-PSOwithoutMM on optimization accuracy and robustness. Specifically, the average error (i.e., the total cost of the resource allocation solution) obtained by MMCC-PSO for 30 independent runs is just 41.9982, which is significantly smaller than 157.2159 obtained by MMCC-PSOwithoutMM. In addition, the best and worst performance obtained by MMCC-PSO is also better than those of MMCC-PSOwithoutMM. Moreover, the standard deviation obtained by MMCC-PSO is just 2.8651, which is smaller than 10.6985 obtained by MMCC-PSOwithoutMM. This implies that with the integration of multi-modal mutation strategy, robustness of the algorithm is also improved.

Figure 8 shown the convergence graphs obtained by MMCC-PSO and MMCC-PSOwithoutMM. Obviously, the MMCC-PSO significantly outperforms MMCC-PSOwithoutMM on both accuracy and convergence speed.

Verification for the developed evolution principle

In this section, the MMCC-PSO with and without the developed evolution principle (described in “Evolution principle for MMCC-PSO”) are compared. Parameter settings for the evaluated D2D communication system are the same with “Parameter setting and tuning”. In the following experiments, the MMCC-PSO integrated with the developed evolution principle is denoted as MMCC-PSO, while MMCC-PSOwithoutEP denotes the opposite. The average result for 30 independent runs is recorded. The final optimization results of MMCC-PSO and MMCC-PSOwithoutEP are compared in Table 8. The corresponding convergence graphs are plotted in Fig. 9.

Table 8 Experimental results of MMCC-PSO and MMCC-PSOwithoutEP for 30 independent runs
Full size table
Fig. 9
figure 9

Average convergence graphs of MMCC-PSO and MMCC-PSOwithoutEP

Full size image

As shown in Table 8 and Fig. 9, with the integration of the developed evolution principle, MMCC-PSO significantly outperforms MMCC-PSOwithoutEP on both optimization accuracy and convergence speed. Specifically, for the 30 independent runs, the average result obtained by MMCC-PSO is just 42.1126, which is significantly smaller than 101.5988 obtained by MMCC-PSOwithoutEP. In addition, the standard deviation of MMCC-PSO and MMCC-PSOwithoutEP is 2.7996 and 17.4325, respectively. The improvement on standard deviation implies a better performance on the algorithm robustness. Moreover, as shown in Fig. 9, the slope for convergence graph of MMCC-PSO is steeper than that of MMCC-PSOwithoutEP, and the location for convergence graph of MMC-PSO is lower than that of MMCC-PSOwithoutEP during most of the evolution process. This implies that the developed evolution principle can increase the convergence speed of algorithm for exploring the potential global optimum.

Comparison with other famous algorithms

In this section, the developed MMCC-PSO algorithm is compared with some famous algorithms for the specialized literature, including the AMCCPSO [34], DTC-DE [35], AMCCDE [36], CCPSO2 [37], VGCC-PSO [38] and DFS-CPSO [39]. Note that this study concerns the resource allocation problem of large-scale D2D communication system, and the developed MMCC-PSO algorithm is also mainly about improving the performance on optimizing ultra-high dimensional model. As a result, the compared algorithms are all chosen from the famous algorithms which are specifically designed for optimizing large-scale optimization problems. Specifically, the compared CCPSO2, AMCCPSO and AMCCDE algorithms are the classic and famous algorithms for optimizing large-scale problem, and the compared DTC-DE, VGCC-PSO and DFS-CPSO are the most recent and competitive large-scale optimization algorithms.

In order to compare the efficiency of these algorithms on optimizing different scales of allocation models, the comparison experiments are conducted on different cases with the dimensionalities from 100 to 1000. The detailed parameter settings of the compared algorithms follow their original studies. The evaluated D2D communication system for different cases are listed in Table 9.

Table 9 D2D communication systems for different cases
Full size table

The distributions of CU and DP for each case are plotted as Fig. 10.

Fig. 10
figure 10

Distributions of CU and DP for Case 1–6

Full size image

The final optimization results for 30 independent runs of each algorithm are compared in Table 10. The convergence graphs of each algorithm are plotted in Fig. 11.

Table 10 Comparisons of MMCC-PSO and some other famous algorithms
Full size table
Fig. 11
figure 11

Convergence graphs for Cases 1–6

Full size image

As shown in Table 10, the developed MMCC-PSO can obtain the best performance on most of the cases of which the model dimensionality varies from 100 to 1000. Specifically, for the 100-dimensional case 1, the performance obtained by MMCC-PSO and CCPSO2 is almost the same (i.e., the average results are 27.2169 for MMCC-PSO and 27.4596 for CCPSO2). In addition, the performance of AMCCPSO, DTC-DE, VGCC-PSO and DFS-CPSO are 33.4569, 38.0889, 39.1930 and 29.1695 respectively, which are slightly worse than those of MMCC-PSO and CCPSO2. However, the performance of AMCCDE is 53.5692 and is significantly worse than the other algorithms.

For the cases 2 and 3, the model dimensionality increases to 200 and 300 respectively. The developed MMCC-PSO algorithm can also obtain the best performance, while the performance of its competitors deteriorates significantly. Specifically, the second-best performers are DFS-CPSO for case 2 and AMCCPSO for case 3, but their performance is significantly worse than that of MMCC-PSO. For example, the second-best performance is 101.3251 for case 2 (obtained by DFS-CPSO) and 143.4239 for case 3 (obtained by AMCCPSO), but the performance obtained by MMCC-PSO is 81.5124 for case 2 and 126.1985 for case 3. Moreover, the performance obtained by AMCCDE deteriorates rapidly with the increasing of model dimensionalities. The final results AMCCDE is 223.5963 for case 2 and 272.8886 for case 3, which are significantly worse than the other algorithms.

When the model dimensionality further increases to 500 in case 4 and 800 in case 5, with the integration of the developed multi-modal mutation strategy and evolution principle, the MMCC-PSO algorithm can still keep its efficiency. However, performance of the compared algorithms deteriorates rapidly with the increasing of model dimensionality. Moreover, when the dimensionality increases to 1000 in case 6, MMCC-PSO still obtains the best performance of 420.1205. However, all the compared algorithms lose their efficacies for optimizing 1000-dimensional model due to the exponential increasing complexity. In addition, as shown in Fig. 11, the developed MMCC-PSO algorithm can obtain the fastest convergence speed for most of the cases.

Conclusion

This study focuses on the optimal resource allocation for large-scale D2D communication system, in order to improve the overall system efficiency. Specifically, the numerical resource allocation model is established as a constrained large-scale optimization problem (LSOP). Then, the variable-coupling relationship of link resource allocation model is analysed in detail. According to the mathematical proof provided in this study, each optimization variable is separable for the fitness function fSEE which is related to the overall system efficiency, while each optimization variable is non-separable for the penalty function fp which is related the system constraints.

Based on the variable-coupling relationship analysis, a novel MMCC-PSO algorithm is developed to overcome the ultra-high dimensional and variable-coupling characteristics of the aforementioned LSOP-based resource allocation problem. According to the result of simulation experiments, the developed multi-modal mutation strategy and evolution principle in MMCC-PSO can significantly improve the performance on optimization accuracy, convergence speed and algorithm robustness.

Finally, efficiency of the developed methodology is verified by a comprehensive set of case studies, and some famous algorithms for the specialized literature are also employed for comparison. According to the experimental results, the developed MMCC-PSO significantly outperforms the compared algorithms on both accuracy and convergence speed, especially on optimizing the ultra-high dimensional problems with up to 500–1000 dimensionalities.

In the future, more efforts will be made to further improve the performance of MMC-PSO on optimizing the resource allocation problem with higher dimensionalities. The effectiveness of the developed model and algorithm will be furtherly verified by hardware system experiments. In addition, the real-world application of the developed methodology will be also considered in our future work.