Introduction

In the industrial sector, a robotic manipulator is often used instead of people to do repetitive jobs like palletizing, picking, and dropping machines, welding, putting things together, soldering, and so on. It was also used to do dangerous jobs in nuclear power plants, such as cleaning up waste. Robotic manipulators are used a lot in many different fields because they increase productivity (both quantity and quality), lower production costs, and improve precision [1, 2]. A great deal of control and stability is required because this is a nonlinear system with a high degree of mechanical instability. Thus, it needs to be controlled meticulously. Many viable approaches have been proposed for robotic systems with a degree of uncertainty due to the influence of environmental disturbances. Hence, a robust adaptive control mechanism is built to guarantee that the system keeps functioning as planned despite the presence of unknown dynamics. The approach underlying adaptive robust schemes has several advantages, one of which is that the control system must be resilient, and its gains must be updated according to the present circumstances in order to guarantee the performance of the required level of stability.

The topic of controlling robotic manipulator systems is receiving a lot of interest from researchers [3]. Advanced proportional-integral controller [4], sliding-mode control (SMC) [5], disturbance-observer based control [6], and fuzzy control [7] are only a few of the solutions offered to the tracking problem in the literature. Enhancements are introduced to manage unknown parametric uncertainties [8]. For uncertain nonlinear systems, two of the most common control strategies are adaptive control and robust control. The estimation of the nonlinear system’s unknown parameters and dynamics is made possible by adaptive control [9]. In addition, the robust approach decreases the computational cost for the nonlinear systems while still requiring defined bounds for the uncertain dynamics.

A growing number of control engineering systems are employing adaptive control, a technique that has been around for a while but is gaining in popularity. It has remarkable potential for adapting to situations with unknown and uncertain dynamics, which improves closed-loop tracking performance [8, 10]. Another nonlinear robust control method that works effectively for robotic manipulators is SMC. As long as the disturbances are bounded, and the system’s features are kept to a minimum, uncertain nonlinear systems can be controlled properly. Terminal SMC (TSMC), nonsingular TSMC (NTSMC), integral TSMC (ITSMC), and fast nonsingular TSMC (FNTSMC) are only some of the many types of SMC that have received improvements over the years [11,12,13,14]. To further boost the controller’s efficiency, fractional-order (Fo) control has been integrated with SMC [15]. Derivatives and integrals of non-integer orders have been of interest to scientists and engineers for over three centuries, and this control method has lately been rediscovered and used in many other areas [16,17,18]. To enhance the performance of SMC, a strategy such as fractional-order TSMC (FoTSMC) has been developed and used in various robotic systems [19, 20].

The time required for a dynamical system to converge in finite time is highly sensitive to the initial circumstances of the system’s states and so varies with the nonlinear system. Hence, a fixed-time control technique is an option that may be used to precisely determine the convergence time regardless of the initial values [21, 22]. The robotic manipulator systems can be employed with a variety of finite-time adaptive FoSMC algorithms that account for the existence of uncertainties and disturbances. For the nonlinear robotic system, an adaptive finite-time FoTSM controller has been developed [4]. Moreover, a finite-time FoSMC was employed to estimate the unknown dynamics of the nonlinear robot using an adaptive controller for modeling internal uncertainties [23]. Furthermore, a robust fractional-order proportional-derivative control was designed with the optimization of fuzzy sliding mode controller parameters using a genetic algorithm for robot manipulator and coupled tanks [24]. In the face of unknown dynamics, a class of high-order FoSMC was used to construct a robust adaptive method [25].

Each of the studies mentioned above employs a different approach to estimating the boundaries of unknown uncertain dynamics, but they all emphasize the importance of an adaptive approach in a finite-time sliding mode scheme. Most importantly, using FtNTSM control eliminates the risk of non-singularity, makes systems more resistant to unknown dynamics and external disturbances, and ensures that the convergence rate is independent of the initial conditions. According to the literature study, FtNTSM with adaptive control has not been investigated, and adaptive fixed-time SMC control is only available in a few works. Thus, the fixed-time approach for externally perturbed robotic manipulator systems is the focus of this study. In particular, the consequences of unknowable system dynamics are investigated. So, the research is conducted to develop the adaptive fractional-order non-singular TSM (AFtNTSM) for the externally perturbed uncertain robotic manipulator dynamics.

The following points represent the most important contributions made by this research.

(i):

A sliding surface with high tracking performance, negligible chattering in control inputs, and a quick rate of convergence was developed using the properties of fixed-time.

(ii):

The efficiency of the closed loop is enhanced by employing the fractional-order method.

(iii):

This work provides adaptive control utilizing FtNTSM for a robotic system, with the goal of achieving resilient and sustainable performance by reducing the impact of uncertainties.

(iv):

The suggested system’s fixed-time stability analysis is investigated using the Lyapunov synthesis.

The remainder of this work is structured as follows: the next section discusses the preliminaries. In the next section, system modeling, adaptive fixed-time control strategy, and the accompanying evidence of stability of the overall system are presented. Following section presents the numerical findings of the proposed method and discusses them. The concluding remarks are given in the last section.

Preliminaries

Definition 1

In the field of fractional calculus, the Riemann–Liouville (RL) definition is commonly employed. The following equation gives the RL fractional integral as well as the derivative of the \(\beta \)th-order as a function z(t) of time t and the provided constant a [4]

$$\begin{aligned} _a\mathcal{I}_t^\beta z(t)= & {} \frac{1}{{\Gamma (\beta )}}\int _a^t {\frac{{z(\tau )}}{{{{(t - \tau )}^{1 - \beta }}}}} \textrm{d}\tau \end{aligned}$$
(1)
$$\begin{aligned} {}_a\mathcal{D}_t^\beta z(t)= & {} \frac{{{\textrm{d}^\beta }z(t)}}{{\textrm{d}{t^\beta }}} = \frac{1}{{\Gamma (1 - \beta )}}\frac{\textrm{d}}{{\textrm{d}t}}\int _a^t {\frac{{z(\tau )}}{{{{(t - \tau )}^\beta }}}} \textrm{d}\tau \end{aligned}$$
(2)

with \(r - 1< \beta < r\), \(r \in {\mathbb {N}}\). The gamma function \(\Gamma ( \cdot )\) using Euler can be defined as

$$\begin{aligned} \Gamma (\beta ) = \int _0^\infty {{\textrm{e}^{ - t}}} {t^{\beta - 1}}\textrm{d}t \end{aligned}$$

where \(\mathcal{I}\) is fractional integral and \(\mathcal{D}\) is fractional derivative.

Property 1

The following is the equality for the RL derivative [26]

$$\begin{aligned} {}_a^{}\mathcal{D}_t^{1 - \beta }\left( {{}_a^{}\mathcal{D}_t^\beta z(t)} \right) = \dot{z}(t). \end{aligned}$$
(3)

Property 2

The RL derivative conforms to the following equality [26]

$$\begin{aligned} {}_a^{}\mathcal{D}_t^\beta \left( {{}_a^{}\mathcal{D}_t^{ - \beta }z(t)} \right) = z(t) \end{aligned}$$
(4)

Lemma 1

Following is a nonlinear equation that is being considered [27]

$$\begin{aligned} \dot{x}(t) = z(t,x),\quad x(0) = {x_0} \end{aligned}$$
(5)

where z(t, x) is continues and nonlinear function. In order to achieve fixed-time stability and convergence, the Lyapunov equation \(\nu (x)\) must satisfy the following conditions

  1. (i)

    \(\nu (x) = 0\,\, \Leftrightarrow \,\,x = 0\)

  2. (ii)

    \({\dot{\nu }}(x) \le - {\kappa _1}{\nu ^{{\varphi _1}}}(x) - {\kappa _2}\nu {(x)^{{\varphi _2}}}\)

with \({\kappa _1},\,{\kappa _2}> 0,\,0< {\varphi _1} < 1\,\,\,and\,\,{\varphi _2} > 1\). Following this, the system is considered to be stable in fixed-time, and the convergence time can be computed as

$$\begin{aligned} T \le \frac{1}{{{\kappa _1}(1 - {\varphi _1})}} + \frac{1}{{{\kappa _2}({\varphi _2} - 1)}} \end{aligned}$$
(6)

Lemma 2

With \(\varepsilon _1,\varepsilon _2,\varepsilon _3,\ldots ,\varepsilon _n > 0\), the inequalities are given as [28]

$$\begin{aligned} \begin{array}{l} \sum \limits _{i = 1}^n {\left| {{\varepsilon _i}} \right| _{}^{1 + \eta }} \ge {\left( {\sum \limits _{i = 1}^n {\left| {{\varepsilon _i}} \right| _{}^2} } \right) ^{\frac{{1 + \eta }}{2}}},\,\,\,\,\,\,\,\textrm{for}\,\,\,0< \eta < 1\\ \sum \limits _{i = 1}^n {\left| {{\varepsilon _i}} \right| _{}^\eta } \ge {n^{1 - \eta }}{\left( {\sum \limits _{i = 1}^n {\left| {{\varepsilon _i}} \right| } } \right) ^\eta },\,\,\,\,\,\,\,\textrm{for}\,\,\eta > 1 \end{array} \end{aligned}$$
(7)

Adaptive fixed-time fractional-order SMC scheme design

This section begins with a discussion of the dynamics of robotic manipulator systems, continues with an examination of an adaptive fixed-time fractional-order sliding surface, and then the development of a proposed scheme AFtNTSM is presented. Moreover, Lyapunov theorem analysis is used to conduct research into the stability of the suggested method.

Dynamics of robotic manipulator

The dynamical expression of a robotic manipulator is written as follows [4]

$$\begin{aligned} M(\theta )\ddot{\theta }+ H(\theta ,{\dot{\theta }}){\dot{\theta }} + G(\theta ) = \tau (t) + \delta _\textrm{dis}(t) + \delta _\textrm{fric}(t) \end{aligned}$$
(8)

where \( \theta \, \in \,{\mathbb {R}}{^n}\) denotes angular position, \({\dot{\theta }}\, \in \,{\mathbb {R}}{^n} \) represents angular velocity and \(\ddot{\theta }\, \in \,{\mathbb {R}}{^n}\) shows angular acceleration. \(M(\theta )\, \in \,{\mathbb {R}}{^{n \times n}}\) is the positive definite inertia matrix and satisfies the condition that \({\mathcal{M}_1}(M(\theta )) \le \left\| M(\theta ) \right\| \le {\mathcal{M} _2}(M(\theta ))\) with \({\mathcal{M} _1}>0\) is smallest and \({\mathcal{M} _2}>0\) is largest eigenvalues of \(M(\theta )\). \(H(\theta ,{\dot{\theta }}) \in \,{\mathbb {R}}{^{n \times n}}\) is the coriolis and centripetal forces, \(G(\theta ) \in \,{\mathbb {R}}{^n}\) is the gravitational force. \({\delta _\textrm{dis}(t)} \in \,{\mathbb {R}}{^n}\) is the bounded external disturbances, \({\delta _\textrm{fric}(t)} \in \,{\mathbb {R}}{^n}\) is the friction forces, \(\tau (t) \in \,{\mathbb {R}}{^n}\) is the vector control torque input.

The dynamics of robotic manipulator (8) can be rewritten to give

$$\begin{aligned} \ddot{\theta }= & {} {M^{ - 1}}(\theta )\tau (t) + {M^{ - 1}}(\theta ){\delta _\textrm{dis}}(t) + {M^{ - 1}}(\theta ){\delta _\textrm{fric}}(t)\nonumber \\{} & {} - {M^{ - 1}}(\theta )\left[ {H(\theta ,{\dot{\theta }}){\dot{\theta }} + G(\theta )} \right] \end{aligned}$$
(9)

To compute the tracking error, one can write it by utilizing (9) in the following way

$$\begin{aligned} \ddot{\tilde{\theta }}(t) = M_{}^{ - 1}(\theta )\tau (t) + \phi (\theta ,t) + \varphi (\ddot{\theta },{\dot{\theta }},\theta ,t) \end{aligned}$$
(10)

where \(\varphi (\ddot{\theta },{\dot{\theta }},\theta ,t) = - {{\ddot{\theta }}_d} - {M^{ - 1}}(\theta )\left[ {H(\theta ,{\dot{\theta }}){\dot{\theta }} + G(\theta )} \right] \) represents the known system dynamics. \(\phi (\theta ,t) = {M^{ - 1}}(\theta ) \)\( {\delta _\textrm{dis}}(t) + {M^{ - 1}}(\theta ){\delta _\textrm{fric}}(t)\) describes uncertain unknown dynamics. Moreover, \(\tilde{\theta }(t) = \theta - \theta _d\) is tracking error equation in which \(\theta _d\) is the desired angular position and \(\theta \) is the robot joint’s angular position.

Assumption 1

The Eq. (11), which can be observed in the following expression, offers a bounded condition for unknown dynamics.

$$\begin{aligned} \left\| {{\mathcal{D}^{ \alpha }}\phi (\theta ,t)} \right\| \le {\omega _1} + \,{\omega _2}\left\| \theta \right\| + \,{\omega _3}{\left\| {{\dot{\theta }}} \right\| ^2} \end{aligned}$$
(11)

where \(\omega _i\) is positive constant.

Fractional-order based sliding surface

This section presents the fractional-order sliding surface that provides fixed-time convergence and superior tracking capability for the nonlinear robotic manipulator system.

$$\begin{aligned} \sigma (t)= & {} {\mathcal{D}^\alpha }e(t) + {\chi _1}{\mathcal{D}^{\alpha - 1}}\left[ {sg{n^{{\kappa _1}}}(e(t))} \right] \nonumber \\{} & {} + {\chi _2}{\mathcal{D}^{\alpha - 1}}\left[ {sg{n^{{\kappa _2}}}(e(t))} \right] \end{aligned}$$
(12)

where \(e (t) = \dot{\tilde{\theta }}(t) + {a_1}sg{n^{{b_1}}}({\tilde{\theta }}(t)) + {a_2}sg{n^{{b_2}}}({\tilde{\theta }}(t))\), \(\sigma (t) \in {\mathbb {R}}{^n}\) is the sliding surface, \(sg{n^\kappa }( \bullet ) = | \bullet {|^\kappa }sign( \bullet )\), \({\chi _1,a_1>0}\) and \({\chi _2,a_2>0}\). The other constants are given as \(0<{\kappa _1, b_1, \alpha }<1\) and \({\kappa _2, b_2}>1\). Error on the sliding surface (\(\sigma (t)=0\)), we get

$$\begin{aligned} {\mathcal{D}^\alpha }e(t)= & {} - {\chi _1}{\mathcal{D}^{\alpha - 1}}\left[ {sg{n^{{\kappa _1}}}(e(t))} \right] \nonumber \\{} & {} - {\chi _2}{\mathcal{D}^{\alpha - 1}}\left[ {sg{n^{{\kappa _2}}}(e(t))} \right] . \end{aligned}$$
(13)

Theorem 1

No instability in the dynamics of the sliding mode (12), thus, the trajectories of its states tend to zero in fixed-time.

Consider the suitable Lyapunov candidate as follows

$$\begin{aligned} {V_1}(t) = 0.5\sum \limits _{i = 1}^n {e_i^2(t)}. \end{aligned}$$
(14)

Equation (14) can be derived as

$$\begin{aligned} {{\dot{V}}_1}(t) = \sum \limits _{i = 1}^n {e_i^{}(t)} \dot{e}_i^{}(t) \end{aligned}$$
(15)

According to Property 1, (15) is expressed as

$$\begin{aligned} {{\dot{V}}_1}(t) = \sum \limits _{i = 1}^n {e_i^{}(t)} {\mathcal{D}^{1 - \alpha }}({\mathcal{D}^\alpha }{e_i}(t)) \end{aligned}$$
(16)

By substitution of (13) into (16), we have

$$\begin{aligned} \dot{V}_1(t)= & {} \sum \limits _{i = 1}^n {e_i^{}(t)}{\mathcal{D}^{1 - \alpha }}\left[ - {\chi _1}{\mathcal{D}^{\alpha - 1}}\left[ {sg{n^{{\kappa _1}}}(e_i(t))} \right] \right. \nonumber \\{} & {} \left. - {\chi _2}{\mathcal{D}^{\alpha - 1}}\left[ {sg{n^{{\kappa _2}}}(e_i(t))} \right] \right] \end{aligned}$$
(17)
$$\begin{aligned} \dot{V}_1(t)= & {} - \sum \limits _{i = 1}^n {e_i^{}(t)}\left[ {{\chi _1}sg{n^{{\kappa _1}}}(e_i(t)) + {\chi _2}sg{n^{{\kappa _2}}}(e_i(t))} \right] \nonumber \\ \end{aligned}$$
(18)
$$\begin{aligned} \dot{V}_1(t)= & {} - {\chi _1}\sum \limits _{i = 1}^n {{{\left| {{e _i}(t)} \right| }^{{\kappa _1} + 1}}} - {\chi _2}\sum \limits _{i = 1}^n {{{\left| {{e _i}(t)} \right| }^{{\kappa _2} + 1}}} \nonumber \\= & {} - {\chi _1}\sum \limits _{i = 1}^n {{{\left( {{{\left| {e _i^{}(t)} \right| }^2}} \right) }^{\frac{{{\kappa _1} + 1}}{2}}}} - {\chi _2}\sum \limits _{i = 1}^n {{{\left( {{{\left| {e _i^{}(t)} \right| }^2}} \right) }^{\frac{{{\kappa _2} + 1}}{2}}}}\nonumber \\ \end{aligned}$$
(19)

According to Lemma 2, one obtains

$$\begin{aligned} \dot{V}_1(t)\le & {} - {\chi _1}{\left( {\sum \limits _{i = 1}^n {{{\left| {e _i^{}(t)} \right| }^2}} } \right) ^{\frac{{{\kappa _1} + 1}}{2}}}\nonumber \\{} & {} - {\chi _2}{n^{\frac{{1 - {\kappa _2}}}{2}}}{\left( {\sum \limits _{i = 1}^n {{{\left| {e _i^{}(t)} \right| }^2}} } \right) ^{\frac{{{\kappa _2} + 1}}{2}}} \end{aligned}$$
(20)
$$\begin{aligned} \dot{V}_1(t)\le & {} - {\chi _1}{\left( {2V_1} \right) ^{\frac{{{\kappa _1} + 1}}{2}}} - {\chi _2}{n^{\frac{{1 - {\kappa _2}}}{2}}}{\left( {2V_1} \right) ^{\frac{{{\kappa _2} + 1}}{2}}} \end{aligned}$$
(21)
$$\begin{aligned} \dot{V}_1(t)\le & {} - {2^{\frac{{{\kappa _1} + 1}}{2}}}{\chi _1}{V_1^{\frac{{{\kappa _1} + 1}}{2}}} - {2^{\frac{{{\kappa _2} + 1}}{2}}}{\chi _2}{n^{\frac{{1 - {\kappa _2}}}{2}}}{V_1^{\frac{{{\kappa _2} + 1}}{2}}} \end{aligned}$$
(22)

According to Lemma 1, one gets the settling time as

$$\begin{aligned} T_\textrm{st1} = \frac{1}{{{2^{\frac{{{\kappa _1} + 1}}{2}}}{\chi _1}\left( {1 - \frac{{{\kappa _1} + 1}}{2}} \right) }} + \frac{1}{{{2^{\frac{{{\kappa _2} + 1}}{2}}}{n^{\frac{{1 - {\kappa _2}}}{2}}}{\chi _2}\left( {\frac{{{\kappa _2} + 1}}{2} - 1} \right) }}\nonumber \\ \end{aligned}$$
(23)

As the construction of the sliding surface is now complete, the proposed FtNTSM approach for the known dynamical systems can be developed to realize the desired robust performance in the face of external disturbances.

Proposed FtNTSM controller design and stability analysis

In this subsection, designing of the proposed controller and the stability analysis of the overall system will be given.

The derivative of the (12) can be deduced as

$$\begin{aligned} {\dot{\sigma }} (t)= & {} {\mathcal{D}^\alpha }\dot{e}(t) + {\chi _1}{\mathcal{D}^{\alpha }}\left[ {sg{n^{{\kappa _1}}}(e(t))} \right] \nonumber \\{} & {} + {\chi _2}{\mathcal{D}^{\alpha }}\left[ {sg{n^{{\kappa _2}}}(e(t))} \right] \nonumber \\ \end{aligned}$$
(24)

By putting (10) into (24), one has

$$\begin{aligned} \begin{array}{*{20}{l}} {\dot{\sigma }} (t) = {\mathcal{D}^\alpha }\left[ {M_{}^{ - 1}(\theta )\tau (t) + \phi (\theta ,t) + \varphi (\ddot{\theta },{\dot{\theta }},\theta ,t)} \right. \\ \qquad \qquad \left. + {a_1}{b_1}{\left| {{\tilde{\theta }} (t)} \right| ^{{b_1} - 1}}\dot{{\tilde{\theta }}} (t) + {a_2}{b_2}{\left| {{\tilde{\theta }} (t)} \right| ^{{b_2} - 1}}\dot{{\tilde{\theta }}} (t) \right] \\ \qquad \qquad { + {\chi _1}{\mathcal{D}^{\alpha }}\left[ {sg{n^{{\kappa _1}}}(e(t))} \right] + {\chi _2}{\mathcal{D}^{\alpha }}\left[ {sg{n^{{\kappa _2}}}(e(t))} \right] } \end{array} \end{aligned}$$
(25)

where \({b_1}{\left| {{\tilde{\theta }} (t)} \right| ^{{b_1} - 1}} = 0\) if \({{\tilde{\theta }} (t)} =0\).

To control and stabilize the nonlinear robotic manipulator system with known bounded disturbances, the FtNTSM control law \(\tau = \tau _n + \tau _s\) can be formulated as given in (26, 27).

$$\begin{aligned} {\tau _n}(t)= & {} - M(\theta )\left[ \begin{array}{l} \varphi (\ddot{\theta },{\dot{\theta }},\theta ,t) {+} {\mathcal{D}^{ {-} \alpha }}[({\omega _1} {+} {\omega _2}\left\| \theta \right\| {+} {\omega _3}{\left\| {{\dot{\theta }} } \right\| ^2})sign(\sigma )]\\ {+} {a_1}{b_1}{\left| {{\tilde{\theta }} (t)} \right| ^{{b_1} {-} 1}}\dot{{\tilde{\theta }}} (t) {+} {a_2}{b_2}{\left| {{\tilde{\theta }} (t)} \right| ^{{b_2} {-} 1}}\dot{{\tilde{\theta }}} (t)\\ {+} {\chi _1}\left[ {sg{n^{{\kappa _1}}}(e(t))} \right] {+} {\chi _2}\left[ {sg{n^{{\kappa _2}}}(e(t))} \right] \end{array} \right] \nonumber \\ \end{aligned}$$
(26)
$$\begin{aligned} {\tau _s}(t)= & {} - M(\theta ){\mathcal{D}^{ - \alpha }}\left[ {K_1}\left[ {sg{n^{{\lambda _1}}}(\sigma (t))} \right] + {K_2}\left[ {sg{n^{{\lambda _2}}}(\sigma (t))} \right] \right] \end{aligned}$$
(27)

where \({K _{1}} >0\) and \({K _{2}} >0\) are constants. \({\lambda _{1}}\) and \({\lambda _{2}}\) have ranges as \(0<{\lambda _{1}}<1\) and \(1<{\lambda _{2}}\), respectively.

Substitution of (26, 27) into (25), one gets the closed system as

$$\begin{aligned} \begin{array}{*{20}{l}} {\dot{\sigma }} (t) \\ \quad = {\mathcal{D}^\alpha }\left[ {\begin{array}{*{20}{l}} {\begin{array}{*{20}{l}} { {-} \varphi (\ddot{\theta },{\dot{\theta }},\theta ,t) {-} {\mathcal{D}^{ {-} \alpha }}[({\omega _1} {+} {\omega _2}\left\| \theta \right\| {+} {\omega _3}{{\left\| {{\dot{\theta }} } \right\| }^2})sign(\sigma )]}\\ { {-} {a_1}{b_1}{{\left| {{\tilde{\theta }} (t)} \right| }^{{b_1} {-} 1}}\dot{{\tilde{\theta }}} (t) {-} {a_2}{b_2}{{\left| {{\tilde{\theta }} (t)} \right| }^{{b_2} {-} 1}}\dot{{\tilde{\theta }}} (t)} \end{array}}\\ { {-} {\chi _1}\left[ {sg{n^{{\kappa _1}}}(e(t))} \right] {-} {\chi _2}\left[ {sg{n^{{\kappa _2}}}(e(t))} \right] }\\ { {-} {\mathcal{D}^{ {-} \alpha }}\left( {{K_1}\left[ {sg{n^{{\lambda _1}}}(\sigma (t))} \right] {+} {K_2}\left[ {sg{n^{{\lambda _2}}}(\sigma (t))} \right] } \right) }\\ {\begin{array}{*{20}{l}} { {+} \phi (\theta ,t) {+} \varphi (\ddot{\theta },{\dot{\theta }},\theta ,t)}\\ { {+} {a_1}{b_1}{{\left| {{\tilde{\theta }} (t)} \right| }^{{b_1} {-} 1}}\dot{{\tilde{\theta }}} (t) {+} {a_2}{b_2}{{\left| {{\tilde{\theta }} (t)} \right| }^{{b_2} {-} 1}}\dot{{\tilde{\theta }}} (t)} \end{array}} \end{array}} \right] \\ \qquad { + {\chi _1}{\mathcal{D}^\alpha }\left[ {sg{n^{{\kappa _1}}}(e(t))} \right] + {\chi _2}{\mathcal{D}^\alpha }\left[ {sg{n^{{\kappa _2}}}(e(t))} \right] } \end{array}\nonumber \\ \end{aligned}$$
(28)

By simplification of (28), one obtains

$$\begin{aligned}{} & {} {\dot{\sigma }} (t) \nonumber \\{} & {} = {\mathcal{D}^\alpha }\left[ {\begin{array}{*{20}{l}} {\phi (\theta ,t) {-} {\mathcal{D}^{ - \alpha }}[({\omega _1} {+} {\omega _2}\left\| \theta \right\| {+} {\omega _3}{{\left\| {{\dot{\theta }} } \right\| }^2})sign(\sigma )]}\\ { {-} {\mathcal{D}^{ {-} \alpha }}\left( {{K_1}\left[ {sg{n^{{\lambda _1}}}(\sigma (t))} \right] {+} {K_2}\left[ {sg{n^{{\lambda _2}}}(\sigma (t))} \right] } \right) } \end{array}} \right] \nonumber \\ \end{aligned}$$
(29)
$$\begin{aligned} {\dot{\sigma }} (t){} & {} = - {K_1}\left[ {sg{n^{{\lambda _1}}}(\sigma (t))} \right] - {K_2}\left[ {sg{n^{{\lambda _2}}}(\sigma (t))} \right] \nonumber \\{} & {} \quad + {\mathcal{D}^\alpha }\phi (\theta ,t)- ({\omega _1} + {\omega _2}\left\| \theta \right\| + {\omega _3}{\left\| {{\dot{\theta }} } \right\| ^2})sign(\sigma )\nonumber \\ \end{aligned}$$
(30)

In order to determine the closed-loop system’s stability in this section, the Lyapunov theorem will be implemented.

Theorem 2

With the robotic manipulator system described in (8), the sliding manifold suggested in (12), and the FtNTSM controller developed in (26, 27), the desired position of the joints can converge in a fixed-time, as long as Assumption 1 holds.

Proof

The expression for the suitable Lyapunov function is as follows

$$\begin{aligned} {V_2}(t) = 0.5\sum \limits _{i = 1}^n {\sigma _i^2(t)} \end{aligned}$$
(31)

Then (31) can be derived as

$$\begin{aligned} {\dot{V}_2}(t) = \sum \limits _{i = 1}^n {\sigma _i(t)} {\dot{\sigma }}_i(t) \end{aligned}$$
(32)

Substitution of (26, 27) into (32), one can have

$$\begin{aligned}{} & {} \dot{V}_2(t) = \sum \limits _{i = 1}^n {\sigma _i(t)}\nonumber \\{} & {} \quad \left( \begin{array}{l} {-} {K_1}\left[ {sg{n^{{\lambda _1}}}(\sigma _i (t))} \right] {-} {K_2}\left[ {sg{n^{{\lambda _2}}}(\sigma _i (t))} \right] {+} {\mathcal{D}^\alpha } \phi _i (\theta ,t)\\ {-} ({\omega _1} {+} {\omega _2}\left\| \theta \right\| {+} {\omega _3}{\left\| {{\dot{\theta }} } \right\| ^2})sign(\sigma _i) \end{array} \right) \nonumber \\ \end{aligned}$$
(33)

Based on condition given in Assumption 1, one can obtain

$$\begin{aligned} \dot{V}_2(t){} & {} \le - {K_1}\sum \limits _{i = 1}^n {\sigma _i(t)}\left[ {sg{n^{{\lambda _1}}}(\sigma _i (t))} \right] \nonumber \\{} & {} \qquad - {K_2}\sum \limits _{i = 1}^n {\sigma _i(t)}\left[ {sg{n^{{\lambda _2}}}(\sigma _i (t))} \right] \end{aligned}$$
(34)
$$\begin{aligned} \dot{V}_2(t){} & {} \le - {K_1}\sum \limits _{i = 1}^n {{{\left| {{\sigma _i}(t)} \right| }^{{\lambda _1} + 1}}} - {K_2}\sum \limits _{i = 1}^n {{{\left| {{\sigma _i}(t)} \right| }^{{\lambda _2} + 1}}} \nonumber \\{} & {} {\le } {-} {K_1}\sum \limits _{i = 1}^n {{{\left( {{{\left| {\sigma _i^{}(t)} \right| }^2}} \right) }^{\frac{{{\lambda _1} + 1}}{2}}}} {-} {K_2}\sum \limits _{i = 1}^n {{{\left( {{{\left| {\sigma _i^{}(t)} \right| }^2}} \right) }^{\frac{{{\lambda _2} + 1}}{2}}}}\nonumber \\ \end{aligned}$$
(35)

According to Lemma 2, we get

$$\begin{aligned}{} & {} \dot{V}_2(t) \le - {K_1}{\left( {\sum \limits _{i = 1}^n {{{\left| {\sigma _i^{}(t)} \right| }^2}} } \right) ^{\frac{{{\lambda _1} + 1}}{2}}} \nonumber \\{} & {} \qquad -{K_2}{n^{\frac{{1 - {\lambda _2}}}{2}}}{\left( {\sum \limits _{i = 1}^n {{{\left| {\sigma _i^{}(t)} \right| }^2}} } \right) ^{\frac{{{\lambda _2} + 1}}{2}}} \end{aligned}$$
(36)
$$\begin{aligned} \dot{V}_2(t)\le & {} - {K_1}{\left( {2V_2} \right) ^{\frac{{{\lambda _1} + 1}}{2}}} - {K _2}{n^{\frac{{1 - {\lambda _2}}}{2}}}{\left( {2V_2} \right) ^{\frac{{{\lambda _2} + 1}}{2}}}\nonumber \\\le & {} - {2^{\frac{{{\lambda _1} + 1}}{2}}}{K_1}{V_2^{\frac{{{\lambda _1} + 1}}{2}}} - {2^{\frac{{{\lambda _2} + 1}}{2}}}{K _2}{n^{\frac{{1 - {\lambda _2}}}{2}}}{V_2^{\frac{{{\lambda _2} + 1}}{2}}} \end{aligned}$$
(37)

As a result, in a fixed-time, the system’s states will arrive to \(\sigma (t)\). In light of Lemma 1, the following formula can be used to determine the fixed settling time

$$\begin{aligned} T_{st2} = \frac{1}{{{2^{\frac{{{\lambda _1} + 1}}{2}}}{K_1}\left( {1 - \frac{{{\lambda _1} + 1}}{2}} \right) }} + \frac{1}{{{2^{\frac{{{\lambda _2} + 1}}{2}}}{n^{\frac{{1 - {\lambda _2}}}{2}}}{K_2}\left( {\frac{{{\lambda _2} + 1}}{2} - 1} \right) }}\nonumber \\ \end{aligned}$$
(38)

As \(T_{1}\) can be calculated for known dynamics of robotic manipulator having the relation \(T_{1}= T_{st1} + T_{st2} + T_{st3}\), where \( T_{st3}\) can be calculated using \( \dot{\tilde{\theta }}(t) = - {a_1}sg{n^{{b_1}}}({\tilde{\theta }}(t)) - {a_2}sg{n^{{b_2}}}({\tilde{\theta }}(t))\) when \(e(t)=0\). \(\square \)

Proposed AFtNTSM controller design and stability analysis

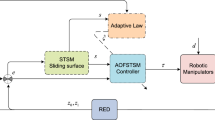
In order to deal with the unknown and uncertain dynamics, the following equation presents the proposed adaptive based FtNTSM control scheme \(\tau (t) = \tau _a(t) + \tau _s(t)\). The proposed model is depicted in Fig. 1.

Fig. 1
figure 1

Proposed model

Full size image
$$\begin{aligned}{} & {} {\tau _a}(t) = - M(\theta )\nonumber \\{} & {} \quad \left[ \begin{array}{l} \varphi (\ddot{\theta },{\dot{\theta }},\theta ,t) + {\mathcal{D}^{ - \alpha }}[({{\hat{\omega }} _1} + {{\hat{\omega }} _2}\left\| \theta \right\| + {{\hat{\omega }} _3}{\left\| {{\dot{\theta }} } \right\| ^2})sign(\sigma )]\\ + {a_1}{b_1}{\left| {{\tilde{\theta }} (t)} \right| ^{{b_1} - 1}}\dot{{\tilde{\theta }}} (t) + {a_2}{b_2}{\left| {{\tilde{\theta }} (t)} \right| ^{{b_2} - 1}}\dot{{\tilde{\theta }}} (t)\\ + {\chi _1}\left[ {sg{n^{{\kappa _1}}}(e(t))} \right] + {\chi _2}\left[ {sg{n^{{\kappa _2}}}(e(t))} \right] \\ \end{array} \right] \nonumber \\ \end{aligned}$$
(39)

where \({\hat{\omega }}\) is the adaptive variable for compensating for unknown dynamics, designed as follows:

(40)

where \( \Delta \Xi = \left[ {1,\left\| \theta \right\| ,{{\left\| {{\dot{\theta }} } \right\| }^2}} \right] ,\ \Xi > 0\) and .

Theorem 3

Under Assumption 1, with the sliding manifold suggested in (12), the AFtNTSM controller produced in (27, 39), and the adaptive control rules designed in (40), the intended position of the joints of the robotic manipulator system under unknown dynamics described in (8) can converge in a fixed-time.

Proof

The function of the Lyapunov candidate is selected as follows

$$\begin{aligned} {{ V}_3}(t) = \frac{1}{2}\sum \limits _{i = 1}^n {\sigma _i^2(t)} + \frac{1}{{2{\varsigma _1}}}{\bar{\omega }} _1^2 + \frac{1}{{2{\varsigma _2}}}{\bar{\omega }} _2^2 + \frac{1}{{2{\varsigma _3}}}{\bar{\omega }} _3^2 \end{aligned}$$
(41)

where \({\bar{\omega }} _i = {\hat{\omega }}_i - \omega _i\) is the estimation error and \({\varsigma _i >0}\).

By taking derivative of (41), one can obtain

$$\begin{aligned} {{\dot{V}}_3}(t) = \sum \limits _{i = 1}^n {\sigma _i^{}(t)} {\dot{\sigma }}_i^{}(t) + \frac{1}{{{\varsigma _1}}}{\bar{\omega }} _1^{}\dot{{\hat{\omega }}} _1^{} + \frac{1}{{{\varsigma _2}}}{\bar{\omega }} _2^{}\dot{{\hat{\omega }}} _2^{} + \frac{1}{{{\varsigma _3}}}{\bar{\omega }} _3^{}\dot{{\hat{\omega }}} _3^{}\nonumber \\ \end{aligned}$$
(42)

Substitution of (25, 27, 39) into (42), one can get

$$\begin{aligned} \begin{array}{*{20}{l}} \dot{V}_3(t) =\sum \limits _{i = 1}^n {\sigma _i^{}(t)}\\ \quad \left\{ {\begin{array}{*{20}{l}} { - {K_1}\left[ {sg{n^{{\lambda _1}}}(\sigma _i (t))} \right] - {K_2}\left[ {sg{n^{{\lambda _2}}}(\sigma _i (t))} \right] }\\ {+ {\mathcal{D}^\alpha }\phi _i (\theta ,t) - ({{{\hat{\omega }} }_1} + {{{\hat{\omega }} }_2}\left\| \theta \right\| + {{{\hat{\omega }} }_3}{{\left\| {{\dot{\theta }} } \right\| }^2})sign(\sigma _i )} \end{array}} \right\} \\ \qquad { + \frac{1}{{{\varsigma _1}}}{\bar{\omega }} _1^{}\dot{{\hat{\omega }}} _1^{} + \frac{1}{{{\varsigma _2}}}{\bar{\omega }} _2^{}\dot{{\hat{\omega }}} _2^{} + \frac{1}{{{\varsigma _3}}}{\bar{\omega }} _3^{}\dot{{\hat{\omega }}} _3^{}} \end{array}\nonumber \\ \end{aligned}$$
(43)

Using adaptive laws (40), one can write

(44)

Equation (44) can be rewritten as

(45)

multiply and divided by \({\varsigma _i}{\left( {\left\| {{\bar{\omega }} _i^{}} \right\| \sqrt{\frac{1}{{2{\varsigma _i}}}} } \right) ^{{\lambda _1}}}\,\,and\,\,{\varsigma _i}\left( \left\| {{\bar{\omega }} _i^{}} \right\| \right. \)\( \left. \sqrt{\frac{1}{{2{\varsigma _i}}}} \right) ^{{\lambda _2}}\), one can realize

(46)

For brevity, (46) can be written in simplified form as

$$\begin{aligned} \begin{array}{*{20}{l}} \begin{array}{l} {{\dot{V}}_3}(t) \le - {K_1}\sum \limits _{i = 1}^n {{{\left| {{\sigma _i}(t)} \right| }^{{\lambda _1} + 1}}} - {\Xi _1}{\left( {\left\| {{\bar{\omega }} _1^{}} \right\| \sqrt{\frac{1}{{2{\varsigma _1}}}} } \right) ^{{\lambda _1} + 1}}\\ \quad - {\Xi _2}{\left( {\left\| {{\bar{\omega }} _2^{}} \right\| \sqrt{\frac{1}{{2{\varsigma _2}}}} } \right) ^{{\lambda _1} + 1}} - {\Xi _3}{\left( {\left\| {{\bar{\omega }} _3^{}} \right\| \sqrt{\frac{1}{{2{\varsigma _3}}}} } \right) ^{{\lambda _1} + 1}} \end{array}\\ \begin{array}{l} \quad - {K_2}\sum \limits _{i = 1}^n {{{\left| {{\sigma _i}(t)} \right| }^{{\lambda _2} + 1}}} - {\Xi _4}{\left( {\left\| {{\bar{\omega }} _1^{}} \right\| \sqrt{\frac{1}{{2{\varsigma _1}}}} } \right) ^{{\lambda _2} + 1}}\\ \quad - {\Xi _5}{\left( {\left\| {{\bar{\omega }} _2^{}} \right\| \sqrt{\frac{1}{{2{\varsigma _2}}}} } \right) ^{{\lambda _2} + 1}} - {\Xi _6}{\left( {\left\| {{\bar{\omega }} _3^{}} \right\| \sqrt{\frac{1}{{2{\varsigma _3}}}} } \right) ^{{\lambda _2} + 1}} \end{array} \end{array}\nonumber \\ \end{aligned}$$
(47)

where

$$\begin{aligned} \dot{V}_3(t){} & {} \le - {K_1}\sum \limits _{i = 1}^n {{{\left( {{{\left| {\sigma _i^{}(t)} \right| }^2}} \right) }^{\frac{{{\lambda _1} + 1}}{2}}}} - {\Xi _1}{{\left( {\frac{{{{\left\| {{\bar{\omega }} _1^{}} \right\| }^2}}}{{2{\varsigma _1}}}} \right) }^{\frac{{{\lambda _1} + 1}}{2}}} \nonumber \\{} & {} \quad - {\Xi _2}{{\left( {\frac{{{{\left\| {{\bar{\omega }} _2^{}} \right\| }^2}}}{{2{\varsigma _2}}}} \right) }^{\frac{{{\lambda _1} + 1}}{2}}} - {\Xi _3}{{\left( {\frac{{{{\left\| {{\bar{\omega }} _3^{}} \right\| }^2}}}{{2{\varsigma _3}}}} \right) }^{\frac{{{\lambda _1} + 1}}{2}}}\nonumber \\{} & {} \quad - {K_2}\sum \limits _{i = 1}^n {{{\left( {{{\left| {\sigma _i^{}(t)} \right| }^2}} \right) }^{\frac{{{\lambda _2} + 1}}{2}}}} - {\Xi _4}{{\left( {\frac{{{{\left\| {{\bar{\omega }} _1^{}} \right\| }^2}}}{{2{\varsigma _1}}}} \right) }^{\frac{{{\lambda _2} + 1}}{2}}} \nonumber \\{} & {} \quad - {\Xi _5}{{\left( {\frac{{{{\left\| {{\bar{\omega }} _2^{}} \right\| }^2}}}{{2{\varsigma _2}}}} \right) }^{\frac{{{\lambda _2} + 1}}{2}}} - {\Xi _6}{{\left( {\frac{{{{\left\| {{\bar{\omega }} _3^{}} \right\| }^2}}}{{2{\varsigma _3}}}} \right) }^{\frac{{{\lambda _2} + 1}}{2}}} \end{aligned}$$
(48)

According to Lemma 2, one can deduce

$$\begin{aligned}{} & {} \begin{array}{*{20}{l}} \dot{V}_3(t) \le - {K_1}{{\left( {\sum \limits _{i = 1}^n {{{\left| {\sigma _i^{}(t)} \right| }^2}} } \right) }^{\frac{{{\lambda _1} + 1}}{2}}} - {\Xi _1}{{\left( {\frac{{{{\left\| {{\bar{\omega }} _1^{}} \right\| }^2}}}{{2{\varsigma _1}}}} \right) }^{\frac{{{\lambda _1} + 1}}{2}}} \\ \qquad \qquad - {\Xi _2}{{\left( {\frac{{{{\left\| {{\bar{\omega }} _2^{}} \right\| }^2}}}{{2{\varsigma _2}}}} \right) }^{\frac{{{\lambda _1} + 1}}{2}}} - {\Xi _3}{{\left( {\frac{{{{\left\| {{\bar{\omega }} _3^{}} \right\| }^2}}}{{2{\varsigma _3}}}} \right) }^{\frac{{{\lambda _1} + 1}}{2}}}\\ \qquad \quad - {K_2}{n^{\frac{{1 - {\lambda _2}}}{2}}}{{\left( {\sum \limits _{i = 1}^n {{{\left| {\sigma _i^{}(t)} \right| }^2}} } \right) }^{\frac{{{\lambda _2} + 1}}{2}}} - {\Xi _4}{{\left( {\frac{{{{\left\| {{\bar{\omega }} _1^{}} \right\| }^2}}}{{2{\varsigma _1}}}} \right) }^{\frac{{{\lambda _2} + 1}}{2}}} \\ \qquad \qquad - {\Xi _5}{{\left( {\frac{{{{\left\| {{\bar{\omega }} _2^{}} \right\| }^2}}}{{2{\varsigma _2}}}} \right) }^{\frac{{{\lambda _2} + 1}}{2}}} - {\Xi _6}{{\left( {\frac{{{{\left\| {{\bar{\omega }} _3^{}} \right\| }^2}}}{{2{\varsigma _3}}}} \right) }^{\frac{{{\lambda _2} + 1}}{2}}} \end{array} \nonumber \\ \end{aligned}$$
(49)
$$\begin{aligned}{} & {} \begin{array}{*{20}{l}} {{\dot{V}}_3}(t) \le - {{{\hat{\Xi }} }_1}\left\{ {{\left( {\frac{{\sum \limits _{i = 1}^n {{{\left| {\sigma (t)} \right| }^2}} }}{2}} \right) }^{\frac{{{\lambda _1} + 1}}{2}}} + {{\left( {\frac{{{{\left\| {{\bar{\omega }} _1^{}} \right\| }^2}}}{{2{\varsigma _1}}}} \right) }^{\frac{{{\lambda _1} + 1}}{2}}} \right. \\ \qquad \qquad \left. + {{\left( {\frac{{{{\left\| {{\bar{\omega }} _2^{}} \right\| }^2}}}{{2{\varsigma _2}}}} \right) }^{\frac{{{\lambda _1} + 1}}{2}}} + {{\left( {\frac{{{{\left\| {{\bar{\omega }} _3^{}} \right\| }^2}}}{{2{\varsigma _3}}}} \right) }^{\frac{{{\lambda _1} + 1}}{2}}} \right\} \\ \qquad \qquad - {{{\hat{\Xi }} }_2}\left\{ {{\left( {\frac{{\sum \limits _{i = 1}^n {{{\left| {\sigma (t)} \right| }^2}} }}{2}} \right) }^{\frac{{{\lambda _2} + 1}}{2}}} + {{\left( {\frac{{{{\left\| {{\bar{\omega }} _1^{}} \right\| }^2}}}{{2{\varsigma _1}}}} \right) }^{\frac{{{\lambda _2} + 1}}{2}}} \right. \\ \qquad \qquad \left. + {{\left( {\frac{{{{\left\| {{\bar{\omega }} _2^{}} \right\| }^2}}}{{2{\varsigma _2}}}} \right) }^{\frac{{{\lambda _2} + 1}}{2}}} + {{\left( {\frac{{{{\left\| {{\bar{\omega }} _3^{}} \right\| }^2}}}{{2{\varsigma _3}}}} \right) }^{\frac{{{\lambda _2} + 1}}{2}}} \right\} \end{array}\nonumber \\ \end{aligned}$$
(50)

where \({{{\hat{\Xi }} }_1} = \min \left( {{2^{\frac{{{\lambda _1} + 1}}{2}}}{K_1},\,{\Xi _1},\,{\Xi _2},\,{\Xi _3}} \right) ,\,\,{{{\hat{\Xi }} }_2} = \min \)\( \left( {{2^{\frac{{{\lambda _2} + 1}}{2}}}{{n^{\frac{{1 - {\lambda _2}}}{2}}}}{K_2},\,{\Xi _4},\,{\Xi _5},\,{\Xi _6}} \right) \).

$$\begin{aligned} {{\dot{V}}_3}(t)\le & {} - {{{\hat{\Xi }} }_1}\left\{ \left( {\frac{{\sum \limits _{i = 1}^n {{{\left| {\sigma (t)} \right| }^2}} }}{2}} \right) + \left( {\frac{{{{\left\| {{\bar{\omega }} _1^{}} \right\| }^2}}}{{2{\varsigma _1}}}} \right) \right. \nonumber \\{} & {} \left. + \left( {\frac{{{{\left\| {{\bar{\omega }} _2^{}} \right\| }^2}}}{{2{\varsigma _2}}}} \right) + \left( {\frac{{{{\left\| {{\bar{\omega }} _3^{}} \right\| }^2}}}{{2{\varsigma _3}}}} \right) \right\} ^{\frac{{{\lambda _1} + 1}}{2}}\nonumber \\{} & {} - {{{\hat{\Xi }} }_2}{4^{\frac{{1 - {\lambda _2}}}{2}}}\left\{ \left( {\frac{{\sum \limits _{i = 1}^n {{{\left| {\sigma (t)} \right| }^2}} }}{2}} \right) + \left( {\frac{{{{\left\| {{\bar{\omega }} _1^{}} \right\| }^2}}}{{2{\varsigma _1}}}} \right) \right. \nonumber \\{} & {} \left. + \left( {\frac{{{{\left\| {{\bar{\omega }} _2^{}} \right\| }^2}}}{{2{\varsigma _2}}}} \right) + \left( {\frac{{{{\left\| {{\bar{\omega }} _3^{}} \right\| }^2}}}{{2{\varsigma _3}}}} \right) \right\} ^{\frac{{{\lambda _2} + 1}}{2}} \end{aligned}$$
(51)
$$\begin{aligned} \dot{V}_3(t)\le & {} - {{{\hat{\Xi }} }_1}(t)V_3{(t)^{\frac{{{\lambda _1} + 1}}{2}}} - {{{\hat{\Xi }} }_2}{4^{\frac{{1 - {\lambda _2}}}{2}}}V_3{(t)^{\frac{{{\lambda _2} + 1}}{2}}} \end{aligned}$$
(52)

Using Lemma 1, one can formulate the fixed settling time as

$$\begin{aligned} T_{st4} = \frac{1}{{{{{\hat{\Xi }} }_1}\left( {1 - \frac{{{\lambda _1} + 1}}{2}} \right) }} + \frac{1}{{{4^{\frac{{1 - {\lambda _2}}}{2}}}{{{\hat{\Xi }} }_2}\left( {\frac{{{\lambda _2} + 1}}{2} - 1} \right) }} \end{aligned}$$
(53)

Hence, \(T_{2}\) can be formulated for unknown uncertain dynamics of robotic manipulator having the relation \(T_{2}= T_{st1} + T_{st3} + T_{st4}\). \(\square \)

Remark 1

According to Lemma 1, the fixed-time, specified by \(T_2\), can have a significant impact on the choice made using the parameters \({\hat{\Xi }}_1\), \({\hat{\Xi }}_2\), \(\chi _1\) and \(\chi _2\). Increasing the values of these parameters substantially increases the convergence rate.

Results and discussions

The robotic system is implemented using a three-degrees-of-freedom (DOF) robot manipulator to demonstrate simulation performance and to put the proposed AFtNTSM approach to the test. A 3-DOF of PUMA 560 robotic manipulator will be implemented in the existence of disturbances and uncertainties [29]. In order to demonstrate the efficacy of the AFtNTSM in coping with uncertainties and disturbances, comparative simulated studies are provided. The results of these investigations are presented with the help of simulations run in MATLAB/Simulink. The authors describe the required parameters, anticipated trajectories, frictions, and disturbances as

$$\begin{aligned} {\theta _d}= & {} \left[ \cos (t\pi /5)\, - 1,\,\cos (t\pi /5\, + \pi /2), \right. \\{} & {} \left. \cos (t\pi /5\, + \pi /2) - 1 \right] ^T\\ {\delta _\textrm{fric}}= & {} \left[ 0.5{{{\dot{\theta }}}_1} + \sin (3{\theta _1}),\,\,1.3{{{\dot{\theta }}}_2} - 1.8\sin (2{\theta _2}),\,\, - 0.1{{{\dot{\theta }}}_3}\right. \\{} & {} \left. - 0.5\sin ({\theta _3}) \right] ^T\\ {\delta _\textrm{dis}}= & {} {\left[ {20.5\sin ({{{\dot{\theta }}}_1}),\,\,21.1\sin ({{{\dot{\theta }}}_2})\,,\,\,10.15\sin ({{{\dot{\theta }}}_3})} \right] ^T}. \end{aligned}$$
Table 1 Parameters of AFtNTSM
Full size table

To apply the appropriate fractional-order value of \(\alpha \), trail-and-error has been applied. Therefore, the suitable value is obtained as \(\alpha = 0.9\). The proposed control parameters are given in Table 1.

In the following section, the AFtNTSM approach that has been suggested is described as being designed to enhance the performance of the uncertain dynamics of the 3-DOF robotic manipulator when it is subjected to unknown external disturbances. This is done so that the robot will be able to accomplish its mission. In order to further prove the efficacy of the developed method, adaptive time delay sliding mode control (ATDSMC) [30] and adaptive fractional-order SMC (AFOSMC) [31] are used to compare with proposed control simulations. In Figs. 2, 3 and 4, the performance of desired trajectory tracking, tracking error, control torque inputs, is validated by comparing the results from the AFtNTSM scheme with those from the ATDSMC and AFOSMC methods in the presence of unknown dynamics. Figure 5 provides a depiction of the adaptive estimation of the unknown parameters.

Fig. 2
figure 2

Position tracking

Full size image
Fig. 3
figure 3

Tracking errors

Full size image
Fig. 4
figure 4

Control inputs

Full size image
Fig. 5
figure 5

Adaptive parameter estimation

Full size image

Figures 2, 3, 4, 5 show the results of the comparisons and illustrate that the AFtNTSM has superior tracking performance, non-chatter control inputs, and precise adaptive compensation despite the presence of unknown uncertain dynamics.

After the evaluation of the suggested control scheme AFtNTSM, ATDSMC, and AFOSMC have been concluded, the constant parameters are then modified in a way that is thought to be appropriate. When looking at Figs. 2 and 3, it becomes abundantly evident that the proposed method results in less angular position error while requiring a minimal amount of convergence time. In addition, Fig. 4 displays the control performance, and it is easy to see that the offered method gives the non-chattering and smooth control input. Figure 5 presents the adaptive estimation, which reveals that the adaptive rules do not experience the problem of drifting. This may be considered as a demonstration that the adaptive rules do not suffer from the issue of drifting.

For the proposed technique, the suitable parameters are those chosen from the given range, which is defined as \(\chi _1, a_1 > 0\), \(\chi _2, a_2> 0\), \(K_1 > 0\), \( K_2 >0 \), \(0< \kappa _{1}, b_1, \lambda _1,\alpha < 1\) and \(\kappa _{2},b_2,\lambda _{2} > 1\). The planned scheme will remain unaffected, however, the system’s fixed-time stability will collapse if these ranges of parameter are ignored. As \(\chi _ i \) is directly related to \(\tau (t)\) in (27, 39), it follows that \(K_i \) is not directly related to \(T_{st2}\) and \(T_{st4}\), respectively. As a result, achieving error convergence in a specified settling time and overall stability of the system requires adjusting \(\chi _i\) to the proper levels. These numbers are crucial since they determine whether or not the system is stable. Because of this familiarity with the parameters’ ranges, an adequate value can be chosen. In this way, picking the right value is actually doable. In addition, this field of research focuses on the robotic manipulator system, which can be affected by other types of frictions and nonlinearities. Therefore, the scope of the work can be significantly expanded in the future [32].

Conclusion

An AFtNTSM has been proposed as a way to improve tracking outcomes for the uncertain robotic manipulator system in the presence of external disturbances. The suggested approach makes use of an adaptive strategy in order to estimate the unknown bounds of uncertain dynamics and external disturbances. With this strategy, the FtNTSM converges within a certain length of time and achieves the targeted tracking performance. The AFtNTSM has been built with unknown dynamics to demonstrate the efficacy of the suggested technique. Findings show that the suggested AFtNTSM strategy outperforms the ATDSMC and AFOSMC methods in terms of response time, tracking error, and the ability to mitigate sources of uncertainty.