Emergency shelter materials under a complex non-linear diophantine fuzzy decision support system

Abstract

The distribution of emergency shelter materials in emergency cases around the world is a hard task, the goal of this research is to offer a Complex Non-linear Diophantine Fuzzy (C-NLDF) decision-making model for earthquake shelter construction. Essentially, the article is divided into three sections to acquire acceptable and precise measures in emergency decision-making situations. First, we present the Complex Non-Linear Diophantine Fuzzy Set (CN-LDFS), a new generalization of the complex linear Diophantine fuzzy set (CLDFS) and q-linear Diophantine fuzzy set (q-LDFS), as well as explore its key aspects. Furthermore, aggregation operators are useful for aggregating uncertainty in decision-making issues. As a result, algebraic norms for CN-LDFSs are produced based on certain operational laws. In the second section of the work, we offer a series of averaging and geometric aggregation operators under CN-LDFS that are based on defined operating laws. In the final section of the work, under complex Non-linear Diophantine fuzzy information, the ranking algorithms based on suggested aggregation operators are present to address the case study regarding emergency situation of earthquakes. In comparison section, results of existing and proposed operators explore the effectiveness of proposed methodologies and provide accurate emergency measures to address the global uncertainty about the construction of emergency shelters in earthquakes.

Introduction

Earthquakes, pandemic, conflicts, and environmental disasters have all caused challenges for architects, planners, designers, and engineers. The purpose is to develop ways to build models and buildings that are more swiftly, simply, and effectively, and that are appropriate for both the circumstances and the place in which they will be used. Those considered “alternative” or unusual—at least in the sense of emergency shelters—might offer enormous chances for experimentation and applicability for emergency buildings when looking for materials that fulfill the requirements for each situation.

Shigeru Ban, a Japanese architect, has worked on buildings for emergency shelters all over the world. He began experimenting with cardboard tubes as a building material in 1986, when he began developing temporary and semi-permanent constructions. His study led him to create pavilions, schools, emergency shelters, and other structures made of this material since. The architect conducted laboratory tests to show that cardboard tubes can withstand 10 megapascals (MPa) when compressed and 15 MPa when bent. In the literature, several work has been presented on the earthquakes pandemic such as [1,2,3].

When all the rules are thought of at the same time, the MCGDM approach involves the evaluation of a restricted number of possibilities and placing them such that they are so trustworthy to decision-maker(s). The rating estimates for each choice in this approach include both exact data and subjective data from experts. However, it is generally assumed that the information they provide is fresh. In any way, the genuine incorporates various MCGDM difficulties where the data is either unclear or questionable in nature due to the unpredictability of the framework step by step. To deal with it, Zadeh [4] proposed the concept of fuzzy set (FS) having membership grade (MG), which showed to be a useful tool for dealing with uncertain and unpredictable information in real-life situations. Many academicians have wondered what would happen if the FS codomain was modified to unit disk instead of real unit interval [0, 1]. So Ramot et al., (2002) [5] proposed the concept of a complex fuzzy set (CFS), which is defined as a complex-valued mapping with a unit circle in the complex plane as the codomain. CFS varies from FS in that its range extends into a unit disk on a complex plane rather than being limited to [0, 1]. The CFS has received considerable attention in the framework of FS theory. A Type-1 fuzzy set, which has been known for fifty years, is an improvement on the idea of an ordinary set. A Type-2 fuzzy set [6, 7], also known as an improvement or extension of a Type-1 fuzzy set and has a degree of membership that is also fuzzy. The three-dimensional membership function of a Type-2 fuzzy set allows new design degrees of freedom to meet larger uncertainty levels. Type-2 fuzzy sets are useful for working with words because it is challenging to identify the appropriate membership function for a fuzzy set. The traditional type-1 fuzzy set has difficulty describing degrees of vagueness, while type-2 fuzzy logic provides this option. For certain fields, the Type-2 fuzzy set is a more effective tool for describing uncertainty in complex problems. The majority of genuine cases are better fit by the symmetric shape of Gaussian functions. This Gaussian feature is used in various fields to explain complex situations in terms of knowledge representation and to address important decision-making issues. As a result, it is hoped that Gaussian Type-2 fuzzy sets will be widely used; yet, due to their complexity, relatively few studies have been published. Similar to this, Castillo et al. use a different notion for their case study of interval type-3 fuzzy aggregations [8,9,10,11,12]

In 1986, Atanassove’s intuitionistic fuzzy set (IFS) [13] was a generalization of FS, which specified the membership and non-membership grades with the requirement that the sum of membership and non-membership grades is less than or equal to one. IFS can assist in dealing with complex and tough data. The human viewpoint is described by IFS as yes or no. The concept of IFS has been employed by several scholars in the context of similarity measures such as [14,15,16,17,18,19,20,21,22,23].

Furthermore, in 2012, Alkouri and Salleh [24] introduced the concept of Complex intuitionistic fuzzy set (CIFS), which is defined by the membership and non-membership grades in the unit circle in the complex plane. Rani and Garg [25] and also [26] recently presented the idea of CIF power aggregation operators, as well as some generalized CIF operators and their implementations in MADM process. Garg and Rani [27] additionally implement a robust correlation coefficient measure of CIFSs and their applications in decision-making.

However, in real-world situations, decision-makers may receive facts where the sum of membership and non-membership grades is larger than one, but the square is less than or equal to one. To address these issues, Yager in 2013 [28] proposed the Pythagorean fuzzy set (PyFS), which proven to be a more powerful tool for dealing with complex situations. Furthermore, IFS is a subset of PyFS. Yager and Abbasov [29] proposed a link between PyFNs and complex numbers based on this hypothesis. To generalize the idea of CIFS, Ullah et al., [30] developed the concept of complex PyFS and extended several distance measurements to take complex PyF values.

As PyFS has fixed many concerns, there are still many cases where PyFS unable to handle the situation. For example, if a decision-maker is given a membership grade (MG) of 0.9 and a non-membership grade (NMG) of 0.6, IFS and PyFS are unable to solve the problem. In 2017, Yager [31] suggested the notion of q-rung orthopair fuzzy set (q-ROFS) for dealing with these kinds of situations, with the restriction that the sum of the q-power of MG and NMG bound between zero and one. q-ROFS essentially combined the concepts of FS, IFS, and PyFS. q-ROFSs have been used by several researchers in a variety of domains, including [32,33,34,35,36]. Garg [37] recently defined and solved the MADM problems using tangential based operational laws and aggregation operators for q-ROFS. To build a decision model, Liu et al. [38] define complex q-ROFS (Cq-ROFS) and Cq-ROF Linguistic set (Cq-ROFLS), as well as various Cq-ROFL Heronian mean (HM) operators.

MG and NMGs are also subject to specific restrictions under the q-ROFS. Riaz and Hashmi [39] (2019) implemented the theory of linear Diophantine fuzzy set (LDFS) in which they included the structure of reference parameters (RPs), in which IFS, PyFS, and q-ROFS cannot manage RPs. In 2021, Kamacı [40] presented the idea of Complex linear Diophantine fuzzy sets (CLDFSs). Many researchers have used the concept of LDFSs in a variety of domains i.e., [41,42,43,44,45].

So, in some real-world situations, the sum of the reference parameters (RPs) obtained by DM is often greater than one, noting that LDFS did not achieve his goal in terms of RPs. The reference parameters have their own constraints in the LDFS. Almagrabi et al. proposed a new extension of LDF, the q-rung linear Diophantine fuzzy set (q-RLDFS), and investigated its important features in [46]. The concept of q-RLDFSs is a novel technique to describe decision-making uncertainty. Because it combines the qth power of RFs or control factors with membership and non-membership grades, q-RLDFS is more versatile and dependable than current ideas, such as IFSs, PyFSs, q-ROFSs, and LDFSs [47]. In this study, we named it Non-linear Diophantine fuzzy sets (N-LDFSs) instead of q-RLDFS because we can freely choose the qth values i.e $q\ge 1.$ In this study, we utilized the complex-valued function for Non-linear Diophantine fuzzy sets (N-LDFSs) and named it complex non-linear Diophantine fuzzy sets (CN-LDFSs) inspired from the above discussion and motivation. As a result, a new method of integrated CN-LDF data is developed. Based on Frank Norms, novel Non-Linear Diophantine Fuzzy Frank (N-LDFF) aggregation operators are established. We noted that there is no complex aggregation operators in the literature for dealing with ambiguity in practical problems using novel N-LDFSs. Following are the main contributions of this work:

• (i) It is the first study that proposes a complex non-linear Diophantine fuzzy (CN-LDF) group decision-making approach that consists of the integrated CN-LDF aggregation operators for effectively evaluating materials for building emergency shelters during emergency situation.

• (ii) To construct a new notion of Complex non-linear Diophantine fuzzy sets (CN-LDFSs) and also construct their operational laws.

• (iii) To create a list of aggregation operators for CN-LDFS and named as CN-LDFWA and CN-LDFWG operators, as well as explain their associated properties.

• (iv) To develop a decision-making (DM) methodology using proposed aggregation operators to aggregate the uncertain information in DM real-world problems.

• (v) To validate the suggested methodology, a numerical case study of a real-life DM problem including the selection of best building shelters in emergency situation.

In brief, within the framework of the above, the contributions of the research are summarized as follows:

Some basic concepts of FS are offered by Sect. 2. Section 3 is about the novel concept of complex Non-Linear Diophantine fuzzy set, their operational laws, and also score and accuracy function. Section 4 provides CN-LDF aggregation operators: CN-LDFWA, CN-LDFOWA, and CN-LDFHWA aggregation operators and also CN-LDFWG, CN-LDFOWG, and CN-LDFHWG and studied some desirable theorem and properties of the proposed operators. Section 5 provides a novel MCGDM problem algorithm under CN-LDF environment. Section 6 addressed the numerical example and a case study regarding to the selection of best building shelters in emergency earthquakes. Section 7 describes an overview comparison of the proposed approach with some existing methods and also advantages of the proposed approach is presented. Section 8 concluded the article.

Following Table 1 represented the detailed description of acronym used in this work. Similarly, Table 2 and summarized all the acronyms and parameters used in this paper.

Table 1 Description of acronyms used in this work

Following Table 2 represented the variables/parameters and their representation and symbols in this work.

Table 2 Representation of variable/parameters used in this work

Preliminaries

We’ll go through the fundamentals of CIFS, CPyFS, Cq-ROFS, and CLDFS in this section. We investigate the essential concepts and properties in order to gain the necessary basic understanding before developing a novel idea of a complex Non-linear Diophantine fuzzy set (CN-LDFS).

Definition 1

[24] A complex intuitionistic fuzzy set (CIFS) I over a fixed set M is defined as:

$$\begin{aligned} I=\{(m,(G_{I}(m),H_{I}(m)):m\in M\}, \end{aligned}$$

(1)

where the membership grade $G_{I}(m)$ and non-membership grade $H_{I}(m)$ defined as

$$\begin{aligned} G_{I}(m)= & {} g_{I}(m).e^{i.2\pi \theta _{g_{I}}(m)}\text { }and\text { }\nonumber \\ H_{I}(m)= & {} h_{I}(m).e^{i.2\pi \xi _{h_{I}}(m)} \end{aligned}$$

(2)

respectively, lie within a unit disk in complex plane with $g_{I}(m),h_{I}(m),\theta _{g_{I}}(m),$ and $\xi _{h_{I}}(m)$ being real valued functions satisfying the condition

$$\begin{aligned} 0\le g_{I}(m)+h_{I}(m)\le 1\text { }and\text { }0\le \theta _{g_{I}}(m)+\xi _{h_{I}}(m)\le 1. \nonumber \\ \end{aligned}$$

(3)

Definition 2

[29] A complex pythagorean fuzzy set (CPyFS) R over a fixed set M is defined as:

$$\begin{aligned} R=\{(m,(G_{R}(m),H_{R}(m)):m\in M\}, \end{aligned}$$

(4)

where

$$\begin{aligned} G_{R}(m)= & {} g_{R}(m).e^{i.2\pi \theta _{g_{R}}(m)}\text { }and\text { }\nonumber \\ H_{R}(m)= & {} h_{R}(m).e^{i.2\pi \xi _{h_{R}}(m)} \end{aligned}$$

(5)

denote complex-valued membership and non-membership grades respectively, satisfying the conditions

$$\begin{aligned} 0\le g_{R}^{2}(m)+h_{R}^{2}(m)\le 1\text { }and\text { }0\le \theta _{g_{R}}^{2}(m)+\xi _{h_{R}}^{2}(m)\le 1. \nonumber \\ \end{aligned}$$

(6)

Definition 3

[38] A complex q-rung orthopair fuzzy set (Cq-ROFS) B over a fixed set M is defined as:

$$\begin{aligned} B=\{(m,(G_{B}(m),H_{B}(m)):m\in M\}, \end{aligned}$$

(7)

where

$$\begin{aligned} G_{B}(m)= & {} g_{B}(m).e^{i.2\pi \theta _{g_{B}}(m)}\text { }and\text { }\nonumber \\ H_{B}(m)= & {} h_{B}(m).e^{i.2\pi \xi _{h_{B}}(m)} \end{aligned}$$

(8)

denote complex-valued membership and non-membership grades respectively, satisfying the conditions

$$\begin{aligned} 0\le g_{B}^{q}(m)+h_{B}^{q}(m)\le 1\text { }and\text { }0\le \theta _{g_{B}}^{q}(m)+\xi _{h_{B}}^{q}(m)\le 1. \nonumber \\ \end{aligned}$$

(9)

Definition 4

[39] A linear Diophantine fuzzy set (LDFS) C over a non-empty reference set M is defined as:

$$\begin{aligned} C=\{(m,\left\langle G_{C}(m),H_{C}(m)\right\rangle ,\left\langle \alpha ,\beta \right\rangle ):m\in M\} \end{aligned}$$

(10)

where $G_{C}(m),H_{C}(m),\alpha ,\beta \in [0,1]$ denoted MG, NMG and RPs respectively and satisfy the restriction;

$$\begin{aligned}{} & {} 0 \le (\alpha )G_{C}(m)+(\beta )H_{C}(m)\le 1\forall m\in M, \nonumber \\{} & {} \text {with }0 \le \alpha +\beta \le 1. \end{aligned}$$

(11)

Definition 5

[40] A complex linear Diophantine fuzzy set (CLDFS) L over a non-empty reference set M is defined as:

$$\begin{aligned} L=\{(m,\left\langle G_{L}(m),H_{L}(m)\right\rangle ,\left\langle \alpha _{L},\beta _{L}\right\rangle ):m\in M\} \end{aligned}$$

(12)

also as;

$$\begin{aligned} L= & {} \bigg \{(m,\left\langle g_{L}(m)e^{i.2\pi \theta _{g_{L}}(m)},h_{L}(m)e^{i.2\pi \xi _{h_{L}}(m)}\right\rangle ,\nonumber \\{} & {} \left\langle \alpha _{L},\beta _{L}\right\rangle ):m\in M\bigg \} \end{aligned}$$

(13)

where $g_{L}(m)e^{i.2\pi \theta _{g_{L}}(m)}$ and $h_{L}(m)e^{i.2\pi \xi _{h_{L}}(m)}$ denoted complex-valued membership and non-membership grades and $\alpha _{L},\beta _{L}$ denoted the reference parameters respectively, such that $g_{L}(m),h_{L}(m),\alpha _{L},\beta _{L},\theta _{g_{L}}(m),\xi _{h_{L}}(m)\in [0,1]$ and $0\le \alpha _{L}+\beta _{L}\le 1$, satisfying

$$\begin{aligned} 0\le & {} g_{L}(m)\alpha _{L}+h_{L}(m)\beta _{L}\le 1\text { }and\text { }\nonumber \\ 0\le & {} \theta _{g_{L}}(m)\alpha _{L}+\xi _{h_{L}}(m)\beta _{L}\le 1. \end{aligned}$$

(14)

Definition 6

[46] A q-rung linear Diophantine fuzzy set (q-RLDFS) S over a non-empty reference set M is defined as:

$$\begin{aligned} S=\{(m,\left\langle G_{S}(m),H_{S}(m)\right\rangle ,\left\langle \alpha ,\beta \right\rangle ):m\in M\} \end{aligned}$$

(15)

where $G_{S}(m),H_{S}(m),\alpha ,\beta \in [0,1]$ denoted MG, NMG and RPs respectively and satisfy the restriction;

$$\begin{aligned}{} & {} 0 \le (\alpha )^{q}G_{C}(m)+(\beta )^{q}H_{C}(m)\le 1\forall m\in M,q\geqslant 1 \nonumber \\{} & {} \text {with }0 \le \alpha ^{q}+\beta ^{q}\le 1,q\ge 1. \end{aligned}$$

(16)

Complex non-linear diophantine fuzzy set (CN-LDFS)

The concept of a complex Non-linear Diophantine fuzzy set (CN-LDFS) is introduced in this section. In number theory, the proposed model is similar to the well-known linear Diophantine equation $ax+by=c$, but here we generalized this concept by addition of the qth power on reference parameters. Because membership and non-membership grades are limited in CIFSs, CPyFSs, and Cq-ROFSs, and in CLDFS, the reference parameters are limited. We offer the notion of CN-LDFS with the addition of qth power on reference parameters to overcome these restrictions. This concept eliminates the limits on membership/non-membership grades and reference parameters, allowing the decision-maker (DM) to choose the desired functions without restriction. Now we introduce the concept of complex Non-linear Diophantine fuzzy set (CN-LDFS) as follows:

Definition 7

A complex Non-linear Diophantine fuzzy set (CN-LDFS) L over a non-empty reference set M is defined as:

$$\begin{aligned} A=\{(m,\left\langle G_{A}(m),H_{A}(m)\right\rangle ,\left\langle \alpha _{A},\beta _{A}\right\rangle ):m\in M\} \end{aligned}$$

(17)

also as;

$$\begin{aligned} A= & {} \bigg \{(m,\left\langle g_{A}(m)e^{i.2\pi \theta _{g_{A}}(m)},h_{L}(m)e^{i.2\pi \xi _{h_{A}}(m)}\right\rangle ,\nonumber \\{} & {} \left\langle \alpha _{L}e^{i.2\pi \varphi _{\alpha _{A}}},\beta _{L}e^{i.2\pi \eta _{\beta _{A}}}\right\rangle ):m\in M\bigg \} \end{aligned}$$

(18)

where $g_{A}(m)e^{i.2\pi \theta _{g_{A}}(m)}$, $h_{A}(m)e^{i.2\pi \xi _{h_{A}}(m)},$ $\alpha _{A}e^{i.2\pi \varphi _{\alpha _{A}}}$ and $\beta _{A}e^{i.2\pi \eta _{\beta _{A}}}$ denoted complex valued membership, non-me mbership grades and reference parameters respectively, such that $g_{A}(m),h_{A}(m),\alpha _{A},\beta _{A},\theta _{g_{A}}(m),\xi _{h_{A}}(m),\varphi _{\alpha _{A}},\eta _{\beta _{A}}\in [0,1]$ and $0\le \alpha _{A}^{q}+\beta _{A}^{q}\le 1$, satisfying

$$\begin{aligned} 0\le & {} g_{A}(m)\alpha _{A}^{q}+h_{A}(m)\beta _{A}^{q}\le 1\text { and }\nonumber \\ 0\le & {} \theta _{g_{A}}(m)\varphi _{\alpha _{A}}^{q}+\xi _{h_{A}}(m)\eta _{\beta _{A}}^{q}\le 1. \end{aligned}$$

(19)

Operational laws of complex non-linear diophantine fuzzy set (CN-LDFS)

In this section, we define the operational laws of complex numbers for two non-linear Diophantine fuzzy numbers, and then some basic proposition for CN-LDFSs are defined—

Definition 8

Let $U_{j}{=}\left\{ \! \begin{array}{c} \left\langle \left[ g_{j}\right] .e^{i2\pi \left[ \theta _{g_{j}}\right] }, \left[ h_{j}\right] .e^{i2\pi \left[ \xi _{h_{j}}\right] }\right\rangle , \\ \left\langle \left[ \alpha _{j}\right] .e^{i2\pi \left[ \varphi _{\alpha _{j}}\right] },\left[ \beta _{j}\right] .e^{i2\pi \left[ \eta _{\beta _{j}} \right] }\right\rangle \end{array} \!\!\right\} , j=1,2,3$ be any three CN-LDFNs, $q\ge 1,$ $K>0.$ Then, we define some basic operations of CN-LDFNs as follow—

$$\begin{aligned}{} & {} (i)\text { }U_{j}^{c}=\left( \begin{array}{c} \left\langle \left[ h_{j}\right] .e^{i2\pi \left[ \xi _{h_{j}}\right] }, \left[ g_{j}\right] .e^{i2\pi \left[ \theta _{g_{j}}\right] }\right\rangle , \\ \left\langle \left[ \beta _{j}\right] .e^{i2\pi \left[ \eta _{\beta _{j}} \right] },\left[ \alpha _{j}\right] .e^{i2\pi \left[ \varphi _{\alpha _{j}} \right] }\right\rangle \end{array} \right) \end{aligned}$$

(20)

$$\begin{aligned}{} & {} (ii)\text { }U_{1}\oplus U_{2}\nonumber \\{} & {} \quad {=}\left[ \begin{array}{c} \left( \begin{array}{c} \left[ \root q \of {g_{1}^{q}{+}g_{2}^{q}-g_{1}^{q}g_{2}^{q}}\right] .e^{i2\pi \left[ \root q \of {\theta _{g_{1}}^{q}{+}\theta _{g_{2}}^{q}{-}\theta _{g_{1}}^{q}\theta _{g_{2}}^{q}}\right] }, \\ \left[ h_{1}h_{2}\right] .e^{i2\pi \left[ \xi _{h_{1}}\xi _{h_{2}}\right] } \end{array} \right) , \\ \left( \begin{array}{c} \left[ \root q \of {\alpha _{1}^{q}{+}\alpha _{2}^{q}{-}\alpha _{1}^{q}\alpha _{2}^{q}}\right] .e^{i2\pi \left[ \root q \of {\varphi _{\alpha _{1}}^{q}{+}\varphi _{\alpha _{2}}^{q}{-}\varphi _{\alpha _{1}}^{q}\varphi _{\alpha _{2}}^{q}}\right] }, \\ \left[ \beta _{1}\beta _{2}\right] .e^{i2\pi \left[ \eta _{\beta _{1}}\eta _{\beta _{2}}\right] } \end{array} \right) \end{array} \right] \nonumber \\ \end{aligned}$$

(21)

$$\begin{aligned}{} & {} (iii)\text { }U_{1}\otimes U_{2}\nonumber \\{} & {} \quad =\left[ \begin{array}{c} \left( \begin{array}{c} \left[ g_{1}g_{2}\right] .e^{i2\pi \left[ \theta _{g_{1}}\theta _{g_{2}} \right] }, \\ \left[ \root q \of {h_{1}^{q}+h_{2}^{q}-h_{1}^{q}h_{2}^{q}}\right] .e^{i2\pi \left[ \root q \of {\xi _{h_{1}}^{q}+\xi _{h_{2}}^{q}-\xi _{h_{1}}^{q}\xi _{h_{2}}^{q}}\right] } \end{array} \right) , \\ \left( \begin{array}{c} \left[ \alpha _{1}\alpha _{2}\right] .e^{i2\pi \left[ \varphi _{\alpha _{1}}\varphi _{\alpha _{2}}\right] }, \\ \left[ \root q \of {\beta _{1}^{q}+\beta _{2}^{q}-\beta _{1}^{q}\beta _{2}^{q}} \right] .e^{i2\pi \left[ \root q \of {\eta _{\beta _{1}}^{q}+\eta _{\beta _{2}}^{q}-\eta _{\beta _{1}}^{q}\eta _{\beta _{2}}^{q}}\right] } \end{array} \right) \end{array} \right] \nonumber \\ \end{aligned}$$

(22)

$$\begin{aligned}{} & {} (iv)\text { }k.U\nonumber \\{} & {} \quad {=}\left[ \begin{array}{c} \left( \left[ \root q \of {\left( 1{-}\left( 1{-}g^{q}\right) ^{k}\right) }\right] .e^{i2\pi \left[ \root q \of {\left( 1{-}\left( 1{-}\theta _{g}^{q}\right) ^{k}\right) }\right] },\left[ h^{k}\right] .e^{i2\pi \left[ \xi _{h}^{k} \right] }\right) , \\ \left( \left[ \root q \of {\left( 1{-}\left( 1{-}\alpha ^{q}\right) ^{k}\right) } \right] .e^{i2\pi \left[ \root q \of {\left( 1{-}\left( 1{-}\varphi _{\alpha }^{q}\right) ^{k}\right) }\right] },\left[ \beta ^{k}\right] .e^{i2\pi \left[ \eta _{\beta }^{k}\right] }\right) \end{array} \right] \nonumber \\ \end{aligned}$$

(23)

$$\begin{aligned}{} & {} (v)\text { }U^{K}\nonumber \\{} & {} \quad {=}\left[ \begin{array}{c} \left( \left[ g^{k}\right] .e^{i2\pi \left[ \theta _{g}^{k}\right] },\left[ \root q \of {\left( 1{-}\left( 1{-}h^{q}\right) ^{k}\right) }\right] .e^{i2\pi \left[ \root q \of {\left( 1{-}\left( 1{-}\xi _{h}^{q}\right) ^{k}\right) }\right] }\right) , \\ \left( \left[ \alpha ^{k}\right] .e^{i2\pi \left[ \varphi _{\alpha }^{k} \right] },\left[ \root q \of {\left( 1{-}\left( 1{-}\beta ^{q}\right) ^{k}\right) } \right] .e^{i2\pi \left[ \root q \of {\left( 1{-}\left( 1{-}\eta _{\beta }^{q}\right) ^{k}\right) }\right] }\right) \end{array} \right] \nonumber \\ \end{aligned}$$

(24)

$$\begin{aligned}{} & {} (vi)\text { }U_{1}\vee U_{2}\nonumber \\{} & {} \quad =\left\{ \begin{array}{c} \left\langle \begin{array}{c} \max \left[ g_{1},g_{2}\right] .e^{i2\pi \max \left[ \theta _{g_{1}},\theta _{g_{2}}\right] }, \\ \min \left[ h_{1},h_{2}\right] .e^{i2\pi \min \left[ \xi _{h_{1}},\xi _{h_{2}}\right] } \end{array} \right\rangle , \\ \left\langle \begin{array}{c} \max \left[ \alpha _{1},\alpha _{2}\right] .e^{i2\pi \max \left[ \varphi _{\alpha _{1}},\varphi _{\alpha _{2}}\right] }, \\ \min \left[ \beta _{1},\beta _{2}\right] .e^{i2\pi \min \left[ \eta _{\beta _{1}},\eta _{\beta _{2}}\right] } \end{array} \right\rangle \end{array} \right\} \end{aligned}$$

(25)

$$\begin{aligned}{} & {} (vii)\text { }U_{1}\wedge U_{2}\nonumber \\{} & {} \quad =\left\{ \begin{array}{c} \left\langle \begin{array}{c} \min \left[ g_{1},g_{2}\right] .e^{i2\pi \min \left[ \theta _{g_{1}},\theta _{g_{2}}\right] }, \\ \max \left[ h_{1},h_{2}\right] .e^{i2\pi \max \left[ \xi _{h_{1}},\xi _{h_{2}}\right] } \end{array} \right\rangle , \\ \left\langle \begin{array}{c} \min \left[ \alpha _{1},\alpha _{2}\right] .e^{i2\pi \min \left[ \varphi _{\alpha _{1}},\varphi _{\alpha _{2}}\right] }, \\ \max \left[ \beta _{1},\beta _{2}\right] .e^{i2\pi \max \left[ \eta _{\beta _{1}},\eta _{\beta _{2}}\right] } \end{array} \right\rangle \end{array} \right\} \end{aligned}$$

(26)

Proposition 1

Suppose we have three CN-LDFNs—

$U_{j}=\left\{ \left\langle \left[ g_{j}\right] .e^{i2\pi \left[ \theta _{g_{j}}\right] },\left[ h_{j}\right] .e^{i2\pi \left[ \xi _{h_{j}}\right] }\right\rangle ,\left\langle \left[ \alpha _{j}\right] .e^{i2\pi \left[ \varphi _{\alpha _{j}}\right] },\right. \right.$ $\left. \left. \left[ \beta _{j}\right] .e^{i2\pi \left[ \eta _{\beta _{j}}\right] }\right\rangle \right\} ,j=1,2,3$ then the following properties are satisfied;

• (1) $U_{1}\subseteq U_{2}$ and $U_{2}\subseteq U_{3}$ then $U_{1}\subseteq U_{3}$

• (2) $U_{1}\cup U_{2}=U_{2}\cup U_{1}$

• (3) $U_{1}\cap U_{2}=U_{1}\cap U_{2}$

• (4) $U_{1}\cup (U_{2}\cup U_{3})=(U_{1}\cup U_{2})\cup U_{3}$

• (5) $U_{1}\cap (U_{2}\cap U_{3})=(U_{1}\cap U_{2})\cap U_{3}$

• (6) $U_{1}\cup (U_{2}\cap U_{3})=(U_{1}\cup U_{2})\cap (U_{1}\cup U_{3})$

• (7) $U_{1}\cap (U_{2}\cup U_{3})=(U_{1}\cap U_{2})\cup (U_{1}\cap U_{3})$

• (8) $(U_{1}\cup U_{2})^{c}=U_{1}^{c}\cap U_{2}^{c}$

• (9) $(U_{1}\cap U_{2})^{c}=U_{1}^{c}\cup U_{2}^{c}$

Proof

Proof of the above statements are obvious. $\square$

Score and accuracy functions for CN-LDFN

Definition 9

Suppose M be a nonempty reference set. For any CN-LDFNS $U=\left\{ \left\langle \left[ g\right] .e^{i2\pi \left[ \theta _{g}\right] }, \left[ h\right] .e^{i2\pi \left[ \xi _{h}\right] }\right\rangle , \left\langle \left[ \alpha \right] .\right. \right.$$\left. \left. e^{i2\pi \left[ \varphi _{\alpha } \right] },\left[ \beta \right] .e^{i2\pi \left[ \eta _{\beta }\right] }\right\rangle \right\} \in$ $CN-LDFN$, the score function (ScF) of U can be defined by the mapping $Sc:CN-LDFN(M)\longrightarrow [-1,1]$; and given as

$$\begin{aligned} Sc(U)=\left[ \frac{(g(\theta _{g})-h(\xi _{h}))+(\alpha ^{q}(\varphi _{\alpha }^{q})-\beta ^{q}(\eta _{\beta }^{q})}{2}\right] ;q\ge 1 \nonumber \\ \end{aligned}$$

(27)

Definition 10

Suppose M be a nonempty reference set. For any CN-LDFNS $U=\left\{ \left\langle \left[ g\right] .e^{i2\pi \left[ \theta _{g}\right] },\left[ h \right] .e^{i2\pi \left[ \xi _{h}\right] }\right\rangle ,\left\langle \left[ \alpha \right] .\right. \right.$ $\left. \left. e^{i2\pi \left[ \varphi _{\alpha }\right] },\left[ \beta \right] .e^{i2\pi \left[ \eta _{\beta }\right] }\right\rangle \right\} \in$ $CN-LDFN$, the Accuracy Function (AcF) of U can be defined by the mapping $Ac:CN-LDFN(M)\longrightarrow [0,1]$; and given as

$$\begin{aligned} Ac(U)=\left[ \frac{g(\theta _{g})+h(\xi _{h})+\alpha ^{q}(\varphi _{\alpha }^{q})+\beta ^{q}(\eta _{\beta }^{q})}{2}\right] ;q\ge 1 \nonumber \\ \end{aligned}$$

(28)

Definition 11

Let $U_{1}$ and $U_{2}$ be two $CN-LDFNs$. Then, using the ScF, the two $CN-LDFNs$ can be easily compared as:

• (i) if $Sc(U_{1})<Sc(U_{2}),$ then $U_{1}<U_{2}$

• (ii) if $Sc(U_{1})>Sc(U_{2}),$ then $U_{1}>U_{2}$

• (iii) if $Sc(U_{1})=Sc(U_{2}),$ then

  • (a) if $Ac(U_{1})<Ac(U_{2}),$ then $U_{1}<U_{2}$

  • (b) if $Ac(U_{1})=Ac(U_{2}),$ then $U_{1}=U_{2},$

Complex non-linear diophantine fuzzy aggregation operators

Throughout this section, we propose the novel aggregation operators based on complex Non-linear Diophantine Fuzzy environments.

Complex non-linear diophantine fuzzy weighted averaging ($CN-LDFWA$) aggregation operator

Throughout this part, we have defined complex non-linear Diophantine fuzzy weighted averaging aggregation operators i.e., CN-LDFWA, CN-LDFOWA and CN-LDFHWA aggregation operators.

Definition 12

Let $U_{j}{=}\!\left\{ \!\! \begin{array}{c} \left\langle \left[ g_{j}\right] .e^{i2\pi \left[ \theta _{g_{j}}\right] }, \left[ h_{j}\right] .e^{i2\pi \left[ \xi _{h_{j}}\right] }\right\rangle , \\ \left\langle \left[ \alpha _{j}\right] .e^{i2\pi \left[ \varphi _{\alpha _{j}}\right] },\left[ \beta _{j}\right] .e^{i2\pi \left[ \eta _{\beta _{j}} \right] }\right\rangle \end{array} \!\!\right\} \!:j=1,2,...n$ be a family of CN-LDFNs over a non-empty reference set M and $\Omega =(\Omega _{1},\Omega _{2},\ldots ,\Omega _{n})^{T}$ is the weight with $\sum \nolimits _{j=1}^{n}\Omega _{j}=1,$ and $q\ge 1;$ then we define the complex non-Linear Diophantine fuzzy weighted averaging (CN-LDFWA) operator as follows and let the transformation $\chi :CN-LDFN(M)\longrightarrow CN-LDFN(M)$

$$\begin{aligned}{} & {} CN-LDFWA(U_{1},U_{2},U_{3},...,U_{n}) \nonumber \\{} & {} \quad =\bigoplus \nolimits _{j=1}^{n}(U_{j}^{\Omega _{j}})=U_{1}^{\Omega _{1}}\oplus U_{2}^{\Omega _{2}}\oplus U_{3}^{\Omega _{3}}\oplus ...\oplus U_{n}^{\Omega _{n}}. \end{aligned}$$

(29)

In CN-LDFWA operator, g denotes MG and h denotes NMG, $\alpha ,\beta$ denotes the RPs and $q\ge 1.$ Weights are represented by $\Omega$, $U_{ {\mathbb {N}} }$ denoted CN-LDFNs, $j\in {\mathbb {N}}$ and CN-LDFN(M) combines all CN-LDFNs.

Theorem 2

Let $U_{j}{=}\left\{ \!\! \begin{array}{c} \left\langle \left[ g_{j}\right] .e^{i2\pi \left[ \theta _{g_{j}}\right] }, \left[ h_{j}\right] .e^{i2\pi \left[ \xi _{h_{j}}\right] }\right\rangle , \\ \left\langle \left[ \alpha _{j}\right] .e^{i2\pi \left[ \varphi _{\alpha _{j}}\right] },\left[ \beta _{j}\right] .e^{i2\pi \left[ \eta _{\beta _{j}} \right] }\right\rangle \end{array} \!\right\} \!:j=1,2,...n$ be a family of CN-LDFNs over a non-empty reference set M and $\Omega =(\Omega _{1},\Omega _{2},...,\Omega _{n})^{T}$ is the weight with $\sum \nolimits _{j=1}^{n}\Omega _{j}=1,$ and $q\ge 1;$ then by applying the CN-LDFWA operator, their aggregated value is also an CN-LDFN, and the transformation $\chi :CN-LDFN(M)\longrightarrow CN-LDFN(M)$ is called CN-LDFWA operator and defined as—

$$\begin{aligned}{} & {} \!\!\!CN-LDFWA(U_{1},U_{2},U_{3},...,U_{n})=\bigoplus \nolimits _{j=1}^{n}U_{j}^{ \Omega _{j}} \nonumber \\{} & {} \quad {=}\!\left( \! \begin{array}{c} \left\langle \begin{array}{c} \left( \root q \of {\left( 1{-}\prod \limits _{j=1}^{n}(1{-}g_{j}^{q})^{\Omega _{j}}\right) .}e^{i2\pi \left[ \root q \of {\left( 1{-}\prod \limits _{j=1}^{n}(1{-}\theta _{g_{j}}^{q})^{\Omega _{j}}\right) }\right] }\right) , \\ \left( \prod \limits _{j=1}^{n}(h_{j})^{\Omega _{j}}.e^{i2\pi \left[ \prod \limits _{j=1}^{n}(\xi _{hj})^{\Omega _{j}}\right] }\right) \end{array} \right\rangle , \\ \left\langle \begin{array}{c} \left( \root q \of {\left( 1{-}\prod \limits _{j=1}^{n}(1{-}\alpha _{j}^{q})^{\Omega _{j}}\right) .}e^{i2\pi \left[ \root q \of {\left( 1{-}\prod \limits _{j=1}^{n}(1{-}\varphi _{\alpha _{j}}^{q})^{\Omega _{j}}\right) } \right] }\right) , \\ \left( \prod \limits _{j=1}^{n}(\beta _{j})^{\Omega _{j}}.e^{i2\pi \left[ \prod \limits _{j=1}^{n}(\eta _{\beta j})^{\Omega _{j}}\right] }\right) \end{array} \right\rangle \end{array} \!\right) ,\nonumber \\{} & {} \qquad q\ge 1. \end{aligned}$$

(30)

Theorem 3

(Idempotency). If $U_{j}=$$\left\{ \begin{array}{c} \left\langle \left[ g_{j}\right] .e^{i2\pi \left[ \theta _{g_{j}}\right] }, \left[ h_{j}\right] .e^{i2\pi \left[ \xi _{h_{j}}\right] }\right\rangle , \\ \left\langle \left[ \alpha _{j}\right] .e^{i2\pi \left[ \varphi _{\alpha _{j}}\right] },\left[ \beta _{j}\right] .e^{i2\pi \left[ \eta _{\beta _{j}} \right] }\right\rangle \end{array} \right\} :j=1,2,...n$ are equal i.e., $U_{j}=$$U=\left. \left\{ \begin{array}{c} \left\langle \left[ g\right] .e^{i2\pi \left[ \theta _{g}\right] },\left[ h \right] .e^{i2\pi \left[ \xi _{h}\right] }\right\rangle , \\ \left\langle \left[ \alpha \right] .e^{i2\pi \left[ \varphi _{\alpha }\right] },\left[ \beta \right] .e^{i2\pi \left[ \eta _{\beta }\right] }\right\rangle \end{array} \right\} \right\}$ then

$$\begin{aligned} CN-LDFWA(U_{1},U_{2},...,U_{n})=U \end{aligned}$$

(31)

Theorem 4

(Boundedness). Let $U_{j}$$=\left\{ \begin{array}{c} \left\langle \left[ g_{j}\right] .e^{i2\pi \left[ \theta _{g_{j}}\right] }, \left[ h_{j}\right] .e^{i2\pi \left[ \xi _{h_{j}}\right] }\right\rangle , \\ \left\langle \left[ \alpha _{j}\right] .e^{i2\pi \left[ \varphi _{\alpha _{j}}\right] },\left[ \beta _{j}\right] .e^{i2\pi \left[ \eta _{\beta _{j}} \right] }\right\rangle \end{array} \right\} :j\in {\mathbb {N}}$ be a family of CN-LDFNs, and consider $U^{-}=\min \nolimits _{j}U_{j},$ $U^{+}=\max \nolimits _{j}U_{j},$ then

$$\begin{aligned} U^{-}\le CN-LDFWA_{\Omega }(U_{1},U_{2},...,U_{n})\le U^{+} \end{aligned}$$

(32)

Theorem 5

(Monotonicity). Let $U_{j}(j\in {\mathbb {N}} )$ and $U_{j}^{*}(j\in {\mathbb {N}} )$ be two set of CN-LDFNs, if $U_{j}\le U_{j}^{*},\forall$ j,  then

$$\begin{aligned}{} & {} CN-LDFWA_{\Omega }(U_{1},U_{2},...,U_{n})\nonumber \\{} & {} \quad \le CN-LDFWA_{\Omega }(U_{1}^{*},U_{2}^{*},...,U_{n}^{*}) \end{aligned}$$

(33)

Furthermore, we shall develop the complex non-linear Diophantine fuzzy ordered weighted averaging (CN-LDF OWA) operator.

Definition 13

Let $U_{j}{=}\!\left\{ \! \begin{array}{c} \left\langle \left[ g_{j}\right] .e^{i2\pi \left[ \theta _{g_{j}}\right] }, \left[ h_{j}\right] .e^{i2\pi \left[ \xi _{h_{j}}\right] }\right\rangle , \\ \left\langle \left[ \alpha _{j}\right] .e^{i2\pi \left[ \varphi _{\alpha _{j}}\right] },\left[ \beta _{j}\right] .e^{i2\pi \left[ \eta _{\beta _{j}} \right] }\right\rangle \end{array} \!\!\right\} \!:j=1,2,...n\}$ be a family of CN-LDFNs over a non-empty reference set M and $\Omega =(\Omega _{1},\Omega _{2},...,\Omega _{n})^{T}$ is the weight with $\sum \nolimits _{j=1}^{n}\Omega _{j}=1,$ and $q\ge 1;$ then by applying the CN-LDFOWA operator their aggregated value is also an CN-LDFN, and the transformation $\chi :CN-LDFN(M)\longrightarrow CN-LDFN(M)$ is called CN-LDFOWA operator and defined as;

$$\begin{aligned}{} & {} CN-LDFOWA(U_{1},U_{2},U_{3},...,U_{n}) \nonumber \\{} & {} \quad =\bigoplus \nolimits _{j=1}^{n}(U_{(\delta )j})^{\Omega _{j}}=U_{(\delta )1}^{\Omega _{1}}\oplus U_{(\delta )2}^{\Omega _{2}}\oplus U_{(\delta )3}^{\Omega _{3}}\oplus ...\oplus U_{(\delta )n}^{\Omega _{n}}.\nonumber \\ \end{aligned}$$

(34)

where the arrangement of $(j\in {\mathbb {N}} )$ is $(\delta (1),$ $\delta (2),$ $\delta (3),$ ...,  $\delta (n))$, for which $U_{\delta (j=1)}\ge U_{\delta (j)}\forall (j\in {\mathbb {N}} ).$

Theorem 6

Let $U_{j}{=}\!\left\{ \! \begin{array}{c} \left\langle \left[ g_{j}\right] .e^{i2\pi \left[ \theta _{g_{j}}\right] }, \left[ h_{j}\right] .e^{i2\pi \left[ \xi _{h_{j}}\right] }\right\rangle , \\ \left\langle \left[ \alpha _{j}\right] .e^{i2\pi \left[ \varphi _{\alpha _{j}}\right] },\left[ \beta _{j}\right] .e^{i2\pi \left[ \eta _{\beta _{j}} \right] }\right\rangle \end{array} \!\!\right\} \!:j=1,2,...n$ be a family of CN-LDFNs over a non-empty reference set M and $\Omega =(\Omega _{1},\Omega _{2},...,\Omega _{n})^{T}$ is the weight with $\sum \nolimits _{j=1}^{n}\Omega _{j}=1,$ and $q\ge 1;$ by applying the CN-LDFOWA operator their aggregated value is also CN-LDFN, and the transformation $\chi :CN-LDFN(M)\longrightarrow CN-LDFN(M)$ are known as CN-LDFOWA operator and defined as;

$$\begin{aligned}{} & {} \!\!\!CN-LDFOWA(U_{1},U_{2},U_{3},...,U_{n})=\bigoplus \limits _{j=1}^{n}(U_{(\delta )j})^{\Omega _{j}} \nonumber \\{} & {} \quad {=}\!\left( \! \begin{array}{c} \left\langle \begin{array}{c} \left( \root q \of {\left( 1{-}\prod \limits _{j=1}^{n}(1{-}g_{(\delta )j}^{q})^{\Omega _{j}}\right) .}e^{i2\pi \left[ \root q \of {\left( 1{-}\prod \limits _{j=1}^{n}(1{-}\theta _{g_{(\delta )j}}^{q})^{\Omega _{j}}\right) }\right] }\right) , \\ \left( \prod \limits _{j=1}^{n}(h_{(\delta )j})^{\Omega _{j}}.e^{i2\pi \left[ \prod \limits _{j=1}^{n}(\xi _{h(\delta )j})^{\Omega _{j}}\right] }\right) \end{array} \right\rangle , \\ \left\langle \begin{array}{c} \left( \root q \of {\left( 1{-}\prod \limits _{j=1}^{n}(1{-}\alpha _{(\delta )j}^{q})^{\Omega _{j}}\right) .}e^{i2\pi \left[ \root q \of {\left( 1{-}\prod \limits _{j=1}^{n}(1{-}\varphi _{\alpha _{(\delta )j}}^{q})^{\Omega _{j}}\right) }\right] }\right) , \\ \left( \prod \limits _{j=1}^{n}(\beta _{(\delta )j})^{\Omega _{j}}.e^{i2\pi \left[ \prod \limits _{j=1}^{n}(\eta _{\beta (\delta )j})^{\Omega _{j}}\right] }\right) \end{array} \right\rangle \end{array} \!\right) ,\nonumber \\{} & {} \qquad q\ge 1. \end{aligned}$$

(35)

where the arrangement of $(j\in {\mathbb {N}} )$ is $(\delta (1),$ $\delta (2),$ $\delta (3),$ ...,  $\delta (n))$, for which $U_{\delta (j=1)}\ge U_{\delta (j)}\forall (j\in {\mathbb {N}} ).$

Above we defined CN-LDFWA and CN-LDFOWA operators, next we are going to establish CN-LDFHWA aggregation operator.

Definition 14

Let $U_{j}{=}\!\left\{ \! \begin{array}{c} \left\langle \left[ g_{j}\right] .e^{i2\pi \left[ \theta _{g_{j}}\right] }, \left[ h_{j}\right] .e^{i2\pi \left[ \xi _{h_{j}}\right] }\right\rangle , \\ \left\langle \left[ \alpha _{j}\right] .e^{i2\pi \left[ \varphi _{\alpha _{j}}\right] },\left[ \beta _{j}\right] .e^{i2\pi \left[ \eta _{\beta _{j}} \right] }\right\rangle \end{array} \!\right\} \!:j\in {\mathbb {N}}$ be a family of CN-LDFNs over a non-empty reference set M and $\Omega =(\Omega _{1},\Omega _{2},...,\Omega _{n})^{T}$ are the weight with $\sum \nolimits _{j=1}^{n}\Omega _{j}=1,$ also $q\ge 1;$ then we define the Complex Non-Linear Diophantine fuzzy hybrid weighted averaging (CN-LDFHWA) operator as follows and let the mapping $\chi :N-LDFN(M)\longrightarrow N-LDFN(M)$

$$\begin{aligned}{} & {} CN-LDFHWA(U_{1},U_{2},U_{3},...,U_{n}) \nonumber \\{} & {} \quad =\bigoplus \limits _{j=1}^{n}(U_{(\delta )j}^{\star })^{\Omega _{j}}=(U_{(\delta )1}^{\star })^{\Omega _{1}}\oplus (U_{(\delta )2}^{\star })^{\Omega _{2}}\nonumber \\{} & {} \qquad \oplus (U_{(\delta )3}^{\star })^{\Omega _{3}}\oplus ...\oplus (U_{(\delta )n}^{\star })^{\Omega _{n}}. \end{aligned}$$

(36)

where $U_{\delta (j)}^{\star }$ is the jth largest weighted N-LDF values $U_{i}^{\star }(U_{j}^{\star }=(U_{j})^{n\Omega _{j}},j\in {\mathbb {N}} )$ and the weights of $U_{j}^{\star }$ are $\Omega =(\Omega _{1},\Omega _{2},...,\Omega _{n})^{T}$ by mean of $\Omega _{j}>0$ with $\sum \nolimits _{j=1}^{n}\Omega _{j}=1.$

Theorem 7

Let $U_{j}{=}\!\left\{ \! \begin{array}{c} \left\langle \left[ g_{j}\right] .e^{i2\pi \left[ \theta _{g_{j}}\right] }, \left[ h_{j}\right] .e^{i2\pi \left[ \xi _{h_{j}}\right] }\right\rangle , \\ \left\langle \left[ \alpha _{j}\right] .e^{i2\pi \left[ \varphi _{\alpha _{j}}\right] },\left[ \beta _{j}\right] .e^{i2\pi \left[ \eta _{\beta _{j}} \right] }\right\rangle \end{array} \!\right\} \!:j\in {\mathbb {N}}$ be a family of CN-LDFNs over a non-empty reference set M and $\Omega =(\Omega _{1},\Omega _{2},...,\Omega _{n})^{T}$ is the weight with $\sum \nolimits _{j=1}^{n}\Omega _{j}=1,$ also $q\ge 1;$ by applying the CN-LDFHWA operator their aggregated value is also an CN-LDFN, and the transformation $\chi :N-LDFN(M)\longrightarrow N-LDFN(M)$ are known as CN-LDFHWA and defined as—

$$\begin{aligned}{} & {} \!\!\!CN-LDFHWA(U_{1},U_{2},U_{3},...,U_{n})=\bigoplus \limits _{j=1}^{n}(U_{(\delta )j}^{\star })^{\Omega _{j}} \nonumber \\{} & {} \quad {=}\left( \begin{array}{c} \left\langle \begin{array}{c} \left( \root q \of {\left( 1{-}\prod \limits _{j=1}^{n}(1{-}g_{(\delta )j}^{\star q})^{\Omega _{j}}\right) .}e^{i2\pi \left[ \root q \of {\left( 1{-}\prod \limits _{j=1}^{n}(1{-}\theta _{g_{(\delta )j}}^{\star q})^{\Omega _{j}}\right) }\right] }\right) , \\ \left( \prod \limits _{j=1}^{n}(h_{(\delta )j}^{\star })^{\Omega _{j}}.e^{i2\pi \left[ \prod \limits _{j=1}^{n}(\xi _{h^{\star }(\delta )j})^{\Omega _{j}}\right] }\right) \end{array} \right\rangle , \\ \left\langle \begin{array}{c} \left( \root q \of {\left( 1{-}\prod \limits _{j=1}^{n}(1{-}\alpha _{(\delta )j}^{\star q})^{\Omega _{j}}\right) .}e^{i2\pi \left[ \root q \of {\left( 1{-}\prod \limits _{j=1}^{n}(1{-}\varphi _{\alpha _{(\delta )j}}^{\star q})^{\Omega _{j}}\right) }\right] }\right) , \\ \left( \prod \limits _{j=1}^{n}(\beta _{(\delta )j}^{\star })^{\Omega _{j}}.e^{i2\pi \left[ \prod \limits _{j=1}^{n}(\eta _{\beta ^{\star }(\delta )j})^{\Omega _{j}}\right] }\right) \end{array} \right\rangle \end{array} \!\!\right) ,\nonumber \\{} & {} \qquad q\ge 1. \end{aligned}$$

(37)

where $U_{\delta (j)}^{\star }$ is the jth biggest weighted CN-LDF values $U_{i}^{\star }(U_{j}^{\star }=(U_{j})^{n\Omega _{j}},j\in {\mathbb {N}} )$ and the weights of $U_{j}^{\star }$ are $\Omega =(\Omega _{1},\Omega _{2},...,\Omega _{n})^{T}$ by mean of $\Omega >0$ with $\ \sum \nolimits _{j=1}^{n}\Omega _{j}=1.$

If $\Omega =(\frac{1}{\Omega },$ $\frac{1}{\Omega },$ ... $,\frac{1}{ \Omega }),$ then CN-LDFWA and CN-LDFOWA operators are supposed to be a particular case CN-LDFHWA. So from this we obtained that CN-LDFHWA operator is the generalized form of CN-LDFWA and CN-LDFOWA operators.

Complex non-linear diophantine fuzzy weighted geometric ($CN-LDFWG$) aggregation operator

Throughout this part, we define complex non-linear Diophantine fuzzy weighted geometric aggregation operators i.e., CN-LDFWG, CN-LDFOWG and CN-LDFHWG aggregation operators.

Definition 15

Let $U_{j}{=}\!\left\{ \!\! \begin{array}{c} \left\langle \left[ g_{j}\right] .e^{i2\pi \left[ \theta _{g_{j}}\right] }, \left[ h_{j}\right] .e^{i2\pi \left[ \xi _{h_{j}}\right] }\right\rangle , \\ \left\langle \left[ \alpha _{j}\right] .e^{i2\pi \left[ \varphi _{\alpha _{j}}\right] },\left[ \beta _{j}\right] .e^{i2\pi \left[ \eta _{\beta _{j}} \right] }\right\rangle \end{array} \!\!\right\} \!:j=1,2,...n$ be a family of CN-LDFNs over a non-empty reference set M and $\Omega =(\Omega _{1},\Omega _{2},...,\Omega _{n})^{T}$ is the weight with $\sum \nolimits _{j=1}^{n}\Omega _{j}=1,$ and $q\ge 1;$ then we define the complex non-Linear Diophantine fuzzy weighted geometric (CN-LDFWG) operator as follows and let the transformation $\chi :CN-LDFN(M)\longrightarrow CN-LDFN(M)$

$$\begin{aligned}{} & {} CN-LDFWG(U_{1},U_{2},U_{3},...,U_{n}) \nonumber \\{} & {} \quad =\bigotimes \nolimits _{j=1}^{n}(U_{j}^{\Omega _{j}})=U_{1}^{\Omega _{1}}\oplus U_{2}^{\Omega _{2}}\oplus U_{3}^{\Omega _{3}}\oplus ...\oplus U_{n}^{\Omega _{n}}. \end{aligned}$$

(38)

Theorem 8

Let $U_{j}{=}\!\left\{ \! \begin{array}{c} \left\langle \left[ g_{j}\right] .e^{i2\pi \left[ \theta _{g_{j}}\right] }, \left[ h_{j}\right] .e^{i2\pi \left[ \xi _{h_{j}}\right] }\right\rangle , \\ \left\langle \left[ \alpha _{j}\right] .e^{i2\pi \left[ \varphi _{\alpha _{j}}\right] },\left[ \beta _{j}\right] .e^{i2\pi \left[ \eta _{\beta _{j}} \right] }\right\rangle \end{array} \!\right\} \!:j=1,2,...n$ be a family of CN-LDFNs over a non-empty reference set M and $\Omega =(\Omega _{1},\Omega _{2},...,\Omega _{n})^{T}$ is the weight with $\sum \nolimits _{j=1}^{n}\Omega _{j}=1,$ and $q\ge 1;$ then by applying the CN-LDFWG operator their aggregated value is also an CN-LDFN, and the transformation $\chi :CN-LDFN(M)\longrightarrow CN-LDFN(M)$ is called CN-LDFWG operator and defined as;

$$\begin{aligned}{} & {} \!\!\!CN-LDFWG(U_{1},U_{2},U_{3},...,U_{n})=\bigotimes \limits _{j=1}^{n}U_{j}^{ \Omega _{j}} \nonumber \\{} & {} \quad {=}\!\left( \! \begin{array}{c} \left\langle \begin{array}{c} \left( \prod \limits _{j=1}^{n}(g_{j})^{\Omega _{j}}.e^{i2\pi \left[ \prod \limits _{j=1}^{n}(\xi _{gj})^{\Omega _{j}}\right] }\right) , \\ \left( \root q \of {\left( 1{-}\prod \limits _{j=1}^{n}(1-h_{j}^{q})^{\Omega _{j}}\right) .}e^{i2\pi \left[ \root q \of {\left( 1{-}\prod \limits _{j=1}^{n}(1{-}\theta _{h_{j}}^{q})^{\Omega _{j}}\right) }\right] }\right) , \end{array} \right\rangle , \\ \left\langle \begin{array}{c} \left( \prod \limits _{j=1}^{n}(\alpha _{j})^{\Omega _{j}}.e^{i2\pi \left[ \prod \limits _{j=1}^{n}(\eta _{\alpha j})^{\Omega _{j}}\right] }\right) , \\ \left( \root q \of {\left( 1{-}\prod \limits _{j=1}^{n}(1{-}\beta _{j}^{q})^{\Omega _{j}}\right) .}e^{i2\pi \left[ \root q \of {\left( 1{-}\prod \limits _{j=1}^{n}(1{-}\varphi _{\beta _{j}}^{q})^{\Omega _{j}}\right) } \right] }\right) , \end{array} \right\rangle \end{array} \!\right) ,\nonumber \\{} & {} \qquad q\ge 1. \end{aligned}$$

(39)

Theorem 9

(Idempotency). If $U_{j}$$=\left\{ \begin{array}{c} \left\langle \left[ g_{j}\right] .e^{i2\pi \left[ \theta _{g_{j}}\right] }, \left[ h_{j}\right] .e^{i2\pi \left[ \xi _{h_{j}}\right] }\right\rangle , \\ \left\langle \left[ \alpha _{j}\right] .e^{i2\pi \left[ \varphi _{\alpha _{j}}\right] },\left[ \beta _{j}\right] .e^{i2\pi \left[ \eta _{\beta _{j}} \right] }\right\rangle \end{array} \right\} :j=1,2,...n$ are equal i.e., $U_{j}=$$U=\left\{ \begin{array}{c} \left\langle \left[ g\right] .e^{i2\pi \left[ \theta _{g}\right] },\left[ h \right] .e^{i2\pi \left[ \xi _{h}\right] }\right\rangle , \\ \left\langle \left[ \alpha \right] .e^{i2\pi \left[ \varphi _{\alpha }\right] },\left[ \beta \right] .e^{i2\pi \left[ \eta _{\beta }\right] }\right\rangle \end{array} \right\} \}$ then

$$\begin{aligned} CN-LDFWG(U_{1},U_{2},...,U_{n})=U \end{aligned}$$

(40)

Theorem 10

(Boundedness). Let $U_{j}$$=\left\{ \begin{array}{c} \left\langle \left[ g_{j}\right] .e^{i2\pi \left[ \theta _{g_{j}}\right] }, \left[ h_{j}\right] .e^{i2\pi \left[ \xi _{h_{j}}\right] }\right\rangle , \\ \left\langle \left[ \alpha _{j}\right] .e^{i2\pi \left[ \varphi _{\alpha _{j}}\right] },\left[ \beta _{j}\right] .e^{i2\pi \left[ \eta _{\beta _{j}} \right] }\right\rangle \end{array} \right\} :j\in {\mathbb {N}}$ be a family of CN-LDFNs, and consider $U^{-}=\min \nolimits _{j}U_{j},$ $U^{+}=\max \nolimits _{j}U_{j},$ then

$$\begin{aligned} U^{-}\le CN-LDFWG_{\Omega }(U_{1},U_{2},...,U_{n})\le U^{+} \end{aligned}$$

(41)

Theorem 11

(Monotonicity). Let $U_{j}(j\in {\mathbb {N}} )$ and $U_{j}^{*}(j\in {\mathbb {N}} )$ be two set of CN-LDFNs, if $U_{j}\le U_{j}^{*},\forall$ j,  then

$$\begin{aligned}{} & {} CN-LDFWG_{\Omega }(U_{1},U_{2},...,U_{n})\nonumber \\{} & {} \quad \le CN-LDFWG_{\Omega }(U_{1}^{*},U_{2}^{*},...,U_{n}^{*}) \end{aligned}$$

(42)

Furthermore, we shall develop the complex non-linear Diophantine fuzzy ordered weighted averaging (CN-LDFOWG) operator.

Definition 16

Let $U_{j}{=}\!\!\left\{ \! \begin{array}{c} \left\langle \left[ g_{j}\right] .e^{i2\pi \left[ \theta _{g_{j}}\right] }, \left[ h_{j}\right] .e^{i2\pi \left[ \xi _{h_{j}}\right] }\right\rangle , \\ \left\langle \left[ \alpha _{j}\right] .e^{i2\pi \left[ \varphi _{\alpha _{j}}\right] },\left[ \beta _{j}\right] .e^{i2\pi \left[ \eta _{\beta _{j}} \right] }\right\rangle \end{array} \!\right\} \!\!:j=1,2,...n$ be a family of CN-LDFNs over a non-empty reference set M and $\Omega =(\Omega _{1},\Omega _{2},...,\Omega _{n})^{T}$ is the weight with $\sum \nolimits _{j=1}^{n}\Omega _{j}=1,$ and $q\ge 1;$ then by applying the CN-LDFOWG operator their aggregated value is also a CN-LDFN, and the transformation $\chi :CN-LDFN(M)\longrightarrow CN-LDFN(M)$ is called CN-LDFOWG operator and defined as;

$$\begin{aligned}{} & {} CN-LDFOWG(U_{1},U_{2},U_{3},...,U_{n}) \nonumber \\{} & {} \quad =\bigotimes \limits _{j=1}^{n}(U_{(\delta )j})^{\Omega _{j}}=U_{(\delta )1}^{\Omega _{1}}\oplus U_{(\delta )2}^{\Omega _{2}}\nonumber \\{} & {} \qquad \oplus U_{(\delta )3}^{\Omega _{3}}\oplus ...\oplus U_{(\delta )n}^{\Omega _{n}}. \end{aligned}$$

(43)

where the arrangement of $(j\in {\mathbb {N}} )$ is $(\delta (1),$ $\delta (2),$ $\delta (3),$ ...,  $\delta (n))$, for which $U_{\delta (j=1)}\ge U_{\delta (j)}\forall (j\in {\mathbb {N}} ).$

Theorem 12

Let $U_{j}{=}\!\!\left\{ \! \begin{array}{c} \left\langle \left[ g_{j}\right] .e^{i2\pi \left[ \theta _{g_{j}}\right] }, \left[ h_{j}\right] .e^{i2\pi \left[ \xi _{h_{j}}\right] }\right\rangle , \\ \left\langle \left[ \alpha _{j}\right] .e^{i2\pi \left[ \varphi _{\alpha _{j}}\right] },\left[ \beta _{j}\right] .e^{i2\pi \left[ \eta _{\beta _{j}} \right] }\right\rangle \end{array} \!\!\right\} \!:j=1,2,...n$ be a family of CN-LDFNs over a non-empty reference set M and $\Omega =(\Omega _{1},\Omega _{2},...,\Omega _{n})^{T}$ is the weight with $\sum \nolimits _{j=1}^{n}\Omega _{j}=1,$ and $q\ge 1;$ by applying the CN-LDFOWG operator their aggregated value is also CN-LDFN, and the transformation $\chi :CN-LDFN(M)\longrightarrow CN-LDFN(M)$ are known as CN-LDFOWG operator and defined as;

$$\begin{aligned}{} & {} \!\!\!CN-LDFOWG(U_{1},U_{2},U_{3},...,U_{n})=\bigotimes \limits _{j=1}^{n}(U_{( \delta )j})^{\Omega _{j}} \nonumber \\{} & {} \quad {=}\!\left( \begin{array}{c} \left\langle \begin{array}{c} \left( \prod \limits _{j=1}^{n}(g_{(\delta )j})^{\Omega _{j}}.e^{i2\pi \left[ \prod \limits _{j=1}^{n}(\xi _{g(\delta )j})^{\Omega _{j}}\right] }\right) , \\ \left( \root q \of {\left( 1{-}\prod \limits _{j=1}^{n}(1-h_{(\delta )j}^{q})^{\Omega _{j}}\right) .}e^{i2\pi \left[ \root q \of {\left( 1{-}\prod \limits _{j=1}^{n}(1{-}\theta _{h_{(\delta )j}}^{q})^{\Omega _{j}}\right) }\right] }\right) , \end{array} \right\rangle , \\ \left\langle \begin{array}{c} \left( \prod \limits _{j=1}^{n}(\alpha _{(\delta )j})^{\Omega _{j}}.e^{i2\pi \left[ \prod \limits _{j=1}^{n}(\eta _{\alpha (\delta )j})^{\Omega _{j}}\right] }\right) , \\ \left( \root q \of {\left( 1-\prod \limits _{j=1}^{n}(1{-}\beta _{(\delta )j}^{q})^{\Omega _{j}}\right) .}e^{i2\pi \left[ \root q \of {\left( 1{-}\prod \limits _{j=1}^{n}(1{-}\varphi _{\beta _{(\delta )j}}^{q})^{\Omega _{j}}\right) }\right] }\right) , \end{array} \right\rangle \end{array} \!\!\right) ,\nonumber \\{} & {} \qquad q\ge 1. \end{aligned}$$

(44)

Above we defined CN-LDFWG and CN-LDFOWG operators, next we are going to establish CN-LDFHWG aggregation operator.

Definition 17

Let $U_{j}{=}!\!\left\{ \!\! \begin{array}{c} \left\langle \left[ g_{j}\right] .e^{i2\pi \left[ \theta _{g_{j}}\right] }, \left[ h_{j}\right] .e^{i2\pi \left[ \xi _{h_{j}}\right] }\right\rangle , \\ \left\langle \left[ \alpha _{j}\right] .e^{i2\pi \left[ \varphi _{\alpha _{j}}\right] },\left[ \beta _{j}\right] .e^{i2\pi \left[ \eta _{\beta _{j}} \right] }\right\rangle \end{array} \!\!\right\} \!:j=1,2,...n$ be a family of CN-LDFNs over a non-empty reference set M and $\Omega =(\Omega _{1},\Omega _{2},...,\Omega _{n})^{T}$ are the weight with $\sum \nolimits _{j=1}^{n}\Omega _{j}=1,$ also $q\ge 1;$ then we define the Complex Non-Linear Diophantine fuzzy hybrid weighted geometric (CN-LDFHWG) operator as follows and let the mapping $\chi :N-LDFN(M)\longrightarrow N-LDFN(M)$

$$\begin{aligned}{} & {} CN-LDFHWG(U_{1},U_{2},U_{3},...,U_{n}) \nonumber \\{} & {} \quad =\bigotimes \limits _{j=1}^{n}(U_{(\delta )j}^{\star })^{\Omega _{j}}=(U_{(\delta )1}^{\star })^{\Omega _{1}}\oplus (U_{(\delta )2}^{\star })^{\Omega _{2}}\nonumber \\{} & {} \qquad \oplus (U_{(\delta )3}^{\star })^{\Omega _{3}}\oplus ...\oplus (U_{(\delta )n}^{\star })^{\Omega _{n}}. \end{aligned}$$

(45)

where $U_{\delta (j)}^{\star }$ is the jth largest weighted N-LDF values $U_{i}^{\star }(U_{j}^{\star }=(U_{j})^{n\Omega _{j}},j\in {\mathbb {N}} )$ and the weights of $U_{j}^{\star }$ are $\Omega =(\Omega _{1},\Omega _{2},...,\Omega _{n})^{T}$ by mean of $\Omega >0$ with $\sum \nolimits _{j=1}^{n}\Omega _{j}=1.$

Theorem 13

Let $U_{j}{=}\!\!\left\{ \! \begin{array}{c} \left\langle \left[ g_{j}\right] .e^{i2\pi \left[ \theta _{g_{j}}\right] }, \left[ h_{j}\right] .e^{i2\pi \left[ \xi _{h_{j}}\right] }\right\rangle , \\ \left\langle \left[ \alpha _{j}\right] .e^{i2\pi \left[ \varphi _{\alpha _{j}}\right] },\left[ \beta _{j}\right] .e^{i2\pi \left[ \eta _{\beta _{j}} \right] }\right\rangle \end{array} \!\!\right\} \!:j\in {\mathbb {N}}$ be a family of CN-LDFNs over a non-empty reference set M and $\Omega =(\Omega _{1},\Omega _{2},...,\Omega _{n})^{T}$ is the weight with $\sum \nolimits _{j=1}^{n}\Omega _{j}=1,$ also $q\ge 1;$ by applying the CN-LDFHWG operator their aggregated value is also an CN-LDFN, and the transformation $\chi :N-LDFN(M)\longrightarrow N-LDFN(M)$ are known as CN-LDFHWG and defined as;

$$\begin{aligned}{} & {} \!\!\!CN-LDFHWG(U_{1},U_{2},U_{3},...,U_{n})=\bigotimes \limits _{j=1}^{n}(U_{( \delta )j}^{\star })^{\Omega _{j}} \nonumber \\{} & {} \quad {=}\!\left( \! \begin{array}{c} \left\langle \begin{array}{c} \left( \prod \limits _{j=1}^{n}(g_{(\delta )j}^{\star })^{\Omega _{j}}.e^{i2\pi \left[ \prod \limits _{j=1}^{n}(\xi _{g^{\star }(\delta )j})^{\Omega _{j}}\right] }\right) , \\ \left( \root q \of {\left( 1{-}\prod \limits _{j=1}^{n}(1{-}h_{(\delta )j}^{\star q})^{\Omega _{j}}\right) .}e^{i2\pi \left[ \root q \of {\left( 1{-}\prod \limits _{j=1}^{n}(1{-}\theta _{h_{(\delta )j}}^{\star q})^{\Omega _{j}}\right) }\right] }\right) , \end{array} \right\rangle , \\ \left\langle \begin{array}{c} \left( \prod \limits _{j=1}^{n}(\alpha _{(\delta )j}^{\star })^{\Omega _{j}}.e^{i2\pi \left[ \prod \limits _{j=1}^{n}(\eta _{\alpha ^{\star }(\delta )j})^{\Omega _{j}}\right] }\right) , \\ \left( \root q \of {\left( 1{-}\prod \limits _{j=1}^{n}(1{-}\beta _{(\delta )j}^{\star q})^{\Omega _{j}}\right) .}e^{i2\pi \left[ \root q \of {\left( 1{-}\prod \limits _{j=1}^{n}(1{-}\varphi _{\beta _{(\delta )j}}^{\star q})^{\Omega _{j}}\right) }\right] }\right) , \end{array} \right\rangle \end{array} \!\!\right) ,\nonumber \\{} & {} \qquad q\ge 1. \end{aligned}$$

(46)

where $U_{\delta (j)}^{\star }$ is the jth biggest weighted q-RDF values $U_{i}^{\star }(U_{j}^{\star }=(U_{j})^{n\Omega _{j}},j\in {\mathbb {N}} )$ and the weights of $U_{j}^{\star }$ are $\Omega =(\Omega _{1},\Omega _{2},...,\Omega _{n})^{T}$ by mean of $\Omega >0$ with $\sum \nolimits _{j=1}^{n}\Omega _{j}=1.$

If $\Omega =(\frac{1}{\Omega },$ $\frac{1}{\Omega },$ ... $,\frac{1}{ \Omega }),$ then CN-LDFWG and CN-LDFOWG operators are supposed to be a particular case CN-LDFHWG. So from this we obtained that CN-LDFHWG operator is the generalized form of CN-LDFWG and CN-LDFOWG operators.

Complex non-linear diophantine fuzzy MCGDM problem

We build algorithms based on the CN-LDFWA and CN-LDFWG aggregation operators all around this area. The goal of providing this technique is to demonstrate the theory of CN-LDFS and their aggregation operators, as well as its versatility in application. The MCGDM problem is utilized to choose the best shelter material using CN-LDF data by applying the CN-LDFWA and CN-LDFWG aggregation operators.

Consider a set of alternatives $F=\{F_{1},F_{2},...,F_{m}\}$ and $H=\{H_{1},H_{2},...H_{n}\}$ denoted criteria’s set with weight vectors $\Omega =(\Omega _{1},\Omega _{2},...,\Omega _{n})^{T}$ with condition $\Omega _{j}>0$, $\sum \nolimits _{j=1}^{n}\Omega _{j}=1.$ Also, consider e number of expert matrix (EMs), $EM_{k}(k=1,2,\ldots ,e)$, about $F_{i}$ alternatives and $H_{j}$ criteria by applying CN-LDFWA $U_{ij}^{(k)}=\left[ \left\langle g_{ij}^{(k)},h_{ij}^{(k)}\right\rangle ,\left\langle \alpha _{ij}^{(k)},\beta _{ij}^{(k)}\right\rangle \right] .$ The kth EM is appeared as follows:

$$\begin{aligned} \left[ U_{ij}^{(k)}\right] _{m\times n}=\left[ \left\langle g_{U_{ij}}^{(k)},h_{U_{ij}}^{(k)}\right\rangle ,\left\langle \alpha _{U_{ij}}^{(k)},\beta _{U_{ij}}^{(k)}\right\rangle \right] _{m\times n}(k=1,2,...,e), \end{aligned}$$

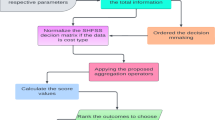
With the help of CN-LDFWA operator and CN-LDFWG operator, we developed the decision steps which are shown as follows:

Step-1: Establish an Experts Matrix (EMs) team in the form of CN-LDFS for an appropriate number of alternatives and criteria’s. Here $EM=\{EM_{1},EM_{2},...,EM_{k}\}$ denotes the expert matrix group. The preferences of each EMs are calculated via CN-LDFWA and CN-LDFWG operators with weight vector $\Omega .$

Step-2: Standardized CN-LDF data, because the experts matrix $E^{(k)}$ may have some benefit and cost criteria that is:

$$\begin{aligned} N_{ij}^{(k)}= & {} \left\{ \begin{array}{ccc} U_{ij}^{(k)} &{} for &{} \text {benefit criteria} \\ (U_{ij}^{(k)})^{c} &{} for &{} \text {cost criteria} \end{array} \right. \end{aligned}$$

(47)

$$\begin{aligned} k= & {} 1,2,\ldots ,e,i=1,2,\ldots ,m,j=1,2,\ldots ,n, \end{aligned}$$

(48)

All criteria in our given problem are of the same types, we don’t require to normalize the data.

Step-3: For each Expert Matrix, we have to suppose the equivalent weights which give priority to each expert matrix $\Omega =(\Omega _{1},\Omega _{2},\Omega _{3})^{T}$.

Step-4: Utilize the Experts information given in matrix $EM_{k}(k=1,2,3)$ into the collective (combine) C-NLDF Expert matrix by applying the C-NLDFWA and C-NLDFWG operators with associated weights $\Omega =(\Omega _{1},\Omega _{2},\Omega _{3})^{T}$ of attribute $H_{j}.$

Step-5: Again compute collective aggregated value for each criteria’s $H_{j}$ with weight vector $\Omega =(\Omega _{1},\Omega _{2},\Omega _{3},\Omega _{4})^{T}$ $\Omega =\{0.35,0.3,0.25,0.1\}$ by using Eqs. 30, 35, 37, 39, 44 and 46 of CN-LDFWA and CN-LDFWG aggregation operators from above definition..

Step-6: From aggregated values, calculate scores of each alternatives $F_{i}$ by applying the above definition of expectation score functions using Eqs. 27 and 28.

Step-7: Rank the alternatives on the base of score values.

Step 8: Higher-score alternatives have the maximum rank and must be selected for the final decision. Following Fig. 1 showed the schematic diagram of the proposed research methodology.

Fig. 1

Schematic diagram of the proposed research methodology

Numerical example

We provide a novel MCGDM method with complex Non-linear Diophantine fuzzy information in this section under the CN-LDFS environment which is CN-LDFWA, CN-LDFOWA, and CN-LDFHWA operators and also CN-LDFWG, CN-LDFOWG, and CN-LDFHWG operators. So for, in this we present algorithm for numerical model and using of SF and AF, we get preventive and control rankings for final decision about emergency shelters, and then the results are compared to the result of previous operators to demonstrate the feasibility and usefulness of the suggested method.

Problem description: materials for building emergency shelters

Earthquakes are important natural disasters that endanger people’s lives, health, and property. Unfortunately, there is currently no reliable technology to predict the specific time, location, and intensity of an earthquake disaster. Therefore, in the face of uncontrollable natural disasters, all countries have established a series of emergency measures after the earthquake, so that after the disaster occurs, the disaster-stricken people can be quickly rescued and their lives and production activities can be restored. Among them, the construction of emergency shelters is an extremely important step [48]. According to known experience, four criteria are generally considered when constructing emergency shelters, namely:

• Availability ($H_{1}$)

• Convenience ($H_{2}$)

• Safety ($H_{3}$)

• Comprehensive support services ($H_{4})$.

At the same time, there are four kinds of materials (alternatives) used to construct emergency shelters, namely Rubber ($F_{1}$), Bamboo ($F_{2}$), Plastic sheeting ($F_{3}$) and 3D printed recycled materials ($F_{4}$).

In order to build a safe and suitable emergency shelter as soon as possible, the emergency command department invited three expert matrices $(EM_{1},EM_{2},EM_{3})$ from government officials, experts in emergency decision-making, experts from international rescue organizations, and local residents to participate in the emergency decision-making. These decision-makers evaluated the four building materials (alternatives) according to four criteria, and these evaluation values have been displayed in Table 3, 4, 5. At the same time, the fuzzy evaluation matrix of the expert makers is marked as $EM_{s}$. Following are the details of four alternatives for emergency shelters—

(1) Rubber ($F_{1}$): Rubber may be recycled for a variety of uses and has even been used in building to manufacture bricks. Unlike traditional bricks, those made from recycled rubber are easy to assemble and ready to use right away. Their greatest advantage is their low density, which results in extremely light blocks. Because the materials are stronger than waterproof fabrics, which are more typically used for emergency tent building, shelters produced using this technology can be used even after emergency has occurred.

(2) Bamboo ($F_{2}$): Bamboo is a very adaptable material that controls pressure and twisting. Another significant advantage is its widespread availability (particularly in hot regions) and quick growth. As a result, bamboo is perfect for temporary structures, such as building structures, sidewalls, and roofing. It has the extra virtue of being quick to assemble and can be left in place for permanent housing when creating emergency shelters. However, in order for bamboo to be regarded a building material with acceptable durability and great mechanical features, it must first be chemically treated to prevent rotting and insect infestation before being used in construction. Another important consideration in bamboo building is that the components must be well sheltered from the sun and rain.

(3) Plastic sheeting ($F_{3}$): People who have been impacted by earthquakes have shown that they prefer to stay in or near their damaged homes instead of migrate to camps or communal centers. Plastic sheeting or tarpaulins are the conventional material of choice for emergency shelter support due to their versatility. Because earthquake victims are frequently able to rescue building materials from their homes, there is usually no need to distribute timber or bamboo poles.

(4) 3D printed recycled materials ($F_{4}$): Despite its relatively expensive cost, 3D printing has grown in popularity over the years and has indicated to be a feasible alternative for building emergency shelters. DUS Architects, for example, has created a totally transportable 3D printer called the “KamerMaker” that can build entire spaces out of recycled materials. 3D printers, on the other hand, can be extremely useful in an emergency when creating small connecting pieces. When it comes to assembly, designing joints to improve installation, and allow parts of different materials to be linked together can be a huge help.

In times of severe pain and loss, temporary solutions and emergency architecture become highly important. The combination of rapid and simple treatments that can respond to the needs and demands of the impacted people must be taken seriously. Architects must be fully engaged in developing thoughtful and serious solutions and engaging in comprehensive research of new materials and alternatives, including the utilization of local resources [49, 50].

Following is the solution of numerical table using above algorithm with the guidance of case related to materials for building emergency shelters on the base of which we will select the best alternative solution for this emergency.

Step-1: Assume three experts are hired to analyze the four material shelters alternatives $F_{i}(i=1,2,3,4)$ in terms of four criteria $H_{j}(j=1,2,3,4)$, and the expert evaluation matrices $E_{k}(k=1,2,3)$ are built in Tables 3, 4, 5. All of the attributes $H_{1},H_{2},H_{3},H_{4}$ are benefits types, according to experts.

Table 3 Expert matrix ($EM_{1}$)

Table 4 Expert matrix ($EM_{2}$)

Table 5 Expert matrix ($EM_{3}$)

Step-2: We have same types of criteria, so we don’t need to normalize the input data.

Step-3: For each Expert matrix/maker’s, we have the equivalent weight vectors $\Omega =\{0.4,0.3,0.3\}$.

Step-4: Now we apply the CN-LDFWA and CN-LDFWG operators with associated weight vectors $\Omega =(0.4,0.3,0.3)^{T},$ to calculate the input data given in Table 3, 4, 5 into collective (combine) CN-RLDF information, following Tables 6 and 7 showed the computed expert matrix for CN-LDFWA and CN-LDFWG aggregation operators using Eq. 30, 35, 37, 39, 44 and 46.

Table 6 Computed expert matrix by CN-LDFWA

Table 7 Computed expert matrix by CN-LDFWG

Similarly, we obtained the collective/computed expert matrix for CN-LDFOWA and CN-LDFOWG aggregation operator showed in Table 8.

Table 8 Computed expert matrix by CN-LDFOWA

Similarly, we obtained the collective/computed expert matrix for CN-LDFHWA and CN-LDFHWG aggregation operator.

Step-5: We again computed the collective aggregated matrix given in Tables 6, 7 and 8 for each criteria $H_{j}$ with weight vector $\Omega =\{0.35,0.3,0.25,0.1\}$ using Eqs. 30, 35 37 3944 and 46 of CN-LDFWA, CN-LDFOWA, and CN-LDFHWA and also CN-LDFWG, CN-LDFOWG, and CN-LDFHWG aggregation operators from the above definition, the result shown in following Table 9.

Similarly, we obtained the aggregated values for CN-LDFOWA, CN-LDFOWA, CN-LDFHWA, and CN-LDFHWG.

Step-6: Table 11 show the overall Score function values of CN-LDFWA, CN-LDFOWA, and CN-LDFHWA and also CN-LDFWG, CN-LDFOWG, and CN-LDFHWG aggregation operators.

Step-7: Ranking of proposed aggregation operators is shown in the following Table 12.

Step-8: From Table 12, we conclude that $F_{3}$ i.e plastic sheeting is chosen the best alternative for emergency situation and earthquakes. Following Fig. 2 represented the graphically ranking of proposed method.

Fig. 2

Graphically ranking of proposed method (CN-LDFW)

Comparison analysis

To state the effectiveness of the proposed method, some existing MCGDM methods are employed and for comparison, we select three existing methods, namely LDFS, q-RLDFS, and CNLDFS. In order to unify the comparison scale, we start to make decisions based on the integrated matrix after group decision-making. We applied the same steps of above algorithm for comparison section also. We get the same ranking results from proposed and existing approach the best and top option are the same throughout the whole methods which approves the stability and validity of the suggested work. The whole comparison’s results are listed in Table 19 below.

Comparison with linear diophantine fuzzy set [39]

In this subsection, we compared the proposed work with LDFS [39]. We applied the LDFS aggregation operators on our input data given in Tables 3, 4, 5, the aggregation operators of existing approach are LDFWA, LDFOWA, and LDFHWA, also LDFWG, LDFOWG, and LDFHWG.

The Score function value matrix for comparison after aggregation by existing LDF operators is shown as follows in Table 13:

Following Fig. 3 represented the graphically ranking of existing LDF method.

Table 9 CN-LDFWA aggregated values

Table 10 CN-LDFWG aggregated values

Comparison with q-Rung linear diophantine fuzzy set [46]

In this subsection, we compared the proposed work with q-RLDFS [46]. We applied the q-RLDFS aggregation operators on our input data given in Tables 3, 4, 5, the aggregation operators of existing approach are q-RLDFWA and q-RLDFWG.

The Score function value matrix for comparison after aggregation by existing q-RLDF operators is shown as follows in Table 15:

The ranking result of compared existing LDF approach is shown in Table 14.

The Ranking result of compared existing q-RLDF approach is shown in following Table 16.

Following Fig. 4 represented the graphically ranking of existing q-RLDF method.

Comparison with complex linear diophantine fuzzy set (CLDFS) [40]

In this subsection, we compared the proposed work with CLDFS [40]. We applied the CLDFS aggregation operators on our input data given in Table 3, 4, 5, the aggregation operators of existing approach are CLDFWA, CLDFOWA, and CLDFHWA, also as CLDFWG, CLDFOWG, and CLDFHWG.

The Score function value matrix for comparison after aggregation by existing CLDF operators is shown as follows in Table 17.

The Ranking result of compared existing CLDF approach is shown in following Table 18.

Table 11 Overall Score function values of proposed operators

Fig. 3

Graphically ranking of existing LDFW operators

Following Fig. 5 represented the graphically ranking of existing CLDF method.

Final overall ranking result of proposed and existing methods are listed in Table 19 as follows:

From this, we conclude that $F_{3}$ i.e., plastic sheeting is chosen the best alternative for emergency situation and earthquakes. From the above Table 19, we get the same ranking order after applying the proposed and existing approach, which shows the flexibility and reliability of proposed method.

Advantages of the proposed approach

We highlight the following effectiveness of the suggested techniques to deal with decision-making in the CN-LDF context based on previous studies and proposed methodologies.

A complex Non-linear Diophantine fuzzy set is a generalization of the earlier approaches, especially CLDFS [65] and q-RLDFS, in which more knowledge about an element is addressed during the process and two-dimensional information in a set is handled. In a variety of domains, this generalized form provides advanced solution to problems involving fuzzy sets and their extensions (as well as decision-making).

Table 12 Whole ranking of proposed method

Table 13 Score values of existing method

The CN-LDFS (which uses complex values for membership, non-membership, and reference parameters) contains more amplitude and phase terms than the LDFS, CLDFS, and q-RLDFS. As a result, the proposed CN-LDFS are modified versions of the current q-RLDF structure [46].

The proposed approaches have the significant advantage of considering severely more information with the qth power of reference parameters in order to obtain the alternative to reduce information loss. Furthermore, the complex membership, non-membership, and complex reference parameter values will aid the decision-maker(s) in more precisely determining the ideal alternative(s). In other words, we believe that the new N-LDF idea will provide decision-makers with a variety of possibilities based on their complicated decision-making behavior.

Fig. 4

Graphically ranking of existing q-RLDF operators

Fig. 5

Graphically ranking of existing CLDF operators

Table 14 Ranking of LDF method

Table 15 Score values of q-RLDF operators

Table 16 Ranking of q-RLDF method

Table 17 Score Values of CLDF operators

Table 18 Ranking of CLDF method

Table 19 Overall ranking of proposed and existing methods

Conclusion

In real-world MCGDM problems, CN-LDFS plays a vital role to freely choose the grades of complex-valued membership complex-valued non-membership, and complex-valued reference parameters without any conditions. Therefore, in this paper, we developed a novel notion of CN-LDFS an extension of CLDFS. The CN-LDFS is more efficient and flexible rather than other approaches due to the role of complex-valued reference parameters. As the CN-LDFS provides a flexible and convenient way for people to express information and make decisions, it can be successfully applied to solve various decision-making problems. Furthermore, we developed score and accuracy function and novel systematic transformation of aggregation operators, such as CN-LDFWA, CN-LDFOWA, and CN-LDFHWA, and similarly, CN-LDFWG, CN-LDFOWG, and CN-LDFHWG aggregation operators for CN-LDFSs. Finally, we developed CN-LDFS-based algorithms with the guidance of a case study regarding emergency situation of earthquakes for the selection of best building material shelters to deal in real-life problems and also compared it with other methods in existence which showed the possibility and implementation of suggested method. The proposed approach provides an accurate ranking of building material shelters validated through a real-world case study. In this case, the ranking obtained from the integrated CN-LDFW aggregation operators is $F_{3}$ i.e., Plastic sheeting is selected the best shelter during the emergency situation.

This study provides a number of interesting topics for future research. More complex non-linear Diophantine fuzzy decision-making techniques can be used in this study, including CN-LDF CODAS, CN-LDF VIKOR, CN-LDF MULTIMOORA, CN-LDF TODIM, CN-LDF FUCOM, CN-LDF LBWA, and their hybrids. Future research can expand on the suggested methodology using picture fuzzy sets, bipolar fuzzy sets, neutrosophic sets, spherical fuzzy sets, and hesitant fuzzy sets. These fuzzy sets can also be used to develop trapezoidal fuzzy sets. The problem of choosing a building material for a shelter can be further improved with additional criteria.