Novel intuitionistic fuzzy Aczel Alsina Hamy mean operators and their applications in the assessment of construction material

Abstract

Aggregation operators (AOs) are utilized to overcome the effects of attributes under some specific degree of weight in the decision-making (DM) process. The AOs have a large capacity to deal with uncertain and unpredictable information in multi-attribute decision-making (MADM) problems. The Hamy mean (HM) aggregation tools are well-known aggregation models, which are utilized to define correlation among different input arguments adequately. The intuitionistic fuzzy (IF) sets (IFS) can express unpredictable and vague information. The Aczel Alsina aggregation expressions are extensions of triangular norms. Recently, Aczel Alsina aggregation tools attained a lot of attentions from numerous research scholars. By inspiring the robustness and reliability of Aczel Alsina aggregation tools, we expose some appropriate operations of Aczel Alsina expressions under consideration of IF information. In this manuscript, we developed an intuitionistic fuzzy Aczel Alsina HM (IFAAHM) and an intuitionistic fuzzy Aczel Alsina weighted HM (IFAAWHM) operator. We also expressed the theory of Dual HM (DHM) tools and established a series of new approaches including intuitionistic fuzzy Aczel Alsina Dual HM (IFAADHM) and intuitionistic fuzzy Aczel Alsina weighted Dual HM (IFAAWDHM) operators. Some reliable characteristics and special cases of our derived approaches are also presented. The authors solved an application of a MADM technique under consideration of our derived approaches. To check the reliability and dependency of our derived mythologies, we gave an experimental case study to evaluate a desirable construction material based on some specific criteria of different Alternatives. To see the advantages and compatibility of our derived approaches, by comparing the results of existing approaches with the results of currently discussed AOs.

Introduction

The MADM is a decision-making process that involves considering multiple criteria or attributes when evaluating options or alternatives. It is a common approach used in many fields, including business, engineering, green supplier management, construction development and public policy. Generally, the decision-makers (DMs) utilize crisp numbers to show their capability about the alternative to accepted MADM issues. Cagri Tolga and Basar [1] expressed a particular estimation of the rate of increasing in population and production resources of foods by using theoretic concepts of multi-criteria DM problems under fuzziness. Tolga et al. [2] utilized a more powerful and effective evaluating strategy to select desirable medical devices for improvement in the health sector under consideration of type-2 fuzzy environments. Moreover, due to a lack of data, the inadequacy of information, and time pressure, the property estimations, particularly for subjective trait values, by and large, can't be appeared by genuine numbers, and some of them are more straightforward to be communicated by fuzzy sets (FSs). Zadeh [3] has been applied in different fields of current culture as DM, design acknowledgement, clinical finding, and so on Afterward, considering that the FS just holds back one membership grade (MG), Atanassov [4] presented the idea of the IFS for expanding the FS into three sensible structures, MG, non-membership grade (NMG) and hesitancy grade(HG). The sum of MG and NMG lies in $\left[ {0,{ }1} \right]$ i.e., $\upkappa\kern-1.0pt\text{\c{}}\left( \tau \right) + \nu \left( \tau \right) \in \left[ {0,1} \right]$. A lot of researchers utilized the theory of IFS and FS to understand the methodologies of our research works [5,6,7].

Many researchers worked in different fields of fuzzy environments to cope with uncertain and vague information and discovered various new AOs such as IF weighted averaging (IFWA) by Xu [6] IF weighted geometric (IFWG) by Xu and Yager [8] IF Dombi weighted averaging (IFDWA) and IF Dombi weighted geometric (IFDWG) by the Seikh and Mandal [9], triangular IFWA and IFWG by the Mahmood et al. [10], interval-valued IFWA by the Wang et al. [11], AOs of interval-valued T-spherical fuzzy (IVTSF) by the Ullah et al. [12], AOs of the Pythagorean fuzzy weighted averaging operator by the Rahman et al. [13]. AOs of interval-valued picture fuzzy (IVPF) weighted averaging (IVPFWA) and IVPF weighted geometric (IVPFWG) by Mahmood et al. [10]. Hussain et al. [14] explored innovative AOs of complex IFSs by using the basic properties of HM operators and established an application for the tourism industry under the system of a MADM technique. Einstein geometric AOs under the interval-valued Pythagorean fuzzy system by Ali et al. [15]. We also studied research work for further development of this article given in [16,17,18,19].

The t-norm (TN) and t-conorm (TCN) play a significant role to investigate logical conjunction and disjunction of fuzzy logic. TNs are the extension of intersection in conjunction and lattice in logic. TNs and TCNs are the binary operations used in probabilistic metric space. First of all, Klement et al. [20] introduced a family of TNs and TCNs and their properties in a fuzzy environment. Moreover, with time several researchers explored the concepts of triangular norms. Bobillo and Straccia [21] explored the algebraic TN and TCN. Klement and Navara [22] generalized the characteristic of TN and TCN under the Lukasiewicz TN. Wang [23] introduced the idea of drastic t-norm and TCN by utilizing the binary operations of triangular norms. Fodor [24] discovered new collections of TN and TCN with the characteristic of nilpotent minimum and its properties. Gál et al. [25] enlarged the concepts of TN and TCN in the form of Hamacher TN and TCN by using the operations of triangular norms. Navara. [26], represented the frank TNs and TCNs by utilizing the concepts of triangular norms and their binary operations. Lin. [27] gave a new tool to aggregate information in the form of Archimedean TN and TCN. Sarkar and Biswas, [28] developed the idea of Bonferroni mean and Dombi TCNs and TNs under a dual hesitant q-rung orthopair fuzzy environment. A lot of mathematicians worked by utilizing the theory of triangular norms given in [29,30,31,32].

Aczel and Alsina [33] presented the new operations namely A-TNM and A-TCNM which are more flexible than TN and TCN. Farahbod and Eftekhari [34] compared different TNs to evaluate the best one. Further, Farahbod and Eftekhari worked on several TNs and after experimental outcomes, obtained that Aczel Alsina is the best operator, Dubois prade operator is the second one and Dombi operator is the third operator. Senapati et al. [35] utilized the operations of TN and TCN based on interval-valued intuitionistic fuzzy (IVIF) information and introduced some new AOs in the form of IVIF weighted averaging (IVIFWA) with special cases. Güneri and Deveci [36] utilized an effective DM technique to evaluate a suitable supplier logistic company in the defence industry under consideration of q-ROF information. Senapati et al. [37] explored the operations of A-TNM and A-TCNM under the environment of IF information with the application of human resource selections and their properties. Senapati. [38], generalized the theory of picture fuzzy set (PFS) in the framework of the PF Aczel Alsina weighted averaging (PFAAWA) operator. Pamučar et al. [39] presented a useful strategy to reduce the impact of healthcare waste management and evaluated a particular case study by using the notion of Aczel Alsina rough FSs under multi-criteria in the DM process. Pamucar et al. [40] utilized the properties of metaverse models to assess different transportation systems based on ordinal property and Aczel Alsina aggregation models. Deveci et al. [41] applied properties of Aczel Alsina aggregation tools to evaluate a desirable parking place for E-scooter under consideration of fuzzy environments. Hussain et al. [42] explored an algorithm to develop a series of new AOs-based Aczel Alsina aggregation expressions under pythagorean fuzzy information. Hussain et al. [43] also utilized the theory of Aczel Alsina aggregation models and the structure of T-spherical fuzzy information for the development of new approaches. Bouraima et al. [44] evaluated a suitable transport infrastructure system and show its robustness by using several criteria in the DM process. We also studied the performance and superiority of Aczel Alsina aggregation expressions in the references [45,46,47,48].

Firstly, Hara et al. [49] introduced the Hamy mean (HM) operator to investigate the refinement of arithmetic and geometric mean. Li et al. [50] explored the concepts of HM operators in Dombi HM and Dual Dombi HM operators. Wu et al. [51] generalized the theory of HM and Dual HM (DHM) in the framework of IVIF Dombi HM (IVIFDHM) and IVIF weighted Dombi HM (IVIFWDHM) operators. Wu et al. [52] utilize the tool of HM operator to investigate the competitiveness of the tourism industry under the IVIF Hamy mean (IVIFHM) operators. Liang [53] expanded the concepts of the HM operator and weighted HM operator under the fuzzy number (FNs) to develop some new AOs such as FN intuitionistic fuzzy (IF) Hamy mean (FNIFHM) operator and FNIF weighted Hamy mean (FNIFWHM) operator. Liu et al. [54] developed some AOs of Intuitionistic Uncertain Linguistic HM Operators by using the theory of HM. Liu and Wang [55] generalized the concepts of HM based on IF Interaction HM Operators. Liu and Liu [56] gave new concepts of Linguistic IFHM operators by utilizing the tool of HM operators. Li et al. [57] extended the concept of HM and dual HM operators based on Pythagorean fuzzy (PyF) Hamy mean (PyFHM), PyF weighted HM (PyFWHM) and PyF weighted Dual HM (PyFWDHM) operators. We understand that DM issues are getting progressively more complicated in reality. To have the option to pick the unmatched alternative for the MADM issues, it is vital to convey the questionable information more favorably.

In the above discussion, we studied several AOs which are used to investigate the vague and uncertain information in the fuzzy system. They cannot adequately handle insufficient information and are unable to provide a smooth approximation of the information. Several types of triangular norms and its extension presented union and intersection based on algebraic sum and algebraic product. But Aczel Alsian sum and Aczel Alsian product have a great capacity to cope with unpredictable and vague information, Aczel Alsina aggregation models also provide a smooth approximation. Due to the robustness of Aczel Alsina aggregation expressions and the powerful structure of the IF environment, we exposed some fundamental operations of Aczel Alsina aggregation expressions under consideration of IF information. The aims of this article are as follows:

• (a) To explore the basic operations of Aczel Alsina aggregation expressions based on IF information.

• (b) We expose the theory of the HM model with some appropriate characteristics under consideration of IF information.

• (c) By utilizing the theory of HM tools, we developed a series of new approaches including IFAAHM, and IFAAWHM operators.

• (d) We also derive new techniques by using the theory of DHM models like IFAADHM, and IFAAWDHM operators with some particular properties.

• (e) To find the flexibility and efficiency of AOs, we gave an application with the help of numerical examples from engineering and construction management enterprises.

• (f) A comprehensive comparative study in which a comparison of current AOs with existing AOs and a conclusion are also present there.

The structure of this paper is organized as follows: In Sect. “Introduction”, we briefly discussed the background of our current work to understand the terminology of this article. In Sect. “Preliminaries”, we recall the notion of IFS, A-TNM, and A-TCNM, and some basic operational laws. In Sect. “Aczel Alsina operations based on IFVs”, we presented previously existing AOs of HM and DHM operators. In Sect. “Aczel Alsina intuitionistic fuzzy Hamy mean operator”, we developed the new idea of IFAAHM, and IFAAWHM operators and listed their properties of Idempotency, monotonicity, and boundedness. In Sect. “Aczel Alsina intuitionistic fuzzy weighted hamy mean operator”, the author generalized the concepts of HM operators in the form of IFAAWHM, and IFAAWDHM operators. In Sect. “Aczel Alsina intuitionistic fuzzy dual Hamy mean operator”, the author utilized the MADM techniques to find the flexibility and reliability of discussed operators. We established an application with the help of a numerical example to check effectiveness and validity by using the IFAAWHM and IFAAWDHM operators. We also compared our proposed AOs with existing AOs and suggested some advantages of our work in Sect. “Intuitionistic Fuzzy Aczel Alsina weighted dual Hamy mean operator”. In the end, we briefly explained this article in Sect. “Multi-attribute decision making with proposed algorithm”.

Preliminaries

In this part, we discuss the fundamental concepts of IFS, the theory of Aczel Alsina aggregation expressions and its basic operations for further development of this paper. A list of symbols and their meaning is stated in Table 1.

Table 1 Covered symbols and their meanings

Definition 1

[4] Consider a non-empty set $\mathtt{U}$. An IFS $B$ is the form as:

$$ B = \left\{ {\left( {\tau ,\left( {\upkappa\kern-1.0pt\text{\c{}}_{B} \left( \tau \right),\nu_{B} \left( \tau \right)} \right)} \right)| \in {\varvec{U}}} \right\}, $$

where $\upkappa\kern-1.0pt\text{\c{}}_{B} \left( \tau \right) \to \left[ {0, 1} \right]$ be the MG and $\nu_{B} \left( \tau \right) \to \left[ {0, 1} \right]$ be the NMG respectively for the$\tau \in \left[ {0, 1} \right]$. The hesitancy degree denoted by ${\mathfrak{E}}\left( \tau \right) = 1 - \left( {\upkappa\kern-1.0pt\text{\c{}}_{B} \left( \tau \right) + \nu_{B} \left( \tau \right)} \right),{ }{\mathfrak{E}}\left( \tau \right) \in \left[ {0,1} \right]$, and $\left( {\upkappa\kern-1.0pt\text{\c{}}_{B} \left( \tau \right),\nu_{B} \left( \tau \right)} \right)$ represents an intuitionistic fuzzy value (IFV) such that:

$$ 0 \le \upkappa\kern-1.0pt\text{\c{}}_{B} \left( \tau \right) + \nu_{B} \left( \tau \right) \le 1. $$

Definition 2

[33] The A-TNM is defined as:

$${{\text{\rlap{\textendash}\kern-0.5pt T}}}_{\acute{\hat{\hbox{A}}}}^{\partial }\left(a, {\d{b}}\right)=\left\{\begin{array}{c}{{\text{\rlap{\textendash}\kern-0.5pt T}}}_{D}\left(a, {\d{b}}\right)\quad if\quad \partial =0\\ min\left(a, {\d{b}}\right)\quad if\quad \partial =\infty \\ {e}^{-{\left({\left(-log\mathcalligra{a}\right)}^{\partial }+{\left(-log\d{b}\right)}^{\partial }\right)}^{\frac{1}{\partial }}} otherwise\end{array}\forall , 0\le \partial \le +\infty \right\},$$

And the A-TCNM is defined as:

$${\dot{\acute{\hbox{S}}}}_{\acute{\hat{\hbox{A}}}}^{\partial }\left(a, {\d{b}}\right)=\left\{\begin{array}{c}{\dot{\acute{\hbox{S}}}}_{D}\left(a, {\d{b}}\right)\quad if \quad\partial =0\\ ma\tau \left(a, {\d{b}}\right) \quad if \quad \partial =\infty \\ 1-{e}^{-{\left({\left(-log\mathcalligra{a}\right)}^{\partial }+{\left(-log\d{b}\right)}^{\partial }\right)}^{\frac{1}{\partial }}} otherwise\end{array}\forall , 0\le \partial \le +\infty \right\},$$

respectively.

Definition 3

[6] Consider $\zeta =\left(\upkappa\kern-1.0pt\text{\c{}}\left(\tau \right),\nu \left(\tau \right)\right)$ be an IFV, so the score function is defined as:

$$\c{S}\left(\zeta \right)=\frac{\left(1+\upkappa\kern-1.0pt\text{\c{}}\left(\tau \right)-\nu \left(\tau \right)\right)}{2}, \c{S}\left(\zeta \right), \in \left[0, 1\right].$$

(1)

Definition 4

[6] Consider $\zeta =\left(\upkappa\kern-1.0pt\text{\c{}}\left(\tau \right),\nu \left(\tau \right)\right)$ be an IFV, so the accuracy function is defined as:

$$\k{A}\left(\zeta \right)=\frac{\left(1+\upkappa\kern-1.0pt\text{\c{}}\left(\tau \right)+\nu \left(\tau \right)\right)}{2}, \k{A}\left(\zeta \right), \in \left[\mathrm{0,1}\right].$$

(2)

Example 1

Let ${\zeta }_{1}=\left(0.62, 0.33\right)$ and ${\zeta }_{2}={\zeta }_{1}=\left(0.05, 0.82\right)$ be two IFVs, then by using Definition 3 and 4 we have:

$$\mathrm{\c{S}}\left({\zeta }_{1}\right)=\frac{\left(1+{\upkappa\kern-1.0pt\text{\c{}}}_{1}\left(\tau \right)-{\nu }_{1}\left(\tau \right)\right)}{2}=\frac{\left(1+0.62-0.33\right)}{2}=0.65\in \left[\mathrm{0,1}\right],$$

$$\mathrm{\c{S}}\left({\zeta }_{2}\right)=\frac{\left(1+{\upkappa\kern-1.0pt\text{\c{}}}_{2}\left(\tau \right)-{\nu }_{2}\left(\tau \right)\right)}{2}=\frac{\left(1+0.05-0.82\right)}{2}=0.12\in \left[\mathrm{0,1}\right],$$

$$\mathrm{\k{A}}\left({\zeta }_{1}\right)=\frac{\left(1+{\upkappa\kern-1.0pt\text{\c{}}}_{1}\left(\tau \right)+{\nu }_{1}\left(\tau \right)\right)}{2}=\frac{\left(1+0.62+0.33\right)}{2}=0.98\in \left[\mathrm{0,1}\right],$$

$$\mathrm{\k{A}}\left({\zeta }_{2}\right)=\frac{\left(1+{\upkappa\kern-1.0pt\text{\c{}}}_{2}\left(\tau \right)+{\nu }_{2}\left(\tau \right)\right)}{2}=\frac{\left(1+0.05+0.82\right)}{2}=0.94\in \left[\mathrm{0,1}\right].$$

Definition 5

[6] Consider $\zeta =\left(\upkappa\kern-1.0pt\text{\c{}}\left(\tau \right),\nu \left(\tau \right)\right)$, ${\zeta }_{1}=\left({\upkappa\kern-1.0pt\text{\c{}}}_{1}\left(\tau \right),{\nu }_{1}\left(\tau \right)\right)$ and ${\zeta }_{2}=\left({\upkappa\kern-1.0pt\text{\c{}}}_{2}\left(\tau \right),{\nu }_{2}\left(\tau \right)\right)$ are three IFVs. So $\c{S}\left({\zeta }_{1}\right)=\upkappa\kern-1.0pt\text{\c{}}\left(\tau \right)-\nu \left(\tau \right)$ and $\c{S}\left({\zeta }_{2}\right)=\upkappa\kern-1.0pt\text{\c{}}\left(\tau \right)-\nu \left(\tau \right)$ be the score values of ${\zeta }_{1}$ and ${\zeta }_{2}$ respectively. Consider $\k{A}\left({\zeta }_{1}\right)=\upkappa\kern-1.0pt\text{\c{}}\left(\tau \right)+\nu \left(\tau \right)$ and $\k{A}\left({\zeta }_{2}\right)=\upkappa\kern-1.0pt\text{\c{}}\left(\tau \right)+\nu \left(\tau \right)$ be the accuracy values of ${\zeta }_{1}$ and ${\zeta }_{2}$ respectively. Now we discuss some basic operations of score function and accuracy function, If $\c{S}\left({\zeta }_{1}\right)<\c{S}\left({\zeta }_{2}\right)$ then ${\zeta }_{1}<{\zeta }_{2}$ and If $\c{S}\left({\zeta }_{1}\right)>\c{S}\left({\zeta }_{2}\right)$ then ${\zeta }_{1}>{\zeta }_{2}$. So, If $\c{S}\left({\zeta }_{1}\right)=\c{S}\left({\zeta }_{2}\right)$ then:

(a) $\mathrm{\k{A}}\left({\zeta }_{1}\right)>\mathrm{\k{A}}\left({\zeta }_{2}\right)$, then ${\zeta }_{1}>{\zeta }_{2}$.

(b) $\mathrm{\k{A}}\left({\zeta }_{1}\right)<\mathrm{\k{A}}\left({\zeta }_{2}\right)$, then ${\zeta }_{1}<{\zeta }_{2}$.

(c) $\mathrm{\k{A}}\left({\zeta }_{1}\right)=\mathrm{\k{A}}\left({\zeta }_{2}\right)$, then ${\zeta }_{1}\approx {\zeta }_{2}$.

Definition 6

[35] Consider $\zeta =\left(\upkappa\kern-1.0pt\text{\c{}}\left(\tau \right),\nu \left(\tau \right)\right)$, ${\zeta }_{1}=\left({\upkappa\kern-1.0pt\text{\c{}}}_{1}\left(\tau \right),{\nu }_{1}\left(\tau \right)\right)$ and ${\zeta }_{2}=\left({\upkappa\kern-1.0pt\text{\c{}}}_{2}\left(\tau \right),{\nu }_{2}\left(\tau \right)\right)$ are three IFVs and $\lambda >0$ be a real number, then we defined some basic rules as follow:

• (1) ${\zeta }_{1}\oplus {\zeta }_{2}=\left(1-\left(1-{\upkappa\kern-1.0pt\text{\c{}}}_{1}\left(\tau \right)\right)\left(1-{\upkappa\kern-1.0pt\text{\c{}}}_{2}\left(\tau \right)\right), {\nu }_{1}\left(\tau \right).{\nu }_{2}\left(\tau \right)\right),$

• (2) ${\zeta }_{1}\otimes{\zeta }_{2}=\left( {\upkappa\kern-1.0pt\text{\c{}}}_{1}\left(\tau \right).{\upkappa\kern-1.0pt\text{\c{}}}_{2}\left(\tau \right), 1-\left(1-{\nu }_{1}\left(\tau \right)\right)\left(1-{\nu }_{2}\left(\tau \right)\right)\right),$

• (3) $\lambda \zeta =\left(1-{\left(1-\upkappa\kern-1.0pt\text{\c{}}\left(\tau \right)\right)}^{\lambda }, {\nu }^{\lambda }\left(\tau \right)\right), \lambda >0,$

• (4) ${\zeta }^{\lambda }=\left({\upkappa\kern-1.0pt\text{\c{}}}^{\lambda }\left(\tau \right), 1-{\left(1-\nu \left(\tau \right)\right)}^{\lambda }\right), \lambda >0,$

• (5) $\overline{\zeta }=\left(\nu \left(\tau \right), \upkappa\kern-1.0pt\text{\c{}}\left(\tau \right)\right).$

By inspiring the theory of Aczel Alsina aggregation models, Senapati et al. [37] illustrated some basic operations of Aczel Alsina aggregation tools and some new approaches under consideration of IF information. Senapati et al. [35] also extended the concepts of Aczel Alsian aggregation expressions under the IVIF framework. Recently, Aczel Alsina aggregation models gain a lot of attention from numerous scholars. The Hamy mean [49] aggregation models are well-known power aggregation models, which are utilized to define correlation among different input arguments. Liang [53] utilized the theory of HM tools based algebraic sum and algebraic product under consideration of IF information, extension of the concepts of the HM tools under consideration of IVIF information seen in [52]. In order to deal with unpredictable and imprecision information realistically, we needed some reliable approaches. Due to the robustness and reliability of Aczel Alsina aggregation tools, we derived a series of new approaches by using the theory HM aggregation tools including IFAAHM, IFAAWHM, IFAAWDHM and IFAAWDHM operators under consideration of IF information.

Aczel Alsina operations based on IFVs

We will explore the fundamental operational laws of Aczel Alsina TN and TCN. The Aczel Alsina product $\left(\text{{\AA }}\otimes\mathcal{B}\right)$ and Aczel Alsina sum $\left(\text{{\AA }}\oplus\mathcal{B}\right)$ of TN $\mathop{\hbox{T}}\limits_{\hat{}}$ and TCN $\check{{{\mathrm{S}}}}$ are defined as follows:

$$\text{{\AA }}\otimes\mathcal{B}=\left\{\tau , \mathop{\hbox{T}}\limits_{\hat{}}\left({\upkappa\kern-1.0pt\text{\c{}}}_{\text{{\AA }}}\left(\tau \right),{\upkappa\kern-1.0pt\text{\c{}}}_{\mathcal{B}}\left(\tau \right)\right), \check{{{\mathrm{S}}}} \left({\nu }_{\text{{\AA }}}\left(\tau \right),{\nu }_{\mathcal{B}}\left(\tau \right)\right) |\tau \in \mathtt{U}\right\}.$$

$$\text{{\AA }}\otimes\mathcal{B}=\left\{\tau , {\check{{{\mathrm{S}}}}}_{\text{{\AA }}}\left(\upkappa\kern-1.0pt\text{\c{}}\left(\tau \right),{\upkappa\kern-1.0pt\text{\c{}}}_{\mathcal{B}}\left(\tau \right)\right), \mathop{\hbox{T}}\limits_{\hat{}}\left({\nu }_{\text{{\AA }}}\left(\tau \right),{\nu }_{\mathcal{B}}\left(\tau \right)\right) |\tau \in \mathtt{U}\right\}.$$

Definition 7

[37] Let $\zeta =\left(\upkappa\kern-1.0pt\text{\c{}}\left(\tau \right),\nu \left(\tau \right)\right)$, ${\zeta }_{1}=\left({\upkappa\kern-1.0pt\text{\c{}}}_{1}\left(\tau \right),{\nu }_{1}\left(\tau \right)\right)$ and ${\zeta }_{2}=\left({\upkappa\kern-1.0pt\text{\c{}}}_{2}\left(\tau \right),{\nu }_{2}\left(\tau \right)\right)$ are three IFVs and $\lambda >0$. Then some basic operations of IFVs based on Definition 4, are given as:

• (a) ${\zeta }_{1}\otimes{\zeta }_{2}=\left(1-{e}^{-{\left({\left(-ln\left(1-{\upkappa\kern-1.0pt\text{\c{}}}_{1}\left(\tau \right)\right)\right)}^{\partial }+ {\left(-ln\left(1-{\upkappa\kern-1.0pt\text{\c{}}}_{2}\left(\tau \right)\right)\right)}^{\partial }\right)}^{\frac{1}{\partial }}},\right.\break \left. {e}^{-{\left({\left(-ln\left({\nu }_{1}\left(\tau \right)\right)\right)}^{\partial }+{\left(-ln\left({\nu }_{2}\left(\tau \right)\right)\right)}^{\partial }\right)}^{\frac{1}{\partial }}}\right),$

• (b) ${\zeta }_{1}\otimes{\zeta }_{2}=\left({e}^{-{\left({\left(-ln\left({\upkappa\kern-1.0pt\text{\c{}}}_{1}\left(\tau \right)\right)\right)}^{\partial }+{\left(-ln\left({\upkappa\kern-1.0pt\text{\c{}}}_{2}\left(\tau \right)\right)\right)}^{\partial }\right)}^{\frac{1}{\partial }}},\right. \break \left. 1-{e}^{-{\left({\left(-ln\left(1-{\nu }_{1}\left(\tau \right)\right)\right)}^{\partial }+ {\left(-ln\left(1-{\nu }_{2}\left(\tau \right)\right)\right)}^{\partial }\right)}^{\frac{1}{\partial }}}\right),$

• (c) $\lambda \zeta =\left(1-{e}^{-{\left(\lambda \left({\left(-ln\left(1-\upkappa\kern-1.0pt\text{\c{}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}, {e}^{-{\left({\lambda \left(-ln\left(\nu \left(\tau \right)\right)\right)}^{\partial }\right)}^{\frac{1}{\partial }}}\right),$

• (d) ${\zeta }^{\lambda }=\left({e}^{-{\left({\lambda \left(-ln\left(\upkappa\kern-1.0pt\text{\c{}}\left(\tau \right)\right)\right)}^{\partial }\right)}^{\frac{1}{\partial }}},1-{e}^{-{\left(\lambda \left({\left(-ln\left(1-\nu \left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right).$

Example 2

Let $\zeta =\left(0.25, 0.45\right)$, ${\zeta }_{1}=\left(0.36, 0.55\right)$ and ${\zeta }_{2}=\left(0.28, 0.45\right)$ be three IFVs, then AA operations by using Definition 7, for $\partial =3$ and $\lambda =2$ we have:

• (a) ${\zeta }_{1}\otimes{\zeta }_{2}=\left(1-{e}^{-{\left({\left(-ln\left(1-\left(0.36\right)\right)\right)}^{3}+ {\left(-ln\left(1-\left(0.28\right)\right)\right)}^{3}\right)}^{\frac{1}{3}}},\right. \break \left. {e}^{-{\left({\left(-ln\left(0.55\right)\right)}^{3}+{\left(-ln\left(0.45\right)\right)}^{3}\right)}^{\frac{1}{3}}}\right)=\left(\mathrm{0.3929,0.4076}\right),$

• (b) ${\zeta }_{1}\otimes{\zeta }_{2}=\left({e}^{-{\left({\left(-ln\left(0.36\right)\right)}^{3}+{\left(-ln\left(0.28\right)\right)}^{3}\right)}^{\frac{1}{3}}},\right. \break \left. 1-{e}^{-{\left({\left(-ln\left(1-\left(0.55\right)\right)\right)}^{3}+ {\left(-ln\left(1-\left(0.45\right)\right)\right)}^{3}\right)}^{\frac{1}{3}}}\right)=\left(0.2316, 0.5924\right),$

• (c) $2\zeta =\left(1-{e}^{-{\left(2\left({\left(-ln\left(1-\left(0.25\right)\right)\right)}^{3}\right)\right)}^{\frac{1}{3}}}, {e}^{-{\left({2\left(-ln\left(0.45\right)\right)}^{3}\right)}^{\frac{1}{3}}}\right)=\left(0.3040, 0.3657\right),$

• (d) $2\zeta =\left({e}^{-{\left({2\left(-ln\left(0.25\right)\right)}^{3}\right)}^{\frac{1}{3}}},1-{e}^{-{\left(2\left({\left(-ln\left(1-\left(0.45\right)\right)\right)}^{3}\right)\right)}^{\frac{1}{3}}}\right)=\left(0.1744, 0.5292\right).$

Theorem 1

Let $\zeta =\left(\upkappa\kern-1.0pt\text{\c{}}\left(\tau \right),\nu \left(\tau \right)\right)$, ${\zeta }_{1}=\left({\upkappa\kern-1.0pt\text{\c{}}}_{1}\left(\tau \right),{\nu }_{1}\left(\tau \right)\right)$ and ${\zeta }_{2}=\left({\upkappa\kern-1.0pt\text{\c{}}}_{2}\left(\tau \right),{\nu }_{2}\left(\tau \right)\right)$ are three IFVs and $\lambda >0$ then:

• (1) ${\zeta }_{1}\oplus {\zeta }_{2}={\zeta }_{2} \oplus {\zeta }_{1}$

• (2) ${\zeta }_{1} \otimes {\zeta }_{2}={\zeta }_{2} \otimes {\zeta }_{1}$

• (3) $\lambda \left({\zeta }_{1}\oplus {\zeta }_{2}\right)=\lambda {\zeta }_{1} \oplus {\lambda \zeta }_{2}, \lambda >0$

• (4) $\left({\lambda }_{1}+{\lambda }_{2}\right)\zeta ={\lambda }_{1}\zeta \oplus {\lambda }_{2}\zeta , {\lambda }_{1}, {\lambda }_{2}>0$

• (5) ${\left({\zeta }_{1}\otimes {\zeta }_{2}\right)}^{\lambda }={\zeta }_{1}^{\lambda } \otimes {\zeta }_{1}^{\lambda }, \lambda >0$

• (6) ${\zeta }^{{\lambda }_{1}} \otimes {\zeta }^{{\lambda }_{2}}={\zeta }^{\left({\lambda }_{1}+{\lambda }_{2}\right)}, {\lambda }_{1},{\lambda }_{2}>0$

Proof

Proof is straightforward.

Aczel Alsina intuitionistic fuzzy Hamy mean operator

In this section, we explore the ideas of HM and DHM operators in the system of IFVs. We will also study innovative concepts of HM operators in the framework of IFSs by using the operational laws of Aczel Alsina TN and TCN defined in Definition 7.

Definition 8

[49] The HM operator is the form:

$$H{M}^{\left(\tau \right)}\left({\zeta }_{1},{\zeta }_{2},\dots ,{\zeta }_{n}\right)=\frac{\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\left(\prod_{i=1}^{\tau }{\zeta }_{{i}_{\mathcalligra{s}}} \right)}^{\frac{1}{\tau }}}{{C}_{n}^{\tau }},$$

(3)

where $\tau$ is such that $1\le \tau \le n$ and ${C}_{n}^{\tau }$ represent the binomial coefficient i.e. ${C}_{n}^{\tau }=\frac{n!}{\tau !\left(n-\tau \right)!}$.

The HM operator satisfies such conditions:

• 1. $H{M}^{\left(\tau \right)}\left({\zeta }_{1},{\zeta }_{2},\dots ,{\zeta }_{n}\right)=\zeta$ if ${\zeta }_{i}=\zeta , \left(i=\mathrm{1,2},3,\dots ,n\right)$.

• 2. $H{M}^{\left(\tau \right)}\left({\zeta }_{1},{\zeta }_{2},\dots ,{\zeta }_{n}\right)\le H{M}^{\left(\tau \right)}\left({\acute{{\upomega}}}_{1},{\acute{{\upomega}}}_{2},\dots ,{\acute{{\upomega}}}_{n}\right)$ if ${\zeta }_{i}\le {\acute{{\upomega}}}_{i}, \left(i=\mathrm{1,2},3,\dots ,n\right)$.

• 3. ${min}\left({\zeta }_{i}\right)\le H{M}^{\left(\tau \right)}\left({\zeta }_{1},{\zeta }_{2},\dots ,{\zeta }_{n}\right)\le ma\tau {\zeta }_{i}.$

• 4. For arithmetic mean operator $H{M}^{\left(\tau \right)}\left({\zeta }_{1},{\zeta }_{2},\dots ,{\zeta }_{n}\right)=\frac{1}{n}\sum_{i=1}^{n}{\zeta }_{i}.$

• 5. For geometric mean operator $H{M}^{\left(\tau \right)}\left({\zeta }_{1},{\zeta }_{2},\dots ,{\zeta }_{n}\right)={\left(\prod_{i=1}^{n}{\zeta }_{i}\right)}^{\frac{1}{\tau }}.$

We recall the notion of the DHM operator by using the basic operational laws.

Definition 9

[49] The DHM operator is defined as:

$$DH{M}^{\left(\tau \right)}\left({\zeta }_{1},{\zeta }_{2},\dots ,{\zeta }_{n}\right)={\left(\prod_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}\left(\frac{\sum_{\mathcalligra{s}=1}^{\tau }{\zeta }_{\mathcalligra{s}}}{\tau }\right)\right)}^{\frac{1}{{C}_{n}^{\tau }}}.$$

(4)

Definition 10

Let ${\zeta }_{i}=\left({\upkappa\kern-1.0pt\text{\c{}}}_{i}\left(\tau \right),{\nu }_{i}\left(\tau \right)\right),i=\mathrm{1,2},\dots ,n$, be the family of IFVs. Then IFAAHM operator is defined as:

$${\mathrm{IFAAHM}}^{\left(\tau \right)}\left({\zeta }_{1},{\zeta }_{2},\dots ,{\zeta }_{n}\right)=\frac{\underset{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\oplus }{\left(\stackrel{\tau }{\underset{\mathcalligra{s}=1}{\otimes}}{\zeta }_{{i}_{\mathcalligra{s}}}\right)}^{\frac{1}{\tau }}}{{C}_{n}^{\tau }}.$$

(5)

Theorem 2

Let ${\zeta }_{i}=\left({\upkappa\kern-1.0pt\text{\c{}}}_{i}\left(\tau \right),{\nu }_{i}\left(\tau \right)\right),i=\mathrm{1,2},\dots ,n$, be the family of IFVs. Then the aggregated value of the IFAAHM operator is defined as:

$${\mathrm{IFAAHM}}^{\left(\tau \right)}\left({\zeta }_{1},{\zeta }_{2},\dots ,{\zeta }_{n}\right) =\left(\begin{array}{c}1-{e}^{-{\left(\left(\frac{1}{{C}_{n}^{\tau }}\right)\left(\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left({\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)\right)\right)}^{\frac{1}{\partial }}},\\ {e}^{-{\left(\left(\frac{1}{{C}_{n}^{\tau }}\right)\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left(1-{\nu }_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\end{array}\right).$$

(6)

Proof

We prove this Theorem 1 by using basic operations of A-TNM and A-TCNM, we have:

$$\stackrel{\tau }{\underset{\mathcalligra{s}=1}{\otimes}}{\zeta }_{\mathcalligra{s}}=\left({e}^{-{\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left({\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)}^{\frac{1}{\partial }}},1-{e}^{-{\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left(1-{\nu }_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)}^{\frac{1}{\partial }}}\right).$$

Further,

$${\left(\stackrel{\tau }{\underset{i=1}{\otimes}}{\zeta }_{\mathcalligra{s}}\right)}^{\frac{1}{\tau }}=\left({e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left({\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}},1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left(1-{\nu }_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right),$$

Therefore,

$${\oplus }_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\left(\stackrel{\tau }{\underset{\mathcalligra{s}=1}{\otimes}}{\zeta }_{\mathcalligra{s}}\right)}^{\frac{1}{\tau }}=\left(\begin{array}{c}1-{e}^{-{\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left({\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)}^{\frac{1}{\partial }}},\\ {e}^{-{\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left(1-{\nu }_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)}^{\frac{1}{\partial }}}\end{array}\right).$$

After the above, we have:

$$\frac{{\oplus }_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\left(\stackrel{\tau }{\underset{\mathcalligra{s}=1}{\otimes}}{\zeta }_{\mathcalligra{s}}\right)}^{\frac{1}{\tau }}}{{C}_{n}^{\tau }}=\left(\begin{array}{c}1-{e}^{-{\left(\left(\frac{1}{{C}_{n}^{\tau }}\right)\left(\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left({\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)\right)\right)}^{\frac{1}{\partial }}},\\ {e}^{-{\left(\left(\frac{1}{{C}_{n}^{\tau }}\right)\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left(1-{\nu }_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\end{array}\right)$$

Now we have to show that Eq. 6 is an IFV. If satisfy the following conditions:

• 1. $0\le \alpha \le 1, 0\le \beta \le 1$

• 2. $0\le {\alpha }_{{i}_{\mathcalligra{s}}}+{\beta }_{{i}_{\mathcalligra{s}}}\le 1$

Consider,

$$\alpha =1-{e}^{-{\left(\left(\frac{1}{{C}_{n}^{\tau }}\right)\left(\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}}=1^{\tau }{\left(-ln\left({\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)\right)\right)}^{\frac{1}{\partial }}}$$

$$\beta ={e}^{-{\left(\!\left(\!\frac{1}{{C}_{n}^{\tau }}\right)\left(\!\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\left(-ln\left(1-{e}^{-{\left(\!\left(\!\frac{1}{\tau }\!\right)\left(\!\sum_{\mathcalligra{s}}=1^{\tau }{\left(-ln\left(1-{\nu }_{{i}_{\mathcalligra{s}}}\left(\tau \right)\!\right)\!\right)}^{\partial }\!\right)\!\right)}^{\frac{1}{\partial }}}\!\right)\!\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}$$

To show this $0\le \alpha \le 1, 0\le \beta \le 1$, we have:

We know that ${\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\in \left[0, 1\right]$

$$\Rightarrow {e}^{-{\left(\sum_{\mathcalligra{s}}=1^{\tau }{\left(-ln\left({\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)}^{\frac{1}{\partial }}}\in \left[0, 1\right].$$

$$\Rightarrow {e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}}=1^{\tau }{\left(-ln\left({\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\in \left[0, 1\right].$$

$$\begin{aligned} &\Rightarrow 1-{e}^{-{\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}}=1^{\tau }{\left(-ln\left({\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)}^{\frac{1}{\partial }}}\nonumber \\ &\quad \in \left[0, 1\right].\end{aligned}$$

$$\begin{aligned} &\Rightarrow {e}^{-{\left(\left(\frac{1}{{C}_{n}^{\tau }}\right){\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{\tau}\! \right)\left(\!\sum_{\mathcalligra{s}}=1^{\tau }{\left(\!-ln\left(1-{\nu }_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\!\right)\!\right)}^{\frac{1}{\partial }}}\!\right)\!\right)}^{\partial }\!\right)}^{\frac{1}{\partial }}\!\right)}^{\frac{1}{\partial }}}\nonumber \\ &\in \left[0, 1\right].\end{aligned}$$

$$\Rightarrow 0\le {\alpha }_{{i}_{\mathcalligra{s}}}\le 1.$$

In this way, we have to show that:

$$\begin{aligned} &{e}^{-{\left(\!\left(\!\frac{1}{{C}_{n}^{\tau }}\right)\left(\!\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\!\sum_{\mathcalligra{s}}=1^{\tau }{\left(-ln\left(1-{\nu }_{{i}_{\mathcalligra{s}}}\left(\tau \right)\!\right)\!\right)}^{\partial }\!\right)\!\right)}^{\frac{1}{\partial }}}\!\right)\!\right)}^{\partial }\!\right)\!\right)}^{\frac{1}{\partial }}} \nonumber \\ &\quad \in \left[0, 1\right].\end{aligned}$$

$$\Rightarrow 0\le {\beta }_{{i}_{\mathcalligra{s}}}\le 1.$$

Next, we have $0\le {\alpha }_{{i}_{\mathcalligra{s}}}+{\beta }_{{i}_{\mathcalligra{s}}}\le 1$.

$$\left(\!\!\begin{array}{c}1-{e}^{-{\left(\!\left(\!\frac{1}{{C}_{n}^{\tau }}\!\right)\left(\!\left(\!\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\left(-ln\left(1-{e}^{-{\left(\!\left(\!\frac{1}{\tau }\!\right)\left(\!\sum_{\mathcalligra{s}=1}^{\tau }{\left(\!-ln\left({\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\!\right)\!\right)}^{\partial }\!\right)\!\right)}^{\frac{1}{\partial }}}\!\right)\!\right)}^{\partial }\!\right)\!\right)\!\right)}^{\frac{1}{\partial }}}+\\ \left({e}^{-{\left(\!\left(\!\frac{1}{{C}_{n}^{\tau }}\!\right)\left(\!\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\left(\!-ln\left(\!1-{e}^{-{\left(\!\left(\!\frac{1}{\tau }\!\right)\left(\!\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left(1-{\nu }_{{i}_{\mathcalligra{s}}}\left(\tau \right)\!\right)\!\right)}^{\partial }\!\right)\!\right)}^{\frac{1}{\partial }}}\!\right)\!\right)}^{\partial }\right)\!\right)}^{\frac{1}{\partial }}}\!\right)\end{array}\!\right)$$

$$\Rightarrow 0\le \left(\begin{array}{c}1-{e}^{-{\left(\left(\frac{1}{{C}_{n}^{\tau }}\right)\left(\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left({\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)\right)\right)}^{\frac{1}{\partial }}},\\ {e}^{-{\left(\left(\frac{1}{{C}_{n}^{\tau }}\right)\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left(1-{\nu }_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\end{array}\right)\le 1$$

Now we illustrate some basic properties of the IFAAHM operator.

Theorem 3

(Idempotency property) let ${\zeta }_{i}=\left({\upkappa\kern-1.0pt\text{\c{}}}_{i}\left(\tau \right),{\nu }_{i}\left(\tau \right)\right),i=\mathrm{1,2},\dots ,n$, be the family of all identical IFVs. Then:

$${\mathrm{IFAAHM}}^{\left(\tau \right)}\left({\zeta }_{1},{\zeta }_{2},\dots ,{\zeta }_{n}\right)=\zeta .$$

Proof

We know that ${\zeta }_{i}=\left({\upkappa\kern-1.0pt\text{\c{}}}_{i}\left(\tau \right),{\nu }_{i}\left(\tau \right)\right),i=\mathrm{1,2},\dots ,n$, be the family of all identical IFVs. Then:

$$ \begin{aligned}{\mathrm{IFAAHM}}^{\left(\tau \right)}\left({\zeta }_{1},{\zeta }_{2},\dots ,{\zeta }_{n}\right) &=\left(\begin{array}{c}1-{e}^{-{\left(\left(\frac{1}{{C}_{n}^{\tau }}\right)\left(\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left({\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)\right)\right)}^{\frac{1}{\partial }}},\\ {e}^{-{\left(\left(\frac{1}{{C}_{n}^{\tau }}\right)\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left(1-{\nu }_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\end{array}\right) \\ & =\left(\begin{array}{c}1-{e}^{-{\left(\left(\frac{1}{{C}_{n}^{\tau }}\right)\left(\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\left(-ln\left(1-{e}^{-{\left({\left(-ln\left({\upkappa\kern-1.0pt\text{\c{}}}_{i}\left(\tau \right)\right)\right)}^{\partial }\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)\right)\right)}^{\frac{1}{\partial }}},\\ {e}^{-{\left(\left(\frac{1}{{C}_{n}^{\tau }}\right)\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\left(-ln\left(1-{e}^{-{\left({\left(-ln\left(1-{\nu }_{i}\left(\tau \right)\right)\right)}^{\partial }\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\end{array}\right) \\ &=\left(\begin{array}{c}1-{e}^{-{\left({\left(-ln\left(1-{e}^{-{\left({\left(-ln\left({\upkappa\kern-1.0pt\text{\c{}}}_{i}\left(\tau \right)\right)\right)}^{\partial }\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)}^{\frac{1}{\partial }}},\\ {e}^{-{\left({\left(-ln\left(1-{e}^{-{\left({\left(-ln\left(1-{\nu }_{i}\left(\tau \right)\right)\right)}^{\partial }\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)}^{\frac{1}{\partial }}}\end{array}\right) \\& =\left(\upkappa\kern-1.0pt\text{\c{}}\left(\tau \right),\nu \left(\tau \right)\right)=\zeta .\end{aligned}$$

Theorem 4

(Monotonicity property) let ${\zeta }_{i}=\left({\upkappa\kern-1.0pt\text{\c{}}}_{i}\left(\tau \right),{\nu }_{i}\left(\tau \right)\right),i=\mathrm{1,2},\dots ,n$ and ${\xi }_{i}=\left({\gamma }_{i}\left(\tau \right),{\delta }_{i}\left(\tau \right)\right), i=\mathrm{1,2},\dots ,n$ be the family of two IFVs, if ${\upkappa\kern-1.0pt\text{\c{}}}_{i}\left(\tau \right)\le {\gamma }_{i}\left(\tau \right),{\nu }_{i}\left(\tau \right)\ge {\delta }_{i}\left(\tau \right), \forall i$, Then:

$${\mathrm{IFAAHM}}^{\left(\tau \right)}\left({\zeta }_{1},{\zeta }_{2},\dots ,{\zeta }_{n}\right)\le {\mathrm{IFAAHM}}^{\left(\tau \right)}\left({\xi }_{1},{\xi }_{2},\dots ,{\xi }_{n}\right)$$

Proof

Consider ${\zeta }_{i}=\left({\upkappa\kern-1.0pt\text{\c{}}}_{i}\left(\tau \right),{\nu }_{i}\left(\tau \right)\right),i=\mathrm{1,2},\dots ,n$ and ${\xi }_{i}=\left({\gamma }_{i}\left(\tau \right),{\delta }_{i}\left(\tau \right)\right), i=\mathrm{1,2},\dots ,n$ be the family of two IFVs, if ${\upkappa\kern-1.0pt\text{\c{}}}_{i}\left(\tau \right)\le {\gamma }_{i}\left(\tau \right),{\nu }_{i}\left(\tau \right)\ge {\delta }_{i}\left(\tau \right), \forall i$, Then:

$${e}^{-{\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left({\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)}^{\frac{1}{\partial }}}\le {e}^{-{\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left({\gamma }_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)}^{\frac{1}{\partial }}}$$

$${e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left({\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\ge {e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left({\gamma }_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}$$

$$\begin{aligned}&1-{e}^{-{\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left({\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)}^{\frac{1}{\partial }}} \\&\quad\le 1-{e}^{-{\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left({\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)}^{\frac{1}{\partial }}}\end{aligned}$$

$$\begin{aligned} &1-{e}^{-{\left(\left(\frac{1}{{C}_{n}^{\tau }}\right)\left(\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left({\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)\right)\right)}^{\frac{1}{\partial }}} \nonumber \\ &\quad \le 1-{e}^{-{\left(\left(\frac{1}{{C}_{n}^{\tau }}\right)\left(\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left({\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)\right)\right)}^{\frac{1}{\partial }}}\end{aligned}$$

This means that ${\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\le {\gamma }_{{i}_{\mathcalligra{s}}}\left(\tau \right).$

Similarly, we can show ${\nu }_{{i}_{\mathcalligra{s}}}\left(\tau \right)\ge {\delta }_{{i}_{\mathcalligra{s}}}\left(\tau \right)$.

If ${\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)<{\gamma }_{{i}_{\mathcalligra{s}}}\left(\tau \right),{\nu }_{{i}_{\mathcalligra{s}}}\left(\tau \right)>{\delta }_{{i}_{\mathcalligra{s}}}\left(\tau \right)$, then:

$${\mathrm{IFAAHM}}^{\left(\tau \right)}\left({\zeta }_{1},{\zeta }_{2},\dots ,{\zeta }_{n}\right)<{\mathrm{IFAAHM}}^{\left(\tau \right)}\left({\xi }_{1},{\xi }_{2},\dots ,{\xi }_{n}\right)$$

If ${\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)={\gamma }_{{i}_{\mathcalligra{s}}}\left(\tau \right),{\nu }_{{i}_{\mathcalligra{s}}}\left(\tau \right)={\delta }_{{i}_{\mathcalligra{s}}} \left(\tau \right)$, then:

$${\mathrm{IFAAHM}}^{\left(\tau \right)}\left({\zeta }_{1},{\zeta }_{2},\dots ,{\zeta }_{n}\right)={\mathrm{IFAAHM}}^{\left(\tau \right)}\left({\xi }_{1},{\xi }_{2},\dots ,{\xi }_{n}\right)$$

Theorem 5

(Boundedness property) let ${\zeta }_{i}=\left({\upkappa\kern-1.0pt\text{\c{}}}_{i}\left(\tau \right),{\nu }_{i}\left(\tau \right)\right),i=\mathrm{1,2},\dots ,n$ be the family of IFVs, if ${\zeta }_{i}^{-}=\wedge \left({\zeta }_{1}, {\zeta }_{2}, {\zeta }_{3}, \dots , {\zeta }_{n}\right)$ and ${\zeta }_{i}^{+}=\vee \left({\zeta }_{1}, {\zeta }_{2}, {\zeta }_{3}, \dots , {\zeta }_{n}\right)$, then:

$${\zeta }^{-}\le \mathrm{IFAAHM}\left({\zeta }_{1},{\zeta }_{2},\dots ,{\zeta }_{n}\right)\le {\zeta }^{+}$$

where symbols $\wedge$ $\vee$ represent the minimum and maximum values of ${\zeta }_{\mathcalligra{s}}$.

Proof

By using Theorem 2 and 3. We have:

$$\mathrm{IFAAHM}\left({\zeta }_{1},{\zeta }_{2},\dots ,{\zeta }_{n}\right)\ge \mathrm{IFAAHM}\left({\zeta }_{1}^{-},{\zeta }_{2}^{-},\dots ,{\zeta }_{n}^{-}\right)={\zeta }^{-}$$

$$\mathrm{IFAAHM}\left({\zeta }_{1},{\zeta }_{2},\dots ,{\zeta }_{n}\right)\le \mathrm{IFAAHM}\left({\zeta }_{1}^{+},{\zeta }_{2}^{+},\dots ,{\zeta }_{n}^{+}\right)={\zeta }^{+}$$

Therefore ${\zeta }^{-}\le \mathrm{IFAAHM}\left({\zeta }_{1},{\zeta }_{2},\dots ,{\zeta }_{n}\right)\le {\zeta }^{+}$

Example 3

Consider ${\zeta }_{1}=\left(0.35, 0.56\right)$,${\zeta }_{2}=\left(0.62, 0.73\right), {\zeta }_{3}=\left(0.72, 0.25\right)$ and ${\zeta }_{4}=\left(0.47, 0.51\right)$ are four IFVs. Then we applied an IFAAHM operator to aggregate given IFVs. Let $\partial =3$ and $\tau =2$.

$$\begin{aligned}{\mathrm{IFAAHM}}^{\left(\tau \right)}\left({\zeta }_{1},{\zeta }_{2},{\zeta }_{3},{\zeta }_{4}\right) &=\left(\begin{array}{c}1-{e}^{-{\left(\left(\frac{1}{{C}_{n}^{\tau }}\right)\left(\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left({\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)\right)\right)}^{\frac{1}{\partial }}},\\ {e}^{-{\left(\left(\frac{1}{{C}_{n}^{\tau }}\right)\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left(1-{\nu }_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\end{array}\right) \\ &=\left(\begin{array}{c}1-{e}^{-{\left(\left(\frac{1}{6}\right)\left(\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{2}\right)\left(\sum_{i=1}^{2}{\left(-ln\left({\upkappa\kern-1.0pt\text{\c{}}}_{i}\left(\tau \right)\right)\right)}^{3}\right)\right)}^{\frac{1}{3}}}\right)\right)}^{3}\right)\right)\right)}^{\frac{1}{3}}},\\ {e}^{-{\left(\left(\frac{1}{6}\right)\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{2}\right)\left(\sum_{i=1}^{2}{\left(-ln\left(1-{\nu }_{i}\left(\tau \right)\right)\right)}^{3}\right)\right)}^{\frac{1}{3}}}\right)\right)}^{3}\right)\right)}^{\frac{1}{3}}}\end{array}\right) \\ &=\left(0.5351, 0.5235\right)\end{aligned}$$

Aczel Alsina intuitionistic fuzzy weighted Hamy mean operator

We explored concepts of HM mean operator in the form of IFAAHM operator by using the basic operational laws of A-TNM and A-TCNM based on IFVs.

Definition 11

Let ${\zeta }_{i}=\left({\upkappa\kern-1.0pt\text{\c{}}}_{i}\left(\tau \right),{\nu }_{i}\left(\tau \right)\right),i=\mathrm{1,2},\dots ,n$, be the family of IFVs, with weight vector $w={\left({w}_{1}, {w}_{2}, \dots , {w}_{n}\right)}^{T}, {w}_{i}\in \left[0, 1\right]$ and $\sum_{i=1}^{n}{w}_{i}=1$. Then IFAAWHM operator is defined as follows:

$$\begin{aligned} & {\mathrm{IFAAWHM}}^{\left(\tau \right)}\left({\zeta }_{1},{\zeta }_{2},\dots ,{\zeta }_{n}\right)\\ & \quad =\left\{\begin{array}{cc}\frac{\underset{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\oplus }\left(1-\sum_{\mathcalligra{s}=1}^{\tau }{w}_{{i}_{\mathcalligra{s}}}\right){\left(\underset{\mathcalligra{s}=1}{\stackrel{\tau }{\otimes}}{\zeta }_{{i}_{\mathcalligra{s}}}\right)}^{\frac{1}{\tau }}}{{C}_{n-1}^{\tau }}& 1\le \tau <n\\ \underset{\mathcalligra{s}=1}{\stackrel{\tau }{\otimes}}{\zeta }_{{i}_{\mathcalligra{s}}}^{\frac{1-{w}_{{i}_{\mathcalligra{s}}}}{n-1}}& \tau =n\end{array}\right..\end{aligned}$$

(7)

Theorem 6

Let ${\zeta }_{i}=\left({\upkappa\kern-1.0pt\text{\c{}}}_{i}\left(\tau \right),{\nu }_{i}\left(\tau \right)\right),i=\mathrm{1,2},\dots ,n$, be the family of IFVs, with weight vector $w={\left({w}_{1}, {w}_{2}, \dots , {w}_{n}\right)}^{T}, {w}_{i}\in \left[0, 1\right]$ and $\sum_{i=1}^{n}{w}_{i}=1$. Then the aggregated value of the IFAAWHM operator is defined as:

$$\begin{aligned} & {\mathrm{IFAAWHM}}^{\left(\tau \right)}\left({\zeta }_{1},{\zeta }_{2},\dots ,{\zeta }_{n}\right)\\ &\quad =\left(\begin{array}{c}1-{e}^{-{\left(\left(\frac{1}{{C}_{n-1}^{\tau }}\right)\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}\left(\left(1-\sum_{\mathcalligra{s}=1}^{\tau }{w}_{{i}_{\mathcalligra{s}}}\right){\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left({\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)\right)\right)}^{\frac{1}{\partial }}},\\ {e}^{-{\left(\left(\frac{1}{{C}_{n-1}^{\tau }}\right)\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}\left({\left(1-\sum_{\mathcalligra{s}=1}^{\tau }{w}_{{i}_{\mathcalligra{s}}}\right)\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left(1-{\nu }_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)\right)\right)}^{\frac{1}{\partial }}}\end{array}\right), 1\le \tau <n \end{aligned} $$

(8)

$$\underset{\mathcalligra{s}=1}{\stackrel{\tau }{\otimes}}{\zeta }_{{i}_{\mathcalligra{s}}}^{\frac{1-{w}_{{i}_{\mathcalligra{s}}}}{n-1}}=\left(\begin{array}{c}{e}^{-{\left(\sum_{\mathcalligra{s}=1}^{\tau }\left({\left(\frac{1-{w}_{{i}_{\mathcalligra{s}}}}{n-1}\right)\left(-ln\left({\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}},\\ 1-{e}^{-{\left(\sum_{\mathcalligra{s}=1}^{\tau }\left(\frac{1-{w}_{{i}_{\mathcalligra{s}}}}{n-1}\right)\left({\left(-ln\left(1-{\nu }_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\end{array}\right), \tau =n$$

Proof

Let ${\zeta }_{i}=\left({\upkappa\kern-1.0pt\text{\c{}}}_{i}\left(\tau \right),{\nu }_{i}\left(\tau \right)\right),i=\mathrm{1,2},\dots ,n$ be the family of IFVs.

Case 1

We prove this theorem for $1\le \tau <n$, by using the basic operations of A-TNM and A-TCNM, we have:

$$\underset{\mathcalligra{s}=1}{\stackrel{\tau }{\otimes}}{\zeta }_{{i}_{\mathcalligra{s}}}=\left({e}^{-{\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left({\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)}^{\frac{1}{\partial }}},1-{e}^{-{\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left(1-{\nu }_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)}^{\frac{1}{\partial }}}\right)$$

$${\left(\mathop{\otimes}^{\tau}_{\mathcalligra{s}=1} {\zeta }_{{i}_{\mathcalligra{s}}}\right)}^{\frac{1}{\tau }}=\left({e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left({\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}},1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left(1-{\nu }_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right) =\left(\begin{array}{c}1-{e}^{-{\left(\left(1-\sum_{\mathcalligra{s}=1}^{\tau }{w}_{{i}_{\mathcalligra{s}}}\right){\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left({\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)}^{\frac{1}{\partial }}},\\ {e}^{-{\left({\left(1-\sum_{\mathcalligra{s}=1}^{\tau }{w}_{{i}_{\mathcalligra{s}}}\right)\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left(1-{\nu }_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)}^{\frac{1}{\partial }}}\end{array}\right)$$

$$\begin{aligned} & \underset{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\oplus }\left(1-\sum_{\mathcalligra{s}=1}^{\tau }{w}_{{i}_{\mathcalligra{s}}}\right){\left(\underset{\mathcalligra{s}=1}{\stackrel{\tau }{\otimes}}{\zeta }_{{i}_{\mathcalligra{s}}}\right)}^{\frac{1}{\tau }} =\left(\begin{array}{c}1-{e}^{-{\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}\left(\left(1-\sum_{\mathcalligra{s}=1}^{\tau }{w}_{{i}_{\mathcalligra{s}}}\right){\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left({\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}},\\ {e}^{-{\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}\left({\left(1-\sum_{\mathcalligra{s}=1}^{\tau }{w}_{{i}_{\mathcalligra{s}}}\right)\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left(1-{\nu }_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\end{array}\right)\end{aligned}$$

$$\begin{aligned} & \frac{\underset{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\oplus }\left(1-\sum_{\mathcalligra{s}=1}^{\tau }{w}_{{i}_{\mathcalligra{s}}}\right){\left(\underset{\mathcalligra{s}=1}{\stackrel{\tau }{\otimes}}{\zeta }_{{i}_{\mathcalligra{s}}}\right)}^{\frac{1}{\tau }}}{{C}_{n-1}^{\tau }}\\ &\quad =\left(\begin{array}{c}1-{e}^{-{\left(\left(\frac{1}{{C}_{n-1}^{\tau }}\right)\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}\left(\left(1-\sum_{\mathcalligra{s}=1}^{\tau }{w}_{{i}_{\mathcalligra{s}}}\right){\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left({\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)\right)\right)}^{\frac{1}{\partial }}}\\ {e}^{-{\left(\left(\frac{1}{{C}_{n-1}^{\tau }}\right)\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}\left({\left(1-\sum_{\mathcalligra{s}=1}^{\tau }{w}_{{i}_{\mathcalligra{s}}}\right)\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left(1-{\nu }_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)\right)\right)}^{\frac{1}{\partial }}}\end{array}\right).\end{aligned}$$

Case 2

Now we prove for $\tau =n$ by using the operational laws of A-TNM and A-TCNM, so we have:

$${\zeta }_{{i}_{\mathcalligra{s}}}^{\frac{1-{w}_{{i}_{\mathcalligra{s}}}}{n-1}}=\left({e}^{-{\left({\left(\frac{1-{w}_{{i}_{\mathcalligra{s}}}}{n-1}\right)\left(-ln\left({\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)}^{\frac{1}{\partial }}},1-{e}^{-{\left(\left(\frac{1-{w}_{{i}_{\mathcalligra{s}}}}{n-1}\right)\left({\left(-ln\left(1-{\nu }_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)$$

$$\underset{\mathcalligra{s}=1}{\stackrel{\tau }{\otimes}}{\zeta }_{{i}_{\mathcalligra{s}}}^{\frac{1-{w}_{{i}_{\mathcalligra{s}}}}{n-1}}=\left(\begin{array}{c}{e}^{-{\left(\sum_{\mathcalligra{s}=1}^{\tau }\left({\left(\frac{1-{w}_{{i}_{\mathcalligra{s}}}}{n-1}\right)\left(-ln\left({\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}},\\ 1-{e}^{-{\left(\sum_{\mathcalligra{s}=1}^{\tau }\left(\frac{1-{w}_{{i}_{\mathcalligra{s}}}}{n-1}\right)\left({\left(-ln\left(1-{\nu }_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\end{array}\right)$$

We have to show that Eq. (8) is IFVs, for this, we have to satisfy the following conditions:

• 1. $0\le \alpha \le 1, 0\le \beta \le 1$

• 2. $0\le \alpha +\beta \le 1$

We show proof above equation for $1\le \tau <n$.

Consider,

$$\alpha =1-{e}^{-{\left(\left(\frac{1}{{C}_{n-1}^{\tau }}\right)\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}\left(\left(1-\sum_{\mathcalligra{s}=1}^{\tau }{w}_{{i}_{\mathcalligra{s}}}\right){\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left({\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)\right)\right)}^{\frac{1}{\partial }}}$$

$$\beta ={e}^{-{\left(\left(\frac{1}{{C}_{n-1}^{\tau }}\right)\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}\left({\left(1-\sum_{\mathcalligra{s}=1}^{\tau }{w}_{{i}_{\mathcalligra{s}}}\right)\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left(1-{\nu }_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)\right)\right)}^{\frac{1}{\partial }}}$$

We know that ${\upkappa\kern-1.0pt\text{\c{}}}_{\mathcalligra{s}}\left(\tau \right)\in \left[0, 1\right]$

$$\Rightarrow {e}^{-{\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left({\mathrm{\upkappa\kern-1.0pt\text{\c{}}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)}^{\frac{1}{\partial }}}\in \left[0, 1\right].$$

$$\Rightarrow {e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left({\mathrm{\upkappa\kern-1.0pt\text{\c{}}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\in \left[0, 1\right].$$

$$\Rightarrow 1-{e}^{-{\left(\left(1-\sum_{\mathcalligra{s}=1}^{\tau }{w}_{{i}_{\mathcalligra{s}}}\right){\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left({\mathrm{\upkappa\kern-1.0pt\text{\c{}}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)}^{\frac{1}{\partial }}}\in \left[0, 1\right].$$

$$\Rightarrow 1-{e}^{-{\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}\left(\left(1-\sum_{\mathcalligra{s}=1}^{\tau }{w}_{{i}_{\mathcalligra{s}}}\right){\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left({\mathrm{\upkappa\kern-1.0pt\text{\c{}}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\in \left[0, 1\right].$$

$$\begin{aligned} & \Rightarrow 1-{e}^{-{\left(\left(\frac{1}{{C}_{n-1}^{\tau }}\right)\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}\left(\left(1-\sum_{\mathcalligra{s}=1}^{\tau }{w}_{{i}_{\mathcalligra{s}}}\right){\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left({\mathrm{\upkappa\kern-1.0pt\text{\c{}}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)\right)\right)}^{\frac{1}{\partial }}}\in \left[0, 1\right].\\ & \Rightarrow 0\le \alpha \le 1.\end{aligned}$$

In this way, we have to show that:

$$\begin{aligned} & {e}^{-{\left(\left(\frac{1}{{C}_{n-1}^{\tau }}\right)\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}\left({\left(1-\sum_{\mathcalligra{s}=1}^{\tau }{w}_{{i}_{\mathcalligra{s}}}\right)\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left(1-{\nu }_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)\right)\right)}^{\frac{1}{\partial }}}\in \left[0, 1\right].\\ & \Rightarrow 0\le \beta \le 1.\end{aligned}$$

Next, we have $0\le \alpha +\beta \le 1$.

$$\begin{aligned} &1-{e}^{-{\left(\left(\frac{1}{{C}_{n-1}^{\tau }}\right)\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}\left(\left(1-\sum_{\mathcalligra{s}=1}^{\tau }{w}_{{i}_{\mathcalligra{s}}}\right){\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left({\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)\right)\right)}^{\frac{1}{\partial }}}\\ &\quad +{e}^{-{\left(\left(\frac{1}{{C}_{n-1}^{\tau }}\right)\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}\left({\left(1-\sum_{\mathcalligra{s}=1}^{\tau }{w}_{{i}_{\mathcalligra{s}}}\right)\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left(1-{\nu }_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)\right)\right)}^{\frac{1}{\partial }}}\end{aligned}$$

$$\Rightarrow 0\le \left(\begin{array}{c}1-{e}^{-{\left(\left(\frac{1}{{C}_{n-1}^{\tau }}\right)\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}\left(\left(1-\sum_{\mathcalligra{s}=1}^{\tau }{w}_{{i}_{\mathcalligra{s}}}\right){\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left({\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)\right)\right)}^{\frac{1}{\partial }}},\\ {e}^{-{\left(\left(\frac{1}{{C}_{n-1}^{\tau }}\right)\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}\left({\left(1-\sum_{\mathcalligra{s}=1}^{\tau }{w}_{{i}_{\mathcalligra{s}}}\right)\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left(1-{\nu }_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)\right)\right)}^{\frac{1}{\partial }}}\end{array}\right)\le 1$$

We prove above equation for $0\le \alpha \le 1, 0\le \beta \le 1$ and $0\le \alpha +\beta \le 1$, for $\tau =n$. We have:

Let $\alpha ={e}^{-{\left({\left(\frac{1-{w}_{{i}_{\mathcalligra{s}}}}{n-1}\right)\left(-ln\left({\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)}^{\frac{1}{\partial }}}$ and $\beta =1-{e}^{-{\left(\left(\frac{1-{w}_{{i}_{\mathcalligra{s}}}}{n-1}\right)\left({\left(-ln\left(1-{\nu }_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}$

We know that ${\upkappa\kern-1.0pt\text{\c{}}}_{\mathcalligra{s}}\left(\tau \right)\in \left[0, 1\right]$

$$\Rightarrow {e}^{-{\left({\left(\frac{1-{w}_{{i}_{\mathcalligra{s}}}}{n-1}\right)\left(-ln\left({\mathrm{\upkappa\kern-1.0pt\text{\c{}}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)}^{\frac{1}{\partial }}}\in \left[0, 1\right].$$

$$\Rightarrow {e}^{-{\left({\left(\frac{1-{w}_{{i}_{\mathcalligra{s}}}}{n-1}\right)\left(-ln\left({\mathrm{\upkappa\kern-1.0pt\text{\c{}}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)}^{\frac{1}{\partial }}}\in \left[0, 1\right].$$

So, $\alpha ={e}^{-{\left({\left(\frac{1-{w}_{{i}_{\mathcalligra{s}}}}{n-1}\right)\left(-ln\left({\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)}^{\frac{1}{\partial }}}\in \left[0, 1\right]$

In the same way, we can show:

$$\beta =1-{e}^{-{\left(\sum_{\mathcalligra{s}=1}^{\tau }\left(\frac{1-{w}_{{i}_{\mathcalligra{s}}}}{n-1}\right)\left({\left(-ln\left(1-{\nu }_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\in \left[0, 1\right]$$

So we have $0\le \alpha +\beta \le 1$.

$${e}^{-{\left({\left(\frac{1-{w}_{{i}_{\mathcalligra{s}}}}{n-1}\right)\left(-ln\left({\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)}^{\frac{1}{\partial }}}+1-{e}^{-{\left(\sum_{\mathcalligra{s}=1}^{\tau }\left(\frac{1-{w}_{{i}_{\mathcalligra{s}}}}{n-1}\right)\left({\left(-ln\left(1-{\nu }_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}$$

$$0\le \left(\begin{array}{c}{e}^{-{\left(\sum_{\mathcalligra{s}=1}^{\tau }\left({\left(\frac{1-{w}_{{i}_{\mathcalligra{s}}}}{n-1}\right)\left(-ln\left({\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}},\\ 1-{e}^{-{\left(\sum_{\mathcalligra{s}=1}^{\tau }\left(\frac{1-{w}_{{i}_{\mathcalligra{s}}}}{n-1}\right)\left({\left(-ln\left(1-{\nu }_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\end{array}\right)\le 1.$$

Example 4

Consider ${\zeta }_{1}=\left(0.22, 0.16\right)$,${\zeta }_{2}=\left(0.86, 0.47\right)$,${\zeta }_{3}=\left(0.57, 0.65\right)$ and ${\zeta }_{4}=\left(0.84, 0.59\right)$ are four IFVs, weight vector $w=\left(0.15, 0.35, 0.20, 0.30\right)$. Then we applied an IFAAWHM operator to aggregate given IFVs. Let $\partial =3$ and $\tau =2$.

$${\mathrm{IFAAWHM}}^{\left(\tau \right)}\left({\zeta }_{1},{\zeta }_{2},\dots ,{\zeta }_{n}\right)=\left(\begin{array}{c}1-{e}^{-{\left(\left(\frac{1}{{C}_{n-1}^{\tau }}\right)\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}\left(\left(1-\sum_{\mathcalligra{s}=1}^{\tau }{w}_{{i}_{\mathcalligra{s}}}\right){\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left({\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)\right)\right)}^{\frac{1}{\partial }}},\\ {e}^{-{\left(\left(\frac{1}{{C}_{n-1}^{\tau }}\right)\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}\left({\left(1-\sum_{\mathcalligra{s}=1}^{\tau }{w}_{{i}_{\mathcalligra{s}}}\right)\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left(1-{\nu }_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)\right)\right)}^{\frac{1}{\partial }}}\end{array}\right)$$

$${\mathrm{IFAAWHM}}^{\left(\tau \right)}\left({\zeta }_{1},{\zeta }_{2},{\zeta }_{3}, {\zeta }_{4}\right)=\left(\begin{array}{c}1-{e}^{-{\left(\left(\frac{1}{6}\right)\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}\left(\left(1-\sum_{\mathcalligra{s}=1}^{2}{w}_{{i}_{\mathcalligra{s}}}\right){\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{2}\right)\left(\sum_{\mathcalligra{s}=1}^{2}{\left(-ln\left({\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{3}\right)\right)}^{\frac{1}{3}}}\right)\right)}^{3}\right)\right)\right)}^{\frac{1}{3}}},\\ {e}^{-{\left(\left(\frac{1}{6}\right)\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}\left({\left(1-\sum_{\mathcalligra{s}=1}^{2}{w}_{{i}_{\mathcalligra{s}}}\right)\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{2}\right)\left(\sum_{\mathcalligra{s}=1}^{2}{\left(-ln\left(1-{\nu }_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{3}\right)\right)}^{\frac{1}{3}}}\right)\right)}^{3}\right)\right)\right)}^{\frac{1}{3}}}\end{array}\right) =\left(0.2744, 0.4579\right)$$

Now we illustrate some basic properties of the IFAAHM operator.

Theorem 7

(Idempotency property) let ${\zeta }_{i}=\left({\upkappa\kern-1.0pt\text{\c{}}}_{i}\left(\tau \right),{\nu }_{i}\left(\tau \right)\right),i=\mathrm{1,2},\dots ,n$, be the family of all identical IFVs, with weight vector $w={\left({w}_{1}, {w}_{2}, \dots , {w}_{n}\right)}^{T}, {w}_{i}\in \left[0, 1\right]$ and $\sum_{i=1}^{n}{w}_{i}=1$. Then:

$${\mathrm{IFAAWHM}}^{\left(\tau \right)}\left({\zeta }_{1},{\zeta }_{2},\dots ,{\zeta }_{n}\right)=\zeta .$$

Proof

Proof is similar to Theorems 2.

Theorem 8

(Monotonicity property) let ${\zeta }_{i}=\left({\upkappa\kern-1.0pt\text{\c{}}}_{i}\left(\tau \right),{\nu }_{i}\left(\tau \right)\right),i=\mathrm{1,2},\dots ,n$ and ${\xi }_{i}=\left({\gamma }_{i}\left(\tau \right),{\delta }_{i}\left(\tau \right)\right), i=\mathrm{1,2},\dots ,n$ be the family of two IFVs, if ${\upkappa\kern-1.0pt\text{\c{}}}_{i}\left(\tau \right)\le {\gamma }_{i}\left(\tau \right),{\nu }_{i}\left(\tau \right)\ge {\delta }_{i}\left(\tau \right), \forall i$, Then:

$${\mathrm{IFAAHM}}^{\left(\tau \right)}\left({\zeta }_{1},{\zeta }_{2},\dots ,{\zeta }_{n}\right)\le {\mathrm{IFAAHM}}^{\left(\tau \right)}\left({\xi }_{1},{\xi }_{2},\dots ,{\xi }_{n}\right).$$

Proof

Proof is straightforward.

Theorem 9

(Boundedness property) let ${\zeta }_{i}=\left({\upkappa\kern-1.0pt\text{\c{}}}_{i}\left(\tau \right),{\nu }_{i}\left(\tau \right)\right),i=\mathrm{1,2},\dots ,n$ be the family of IFVs, if: ${\zeta }_{i}^{-}=\wedge \left({\zeta }_{1}, {\zeta }_{2}, {\zeta }_{3}, \dots , {\zeta }_{n}\right)$ and ${\zeta }_{i}^{+}=\vee \left({\zeta }_{1}, {\zeta }_{2}, {\zeta }_{3}, \dots , {\zeta }_{n}\right)$, then:

$${\zeta }^{-}\le \mathrm{IFAAHM}\left({\zeta }_{1},{\zeta }_{2},\dots ,{\zeta }_{n}\right)\le {\zeta }^{+}.$$

where symbols $\wedge$ $\vee$ represent the minimum and maximum values of ${\zeta }_{i}$.

Proof

Proof is analogous.

Aczel Alsina intuitionistic fuzzy dual Hamy mean operator

We discussed an innovative idea of the HM operator based on IFVs by using the basic operations of A-TNM and A-TCNM in the form of an intuitionistic fuzzy Aczel Alsina Dual Hamy mean (IFAADHM) operator. Moreover, we also explored the basic properties of our proposed work.

Definition 12

Let ${\zeta }_{i}=\left({\upkappa\kern-1.0pt\text{\c{}}}_{i}\left(\tau \right),{\nu }_{i}\left(\tau \right)\right),i=\mathrm{1,2},\dots ,n$, be the family of IFVs. Then an IFAADHM operator is defined as:

$${\mathrm{IFAADHM}}^{\left(\tau \right)}\left({\zeta }_{1},{\zeta }_{2},\dots ,{\zeta }_{n}\right)={\left(\underset{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\otimes}\frac{\left(\stackrel{\tau }{\underset{\mathcalligra{s}=1}{\oplus }}{\zeta }_{{i}_{\mathcalligra{s}}}\right)}{{\varvec{\tau}}}\right)}^{\frac{1}{{C}_{n}^{\tau }}}.$$

(9)

Theorem 10

Let ${\zeta }_{i}=\left({\upkappa\kern-1.0pt\text{\c{}}}_{i}\left(\tau \right),{\nu }_{i}\left(\tau \right)\right),i=\mathrm{1,2},\dots ,n$, be the family of IFVs. Then an IFAADHM operator is given as:

$${\mathrm{IFAADHM}}^{\left(\tau \right)}\left({\zeta }_{1},{\zeta }_{2},\dots ,{\zeta }_{n}\right) =\left(\begin{array}{c}{e}^{-{\left(\left(\frac{1}{{C}_{n}^{\tau }}\right)\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left(1-{\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}},\\ 1-{e}^{-{\left(\left(\frac{1}{{C}_{n}^{\tau }}\right)\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left({\nu }_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\end{array}\right)$$

(10)

Proof

Let ${\zeta }_{i}=\left({\upkappa\kern-1.0pt\text{\c{}}}_{i}\left(\tau \right),{\nu }_{i}\left(\tau \right)\right),i=\mathrm{1,2},\dots ,n$ be the family of IFVs, we prove this theorem by using basic operations of A-TNM and A-TCNM, we have:

$$\stackrel{\tau }{\underset{\mathcalligra{s}=1}{\oplus }}{\zeta }_{{i}_{\mathcalligra{s}}}=\left(1-{e}^{-{\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left(1-{\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)}^{\frac{1}{\partial }}}, {e}^{-{\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left({\nu }_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)}^{\frac{1}{\partial }}}\right)$$

$$ \frac{\left(\stackrel{\tau }{\underset{\mathcalligra{s}=1}{\oplus }}{\zeta }_{{i}_{\mathcalligra{s}}}\right)}{{\varvec{\tau}}}=\left(1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left(1-{\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}, {e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left({\nu }_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)$$

$$\begin{aligned}& \underset{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\otimes}\frac{\left(\stackrel{\tau }{\underset{\mathcalligra{s}=1}{\oplus }}{\zeta }_{{i}_{\mathcalligra{s}}}\right)}{{\varvec{\tau}}} =\left(\begin{array}{c}{e}^{-{\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left(1-{\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)}^{\frac{1}{\partial }}},\\ 1-{e}^{-{\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left({\nu }_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)}^{\frac{1}{\partial }}}\end{array}\right)\end{aligned}$$

$${\left(\underset{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\otimes}\frac{\left(\stackrel{\tau }{\underset{\mathcalligra{s}=1}{\oplus }}{\zeta }_{{i}_{\mathcalligra{s}}}\right)}{{\varvec{\tau}}}\right)}^{\frac{1}{{C}_{n}^{\tau }}}=\left(\begin{array}{c}{e}^{-{\left(\left(\frac{1}{{C}_{n}^{\tau }}\right)\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left(1-{\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}},\\ 1-{e}^{-{\left(\left(\frac{1}{{C}_{n}^{\tau }}\right)\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left({\nu }_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\end{array}\right)$$

Now we have to show that Eq. 10 is an IFV. If satisfy the following conditions:

• 1. $0\le \alpha \le 1, 0\le \beta \le 1$

• 2. $0\le \alpha +\beta \le 1$

Consider,

$$\alpha ={e}^{-{\left(\left(\frac{1}{{C}_{n}^{\tau }}\right)\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left(1-{\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}$$

$$\beta =1-{e}^{-{\left(\left(\frac{1}{{C}_{n}^{\tau }}\right)\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{i\mathcalligra{s}=1}^{\tau }{\left(-ln\left({\nu }_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}$$

We know that ${\upkappa\kern-1.0pt\text{\c{}}}_{\mathcalligra{s}}\left(\tau \right)\in \left[0, 1\right]$

$$\Rightarrow {e}^{-{\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left(1-{\mathrm{\upkappa\kern-1.0pt\text{\c{}}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)}^{\frac{1}{\partial }}}\in \left[0, 1\right].$$

$$1-{e}^{-{\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left(1-{\mathrm{\upkappa\kern-1.0pt\text{\c{}}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)}^{\frac{1}{\partial }}}\in \left[0, 1\right].$$

$$\Rightarrow 1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left(1-{\mathrm{\upkappa\kern-1.0pt\text{\c{}}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\in \left[0, 1\right].$$

$$\Rightarrow {e}^{-{\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left(1-{\mathrm{\upkappa\kern-1.0pt\text{\c{}}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)}^{\frac{1}{\partial }}}\in \left[0, 1\right].$$

$$\begin{aligned}&\Rightarrow {e}^{-{\left(\left(\frac{1}{{C}_{n}^{\tau }}\right)\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left(1-{\mathrm{\upkappa\kern-1.0pt\text{\c{}}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\in \left[0, 1\right].\\ &\Rightarrow 0\le \alpha \le 1.\end{aligned}$$

In this way, we have to show that:

$$1-{e}^{-{\left(\left(\frac{1}{{C}_{n}^{\tau }}\right)\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left({\nu }_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\in \left[0, 1\right].$$

$$\Rightarrow 0\le \beta \le 1.$$

Next, we have $0\le \alpha +\beta \le 1$.

$$\left(\begin{array}{c}{e}^{-{\left(\left(\frac{1}{{C}_{n}^{\tau }}\right)\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left(1-{\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}+\\ \left(1-{e}^{-{\left(\left(\frac{1}{{C}_{n}^{\tau }}\right)\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left({\nu }_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)\end{array}\right)$$

$$\Rightarrow 0\le \left(\begin{array}{c}{e}^{-{\left(\left(\frac{1}{{C}_{n}^{\tau }}\right)\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left(1-{\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}},\\ 1-{e}^{-{\left(\left(\frac{1}{{C}_{n}^{\tau }}\right)\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left({\nu }_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\end{array}\right)\le 1.$$

Theorem 3

Let ${\zeta }_{i}=\left({\upkappa\kern-1.0pt\text{\c{}}}_{i}\left(\tau \right),{\nu }_{i}\left(\tau \right)\right),i=\mathrm{1,2},\dots ,n$, be the family of all identical IFVs. Then:

$${\mathrm{IFAADHM}}^{\left(\tau \right)}\left({\zeta }_{1},{\zeta }_{2},\dots ,{\zeta }_{n}\right)=\zeta $$

Theorem 4

Let ${\zeta }_{i}=\left({\upkappa\kern-1.0pt\text{\c{}}}_{i}\left(\tau \right),{\nu }_{i}\left(\tau \right)\right),i=\mathrm{1,2},\dots ,n$ and ${\xi }_{i}=\left({\gamma }_{i}\left(\tau \right),{\delta }_{i}\left(\tau \right)\right), i=\mathrm{1,2},\dots ,n$ be the family of two IFVs, if ${\upkappa\kern-1.0pt\text{\c{}}}_{i}\left(\tau \right)\le {\gamma }_{i}\left(\tau \right),{\nu }_{i}\left(\tau \right)\ge {\delta }_{i}\left(\tau \right), \forall i$, Then:

$${\mathrm{IFAADHM}}^{\left(\tau \right)}\left({\zeta }_{1},{\zeta }_{2},\dots ,{\zeta }_{n}\right)\le {\mathrm{IFAADHM}}^{\left(\tau \right)}\left({\xi }_{1},{\xi }_{2},\dots ,{\xi }_{n}\right)$$

Theorem 5

Let ${\zeta }_{i}=\left({\upkappa\kern-1.0pt\text{\c{}}}_{i}\left(\tau \right),{\nu }_{i}\left(\tau \right)\right),i=\mathrm{1,2},\dots ,n$ be the family of IFVs, if ${\zeta }_{i}^{-}=\wedge \left({\zeta }_{1}, {\zeta }_{2}, {\zeta }_{3}, \dots , {\zeta }_{n}\right)$ and ${\zeta }_{i}^{+}=\vee \left({\zeta }_{1}, {\zeta }_{2}, {\zeta }_{3}, \dots , {\zeta }_{n}\right)$, then:

$${\zeta }^{-}\le \mathrm{IFAADHM}\left({\zeta }_{1},{\zeta }_{2},\dots ,{\zeta }_{n}\right)\le {\zeta }^{+}$$

where symbols $\wedge$ $\vee$ represent the minimum and maximum values of ${\zeta }_{\mathcalligra{s}}$.

Example 5

Consider ${\zeta }_{1}=\left(0.42, 0.34\right)$,${\zeta }_{2}=\left(0.62, 0.31\right), {\zeta }_{3}=\left(0.55, 0.28\right)$ and ${\zeta }_{4}=\left(0.63, 0.29\right)$ are four IFVs. Then we applied an IFAAHM operator to aggregate given IFVs. Let $\partial =3$ and $\tau =2$.

$$\begin{aligned}{\mathrm{IFAADHM}}^{\left(\tau \right)}\left({\zeta }_{1},{\zeta }_{2},\dots ,{\zeta }_{n}\right) =&\,\left(\begin{array}{c}{e}^{-{\left(\left(\frac{1}{{C}_{n}^{\tau }}\right)\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left(1-{\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}},\\ 1-{e}^{-{\left(\left(\frac{1}{{C}_{n}^{\tau }}\right)\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left({\nu }_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\end{array}\right)\\ =&\left(\begin{array}{c}{e}^{-{\left(\left(\frac{1}{6}\right)\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{2}\right)\left(\sum_{\mathcalligra{s}=1}^{2}{\left(-ln\left(1-{\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{3}\right)\right)}^{\frac{1}{3}}}\right)\right)}^{3}\right)\right)}^{\frac{1}{3}}},\\ 1-{e}^{-{\left(\left(\frac{1}{6}\right)\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\left(-ln\left(1-{e}^{-{\left(\left(\frac{1}{2}\right)\left(\sum_{\mathcalligra{s}=1}^{2}{\left(-ln\left({\nu }_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{3}\right)\right)}^{\frac{1}{3}}}\right)\right)}^{3}\right)\right)}^{\frac{1}{3}}}\end{array}\right)\\ =&\left(0.5581, 0.3046\right).\end{aligned}$$

Intuitionistic fuzzy Aczel Alsina weighted dual Hamy mean operator

We developed a new AOs of DHM operator in the form of intuitionistic fuzzy Aczel Alsina Weighted Dual Hamy mean (IFAAWDHM) by using the basic operations of A-TNM and A-TCNM.

Definition 13

Let ${\zeta }_{i}=\left({\upkappa\kern-1.0pt\text{\c{}}}_{i}\left(\tau \right),{\nu }_{i}\left(\tau \right)\right),i=\mathrm{1,2},\dots ,n$, be the family of IFVs, with weight vector $w={\left({w}_{1}, {w}_{2}, \dots , {w}_{n}\right)}^{T}, {w}_{i}\in \left[0, 1\right]$ and $\sum_{i=1}^{n}{w}_{i}=1$. Then an IFAAWDHM operator is defined as:

$${\mathrm{IFAAWDHM}}^{\left(\tau \right)}\left({\zeta }_{1},{\zeta }_{2},\dots ,{\zeta }_{n}\right) =\left\{\begin{array}{cc}{\left(\underset{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\otimes}\left(1-\sum\limits_{\mathcalligra{s}=1}^{\tau }{w}_{{i}_{\mathcalligra{s}}}\right)\left(\frac{\underset{\mathcalligra{s}=1}{\stackrel{\tau }{\oplus }}{\zeta }_{{i}_{\mathcalligra{s}}}}{\tau }\right)\right)}^{\frac{1}{{C}_{n-1}^{\tau }}}& 1\le \tau <n\\ \underset{\mathcalligra{s}=1}{\stackrel{\tau }{\oplus }}{\zeta }_{{i}_{\mathcalligra{s}}}^{\frac{1-{w}_{{i}_{\mathcalligra{s}}}}{n-1}}& \tau =n\end{array}\right.$$

(11)

Theorem 11

Let ${\zeta }_{i}=\left({\upkappa\kern-1.0pt\text{\c{}}}_{i}\left(\tau \right),{\nu }_{i}\left(\tau \right)\right),i=\mathrm{1,2},\dots ,n$, be the family of IFVs. Then the aggregated value of the IFAAWDHM operator is given as:

$${\mathrm{IFAAWDHM}}^{\left(\tau \right)}\left({\zeta }_{1},{\zeta }_{2},\dots ,{\zeta }_{n}\right) =\left(\begin{array}{c}{e}^{-{\left(\left(\frac{1}{{C}_{n-1}^{\tau }}\right)\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\left(-ln\left(1-{e}^{-{\left(\left(1-\sum_{\mathcalligra{s}=1}^{\tau }{w}_{{i}_{\mathcalligra{s}}}\right)\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left(1-{\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}},\\ 1-{e}^{-{\left(\left(\frac{1}{{C}_{n-1}^{\tau }}\right)\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\left(-ln\left(1- {e}^{-{\left(\left(1-\sum_{\mathcalligra{s}=1}^{\tau }{w}_{{i}_{\mathcalligra{s}}}\right)\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left({\nu }_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\end{array}\right), 1\le \tau <n$$

$$\begin{aligned} & {\mathrm{IFAAWDHM}}^{\left(\tau \right)}\left({\zeta }_{1},{\zeta }_{2},\dots ,{\zeta }_{n}\right) =\left(\begin{array}{c}1-{e}^{-{\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left(1-{e}^{-{\left({\left(\frac{1-{w}_{{i}_{\mathcalligra{s}}}}{n-1}\right)\left(-ln\left({\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)}^{\frac{1}{\partial }}},\\ {e}^{-{\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left(1-{e}^{-{\left(\left(\frac{1-{w}_{{i}_{\mathcalligra{s}}}}{n-1}\right)\left({\left(-ln\left(1-{\nu }_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)}^{\frac{1}{\partial }}}\end{array}\right), \tau =n\end{aligned}$$

(12)

Proof

Let ${\zeta }_{i}=\left({\upkappa\kern-1.0pt\text{\c{}}}_{i}\left(\tau \right),{\nu }_{i}\left(\tau \right)\right),i=\mathrm{1,2},\dots ,n$, be the family of IFVs, we prove the above theorem by using the basic operations of A-TNM and A-TCNM as follows:

Case 1

For $1\le \tau <n$.

$$\underset{\mathcalligra{s}=1}{\stackrel{\tau }{\oplus }}{\zeta }_{{i}_{\mathcalligra{s}}}=\left(1-{e}^{-{\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left(1-{\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)}^{\frac{1}{\partial }}}, {e}^{-{\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left({\nu }_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)}^{\frac{1}{\partial }}}\right)$$

$$\left(\frac{{{\oplus_{\mathcalligra{s}=1}^{\tau }}}{\zeta }_{{i}_{\mathcalligra{s}}}}{\tau }\right)=\left(1-{e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left(1-{\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}, {e}^{-{\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left({\nu }_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)$$

$$\left(1-\sum_{\mathcalligra{s}=1}^{\tau }{w}_{{i}_{\mathcalligra{s}}}\right)\left(\frac{{{\oplus_{\mathcalligra{s}=1}^{\tau } }}{\zeta }_{{i}_{\mathcalligra{s}}}}{\tau }\right)=\left(\begin{array}{c}1-{e}^{-{\left(\left(1-\sum_{\mathcalligra{s}=1}^{\tau }{w}_{{i}_{\mathcalligra{s}}}\right)\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left(1-{\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)\right)}^{\frac{1}{\partial }}},\\ {e}^{-{\left(\left(1-\sum_{\mathcalligra{s}=1}^{\tau }{w}_{{i}_{\mathcalligra{s}}}\right)\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left({\nu }_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)\right)}^{\frac{1}{\partial }}}\end{array}\right)$$

$$\underset{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\otimes}\left(1-\sum_{\mathcalligra{s}=1}^{\tau }{w}_{{i}_{\mathcalligra{s}}}\right)\left(\frac{{{\oplus_{\mathcalligra{s}=1}^{\tau } }}{\zeta }_{{i}_{\mathcalligra{s}}}}{\tau }\right)=\left(\begin{array}{c}{e}^{-{\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\left(-ln\left(1-{e}^{-{\left(\left(1-\sum_{\mathcalligra{s}=1}^{\tau }{w}_{{i}_{\mathcalligra{s}}}\right)\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left(1-{\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)}^{\frac{1}{\partial }}},\\ 1-{e}^{-{\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\left(-ln\left(1- {e}^{-{\left(\left(1-\sum_{\mathcalligra{s}=1}^{\tau }{w}_{{i}_{\mathcalligra{s}}}\right)\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left({\nu }_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)}^{\frac{1}{\partial }}}\end{array}\right)$$

$${\left(\underset{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\otimes}\left(1-\sum_{\mathcalligra{s}=1}^{\tau }{w}_{{i}_{\mathcalligra{s}}}\right)\left(\frac{{{\oplus_{\mathcalligra{s}=1}^{\tau } }}{\zeta }_{{i}_{\mathcalligra{s}}}}{\tau }\right)\right)}^{\frac{1}{{C}_{n-1}^{\tau }}}=\left(\begin{array}{c}{e}^{-{\left(\left(\frac{1}{{C}_{n-1}^{\tau }}\right)\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\left(-ln\left(1-{e}^{-{\left(\left(1-\sum_{\mathcalligra{s}=1}^{\tau }{w}_{{i}_{\mathcalligra{s}}}\right)\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left(1-{\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}},\\ 1-{e}^{-{\left(\left(\frac{1}{{C}_{n-1}^{\tau }}\right)\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\left(-ln\left(1- {e}^{-{\left(\left(1-\sum_{\mathcalligra{s}=1}^{\tau }{w}_{{i}_{\mathcalligra{s}}}\right)\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left({\nu }_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\end{array}\right)$$

Case 2

For $\tau =n$.

$${\zeta }_{{i}_{\mathcalligra{s}}}^{\frac{1-{w}_{{i}_{\mathcalligra{s}}}}{n-1}}=\left({e}^{-{\left({\left(\frac{1-{w}_{{i}_{\mathcalligra{s}}}}{n-1}\right)\left(-ln\left({\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)}^{\frac{1}{\partial }}},1-{e}^{-{\left(\left(\frac{1-{w}_{{i}_{\mathcalligra{s}}}}{n-1}\right)\left({\left(-ln\left(1-{\nu }_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)$$

$$\underset{\mathcalligra{s}=1}{\stackrel{\tau }{\oplus }}{\zeta }_{{i}_{\mathcalligra{s}}}^{\frac{1-{w}_{{i}_{\mathcalligra{s}}}}{n-1}}=\left(\begin{array}{c}1-{e}^{-{\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left(1-{e}^{-{\left({\left(\frac{1-{w}_{{i}_{\mathcalligra{s}}}}{n-1}\right)\left(-ln\left({\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)}^{\frac{1}{\partial }}},\\ {e}^{-{\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left(1-{e}^{-{\left(\left(\frac{1-{w}_{{i}_{\mathcalligra{s}}}}{n-1}\right)\left({\left(-ln\left(1-{\nu }_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)}^{\frac{1}{\partial }}}\end{array}\right)$$

Example 6

Consider ${\zeta }_{1}=\left(0.58, 0.38\right)$,${\zeta }_{2}=\left(0.26, 0.17\right)$,${\zeta }_{3}=\left(0.31, 0.42\right)$ and ${\zeta }_{4}=\left(0.76, 0.29\right)$ are four IFVs, weight vector $w=\left(0.20, 0.15, 0.35, 0.30\right)$. Then we applied an IFAAWDHM operator to aggregate given IFVs. Let $\partial =3$ and $\tau =2$.

$${\mathrm{IFAAWDHM}}^{\left(\tau \right)}\left({\zeta }_{1},{\zeta }_{2},\dots ,{\zeta }_{n}\right)=\left(\begin{array}{c}{e}^{-{\left(\left(\frac{1}{{C}_{n-1}^{\tau }}\right)\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\left(-ln\left(1-{e}^{-{\left(\left(1-\sum_{\mathcalligra{s}=1}^{\tau }{w}_{{i}_{\mathcalligra{s}}}\right)\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left(1-{\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}},\\ 1-{e}^{-{\left(\left(\frac{1}{{C}_{n-1}^{\tau }}\right)\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\left(-ln\left(1- {e}^{-{\left(\left(1-\sum_{\mathcalligra{s}=1}^{\tau }{w}_{{i}_{\mathcalligra{s}}}\right)\left(\left(\frac{1}{\tau }\right)\left(\sum_{\mathcalligra{s}=1}^{\tau }{\left(-ln\left({\nu }_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{\partial }\right)\right)\right)}^{\frac{1}{\partial }}}\right)\right)}^{\partial }\right)\right)}^{\frac{1}{\partial }}}\end{array}\right)$$

$$\begin{aligned}{\mathrm{IFAAWDHM}}^{\left(\tau \right)}\left({\zeta }_{1},{\zeta }_{2},{\zeta }_{3}, {\zeta }_{4}\right)=&\left(\begin{array}{c}{e}^{-{\left(\left(\frac{1}{6}\right)\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\left(-ln\left(1-{e}^{-{\left(\left(1-\sum_{\mathcalligra{s}=1}^{2}{w}_{{i}_{\mathcalligra{s}}}\right)\left(\left(\frac{1}{2}\right)\left(\sum_{\mathcalligra{s}=1}^{2}{\left(-ln\left(1-{\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{3}\right)\right)\right)}^{\frac{1}{3}}}\right)\right)}^{3}\right)\right)}^{\frac{1}{3}}},\\ 1-{e}^{-{\left(\left(\frac{1}{6}\right)\left(\sum_{1\le {i}_{1}<, \dots , {<i}_{\tau }\le n}{\left(-ln\left(1- {e}^{-{\left(\left(1-\sum_{\mathcalligra{s}=1}^{2}{w}_{{i}_{\mathcalligra{s}}}\right)\left(\left(\frac{1}{2}\right)\left(\sum_{\mathcalligra{s}=1}^{2}{\left(-ln\left({\nu }_{{i}_{\mathcalligra{s}}}\left(\tau \right)\right)\right)}^{3}\right)\right)\right)}^{\frac{1}{3}}}\right)\right)}^{3}\right)\right)}^{\frac{1}{3}}}\end{array}\right)\\ =&\,\left(0.0108, 0.7044\right).\end{aligned}$$

Remark 2

We can prove all the properties of the IFAAWDHM operator namely idempotency, monotonicity and boundedness by using the method of Theorem 3, 4 and 5 respectively.

Multi-attribute decision making with proposed algorithm

In this section, we develop the algorithm for investigating the MADM problem by using the IFAAWHM and IFAAWDHM operators. We select the most suitable alternative on the base of some attributes. Consider $\left\{{\mathcal{a}}_{1}, {\mathcal{a}}_{2}, {\mathcal{a}}_{3}, \dots , {\mathcal{a}}_{\rho }\right\}$ be the family of alternatives and $\left\{{\mathcal{l}}_{1}, {\mathcal{l}}_{2}, {\mathcal{l}}_{3}, \dots , {\mathcal{l}}_{\rho }\right\}$ be the family of attributes with an assigned weight vector$\left\{{w}_{1}, {w}_{2}, {w}_{3}, \dots , {w}_{\rho }\right\}, {w}_{\rho }>0, \sum_{\mathcalligra{s}=1}^{\rho }{w}_{\rho }=1, \mathcalligra{s}=1, 2, 3, \dots , \rho$. Consider a decision matrix ${\mathcal{B}}_{b}=\left({\mathfrak{C}}_{{i}_{\mathcalligra{s}}}^{c}\right)={\left({\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}^{c},{\nu }_{{i}_{\mathcalligra{s}}}^{C}\right)}_{n\times m}, c=1, 2, 3, \dots , \rho$ given by the decision-maker. Where${\mathfrak{C}}_{{i}_{\mathcalligra{s}}}^{c}={\upkappa\kern-1.0pt\text{\c{}}}_{{i}_{\mathcalligra{s}}}^{c},{\nu }_{{i}_{\mathcalligra{s}}}^{C}, , i==1, 2, 3, \dots n, \mathcalligra{s}=1, 2, 3, \dots m$.

Engineering and construction industry

In the current era, the engineering and construction sector is crucial and has a big impact on any country’s economic growth. Any structure or piece of land that is built around us is attempted by pieces of the construction industry. The scope of the building sector is extremely broad, and lifting is making a big commitment to expanding it further. A professional development industry completes any type of improvements to system properties. Traditional construction methods or structural design can both be used. The construction industry completes projects like building a dam, a street, a monument, wooden structures, and other resources using accurate calculations.

A big sector that makes a considerable financial contribution to a nation is construction. The government has a huge interest in the construction industry because it is a venture-driven sector. To promote a framework for well-being, transportation, and training, the government enters into contracts with the construction industry. The construction industry is fundamental to any nation's growth.

Numerical example

In section, we established a numerical example to find the flexibility and capability of proposed AOs, for the construction of building materials that are utilized in constructing a building. Construction materials play a significant role in the safety and long-lasting life of a building. In this numerical example, we specified suitable construction materials like bricks based on different kinds of bricks Ђ_i = (Ђ₁, Ђ₂, Ђ₃, Ђ₄, Ђ₅). The selection process of suitable bricks is based on four characteristics as ${J}_{\mathcalligra{s}}=\left({J}_{1}, {J}_{2}, {J}_{3}, {J}_{4}\right)$. The details of these attributes such as: ${\mathrm{J}}_{1}$ represent the hardness of bricks, ${\mathrm{J}}_{2}$ represents the water absorption of bricks, ${\mathrm{J}}_{3}$ represents the uniform in shape, size and color,${\mathrm{J}}_{4}$ about the compressive strength of bricks.

The corresponding weight vector is $w={\left(0.30, 0.35, 0.15, 0.20\right)}^{T}$ by the decision maker. A decision matrix given by the decision-maker is shown in Table 1. We aim to select a suitable construction material like bricks for building construction by ordering and ranking the alternatives (bricks) by using the Algorithm depicted in Table 2.

Table 2 Algorithm

The following Table 3. shows the information of applicants under the environment of an intuitionistic fuzzy system established by the decision maker. We have to investigate the suitable applicants by using the algorithm that depicts in Table 2.

Table 3 Show the information in the form of IFVs by the decision-maker

To aggregate the information on IFVs given by the decision-maker, we applied AOs of IFAAWHM and IFAAWDHM operators, by using the information in Table 3.

We applied our proposed methodology to the given decision matrix by the decision maker and show all the results of our proposed AOs in the following Table 4.

Table 4 Show the results of IFAAWHM and IFAAWDHM operators

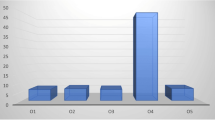
To find a suitable alternative (brick), we investigate score values shown in the following Table 5 by using the information that is depicted in above Table 4. We show score values of the IFAAWHM and IFAAWDHM operates in a graphical representation in Fig. 1.

Table 5 shows the Score values of the IFAAWHM and IFAAWDHM operators

Fig. 1

Shows the score values of our proposed methodology

Influence study

This section aims to evaluate the impact of the parameter $\tau$ on the consequences of the IFAAWHM operator. We change the value of ${\tau }_{\mathcalligra{s}},\mathcalligra{s}=1, 2, 3, 4$ but $\partial =1$ which remains to fix and applied our proposed AOs IFAAWHM operator. When we change the value of $\tau$ then the results of the combination ${C}_{n}^{\tau }$ must be changed and affected the results of the IFAAWHM operator. Therefore, we depicted all the results of the IFAAWHM operator in the following Table 6. We also observed that the suitable alternative is Ђ₅ for all the values of ${\tau }_{\mathcalligra{s}},\mathcalligra{s}=1, 2 , 3, 4$ at $\partial =1$.

Table 6 Shows the outcomes of the IFAAWHM operator at ∂ = 1

In the following Fig. 2, we also present a graphical representation of the results which are depicted in the above Table 6.

Fig. 2

Shows the outcomes of the IFAAWHM operator

We also observe the impact of ${\tau }_{\mathcalligra{s}},\mathcalligra{s}=1, 2, 3, 4$ on discussed AO of IFAAWDHM operator. If the value of $\tau$ is changed then the results of the combination must be changed ${C}_{n}^{\tau }$ and effect the consequences of the AO of the IFAAWDHM operator. We analyse the results of our proposed methodology for all the values of ${\tau }_{\mathcalligra{s}},\mathcalligra{s}=1, 2, 3, 4$ at fixed parameter $\partial =1$. The investigated results of our proposed technique are depicted in the following Table 7 with the ordering and ranking of the alternatives.

Table 7 Shows the outcomes of the IFAAWDHM operator at ∂ = 1

We also explored the results of the IFAAWDHM operator in a graph representation of Fig. 3 that are shown in the following Table 7.

Fig. 3

Shows the outcomes of the IFAAWDHM operator

The effect of the parameter $\partial$ on our purposed methodology

To find the flexibility and reliability of the proposed AOs, we illustrated the impact of the parameter $\partial$ on our proposed AOs of IFAAWHM and IFAAWDHM operators. Table 8 and Table 9 depict the results of IFAAWHM and IFAAWDHM AOs by the variation of the parameters $\partial$. We see that a suitable alternative is Ђ₅ as a result of the AO of the IFAAWHM operator for all discussed variations of the $\partial$. All the results of the IFAAWHM operator are depicted in the following Table 8. Similarly, we also observe the variation of $\partial$ for AO of the IFAAWDHM operator at a fixed value of $\tau =2$. After investigating, ordering and ranking the score values, we establish that the best alternative is ${\upkappa\kern-1.0pt\text{\c{}}}_{2}$ at $\partial =1$ and ${\upkappa\kern-1.0pt\text{\c{}}}_{5}$ is the most suitable alternative for all values of $\partial \ge 3$. All the consequences of the IFAAWDHM operator are depicted in the following Table 9.

Table 8 Shows the score values of the IFAAWHM operator for variations $\partial$

Table 9 Shows the score values of the IFAAWDHM operator for variations$\partial$

We explored all the results of score values by the IFAAWHM and IFAAWDHM operators in the following graphical representations in Figs. 4 and 5.

Fig. 4

Covered the results of score values by the IFAAWHM operator for the variations $\partial$

Fig. 5

Covered the results of score values by the IFAAWDHM operator for the variations $\partial$

Comparative analysis

Many researchers utilized different kinds of speculative theories to evaluate MADM problems and to ratify the reliability and flexibility of proposed techniques. To show the robustness and efficiency of our proposed approaches, by verifying and contrasting the results of existing approaches with our current methodologies. For this determination, we applied some existing approaches by utilizing discussed algorithm in Table 2 and investigating the consequences. Some existing approaches like the IFDWA and IFDWG by Seikh and Mandal [9], IFWA by Xu [6], IFWG by Xu and Yager [8], IFWDHM and IFWDDHM AOs by Li et al. [50], IVIFWHM and IVIFWDHM AOs by the Wu et al. [52], Senapati et al. [37] gave IF Aczel Alsina weighted average (IFAAWA) operator, Senapati et al. [58] also illustrated IF Aczel Alsina weighted geometric (IFAAWG) operator, AOs of PF Aczel Alsina weighted averaging (PFAAWA) by Senapati. [38], AOs of T-spherical fuzzy Aczel Alsina weighted averaging (TSFAAWA) by Hussain et al. [43], complex IF weighted averaging (CIFWA) by Garg and Rani. [59]. The outcomes of AOs are depicted in Table 4. We observed that AOs [38, 43, 52, 59] failed to investigate the given MADM techniques by the decision-maker in Table 1. We applied different AOs of IFDWA and IFDWG [9], IFWA [6], IFWG [8], IFAAWA [37], IFAAWG [58], IFWDHM, and IFWDDHM [50] to the given information by the decision-maker shown in Table 3. We established a comparison of this article with the previous paper and the consequences of all discussed AOs are shown in Table 10.

Table 10 Comparative study of currently discussed AOs with existing AOs

We analyzed that the consequences of IFAAWHM and IFAAWDHM operators are more reliable than existing ones. The currently developed methodologies provide authentic and smooth approximation due to different parametric values. We see our proposed methods easily deal with vague and uncertain information under consideration of IF information, and are more powerful than existing approaches seen in [38, 43, 52, 59]. The graphical representation shows the consequences of current AOs with previously existing AOs in Fig. 6.

Fig. 6

The results of the comparative study

Conclusion

The MADM technique is a well-known aggregation DM tool, which is utilized in several fields of life including computational science, environmental biology, green supplier system, renewable energy enterprises and social DM process. In this article, the author illustrates the notion of IFSs and some basic operational laws which are related to IF information. The theory of Aczel Alsina aggregation tools is a powerful and robust mathematical expression, which is utilized to overcome the loss of information during the aggregation process. The theory of HM aggregation models is utilized to express interrelationships among different input arguments in several DM processes. In this article, some appropriate aggregation approaches including IFAAHM, IFAAWHM, IFAADHM and IFAAWDHM operators. To reveal the robustness of our derived approaches, we exposed some prominent properties of our derived methodologies. The authors developed an algorithm of a MADM approach to evaluate IF information associated with several alternatives based on some particular criteria. In order to show the robustness and reliability of our proposed mythologies, we gave an experimental case study to evaluate reliable construction material from different optimal options. To see the advantages and capability of our derived approaches, a comprehensive comparative study is presented in which the results of exiting approaches contrast with the results of currently proposed AOs.

Our developed approaches are more efficient and flexible, but sometimes unable to deal with imprecision and vague information. To express such a scenario, we will enlarge the circle of our research works in several fuzzy environments including pythagorean FSs, and q-rung orthopair FSs. Moreover, we will try to solve different real-life challenges such as medical diagnosis, advanced renewable energy enterprises, construction development, and computational and information science by the implementation of our derived methodologies. We will also generalize our current research works in the environment of the bipolar-valued hesitant fuzzy system [60] and the frame of complex q-rung orthopair fuzzy planar graphs [61]. Moreover, we will enlarge our proposed work in the environment of picture fuzzy Maclaurin symmetric mean operators [62, 63].