Introduction

Due to the advantage of convenience and the universality of application, there is an increasing interest in mobile robots. Path planning is one of the prime concerns to be explored in mobile robots. Generally speaking, path planning is to generate a feasible and optimal path between the source and destination in a preset environment with several performance indicators, such as distance cost and work time. Nowadays, path planning algorithms have been applied substantially in many fields including, but not limited to, unmanned aerial vehicles [1, 2], additive manufacturing [3, 8] and biology [9]. It is worth noting that the detection algorithm [10] lays the foundation for path planning by identifying the external environment.

Path planning becomes a hot issue and a lot of research is being conducted. Nowadays, there are several commonly used path-planning algorithms: artificial potential field methods [11], geometric algorithms [12], grid-based searches [13], sampling-based algorithms [14, 15], and learning-based algorithms [16, 17]. Although the learning-based algorithm shows superior performance in path planning, its reliability of it needs to be further verified theoretically. Benefiting from the excellent performance, increasing attention has been focused on the sample-based algorithm in the current study. Rapidly exploring Random Trees (RRT) is a typical representation of sample-based algorithm. Compared to other algorithms, RRT can find a feasible solution without complicated computation. However, the path created by RRT is not optimal. To solve this problem, the RRT* is proposed [18]. It mainly introduces two procedures, ChooseParent and Rewire procedure, into RRT to increase the number of samples and generate an optimal path. However, the increased number of samples leads to its slow convergence. It cannot generate the optimal path during the limited time. In addition, the optimization effect is not satisfactory. To solve the problem, researchers have proposed many RRT*-variants in recent years.

Introducing a sampling strategy is one of the useful ways. On the one hand, the sampling strategy can be applied to the initial path of RRT*. RRT*-Smart [19] obtains an optimal path by applying the intelligent sampling method in RRT*. However, the algorithm only adapted to the environment containing obstacles with simple geometries. Informed-RRT* [20] generates an elliptical sampling region according to the start and goal point, which is continuously narrowed with the sampling process, to quickly gain the optimal path. However, once the generated prolate hyper-spheroid is bigger than the planning problem domain, the algorithm has poor performance. On the other hand, the sampling strategy can also be applied to searching the nodes during the path planning process. P-RRT* [21] determines the extension direction by artificial potential fields. Based on it, PQ-RRT* [22] combines it with Quick-RRT* [23] to further shorten the convergence time. Moreover, AFG-RRT* [24] and improved bidirectional RRT∗ [25] are also applied to the artificial field to ensure directional exploration. Wang et al. use a CNN model trained with the successful example to predict the extension direction and guide the generation of nodes [26]. G-RRT* [27] and ED-RRT* [28] shorten the sampling process by goal-oriented sampling. The Fast-RRT* [29] introduces the hybrid sampling strategy to narrow the sampling area and shorten the convergence rate. It is worth noting that the applicability of the hybrid sampling method is poor in the complex environment with concave cavity obstacle. Since these algorithms mainly reduce the convergence rate by improving the quality of sampling, the optimization effect is still not satisfactory.

In addition to the improved sampling strategy, reducing nodes is another effective way. Karaman et al. use the heuristic function to calculate the path cost [30]. The point will be cut off if it cannot decrease the cost. MOD-RRT* [31] expands the tree with a goal point to calculate the cost between nodes and the goal point and cut off the node which brings the additional cost. Except for reducing the tree nodes, reducing path nodes can also improve the convergence rate. In this field, Jeong et al. propose Quick-RRT* [23], which applies triangular inequality to improve the RRT*. Inspired by Quick-RRT*, Kang et al. [32] use the triangular inequality to improve the performance of RRT-Connect [33]. Furthermore, Liao et al. proposed the F-RRT* [34]. By applying the FindReachest procedure with triangular inequality and the CreatNode procedure with dichotomy method, the path cost is greatly reduced. It is worth noting that the parameter Ddichotomy needs to be identified because F-RRT ∗ with a smaller Ddichotomy not only improves the quality of the path but also increases the computation time. It is useful to combine the sampling strategy algorithm with F-RRT* to improve the quality of sampling to compensate for the increasing computation time.

This paper proposes a sampling-improved path planning algorithm, FF-RRT*. FF-RRT* takes advantage of Fast-RRT* and F-RRT* and overcomes the weakness of these two algorithms. The hybrid sampling method is improved to achieve effective sampling and overcome the application limitation of the original hybrid sampling method. The search scopes of the ChooseParent and Rewire procedures are expanded to optimize the path and shorten the convergence time. The CreatNode process creates a new parent node based on the dichotomy method to get an optimal parent node to \(x_{{{\text{rand}}}}\). Compared with F-RRT* and Fast-RRT*, FF-RRT* generates an optimal path with a short convergence time and has superior environment adaptability. The theoretical analysis is provided for the characteristics of FF-RRT*. And the superior performance of FF-RRT* is validated by the comparative simulations with four simulation environments.

This paper is organized as follows: "Problem definition" introduces the path planning problem. "Related work" introduces the related work of FF-RRT*. "FF-RRT*" states the FF-RRT*. "Analysis" presents a theoretical analysis of completeness, optimality, and computational complexity. Four simulation environments are used in "Simulation results" to demonstrate the performance of FF-RRT* compared with F-RRT* and Fast-RRT*. Finally, a summary is given in "Conclusion".

Problem definition

Let \(X \subseteq R^{c}\) be the workspace, where \(c \in N,c \ge 2\). Let \(X_{{{\text{obs}}}} \subset X\) be the obstacle region, and the collision-free region is \(X_{{{\text{free}}}} = X - X_{{{\text{obs}}}}\). \(x_{{\text{s}}}\) and \(x_{{\text{g}}}\) are source and destination. The path is described as a function \(\phi\).

Path planning aims to generate a path \(\phi\) that begins at the initial point \(\phi (0) = x_{{\text{s}}}\) and reaches the destination \(\phi (1) = x_{{\text{g}}}\) and \(\phi (\upsilon ) \in X_{{{\text{free}}}}\) for all \(\upsilon \in [0,1][0,1]\). The \(\phi\) that fulfills the requirement is called a feasible path. Based on the definition above, the path planning problem can be described as generate a feasible path in the workspace \(X\) with the initial conditions \(\{ x_{{\text{s}}} ,X_{{{\text{obs}}}} ,x_{{\text{g}}} \}\). Definitions 1 and 2 present, respectively, the feasibility and optimal path planning problem.

Definition 1.

Feasible path planning is to generate \(\phi\) such that \(\phi (0) = x_{{\text{s}}}\), and \(\phi (1) = x_{{\text{g}}}\) and \(\phi (\upsilon ) \in X_{{{\text{free}}}}\) for all \(\upsilon \in [0,1]\).

Definition 2.

Optimal path planning is to find a \(\phi^{*}\) that match the optimal condition \(c(\phi^{*} ) = \min \{ c(\phi ):\phi {\text{ is feasible}}\}\), where \(c(\phi )\) represents the cost of \(\phi\).

Related work

This section mainly introduces the related work of the proposed method. The main improvement of Fast-RRT* [29] and F-RRT* [34] compared to RRT* is introduced subsequently.

Fast-RRT*

The pseudocode of Fast-RRT* is outlined in Algorithm 1. Fast-RRT* has two improvements compared to RRT*. Firstly, hybrid sampling is used to select the \(x_{{{\text{rand}}}}\) instead of random sampling by RRT. The goal bias strategy and the constraint sampling are combined to improve the sampling quality. The position of the previous sampling node \(x_{{{\text{p\_rand}}}}\) and a value \(\lambda\) are used in the sampling process, and \(0 < \lambda < 1\). HybridSampling procedure is outlined in Algorithm 2. Secondly, the Backtracking procedure is applied to improve the ChooseParent procedure. The ancestor node set of \(x_{{{\text{rand}}}}\) is generated by tracking from the temporary parent node to the start point. And the parent node of \(x_{{{\text{rand}}}}\) is replaced by the node with the lowest path cost in the set. The improved ChooseParent procedure of Fast-RRT* is shown in Algorithm 3. The Backtracking procedure is outlined in Algorithm 4. However, although the hybrid sampling method accelerates the sampling process, it has applicability limitation towards some special obstacle scenes.

figure a
figure b
figure c
figure d

F-RRT*

The F-RRT* is outlined in Algorithm 5. F-RRT* has also two improvements compared to RRT*, the FindReachest and CreatNode procedure. By comparison, the FindReachest procedure is the same as the Backtracking procedure. Hence, in Algorithm 5, the improved ChooseParent procedure is the same as in Fast-RRT*. Compared to Fast-RRT*, F-RRT* introduces the CreatNode procedure to get an optimal path. The CreatNode procedure creates a new parent node \(x_{{{\text{create}}}}\) based on the dichotomy method. A parameter Ddichotomy is used to determine whether satisfies the requirements. The CreatNode procedure is shown in Algorithm 6. Meanwhile, compared with Fast-RRT*, F-RRT* continues to adopt the Rewire procedure of RRT*, which is shown in Algorithm 7. However, the CreatNode procedure not only improves the quality of the path but also increases the computation time.

figure e
figure f
figure g

FF-RRT*

This paper proposes the FF-RRT* algorithm, which combines the advantages of Fast-RRT* and F-RRT* and overcomes the weakness of these two algorithms. FF-RRT is shown in Algorithm 8. The improved hybrid sampling method is used to improve the sampling quality to compensate for the large computation time generated by the CreatNode procedure of F-RRT* and remove the applicability limitation of Fast-RRT*.

First, the tree node is sampled by the improved HybridSampling procedure. The improved HybridSampling procedure is outlined in Algorithm 9. Different from the original hybrid sampling outlined in Algorithm 2, the improved hybrid sampling combines the random sampling strategy and the constrained sampling strategy to overcome the application limits of the original hybrid sampling. Second, the search scopes of the ChooseParent and Rewire procedures are expanded to the ancestor of the temporary parent node to accelerate the convergence rate. The improved ChooseParent procedure is the same as Fast-RRT* and F-RRT*. The improved Rewire procedure is shown in Algorithm 10. Thirdly, the CreatNode procedure is adopted to generate an optimal parent node for \(x_{{{\text{rand}}}}\) based on the dichotomy method to generate an optimal path. The FF-RRT* is constructed as shown in Fig. 1. And the comparison between FF-RRT* and related works is illustrated in Table 1.

Fig. 1
figure 1

The construction process of FF-RRT*

Full size image
Table 1 Research gaps between FF-RRT* and related work of previous author(s)
Full size table
figure h
figure i
figure j

The improved HybridSampling procedure

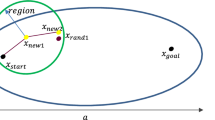
Inspired by the Fast-RRT*, we replace the random sampling with improved hybrid sampling to achieve goal-orientation. Figure 1 illustrates the sampling area of both random sampling and original hybrid sampling in a simple environment. Figure 2a shows the sampling area of random sampling in the pink area, and Fig. 2b shows the node created by the original hybrid sampling is constrained in the green area. It is obvious that the quality of the node sampled by hybrid sampling is greater than the random sampling in the simple obstacle environment. However, in a complex environment with a concave cavity obstacle, the performance of the original hybrid sampling is poor, which is shown in Fig. 3. The original hybrid sampling cannot generate the node to escape from the obstacle in one iteration. In contrast, random sampling can do it. Hence, we combine the random and constrained sampling to improve the original hybrid sampling procedure, shown in Algorithm 11. Compared to the original hybrid sampling, the goal bias strategy is replaced by the random sampling method. And the sampling process can quickly escape from the concave cavity obstacle with random sampling under a certain probability. As a result, the applicability of hybrid sampling is increased.

Fig. 2
figure 2

Comparison of the sampling area of random sampling and Hybrid Sampling in the simple environment (a shows the sampling area of random sampling in pink area, b shows the sampling area of hybrid sampling in green area)

Full size image
Fig. 3
figure 3

Comparison of the sampling area of random sampling and hybrid sampling with concave cavity obstacle (a shows the sampling area of random sampling in pink area, b shows the sampling area of hybrid sampling in green area)

Full size image

The improved ChooseParent procedure

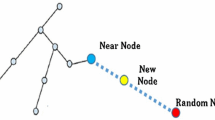
Compared to RRT*, the ChooseParent procedure is shown in Fig. 4. The parent node of \(x_{{{\text{rand}}}}\) is replaced by the farthest ancestor node that can be reached. The rad pot represents the \(x_{rand}\), the blue pot represents the \(x_{{{\text{present}}}}\), the green pots represent the nodes in \(X_{{{\text{near}}}}\), the red line presents the created connection relationship. The parent node of \(x_{{{\text{rand}}}}\) will be replaced by the farthest ancestor node that can be reached.

Fig. 4
figure 4

Comparison of the ChooseParent procedure and the improved ChooseParent procedure (a shows the ChooseParent procedure of RRT*, b shows the improved ChooseParent procedure of FF-RRT*)

Full size image

The CreatNode procedure

To get close to the obstacle to decrease the path cost, we create an optimal parent node for \(x_{{{\text{rand}}}}\) during the CreatNode procedure. The CreatNode procedure is shown in Fig. 5.

Fig. 5
figure 5

The CreatNode procedure of FF-RRT*

Full size image

The improved Rewire procedure

Compared to F-RRT*, the improved Rewire procedure is shown in Fig. 6. As long as there are no obstacles between \(X_{{{\text{near}}}}\) and \(x_{{{\text{present}}}}\), the parent node of \(X_{{{\text{near}}}}\) will be replaced by \(x_{{{\text{present}}}}\). The grey dashed lines present the rewired nodes’ original connection relationship.

Fig. 6
figure 6

Comparison of the Rewire procedure and the improved Rewire procedure (a shows the Rewire procedure of F-RRT*, b shows the improved Rewire procedure of FF-RRT*)

Full size image

Analysis

Probabilistic completeness

RRT processes the probabilistic completeness characteristic and RRT* inherits it [18]. Additionally, Li et al. prove Fast-RRT* inherits this property [29]. Theorem 1 describes the probabilistic completeness of FF-RRT*.

Theorem 1.

For any feasible path planning problems, the probability of finding a feasible path by FF-RRT* approaches one, i.e.,

$$ \mathop {\lim }\limits_{n \to \infty } P(\{ Q_{n}^{{{\text{FF - RRT}}*}} \cap x_{{\text{g}}} \ne \phi \} {\text{ such that x}}_{{\text{s}}} {\text{ is connected to }}x_{{\text{g}}} ) = 1 $$

where \(Q_{n}^{{{\text{FF - RRT}}*}}\) is the set of nodes generated by FF-RRT* after n iteration.

Proof of Theorem 1.

In the FF-RRT*, the improved HybridSampling method is just used to improve the sampling quality. Additionally, the CreateNode and improved Rewire procedure just optimal the path and change the connection relationship. The adjustments of FF-RRT* do not destroy the connectivity. The path can still connect \({\text{x}}_{{\text{s}}}\) and \(x_{{\text{g}}}\). Hence, the FF-RRT* processes the probabilistic completeness as Fast-RRT*.

Asymptotic optimality

RRT* has the asymptotic optimality characteristic compared to RRT [18]. Theorem 2 states that FF-RRT* inherits the asymptotic optimality characteristic.

Theorem 2.

For any given feasible path planning problem, the FF-RRT* can generate the optimum path as the number of iterations approaches infinity:

$$ \mathop {\lim }\limits_{n \to \infty } P(\sup Y_{n}^{{{\text{FF - RRT}}*}} = C^{*} ) = 1 $$

where \(Y_{n}^{{{\text{FF - RRT}}*}}\) represents the cost of the path generated by FF-RRT* after n iterations, \(C^{*}\) represents the minimum cost.

Proof of Theorem 2.

Firstly, the differences between Fast-RRT* and RRT* are HybridSampling and Rewire procedure. The HybridSampling procedure is used to improve the sampling quality, which does not influence the asymptotic optimality characteristic. Additionally, Fast-RRT* does not adopt the Rewire procedure as RRT*. Therefore, the Fast-RRT* combined with the Rewire procedure can inherit the asymptotic optimality characteristic. With the improved HybridSampling procedure and the improved Rewire procedure, the FF-RRT* is just an improved method of Fast-RRT* combined with the Rewire procedure, so the FF-RRT* also inherits the asymptotic optimality characteristic.

Computational complexity

Theorem 3 states FF-RRT* has the same computational complexity as F-RRT*.

Theorem 3.

For any given feasible path planning problem, there will be a constant \(\varepsilon_{1}\) to match:

$$ \mathop {\lim }\limits_{n \to \infty } \, \exp \left( {\frac{{S_{n}^{{{\text{FF - RRT}}*}} }}{{S_{n}^{{{\text{F - RRT}}*}} }}} \right) \le \varepsilon_{1} $$

where \(S_{n}^{i}\) is the number of procedures executed by algorithm i after n iterations.

Proof of Theorem 3.

The differences between FF-RRT* and F-RRT* are the improved HybridSampling procedure and the improved Rewire procedure. For the improved HybridSampling procedure, it just improves the sampling quality by constraining the sampling area and does not increase the computation amount. For the improved Rewire procedure, it just changes the connection between nodes compared to Rewire procedure. Hence, Theorem 3 is proved.

Simulation results

FF-RRT* is simulated in 2-dimensional map, which contains four test environments. In the simulation, the performance of FF-RRT* is compared with Fast-RRT* and F-RRT, because they are the basement of FF-RRT* and are the latest representations of the variant of RRT*. Every algorithm was repeated 100 times during the simulation to resist randomness.

The simulation will compare the performance of algorithms by three indicators: Ci, which is the cost of the generated path by algorithm i; Ni, which is the number of iterations to generate the path by algorithm i, Ti, which is the time of generating the path by algorithm i. The algorithm will stop once the feasible path is found or the max iteration is reached. The simulation is implemented on an AMD Ryzen 7 5800X CPU with 8G of RAM. The simulation environments are illustrated in Fig. 7. The four simulation environments are the same size 9000 × 6000.

Fig. 7
figure 7

The simulation environments (the green dot: \(x_{{\text{s}}}\), the red dot: \(x_{{\text{g}}}\))

Full size image

During the simulation process, the parameters that need to be identified are \(R_{{{\text{near}}}}\),\(n_{\max }\), Ddichotomy, \(\lambda\). In the simulation process, \(n_{\max } = 30,000\). In the sampling procedure, \(\lambda = 0.5\). In the improved ChooseParent procedure, \(R_{{{\text{near}}}} = 200\). And in CreatNode procedure, referring to the Reference [34], we did the simulation to choose the value of \(D_{{{\text{dichotomy}}}}\). The relationship between the performance of the F-RRT* in the cluttered environment and \(D_{{{\text{dichotomy}}}}\) is shown in Fig. 8. It can be seen that when the \(D_{{{\text{dichotomy}}}}\) increases, CF-RRT* increases, while TF−RRT* decreases simultaneously. To avoid the additional computation time, the value of \(D_{{{\text{dichotomy}}}}\) is set as 300.

Fig. 8
figure 8

The relationship between the performance of the F-RRT* and the value of \(D_{{{\text{dichotomy}}}}\) in the cluttered environment

Full size image

Simple maze

Figure 9 shows the performance of the three algorithms in a simple maze environment. It can be seen that F-RRT* and the proposed algorithm, FF-RRT* generate a path that is closer to obstacles and have a better initial solution than Fast-RRT*. Figure 10 shows the statistics of Ci, Ni, Ti and Table 2 illustrates the average value of Ci, Ni, Ti with 100 simulations. The average of Ci for Fast-RTT* is higher than the average of Ci for F-RRT* and FF-RRT*, which also shows that the last two algorithms generate a more optimal path than Fast-RRT*. And according to the box height, the performances of the last two algorithms are more stable. Additionally, the average value of Ni and Ti for FF-RRT* are lower than the F-RRT*. By the improved HybridSampling procedure, there is a 35% reduction in the average value of Ni and a 25% reduction in the average value, which shows that FF-RRT* has a faster convergence rate than F-RRT*. Meanwhile, since the Ni for FF-RRT* has no significant difference from it for Fast-RRT*, the Ti for FF-RRT* is still higher than the Ti for Fast-RRT*. It is because that the application of dichotomy. Based on the above analysis, the proposed method, FF-RRT* can generate a more optimal path than Fast-RTT* with a less convergence time than F-RRT*.

Fig. 9
figure 9

Performance of algorithms in a simple maze environment

Full size image
Fig. 10
figure 10

The statistical results of Ci, Ni, Ti

Full size image
Table 2 The average value of Ci, Ni, Ti
Full size table

Complex maze

Figure 11 shows the performance of algorithms in complex maze environment. It can be also clearly seen that F-RRT* and the proposed algorithm, FF-RRT* generate a path that is closer to obstacles and have better performance than Fast-RRT*. Figure 12 shows the statistics Ci, Ni, Ti. The statistics result show that FF-RRT* can generate a more optimal path than Fast-RTT* with a less convergence time than F-RRT* in a complex maze environment. Table 3 illustrates the average value of Ci, Ni, Ti in a complex maze environment. Combing with statistics in Table 2, the FF-RRT* shortens 32% of the Ti in a complex maze environment and 25% of the Ti in a simple maze environment compared to F-RRT*, which shows that the more complex the maze environment becomes, the better the FF-RRT* performs compared to F-RRT*.

Fig. 11
figure 11

Performance of algorithms in a complex maze environment

Full size image
Fig. 12
figure 12

The statistical results of Ci, Ni, Ti

Full size image
Table 3 The average value of Ci, Ni, Ti
Full size table

Complex maze with concave cavity obstacle

Figure 13 illustrated the performance of algorithms in the complex maze with a concave cavity obstacle environment. It can be seen that the Fast-RRT* needs to take much more iterations to get out of the concave cavity obstacle compared to F-RRT* and FF-RRT*, which shows the applicability limits of the original hybrid sampling method. Figure 14 shows the performance of the three algorithms of Ci, Ni, Ti. It can be also seen from the box that the average of Ni for Fast-RTT* is higher than the average of Ni for F-RRT* and FF-RRT*, which also shows the poor performance of Fast-RRT* towards concave cavity obstacle. However, the Ti of Fast-RRT* is still the lowest of the three algorithms. It is because the increased iterations mainly appear in the beginning and most of them are quickly skipped over, leading to a low cost per iteration. Table 4 illustrates the average value of Ci, Ni, Ti. It can be obtained by calculation that the average Ti of Fast-RRT* in this environment is 134% more than in the complex maze environment compared to 12% with F-RRT* and 34% with FF-RRT*. The comparison result shows the poor performance of the original hybrid sampling method and the effectiveness of the improved hybrid sampling method for concave cavity obstacle. Based on the above analysis, the proposed method, FF-RRT*, has stronger applicability compared to Fast-RRT* by the improved hybrid sampling method.

Fig. 13
figure 13

Performance of algorithms in a complex maze with concave cavity obstacle environment

Full size image
Fig. 14
figure 14

The statistical results of Ci, Ni, Ti

Full size image
Table 4 The average value of Ci, Ni, Ti
Full size table

Cluttered environment

Figure 15 illustrates the performances of algorithms in a cluttered environment. Different from the other two environments, it cannot be seen that F-RRT* and FF-RRT* generate a more optimal path than Fast-RRT*. It is because the distance between two obstacles is relatively small, which weakens the performance of the dichotomy method. Additionally, comparing Fig. 15c to (b), the quality of searching direction is improved by the improved HybridSampling procedure. Figure 16 shows the statistics Ci, Ni, Ti. The statistics result show that FF-RRT* can generate a more optimal path than Fast-RTT* with a less convergence time than F-RRT*. Table 5 illustrates the average value of Ci, Ni, Ti. Combing with the statistics in Table 3, the last two algorithms shorten 15% of the Ci in a cluttered environment compared to 20% in a complex maze environment, which shows that FF-RRT* performs better in a maze environment.

Fig. 15
figure 15

Performance of algorithms in a cluttered environment

Full size image
Fig. 16
figure 16

The statistical results of Ci, Ni, Ti

Full size image
Table 5 The average value of Ci, Ni, Ti
Full size table

From the above analysis, FF-RRT* has a superior performance compared to Fast-RRT* and F-RRT*. The boxes show that FF-RRT* can generate a more optimal solution than Fast-RRT* and the optimal path generated by the FF-RRT* requires fewer iterations than F-RRT*. Moreover, the application limits of the original hybrid sampling method are overcome by the improved HybridSampling procedure. We sum up that FF-RRT* is suitable for more complex environments than Fast-RRT* and can generate an optimal path with a faster convergence rate.

Conclusion

A novel sampling-improved path planning algorithm, FF-RRT* is proposed in the paper. By combining and improving the adjustments of F-RRT* and Fast-RRT*, the FF-RRT* can obtain an optimal path with a short convergence time. The major imp of FF-RRT* is to propose the improved HybridSampling procedure and introduce it into the F-RRT* to improve sampling quality and decrease the iterations to increase the convergence rate. Additionally, the improved HybridSampling procedure is applicable to the environment with concave cavity obstacle, which overcomes the application limitation of the original HybridSampling procedure in Fast-RRT*. The superior performance of the FF-RRT* was verified by numerical simulation compared to F-RRT* and Fast-RRT*. The FF-RRT* shortens 32% of the convergence time in complex maze environment and 25% of the convergence time in simple maze environment compared to F-RRT*. And in a complex maze with a concave cavity obstacle, the average convergence time of Fast-RRT* in this environment is 134% more than the complex maze environment compared to 12% with F-RRT* and 34% with FF-RRT*.

Although the FF-RRT* algorithm can effectively decrease the convergence time by improved HybridSampling procedure, the increased computation problem caused by the application of dichotomy has not been fundamentally solved. Additionally, the applicability to three-dimensional environment [35, 36] is also a valuable research direction. Meanwhile, when actually used for certain robots, such as drones, the continuity of the generated paths needs to be guaranteed [37, 38]. Hence, how to decrease the computation time of dichotomy fundamentally and maintain the continuity of the generated path in a three-dimensional environment is our future study direction.