BRCE: bi-roles co-evolution for energy-efficient distributed heterogeneous permutation flow shop scheduling with flexible machine speed

Abstract

Distributed manufacturing is the mainstream model to accelerate production. However, the heterogeneous production environment makes engineer hard to find the optimal scheduling. This work investigates the energy-efficient distributed heterogeneous permutation flow scheduling problem with flexible machine speed (DHPFSP-FMS) with minimizing makespan and energy consumption simultaneously. In DHPFSP-FMS, the local search misleads the population falling into local optima which reduces the convergence and diversity. To solve this problem, a bi-roles co-evolutionary algorithm is proposed which contains the following improvements: First, the global search and local search is divided into two swarms producer and consumer to balance computation. Second, three heuristic rules are designed to get a high-quality initialization population. Next, five problem-based local search strategies are designed to accelerate converging. Then, an efficient energy-saving strategy is presented to save energy. Finally, to verify the performance of the proposed algorithm, 22 instances are generated based on the Taillard benchmark, and a number of numerical experiments are adopted. The experiment results state that our algorithm is superior to the state-of-arts and more efficient for DHPFSP-FMS.

Introduction

With the development of industrial technology and global trade, the order quantity increases fast for enterprises. However, limited to the production capacity of a single factory, the jobs are distributed to different factories to parallel production [1,2,3]. This manufacturing mechanism is called distributed production. Thus, distributed permutation flow shop scheduling problem (DPFSP) received more attention than the classical flow shop scheduling problem [4] based on the above situation in recent years. For example, DPFSP with assembly stage [5], DPFSP with no-wait time [6, 7], DPFSP with limited buffer [8], DPFSP with blocking [9], DFSP with lot-streaming [10]. However, after summarizing the previous work for DPFSP, it is found that the processing time of each operation in each factory is the same which is called homogeneous factories. Nevertheless, in most situations, the processing time might be different in each factory because the machine type is different and limited to the cost, which is called heterogeneous factories [11]. Thus, researching distributed heterogeneous permutation flow shop scheduling problem (DHPFSP) is more realistic. Because of the variation in processing time, the optimization will be more difficult than DPFSP which is more challenging. Moreover, in flow shop environment, the machine processing speed can be adjusted due to the features of the numerical control machine tool. The faster processing speed, the higher energy consumption, and the shorter processing time [12].

Energy consumption is a key indicator reflecting the carbon emission [13]. After Industrial 4.0 is proposed, green manufacturing became a trend of industrial development [14]. To protect our environment and promote sustainable manufacturing, green scheduling has been concerned more in recent years [15, 16]. Thus, the green indicator should be also considered in DHPFSP.

The co-evolutionary algorithm is an efficient framework that has been successfully applied to many fields [17]. Meanwhile, it is based on the thought of divide-and-conquer and decomposes the difficult problem into several sub-problem to solve [18]. The key idea is to assign different tasks to each sub-population and solve the hard problem in the merged population [19]. Considering the complexity of DHPFSP, this work designs a framework called bi-roles co-evolution (BCCE) which defines two populations producer ${\mathcal {P}}$ and consumer ${\mathcal {C}}$ for DHPFSP. Moreover, the producer and consumer are two concepts from biology. The producer ${\mathcal {P}}$ takes charge of exploring the potential region to generate solutions with great diversity. Furthermore, the consumer ${\mathcal {C}}$ buys the Pareto solutions from ${\mathcal {P}}$ to preserve the historical elite solutions without reducing the diversity of ${\mathcal {P}}$. Meanwhile, the consumer ${\mathcal {C}}$ will rewards ${\mathcal {P}}$ by replacing the worst individuals of ${\mathcal {P}}$ with some high-quality solutions. This framework is first proposed for DHPFSP which is never proposed before. Meanwhile, it can efficiently balance the computation resources between exploration and exploitation.

This study focuses on solving the multi-objective distributed heterogeneous permutation flow shop scheduling problem with flexible machine speed (DHPFSP-FMS), where the makespan and total energy consumption (TEC) are minimized simultaneously. The processing time is different in each factory and each machine has a flexible speed selection. To solve this problem, a novel co-evolutionary framework for DHPFSP-FMS is proposed. First, the BRCE is designed to balance computation resources. Second, three heuristic rules are designed to get a high-quality population. Then, five local search strategies based on problem features are presented to improve the convergence. Finally, an efficient energy-saving strategy is proposed. The motivation for designing BRCE is stated as follows: (1) due to the complexity of DHPFSP-FMS, the global search needs to be allocated many computation resources. Moreover, if directly adopting local search to the whole population, fast convergence reduces the chance to approach potential object space, which reduces the diversity. Thus, a big swarm with much computation is used for global search without influence by enhanced operators and a small swarm is applied to local search to improve the quality of Pareto solutions. (2) Traditional NEH is based on several insertions that waste too much computation. Nevertheless, based on the features of DHPFSP-FMS, the heuristic construction rule like adjusting speed can vastly improve the convergence and diversity of the initial population by one-time initialization. (3) Designing neighborhood structures based on the critical path and problem features can greatly increase the efficiency of local search. (4) Adjusting speed selection can reduce the idle gap to efficiently save energy consumption.

The rest of this work is mainly divided four parts. The literature review and research gap are described in “Related work”. The MILP model for DHPFSP-FMS is built and its features are introduced in “Problem statement and modeling”. “Our approach: BRCE” described the proposed algorithm. The experimental results are shown in “Experimental results”. Finally, the conclusion of this work is described in “Conclusions”.

Related work

Distributed permutation flow shop scheduling

DPFSP is first suggested by Naderi and Ruiz [20] which defines the original model. The representative publications of DPFSP in the recent 3 years will be introduced as follows. Wang and Wang proposed a knowledge-based cooperative algorithm for DPFSP with variable speed [17]. Moreover, they designed an improved Nawaz–Enscore–Ham (NEH) [21] initialization strategy by reducing processing speed to get a high-quality population. Wang proposed a multi-objective whale swarm algorithm with a problem-dependent local search strategy for DPFSP with identical factory [22]. Shao studied blocking DPFSP with fuzzy processing time and designed improved NEH to get an efficient population [23]. Hamzadayi thinks DPFSP is a decision-making process and proposed a bender decomposition algorithm with an enhanced NEH strategy to solve it [24]. Jing studied DPFSP with due window and applied iterated greedy algorithm (IGA) by insertion operation [25]. Huang extended DPFSP with sequence-dependent set-up time and also used IGA with local search to solve it [26]. Meanwhile, Rifai designs an adaptive strategy to balance exploration and exploitation for the same model [27]. Zhao considered the DPFSP with blocking time and proposed a differential evolutionary algorithm with ensemble initial strategy [28]. A parameter adaptive social engineering algorithm is proposed by Fard for DPFSP [29]. Shao mixed different blocking constrain with DPFSP and designed an efficient IGA to solve it [30]. Furthermore, Li improved IGA with an adaptive probability to accept worse solutions for escaping local optima [31]. Moreover, Chen proposed a population-based IGA for blocking DPFSP [32]. Zhao added a assemble stage for DPFSP and adopted a matrix-cube encoding mechanism which contains more information on the relationship between the best solution and the others [33]. Moreover, Song extend the model based on the former work with sequence-dependent setup time and applied the genetic programming for selecting the heuristics [34]. Zhen studied no-wait DPFSP with sequence-dependent setup time [35]. Mao considered DPFSP with machine preventive maintenance and used a restart strategy to jump out of local optima [36]. Jing extended DPFSP with uncertain processing time and applied to improve IGA for it [37]. Li studied green DPFSP by minimizing total flow time and energy consumption and designed an NSGA-II with speed adjustment local search and right-shift energy-saving strategy [38]. Schulz considered DPFSP with transportation time and minimizing the makespan and energy consumption of production and transportation [39]. Yang combined blocking and assembly constraints to DPFSP and designed a knowledge-driven heuristic to solve it [40]. Zhu added no-wait and due window constraints to DPFSP [41]. Wang studied DPFSP with assembly stage, set-up, and transportation time [5]. Moreover, Miyata fixed blocking time and maintenance operation with DPFSP [42]. Li studied parallel batching DPFSP with the deteriorating job and designed a hybrid artificial bee colony algorithm for solving it [43]. Pan researched lot-streaming DPFSP and bind several jobs together to schedule [44]. The same publications with different names but same the accepted are [45].

In conclusion, the extension model of DPFSP can be summarized as the following features: blocking time (mixed blocking), assembly stage, sequence-dependent set-up time, fuzzy processing time (uncertain time), variable machine processing speed, no-wait (no-idle) time, machine maintenance time, lot-streaming (parallel batching or group) scheduling, due window, and green (carbon- or energy-efficient) scheduling. All of their publications are combined these features and add them to DPFSP. The algorithm they use most is IGA combined with local search (swap and insert) and improve NEH strategies for initialization. However, the factory type is the same in the above work. Nevertheless, the factory type is not identical to practical manufacturing.

Distributed heterogeneous flow shop scheduling

DHFSJP has received growing concern in recent years. Chen proposed an improved estimation distribution algorithm for DHPFSP-FMS with the content machine speed and got a better performance [46]. Shao designs multi-local search strategies for DHPFSP-FMS which efficiently increase the exploitation [47]. Li combined decomposition-based multi-objective evolutionary algorithm with bee behavior for DHPFSP-FMS which balances the convergence and diversity [48]. Zhao designed a self-adaptive operators selection strategy for DHPFSP-FMS which improves the efficiency of local search [7]. Lu proposed a turn-off/on strategy to save energy for DHPFSP-FMS by minimizing makespan, energy consumption, and negative social impact [49]. Meng studied DHPFSP-FMS with lot-streaming which binds a group of jobs to be processed together and sequence-dependent set-up time [50]. Lu fixed flow shop and hybrid flow shop as DHPFSP-FMS [11]. However, the DHPFSP-FMS with variable machine speed has few works.

Research gap and discussion

The previous work mainly focuses on DPFSP with the flexible machine speed and DHPFSP-FMS with content speed. The DHPFSP-FMS with flexible machine speed is never considered before.

The works about DHPFSP-FMS focus on combining global search with local search in one population, which will consume much computation on local search. The performance of the final results is based on exploration period. Thus, dividing global search and local search into two populations and dispatch more computation resource can increase diversity of population. Meanwhile, the convergence can keep in elite swarms.

The initialization strategy applied most is improved NEH which inserts a job to every place to search for the best local solution. However, this method will waste too much computation. The feature of DHPFSP-FMS with variable speed is based on speed. Construct heuristics about speed can greatly save computation to increase diversity and convergence.

The local search strategies of DHPFSP-FMS are so random, which is efficient to search for better solutions. The knowledge of features of DHPFSP-FMS is mainly based on the critical path. Designing search strategies based on the critical path can improve efficiency.

The publications of DHPFSP-FMS with variable speed pay little attention to energy-saving strategy. Saving energy can promote economic profit vastly, which is worth researching.

Problem statement and modeling

Problem statement

The DHPFSP-FMS with flexible speed has to solve three sub-problems: (i) assign each job to different factories; (ii) determine the job processing sequence in each factory; and (iii) select a machine processing speed for each operation. In DHPFSP-FMS, there are n jobs that need to be allocated to $n_f$ factories. Each factory has m machines with different processing times for each the same operation. Meanwhile, each job has $n_i$ operations which must be processed in the same factory. Each factory shares a permutation flow shop scheduling problem. Moreover, each job will be processed from $M_1$ to $M_{n_m}$ which is the same for all jobs. By adjusting the processing sequence in each factory and selecting different speed $v_{f, i,k}$, the makespan and energy consumption is different. The real processing time $p_{f,i,k}^{r}$ equals to original processing time $p_{f,i,j}^{o}$ divided $v_{f,i,k}$. Moreover, the processing power equals to $p_{f,i,j}^{r}\times v_{f,i,k}^{2}$.

The assumptions of DHPFSP-FMS are given as below:

• All the factories start processing operations at time zero. Moreover, all jobs and machines are available at time zero in each factory.

• Each machine can only process one operation at the same time. Meanwhile, interruption is not considered for each operation.

• The processing times and energy consumption are certain values.

• Every job can only select one factory and each job can only be processed on one machine at a moment.

• The processing time of each operation on different machine is different in each factory. Meanwhile the machine speed $v_{f,i,k}\in [1,5]$.

• Transportation time, setup time, and energy consumption are not considered. Moreover, machine breakdown and dynamic events would not happen.

Table 1 gives an example of DHPFSP-FMS with two factories, eight jobs, and two machines. Assuming the processing sequence is $\Pi =\{1,5,2,6,4,7,3,8\}$ and factory assignment is $FA=\{1,1,2,2,1,1,2,2\}$. The original processing time of each job on each machine is can be seen in Table 1 and the speed selections are at the right. Figure 1 shows the Gantt chart of this example. $J_1,J_2,J_5$ and $J_6$ are assigned to $F_1$, and the others are assigned to $F_2$. The processing time of each operation is accelerated by $v_{f, i,k}$. Finally, the makespan of all factories depends on the max completion time factory.

Table 1 An example for DHPFSP-FMS

Fig. 1

The gantt chart of the example in Table 1

MILP model for DHPFSP-FMS

Before modeling the DHPFSP-FMS, the notations used throughout the study are defined as follows:

Indices:

• $i,i'$: indices of all jobs, $i\in \{1,\ldots ,n\}$;

• $k,k'$: indices of machines, $k\in \{1,\ldots ,m\}$;

• $v,v'$: indices of speed, $v\in \{1,\ldots ,n_v\}$;

• f: indices of factories, $f\in \{1,\ldots ,n_f\}$;

• t: job position of machine $M_k$ in factory f, $l\in \{1,\ldots ,n_t\}$;

Parameters:

• n: the number of all jobs;

• $n_f$: the number of factories;

• m: the number of all machines;

• $n_v$: the max level of machine speed;

• $n_t$: the number of all positions;

• I: set for jobs and $I=\{1,2,\ldots ,n\}$;

• F: set of factories and $F=\{1,2,\ldots ,n_f\}$;

• M: set of machines and $M=\{1,2,\ldots ,m\}$;

• $T_{f,k}$: set of job positions on machines $M_K$ in factory f and $T_{f,k}=\{1,2,\ldots ,n_t\}$;

• $T_{f,k}^{'}$: set of top $n_t-1$ positions on machines $M_K$ in factory f and $T_{f,k}=\{1,2,\ldots ,n_t-1\}$;

• V: set of speeds and $V=\{1,2,\ldots ,n_v\}$;

• $p_{f,i,k}^o$: The original processing time for operation $O_{i,k}$ job $I_i$ processed by machine $M_k$ in factory f;

• $W_{I}$ the idle power when machine stands by;

• $W_{O}$ processing power when machine processing operation;

• L: a large integer for keeping the consistency of the inequality;

Decision variables:

• $O_{i,k}$: The $k_{th}$ operation of job $I_i$ on machine $M_k$;

• $v_{f,i,k}$: The speed selection of operation $O_{i,k}$ on machine $M_k$ in factory f;

• $p_{f,i,k}^{r}$: The real processing time of operation $O_{i,k}$ on machine $M_k$ in factory f;

• $S_{f,i,k}$: the starting time of operation $O_{i,j}$ in factory f;

• $F_{f,i,k}$: the finishing time of operation $O_{i,j}$ in factory f;

• $B_{f,k,t}$: the beginning time of machine $M_k$ at position t in factory f;

• $C_{f,k,t}$: the completion time of machine $M_k$ at position t in factory f;

• $E_P$: total processing energy consumption;

• $E_I$: total idle energy consumption;

• $E_{f,k,t}^M$: idle energy consumption of machine $M_k$ at position t in factory f;

• ${\text {TEC}}$: total energy consumption;

• $C_{\max }$: the makespan of a schedule;

• ${\textbf{X}}_{f,i,k,v,t}$: The value is equals to 1, if operation $O_{i,k}$ is processed on machine $M_k$ with speed $V_v$ at position t in factory f; otherwise it is set to 0;

• ${\textbf{Y}}_{i,f}$: The value is equals to 1, if job $I_i$ is assigned to factory f; otherwise is set to 0;

The objectives of DHPFSP-FMS include makespan and TEC. The machine speed is faster, the makespan is lower and the TEC is higher. Thus, makespan and TEC conflict. Their equations are elaborated as follows:

$$\begin{aligned} \min ~F_1= & {} C_{\max }=\max \left\{ F_{f,i,m}\right\} , {\forall i \in I, f \in F}. \end{aligned}$$

(1)

$$\begin{aligned} \min ~F_2= & {} {\text {TEC}}=E_P+E_I \end{aligned}$$

(2)

$$\begin{aligned} E_P= & {} \sum _{f\in F}\sum _{i\in I}\sum _{k\in M}\sum _{v\in V}\sum _{t\in T_{f,k}}W_{O}\cdot p_{f,i,k}^r\nonumber \\{} & {} \cdot v_{f,i,k}^2\cdot {\textbf{X}}_{f,i,k,v,t} \end{aligned}$$

(3)

$$\begin{aligned} E_I= & {} \sum _{f\in F}\sum _{k\in K}\sum _{t\in T_{f,k}^{'}}W_{I}\cdot (B_{f,k,t}-C_{f,k,t-1}) \end{aligned}$$

(4)

The mixed-integer linear programming model of DHPFSP-FMS with two objective functions is introduced as follows:

$$\begin{aligned} \left\{ \begin{aligned}&\min ~F_1=C_{\max }\\&\min ~F_2={\text {TEC}} \end{aligned}\right. \end{aligned}$$

(5)

subject to:

$$\begin{aligned}{} & {} \sum _{f\in F}{\textbf{Y}}_{i,f}=1, \quad \forall i\in I\end{aligned}$$

(6)

$$\begin{aligned}{} & {} \sum _{v\in V}{\textbf{X}}_{f,i,k,v}=1,\forall i\in I, \quad k \in M, f \in F \end{aligned}$$

(7)

$$\begin{aligned}{} & {} S_{f,i,m}+\sum _{v\in V}\sum _{t\in T_{f,k}}p_{f,i,m}^o/v_{f,i,m}\cdot {\textbf{X}}_{f,i,m,v,t}\leqslant C_{f,m,n_t}, \nonumber \\{} & {} \quad \forall i\in I,\quad f \in F \end{aligned}$$

(8)

$$\begin{aligned}{} & {} C_{f,m,n_t}\leqslant C_{\max },\quad \forall f \in F \end{aligned}$$

(9)

$$\begin{aligned}{} & {} S_{f,i,k}+\sum _{v\in V}\sum _{t\in T_{f,k}}p_{f,i,k}^o/v_{f,i,k}\cdot {\textbf{X}}_{f,i,m,v,t}\leqslant S_{f,i,k+1},\nonumber \\{} & {} \quad \forall i\in I, k \in \{1,\ldots ,m-1\},\quad f \in F \end{aligned}$$

(10)

$$\begin{aligned}{} & {} \sum _{i\in I}\sum _{k\in K}{\textbf{X}}_{f,i,k,v,t}\ge \sum _{i\in I}\sum _{k\in K}{\textbf{X}}_{f,i,k,v,t+1},\nonumber \\{} & {} \quad \forall f\in F, v\in V,\quad t \in T_{f,k}^{'} \end{aligned}$$

(11)

$$\begin{aligned}{} & {} B_{f,k,t+1}-B_{f,k,t}\ge \sum _{i\in I}\sum _{k\in K}{\textbf{X}}_{f,i,k,v,t}\cdot p_{f,i,k}^o/v_{f,i,k},\nonumber \\{} & {} \quad \forall f\in F, \quad v\in V, t \in T_{f,k}^{'} \end{aligned}$$

(12)

$$\begin{aligned}{} & {} E_{f,k,t}^M+L\ge \Big (B_{f,k,t+1}-B_{f,k,t} \nonumber \\{} & {} \quad -\sum _{i\in I}\sum _{k\in K}{\textbf{X}}_{f,i,k,v,t}\cdot p_{f,i,k}^o/v_{f,i,k}\Big )\cdot W_{I},\nonumber \\{} & {} \quad \forall f\in F, v\in V, t \in T_{f,k} \end{aligned}$$

(13)

$$\begin{aligned}{} & {} B_{f,k,t}\ge S_{f,i,k}-L\cdot (1-{\textbf{X}}_{f,i,k,v,t}), \nonumber \\{} & {} \quad \forall i\in I, \quad k\in K,\quad f\in F, v\in V,\quad t \in T_{f,k} \end{aligned}$$

(14)

$$\begin{aligned}{} & {} B_{f,k,t}\leqslant S_{f,i,k}-L\cdot (1-{\textbf{X}}_{f,i,k,v,t}),\nonumber \\{} & {} \quad \forall i\in I,\quad k\in K, f\in F, \quad v\in V,\quad t \in T_{f,k}\end{aligned}$$

(15)

$$\begin{aligned}{} & {} 0\leqslant S_{f,i,k}\leqslant L, \quad \forall i\in I, k \in K, f\in F \end{aligned}$$

(16)

$$\begin{aligned}{} & {} L\ge B_{f,k,t}\ge 0,\quad \forall f\in F,\quad k\in K, \quad t \in T_{f,k} \end{aligned}$$

(17)

where Eq. (5) is objective function which is makespan and TEC. Equation (6) makes sure a job only be dispatched to one factory. Equation (7) guarantees that every job has to be processed on one machine at the same time. Equations (8)–(9) state the makespan constrain. Equation (10) states that the proceeding must be finished before the current operation starts. Equation (11) indicates that each operation must be delivered to the preceding positions only when they are free. Equation (12) guarantees that the idle time is more than zero. Equation (13) defines the energy consumption between two adjacent positions on the same machine. Equations (14)–(15) ensure the constrain between operation start time and machine start time. Equations (16)–(17) are value boundaries.

Problem features

Property 1: The makespan is mainly determined by speed selection. Increasing the speed of the critical path can reduce makespan.

Proof 1: Assuming the original makespan is $C(\pi )$, where $\pi$ is the critical path. Then, increase the speed of an operation $v_1$ to $v_2$. Suppose the makespan $C(\pi )=A+p_{f,i,k}^{o}/v_1$, where A is the total processing time of other critical operations and is constant. For $v_2>v_1$, so that $p_{f,i,k}^{o}/v_1>p_{f,i,k}^{o}/v_2$. Moreover, $C(\pi ^{'})=A+p_{f,i,k}^{o}/v_2<C(\pi )$. Thus, the property 1 has been proved.

Property 2: The TEC is based on speed selection and idle time. Select smaller speed can lower the TEC when it does not change $C_{\text {max}}$.

Proof 2: Assuming the original TEC is $E_1$ and the critical path is $\pi$. Suppose that there exists an idle time gap $T_1$ which is sufficiently big, which is more than the change of finish time of an operation $\Delta F$. Reduce the speed of the operation $v_1$ to $v_2$. First, $E_1=B+T_1*W_{I}$ where B is other energy consumption, and $\Delta F=p_{f,i,k}^{o}/v_1-p_{f,i,k}^{o}/v_2<0$. Then, the $T_2=T_1+\Delta F<T_1$. Thus, $E_2=B+T_2*W_{I}<E_1$ and property 2 have been proved.

Property 3: Inserting one job in the critical factory to the factory with a sufficiently small finish time can reduce the makespan.

Proof 3: Supposing the original makespan is $C_{f_1}(\pi )$, where $\pi$ is the critical path. Assume that there exists a factory $f_2$ which has a sufficiently small makespan $C_{f_2}<C_{f_1}(\pi )$. Randomly select a job from the critical factory and insert it into factory $f_2$. Then, $C(\pi )=C(\pi )-p_{f_1,i,k}$ and $C_{f_2}=C_{f_2}+p_{f_2,i,k}<C(\pi )$. Thus, the makespan is reduced and property 3 has been proved.

In conclusion, frequently changing speed selection and factory assignment can efficiently reduce makespan and TEC.

Our approach: BRCE

Framework of BRCE

There are two different roles in BRCE which are producer swarm ${\mathcal {P}}$ and consumer swarm ${\mathcal {C}}$. ${\mathcal {P}}$ has content size ps and ${\mathcal {C}}$ sizes dynamically. Moreover, ${\mathcal {P}}$ executes global searching without being affected and generates the Pareto solutions as production. Meanwhile, ${\mathcal {C}}$ absorbs Pareto solutions and adopts enhanced operators to them. The producer plays a role in keeping diversity and the consumer has to keep convergence and save computation resources. As shown in Fig. 2, first, the heuristic initialization is adopted to get high-quality solutions. Second, the producer ${\mathcal {P}}$ generates offspring and environment selection by the fast non-dominated sorting genetic algorithm (NSGA-II) [51]. Next, the consumer ${\mathcal {C}}$ absorbs the Pareto solutions from ${\mathcal {P}}$. Then, the consumer executes problem-specific local search strategies to enhance convergence and diversity. Moreover, the energy-saving strategy is executed to reduce TEC. Furthermore, ${\mathcal {C}}$ adopts preserves the Pareto solutions of itself as a new swarm. Finally, the final Pareto solutions set will be output by ${\mathcal {C}}$.

Encoding and decoding

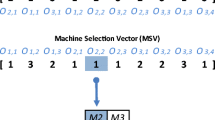
In this work, two vectors and a matrix are used to represent a solution for DHPFSP-FMS. Figure 3 shows the encoding schema for DHPFSP-FMS. Moreover, the encoding and decoding schema is as follows: Encoding schema: there are three vectors which are job sequence (JS), speed selection (SS), and factory assignment (FA). Moreover, all operations of each job must be dispatched to the same factory.

Decoding schema First, all jobs are allocated to different factories according to the FA. Second, the job sequence of each factory can be obtained from JS. Next, each job will be processed from machine $M_1$ to $M_m$ and the real processing time is got by dividing the speed by SS. Finally, the makespan and TEC can be get after all jobs are processed.

Fig. 2

Parasitic evolutionary framework for distributed shop scheduling

Initialization

Initialization strategy is essential for the shop scheduling problems problems [13]. To vastly improve convergence and save computation, three heuristics are proposed as follows:

Maximum speed rule: Randomly initial JS and FA. Select the biggest speed for all operations. The Cmax can reduce to the smallest range to explore.

Minimum speed rule: Randomly initial JS and FA. Select the smallest speed for all operations. The ${\text {TEC}}$ can reduce to the smallest interval to explore.

Balance load rule: Randomly initial JS and SS. Calculate the sum of the processing time of each job on all machines in each factory. $T_{f,i}=\sum _{1}^{m}p_{f,i,k}^{o}, \forall i\in I, f\in F$. For each job, select the factory with the smallest workload of current scheduling. If there are factories with the same load, select the one with smaller T.

Based on those rules mentioned above, the initial population consists of four sub-populations sizing ps/4, which are generated by executing three rules and random initialization. Moreover, initialized producer swarm ${\mathcal {P}}$ can cover the extreme space of two objectives which increases the convergence and diversity and saves computation resources.

Fig. 3

An example for encoding schema for DHPFSP-FMS

Global search

Mating selection To improve search efficiency, two players’ tournament selection is applied to generate a mating pool [51, 52].

Genetic operator Due to the complexity of DHPFSP-FMS, a large step perturbation is necessary. In this study, the partial match crossover (PMX) is adopted for JS [11]. Meanwhile, the uniform crossover (UX) is applied to SS and FA [53]. Figure 4 gives the procedure of PMX and UX. It is worth noting that the SS also applied UX for crossover. Moreover, each child generated by the crossover step has a probability $P_m$ to adopt two mutation strategies. JS mutation: randomly swap two positions. SS mutation: randomly reselect a speed for an operation. FA mutation: randomly reassign a factory for a job. If there exists an empty factory, regenerate a FA vector.

Environmental selection I The offspring generated by the genetic operator is merged with producer ${\mathcal {P}}$. The combined population is selected by fast non-dominated sorting and crowding distance strategy [51].

Fig. 4

a PMX and b UX

Knowledge-driven local search

In shop scheduling problems, designing local search strategies according to problem features can greatly improve efficiency. Based on the features of DHPFSP-FMS, five neighborhood structures ${\mathcal {N}}_i, i\in [1,5]$ are proposed to enhance convergence and diversity which are described as follows:

${\mathcal {N}}_1$ (Swap in whole JS) This is a simple structure that aims to increase the diversity and search step.

${\mathcal {N}}_2$ (swap in critical factory) Randomly selecting two critical operations in the critical factory and swapping their positions can reduce makespan.

${\mathcal {N}}_3$ (insert in critical factory) Randomly select two operations in the critical factory and insert the latter into the front of the former.

${\mathcal {N}}_4$ (Increase speed of critical job) Based on property 1 mentioned in Section III-C, randomly selecting a critical job and increasing its speed can reduce makespan.

${\mathcal {N}}_5$ (Randomly factory assignment) Based on property 3, randomly selecting a critical job and assigning it to another factory can reduce makespan.

From those neighborhood structures mentioned above, this work adopts a variable neighborhood search to consumer ${\mathcal {C}}$ with random selection. If the new solution dominated the old, it will replace the old. If they do not dominate each other, add the new solution to ${\mathcal {C}}$.

Energy-saving strategy

The energy-saving technique is a critical step for green scheduling [13]. However, the strategy has to be designed according to problem features. Based on property 2, the TEC mainly depends on idle time and speed selection. Thus, a speed-decreasing strategy is proposed to save energy. In conclusion, idle time can be summarized as two following conditions (Fig. 5):

Fig. 5

Energy-saving strategy

Condition 1 The start time of current operation $S_{f,i,k}$ equals to the former operation’s $F_{f,i',k}$ finish time on the same machine but the last operation of the same job’s finish time $F_{f,i,k-1}$ is less than $S_{f,i,k}$.

Rule 1: If $S_{f,i,k}>F_{f,i,k-1}$, decrease the speed of $O_{i,k-1}$. If the new finish time of $O_{i,k-1}$ is smaller than $S_{f,i,k}$, accept the speed change. Repeat above step until the $S_{f,i,k}<F_{f,i,k-1}$.

Condition 2 $S_{f,i,k}$ equals to the last operation of the same job’s finish time $F_{f,i,k-1}$ but the former operation’s $F_{f,i',k}$ finish time on the same machine is less than $S_{f,i,k}$.

Rule 2: If $S_{f,i,k}==F_{f,i,k-1}$ and $S_{f,i,k}>F_{f,i',k}$, decrease the speed of $O_{i',k}$. If the new finish time of $O_{i',k}$ is smaller than $S_{f,i,k}$, accept the speed change. Repeat above step until the $S_{f,i,k}<F_{f,i',k}$. It is worth noting that this change will delay the latter operation and increase makespan. Thus, to overcome this problem, if the start time of latter operation $O_{i',k+1}$ cannot be obtained ahead or $S_{f,i',k+1}==F_{f,i',k}$, the speed will not change. To simplify the rule, only the operation stays on the last machine, the rule 2 is executed.

The energy strategy is executed as follows:

Step 1: if the solution has not executed the energy-saving strategy and the number of function evaluations has been consumed over 90%, divide all jobs into each factory based on FA.

Step 2: for each factory, calculate the start time of current operation $S_{f,i,k}$. and judge the condition by comparing $F_{f,i',k}$ and $F_{f,i,k-1}$.

Step 3: execute rule 1 or rule 2 to decrease speed selection.

Step 4: repeat the above step until all factories have been slowed down speed.

Experimental results

The proposed algorithm BRCE has been described in detail in “Our approach: BRCE”. In this section, detailed experiments are designed to evaluate the performance of BRCE. All algorithms are coded in MATLAB on an Intel(R) Xeon(R) Gold 6246R CPU @ 3.4GHz with 384 G RAM. The running experiment is Matlab2020b with the parallel toolbox.

Instances and metrics

Because DHPFSP-FMS cannot find an open source benchmark, this work generates 22 different scales of instances for DHPFSP-FMS based on the Taillard benchmark to evaluate the performance of the proposed BRCE [54]. The job number ranges from $n\in \{20,50,100,200\}$ and the number of factories belongs to $n_f\in \{2,3\}$. The number of machines in each factory $n_m=\in \{5,10,20\}$. The processing time of each operation is different in heterogeneous factories. The processing power $W_{O}=2.0$ kWh and the idle power $W_{I}=1.0$ kWh. Finally, 22 instances are generated with different scales which are named by $n\_m\_n_f$. The stop criterion is MaxNEFs $=400\times n$ (at least 20,000). The dataset can be downloaded from https://cuglirui.github.io/downloads.htm.

Three multi-objective optimization metrics are used to measure the performance of different algorithms which are Hypervolume (HV) [55], Generation distance (GD) [51], and Spread [51]. Meanwhile, their formulations are given as below:

$$\begin{aligned} HV(P,r)=\bigcup _{{\textbf{x}} \in P}^{P} v({\textbf{x}},r), \end{aligned}$$

(18)

where P is the Pareto solutions got by each algorithm, and r is the reference point. Moreover, for calculating the boundary solutions for HV, r is set (1.1, 1.1). ${\textbf{x}}$ is a normalized Pareto solution. v is the volume value of the hypercube. Moreover, the higher HV, the better the comprehensive performance of an algorithm.

$$\begin{aligned} GD(P,P^*)=\frac{\sqrt{\sum _{y\in P}\min _{x\in P^*}d(x,y)^2}}{|P|}, \end{aligned}$$

(19)

where $P^*$ is the best Pareto solutions got by all algorithms, P is the Pareto solutions set of each algorithm, and d(x, y) states the Euclidean distance between $x\in P$ and $y\in P^*$. Moreover, the lower the GD value, the better the performance of an algorithm

$$\begin{aligned} {\text {Spread}} =\frac{d_l+d_f+\sum _{i=1}^{N-1}\Vert d_i-{\bar{d}} \Vert }{d_l+d_f+(N-1){\bar{d}}} \end{aligned}$$

(20)

where d is the Euclidean distance of adjacent Pareto solutions. Moreover, the lower the Spread value, the better.

Fig. 6

Main effects plot of three metrics: a HV, b GD, and c spread

Table 2 Overall ranks through the Friedman test among all variant algorithms (a level of significant $\alpha =0.05$)

Parameters calibration

The parameter configuration has a great impact on the performance of an algorithm in solving DHPFSP-FMS. The proposed BRCE contains three parameters which are population size ps, mutation rate $P_m$, and the enhancement strategies start rate of the whole computation resource $E_t$. A Taguchi approach of design-of-experiment (DOE) [56] is adopted by the software Mintab18. The parameter level is given as follows: $ps=\{100,150,200\}$; $P_m=\{0.1,0.15,0.2\}$; $E_t=\{0,0.5,0.9\}$. An orthogonal array is $L_{9}(3^3)$ generated in this calibration experiment. For fairness, each parameter runs 10 independent times with the same stop criteria (MaxNFEs $=400\times n$). The means of all metrics for 10 runs are collected. Figure 6 shows the main effects plot of three parameters for three metrics. The bigger the HV metrics values, the better the performance. Moreover, GD and Spread have the opposite regular of HV. Based on comprehensive observation, the best configure of parameter setting is that $ps=100$, $P_m=0.2$, and $E_t=0.9$.

Table 3 Overall ranks through the Friedman test among all comparison algorithms (a level of significant $\alpha =0.05$)

Effectiveness of the components in BRCE

To evaluate each improvement part of BRCE, some variant algorithms are generated as follows: (i) BRCE-C without the coevolutionary framework is set only the traditional one population evolution which is used to prove the effectiveness of the proposed framework; (ii) to evaluate the effectiveness of the proposed energy-saving strategy, BRCE with energy-saving strategy called (BRCE + E) is set; (iii) BRCE + EV is set with energy-saving strategy and variable neighborhood search and compared with the former variant to prove the effectiveness of local search; (iv) BRCE + EVH embedded with heuristic initialization is compared to the former algorithm to prove the effectiveness initialization strategy. For fairness comparison, each algorithm runs 20 independent times on all instances with the same stop criteria (MaxNFEs $=400\times n$ at least 20,000). All algorithms are coded by MATLAB.

Table S-I shows the statistical results of all metrics of all variant algorithms. Moreover, the bold values mean the best. Furthermore, Table 2 lists the Friedman test results, where the confidence level $\alpha =0.05$. Some conclusions can be obtained as follows: (1) the p value is less than 0.05, which means a significant difference between all variants. (2) the comparison results of BRCE and BRCE-C can prove the effectiveness of the proposed bi-roles coevolutionary framework for the distributed shop scheduling problem. (3) Comparing BRCE + E with BRCE can prove the effectiveness of the proposed energy-saving strategy. (4) Comparing BRCE + E and BRCE + EV, the HV and GD metrics rank higher but Spread ranks lower, which ensures the proposed local search can efficiently increase convergence whereas the diversity is reduced. This is because the Pareto solutions are closer to each other. (5) Comparing BRCE + EVH and BRCE + EV, the HV and Spread rank first but GD sharply reduces. This is because the proposed heuristic initialization rules generate many solutions with the smallest $C_{\text {max}}$ and TEC. Thus, the diversity of producer ${\mathcal {P}}$ vastly increases and the computation resource is divided into more search directions. BRCE + EV has a population with higher density which can converge to the middle range well and result in increasing the distance between the middle of Pareto Front and the middle of Pareto solutions of BRCE + EVH. Finally, the BRCE + EVH can find solutions with the smallest $C_{\text {max}}$ and TEC and more Pareto solutions than BRCE + EV, which provides a more practical reference to manufacturing. It is acceptable that the GD metric is worse than other variants.

Comparison and discussions

To further evaluate the effectiveness of our approach, BRCE is compared to the classical MOEAs like MOEA/D [57] and NSGA-II [51]. Furthermore, two state-of-art algorithm for DHPFSP-FMS named PMMA [46] and KCA [17] is compared. The parameters are set with the best configuration in each reference. The crossover rate $P_c=1.0$, mutation rate $P_m=0.2$ and population size $ps=100$ for MOEA/D, NSGA-II and BRCE. The population size $ps=40$, elite rate $\eta =0.2$ and update rate $\alpha =0.1$ for PMMA. The population size $ps=10$, local search times $LS=100$ and energy-efficient rate $P_E=0.6$ for KCA. The number of neighborhoods $T=10$ for MOEA/D. To conduct a fair comparison, all MOEAs share the same stop criteria (MaxNFEs $= 400\times n\geqslant$ 20,000). Because of the complexity of DHPFSP-FMS, this comparison experiment adopted 20 independent runs in 22 instances.

Table S-II shows statistical results (mean and standard deviation values) of all comparison algorithms for three metrics in 22 instances. Moreover, the symbol “−/=/+” means significantly inferior, equal, or superior to BRCE. Meanwhile, the best value is marked with bold. As Table S-II shows, as for HV and Spread metrics BRCE is significantly better than all comparison algorithms, which proves BRCE has better comprehensive performance and diversity than comparison algorithms. As for the GD metric, BRCE is significantly superior to MOEA/D, PMMA, and KCA over 20 instances. This is because it is designed based on problem feature and the advantage of the framework which balance the computation resource. However, the BRCE is worse than NSGA-II in eight instances. This is because the number of Pareto solutions of BRCE is too many and cannot focus on converging in the middle range. Although the metric is lower, the BRCE can find solutions with smaller objectives, which is acceptable. Table 3 indicates the Friedman rank test results among all comparison algorithms in all instances, where the confidence level $\alpha$ = 0.05. BRCE ranks first for all metrics, where p value is less than 0.05, which proves BRCE is significantly better than comparison algorithms.

The success of BRCE relays on its design. First, the proposed bi-roles coevolutionary framework can efficiently balance computation resources between exploration and exploitation. Second, three heuristic rules are proposed to vastly converge to the boundary of objectives. Next, aiming at the problem characteristics five neighborhood structures are designed to enhance convergence. Next, to enhance the success rate of local search, a deep Q-network is adopted. Finally, an efficient energy-saving strategy is introduced to efficiently lower idle time to reduce TEC. Moreover, Fig. 7 shows their Pareto front with the best HV metric overall 20 runs. Considering the convergence and diversity of PF, BRCE can find better Pareto solutions on two sides than all comparison algorithms, which means BRCE can find solutions with smaller objective functions and get closer approximations toward practical PF. Because of the large number of Pareto solutions, BRCE has not enough resources to explore the middle reign. Thus, the convergence of the middle region is worse than NSGA-II. However, BRCE can find solutions with better $C_{\text {max}}$ and TEC, which states the proposed BRCE can solve DHPFSP-FMS well.

Fig. 7

Pareto front approximately by different algorithms on 100J4F

Conclusions

This paper proposed a bi-roles coevolutionary algorithm for energy-efficient distributed heterogeneous permutation flow shop scheduling problems with flexible machine speed. First, a novel bi-roles coevolutionary framework was proposed to solve DHPFSP-FMS. Second, three heuristic rules are proposed to get an initialization population with high quality. Next, five knowledge-driven neighborhood structures were designed for optimizing DHPFSP-FMS based on three features. Then, an energy-saving strategy based on reducing speed was presented to efficiently save TEC. Finally, the experimental results indicated that BRCE is significantly better than different types of comparison algorithms in terms of getting Pareto solutions with better convergence and diversity.

In our future work, we will consider the following task: (i) apply BRCE to other distributed heterogeneous shop scheduling problems; (ii) consider an assembly stage of DHPFSP-FMS; and (iii) consider the dynamic situations in DHPFSP-FMS.