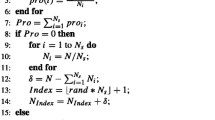Introduction

Many optimization problems in both academia and industry, such as structure optimization [1,2,3], production scheduling [4], and battery model optimization [5], involve constraints. These constrained optimization problems (COPs) can be formulated as follows:

$$\begin{aligned}{} & {} \mathrm{{minimize}} \, f(\textbf{x}), \, \textbf{x} = ({x_1},{x_2},\ldots ,{x_D}) \in {\mathbb {S}}, \, {L_i} \le {x_i} \le {U_i}, \\{} & {} \quad i=1,\cdots ,D\\{} & {} \quad \mathrm{subject \, to:} \, {g_j}(\textbf{x}) \le 0, \, \mathrm{{ }}j = 1,2,\ldots ,p \\{} & {} \quad {h_j}(\textbf{x}) = 0, \, j = p + 1, \, p + 2,\ldots ,q, \end{aligned}$$

where \(f(\textbf{x})\) is the objective function, \({x_i}\in [L_i,U_i]\) is the ith dimension of a decision vector/solution (denoted as \(\textbf{x}\)), \(\mathrm{{{\mathbb {S}} = }}\prod \nolimits _{i = 1}^D {\left[ {{L_i},{U_i}} \right] }\) denotes the decision space, and \({g_j}(\textbf{x})\) and \({h_j}(\textbf{x})\) represent an inequality constraint and an equality constraint, respectively.

For a decision vector (i.e., \(\textbf{x}\)), the violation of the jth constraint is calculated as follows [6]:

$$\begin{aligned} G_{j}(\textbf{x})=\left\{ \begin{array}{ll} \textrm{max}(0,g_{j}(\textbf{x})), \quad 1 \le j \le p \\ \textrm{max}(0,\left| h_{j}(\textbf{x})\right| -\delta ), \quad p+1 \le j \le q \end{array} \right. \end{aligned}$$
(1)

where \(\delta \) is a tolerance value. The degree of constraint violation of all constraints is calculated as: \({G}(\textbf{x}) = \sum \nolimits _{j = 1}^q {{G_j}(\textbf{x})}\). The feasible domain (denoted as \(\varOmega \)) is represented as \(\{\textbf{x}\in {\mathbb {S}}|G(\textbf{x})=0\}\). The ultimate goal of constrained optimization is to locate the feasible optimum in \(\varOmega \) [7].

Evolutionary algorithms (EAs) have been demonstrated as reliable tools for optimization during past years [8,9,10]. For COPs, EAs play the role of generating new solutions. They require additional mechanisms to deal with constraints [11, 12]. Specifically, a constrained optimization evolutionary algorithm (COEA) needs to balance constraints and objective function. The key lies in how to use constraints or objective function to select solutions, which still remains an open question. Constraint handling techniques (CHTs), which provide a basis for the environment selection of a COEA, are designed to address this issue [13]. In general, there are four cases in CHTs, namely those based on penalty function [6, 14], separation of constraints and objective function [15,16,17], multiobjective optimization [18,19,20], and hybrid methods [21, 22], respectively. Additionaly, some researchers have designed non-penalty-based CHTs by using supervised learning technology [23] or special operators [24]. In [23], the non-penalty-based CHT for the particle swarm optimization (PSO) was implemented by adopting the support vector machine (SVM). After a training phase on the current positions of the swarm, the new trial positions were labeled as feasible or unfeasible positions using the trained predictive model. In [24], a variant of the PSO was developed for COPs. And a new local search operator was implemented to help localize the feasible region in challenging optimization problems.

Among the aforementioned CHTs, the penalty function method has attracted increasing attention [6, 12, 14]. In this kind of CHTs, a penalty factor is used to balance the satisfaction of all constraints and the search for global optimum. However, how to determine a proper penalty factor is far from trivial [13]. Many attempts have been made to address this open question and numerous CHTs based on penalty function have been proposed. According to the way of adjusting the penalty factor, these CHTs are classified into the following three categories:

  • CHTs based on static penalty factor [25],

  • CHTs based on dynamic penalty factor [26], and

  • CHTs based on adaptive penalty factor [6, 22].

In the first type of CHTs, the penalty factor remains constant throughout the evolutionary process, while it varies dynamically according to a predefined function in CHTs based on dynamic penalty function. In the third type of CHTs, the penalty factor is adjusted adaptively based on the situation of the population. Michalewicz et al. [27] pointed out that adaptive penalty function methods have better performance in solving COPs. Thus, most existing penalty function methods adopt adaptive strategies [6].

Among various kinds of adaptive strategies, co-evolution provides a promising direction for the setting of an effective penalty factor [28,29,30]. In general, co-evolution refers to that two or more populations evolve simultaneously and complete information interaction during the evolutionary process [31]. Due to its numerous advantages, co-evolution has been used to solve a variety of challenging COPs [32, 33]. In the co-evolution framework, the penalty factors and solutions are updated in a collaborative manner. Due to the information interaction mechanism, the penalty factor can be adjusted according to the information of the solution population; thus, this strategy will be effective to solve various kinds of COPs [28,29,30]. Coello [34] conducted a pioneer study using co-evolution for penalty factor adaptation, in which a population of penalty factors is maintained and each of them is updated based on the performance of the solution population. Although Coello’s method achieves satisfactory results, its effectiveness will be limited from two aspects. First, each penalty factor is evaluated based on the feasible solutions in the solution population. For many complex COPs, the method using a static penalty factor may not get a feasible solution. In this case, all penalty factors have the same performance. The evolution will become a random search process. Second, the solution population evolves based on different penalty factors in succession, which may cause oscillation. Huang et al. [29] improved Coello’s method and integrated it with differential evolution (DE). When solutions are infeasible, penalty factors are evaluated based on constraint violation. Due to the preference for constraints, Huang’s method is likely to trap the population into a local feasible domain. Krohling et al. [30] formulated the original COP as a minimax optimization problem and solved it through co-evolution. When the penalty factors are being updated, the solution population is maintained frozen, and vice versa. As we know, a minimax optimization problem is challenging to solve. Thus, the effectiveness of the formulation is questionable. Fan and Yan [28] used the Alopex algorithm for the co-evolution of symbiotic individuals including penalty factors and control parameters of DE. Each penalty factor is evaluated by its corresponding solution. This way, a good penalty factor will be eliminated simply for the inferior performance of the corresponding solution. In summary, although the adaptive scheme using co-evolution is promising, the classical co-evolution framework may exhibit the following shortcomings:

  • First, the additional population of penalty factors will consume a lot of computing resources. As a result, the efficiency will be sacrificed to a certain degree.

  • Second, when evaluating the performance of a penalty factor, the classical co-evolution framework puts too much emphasis on constraints. This way, it will fail to tackle complex COPs.

  • Finally, some valuable knowledge that is beneficial for constrained evolutionary optimization has not been used fully.

To leverage the strengths of co-evolution and remedy the weaknesses of the classical framework, this paper proposes a two-stage adaptive penalty method based on co-evolution (abbreviated as TAPCo). The evolutionary process in TAPCo consists of two stages, namely the co-evolution stage and the shuffle stage. In the co-evolution stage, the solution population is divided into multiple subpopulations. Each is associated with a penalty factor and the best one is determined by the co-evolution of these subpopulations. Since different penalty factors are used, these subpopulations will search along different directions. Thus, the co-evolution stage can enhance exploration. In the shuffle stage, multiple subpopulations are merged into a single population, which uses the best penalty factor from the co-evolution stage to facilitate exploitation. By executing the co-evolution stage and shuffle stage iteratively, TAPCo is able to balance exploration and exploitation. Additionally, assisted by the adaptive penalty factor, TAPCo can also achieve a tradeoff between constraints and objective function. Thus, it is able to find a satisfactory solution finally. The main advantages of TAPCo are summarized as follows:

  • TAPCo adjusts the penalty factor adaptively by the co-evolution of multiple subpopulations. Without using an additional population to evaluate penalty factors, TAPCo is more efficient than the classical framework. Additionally, TAPCo combines objective function with constraints to evaluate the quality of the penalty factor. Moreover, TAPCo also leverages some valuable knowledge from the community of constrained evolutionary optimization.

  • TAPCo combines two trial vector generation strategies of DE for solution reproduction in the co-evolution stage and the shuffle stage. The proposed search algorithm can achieve a tradeoff between constraints and objective function as well as a tradeoff between exploration and exploitation.

  • In TAPCo, a restart mechanism is designed by judging whether the population stagnates in the infeasible region. With this strategy, TAPCo is able to tackle COPs with flat landscape.

  • Extensive experiments have been executed on three sets of benchmark test instances to prove the effectiveness of TAPCo for solving COPs.

The rest of this paper consists of four sections. Section “Basic knowledge” provides a brief introduction of the basic knowledge. The details of TAPCo are described in Section “Proposed method–TAPCo”. The empirical study is introduced in Section “Experimental study”. Section “Conclusion” provides a summary and outlook of this paper.

Basic knowledge

Penalty function method

The penalty function method uses penalty factors to incorporate constraints into objective function. Its general expression is shown below:

$$\begin{aligned} ~ F(\textbf{x}) = f(\textbf{x}) + \gamma \cdot G(\textbf{x}), \end{aligned}$$
(2)

where \(\gamma \) is a penalty factor. Compared to normalizing only the average fitness [35], the penalty function method normalizes \(f(\textbf{x})\) and \(G(\textbf{x})\) of all individuals in the current population [6, 36]. This way is conducive to make a COEA less problem-dependent [37].

$$\begin{aligned} {f^{\mathrm{{norm}}}}({{\textbf{x}}})= & {} \frac{{f({{\textbf{x}}}) - {f_{\min }}}}{{{f_{\max }} - {f_{\min }}}}, \end{aligned}$$
(3)
$$\begin{aligned} {G^{\mathrm{{norm}}}}({{\textbf{x}}})= & {} \frac{{G({{\textbf{x}}}) - {G_{\min }}}}{{{G_{\max }} - {G_{\min }}}}, \end{aligned}$$
(4)

where \({f_{\max }}\) and \({f_{\min }}\) are the maximum and minimum objective function values in the current population, respectively, and \({G_{\max }}\) and \({G_{\min }}\) are the maximum and minimum degree of constraint violation in the current population, respectively.

In general, an appropriate value of \(\gamma \) is difficult to determine. Similar to [6], we replace \(\gamma \) by a weight value w: \(\gamma =\frac{1-w}{w},0<w\le 1\). Thus, the penalty function in Eq. (2) is reformulated as follows:

$$\begin{aligned} F(\textbf{x}) = \frac{{w}\cdot {f^{\mathrm{{norm}}}}(\textbf{x}) + (1 - {w})\cdot {G^{\mathrm{{norm}}}}(\textbf{x})}{w}. \end{aligned}$$
(5)

As described in Eq. (5), a smaller value of w will lead to a higher penalty, while a larger value will result in a lower penalty.

Fig. 1
figure 1

The classical co-evolution for penalty factor adaptation. Both the penalty factor population and the solution populations are updated by an EA

Full size image

Classical co-evolution for penalty factor adaptation

In this paper, we denote the co-evolution framework proposed by Coello [34] as the classical framework. Genetic algorithm (GA) [34], particle swarm optimization (PSO) [38], and DE [29] have been used in this framework for constrained optimization. As shown in Fig. 1, a population of penalty factors (denoted as \(\{\gamma _1,\cdots ,\gamma _k\}\)) is maintained. Each penalty factor (i.e., \(\gamma _i,1\le i\le k\)) is used to update a population of solutions for T generations. Next, the performance of the penalty factor is evaluated by the solution population. Note that in the classical framework, penalty factors can be evaluated by a single solution population [34] or k different solution populations [29, 38], respectively. Specifically, when k different solution populations are used, the performance of the ith penalty factor (denoted as \(\eta (\gamma _i)\) ) is evaluated as follows [29, 38]. If there exist feasible solutions in the ith solution population, \(\eta (\gamma _i)\) is calculated according to:

$$\begin{aligned} \eta (\gamma _i)=\frac{\sum _{\textbf{x}_i \in {\mathbb {Q}}}f(\textbf{x}_i)}{|{\mathbb {Q}}|}+|{\mathbb {Q}}|, \end{aligned}$$
(6)

where \({\mathbb {Q}}\) is a set including the feasible solutions in the ith solution population, and \(|{\mathbb {Q}}|\) represents the cardinality of \({\mathbb {Q}}\). In this case, \(\gamma _i\) is called a valid penalty factor. If there are no feasible solutions in the ith solution population, \(\eta (\gamma _i)\) is calculated as follows:

$$\begin{aligned} \eta (\gamma _i)=\mathop {\text {max}}\limits _{\gamma _v\in {\mathbb {V}}} \eta (\gamma _v)+\frac{\sum _{\textbf{x}_j\in {\mathbb {P}}_i}G(\textbf{x}_j)}{N}-N, \end{aligned}$$
(7)

where \({\mathbb {V}}\) is the set of valid penalty factors, \({\mathbb {P}}_i\) denotes the ith solution population, and N is the number of violated constraints of all solutions in \({\mathbb {P}}_i\). After being evaluated, the penalty factors will be updated by an EA. The above steps will be executed iteratively until a satisfactory solution is found.

Proposed method–TAPCo

First, we introduce TAPCo’s framework in Section “Framework of TAPCo”. Then, the details of TAPCo are illustrated in Sections “Two-stage adaptive penalty method based on co-evolution”–“Restart mechanism”. Finally, Section “Computational time complexity analysis” analyzes the computational time complexity of TAPCo.

Fig. 2
figure 2

Flowchart of TAPCo

Full size image
figure a

Framework of TAPCo

The flowchart and the framework of TAPCo are given in Fig. 2 and Algorithm 1, respectively. First, algorithm-specific parameters are initialized and a population of solutions is sampled from the decision space (Line 1). In the main loop, a set of weight valuesFootnote 1 is generated, which are then updated based on some valuable knowledge and co-evolution (Line 3). Next, the two-stage adaptive penalty method based on co-evolution and the restart mechanism are executed iteratively to search for the feasible optimum (Lines 4–11). The two-stage adaptive penalty method includes a co-evolution stage and a shuffle stage. In the co-evolution stage, the main population is divided into \(N_s\) subpopulations and each is associated with a weight value (Line 4). These subpopulations will evolve for T generations (Lines 5–6). In the shuffle stage, a weight value is evaluated based on the performance of the corresponding subpopulation (Line 7). Thereafter, all subpopulations are merged into the main population and the best weight value from the co-evolution stage is used for population evolution (Lines 8–10). In both stages, a search algorithm based on DE is developed to generate promising offsprings. If the function evaluations are exhausted, TAPCo will output the best solution in the main population (Line 12).

As shown in Fig. 2, TAPCo consists of four key ingredients, those are, the two-stage adaptive penalty method based on co-evolution (including a co-evolution stage and a shuffle stage), the weight value generation, the search algorithm, and the restart mechanism. We will focus on these four ingredients in next subsections.

Two-stage adaptive penalty method based on co-evolution

Fig. 3
figure 3

The two-stage adaptive penalty method based on co-evolution

Full size image

The two-stage adaptive penalty method consists of a co-evolution stage and a shuffle stage. As shown in Fig. 3, in the co-evolution stage, a population of solutions (denoted as \({\mathbb {P}}=\{\textbf{x}_1,\cdots , \textbf{x}_{Ps}\}\)) is divided into \(N_s\) subpopulations, each of which consists of \(O_s=P_s/N_s\) solutions. For the ith (\(i=1,\dots , N_s\)) subpopulation, a weight value (denoted as \(w_i\)) is used for solution selection. All subpopulations will co-evolve for T generations. Afterward, the shuffle stage begins. In this stage, all subpopulations are merged into the main population. The main population will evolve for another T generations. The best weight value in the co-evolution stage (denoted as \(w_{best}\)) is used for solution selection. These two stages will be executed iteratively until the computing resources are exhausted.

As shown in Fig. 1, in the classical framework, the co-evolution means that the population of penalty factors and the population of solutions evolve in a collaborative manner, with the aim of adjusting the penalty factor adaptively as well as locating the feasible optimum. Different from the classical framework, TAPCo does not maintain a population of penalty factors. The co-evolution in our framework means that multiple subpopulations co-evolve based on different weight values. A weight value can be evaluated by the performance of the corresponding subpopulation easily and the best one is used to further facilitate the optimization. In this way, TAPCo can remedy the weaknesses of the classical framework. The details of the co-evolution stage and the shuffle stage are elaborated as follows.

Co-evolution stage

figure b

The details of the co-evolution stage are given in Algorithm 2. First, the main population (i.e., \({\mathbb {P}}\)) is divided into \(N_s\) subpopulations (denoted as \(\{{\mathbb {O}}_1,\cdots ,{\mathbb {O}}_{N_s}\}\)). Additionally, a weight value is assigned to each subpopulation (Lines 1–4). Afterward, the \(N_s\) subpopulations co-evolve for T generations (Lines 5–13). Specifically, for the ith subpopulation, the search algorithm described in Algorithm 4 is executed to generate a population of trial vectors (denoted as \({\mathbb {U}}_i=\{\textbf{u}_{i,1},\cdots ,\textbf{u}_{i,O_s}\}\)) (Line 7). Finally, each pair of solution and trial vector are evaluated by \(w_i\) according to Eqs. (3)–(5) and the pairwise selection is conducted based on penalty function values (Lines 8–13). Note that all subpopulations interact with each other through the search algorithm described in Section “Search algorithm”.

As described in Algorithm 2, each weight value is used to update a subpopulation for T generations. Thus, it can be evaluated according to the performance of the subpopulation directly. Since these subpopulations adopt different weight values, they will evolve along various directions. In this manner, the decision space can be explored adequately.

Shuffle stage

The details of the shuffle stage are given in Algorithm 3. First, each weight value is evaluated by the performance of its subpopulation (Lines 1–2). As we know, the final goal of COEAs is to find a feasible optimum. Thus, the primary task of a weight value is to improve the feasibility. In view of this, the feasibility rule [39] is used to evaluate the performance of a weight value. The feasibility rule is the most popular CHT as it is free of parameter and easy to implement. To be specific, for \({\mathbb {O}}_i\), we sort the solutions in the subpopulation according to the feasibility rule and pick the best one (denoted as \(\textbf{x}_{i,best}\)) to represent the whole subpopulation. Afterward, we select the best weight value (denoted as \(w_{best}\)) according to the best solutions in the subpopulations. The weight value associated with the best solution in \(\{\textbf{x}_{1,best},\dots ,\textbf{x}_{N_s,best}\}\) is selected based on the feasibility rule (Line 3). Next, all subpopulations are merged into the main population (Line 4). The main population will evolve for T generations (Lines 5–12). Specifically, the search algorithm described in Algorithm 4 is executed to generate a population of trial vectors (denoted as \({\mathbb {U}}=\{\textbf{u}_{i},\cdots ,\textbf{u}_{P_s}\}\)) (Line 6). Finally, each pair of solution and trial vector are evaluated by \(w_{best}\) according to Eqs. (3)–(5) and the pairwise selection is conducted based on penalty function values (Lines 7–12).

The shuffle stage in TAPCo is different from the shuffle mechanism in [40]. In the shuffle mechanism, the individuals of all subpopulations are moved into a provisional list. Then the individuals are randomly re-distributed over the subpopulations. The shuffle mechanism is executed with a certain probability in each generation. However, in the shuffle stage of TAPCo, the population consisting of multiple subpopulations evolves for a certain generations. Since all solutions adopt a single weight value for evolution, the exploitation can be enhanced. Additionally, the best weight value in the co-evolution stage is used. Thus, the shuffle stage can also further facilitate the balance between constraints and objective function.

In summary, by executing the co-evolution stage and the shuffle stage iteratively, the two-stage adaptive penalty method based on co-evolution can achieve the two tradeoffs which are critical to COEAs.

Weight value generation

As described in Section “Penalty function method”, a weight value w is bounded between 0 and 1. Additionally, a smaller w represents a higher penalty, while a larger value will result in a lower penalty. In this subsection, we discuss how to generate a set of weight values by using some valuable knowledge and taking advantage of co-evolution.

figure c

As discussed in [16, 21], theoretically, a weight value \(w\in (0,w_{opt}]\) is helpful to achieve the feasible optimum, where \(w_{opt}\) denotes the optimal weight value leading to the feasible optimum. If \(w_{opt}\) is known a priori, we can sample a set of weight values from \(w\in (0,w_{opt}]\) uniformly as follows:

$$\begin{aligned} w_i=i\cdot \frac{w_{opt}}{N_s},\;i=1,\cdots ,N_s. \end{aligned}$$
(8)

Afterward, each weight value is assigned to a subpopulation. However, \(w_{opt}\) is problem-dependent and cannot be known beforehand. To address this issue, we approximate \(w_{opt}\) iteratively by the co-evolution of all subpopulations.

In the initialization stage, a set of weight values is sampled from (0,1] uniformly: \(\{\frac{1}{N_s},\frac{2}{N_s},\dots ,1\}\). Although a weight value \(w\in (w_{opt},1]\) cannot explicitly guide the population to a feasible optimal solution, it can facilitate the exploration of the infeasible domain. The reason for this is that such a weight value can provide the high-quality information of objective function for search in the early stage [16, 21]. As detailed in Section “Shuffle stage”, after T generations of co-evolution, the ith weight value (i.e., \(w_i=\frac{i}{N_s}\)) can be evaluated according to the performance of the ith subpopulation. Afterward, the best weight value (i.e., \(w_{best}\)) is considered as an approximated value of \(w_{opt}\). The set of weight values is updated as follows:

$$\begin{aligned} w_i=i\cdot \frac{w_{best}}{N_s},\;i=1,\cdots ,N_s. \end{aligned}$$
(9)

As shown in Fig. 2, the weight value generation procedure will be repeated in the main loop. Thus, \(w_{best}\) will be adjusted by co-evolution and the set of weight values will be updated according to Eq. (9).

In summary, by utilizing some valuable knowledge and taking advantage of co-evolution, promising weight values can be used for constrained optimization effectively.

Search algorithm

An effective search algorithm needs to satisfy two tradeoffs: (1) the tradeoff between constraints and objective function; (2) the tradeoff between exploration and exploitation. DE has been used to solve various kinds of optimization problems successfully [41,42,43,44]. It contains four sections: initialization of vectors, mutation, crossover and selection operations [45]. Compared to other EAs, DE differs mainly in its mutation operation which is achieved by random vectors and difference vectors. Therefore no separate probability distribution has to be used for generating the offsprings. DE has a simpler structure and greater search capability [46]. We adopt DE to develop the search algorithm for the co-evolution stage and the shuffle stage. Inspired by our previous studies [6, 17], to satisfy two tradeoffs, we combine the following two trial vector generation strategies:

DE/rand-to-best/1/bin

$$\begin{aligned} {\textbf{v}_i} = {\textbf{x}_{r1}} +F\cdot ({\textbf{x}_{best}} - {\textbf{x}_{r1}})+ F\cdot ({\textbf{x}_{r2}} - {\textbf{x}_{r3}}), \end{aligned}$$
(10)
$$\begin{aligned} u_{i,j}=\left\{ \begin{array}{ll} v_{i,j}, \quad {\textrm{if}} \, rand_{j}<CR \, {\textrm{or}} \, j=j_{rand} \\ x_{i,j}, \quad {\textrm{otherwise}} \end{array} \right. , \end{aligned}$$
(11)

DE/current-to-rand/1

$$\begin{aligned} {\textbf{u}_i} = {\textbf{x}_{i}} +rand\cdot ({\textbf{x}_{r1}} - {\textbf{x}_{i}})+ F\cdot ({\textbf{x}_{r2}} - {\textbf{x}_{r3}}), \end{aligned}$$
(12)

where \(\textbf{x}_{best}\) denotes the best solution in the current population/subpopulation, \({\textbf{x}_{r1}}\ne {\textbf{x}_{r2}}\ne {\textbf{x}_{r3}}\in {\mathbb {P}}/\textbf{x}_i\), F denotes the scaling factor, \(u_{i,j}\in \textbf{u}_i\), \(v_{i,j}\in \textbf{v}_i\), \(x_{i,j}\in \textbf{x}_i\), \(rand_j\in [0,1]\) is a random value, CR is the crossover control parameter, and \({j_{rand}}\in \{1,\cdots ,D\}\).

figure d

As shown in Eq. (10), “DE/rand-to-best/1/bin” leverages the best solution to generate a trial vector. Thus, it is able to facilitate exploitation. As shown in Eq. (12), in “DE/current-to-rand/1”, the target vector utilizes information from randomly selected individuals; thus, it can facilitate exploration. Similar to [17], TAPCo executes these two strategies with the same probability (i.e., 0.5). By doing so, TAPCo can balance exploration and exploitation. The other tradeoff is closely related to how to select \(\textbf{x}_{best}\). In TAPCo, \(\textbf{x}_{best}\) is selected according to Eqs. (3)–(5). Since the weight value in Eq. (5) is adjusted by the two-stage adaptive penalty method based on co-evolution, a balance between constraints and objective function can be realized. As the same in [6, 17], F and CR are selected from \(F_{pool}=\{0.6, 0.8, 1.0\}\) and \(CR_{pool}=\{0.1, 0.2, 1.0\}\), respectively.

The search algorithm is used in both the co-evolution stage and the shuffle stage. In the co-evolution stage, for the \(i\hbox {th}\) subpopulation, \(\textbf{x}_{best}\) is selected from the subpopulation according to Eqs. (3)–(5) in which \(w_i\) is used. In the shuffle stage, \(\textbf{x}_{best}\) is selected from the entire population according to Eqs. (3)–(5) in which \(w_{best}\) is used. Note that, in the co-evolution stage, to facilitate the interaction among different subpopulations, \({\textbf{x}_{r1}}\), \({\textbf{x}_{r2}}\), and \({\textbf{x}_{r3}}\) are selected from the entire population rather than a single subpopulation. In summary, the search algorithm is detailed in Algorithm  4.

Restart mechanism

In some practical cases, the landscape of a few constraints is flat. To tackle the COPs with this kind of constraints, constraint information should be used adequately. In the early stage of TAPCo, most weight values are larger than \(w_{opt}\); thus, much objective function information is used for search. As a result, TAPCo could not enter a feasible region, even until it converges in the infeasible region. We propose a restart mechanism to remedy this weakness.

Table 1 Maximum number of function evaluations (denoted as MaxFEs) and population size (denoted as \(P_s\))
Full size table

In the restart mechanism, when all solutions are infeasible and the standard deviation of the degree of constraint violation is below a threshold \(\mu \), it indicates that the population has converged to the infeasible domain. In this case, we will regenerate the population in the decision space. Some scholars have proposed a local restart mechanism [47], which inherits some information of the optimal individual in the current population and then restarts the search. However, The population which has converged in infeasible domains cannot provide any valuable information for the search process. Thus, our restart mechanism will regenerate the population. Additionally, since the two-stage adaptive penalty method based on co-evolution has been executed for some generations, a proper \(w_{best}\) could be obtained. In this way, the new population can make full use of constraint information to locate the feasible optimum.

Computational time complexity analysis

The computational time complexity of TAPCo is analyzed as follows. As shown in Fig. 2, in the main loop of TAPCo, the weight value generation, the co-evolution stage, the shuffle stage, and the restart mechanism are executed iteratively. The complexity of the weight value generation is \(O(N_s)\). In the co-evolution stage, the complexity of assigning the weight values to subpopulations is \(O(N_s)\). The complexity of the search algorithm for each subpopulation is \(O(D\cdot O_s)\). Thus, the complexity of the co-evolution of multiple subpopulations is \(O(P_s\cdot D)\). The complexity of the selection is \(O(P_s)\). In summary, the complexity of the co-evolution stage is \(O(T\cdot D\cdot P_s )\). In the shuffle stage, the complexity of evaluating the weight values is \(O(P_s)\). The complexity of selecting the best weight value is \(O(N_s)\). The complexity of the search algorithm is \(O( D\cdot P_s)\). The complexity of the selection is \(O(P_s)\). In summary, the complexity of the shuffle stage is \(O(T\cdot D\cdot P_s)\). The complexity of the restart mechanism is \(O(P_s)\). In summary, the computational time complexity of TAPCo is \(O((N_s+2\cdot P_s\cdot D\cdot T+P_s)\cdot I_t)=O(T_{max}\cdot D\cdot P_s)\) where \(I_t\) is iteration number and \(T_{max}=T\cdot I_t\) denotes the maximum generation number.

Experimental study

We investigated the performance of TAPCo through extensive experiments. The experimental settings are introduced in Section “Experimental settings”. The performance of TAPCo is demonstrated by comparing it with other excellent COEAs in Section “Performance comparison”. Some further analyses and discussions are carried out in Section “Further analyses and discussions”.

Experimental settings

Table 1 summarized the test instances and the corresponding parameters. The common parameters of these functions are the same as in [6, 17]. In all experiments, MaxFEs represents the computing resources. \(P_s\), the population size, mainly depends on the dimensions of the search space. Additionally, the tolerance value (i.e., \(\delta \)) was set to \(10^{-4}\), as suggested in [16, 34]. In Section “Performance comparison”, five advanced competitors were selected for the IEEE CEC 2016 and the IEEE CEC 2010 test instances with 10D and 30D, respectively. Two representative competitors were selected for the IEEE CEC 2017 test instances with 50D and 100D. In Section “Further analyses and discussions”, the experiments focused on verifying the effectiveness of TAPCo’s strategies on the IEEE CEC2010 test instances with 30D. For each test instance, a COEA was repeated for 25 independent runs. The mean and standard deviation of the objective function values obtained from 25 independent runs were used as common test metrics for all test instances. The aforementioned parameters (i.e., MaxFEs, the number of runs, and \(\delta \)) were kept constant in all comparison COEAs. The specific algorithm parameters in TAPCo were: \(N_s=10, T=50\), and \(\mu =10^{-6}\). In terms of statistical significance test, the multiple-problem statistical significance tests were used for performance comparison [48].

Performance comparison

Experiments on the 22 IEEE CEC2006 test instances

The effectiveness of TAPCo was demonstrated by experiments on the IEEE CEC 2006 test instances. TAPCo was compared with other five representative COEAs, namely fpenalty [14], NSES [49], DW [19], FROFI [17], and SR_C\(^2\)oDE [50]. The experimental results of all six COEAs were summarized in Table S1 in the supplementary file. In Table S1, “Mean OFV” and “Std Dev” denote the mean and standard deviation of the objective function values obtained over 25 independent runs, respectively. A successful run was defined as: \(f({\textbf{x}^*}) - f(\hat{\textbf{x}}) \le 0.0001\) where \(\hat{\textbf{x}}\) was the true feasible optimum, and \({\textbf{x}^*}\) was obtained by a COEA. If a COEA runs successfully 25 times on a test function, there will be a “\(*\)” in Table S1. For a COEA, we counted the number of “\(*\)” obtained over 22 test instances. As described in Table S1, except for DW and fpenalty, the other COEAs achieve the success condition consistently on 22 test instances. The above results demonstrate that TAPCo has the ability to solve the IEEE CEC2006 test instances.

Table 2 Multiple-problem Wilcoxon’s test results on C01–C18 with 10D
Full size table
Table 3 Multiple-problem Friedman’s test results on C01-C18 with 10D
Full size table

Experiments on the 36 IEEE CEC2010 test instances

A further comparison of  TAPCo with other advanced COEAs was executed on the IEEE CEC2010 test instances. Note that the optimal solutions of these test instances are not provided; thus, the way in Section “Experiments on the 22 IEEE CEC2006 test instances” to assess the performance of a COEA was no longer applicable. The mean objective function value (i.e., “Mean OFV”) and standard deviation (i.e., “Std Dev”) were used as comparison indicators for different COEAs. First, six COEAs were ranked based on “Mean OFV” for a test function. Then, for a COEA, the total rank value was the sum of the rank values on all functions. Intuitively, the smaller the total rank value, the better the performance of a COEA. Additionally, the multiple-problem statistical significance tests were also implemented [48].

For the 10D test instances, TAPCo was compared with five COEAs (i.e., ITLBO [51], FROFI [17], CACDE [52], AIS-IRP [53], and fpenalty [14]). The mean objective function values and standard deviations of TAPCo and these five peer COEAs were collected in Table S2 in the supplementary file. The statistical significance test results were recorded in Tables 2 and 3. In Table S2, TAPCo gets the first rank on 13 test instances. In Table 2, the \(R^+\) values are much larger than the \(R^-\) values. The larger the difference between the \(R^+\) value and the \(R^-\) value, the more significant the superiority of TAPCo. In addition, TAPCo significantly outperforms fpenalty and ITLBO at the significant difference with \(\alpha =0.05\). As shown in Table 3, TAPCo is the best among these six COEAs. In summary, the results indicate that TAPCo can handle the IEEE CEC2010 test instances with 10D.

Table 4 Multiple-problem Wilcoxon’s test results on C01–C18 with 30D
Full size table
Table 5 Multiple-problem Friedman’s test results on C01–C18 with 30D
Full size table

For the 30D test instances, the mean objective function values and standard deviations were collected in Table S3 in the supplementary file. The statistical significance test results were recorded in Tables 4 and 5. Since the results of C01-C18 with 30D were not provided in its original paper, fpenalty was replaced by Co-CLPSO [54]. Compared with C01-C18 with 10D, these test instances are more challenging; thus, a COEA might fail in finding a feasible solution of some test instances over all 25 runs. In this case, a symbol “\(\varDelta \)” was marked. As described in Table S3, TAPCo ranks the first on 12 test instances. Note that Co-CLPSO performs worst and cannot find a feasible solution of three test instances. The reason is that, for complex COPs, PSO is easy to be trapped into a local optimum. In Table 4, since all the \(R^+\) values are greater than the \(R^-\) values, TAPCo is better than the other five COEAs. Moreover, the p-value is below 0.05 in four cases. In Table 5, TAPCo ranks first in the multiple-problem Friedman’s test. The experimental results indicate that TAPCo has an advantage on the IEEE CEC2010 30D test instances.

Experiments on the 56 IEEE CEC2017 test instances

The IEEE CEC2017 includes 28 test instances with 50D and 28 test instances with 100D. We used TAPCo to solve these high-dimensional COPs. Specifically, we compared the performance of TAPCo with that of LSHADE44 [55] and UDE [56], which rank the first two places in the IEEE CEC2017 competition. The experimental results of these three COEAs were recorded in Table S4 in the supplementary file, where “voi” denotes the mean value of the minimum degree of constraint violation, and “FR” denotes the percentage of feasible runs. Additionally, the statistical significance test results were recorded in Tables 6 and 7, respectively.

Table 6 Multiple-problem Wilcoxon’s test results on the 56 IEEE CEC2017 test instances
Full size table
Table 7 Multiple-problem Friedman’s test results on the 56 IEEE CEC2017 test instances
Full size table

For a test function, we compared every two COEAs according to the following rules: (1) if both these two COEAs fail to find a feasible solution in all runs, the one with the smaller “voi” is better; (2) if both these two COEAs can find a feasible solution in each run, the one with the smaller “Mean OFV” is better; (3) otherwise, the one with the larger “FR” is better. For a COEA, all rank values of the test instances are summed to obtain the total rank. In Table S4, TAPCo gets the best total rank value among these three COEAs. As described in Table 6, all the \(R^+\) values are much larger than the \(R^-\) values. Additionally, the p-value is much smaller than 0.05. In Table 7, TAPCo gets the first rank. In summary, the results demonstrate that TAPCo has the ability to solve the high-dimensional COPs in the IEEE CEC2017 test set successfully.

Further analyses and discussions

Advantages over the classical co-evolution framework

We designed a comparison experiment to illustrate the advantages of TAPCo over the classical co-evolution framework. To this end, we implemented a COEA called Co_DE in the framework of the classical co-evolution [34, 38]. For a fair comparison, the search algorithm in Section “Search algorithm” was used in Co_DE. Next, The experiments of Co_DE and TAPCo were executed based on the IEEE CEC2006 and IEEE CEC2010 test sets. The comparison results were recorded in Table 8 where “+”, “\(\approx \)”, and “-” denote that Co_DE is better than, similar to, and worse than TAPCo, respectively. In Table 8, Co_DE is worse than TAPCo on all test instances significantly. The experimental results show that TAPCo can remedy the weaknesses of the classical co-evolution framework and thus is more effective to solve COPs.

Table 8 Comparison results of Co_DE versus TAPCo on different test sets
Full size table

Effectiveness of the co-evolution stage

As discussed in Section “Two-stage adaptive penalty method based on co-evolution”, both the co-evolution stage and the shuffle stage are critical to TAPCo. To verify the advantages of the co-evolution stage, we designed four variants (denoted as TAPCo-rSh, TAPCo-fSh1, TAPCo-fSh2, and TAPCo-fSh3) for a comparative experiment. In TAPCo-rSh, for every T generations, a weight value was selected from \(\{\frac{1}{N_s},\frac{2}{N_s},\cdots ,1\}\) randomly. In TAPCo-fSh1, TAPCo-fSh2, and TAPCo-fSh3, the weight value was kept unchanged. To be specific, the weight values were set to 0.1, 0.5, and 1 in these three variants, respectively. We evaluated these COEAs based on the IEEE CEC2010 test instances with 30D. The comparison results were summarized in Table S5 in the supplementary file where “+”, “\(\approx \)”, and “-” denote that a variant is better than, similar to, and worse than TAPCo, respectively. When a COEA fails to find a feasible solution in each run, “FR” will be given in the table. As described in Table S5, TAPCo has an advantage over TAPCo-rSh, TAPCo-fSh1, TAPCo-fSh2, and TAPCo-fSh3 on most of the test instances. The results show that neither a random weight value nor a fixed weight value can be better than a weight value adjusted by the co-evolution. It reflects that the co-evolution stage is critical to TAPCo.

Effectiveness of the shuffle stage

Similarly, to verify the necessity of the shuffle stage, we deleted the shuffle stage from TAPCo and obtained a variant called TAPCo-Co. The comparison results of TAPCo-Co and TAPCo were collected in Table S5 in the supplementary file. In Table S5, TAPCo has an advantage over TAPCo-Co on 9 test instances. In addition, TAPCo-Co cannot get a feasible solution of C04 with 10D consistently. The results show that TAPCo is significantly better than TAPCo-Co. That is to say, the shuffle stage can improve TAPCo’s capability to solve COPs.

In addition, TAPCo-Co is better than the other four variants in which the co-evolution stage is deleted. It implies that the co-evolution stage is more important than the shuffle stage. The main reason is that a proper weight value is decided in the co-evolution stage. In addition, the interaction of subpopulations in the co-evolution stage can be realized by the search algorithm to some extent.

Table 9 Experimental results of TAPCo and TAPCo-wor on 5 IEEE CEC2010 test instances
Full size table

Effectiveness of the search algorithm

To demonstrate the ability of the search algorithm, we implemented six variants of TAPCo (denoted as TAPCo-Cf, TAPCo-Cc, TAPCo-Con, TAPCo-Obj, TAPCo-Div, and TAPCo-rand1). Both TAPCo-Cf and TAPCo-Cc used “DE/current-to-rand/1” and “DE/rand-to-best/1/bin” for mutation. Whereas, \(\textbf{x}_{best}\) was obtained in different ways. In TAPCo-Cf, \(\textbf{x}_{best}\) was selected based on \(G(\textbf{x})\), while in TAPCo-Cc, \(\textbf{x}_{best}\) was got based on \(f(\textbf{x})\). By comparing TAPCo with them, we can see that the tradeoff between \(f(\textbf{x})\) and \(G(\textbf{x})\) plays an important role in the search algorithm. In TAPCo-Con and TAPCo-Obj, only “DE/rand-to-best/1/bin” was adopted. The former variant selected \(\textbf{x}_{best}\) based on \(G(\textbf{x})\), while the latter selected \(\textbf{x}_{best}\) based on \(f(\textbf{x})\). TAPCo-Div only utilized “DE/current-to-rand/1”. “DE/rand/1/bin” was adopted in TAPCo-rand1. By comparing TAPCo with each of TAPCo-Con, TAPCo-Obj, TAPCo-Div, and TAPCo-rand1, we can find that the tradeoff between exploration and exploitation is also important in the search algorithm. The experiments of TAPCo and these variants on the IEEE CEC2010 test instances with 30D were summarized in Table S6 in the supplementary file. In Table S6, “FR” represents the percentage of infeasible runs. In Table S6, there are no variants better than TAPCo on more than two test instances. The experimental results show that the search algorithm can achieve the aforementioned two tradeoffs effectively.

Effectiveness of the restart mechanism

In TAPCo, a restart mechanism was designed to avoid stagnating in the infeasible region. To verify the effectiveness of the restart mechanism, we removed it from TAPCo and obtained a variant called TAPCo-wor. Experiments were conducted on the thirty-six IEEE CEC2010 test instances. As shown in Table 9, we can find that TAPCo-wor cannot enter into a feasible region of 5 test instances. Such this case occurs because the landscape of these functions is relatively complex and flat. Thus, we can conclude that the restart mechanism is beneficial for TAPCo to avoid stagnating in the infeasible region.

Parameter sensitivity analysis

There are two key parameters (i.e., T and \(N_{s}\)) in TAPCo. To investigate the impact of these two parameters on TAPCo, we designed two parameter sensitivity experiments.

For T, we chose five values (i.e., \(T=5\), \(T=25\), \(T=50\), \(T=100\), and \(T=250\)) to participate in the comparative experiment, where \(T=50\) is the default value used in TAPCo. We summarized “Mean OFV”, “Std Dev”, and “FR” of all variants in Table S7 in the supplementary file. Compared with the variants with \(T=5\), \(T=25\), \(T=100\), and \(T=250\), TAPCo reveals better results on 6, 7, 9, and 9 test instances, respectively. It is easy to see from Table S7 that \(T=50\) is more proper for TAPCo.

To determine an appropriate \(N_{s}\), we also chose five fixed values (\(N_{s}=2\), \(N_{s}=5\), \(N_{s}=7\), \(N_{s}=10\), and \(N_{s}=14\)), where \(N_{s}=10\) is the default value used in TAPCo. Similarly, “Mean OFV”, “Std Dev”, and “FR” of all variants were recorded in Table S8 in the supplementary file. There are no variants better than TAPCo on more than 4 test instances. The above experimental results indicate that \(N_{s}=10\) is more appropriate for TAPCo.

Conclusion

This paper proposed a two-stage adaptive penalty method based on co-evolution (abbreviated as TAPCo) for constrained evolutionary optimization. Different from the classical co-evolution framework in which a population of solutions and a population of penalty factors co-evolve, TAPCo adjusted the penalty factor adaptively through the co-evolution of multiple subpopulations of solutions. Specifically, in the co-evolution stage, multiple subpopulations, each of which was associated with a weight value, co-evolved along different directions. In the shuffle stage, these subpopulations were merged into the main population. The best weight value from the co-evolution stage was used for evolution of the main population. By executing these two stages iteratively, TAPCo can achieve a tradeoff  between constraints and objective function as well as a tradeoff between exploration and exploitation. In addition, a DE-based search algorithm was designed to produce promising candidate solutions in these two stages and a restart mechanism was developed to help the population avoid stagnating in infeasible regions. Extensive experiments on three test sets owning various challenging characteristics verified that:

  • TAPCo shows better or at least competitive performance against some other state-of-the-art COEAs.

  • TAPCo has an edge over the classical co-evolution framework for constrained evolutionary optimization.

  • Both the co-evolution stage and the shuffle stage are critical to TAPCo.

  • The search algorithm and the restart mechanism can improve TAPCo’s capability to handle complex COPs.

In addition, TAPCo also has some disadvantages. TAPCo’s co-evolution stage may waste computing resources and slow down the convergence speed. The reason is as follows. In this stage, \(N_s\) subpopulations evolve along directions of their respective weights. But only one direction is promising to converge to the optimal solution. The search behaviors of the remaining (\(N_s\)-1) subpopulations may waste computing resources. Therefore, TAPCo has difficulties in dealing with COPs that require a lot of computing resources, such as large-scale COPs. In the future, efforts will be devoted to improving and further extending TAPCo.