A hybrid temporal convolutional network and Prophet model for power load forecasting

Abstract

Accurate and effective power system load forecasting is an important prerequisite for the safe and stable operation of the power grid and the normal production and operation of society. In recent years, convolutional neural networks (CNNs) have been widely used in time series prediction due to their parallel computing and other characteristics, but it is difficult for CNNs to capture the relationship of sequence context and meanwhile, it easily leads to information leakage. To avoid the drawbacks of CNNs, we adopt a temporal convolutional network (TCN), specially designed for time series. TCN combines causal convolution, dilated convolution, and residual connection, and fully considers the causal correlation between historical data and future data. Considering that the power load data has strong periodicity and is greatly influenced by seasons and holidays, we adopt the Prophet model to decompose the load data and fit the trend component, season component, and holiday component. We use TCN and Prophet to forecast the power load data respectively, and then use the least square method to fuse the two models, and make use of their respective advantages to improve the forecasting accuracy. Experiments show that the proposed TCN-Prophet model has a higher prediction accuracy than the classic ARIMA, RNN, LSTM, GRU, and some ensemble models, and can provide more effective decision-making references for power grid departments.

Introduction

Under the background of the pursuit of carbon peaking and carbon neutralization, the balance between energy supply and demand is the development trend, and accurate power system load forecasting can achieve this balance in a maximum manner and achieve global energy emission reduction. Short-term load forecasting is a kind of time series forecasting problem, which models the historical observation data and predicts the change of trend in the future, to realize the purpose of early perception and efficient regulation.

Traditional prediction methods, such as ARMA (autoregressive moving average) [1], combine autoregressive and moving average methods. It is considered that the value to be predicted is a multivariate linear function of the sequence value of the previous p period and the random disturbance value of the previous q period, which is recorded as ARMA(p, q). However, the ARMA model is only suitable for stationary time series. Box et al. proposed the ARIMA (Autoregressive Integrated Moving Average) model [2], which converts the non-stationary time series by d-order difference into a stationary sequence, and then uses autoregression and moving average methods to predict future sequences. The model can be written as ARIMA(p,d,q).

Due to the simplicity of ARMA and ARIMA models, they can only capture linear relationships in essence, but cannot capture nonlinear relationships [3]. Many researchers have tried to apply machine learning methods to time series forecasting. This type of method is mainly based on Xgboost and LightGBM, which converts time series problems into supervised learning problems [4], integrates feature engineering, and realizes the prediction of complex sequences. Abbasi et al. [5] used Xgboost to extract power load data features, and after feature selection, short-term load forecasting was achieved, and a better forecasting effect than traditional methods was achieved. In addition, such features could be multimodal [6] and complex to select. Park et al. [7] proposed a sliding-window-based LightGBM model for short-term load forecasting using anomaly detection and repair, and achieved good forecasting performance.

However, machine learning methods require more complex feature engineering [8], and the quality of feature engineering determines the upper limit of the model. With the continuous development of artificial intelligence, deep learning algorithms are also widely used in load forecasting. Because the traditional convolutional neural networks (CNNs) do not consider the time series characteristics of data, it is easy to cause information leakage when applied to time series prediction [9], and the obtained prediction results are unreliable. The recurrent neural network (RNN) has added the memory function, and the discrimination and prediction of input data are related to historical data, but there is a problem of gradient disappearance or gradient explosion [10], which makes it only rely on the adjacent data, and the prediction effect of long series is not good. Therefore, researchers have improved it by introducing a gating mechanism and unit state into Long short-term memory networks (LSTM), which solves the problem of RNN gradient disappearance or gradient explosion [11]. Kong et al. [12] proposed a recursive neural network framework based on LSTM to predict the power load of a single energy user. Gated recurrent units (GRU), one of the variants of LSTM, no longer uses separate memory cells to store memory information, but directly uses hidden units to record historical states, reducing matrix calculations inside hidden units [13]. Zheng et al. [14] proposed a short-term load forecasting method for residential communities based on GRU neural network. David et al. [15] proposed an accurate probability prediction model DeepAR, and achieved the best results on multiple time series data sets. simulation results show that the proposed method is faster with similar forecasting accuracy compared with LSTM and RNN. At present, many researchers also apply the Transformer model to time series prediction, Zhou et al. [16] proposed the Informer model, which can effectively capture the accurate long-term correlation coupling between the output and the input.

Different time series forecasting models have their own advantages and disadvantages, and more and more scholars are now trying to integrate these models. The fusion models can be roughly divided into two modes, which we generalize as series modes and parallel modes. Series modes mean that two or more models operate in turn, and the output of the previous model is used as the input of the next model. Guo et al. [17] used a CNN network to cascade features of different scales, and fused feature vectors of different scales as the input of the LSTM network, which was used for short-term load prediction. Wang et al. [18] proposed a short-term load forecasting model based on variational mode decomposition (VMD) and deep neural network (DNN), where the VMD algorithm was used to decompose the load sequence into different intrinsic mode functions (IMF) and combine each IMF with DNN for forecasting. Parallel modes refer to the establishment of time series prediction models based on historical time series data, and then the weighted fusion method is used to combine the models to achieve higher accuracy prediction than a single model. Chen et al. [19] proposed a combined prediction model based on LSTM and XGBoost, and finally merged the results of the two single models through the reciprocal error method. Wei et al. [20] designed a combined forecasting model based on LSTM, random forest (RF) and support vector machine (SVM), then the optimal weighted combination method was used to fuse the three models to achieve short-term load forecasting.

In this paper, a forecasting model belonging to a parallel mode is proposed, combining temporal convolutional network (TCN) and Prophet for power load forecasting. TCN was proposed by Bai et al [21]. It combines causal convolution, dilated convolution and residual connection, which not only realizes the functions of parallel computing and efficient extraction of time series features, but also mitigates the phenomenon of gradient disappearance and gradient explosion by introducing residual structure. It also outperforms most mainstream deep learning models on different test sets. Prophet [22] is a time series prediction model that is widely used in the industry. It decomposes data into several items, including trend items, seasonal items, and holiday items. It can fit time series data in complex situations, achieve high-precision prediction, and has Interpretability that deep learning models do not have. Electricity load data is easily affected by seasons and holidays.In order to improve the prediction accuracy, we combine the deep learning model TCN with the interpretable model Prophet. Using the efficient extraction ability of TCN for time series features and the high adaptability of Prophet to season and seasonal day factors, we construct TCN and Prophet models respectively. Finally, we fuse the two models by least square multiplication to form a TCN-Prophet combination model. Based on the hourly power load data of eight regions in Texas provided by the Electric Reliability Commission of Texas (ERCOT), the experiments show that the prediction accuracy of the proposed model exceeds other classical time series forecasting models.

The remainder of this paper is organized as follows. In the next section, causal convolution, extended convolution and residual connection of temporal convolutional network are introduced. In the subsequent section, the decomposition principle and components of the Prophet model are introduced followed by which the overall framework of the TCN-Prophet prediction model are presented. The penultimate section provides a case study. The conclusion of this paper and the future work are given in the final section.

Principle of temporal convolutional network

The temporal convolutional network (TCN) is a neural network dedicated to time series prediction that combines causal convolution, dilated convolution and residual connection based on CNNs. TCN retains the advantages of parallel computing of CNNs, and adds a flexible receptive field, which can be flexibly customized according to different tasks, and the residual connection ensures that TCN has a stable gradient. These advantages of TCN are beneficial for modeling and forecasting time series. The three main components of TCN are introduced below.

Causal convolution

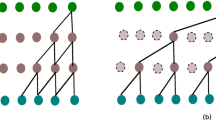
When the traditional convolutional neural network performs feature extraction, it is easy to cause the leakage of information from the future to the past. Taking the CNN network with kernel size equal to 3 as an example, the progress of extracting features is shown in Fig. 1. It can be seen that a certain point $y_t$ in the output sequence depends on the input $x_{t+1}$ at the next moment. For the time series prediction problem, given the input sequence $\mathcal {X}=\{x_0,x_1...x_T\}$, the corresponding output $\mathcal {Y}=\{y_0,y_1...y_T\}$ needs to be predicted. The causal convolution needs to satisfy that the output $y_T$ is only related to the t time states before the current state $x_T$, that is, the input $\mathcal {X}$ and the output $\mathcal {Y}$ satisfy a mapping f. The mapping relation can be expressed as Eq. (1).

$$\begin{aligned} \hat{y_0},...,\hat{y_T}=f(x_0,...,x_T). \end{aligned}$$

(1)

Fig. 1

The progress of extracting time series features using CNNs

The middle layer of TCN has the same input and output length. In order to ensure this, the input sequence needs to be filled with zero value. From the previous introduction, zero values can only be filled at the left end of the input sequence to ensure that the output sequence does not involve future information. Also taking kernel size equal to 3 as an example, the schematic diagram of causal convolution is shown in Fig. 2. We can see that padding with two zeros on the left can achieve the same output length while adhering to the rules of causality. In fact, without dilation, the number of zero-padded entries required for the input length is always equal to kernel size $- 1$.

Fig. 2

Schematic diagram of causal convolution with kernel size equal to 3

Dilated convolution

A simple causal convolution can only review a few historical data. Even if multiple hidden layers are added, the receptive field size only increases linearly. In the dilated convolution, d stands for dilation factor, which controls the interval between input data in the layer. d is equal to 1, indicating that the features extracted from the input sequence are adjacent. The previous Fig. 2 shows the dilated convolution with d equal to 1, and the receptive field size of one-dimensional causal convolution equals kernel size.

In order to increase the size of the receptive field, it is also necessary to introduce the dilation base, which is recorded as b. There is a formula, $d = b ^ i$, where i represents the number of layers below. Assuming that b is equal to 2, correspondingly, the expansion factor d of each layer forms the set {1, 2, 4, ...}. It should be noted that the kernel size must be greater than or equal to the value of the dilation base b, otherwise all the data contained in the receptive field is only a part of the input sequence, which is not conducive to capturing all historical data for modelling. The schematic diagram of multi-layer dilated convolution with b equal to 2 and kernel size equal to 3 is shown in Fig. 3.

In principle, if we construct a three-layer dilated convolution model for sufficiently long-term time series, the receptive field size corresponding to the last output value will be 15 (the input of the leftmost data of the first hidden layer is not drawn), and cover all historical data within the obtained receptive field range. When there is only one layer, the receptive field size remains the same, still as 3. When constructing a two-layer dilated convolution, the receptive field size is 7, which is 2 more than the two-layer causal convolution with d fixed at 1. Generally speaking, adding one layer of dilated convolution will increase the size of the receptive field by $(k-1)\times d$, so we can get the calculation expression for the size of the receptive field s:

$$\begin{aligned} s=1+\sum _{i=0}^{n-1}(k-1) \cdot b^{i}=1+(k-1) \cdot \frac{b^{n}-1}{b-1}, \end{aligned}$$

(2)

where n is the number of layers of extended convolution and k is kernel size, b is the dilation base.

The formula shows that the receptive field size increases exponentially with the increase of the number of layers. Fewer layers can be constructed for the time series with a large amount of data to realize the full data coverage.

Fig. 3

A schematic diagram of causal convolution with dilation base b equal to 2

Residual connection

Residual connection is an improvement of one-dimensional causal convolution, which is modified to residual block connection. Each residual block can be represented by residual block (k, d), where k is kernel size, d is dilation base. Two convolution layers are added to each residual block to produce the input of the next block. The residual connection can speed up the feedback and convergence of the deep network and solve the degradation phenomenon with the deepening of the network level. The following three methods are adopted:

• Weight normalization: normalizes the input of each layer (this offsets the gradient explosion problem, etc.)

• ReLU activation function: increases the nonlinear fitting ability of TCN

• Dropout regularization: alleviates the over fitting of the model and improves the prediction ability of the model

The TCN model with residual connections can be expressed in Fig. 4. The 1 $\times$ 1 convolution on the right of Fig. 4 is to reduce the dimension of high-dimensional data when the original input and final output dimensions of the residual block are different, to meet the requirements of the output sequence. The input sequence $\varvec{x}$ of the residual block is the output of the previous residual block. The relationship between the output $f(\varvec{x})$ of the residual block and $\varvec{x}$ is:

$$\begin{aligned} f(\varvec{x})=h(\varvec{x})+\varvec{x}. \end{aligned}$$

(3)

Fig. 4

Complete TCN model structure

Principle of Prophet model

The Prophet model is a tool developed by Facebook for time series forecasting and has a special python package that can be applied. Prophet regards time series as an additive or multiplicative model, and decomposes it into several items, including trend component, seasonal component, holiday component and residual component. It has good forecasting ability for complex nonlinear data and has become an industry widely used time series forecasting model.

Traditional sequence decomposition algorithms, such as the Seasonal-Trend decomposition procedure based on Loess (STL) [23], only decompose time series into trend component, seasonal component and remainder component. The Prophet model adds the influencing factors of the holiday component and can also refer to other external variables, which greatly improves the prediction effect of time series greatly affected by holidays or other external factors. Power load data is greatly affected by holidays and seasons, and the Prophet model can be used to fit the degree of their influence on the data. In this paper, the additive model is used to decompose the sequence, and the specific expression is as follows.

$$\begin{aligned} y(t)=g(t)+s(t)+h(t)+\varepsilon _{\textrm{t}}, \end{aligned}$$

(4)

where g(t) represents the trend component, s(t) represents the seasonal component, h(t) represents the holiday component (or other external variables), and $\varepsilon _{\textrm{t}}$ represents the residual component.

After Prophet decomposes the time series into four components, it predicts the trend component, the seasonal component and the holiday component, but does not predict the residual component, and adds the predicted three component results to obtain the final forecast result. The four components are briefly described below.

Trend component

Trend component is used to fit aperiodic changes such as piecewise linear growth or logical growth in time series, and can be divided into the following two types.

• 1. Saturation trend component: a saturated value that increases or decreases nonlinearly to control the extent of the trend. The logistic growth model is often used, and the specific form is as follows.

  $$\begin{aligned} g(t)=\frac{C}{1+\exp (-k(t-m))}, \end{aligned}$$

  (5)

  where C is the upper limit of capacity, which refers to the upper bound that g(t) can reach; k refers to the growth rate. The greater the absolute value of k, the faster the change; m refers to the turning point where the slope of the trend term changes. When t equals m, the slope reaches the maximum.

• 2. Linear trend component: there is always an upward or downward trend. The linear trend component is expressed as follows.

  $$\begin{aligned} g(t)=k t+m, \end{aligned}$$

  (6)

  where k is the trend growth rate and m is the offset.

Seasonal component

The seasonal component simulates the periodicity of time series through the Fourier series. The specific form is:

$$\begin{aligned} s(t)=\sum _{n=1}^{N}\left( a_{n} \cos \left( \frac{2 \pi n t}{P}\right) +b_{n} \sin \left( \frac{2 \pi n t}{P}\right) \right) , \end{aligned}$$

(7)

where P represents the size of the period, such as 365.25 for the year and 7 for the week, and N represents the number of fitting items. Obviously, the higher the N is, the better the fitting effect will be, but it will cause overfitting of the model, and conversely will cause the underfitting of the model. N is generally taken as 10 in annual seasonality and 3 in weekly seasonality [22].

Fig. 5

The framework of the TCN-Prophet model

Taking annual seasonality as an example, let x(t) denote the vector set consisting of the sine or cosine terms following $a_{n},b_{n}$.

$$\begin{aligned} x(t)=\left[ \cos \left( \frac{2 \pi (1) t}{365.25}\right) , \ldots , \sin \left( \frac{2 \pi (10) t}{365.25}\right) \right] , \end{aligned}$$

(8)

The seasonal component can be expressed more succinctly as $s(t)=x(t)\beta$. Fitting the seasonal component theoretically needs to learn the value of $a_{n},b_{n}(n=1,...,N)$, and now only needs to learn $\beta$. In Prophet model, $a_{n},b_{n}$ is regarded as a normally distributed random variable with mean 0 and variance $\sigma ^2$.

$$\begin{aligned} \beta \sim \mathrm{{Normal}}(0,\sigma ^2), \end{aligned}$$

(9)

where standard deviation $\sigma$ represents seasonality prior scale, and the larger $\sigma$, the more obvious the effect of the seasonal component, but it is easy to cause overfitting.

Holiday component

The holiday component is used to fit factors that impact the time series but is not a seasonal component. It generally refers to holiday factors, and can also refer to other external variables. Suppose there are L kinds of holidays, and $D_i$ represents the set of ith holiday dates in the past and the future. The vacation component can be expressed as follows.

$$\begin{aligned}&h(t)=Z(t) \kappa \end{aligned}$$

(10)

$$\begin{aligned}&Z(t)=\left[ \textbf{1}\left( t \in D_{1}\right) , \ldots , \textbf{1}\left( t \in D_{L}\right) \right] \end{aligned}$$

(11)

$$\begin{aligned}&\kappa \sim \mathrm{{Normal}}\left( 0, v^{2}\right) . \end{aligned}$$

(12)

Similar to the seasonal component, the model fits the holiday component by learning parameter $\kappa$. In the above formula, v represents the holiday prior scale, and the higher the v, the more the model will be affected by the holiday component more.

Residual component

The residual component refers to the component that cannot be explained by the above three components, generally referring to the noise in the sequence. When Prophet makes predictions, it does not consider the residual component and sums the prediction results of the remaining three components, which has good robustness. The final predicted sequence is expressed as

$$\begin{aligned} \hat{y}(t)=g(t)+s(t)+h(t). \end{aligned}$$

(13)

Load forecasting model based on TCN-Prophet

Power load data is a series of complex discontinuous time series, which is affected by many surrounding factors. For power load data prediction, first, TCN is used to extract the features of the series, and then the sliding window method is used to predict the future power load data. Then use the Prophet model to decompose the load data, and predict the future series according to the addition model. Finally, the least square method is used to fit the weight coefficients of the TCN and Prophet models, so that the difference between the predicted results of the hybrid TCN-Prophet model and the real data is minimal. Define the output sequence of the TCN model as T(t), the output sequence of the Prophet model as P(t), and the least squares method assigns the weights to the two as $w_1,w_2$. The final predictions of the TCN-Prophet model are as follows.

$$\begin{aligned}&\hat{Y}{(t)}=w_1T(t)+w_2P(t) \end{aligned}$$

(14)

$$\begin{aligned}&w_1+w_2=1. \end{aligned}$$

(15)

The framework of the TCN-Prophet model is shown in Fig. 5.

In order to minimize the difference between the predicted results of the TCN-Prophet model and the real results, we define the distance function as the two-norm between the predicted results and the real results, to select appropriate weight coefficients $w_1$ and $w_2$ to minimize the two-norm. The two-norm is a function of $w_1$ and $w_2$, expressed as follows.

$$\begin{aligned} \min f(w_1,w_2)= & {} \left\| \hat{Y} -Y \right\| \nonumber \\= & {} \sum _{i\in T}^{} (\hat{y} _i-y_i)^2 \nonumber \\= & {} \sum _{i\in T}^{}(w_1T_i+w_2P_i-y_i)^2. \end{aligned}$$

(16)

T in the above formula $i\in T$ represents the time set for calculating the weight coefficient, which can take the time range of the whole training set. To better predict future data, we split the training set into new training and validation sets, and take T as the set of validation set times. Taking the partial derivatives of Eq. (16) for $w_1$ and $w_2$, respectively, we can get

$$\begin{aligned}&\frac{\partial f(w_{1}, w_{2})}{\partial w_{1}}=\sum _{i\in T}^{} 2(w_1T_i+w_2P_i-y_i)T_i=0 \end{aligned}$$

(17)

$$\begin{aligned}&\frac{\partial f(w_{1}, w_{2})}{\partial w_{2}}=\sum _{i\in T}^{} 2(w_1T_i+w_2P_i-y_i)P_i=0 \end{aligned}$$

(18)

$$\begin{aligned}&w_1+w_2=1. \end{aligned}$$

(19)

The weight coefficients $w_1$ and $w_2$ can be obtained by simultaneous Eqs.  (17)–(19).

$$\begin{aligned} w_1&=\frac{\sum _{i\in T}^{} (y_i-P_i)T_i}{\sum _{i\in T}^{} (T_i-P_i)T_i} \end{aligned}$$

(20)

$$\begin{aligned} w_2&=\frac{\sum _{i\in T}^{} (T_i-y_i)T_i}{\sum _{i\in T}^{} (T_i-P_i)T_i}. \end{aligned}$$

(21)

Case study

This paper forecasts the hourly power load of eight regions in Texas provided by ERCOT. The hourly data can be obtained from this website, http://www.ercot.com. The dataset includes power load data from 1:00 on January 1, 2004, to 0:00 on September 1, 2021, in eight regions of Texas, with 154,854 h of data in each region.

Different from traditional machine learning segmentation datasets, to ensure the continuity of time series information and avoid information leakage, the training set, validation set and test set should be continuous. We select the data of the last 60 days as the test set, then selects the last 60 days of the remaining data as the validation set, and the rest of the data as the training set. Then, the TCN-Prophet model proposed in this paper is used for prediction, and compared with ARIMA, RNN, LSTM, GRU, TCN, Prophet and some ensemble models. All experimental models run in the Python 3.9 programming environment. The hardware is a PC with an AMD core R7-5800H CPU and 16GB memory.

Data preprocessing

Through a simple exploration of the load data, it was found that there were 18 data shortages in each of the eight regions. We use the “fillna” method in Pandas to deal with missing values, and set the filling method to “pad”, that is, we use the data of the previous row to fill the null values of the current row.

There are differences in electricity consumption in different regions, so we adopt Min–Max Normalization for the eight regions respectively. Scaling the data to the range of [0, 1] can eliminate the adverse effects caused by singular sample data, and at the same time improve the model accuracy and accelerate the model convergence speed. It should be noted that, not to cause information leakage, when performing normalization, the training set should be normalized first. Then the validation set and test set should be scaled based on the training set. The Min–Max Normalization can be expressed as:

$$\begin{aligned} \varvec{x}^\prime =\frac{\varvec{x}-\min (\varvec{x})}{\max (\varvec{x})-\min (\varvec{x})}, \end{aligned}$$

(22)

where $\varvec{x}$ is the training set of power load data in any region, $\min (\varvec{x})$ and $\max (\varvec{x})$ are their minimum and maximum level, respectively, and $\varvec{x}^\prime$ is the normalized data sequence.

Parameter setting of TCN model

When using the TCN model for prediction, it is necessary to specify the length of input sequence input_length and the length of output sequence output_length of each sliding window. Then, using the sliding window method, the time is sequentially advanced to form multiple sets of prediction pairs consisting of the input and output sequence. We forecast the load of the next day according to the historical 10 day power load data, that is, input_length equals 240, output_length equals 24.

In each iteration of the model, the Adam optimizer is used to optimize the parameters to reduce the value of the loss function in the training process. Adam combines the advantages of the two optimization algorithms AdaGrad and RMSProp, comprehensively considers the first-moment estimation of the gradient (the mean value of the gradient) and the second-moment estimation (the uncentered variance of the gradient), and calculates the update step size. The loss function Loss selects the mean square error MSE.

$$\begin{aligned} \mathrm{{Loss}} =\frac{1}{n} \sum _{i=1}^{n}(\varvec{Y}_{i}-\hat{\varvec{Y}}_{i})^2, \end{aligned}$$

(23)

where $\varvec{Y}_{i}$ is the real load data in the validation set, $\hat{\varvec{Y}}_{i}$ is the load data predicted by TCN model, and n is the size of the validation set.

To mitigate model overfitting, set dropout to 0.1. At the same time, an early stop mechanism is added to the model. When the performance of the model on the validation set begins to decline, stopping training can also alleviate the problem of overfitting. The early stop parameter patience is set to 50.

The main parameters of the TCN model are shown in Table 1.

Table 1 The main parameters of the TCN model

Parameter settings of Prophet

We use a piecewise linear model to describe the trend component of the Prophet model. That is, the parameter growth is set to “linear”. Meanwhile, changepoint_range, the parameter controlling the range of change points, is set to 0.8, indicating that mutation points occur in the range of 80% before the training set. The parameter changepoint_ prior_scale controls the number of mutation points, and a larger value allows more mutation points, but will cause overfitting of the model, so set it to 0.2.

As the seasonal component is an important part of Prophet, we set yearly, monthly, weekly and daily seasonality to analyze power load data. The period P corresponding to the year, month, week, and the “day” is set to 365.25, 30.5, 7, and 1, respectively, and the corresponding Fourier series N is set to 10, 5, 3, and 4, respectively. Their seasonal impact factors, seasonality_prior_scale, are all set to 10.

In the holiday component, because the power load data come from Texas, the United States, we introduce the main holidays in the United States to fit the mutation of the load data caused by the holiday. We import the dates of the top ten legal holidays in the United States into the Prophet model. Taking 2020 year as an example, the specific imported holidays and their times are shown in Table 2. The Prophet model will pay more attention to the load data of these times and fit the change value of these times to the load.

Table 2 US holidays in 2021 with Prophet model

Table 3 The main parameters of Prophet

Table 4 MAPE for single model comparative experiments, all values are in units of $10^{-2}$

The main parameters of Prophet are set according to Table 3. Through experiments, we can obtain the fitting diagram of each component after the decomposition of the power load data by the Prophet model. The Prophet model does just that by fitting out the individual components and accumulating them to get the predicted electricity load series.

Table 5 MSE for single model comparative experiments, all values are in units of $10^{-3}$

Evaluating indicators

We introduce commonly used metrics for time series forecasting, mean square error (MSE), mean absolute error (MAE) and mean absolute percentage error (MAPE), to compare the proposed TCN-Prophet model with other classic time series forecasting models. The calculation formulas of the three evaluation indicators are as follows.

$$\begin{aligned}&\mathrm{{M A P E}}=\frac{1}{n} \sum _{i=1}^{n}|\frac{\hat{Y} _{\text{ test } }(i)-Y_{\text{ test } }(i)}{Y_{\text{ test } }(i)}|\end{aligned}$$

(24)

$$\begin{aligned}&\mathrm{{M S E}}=\sqrt{\frac{1}{n} \sum _{i=1}^{n}\left( \hat{Y} _{\text{ test } }(i)-Y_{\text{ test } }(i)\right) ^{2}} \end{aligned}$$

(25)

$$\begin{aligned}&\mathrm{{M A E}}=\frac{1}{n} \sum _{i=1}^{n}|\hat{Y} _{\text{ test } }(i)-Y_{\text{ test } }(i)|, \end{aligned}$$

(26)

where $Y_{\text{ test } }$ is the actual load data sequence of any region in the test set, $\hat{Y}_{\text{ test } }$ is the sequence predicted by models, and n is the size of the test set.

Table 6 MAE for single model comparative experiments, all values are in units of $10^{-2}$

Analysis of experimental results

Compared with the traditional single model

Tables 4, 5 and 6 show the average values of MAPE, MSE and MAE indexes of the test set calculated after 10 times experiments have been done by the seven models based on the power load data of eight regions, and the best indicators in each dataset are shown in bold. It can be seen from the three tables that the traditional ARIMA model has a lower effect on the prediction of long-term series than the neural network algorithm, and LSTM performs better in models based on the recurrent neural network prediction. The optimal values of different indicators in each region are shown in bold, the three indicators of the TCN-Prophet model proposed in this paper all perform the best on the eight regional datasets. Taking the MAPE indicator in the COAST region as an example, the performance of this model has been improved by 19% than Prophet, 51% than TCN, and even 67% than the next RNN model. The experimental results show that the TCN-Prophet model has much higher forecasting accuracy than the listed classical models in time series forecasting. Figure 6 shows the visualization results of different models on the test set of power load data in the COAST region. In Fig. 6, the seven small graphs at the top and right show the degree of correlation between the predicted results of each model and the true values, we can see that the prediction result of the ARIMA model deviates greatly from the actual value and is unstable, and Prophet model performs better than other single models. The large graph in the middle of Fig. 6 summarizes the predicted results of models, and the three graphs at the bottom clearly show the visualization results of the three indicators. Now we can find that the three indicators of the prediction effect of our proposed TCN-Prophet model have a certain improvement over the Prophet model, and are significantly better than other single models. It should be mentioned that, for better visualization, only the prediction results of the last five days of the different models are shown (data are normalized).

Fig. 6

Visualization of prediction results of single models

Fig. 7

Visualization of prediction results of ensemble models

Compared with various ensemble models

To ensure the rigor of the experiments, we also compare the proposed model with various ensemble models. We added the bagging ensemble method and established the bagging ensemble model of TCN and Prophet, denoted as TCN-Prophet (Bagging), to verify the accuracy of the ensemble method proposed in this paper. In order to compare the good performance of the selected single model TCN and Prophet compared with other traditional single models in time series prediction, we also use the least squares method to integrate several models with better performance in the single model to compare their effects. Specifically, TCN-GRU, Prophet-GRU and GRU-LSTM models are included.

Due to the limitation of the paper’s length, only the ensemble models’ prediction results are shown here. In Fig. 7, we can clearly see that the prediction curve of the TCN-Prophet model is the closest to the real data, and the prediction effect of other ensemble models is not even comparable to that of the single models.

Conclusions

Accurate load forecasting can maintain the safety and stability of power grid operation and save unnecessary equipment operation, maintenance and other costs. This paper proposes a power load prediction model based on TCN-Prophet. The TCN model adopts causal convolution, dilated convolution and residual connection, which is suitable for extracting long-term time series features and making predictions. The Prophet model decomposes the sequence, and by adding the seasonal component and the holiday component, the changing effect of the power load data in different periods and different holidays can be fitted. Finally, the advantages of the two models are fully utilized, and the least squares method is used to fuse them to improve the accuracy of the prediction results. The experimental results show that TCN-Prophet model has the best prediction indicators whether compared with single models or other ensemble models. Taking the COAST region as an example, the MAPE indicator is at least 19% higher than other models.

Moreover, the model proposed in this paper can also be extended to other fields, such as stock forecasting, precipitation forecasting, sales forecasting and so on. We only mine and analyze the historical data of the power load itself, and fully consider the impact of time factors on the sequence. However, in real life, power load data is affected by some potential factors, such as temperature, humidity, wind power, etc. The follow-up work will consider adding potential factors to the model to construct a more accurate prediction model. In addition, the time series prediction model based on the transformer variant has achieved better results, providing ideas for our follow-up research.