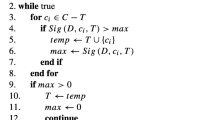Feature selection based on self-information and entropy measures for incomplete neighborhood decision systems

Abstract

For incomplete datasets with mixed numerical and symbolic features, feature selection based on neighborhood multi-granulation rough sets (NMRS) is developing rapidly. However, its evaluation function only considers the information contained in the lower approximation of the neighborhood decision, which easily leads to the loss of some information. To solve this problem, we construct a novel NMRS-based uncertain measure for feature selection, named neighborhood multi-granulation self-information-based pessimistic neighborhood multi-granulation tolerance joint entropy (PTSIJE), which can be used to incomplete neighborhood decision systems. First, from the algebra view, four kinds of neighborhood multi-granulation self-information measures of decision variables are proposed by using the upper and lower approximations of NMRS. We discuss the related properties, and find the fourth measure-lenient neighborhood multi-granulation self-information measure (NMSI) has better classification performance. Then, inspired by the algebra and information views simultaneously, a feature selection method based on PTSIJE is proposed. Finally, the Fisher score method is used to delete uncorrelated features to reduce the computational complexity for high-dimensional gene datasets, and a heuristic feature selection algorithm is raised to improve classification performance for mixed and incomplete datasets. Experimental results on 11 datasets show that our method selects fewer features and has higher classification accuracy than related methods.

Introduction

With the rapid development of information technology, the databases expand rapidly. In daily production and life, more and more information is obtained and stored [1,2,3,4,5]. However, these information may contain a great quantity of redundancy, noise, or even missing feature values [6,7,8]. Nowadays, how to deal with missing values, reduce redundant features, and simplify the complexity of the classification model, so as to improve the generalization ability of model classification is a huge challenge we are facing [9,10,11,12,13,14,15]. As an important step of data preprocessing, feature selection based on granular computing has been widely used in knowledge discovery, data mining, machine learning, and other fields [16,17,18,19,20,21,22,23].

Related work

Neighborhood rough sets [24] and multi-granularity rough sets [25] models, as two commonly used mathematical tools for dealing with uncertainty and incomplete knowledge, are widely employed in feature selection and attribute reduction [26,27,28,29,30,31,32]. Hu et al. [33]introduced the neighborhood relationship into different weights, constructed a weighted rough set model based on the weighted neighborhood relationship, and fully tapped the correlation between attributes and decision. Yang et al. [34] introduced fuzzy preference relations to propose a neighborhood rough set model based on the degree of dominance and applied it to the problem of attribute reduction in large-scale decision problems. Wang et al. [28] presented a neighborhood discriminant index to characterize the discriminative relationship of neighborhood information, which reflects the distinguishing ability of a feature subset. Qian et al. [35] developed a pessimistic multi-granulation rough sets decision model based on attribute reduction. Lin et al. [36] advanced a neighborhood-based coverage reduction multi-granulation rough set model. Sun et al. [37] combined the fuzzy neighborhood rough sets with the multi-granulation rough set model, and proposed a new fuzzy neighborhood multi-granulation rough set model, which expanded the types of rough set models. Meanwhile, the neighborhood multi-granulation rough sets’ (NMRS) model has been widely used. Ma et al. [38] constructed an NMRS model based on the two-particle criterion, which effectively reduced the number of iterations in the attribute reduction calculation. Hu et al. [39] presented a matrix-based incremental method to update the knowledge in NMRS. To obtain more accurate rough approximation and reduce the interference of noise data, Luo et al. [40] developed a neighborhood multi-granular rough set variable precision decision method based on multi-threshold. Although a variety of NMRS-based feature selection methods have been proposed and applied, most of the evaluation functions of them are constructed only based on the lower approximation of decision. This construction method ignores the information contained in the upper approximation, which easily leads to the loss partial information [58].

In various fields datasets, missing values (null or unknown values) often occur [9, 41]. Recently, tolerance relation or tolerance rough sets have emerged in the field of processing incomplete datasets [42]. Qian et al. [43] presented an incomplete rough set model based on multiple tolerance relations from the multi-granulation view. Yang et al. [44] proposed supporting feature functions for processing multi-source datasets through the perspective of multi-granulation. Sun et al. [45] developed neighborhood tolerance-dependent joint entropy for feature selection and revealed better classification performance on incomplete datasets. Zhao et al. [42] constructed an extended rough set model based on neighborhood tolerance relation, which was successfully applied to incomplete datasets with mixed categories and numbers. Inspired by these research achievements, this paper is dedicated to developing a heuristic feature selection method based on neighborhood tolerance relation to solve mixed incomplete datasets.

In recent years, the uncertainty measures had developed rapidly from the algebra view or the information view [46, 47]. Hu et al. [39] constructed a matrix-based feature selection method to realize the uncertainty of the boundary region in the NMRS model. You et al. [48] proposed the relative reduction for covering information system. Zhang et al. [49] employed local pessimistic multi-granulation rough set to deal with larger size datasets. In general, the above studies are only from algebra view. Unfortunately, the attribute importance based on algebra view only describes the influence of the features contained in the subset. In the past decades, information entropy and its variants have been extensively used in feature selection as an important method [50, 51]. Zeng et al. [52] improved multi-granulation entropy by developing multiple binary relations. Feng et al. [53] studied the reduction problem of multi-granulation fuzzy information system according to merging entropy and conditional entropy. In short, these literatures discussed feature selection only from information view. However, feature significance only from the information view barely reflects the significance on features in uncertainty classification [54, 55]. It would be a better topic to integrate the two views to improve the uncertainty measure quality in feature selection for incomplete neighborhood decision systems. Wang et al. [56] studied rough reduction and relative reduction from two views simultaneously. Chen et al. [57] proposed the roughness based on entropy and the approximate roughness measurement of the neighborhood system. Xu et al. [58] presented a feature selection method using fuzzy neighborhood self-information measures and entropy in combination with algebra and information views. Table 1 summarizes and highlights some feature selection methods from the perspective of whether to deal with missing data and uncertainty measure views.

Table 1 Summary of some feature selection methods

Our work

To solve the problem, some feature evaluation functions only consider the information contained in the lower approximation of the decision, which may lead to loss some information, moreover comprehensively evaluate the uncertainty of the incomplete neighborhood decision systems. This paper will focus on researching a new feature selection method in multi-granulation terms. The main work of this paper is as follows:

• Based on the related definitions of NMRS, the shortcomings of the related neighborhood functions are analyzed.

• Three kinds of uncertain indices are proposed, including decision index, sharp decision index, and blunt decision index, using upper and lower approximations of NMRS. Then, we redefine three types of precision and roughness based on three indices. Next, combining with the concept of self-information, four kinds of neighborhood multi-granulation self-information measures are proposed and their related properties are studied. According to theoretical analysis, the fourth measure, named lenient neighborhood multi-granulation self-information (NMSI), is suitable for select the optimal feature subsets.

• To better study the uncertainty measure for the incomplete neighborhood decision systems from the algebra and information views, the self-information measures and information entropy are combined to propose a neighborhood multi-granulation self-information-based pessimistic neighborhood multi-granulation tolerance joint entropy (PTSIJE). PTSIJE not only considers the upper and lower approximations of the incomplete decision systems at the same time, but also can measure the uncertainty of the incomplete neighborhood decision systems from the algebra and information views simultaneously.

The structure of the rest of this paper is as follows: some related concepts of self-information and NMRS are reviewed in “Previous knowledge”. “The deficiency of relative function and PTSIJE- based uncertainty measures” illustrates the shortcomings of neighborhood correlation function. Then, to improve the shortcomings, we propose four neighborhood multi-granulation self-information measures and study their related properties. Finally, the fourth measure is combined with neighborhood tolerance joint entropy to construct a feature selection model based on PTSIJE. “PTSIJE-based feature selection method in incomplete neighborhood decision systems” designs a heuristic feature subset selection method. In “Experimental results and analysis” six UCI datasets and five gene expression profile datasets were used to verify the results. “Conclusion” is the conclusion of this paper and our future work.

Previous knowledge

Self-information

Definition 1

[59] Metric I(x) is proposed by Shannon to represent the uncertainty of a signal x, is called the self-information of x if it met the following properties:

• (1) Non-negative:$I(x) \ge 0$.

• (2) If $p(x) \rightarrow 0$ , then $I(x) \rightarrow \infty$.

• (3) If $p(x)\mathrm{{ = }}0$ , then $I(x) = 1$.

• (4) Monotonic: If $p(x) < p(y)$ , then $I(x) < I(y)$.

Here, p(x) is the probability of x.

Neighborhood multi-granulation rough sets

Given a neighborhood decision $NDS=<U,CA,D,V,f,$ $\varDelta ,\lambda >$, $U = \{ {x_1},{x_2},...,{x_m}\}$ is an universe, $CA\mathrm{{ = }}{B_S} \cup {B_N}$ is a conditional attribute set that depicts the samples with mixed data, here ${B_S}$ is a symbolic attribute set, ${B_N}$ is the a numerical attribute set; D is the decision attribute set; $V = { \cup _{a \in CA \cup DS}}{V_a}$ which ${V_a}$ is a value of attribute a; f is the map function; $\varDelta$ is the distance function; $\lambda$ is the neighborhood radius and $\lambda \in [0,1]$. Suppose that $x \in U$ and f(a, x) is equal to a missing value (an unknown value or a null, recorded as “*”), which means that there is at least one attribute $a \in CA$, $f(a,x)\mathrm{{ = *}}$, then this decision systems can be called an incomplete neighborhood decision system $INDS\mathrm{{ = }} < U,CA,D,V,f,\varDelta ,\lambda>$, it can be abbreviated as $INDS = < U,CA,D,\lambda >$.

Definition 2

Suppose an incomplete neighborhood decision system $INDS = < U,CA,D,\lambda >$ with any $B \in CA$ and $B\mathrm{{ = }}{B_S} \cup {B_N}$, then the neighborhood tolerance relation of B is described as [42]

$$\begin{aligned} \begin{aligned} NT_B^\lambda&= \{ (x,y) \in U \times U|\forall a \in B(f(a,x) = *) \vee \\&(f(a,y) = *) \vee (a \in {B_S} \rightarrow {\varDelta _a}(x,y) = 0) \\&\wedge (a \in {B_N} \rightarrow {\varDelta _a}(x,y) \le \lambda )).\} \end{aligned} \end{aligned}$$

(1)

For any $x,y \in U$, the neighborhood tolerance class is expressed as [42]

$$\begin{aligned} NT_B^\lambda (x) = \{ y \in U|(x,y) \in NT_B^\lambda \}. \end{aligned}$$

(2)

Definition 3

Given $INDS = < U,CA,D,\lambda >$ with $X \subseteq U$, $A = \{ {A_1},{A_2},...,{A_r}\}$ and $A \subseteq CA$, the optimistic neighborhood multi-granulation lower and upper approximations of X with regard to ${A_1},{A_2},...,{A_r}$ are denoted, respectively, as

$$\begin{aligned}&\underline{\sum \limits _{i = 1}^r {A_i^{O,\lambda }} } (X) = \{ x \in U|NT_{{A_1}}^\lambda (x) \subseteq X \vee \nonumber \\&\quad NT_{{A_2}}^\lambda (x) \subseteq X\vee ... \vee NT_{{A_r}}^\lambda (x) \subseteq X\} \end{aligned}$$

(3)

$$\begin{aligned}&\quad \overline{\sum \limits _{i = 1}^r {A_i^{O,\lambda }} } (X) = \sim \left( \sum \limits _{i = 1}^r {A_i^{O,\lambda }} (\sim X)\right) ; \end{aligned}$$

(4)

here, $NT_{{A_i}}^\lambda (x)$ represents the neighborhood tolerance class, ${A_i} \subseteq A$ with $i = 1,2,...,r$ . Then, $\underline{\Bigg (\sum \nolimits _{i = 1}^r {A_i^{O,\lambda }} } (X),$ $\overline{\sum \nolimits _{i = 1}^r {A_i^{O,\lambda }} } (X)\Bigg )$ can be called an optimistic NMRS model (ONMRS) in incomplete neighborhood decision systems [60].

Definition 4

Assume that an incomplete neighborhood decision system $INDS = < U,CA,D,\lambda >$ with ${A_i} \subseteq A$, $A = \{ {A_1},{A_2},...,{A_r}\}$, and $U/D = \{ {D_1},{D_2},...,{D_t}\}$, the optimistic positive region and the optimistic dependency degree of D with respect to A based on ONMRS are expressed[60], respectively, as

$$\begin{aligned} POS_A^{O,\lambda }(D)= & {} \bigcup \limits _{l = 1}^t {\sum \limits _{i = 1}^r {A_i^{O,\lambda }} } ({D_l}) \end{aligned}$$

(5)

$$\begin{aligned} \gamma _A^{O,\lambda }(D)= & {} \frac{{\left| {POS_{{A_i}}^{O,\lambda }(D)} \right| }}{{\left| U \right| }}, \end{aligned}$$

(6)

where ${A_i} \subseteq A$, $i = 1,2,...,r$, ${D_l} \in U/D$, $l = 1,2,...,t$.

Definition 5

Let $INDS = < U,CA,D,\lambda >$ with $X \subseteq U$, $A = \{ {A_1},{A_2},...,{A_r}\}$ and $A \subseteq CA$ , then the pessimistic neighborhood multi-granulation lower and upper approximations of X with respect to ${A_1},{A_2},...,{A_r}$ are denoted [60], respectively, as

$$\begin{aligned}&\quad \underline{\sum \limits _{i = 1}^r {A_i^{P,\lambda }} } (X) = \{ x \in U|NT_{{A_1}}^\lambda (x) \subseteq X \nonumber \\&\quad \wedge NT_{{A_2}}^\lambda (x) \subseteq X \wedge ... \wedge NT_{{A_r}}^\lambda (x) \subseteq X\} \end{aligned}$$

(7)

$$\begin{aligned}&\quad \overline{\sum \limits _{i = 1}^r {A_i^{P,\lambda }} } (X) = \sim \left( \sum \limits _{i = 1}^r {A_i^{P,\lambda }} (\sim X)\right) ; \end{aligned}$$

(8)

here, $NT_{{A_i}}^\lambda (x)$ represents the neighborhood tolerance class, ${A_i} \subseteq A$ with $i = 1,2,...,r$ .

Then,$\underline{\Bigg (\sum \nolimits _{i = 1}^r {A_i^{P,\lambda }} } (X),\overline{\sum \nolimits _{i = 1}^r {A_i^{P,\lambda }} } (X)\Bigg )$ can be called a pessimistic NMRS model (PNMRS) in incomplete neighborhood decision systems [60].

Definition 6

Given $I\!N\!D\!S = <U,CA,D,\lambda>$ with ${A_i} \subseteq A$, $A = \{ {A_1},{A_2},...,{A_r}\}$, and $U/D = \{ {D_1},{D_2},...,{D_t}\}$, the pessimistic positive region and the pessimistic dependency degree of D with respect to A based on PNMRS are expressed [60], respectively, as

$$\begin{aligned} POS_A^{P,\lambda }(D)= & {} \bigcup \limits _{l = 1}^t {\sum \limits _{i = 1}^r {A_i^{P,\lambda }} } ({D_l}) \end{aligned}$$

(9)

$$\begin{aligned} \gamma _A^{P,\lambda }(D)= & {} \frac{{\left| {POS_{{A_i}}^{P,\lambda }(D)} \right| }}{{\left| U \right| }}, \end{aligned}$$

(10)

where ${A_i} \subseteq A$, $i = 1,2,...,r$, ${D_l} \in U/D$, $l = 1,2,...,t$.

The deficiency of relative function and PTSIJE-based uncertainty measures

The deficiency of relative function

The classic NMRS model employs Eq. (10) as the evaluation function for feature selection. However, this construction method only considers the positive region, that is to say, only a part of the decision information is taken into account, and the information contained in the upper approximation of the decision is often not negligible, so this construction method is easy to cause the loss of some information. Thus, an ideal evaluation function should take into account the information whether it is consistent with the decision. For this reason, in the next part, we construct PTSIJE to measure the uncertainty in the mixed incomplete neighborhood decision systems, making the feature selection mechanism more comprehensive and reasonable.

PTSIJE-based uncertainty measures

Definition 7

Let $INDS = < U,CA,D,\lambda >$, $U/D = \{ {D_1},{D_2},...,{D_t}\}$, $A \subseteq CA$, $A = \{ {A_1},{A_2},...,{A_r}\}$, ${A_i} \subseteq A$, $NT_A^\lambda$ is a neighborhood tolerance relation induced by A. The decision index $dec({D_k})$, the sharp decision index $sha{r_A}({D_k})$, and the blunt decision index $blu{n_A}({D_k})$ of ${\mathrm{{D}}_k}$ are denoted, respectively, by

$$\begin{aligned} dec({D_k})= & {} \left| {NT_A^\lambda } \right| \end{aligned}$$

(11)

$$\begin{aligned} sha{r_A}({D_k})= & {} \left| {\underline{\sum \limits _{i = 1}^r {A_i^{P,\lambda }} } ({D_k})} \right| \end{aligned}$$

(12)

$$\begin{aligned} blu{n_A}({D_k})= & {} \left| {\overline{\sum \limits _{i = 1}^r {A_i^{P,\lambda }} } ({D_k})} \right| , \end{aligned}$$

(13)

where the sharp decision index $sha{r_A}({D_k})$ of ${D_k}$ is illustrated as the cardinal number of its lower approximation, which is expressing the number of samples with consistent neighborhood decision classification. The blunt decision index $blu{n_A}({D_k})$ of ${D_k}$ is showed by the cardinal number of its upper approximation, which representing number of samples may belong to ${D_k}$. $\left| \cdot \right|$ means the cardinality of the set.

Property 1

$sha{r_A}({D_k}) \le dec({D_k}) \le blu{n_A}({D_k})$.

Proof

The detailed proof can be found in the supplementary file.

Property 2

Assume $A1 \subseteq A2 \subseteq CA$ and ${D_k} \in U/D = \{ {D_1},{D_2},...,{D_t}\}$, then

• (1) $sha{r_{A1}}({D_k}) \le sha{r_{A2}}({D_k})$.

• (2) $blu{n_{A1}}({D_k}) \ge blu{n_{A2}}({D_k})$.

Proof

The detailed proof can be found in the supplementary file.

Property 2 reveals that both the sharp decision and the blunt decision indices are monotonic. The sharp decision index $sha{r_A}({D_k})$ boosts and the consistency of decision is enhanced with the increase of the number of features. A smaller blunt decision index $blu{n_A}({D_k})$ is generates by decrease of decision uncertainty. In other words, attribute reduction is produced by the uncertainty of decision decreases.

Definition 8

For an incomplete neighborhood decision system $INDS = < U,CA,D,\lambda >$ with $A \subseteq CA$, ${D_k} \in U/D$, the precision and roughness of the sharp decision index are defined, respectively, as

$$\begin{aligned} \theta _A^{(1)}({D_k})= & {} \frac{{sha{r_A}({D_k})}}{{dec({D_k})}} \end{aligned}$$

(14)

$$\begin{aligned} \sigma _A^{(1)}({D_k})= & {} 1 - \frac{{sha{r_A}({D_k})}}{{dec({D_k})}} = 1 - \theta _A^{(1)}({D_k}). \end{aligned}$$

(15)

Evidently, $0 \le \theta _A^{(1)}({D_k}),\sigma _A^{(1)}({D_k}) \le 1$, $\theta _A^{(1)}({D_k})$ shows the degree to which the sample is completely grouped into $D_k$. $\sigma _A^{(1)}({D_k})$ indicates that the sample is not classified to the degree of correct decision $D_k$. Both $\theta _A^{(1)}({D_k})$ and $\sigma _A^{(1)}({D_k})$ mean the classification ability of feature subset in different ways.

If $\theta _A^{(1)}({D_k}) = 1$, $\sigma _A^{(1)}({D_k}) = 0$, then $dec({D_k}) = sha{r_A}({D_k})$; it describes that all samples can be correctly divided into corresponding decision by feature subset A; at this time, feature subset reaches the optimal classification ability. If $\theta _A^{(1)}({D_k}) = 0$, $\sigma _A^{(1)}({D_k}) = 1$, then $sha{r_A}({D_k}) = 0$; it indicates that all samples cannot be classified into correct decision $D_k$ through A; in this case, feature subset A has the weakest classification ability.

Property 3

Assume that $A1 \subseteq A2 \subseteq CA$ with ${D_k} \in U/D$, then

• (1) $\theta _{A1}^{(1)}({D_k}) \le \theta _{A2}^{(1)}({D_k})$.

• (2) $\sigma _{A1}^{(1)}({D_k}) \ge \sigma _{A2}^{(1)}({D_k})$.

Proof

The detailed proof can be found in the supplementary file.

Property 3

explains that the precision and roughness of the sharp decision index are monotonic. As the number of new features increases, higher precision and lower roughness of the sharp decision index will be generated.

Definition 9

Let $A \subseteq CA$, ${D_k} \in U/D$, the sharp decision self-information of $D_k$ is defined as

$$\begin{aligned} I_A^1({D_k}) = - \sigma _A^{(1)}({D_k})\ln \theta _A^{(1)}({D_k}). \end{aligned}$$

(16)

It is obvious to testify that $I_A^1({D_k})$ meets properties (1), (2), and (3) of the definition of self-information. Then, (4) can be confirmed according to Property 4.

Property 4

Let $A1 \subseteq A2 \subseteq CA$ and ${D_k} \in U/D$, then $I_{A1}^1({D_k}) \ge I_{A2}^1({D_k})$.

Proof

The detailed proof can be found in the supplementary file.

Definition 10

Given $INDS = < U,CA,D,\lambda >$, $U/D = \{ {D_1},{D_2},...,{D_t}\}$, $A \subseteq CA$, then the sharp decision self-information of INDS can be defined as

$$\begin{aligned} I_A^1(D) = \sum \limits _{k = 1}^t {I_A^1({D_k})}. \end{aligned}$$

(17)

As we know, self-information was originally used to characterize the instability of signal output. Here, the application of self-information in the incomplete neighborhood decision systems can be used to picture the uncertainty of decision, which it is an effective medium to evaluating decision ability.

$I_A^1(D)$ delivers the classification information of the feature subset about the sharp decision. The smaller $I_A^1(D)$ is, the stronger classification ability of feature subset A is. When $I_A^1(D) = 0$, illustrates that all samples in U can be completely classified into the correct categories according to feature subset A.

However, the feature subset selected by sharp decision only focuses on the information contained in the consistent decision, while ignoring the information contained in the uncertain classification object. In addition, these uncertain informations are essential to decision classification, which cannot be ignored. Therefore, it is vital to analyze the information which contained in the uncertain classification objects. Next, we will define the precision and roughness of blunt decision to discuss the classification ability of feature subset.

Definition 11

Letting $INDS = < U,CA,D,\lambda >$, $U/D = \left\{ {{D_1},{D_2}, \cdots ,{D_t}} \right\}$, then precision and roughness of the blunt decision index are denoted, respectively, as

$$\begin{aligned} \theta _A^{(2)}({D_k})= & {} \frac{{dec({D_k})}}{{blu{n_A}({D_k})}} \end{aligned}$$

(18)

$$\begin{aligned} \sigma _A^{(2)}({D_k})= & {} 1 - \frac{{dec({D_k})}}{{blu{n_A}({D_k})}} = 1 - \theta _A^{(2)}({D_k}). \end{aligned}$$

(19)

Clearly, $0 \le \theta _A^{(2)}({D_k}),\sigma _A^{(2)}({D_k}) \le 1$. $\theta _A^{(2)}({D_k})$ shows the uncertain information contained in $D_k$. $\sigma _A^{(2)}({D_k})$ expresses the degree that the samples cannot be completely classified into the corresponding decision class. When $\theta _A^{(2)}({D_k}) = 1$, $\sigma _A^{(2)}({D_k}) = 0$, then $dec({D_k}) = blu{n_A}({D_k})$. It explains that all possible decisions are correctly divided into the decision $D_k$, and the feature subset has the strongest classification ability. On the contrary, feature subset A has no classification ability.

Property 5 Suppose that $A1 \subseteq A2 \subseteq CA$ and ${D_k} \in U/D$, then

• (1) $\theta _{A1}^{(2)}({D_k}) \le \theta _{A2}^{(2)}({D_k})$.

• (2) $\sigma _{A1}^{(2)}({D_k}) \ge \sigma _{A2}^{(2)}({D_k})$.

Proof

The detailed proof can be found in the supplementary file.

According to Property 5, it explicitly illustrates that the precision and roughness of the blunt decision index are monotonic. When new features are added, the precision of the blunt decision increases with the roughness falls.

Definition 12

Suppose that ${A} \subseteq {CA}$ with $D_k \in U/D$, then blunt decision self-information of $D_k$ can be defined as

$$\begin{aligned} I_A^2({D_k}) = - \sigma _A^{(2)}({D_k})\ln \theta _A^{(2)}({D_k}). \end{aligned}$$

(20)

It is obvious to testify that $I_A^2({D_k})$ meets properties (1), (2), and (3) of the definition of self-information, (4) can be confirmed according to Property 6.

Property 6

Letting $A1 \subseteq A2 \subseteq CA$ and ${D_k} \in U/D$, then $I_{A1}^2({D_k}) \ge I_{A2}^2({D_k})$.

Proof

The detailed proof can be found in the supplementary file.

Definition 13

Assume an incomplete decision system $INDS = < U,CA,D,\lambda >$ with $U/D = \left\{ {{D_1},{D_2}, \cdots , {D_t}} \right\}$, and $A \subseteq CA$, then the blunt decision self-information of INDS is defined as

$$\begin{aligned} I_A^2(D) = \sum \limits _{k = 1}^t {I_A^2({D_k})}. \end{aligned}$$

(21)

Through the above analysis, we can obtain that sharp decision self-information $I_A^1(D)$ relies on samples with consistent decision classification, while blunt decision self-information $I_A^2(D)$ considers samples with inconsistent classification information, but it cannot ensure that all classification information is definitive. Therefore, both $I_A^1(D)$ and $I_A^2(D)$ have insufficient classification capabilities in describing feature subsets, and they are rather one-sided. For this reason, we will propose two other kinds of self-information about classification decision to measure the uncertainty of incomplete neighborhood systems.

Definition 14

Let $A \subseteq CA$ and ${D_k} \in U/D$, the sharp-blunt decision self-information of $D_k$ can be denoted as

$$\begin{aligned} I_A^3({D_k}) = I_A^1({D_k}) + I_A^2({D_k}). \end{aligned}$$

(22)

It is obvious to testify that $I_A^3({D_k})$ meets properties (1), (2), and (3) of the definition of self-information, (4) can be proofed by Property 7.

Property 7

Assume $A1 \subseteq A2 \subseteq CA$ and ${D_k} \in U/D$, then $I_{A1}^3({D_k}) \ge I_{A2}^3({D_k})$.

Proof

The detailed proof can be found in the supplementary file.

Definition 15

Suppose that $INDS = < U,CA,D,\lambda >$, $U/D = \left\{ {{D_1},{D_2}, \cdots ,{D_t}} \right\}$ and , then the sharp-blunt decision self-information of INDS is defined as

$$\begin{aligned} I_A^3(D) = \sum \limits _{k = 1}^t {I_A^3({D_k})} \end{aligned}$$

(23)

Definition 16

Let $A \subseteq CA$ and ${D_k} \in U/D$, the precision and roughness of the lenient decision index are defined as

$$\begin{aligned} \theta _A^{(3)}({D_k})= & {} \frac{{sha{r_A}({D_k})}}{{blu{n_A}({D_k})}} \end{aligned}$$

(24)

$$\begin{aligned} \sigma _A^{(3)}({D_k})= & {} 1 - \frac{{sha{r_A}({D_k})}}{{blu{n_A}({D_k})}} = 1 - \theta _A^{(3)}({D_k}). \end{aligned}$$

(25)

Apparently, $0 \le \theta _A^{(3)}({D_k}),\sigma _A^{(3)}({D_k}) \le 1$. $\theta _A^{(3)}({D_k})$ portrays the proportion of the cardinal number of sharp and blunt decision-making samples. In other words, $\theta _A^{(3)}({D_k})$ characterizes the classification ability of feature subset A according to compare sharp decision index with blunt decision index.

When $\theta _A^{(3)}({D_k}) = 1$, $\sigma _A^{(3)}({D_r}) = 0$. It is the ideal state of the feature subset. At this time, the feature subset A has the strongest classification ability. On the contrary, when $\theta _A^{(3)}({D_r}) = 0$, the feature subset A has no effect on classification and has the weakest classification ability.

Property 8

Let $A1 \subseteq A2 \subseteq CA$ and ${D_k} \in U/D$, then

• (1) $\theta _{A1}^{(3)}({D_k}) \le \theta _{A2}^{(3)}({D_k})$, $\sigma _{A1}^{(3)}({D_k}) \ge \sigma _{A2}^{(3)}({D_k})$.

• (2) $\theta _A^{(3)}({D_k}) = \theta _A^{(1)}({D_k}) \cdot \theta _A^{(2)}({D_k})$.

• (3) $\sigma _A^{(3)}({D_k}) = \sigma _A^{(1)}({D_k}) + \sigma _A^{(2)}({D_k}) - \sigma _A^{(1)}({D_k}) \cdot \sigma _A^{(2)}({D_k})$.

Proof

The detailed proof can be found in the supplementary file.

Definition 17

Assume $A \subseteq CA$ and ${D_k} \in U/D$, the lenient self-information of ${D_k}$ can be defined as

$$\begin{aligned} I_A^4({D_k}) = - \sigma _A^{(3)}({D_k})\ln \theta _A^{(3)}({D_k}). \end{aligned}$$

(26)

It is obvious to testify that $I_A^4({D_k})$ meets properties (1), (2), and (3) of the definition of self-information, and (4) can be confirmed according to Property 9.

Property 9 Letting $A1 \subseteq A2 \subseteq CA$ with ${D_k} \in U/D$, then $I_{A1}^4({D_k}) \ge I_{A2}^4({D_k})$.

Proof

The detailed proof can be found in the supplementary file.

Property 10

$I_A^4({D_k}) \ge I_A^3({D_k})$.

Proof

The detailed proof can be found in the supplementary file.

Definition 18

Suppose an incomplete neighborhood decision system $INDS = < U,CA,D,\lambda >$ with $U/D = \left\{ {{D_1},{D_2}, \cdots ,{D_t}} \right\}$, and $A \subseteq CA$, the lenient self-information of INDS is defined as

$$\begin{aligned} I_A^4(D) = \sum \limits _{k = 1}^t {I_A^4({D_k})}. \end{aligned}$$

(27)

Property 11

Let $A1 \subseteq A2 \subseteq CA$, then $I_{A1}^4(D) \ge I_{A2}^4(D)$.

Proof

The detailed proof can be found in the supplementary file.

Remark 1

Through the above theoretical analysis, we receive that the lenient neighborhood multi-granulation self-information (NMSI) not only considers the upper and lower approximations of decision-making, but also can measure the uncertainty of the incomplete neighborhood decision-making system from a more comprehensive perspective. In addition, NMSI is more sensitive for the change of feature subset, and hence, it is more suitable for feature selection.

Definition 19

[45] Assume an incomplete neighborhood decision system $INDS = < U,CA,D,\lambda >$, $A \subseteq CA$, $A = \{ {A_1},{A_2},...,{A_r}\}$, ${A_i} \subseteq A$, $NT_{{A_i}}^\lambda (x)$ is a neighborhood tolerance class for $x \in U$, the neighborhood tolerance entropy of A is defined as

$$\begin{aligned} NT{E_\lambda }(A) = - \frac{1}{{\left| U \right| }}\sum \limits _{i = 1}^{\left| U \right| } {{{\log }_2}} \frac{{\left| {NT_{{A_i}}^\lambda (x)} \right| }}{{\left| U \right| }}. \end{aligned}$$

(28)

Definition 20

Letting $INDS = < U,CA,D,\lambda >$, $U/D = \left\{ {{D_1},{D_2}, \cdots ,{D_t}} \right\}$, $A = \{ {A_1},{A_2},...,{A_r}\}$, $A \subseteq CA$, $NT_{{A_i}}^\lambda (x)$ is a neighborhood tolerance class. Then, the neighborhood tolerance joint entropy of A and D is defined as

$$\begin{aligned} N\!T\!{E_\lambda }\!(\!A\!\cup \!D\!)\!=\!\!-\!\frac{1}{{\left| U \right| }}\!\sum \limits _{i = 1}^r {\!\!\sum \limits _{k = 1}^t {\frac{{\left| {\!N\!T_{{A_i}}^\lambda (x)\! \!\cap \! {D_k}} \right| }}{{\left| U \right| }}{{\log }_2}} \frac{{\left| {\!N\!T_{{A_i}}^\lambda (x) \!\!\cap \! {D_k}} \right| }}{{\left| U \right| }}}. \end{aligned}$$

(29)

Definition 21

Assume an incomplete neighborhood decision system $I\!N\!D\!S\! = < U,CA,D,\lambda >$, $A = \{ {A_1},{A_2},...,{A_r}\}$, $U/D = \left\{ {{D_1},{D_2}, \cdots ,{D_t}} \right\}$, $NT_{{A_i}}^\lambda (x)$ is a neighborhood tolerance class for $x \in U$, the neighborhood multi-granulation self-information-based pessimistic neighborhood multi-granulation tolerance joint entropy (PTSIJE) of A and D is defined as

$$\begin{aligned} \begin{aligned}&PTSIJE_{_\lambda }^p(A\cup D) = - I_B^4(D)\\&\times \frac{1}{{\left| U \right| }}\sum \limits _{i = 1}^r {\sum \limits _{k = 1}^t {\frac{{\left| {NT_{{A_i}}^\lambda (x) \cap {D_k}} \right| }}{{\left| U \right| }} {{\log }_2}} \frac{{\left| {NT_{{A_i}}^\lambda (x) \cap {D_k}} \right| }}{{\left| U \right| }}}. \end{aligned} \end{aligned}$$

(30)

Here, $I_B^4(D)$ is the lenient NMSI measure of INDS.

Property 12

Letting $INDS = < U,CA,D,\lambda >$, $U/D = \left\{ {{D_1},{D_2}, \cdots ,{D_t}} \right\}$, $A \subseteq CA$, $A = \{ {A_1},{A_2},...,{A_r}\}$, $NT_{{A_i}}^\lambda (x)$ is a neighborhood tolerance class for $x \in U$, then

$$\begin{aligned} PTSIJE_{_\lambda }^p(A\cup D)\mathrm{{ }} = I_A^4(D) \times NT{E_\lambda }(A\cup D) \ge 0. \end{aligned}$$

Remark 2

From Definition 20 and Property 12, we can vividly realize that $I_A^4(D)$ represents the lenient NMSI measure in algebraic view, and $NT{E_\lambda }(A\cup D)$ is the neighborhood tolerance joint entropy of A and D in information view. Therefore, PTSIJE can measure the uncertainty of incomplete neighborhood decision systems from both algebraic and information views based on self-information measures and entropy.

Fig. 1

Process flow of the feature selection method for data classification

PTSIJE-based feature selection method in incomplete neighborhood decision systems

Feature selection based on PTSIJE

Definition 22

Letting $INDS = < U,CA,D,\lambda >$, $A = \{ {A_1},{A_2},...,{A_r}\}$, $A' \subseteq A \subseteq CA$, then $A'$ is the reduction of A and D if:

• (1) $PTSIJE_\lambda ^p(A',D) = PTSIJE_\lambda ^p(CA,D)$.

• (2) For any ${A_i}\! \subseteq \!A'$, $PTSIJE_\lambda ^p(A',D)\!<PTSIJE_{_\lambda }\!^p(A' - \!{A_i},\!D)$.

Here, the formula (1) illustrates that the reduced subset and the entire dataset have the same classification ability, and the formula (2) guarantees that the reduced subset has no redundant attributes.

Definition 23

Let $INDS = < U,CA,D,\lambda >$, $A = \{ {A_1},{A_2},...,{A_r}\}$, $A' \subseteq A \subseteq CA$, for any ${A_i} \subseteq A'$, $i = 1,2,...,r$, the attribute significance of attribute subset $A'$ with respect to D in granularity set ${A_i}$ is defined as

$$\begin{aligned} \!S\!I\!G(\!{A_i},\!A',\!D) = PTSIJE_{_\lambda }^p(A' - {A_i},\!D)-PTSIJE_{_\lambda }^p(\!A',\!D)\! \end{aligned}$$

(31)

Feature selection algorithm

To show the feature selection method more clearly, the process of data classification for feature selection is expressed in Fig. 1, and the algorithm description is shown in Algorithm 1.

For the PTSIJE-FS algorithm, it mainly involves two aspects: getting neighborhood tolerance classes and counting PTSIJE. The calculation of neighborhood tolerance class has a great impact on the time complexity. To reduce the computational complexity of the neighborhood tolerance classes, the bucket sorting algorithm [37] is used here, and the time of complexity of neighborhood tolerance classes is cut back to O(mn). Here, m is the number of samples and n is the number of features. Meanwhile, the computational time complexity of the PTSIJE is O(n) . The PTSIJE-FS algorithm is a loop in steps 8-14. In the worst case, its time complexity is $O({n^3}m)$. Assuming that the number of selected granularities is ${n_R}$, since only candidate granularities need to be considered but not all granularities, the time complexity of calculating the neighborhood tolerance classes is $O({n_R}m)$. In most cases ${n_R} \ll n$, so the time complexity of PTSIJE-FS is about O(mn).

Experimental results and analysis

Experiment preparation

To demonstrate the effectiveness and robustness of our proposed feature selection method, we conducted experiments on 11 public datasets, including 6 UCI datasets and 5 high-dimensional microarray gene expression data- sets. The datasets used are listed in Table 1. Among them, six UCI datasets can be downloaded from http://archive.ics.uci.edu/ml/datasets.php, and five gene expression datasets can be downloaded from http://portals.broadinstitute.org/cgi-bin/cancer/datasets.cgi. It should be noted here that the Wine, Wdbc, Sonar, Heart datasets and five gene expression datasets are usually complete. Therefore, to convenience, we randomly modify some known feature values to missing values to achieve incomplete neighborhood decision systems.

Table 2 lists all datasets.

Table 2 Eleven datasets in experiments

All simulation experiments are running on MATLAB 2016a, under Window10 operating system with an Intel(R) i5 CPU at 3.20 GH and 4.0 GB RAM. The classification accuracy is verified by three classifiers KNN, CART, and C4.5 whose default values of all parameters are selected under Weka 3.8 software. To ensure the consistency of experiments, we use the tenfold cross-validation method in all our experiments.

Effect of different neighborhood parameters

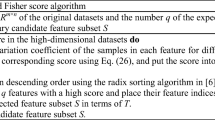
This subsection will focus on the analysis of the impact of different neighborhood parameters $\lambda$ on the classification performance of our method, and find the best parameters for each dataset. For five high-dimensional gene expression datasets (hereinafter referred to as gene datasets), to effectively reduce the time cost, we use Fisher score (FS) [45] for preliminary dimensionality reduction. There are some advances of FS: less calculation, strong operability, and can effectively reduce the computational complexity. Figure 2 illustrates the variation trend of the accuracy of the number of selected genes under the classifier KNN in different dimensions (10, 50, 100, 200, 300, 400, 500) on the five gene datasets.

Fig. 2

Classification accuracy via the size of gene subsets on five gene datasets

As shown in Fig. 2, the accuracy in most cases changes with the size of the gene subset. The optimal balance between the size and accuracy of the selected feature gene subset is found to obtain the appropriate dimension of each gene subset for the next feature selection. Therefore, the values of two datasets DLBCL and Lung are set as 100 dimensions, the 200 dimensions are favorable for datasets Leukemia and MLL, and the 400 dimensions are appropriate for dataset Prostate.

The classification accuracy of selected feature subsets using PTSIJE-FS on 11 datasets is obtained with different neighborhood parameters. For six UCI datasets, the classification performance is evaluated under two classifiers KNN (k=10) and CART, which is displayed in Fig. 3a–f, and the classification performance for five gene datasets under three classifiers KNN (k=10), CART, and C4.5 is illustrated in Fig. 3g–k. The classification accuracy under different parameters $\lambda$ is shown in Fig. 3, where the abscissa represents different neighborhood parameters $\lambda \in [0.05,1]$, and the ordinate is the classification accuracy.

Fig. 3

Classification accuracy for 11 datasets with different neighborhood parameter values

Table 3 The number of selected features with the seven methods on the six UCI datasets

Table 4 Optimal feature subset with PTSIJE-FS for six UCI datasets

Figure 3 reveals that the neighborhood parameters increase from 0.05 to 1, and the classification accuracy of features selected by PTSIJE-FS is changing. Different parameters have a certain impact on the classification performance of PTSIJE-FS. Fortunately, every dataset can reach the high result in the wider range of $\lambda$. Figure 3a displays that for Credit dataset, the neighborhood parameter will be 0.4 under KNN and 0.1 under CART. From Fig. 3b, for Heart dataset, the neighborhood parameter set 1.0 under classifier KNN and 0.75 under classifier CART, the classification accuracy achieves maximum. In Fig. 3c, for Sonar dataset, the classification performance is at best level when neighborhood parameters are 0.5 and 0.6 under classifiers KNN and CART, respectively. As shown in Fig. 3d, when the neighborhood parameter is set to 0.15 under classifiers KNN and CART, the classification performance is optimal. It can be seen from Fig. 3e that for the Wine dataset, the classification performance is best when the neighborhood parameter is set to 0.8 under the classifier KNN, and the neighborhood parameter is set to 0.2 under the classifier CART. From Fig. 3f that on the Wpbc dataset, when the neighborhood parameters are set to 0.15 and 0.3, the classification performance of the selected feature subset under the classifiers KNN and CART reaches the high level at the same time. Figure 3g shows the accuracy of DLBCL dataset and the neighborhood parameters will be set 0.45, 1.0, and 0.4 under three classifiers KNN, CART, and C4.5, respectively. In Fig. 3h, for the gene dataset Leukemia, when the neighborhood parameter is set to 0.35 under KNN, 0.05 under CART, and 0.45 under C4.5, the gene subset with the best classification performance can be obtained. As shown in Fig. 3i, when the neighborhood parameter under KNN is set to 0.8, CART is set to 0.05, and C4.5 is set to 0.7, the classification performance of the gene subset selected from Lung dataset achieves the best level. Figure 3j demonstrates that the optimal neighborhood parameter values should be set to 0.4 under KNN, and set to 0.65 under classifiers CART and C4.5 for MLL. Similarly, for the Prostate dataset, the parameter values are 0.75, 0.8, and 0.3 under classifiers KNN, CART, and C4.5, respectively.

Classification results of the UCI datasets

In this subsection, to illustrate the classification performance of the method PTSIJE-FS on the low-dimensional UCI datasets, the PTSIJE-FS is compared with six existing feature selection methods: (1) the neighborhood tolerance dependency joint entropy-based feature selection method (FSNTDJE) [45], (2) the discernibility matrix-based reduction algorithm (DMRA) [27], (3) the fuzzy positive region-based accelerator algorithm (FPRA) [61], (4) the fuzzy boundary region-based feature selection algorithm (FRFS) [62], (5) the intuitionistic fuzzy granule-based attribute selection algorithm (IFGAS) [63], and (6) the pessimistic neighborhood multi-granulation dependency joint entropy (PDJE-AR) [60].

The first part of this subsection focuses on the size of feature subsets selected by all comparative feature selection methods. Using neighborhood parameters $\lambda$, the tenfold cross-validation method is used on six UCI datasets. The original data and average size of the selected feature subset by the above seven feature selection methods are shown in Table 3. Under two classifiers KNN and CART, PTSIJE-FS selects the optimal feature subset for six UCI datasets as displayed in Table 4 where “original” represents the original dataset.

Table 3 shows the average number of the selected feature subset by seven feature selection methods. Compared with method IFGAS, PTSIJE-FS selects more features for datasets Heart and Sonar. The average size of the selected feature subsets by PTSIJE-FS is 7.2, 5.5, and 5.0, respectively, and reaches the minimum on datasets Credit, Wine, and Wpbc. In a word, the mean number of the selected feature subset by PTSIJE-FS is the minimum compare with six related methods for six UCI datasets.

The second part in this subsection is to exhibit the classification effectiveness for PTSIJE-FS. There are six feature selection methods, including FSNTDJE, DMRA, FPRA, FRFS, IFGAS, and PDJE-AR, are used to prove the accuracy on the selected feature subsets under two classifiers KNN and CART for six UCI datasets. Tables 5 and 6, respectively, list the average classification accuracy using the seven methods of selected feature subsets under two classifiers KNN and CART. In Tables 3, 7, the bold font shows that the size of the reduced datasets is least with respect to other methods. In Tables 5, 6, 9, 10, the bold numbers indicate that the classification accuracy of the selected feature subsets is the highest with respect to other methods.

Table 5 Classification accuracy of the seven methods under the KNN classifier

Table 6 Classification accuracy of the seven methods under the CART classifier

Combined with Tables 3 and 5, we can clearly see the differences between the seven methods. For almost all UCI datasets, the classification accuracy of the selected feature subsets by PTSIJE-FS apparently outperforms the other six methods under the KNN classifier. In addition, PTSIJE-FS not only selects the fewer features, but also has the highest classification accuracy on datasets Credit, Wine, and Wpbc. In brief, the PTSIJE-FS method deletes redundant features to the greatest extent and still shows better classification performance than six compared methods on UCI datasets.

Similarly, from Tables 3 and 6, the differences among seven feature selection methods are illustrated under the classifier CART. The average accuracy of PTSIJE-FS is larger than other six comparison methods on the datasets Heart, Sonar, Wine, and Wpbc, which are 82.22%, 75.96%, 91.57%, and 76.26%, respectively. Although the average accuracy of the feature subset selected by PTSIJE-FS on the dataset Credit is 0.95% lower than that of the feature subset selected by DMRA, PTSIJE-FS selects the fewer features for the dataset Credit.

In terms of time complexity, the time complexity of DMRA and IFGAS is $O(m^{2}n)$ [27, 63], the time complexity of FPRA is O(mlogn) [61], the time complexity of FRFS is $O(n^{2})$ [62], and the time complexity of PDJE-AR and FSNTDJE is O(mn) [45, 60]. Therefore, the rough ranking of the seven methods on times complexity is as follows: $O(FRFS)<O(FPRA)<O(PDJE-AR)=O(FSNTDJE)=O(PTSIJE-FS)<O(DMRA)=O(IFGAS)$.

Under different classifiers and learning tasks, no one method always performs better than other methods. PTSIJE-FS shows superior classification performance and stability under the classifiers KNN and CART.

In summary, PTSIJE-FS can eliminate redundant features as a whole, and shows outstanding classification performance on UCI datasets.

Classification results of the gene expression datasets

This subsection illustrates the classification performance of the method PTSIJE-FS on high-dimensional gene expression datasets. PTSIJE-FS is compared with six existing feature selection methods: (1) the neighborhood tolerance dependency joint entropy-based feature selection method (FSNTDJE) [45], (2) the mutual information-based attribute reduction algorithm for knowledge reduction (MIBARK) [64], (3) the decision neighborhood entropy-based heuristic attribute reduction algorithm (DNEAR) [21], (4) the entropy gain-based gene selection algorithm (EGGS) [65], (5) EGGS [65] algorithm combined with Fisher Score (EGGS-FS) [66], and (6) the pessimistic neighborhood multi-granulation dependency joint entropy (PDJE-AR) [60].

The performance of seven feature selection methods is verified on the gene datasets DLBCL, Leukemia, Lung, MLL, and Prostate under tenfold cross-validation. Table 7 lists the average size of gene subsets selected by each feature selection method, where “Original” represents the original dataset and “-” denotes that we have not obtained the result of this method. Under the three classifiers KNN, CART, and C4.5, The optimal gene subsets selected by PTSIJE-FS method for five gene datasets under three classifiers KNN, CART, and C4.5 are demonstrated in Table 8 .

Table 7 Optimal gene subset with PSINTE-FS for five gene datasets

Table 8 Optimal feature subset with PTSIJE-FS for five gene datasets

Table 7 reveals the average size of gene subsets selected by seven feature selection methods. PTSIJE-FS do select more genes for five gene datasets, and the average size of the gene subset selected by PTSIJE-FS is smaller than EGGS.

In the next part, according to the results of Tables 7 and 8 , PTSIJE-FS and related six feature selection methods are used to verify the average classification accuracy of gene subsets under the two classifiers KNN and C4.5, and the results are exhibited in Tables 9 and 10 .

Table 9 Classification accuracy of the seven methods under the KNN classifier

Table 10 Classification accuracy of the seven methods under the C4.5 classifier

From Tables 9 and 10, PTSIJE-FS displays the highest classification accuracy, expect for dataset Prostate under the C4.5 classifier. Especially on the datasets leukemia and MLL, the average classification accuracy of the gene subset selected by PTSIJE-FS is significantly higher than the other six feature selection methods under classifier KNN, and the average accuracy is increased by about 8%-42% and 10%-32%, respectively. As we have seen, the gene subsets selected by PTSIJE-FS show better classification performance on the gene datasets DLBCL, Leukemia, Lung, and MLL under classifier C4.5. There are 4%-39% gaps which obviously exist between PTSIJE-FS and FSNTDJE, MIKARK, DNEAR, EGGS, and EGGS-FS, only lower 0.76% than PDJE-AR. In general, under the classifiers KNN and C4.5, the mean classification accuracy of PTSIJE-FS is higher than the other six feature selection methods, and reach the highest level for five gene datasets.

In terms of time complexity, the time complexity of FSNTDJE, DNEAR, and PDJE-AR is O(mn) [21, 45, 60], the time complexity of MIBARK is $O(m^{2})$ [64], and the time complexity of EGG and EGG-FS is $O(m^{3}n)$ [65]. Therefore, the rough ranking of the seven methods on times complexity is as follows: $O(MIBARK)<O(PDJE-AR)=O(DENAR)=O(FSNTDJE)=O(PTSIJE-FS)<O(EGG)=O(EGG-FS)$.

In summary, PTSIJE-FS can eliminate redundant features as a whole on five gene datasets, and shows better classification performance against the six related methods.

Statistical analysis

To systematically compare the statistical performance of classification accuracy of all methods, Friedman test and corresponding post-test will be employed in this subsection. The Friedman statistic [67] is expressed as

$$\begin{aligned} {\chi ^2}= & {} \frac{{12n}}{{k(k + 1)}}\sum \limits _{i = 1}^k {r_i^2} - \frac{{k{{(k + 1)}^2}}}{4} \end{aligned}$$

(32)

$$\begin{aligned} F= & {} \frac{{(n - 1){\chi ^2}}}{{n(k - 1) - {\chi ^2}}}. \end{aligned}$$

(33)

Here, $r_i$ is the mean rank, and n and k represent the number of datasets and methods, respectively. F obeys the distribution with $\left( {k - 1} \right)$ and $\left( {k - 1} \right) \left( {n - 1} \right)$ degrees of freedom. For the six low-dimensional UCI datasets in Tables 5 and 6, PTSIJE-FS, FSNTDJE, DMRA, FPRA, FRFS, IFGAS, and PDJE-AR are employed to conduct the Friedman statistic. According to the classification accuracy obtained in Tables 5 and 6, the rankings of the seven feature selection methods under the classifiers KNN and CART are shown in Tables 11 and 12.

Table 11 Rank of the seven methods with KNN

Table 12 Rank of the seven methods with CART

Table 13 Rank of the seven methods with KNN

Table 14 Rank of the seven methods with C4.5

Calling icdf calculation in MATLAB 2016a, when $\alpha \mathrm{{ = }}0.1$, F(6,30)=1.9803. Assuming that these seven methods are equivalent in classification performance, then the value of Friedman statistics will not exceed the critical value F(6,30). Otherwise, it is said that these seven methods have significant differences in feature selection performance. According to Friedman statistics, F=7.4605 for the classifier KNN and F=5.3738 for the classifier CART. Obviously, the F values under the classifiers KNN and CART are far greater than the critical value F(6,30), indicating that these seven methods are significantly different under the classifiers KNN and CART on six UCI datasets.

Subsequently, we need to perform post-testing on the differences between the seven methods. The post-hoc test used here is the Nemenyi test [68]. The statistics needs to determine the critical value of the mean distance between rankings, which is defined as

$$\begin{aligned} C{D_\alpha } = {q_a}\sqrt{\frac{{k\left( {k + 1} \right) }}{{6n}}}, \end{aligned}$$

(34)

where $q_a$ means a critical value. It is can be obtained that $q_0.1$ =2.693 when the methods number is 7 and $\alpha = 0.1$. Then, from formula (33), we can know that ${CD_{0.1}}$=3.3588(k=7, n=6). According to Table 10, the distance between mean rankings of PTSIJE-FS to FSNTDJE, DMRA, FRFS, and IGFAS are 4.25, 4.25, 3.75, and 3.92, respectively, which are greater than 3.3588 for classifier KNN. In this case, Nemenyi test reveals that PSITE-FS is far superior to FSNTDJE, DMRA, FRFS, and IGFAS under the classifier KNN at $\alpha = 0.1$. In the same way, from Table 11, the distances between mean rankings of PTSIJE-FS to FSNTDJE, FPRA, FRFS, and FSNTDJE are 4.17, 3.84, and 3.84, respectively, indicating that PSINTE-FS is significantly better than FSNTDJE, FPRA, and FRFS.

In the second part of this subsection, Friedman test is performed on the classification accuracy of the seven feature selection methods in Tables 9 and 10 under the classifiers KNN and C4.5. Tables 13 and 14, respectively, list the mean rankings of the seven methods under the classifiers KNN and C4.5.

After calculation, when $\alpha = 0.1$, the critical value F(6, 24)=2.0351, F=8.2908 for the classifier KNN and F=3.4692 for the classifier C4.5. It is clear that above two values are both greater than the critical value F(6,24). It explains that these seven methods have significant differences on the classifiers KNN and C4.5 on the five gene datasets.

Next, Nemenyi test is performed on the classification accuracy of the seven feature selection methods in Tables 9 and 10 under the classifiers KNN and C4.5. It can be computed that $C{D_{0.1}}$=3.6793(k=7, n=5) when the number of methods is 7, and $q_{0.1}$=2.693. The distances between mean rankings of PTSIJE-FS to IBARK, DNEAR, EGGS under the classifier KNN are 4, 5.75, 4.25. This result demonstrates PTSIJE-FS is apparently better than IBARK, DNEAR, EGGS. The distance between mean rankings of PTSIJE-FS to DNEAR is 5.55 greater than the critical value, showing that PTSIJE-FS is far better than DNEAR under the classifier C4.5.

In a word, the PTSIJE-FS method is superior than the other corresponding methods through the Friedman statistic test.

Conclusion

NMRS model is an effectively tool to improve the classification performance in incomplete neighborhood decision systems. However, most feature evaluation functions based on NMRS only consider the information contained in the lower approximation. Such a construction method is likely to lead to the loss of some information. In fact, the upper approximation also contains some classification information that cannot be ignored. To solve this problem, we propose a feature selection model based on PTSIJE. First, from the algebra view, using the upper and lower approximations in NMRS and combining the concept of self-information, four types of neighborhood multi-granulation self-information measures are defined, and related properties are discussed in detail. The proof proves that the fourth neighborhood multi-granulation self-information measure is more sensitive and helps to select the optimal feature subset. Second, from the information views, the neighborhood tolerance joint entropy is given to analyze the redundancy and noise in the incomplete decision systems. Then, inspiring by both algebra and information view, combined with self-information measure and information entropy, a PTSIJE model is proposed to analyze the uncertainty of incomplete neighborhood decision systems. Finally, a heuristic forward feature selection method is designed and compared with other relevant methods. The experimental results show that our proposed method can select fewer features and have higher classification accuracy than related methods. In the future, we will not only focus on more efficient search strategies based on NMRS and self-information measures to achieve the best balance between classification accuracy and feature subset size, but also on constructing more general feature selection methods.