Introduction

Extreme learning machine (ELM) [1] is the latest research result of single-hidden layer feedforward networks (SLFNs) and attracts much attention in pattern recognition and machine learning fields. The unique principle of the ELM is that the input weights and biases of hidden layer are randomly chosen without fine-tuning, and the output weights are the global optimal solution determined by the least square method, avoiding the dilemma of local optimum. The ELM is proven to have the universal approximation capability [2] and is adequate for regression and classification tasks [3]. And to overcome the problems of online learning, unbalanced learning, and structural redundancy, many methods of improvement have been introduced into the ELM [4,5,6,7,8]. By virtue of strong generalization ability and fast training, the ELM has been successfully applied for speech emotion recognition [9, 10], power load forecasting [11, 12], and medical diagnoses [13, 14].

As a focus of research in recent years, deep learning [15] attaches importance to the hierarchical abstract representation learning and realizes the approximation of complex function. However, deep learning is confronted with the expensive computational cost [16]. To deal with this, Kasun et al. [17] proposed the extreme learning machine autoencoder (ELM-AE) and stacked the ELM-AE to create a multilayer extreme learning machine (ML-ELM). The ELM-AE is the combination of the ELM and the autoencoder (AE), and is utilized to extract abstract feature of samples for the final mapping from feature to targets. Different from traditional deep learning algorithm, the network parameters of the ML-ELM do not need fine-tuning, which greatly reduces training time. Having both excellent generalization performance of deep learning and high training efficiency of the ELM, the ML-ELM is gradually applied in many fields, such as text classification [18], activity recognition [19], and dynamics identification [20].

To enhance the performance of the ML-ELM, many methods of improvement have been introduced into the ML-ELM. Based on the denoising autoencoder (DAE), Zhang et al. [21] proposed the extreme learning machine denoising autoencoder (ELM-DAE) by introducing denoising criterion into the ELM-AE, and developed the denoising multilayer extreme learning machine (D-ML-ELM). To avoid the uncertain influence caused by the number of hidden nodes, Wong et al. [22] combined the kernel learning with the ML-ELM and proposed the multilayer kernel extreme learning machine (ML-KELM) to improve the performance of the ML-ELM. Sun et al. [23] proposed the generalized extreme learning machine autoencoder (GELM-AE) by integrating the manifold regularization into the ELM-AE, and built a deep network called multilayer generalized extreme learning machine (ML-GELM). To improve the sparsity and robustness of the ML-ELM, Li et al. [24] replaced the mean square error with L21-norm loss, and proposed the hierarchical extreme learning machine with L21‑norm loss and regularization (H-LR21-ELM). In addition, many methods [25,26,27] are studied for the development and application of the ML-ELM.

However, the unsupervised learning of the ELM-AE may not be suitable for building the discriminative feature space given the label information and lead to the performance limitation of the ML-ELM for classification tasks. Thus, in the hierarchical feature extraction, it is necessary for the ML-ELM to use the class labels to learn a discriminative feature space. The Fisher criterion is the basis of Fisher discriminant analysis (FDA) and aims to extract discriminative abstract feature by maximizing the between-class distance and minimizing the within-class distance [28]. Based on the fact, the Fisher extreme learning machine autoencoder (FELM-AE) is proposed in this study and used as the basic component for the multilayer Fisher extreme learning machine (ML-FELM). The FELM-AE introduces the Fisher criterion into the ELM-AE and adds the Fisher regularization term about output weights to objective function to enforces the samples of different classes to be far in feature space. The ML-FELM stacked the FELM-AE layer-by-layer to extract abstract feature, and then utilized the ELM to map feature to labels. According to our best knowledge, this study is the first to combine the ELM-AE with the Fisher criterion to extract discriminative feature. Compared with the ELM-AE, the label information contained in the Fisher criterion guides the FELM-AE to learn discriminative feature, and it effectively improves the classification performance of the ML-FELM.

The contributions of this study are summarized as follows:

  1. 1.

    A new regularized ELM-AE named the FELM-AE is proposed for representation learning. By combining the Fisher criterion with the ELM-AE, the Fisher regularization term added to objective function makes the abstract feature learned by the FELM-AE can increase the distance between classes and reduce the distance within a class.

  2. 2.

    A novel ML-ELM called the ML-FELM is proposed for classification tasks. Resembling the ML-ELM, the ML-FELM uses the FELM-AE and ELM for feature extraction and classification, respectively.

  3. 3.

    Comprehensive experiments are conducted to evaluate the performance of the proposed methods. Visualization and classification experiments on various benchmark datasets demonstrate that the feature extracted by the FELM-AE is discriminative and the ML-FELM outperforms the other state-of-the-art ML-ELM.

The rest of this paper is organized as follows. In section “Related works”, a brief review of ELM and ELM-AE is introduced. In section “Multilayer Fisher extreme learning machine”, the details of the proposed FELM-AE and ML-FELM are described. In section “Experiments”, experimental implementation and results over benchmark datasets are reported. In section “Conclusion”, the conclusion of this paper is summarized.

Related works

Extreme learning machine

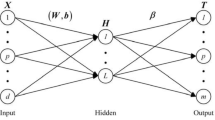
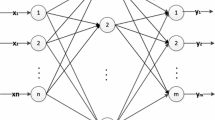
ELM is an efficient single-hidden layer feedforward neural network, and its network structure is shown in Fig. 1.

Fig. 1
figure 1

Network structure of the ELM

Full size image

Given training samples \(\left\{ {{\varvec{X}},{\varvec{T}}} \right\} = \left\{ {({\varvec{x}}_{j} ,{\varvec{t}}_{j} )} \right\}_{j = 1}^{N}\), the output of the ELM is formulated as follows:

$$ f\left( {{\varvec{x}}_{j} } \right) = \sum\limits_{i = 1}^{L} {{\varvec{\beta}}_{i} g\left( {{\varvec{w}}_{i} ,b_{i} ,{\varvec{x}}_{j} } \right)} ,j = 1, \ldots ,N, $$
(1)

where \({\varvec{x}}_{j} = \left[ {x_{j1} ,x_{j2} , \ldots ,x_{jd} } \right] \in {\varvec{R}}^{d}\) and \({\varvec{t}}_{j} = \left[ {t_{j1} ,t_{j2} , \ldots ,t_{jm} } \right] \in {\varvec{R}}^{m}\) are the input and target of the \(j{\text{th}}\) training sample, \(d\) and \(m\) are the dimension of input and target, respectively. \({\varvec{w}}_{i}\) is the input weights of \(i{\text{th}}\) hidden node, and \(b_{i}\) is the bias. \({\varvec{w}}_{i}\) and \(b_{i}\) are both randomly assigned. \(g\left( \cdot \right)\) is the activation function and \({\varvec{\beta}}_{i} = \left[ {\beta_{i1} ,\beta_{i2} , \ldots ,\beta_{im} } \right]^{T}\) is the output weights of \(i{\text{th}}\) hidden node.

Due to the universal approximation capability, the ELM can fit the given samples with zero error. Therefore, the matrix form of the above Eq. (1) can be written as follows:

$$ \user2{H\beta } = \user2{T,} $$
(2)

where \({\varvec{H}}\) is the output matrix of hidden layer; \({\varvec{\beta}}\) is the output weights matrix

$$ {\varvec{H}} = \left[ \begin{gathered} g\left( {{\varvec{w}}_{1} ,b_{1} ,{\varvec{x}}_{1} } \right)\quad \cdots \quad g\left( {{\varvec{w}}_{L} ,b_{L} ,{\varvec{x}}_{1} } \right) \hfill \\ \quad \quad \; \vdots \quad \quad \;\quad \cdots \quad \quad \;\quad \vdots \hfill \\ g\left( {{\varvec{w}}_{1} ,b_{1} ,{\varvec{x}}_{N} } \right){\kern 1pt} \;\,{\kern 1pt} \cdots \quad g\left( {{\varvec{w}}_{L} ,b_{L} ,{\varvec{x}}_{N} } \right) \hfill \\ \end{gathered} \right]_{N \times L} $$
(3)
$$ \user2{\beta} = \left[ \begin{gathered} {\varvec{\beta}}_{1}^{T} \hfill \\ {\varvec{\beta}}_{2}^{T} \hfill \\ \;\, \vdots \hfill \\ {\varvec{\beta}}_{L}^{T} \hfill \\ \end{gathered} \right]_{L \times m} ,\user2{T} = \left[ \begin{gathered} {\varvec{t}}_{1}^{T} \hfill \\ {\varvec{t}}_{2}^{T} \hfill \\ \;\, \vdots \hfill \\ {\varvec{t}}_{N}^{T} \hfill \\ \end{gathered} \right]_{N \times m} . $$
(4)

To improve its generalization ability, the ELM aims to find the optimal \({\varvec{\beta}}\) to minimize the following formula:

$$ \min L_{{\rm {ELM}}} = \frac{1}{2}\left\| {\varvec{\beta}} \right\|^{2} + \frac{C}{2}\left\| {{\varvec{T}} - \user2{H\beta }} \right\|^{2}, $$
(5)

where \(C\) is the regularization parameter to control the balance of empirical and structural risk. By setting the gradient of \(L_{{\rm {ELM}}}\) with respect to \({\varvec{\beta}}\) to zero, the closed-form solution of \({\varvec{\beta}}\) can be obtained as follows:

$$ \user2{\beta = }\left\{ \begin{gathered} \left( {\frac{{\varvec{I}}}{C} + {\varvec{H}}^{T} {\varvec{H}}} \right)^{ - 1} {\varvec{H}}^{T} {\varvec{T}},\quad N \ge L \hfill \\ {\varvec{H}}^{T} \left( {\frac{{\varvec{I}}}{C} + {\varvec{HH}}^{T} } \right)^{ - 1} {\varvec{T}},\quad N < L \hfill \\ \end{gathered} \right., $$
(6)

where \({\varvec{I}}\) is the identity matrix.

Extreme learning machine autoencoder

As a special ELM, the ELM-AE is an unsupervised learning algorithm and its input is also used as output. The ELM-AE consists of an encoder and a decoder. The encoder realizes the encoding of samples and extracts a random feature representation of the input samples. The decoder realizes the decoding of abstract feature and learns the mapping from abstract feature to reconstructed samples. Compared with the traditional AE, the ELM-AE accomplishes fast extraction of abstract feature by applying ELM to AE, and avoids iterative fine-tuning of network parameters.

The network structure of the ELM-AE is shown in Fig. 2.

Fig. 2
figure 2

Network structure of the ELM-AE

Full size image

Assume that the number of nodes in each layer of the ELM-AE is \(d\), \(L\) and \(d\). For the training sample \({\varvec{X}} = \left\{ {{\varvec{x}}_{i} \in {\varvec{R}}^{d} } \right\}_{i = 1}^{N}\), the output of hidden layer \({\varvec{H}}\) can be calculated as Eq. (7), and the relationship between \({\varvec{H}}\) and the output \({\varvec{X}}\) is shown in Eq. (8)

$$ {\varvec{H}} = g\left( {{\varvec{WX}} + {\varvec{b}}} \right) $$
(7)
$$ \user2{H\beta } = {\varvec{X}}\user2{.} $$
(8)

It should be noted that the input weights \({\varvec{W}}\) and biases \({\varvec{b}}\) randomly generated by the ELM-AE need to be orthogonal, that is

$$ {\varvec{WW}}^{T} = \user2{I,bb}^{T} = {\varvec{I}}\user2{.} $$
(9)

According to the number of nodes in input and hidden layer, the ELM-AE represents the input samples in different representation: (1) \(d > L\), compressed representation; (2) \(d = L\), equal dimension representation; (3) \(d < L\), sparse representation.

The output weights \({\varvec{\beta}}\) of the ELM-AE is calculated as

$$ \user2{\beta = }\left\{ \begin{gathered} \left( {\frac{{\varvec{I}}}{C} + {\varvec{H}}^{T} {\varvec{H}}} \right)^{ - 1} {\varvec{H}}^{T} {\varvec{X}},\quad N \ge L \hfill \\ {\varvec{H}}^{T} \left( {\frac{{\varvec{I}}}{C} + {\varvec{HH}}^{T} } \right)^{ - 1} {\varvec{X}},\quad N < L \hfill \\ \end{gathered} \right.. $$
(10)

Once \({\varvec{\beta}}\) is got, the ELM-AE then obtains the final abstract representation of the samples by Eq. (11)

$$ {\varvec{H}}_{New} = \user2{X\beta }^{T} . $$
(11)

Multilayer Fisher extreme learning machine

Fisher extreme learning machine autoencoder

The unsupervised learning of the ELM-AE can learn the intrinsic structure of samples for feature extraction. However, for classification tasks, the ELM-AE fails to make full use of the complete sample labels to guide the feature extraction and enrich the category information contained in the feature. To address this problem, the Fisher criterion is integrated into the ELM-AE, and a new regularized ELM-AE called the FELM-AE is proposed. The Fisher criterion aims to maximize the between-class distance and minimize the within-class distance of feature. Based on the Fisher criterion, class labels are utilized in the training of the FELM-AE, so that the abstract feature learned by the FELM-AE can enhance the class separability of samples in the feature space and improve the performance of classifiers. Compared to the ELM-AE, the major innovation of the FELM-AE is the Fisher regularization about output weights to find a discriminative feature space.

The network structure of the FELM-AE is similar to that of the ELM-AE, as shown in Fig. 2. According to the Fisher criterion, the between-class distance is quantified by the between-class scatter matrix to measure the dispersion of different classes of samples, and the within-class distance is quantified by the within-class scatter matrix to measure the dispersion of a specific class of samples. In the FELM-AE, assume that the output of hidden nodes is \(\left\{ {{\varvec{h}}_{j}^{(i)} ,i = 1, \ldots ,c,j = 1, \ldots ,n_{i} } \right\}\) and that \(S_{b}\) and \(S_{w}\) denote the between-class scatter matrix and within-class scatter matrix, respectively. \(S_{b}\) and \(S_{w}\) are formulated as follows:

$$ S_{b} { = }\sum\limits_{i = 1}^{c} {n_{i} \left( {\overline{\user2{h}}^{(i)} - \overline{\user2{h}}} \right)} \left( {\overline{\user2{h}}^{(i)} - \overline{\user2{h}}} \right)^{T} $$
(12)
$$ S_{w} { = }\sum\limits_{i = 1}^{c} {\sum\limits_{j = 1}^{{n_{i} }} {\left( {{\varvec{h}}_{j}^{(i)} - \overline{\user2{h}}^{(i)} } \right)} \left( {{\varvec{h}}_{j}^{(i)} - \overline{\user2{h}}^{(i)} } \right)^{T} } , $$
(13)

where \(\overline{\user2{h}}^{(i)}\) is the mean output vector of hidden nodes of the \(i{\text{th}}\) class and \(\overline{\user2{h}}\) is the mean output vector of all hidden nodes. \(\overline{\user2{h}}^{(i)}\) and \(\overline{\user2{h}}\) are calculated as Eqs. (14) and (15), respectively

$$ \overline{\user2{h}}^{(i)} = \frac{1}{{n_{i} }}\sum\limits_{j = 1}^{{n_{i} }} {{\varvec{h}}_{j}^{(i)} } $$
(14)
$$ \overline{\user2{h}} = \frac{1}{N}\sum\limits_{i = 1}^{c} {\sum\limits_{j = 1}^{{n_{i} }} {{\varvec{h}}_{j}^{(i)} } } . $$
(15)

Using these distance criteria, the FELM-AE introduces the Fisher regularization matrix \({\varvec{S}}\) to control the different distance criterion, which is calculated as

$$ {\varvec{S}} = \frac{{S_{w} }}{{{\varvec{D}}S_{b} }}, $$
(16)

where \({\varvec{D}}\) is a diagonal matrix with a same element and is usually set to the identity matrix. The Fisher criterion is formulated to maximize the between-class distance and to minimize the within-class distance, i.e., maximizing \(S_{b}\) and minimizing \(S_{w}\). Thus, the objective function of FELM-AE is formulated as

$$ \min L_{{\rm{FELM - AE}}} = \frac{\lambda }{2}{\varvec{\beta}}^{T} \user2{S\beta } + \frac{1}{2}\left\| {{\varvec{X}} - \user2{H\beta }} \right\|^{2} , $$
(17)

where \(\lambda\) the Fisher regularization parameter. The gradient of the objective function with respect to \({\varvec{\beta}}\) is derived as

$$ \nabla L_{{\rm{FELM - AE}}} = \lambda \user2{S\beta - H}^{T} \left( {{\varvec{X}} - \user2{H\beta }} \right). $$
(18)

By setting the gradient to zero, the closed-form solution of Eq. (18) can be obtained. Depending on the number of samples and hidden nodes, the \({\varvec{\beta}}\) is calculated differently

$$ \user2{\beta} = \left\{ \begin{gathered} \left( {\lambda {\varvec{S}} + {\varvec{H}}^{T} {\varvec{H}}} \right)^{ - 1} {\varvec{H}}^{T} {\varvec{X}},\quad N \ge L \hfill \\ {\varvec{H}}^{T} \left( {\lambda {\varvec{S}} + {\varvec{HH}}^{T} } \right)^{ - 1} {\varvec{X}},\quad N < L \hfill \\ \end{gathered} \right.. $$
(19)

After getting \({\varvec{\beta}}\), the FELM-AE can obtain the abstract representation of samples by Eq. (11).

Therefore, the feature extraction based on the FELM-AE can be summarized as Algorithm 1.

figure a

Multilayer Fisher extreme learning machine

Similar to the ML-ELM, the ML-FELM needs to be created by stacking the FELM-AE and adding ELM to complete the classification tasks. Therefore, the training process of the ML-FELM can be divided into two stages: feature extraction and classification. In the feature extraction stage, the ML-FELM extracts representative and discriminative feature by stacking the FELM-AE to train the network parameters layer-by-layer. In the classification stage, the ML-FELM puts the extracted feature into the ELM to implement classification, completing the mapping from feature to class labels.

Suppose that the training samples is \(\left\{ {{\varvec{X}},{\varvec{T}}} \right\} = \left\{ {({\varvec{x}}_{i} ,{\varvec{t}}_{i} )} \right\}_{i = 1}^{N}\) and the number of hidden nodes is \(d,L_{1} ,L_{2} , \ldots ,L_{k} ,L,m\), where \(d\) is the dimension of samples, \(m\) is the dimension of targets, \(\left\{ {L_{i} } \right\}_{i = 1}^{k}\) is the number of hidden nodes in each FELM-AE, and \(L\) is the number of hidden nodes in ELM. The network structure of the ML-FELM is shown in Fig. 3.

Fig. 3
figure 3

Network structure of the ML-FELM

Full size image

In the feature extraction stage, the ML-FELM uses the FELM-AE to learn the abstract representation of samples. The relationship between the output of hidden layers is formulated as

$$ {\varvec{H}}_{i} = \left\{ \begin{gathered} g\left( {\user2{X\beta }_{1}^{T} } \right),i = 1 \hfill \\ g\left( {{\varvec{H}}_{i - 1} {\varvec{\beta}}_{i}^{T} } \right),1 < i \le k \hfill \\ \end{gathered} \right., $$
(20)

where \({\varvec{H}}_{i}\) is the output of \(i{\text{th}}\) hidden layer and \({\varvec{\beta}}_{i}\) is the output weights of \(i{\text{th}}\) FELM-AE. \({\varvec{H}}_{k}\) is the final abstract feature extracted by the stacked FELM-AE and will be used as the input of the ELM to complete the training of the ML-FELM.

In the classification stage, the input of the ELM is \({\varvec{H}}_{k}\). Assume that the input weights of hidden layer are \({\varvec{W}}\) and the biases are \({\varvec{b}}\). The output \({\varvec{H}}_{ELM}\) and output weights \({\varvec{\beta}}\) of hidden layer are calculated as Eqs. (3) and (6), respectively.

Thus, the training process of the ML-FELM is presented in Algorithm 2.

figure b

Experiments

To verify the performance of the FELM-AE and ML-FELM, the following experiments were carried out:

Experiment 1: Visualization of the original data and abstract feature. Visualize the original data and the abstract feature extracted by the ELM-AE and FELM-AE to compare their class separability.

Experiment 2: Influence of the hyperparameters. Observe the classification accuracy of the ML-FELM with different Fisher regularization parameter and different number of hidden layers and hidden nodes, and then analyze the performance change of the ML-FELM.

Experiment 3: Performance comparison with other models. Compare the classification performance of the ML-FELM with the ELM, one-dimensional convolutional neural network (1D-CNN), ML-ELM, D-ML-ELM, ML-GELM, and H-LR21-ELM on various benchmark datasets, and observe the influence of noise on the generalization performance of the ML-ELM, D-ML-ELM, ML-GELM, and ML-FELM.

Experimental settings

Data description

The empirical experiments are carried out over various benchmark datasets including five image datasets. The image datasets are the Convex, USPS [29], Rectangles, MNIST [30], and Fashion-MNIST [31]. Most datasets are taken from UCI Machine Learning Repository [32]. All datasets have been normalized to \(\left[ {0,1} \right]\). The image datasets have been pre-divided by the proposers, and the rest of benchmark datasets need to be randomly divided into a training set and a testing set. For the Image segmentation, Satellite image, Dry bean, Letter recognition, and Gamma telescope, the number ratio of training samples to testing samples is roughly 1:1. While for the Drive diagnosis, Codon usage, and Internet firewall, the ratio is roughly 3:2. Because these ELM algorithms do not need the fine-tuning, there is usually no need to set up the validation samples. Detailed information of the above datasets is shown in Table 1, and a brief description of the image datasets is as follows:

Table 1 The datasets used in the experiments
Full size table

Convex: Convex is an artificial dataset to discriminate between convex and nonconvex shapes. It consists of 8000 training images and 50,000 testing images, and the size of each image is \(28 \times 28\) pixels in gray scale.

USPS: USPS is the US Postal handwritten digit dataset. The training set has 7291 images, and the testing set has 2007 images. Each image is \(16 \times 16\) pixels in gray scale and belongs to the digits 0–9.

Rectangles: Rectangles is an artificial dataset to discriminate between wide and tall rectangles. It contains 1200 images for training and 50,000 images for testing. Each image is in gray scale and of size \(28 \times 28\).

MNIST: MNIST is a commonly used handwritten dataset of digits 0–9. The training samples and testing samples are 60,000 images and 10,000 images with \(28 \times 28\) pixels in gray scale, respectively.

Fashion-MNIST: Fashion-MNIST is a fashion products dataset with 10 categories. It consists of 60,000 training images and 10,000 testing images, and each image is \(28 \times 28\) pixels in gray scale. Compared with MNIST, the images in Fashion-MNIST are more difficult to classify.

Implementation details

All experiments were carried out in MATLAB 2019(b) running on a laptop with a 3.2 GHz AMD 5800H CPU, 16 GB RAM, and a 1 TB hard disk. To ensure the fairness, all algorithms adopt a same network structure, and each experiment is repeated 20 times to obtain the mean results. The trial-and-error method is used to determine the network structure, considering the balance of generalization performance and computational complexity with different number of hidden layer and hidden nodes.

The implementation details for experiment 1 are as follows: the used datasets are MNIST and Fashion-MNIST, the network structure is 784-500-784, the activation function is sigmoid function, the regularization parameter of ELM-AE is \(C\;{ = }\;{10}^{ - 1}\), and the regularization parameter of FELM-AE is \(\lambda \;{ = }\;{10}^{2}\). The original data and abstract feature both need a dimensionality reduction by the T-distribution stochastic neighbor embedding (T-SNE).

The implementation details for experiment 2 are as follows: the used dataset is MNIST, the activation function is sigmoid function. When changing the regularization parameter, the network structure is 784-500-500-2000-10, the range of Fisher regularization parameter is \(\lambda \in \left\{ {{10}^{ - 5} ,{10}^{ - 4} , \ldots ,{10}^{4} ,{10}^{5} } \right\}\), and the range of parameter \(C\) is \(C \in \left\{ {{10}^{ - 3} ,{10}^{ - 2} , \ldots ,{10}^{6} ,{10}^{7} } \right\}\). When changing the number of hidden layers \(k\), the range of \(k\) is \(k \in \left\{ {1,2,3,4,5} \right\}\), the number of hidden nodes in the extraction stage is 500, the number of hidden nodes in the classification stage is 2000, the parameter \(\lambda\) is \(\lambda { = 10}^{5}\) and the parameter \(C\) is \(C{ = }10^{5}\).When changing the number of hidden nodes, the network structure is \(784 - L_{1} - L_{1} - L_{2} - 10\), the range of \(L_{1}\) is \(L_{1} \in \left\{ {100,200, \ldots ,900,1000} \right\}\), the range of \(L_{2}\) is \(L_{2} \in \left\{ {1000,2000, \ldots ,9000,10{,}000} \right\}\), the parameter \(\lambda\) is \(\lambda { = 10}^{5}\), and the parameter \(C\) is \(C{ = }10^{5}\).

The implementation details for experiment 3 are as follows: The network structure of algorithms is shown in Table 2, the activation function is sigmoid function, the Fisher regularization parameter \(\lambda\) is selected from \(\lambda \in \left\{ {{10}^{ - 3} ,{10}^{ - 2} , \ldots ,{10}^{4} ,{10}^{5} } \right\}\), and the parameter \(C\) is selected from \(C \in \left\{ {{10}^{ - 2} ,{10}^{ - 1} , \ldots ,{10}^{7} ,{10}^{8} } \right\}\). For the 1D-CNN, the number of convolutional layers and pooling layers are both 2, the size of convolution kernel is \(1\; \times \;3\), the number of convolution kernel is 4, the max-pooling is used for the down-sampling, the size of pooling kernel is \(1 \times 2\), the activation function is relu function, the learning rate of the stochastic gradient descent method is 0.05, the batch size is 100, and the number of epochs is 100. The Signal-to-Noise Ratio (SNR) is introduced to represent different levels of noise and the range of SNR is \({\rm{SNR}} \in \left\{ {30,25,20,15,10} \right\}\). In the performance comparison for multiclass and binary classification tasks, the evaluation metrics are the accuracy, recall, G-Mean, and F1-Measure. In multiclass classification tasks, the recall, G-Mean, and F1-Measure are the averages of all classes.

Table 2 The network architecture of ELM, ML-ELM, D-ML-ELM, ML-GELM, H-LR21-ELM, and ML-FELM
Full size table

Visualization of the original data and abstract feature

Visualization is a direct way to observe the distribution of abstract feature and to evaluate the effectiveness of feature extraction. To verify that the Fisher criterion can improve the class separability of abstract feature and enrich the category information, the original data and the abstract feature extracted by the ELM-AE and FELM-AE are visualized and analyzed. The distributions of original data and abstract feature on MNIST and Fashion-MNIST are shown in Figs. 4 and 5, respectively. The X-axis and Y-axis in each figure represent different feature value after the dimensionality reduction by the TSNE.

Fig. 4
figure 4

Visualization of original data and abstract feature on MNIST dataset: a original data, b the ELM-AE, and c the FELM-AE

Full size image
Fig. 5
figure 5

Visualization of original data and abstract feature on Fashion-MNIST dataset: a original data, b the ELM-AE, and c the FELM-AE

Full size image

As shown in Figs. 4 and 5, compared with the original data and the abstract feature extracted by the ELM-AE, the between-class distance of abstract feature extracted by the FELM-AE is larger and the within-class distance is smaller, which indicates that the abstract feature extracted by the FELM-AE is more discriminative. The result shows that the introduction of Fisher criterion into the FELM-AE is effective way to enhance the class separability of abstract feature. This is because that adding the Fisher regularization term to objective function enforces the network to balance the reconstruction error and Fisher regularization loss, and makes the output weights can both reduce the reconstruction error and Fisher regularization loss. Thus, the between-class distance of abstract feature is increased, and the within-class distance is decreased. However, the ELM-AE introduces the L2-norm regularization term about the output weights to prevent the over-fitting rather than to improve the class separability of feature.

Influence of the hyperparameters

The regularization parameter and the number of hidden layers and hidden nodes are important hyperparameters of the ML-FELM. The regularization parameter controls the effectiveness of regularization, and the number of hidden layers and hidden nodes control the generalization ability of the ML-FELM. To clarify the influence of the hyperparameters on the ML-FELM, different regularization parameter and different number of hidden layers and hidden nodes are used to observe the change of generalization performance. With variable regularization parameters, the classification accuracy of the ML-FELM is shown in Fig. 6. With variable number of hidden layers, the classification accuracy of the ML-FELM is shown in Fig. 7. And with variable number of hidden nodes, the classification accuracy and training time of the ML-FELM are shown in Fig. 8.

Fig. 6
figure 6

The influence of the regularization parameter on the generalization performance

Full size image
Fig. 7
figure 7

The influence of the number of hidden layers on the generalization performance

Full size image
Fig. 8
figure 8

The influence of the hidden nodes on a accuracy and b training time

Full size image

As is shown in Fig. 6, increasing the regularization parameter \(\lambda\) and \(C\) properly can improve the generalization performance of the ML-FELM. When \(\lambda\) is fixed, the classification accuracy increases with the increase of \(C\). When \(C \le 10^{2}\), the classification accuracy increases and then decreases with the increase of \(\lambda\). When \(C > 10^{2}\), the classification accuracy increases with the increase of \(\lambda\). The reason is that the increase of Fisher regularization parameter \(\lambda\) can enhance the class separability of the extracted feature and make them easy to classify, but an excessively large \(\lambda\) will cause the FELM-AE to ignore the effect of reconstruction error, leading to a under-fitting. And the parameter \(C\) controls the empirical risk of the ELM. An increase \(C\) will drive the ELM to further reduce the reconstruction error and improve the classification performance, but in practical applications, an excessively large \(C\) is likely to lead to an over-fitting. Therefore, the proper regularization parameters \(\lambda\) and \(C\) need to be chosen according to the specific samples.

As is shown in Fig. 7, with the increase of hidden layers, the classification accuracy of the ML-FELM increases. This indicates that the proper number of hidden layers can improve the approximation capability of the ML-FELM. When \(k = 1\), the ML-FELM do not adopt the FELM-AE to extract feature and its performance is not competitive. With the increase of hidden layer, the FELM-AE is used for representation learning, and the abstract feature learned by the stacked FELM-AE is more discriminative and representative. The discriminative and representative feature can enhance the classification capability of the ELM and the comprehensive performance of ML-FELM.

As is shown in Fig. 8, the generalization performance and training time of the ML-FELM both increase as hidden nodes of the FELM-AE and ELM increases. This is because the ELM has universal approximation capability. With the increase of hidden nodes, the performance of the FELM-AE and ELM both gradually improves, making the FELM-AE extract more representative feature and the ELM more capable of approximating nonlinear mappings. Moreover, when the number of samples is not less than hidden nodes, i.e., \(N \ge L\), the computational complexity of the FELM-AE and ELM is \(O\left( {NL^{2} } \right)\), and when \(N < L\), that is \(O\left( {N^{2} L} \right)\). Therefore, as hidden nodes increase, the computational complexity and training time of the ML-FELM both increase.

Performance comparison

To test the comprehensive performance of the ML-FELM, all benchmark datasets are used in the comparison and analysis of the ELM, 1D-CNN, ML-ELM, D-ML-ELM, ML-GELM, H-LR21-ELM, and ML-FELM. First, different evaluation metrics are recorded to evaluate the classification performance and computational complexity of each algorithm. Then, by adding the different levels of noise to training samples, the change of classification accuracy is recorded to evaluate the robustness of each algorithm.

  1. 1.

    Classification results over benchmark datasets.

Since the number of hidden nodes has a significant effect on the generalization performance, the same network structure is required for all algorithms to ensure a fair comparison. And variable regularization parameters are selected to find the best results. The classification performance of each algorithm for multiclass and binary classification tasks are shown in Tables 3 and 4, respectively. The training time and testing time of each algorithm are shown in Tables 5 and 6, respectively. The ‘–’ indicates that the results could not be obtained, and the numbers in boldface represent the best results.

Table 3 The performance comparison of each algorithm for multiclass classification tasks
Full size table
Table 4 The performance comparison of each algorithm for binary classification tasks
Full size table
Table 5 The training time (s) of ELM, 1D-CNN, ML-ELM, D-ML-ELM, ML-GELM, H-LR21-ELM, and ML-FELM
Full size table
Table 6 The testing time (s) of ELM, 1D-CNN, ML-ELM, D-ML-ELM, ML-GELM, H-LR21-ELM, and ML-FELM
Full size table

As shown in Tables 3 and 4, the classification performance of ML-FELM is better than that of ELM, 1D-CNN, ML-ELM, D-ML-ELM, ML-GELM, and H-LR21-ELM on most of benchmark datasets and the generalization improvement is about 0.5–3%. The reason is that the FELM-AE in the ML-FELM introduces the Fisher criterion and uses the category information to guide the feature extraction, which makes the extracted feature more discriminative and the classification boundaries of classifiers more evident. Moreover, the balance of Fisher regularization loss and empirical error prevents the over-fitting of the ML-FELM and improves the generalization performance. The importance difference of labels is not considered by all algorithms; thus, the algorithms with better classification performance tend to have higher accuracy, recall, G-Mean, and F1-Measure. In addition, the ML-GELM needs to calculate the similarity matrix and Laplacian matrix of samples, and there is a memory overflow problem. Thus, dealing with large-scale datasets such as Drive diagnosis, Internet firewall, MNIST, and Fashion-MNIST, the ML-GELM does not obtain effective results.

As shown in Tables 5 and 6, the training speed and testing time of the ML-FELM are both fast. The training time of the ML-FELM is approximately the same as the ML-ELM and D-ML-ELM, and less than the 1D-CNN, ML-GELM and H-LR21-ELM. The testing time of the ML-FELM is approximately the same as other deep learning algorithms. The reason is that compared with ELM, the ML-FELM adopts a deep network structure, and the feature extraction requires additional training time and testing time. Since the number of hidden nodes in feature extraction is much less than that in classification stage and the computational complexity of Fisher matrix in the ML-FELM is same as that of corruption in the D-ML-ELM, the training time of the ML-FELM is approximately the same as the ML-ELM and D-ML-ELM. Compared with the 1D-CNN, ML-GELM, and H-LR21-ELM, the ML-FELM does not need the time-consuming calculation of the similarity matrix and Laplacian matrix in the ML-GELM, neither the fine-tuning of network parameters in 1D-CNN and H-LR21-ELM. Thus, the training efficiency of the ML-FELM is higher than the ML-GELM and the H-LR21-ELM. It should be noted that the testing time is only related to the network structure and the number of samples. Under the same network structure and testing samples, the testing speed of each ML-ELM algorithms differs very little.

  1. 2.

    Robustness performance of the ML-FELM.

In comparison of robustness, the classification accuracy of the ML-ELM, D-ML-ELM, ML-GELM, and ML-FELM are observed and analyzed. The experimental datasets are Satellite image, Letter recognition and Rectangles, and the noise added to training samples is the Gaussian white noise. The classification accuracy of each algorithm with different SNR is shown in Table 7, and the accuracy change curves are shown in Fig. 9.

Table 7 The classification accuracy (%) of ML-ELM, D-ML-ELM, ML-GELM, and ML-FELM with different SNR
Full size table
Fig. 9
figure 9

The variation of classification accuracy with different SNR on datasets: a Satellite image, b letter recognition, and c rectangles

Full size image

As is shown in Table 7 and Fig. 9, the classification accuracy of ML-FELM is higher than that of ML-ELM, D-ML-ELM, and ML-GELM with different SNR, and the performance improvement increases as the SNR decreases. With the decrease of SNR, the noise in the datasets is gradually enhanced, and the generalization performance of each algorithm is affected. However, the performance decline of the ML-FELM and ML-GELM is slower than that of ML-ELM and D-ML-ELM. This is because, by introducing the Fisher regularization, the ML-FELM uses the class labels that are not affected by noise to guide feature extraction. The maximizing of between-class distance and the minimizing of within-class distance can increase the distance among classification boundaries and weaken the influence of noise. In addition, the ML-GELM enhance its robustness by introducing the manifold regularization and learning the intrinsic manifold structure of data.

Conclusion

To enhance the class separability of feature extracted by the ELM-AE and improve the generalization performance of the ML-ELM for classification tasks, this study integrates the Fisher criterion into the ELM-AE and proposes the FELM-AE and ML-FELM. The FELM-AE uses class labels to guide the feature extraction and enhance the class separability of feature by adding Fisher regularization term to the loss function. The ML-FELM stacks the FELM-AE to extract feature and adopts the ELM to classify. The experimental results on various benchmark datasets show that the abstract feature extracted by the FELM-AE is more discriminative than the ELM-AE, and the classification accuracy of the ML-FELM is higher than ML-ELM, 1D-CNN, D-ML-ELM, ML-GELM, and H-LR21-ELM.

However, due to the inefficiency of the trial-and-error method, it is difficult for the ML-FELM to choose proper Fisher regularization parameters in different datasets. Thus, the automatic setting of the regularization parameter is an important issue. One feasible method is to replace the trial-and-error method with the particle swarm optimization (PSO) [33] or genetic algorithm (GA) [34]. The PSO and GA are both the intelligent search algorithms. By setting the regularization parameters as the optimization objects and the generalization performance as the evaluation criteria, they can automatically search the optimal regularization parameters of the FELM-AE and ML-FELM. Moreover, all datasets used in the experiments are complete and balanced, which is contrary to the practical applications. Thus, further works needs to analyze the influence of the incomplete and unbalanced datasets on the performance of the ML-ELM and find the improvement methods. Combining the ML-ELM with data augmentation methods [35] or the semi-supervised learning [36] is a worthwhile attempt.