Abstract
The T-spherical uncertain linguistic (TSUL) sets (TSULSs) integrated by T-spherical fuzzy sets and uncertain linguistic variables are introduced in this article. This new concept is not only a generalized form but also can integrate decision-makers’ quantitative evaluation ideas and qualitative evaluation information. The TSULSs serve as a reliable and comprehensive tool for describing complex and uncertain decision information. This paper focuses on an extended MARCOS (Measurement of Alternatives and Ranking according to the Compromise Solution) method to handle the TSUL multi-attribute group decision-making problems where the weight information is completely unknown. First, we define, respectively, the operation rules and generalized distance measure of T-spherical uncertain linguistic numbers (TSULNs). Then, we develop two kinds of aggregation operators of TSULNs, one kind of operator with independent attributes is T-spherical uncertain linguistic weighted averaging and geometric (TSULWA and TSULWG) operators, and the other is T-spherical uncertain linguistic Heronian mean aggregation operators (TSULHM and TSULWHM) considering attributes interrelationship. Their related properties are discussed and a series of reduced forms are presented. Subsequently, a new TSUL-MARCOS-based multi-attribute group decision-making model combining the proposed aggregation operators and generalized distance is constructed. Finally, a real case of investment decision for a community group-buying platform is presented for illustration. We further test the rationality and superiorities of the proposed method through sensitivity analysis and comparative study.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Multiple decision agents, including experts or stakeholders in different fields, select the optimal option(s) from several alternatives, this process is named multi-attribute group decision-making (MAGDM) [1, 2]. On the one hand, group decision-making can overcome the lack of personal knowledge or experience, and at the same time can fully reflect democracy in the decision process, so it has been widely used in product research and development, the credit assessment, strategic planning evaluation, investment decision, and other fields, it has become the focus of current research. Due to the complexity of practical MAGDM problems, the decision problem itself has a lot of uncertain information, including unquantifiable, incomplete, or unattainable information. However, it is difficult for decision-makers to represent the degree of uncertainty by relying on accurate data. Especially when assessing system performance, the decision-makers prefer to use linguistic evaluation [3, 4], such as “good”, “very likely”, “low”, etc. These linguistic terms can be intuitive and easy to understand, close to people’s cognition. However, considering that a single linguistic variable cannot completely portray the actual ideas of decision-makers, some scholars extend and propose various linguistic information models from specific requirements, such as hesitant fuzzy linguistic term sets [5], intuitionistic linguistic sets [6], 2-tuple fuzzy linguistic representation model [7], etc. Xu [8] believed that the uncertain information of evaluation can be expressed more accurately through linguistic terms interval, while a single linguistic variable cannot be realized. Therefore, Xu [8] proposed the concept of uncertain linguistic variables. Since then, the uncertain linguistic sets have received extensive attention, and various extended studies have emerged.
The intuitionistic uncertain linguistic sets (IULSs) [9] have the advantages of both uncertain linguistic variables and intuitionistic fuzzy sets. The intuitionistic uncertain linguistic number consists of an uncertain linguistic part and an intuitionistic fuzzy part. The former represents the qualitative evaluation value of a certain attribute by decision-makers, and the latter indicates the level of subordination and non-subordination to the uncertain linguistic part [10,11,12], the intuitionistic fuzzy part meets the sum of membership degree (MD) and non-membership degree (ND) is not greater than one [13]. The IULSs cannot be adopted once the sum of MD and ND is greater than one, many scholars explored the combination of an uncertain linguistic variable and Pythagorean fuzzy set [14], then introduced Pythagorean uncertain linguistic sets (PyULSs) [15,16,17,18,19], so the modeling ability of uncertain information is improved to a certain extent. However, the PyULSs cannot be applied if the sum of squares of MD and ND of Pythagorean fuzzy numbers is more than one. Scholars proposed q-rung orthopair uncertain linguistic sets (q-ROULSs) [21,22,23,24,25,26] by pooling the strengths of q-rung orthopair fuzzy sets [20] and uncertain linguistic variables, in which q-rung orthopair fuzzy part satisfies the q-power sum of MD and ND degree less than or equal to one. The q value can be adjusted by decision-makers to expand the expression range of acceptable q-rung orthopair uncertain linguistic information and further improve the modeling ability of uncertain information. The IULSs and PyULSs are particular forms of the q-ROULSs (when q = 1 and q = 2). Therefore, the q-rung orthopair uncertain linguistic sets are more flexible and comprehensive than intuitionistic uncertain linguistic sets and Pythagorean uncertain linguistic sets in describing qualitative evaluation information. In addition, Cuong [27] found that picture fuzzy sets theory can manage awkward and complicated information. This concept makes the description and evaluation information more reliable and widely proficient by adding an abstinence degree (AD) [28, 29]. Wei et al. [30, 31] proposed picture uncertain linguistic sets (PULSs) by combining picture fuzzy sets with uncertain linguistic sets, in which the sum of MD, AD, and ND in the picture fuzzy part is less than or equal to one. Furthermore, Naeem et al. [32] extended interval-valued PULSs to solve the problem of supplier selection. Some weighted and ordered weighted generalized Hamacher aggregation operators (AOs) based on interval-valued PULSs are developed by Garg et al.[33]
In 2019, Mahmood et al.[34] proposed the concept of T-spherical fuzzy set (T-SFS), which not only has the same structural framework of MD, AD and ND as PFS, but also has a larger and more flexible decision space, that is, it has the sum of the q-powers of MD, AD and ND less than or equal to one. Obviously, the T-SFS is reduced to the spherical fuzzy set, PFS, q-ROFS, PyFS and IFS under certain conditions. Therefore, the T-SFS can better represent the uncertainty of evaluation information. Since the generalized feature of T-SFS with no limitations, it has widely concerned by many scholars. Current studies on T-SFS mainly focus on the following three aspects: (1) Some information measures of T-spherical fuzzy number have been studied by scholars, such as entropy measure [35], similarity measure [35,36,37], divergence measure [38], correlation coefficient [39], etc. (2) Some AOs have been developed in the T-SFS environment. Some focused on operational rules, such as Algebraic [40], Hamacher [41], Einstein [42], Frank [43], Dombi [44], and interactional operational laws [45,46,47,48], etc., and some focused on AOs extension, such as power operator [40, 49], Muirhead mean [40], Heronian mean [47, 48], Bonferroni mean [50], etc. (3) The existing alternative ranking technologies have been extended in T-SFS environment, such as TODIM [46], MULTIMOORA [44], ELECTRE [51]. These studies not only enrich the T-SFS theory, but also are applied to practical problems. Based on the above uncertain linguistic set and T-SFS, therefore, inspired by the q-ROULSs, we combine the generalized structure of T-SFSs [34] with uncertain linguistic variables and propose a new linguistic expression model, which is called TSULSs and is used to describe qualitative linguistic information. TSULS is a generalized and effective theory for managing awkward and unreliable information. On the one hand, the merits of uncertain linguistic variables and T-SFSs are integrated into the TSULSs. On the other hand, the IULSs [9], PyULs [15,16,17,18,19], q-ROULSs [21,22,23,24,25,26] and PULSs [30, 31] can all be regarded as special cases. Hence, it is of great theoretical and practical importance for us to research relevant theories and methods of TSULs and its application in MAGDM.
For MAGDM problems, the MARCOS method is a relatively new and stable technique for selecting the best candidate(s) for decision problems. In 2020, Stevič et al. [52] first proposed the MARCOS method, whose basic idea is to determine the utility function of the alternative by determining the connection between the alternative and the reference points and to achieve compromise ordering related to ideal solutions and anti-ideal solutions. Different from existing methods (TOPSIS [53], VIKOR [54], EDAS [55], TODIM [46], etc.), which have disadvantages such as complex calculation, pre-setting of parameters, and ignoring the relative importance of distance, the MARCOS method has below merits: (1) The reference points are determined at the beginning of the model; (2) The utility degree is more accurately determined from ideal and anti-ideal perspectives; (3) A new method to determine utility functions is proposed, which is different from the TOPSIS’s distance approximation and VIKOR’s compromise mechanism; (4) Ability to handle a large number of conflicting attributes and alternatives [56]. So far, the MARCOS method has been extended and applied in different decision environments to deal with various real MAGDM problems, as shown in Table 1.
We can find that there are still some spaces for expansion and improvement of MARCOS method from Table 1. This study aims to modify the MARCOS method for MAGDM problems with interrelationship among decision attributes in T-spherical uncertain linguistic environment. The motivation of this article as follows:
-
(1)
As a generalized form for expressing uncertain and vague information, the TSULSs can effectively characterize and identify decision-makers’ preference information in a decision-making environment with increasing complexity. The existing MARCOS methods have been extended and applied in different MAGDM environments, like IFNs [58], q-ROFNs [56], SFNs [57], IT2FNs [60, 63], RNs [59, 61] and SVNFNs [65], etc. However, the capabilities of these fuzzy numbers are not as good as TSULNs, and MARCOS has not been extended in the TSULSs environment. Thus, it is necessary to investigate the integration of MARCOS and TSULS in this paper.
-
(2)
Expert weights play an important role in MAGDM problems. From Table 1, many scholars adopted the ways of subjective assessment [56,57,58] and assumed weight [59,60,61, 63,64,65] in the process of solving MAGDM problems, but these approaches are too subjective and arbitrary to fully reflect the objective importance of experts. Although there are less distance-based approaches [62, 66] in Table 1, these distance measures did not take into account the psychological behavior of decision-makers. Hence, it is necessary to propose a new distance measure to calculate expert weights in the TSUL environment, which can not only meet the axiomatic definition of distance measure, but also flexibly reflect the psychological behavior of decision-makers.
-
(3)
The attribute weight is critical and can influence the decision results in the process of MAGDM. In Table 1, scholars used the FUCOM [64,65,66], BWM [61,62,63], AHP [60], and PIPRECIA [59] methods to obtain the subjective attribute weights. These subjective weight techniques can make the decision results adhere to the subjectivity of the decision-makers. In addition, the CRITIC [56, 57] approach was employed to obtain the attributes’ objective weights using standard deviation and correlation coefficient. However, under the situation that the decision-makers are completely unknown to the weight information of attributes, an objective weight determination method considering experts’ preferences has not been developed. Thus, the MDM is adopted to calculate the optimal attribute weight in a T-spherical uncertain linguistic context.
-
(4)
In existing MARCOS methods, the evaluation values under each attribute are aggregated to generate the comprehensive evaluation value of each alternative. Unfortunately, the interrelationship between attributes is ignored, but the correlations between attributes do exist objectively in complex real-world decision problems, it can be more in line with the actual situation of decision-making. Therefore, we try to develop some new Heronian mean AOs with TSULNs based on the characteristics and advantages of the Heronian mean operator [12, 47, 48, 68, 69].
-
(5)
In the existing MARCOS methods, the utility degrees (Ki− and Ki+) of alternative solutions to ideal and anti-ideal solutions are calculated by division operation or division operation after defuzzification. However, the division operation may have two disadvantages: first, the value may be 0 when the anti-ideal solution is determined, which causes the division operation to fail. Second, the process of defuzzification may result in the loss of some evaluation information of various types of fuzzy numbers. Therefore, inspired by Euclidean distance in Rf. [34], we try to integrate a new distance measure in the MARCOS method to calculate the utility degrees. The new distance measure is employed to eliminate the above shortcomings, which not only includes the information of MD, AD, ND and refusal degree in TSULNs, but also can achieve the same effect as the division operation.
To sum up the above arguments and motivations, some contributions of this paper are presented as below:
-
(1)
A new notion of TSULSs is introduced to express the decision-maker's view and preferences in complex MAGDM problems, and the operation rules and generalized distance measures of TSULNs are defined.
-
(2)
Two classes of TSUL AOs considering the relationship (independent and correlative) between attributes are developed, their related properties are analyzed and these operators are reduced into some special cases.
-
(3)
Based on the TSUL generalized distance measure, the TSUL similarity is defined to calculate the decision-makers' weight and the MDM is applied to obtain the weight of the attribute.
-
(4)
A novel TSUL-MARCOS method based on the TSULWHM operator and generalized distance measure is designed. We test the practicability and effectiveness of the proposed method by dealing with an investment decision for the community group-buying (CGB) platform.
The other segments are arranged as follows: some related basic concepts are briefly reviewed in “Preliminaries”. “Some notions of T-spherical uncertain linguistic sets” defines the related notions of TSULSs, including the TSULSs, operation rules of TSULNs, and the TSUL generalized distance measure. “The TSUL-weighted AOs and TSULHM AOs” develops the TSULWA, TSULWG, TSULHM, and TSULWHM operators. “ A novel MAGDM framework based on TSUL-MARCOS” builds the TSUL-MARCOS model for the MAGDM problems. A case of the investment decision for the CGB platform is employed to illustrate the practicability of the developed method in “A case study”. Meanwhile, the sensitivity analysis and comparative study are performed. “Conclusions” summarizes the work of this article and introduces the plans.
Preliminaries
We briefly describe some basic concepts of ULS and T-SFS in this section.
Linguistic terms sets S = {s0, s1, …, sk-1} is composed of k elements, in which k is an odd number. Generally, k = 3, 5, 7, 9. For instance, k = 7, S = {s0, s1, s2, s3, s4, s5, s6} = {very low, low, medium low, medium, medium high, high, very high}.
For any linguistic set S, the following conditions should be satisfied [70]:
-
(1)
If m > n, then sm > sn;
-
(2)
If there is a negative operator neg(sm) = sn, then n = k-1-m;
-
(3)
If sm ≥ sn, then max(sm,sn) = sm;
-
(4)
If sm ≤ sn, then min(sm,sn) = sm.
Definition 1
[8]. Suppose \(\tilde{s} = [s_{\alpha } ,s_{\beta } ]\), sα, sβ∈S and α ≤ β, in which sα and β is the lower limit and the upper limit of \(\tilde{s}\), then \(\tilde{s}\) is called the uncertain linguistic variable (ULV). Suppose \(\tilde{S}\) is the set of all ULVs, namely uncertain linguistic set (ULS).
To eliminate some shortcomings of Xu [8] proposed operation rules, Liu and Zhang [12] proposed some new ULVs operation rules and defined them as follows:
Definition 2
[12]. Suppose \(\tilde{s}_{1} = [s_{{\alpha_{1} }} ,s_{{\beta_{1} }} ]\), \(\tilde{s}_{2} = [s_{{\alpha_{2} }} ,s_{{\beta_{2} }} ]\) are any two ULVs in \(\tilde{S} = \{ s_{0} ,s_{1} ,s_{2} , \ldots ,s_{k - 1} \}\), then the new operational laws of ULVs as follows:
-
(1)
\(\tilde{s}_{1} \oplus \tilde{s}_{2} = \left[ {s_{{\alpha_{1} + \alpha_{2} - \frac{{\alpha_{1} \alpha_{2} }}{k}}} ,s_{{\beta_{1} + \beta_{2} - \frac{{\beta_{1} \beta_{2} }}{k}}} } \right]\);
-
(2)
\(\tilde{s}_{1} \otimes \tilde{s}_{2} = \left[ {s_{{\frac{{\alpha_{1} \alpha_{2} }}{k}}} ,s_{{\frac{{\beta_{1} \beta_{2} }}{k}}} } \right]\);
-
(3)
\(\lambda \tilde{s}_{1} = \left[ {s_{{k - k\left( {1 - \frac{{\alpha_{1} }}{k}} \right)^{\lambda } }} ,s_{{k - k\left( {1 - \frac{{\beta_{1} }}{k}} \right)^{\lambda } }} } \right],\lambda \ge 0\);
-
(4)
\(\left( {\tilde{s}_{1} } \right)^{\lambda } = \left[ {s_{{k\left( {\frac{{\alpha_{1} }}{k}} \right)^{\lambda } }} ,s_{{k\left( {\frac{{\beta_{1} }}{k}} \right)^{\lambda } }} } \right],\lambda \ge 0\).
Definition 3
[34]. Suppose X is a universe set, and then the form of T-SFS is described as below:
in which \(\tau_{\Im } (x),\eta_{\Im } (x),\vartheta_{\Im } (x)\) are respectively the MD, AD and ND of element x ∈ ℑ in X, that is, \(\tau_{\Im } (x),\eta_{\Im } (x),\vartheta_{\Im } (x) \in [0,1][0,1]\), and meeting \(0 \le \tau_{\Im }^{q} (x) + \eta_{\Im }^{q} (x) + \vartheta_{\Im }^{q} (x) \le 1\), q ≥ 1 for ∀x ∈ X. \(\pi_{\Im } (x) = \sqrt[q]{{1 - \tau_{\Im }^{q} (x) - \eta_{\Im }^{q} (x) - \vartheta_{\Im }^{q} (x)}}\) is named the refusal degree. For simplicity, the T-spherical fuzzy number (T-SFN) is represented as a triplet of τ, η and ϑ, and denoted as χ = (τ, η, ϑ).
Definition 4 [46]. For a T-SFN χ = (τ, η, ϑ), the score function sc(χ) and accuracy function ac(χ) are defined as:
To compare the two T-SFNs χ1 = (τ1, η1, ϑ1) and χ2 = (τ2, η2, ϑ2), the comparative rules are as follows:
-
(1)
If sc(χ1) > sc(χ2), then χ1 is greater than χ2, namely, χ1 > χ2;
-
(2)
If sc(χ1) = sc(χ2), then if ac(χ1) > ac(χ2), then χ1 is greater than χ2, namely, χ1 > χ2; (ii) if ac(χ1) = ac(χ2), then χ1 is equal to χ2, namely, χ1 = χ2.
Definition 5
[34]. Let χ = (τ, η, ϑ), χ1 = (τ1, η1, ϑ1) and χ2 = (τ2, η2, ϑ2) be three arbitrary T-SFNs, then their operational rules are described as below:
-
(1)
\(\chi_{1} \oplus \chi_{2} = \left( {\sqrt[q]{{\tau_{1}^{q} + \tau_{2}^{q} - \tau_{1}^{q} \tau_{2}^{q} }},\eta_{1} \eta_{2} ,\vartheta_{1} \vartheta_{2} } \right)\);
-
(2)
\(\chi_{1} \otimes \chi_{2} = \left( {\tau_{1} \tau_{2} ,\sqrt[q]{{\eta_{1}^{q} + \eta_{2}^{q} - \eta_{1}^{q} \eta_{2}^{q} }},\sqrt[q]{{\vartheta_{1}^{q} + \vartheta_{2}^{q} - \vartheta_{1}^{q} \vartheta_{2}^{q} }}} \right)\);
-
(3)
\(\lambda \cdot \chi = \left( {\sqrt[q]{{1 - (1 - \tau^{q} )^{\lambda } }},\eta^{\lambda } ,\vartheta^{\lambda } } \right)\), λ > 0;
-
(4)
\(\chi^{\lambda } = \left( {\tau^{\lambda } ,\sqrt[q]{{1 - (1 - \eta^{q} )^{\lambda } }},\sqrt[q]{{1 - (1 - \vartheta^{q} )^{\lambda } }}} \right)\), λ > 0.
Definition 6
[71]. Suppose the parameters σ, ρ ≥ 0, σ and ρ are not 0 at the same time,\(x_{\varsigma } (\varsigma = 1,2,...,\kappa )\) be any family of non-negative real number, if.
The HMσ, ρ is known as the Heronian mean operator.
Some notions of T-spherical uncertain linguistic sets
In this segment, we introduce a notion of TSULs based on the ULVs and T-SFSs, and define a series of relevant definitions, including operation rules and generalized distance measure of TSULNs.
Definition 7
Suppose X is a given domain. The T-spherical uncertain linguistic set (TSULS) \(\widetilde{Q}\) in X is defined as there is \(\left[ {s_{\alpha (x)} ,s_{\beta (x)} } \right] \in X\), then
where \(\left[ {s_{\alpha (x)} ,s_{\beta (x)} } \right] \in S\), \(\tau_{{\tilde{Q}}} (x):X \to [0,1]\), \(\eta_{{\tilde{Q}}} (x):X \to [0,1]\) and \(\vartheta_{{\tilde{Q}}} (x): \to [0,1]\) respectively represents the MD, AD and ND of elements x to ULV \([s_{\alpha (x)} ,s_{\beta (x)} ]\), and satisfy \(0 \le \left( {\tau_{{\tilde{Q}}} (x)} \right)^{q} + \left( {\eta_{{\tilde{Q}}} (x)} \right)^{q} + \left( {\vartheta_{{\tilde{Q}}} (x)} \right)^{q} \le 1\), q ≥ 1, for ∀ x ∈ X. \(\pi_{{\tilde{Q}}} (x) = \sqrt[q]{{1 - \tau_{{\tilde{Q}}}^{q} (x) - \eta_{{\tilde{Q}}}^{q} (x) - \vartheta_{{\tilde{Q}}}^{q} (x)}}\) is named the refusal degree \(\tilde{Q}\) in X. For convenience, the TSULN is represented as \(\delta = ([s_{\alpha } ,s_{\beta } ],(\tau ,\eta ,\vartheta ))\). If q = 1, then the TSULN reduces to the PULS; If q = 2, then the TSULN reduces to the SULN.
Definition 8
For a TSULN \(\delta = ([s_{\alpha } ,s_{\beta } ],(\tau ,\eta ,\vartheta ))\), the score function sc(δ) and accuracy function ac(δ) are defined as:
To compare the two TSULNs \(\delta_{1} = ([s_{{\alpha_{1} }} ,s_{{\beta_{1} }} ],(\tau_{1} ,\eta_{1} ,\vartheta_{1} ))\) and \(\delta_{2} = ([s_{{\alpha_{2} }} ,s_{{\beta_{2} }} ],(\tau_{2} ,\eta_{2} ,\vartheta_{2} ))\), the comparative rules are as follows:
-
(1)
If sc(δ1) > sc(δ2), then δ1 is greater than δ2, namely, δ1 > δ2;
-
(2)
If sc(δ1) = sc(δ2), then (i) if ac(δ1) > ac(δ2), then δ1 is greater than δ2, namely, δ1 > δ2; (ii) if ac(δ1) = ac(δ2), then δ1 is equal to δ2, namely, δ1 = δ2.
Definition 9
Suppose \(\delta = ([s_{\alpha } ,s_{\beta } ],(\tau ,\eta ,\vartheta ))\), \(\delta_{1} = ([s_{{\alpha_{1} }} ,s_{{\beta_{1} }} ],(\tau_{1} ,\eta_{1} ,\vartheta_{1} ))\) and \(\delta_{2} = ([s_{{\alpha_{2} }} ,s_{{\beta_{2} }} ],(\tau_{2} ,\eta_{2} ,\vartheta_{2} ))\) are three arbitrary TSULNs, then their operational rules based on Definitions 2 and 5 are described as below:
Theorem 1. Suppose \(\delta = ([s_{\alpha } ,s_{\beta } ],(\tau ,\eta ,\vartheta ))\), \(\delta_{1} = ([s_{{\alpha_{1} }} ,s_{{\beta_{1} }} ],(\tau_{1} ,\eta_{1} ,\vartheta_{1} ))\) and \(\delta_{2} = ([s_{{\alpha_{2} }} ,s_{{\beta_{2} }} ],(\tau_{2} ,\eta_{2} ,\vartheta_{2} ))\) are three TSULNs, λ1, λ2, λ ≥ 0. Then their operational properties are as below:
-
(1)
\(\delta_{1} \oplus \delta_{2} = \delta_{2} \oplus \delta_{1}\);
-
(2)
\(\delta_{1} \otimes \delta_{2} = \delta_{2} \otimes \delta_{1}\);
-
(3)
\(\lambda \cdot (\delta_{1} \oplus \delta_{2} ) = \lambda \cdot \delta_{2} \oplus \lambda \cdot \delta_{1}\);
-
(4)
\(\lambda_{1} \cdot \delta \oplus \lambda_{2} \cdot \delta = (\lambda_{1} + \lambda_{2} ) \cdot \delta\);
-
(5)
\(\delta^{{\lambda_{1} }} \otimes \delta^{{\lambda_{2} }} = \delta^{{(\lambda_{1} + \lambda_{2} )}}\);
-
(6)
\(\delta_{1}^{\lambda } \otimes \delta_{2}^{\lambda } = (\delta_{1} \otimes \delta_{2} )^{\lambda }\).
Proof
(i) We can easily prove properties (1) and (2) according to Eqs. (8) and (9).
(ii) For property (3), since
According to Eq. (10), we can get
Since \(\begin{aligned}&\lambda \cdot \delta = \left( \left[ {s_{{k - k\left( {1 - \frac{\alpha }{k}} \right)^{\lambda } }} ,s_{{k - k\left( {1 - \frac{\beta }{k}} \right)^{\lambda } }} } \right],\right. \nonumber\\ &\left.\left( \begin{array}{l} \sqrt[q]{{1 - (1 - \tau^{q} )^{\lambda } }},\sqrt[q]{{(1 - \tau^{q} )^{\lambda } - (1 - \tau^{q} - \eta^{q} )^{\lambda } }}, \hfill \\ \sqrt[q]{{(1 - \tau^{q} - \eta^{q} )^{\lambda } - (1 - \tau^{q} - \eta^{q} - \vartheta^{q} )^{\lambda } }} \hfill \\ \end{array} \right) \right)\end{aligned}\).
According to Eq. (8), we can get
Thus, \(\lambda \cdot (\delta_{1} \oplus \delta_{2} ) = \lambda \cdot \delta_{2} \oplus \lambda \cdot \delta_{1}\), which completes the proof of property (3).
(iii) Similar to property (3), the proofs of properties (4) ~ (6) are omitted here.
We propose a new generalized distance to measure the difference between two TSULNs. This distance measure contains parameter, and the decision-makers can adjust parameter value according to the actual situation of decision-making to represent the decision-makers’ psychological preference behavior. The definition of this distance is as below.
Definition 10
For any two TSULNs \(\delta_{1} = ([s_{{\alpha_{1} }} ,s_{{\beta_{1} }} ],(\tau_{1} ,\eta_{1} ,\vartheta_{1} ))\) and \(\delta_{2} = ([s_{{\alpha_{2} }} ,s_{{\beta_{2} }} ],(\tau_{2} ,\eta_{2} ,\vartheta_{2} ))\), q ≥ 1, the TSUL generalized distance between them is defined as:
where φ is a distance parameter, with φ ≥ 1.
When φ = 1, the Eq. (12) reduces to the TSUL Hamming distance:
When φ = 2, the Eq. (12) reduces to the TSUL Euclidean distance:
When φ → ∞, the Eq. (12) reduces to the TSUL Chebyshev distance:
Theorem 2
Let \(\delta_{1} = ([s_{{\alpha_{1} }} ,s_{{\beta_{1} }} ],(\tau_{1} ,\eta_{1} ,\vartheta_{1} ))\), \(\delta_{2} = ([s_{{\alpha_{2} }} ,s_{{\beta_{2} }} ],(\tau_{2} ,\eta_{2} ,\vartheta_{2} ))\) and \(\delta_{3} = ([s_{{\alpha_{3} }} ,s_{{\beta_{3} }} ],(\tau_{3} ,\eta_{3} ,\vartheta_{3} ))\) be any three TSULNs and q ≥ 1, the generalized distance for TSULNs satisfies the below properties:
-
(1)
If δ1 = δ2, then the \(D_{\varphi } (\delta_{1} ,\delta_{2} ) = 0\),
-
(2)
\(D_{\varphi } (\delta_{1} ,\delta_{2} ) = D_{\varphi } (\delta_{2} ,\delta_{1} )\),
-
(3)
\(0 \le D_{\varphi } (\delta_{1} ,\delta_{2} ) \le 1\),
-
(4)
\(D_{\varphi } (\delta_{1} ,\delta_{2} ) + D_{\varphi } (\delta_{2} ,\delta_{3} ) \ge D_{\varphi } (\delta_{1} ,\delta_{3} )\).
Proof
(i) The properties (1) and (2) can be easily proved.
(ii) According to Definitions 7 ~ 10, we have \(\alpha_{i} ,\beta_{i} \in [0,k - 1]\), \(\tau_{i} ,\eta_{i} ,\vartheta_{i} \in [0,1]\), \(0 \le \tau_{i}^{q} + \eta_{i}^{q} + \vartheta_{i}^{q} \le 1\), q, φ ≥ 1 (i = 1,2 ,3), then
Since \(f(\varphi ) = \left( {a^{\varphi } + b^{\varphi } + c^{\varphi } } \right)^{{\frac{1}{\varphi }}}\)(a, b, c > 0; φ ≥ 1) decreases monotonically with the parameter φ. Let φ = 1, then we have \(D_{\varphi } (\delta_{1} ,\delta_{2} ) \le D_{1} (\delta_{1} ,\delta_{2} )\).
Further, we can easily prove that \(D_{\varphi } (\delta_{1} ,\delta_{2} ) \ge 0\).
Therefore, we can get \(0 \le D_{\varphi } (\delta_{1} ,\delta_{2} ) \le D_{1} (\delta_{1} ,\delta_{2} ) \le 1\), that is, the proof of property (3) is complete.
Since \((a + b)^{{\frac{1}{\varphi }}} \le a^{{\frac{1}{\varphi }}} + b^{{\frac{1}{\varphi }}}\)(φ ≥ 1), then we have
Therefore, the proof of property (4) is complete.
Example 1
Suppose \(\delta_{1} = ([s_{4} ,s_{6} ],(0.8,0.3,0.5))\) and \(\delta_{2} = ([s_{3} ,s_{4} ],(0.3,0.6,0.6))\) are two TSULNs, then the Hamming and Euclidean distances between δ1 and δ2 can be obtained by Eqs. (13) ~ (14) respectively (q = 2,k = 7). It is easy to get \(\pi_{1} = \sqrt {1 - 0.8^{2} - 0.3^{2} - 0.5^{2} } { = }0.141\) and \(\pi_{2} = \sqrt {1 - 0.3^{2} - 0.6^{2} - 0.6^{2} } { = }0.436\), then.
Hamming distance:
Euclidean distance:
The TSUL-weighted AOs and TSULHM AOs
We propose the TSULWA and TSULWG operators based on the operation rules of TSULNs, and then we devise the TSULHM and TSULWHM operators considering the interrelationship between input arguments.
The TSUL-weighted AOs
In this sub-section, we define two TSUL-weighted AOs, namely TSULWA and TSULWG operators. They do not concern the correlation between input arguments.
Definition 11
Suppose \(\delta_{j} = ([s_{{\alpha_{j} }} ,s_{{\beta_{j} }} ],(\tau_{j} ,\eta_{j} ,\vartheta_{j} ))\) (j = 1, 2 ,…,n) are a set of TSULNs, w = (w1,w2,…,wn)T is weight vector of δj(j = 1, 2,…,n), with wj > 0 and \(\sum\nolimits_{j = 1}^{n} {w_{j} = 1}\). The TSULWA and TSULWG operators are defined as.
Theorem 3.
Suppose \(\delta_{j} = ([s_{{\alpha_{j} }} ,s_{{\beta_{j} }} ],(\tau_{j} ,\eta_{j} ,\vartheta_{j} ))\)(j = 1,2,..,n) are a set of TSULNs, then the aggregated results of Eqs. (16) and (17) are still TSULNs, where.
Proof: it is easy to prove that the aggregated results of TSULWA and TSULWG operators are still TSULNs, and the proof process is omitted here. Next, we utilize the mathematical induction method to prove the Eqs. (18) and (19). We first prove the TSULWA operator, and the proof process is as follows:
(1) when n = 1, the Eq. (18) is clearly true. And when n = 2, according to Definition 9, we can get.
\(w_{1} \cdot \delta_{1} = \Biggl( \left[ {s_{{k - k\left( {1 - \frac{{\alpha_{1} }}{k}} \right)^{{w_{1} }} }}, s_{{k - k\left( {1 - \frac{{\beta_{1} }}{k}} \right)^{{w_{1} }} }} } \right],\left( {\sqrt[q]{{1 - (1 - \tau_{1}^{q} )^{{w_{1} }} }},(\eta_{1} )^{{w_{1} }} ,(\vartheta_{1} )^{{w_{1} }} } \right) \Biggr)\),\(w_{2} \cdot \delta_{2} = \Biggl( \left[ {s_{{k - k\left( {1 - \frac{{\alpha_{2} }}{k}} \right)^{{w_{2} }} }} ,s_{{k - k\left( {1 - \frac{{\beta_{2} }}{k}} \right)^{{w_{2} }} }} } \right],\Biggl( {\sqrt[q]{{1 - (1 - \tau_{2}^{q} )^{{w_{2} }} }},(\eta_{2} )^{{w_{2} }} ,(\vartheta_{2} )^{{w_{2} }} } \Biggr) \Biggr)\).
Then
When n = 2, the Eq. (18) holds.
(2) when n = m, the Eq. (18) holds. That is,
(3) when n = m + 1, we can get
Obviously, when n = m + 1, the Eq. (18) also holds. From the above proof, we can know that Eq. (18) holds for any j. In the same way, the Eq. (19) holds for any j can be proved.
According to Theorems 1 and 3, we can easily prove that the TSULWA and TSULWG operators have the following properties:
Theorem 4
Suppose δj (j = 1, 2,…, n) is a family of TSULNs,
-
(1)
(Idempotency). If δj = δ for all j, then
$$ TSULWA(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = TSULWG(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = \delta $$(20) -
(2)
(Monotonicity). If δj* (j = 1, 2,…, n) is also a set of TSULNs, and δj ≤δj*, then
$$ TSULWA(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) \le TSULWA(\delta_{1}^{*} ,\delta_{2}^{*} , \ldots ,\delta_{n}^{*} ) $$(21)$$ TSULWG(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) \le TSULWG(\delta_{1}^{*} ,\delta_{2}^{*} , \ldots ,\delta_{n}^{*} ) $$(22) -
(3)
(Boundedness). If \(P^{ - } = \min \delta_{j} = \left( {[s_{{\mathop {\min }\nolimits_{j} \alpha_{j} }} ,s_{{\mathop {\min }\nolimits_{j} \beta_{j} }} ],(\mathop {\min }\nolimits_{j} (\tau_{j} ),\mathop {\max }\nolimits_{j} (\eta_{j} ),\mathop {\max }\nolimits_{j} (\vartheta_{j} ))} \right)\),
\(P^{ + } = \max \delta_{j} = \left( {[s_{{\mathop {\max }\nolimits_{j} \alpha_{j} }} ,s_{{\mathop {\max }\limits_{j} \beta_{j} }} ]} \right)(\mathop {\max }\nolimits_{j} (\tau_{j} ),\mathop {\min }\nolimits_{j} (\eta_{j} ),\mathop {\min }\nolimits_{j} (\vartheta_{j} ))\), then
The following particular cases of the TSULWA and TSULWG operators are discussed when different elements in TSULN \(\delta_{j} = ([s_{{\alpha_{j} }} ,s_{{\beta_{j} }} ],(\tau_{j} ,\eta_{j} ,\vartheta_{j} ))\) are valued in various situations:
-
(1)
If q = 1, the TSULWA, and TSULWG operators are reduced into the picture of uncertain linguistic weighted averaging and geometric operators, i.e., PULWA and PULWG.
$$ PULWA(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = \left( {\left[ {s_{{k - k\prod\limits_{j = 1}^{n} {\left( {1 - \frac{{\alpha_{j} }}{k}} \right)^{{w_{j} }} } }} ,s_{{k - k\prod\limits_{j = 1}^{n} {\left( {1 - \frac{{\beta_{j} }}{k}} \right)^{{w_{j} }} } }} } \right],\left( {1 - \prod\limits_{j = 1}^{n} {(1 - \tau_{j} )^{{w_{j} }} } ,\prod\limits_{j = 1}^{n} {\eta_{j}^{{w_{j} }} } ,\prod\limits_{j = 1}^{n} {\vartheta_{j}^{{w_{j} }} } } \right)} \right) $$(25)$$ PULWG(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = \left( {\left[ {s_{{k\prod\limits_{j = 1}^{n} {\left( {\frac{{\alpha_{j} }}{k}} \right)^{{w_{j} }} } }} ,s_{{k\prod\limits_{j = 1}^{n} {\left( {\frac{{\beta_{j} }}{k}} \right)^{{w_{j} }} } }} } \right],\left( {\prod\limits_{j = 1}^{n} {\tau_{j}^{{w_{j} }} } ,1 - \prod\limits_{j = 1}^{n} {(1 - \eta_{j} )^{{w_{j} }} } ,1 - \prod\limits_{j = 1}^{n} {(1 - \vartheta_{j} )^{{w_{j} }} } } \right)} \right) $$(26)Note that Eqs. (25–26) differ from the PULWA and PULWG operators[30] in the uncertain linguistic part.
-
(2)
If q = 2, αj = βj, the TSULWA operator is reduced into the spherical linguistic fuzzy weighted averaging (SLFWA) operator and geometric (SLFWG) operator.
$$ SLFWA(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = \left( {s_{{k - k\prod\limits_{j = 1}^{n} {\left( {1 - \frac{{\alpha_{j} }}{k}} \right)^{{w_{j} }} } }} ,\left( {\left( {1 - \prod\limits_{j = 1}^{n} {(1 - \tau_{j}^{2} )^{{w_{j} }} } } \right)^{\frac{1}{2}} ,\prod\limits_{j = 1}^{n} {\eta_{j}^{{w_{j} }} } ,\prod\limits_{j = 1}^{n} {\vartheta_{j}^{{w_{j} }} } } \right)} \right) $$(27)$$ SLFWG(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = \left( {s_{{k\prod\limits_{j = 1}^{n} {\left( {\frac{{\alpha_{j} }}{k}} \right)^{{w_{j} }} } }} ,\left( {\prod\limits_{j = 1}^{n} {\tau_{j}^{{w_{j} }} } ,\left( {1 - \prod\limits_{j = 1}^{n} {(1 - \eta_{j}^{2} )^{{w_{j} }} } } \right)^{\frac{1}{2}} ,\left( {1 - \prod\limits_{j = 1}^{n} {(1 - \vartheta_{j}^{2} )^{{w_{j} }} } } \right)^{\frac{1}{2}} } \right)} \right) $$(28)Note that Eq. (27) differs from the SLFWA operator [72] in the linguistic part.
-
(3)
If ηj = 0, the TSULWA and TSULWG operators are reduced into the q-rung orthopair uncertain linguistic weighted averaging and geometric operators, i.e., q-ROULWA and q-ROULWG.
$$ q - ROULWA(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = \left( {\left[ {s_{{k - k\prod\limits_{j = 1}^{n} {\left( {1 - \frac{{\alpha_{j} }}{k}} \right)^{{w_{j} }} } }} ,s_{{k - k\prod\limits_{j = 1}^{n} {\left( {1 - \frac{{\beta_{j} }}{k}} \right)^{{w_{j} }} } }} } \right],\left( {\left( {1 - \prod\limits_{j = 1}^{n} {(1 - \tau_{j}^{q} )^{{w_{j} }} } } \right)^{\frac{1}{q}} ,\prod\limits_{j = 1}^{n} {\vartheta_{j}^{{w_{j} }} } } \right)} \right) $$(29)$$ q - ROULWG(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = \left( {\left[ {s_{{k\prod\limits_{j = 1}^{n} {\left( {\frac{{\alpha_{j} }}{k}} \right)^{{w_{j} }} } }} ,s_{{k\prod\limits_{j = 1}^{n} {\left( {\frac{{\beta_{j} }}{k}} \right)^{{w_{j} }} } }} } \right],\left( {\prod\limits_{j = 1}^{n} {\tau_{j}^{{w_{j} }} } ,\left( {1 - \prod\limits_{j = 1}^{n} {(1 - \vartheta_{j}^{q} )^{{w_{j} }} } } \right)^{\frac{1}{q}} } \right)} \right) $$(30)Note that Eqs. (29–30) differ from the q-ROULWA and q-ROULWG operators [25] in the uncertain linguistic part.
-
(4)
If q = 2, ηj = 0, the TSULWA and TSULWG operators are reduced into the Pythagorean uncertain linguistic weighted averaging and geometric operators, i.e., PyULWA and PyULWG.
$$ PyULWA(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = \left( {\left[ {s_{{k - k\prod\limits_{j = 1}^{n} {\left( {1 - \frac{{\alpha_{j} }}{k}} \right)^{{w_{j} }} } }} ,s_{{k - k\prod\limits_{j = 1}^{n} {\left( {1 - \frac{{\beta_{j} }}{k}} \right)^{{w_{j} }} } }} } \right],\left( {\left( {1 - \prod\limits_{j = 1}^{n} {(1 - \tau_{j}^{2} )^{{w_{j} }} } } \right)^{\frac{1}{2}} ,\prod\limits_{j = 1}^{n} {\vartheta_{j}^{{w_{j} }} } } \right)} \right) $$(31)$$ PyULWG(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = \left( {\left[ {s_{{k\prod\limits_{j = 1}^{n} {\left( {\frac{{\alpha_{j} }}{k}} \right)^{{w_{j} }} } }} ,s_{{k\prod\limits_{j = 1}^{n} {\left( {\frac{{\beta_{j} }}{k}} \right)^{{w_{j} }} } }} } \right],\left( {\prod\limits_{j = 1}^{n} {\tau_{j}^{{w_{j} }} } ,\left( {1 - \prod\limits_{j = 1}^{n} {(1 - \vartheta_{j}^{2} )^{{w_{j} }} } } \right)^{\frac{1}{2}} } \right)} \right) $$(32)Note that Eqs. (31–32) differ from the PyULWA and PyULWG operators [17] in the uncertain linguistic part.
-
(5)
If q = 2, αj = βj, ηj = 0, the TSULWA and TSULWG operators are reduced into the Pythagorean linguistic weighted averaging and geometric operators, i.e., PyLWA and PyLWG.
$$ PyLWA(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = \left( {s_{{k - k\prod\limits_{j = 1}^{n} {\left( {1 - \frac{{\alpha_{j} }}{k}} \right)^{{w_{j} }} } }} ,\left( {\left( {1 - \prod\limits_{j = 1}^{n} {(1 - \tau_{j}^{2} )^{{w_{j} }} } } \right)^{\frac{1}{2}} ,\prod\limits_{j = 1}^{n} {\vartheta_{j}^{{w_{j} }} } } \right)} \right) $$(33)$$\begin{aligned} &PyLWG(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} )\\ &\quad = \left(s_{{k\prod\limits_{j = 1}^{n} {\left( {\frac{{\alpha_{j} }}{k}} \right)^{{w_{j} }} } }}, \left( {\prod\limits_{j = 1}^{n} {\tau_{j}^{{w_{j} }} } ,\left( {1 - \prod\limits_{j = 1}^{n} {(1 - \vartheta_{j}^{2} )^{{w_{j} }} } } \right)^{\frac{1}{2}} } \right)\right) \end{aligned}$$(34)Note that Eqs. (33–34) differ from the PyLWA and PyLWG operators [73] in the linguistic part.
-
(6)
If q = 1, ηj = 0, the TSULWG operator is reduced into the intuitionistic uncertain linguistic weighted geometric operator, i.e., IULWG.
$$\begin{aligned} &IULWG(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n}) \\ &\quad = \left(\left[{s_{{k\prod\limits_{j = 1}^{n} {\left( {\frac{{\alpha_{j} }}{k}} \right)^{{w_{j} }} } }} ,s_{{k\prod\limits_{j = 1}^{n} {\left( {\frac{{\beta_{j} }}{k}} \right)^{{w_{j} }} } }} } \right],\right.\\ &\qquad \left.\left({\prod\limits_{j = 1}^{n} {\tau_{j}^{{w_{j} }} } ,1 - \prod\limits_{j = 1}^{n} {(1 - \vartheta_{j} )^{{w_{j} }}}}\right)\right) \end{aligned}$$(35)Note that Eq. (35) differs from the IULWG operator [9] in the uncertain linguistic part.
-
(7)
If q = 1, αj = βj, ηj = 0, the TSULWA operator is reduced into the intuitionistic linguistic weighted averaging (ILWA) operator.
$$\begin{aligned}& ILWA(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} )\\&\quad = \left( {s_{{k - k\prod\limits_{j = 1}^{n} {\left( {1 - \frac{{\alpha_{j} }}{k}} \right)^{{w_{j} }} } }} ,\left( {1 - \prod\limits_{j = 1}^{n} {(1 - \tau_{j} )^{{w_{j} }} } ,\prod\limits_{j = 1}^{n} {\vartheta_{j}^{{w_{j} }} } } \right)} \right)\end{aligned}$$(36)
Note that Eq. (36) differs from the ILWA operator [6] in the linguistic part.
Example 2. Let δ1 = ([s5, s5], (0.3, 0.5, 0.8)), δ2 = ([s2, s3], (0.7, 0.3, 0.6)) and δ3 = ([s4, s6], (0.6, 0.6, 0.4)) be three TSULNs and q = 2, k = 7, the weight vector of δj (j = 1, 2, 3) is w = (0.3, 0.4, 0.3), then
The TSULHM AOs
In this sub-section, we define the TSULHM operator and its weighted form. They have the ability to capture the interrelationship between input arguments.
Definition 12
Suppose \(\delta_{j} = ([s_{{\alpha_{j} }} ,s_{{\beta_{j} }} ],(\tau_{j} ,\eta_{j} ,\vartheta_{j} ))\)(j = 1,2,…,n) is a family of TSULNs, σ, ρ ≥ 0 and σ + ρ > 0. The TSULHM is a mapping Ω n → Ω:
We can obtain the below result based on Definition 9.
Theorem 5
Let σ, ρ ≥ 0 and σ + ρ > 0, \(\delta_{j} = ([s_{{\alpha_{j} }} ,s_{{\beta_{j} }} ],(\tau_{j} ,\eta_{j} ,\vartheta_{j} ))\)(j = 1, 2, …, n) is a family of TSULNs. By using Eq. (38), we can obtain that the aggregated result of TSULNs is still a TSULN, and.
Proof: On the basis of Definition 9, we can obtain.
\(\delta_{j}^{\sigma } = \bigg(\Big[s_{{k\left( {\frac{{\alpha_{j} }}{k}} \right)^{\sigma } }} ,s_{{k\left( {\frac{{\beta_{j} }}{k}} \right)^{\sigma } }} \Big], \bigg(\tau_{j}^{\sigma } ,\sqrt[q]{{1 - \left( {1 - \eta_{j}^{q} } \right)^{\sigma } }},\sqrt[q]{{1 - \left( {1 - \vartheta_{j}^{q} } \right)^{\sigma } }}\bigg)\bigg)\), \(\delta_{l}^{\rho } = \bigg( \Big[s_{{k\left( {\frac{{\alpha_{l} }}{k}} \right)^{\rho } }} ,s_{{k\left( {\frac{{\beta_{l} }}{k}} \right)^{\rho } }} \Big], \bigg(\tau_{l}^{\rho } ,\sqrt[q]{{1 - \left( {1 - \eta_{l}^{q} } \right)^{\rho } }},\sqrt[q]{{1 - \left( {1 - \vartheta_{l}^{q} } \right)^{\rho } }} \bigg)\bigg)\).
And \(\delta_{j}^{\sigma } \otimes \delta_{l}^{\rho } = \bigg(\left[ {s_{{k\left( {\frac{{\alpha_{j} }}{k}} \right)^{\sigma } \left( {\frac{{\alpha_{l} }}{k}} \right)^{\rho } }} ,s_{{k\left( {\frac{{\beta_{j} }}{k}} \right)^{\sigma } \left( {\frac{{\beta_{l} }}{k}} \right)^{\rho } }} } \right],\bigg(\tau_{j}^{\sigma } \tau_{l}^{\rho } ,\sqrt[q]{{1 - \left( {1 - \eta_{j}^{q} } \right)^{\sigma } \left( {1 - \eta_{l}^{q} } \right)^{\rho } }}, \sqrt[q]{{1 - \left( {1 - \vartheta_{j}^{q} } \right)^{\sigma } \left( {1 - \vartheta_{l}^{q} } \right)^{\rho } }}\bigg)\bigg)\).
Then
So,
Thus, Eq. (38) holds. Meanwhile, Eq. (38) can be easily proved to be TSULN. Therefore, Theorem 5 is true.
According to Theorem 1 and Theorem 5, the following properties of the TSULHM operator can be easily proved:
Theorem 6
Suppose δj (j = 1, 2,…, n) is a family of TSULNs,
-
(1)
(Idempotency). If δj = δ for all j, then
$$ TSULHM(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = \delta $$(39) -
(2)
(Monotonicity). If δj* (j = 1, 2,…, n) is also a set of TSULNs, and δj ≤δj*, then
$$ TSULHM^{\sigma ,\rho } (\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) \le TSULHM^{\sigma ,\rho } (\delta_{1}^{ * } ,\delta_{2}^{ * } , \ldots ,\delta_{n}^{ * } ) $$(40) -
(3)
(Boundedness). If.
\(P^{ - } = \min \delta_{j} = \big([s_{{\mathop {\min }\nolimits_{j} \alpha_{j} }} ,s_{{\mathop {\min }\nolimits_{j} \beta_{j} }}], (\mathop {\min }\limits_{j} (\tau_{j} ),\mathop {\max }\nolimits_{j} (\eta_{j} ),\mathop {\max }\nolimits_{j} (\vartheta_{j}))\big)\), \(P^{+} = \max \delta_{j} = ([s_{{\mathop {\max }\limits_{j} \alpha_{j} }} ,s_{{\mathop {\max }\nolimits_{j} \beta_{j}}}]) (\mathop{\max }\nolimits_{j} (\tau_{j}), \mathop{\min}\limits_{j} (\eta_{j}), \mathop{\min}\nolimits_{j} (\vartheta_{j}))\), then
Next, some particular cases of the TSULHM operator are discussed about the parameters σ and ρ.
-
(1)
If σ → 0, the Eq. (38) is reduced to a TSUL generalized linear ascending weighted mean operator, i.e.,
$$ \begin{gathered} \mathop {\lim }\limits_{\sigma \to 0} TSULHM^{\sigma ,\rho } (\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) \hfill \\ = \left( {\left[ \begin{gathered} s_{{k\left( {1 - \prod\limits_{j = 1}^{n} {\left( {1 - j\left( {\frac{{\alpha_{j} }}{k}} \right)^{\rho } } \right)^{{\tfrac{2}{n(n + 1)}}} } } \right)^{{\tfrac{1}{\rho }}} }} , \hfill \\ s_{{k\left( {1 - \prod\limits_{j = 1}^{n} {\left( {1 - j\left( {\frac{{\beta_{j} }}{k}} \right)^{\rho } } \right)^{{\tfrac{2}{n(n + 1)}}} } } \right)^{{\tfrac{1}{\rho }}} }} \hfill \\ \end{gathered} \right],\left( \begin{gathered} \left( {1 - \prod\limits_{j = 1}^{n} {\left( {1 - (\tau_{j}^{q} )^{\rho } } \right)^{{\tfrac{2i}{{n(n + 1)}}}} } } \right)^{{\tfrac{1}{q\rho }}} ,\left( {1 - \left( {1 - \prod\limits_{j = 1}^{n} {\left( {1 - (1 - \eta_{j}^{q} )^{\rho } } \right)^{{\tfrac{2i}{{n(n + 1)}}}} } } \right)^{{\tfrac{1}{\rho }}} } \right)^{{\tfrac{1}{q}}} , \hfill \\ \left( {1 - \left( {1 - \prod\limits_{j = 1}^{n} {\left( {1 - (1 - \vartheta_{j}^{q} )^{\rho } } \right)^{{\tfrac{2i}{{n(n + 1)}}}} } } \right)^{{\tfrac{1}{\rho }}} } \right)^{{\tfrac{1}{q}}} \hfill \\ \end{gathered} \right)} \right) \hfill \\ \end{gathered} $$(42) -
(2)
If ρ → 0, the Eq. (38) is reduced to a TSUL generalized linear descending weighted men operator, i.e.,
$$ \begin{gathered} \mathop {\lim }\limits_{\rho \to 0} TSULHM^{\sigma ,\rho } (\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) \hfill \\ = \left( {\left[ \begin{gathered} s_{{k\left( {1 - \prod\limits_{j = 1}^{n} {\left( {1 - (n + 1 - j)\left( {\frac{{\alpha_{j} }}{k}} \right)^{\sigma } } \right)^{{\tfrac{2}{n(n + 1)}}} } } \right)^{{\tfrac{1}{\sigma }}} }} , \hfill \\ s_{{k\left( {1 - \prod\limits_{j = 1}^{n} {\left( {1 - (n + 1 - j)\left( {\frac{{\beta_{j} }}{k}} \right)^{\sigma } } \right)^{{\tfrac{2}{n(n + 1)}}} } } \right)^{{\tfrac{1}{\sigma }}} }} \hfill \\ \end{gathered} \right],\left( \begin{gathered} \left( {1 - \prod\limits_{j = 1}^{n} {\left( {1 - (\tau_{j}^{q} )^{\sigma } } \right)^{{\tfrac{2(n + 1 - j)}{{n(n + 1)}}}} } } \right)^{{\tfrac{1}{q\sigma }}} ,\left( {1 - \left( {1 - \prod\limits_{j = 1}^{n} {\left( {1 - (1 - \eta_{j}^{q} )^{\sigma } } \right)^{{\tfrac{2(n + 1 - j)}{{n(n + 1)}}}} } } \right)^{{\tfrac{1}{\sigma }}} } \right)^{{\tfrac{1}{q}}} , \hfill \\ \left( {1 - \left( {1 - \prod\limits_{j = 1}^{n} {\left( {1 - (1 - \vartheta_{j}^{q} )^{\sigma } } \right)^{{\tfrac{2(n + 1 - j)}{{n(n + 1)}}}} } } \right)^{{\tfrac{1}{\sigma }}} } \right)^{{\tfrac{1}{q}}} \hfill \\ \end{gathered} \right)} \right) \hfill \\ \end{gathered} $$(43) -
(3)
If σ = ρ = 0.5, the Eq. (38) is reduced to a TSUL basic HM operator, i.e.,
$$ \begin{gathered} TSULHM^{0.5,0.5} (\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) \hfill \\ \quad =\left( {\left[ \begin{gathered} s_{{k\left( {1 - \prod\limits_{j = 1,l = j}^{n} {\left( {1 - \left( {\frac{{\alpha_{j} }}{k}} \right)^{0.5} \left( {\frac{{\alpha_{l} }}{k}} \right)^{0.5} } \right)^{{\tfrac{2}{n(n + 1)}}} } } \right)}} , \hfill \\ s_{{k\left( {1 - \prod\limits_{j = 1,l = j}^{n} {\left( {1 - \left( {\frac{{\beta_{j} }}{k}} \right)^{0.5} \left( {\frac{{\beta_{l} }}{k}} \right)^{0.5} } \right)^{{\tfrac{2}{n(n + 1)}}} } } \right)}} \hfill \\ \end{gathered} \right],\left( \begin{gathered} \left( {1 - \prod\limits_{j = 1,l = j}^{n} {\left( {1 - (\tau_{j}^{q} )^{0.5} (\tau_{l}^{q} )^{0.5} } \right)^{{\tfrac{2}{n(n + 1)}}} } } \right)^{{\tfrac{1}{q}}} ,\left( {1 - \left( {1 - \prod\limits_{j = 1,l = j}^{n} {\left( {1 - (1 - \eta_{j}^{q} )^{0.5} (1 - \eta_{l}^{q} )^{0.5} } \right)^{{\tfrac{2}{n(n + 1)}}} } } \right)} \right)^{{\tfrac{1}{q}}} , \hfill \\ \left( {1 - \left( {1 - \prod\limits_{j = 1,l = j}^{n} {\left( {1 - (1 - \vartheta_{j}^{q} )^{0.5} (1 - \vartheta_{l}^{q} )^{0.5} } \right)^{{\tfrac{2}{n(n + 1)}}} } } \right)} \right)^{{\tfrac{1}{q}}} \hfill \\ \end{gathered} \right)} \right) \hfill \\ \end{gathered} $$(44) -
(4)
If σ = ρ = 1, the Eq. (38) is reduced to a TSUL line HM operator, i.e.,
$$ \begin{gathered} TSULHM^{1,1} (\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) \hfill \\ \quad =\left( {\left[ \begin{gathered} s_{{k\left( {1 - \prod\limits_{j = 1,l = j}^{n} {\left( {1 - \left( {\frac{{\alpha_{j} }}{k}} \right)\left( {\frac{{\alpha_{l} }}{k}} \right)} \right)^{{\tfrac{2}{n(n + 1)}}} } } \right)^{{\tfrac{1}{2}}} }} , \hfill \\ s_{{k\left( {1 - \prod\limits_{j = 1,l = j}^{n} {\left( {1 - \left( {\frac{{\beta_{j} }}{k}} \right)\left( {\frac{{\beta_{l} }}{k}} \right)} \right)^{{\tfrac{2}{n(n + 1)}}} } } \right)^{{\tfrac{1}{2}}} }} \hfill \\ \end{gathered} \right],\left( \begin{gathered} \left( {1 - \prod\limits_{j = 1,l = j}^{n} {\left( {1 - \tau_{j}^{q} \tau_{l}^{q} } \right)^{{\tfrac{2}{n(n + 1)}}} } } \right)^{{\tfrac{1}{2q}}} ,\left( {1 - \left( {1 - \prod\limits_{j = 1,l = j}^{n} {\left( {1 - (1 - \eta_{j}^{q} )(1 - \eta_{l}^{q} )} \right)^{{\tfrac{2}{n(n + 1)}}} } } \right)^{{\tfrac{1}{2}}} } \right)^{{\tfrac{1}{q}}} , \hfill \\ \left( {1 - \left( {1 - \prod\limits_{j = 1,l = j}^{n} {\left( {1 - (1 - \vartheta_{j}^{q} )(1 - \vartheta_{l}^{q} )} \right)^{{\tfrac{2}{n(n + 1)}}} } } \right)^{{\tfrac{1}{2}}} } \right)^{{\tfrac{1}{q}}} \hfill \\ \end{gathered} \right)} \right) \hfill \\ \end{gathered} $$(45)
Example 3. Let δ1 = ([s5, s6],(0.5, 0.5, 0.7)), δ2 = ([s3, s5],(0.8, 0.6, 0.4)) and δ3 = ([s0,s2],(0.7, 0.8, 0.4)) be three TSULNs, q = 3, k = 7, σ = ρ = 1, then
From Definition 12, we realize that the TSULHM operator does not take into account the importance of arguments for aggregation. However, in many practical decision-making scenarios, attribute weights play a major role in the aggregation process. For this, we should embed weights in the TSULHM operator, thus the TSULWHM operator is proposed as below:
Definition 13
Suppose \(\delta_{j} = ([s_{{\alpha_{j} }} ,s_{{\beta_{j} }} ],(\tau_{j} ,\eta_{j} ,\vartheta_{j} ))\)(j = 1,2 ,…,n) is a family of TSULNs, σ, ρ ≥ 0 and σ + ρ > 0. w = (w1,w2,…,wn)T is the weight vector of δj (j = 1,2 ,…,n), with wj > 0 and \(\sum\nolimits_{j = 1}^{n} {w_{j} = 1}\). The TSULWHM is a mapping Ω n → Ω:
Similar to Theorem 5, Theorem 7 can be derived easily as below.
Theorem 7
Suppose \(\delta_{j} = ([s_{{\alpha_{j} }} ,s_{{\beta_{j} }} ],(\tau_{j} ,\eta_{j} ,\vartheta_{j} ))\)(j = 1,2 ,…,n) is a family of TSULNs, σ, ρ ≥ 0 and σ + ρ > 0. w = (w1, w2,…,wn)T is the weight vector of δj(j = 1,2 ,…,n), with wj > 0 and \(\sum\nolimits_{j = 1}^{n} {w_{j} = 1}\). Then according to Eq. (47), the aggregated result is still a TSULN, and even.
Similar to Theorem 4, Theorem 5 is true and can be proved.
It is worth noting that we also can prove that the TSULWHM operator has the Boundedness and Monotonicity, but it has not the property of Idempotency.
A novel MAGDM framework based on TSUL-MARCOS
The MAGDM problems with TSULNs are described as: Suppose H = {h1, h2,…,hm} is a finite alternative set, A = {a1, a2,…,an} is an attribute set, and the attribute weight vector is W = {w1, w2,…,wn}T,\({\sum }_{j=1}^{n}{w}_{j}=1, {w}_{j}\in [\mathrm{0,1}]\). E = {e1, e2,…,ep} is a collection of experts. As different experts possess different knowledge, experience and industries, different weights are assigned to the corresponding attributes of different experts, but not the same weight is assigned to all attributes, so more reasonable decision-making results can be obtained. Let the weight of expert eε corresponding to attribute aj be \({\omega }_{\varepsilon }^{(j)}\), with \(0\le {\omega }_{\varepsilon }^{\left(j\right)}\le 1, {\sum }_{\varepsilon =1}^{p}{\omega }_{\varepsilon }^{(j)}=1\). The evaluation value given by expert eε (ε = 1,2 ,…,p) of alternative hi(i = 1,2 ,…,m) under the attribute aj(j = 1,2 ,…,n) is represented by TSULN \(d_{ij}^{\varepsilon } = \left( {[s_{{\alpha_{ij}^{\varepsilon } }} ,s_{{\beta_{ij}^{\varepsilon } }} ],\left( {\tau_{ij}^{\varepsilon } ,\eta_{ij}^{\varepsilon } ,\vartheta_{ij}^{\varepsilon } } \right)} \right)\), the constructed evaluation matrix is expressed as Dε = [dijε]m×n,(i = 1,2 ,…,m; j = 1,2,…,n; ε = 1,2,…,p).
Calculate expert weights based on TSUL similarity
According to the difference of judgment information given by experts, we propose a distance measure-based similarity approach to determine the expert weight with regard to attribute in TSUL environment. Under one attribute, when the expert’s judgment information is more consistent with the information provided by other experts, the expert’s weight is higher; On the contrary, experts are assigned a lower weight.
Firstly, the decision matrix Dk(k = 1,2 ,…,p) provided by the expert ek is transformed into an evaluation matrix for each attribute, that is, F(j)( j = 1,2 ,…,n), it is denoted as follows:
where \(\xi_{ki}^{(j)}\) is equivalent to dijk.
For the matrix F(j), the evaluation means the value of the alternative hi for the attribute aj is \(\hat{\xi }_{i}^{(j)} = \left( {[s_{{\hat{\alpha }_{i}^{(j)} }} ,s_{{\hat{\beta }_{i}^{(j)} }} ],(\hat{\tau }_{i}^{(j)} ,\hat{\eta }_{i}^{(j)} ,\hat{\vartheta }_{i}^{(j)} )} \right)\).
As for the alternative hi ∈ H, the TSUL similarity measure \(sim_{ki}^{(j)}\) between \(\xi_{ki}^{(j)}\) and \(\hat{\xi }_{i}^{(j)}\) based on the TUSL generalized distance measure can be defined as
where \(D_{\varphi } (\xi_{ki}^{(j)} ,\hat{\xi }_{i}^{(j)} )\) is the TSUL generalized distance measured between \(\xi_{ki}^{(j)}\) and \(\hat{\xi }_{i}^{(j)}\) defined by Eq. (12).
For attribute aj ∈ A, we can construct the similarity matrix S(j) by using the TSUL similarity measure \(sim_{ki}^{(j)}\).
Based on the similarity matrix S(j), we can use Eq. (52) to calculate the overall similarity degree of expert ek for attribute aj ∈ A.
Lastly, the weight of expert ek on the attribute aj ∈ A can be obtained as below:
Obviously, \(0\le {\omega }_{k}^{\left(j\right)}\le 1, {\sum }_{k=1}^{p}{\omega }_{k}^{(j)}=1\).
Calculate attribute weights based on MDM
When attribute weight information is completely unknown, the uncertainty of attribute weight can affect the final ranking result of alternatives. Generally, if there is a small difference between the attribute values rij(i = 1,2,…,m; j = 1,2,…,n) in attribute aj of all alternatives, it means that the attribute aj is of low importance in the ranking of all alternatives, and we can assign a small weight to this attribute. Otherwise, a larger weight is assigned. Therefore, we can adopt the MDM [74, 75] to obtain the attribute weight vector.
For the attribute aj ∈ A, the deviation of alternative hi to all other alternatives hl (l = 1,2,…,m, l ≠ i) can be expressed as:
Dj(w) represents the deviation value from all alternatives to other alternatives for attribute aj ∈ A, so it can be expressed as:
where \(D_{\varphi } (r_{ij} ,r_{lj} )\) represents the TSUL generalized distance measure between rij and rlj, which can be obtained from Eq. (12).
Therefore, we can build a linear mathematical model that maximizes all deviations for all attributes to assign weight vector W, as follows:
To solve Eq. (56), we apply the Lagrange function with the Lagrange multiplier λ. Then we have
Let \(\left\{ {\begin{array}{*{20}c} {\frac{{\partial L(w_{j} ,\lambda )}}{{\partial w_{j} }} = \sum\nolimits_{i = 1}^{m} {\sum\nolimits_{l = 1}^{m} {D_{\varphi } (r_{ij} ,r_{lj} )w_{j} } + 2\lambda w_{j} } = 0} \\ {\frac{{\partial L(w_{j} ,\lambda )}}{\partial \lambda } = \sum\nolimits_{j = 1}^{n} {w_{j}^{2} } - 1 = 0 \, } \\ \end{array} } \right.\)
Thus, we can obtain a formula for the optimal weight of attributes as follows:
By normalizing wj*, we get the attribute weight wj(j = 1,2,…,n).
Rank the alternatives by extended MARCOS
The existing MARCOS methods cannot handle TSULNs. In this sub-section, we extend the MARCOS method to the TSUL environment. The specific steps are as below:
Step 1: the TSUL evaluation matrix Dk = [dijk]m×n,(i = 1, 2 ,…,m; j = 1, 2 ,…,n; k = 1, 2,…,p) is constructed and normalized to the normalized decision matrix Rk = [rijk]m×n,(i = 1, 2 ,…,m; j = 1, 2 ,…,n; k = 1, 2 ,…,p).
where \((d_{ij}^{k} )^{c}\) is the complement set of TSULN \(d_{ij}^{k}\), Ψ1, and Ψ2 indicate benefit and cost attributes, respectively.
Step 2: the expert weight determination method in sub-Sect. 5.1 is utilized to calculate the weight of experts for different attributes \({\omega }_{k}^{\left(j\right)}\)(j = 1,2 ,…,n; k = 1,2 ,…,p).
Step 3: the TSULWA (Eq. (18)) or TSULWG (Eq. (19)) operator is utilized to fuse the evaluation information given by different experts under the attribute aj of alternative hi, then the individual TSUL decision matrix Rk is aggregated into group TSUL decision matrix G = [gij]m × n, \(g_{ij} = \left( {[s_{{\theta_{ij} }} ,s_{{\rho_{ij} }} ],\left( {\tau_{ij} ,\eta_{ij} ,\vartheta_{ij} } \right)} \right)\)(i = 1,2 ,…,m; j = 1, 2 ,…,n). Further, we can obtain the extended group TSUL decision matrix Ğ by Eq. (60).

where the anti-ideal solution hAAI represents the worst alternative, which can be obtained by \(g_{AAIj} = \left( {[s_{{\mathop {\min }\nolimits_{i} \{ \theta_{ij} \} }} ,s_{{\mathop {\min }\limits_{i} \{ \rho_{ij} \} }} ],\left( {\mathop {\min }\nolimits_{i} \{ \tau_{ij} \} ,\mathop {\max }\nolimits_{i} \{ \eta_{ij} \} ,\mathop {\max }\nolimits_{i} \{ \vartheta_{ij} \} } \right)} \right)\); the ideal solution hAI means the best alternative, which can be obtained by \(g_{AIj} = \left( {[s_{{\mathop {\max }\nolimits_{i} \{ \theta_{ij} \} }} ,s_{{\mathop {\max }\nolimits_{i} \{ \rho_{ij} \} }} ],\left( {\mathop {\max }\nolimits_{i} \{ \tau_{ij} \} ,\mathop {\min }\nolimits_{i} \{ \eta_{ij} \} ,\mathop {\min }\nolimits_{i} \{ \vartheta_{ij} \} } \right)} \right)\).
Step 4: we apply the attribute weight determination method in sub-Sect. 5.2 to get the optimal attribute weight wj (j = 1,2,…,n).
Step 5: all attribute evaluation values gij corresponding to alternative hi are aggregated by the TSULWHM operator (Eq. (38)), then the comprehensive evaluation values of each alternative xi (i = 1, 2 ,…,m). Similarly, we can get the comprehensive evaluation values xAAI of hAAI and xAI of hAI.
Step 6: calculate the utility function f(Ki) of the alternative hi(i = 1, 2,..m).
The utility degrees Ki− and Ki+ of each alternative are obtained from the TSUL generalized distance measure between the comprehensive evaluation value xi and xAAI, xAI, respectively, that is, \(K^{ + } = D_{\varphi } (x_{i} ,x_{AI} )\) and \(K^{ - } = D_{\varphi } (x_{i} ,x_{AAI} )\). The calculation formulas of ideal utility function f(Ki+) and anti-ideal utility function f(Ki−) are shown below:
Step 7: we rank the alternatives according to the utility function value. The alternative with the maximum utility function value is the optimal option.
A case study
The CGB is a kind of shopping and consumption behavior with a low discount that a certain number of consumer groups in real living communities purchase goods online and pick up goods offline. Compared with online group buying, the CGB requires the establishment of a service center in the community or other specific places, where consumers can pay the money and obtain after-sales protection in case of problems with commodities. Meanwhile, group buying organizations can collect consumers’ purchasing demands through the service center and contact appropriate merchants to provide commodities and services. At present, there are hundreds of large-scale CGB platforms in China, which are similar in the use of methods and play their due role in the speed of expansion, cross-regional management ability, supply chain ability, commodity system, technical ability, brand power, and other aspects. According to industry experts, the scale of CGB in China will reach 500 billion CNY in 2025.
Currently, there are many CGB platforms in the group-buying market in China, such as Xingsheng, Meituan, Duoduo, Shihui, etc. Due to the fierce competition in the group-buying market, the investment and financing funds obtained by the CGB platform from the capital market increased from 2.402 billion CNY in 2016 to 20.073 billion CNY in 2020 to seize the market share. However, for investors, how to select a potential CGB platform as the investment object has become a challenging decision-making problem. LXC is a venture capital and private equity fund management company owned by Legend Holdings of China. At present, LXC has a fund to invest in the CGB platform. According to the market survey and preliminary screening, there are five CGB platforms as potential investment objects, for which the best investment projects need to be determined. A brief introduction of alternative CGB platforms is shown in Table 2.
To screen out the best CGB platform project, five options are evaluated from six attributes. There are six attributes used to evaluate the alternatives, including platform operation and maintenance ability (a1), expected revenue (a2), market competitiveness (a3), risk resistance ability (a4), supply chain management ability (a5), and product and service innovation ability (a6). Their weight information is completely unknown. To assess the five CGB platforms with six attributes, LXC company invited three senior investment experts E = {e1,e2,e3}, and they are required to use the linguistic term set S = {s0 = Extremely bad, s1 = Very bad, s2 = Bad, s3 = Medium bad, s4 = Medium, s5 = Medium good, s6 = Good, s7 = Very good, s8 = Extremely good}to assess the five alternatives, respectively. The evaluation information of the experts on the five alternatives can be obtained, which is presented in Table 3.
Decision process
Step 1: since all attributes are benefit types, the TSULDM Dk does not need to be normalized in Table 1, that is, Dk = Rk.
Step 2: first, the evaluation matrix Dk provided by ek(k = 1,2,…,p) is converted into an evaluation matrix for each attribute F(j) ( j = 1,2,…,n). E.g. the evaluation matrix F(1) for attribute a1.

Then, Eq. (49) is used to calculate the evaluation mean value of alternative hi regarding attribute aj. E.g. \(\hat{\xi }_{1}^{(1)} = ([s_{5.333} ,s_{6.667} ],(0.667,0.300,0.367))\).
The Eq. (50) is used to calculate the similarity degree \(sim_{ki}^{(j)}\) between \(\xi_{ki}^{(j)}\) and \(\hat{\xi }_{i}^{(j)}\). We employ the TSUL Hamming distance measure (φ = 1)(Eq. (13)). Thus, the similarity matrix S(j) is constructed. E.g. the similarity matrix S(1) for attribute a1.

Lastly, Eq. (53) is used to calculate the weight of expert ek on attribute aj.
.
Step 3: The TSULWA (Eq. (18)) operator is utilized to aggregate the evaluation information of alternative hi under attribute aj given by experts, then we can obtain the group TSUL decision matrix G. Further, we the G is expanded to the extended group TSUL decision matrix Ğ according to Eq. (60). See Table 4.
Step 4: under the situation of the attribute weight information is completely unknown, we obtain the attribute weight W by Eq. (58), W = (0.185, 0.176, 0.184, 0.143, 0.109, 0.203,)T, where we adopt TSUL Hamming distance measure (φ = 1)(Eq. (13)).
Step 5: we use the TSULWHM operator (Eq. (38)) to obtain the comprehensive evaluation value xi (i = 1,2,…,5), xAAI and xAI.
x1 = ([s3.332,s4.709],(0.650, 0.514, 0.454)); x2 = ([s3.216,s4.855],(0.602, 0.472, 0.545));
x3 = ([s2.434,s3.853],(0.666, 0.483, 0.493)); x4 = ([s2.788,s4.061],(0.535, 0.489, 0.513));
x5 = ([s3.043,s4.382],(0.697, 0.372, 0.454));
xAAI = ([s1.708,s3.167],(0.507, 0.582, 0.655)); xAI = ([s4.083,s5.422],(0.723, 0.339, 0.348)).
Step 6: the Eqs. (61–62) are used to calculate the utility function value of each alternative.
f(K1) = 0.08233; f(K2) = 0.08101; f(K3) = 0.07698; f(K4) = 0.07727; f(K5) = 0.07114.
Step 7: according to the utility function value of each alternative, we rank the alternative: h1 > h2 > h4 > h3 > h5. Therefore, h1(Xingsheng) is the optimal option and h2(Meituan) is the second best solution.
Sensitivity investigation
The parameters q, φ, σ and ρ play an major role in the influence of alternative ranking results. We first investigate the effect of different values in q ∈ [3, 10] on alternative ranking results (φ = 1, σ = ρ = 1). The alternative ranking results are shown in Table 5.
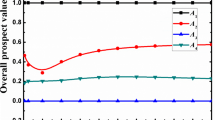
As the parameter q increases, each alternative’s utility function decreases gradually in Table 3. When q takes different values, the ranking of alternatives also changes, see Fig. 1. Specifically, when q = 3, the ranking of alternatives is h1 > h2 > h4 > h3 > h5, the best alternative is h1, and the second-best alternative is h2. When q = 4, the ranking of alternatives is h2 > h4 > h3 > h1 > h5, and the optimal and second alternatives are h2 and h4, respectively. When q ∈ [5, 10], the ranking of alternatives changes from h4 > h3 > h2 > h5 > h1 to h4 > h5 > h3 > h2 > h1, and tends to be stable. As we know, the value of parameter q not only reflects the ability of TSULSs to model uncertain information but also reflects the evaluation preference of decision-makers in the actual decision-making environment. Therefore, the appropriate parameter q value needs to be chosen by the decision-makers. Generally, the parameter can be the smallest integer satisfying the condition \(0 \le \left( {\tau_{{\tilde{Q}}} (x)} \right)^{q} + \left( {\eta_{{\tilde{Q}}} (x)} \right)^{q} + \left( {\vartheta_{{\tilde{Q}}} (x)} \right)^{q} \le 1\)(q ≥ 1) depending on the evaluation value of the attribute. Therefore, h1 and h2 are the best and second-best alternatives in this paper.
Next, the effect of the parameter φ on the ranking results of each alternative is analyzed. When parameters q = 3, σ = ρ = 1, we take various values for the parameterφ, and the results of each alternative are shown in Table 6.
From Table 6, when the parameter φ in the TSUL generalized distance measure is set to different values, the alternative ranking changes from h1 > h2 > h4 > h3 > h5 to h1 > h2 > h3 > h4 > h5. The best alternative and the second-best alternative are always h1 and h2, but the ranking of h3 and h4 changes slightly. On the whole, the effect of the parameter φ on the alternative ranking is not obvious, and the ranking of alternatives is stable in Fig. 2.
We take various values for parameters σ and ρ, then analyze the effect of σ and ρ on alternative ranking in Step 5 of our method. The utility function values of each alternative are shown in Table 7(q = 3, φ = 1).
The ranking of all alternatives varies with the value of parameters σ and ρ, but the optimal option is h2 in Table 7. The parameters σ and ρ represent the degree of correlation between attributes, which is also the main reason for the variation of alternative ranking. When σ = 0,ρ = 1 and σ = 1,ρ = 0, there is no correlation between attributes. Except for the best alternative h2, the order of other alternatives is completely different, namely h2 > h4 > h3 > h1 > h5 and h2 > h3 > h5 > h4 > h1. As the values of σ and ρ increase, the correlation level between attributes increases. Therefore, once various values of parameters σ and ρ are chosen, the relationship structure between attributes simulated by the TSULWHM operator changes. In general, the decision-makers usually take σ = ρ = 1, which can reduce the complexity of calculation and capture the interrelationship between attributes.
Comparative study
We applied some existing MADM approaches, including q-rung orthopair uncertain linguistic weighted geometric Heronian mean (q-ROULWGHM) [76], picture uncertain linguistic weighted averaging and geometric (PULWA and PULWG) [30], picture uncertain linguistic weighted Bonferroni mean and geometric form (PULWBM and PULWGBM) [31] operators and linguistic T-spherical fuzzy ARAS (Lt-SF-ARAS) method [77] to the case in this paper, and the results of alternatives are shown in Table 8.
We apply the existing AOs (q-ROULWGHM, PULWA, PULWG, PULWBM and PULWGBM) and ranking technique (Lt-SF-ARAS) to this case. This results in Table 8 show that the existing methods are not applicable to this case. Due to the lack of AD in q-ROULS, the ability of Lt-SFS to represent uncertain information is not as good as TSULS, and the PULS cannot process the TSULNs in Table 3 and these TSULNs require the parameter q to take the minimum integer as 3. Therefore, these existing methods cannot be used to solve the decision-making problem in above case. However, the proposed method based on the TSULWA (or TSULWG), TSULWHM operators, and TSUL-MARCOS can process the evaluation information in Table 3. It can be seen that our method has a wider scope of application than the existing methods. For this reason, we further use an example from Ref. [31] to demonstrate that the proposed method is more generalized.
Example 4
[31]. Assume that there are five service outsourcing providers (P1, P2,…, P5) to select for the communication industry. The panel selected four criteria (Business reputation C1, technical capability C2, Management capability C3, Quality of Service C4) to evaluate the five possible service outsourcing providers (P1, P2,…, P5). The PULNs are applied to represent the evaluation values of the alternative concerning criteria, and the weight vector of the attribute is W = (0.2,0.1,0.3,0.4)T. Thus, the decision matrix is constructed as shown in Table 9.
We adopt Steps 5 ~ 7 in sub-Sect. 5.3 to solve the selection of service outsourcing providers, and compared the results of the q-ROULWGHM, PULWA, PULWG, PULWBM, PULWGBM operators and Lt-SF-ARAS method, as listed in Table 10.
From Table 10, the q-ROULWGHM operator and Lt-SF-ARAS method are not applicable to Example 2, because q-ROULS and Lt-SFS cannot process the data in Table 9, although the parameter q in these TSULNs is 1. The best alternative obtained by our method is P4 and the sub-best alternative is P3, while P3 is obtained by the PULWA, PULWG, PULWBM, and PULWGBM operators as the optimal option, the second-best alternative is P1 and P4 respectively. This is completely inconsistent with the results of this paper. The specific reasons are as follows:
-
(1)
The operation rules of the linguistic part in PULWA, PULWG, PULWBM, and PULWGBM operators are based on Rf. [8], while the operation of the linguistic part of TSULNs in this paper is based on Definition 2 and can ensure that the calculation results are still within the range of linguistic level.
-
(2)
The PULWA and PULWG operators ignore the correlation between attributes, while the PULWBM and PULWGBM operators are similar to the TSULWHM operator, which can not only concern the interrelationship between attributes but also reflect the preferences of decision-makers by adjusting parameters. However, the PULWA, PULWG, PULWBM, and PULWGBM operators all use score functions that do not contain the degree of refusal to defuzzify, but we apply the TSUL generalized distance measure to compute the utility of alternative in the improved MARCOS.
-
(3)
The existing approaches aggregate the evaluation information and obtain the comprehensive evaluation value of the alternative. This information fusion process is relatively direct and rigid, while the deviation between the alternative and the ideal and anti-ideal solution is considered in the TSUL-MARCOS method, which reflects the characteristics of compromise in the calculation of the alternative’s utility function.
Therefore, in addition to being more generalized than the existing methods, the methodology of this paper is more rationality.
Next, we further compare with the traditional MARCOS method. For the multi-criteria decision-making problems, we can have the general ideal of traditional MARCORS method to solve the TSUL decision-making problems based on the existing works [56,57,58, 63,64,65, 67]: (1) Use the Eq. (6) to de fuzzify the evaluation matrix D = [dij]m×n to obtain the decision matrix G. (2) the hAAI and hAI are obtained, and the extended matrix EG is built. (3) Construct normalized decision matrix NG. (4) Build weighted matrix WG. (5) Obtain the comprehensive evaluation values xi, xAAI and xAI of alternatives (without considering the correlation between attributes). (6) Calculate the ratio of xi to xAI and xAAI respectively, and determine the utility degree Ki+ and Ki− of each alternative. (7) Calculate the utility functions f(Ki+) and f(Ki−) of ideal solution and anti-ideal solution, and calculate the utility function f(Ki) of alternatives. (8) The alternatives are ranked and the optimal one is selected. We compare the traditional MARCOS method with improved MARCOS method (Steps 3 ~ 7 in sub-Sect. 5.3) through example 5 in TSUL environment, so as to illustrate the advantages of our method.
Example 5
Let alternative set be H = {h1,h2,h3}, attribute set be C = {c1,c2,c3}, and the weight vector of attribute be W = (0.3, 0.4, 0.3)T. Assuming that all attributes are benefit types, the TSUL evaluation matrix D (k = 7,q = 2).

Then, we can get the results of the traditional MARCOS method and the improved MARCOS method, as shown in Table 11.
From Table 11, the ranking result of traditional MARCOS method is h1 = h2 > h3, while the ranking result of improved MARCOS method is h1 > h2 > h3. The former cannot distinguish between the optimal alternative h1 and h2, but the latter can clearly obtain the optimal alternative h1. The detailed reasons are as follows: first, we used the score function (Eq. (6)) in the traditional MARCOS method to de fuzzify the evaluation matrix in the early stage. In this process, it is impossible to distinguish the TSUL evaluation values of h1 and h2 under each attribute, such as the score function values of d11 and d21 are s0.750. In the later stage of the improved MARCOS method, the proposed TSUL Hamming distance measure was applied for de fuzzification, and this measure contains refusal degree information of TSULN. In contrast, the traditional MARCOS method loses part of the decision information in the process of de fuzzification. Second, the standardized evaluation values of alternative were summed simply in the traditional MARCOS method to obtain the comprehensive evaluation vale xi of alternative, while the TSULWHM operator was applied to aggregate the TSUL evaluation values of alternative in the improved MARCOS method, which takes into account the correlation between attributes. In contrast, the former method ignores the relationship between attributes, which makes it impossible to mine the potential information in decision information. To sum up, our improved MARCOS method can rank the alternative more effectively in the TSUL environment. Therefore, the improved method in this paper has more superiority compared with the traditional MARCOS method.
Conclusions
In this paper, we define some new concepts of TSULSs inspired by q-rung orthopair uncertain linguistic sets, including operation rules and generalized distance measures of TSULNs. The TSULSs can express more freely and deal with uncertainty in data more effectively. We not only propose the TSULWA and TSULWG operators but also develop the TSULHM and TSULWHM operators which can capture the interrelationship of attributes. Furthermore, we construct the improved MARCOS-based MAGDM framework with TSUL information. In it, based on the generalized distance measure of TSULNs, the TSUL similarity is defined to calculate attribute weights and the MDM is applied to determine the attribute weights, respectively. At the same time, we integrate the TSULWHM operator and generalized distance measure into the MARCOS method, so that this method can capture the interrelationship of attributes and calculate the alternative’s utility degree more accurately. Finally, an illustrative example of a CGB platform investment decision is presented using the proposed method, and sensitivity analysis and comparative study are performed to test the validity of the proposed method.
Although the proposed method can effectively solve the MAGDM problems with TSULNs, there are still some limitations: (1) The HM is included in our method, which can consider the correlation between two attributes, but the HM cannot capture the interrelationship among multiple attributes. (2) Furthermore, there is an objective priority relationship and degree between attributes in the real decision-making problems, but it is not concerned in this case. (3) In addition, the attribute subjective weight is not taken into account in the proposed method, which ignores the intuitive judgment of experts on the importance of attributes.
To this end, a series of new AOs will be further developed in the TSULSs environment in the future. For example, Muirhead mean [40], Hamy mean [78], Maclaurin Symmetric mean [24]. These operators can capture the interrelationship among multiple attributes. Further, we will try to integrate Softmax function [79] into above operators, so that they can focus on the priority and degree between attributes. The attribute combined weight will be adopted in the future, in which the attribute subjective weight will be determined by SWARA (Step-wise Weight Assessment Ratio Analysis) [80] or BWM (Best–Worst Method) [81]. We will try to integrate the TSULSs with other decision-making techniques, such as WASPAS (Weighted Aggregated Sum Product ASsessment) [82], MABAC (Multi-Attribute Border Approximation area Comparison) [83], CoCoSo (Combined Compromise Solution) [84], and so on. In addition, we will expand the improved MARCOS method in various decision-making environments, such as probabilistic T-spherical hesitant fuzzy set [85], probabilistic linguistic term set [86, 87], probabilistic uncertain linguistic term set [88]. Apart from these, we can also test our methodology with real-world decision scenarios, such as firm business decisions, capital item selection, and consumer purchasing decisions.
References
Chen SM, Hong JA (2014) Fuzzy multiple attributes group decision making based on ranking interval type-2 fuzzy sets and the TOPSIS method. IEEE Trans Syst Man Cybern Syst 44(12):1665–1673
Ju YB, Liu XY, Wang AH (2016) Some new Shapley 2-tuple linguistic Choquet aggregation operators and their applications to multiple attribute group decision making. Soft Comput 20:4037–4053
Herrera F, Herrera-Viedma E, Verdegay JL (1996) A model of consensus in group decision making under linguistic assessment. Fuzzy Sets Syst 78(1):73–87
Zadeh LA (1975) The concept of a linguistic variable and its application to approximate reasoning. Inf Sci 8(3):199–249
Rodriguez RM, Martinez L, Herrera F (2012) Hesitant fuzzy linguistic term sets for decision making. IEEE Trans Fuzzy Syst 20(1):109–119
Liu PD (2013) Some generalized dependent aggregation operators with intuitionistic linguistic numbers and their application to group decision making. J Comput Syst Sci 79(1):131–143
Herrera F, Martinez L (2000) A 2-tuple fuzzy linguistic representation model for computing with words. IEEE Trans Fuzzy Syst 8(6):746–752
Xu ZS (2044) Uncertain linguistic aggregation operators based approach to multiple attribute group decision making under uncertain linguistic environment. Inf Sci 168(1–4): 171–184.
Liu PD, Jin F (2012) Methods for aggregating intuitionistic uncertain linguistic variables and their application to group decision making. Inf Sci 205:58–71
Liu PD, Liu ZM, Zhang X (2014) Some intuitionistic uncertain linguistic Heronian mean operators and their application to group decision making. Appl Math Comput 230:570–586
Liu ZM, Liu PD (2017) Intuitionistic uncertain linguistic partitioned Bonferroni means and their application to multiple decision-making. Int J Syst Sci 48(5):1092–1105
Liu PD, Zhang XH (2019) Some intuitionistic uncertain linguistic Bonferroni mean operators and their application to group decision. Soft Comput 23:3869–3886
Atanassov KT (1986) Intuitionistic fuzzy sets. Fuzzy Sets Syst 20:87–96
Yager RR, Abbasov AM (2013) Pythagorean membership grades, complex numbers, and decision making. Int J Intell Syst 28(5):436–452
Liu ZM, Liu PD, Liu WL, Pang JY (2017) Pythagorean uncertain linguistic partitioned Bonferroni mean operators and their application in multi-attribute decision making. J Intell Fuzzy Syst 32(3):2779–2790
Geng Y, Liu PD, Teng F, Liu Z (2017) Pythagorean fuzzy uncertain linguistic TODIM method and their application to multiple criteria group decision making. J Intell Fuzy Syst 33(6):3383–3395
Lu M, Wei GW (2017) Pythagorean uncertain linguistic aggregation operators for multiple attribute decision making. Int J of Knowl Intell Eng Syst 21(3):165–179
Liu HC, Ding XF (2019) A new approach for emergency decision-making based on zero sum game with Pythagorean fuzzy uncertain linguistic variables. Int J Fuzzy Syst 34(7):1667–1684
Wang HD, He SF, Li CD (2019) Pythagorean uncertain linguistic variable Hamy mean operator and its application to multi-attribute group decision making. IEEE/CAA J Automatica Sinica 6(2):527–539
Yager RR (2017) Generalized orthopair fuzzy sets. IEEE Trans Fuzzy Syst 25:1222–1230
Bai KY, Zhu XM, Wang J, Zhang RT (2020) Power partitioned Heronian mean operators for q-rung orthopair uncertain linguistic sets with their application to multi-attribute group decision making. Int J Intell Syst 35:3–37
Xing YP, Zhang RT, Zhu XM, Bai KY (2019) q-Rung orthopair fuzzy uncertain linguistic Choquet integral operators and their application to multi-attribute decision making. J Intell Fuzzy Syst 37:1123–1139
Liu ZM, Li L, Li JQ (2019) q-Rung orthopair uncertain linguistic partitioned Bonferroni mean operators and its application to multiple attribute decision-making method. Int J Intell Syst 34:2490–2520
Yang Z, Garg H (2021) Interaction power partitioned Maclaurin symmetric mean operators under q-rung orthopair uncertain linguistic information. Int J Fuzzy Syst. https://doi.org/10.1007/s40815-021-01062-5
Liu ZM, Xu HX, Yu YN, Li JQ (2019) Some q-rung orthopair uncertain linguistic aggregation operators and their application to multiple attribute group decision making. Int J Intell Syst 34(10):2521–2555
Wang J, Zhang RT, Li L, Zhu XM, Shang XP (2019) A novel approach to multi-attribute group decision making based on q-rung orthopair uncertain linguistic information. J Intell Fuzzy Syst 36(6):5565–5581
Cuong BC (2014) Picture fuzzy sets. J Comput Sci Cyber 30(4):409–420
Ganie AH, Singh S, Bhatia PK (2020) Some new correlation coefficients of picture fuzzy sets with applications. Neural Comput & Applic 32:12609–12625
Luo MX, Zhang Y (2020) A new similarity measure between picture fuzzy sets and its application. Eng Appl Artif Intel 96:103956
Wu SJ, Wei GW (2017) Picture uncertain linguistic aggregation operators and their application to multiple attribute decision making. Int J Know Intell Eng Syst 21:243–256
Wei GW (2017) Picture uncertain linguistic Bonferroni mean operators and their application to multiple attribute decision making. Kybernetes 46(10):1777–1800
Naeem M, Qiyas M, Abdullah S (2021) An approach of interval-valued picture fuzzy uncertain linguistic aggregation operator and their application on supplier selection decision-making in logistics service value concretion. Math Probl Eng 10.115/2021/8873230
Garg H, Ali Z, Mahmood T (2021) Interval-valued picture uncertain linguistic generalized Hamacher aggregation operators and their application in multiple attribute decision-making process. Arab J Sci Eng 46:10153–10170
Mahmood T, Ullah K, Khan Q, Jan N (2019) An approach toward decision-making and medical diagnosis problems using the concept of spherical fuzzy sets. Neural Comput Appl 31(11):7041–7053
Ullah K, Ali Z, Mahmood T, Garg H, Chinram R (2022) Methods for multi-attribute decision making, pattern recognition and clustering based on T-spherical fuzzy information measures. J Intell Fuzzy Syst 42(4):2957–2977
Wu MQ, Chen TY, Fan JP (2020) Similarity measures of T-spherical fuzzy sets based on the Cosine function and their applications in pattern recognition. IEEE Access 8:98181–98192
Ullah K, Mahmood T, Jan N (2018) Similarity measures for T-spherical fuzzy sets with applications in pattern recognition. Symmetry 10(6):193
Wu MQ, Chen TY, Fan JP (2020) Divergence measure of T-spherical fuzzy sets and its applications in pattern recognition. IEEE Access 8:10208–10221
Uallah K, Garg H, Mahmood T, Jan N, Ali Z (2020) Correlation coefficients for T-spherical fuzzy sets and their applications in clustering and multi-attribute decision making. Soft Comput 24:167–1659
Liu PD, Khan Q, Mahmood T, Hassan N (2019) T-spherical fuzzy power Muirhead mean operator based on novel operational laws and their application in multi-attribute group decision making. IEEE Access 7:22613–22632
Ullah K, Mahmood T, Garg H (2020) Evaluation of the performance of search and rescue robots using T-spherical fuzzy Hamacher aggregation operators. Int J Fuzzy Syst 22(2):570–582
Munir M, Kalsoom H, Ullah K, Mahmood T, Chu YM (2020) T-spherical fuzzy Einstein hybrid aggregation operators and their applications in multi-attribute decision making problems. Symmetry 12:365
Mahnaz S, Ali J, Malik MGA, Bashir Z (2022) T-spherical fuzzy Frank aggregation operators and their application to decision making with unknown weight information. IEEE Access 10:7408–7438
Mahmood T, Warraich MS, Ali Z, Pamucar D (2021) Generalized MULTIMOORA method and Dombi prioritized weighted aggregation operators based on T-spherical fuzzy sets and their applications. Int J Intell Syst 36(9):4659–4692
Garg H, Munir M, Ullah K, Mahmood T, Jan N (2018) Algorithm for T-spherical fuzzy multi-attribute decision making based on improved interactive aggregation operators. Symmetry 10:670
Ju YB, Liang YY, Luo C, Dong PW, Gonzalez EDRS, Wang AH (2021) T-spherical fuzzy TODIM method for multi-criteria group decision-making problem with incomplete weight information. Soft Comput 25:2981–3001
Wang HL, Zhang FM (2022) Interaction power Heronian mean aggregation operators for multiple attribute decision making with T-spherical fuzzy information. J Intell Fuzzy Syst 42(6):5715–5739
Wang HL (2021) T-spherical fuzzy rough interactive power Heronian mean aggregation operators for multiple attribute group decision-making. Symmetry 13(12):2422
Garg H, Ullah K, Mahmood T, Hassan N, Jan N (2021) T-spherical fuzzy power aggregation operators and their applications in multi-attribute decision making. J Ambient Intell Human Comput 12:9067–9080
Yang W, Pang YF (2022) T-spherical fuzzy Bonferroni mean operators and their application in multiple attribute decision making. Mathematics 10(6):988
Wang JC, Chen TY (2021) A T-spherical fuzzy ELECTRE approach for multiple criteria assessment problem from a comparative perspective of score functions. J Intell Fuzzy Syst 41(2):3751–3770
Stevič Z, Pamucar D, Puska A, Chatterjee P (2020) Sustainable supplier selection in healthcare industries using a new MCDM method: measurement of alternatives and ranking according to compromise solution (MARCOS). Comput Ind Eng 140:106231
Zhang XL, Xu ZS. Extension of TOPSIS to multiple criteria decision making with Pythagorean fuzzy sets. Int J Intell Syst 29(12): 1061–1078.
Opricovic S, Tzeng GH (2004) Compromise solution by MCDM methods: a comparative analysis of VIKOR and TOPSIS. European J Oper Res 156:445–455
Ghorabaee MK, Zavadskas EK, Olfat L, Turskis Z (2015) Multi-criteria inventory classification using a new method of evaluation based on distance from average solution (EDAS). Informatica 26(3):435–451
Ali J (2021) A q-rung orthopair fuzzy MARCOS method using novel score function and its application to solid waste management. Appl Intell. https://doi.org/10.1007/s10489-021-02921-2
Ali J (2021) A novel score function based CRITIC-MARCOS method with spherical fuzzy information. Comput Appl Math 40:280
Ecer F, Pamucar D (2021) MARCOS technique under intuitionistic fuzzy environment for determining the COVID-19 pandemic performance of insurance companies in terms of healthcare services. Appl Soft Comput 104:107199
Stevic Z, Karamasa C, Demir E, Korucuk S (2021) Assessing sustainable production under circular economy context using a novel rough-fuzzy MCDM model: a case of the forestry industry in the Eastern Black Sea region. J Enterp Inf Manag. https://doi.org/10.1108/JEIM-10-2020-0419
Boral S, Chakraborty S (2021) Failure analysis of CNC machines due to human errors: an integrated IT2F-MCDM-based FMEA approach. Eng Fail Anal 130:105763
Deveci M, Ozcan E, John R, Pamucar D, Karaman H (2021) Offshore wind farm site selection using interval rough numbers based Best-Worst Method and MARCOS. Appl Soft Comput 109:107532
Fan JP, Wang ST, Wu MQ (2021) An integrated FMEA approach using best-worst and MARCOS methods based on D numbers for prioritization of failures. J Intell Fuzzy Syst 41:2833–2846
Gong XM, Yang M, Du PL (2021) Renewable energy accommodation potential evaluation of distribution network: a hybrid decision-making framework under interval type-2 fuzzy environment. J Clean Prod 286:124918
Puska A, Pamucar D, Stojanovic I, Cavallaro F, Kaklauskas A, Mardani A (2021) Examination of the sustainable rural tourism potential of the Brčko district of Bosnia and Herzegovina using a fuzzy approach based on group decision making. Sustainability 13:583
Pamucar D, Ecer F, Deveci M (2021) Assessment of alternative fuel vehicles for sustainable road transportation of United States using integrated fuzzy FUCOM and neutrosophic fuzzy MARCOS methodology. Sci Total Environ 788:147763
Saha A, Mishra AR, Rani P (2021) FUCOM-MARCOS based group decision-making using Dombi power aggregation of dual probabilistic linguistic information. Research Square https://doi.org/10.21203/rs.3.rs-371236/v1
Simic V, Ebadi Torkayesh A, Ijadi Maghsoodi A (2022) Locating a disinfection facility for hazardous healthcare waste in the COVID-19 era: a novel approach based on Fermatean fuzzy ITARA-MARCOS and random forest recursive feature elimination algorithm. Ann Oper Res. https://doi.org/10.1007/s10479-022-04822-0
Liu PD, Chen SM (2017) Group decision making based on Heronian aggregation operators of intuitionistic fuzzy numbers. IEEE T Cybernetics 47(9):2514–2530
Liu PD, Liu JL, Merigo JM (2018) Partitioned Heronian means based on linguistic intuitionistic fuzzy numbers for dealing with multi-attribute group decision making. Appl Soft Comput 62:395–422
Herrera F, Herrera-Viedma E (2000) Linguistic decision analysis: steps for solving decision problems under linguistic information. Fuzzy Set Syst 115(1):67–82
Guan K, Zhu H (2006) The generalized Heronian mean and its inequalities. Univ Beograd Publ Elektrotehn Fak-Ser Ma 17(17):60–75
Ashraf S, Abdullah S, Mahmood T (2018) GRA method based on spherical linguistic fuzzy Choquet integral environment and its application in multi-attribute decision-making problems. Math Sci 12:263–275
Mandal P, Samanta S, Pal M, Ranadive AS (2020) Pythagorean linguistic preference relations and their applications to group decision making using group recommendations based on consistency matrices and feedback mechanism. Int J Intell Syst 35(5):826–849
Wei GW (2008) Maximizing deviation method for multiple attribute decision making in intuitionistic fuzzy setting. Knowl –Based Syst 21: 833–836.
Wang YM (1997) Using the method of maximizing deviation to make decision for multiindices. J Syst Eng Electron 8:21–26
Wang HD, Zhang Y, Bai CZ (2022) A new three-way group decision-making model based on geometric Heronian mean operators with q-rung orthopair uncertain linguistic information. J Intell Fuzzy Syst 43(1):525–544
Wang HL (2022) Sustainable circular supplier selection in the power battery industry using a linguistic T-spherical fuzzy MAGDM model based on the improved ARAS method. Sustainability 14(13):7816
Hara T, Uchiyama M, Takahasi SE (1998) A refinement of various mean inequalities. J Inequal Appl 2:387–395
Torres R, Salas R, Astudillo H (2014) Time-based hesitant fuzzy information aggregation approach for decision making problems. Int J Intell Syst 29(6):579–595
Kersuliene V, Zavadskas EK, Turskis Z (2010) Selection of rational dispute resolution method by applying new step-wise weight assessment ratio analysis (SWARA). J Bus Econ Manage 11(2):243–258
Rezaei J (2016) Best-worst multi-criteria decision-making method: Some properties and a linear model. Omega 64:126–130
Zavadskas EK, Turskis Z, Antucheviciene J, Zakarevicius A (2012) Optimization of weighted aggregated sum product assessment. Elektronika Ir Elektrotechnika 122(6):3–6
Pamucar D, Cirovic G (2015) The selection of transport and handling resources in logistics centers using multi-attributive border approximation area comparison (MABAC). Expert Syst Appl 42:3016–3028
Yazdani M, Zarate P, Kazimieras Zavadskas E, Turskis Z (2019) A combined compromise solution (CoCoSo) method for multi-criteria decision-making problems. Manage Decisi 57(9):2501–2519
Gurmani SH, Chen HY, Bai YH (2022) An extended MABAC method for multiple-attribute group decision making under probabilistic T-spherical hesitant fuzzy environment. Kybernetes. https://doi.org/10.1108/K-01-2022-0137
Liu PD, Li Y, Zhang XH, Pedrycz W (2022) A multiattribute group decision-making method with probabilistic linguistic information based on an adaptive consensus reaching model and evidential reasoning. IEEE T Cybernetics. https://doi.org/10.1109/TCYB.2022.3165030
Liu PD, Wang P, Pedryz W (2021) Consistency- and consensus- based group decision-making method with incomplete probabilistic linguistic preference relations. IEEE T Fuzzy Syst 29(9):2565–2579
Bashir Z, Ali J, Rashid T (2021) Consensus-based robust decision making methods under a novel study of probabilistic uncertain linguistic information and their application in Forex investment. Artif Intell Rev 54(3):2091–2132
Acknowledgements
This work is supported by the Humanities and Social Sciences Foundation of Ministry of Education of the People’s Republic of China (No.19YJC630164), and the Postdoctoral Science Foundation of Jiangxi Province (No. 2019KY14).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wang, H., Ullah, K. T-spherical uncertain linguistic MARCOS method based on generalized distance and Heronian mean for multi-attribute group decision-making with unknown weight information. Complex Intell. Syst. 9, 1837–1869 (2023). https://doi.org/10.1007/s40747-022-00862-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40747-022-00862-y