Introduction

With the development of management, social sciences, operations research, medicine, economics, artificial intelligence, and decision problems, the structure methods have been implemented to unravel the limitations and restrictions encountered by managers and researchers under existing conditions, but decision makers frequently supply little information, and their subjective judgments are utilized to create uncertainty [1]. Multi-criteria decision-making (MCDM) is a prominent strategy for managing difficult decision-making issues facing several typically contradicting factors. Under the circumstances, the combination of structured evaluation methods with scientific data in MCDM is one of the key prerequisites for making the right decisions. But meanwhile existing evaluation methods often ignore the correlation between indicators and the ambiguity of the preferences expressed by experts [2].

To handle and manage the influence of ambiguity, the research of fuzzy logic is an excellent tool in MCDM, pioneered by Zadeh in 1965, which is frequently employed and developed nowadays. The fuzzy logic has the ability to deal with the information of partial truth, which is prevalent with ambiguous, inadequate, unclear, and inaccurate data. So it can formalize the human ability to make rational decisions for ambiguity problems without precision or calculations [3]. The issues with interdependent variables in MCDM, fuzzy logic utilizes a linguistic scale to represent the strength of cause-effect interactions. This scale is transformed into numerical values using fuzzy sets [4].

Dempster–Shafer evidence theory (DST) [5, 6] was established as a useful method to analyze the dynamic and unpredictable context as an extension of Bayesian probability theory, which has the advantage of describing the uncertain data by assigning a level of confidence. Consequently, DST is preferred by many researchers than the traditional methodologies as Bayesian probability theory [7]. Aside from the betterment that DST can tackle many issues, such as decision-making problems and risk theory [8, 9], it also has drawbacks as the limitation of mutually exclusive and collectively extensive set, as well as the sum of the values of the basic probability assignment must be one, which is hard to unravel in the real-world applications [10]. Exclusivity is one restriction which limits the wider practical implementation of DST while parsing elements of a subset. To overcome this shortage, Deng created a model to tackle the antagonistic issue as D numbers under uncertainty. D numbers theory appropriately eliminates this significant restriction, which can deal with these sorts of uncertainties by the trustworthy and effective depiction of uncertain information [11]. Therefore, D number theory is a powerful mathematical paradigm for coping with ambiguity and imperfect information [12]. Its border area provides the concept of ambiguity, which can be addressed using upper and lower approximations of the actual set using any equivalence relation [10]. As a result, it has been applied in a variety of application areas, including risk assessment [13], quality assessment [14, 15], supplier selection [16, 17], healthcare assessment [18, 19], and building assessment [20, 21].

A decision support model can be used and the results must be designed and configured in a real-world scenario. It is critical to ensure that the model can be dictated and guided to achieve its goals. In 1980, Saaty popularized the AHP as an MCDM technique [22]. The hierarchical structure in AHP can be shown as a visualization of the effect of criteria on the alternatives. ANP is extension of AHP which considers complicated interaction of selection factors in the hierarchical structure. In various disciplines, the fuzzy AHP and ANP have been utilized to deal with the fuzzy condition, such as Tolga et al. [23] used the fuzzy ANP method in location selection problem. Kumar et al. [24] estimated barriers in the agriculture supply chain by ANP. In addition, many other methods could be combined to solve the real problems. Kashav et al. [25] combined FAHP and TOPSIS, Buyukozkan and Guler [26] coupled AHP and VIKOR method to estimate the supply chain. Kumar and Barman [27] associated fuzzy TOPSIS and VIKOR in selecting green suppliers.

DEMATEL is a popular decision-making tool for dealing with interdependencies in MCDM environments with structure of complex causal relationships [28]. DEMATEL approach has been widely used in many areas, such as Shahidzadeh and Shokouhyar [29] discussed the logistics performance by fuzzy DEMATEL. Rajabpour et al. [30] combined Fuzzy AHP and type-2 fuzzy DEMATEL. Gao et al. [31] and Sun et al. [32] analyzed green supplier evaluation with DEMATEL, respectively. Liu et al. [33] studied Green supply chain management with the Grey-DEMATEL method.

Michnik created Weighted Influence Nonlinear Gauge System method [34]. Compared with DEMATEL method analyzing the direction and power of criteria, WINGS method utilizes the strength of factors, which can provide theoretical support and practical assistance for supply chain management. Reviewing the existing literature, integrated AHP, ANP, TOPSIS, and DEMATEL have been utilized to address hierarchical decision-making issues with interlaced factors, as shown in Table 1. These complicated issues can also be solved using the WINGS approach. The benefit of adopting WINGS over these integrated approaches is that the computational cost does not rise significantly when the number of criteria, sub-criteria, or alternatives grows. So far, it has been used in a few areas, as advanced technology projects [7], a case study in the automotive industry [35], green building development [20].

Table 1 The comparison of the different methods
Full size table

In this work, one of the main goals is to develop an integrated WINGS method with D number theory and MICMAC. The WINGS approach could be applied to find interrelations between assessment criteria by determining the direction of components, the intensity of the factors, and the strength of assessment criteria. The fuzzy logic can reduce the influence of ambiguous information and present subjective opinions in the form of a linguistic scale. D numbers has absolute advantage in dealing with the uncertain information, which can eliminate the restriction of mutually exclusive and collectively extensive set. Obviously, it is clear that the mutual influence of factors in supply chain management is interacting and ambiguous, which need to apply more objective and accurate evaluation in MCDM. Therefore, fuzzy logic and D number are employed to combine with the WINGS method. In addition, we use the MICMAC method to explain the interrelationships of the components more clearly. Finally, a case in ASCM is presented to illustrate the applicability of the fuzzy D-WINGS–MICMAC approach in this study. And the main contributions of the paper list as:

  1. 1.

    This study contributes to decision theory by presenting a complete fuzzy D-WINGS–MICMAC approach that may be used by researchers to simultaneously modify judgement ambiguity, group choice variety, complicated interrelationships, and excessive computation effort in evaluation problems.

  2. 2.

    The D number is extended to the fuzzy WINGS method. The combination of D number and fuzzy set can provide viable technique to reduce the subjectivity of expert preferences, as the D numbers theory can integrate group information more accurately.

  3. 3.

    The factors affecting agriculture supply chain management are evaluated by previous features to demonstrate preferences of every expert group and aggregated into a complete result. The proposed technique is more objective than fuzzy WINGS since it overcomes the influence limitations of similar group perspectives.

The remainder of this article is shown as below. Section “Preliminaries” focuses on the preliminaries. Section “Methodology” details the fuzzy D-WINGS–MICMAC research methodology. Section “Empirical analysis” shows empirical analysis. Whereas, section “Conclusion” covers conclusion.

Preliminaries

D numbers

D numbers can handle uncertainty in the information being processed more efficiently. D numbers do not require the exclusivity of set components, which considerably broadens the practical application of D numbers [12].

Definition 1

([12]). Let T be a bounded non-empty set, and the mapping is D:T → [0,1],

\(\sum\nolimits_{S \subseteq T} {D(S) \le 1}\) and \(D(\emptyset ) = 0\), where \(S\) is any subset of \(T\) and \(\emptyset\) is an empty set.

The theory of D numbers, as described previously, has the advantage that does not need to be mutually exclusive. So, D numbers can be referred to presenting full information, such as \(\sum\nolimits_{S \subseteq T} {D(S) < 1}\).

If \(G\) is an individual set of ingredients \(G = \left\{ {a_{1,} a_{2} ,...,a_{j,} a_{k} ,...,a_{n} } \right\}\), where \(a_{j} \in R\) and \(a_{j} \ne a_{k}\) (when \(j \ne k\)), then the form of D numbers can be expressed as:

$$ D(a_{1} ) = u_{1} ,D(a_{2} ) = u_{2} ,...,D(a_{j} ) = u_{j} ,D(a_{k} ) = u_{k} ,...,D(a_{n} ) = u_{n} . $$
(1)

And the simplified description is \(D =[ ( {a_{1} ,u_{1} } ),( {a_{2} ,u_{2} } ),...,( {a_{j} ,u_{j} }),( {a_{k} ,u_{k} } ),...,( {a_{n} ,u_{n} } )]\). This presentation also satisfies the condition as \(u_{j} > 0\) and \(\sum\nolimits_{j = 1}^{n} {u_{j} \le 1}\).

Definition 2

([12]). Two D numbers defined as \(D_{1} = \left[ {\left( {a_{1} ,u_{1}^{1} } \right),...,\left( {a_{j} ,u_{j}^{1} } \right),...,\left( {a_{n} ,u_{n}^{1} } \right)} \right]\) and \(D_{2} = \left[ {\left( {a_{1} ,u_{1}^{2} } \right),...,\left( {a_{j} ,u_{j}^{2} } \right),...,\left( {a_{n} ,u_{n}^{2} } \right)} \right]\), then the combination of D numbers: \(C = D_{1} \odot D_{2}\):

$$ \begin{gathered} D(\emptyset ) = 0, \hfill \\ D(I) = \frac{1}{{1 - X_{D} }}\sum\limits_{{I_{1} \cap I_{2} = I}} {D_{1} (I_{1} )D_{2} (I_{2} )} ,I \ne \emptyset , \hfill \\ \end{gathered} $$
(2)

with

$$ \begin{gathered} X_{D} = \frac{1}{{P_{1} P_{2} }}\sum\limits_{{I_{1} \cap I_{2} = \emptyset }} {D_{1} (I_{1} )D_{2} (I_{2} )} , \hfill \\ P_{1} = \sum\limits_{{I_{1} \subseteq \Omega }} {D_{1} (I_{1} )} , \hfill \\ P_{2} = \sum\limits_{{I_{2} \subseteq \Omega }} {D_{2} (I_{2} )} . \hfill \\ \end{gathered} $$

Rule (2) generalizes the rule of Dempster [10]. Such as Q1 = Q2 = 1, then Rule (2) converts into Dempster’s rule. Rule (2) shows as a method for combining and fusing ambiguous data. For an individual \(D = \left[ {\left( {a_{1} ,u_{1} } \right),...,\left( {a_{j} ,u_{j} } \right),...,\left( {a_{n} ,u_{n} } \right)} \right]\), the integration operator presents as: \(M(D) = \sum\nolimits_{j = 1}^{n} {a_{j} u_{j} }\),where \(a_{j} \in R^{ + } ,u_{j} > 0,\sum\nolimits_{j = 1}^{n} {u_{j} \le 1}\).

Triangular fuzzy numbers

Zadeh initially introduces fuzzy set theory, which could effectively characterize the limitation of human cognitive processes. Because the advantage of fuzzy set can shift degrees of membership [36]. A Triangular fuzzy number symbolizes as \(\widetilde{\psi } = \left( {w,v,b} \right)\), where \(w \le v \le b\), then the membership function can be described by:

$$ m_{{\widetilde{\psi }}} \left( z \right) = \left\{ \begin{gathered} 0, z < w {\text{or }}z > q \hfill \\ \frac{z - w}{{v - w}}, w \le z \le v \hfill \\ \frac{q - z}{{q - v}}, v \le z \le q \hfill \\ \end{gathered} \right.. $$

The basic operations can be denoted as:

$$ \begin{gathered} (1)\,\,\widetilde{\gamma }_{1} + \widetilde{\gamma }_{2} = \left( {w_{1} ,v_{1} ,q_{1} } \right) + \left( {w_{2} ,v_{2} ,q_{2} } \right) = \left( {w_{1} + w_{2} ,v_{1} + v_{2} ,q_{1} + q_{2} } \right); \hfill \\ (2)\,\,\widetilde{\gamma }_{1} \!-\! \widetilde{\gamma }_{2} \!=\! \left( {w_{1} ,v_{1} ,q_{1} } \right) \!-\! \left( {w_{2} ,v_{2} ,q_{2} } \right) = \left( {w_{1} - w_{2} ,v_{1} - v_{2} ,q_{1} - q_{2} } \right); \hfill \\ (3)\,\,\widetilde{\gamma }_{1} \times \widetilde{\gamma }_{2} = \left( {w_{1} ,v_{1} ,q_{1} } \right) \times \left( {w_{2} ,v_{2} ,q_{2} } \right) = \left( {w_{1} w_{2} ,v_{1} v_{2} ,q_{1} q_{2} } \right); \hfill \\ (4)\,\,\widetilde{\gamma }_{1} \div \widetilde{\gamma }_{2} = \left( {w_{1} ,v_{1} ,q_{1} } \right) \div \left( {w_{2} ,v_{2} ,q_{2} } \right) = \left( {w_{1} /q_{2} ,v_{1} /v_{2} ,q_{1} /w_{2} } \right); \hfill \\ \end{gathered} $$

where \(w_{1} ,w_{2} > 0;v_{1} ,v_{2} > 0;q_{1} ,q_{2} > 0.\)

Methodology

The fuzzy WINGS technique is expanded using D numbers under the vagueness present in group decision-making. The D numbers can be used to demonstrate include: (1) accounting for the ambiguity which processes in the expert comparison process; (2) constructing a range of fuzzy linguistic forms based on the inconsistencies and inaccuracies in expert preferences. Many multi-criteria models use fuzzy numbers to depict the ambiguity. With the advantage of D numbers, it is now feasible to handle the uncertainties in selecting fuzzy linguistic elements. D numbers presents the likelihood degree of each fuzzy linguistic variable. Furthermore, D numbers improve the effectiveness of the data collected by expert group. The next part describes the algorithm, which involves nine steps:

Step 1. Select the fuzzy linguistic scale for evaluation.

The corresponding numbers and scale defined as:

Step 2. Generate fuzzy initial strength-relation matrix of different group.

Factors analyzed by experts: Assuming that m experts are divided into two homogenous groups, GP1 and GP2, with comparing the n criteria, then the comments are transformed into the form of Triangular fuzzy numbers, where \(x = \left[ {x_{a} ,a = 1,2,...,n} \right]\).

The members in expert group should determine the degree of influence of criteria l on criteria m. The D numbers denote each expert group's comparative evaluation of the pair of jth and kth criteria.

\(D_{lm}^{1} = \left[ {\left( {a_{lm(1)}^{1} ,u_{lm(1)}^{1} } \right),...,\left( {a_{lm(j)}^{1} ,u_{lm(j)}^{1} } \right),...,\left( {a_{lm(s)}^{1} ,u_{lm(s)}^{1} } \right)} \right]\) and \(D_{lm}^{2} = \left[ {\left( {a_{lm(1)}^{2} ,u_{lm(1)}^{2} } \right),...,\left( {a_{lm(j)}^{2} ,u_{lm(j)}^{2} } \right),...,\left( {a_{lm(s)}^{2} ,u_{lm(s)}^{2} } \right)} \right],\) where \(D_{jk}^{1}\) and \(D_{jk}^{2}\) explicit the subjective preferences of GP1 and GP2. Then two nonnegative matrices can be gained as \(X_{{}}^{1} = \left[ {D_{lm}^{1} } \right]_{n \times n}\) and \(X_{{}}^{2} = \left[ {D_{lm}^{2} } \right]_{n \times n}\), which represents each expert group by the form of D numbers.

Step 3. Constructing a Triangular fuzzy strength-relation matrix X: Three stages are processed the conversion of D matrices values.

Phase 1: The vagueness indicated by the experts’ choices could be intermingled. As a result, using the property of \(D_{lm} = D_{l} \odot D_{m}\)(Eq. 3) to combine the numbers, the data given by experts as \(X_{{}}^{1} = \left[ {D_{lm}^{1} } \right]_{n \times n}\) and \(X_{{}}^{2} = \left[ {D_{lm}^{2} } \right]_{n \times n}\) could be analyzed and synthesized.

Phase 2: The ambiguities presented at the intersection of FLVs are converted into distinctive FLVs after performing the criterion for the combination of D numbers. FLVs may be defined as the term-set \(X = \left[ {x_{a} ,a = 1,2,...,n} \right]\), where \(x_{a}\) is a FLV seen in \(D_{lm}^{1}\) and \(D_{lm}^{2}\). Each term \(x_{a}\) is represented as a triangle fuzzy number as \(\widetilde{x} = \left( {x^{w} ,x^{v} ,x^{q} } \right)\), where \(x^{v}\) is the Triangular fuzzy number's (TriFN) center point, and \(x^{w}\) and \(x^{q}\) are the lower and higher boundaries.

The ratio between element \(e_{l,l + 1}\) of the FLVs can be used to process as follows:

$$ D\left( {I_{l} } \right) = D\left( {I_{l} } \right) + D\left( {I_{l} ,I_{l + 1} } \right)\frac{{{\raise0.5ex\hbox{$\scriptstyle {e_{l,l + 1} }$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {e_{j} }$}}}}{{{\raise0.5ex\hbox{$\scriptstyle {e_{l,l + 1} }$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {e_{l} }$}} + {\raise0.5ex\hbox{$\scriptstyle {e_{l,l + 1} }$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {e_{l + 1} }$}}}}, $$
(4)
$$ D\left( {I_{l + 1} } \right) = D\left( {I_{l + 1} } \right) + D\left( {I_{l} ,I_{l + 1} } \right)\frac{{{\raise0.5ex\hbox{$\scriptstyle {e_{l,l + 1} }$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {e_{l} }$}}}}{{{\raise0.5ex\hbox{$\scriptstyle {e_{l,l + 1} }$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {e_{l} }$}} + {\raise0.5ex\hbox{$\scriptstyle {e_{l,l + 1} }$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {e_{l + 1} }$}}}}, $$
(5)

where \(e_{l,l + 1}\) symbolizes the ratio of intersection between the linguistic values \(Q_{l}\) and \(Q_{l + 1}\), \(e_{l}\) and \(e_{l + 1}\) represent the linguistic value \(L_{l}\) and \(L_{l + 1}\). Then, a D matrix \(M = \left[ {D_{lm}^{{}} } \right]_{n \times n}\) can be obtained.

Phase 3: We translate the matrix \(M = \left[ {D_{lm}^{{}} } \right]_{n \times n}\) into the Triangular fuzzy strength-relation matrix \(\tilde{X} = \left[ {\tilde{x}_{lm}^{{}} } \right]_{n \times n}\), and the elements in \(\tilde{X}\) expressed by \(\widetilde{x}_{lm} = \left( {x_{lm}^{w} ,x_{lm}^{v} ,x_{lm}^{q} } \right)\), where n represents the number of FLVs.

Step 4. Generate the normalized fuzzy direct strength-influence matrix.

After forming the single fuzzy direct strength-influence matrix \(\tilde{X} = \left[ {\tilde{x}_{jk}^{{}} } \right]_{n \times n}\), the normalized fuzzy direct strength-influence matrix shows as \(\tilde{Z} = \left\{ {Z^{w} ,Z^{v} ,Z^{q} } \right\}\).

$$ \tilde{Z} = \left[ {\begin{array}{*{20}c} {\tilde{z}_{11} } &\quad {\tilde{z}_{12} } &\quad \cdots &\quad {\tilde{z}_{1n} } \\ {\tilde{z}_{21} } &\quad {\tilde{z}_{22} } &\quad \cdots &\quad {\tilde{z}_{2n} } \\ \vdots &\quad \vdots &\quad \ddots &\quad \vdots \\ {\tilde{z}_{n1} } &\quad {\tilde{z}_{n2} } &\quad \cdots & {\tilde{z}_{nn} } \\ \end{array} } \right], $$

where \(\tilde{z}_{lm} = \left\{ {z_{lm}^{w} ,z_{lm}^{v} ,z_{lm}^{q} } \right\}\) indicates the values after normalized the matrix \(\tilde{X}\) by utilizing the following equations:

$$ \tilde{z}_{lm} = \frac{{\tilde{x}_{lm} }}{{\tilde{y}}}\left\{ {\frac{{z_{lm}^{w} }}{{y_{w} }},\frac{{z_{lm}^{v} }}{{y_{v} }},\frac{{z_{lm}^{q} }}{{y_{q} }}} \right\}, $$
(6)
$$ \tilde{y} = \max \left(\sum\nolimits_{m = 1}^{n} {\tilde{x}_{lm} } \right) = \left\{ {\max \left(\sum\nolimits_{m = 1}^{n} {x_{lm}^{w} } \right),\max \left(\sum\nolimits_{m = 1}^{n} {x_{lm}^{v} } \right),\max \left(\sum\nolimits_{m = 1}^{n} {x_{lm}^{q} } \right)} \right\}. $$
(7)

Step 5. The fuzzy total direction matrix \(H\left( {\tilde{Q}} \right)\) is obtained by the following equation:

$$ H\left( {\tilde{Q}} \right) = \mathop {\lim }\limits_{w \to \infty } H\left( {\tilde{Z}} \right)\left( {I + H\left( {\tilde{Z}} \right) + H\left( {\tilde{Z}} \right)^{2} + \cdots + H\left( {\tilde{Z}} \right)^{w} } \right) = H\left( {\tilde{Z}} \right)\left( {I - H\left( {\tilde{Z}} \right)} \right)^{ - 1} . $$
(8)

Let \(H\left( {\tilde{Q}} \right) = \left[ {H\left( {\tilde{q}} \right)} \right]_{n \times n}\), where \(H\left( {\tilde{q}} \right) = \left[ {\left( {q_{lm}^{w} ,q_{lm}^{v} ,q_{lm}^{q} } \right)} \right]\), then:

$$ Q_{{}}^{w} = \left[ {q_{lm}^{w} } \right]_{n \times n} = Z^{w} \left( {I - Z^{w} } \right)^{ - 1} { ,} $$
$$ Q_{{}}^{v} = \left[ {q_{lm}^{v} } \right]_{n \times n} = Z^{v} \left( {I - Z^{v} } \right)^{ - 1} { ,} $$
$$ Q_{{}}^{q} = \left[ {q_{lm}^{q} } \right]_{n \times n} = Z^{q} \left( {I - Z^{q} } \right)^{ - 1} \, {.} $$

Step 6. Obtain dependence matrix.

Let \(H\left( Q \right) = \left[ {H\left( {q_{lm} } \right)} \right]_{n \times n}\), then \(q_{jk}^{{}}\) can be calculated as follows:

$$ q_{lm}^{{}} = \frac{{y_{lm}^{b} + 4y_{lm}^{c} + y_{lm}^{d} }}{6}. $$
(9)

Step 7. Achieve the sums of row and column in matrix Q.

We can sum the values in the directions of rows (R) and columns (L) in the dependence matrix Q as:

$$ R = [R_{l} ] = \sum\nolimits_{l = 1}^{n} {q_{lm} } , l = 1,2, \ldots ,n - 1,n, $$
(10)
$$ L = [L_{m} ] = \sum\nolimits_{m = 1}^{n} {q_{lm} } , m = 1,2,...,n - 1,n. $$
(11)

R depicts overall effect of element j as a cause on other elements, while L depicts the complete effect of other elements on element k as an effect.

Step 8. Delineate the cause-effect relationship chart.

In cause-effect chart, the value of (R + L) represents total degree of influence on the elements, which can be used to calculate the prominence of this element. A positive value evinces that the element is dominant, while the negative value expresses that the element is influenced. (R + L) and (R − L) are the symptoms of the horizontal and vertical axes of the cause-effect diagram. Furthermore, the WINGS methodology is more suited for studying real-world scenarios than DEMATEL, since it takes strength of elements into account. Using WINGS technique, it is possible to estimate and exploit the degree of correlation between the elements, as well as the dependencies and feedbacks of the elements in the network structure [20].

Step 9. Reachability matrix and MICMAC analysis.

The development of reachability matrix is remarkable for its ability to analyze the degree of impact. If the influence of a criterion on other criteria exceeds a threshold, the stimulus receives a response, indicating that the factor can directly influence other criteria; if the criterion's influence on other criteria is less than a threshold, the stimulus does not receive a response, indicating that the criteria have no effect on other. After that, the reachability matrix was separated into levels. MICMAC was developed by taking into consideration the interrelationships in the reachability matrix, which was developed to analyze the interrelationships and interactions between elements in a system [37]. The influence (driving) power of an element is calculated by adding all the "1" in the rows, while the dependency is calculated by adding all the "1" in the columns. This leads to an analytical representation of the correlation matrix, which consists of four components: autonomous, dependence, driving, and linkage factors. The autonomous part is composed of stimulus factors with low impact and low dependence. The driving part consists of factors with strong drive and low dependence. Influential factors with weak drive and high dependence make up the dependence part. The linkage part is composed of influences with strong drivers and dependencies.

Empirical analysis

This chapter demonstrates the implementation of the TriFN D-WINGS approach for measuring supply chain quality to gain an appropriate understanding the aspects affecting agriculture supply chain management (ASCM), which were precisely extracted and assessed using the TriFN D-WINGS–MICMAC methodology.

Evaluation system with D number and Triangular fuzzy number

Step 1: Construction of the influencing factors of ASCM.

An evaluation technique of the influencing aspects of ASCM has been established based on the state of ASCM and structural analysis methodologies used in supply chain management. We selected ten criteria as monitoring and licensing (P1), Government subsidies (P2), technical level (P3), customer demand/requirement (P4), environmental consciousness (P5), green design (P6), quality of produce (P7), cost and benefits (P8), infrastructure (P9), market channels (P10). To ensure the availability, we got the help from experts in economics, management, and agriculture.

Step 2: Experts’ analysis of factors.

The study included eight experts who were separated into two expert groups: GP1 and GP2, and propose their idea using fuzzy linguistic scale as Table 2. The evaluation values can be seen in Table 3.

Table 2 The corresponding Triangular fuzzy numbers
Full size table
Table 3 Group experts’ evaluation
Full size table

Step 3: Obtain aggregated experts’ preferences.

The values of expert preferences should be aggregated into appropriate fuzzy values using Eqs. (3–5). Table 4 shows the use of the combination criterion within the expert dimensional analysis.

Table 4 Aggregated D matrix of experts’ preferences (GP1 and GP2)
Full size table

Step 4: Calculate the components of the normalized total fuzzy strength-influence matrix.

The components can be esteemed in Table 5 by Eqs. (6) and (7), which provides uncertainty by turning D numbers into Triangular fuzzy numbers. And the matrix is gained with the Eqs. (8) and (9) as shown in Table 6.

Table 5 Normalized fuzzy strength-influence matrix
Full size table
Table 6 Total strength-influence matrix
Full size table

Step 5: Achieve the sums of row and column in the fuzzy total strength-influence matrix.

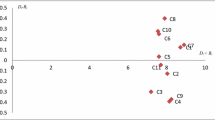
The optimal weight coefficients are determined by the total direct/indirect effects, while Eqs. (10) and (11) are used to enumerate the sums of R and L, which can be shown in Table 7 and Fig. 1.

Table 7 The R&L values and types of factors with WINGS and DEMATEL
Full size table
Fig. 1
figure 1

The chart of interactive influence degree

Full size image

Analysis of prominence

As indicated in Fig. 1 and Table 7, the terminal level of influencing components is P1 > P2 > P4 > P7 > P10 > P3 > P8 > P9 > P6 > P5. The findings show that monitoring and licensing (P1) is the most important component, meaning that P1 has the most direct and significant effect on ASCM. Government subsidies (P2), customer demand (P4), and quality of produce (P7) all have a significant influence. Environmental consciousness (P5), green design (P6), cost and benefits (P8), and infrastructure (P9) have the low level, meaning that these factors get low direct effect on ASCM. These data indicate that the ASCM is primarily impacted by the government, which provides monitoring, licensing and subsidies, as well as technology, which improves efficiency and quality.

Analysis of relation

Based on the R–L values, the fourteen contributing factors may be divided into two groups. As shown in Table 7 and Fig. 1, the cause group with high R–L values includes P4, P5, P6, P9, and P10, with the order P10 > P4 > P9 > P6 > P5. Market channels (P10) has the highest R–L value of these components, suggesting that market channels have the biggest influence on the ASCM and has a higher impact on other variables than other factors. The customer demand (P4) variable has the second highest R–L value, suggesting that it has a considerable impact on ASCM. Infrastructure (P9) has the third highest R–L score. The environmental factors are conventional roles for ASCM, include environmental consciousness (P5) and green design (P6). Through economic and social factors, they will impact the other aspects and the effect of ASCM.

Members of the effect group with negative R–L values are P1, P2, P3, P7, and P8, and their sequence is P8 > P3 > P7 > P2 > P1. Variables have more influence on other than receive influence by other variables, which is the effect group. The greater the variable influences on other variables, the lower R–L value is. Monitoring and licensing (P1) has the lowest R–L score, suggesting that other variables have the greatest impact on the market channel. Furthermore, cost and benefits (P8) have a high R–L value, indicating that it is a significant variable impacting ASCM. Government subsidies (P2) had the second lowest R–L value, showing that other variables have a significant effect on government subsidies. Technical level (P3) and quality of produce (P7) are the technical factors that are highly impacted by external variables.

To demonstrate the effect of the strength of the criteria, we use DEMATEL to compare with the results, for the reason that WINGS and DEMATEL have the similar type of date and simpler operation process than other methods. Through Table 7, we can find that the cause-effect type of the factors is same between two results, but the rank of the prominence is divergent. Obviously, the order of DEMATEL is P1 > P2 > P4 > P10 > P8 > P3 > P7 > P9 > P6 > P5, and the discordant components include P3, P7, P8, and P10. We think the main reason for the difference is the effect of the strength from these factors themselves, which plays an important role in the dimension of prominence.

Strategy analysis

We further separated criteria into four zones at the dimensions of prominence and relation depicted in Fig. 1 using Pan and Chen's [38] notion.

  1. 1.

    Priority zone (high prominence and relationship): customer demand (P4) and market channels (P10) are all primarily from the economic dimension. These are the cause criteria and the basic components that influence the other criteria.

  2. 2.

    Long-term zone (high prominence and low relation): monitoring and licensing (P1), government subsidies (P2), technical level (P3), quality of produce (P7), and cost and benefits (P8) perspectives can be enhanced when other indicators improve.

  3. 3.

    Contingency zone (low prominence and high relationship): environmental consciousness (P5), green design (P6), and infrastructure (P9) are in economic dimension, which have a moderate influence on other components but are less influenced by other elements.

  4. 4.

    No-priority zone (low prominence and relationship): there are no items in this category, which suggests that it’s difficult to have a direct improvement of the indicators in the short term.

Reachability matrix and structural model

We can utilize the threshold equal (1.118), which is determined by average value of all the elements in the total strength-relation matrix, to form the matrix of influence among criteria in Table 8, which is formed by deleting entries with values smaller than those in the total strength–relation matrix.

Table 8 The reachability matrix
Full size table

The data are summed by rows and columns separately to obtain the driving and dependence forces for each factor. Figure 2 shows a graph of driving and dependence power of criteria. The first autonomous component is infrastructure (P9) with a driving force of 4 and no dependencies, indicating that infrastructure is relatively independent in the AGSC. Environmental consciousness (P5) and green design (P6) are the drivers with high drivers and low dependencies, and can be the core factors driving the development of AGSC. In the dependence section, technical level (P3) and quality of produce (P7) have driving force less than 4 and dependency greater than 7, indicating that they receive more influence from other factors and cannot develop these factors independently, but must be developed in combination with other driving forces. The group of linkage factors are the most important factors that policy makers must prioritize for improving the effectiveness of agricultural supply chain management, and these factors include monitoring and licensing (P1), government subsidies (P2), and cost and benefits (P8), where P2 has driving force of 5 and dependency of 9; P1 has driving force and dependency of 5 and 10, respectively; P3 has driving force of 4 and dependency of 7. In the driving section, customer demand (P4) and market channels (P10) have driving force 7 and dependency 2, indicating that they have a high influence on other factors and can develop them independently.

Fig. 2
figure 2

The driving and dependence power diagram

Full size image

Conclusion

The fuzzy WINGS approach is extended by D numbers in this study to resolve uncertainty which is unavoidable in the traditional decision-making procedures, particularly when there are many decision makers. With the combination of D numbers, it is feasible to consider additional uncertainty in the selection of fuzzy linguistic variables. As a complement to the fuzzy set, D numbers have the advantage of catching the likelihood of picking the fuzzy linguistic variable and improving the validity of current estimation within MCDM. WINGS technique can count both the strength and influence of interdependence, which cannot be captured in other similar approaches as DEMATEL. In addition, this integrated framework also has the capacity to efficiently capture and graphically represent intricate interwind interactions in situations with hierarchical structures, as well as user-friendliness and minimal computational complexity. Furthermore, with the information to capture uncertainties in the experts’ comparisons, the initial strength–influence matrix is then converted into a total strength–influence matrix, and causality is generated through the interaction, centrality, and causality of each component. Finally, the reachability matrix is created by setting a threshold to show the results of MICMAC. Through the ASCM example, this novel integrated fuzzy D-WINGS–MICMAC technique is obviously effective and adaptable, because it does not obey the restriction of mutually exclusive and collectively extensive set, as well as can analyze both the strength and the influence of dependence among the criteria or levels in decision issues.

For future study, other types of fuzzy numbers, such as type-2 fuzzy numbers or Gaussian fuzzy numbers, might be extended in this framework according to their applicability and related membership functions. We also recommend greater study into the MCDM models with evaluation of the degree and intensity of interdependence under the limits of subjective assessments. For this purpose, any other MCDM method (ANP, VIKOR, or DEMATEL, etc.) could be compared to test the suitability and validity of the introduced method. Finally, this method of our paper may be used in various situations such as the healthcare, transportation, risk management, and so on.