Introduction

The influential solution for solving complex and uncertain decision-making problems is RL. This algorithm uses reward functions that help an agent converse with the dynamic environment. The output is a policy that helps in dealing with uncertain and complex problems. The policy is a probability of action that can take place in a state. RL is different from supervised learning (SL). It does not require target labels and this helps in building generalization abilities. However, it is hard to set down reward function in advance for handling unpredictable, large, and intricate problems. This leads to the development of IRL which helps in tackling complex problems by understanding reward function through expert demonstrations [1]. IRL is a stream of Learning from Demonstration (LfD) [2] or imitation learning [3, 4], or theory of mind [5]. In IRL, the policy is modified according to the demonstrated behavior. Function mapping and reward function are generally two methods of deriving the policy. Both have their limitations. Function mapping is used in SL and it requires target labels that are expensive and complex methods, whereas reward function is used in RL and knowing the reward function in advance for large and complex problems is a tedious task. These problems can be overcome using LfD and IRL. IRL helps in using the experts’ knowledge in such a way that it can be used in other scenarios.

IRL is formulated by the author Russell [6] as:

  1. 1.

    Given: Agents behavior estimation, sensory inputs to agents, environment model

  2. 2.

    Output: Reward function.

IRL is formally defined by the authors Ng and Russell [7], for the machine learning community as:

To optimize the reward function R for justification of agent behavior by figuring out the optimal policy for the function (S, A, T, D, P) where S is a finite state of space, A is a set of actions, P is transition probability, D is a discount factor, and P is policy [7].

The motivation of the current study

  • Researchers in the current and the past are developing programs for successful IRL implementation by targeting one or two identified problems that may or may not be important at present in the real-time scenario [8,9,10,11]. The current study tries to fill this research gap by prioritizing the IRL implementation problems using fuzzy AHP.

  • The past literature shows that IRL’s theoretical background including problems and solutions is not disclosed comprehensively much by researchers.

  • Different researchers have mentioned different solutions for the IRL problems, and these solutions are not been properly organized and analyzed in the past [12,13,14,15,16]. The current study analyzes and ranks the solutions using the fuzzy TOPSIS method, and helps the decision-makers to make decisions by targetting the prioritized solutions for IRL problems.

Contributions to the paper

  • This is the first study that uses the fuzzy AHP approach to rank the IRL implementation barriers/problems.

  • This is the first study that uses a fuzzy TOPSIS approach to rank the solutions that will overcome the IRL implementation problems.

  • To the best of our knowledge, no other research exists that reports the scope and analysis of this current study about IRL barriers and their solutions. The only hybrid fuzzy AHP–TOPSIS proposed study can be a torchbearer for the researchers to understand the barriers and their solutions in the IRL field.

  • The experts’ opinions in the IRL have been collected in the form of linguistics scales for fuzzy AHP and fuzzy TOPSIS implementation. The current study has used fuzzy MCDM methods as they are capable to handle vagueness and uncertainties in decision-makers’ judgments.

  • The results of the current study can be beneficial to the software companies, industries, and governments that are using reinforcement learning in real-time scenarios.

  • The results show that the most important solution is ‘Supports optimal policy and rewards functions along with stochastic transition models’ and the most significant problem that should be taken care of, while IRL implementation is ‘lack of robust reward functions’.

Hybrid fuzzy AHP–TOPSIS approach performance aspects in IRL

  • Traditional IRL methods are unable to estimate the reward function when there are no state-action trajectories available. The hybrid approach helps to look for the solutions to solve the above problem. Let us illustrate the issue with an example, “Person A can go from position X to position Y with any route. There exists different scenery while going routing through different routes. Person A has some specific preferences for the scenery while routing from position X to position Y. Let’s suppose, the routing time is known, Can we predict person A preferences regarding scenery?” [17]. This is a classical IRL problem having a large problem size or large state spaces. The fuzzy AHP approach of the current study has weighted and ranked this problem high and this is the problem of scalability with large problem sizes or large state spaces. The fuzzy TOPSIS of the current study has focused on solving such problems using “Support multiple rewards and non-linear reward functions for large state spaces”. The new algorithms which support non-linearity for large state spaces or large problem sizes will be used for the proper estimation of reward functions, and it also motivates the researchers and companies to develop new algorithms that can solve such problems in better ways.

  • Feature expectation is another issue with IRL. This is the quality evaluation or assessment of the reward function. The fuzzy AHP approach of the current study has ranked this issue as the number one issue “Lack of robust reward functions” and the fuzzy TOPSIS approach has advocated the use of a solution “Supports optimal policy and rewards functions along with stochastic transition models” that is also ranked one solution to solve the above-mentioned issue. The solution advocated for the building up of algorithms for handling robust reward functions.

  • Using the results of the hybrid approach, the failure rate of IRL projects in the software companies and manufacturing industries can be minimized or reduced.

Literature review

The comprehensive literature review of the current study is carried out in two different phases: the first phase targets to figure out the problems associated with the implementation of IRL, and the second phase targets to find out the solutions to overcome the identified problems.

Problems in the implementation of IRL

IRL mainly targets learning from demonstration or imitation learning [2]. Imitation learning is a way of learning and thriving new skills by perceiving the actions executed by another agent. IRL suffers from various problems. IRL is ill-posed [18], which means that multiple reward functions are consistent with the same optimal policy, and multiple policies exist with the same reward function [18, 19]. The reward function is typically anticipated to be a linear grouping of features [1] which is erroneous. One more thing, original IRL implementation codes consider that demonstrations given by experts’ are optimal, but usually, this thing is not performed in practice. These codes should handle noisy and shabby demonstrations [1, 20]. The policy imitated from the apprenticeship IRL is stochastic, which may not be a good discretion if the expert’s policy is deterministic [1]. When a new reward function is added to iteratively solve IRL problems, the overall computational overhead is hefty [1, 21, 22]. The demonstrations cannot be representative enough and the algorithms should be generalized demonstrations to uncover areas [1]. Different solutions are proposed for solving IRL algorithms. IRL fails to learn robust reward functions [23, 24]. IRL suffers from Ill-posed problems [1]. IRL algorithms have a lack of scalability, which means existing techniques unable to handle large systems due to their run-down performance and incompetence [9] as well as lack of reliability, which means a lack of learning of the reward function by existing techniques due to their incompetence in the learning process [9]. The algorithms have an obstacle to accurate inference [23] Sensitivity to Correctness of Prior Knowledge [23], Disproportionate Growth in Solution Complexity with Problem Size [23], and Direct learning of reward function or policy matching [23]. Table 1 shows the problems associated with the implementation of IRL.

Table 1 Problems in the implementation of IRL
Full size table

Eight problems have been identified in the IRL implementation from the literature, as shown in Table 1. All these problems have arisen due to the IRL basic assumptions and IRL goal to learn the reward function, find the right policy, and deal with complex and large state spaces. IRL is a machine learning framework that has been recently developed to solve the inverse problem of reinforcement learning. IRL targets to figure out the reward function by learning from the observed behavior of the agents and the underlying control model in the process of IRL implementation is the Markov decision process (MDP). In other words, it can be said that IRL portrays learning from humans. IRL also works on the assumptions; one assumption is that the observed behavior of the agent is optimal (this is a very strong assumption when talking about human behavior learning) and the other assumption is that agent policies are optimal when there is an unknown reward function. These assumptions can result in inaccurate inferences and lead to incorrect reward function learning. This reduces the overall performance of the IRL. The IRL problems can arise due to the agent's action, information available to the agent as well as long-term plans of the agent [33]. The correct reward function estimation becomes very difficult when data are complex, inaccurate and agent actions on this data lead to many large state spaces. For most observations of the agent behavior, there exist multiple fitting reward functions and the selection of the best reward function is a challenge. The short-term action of an agent is quite different from its long-term plan and it also acts as a hurdle to estimating the reward function properly. There exist many problems in the IRL implementation and their solutions have also been proposed in the literature and these are described in Sect. Solutions to overcome the identified problems.

Solutions to overcome the identified problems

Different solutions have been proposed to solve the problems faced by the classical IRL algorithm. One is to modify the existing algorithm that improves imitation learning and rewards functions learning. Some of the algorithms are adversarial inverse reinforcement learning (AIRL) [24], cooperative inverse reinforcement learning (CIRL) [34], DeepIRL [16, 35], gradient-based IRL approach [36], relative entropy IRL (REIRL) [37, 38], Bayesian IRL [1, 23], and score-based IRL [25]. Other solutions like maximum margin optimization. It means to introduce the loss functions that optimize the demonstrations for other available solutions by a margin [18]. It also solves the problem of ill-posed. Bayesian IRL uses the probabilistic model to pact with the uncertainty that is allied with the reward function as in IRL. Moreover, this model if extended helps in uncovering the posterior distribution of the expert’s preference [9, 12, 18, 28, 39]. IRL can also accommodate incorrect and partial policies along with noisy observations [8, 23]. One of the solutions is maximum entropy or its optimization [16, 18, 21, 23, 40], and it mainly solves the problem of ill-posed. To extract rewards in problems with large state spaces [29,30,31] and support for non-linear reward functions [41]. More advancements in the field for support of stochastic transition models and transition models are optimized [22, 36]. Many researchers have worked on rewards and optimal policies [10, 13,14,15, 20, 25,26,27, 42,43,44,45], and multiple reward functions [46]. Learning from failed and successful demonstrations [12, 13, 15, 32]. Some authors have worked to cover the risk factors involved in IRL like risk-aware active IRL [47] and risk-sensitive inverse reinforcement learning [12]. Table 2 shows the solutions that are implemented to overcome the identified problems of IRL.

Table 2 Solutions to overcome the problems
Full size table

By analyzing the literature, the IRL algorithms have been divided into four categories to find out the optimal reward function. The first category is the development of max-margin planning methods as they try to match feature expectations. In other words, these methods estimate reward functions that try to maximize the margin between the value function or optimal policy and other policies or value functions. The second category is maximum entropy methods. These methods try to estimate the reward function using the maximum entropy concept in the optimization routine. These methods can handle large state spaces as well as sub-optimal issues of expert demonstrations. These methods try to handle the trajectory noises and agent imperfect behavior. The third category develops improved IRL algorithms like AIRl, CIRL, DeepIRL, Gradient IRL, REIRL, Score-based IRL, and Bayesian IRL for improving imitation learning. The fourth category is the miscellaneous category that targets the development of IRL algorithms that considers risk-awareness factors, learn from failed demonstration, support multiple and non-linear reward functions, and posterior distribution on the agent’s preferences [33]. All the above algorithms solve different IRL problems. The selection of these algorithms is an important step while working on IRL implementation.

IRL has been used in many domains and its applications have been divided into three categories [33]. The first one is the development of autonomous intelligent agents that mimic the expert. Some of the examples of this category include the development of autonomous helicopters [48], robot autonomous systems [38, 49], path planning [50, 51], autonomous vehicles [16, 52], and playing games [12, 34]. The second category is the agent's interaction with other systems to improve the reward function estimation. Some of the examples of this category include pedestrians trajectory [53,54,55,56], haptic assistance, and dialogue system [57,58,59]. The third category is learning about the system using the estimated reward function. Some of the examples of this third category include cyber-physical systems [60], finance trading [61], and market estimation [62].

Fuzzy AHP

AHP is a quantitative technique that was introduced by the author Saaty [63]. This technique armatures a multi-person, multi-criteria, multi-period problem hierarchically, so that solutions are simplified. AHP also has some limitations. These are listed below:

  1. (a)

    Unable to handle ambiguity and vagueness related to human judgments.

  2. (b)

    Experts’ opinions and preferences influence the AHP method.

  3. (c)

    AHP ranking method is imprecise.

  4. (d)

    It uses an unbalanced scale of judgment.

To overcome these limitations, fuzzy set theory is integrated with AHP. This fuzzy AHP helps in capturing the vagueness, impreciseness, and ambiguity of human judgments by better handling linguistic variables. This approach has been used extensively in many different applications like risk assessment in construction sites [64], gas explosion risk assessment in coal mines [65], selection of strategic renewable resources [66], steel pipes supply selection [67], aviation industry [68], banking industry [69], supply chain management [70], etc. Fuzzy AHP was introduced by the author Chang [71]. The pairwise comparison scale uses mostly triangular fuzzy numbers (TFNs), and for synthetic extent value of pairwise comparisons, the extent analysis method is used. It is important why fuzzy AHP has been preferred over other MCDM methods, this is because:

  1. (1)

    Fuzzy AHP is having less computational complexity as compared with other MCDM methods like ANP, TOPSIS, ELECTRE, and multi-objective programming.

  2. (2)

    It is the most widely used MCDM method [72].

  3. (3)

    One of the main advantages of the fuzzy AHP method is that it can simultaneously evaluate the effects of different factors in realistic situations.

  4. (4)

    To deal with imprecision and vagueness of judgments, fuzzy AHP uses a pairwise comparison.

Definition1: A fuzzy set S is represented as {E, μS (x) | x € X} where X = {x1, x2, x3 …} and μS (x) = [73] For a TFN (u, v, w), its membership function is defined in Eq. (1)

Equation (1) states that u ≤  v ≤  w where u means lower value and w means the upper value of the fuzzy set M and v lies between p and r or, in other words, it is the modal value. Different operations can be performed on the TFNs S1 = (u1, v1, w1) and S2 = (u2, v2, w2). These are mentioned below in Eqs. (2)–(6)

$$\begin{aligned} S_{1}-S_{2} &= ( {u_{1} ,v_{1} ,w_{1} } ) - ( {u_{2} ,v_{2} ,w_{2} }) \\& = ( {u_{1} - u_{2} ,v_{1} - v_{2} ,w_{1} - w_{2} } )\\& {\text{where}} \,u_{1} ,u_{2} \geq 0,v_{1} ,v_{2} \geq 0,w_{1} ,w_{2} \geq 0 \end{aligned}$$
(2)
$$\begin{aligned} {{S}}_{{1}} + {{S}}_{{2}} & = \left( {{{u}}_{{1}} ,{{v}}_{{1}} ,{{w}}_{{1}} } \right) \, + \, \left( {{{u}}_{{2}} ,{{v}}_{{2}} ,{{w}}_{{2}} } \right) \\ & = \left( {{{u}}_{{1}} + {{u}}_{{2}} ,{{ v}}_{{1}} + {{v}}_{{2}} ,{{ w}}_{{1}} + {{w}}_{{2}} } \right)\\& {\text{where}} {{u}}_{{1}} ,{{u}}_{{2}} \ge \, 0,{{ v}}_{{1}} ,{{v}}_{{2}} \ge \, 0,{{ w}}_{{1}} ,{{w}}_{{2}} \ge \, 0 \\ \end{aligned}$$
(3)
$$\begin{aligned} {{S}}_{{1}} / {{S}}_{{2}} & = \left( {{{u}}_{{1}} ,{{v}}_{{1}} ,{{w}}_{{1}} } \right) \, / \, \left( {{{u}}_{{2}} ,{{v}}_{{2}} ,{{w}}_{{2}} } \right) \\ & = \left( {{{u}}_{{1}} /{{u}}_{{2}} ,{{ v}}_{{1}} /{{v}}_{{2}} ,{{ w}}_{{1}} /{{w}}_{{2}} } \right) \\& {\text{where}} {{u}}_{{1}} ,{{u}}_{{2}} \ge \, 0,{{ v}}_{{1}} ,{{v}}_{{2}} \ge \, 0,{{ w}}_{{1}} ,{{w}}_{{2}} \ge \, 0 \\ \end{aligned}$$
(4)
$$\begin{aligned} {{S}}_{{1}} * {{S}}_{{2}} & = \left( {{{u}}_{{1}} ,{{v}}_{{1}} ,{{w}}_{{1}} } \right) \, * \, \left( {{{u}}_{{2}} ,{{v}}_{{2}} ,{{w}}_{{2}} } \right) \\ & = \left( {{{u}}_{{1}} *{{u}}_{{2}} ,{{ v}}_{{1}} *{{v}}_{{2}} ,{{ w}}_{{1}} *{{w}}_{{2}} } \right)\\& {\text{where u}}_{{1}} ,{{u}}_{{2}} \ge \, 0,{{ v}}_{{1}} ,{{v}}_{{2}} \ge \, 0,{{ w}}_{{1}} ,{{w}}_{{2}} \ge \, 0 \\ \end{aligned}$$
(5)
$$\begin{aligned} {{S}}_{{1}}^{{ - {1}}} & = \left( {{{u}}_{{1}} ,{{v}}_{{1}} ,{{w}}_{{1}} } \right)^{{ - {1}}} \\ & = \left( {{1}/{{w}}_{{1}} ,{ 1}/{{v}}_{{1}} ,{ 1}/{{u}}_{{1}} } \right)\\& {\text{where}} {{u}}_{{1}} ,{{u}}_{{2}} \ge \, 0,{{ v}}_{{1}} ,{{v}}_{{2}} \ge \, 0,{{ w}}_{{1}} ,{{w}}_{{2}} \ge \, 0. \\ \end{aligned}$$
(6)

The linguistic variables and corresponding TFNs are shown in Table 3.

Table 3 Fuzzy linguistic rating scale
Full size table

The steps used by the author Chang [71] are mentioned below:

Step 1: The pairwise fuzzy matrix (\(\tilde{S}\)) is created using the mathematical Eq. (7). TFNs are used while creating a pairwise fuzzy matrix

$$\begin{aligned} \tilde{S} = \left[ {\begin{array}{*{20}c} {1,1,1} & {\tilde{s}_{12} } & {\tilde{s}_{13 } } & {\tilde{s}_{14 } } & \cdots & {\tilde{s}_{1n } } \\ {\tilde{s}_{21} } & {1,1,1} & {\tilde{s}_{23} } & {\tilde{s}_{24} } & \cdots & {\tilde{s}_{2n} } \\ {\tilde{s}_{31} } & {\tilde{s}_{32} } & {1,1,1} & {\tilde{s}_{34} } & \cdots & {\tilde{s}_{3n} } \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ {\tilde{s}_{n1} } & {\tilde{s}_{n2} } & {\tilde{s}_{n3} } & {\tilde{s}_{n4} } & \cdots & {1,1,1} \\ \end{array} } \right], \end{aligned}$$
(7)

where \(\tilde{s}\) = (ugh, vgh, wgh) where g, h = 1, 2, 3, ……n are the criterion and u, v, w are triangular fuzzy numbers. Here, \(\tilde{s}_{gh}\) indicates the decision makers' preference with the help of fuzzy numbers of gth criterion over hth criterion. Parameter u represents minimal value, parameter v depicts median value and parameter w characterizes maximum possible value.

The pairwise fuzzy matrix is an n x n matrix having fuzzy numbers \(\tilde{s}_{gh}\) as shown in Eq. (8)

$$\tilde{S}_{gh} = \left\{ {\begin{array}{cc} 1,2,3 \ldots .9 \ or \ 1^{ - 1} 2^{ - 1} 3^{ - 1} ......9^{ - 1} & g \ne h \\ 1 & g = h \\ \end{array} } \right..$$
(8)

The values in the pairwise fuzzy matrix \(\tilde{S}_{gh}\) are filled using the linguistic scale as mentioned in Table 3.

Step 2: The fuzzy synthetic extent values (CVs) are calculated using Eq. (9) for the xth object for all criteria (C) as

$$\begin{aligned} CV_{x} = \left( { \mathop \sum \limits_{h = 1}^{n} u_{h } ,\mathop \sum \limits_{h = 1}^{n} v_{h } ,\mathop \sum \limits_{h = 1}^{n} w_{h } } \right)\\ \quad *\left( {\frac{1}{{\mathop \sum \nolimits_{g = 1}^{n} w_{g } }} , \frac{1}{{\mathop \sum \nolimits_{g = 1}^{n} v_{g } }} ,\frac{1}{{\mathop \sum \nolimits_{g = 1}^{n} u_{g } }}} \right). \end{aligned}$$
(9)

Parameters u and w are lower limit and upper limit, respectively, whereas v is the modal limit. Parameters g and h are the criteria, and n denotes the maximum number of criteria.

Step 3: Suppose, S1 = (u1, v1, w1) and S2 = (u2, v2, w2) are two fuzzy matrices. S1 and S2 denote the values of extent analysis. The degree of possibility of S1 ≥ S2 can be defined in Eq. (10) as

$${\text{D}}\left( {S_{1} \ge S_{2} } \right) = \left\{ {\begin{array}{ll} 1 & iff v_{1} \ge v_{2} \\ 0 & iff u_{1} \ge w_{1} \\ \frac{{u_{2} - w_{1} }}{{(v_{1} - w_{{1) - \left( {v_{2} - u_{2} } \right)}} }}, & otherwise \\ \end{array} } \right..$$
(10)

Here, D denoted the degree of possibility. For comparing S1 and S2, it is essential to calculate both D (S1 ≥ S2) and D (S2 ≥ S1). The degree of possibility for convex fuzzy numbers to be greater than t convex fuzzy numbers Sg (g = 1, 2, 3, t) can be illustrated as Eq. (11)

$${\text{D}}\left( {{{S}} \ge {{S}}_{{1}} ,{\text{ S}}_{{2}} ,{\text{ S}}_{{3}} ,{\text{ S}}_{{4}} , \, \ldots ..{\text{ S}}_{{\text{t}}} } \right) = {\text{ min D}}({{S}} \ge {{S}}_{{\text{g}}} ){{ \text{ where }g }} = { 1},{ 2},{ 3}, \ldots {\text{t}}{.}$$
(11)

In Eq. 11, g is denoted as complex fuzzy numbers, and n denotes the limit of complex fuzzy numbers.

Step 4: Calculate fuzzy weight (FW`) and non-fuzzy weight or normalized weight (FW) using Eqs. (12) and (13) for all criteria (i.e., problems). In Eq. 12, d` (Ag) denotes the minimum degree of programming among associated criteria. In Eq. 12, d` (Ag) denotes the minimum value of criteria g among all criteria, and in Eq. 13, d (An) denotes the normalized value of d` (An)

$$\begin{aligned} {\text{FW}}` \, & = \left( {{\text{d}}`\left( {{\text{A}}_{{1}} } \right),{\text{ d}}`\left( {{\text{A}}_{{2}} } \right),{\text{ d}}`\left( {{\text{A}}_{{3}} } \right) \ldots \ldots .{\text{ d}}`\left( {{\text{A}}_{{\text{n}}} } \right)} \right)^{{\text{T}}} \\ &{\text{where d}}`\left( {{\text{A}}_{{\text{g}}} } \right) \, = {\text{ min D}}\left( {{\text{C}}_{{\text{g}}} > = {\text{ C}}_{{\text{t}}} } \right) \\ & {\text{and g}},{\text{t }} = {1},{2},{3} \ldots {\text{n and g}} \ne {\text{t}} \\ \end{aligned}$$
(12)
$${\text{FW }} = \left( {{\text{d}}\left( {{\text{A}}_{{1}} } \right),{\text{ d}}\left( {{\text{A}}_{{2}} } \right),{\text{ d}}\left( {{\text{A}}_{{3}} } \right),{\text{ d}}\left( {{\text{A}}_{{4}} } \right) \ldots \ldots .{\text{ d}}\left( {{\text{A}}_{{\text{n}}} } \right)} \right)^{{\text{T}}} .$$
(13)

Fuzzy TOPSIS

Huang and Yoon [74] have introduced this classical multi-criteria decision-making TOPSIS method. The concept of TOPSIS is based on the ideal solution determination. It differentiates between the cost and benefit category, and selects the solution that is closer to the ideal solution. The solution is selected when it is far away from the negative ideal solution (NIS) and closer to the positive ideal solution (PIS). In the classical TOPSIS, human judgments are based on crisp values, but this representation method is not always suitable for real life as some uncertainty and vagueness are associated with judgments. Therefore, the fuzzy approach is the best method to handle the uncertainty and vagueness of human judgments. In other words, it can be said that fuzzy linguistic values are preferred over crisp values. For this reason, fuzzy TOPSIS is used for handling real-life problems that are multifaceted as well as not well defined [75,76,77,78]. The current study has used TFNs for the implementation of fuzzy TOPSIS as they are easy to understand, calculate, and analyze.

The steps used in this approach are mentioned below:

Step 1: Use the linguistic rating scale as mentioned in Table 3 for the computation of the fuzzy matrix. Here, linguistic values are apportioned to each solution (i.e., alternatives) corresponding to the identified problems (i.e., criteria).

Step 2: After the computation of the fuzzy matrix, compute the aggregate fuzzy evaluation matrix for the solutions.

Suppose, there are ‘i’ experts then fuzzy rating for ith expert is Tghi = (aghi, bghi, cghi) where g = 1, 2, 3…….m and h = 1, 2, 3……n. Tghi depicts a fuzzy evaluation matrix and it is denoted by TFNs having parameters letters a, b, c where parameter a is the minimum value, b is the average value, and c denotes the maximum possible value. Parameter g denotes alternatives, h denotes criteria, and i denotes the expert. Here, m denotes maximum alternatives and n denotes maximum criteria. The aggregate fuzzy rating of solutions for 8 identified problems is computed as mentioned in Eq. (14)

$${\text{ a }} = {\text{ min }}\left( {\mathop \sum \limits_{i = 1}^{i} a_{ghi } } \right), {\text{b }} = \frac{1}{{i\mathop \sum \nolimits_{i = 1}^{i} b_{ghi } }}, {\text{c }} = {\text{ max}}\left( {\mathop \sum \limits_{i = 1}^{i} c_{ghi } } \right),$$
(14)

where g denotes alternatives, h denotes criteria, and i denotes the expert.

Step 3: Create the normalized fuzzy matrix. In this, the raw data are normalized using the linear scale transformations, such that all solutions are comparable. The normalized fuzzy matrix is depicted in Eqs. 15, 16, and 17 as

$$\tilde{Q} = \left[ {{\text{q}}_{\text{gh}}} \right]_{\text{m*n }},{\text{ g}} = 1,2,3,4 \ldots ..{\text{m and h}} = 1,2,3,4 \ldots {\text{n,}}$$
(15)

where \(\tilde{Q}\) depicts the normalized fuzzy matrix, g denotes alternatives, m denotes maximum alternatives, h denotes criteria, and n denotes maximum criteria in the approach

$$\tilde{q}_{gh} = \left( {\frac{{a_{gh} }}{{c_{h}^{*} }},\frac{{b_{gh} }}{{c_{h}^{*} }}, \frac{{c_{gh} }}{{c_{h}^{*} }}} \right)\,\,\,{\text{where }}c_{h}^{*} = \begin{array}{*{20}c} {max} \\ g \\ \end{array} {\text{cgh }}\left( {\text{benefit criteria}} \right)$$
(16)
$$\tilde{q}_{gh} = \left( {\frac{{a_{h}^{ - } }}{{c_{gh} }},\frac{{a_{h}^{ - } }}{{c_{gh} }}, \frac{{a_{h}^{ - } }}{{c_{gh} }}} \right) {\text{where, }}a_{h}^{ - } = \begin{array}{*{20}c} {min} \\ g \\ \end{array} {\text{a}}_{{{\text{gh}}}} ({\text{cost criteria);}}$$
(17)

\(\tilde{q}_{gh}\) also denotes the normalized fuzzy matrix, in Eq. 16, it is first calculated by dividing the each TFNs value by \(c_{h}^{*}\) (it denotes the maximum possible value of benefit criteria), and Eq. 17 shows the updated value of normalized fuzzy matrix values by dividing \(a_{h}^{ - }\) (it denotes the minimum value of cost criteria) with maximum possible value.

Step 4: Calculate the weighted normalized fuzzy matrix.

It is calculated when its weight wh is multiplied by a normalized fuzzy matrix \(\tilde{q}_{gh}\). It is denoted as \(\tilde{Z}\) in Eq. (18)

$$\tilde{Z} = \left[ {\tilde{z}_{gh } } \right]_{m*n} {\text{g }} = { 1},{2},{3},{4} \ldots \ldots {\text{m }}, {\text{h}} = {1},{2},{3},{4} \ldots \ldots \ldots .{\text{n}} {\text{where}}\;\tilde{z}_{gh } \;\tilde{q}_{gh } \left( . \right)W_{j} .$$
(18)

Step 5: Compute fuzzy PIS (FPIS) and fuzzy NIS (FNIS) using Eqs. (19) and (20)

$$A^{*} = (\tilde{z}_{1}^{*} , \tilde{z}_{2}^{*} \ldots \ldots \tilde{z}_{n}^{*} ){\text{where}}\;\tilde{z}_{h}^{*} \; = \;\tilde{c}_{h}^{*} , \tilde{c}_{h}^{*} ,\tilde{c}_{h}^{*} {\text{and}} \tilde{c}_{h}^{*} = \begin{array}{*{20}c} {max} \\ g \\ \end{array} \left\{ {\tilde{c}_{gh } } \right\},$$
(19)

where \(A^{*}\) is fuzzy positive ideal solution (FPIS), \(\tilde{z}_{n}^{*}\) denotes TFNs having FPIS, and \(c_{h}^{*}\) denotes the maximum possible value of benefit criteria

$$A^{ - } = (\tilde{z}_{1}^{ - } , \tilde{z}_{2}^{ - } \ldots \ldots \tilde{z}_{n}^{ - } ){\text{where}}\;\tilde{z}_{h}^{ - } = (a_{h}^{ - } , \tilde{a}_{h}^{ - } ,\tilde{a}_{h}^{ - } )\;{\text{and}} \; \tilde{a}_{h}^{ - } = \begin{array}{*{20}c} {min} \\ g \\ \end{array} \left\{ {\tilde{a}_{gh } } \right\},$$
(20)

where \(A^{ - }\) is fuzzy negative ideal solution (FNIS), \(\tilde{z}_{n}^{ - }\) denotes TFNs having FNIS, and \(\tilde{a}_{h}^{ - }\) denotes the minimum possible value of cost criteria.

Step 6: Compute the distance (\(d_{g}^{ + }\), \(d_{g}^{ - } )\) of each solution from \(A^{*}\) and \(A^{ - }\) with the help of Eqs. (21) and (22)

$$d_{g}^{ + } = \mathop \sum \limits_{h = 1}^{n} dv\;(\tilde{z}_{gh } , \tilde{z}_{h}^{*} ){\text{g }} = { 1},{2} \ldots \ldots ..{\text{m}}$$
(21)
$$d_{g}^{ - } = \mathop \sum \limits_{h = 1}^{n} dv\;(\tilde{z}_{gh } , \tilde{z}_{h}^{ - } )\;{\text{g }} = { 1},{2} \ldots \ldots ..{\text{m}}{.}$$
(22)

Step 7: The last step is to compute CofC using Eq. (23) and rank the solutions based on CofC

$$CofC_{g} = \frac{{d_{g}^{ - } }}{{d_{g}^{ - } + d_{g}^{ + } }}.$$
(23)

The ranking is done for all the solutions by looking at the values of \(CofC_{g}\). The highest value is ranked highest and the lowest value is ranked lowest.

Proposed method

The current study is based on a hybrid fuzzy AHP–TOPSIS approach. It consists of three phases. Phase 1 is about identifying and finalizing the barriers and solutions of IRL (explained in Sect. Literature review). Phase 2 is about the fuzzy AHP that is used to calculate the weights for each barrier/problem that is associated with IRL (results are mentioned in Sect. Fuzzy analytical hierarchical process experimental results). Phase 3 targets the fuzzy TOPSIS approach that is used to rank the solutions/alternatives for the identified problems (results are mentioned in Sect. Fuzzy TOPSIS experimental results). In the proposed method, some key assumptions have been taken into consideration regarding the experts’ evaluation:

  • TFNs are used for the formalization of the experts’ evaluation as pairwise comparison matrix and fuzzy evaluation matrix are involved in the proposed method phases.

  • For any subjective evaluation process, there are imprecision and vagueness associated inherently. Therefore, all experts’ evaluations are affected by uncertainty and ambiguity as all experts have a different level of cognitive vagueness (based on their experience and knowledge). This is the reason for the usage of the fuzzy approach with TFNs, so that uncertainty and ambiguity can be handled in a better way.

  • There are no external conditions that impact the uncertainty as experts’ are confident about their evaluation in the proposed method phases and there is no necessity for the usage of more complex fuzzy tools like type-2 fuzzy sets, neutrosophic, etc.

There are some other methods for multi-criteria decision-making (MCDM) like interpretive structural modeling (ISM), elimination and choice expressing reality (ELECTRE), and analytic network process (ANP), but these decision-making processes take a lot of computation time and experts' judgments are not precise as fuzzy AHP. However, for better decision-making, fuzzy AHP has been used and integrated with TOPSIS [79]. The fuzzy-based approach is more suitable for handling uncertainty, ambiguity, and imprecision of the experts' linguistic inputs. Therefore, the hybrid fuzzy AHP–TOPSIS approach has been preferred and implemented in the current study to rank the solutions identified for IRL problems.

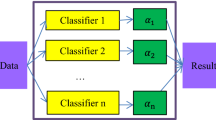
Figure 1 shows the architectural schematization of the proposed method. In the first phase, literature and the decision group play a key role in the finalization of the problems and solutions of IRL. The decision group consists of experts from the software industry, academics, and startups. At the end of the first phase, eight problems of IRL have been finalized with eight solutions have also been finalized that can overcome these IRL problems. Most importantly, decision hierarchy structuring is finalized in this phase, as shown in Fig. 2. In the second phase, the fuzzy AHP approach is implemented. The fundamental step in this approach is to create a pairwise matrix with experts’ opinions.

Fig. 1
figure 1

Architectural schematization of the proposed method

Full size image
Fig. 2
figure 2

Decision hierarchy for overcoming barriers to IRL implementation

Full size image

The linguistic terms are used to define the relative importance of identified criteria (IRL problems) with one another, and then, they are mapped with the fuzzy set, so that the same experts' opinions are produced. TFNs are one of the most popular ways of representing experts' opinions. In the proposed method, they are represented with three letters u, v, and w. These letters represent minimum possible value, median value, and maximum possible value, respectively. After this fundamental step, fuzzy synthetic criteria values, degree of possibility along with normalized weights are computed. These normalized weights act as an input to the third and final phase. The identified IRL problems can also be ranked according to the computed normalized weights. The weight with the highest value is the top most priority IRL problem and the weight with the lowest value is the least priority IRL problem among all the identified IRL problems. In the third phase, the fuzzy TOPSIS approach is implemented. The fundamental step in this approach is to create a fuzzy evaluation matrix with experts’ opinions, and then, aggregated fuzzy evaluation matrix is created followed by a normalized fuzzy evaluation matrix and a weighted normalized fuzzy evaluation matrix. Further computes FPIS and FNIS and computes the distance of each solution from FPIS and FNIS. In the end, calculate the closeness coefficient that is used to rank the solutions based on the identified weights of the IRL problems. The top priority is given to the solutions that are ranked 1 followed by 2 and so on. The pseudocode schematization of the proposed approach is mentioned below.

figure a

The decision hierarchy for overcoming barriers/problems of IRL implementation is mentioned in Fig. 2. It consists of three levels where level 1 states the overall goal (overcoming barriers/problems of IRL implementation). Level 2 (Barrier criteria) focuses on the identified barriers/problems of IRL implementation and Level 3 (Solution Alternatives) focuses on the identified solutions that can be used for achieving the overall goal of the successful implementation of IRL.

Experimental results

Fuzzy analytical hierarchical process experimental results

To implement fuzzy AHP for rating the IRL problems, first, the linguistic scale should be finalized which is shown in Table 3. After the finalization of the linguistic scale, the TFNs’ decision matrix for IRL problems is made using experts’ opinions. Table 4 shows the decision matrix that has been made using one expert opinion. Table 5 shows the aggregated decision matrix that has been made using 15 experts’ opinions. Out of these, six are software developers of industries, two are project managers who have used IRL in their projects, two are software engineers, three are academic professors, and two are directors of startups.

Table 4 TFN decision matrix for IRL problems
Full size table
Table 5 Aggregated TFN decision matrix for IRL problems
Full size table

After computing aggregated decision matrix, fuzzy synthetic extent values (CVs) for all IRL problems are calculated for all fuzzy synthetic criteria (Cs), as shown in Table 6. After performing this, compute the degree of possibility and a minimum degree of possibility for convex fuzzy numbers (see Table 7).

Table 6 Fuzzy synthetic extent values (CVs) for IRL problems
Full size table
Table 7 Degree of possibility (D) and minimum degree of possibility (MinD) for the IRL problems
Full size table

The last step is to compute the fuzzy weight and normalized weight using Eqs. (12) and (13). After figuring out the normalized weights, the IRL problems are prioritized. The highest weight is ranked highest and the lowest weight is ranked the lowest among IRL problems as can be seen in Table 8.

The results show that the most weighted IRL problem is ‘Lack of robust reward functions’ and the least weighted IRL problem is ‘inaccurate inferences’. To tackle different problems, different solutions have been identified and they are ranked using the approach fuzzy TOPSIS.

Performance analysis metrics

Many performance metrics are used to evaluate the fuzzy AHP model. These are mean, mean absolute error (MAE), root-mean-squared error (RMSE), mean-squared error (MSE), and relative error. The lower the value of MSE, RMSE, and MAE, the better the model fits and the higher the relative accuracy, the better the model fits. All the performance analysis metrics of FAHP are calculated using the normalized weights of Table 8. The performance metrics calculations for the current study are mentioned below using Eqs. (24) to (29)

  1. (a)

    Mean

$$\overline{x} = \frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {x_{i} } \right)}}{n},$$
(24)

where \(\overline{x}\) is the arithmetic mean, n is the number of weight vectors, and \(x_{i}\) is the result of ith measurement.

$$\overline{x} = 0.{125}.$$
  1. (b)

    Mean absolute error (MAE)

Table 8 Comparison of weights and ranking of IRL problems
Full size table

It is the average magnitude difference between the observations and its mean. It will be good for the model if the value of this metric is low

$${\text{MAE }} = \frac{{\mathop \sum \nolimits_{i = 1}^{n} \left| {X_{i} - \overline{X}_{i} } \right| }}{n},$$
(25)

where \(\overline{x}_{i}\) is the arithmetic mean, n is the number of weight vectors, and \(x_{i}\) is the magnitude of ith observation

$${\text{MAE }} = 0.0{27}.$$
  1. (iii)

    Mean-squared error (MSE)

It is the average squared difference between the estimated values and the actual value. For value to be model fit, it should be on the lower side

$${\text{MSE}} = \frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {X_{i} - \overline{X}_{i} } \right)^{2} }}{n},$$
(26)

where \(\overline{x}_{i}\) is the arithmetic mean, n is the number of weight vectors, and \(x_{i}\) is the magnitude of ith observation

$${\text{MSE }} = 0.00{12}.$$
  1. (iv)

    Root-mean-squared error (RMSE)

It is known as a good measure to predict the error of a model while working on quantitative data

$${\text{RMSE}} = \sqrt {\frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {\left| {X_{i} - \overline{X}_{i} } \right|} \right)^{2} }}{n}} ,$$
(27)

where \(\overline{x}_{i}\) is the arithmetic mean, n is the number of weight vectors, and \(x_{i}\) is the magnitude of ith observation

$${\text{RMSE }} = 0.0{349}.$$
  1. (e)

    Relative accuracy

It is used to find out the relative accuracy of the model. The value of relative accuracy should be higher, such that model is a good fit

$${\text{Relative Error }} = \frac{{\left| {\overline{X}_{i} - X_{i} } \right|{ }}}{{X_{i} { }}},$$
(28)

where \(\overline{x}_{i}\) is the arithmetic mean, n is the number of weight vectors, and \(x_{i}\) is the magnitude of ith observation

$${\text{Relative Accuracy }} = { 1}00 \, {-}{\text{ Relative Error}}$$
(29)
$${\text{Relative Error }} = { 2}.{25}0{682}$$
$${\text{Relative Accuracy }} = { 97}.{74932}.$$

Fuzzy TOPSIS experimental results

The experts’ inputs help in building the fuzzy evaluation matrix using linguistic variables as mentioned in Table 3. These variables are then transformed into TFNs as mentioned in Table 3. The current study has rated eight solutions corresponding to eight problems with the help of 15 experts. Table 9 shows the fuzzy evaluation matrix created by expert 1 only, whereas Table 10 shows the aggregated fuzzy evaluation matrix of all 15 experts. The aggregation rule is already mentioned in Eq. (14).

Table 9 Fuzzy TOPSIS evaluation matrix for solutions (EXPERT 1)
Full size table
Table 10 Aggregated fuzzy TOPSIS evaluation matrix for solutions
Full size table

The current study targets to reduce the problems and these problems are reflected as cost criteria. A normalized fuzzy matrix (see Table 11) is built using Eqs. (15) to (17) and a weighted normalized matrix (see Table 12) is built using Eq. (18).

Table 11 Normalized fuzzy evaluation matrix for solutions
Full size table
Table 12 Weighted fuzzy evaluation matrix for solutions
Full size table

All the problems are considered as cost criteria in the current study. Therefore, FPIS (\(A^{*}\)) and FNIS (\(A^{ - }\)) are mentioned as \(z^{*}\) = (0, 0, 0) and \(z^{ - }\) = (1, 1, 1), respectively, for each problem. The distance (\(d_{g}^{ + }\), \(d_{g}^{ - } )\) of each solution from FPIS and FPIN is computed with the help of Eqs. (21) and (22). For example, the distance d (A1, \(A^{*}\)) of S-IRL1 and d (A1, \(A^{ - }\)) of P-IRL1 from FPIS and FNIS is calculated as follows:

$${\text{d}}({\text{A}}_{{1}} ,A^{*} ) = \sqrt {\frac{1}{3}[\left( {0 - 0.03} \right)^{2} + \left( {0 - 0.03} \right)^{2 } + \left( {0 - 0.18} \right)^{2 } ]} = 0.{1}0{6771}$$
$${\text{d}}({\text{A}}_{{1}} ,A^{ - } ) = \sqrt {\frac{1}{3}[\left( {1 - 0.155} \right)^{2} + \left( {1 - 0.456} \right)^{2 } + \left( {1 - 0.456} \right)^{2 } ]} = 0.{9229}0{7}.$$

Using these CofC for all solutions is calculated using Eq. 23.

Table 13 shows d (A1, \(A^{*}\)), d (A1, \(A^{ - }\)) and CofCg for all solutions, and they are ranked based on CofC in descending order.

Table 13 Ranking of the solutions based on closeness coefficient (CofCg)
Full size table

Results and discussion

Hybrid fuzzy systems are used in the past for understanding customer behavior [80], heart disease diagnosis [81], and diabetes prediction [81]. Fuzzy logic classifier along with reinforcement learning is used for the development of an intelligent power transformer [82], for handling continuous inputs and learning from continuous actions [83], for small lung nodules detection [84], for finding appropriate pedagogical content [85], for robotic soccer games [44, 45], for water blasting system for ship hull corrosion cleaning [86], and for classification of diabetes [73]. All the above mentioned have used fuzzy systems to figure out the issues and solutions in different concepts, but none of them has prioritized the problems or solutions identified in the different concepts. The same case is also applied to the IRL. Therefore, the first-ever hybrid fuzzy AHP–TOPSIS approach has been used in the current study which turns out to be the elementary and rudimental approach for digging out the important problems and solutions for successful implementation of IRL technique in real life by ranking all the solutions. There are 8 problems and 8 solutions that are identified through literature. Fuzzy AHP has been used to get the weights of the problems and these calculated weights by fuzzy TOPSIS to rank the solutions. The computed weights during the fuzzy AHP approach are compared to rank the IRL problems. These are ranked as P-IRL1 > P-IRL7 > P-IRL6 > P-IRL4 > P-IRL3 > P-IRL2 > P-IRL8 > P-IRL5, as shown in Table 8. The major concern that is identified during the accurate implementation of IRL is ‘lack of robust reward functions’. The next ranked problem is ‘Lack of scalability with large problem size’. It tells the IRL users to need to put more emphasis on scalability with large problem sizes instead of only concentrating on just solving problems. ‘Sensitivity to Correctness of Prior Knowledge’ is the next ranked category that tells experts should be aware of the feature functions and transition functions of the Markov decision process, such that human judgment is not too subjective for taking decisions. ‘Ill-posed problems’ is ranked fourth in IRL implementation and it states that uncertainty is involved in obtaining the reward functions, or in other words, it can be said that loss functions are not introduced extensively in classical IRL algorithms. The problem category based on ‘Stochastic policy’ is ranked fifth. If experts’ behavior is deterministic in nature, then mixed or dynamic policy can be inaccurate due to its stochastic nature. The next ranked problem is ‘Imperfect and Noisy inputs’. If in real-life implementation of IRL, the inputs are incorrect and noisy, then it leads to failure of IRL in real life. The next ranked category is ‘Lack of reliability. This means inappropriate learning of classical IRL algorithm from reward functions for failed and successful demonstrations. The last ranked category is ‘Inaccurate inferences’. It states that generalization of learned information of states and actions to other initial states is difficult, or in other words, greater approximation errors in reward functions. For the effective implementation of IRL, the fuzzy TOPSIS approach has been used to rank the solutions based on the closeness coefficient, as shown in Table 13. The ranking of the solutions is S-IRL2 > S-IRL8 > S-IRL3 > S-IRL7 > S-IRL4 > S-IRL1 > S-IRL6 > S-IRL5. The results show that the least important solution is ‘Inculcate risk- awareness factors in IRL algorithms’ and the most important solution is ‘Supports optimal policy and rewards functions along with stochastic transition models’. The current study reveals that usage of optimal policy and learning of rewards functions is necessary for the IRL implementation success.

Conclusion and future scope

In the present scenario, the demand for autonomous agents is at a great height as they can do mundane and complex tasks without the help of other sources. IRL is used in autonomous agents’ example cars without drivers. IRL is mostly used in the automotive industry, textile industry, automatic transport system, supply and chain management, etc. IRL is also suffering from many problems. Majorly eight problems have been identified from the literature and different solutions have been proposed for mitigating these IRL problems. It is very difficult to implement all the solutions together, so these solutions are prioritized while doing decision-making. The current study has used a hybrid fuzzy AHP–TOPSIS approach for ranking the solutions. The fuzzy AHP method is used to obtain the weights of the IRL problems, whereas the fuzzy TOPSIS method ranks the solutions for the implementation of IRL in a real-life scenario. The important thing to note is, computed weights are used in figuring out the rank of solutions. Fifteen expert opinions are used to compute weights and rank the solutions. Results show that the most significant issue in IRL is of ‘lack of robust reward functions’ with a weight of 0.180. The least significant problem in IRL real-life implementation is ‘Inaccurate inferences’ with a weight of 0.063. It mainly focuses that human judgments fail to do a generalization of outputs. The most significant solution is ‘Supports optimal policy and rewards functions along with stochastic transition models’ and the least significant solution is ‘Inculcate risk- awareness factors in IRL algorithms’. This ranking is based on the CofC having the value of 0.967156846 and 0.94958721, respectively. These solutions help the industries in their decision-making, so that projects will become successful. The findings of the current study provide the following insights for the future research:

  • The fuzzy TOPSIS results can be influenced by the distance measures, approaches like weighted correlation coefficients [87] and picture fuzzy information measure, [88] should be used to improve the reliability of results.

  • In the future, other multi-criteria and multi-facet decision-making criteria can be used like fuzzy VIKOR, fuzzy PROMETHEE, or fuzzy ELECTRE, and the results can be compared with the current study results.

  • The experts' experience and knowledge play important role in the results of the current study and there are chances of biases in the results. This can be minimized or eliminated in the future by adding more experts to the study.

  • In the future, case studies can be done in industries that are using IRL implementation in their processes.

  • As there is up-gradation of technology in the future, some other barriers, as well as solutions, may be identified [89] and they can be taken into the future study.

  • IRL methods should be studied in the future in the context of multi-view learning and transfer learning approaches [56].